Algebraic Properties of the Category of Involutive m-Semilattices and Its Limits

Abstract

An involutive m-semilattice is a kind of algebraic structure with symmetry. Symmetry is reflected from partial-order relations to algebraic operations and even categorical properties. In this study, firstly, the concepts of the nucleus and congruence in involutive m-semilattices are introduced, and their interrelationships are discussed. On this basis, the concrete structure of a coequalizer in the category of involutive m-semilattices is obtained. We introduce the definition of free involutive m-semilattices, and the concrete structure of involutive m-semilattices is discussed. In addition, It is shown that the category of involutive m-semilattices is algebraic. Secondly, the colimit in the category of involutive m-semilattices is shown to be a very difficult problem. We obtain the concrete structure of the colimit for a full subcategory of the category of involutive m-semilattices. Thirdly, we introduce the definition of an inverse system in the category of involutive m-semilattices and give the concrete structure of the inverse limit of an inverse system. We establish the concept of a mapping between two inverse systems. The properties of inverse limits are discussed. Finally, we study the direct limit of the category of involutive m-semilattices and give its concrete structure.

1. Introduction

The quantale was proposed by Mulvey in 1986 in [1] as a combination of quantum logic and locale. The algebraic structure of a quantale inherently exhibits symmetry. For instance, the distributive property of multiplication over a supremum operation embodies a form of symmetric relation. Additionally, symmetry is reflected in the characteristics of multiplication operations under arbitrary permutations of elements. Quantale theory provides a powerful tool for studying non-commutative structures and a new mathematical model for quantum mechanics. Hence, the theory of quantales has attracted the attention of many scholars. Quantale theory has a wide range of applications, especially when studying non-commutative structures [2], linear logic [3,4,5], C*-algebras [6], topological space [7,8,9], category [10,11,12], roughness theory [13], and so on. A systematic introduction to quantale theory written by Rosenthal in 1990 can be found in [14].

m-semilattices are important structures that are related to quantales. Rosenthal proved that each coherent quantale is isomorphic to a quantale consisting of all ∨-semilattice ideals of an m-semilattice with a top element. A coherent quantale is a special type of quantale characterized by properties such as symmetry, right-sidedness, and semiprimeness. These characteristics confer upon it a significant role in the study of mathematical logic and algebraic structures. Since m-semilattices connect the structures of ∨-semilattices with multiplications of semigroups, m-semilattices can be regarded as generalizations of residual lattices, lattice-ordered semigroups, quantales, and frames. m-semilattice theory has aroused great interest from many scholars. In [15], by using the fuzzy set method, the concept of (prime) ideals of an m-semilattice was introduced. Equivalent characterizations of (prime) ideals and (prime) ideas were given. In [16], Zhou and Zhao proposed the congruences induced by the fuzzy (prime) ideals of an m-semilattice, studied the properties of the upper (lower) rough fuzzy approximation operators with respect to these congruences, and introduced the notion of rough fuzzy (prime) ideals of m-semilattices. In [17], a minimal neighborhood approximation operator on m-semilattices was studied, and the definition of fuzzy rough sets based on fuzzy coverings of m-semilattices was introduced. In [18], Su and Zhao introduced the concept of filters in m-semilattices, and a filter topology on m-semilattices was constructed. A series of properties of filter spaces was studied. In [19], Pan and Han proved that the category of coherent quantales is a reflective subcategory of the category of m-semilattices. Based on the definition of m-semilattices, the concept of involutive m-semilattices was given. A series of important properties of involutive m-semilattices were studied, and it was proven that the category of involutive m-semilattices is complete ([20]). In [21], the definition of the generalized M-P inverse of an m-semilattice matrix was introduced. The necessary and sufficient condition for the existence of a generalized M-P inverse of an m-semilattice matrix was obtained. Some scholars have also provided different definitions of m-semilattices against various research backgrounds [22,23,24,25].

The category theory provides a new language that affords economy of thought and expression, in addition to allowing easier communication among investigators in different areas. The symmetry within a semilattice is manifested through its operational rules and partial-order relations, representing a form of mathematical abstract symmetry. Symmetry is a highly abstract mathematical concept in category theory, and it is manifested through the properties of morphisms and the structure of categories. For example, natural equivalences, symmetric categories, the commutativity of morphisms, and duality are all manifestations of symmetry. This symmetry not only reveals the deep connections between different areas of mathematics but also plays a significant role in fields such as physics. Understanding symmetry in category theory helps us gain a deeper insight into the nature of mathematical and physical phenomena.

In the literature on the study of m-semilattices, the focus has primarily been on ideals, filters, topological properties, roughness, fuzzy roughness, and matrices, with little discussion on categorical properties. We have added a unary involution operation to the m-semilattice, similar to the negation operator in algebraic logic, making the involution m-semilattice an extension of the m-semilattice. This article investigates the properties of involutive m-semilattices from a categorical perspective. The algebraic properties and limit structures of a category are important research focuses. If the algebraic properties of a category are proven and its limit structures are provided, then many categorical properties naturally hold. This study researches the algebraic properties of the category of involutive m-semilattices, as well as the structures of its colimits, direct limits, and inverse limits. In the following, some simple concepts of category theory are taken from [26].

This article is organized as follows. In Section 1, we show some basic concepts and the results needed in this article. In Section 2, the concepts of the nucleus and congruence are introduced. The category of involutive m-semilattices is proven to be algebraic. In Section 3, we discuss the structure of the coproduct and colimit in the category of involutive m-semilattices. In Section 4, we study the inverse limit and direct limit in the category of involutive m-semilattices. The properties of inverse limits are discussed.

For the convenience of readers, the important symbols used in this article can be found in the table below (Table 1).

Table 1. Symbol description.

Symbols	Explanation
$Ob\left(\mathcal{C}\right)$	All objects in category $\mathcal{C}.$
$Mor\left(\mathcal{C}\right)$	All morphisms in category $\mathcal{C}.$
$Ho{m}_{\mathcal{C}}(A,B)$	Morphism set form object A to B.
${\displaystyle \prod _{i\in I}}{A}_i$	The product of ${\left\{A_i\right\}}_{i\in I}$.
${\displaystyle \coprod _{i\in I}}{A}_i$	The product of ${\left\{A_i\right\}}_{i\in I}$.
$N\left(S\right)$	The set of all nuclei on S.
$Con\left(S\right)$	The set of all congruences on S.
$S_j$	The set of all fixed points of j.
$S/R$	Equivalence class of S with respect to R.
$IMSLatt$	The category of involutive m-semilattices.
$P_F\left(\tilde{X}\right)$	All finite subsets of the set $\tilde{X}$.
$i_{P_F\left(\tilde{X}\right)}$	The dentity morphism on $P_F\left(\tilde{X}\right)$.

2. Preliminaries

Definition 1. 

Let $(S,\vee )$ be a ∨-semilattice, let $(S,·)$ be a semigroup, and let ∗ be a unary operation on S satisfying the following:

(1) 

$a·(b\vee c)=(a·b)\vee (a·c),(b\vee c)·a=(b·a)\vee (c·a)$ for all $a,b\in S$.

(2) 

$a**=a$ for all $a\in S$.

(3) 

$(a·b)*=b*·a*$ for all $a,b\in S$.

(4) 

$(a\vee b)*=a*\vee b*$ for all $a,b\in S$.

Then, $(S,\vee ,·,\ast )$ is called an involutive m-semilattice.

The definition of the involutive m-semilattice given in this paper is an extension of the definition of the involutive m-semilattice introduced in reference [20].

Definition 2. 

Let $S_1$ and $S_2$ be two involutive m-semilattices. A mapping $f:S_1\to S_2$ is said to be an involutive m-semilattice homomorphism if it satisfies the following:

(1) 

$f(a·b)=f\left(a\right)·f\left(b\right)$;

(2) 

$f(a\vee b)=f\left(a\right)\vee f\left(b\right)$;

(3) 

$f\left(a^{*}\right)=\left(f\left(a\right)\right)*$.

Example 1. 

(1) Let $(B,\wedge ,\vee ,\neg )$ be a Boolean algebra. We define a semigroup multiplication · on B and an involution operation ∗ on B as follows:

$$\forall a,b\in B,a·b=a\wedge b,a^{*}=a.$$

It can be verified that $(B,\vee ,·,\ast )$ is an involutive m-semilattice, and it is commutative. Let $(\acute{B},\vee ,\wedge ,\neg ,0,1)$ B be a two-element Boolean algebra. We define a mapping $f:B\to \acute{B}$ as follows: $f\left(x\right)=\left\{\begin{array}{c}0,x=0,\hfill \\ 1,x\ne 0,\hfill \end{array}\right.$, then the mapping f is both a Boolean algebra homomorphism and an involution m-semilattice homomorphism.

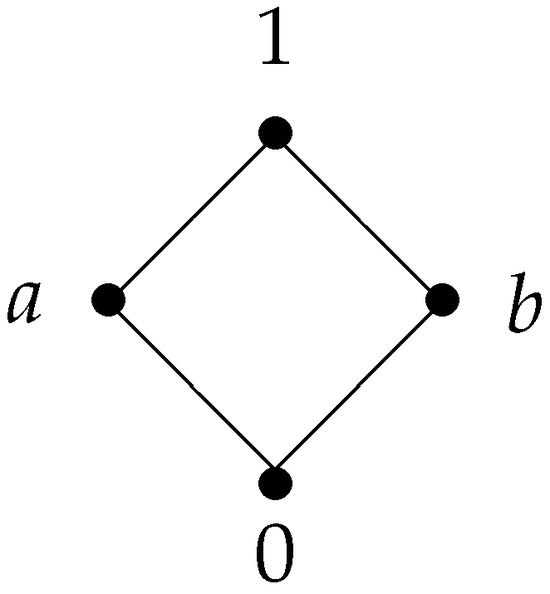
(2) Let $S=\{0,a,b,1\}$ be a lattice determined by Figure 1. A semigroup multiplication on S and an involution operation on S are determined by the tables below (Table 2 and Table 3).

Figure 1. The partial order on S.

Table 2. The semigroup multiplication on S.

·	0	a	b	c
0	0	0	0	0
a	0	a	1	1
b	0	1	b	1
1	0	1	1	1

Table 3. The involution operation on S.

∗	0	a	b	1
	0	b	a	1

It can be verified that $(S,·,\ast )$ is an involutive m-semilattice, and it is symmetric and commutative. By the definitions of m-semilattice ideals and filters, the sets $\downarrow 0$, $\downarrow a$, $\downarrow b$, and $\downarrow 1$ are ideals of S, while $\uparrow 0$, $\uparrow a$, $\uparrow b$, and $\uparrow 1$ are filters of S.

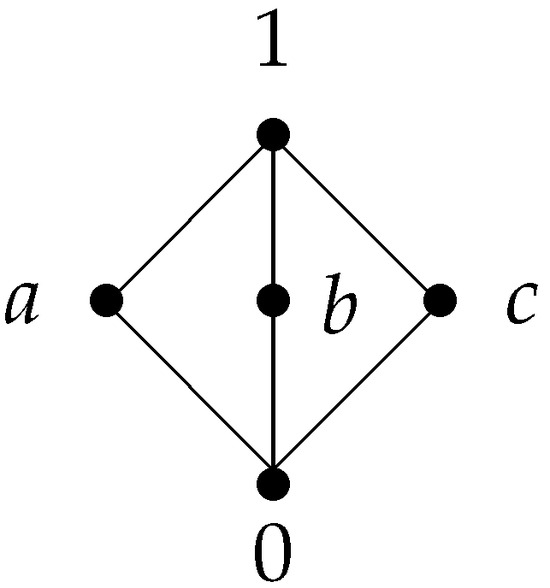
(3) Let $S=\{0,a,b,c,1\}$ be a lattice determined by Figure 2. A semigroup multiplication on S and an involution operation on S are determined by the tables below (Table 4 and Table 5).

Figure 2. The partial order on S.

Table 4. The semigroup multiplication on S.

·	0	a	b	c	1
0	0	0	0	0	0
a	0	b	c	a	1
b	0	c	a	b	1
c	0	a	b	c	1
1	0	1	1	1	1

Table 5. The involution operation on S.

∗	0	a	b	c	1
	0	b	a	c	1

It can be verified that $(S,·,\ast )$ is an involutive m-semilattice, and it is symmetric and commutative. By the definitions of m-semilattice ideals and filters, the sets $\downarrow 0$, $\downarrow a$, $\downarrow b$, $\downarrow c$, and $\downarrow 1$ are ideals of S, while $\uparrow 0$, $\uparrow a$, $\uparrow b$, $\uparrow c$ and $\uparrow 1$ are filters of S.

Definition 3 ([26]). 

A category is a quintuple $\mathcal{C}=(\mathcal{O},\mathcal{M},dom,cod,\circ )$, where

(1) $\mathcal{O}$ is a class whose members are called $\mathcal{C}$-objects;

(2) $\mathcal{M}$ is a class whose members are called $\mathcal{C}$-morphisms;

(3) $dom$ and $cod$ are functions from $\mathcal{M}$ to $\mathcal{O}$; ($dom\left(f\right)$) is called the domain of f, and $cod\left(f\right)$ is called the codomain of f;

(4) ∘ is a function from $D=\left\{\right(f,g\left)\right|f,g\in \mathcal{M},dom\left(f\right)=cod\left(g\right)\}$ to $\mathcal{M}$, and this is called the composition law of $\mathcal{C}(\circ (f,g\left)\right)$, which is usually written as $f\circ g$. We say that $f\circ g$ is defined if, and only if, c$(f,g)\in D$ such that the following conditions are satisfied:

(i) Matching Condition: If $f\circ g$ is defined, then $dom(f\circ g)=dom\left(g\right)$ and $cod(f\circ g)=cod\left(f\right)$;

(ii) Associativity Condition: If $f\circ g$ and $h\circ f$ are defined, then $h\circ (f\circ g)=(h\circ f)\circ g$;

(iii) Identity Existence Condition: For each $\mathcal{C}$-object A, there exists a $\mathcal{C}$-morphism e such that $dom\left(e\right)=A=cod\left(e\right)$ and

(a) 

$f\circ e=f$ whenever $f\circ e$ is defined;

(b) 

$e\circ g=g$ whenever $e\circ g$ is defined.

(iv) Smallness of Morphism Class Condition: For any pair $(A,B)$ of $\mathcal{C}$-objects, the class

$$ho{m}_{\mathcal{C}}(A,B)=\left\{f\right|f\in \mathcal{M},dom\left(f\right)=Aandcod\left(f\right)=B\}$$

is a set.

For a given category $\mathcal{C}$, the class of $\mathcal{C}$-objects will be denoted by $Ob\left(\mathcal{C}\right)$, whereas $Mor\left(\mathcal{C}\right)$ will stand for the class of $\mathcal{C}$-morphisms.

Example 2 ([26]). 

In the category Set, the class of objects is the class of all sets, the morphisms sets $hom(A,B)$ are all functions from A to B, and the composition law is the usual composition of functions. Set is commonly called the category of sets.

Definition 4 ([26]). 

A category $\mathcal{C}$ is said to be the following:

(1) small provided that $\mathcal{C}$ is a set;

(2) discrete provided that all of its morphisms are identities;

(3) connected provided that for each pair $(A,B)$ of $\mathcal{C}$-objects, $ho{m}_{\mathcal{C}}(A,B)\ne \varnothing$.

Definition 5 ([26]). 

Let $\mathcal{C}$ and $\mathcal{D}$ be categories, A functor from $\mathcal{C}$ to $\mathcal{D}$ is a triple $(\mathcal{D},F,\mathcal{D})$, which is a function from the class of morphisms with respect to the class of morphisms of $\mathcal{D}$ (i.e., $F:Mor\left(\mathcal{C}\right)\to Mor\left(\mathcal{D}\right))$ satisfying the following conditions:

(1) F preserves identities, i.e., if e is a $\mathcal{D}$-identity, then $F\left(e\right)$ is a $\mathcal{D}$-identity.

(2) F preserves composition; $F(f\circ g)=F\left(f\right)\circ F\left(g\right)$, i.e., whenever $dom\left(f\right)=cod\left(g\right)$, then $dom\left(F\right(f\left)\right)=cod\left(F\right(g\left)\right)$, and the above equality holds.

For any concrete category $\mathcal{C}$, there is a functor $U:\mathcal{C}\to Set$ that assigns to any object A the underlying set $U\left(A\right)$ and to any morphism the corresponding function on the underlying sets. U is called a forgetful functor on $\mathcal{C}$.

Definition 6 ([26]). 

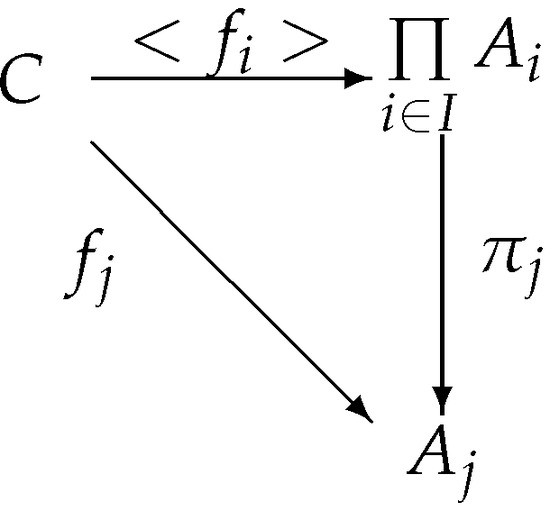
A product of a family ${\left(A_i\right)}_{i\in I}$ of $\mathcal{C}$-objects is a pair $({\displaystyle \prod _{i\in I}}{A}_i,{\left(\pi \right)}_{i\in I})$ satisfying the following properties:

(1) ${\displaystyle \prod _{i\in I}}{A}_i$ is a $\mathcal{C}$-object.

(2) For each $j\in J$, ${\pi }_j:{\displaystyle \prod _{i\in I}}{A}_i\to A_j$ is a $\mathcal{C}$-morphism (called the projection from ${\displaystyle \prod _{i\in I}}{A}_i$ to $A_j$).

(3) For each pair $(C,{\left(f_i\right)}_{i\in I})$, where C is a $\mathcal{C}$-object and for each $j\in J$, $f_j:C\to {\displaystyle \prod _{i\in I}}{A}_i$, there exists a unique $\mathcal{C}$-morphism $<f_i>:C\to {\displaystyle \prod _{i\in I}}{A}_i$ such that, for each $j\in J$, Figure 3 commutes.

Figure 3. Product diagram.

Definition 7 ([26]). 

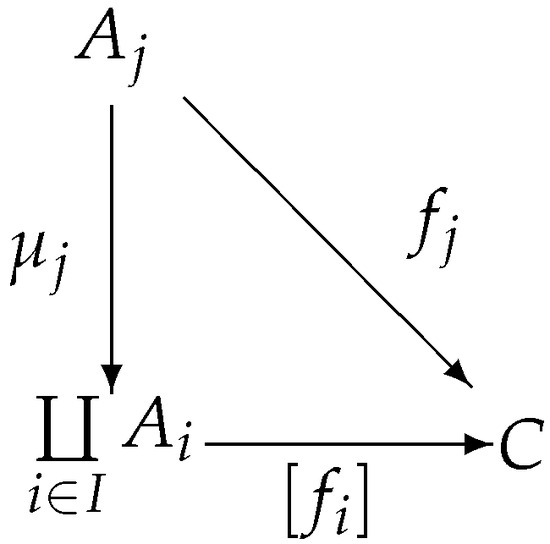
A coproduct of a family ${\left(A_i\right)}_{i\in I}$ of $\mathcal{C}$-objects is a pair $({\left({\mu }_i\right)}_{i\in I},{\displaystyle \coprod _{i\in I}}{A}_i)$ satisfying the following properties:

(1) ${\displaystyle \coprod _{i\in I}}{A}_i$ is a $\mathcal{C}$-object.

(2) For each $j\in J$, ${\mu }_j:A_j\to {\displaystyle \coprod _{i\in I}}{A}_i$ is a $\mathcal{C}$-morphism (which is called the injection from $A_j$ to ${\displaystyle \coprod _{i\in I}}{A}_i$).

(3) For each pair $({\left(f_i\right)}_{i\in I},C)$, where C is a $\mathcal{C}$-object and for each $j\in J$, $f_j:A_j\to C$, there exists a unique $\mathcal{C}$-morphism $\left[f_i\right]:{\displaystyle \coprod _{i\in I}}{A}_i\to C$ such that for each $j\in J$, Figure 4 commutes.

Figure 4. Coproduct diagram.

Definition 8 ([26]). 

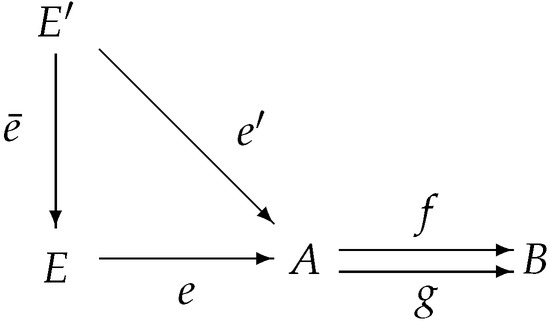
Let $A\stackrel{f}{\underset{g}{\rightrightarrows }}B$ be a pair of $\mathcal{C}$-morphisms. A pair $(E,e)$ is called an equalizer in $\mathcal{C}$ of f and g provided that the following hold:

(1) $e:E\rightrightarrows A$ is a $\mathcal{C}$-morphism;

(2) $f\circ e=g\circ e$;

(3) For any $\mathcal{C}$-morphism $e^{\prime }:E^{\prime }\to A$ such that $f\circ e^{\prime }=g\circ e^{\prime }$, there exists a unique $\mathcal{C}$-morphism $\overline{e}:E^{\prime }\to E$ such that Figure 5 commutes.

Figure 5. Equalizer diagram.

Dually, if $c:B\to \mathcal{C}$, then $(c,\mathcal{C})$ is called a coequalizer in $\mathcal{C}$ for a pair $A\stackrel{f}{\underset{g}{\rightrightarrows }}B$ if, and only if, $c\circ f=c\circ g$ and each morphism $c^{\prime }$ with the property that $c^{\prime }\circ f=c^{\prime }\circ g$ can be uniquely factored through c.

Definition 9 ([26]). 

A category $\mathcal{C}$ is called algebraic provided that it satisfies the following conditions:

(1) The category $\mathcal{C}$ has coequalizers;

(2) The forgetful functor $U:\mathcal{C}\to Set$ has a left adjoint;

(3) The forgetful functor $U:\mathcal{C}\to Set$ preserves and reflects regular epimorphisms.

3. The Category of Involutive m-Semilattices Is Algebraic

In algebraic structure research, nucleus and congruences stand out as two key areas of focus. Both concepts are instrumental in constructing quotient structures, which, in turn, facilitates a deeper exploration of their important properties. Furthermore, nucleus and congruences often exhibit a mutually determining relationship. Showing a category is algebraic involves proving the existence of coequalizers, with congruences being the basis for their construction. Next, we will introduce nucleus mappings and congruences in involutive m-semilattices. “A category is algebraic” means that it possesses good properties similar to those of classical algebraic structures (such as groups, rings, modules, etc.) and their homomorphisms. It provides an abstract and unified perspective for understanding and connecting various algebraic theories. In [27]. Liu and Zhao proved that the category of quantales is algebraic. Next, we will discuss the algebraicity of the involutive m-semilattice category.

Definition 10. 

Let S be an involutive m-semilattice. A closure (coclosure) operator is an order-preserving increasing (decreasing), idempotent map $j:S\to S$. If j is a closure (coclosure) operator on S, then $a\le j\left(b\right)\left(j\right(a)\le b)$ if, and only if, $j\left(a\right)\le j\left(b\right)$ for all $a,b\in S$.

Definition 11. 

Let S be an involutive m-semilattice. An involutive m-semilattice nucleus on S is a closure operator j such that $j\left(a\right)·j\left(b\right)\le j(a·b)$ and $j\left(a^{*}\right)={\left(j\left(a\right)\right)}^{*}$ for all $a,b\in S$. Let $N\left(S\right)$ denote the set of all involutive m-semilattice nuclei on S.

Lemma 1. 

Let j be an involutive m-semilattice nucleus on S; then, $j(a·b)=j(a·j(b\left)\right)=j\left(j\right(a)·b)=j\left(j\right(a\left)j\right(b\left)\right)$ for all $a,b\in S$.

Definition 12. 

Let S be an involutive m-semilattice with a maximum element 1, $\forall j\in N\left(S\right)$.

(1) j is right-sided (left-sided) if, and only if, $j(a·1)\le j\left(a\right)$ for all $a\in S$.

(2) j is commutative if, and only if, $j(a·b)=j(b·a)$ for all $a,b\in S$.

(3) j is idempotent if, and only if, $j\left(a^2\right)=j\left(a\right)$ for all $a\in S$.

(4) Let $S_j$ be the set of all fixed points of j; then, $S_j=\{a\in S|j\left(a\right)=a\}$ is called a quotient of S.

$\forall a,b\in S_j$, $a{·}_{j}b=j(a·b),a{\vee }_{j}b=j(a\vee b),a^{{*}_j}=j\left(a^{*}\right)$. It can be verified that the three operations mentioned above are well defined.

Theorem 1. 

Let S be an involutive m-semilatticewith a maximum element 1, $\forall j\in N\left(S\right)$; then,

(1) j is right-sided (left-sided) if, and only if, $S_j$ is right-sided (left-sided).

(2) j is commutative if, and only if, $S_j$ is commutative.

(3) j is idempotent if, and only if, $S_j$ is idempotent.

Proof. 

(1) Assume j is right-sided, then, $\forall a\in S_j$, $a·1\le j(a·1)=j\left(a\right)=a$, i.e., $a·1\le a$. Hence, $S_j$ is right-sided.

Conversely, when $S_j$ is right-sided, it follows that $j\left(a\right)\in S_j$ for all $a\in S$. Then, $j\left(a\right)·1\le j\left(a\right)$. Since j is increasing, therefore $j(a·1)=j\left(j\right(a)·1)\le j\left(j\right(a\left)\right)=j\left(a\right)$, i.e., $j(a·1)\le j\left(a\right)$. Hence, j is right-sided.

Similarly, the case on the left can be proven.

(2) Assume j is commutative, then, $\forall a,b\in S_j$, $a{·}_{j}b=j(a·b)=j(b·a)=b{·}_{j}a$. Thus, $a{·}_{j}b=b{·}_{j}a$. Therefore, $S_j$ is commutative.

Conversely, when $S_j$ is commutative. By Lemma 1, it follows that $\forall a,b\in S$, $j(a·b)=j(j\left(a\right)·j\left(b\right)))=j\left(a{·}_{j}b\right)=j\left(b{·}_{j}a\right)=j(j\left(b\right)·j\left(a\right)))=j(b·a)$. Thus, $j(a·b)=j(b·a)$. Therefore, j is commutative.

(3) Let j be idempotent. then, $\forall a\in S_j$, $a{·}_{j}a=j(a·a)=j\left(a\right)=a$. Thus, $S_j$ is idempotent.

Conversely, Assume $S_j$ is commutative. By Lemma 1, it follows that $\forall a\in S$, $j(a·a)=j\left(j\right(a)·j(a\left)\right)=j\left(j\right(a\left)\right)=j\left(a\right)$. This shows that j is idempotent. □

Definition 13. 

Let S be an involutive m-semilattice; the relation $R\subseteq S\times S$ satisfies the following:

(1) $(a,b),(c,d)\in R$ implies $(a\vee c,b\vee d)\in R$ for all $a,b,c,d\in S$;

(2) $(a,b),(c,d)\in R$ implies $(a·c,b·d)\in R$ for all $a,b,c,d\in S$;

(3) If $(a,b)\in R$, then $(a^{*},b^{*})\in R$.

Then, R is called an involutive m-semilattice congruence on S.

For any $x\in S$, let ${\left[x\right]}_R$ denote the congruence class of x, and let $Con\left(S\right)$ denote the set of all congruences on S. Then, $Con\left(S\right)$ is a complete lattice with respect to the inclusion order.

Theorem 2. 

Let S be an involutive m-semilattice, and let j be a nucleus on S. Then, $(S_j,{\vee }_j,{·}_j,{\ast }_j)$ is an involutive m-semilattice, and $j:S\to S_j$ is an involutive m-semilattice homomorphism, where $\forall a,b\in S_j$, $a{·}_{j}b=j(a·b),a{\vee }_{j}b=j(a\vee b),a^{{*}_j}=j\left(a^{*}\right)$.

Proof. 

It can be verified that $(S_j,{\vee }_j)$ is a joint semilattice with a maximum element.

We will show that $(S_j,{\vee }_j,{·}_j,{\ast }_j)$ is an involutive m-semilattice. For any $a,b\in S$, by the definition of ${·}_j$ and Lemma 1, we have $\left(a{·}_{j}b\right){·}_{j}c=j(a·b){·}_{j}c=j(j(a·b)·c)=j((a·b)·j\left(c\right))=j(a·(b·j\left(c\right)))=j(a·(j\left(b\right)·j\left(c\right)))=j(a·\left(b{·}_{j}c\right))=a{·}_j\left(b{·}_{j}c\right)$. Thus, the associativity of ${·}_j$ is valid.

Next, we will show that the distributive law is valid. For any $a,b,c\in S_j$,

(1) $a{·}_j\left(b{\vee }_{j}c\right)\ge \left(a{·}_{j}b\right){\vee }_j\left(a{·}_{j}c\right)$.

(2) By Lemma 1, we have $a{·}_j\left(b{\vee }_{j}c\right)=j(a·j(b\vee c))=j(a·(b\vee c))=j((a·b)\vee (c·d))\le j(j(a·b)\vee j(a·c))=j(\left(a{·}_{j}b\right)\vee \left(a{·}_{j}c\right))=\left(a{·}_{j}b\right){\vee }_j\left(a{·}_{j}c\right)$.

Hence, $a{·}_j\left(b{\vee }_{j}c\right)=\left(a{·}_{j}b\right){\vee }_j\left(a{·}_{j}c\right)$. Similarly, it can be proven that the right-distributive law $\left(b{\vee }_{j}c\right)·a_j=\left(b{·}_{j}a\right){\vee }_j\left(c{·}_{j}a\right)$ holds.

Finally, we will prove that ${*}_j$ is an involutive operation on $S_j$.

For any $a,b\in S_j$,

(1) ${\left(a^{{*}_j}\right)}^{{*}_j}={\left(j(a*)\right)}^{{*}_j}={\left({\left(j\left(a\right)\right)}^{*}\right)}^{{*}_j}=j{\left({\left(j\left(a\right)\right)}^{*}\right)}^{*})=j\left({\left(j\left(a\right)\right)}^{*}\right)={\left(j\left(j\left(a\right)\right)\right)}^{*}={\left(j\left(a\right)\right)}^{*}=j\left(a^{*}\right)=a^{{*}_j}$.

(2) ${\left(a{·}_{j}b\right)}^{{*}_j}={\left(j(a·b)\right)}^{{*}_j}=j\left({\left(j(a·b)\right)}^{*}\right)=j\left(j\left({(a·b)}^{*}\right)\right)=j\left(j(b^{*}·a^{*})\right)=j(b^{*}·a^{*})$. By Lemma 1, it follows that $b^{{*}_j}{·}_j{a}^{{*}_j}=j(b^{{*}_j}·a^{{*}_j})=j(j\left(b^{*}\right)·j\left(a^{*}\right))=j(b^{*}·a^{*})$. Thus ${\left(a{·}_{j}b\right)}^{{*}_j}=b^{{*}_j}{·}_j{a}^{{*}_j}$.

(3) ${\left(a{\vee }_{j}b\right)}^{{*}_j}={\left(j(a\vee b)\right)}^{{*}_j}=j\left({\left(j(a\vee b)\right)}^{*}\right)=j(j\left(a^{*}\right)\vee j\left(b^{*}\right))=j\left(a^{*}\right){\vee }_{j}j\left(b^{{*}_j}\right)=a^{{*}_j}{\vee }_j{b}^{{*}_j}.$

Therefore, ${\ast }_j$ is an involutive operation on $S_j$.

For any $a,b\in S$,

(1) $j(a\vee b)\le j(j\left(a\right)\vee j\left(b\right))=j\left(a\right){\vee }_{j}j\left(b\right)$. By the definition of j, it follows that $j(a\vee b)=j\left(j(a\vee b)\right)\ge j(j\left(a\right)\vee j\left(b\right))=j\left(a\right){\vee }_{j}j\left(b\right)$. Thus, $j(a\vee b)=j\left(a\right){\vee }_{j}j\left(b\right)$.

(2) From Lemma 1, it follows that $j\left(a\right){·}_{j}j\left(b\right)=j(j\left(a\right)·j\left(b\right))=j(a·b)$. Thus, j preserves operation ${·}_j$.

(3) $j\left(a^{*}\right)=a^{{*}_j}\le {\left(j\left(a\right)\right)}^{{*}_j}$, but ${\left(j\left(a\right)\right)}^{{*}_j}=j\left({\left(j\left(a\right)\right)}^{*}\right)\ge j\left(a^{*}\right)$; thus, $j\left(a^{*}\right)={\left(j\left(a\right)\right)}^{{*}_j}$.

From (1), (2), and (3), we know that mapping $j:S\to S_j$ is an involutive m-semilattice homomorphism. □

Theorem 3. 

Let S be an involutive m-semilattice. $\forall j\in N\left(S\right)$, an equivalence R is defined as follows: $(a,b)\in R$ if, and only if, $j\left(a\right)=j\left(b\right)$ for all $a,b\in S$. Then, R is a congruence on S.

Theorem 4. 

Let S be an involutive m-semilattice, and let R be a congruence of S. For all $a,b,c\in S$, define $\left[a\right]\le \left[b\right]\iff [a\vee b]=\left[b\right]$; $\left[a\right]\vee \left[b\right]=[a\vee b]$; $\left[a\right]·\left[b\right]=[a·b]$; ${\left(\left[a\right]\right)}^{*}=\left[a^{*}\right]$. The mapping $\pi :S\to S/R$ such that $\pi \left(a\right)=\left[a\right]$. Then, $(S/R,·,\ast )$ is an involutive m-semilattice, and the mapping π is an involutive m-semilattice homomorphism.

Proof. 

We first show that ≤ is a partial order on $S/R$.

For any $\left[a\right],\left[b\right],\left[c\right]\in S/R$,

(1) It is clear that $\left[a\right]\le \left[a\right]$.

(2) If $\left[a\right]\le \left[b\right]$ and $\left[b\right]\le \left[a\right]$, then $[a\vee b]=\left[b\right]$ and $[b\vee a]=\left[a\right]$; thus, $\left[a\right]=\left[b\right]$.

(3) If $\left[a\right]\le \left[b\right]$ and $\left[b\right]\le \left[c\right]$, then $[a\vee c]=[a\vee (b\vee c\left)\right]=\left[\right(a\vee b)\vee (b\vee c\left)\right]=[b\vee c]=\left[c\right]$, i.e., $\left[a\right]\le \left[c\right]$.

It is easy to verify that the above operations $·,\vee ,$ and ∗ are well defined, and $(S/R,\vee )$ is a semilattice with a maximum element $\left[1\right]$.

Next, for any $\left[a\right],\left[b\right],\left[c\right]\in S/R$, we have

(1) $\left(\right[a]·[b\left]\right)·\left[c\right]=[a·b]·\left[c\right]=\left[\right(a·b)·c)]=[a·(b·c)]=[a]·(\left[b\right]·\left[c\right])$.

(2) $\left[a\right]·\left(\right[b]\vee [c\left]\right)=\left[a\right]·[b\vee c]=[a·(b\vee c\left)\right]=\left[\right(a·b)\vee (a·c\left)\right]=[a·b]\vee [a·c]=\left(\right[a]·[b\left]\right)\vee \left(\right[a]·[c\left]\right)$. Similarly, it can be proven that $\left(\right[b]\vee [c\left]\right)·\left[a\right]=\left(\right[b]·[a\left]\right)\vee \left(\right[c]·[a\left]\right)$ also holds.

(3) We verify that ∗ is an involution operation on $S/R$.

(i) ${\left(\left[a\right]\right)}^{**}=\left[a^{**}\right]=\left[a^{*}\right]={\left[a\right]}^{*}$.

(ii) ${\left([a·b]\right)}^{*}=\left[{(a·b)}^{*}\right]=[b^{*}·a^{*}]={\left(\left[b\right]\right)}^{*}·{\left(\left[a\right]\right)}^{*}$.

(iii) ${\left([a\vee b]\right)}^{*}=\left[{(a\vee b)}^{*}\right]=[a^{*}\vee b^{*}]={\left(\left[a\right]\right)}^{*}\vee {\left(\left[b\right]\right)}^{*}$

Therefore, $(S/R,·,\ast )$ is an involutive m-semilattice.

Finally, we will prove that the mapping $\pi :S\to S/R$ is an involutive m-semilattice homomorphism.

For any $\left[a\right],\left[b\right]\in S/R$,

(1) $\pi (a\vee b)=[a\vee b]=\left[a\right]\vee \left[b\right]=\pi \left[a\right]\vee \pi \left[b\right]$.

(2) $\pi (a·b)=[a·b]=\left[a\right]·\left[b\right]=\pi \left(a\right)·\pi \left(b\right)$.

(3) $\pi \left(a^{*}\right)=\left[a^{*}\right]={\left[a\right]}^{*}={\left[\pi \left(a\right)\right]}^{*}$. □

Definition 14. 

Let $IMSLatt$ be a category whose objects are involutive m-semilattices and whose morphisms are involutive m-semilattice homomorphisms. Obviously, the category $IMSLatt$ is a concrete category.

Lemma 2. 

Let $f:S\to P$ be an involutive m-semilattice homomorphism; then, $f^{-1}(△)=\{(x,y)\in S\times S|f\left(x\right)=f\left(y\right)\}$ is an involutive m-semilattice congruence on S.

Let S be an involutive m-semilattice, and let R be a binary relation on S. The smallest congruence containing R is the intersection of all the involutive m-semilattice congruences containing R on S. We say that this congruence is generated by R and is denoted by $<R>$.

Theorem 5. 

$IMSLatt$ has a coequalizer.

Proof. 

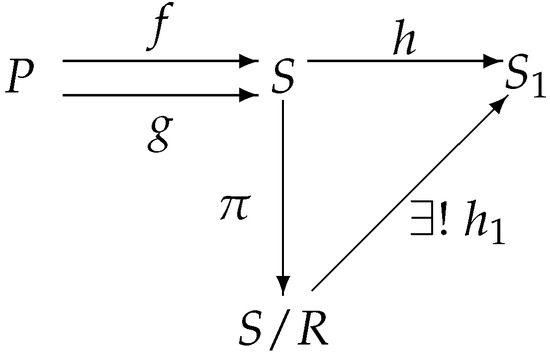
Let S and P be two involutive m-semilattices, let $f,g:S\to P$ be two involutive m-semilattice homomorphisms, and let R be the smallest congruence, which contains $\left\{\right(f\left(a\right),g\left(a\right)|a\in P\}$.

Suppose that $\pi :S\to S/R$ is the canonical mapping. Then, the mapping $\pi$ is an involutive m-semilattice homomorphism according to Theorem 4. We will show that $(\pi ,S/R)$ is the coequalizer of f and g.

(1) Let $a\in P$; then, $(\pi \circ f)\left(a\right))=\pi (f\left(a\right))=[f\left(a\right)]$ and $(\pi \circ g)\left(a\right))=\pi (g\left(a\right))=[g\left(a\right)]$. Since $\left(f\right(a),g(a\left)\right)\in R$, this implies that $\left[f\right(a\left)\right]=\left[g\right(a\left)\right]$, i.e., $\pi \circ f=\pi \circ g$.

(2) Let $h:S\to S_1$ be an involutive m-semilattice homomorphism such that $h\circ f=h\circ g$. Let $R_1={\left(h\right)}^{-1}(▵)$ and $▵=\left\{(x,x)\right|x\in S_1\}$. According to Lemma 2, it follows that $R_1$ is a congruence of S. $\forall a\in P$, then $h\left(f\right(a\left)\right)=h\left(g\right(a\left)\right)$. This implies that $(f\left(a\right),g\left(a\right))\in R_1$; thus, $R\subseteq R_1$.

We define a mapping $h_1:S/R\to S$ such that $h_1\left(\left[a\right]\right)=h\left(a\right)$ for all $\left[a\right]\in S/R$. Let $(a,b)\in R$; then, $(a,b)\in R_1$, i.e., $h_1\left(a\right)=h_1\left(b\right)$. This means that $h_1$ is well defined.

Let $\left[a\right],\left[b\right]\in S/R$; then,

(1) $h_1(\left[a\right]·\left[b\right])=h_1\left([a·b]\right)=h(a·b)=h\left(a\right)·h\left(b\right)=h_1\left(\left[a\right]\right)·h_1\left(\left[b\right]\right)$.

(2) $h_1(\left[a\right]\vee \left[b\right])=h_1\left([a\vee b]\right)=h(a\vee b)=h\left(a\right)\vee h\left(b\right)=h_1\left(\left[a\right]\right)\vee h_1\left(\left[b\right]\right)$.

(3) $h_1\left({\left(\left[a\right]\right)}^{*}\right)=h_1\left(\left[a^{*}\right]\right)=h\left(a^{*}\right)={\left(h\left(a\right)\right)}^{*}={\left[h_1\left(\left[a\right]\right)\right]}^{*}$.

Hence, the mapping $h_1:S/R\to S$ is an involutive m-semilattice homomorphism.

Let $x\in S$; then, $h_1\circ \pi \left(x\right)=h_1\left(\left[x\right]\right)=h\left(x\right)$, i.e., $h_1\circ \pi =h$. Thus, Figure 6 commutes.

Figure 6. Coequalizer diagram.

Let $h_2:S/R\to S$ such that $h_2\circ \pi =h$; then, $h_2\left(\left[x\right]\right)=(h_2\circ \pi )\left(x\right)=(h_1\circ \pi )\left(x\right)=h_1\left(\left[x\right]\right)$, i.e., $h_2=h_1$. Therefore, $(\pi ,S/R)$ is the coequalizer of f and g. □

The problem of free generation plays a crucial role in algebra, and the free generation of some mathematical structures has been widely studied ([28,29]). Next, we will discuss the structure of free involutive m-semilattices in detail.

Let X be a set; we use $\tilde{X}=\{x_1{x}_2\dots x_n|x_n\in X,n\in Z^{+}\}$ to denote the set of all finite strings composed of elements from X. A binary operation ★ is defined as follows:

$$\begin{array}{c}\forall x_1{x}_2\dots x_n,y_1{y}_2\dots y_m\in \tilde{X},\hfill \\ (x_1{x}_2\dots x_n)★(y_1{y}_2\dots y_m)=x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m.\hfill \end{array}$$

It is easy to verify that the binary operation ★ satisfies the associative law. $(\tilde{X},★)$ is called the free semigroup generated by the set X.

Let $P_F\left(\tilde{X}\right)$ denote the set of all finite subsets of the set $\tilde{X}$. Two binary operations are defined on the set $P_F\left(\tilde{X}\right)$ as follows:

$$\begin{array}{c}\forall A,B\in P_F\left(\tilde{X}\right),\hfill \\ A•B=\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B,n,m\in Z^{+}\},\hfill \\ A^{*}=\{x_n{x}_{n-1}\dots x_1|x_1{x}_2\dots x_n\in A,n\in Z^{+}\}.\hfill \end{array}$$

Theorem 6. 

The triple $(P_F\left(\tilde{X}\right),•,\ast )$ is an involutive m-semilattice with respect to the set inclusion order.

Proof. 

We first show that the above operations $•,\cup ,$ and ∗ are well defined, and $(P_F\left(\tilde{X}\right),\cup )$ is a semilattice. For any $A,B\in P_F\left(\tilde{X}\right)$. Since A and B are finite sets, suppose the cardinalities of A and B are $\kappa$ and $\lambda$, respectively, i.e., $\mid A\mid =\kappa$, $\mid B\mid =\lambda$. We have

(1) $A•B=\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B,n,m\in Z^{+}\}$. Hence, $\mid A•B\mid =\kappa \lambda$. Therefore, $A•B\in P_F\left(\tilde{X}\right)$.

(2) $\mid A\cup B\mid =\kappa \lambda$. Hence, $A\cup B\in P_F\left(\tilde{X}\right)$, Therefore, $(P_F\left(\tilde{X}\right),\cup )$ is a semilattice.

(3) $A^{*}=\{x_n{x}_{n-1}\dots x_1|x_1{x}_2\dots x_n\in A,n\in Z^{+}\}$. Then, $A^{*}\in P_F\left(\tilde{X}\right)$.

Next, For any $A,B,C\in P_F\left(\tilde{X}\right)$,

(1)

$$\begin{array}{cc}A•(B\cup C)\hfill & =\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B\cup C\}\hfill \\ \hfill & =\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|y_1{y}_2\dots y_m\in B\mathrm{or}{y}_1{y}_2\dots y_m\in C\}\hfill \\ \hfill & =(A•B)\cup (A•C).\hfill \end{array}$$

Similarly, it follows that $(B\cup C)•A=(B•A)\cup (C•A)$.

(2)

$$\begin{array}{cc}(A•B)•C\hfill & =\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B\}•C\hfill \\ \hfill & =\{(x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m)★(z_1{z}_2\dots z_s)|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\hfill \\ \hfill & \in B,z_1{z}_2\dots z_s\in C\}\hfill \\ \hfill & =\{(x_1{x}_2\dots x_n)★(y_1{y}_2\dots y_m{z}_1{z}_2\dots z_s)|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\hfill \\ \hfill & \in B,z_1{z}_2\dots z_s\in C\}\hfill \\ \hfill & =A•(B•C).\hfill \end{array}$$

(3)

$$\begin{array}{cc}(A*)*& ={\left(\{x_n{x}_{n-1}\dots x_1|x_1{x}_2\dots x_n\in A\}\right)}^{*}=\{x_1{x}_2\dots x_n|x_1{x}_2\dots x_n\in A\}=A.\\ (A•B)*\hfill & =\left(\right\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B\})*\hfill \\ \hfill & =\{y_m{y}_{m-1}\dots y_1{x}_n{x}_{n-1}\dots x_1|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B\}\hfill \\ \hfill & =\{y_m{y}_{m-1}\dots y_1{x}_n{x}_{n-1}\dots x_1|x_n{x}_{n-1}\dots x_1\in A*,y_m{y}_{m-1}\dots y_1\in B*\}\hfill \\ \hfill & =B*•A*.\hfill \end{array}$$

(4)

$$\begin{array}{cc}{(A\cup B)}^{*}\hfill & =\left(\{x_1{x}_2\dots x_n|x_1{x}_2\dots x_n\in A\cup B\}\right)*\hfill \\ \hfill & =\{x_n{x}_{n-1}\dots x_1|x_1{x}_2\dots x_n\in A\mathrm{or}{x}_1{x}_2\dots x_n\in B\}\hfill \\ \hfill & =A^{*}\cup B^{*}.\hfill \end{array}$$

From the above proof, it can be seen that $(P_F\left(\tilde{X}\right),•,\cup ,\ast )$ is an involutive m-semilattice. □

Theorem 7. 

There is a functor $P_F:Set\to IMSLatt$ that is left adjoint to the forgetful functor $U:IMSLatt\to Set$.

Proof. 

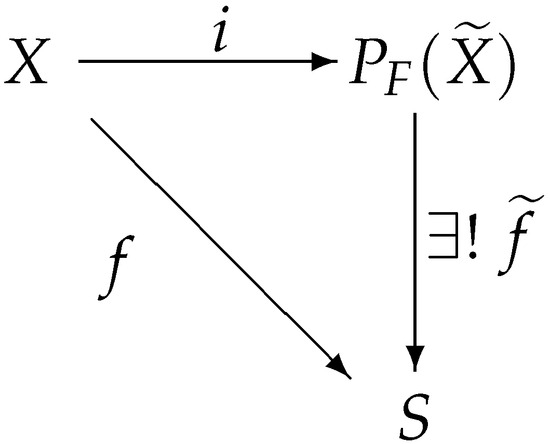
Let X and Y be nonempty sets, and let $f:X\to Y$ be a mapping. According to Theorem 6, it follows that $P_F\left(\tilde{X}\right)$ and $P_F\left(\tilde{Y}\right)$ are involutive m-semilattices. We define $P_F\left(f\right):P_F\left(\tilde{X}\right)\to P_F\left(\tilde{Y}\right)$ such that $P_F\left(f\right)\left(A\right)=\{f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\}$ for all $A\in P_F\left(\tilde{X}\right)$; then, the mapping $P_F\left(f\right)$ is well defined.

Next, we will prove that the mapping $P_F\left(f\right)$ is an involutive m-semilattice homomorphism. For any $A,B\in P_F\left(\tilde{X}\right)$,

(1)

$$\begin{array}{ll}{P}_F\left(f\right)(A\cup B)& =\{f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\cup B\}\\ & =\{f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\mathrm{or}{x}_1{x}_2\dots x_n\in B\}\\ & =P_F\left(f\right)\left(A\right)\cup P_F\left(f\right)\left(B\right).\end{array}$$

Therefore, the mapping f preserves the union of sets.

(2)

$$\begin{array}{ll}{P}_F\left(f\right)(A•B)& =\{f\left(x_1\right)\dots f\left(x_n\right)f\left(y_1\right)\dots f\left(y_m\right)|x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m\in A•B\}\\ & =\{f\left(x_1\right)\dots f\left(x_n\right)f\left(y_1\right)\dots f\left(y_m\right)|x_1\dots x_n\in A,y_1\dots y_m\in B\}\\ & =\{f\left(x_1\right)\dots f\left(x_n\right)|x_1\dots x_n\in A\}•\{f\left(y_1\right)\dots f\left(y_m\right)|y_1\dots y_m\in B\}\\ & =P_F\left(f\right)\left(A\right)•P_F\left(f\right)\left(B\right).\end{array}$$

Therefore, the mapping $P_F\left(f\right)$ preserves the operation •.

(3)

$$\begin{array}{ll}{P}_F\left(f\right){\left(A\right)}^{*}& =\{f\left(x_n\right)f\left(x_{n-1}\right)\dots f\left(x_1\right)|x_n{x}_{n-1}\dots x_1\in A^{*}\}\\ & =\left\{{(f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right))}^{*}\right|x_1{x}_2\dots x_n\in A\}\\ & ={\left(\{f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\}\right)}^{*}\\ & ={\left(P_F\left(f\right)\left(A\right)\right)}^{*}.\end{array}$$

Hence, the mapping $P_F\left(f\right)$ preserves the involutive operation ∗.

From the above proof, it can be concluded that the mapping $P_F\left(f\right)$ is an involutive semilattice homomorphism.

Next, we will check that $P_F:Set\to IMSLatt$ is a functor.

We define a mapping $i_X:X\to X$ such that $i_X\left(x\right)=x$ for all $x\in X$. For any $A\in P_F\left(\tilde{X}\right)$,

(1)

$$\begin{array}{cc}{P}_F\left(i_X\right)\left(A\right)\hfill & =\{i_X\left(x_1\right)i_X\left(x_2\right)\dots i_X\left(x_n\right)|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =\{x_1{x}_2\dots x_n|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =A\hfill \\ \hfill & =i_{P_F\left(X\right)}\left(A\right).\hfill \end{array}$$

This means that the functor $P_F$ preserves identity mappings.

(2) Let $f:X\to Y$, $g:Y\to Z$; then,

$$\begin{array}{cc}{P}_F(f\circ g)\left(A\right)\hfill & =\{(f\circ g)\left(x_1\right)(f\circ g)\left(x_2\right)\dots (f\circ g)\left(x_n\right)|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =\left\{(f\circ g)(x_1{x}_2\dots x_n)\right|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =\left\{f\left(g(x_1{x}_2\dots x_n)\right)\right|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =\left\{f(g\left(x_1\right)g\left(x_2\right)\dots g\left(x_n\right))\right|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =P_F\left(f\right)\left(\{g\left(x_1\right)g\left(x_2\right)\dots g\left(x_n\right)|x_1{x}_2\dots x_n\in A\}\right)\hfill \\ \hfill & =(P_F\left(f\right)\circ P_F\left(g\right))\left(A\right).\hfill \end{array}$$

Thus, the functor $P_F$ preserves the composition of f and g.

Finally, we will prove that $P_F:Set\to IMSLatt$ is the left adjoint to the forgetful functor $U:IMSLatt\to Set$.

Let X be a non-empty set; we define a mapping $i:X\to P_F\left(\tilde{X}\right)$ such that $i\left(x\right)=x$ for all $x\in X$. Let S be an involutive semilattice and mapping $f:X\to S$; we define a mapping $\tilde{f}:P_F\left(\tilde{X}\right)\to S$ such that $\tilde{f}\left(A\right)=\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_1\dots x_n\in A)\}$ for all $A\in P_F\left(\tilde{X}\right)$. Since $\{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_1\dots x_n\in A\left)\right\}$ is a finite set, then $\tilde{f}\left(A\right)\in S$. This shows that the mapping $\tilde{f}$ is well defined.

For any $A,B\in P_F\left(\tilde{X}\right)$,

(1)

$$\begin{array}{cc}\tilde{f}(A\cup B)\hfill & =\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\cup B\}\hfill \\ \hfill & =(\bigvee \{f\left(y_1\right)·f\left(y_2\right)\dots f\left(y_m\right)|y_1{y}_2\dots y_m\in A\})\hfill \\ \hfill & \vee (\bigvee \{f\left(z_1\right)·f\left(z_2\right)\dots f\left(z_s\right)|z_1{z}_2\dots z_s\in B\})\hfill \\ \hfill & =\tilde{f}\left(A\right)\vee \tilde{f}\left(B\right).\hfill \end{array}$$

(2)

$$\begin{array}{cc}\tilde{f}(A•B)\hfill & =\bigvee \{f\left(y_1\right)·f\left(y_2\right)\dots f\left(y_n\right)·f\left(z_1\right)·f\left(z_2\right)\dots f\left(z_s\right)|y_1{y}_2\dots y_m\in A,\hfill \\ \hfill & z_1{z}_2\dots z_s\in B)\}\hfill \\ \hfill & =(\bigvee \{f\left(y_1\right)·f\left(y_2\right)\dots f\left(y_m\right)|y_1{y}_1\dots y_m\in A\})\hfill \\ \hfill & ·(\bigvee \{f\left(z_1\right)·f\left(z_2\right)\dots f\left(z_s\right)|z_1{z}_2\dots z_s\in B\})\hfill \\ \hfill & =\tilde{f}\left(A\right)·\tilde{f}\left(B\right).\hfill \end{array}$$

(3)

$$\begin{array}{cc}\tilde{f}\left(A^{*}\right)\hfill & =\bigvee \{f\left(x_n\right)·f\left(x_{n-1}\right)\dots f\left(x_1\right)|x_n{x}_{n-1}\dots x_1\in A^{*})\}\hfill \\ \hfill & =\bigvee \left(\{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A)\right\})*\hfill \\ \hfill & =(\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A)\})*\hfill \\ \hfill & ={\left(\tilde{f}\left(A\right)\right)}^{*}.\hfill \end{array}$$

Hence, the mapping $P_F\left(f\right)$ is an involutive semilattice homomorphism.

For any $x\in X$, $(\tilde{f}\circ i)\left(x\right)=\tilde{f}\left(\left\{x\right\}\right)=f\left(x\right)$, i.e., $\tilde{f}\circ i=f$; hence, Figure 7 commutes.

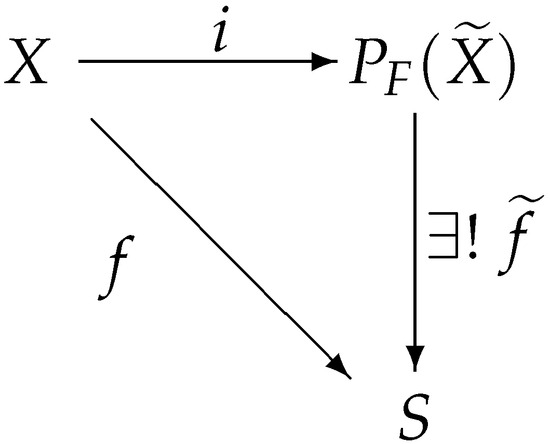
Figure 7. Universal property diagram.

Suppose that $\widetilde{f^{\prime }}:P_F\left(f\right)\to S$ is another homomorphism such that $\widetilde{f^{\prime }}\circ i=f$.

Then, $\tilde{f}\left(\left\{x\right\}\right)=(\tilde{f}\circ i)\left(x\right)=f\left(x\right)=(\widetilde{f^{\prime }}\circ i)\left(x\right)=\widetilde{f^{\prime }}\left(\left\{x\right\}\right)$, i.e., $\tilde{f}\left(\left\{x\right\}\right)=\widetilde{f^{\prime }}\left(\left\{x\right\}\right)$.

For any $A\in P_F\left(\tilde{X}\right)$,

$$\begin{array}{cc}\tilde{f}\left(A\right)\hfill & =\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =\bigvee \{\widetilde{f^{\prime }}\left(\left\{x_1\right\}\right)·\widetilde{f^{\prime }}\left(\left\{x_2\right\}\right)\dots \widetilde{f^{\prime }}\left(\left\{x_n\right\}\right)|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =\bigvee \left\{\widetilde{f^{\prime }}(\left\{x_1\right\}•\left\{x_2\right\}\dots •\left\{x_n\right\})\right|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =\bigvee \left\{\widetilde{f^{\prime }}(x_1{x}_2\dots x_n)\right|x_1{x}_2\dots x_n\in A\}\hfill \\ \hfill & =\widetilde{f^{\prime }}(\bigcup \{x_1{x}_2\dots x_n|x_1{x}_2\dots x_n\in A\})\hfill \\ \hfill & =\widetilde{f^{\prime }}\left(A\right).\hfill \end{array}$$

Thus, $\tilde{f}=\widetilde{f^{\prime }}$. This means that $\tilde{f}$ is a unique involutive m-semilattice homomorphism and satisfies the commutativity of Figure 7.

The above proof shows that the functor $P_F$ is left adjoint to the forgetful functor U. □

Definition 15 ([26]). 

A morphism $f:A\to B$ is said to be a monomorphism in $\mathcal{C}$ provided that for all $\mathcal{C}$-morphisms h and k such that $f\circ h=f\circ k$, it follows that $h=k$ (i.e., f is left-cancellable with respect to the composition in $\mathcal{C}$).

Dually, a morphism $f:A\to B$ is said to be an epimorphism in $\mathcal{C}$ provided that for all $\mathcal{C}$-morphisms h and k such that $h\circ f=k\circ f$, it follows that $h=k$ (i.e., f is right-cancellable with respect to the composition in $\mathcal{C}$).

Every morphism in a concrete category that is an injective function on underlying sets is a monomorphism; every morphism in a concrete category that is a surjective function on underlying sets is an epimorphism.

Theorem 8. 

In IMSLatt, the monomorphisms are precisely the morphisms that are injective on the underlying sets, and the epimorphisms are precisely the morphisms that are surjective on the underlying sets.

Proof. 

This proof is similar to Proposition 3.3 in the Reference [27]. □

Definition 16 ([26]). 

If $e:E\to A$ is a $\mathcal{C}$-morphism, then e is called a regular monomorphism if, and only if, there are $\mathcal{C}$-morphisms f and g such that $(E,e)$ is the equalizer of f and g.

Dually, if $e:A\to E$ is a $\mathcal{C}$-morphism, then e is called a regular epimorphism if, and only if, there are $\mathcal{C}$-morphisms f and g such that $(e,E)$ is the coequalizer of f and g.

Theorem 9. 

The forgetful functor $U:IMSLatt\to Set$ preserves and reflects regular epimorphisms.

Proof. 

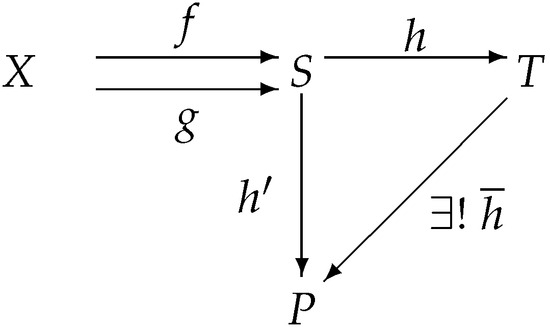
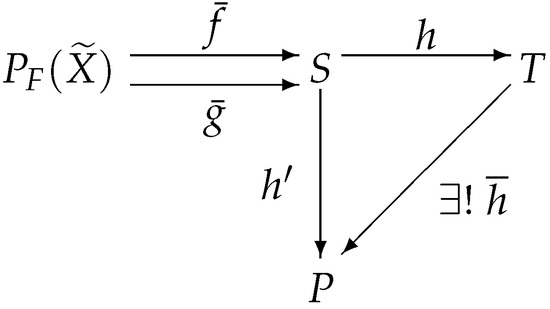
Obviously, the forgetful functor $U:IMSLatt\to Set$ preserves regular epimorphisms. We will prove that the forgetful functor $U:IMSLatt\to Set$ reflects regular epimorphisms, which requires proving that the epimorphisms are precisely the regular epimorphisms in the category IMSLatt.

Let $h:S\to T$ be an epimorphism in the category IMSLatt. Since the surjection is a regular epimorphism in the category Set, then the mapping h is a regular epimorphism in the category Set. This means that there is a set X and mappings $f,g:X\to S$ such that $(h,T)$ is the coequalizer of f and g. Then, Figure 8 commutes.

Figure 8. Coequalizer diagram.

For any $A\in P_F\left(\tilde{X}\right)$, define two mappings $\tilde{f}:P_F\left(\tilde{X}\right)\to S$ and $\tilde{g}:P_F\left(\tilde{X}\right)\to S$ as follows:

$$\begin{gathered} \tilde{f}\left(A\right)=\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\}, \\ \tilde{g}\left(A\right)=\bigvee \{g\left(x_1\right)·g\left(x_2\right)\dots g\left(x_n\right)|x_1{x}_2\dots x_n\in A\}. \end{gathered}$$

According to the proof of Theorem 6, we know that mappings $\tilde{f}$ and $\tilde{g}$ are involutive m-semilattice homomorphisms. Since $h\circ f=h\circ g$,

$$\begin{array}{cc}h\circ \tilde{f}\left(A\right)\hfill & =h(\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\})\hfill \\ \hfill & =\bigvee \{(h\circ f)\left(x_1\right)·(h\circ f)\left(x_2\right)\dots (h\circ f)\left(x_n\right)|x_1{x}_2\dots x_n\in A\left\}\right)\hfill \\ \hfill & =\bigvee \{(h\circ g)\left(x_1\right)·(h\circ g)\left(x_2\right)\dots (h\circ g)\left(x_n\right)|x_1{x}_2\dots x_n\in A\left\}\right)\hfill \\ \hfill & =h(\bigvee \{g\left(x_1\right)·g\left(x_2\right)\dots g\left(x_n\right)|x_1{x}_2\dots x_n\in A\}).\hfill \end{array}$$

Hence, $h\circ \tilde{f}=h\circ \tilde{g}$.

Let mapping $h^{\prime }:S\to P$ such that $h^{\prime }\circ \tilde{f}=h^{\prime }\circ \tilde{g}$; then, $h^{\prime }\circ f=h^{\prime }\circ g$. Since $(h,T)$ is the coequalizer of f and g, this shows that there exists a unique mapping $\overline{h}:T\to P$ such that $h^{\prime }=\overline{h}\circ h$.

For any $x,y\in S$, since h is a surjective function, there are $x_1,y_1\in S$ such that $h\left(x_1\right)=x$ and $h\left(y_1\right)=y$. We have

(1) $\overline{h}(x·y)=\overline{h}(h\left(x_1\right)·h\left(y_1\right))$ $=(\overline{h}\circ h)(x_1·y_1)=h^{\prime }(x_1·y_1)$ $=h^{\prime }\left(x_1\right)·h^{\prime }\left(y_1\right)$ $=(\overline{h}\circ h)\left(x_1\right)·(\overline{h}\circ h)\left(y_1\right)$ $=\overline{h}\left(h\left(x_1\right)\right)·\overline{h}\left(h\left(y_1\right)\right)$ $=\overline{h}\left(x\right)·\overline{h}\left(y\right)$.

(2) $\overline{h}(x\vee y)=\overline{h}(h\left(x_1\right)\vee h\left(y_1\right))=\left((\overline{h}\circ h)\left(x_1\right)\right)\vee \left((\overline{h}\circ h)\left(y_1\right)\right)=h^{\prime }\left(x_1\right)\vee h^{\prime }\left(y_1\right)=\overline{h}\left(h\left(x_1\right)\right)\vee \overline{h}\left(h\left(y_1\right)\right)=\overline{h}\left(x\right)\vee \overline{h}\left(y\right)$.

(3) $\overline{h}\left(x^{*}\right)=\overline{h}\left({\left(h\left(x_1\right)\right)}^{*}\right)=\overline{h}\left(h\left(x_1^{*}\right)\right)=(\overline{h}\circ h)\left(x_1^{*}\right)=h^{\prime }\left(x_1^{*}\right)={\left(h^{\prime }\left(x_1\right)\right)}^{*}={\left((\overline{h}\circ h)\left(x_1\right)\right)}^{*}={\left(\overline{h}\left(x\right)\right)}^{*}$.

Thus, the mapping $\overline{h}$ is an involutive m-semilattice homomorphism.

The above proof shows that $(h,T)$ is a coequalizer of f and g in the category IMSLatt. Then, Figure 9 commutes.

Figure 9. Coequalizer diagram.

Therefore, the mapping h is a regular epimorphism in IMSLatt. □

Using Theorems 5, 7, and 9, we can obtain Theorem 10.

Theorem 10. 

The category $IMSLatt$ is algebraic.

4. The Colimit of the Functor in ${\mathit{IMCSLatt}}_{\mathbf{0}}$

Limits provide a highly abstract and unified way to describe various concrete mathematical constructions. The limit of a functor is a generalization of each of the notions of a “terminal object”, “equalizer”, “product”, and “intersection”. Therefore, the study of limits is very important for a category. The colimit is the dual definition of the limit. Limits are not only fundamental constructions within category theory itself but also powerful tools for connecting different mathematical fields and unifying various mathematical concepts. Limits and colimits have been systematically studied in some categories [30,31,32,33]. It is well known that to prove that a category is cocomplete, one must verify that the colimit of a functor from a small category to this category exists, and the construction of colimits relies on coproducts. Building coproducts in the involutive m-semilattice category is a complex and difficult task. In this study, we prove that a full subcategory of involutive m-semilattices is cocomplete, providing some insights for the proof of cocompleteness in the category of involutive m-semilattices.

Definition 17 ([26]). 

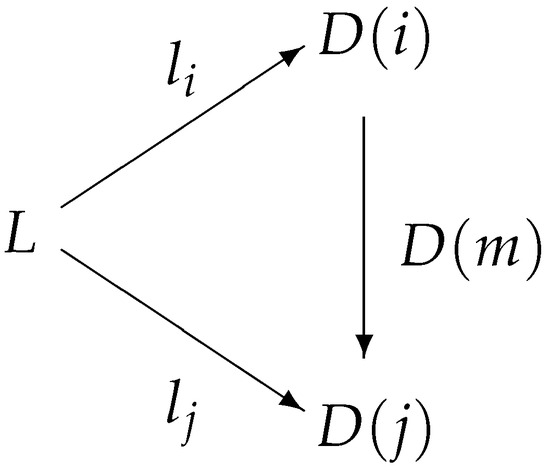
If I and $\mathcal{C}$ are categories and $D:I\to \mathcal{C}$ is a functor, then a natural source for D is a source $(L,{\left(l_i\right)}_{i\in Ob\left(I\right)})$ in $\mathcal{C}$ such that for each $i\in Ob\left(I\right)$, $l_i:L\to D\left(i\right)$ and for all morphisms $m:i\to j$, Figure 10 commutes.

Figure 10. Natural source diagram.

Dually, a natural sink for D is a sink $({\left(k_i\right)}_{i\in Ob\left(I\right)},K)$ where ${\left(k_i\right)}_{i\in Ob\left(I\right)}$ is a natural transformation from D to the constant functor $K:I\to \mathcal{C}$.

Definition 18 ([26]). 

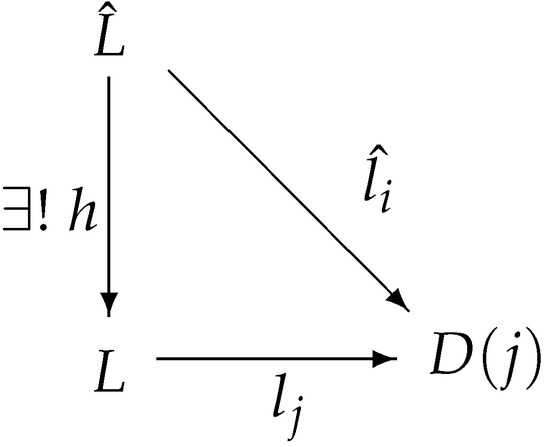
If $D:I\to \mathcal{C}$ is a functor, then a natural source $(L,l_i)$ for D is called a limit of D provided that if $(\widehat{L},\widehat{l_i})$ is any natural source for D, then there is a unique morphism $h:\widehat{L}\to L$ such that for each $j\in Ob\left(I\right)$, Figure 11 commutes.

Figure 11. Limit diagram.

Dually, a natural sink $({\left(k_i\right)}_{i\in Ob\left(I\right)},K)$ is called a colimit of D provided that every natural sink for D factors uniquely through it.

Definition 19. 

Let S be an involutive m-semilattice. $\forall \left\{a_i\right\},\left\{b_i\right\}\subseteq S$, and I is a finite set. If S satisfies the condition (CD) $\underset{i\in I}{\vee }(a_i·b_i)=\left(\underset{i\in I}{\vee }{a}_i\right)·\left(\underset{i\in I}{\vee }{b}_i\right)$, then $(S,\vee ,·,\ast )$ is called an involutive mc-semilattice. It is clear that if S satisfies (CD), then S satisfies Definition 1(1).

Theorem 11. 

Let S be an involutive mc-semilattice, and let R be a congruence of S. For any $a,b,c\in S$, we define $\left[x\right]\le \left[y\right]\iff [a\vee b]=\left[b\right]$; $\left[a\right]\vee \left[b\right]=[a\vee b]$; $\left[a\right]·\left[b\right]=[a·b]$; ${\left(\left[a\right]\right)}^{*}=\left[a^{*}\right]$. The mapping $\pi :S\to S/R$ such that $\pi \left(a\right)=\left[a\right]$. Then, $(S/R,·,\ast )$ is an involutive mc-semilattice, and the mapping π is an involutive m-semilattice homomorphism.

Proof. 

The proof of Theorem 11 is similar to the proof of Theorem 4. □

Definition 20. 

Let ${\left\{S_i\right\}}_{i\in I}$ be a family of involutive mc-semilattices with a minimum element, and let ${\displaystyle \prod _{i\in I}}{S}_i$ be the Cartesian product of ${\left\{S_i\right\}}_{i\in I}$. For any $i\in S$, we define a mapping ${ϵ}_i:S_i\to {\displaystyle \prod _{i\in I}}{S}_i$ by $\forall x\in I$, ${\left({ϵ}_i\left(x\right)\right)}_j=\left\{\begin{array}{c}x,i=j,\hfill \\ 0_i,i\ne j,\hfill \end{array}\right.$ where $0_i$ denotes the minimal element of $S_i$. Then, mapping ${ϵ}_i$ is called a standard injection.

Lemma 3 ([20]). 

Let ${\left\{S_i\right\}}_{i\in I}$ be a family of involutive m-semilattices, and let ${\displaystyle \prod _{i\in I}}{S}_i$ be the Cartesian product of ${\left\{S_i\right\}}_{i\in I}$. $\forall s={\left(s_i\right)}_{i\in I},t={\left(t_i\right)}_{i\in I}{\displaystyle \prod _{i\in I}}{S}_i$, we define a semigroup multiplication "·" and an involutive operation on ${\displaystyle \prod _{i\in I}}{S}_i$ as follows: $s·t={(s_i·t_i)}_{i\in I},s^{*}={\left(s_i^{*}\right)}_{i\in I}.$ Then, $({\displaystyle \prod _{i\in I}}{S}_i,·,\ast )$ is an involutive m-semilattice.

Theorem 12. 

Let ${\displaystyle \coprod _{i\in I}}{S}_i=\{x={\left(x_i\right)}_{i\in I}\in {\displaystyle \prod _{i\in I}}{S}_i|\{i\in I|x_i\ne 0_i\}$ is a finite set }. $\forall s={\left(s_i\right)}_{i\in I},t={\left(t_i\right)}_{i\in I}\subseteq {\displaystyle \coprod _{i\in I}}{S}_i$, $s·t={(s_i·t_i)}_{i\in I},s^{*}={\left(s_i^{*}\right)}_{i\in I}.$ Then, $({\displaystyle \coprod _{i\in I}}{S}_i,·,\ast )$ is an involutive mc-semilattice under the pointwise order of the Cartesian product.

Proof. 

The proof is similar to the proof of Lemma 3. □

Definition 21. 

Let $IMCSLat{t}_0$ be a category whose objects are involutive mc-semilattices with a minimum element and whose morphisms are involutive m-semilattice homomorphisms. Obviously, the category $IMCSLat{t}_0$ is a full subcategory of $IMSLatt$.

Theorem 13. 

Let ${\left\{S_i\right\}}_{i\in I}$ be a family of involutive mc-semilattices with a minimum element; then, $({\displaystyle \coprod _{i\in I}}{S}_i,{\left\{{ϵ}_i\right\}}_{i\in I})$ is the coproduct of ${\left\{S_i\right\}}_{i\in I}$ in $IMCSLat{t}_0$, where $\forall i\in I$ and the mapping ${ϵ}_i:S_i\to {\displaystyle \coprod _{i\in I}}{S}_i$ is an injection.

Proof. 

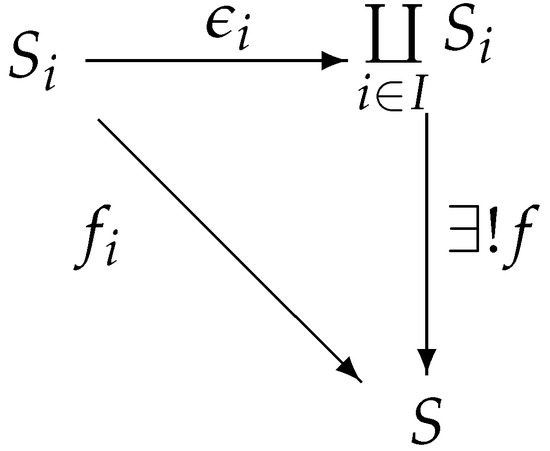
We shall show that ${ϵ}_i$ is an involutive m-semilattice homomorphism.

$\forall i\in I,\forall x,y\in S_i$,

(1)

$$\begin{array}{c}{\left({ϵ}_i(x\vee y)\right)}_i=x\vee y={\left({ϵ}_i\left(x\right)\right)}_i\vee ({ϵ}_i{\left(y\right)}_i={({ϵ}_i\left(x\right)\vee {ϵ}_i\left(y\right))}_i.\hfill \\ \forall j\in I,\mathrm{if}i\ne j,{\left({ϵ}_i(x\vee y)\right)}_j=0_j={\left({ϵ}_i\left(x\right)\right)}_j\vee {\left({ϵ}_i\left(y\right)\right)}_j={({ϵ}_i\left(x\right)\vee {ϵ}_i\left(y\right))}_j.\hfill \end{array}$$

Thus, ${ϵ}_i(x\vee y)={ϵ}_i\left(x\right)\vee {ϵ}_i\left(y\right)$.

(2)

$$\begin{array}{c}{\left({ϵ}_i(x·y)\right)}_i=x·y={\left({ϵ}_i\left(x\right)\right)}_i·{\left({ϵ}_i\left(y\right)\right)}_i={({ϵ}_i\left(x\right)·{ϵ}_i\left(y\right))}_i.\hfill \\ \forall j\in I,\mathrm{if}i\ne j,{\left({ϵ}_i(x·y)\right)}_j=0_j={\left({ϵ}_i\left(x\right)\right)}_j·{\left({ϵ}_i\left(y\right)\right)}_j={({ϵ}_i\left(x\right)·{ϵ}_i\left(y\right))}_j.\hfill \end{array}$$

Thus, ${ϵ}_i(x·y)={ϵ}_i\left(x\right)·{ϵ}_i\left(y\right)$.

(3)

$$\begin{array}{c}{\left({ϵ}_i\left(x^{*}\right)\right)}_i=x^{*}={\left({\left({ϵ}_i\left(x\right)\right)}_i\right)}^{*}.\hfill \\ \forall j\in I,ifi\ne j,{\left({ϵ}_i(x*)\right)}_j=0_j=\left(0_j\right)*=\left({\left({ϵ}_i\left(x\right)\right)}_j\right)*.\hfill \end{array}$$

Thus, ${ϵ}_i\left(x^{*}\right)={\left({ϵ}_i\left(x\right)\right)}^{*}$.

Therefore, ${ϵ}_i$ is an involutive m-semilattice homomorphism.

Let S be an arbitrary involutive mc-semilattice with a minimum element 0. $\forall i\in I$, mapping $f_i:S_i\to S$ is an involutive m-semilattice homomorphism. We define $f:{\displaystyle \coprod _{i\in I}}{S}_i\to S$ by $\forall x={\left(x_i\right)}_{i\in I}\in {\displaystyle \coprod _{i\in I}}{S}_i$, $f\left(x\right)={\displaystyle \underset{i\in I}{\bigvee }}\left\{f_i\left(x_i\right)\right|x_i\ne 0_i\}$. We first show that f is well defined for any $x={\left(x_i\right)}_{i\in I}\in {\displaystyle \coprod _{i\in I}}{S}_i$. By the definition of ${\displaystyle \coprod _{i\in I}}{S}_i$, it follows that $\{i\in I|x_i\ne 0_i\}$ is a finite set. Since $\forall i\in I$, mapping $f_i:S_i\to S$ is an involutive m-semilattice homomorphism; then, $f\left(0_i\right)=0$ (i.e., $f_i$ preserves the minimum element). Thus, the set $\{i\in I|f_i\left(x_i\right)\ne 0\}$ is finite. Therefore, the supremum of the set $\{i\in I|f_i\left(x_i\right)\ne 0\}$ in the semilattice S exists. This shows that f is well defined.

Next, we prove that f is an involutive m-semilattice homomorphism.

$\forall a={\left(a_i\right)}_{i\in I},b={\left(b_i\right)}_{i\in I},c={\left(c_i\right)}_{i\in I}\in {\displaystyle \coprod _{i\in I}}{S}_i$; then,

(1) $f(a\vee b)={\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left({(a\vee b)}_i\right)={\displaystyle \underset{i\in I}{\bigvee }}(f_i\left(a_i\right)\vee \left(f_i\left(b_i\right)\right)=({\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left(a_i\right))\vee ({\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left(b_i\right))=f\left(a\right)\vee f\left(b\right)$.

(2) $f(a·b)={\displaystyle \underset{i\in I}{\bigvee }}\left(f_i\left({(a·b)}_i\right)\right)={\displaystyle \underset{i\in I}{\bigvee }}(f_i\left(a_i\right)·f_i\left(b_i\right))$, and by Definition 19, it follows that ${\displaystyle \underset{i\in I}{\bigvee }}(f_i\left(a_i\right)·f_i\left(b_i\right))=({\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left(a_i\right))·({\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left(b_i\right))=f\left(a\right)·f\left(b\right)$. Then, $f(a·b)=f\left(a\right)·f\left(b\right)$.

(3) $f\left(c^{*}\right)={\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left({\left(c^{*}\right)}_i\right)$ $={\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left(c_i^{*}\right)$ $={\displaystyle \underset{i\in I}{\bigvee }}{\left(f_i\left(c_i\right)\right)}^{*}$ $={({\displaystyle \underset{i\in I}{\bigvee }}{f}_{i\in I}\left(c_i\right))}^{*}={\left(f\left(x\right)\right)}^{*}$.

In the following, we prove that $f_i=f\circ {ϵ}_i$ for all $i\in I$. $\forall x\in S_i$, $(f\circ {ϵ}_i)\left(x\right)={\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left({\left({ϵ}_i\right)}_i\right)=f_i\left(x_i\right)$. Then, Figure 12 commutes.

Figure 12. Coproduct diagram.

Finally, we prove the uniqueness of the involutive m-semilattice homomorphism f that satisfies the conditions $f_i=f\circ {ϵ}_i$.

We assume that g is another involutive m-semilattice homomorphism that satisfies the above condition, i.e., $\forall i\in I$, $f_i=g\circ {ϵ}_i$. Then, $\forall x\in {\displaystyle \coprod _{i\in I}}{S}_i$, we have

$$g\left(x\right)=g(\underset{i\in I}{\bigvee }{ϵ}_i\left(x_i\right))={\displaystyle \underset{i\in I}{\bigvee }}g\left({ϵ}_i\left(x_i\right)\right)={\displaystyle \underset{i\in I}{\bigvee }}(g\circ {ϵ}_i)\left(x_i\right)={\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left(x_i\right)=f\left(x\right).$$

Therefore, $({\displaystyle \coprod _{i\in I}}{S}_i,{\left\{{ϵ}_i\right\}}_{i\in I})$ is the coproduct of ${\left\{S_i\right\}}_{i\in I}$ in $IMCSLat{t}_0$. □

Definition 22 ([26]). 

A category $\mathcal{C}$ is said to be small provided that $\mathcal{C}$ is a set.

Theorem 14. 

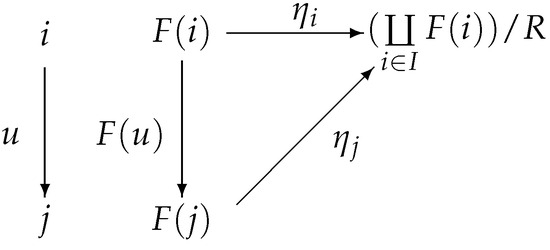
Let I be a small category, and let $F:I\to IMCSLat{t}_0$ be a functor; then, the colimit of F is $({({\eta }_i)}_{i\in I},({\displaystyle \coprod _{i\in I}}F(i))/R)$, where R is the smallest involutive m-semilattice congruence relation that contains the set $\bigcup \left\{({ϵ}_i(a),{ϵ}_j(F(u)(a)))\right|u:i\to j\in Mor(I),a\in D(i)\}$, $\forall i\in I$, ${ϵ}_i:F(i)\to {\displaystyle \coprod _{i\in I}}F(i)$ is an injection, and $\pi :{\displaystyle \coprod _{i\in I}}F(i)\to ({\displaystyle \coprod _{i\in I}}F(i))/R$ is a projection.

Proof. 

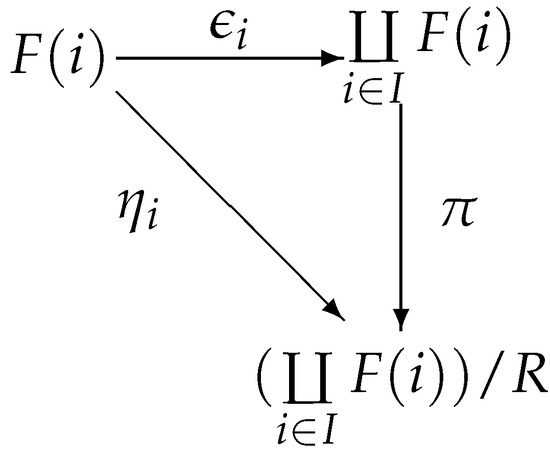
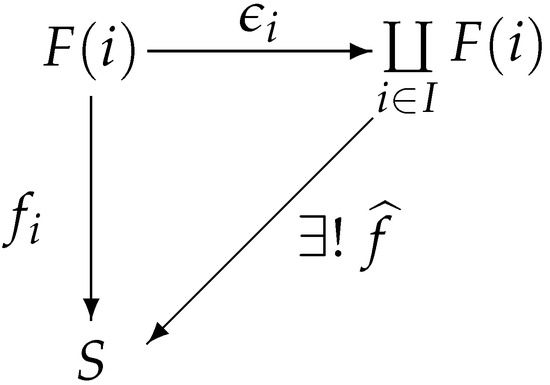
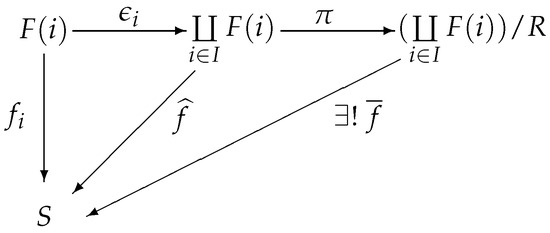
(1) We first show that $({({\eta }_i)}_{i\in I},({\displaystyle \coprod _{i\in I}}F(i))/R)$ is the natural sink of the functor F.

According to Theorems 11 and 13, it follows that projection $\pi$ and injection ${ϵ}_i$ are both involutive m-semilattice homomorphisms. Then, the mapping ${\eta }_i=\pi \circ {ϵ}_i$ is also an involutive m-semilattice homomorphism. Then, Figure 13 commutes.

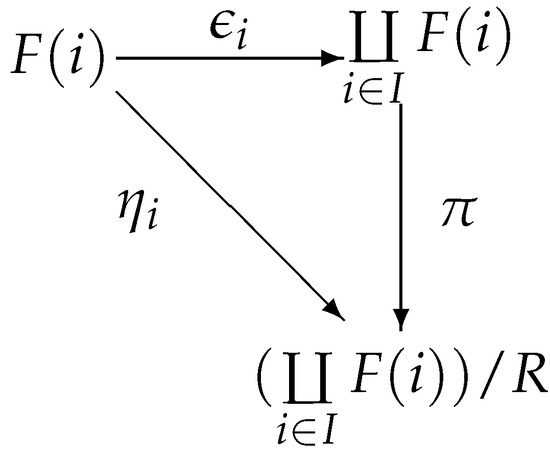
Figure 13. Canonical mapping diagram.

$\forall u:i\to j\in MOr(I)$, $\forall x\in F(i)$. Because R is the smallest involutive m-semilattice congruence relation that contains the set $\tilde{R}=\bigcup \left\{({ϵ}_i(a),{ϵ}_j(F(u)(a)))\right|u:i\to j\in Mor(I),a\in F(i)\}$, and $\forall i\in I$, then $({ϵ}_i(x),{ϵ}_j(F(u)(x))\in R$; thus, $({\eta }_j\circ F(u))(x)=(\pi \circ {ϵ}_j)(F(u)(x))=\pi ({ϵ}_j(F(u)(x)))=[{ϵ}_j\circ F(u)(x)]=\left[{ϵ}_i(x)\right]=\left[(\pi \circ {ϵ}_i)(x)\right]={\eta }_i(x)$. Then, Figure 14 commutes.

Figure 14. Natural sink diagram.

Therefore, $({({\eta }_i)}_{i\in I},({\displaystyle \coprod _{i\in I}}F(i))/R)$ is the natural sink of the functor F.

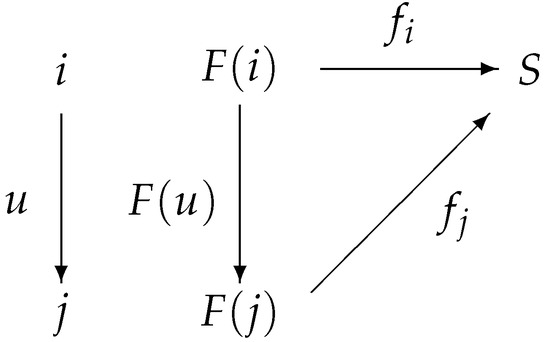
(2) Let S be an involutive mc-semilattice with a minimum element, let $\left\{f_i\right|F(i)\to S,i\in I\}$ be a family of involutive m-semilattice homomorphisms, and let $({(f_i)}_{i\in I},S)$ be the natural sink of the functor F. Then, $f_i=f_j\circ (F(u))$, i.e., Figure 15 commutes.

Figure 15. Natural sink diagram.

$\forall x={(x_i)}_{i\in I}\in {\displaystyle \coprod _{i\in I}}F(i)$, we define $\overline{f}:({\displaystyle \coprod _{i\in I}}F(i))/R\to S$ such that $\overline{f}(\left[x\right])={\displaystyle \underset{i\in I}{\bigvee }}{f}_i(x_i)$. Since $\left\{f_i(x_i)\right|i\in I,x_i\ne 0\}$ is a finite set, ${\displaystyle \underset{i\in I}{\bigvee }}\left\{f_i(x_i)\right|i\in I,x_i\ne 0\}\in S$; thus, the mapping is well defined.

From Theorem 13, we know that $({\displaystyle \coprod _{i\in I}}F(i),{\left\{{ϵ}_i\right\}}_{i\in I})$ is the coproduct of ${\left\{F(i)\right\}}_{i\in I}$ in $IMCSLat{t}_0$, and there exists a unique involutive m-semilattice homomorphism $\widehat{f}:{\displaystyle \coprod _{i\in I}}F(i)\to S$ satisfying $f_i=\widehat{f}\circ {ϵ}_i$; then, Figure 16 commutes.

Figure 16. Coproduct diagram.

Let $△=\{(y,y)|y\in S\}$, $\forall u:i\to j\in Mor(I)$, $\forall x\in F(i)$; then, $\widehat{f}({ϵ}_i(x))=f_i(x)=f_j(F(u)(x))=(\widehat{f}\circ {ϵ}_i)(F(u)(x))=\widehat{f}(({ϵ}_i\circ F(u))(x))$, i.e., $({ϵ}_i(x),{ϵ}_j(F(u)(x)))\in f^{-1}(△)$. Hence, $\tilde{R}=\bigcup \left\{({ϵ}_i(a),{ϵ}_j(F(u)(a)))\right|u:i\to j\in Mor(I),a\in D(i)\}\subseteq f^{-1}(△)$. Since R is the smallest involutive m-semilattice congruence relation that contains the set $\tilde{R}$, $R\subseteq f^{-1}(△)$.

$\forall x={\left(x_i\right)}_{i\in I},y={\left(y_i\right)}_{i\in I}\in {\displaystyle \coprod _{i\in I}}{F}_i$, if $(x,y)\in R$, then $(x,y)\in f^{-1}(△)$; hence, $\widehat{f}\left(x\right)=\widehat{f}\left(y\right)$. Therefore, ${\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left(y_i\right)={\displaystyle \underset{i\in I}{\bigvee }}{f}_i\left(x_i\right)$, which implies that $\overline{f}\left(\left[x\right]\right)=\overline{f}\left(\left[y\right]\right)$. Thus, the mapping $\overline{f}$ is well defined. $\forall i\in I$, $\forall z_i\in F\left(i\right)$, then $\overline{f}\left({\eta }_i\left(z_i\right)\right)=\overline{f}\left((\pi \circ {ϵ}_i)\left(z_i\right)\right)=\overline{f}\left(\left[{ϵ}_i\left(z_i\right)\right]\right)={\displaystyle \underset{j\in I}{\bigvee }}{f}_j\left({\left({ϵ}_i\left(z_i\right)\right)}_j\right)=f_i\left(z_i\right)$. Thus, $\overline{f}\circ {\eta }_i=f_i$; then, Figure 17 commutes.

Figure 17. Colimit diagram.

(3) We shall show that the mapping $\overline{f}:({\displaystyle \coprod _{i\in I}}F(i))/R\to S$ is an involutive m-semilattice homomorphism. $\forall x,y\in ({\displaystyle \coprod _{i\in I}}F(i))/R$, we have

(i) $\overline{f}(\left[x\right]\vee \left[y\right])=\overline{f}([x\vee y])={\displaystyle \underset{i\in I}{\bigvee }}{f}_i({(x\vee y)}_i)={\displaystyle \underset{i\in I}{\bigvee }}(f_i(x_i)\vee f_i(y_i))=({\displaystyle \underset{i\in I}{\bigvee }}{f}_i(x_i))\vee ({\displaystyle \underset{i\in I}{\bigvee }}{f}_i(y_i))=\overline{f}(\left[x\right])\vee \overline{f}(\left[y\right])$; then, $\overline{f}(\left[x\right]\vee \left[y\right])=\overline{f}(\left[x\right])\vee \overline{f}(\left[y\right])$.

(ii) $\overline{f}(\left[x\right]·\left[y\right])=\overline{f}([x·y])={\displaystyle \underset{i\in I}{\bigvee }}{f}_i({(x·y)}_i)={\displaystyle \underset{i\in I}{\bigvee }}{f}_i(x_i·y_i)={\displaystyle \underset{i\in I}{\bigvee }}(f_i(x_i)·f_i(y_i))$. By Definition 19, we know that ${\displaystyle \underset{i\in I}{\bigvee }}(f_i(x_i)·f_i(y_i))=({\displaystyle \underset{i\in I}{\bigvee }}{f}_i(x_i))·({\displaystyle \underset{i\in I}{\bigvee }}{f}_i(y_i))=\overline{f}(\left[x\right])·\overline{f}(\left[y\right])$. Hence, $\overline{f}(\left[x\right]·\left[y\right])=\overline{f}(\left[x\right])·\overline{f}(\left[y\right])$.

(iii) $\overline{f}(\left[x^{*}\right])={\displaystyle \underset{i\in I}{\bigvee }}{f}_i({(x^{*})}_i)={\displaystyle \underset{i\in I}{\bigvee }}{f}_i(x_i^{*})={\displaystyle \underset{i\in I}{\bigvee }}{(f_i(x_i))}^{*}={({\displaystyle \underset{i\in I}{\bigvee }}{f}_i(x_i))}^{*}={(\overline{f}(\left[x\right]))}^{*}$; then, $\overline{f}(\left[x^{*}\right])={(\overline{f}(\left[x\right]))}^{*}$.

(4) We will prove the uniqueness of the involutive m-semilattice homomorphism $\overline{f}:({\displaystyle \coprod _{i\in I}}F(i)/R\to S$ that satisfies the conditions $f_i=\overline{f}\circ {\eta }_i$. Assuming that $\tilde{f}:({\displaystyle \coprod _{i\in I}}F(i))/R\to S$ is another involutive m-semilattice homomorphism that satisfies $f_i=\tilde{f}\circ {\eta }_i$, then $\tilde{f}(\left[x\right])=\tilde{f}(\pi (x))=\tilde{f}(\pi ({\displaystyle \underset{i\in I}{\bigvee }}{ϵ}_i(x_i)))=\tilde{f}({\displaystyle \underset{i\in I}{\bigvee }}(\pi ({ϵ}_i(x_i))))=\tilde{f}({\displaystyle \underset{i\in I}{\bigvee }}\left[x_i\right])={\displaystyle \underset{i\in I}{\bigvee }}\tilde{f}(\left[x_i\right])={\displaystyle \underset{i\in I}{\bigvee }}\tilde{f}((\pi \circ {ϵ}_i)(x_i))={\displaystyle \underset{i\in I}{\bigvee }}\tilde{f}({\eta }_i(x_i))={\displaystyle \underset{i\in I}{\bigvee }}(\tilde{f}\circ {\eta }_i)(x_i)={\displaystyle \underset{i\in I}{\bigvee }}{f}_i(x_i)=\overline{f}(\left[x\right])$. Hence, $\tilde{f}=\overline{f}$.

From (1), (2), (3), and (4), it can be concluded that $({({\eta }_i)}_{i\in I},({\displaystyle \coprod _{i\in I}}F(i))/R)$ is the colimit of the functor F. □

Corollary 1. 

$IMCSLat{t}_0$ is cocomplete.

5. The Inverse Limit and Direct Limit in $\mathit{IMSLatt}$

Definition 23. 

Let I be a downward-directed set; then, I can be taken for a category, where its objects are the elements in I. Let $i,j\in I$; if $i\le j$, then a morphism $u_{ij}:i\to j$ is taken naturally in the category I.

A functor $F:I\to IMSLatt$ is called an inverse system in the category of involutive m-semilattices. An inverse system in IMSLatt can be described by the following statements without using the notion of a functor. Let I be a downward-directed set. For any $i,j\in I$ and $i\le j$, there exists an involutive m-semilattice homomorphism $f_{ij}:S_i\to S_j$. Further, $f_{ij}=f_{jk}·f_{ik}$ for all $i,j,k\in I$ satisfying $i\le j\le k,f_{ii}=i{d}_{S_i}:S_i\to S_i$. The triple $(S_i,f_{ij},I)$ is called an inverse system in IMSLatt.

Definition 24. 

Let I be a downward-directed set, and let $F:I\to IMSLatt$ be an inverse system in IMSLatt. Then, the limit of F is called the inverse limit of the inverse system $F:I\to IMSLatt$.

Dually, this holds for an upward-directed set in a direct system with a direct limit.

From the definitions of the inverse limit and direct limit in IMSLatt, it is clear that the inverse limits are defined to be particular limits, and direct limits are particular colimits. Inverse limits and directed limits have been extensively studied in some categories [27,34,35,36,37,38,39,40]. The following will give the inverse limit and direct limit in IMSLatt.

5.1. The Inverse Limit of the Inverse System in $IMSLatt$

Theorem 15 ([20]). 

Let I be a small category, and let $F:I\to IMSLatt$ be a functor; then, the limit of F is $(L,{\left(p_i\right)}_{i\in I})$, where $L=\{f\in {\displaystyle \prod _{i\in I}}F\left(i\right)|\forall u:i\to j\in Mor\left(I\right)$ such that $f\left(j\right)=F\left(u\right)\left(f\right(i\left)\right)\}$. $\forall i\in I$, $f\in {\displaystyle \prod _{i\in I}}F\left(i\right)$, the mapping $p_i:{\displaystyle \prod _{i\in I}}F\left(i\right)\to F\left(i\right)$ is projection, and $p_i\left(f\right)=f\left(i\right)$.

Theorem 16. 

Let I be a downward-directed set, and let $F:I\to IMSLatt$ be an inverse system in IMSLatt. Then, the inverse limit of inverse system F is $(T,{\left(p_i\right)}_{i\in I})$, where $T=\{{\left\{x_i\right\}}_{i\in I}\in {\displaystyle \prod _{i\in I}}F\left(i\right)|\forall i,j\in I,$ if $i\le j,$ then $\exists f_{ij}:F\left(i\right)\to F\left(j\right)\in Mor\left(IMSLatt\right)$ such that $f_{ij}\left(x_i\right)=x_j\}$, and $\forall i\in I$, $\forall x={\left(x_i\right)}_{i\in I}\in {\displaystyle \prod _{i\in I}}F\left(i\right)$, $p_i:{\displaystyle \prod _{i\in I}}F\left(i\right)\to F\left(i\right)$ is a projection (i.e., $p_i\left({\left(x_i\right)}_{i\in I}\right)=x_i$).

Proof. 

The proof of Theorem 16 is similar to the proof of Theorem 15 in Reference [20]. □

Suppose that $F:I\to IMSLatt$ and $G:I^{\prime }\to IMSLatt$ are two inverse systems in IMSLatt. Let $(T,{\left(p_i\right)}_{i\in I})$ and $(T^{\prime },{\left(p_i^{\prime }\right)}_{i\in I})$ be the inverse limits of inverse systems F and G, respectively, where I and $I^{\prime }$ are downward-directed sets.

$\forall i,j\in I$, $\forall i^{\prime },j^{\prime }\in I^{\prime }$, $F\left(i\right)=S_i$, $F\left(i^{\prime }\right)=S_{i^{\prime }}$ are involutive m-semilattices. If $i\le j$ and $i^{\prime }\le j^{\prime }$, then $F(i\to j)=F_{ij}:F\left(i\right)\to F\left(j\right)$ and $G(i^{\prime }\to j^{\prime })=G_{i^{\prime }{j}^{\prime }}:F\left(i^{\prime }\right)\to F\left(j^{\prime }\right)$ are involutive m-semilattice homomorphisms. $\forall i,j,k\in I$, $\forall i^{\prime },j^{\prime },k^{\prime }\in I^{\prime }$, if $i\le j\le k$ and $i^{\prime }\le j^{\prime }\le k^{\prime }$, $F_{jk}·F_{ij}=F_{ik}$, $G_{j^{\prime }{k}^{\prime }}·G_{i^{\prime }{j}^{\prime }}=G_{i^{\prime }{k}^{\prime }}$, $F_{ii}=i{d}_{F\left(i\right)}$, $G_{i^{\prime }{i}^{\prime }}=i{d}_{G\left(i^{\prime }\right)}$. The homomorphisms $F_{ij}$ and $G_{i^{\prime }{j}^{\prime }}$ are called the bonding mappings of the inverse systems F and G, respectively.

Definition 25 ([36]). 

Let I be a downward-directed set, and $I^{\prime }\subseteq I$. If $\forall i\in I$, there is $i^{\prime }\in I^{\prime }$ such that $i^{\prime }\le i$, and the set $I^{\prime }$ is called a downward cofinal subset of I.

Based on Definition 3.1 in [37], the definition of the mapping between two inverse systems can be given as follows.

Definition 26. 

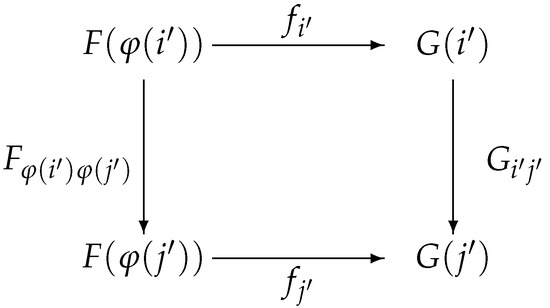
Let $F:I\to IMSLatt$ and $G:I^{\prime }\to IMSLatt$ be two inverse systems in IMSLatt. $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ is called the mapping from inverse system F to inverse system G if it satisfies the following conditions:

(1) $\phi :I^{\prime }\to I$ is an order-preserving mapping and $\phi \left(I^{\prime }\right)$ is a downward cofinal subset of I.

(2) $\forall i^{\prime }\in I^{\prime }$, $f_{i^{\prime }}:F\left(\phi \left(i^{\prime }\right)\right)\to G\left(i^{\prime }\right)$ is an involutive m-semilattice homomorphism, and $\forall i^{\prime },j^{\prime }\in I^{\prime }$, if $i^{\prime }\le j^{\prime }$, then $G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }}=f_{j^{\prime }}\circ F_{\phi \left(i^{\prime }\right)\phi \left(j^{\prime }\right)}$, i.e., Figure 18 commutes.

Figure 18. Commutative square.

Theorem 17. 

Let $F:I\to IMSLatt$ and $G:I^{\prime }\to IMSLatt$ be two inverse systems in IMSLatt. $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ is the mapping from inverse system F to inverse G. Then, the mapping $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ induces an involutive m-semilattice homomorphism $f:T\to T^{\prime }$, where $\forall x={\left(x_i\right)}_{i\in I}\in T$, $f\left(x\right)=f\left({\left(x_i\right)}_{i\in I}\right)={\left(x_{i^{\prime }}^{\prime }\right)}_{i^{\prime }\in I^{\prime }}=x^{\prime }\in T^{\prime }$, $x_{i^{\prime }}^{\prime }=(f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left({\left(x_i\right)}_{i\in I}\right)$, and $p_i:{\displaystyle \prod _{i\in I}}F\left(i\right)\to F\left(i\right)$ is a projection (i.e., $p_i\left({\left(x_i\right)}_{i\in I}\right)=x_i$).

Proof. 

$\forall i^{\prime },j^{\prime }\in I^{\prime }$, if $i^{\prime }\le j^{\prime }$, then $\phi \left(i^{\prime }\right)\le \phi \left(j^{\prime }\right)$. $\forall x={\left(x_i\right)}_{i\in I}\in T$, by Definition 26(2) and Theorem 16, we know that $(G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }})\left(x_{\phi \left(i^{\prime }\right)}\right)=(f_{j^{\prime }}\circ F_{\phi \left(i^{\prime }\right)\phi \left(j^{\prime }\right)})\left(x_{\phi \left(i^{\prime }\right)}\right)$; then, $F_{\phi \left(i^{\prime }\right)\phi \left(j^{\prime }\right)}\left(x_{\phi \left(i^{\prime }\right)}\right)=x_{\phi \left(j^{\prime }\right)}=p_{\phi \left(j^{\prime }\right)}\left({\left(x_i\right)}_{i\in I}\right)$. Thus, $G_{i^{\prime }{j}^{\prime }}\left(x_{i^{\prime }}^{\prime }\right)=G_{i^{\prime }{j}^{\prime }}\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left({\left(x_i\right)}_{i\in I}\right)\right)=(G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left({\left(x_i\right)}_{i\in I}\right)=(G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }})\left(p_{\phi \left(i^{\prime }\right)}{\left(x_i\right)}_{i\in I}\right)=(G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }})\left(x_{\phi \left(i^{\prime }\right)}\right)=(f_{j^{\prime }}\circ F_{\phi \left(i^{\prime }\right)\phi \left(j^{\prime }\right)})\left(x_{\phi \left(i^{\prime }\right)}\right)=(f_{j^{\prime }}\circ p_{\phi \left(j^{\prime }\right)})\left({\left(x_i\right)}_{i\in I}\right)=x_{j^{\prime }}^{\prime }$. This implies that there exists an involutive m-semilattice homomorphism $G_{i^{\prime }{j}^{\prime }}:G_{i^{\prime }}\to G_{j^{\prime }}$ such that $G_{i^{\prime }{j}^{\prime }}\left(x_{i^{\prime }}^{\prime }\right)=x_{j^{\prime }}^{\prime }$. From Theorem 16, it follows that $x^{\prime }={\left(x_{i^{\prime }}^{\prime }\right)}_{i^{\prime }\in I^{\prime }}\in T^{\prime }$. Hence, f is well defined.

$\forall x={\left(x_i\right)}_{i\in I},y={\left(y_i\right)}_{i\in I},z={\left(z_i\right)}_{i\in I}\in T$, $\forall i\in I^{\prime }$; then,

(1) ${\left(f(x\vee y)\right)}_{i^{\prime }}=(f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})(x\vee y)=f_{i^{\prime }}{\left((x\vee y)\right)}_{\phi \left(i^{\prime }\right)})=\left(f_{i^{\prime }}\left(x_{\phi \left(i^{\prime }\right)}\right)\right)\vee \left(f_{i^{\prime }}\left(y_{\phi \left(i^{\prime }\right)}\right)\right)=\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(x\right)\right)\vee \left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(y\right)\right)={\left(f\left(x\right)\right)}_{i^{\prime }}\vee {\left(f\left(y\right)\right)}_{i^{\prime }}={(f\left(x\right)\vee f\left(y\right))}_{i^{\prime }}$. This implies that $f(x\vee y)=f\left(x\right)\vee f\left(y\right)$. Thus, f preserves the union.

(2) ${\left(f(h_1·h_2)\right)}_{i^{\prime }}=(f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})(x·y)={\left(f_{i^{\prime }}(x·y)\right)}_{\phi \left(i^{\prime }\right)}=\left({\left(f_{i^{\prime }}\left(x\right)\right)}_{\phi \left(i^{\prime }\right)}\right)·\left({\left(f_{i^{\prime }}\left(y\right)\right)}_{\phi \left(i^{\prime }\right)}\right)=\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(x\right)\right)·\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(y\right)\right)={(f\left(x\right)·f\left(y\right))}_{i^{\prime }}$. This shows that $f(x·y)=f\left(x\right)·f\left(y\right)$. Thus, f preserves the semigroup operation ·.

(3) ${\left(f\left(z^{*}\right)\right)}_{i^{\prime }}={\left(f_{i^{\prime }}\left(z^{*}\right)\right)}_{\phi \left(i^{\prime }\right)}={\left({\left(f_{i^{\prime }}\left(z\right)\right)}_{\phi \left(i^{\prime }\right)}\right)}^{*}={\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(z\right)\right)}^{*}={\left({\left(f\left(z\right)\right)}_{i^{\prime }}\right)}^{*}={\left({\left(f\left(z\right)\right)}^{*}\right)}_{i^{\prime }}$. Thus, f preserves the involution operation *.

Therefore, the mapping f is an involutive m-semilattice homomorphism. □

Definition 27. 

Let $F:I\to IMSLatt$ and $G:I^{\prime }\to IMSLatt$ be two inverse systems in IMSLatt. Let $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ be a mapping from the inverse F to the inverse G. Then, the morphism $f:T\to T^{\prime }$ induced above is called the limit mapping. It can be denoted by $lim(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$.

Theorem 18. 

Let $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ be a mapping from the inverse F to the inverse G. For any $i^{\prime }\in I^{\prime }$, if $f_{i^{\prime }}$ is a monomorphism, then the induced mapping $f:T\to T^{\prime }$ is also a monomorphism.

5.2. The Direct Limit of the Direct System on IMSLatt

Definition 28 ([26]). 

Let I be a set; if every subset of I has an upper bound, then I is called upward-bound.

Definition 29. 

Let I be a upward-bound set. The functor $D:I\to IMSLatt$ is called a direct system in IMSLatt, where $\forall i,j\in I$, $D\left(i\right)=S_i$ and $D\left(j\right)=S_j$; if $i\le j$, then $D(i\to j)=f_{ij}:S_i\to S_j$ is an involutive m-semilattice homomorphism. For the convenience of the following description, let $f_{ij}$ denote the mapping $D(i\to j)=f_{ij}:S_i\to S_j$.

Lemma 4. 

Let $U:IMSLatt\to Set$ be a forgetful functor, and let $(u_i,S)$ be the coproduct of ${\left\{U\left(S_i\right)\right\}}_{i\in I}$ in the category of sets (i.e., the disjoint union of sets ${\left\{U\left(S_i\right)\right\}}_{i\in I}$). The binary relation $"\sim "$ on S is defined by the following: $x,y\in S,$ such that $x\in U\left(S_i\right)$, $y\in U\left(S_j\right)$, $x\sim y$ if, and only if, there is a $k\in K$ such that $i\le k,j\le k$, and $f_{ik}\left(x\right)=f_{jk}\left(x\right)$. Let $\overline{S}=S/\sim$ represent the equivalence class of S under relation "∼"; the order relation and three operations on S are defined by the following:

$\forall \left[x\right],\left[y\right]\in \overline{S}$, such that $x\in S_i$ and $y\in S_j$,

(1) $\left[x\right]\le \left[y\right]$ if, and only if, there is a $k\in I$ that satisfies $i,j\le k$ and $f_{ik}\left(x\right)\le f_{jk}\left(x\right)$.

(2) $\left[x\right]\vee \left[y\right]=[f_{ik}\left(x\right)\vee f_{jk}\left(y\right)]$.

(3) $\left[x\right]·\left[y\right]=[f_{ik}\left(x\right)·f_{jk}\left(y\right)]$.

(4) ${\left(\left[x\right]\right)}^{*}=\left[f_{ik}\left(x^{*}\right)\right]$.

Then, $(\overline{S},\vee ,·,*)$ is an involution m-semilattice.

Proof. 

The proof of this theorem is similar to the proof of Proposition 2 in Reference [40]. □

Theorem 19. 

Let I be an upward-bound set, and let $D:I\to IMSLatt$ be a direct system in IMSLatt. $\forall i,j\in I$, if $i\le j$, and $D(i\to j)=f_{ij}:S_i\to S_j$ is an involutive m-semilattice homomorphism, then the direct limit of direct system D is $(l_i,\overline{S})$, where $\overline{S}$ is defined above in Lemma 5, $l_i=\pi \circ u_i:A_i\to S_i$, and the mapping $\pi :S\to S/\sim$ represents the projection from S to its equivalence class $S/\sim$.

Proof. 

The proof of this theorem is similar to the proof of Theorem 14. □

Corollary 2. 

IMSLAtt is directed and complete.

Theorem 20. 

Let I be an upward-bound set, let functor $D:I\to IMSLatt$ be a direct system in IMSLatt, and let $(l_i,\overline{S})$ be the direct limit of direct system D. $\forall i,j\in I$, if $i\le j$, mapping $f_{ij}=D(i\to j):S_i\to S_j$ is a monomorphism; then, $l_i$ is also a monomorphism.

Proof. 

Let $x,y\in S_i$, $l_i\left(x\right)=l_i\left(y\right)$. Figure 19 commutes. Then, $l_j\left(f_{ij}\left(x\right)\right)=l_i\left(x\right)=l_i\left(y\right)=l_j\left(f_{ij}\left(x\right)\right)$. Since mapping $f_{ij}=D(i\to j):S_i\to S_j$ is a monomorphism. Thus, $\left[f_{ij}\left(x\right)\right]=\left[f_{ij}\left(y\right)\right]$, i.e., $f_{ij}\left(x\right)\sim f_{ij}\left(y\right)$. Because I be an upward-bound set, there exists $k\in I$ such that $i.j\le k$, $f_{jk}\left(f_{ij}\left(x\right)\right)=f_{jk}\left(f_{ij}\left(y\right)\right)$. Since mapping $f_{jk}=D(j\to k):S_j\to S_k$ is a monomorphism. Then, $f_{ij}\left(x\right)=f_{ij}\left(y\right)$. This means that $x=y$. Thus, $l_i$ is a monomorphism. □

Figure 19. Commutative triangle.

6. Conclusions

This paper mainly conducts an in-depth study on the properties of the category of involutive m-semilattices. The concepts of the nucleus and congruence are introduced. The concrete structure of a coequalizer in the category of involutive m-semilattices is obtained. It is shown that the category of involutive m-semilattices is algebraic. Based on the study of limits, we conduct a systematic investigation of limits within the category of involutive m-semilattices, obtaining the specific forms of colimits, inverse limits, and directed limits. These findings expand new horizons for the study of involutive m-semilattice theory and provide a theoretical foundation for the research on the applications of involutive m-semilattices. The research ideas and methods presented in this paper hold application value in the study of lattice structures, topological structures, fuzzy mathematics, rough sets, and logical algebra, among others, which represent the directions for future research.