Abstract
A rational exchange protocol is a type of e-commerce protocol that aims to maximize the participants’ own interests. The Buttyan model is commonly used to analyze the security of such protocols. However, this model has limitations in dealing with uncertainties and false messages in rational exchanges. To address these shortcomings, this paper proposes a formal analysis method based on Bayesian games. By incorporating participants’ types and beliefs, the Buttyan model is extended to enhance its ability to express uncertainties. Additionally, attack messages are introduced to simulate the potential fraudulent behaviors that participants may exploit through the security vulnerabilities in the protocol. Finally, the improved model is applied to conduct a formal analysis of a rational electronic contract signing protocol, and it is found that the protocol meets the usability requirements. The results show that this method can be effectively applied to the security analysis of rational exchange protocols, thereby enhancing the security of the e-commerce transaction process.
1. Introduction
Rational exchange protocols are a special type of cryptographic protocol [1]. In the absence of a trusted third party (TTP), they ensure secure and fair transactions among self-interested participants through game theory. These protocols are widely used in various fields such as electronic contracts [2,3], micropayment systems, secure communications, online voting, and auctions. They improve transaction efficiency and security while reducing dependence on trusted third parties. Currently, research on game theory-based cryptography mainly focuses on three areas: rational exchange protocols, rational secret sharing [4,5], and rational secure multi-party computation [6,7].
In [8], Syverson first proposed the concept of rational exchange and designed the Syverson protocol, a rational exchange protocol based on weak bit commitment functions. Buttyan [9] analyzed rational exchange protocols using a basic game-theoretic formal model, defining rational exchange and exploring its relationship with fair exchange. They also proved the rationality of the Syverson protocol under the assumption of a reliable network. Subsequently, Almudena Alcaide [10,11] proposed a rational exchange protocol model based on the Bayesian game theory, extending the Buttyan model and first proposing a rational fair exchange protocol for multiple parties. These studies mainly focused on the fairness of the exchange results, without covering the fairness during the protocol process.
Bayesian games are games of incomplete information. Munyque Mittelmann [12] first studied the formal verification of Bayesian mechanisms through strategy reasoning, using the probabilistic strategy logic (PSL) framework to transform the verification problem into a PSL model checking problem. Liu [13] proposed a generalized method to solve the Perfect Bayesian Nash Equilibrium (PBNE) in practical network attack and defense scenarios. Many researchers have designed a series of effective incentive schemes based on Bayesian games [14,15]. In addition, some scholars have applied Bayesian games to LoRa networks to defend against link flooding attacks [16,17].
The Buttyan model has built a game-theoretic mathematical framework for the analysis of rational exchange protocols. However, it has certain limitations in dealing with uncertainties and false messages in rational exchanges. These limitations may lead to inaccurate assessments of the protocol’s robustness, reliability, and adaptability and may even cause incorrect decisions and behavioral deviations during the protocol execution process. Therefore, this paper improves the Buttyan model based on its shortcomings. The main contributions are as follows:
- Based on Bayesian games, the Buttyan model is extended by incorporating participant types and beliefs, enhancing the expression of uncertainties.
- Introduce attack messages to simulate the potential fraudulent behaviors that participants may exploit through security vulnerabilities in the protocol.
- Taking the rational electronic contract signing protocol as an example, the improved model is used to formally analyze it, resulting in a set of clear judgment conditions to assess whether users follow the protocol agreement for transactions.
The rest of this paper is arranged as follows: Section 2 reviews the rational exchange protocol model and the application of game theory in network security. Section 3 introduces the basic knowledge of game theory and the Buttyan model. Section 4 proposes an improved Buttyan model. Based on the Bayesian game, the Buttyan model is extended and improved by incorporating participant types and beliefs and introducing attack messages . Section 5 applies the improved model to formally analyze the rational electronic contract signing protocol. Section 6 compares it with other existing security models and discusses the limitations of the model. Section 7 summarizes the research results and elaborates on future research directions.
2. Related Work
This section introduces the application of the rational exchange protocol model and game theory in network security, which provides the theoretical basis and research background for the improved Buttyan model proposed in this paper.
2.1. Rational Exchange Protocol Model
The rational exchange protocol model is an important research direction in the field of e-commerce and network security. The early model proposed by Buttyan and Alcaide did not involve the fairness analysis of the protocol process. To this end, Ding et al. [18] proposed a rational exchange protocol model based on a mixed strategy, which used the mixed strategy theory of an extended game to simulate the exchange protocol and entropy theory to describe the fairness in the exchange process. However, it did not consider the situation where the network is unreliable and the process is not strictly fair. Tao et al. [19] proposed a model for analyzing the Internet of Things (IoT) protocol based on an incomplete information extended game, defined rationality and fairness properties, and verified these properties using tree analysis methods and linear time algorithms. Although the aforementioned studies provide an important theoretical basis for understanding the security and fairness of rational exchange protocols, none of them consider the risks posed by attack messages.
2.2. Application of Game Theory in Network Security
Game theory is widely used in network security, especially in blockchain [20], wireless sensor networks [21,22], and multi-agent systems [23]. Existing blockchain-related reviews do not discuss the application of game theory in depth. Some reviews only focus on blockchain security and privacy issues or the combination of blockchain with the Internet of Things and edge computing. In this regard, the literature [24] classified and reviewed the specific models and application scenarios of game theory in blockchain, filling the gap in the systematic analysis of the application of game theory in blockchain, mining management, and economic models. Chen [25] proposed an incentive-compatible rational secret sharing scheme based on blockchain and smart contracts. By redesigning the secret-sharing process, introducing incentive mechanisms, and adding verifiers, it solved the prisoner’s dilemma problem faced by rational participants in secret sharing. The application of game theory in wireless sensor networks has involved clustering and power control but has not combined state-switching thresholds and penalty mechanisms. Therefore, Yan [26] proposed an idle listening-sleep state switching model based on game theory and introduced a penalty mechanism to suppress node selfish behavior. Tian [27] proposed a one-time rational secret sharing scheme based on a Bayesian game, which solved the cooperation problem in one-time rational secret sharing and achieved perfect Bayesian equilibrium. Although this method has advantages in dealing with information asymmetry and participant uncertainty, it has high communication overhead. These studies show that game theory provides a powerful tool for the design and analysis of network security protocols.
3. Fundamentals
3.1. Game Theory
Game theory is a mathematical theory that studies the strategic interactions among decision-makers (participants or players) with characteristics of conflict and cooperation, where each participant attempts to maximize their own interests by selecting the optimal strategy. The main concepts related to game theory are as follows:
- 1.
- Utility Function
The utility function is a measure of the payoff or degree of satisfaction for each participant given a combination of strategies, usually denoted by . For a given sequence of terminal actions , the utility function of participant can be expressed as
where and are the payoff and loss (cost) of participant when executing the sequence of terminal actions , respectively.
- 2.
- Nash Equilibrium
In a game, if each participant’s strategy is optimal given the strategies of the other participants, this combination of strategies constitutes a Nash equilibrium. It can be formally represented as: for a game with participants, if the strategy combination is a Nash equilibrium, then for the participant , there is
where is the utility function of participant , is the strategy combination of participant in the equilibrium state, is the strategy combination of the other participants in the equilibrium state, and is the strategy set of participant .
3.2. The Buttyan Model
The Buttyan model [9] is a mathematical model based on game theory, proposed by Levente Buttyan et al., to analyze and define rational exchange protocols, especially for the analysis of the Syverson protocol. The model constructs an extensive-form game [28] through a series of elements to describe the interactions between protocol participants, which can be represented by a six-tuple to indicate a rational exchange protocol , where
- is the set of participants, including all individuals involved in the protocol. It can be expressed as , where and represent the two parties involved in the protocol, and represents the network used by participants for communication, which is assumed to be fully reliable in this model.
- is the set of actions for participants, including all possible actions that participants can take at each stage of the game. Protocol participants face three basic strategic choices: first, to follow the protocol and send honest messages ; second, to engage in deceptive behavior by sending false messages ; and third, to withdraw from the protocol .
- is the set of action sequences. For any action , indicates the action following the non-terminal action sequence , and represents the set of optional actions for participant following the non-terminal action sequence . If is a terminal action sequence, it indicating the end of the protocol execution. The empty sequence is also a subset of the action sequence set, representing the starting point of the game. The Buttyan model does not allow protocol parties to run multiple protocol instances simultaneously; that is, it does not consider interleaving attacks.
- is the information set for participant . For any two non-terminal action sequences and , if and , then and belong to the same information set of participant .
- is the participant function used to determine which participant should take the next action following a non-terminal action sequence. It can be expressed as: , where is the terminal action sequence. For any non-terminal action sequence , indicates which participant will take the next action following sequence .
- is the preference relation for participant . It indicates the preference ranking of each participant for different outcomes, describing the rational behavior of participants in the protocol, that is, the tendency to choose actions that can maximize their own interests.
4. The Extension of the Buttyan Model
4.1. The Shortcomings of the Buttyan Model
Although the Buttyan model has demonstrated certain capabilities in formally analyzing rational exchange protocols, a deeper investigation reveals that it is essentially a framework with many limitations. Its shortcomings are mainly reflected in the following two aspects:
- 1.
- Lack of ability to handle uncertainties.
First, in the Buttyan model, action sequences are indistinguishable to participants and belong to the same information set. This means that the protocol participants have complete information about the structure of the game. However, in reality, information is often asymmetric. Participants may not fully understand the strategies or payoff functions of other participants. Therefore, using a complete information game is not realistic in actual operation. Second, the model assumes that the network is reliable, meaning that all messages can be accurately delivered within the scheduled time. However, in practical applications, the network may be unreliable. Messages may be delayed, lost, or tampered with. Therefore, when conducting security analysis, the trust level in other participants and the reliability of the network are two key factors that must be considered comprehensively to ensure the comprehensiveness and accuracy of the analysis.
- 2.
- There are certain limitations in describing the malicious behaviors of participants, and the handling of false messages is not sufficient.
Figure 1 shows the interaction process of the Syverson protocol, where and represent the sender and receiver of the protocol, respectively. In this protocol, the items exchanged by the two parties are marked as and , where is a description of , is an encryption algorithm that encrypts the message with key , and is a temporary secret commitment function used to keep the message confidential for a certain period of time (see reference [11] for details).
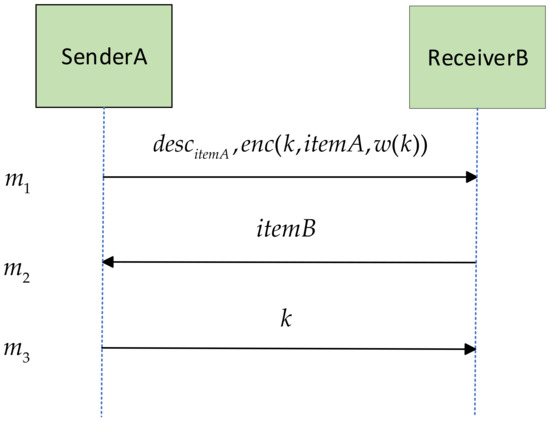
Figure 1.
Interaction process of the Syverson protocol.
Figure 2 shows the game tree description of the Syverson protocol by the Buttyan model. The nodes represent the participants of the protocol, and the lines between the nodes represent the actions taken (sending messages or exiting the protocol). Participants will have corresponding benefits at each leaf node (see reference [11] for details). In the first round of interaction of the Buttyan model analysis protocol, participant can not only transmit true information to participant but also send false message . Once sends a false message to , will always be punished by . This means that the Buttyan model presupposes that participants can identify all false messages. It only focuses on those false messages that participants can detect, without fully considering those that are not identified. In the actual operation of the protocol, participants’ detection capabilities may be limited by technology. At the same time, attackers continuously develop new attack methods and tools. These new methods and tools may not be widely recognized for a period of time, making it difficult for participants to update their detection mechanisms in time to identify these new types of false messages. Therefore, in reality, it is not possible to expect all false messages to be identified by participants . This limitation means that the Buttyan model needs further development and improvement.
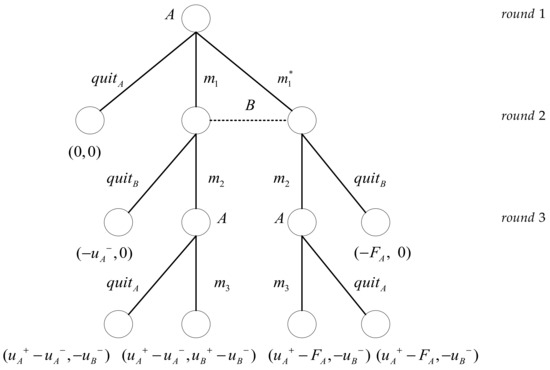
Figure 2.
Game tree description of the Syverson protocol by the Buttyan model.
The following are the main notational representations of the Buttyan model and the improved Buttyan model, as shown in Table 1.

Table 1.
Notational Representation.
4.2. The Improved Buttyan Model
4.2.1. Bayesian Game
To address the aforementioned shortcomings, a formal analysis method based on Bayesian games is proposed, which can more accurately simulate uncertainty and information asymmetry in the real world. The Buttyan model can be extended to an octuple: .
Definition 1.
Participant types and type spaces: If participant has a type , then is the type of combination of participants, and is the type combination space of participants, where is the type space of participant . Each participant may have multiple types, which determine their utility functions.
Definition 2.
Beliefs: Participants’ beliefs are represented in the form of probability distributions, which can be expressed using Greek letters such as , , , etc. Participant ’s belief about the types of other participants is expressed through a probability distribution over the type space of , and the set of all beliefs can be denoted by the letter .
The Bayesian game proposed in this paper is based on the framework of Bayesian rationality [11,29], which is used to reason and analyze rational exchange protocols. By introducing the concepts of participant types and beliefs, it can simultaneously incorporate the complete information game adopted by the Buttyan model and the unreliable network factors, thereby constructing a more complex and realistic model. Under this framework, participants do not fully understand the types of other participants. This uncertainty enhances the realism of the model. The types of participants are key factors in determining the payoffs participants receive in the protocol. Different types of participants may achieve different payoff outcomes under the same strategy choices, reflecting the impact of individual differences and information asymmetry in the real world on the decision-making process.
Moreover, “Nature” , as an abstract entity, is responsible for assigning a type to each participant. This process is randomly conducted based on the probability distribution over each participant’s type space, enabling the Bayesian game to more realistically reflect participants’ decision-making under uncertainty. Compared with the basic game-theoretic framework in the Buttyan model, the Bayesian game provides a richer and more realistic analytical tool.
To highlight the improvements of the model, we introduce the types and beliefs of the participants based on Figure 1, as shown in Figure 3. Nature randomly assigns types to participant , where , , …, represents the probability of assigning each type (Equation (3)), , , …, indicates that participant has types, and , , represent the probabilities of sending messages , and . During the protocol analysis, the network can be regarded as a participant of a specific type, and its behavior (such as the reliability of message transmission) can be uncertain. In the game tree, the leaf nodes symbolize the end of the protocol, while the other nodes (except for leaf nodes and Nature ) represent the decision points of the participants in the game process. The dashed lines indicate that participant does not know the actions or strategy choices of participant , reflecting the uncertainty of the game.
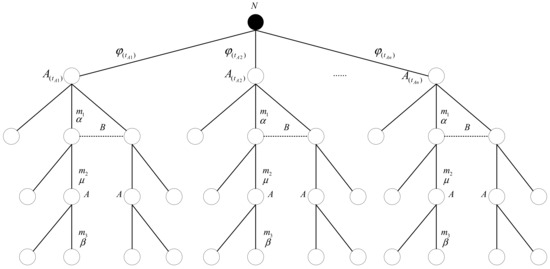
Figure 3.
The game tree description with the introduction of types and beliefs.
The probability distribution over is represented by , which can be expressed as
During the interaction of the protocol, participant may exploit the potential unknown vulnerabilities [30] in the protocol to send fraudulent messages to . Therefore:
Definition 3.
Attack message : During the transaction, a participant may send an attack message (such as a forged message) to another participant. Attack messages include false messages that the participant can identify and false messages that the participant cannot identify.
When sends an attack message to , for the recognizable false messages, can choose to exit the protocol . However, to ensure that does not commit fraud against again in the future, a certain punishment () will be given to . For the false messages that are not recognized by participant , since the content and specific form of the false messages are unknown to , may choose to continue the transaction or exit the protocol . In rational exchange protocols, and are rational participants who maximize their own interests. Therefore, in the third round of the interaction, will not send or to , but will directly exit the protocol . The introduction of the attack message not only enhances the model’s adaptability to reality but also provides a more comprehensive perspective for analyzing participants’ behavior when facing potential fraud, more accurately reflecting the content of the messages. The interaction diagram with the introduction of the attack message is shown in Figure 4.
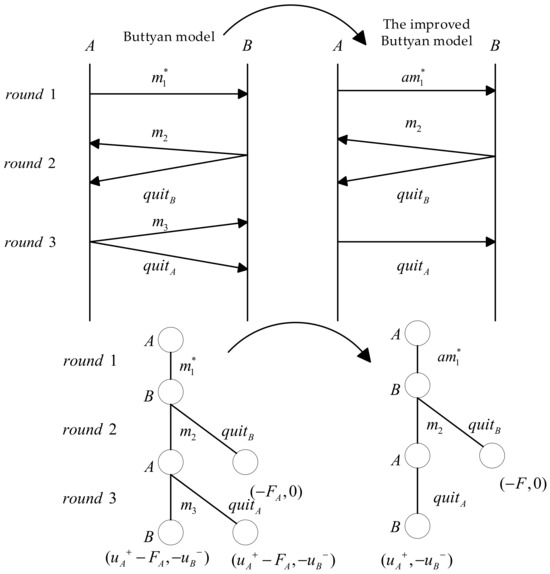
Figure 4.
The interaction diagram with the introduction of attack message .
4.2.2. Analysis Method
Based on the Buttyan model, this paper proposes two key improvements. The following is the flowchart of the improved Buttyan model for rational exchange protocol analysis, as shown in Figure 5. Appendix A shows a brief analysis process of the payment protocol based on the improved Buttyan model.
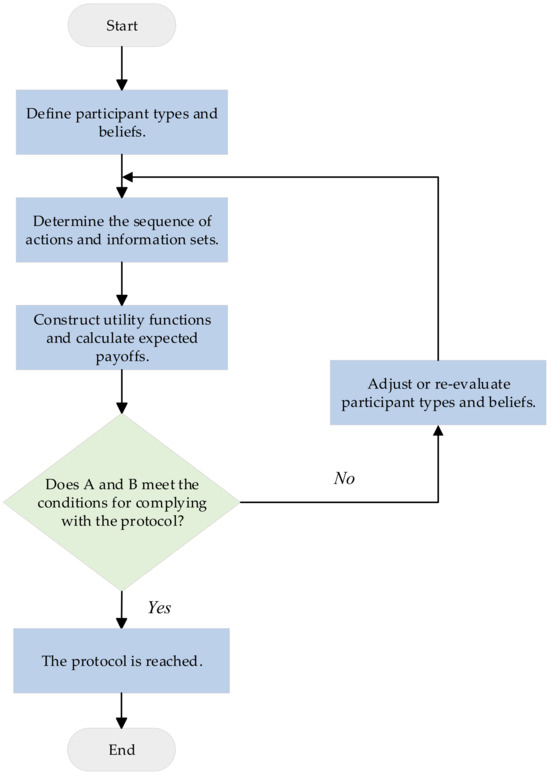
Figure 5.
Flowchart of Bayesian game analysis of the protocol.
The flowchart describes the process of protocol analysis: starting from the “Start” node, first define the participant type and belief, then determine the sequence of actions and information sets, then build the utility function and calculate the expected return, and then check whether participants and meet the conditions for complying with the protocol. If they do, the agreement is reached and the process ends; if not, it is necessary to adjust or re-evaluate the participant type and belief and then return to redetermine the sequence of actions and information sets until the conditions are met.
5. Formal Analysis of the Protocol
5.1. Description of the Rational Electronic Contract Signing Protocol
To further illustrate the improved Buttyan model, this paper takes the rational electronic contract signing protocol as an example [31] and provides a detailed analysis. It is assumed that user and user each have a private key and , and both are rational participants who do not rely on the involvement of the Contract Management Party (CMP). The specific content of the protocol is shown in Figure 6. Item is the description related to the contract signature . User encrypts with a random number to obtain . Items , , and represent the operation of the sender signing the message with their own private key. Essentially, this protocol is a rational exchange protocol aimed at achieving the exchange between and . It should be noted that during the signature transaction, may send an attack message (forged signature information) to .
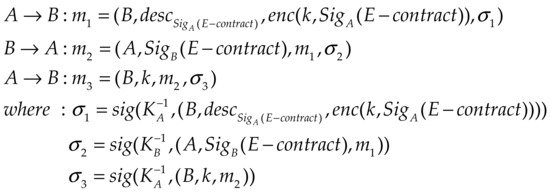
Figure 6.
Rational electronic contract signing protocol.
Table 2 shows the abbreviations and the meanings of some of the main notations in this chapter.

Table 2.
Abbreviations/main notations.
- Step 1 (): Participant sends and to , signs these pieces of information with , and then sends the entire message to .
- Step 2 (): Participant sends to . Since contains a copy of , can confirm that has received message .
- Step 3 (): Participant sends to . receives and uses it to decrypt the signature of the contract , thereby obtaining .
After the three-step electronic contract signing protocol is executed, both parties can obtain the contract signature from the other party, and the transaction is completed. As shown in Figure 5, participant takes on more unknown risks in the transaction process compared to . This is because first lose control of their digital signature, so should carefully evaluate factors such as the type and reputation of .
5.2. Participant Types and Action Sets
To facilitate the analysis of the protocol, this paper only considers the types of and . The participant can be divided into two categories: cooperative type and non-cooperative type . Participant has only one cooperative type, denoted as . It should be noted that the cooperative type may send false messages, and the non-cooperative type may also send true messages. Since sending message from to is agreed upon in advance by both parties of the protocol, and can also verify the correctness of , is always honest. The participant set of this protocol is , and the type combination space can be represented as . and represent the type spaces of participants and , respectively.
The action set of participants is composed of the action set of participant and the action set of participant , which can be represented as
Among them, represents the sending message , and represent the protocol exit operations executed by participants and , respectively, and indicates that the first message in the protocol is an attack message.
5.3. Beliefs and Strategies
Suppose is a probability distribution over , which can be represented as
The belief of is represented by a probability distribution over :
The belief of is represented by a probability distribution over :
In addition, based on maximizing its own interests, participant should also have the following belief:
In game theory, a strategy refers to the course of action that a participant takes during the game. The strategy profile can be represented as: .
The pure strategy of participant can be represented by a tuple:
where the elements in and represent the optional actions of participant in the first and third steps of the protocol, respectively, and the elements in represent the pure strategies of participant for the cooperative and non-cooperative types, respectively. When expanded, it can be obtained as
The pure strategy of participant can be represented as
where the elements in represent the optional actions of participant in the second step of the protocol.
5.4. Action Sequences and Information Sets
In this paper, taking the cooperative type as an example, the action sequence can be represented as
Then, the set of non-terminal sequences can be represented as
The participant function is used to determine the next participant in a nonterminal sequence, which can be represented as follows:
In this protocol, only takes actions in the first and third steps. Since has no prior information to refer to in the first step, the information set of is, and can only update its own information set after observing execute in the third step:
Participant takes action in the second step and cannot know the type of , so the information set of is represented as
5.5. Utility Functions and Expected Payoffs
In the rational electronic contract signing protocol mentioned above, to maintain the authenticity of the information, it can be assumed that: if sends an attack message to , and it is recognized by , then should be given a certain punishment ; if it is not recognized by , there will be no punishment. If sends a signature to , then will gain a profit ( will suffer a loss of profit ). If sends to , then will incur certain costs and suffer a certain loss of profit . Since is always honest, there is no punishment value for . If sends to , will gain a profit . Note that
For this protocol, the utility function can be represented as
where and are the profits of participants and , respectively, is the type space of , and is the terminal action sequence.
In each terminal action sequence , the pure profit of the cooperative type is as follows:
Table 3 and Table 4 show the payoff matrices of the cooperative types and , and non-cooperative types and , respectively. The horizontal axis represents the different pure strategies of and in the protocol, and the vertical axis represents the different pure strategies of in the protocol. The pure strategies of and together constitute each terminal action sequence in the protocol, and the table corresponds to the pure payoffs of each terminal action sequence and , and and , respectively.

Table 3.
The payoff matrix of and .

Table 4.
The payoff matrix of and .
Based on the improved Buttyan model, by setting the types and beliefs of participants and elaborately describing the action sequences, information sets, and payoffs, we can precisely represent the rational electronic contract signing protocol as a game tree, as shown in Figure 7.
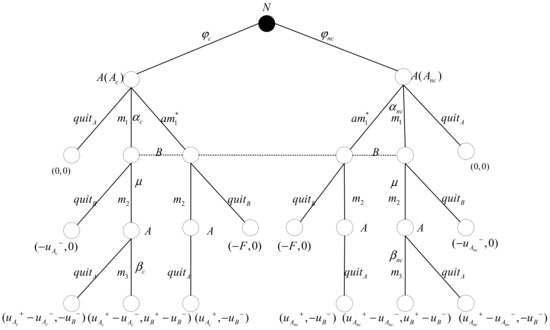
Figure 7.
Game tree description of the rational electronic contract signing protocol.
In the Buttyan model, the payoffs for when taking action sequences and are and , respectively. Participant will be penalized for sending the false message to , and the false information is assumed to be recognizable by . From the perspective of rational participants, false messages that can be recognized by do not need to be emphasized because will always choose to exit the protocol to safeguard their own interests. On the contrary, false messages that are not recognized by participant pose a potential threat to . Therefore, the focus of the analysis in this paper is on the false messages that are not recognized.
Different strategies correspond to different payoffs. The following will discuss the expected payoffs of participants and under different pure strategies. For participant :
From the expected payoffs mentioned above, when the type of is , to ensure that participant complies with the protocol rules and does not engage in fraudulent behavior, it is only necessary that:
That is,
When remains constant, increasing the penalty value means that the value of becomes larger. In other words, the probability of sending message will increase, which is more conducive to the successful completion of the protocol. Therefore, during the contract signing process, appropriately increasing the penalty for sending attack messages can effectively encourage users to comply with the protocol. However, an excessively large penalty may backfire, as participants may be deterred by the high penalty and become reluctant to participate, thereby affecting the success rate of the protocol.
When the penalty value remains unchanged, reducing the cost means that the value of becomes larger. Therefore, in the signing of small contracts (where the cost is low), user is more likely to comply with the protocol. However, in the signing of large contracts, user should be more cautious and improve their ability to identify false messages to ensure that both parties in the protocol comply as much as possible. This not only helps protect their own interests but also helps maintain the fairness and effectiveness of the contract.
Similarly, when the type of is , they will be more willing to comply with the protocol rules and avoid fraudulent behavior only when condition is satisfied. For participant :
It can be denoted that is represented by . To ensure that participant complies with the protocol rules, it is only necessary that , that is,
Assign a set of values to , , , , , , namely , , , , , . The calculated result is 0.6285. The five groups of strategies for ’s instances are shown in Table 5. The table shows the specific values of and under different instance numbers, as well as the ratio of and the corresponding strategy . For example, the value of in instance 1 is 3, the value of is 8, and the ratio is 0.375. At this time, 0.6285 > 0.3750, so ’s strategy is . In the first three groups of instances, is 8. As increases, the value of increases, and the possibility of choosing increases, which is not conducive to the agreement. In the last three groups of instances, is 6. As increases, the value of decreases, and is more willing to choose , which is more conducive to the agreement.

Table 5.
Strategy Table for ’s Instances.
The following conclusions can be drawn from the table:
When is fixed, the ratio of cost to benefit should be minimized as much as possible; that is, increasing the benefit and reducing the cost . When the ratio of cost to benefit decreases, will be more inclined to exchange signatures after weighing the pros and cons. On the one hand, increasing the benefit lets see more room for profit and development opportunities, enhancing the motivation to participate; on the other hand, reducing the cost lowers the participation threshold and potential risks for , alleviating concerns. This combined effect will effectively increase the success rate and execution efficiency of the protocol, promoting cooperation and win-win outcomes for both parties.
When is fixed, increasing the value of , that is, enhancing ’s trust in , makes more willing to exchange signatures, which is another important factor in promoting the successful conclusion of the protocol.
The following are the strategy diagrams for participant under parameter and participant under parameter , as shown in Figure 8. (a): When , participant adopts the pure strategy . (b): When , participant adopts the pure strategy . Both parties interactively sign and reach an agreement.
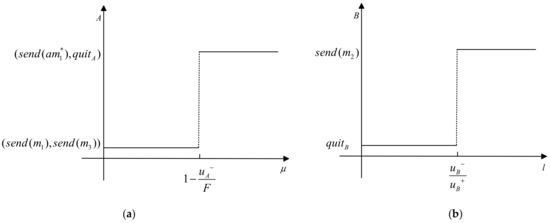
Figure 8.
(a) The strategy diagram of participant under parameter ; (b) The strategy diagram of participant under parameter .
In summary, both parties are willing to comply with the protocol rules only when and are satisfied simultaneously. In the process of signing electronic contract agreements, to ensure the cooperation and willingness of both parties, the agreement should include an appropriate penalty mechanism for sending false messages. In addition to this, it is also essential to enhance users’ ability to identify false messages. Furthermore, establishing a trust mechanism within the agreement can further strengthen both parties’ willingness to comply with the protocol.
6. Discussion
To better illustrate the advantages and unique features of our improved Buttyan model, we compare it with several existing security models, including the original Buttyan model, Alcaide’s rational exchange protocol model (referred to as the Alcaide model in this paper), Ding’s mixed strategy rational exchange protocol model (referred to as the Ding model in this paper), and Tao’s IoT protocol model (referred to as the Tao model in this paper). The comparison is conducted from multiple dimensions, such as handling uncertainty, handling false information, outcome fairness, process fairness, fraud prevention ability, and computational complexity. Table 6 shows the results of the comparison of different security models in multiple dimensions.

Table 6.
Comparison results of different security models.
- Handling uncertainty: The original Buttyan model assumes complete information and reliable networks, which is not realistic in real-life scenarios. Our model solves the problems of uncertainty and information asymmetry by introducing Bayesian games and increasing participant types and beliefs.
- Handling attack messages: None of the existing models adequately handle attack messages or potential fraud. Our model introduces attack messages to simulate and analyze potential vulnerabilities, enhancing the robustness of the protocol.
- Result and process fairness: While the original Buttyan and Alcaide models focus on outcome fairness, they ignore fairness in the protocol process. Our model ensures fairness of the results and processes by introducing Bayesian game and attack messages.
- Fraud prevention capability: The original model lacks processing of false messages. Our model enhances fraud prevention capabilities by introducing attack messages and penalties for sending false information.
This study proposes an improved Buttyan model that aims to formally analyze rational exchange protocols, with a particular focus on improving the model’s ability to handle uncertainty and potential fraud. By introducing participant types and beliefs, the model is extended to more accurately reflect the complexity of real-world scenarios. In addition, the introduction of attack messages further enhances the model’s ability to simulate and analyze potential security vulnerabilities. The improved model is applied to rational electronic contract signing protocols, and a set of judgment conditions for evaluating whether users follow the protocol is obtained.
However, an important limitation of our model is the assumption that participant is always honest. Although this assumption simplifies the analysis process, in real scenarios, participant may have an incentive to deviate from honest behavior. This limitation limits the applicability of the model in dealing with scenarios where participant may engage in fraudulent activities. Future research should consider relaxing this assumption and exploring mechanisms to deal with ’s dishonest behavior, such as introducing reputation mechanisms or additional cryptographic techniques to ensure the integrity of the protocol. In addition, the current model is only applicable to two-party protocols, and extending it to multi-party scenarios can provide a more comprehensive framework for analyzing complex e-commerce transactions. Through experiments and actual tests, the effectiveness of the model can be verified, and the direction of improvement can be further determined.
7. Conclusions and Future Work
This paper proposes an improved Buttyan model. Through Bayesian game theory, it incorporates participant types and beliefs, expands the Buttyan model, and enhances the model’s ability to express real-world uncertainties. In addition, attack messages are introduced to simulate the potential fraudulent behavior of participants exploiting protocol security vulnerabilities. Finally, taking the rational electronic contract signing protocol as an example, the paper demonstrates how to apply the improved model for formal analysis and derives clear judgment conditions to assess whether users follow the protocol for transactions. The improved model is more in line with actual operating conditions and provides theoretical support for the design and optimization of e-commerce protocols.
In future research, there are two main directions for development: First, the analysis method can be extended to multi-party exchange protocols to enhance the security of e-commerce protocols [32,33]. Second, while the existing model has achieved certain results in theoretical design, there are still some shortcomings in practical application. For example, when facing complex real-world scenarios, the current model may not fully consider practical factors such as network latency and irrational behavior of participants, thereby affecting its adaptability and stability. To further improve the model’s practical adaptability, it can be verified and tested through experiments and practical applications.
Author Contributions
Conceptualization, M.X. and K.Y.; methodology, L.C.; formal analysis, L.C.; investigation, L.C. and K.Y.; writing—original draft preparation, L.C.; writing—review and editing, M.X. and Z.L.; supervision, K.Y. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 62362033, 61962020), the Double Thousand Talent Plan of Jiangxi Province (No. jxsq2023201009), the Natural Science Foundation of Jiangxi Province (No. 20224ACB202006), and the Jiangxi Province Early Career Youth Science and Technology Talent Training Special Project (No. 20244BCE52146).
Data Availability Statement
The data supporting the findings of this study are available within the article.
Acknowledgments
The authors would like to express their sincere thanks to the reviewers for their valuable feedback and insightful comments.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This appendix briefly explains how to apply the improved Buttyan model to the analysis process of actual e-commerce protocols through an electronic payment case. For the specific application process, please refer to Section 5 of the main text.
Figure A1 shows the process of electronic payment. Both parties to the agreement are rational. Seller sends information such as item description and payment amount to the buyer , and then the buyer pays the seller, and the seller finally sends the item or service to the buyer.
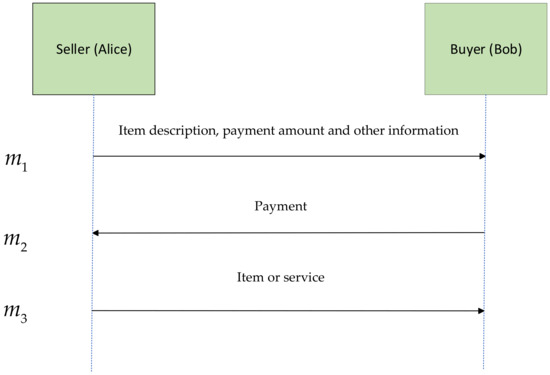
Figure A1.
Electronic payment process.
The improved Buttyan model in this paper mainly introduces participant types, beliefs, and attack messages. The details are as follows:
- Define the types of sellers and buyers: Sellers can be divided into cooperative types and non-cooperative types. In the process of electronic payment, since buyers only pay for goods, there is no equal description of buyers. There is only one cooperative type, and they remain honest;
- Define beliefs: In electronic contracts, naturally assigns types to sellers with a certain probability and represents the messages sent with a certain probability;
- Introduce attack messages: During the transaction, the seller may send an attack message (such as forged product information) to the buyer to mislead the buyer. Attack messages include false messages that the buyer can identify and false messages that the buyer cannot identify. For false messages identified by buyers, based on maximizing the interests of buyers, buyers should choose to exit the agreement in the second round; for false messages that cannot be identified, buyers continue to trade, and in the third round, based on maximizing the interests of sellers, sellers should choose to exit the agreement;
- Calculate expected benefits: According to probability and net benefits, the expected benefits of sellers and buyers can be calculated, respectively. By comparing expected benefits, the judgment conditions for reaching two sets of agreements can be obtained. These conditions ensure that participants have an incentive to follow the protocol given their beliefs and strategies.
- Through a series of steps, the improved Buttyan model is able to more accurately simulate uncertainty in reality, thus providing a more comprehensive perspective for the security analysis of electronic payment protocols.
References
- Shen, Y.; Shepherd, C.; Ahmed, C.M.; Shen, S.; Wu, X.; Ke, W.; Yu, S. Game-theoretic analytics for privacy preservation in Internet of Things networks: A survey. Eng. Appl. Artif. Intell. 2024, 133, 108449. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Pang, J.; Mauw, S. Game-based verification of contract signing protocols with minimal messages. Innov. Syst. Softw. Eng. 2012, 8, 111–124. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, Y.; Sangaiah, A.K.; Li, X.; Castiglione, A.; Zheng, X. CSP-E2: An abuse-free contract signing protocol with low-storage TTP for energy-efficient electronic transaction ecosystems. Inf. Sci. 2019, 476, 505–515. [Google Scholar] [CrossRef]
- Maitra, A.; De, S.J.; Paul, G.; Pal, A.K. Proposal for quantum rational secret sharing. Phys. Rev. A 2015, 92, 022305. [Google Scholar] [CrossRef]
- Harn, L.; Lin, C.; Li, Y. Fair secret reconstruction in (t, n) secret sharing. J. Inf. Secur. Appl. 2015, 23, 1–7. [Google Scholar] [CrossRef]
- Abate, A.; Gutierrez, J.; Hammond, L.; Harrenstein, P.; Kwiatkowska, M.; Najib, M.; Perelli, G.; Steeples, T.; Wooldridge, M. Rational verification: Game-theoretic verification of multi-agent systems. Appl. Intell. 2021, 51, 6569–6584. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, X.; Song, A.; Chen, W.-N.; Lai, K.-K.; Zhang, J.; Deng, R.H. Primpso: A privacy-preserving multiagent particle swarm optimization algorithm. IEEE Trans. Cybern. 2022, 53, 7136–7149. [Google Scholar] [CrossRef]
- Syverson, P. Weakly secret bit commitment: Applications to lotteries and fair exchange. In Proceedings of the 11th IEEE Computer Security Foundations Workshop, Rockport, MA, USA, 9–11 June 1998; pp. 2–13. [Google Scholar]
- Buttyán, L.; Hubaux, J.-P.; Čapkun, S. A formal model of rational exchange and its application to the analysis of Syverson’s protocol. J. Comput. Secur. 2004, 12, 551–587. [Google Scholar] [CrossRef]
- Alcaide, A.; Estevez-Tapiador, J.M.; Hernandez-Castro, J.C.; Ribagorda, A. A multi-party rational exchange protocol. In Proceedings of the On the Move to Meaningful Internet Systems 2007: OTM 2007 Workshops, Vilamoura, Portugal, 25–30 November 2007; pp. 42–43. [Google Scholar]
- Estevez-Tapiador, J.M.; Alcaide, A.; Hernandez-Castro, J.C.; Ribagorda, A. Bayesian rational exchange. Int. J. Inf. Secur. 2008, 7, 85–100. [Google Scholar] [CrossRef]
- Mittelmann, M.; Maubert, B.; Murano, A.; Perrussel, L. Formal verification of bayesian mechanisms. In Proceedings of the 37th AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 11621–11629. [Google Scholar]
- Liu, L.; Zhang, L.; Liao, S.; Liu, J.; Wang, Z. A generalized approach to solve perfect Bayesian Nash equilibrium for practical network attack and defense. Inf. Sci. 2021, 577, 245–264. [Google Scholar] [CrossRef]
- Cai, L.; Dai, Y.; Hu, Q.; Zhou, J.; Zhang, Y.; Jiang, T. Bayesian Game-Driven Incentive Mechanism for Blockchain-Enabled Secure Federated Learning in 6 G Wireless Networks. IEEE Trans. Netw. Sci. Eng. 2024, 11, 4951–4964. [Google Scholar] [CrossRef]
- Dahiya, A.; Gupta, B.B. A reputation score policy and Bayesian game theory based incentivized mechanism for DDoS attacks mitigation and cyber defense. Future Gener. Comp. Syst. 2021, 117, 193–204. [Google Scholar] [CrossRef]
- Kumari, P.; Gupta, H.P.; Dutta, T. A Bayesian game based approach for associating the nodes to the gateway in LoRa network. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4583–4592. [Google Scholar] [CrossRef]
- Chen, X.; Feng, W.; Luo, Y.; Shen, M.; Ge, N.; Wang, X. Defending against link flooding attacks in internet of things: A bayesian game approach. IEEE Internet Things J. 2021, 9, 117–128. [Google Scholar] [CrossRef]
- Ding, H.; Peng, C.; Kuang, Q. A Rational Exchange Protocol Model under Mixed Strategies. J. Netw. Inf. Secur. 2016, 2, 68–75. (In Chinese) [Google Scholar]
- Tao, X.; Li, G.; Sun, D.; Cai, H. A game-theoretic model and analysis of data exchange protocols for Internet of Things in clouds. Future Gener. Comp. Syst. 2017, 76, 582–589. [Google Scholar] [CrossRef]
- Lohr, M.; Skiba, K.; Konersmann, M.; Jürjens, J.; Staab, S. Formalizing cost fairness for two-party exchange protocols using game theory and applications to blockchain. In Proceedings of the 2022 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Shanghai, China, 2–5 May 2022; pp. 1–5. [Google Scholar]
- Cai, L.; Luo, L.; Li, Z.; Xiong, Z. A game-based dynamic clustering routing strategy for mobile wireless sensor networks. IEEE Internet Things J. 2024, 11, 26481–26491. [Google Scholar] [CrossRef]
- Lv, Z.; Peng, C.; Peng, Y.; Zhang, J.; Computing, M. A rational exchange protocol under asymmetric information in wireless sensor networks. Wirel. Commun. Mob. Comput. 2018, 2018, 9437936. [Google Scholar] [CrossRef]
- Luo, J.R.; Zhang, W.P.; Su, J.M.; Yuan, W.L.; Chen, J. Research Progress on Multi-Agent Game Learning. Syst. Eng. Electron. 2024, 46, 1628–1655. (In Chinese) [Google Scholar]
- Liu, Z.; Luong, N.C.; Wang, W.; Niyato, D.; Wang, P.; Liang, Y.-C.; Kim, D.I. A survey on applications of game theory in blockchain. arXiv 2019. [Google Scholar] [CrossRef]
- Chen, Z.; Tian, Y.; Peng, C. An incentive-compatible rational secret sharing scheme using blockchain and smart contract. Sci. China Inf. Sci. 2021, 64, 202301. [Google Scholar] [CrossRef]
- Yan, X.; Huang, C.; Gan, J.; Wu, X. Game theory-based energy-efficient clustering algorithm for wireless sensor networks. Sensors 2022, 22, 478. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Ma, J.; Peng, C.; Chen, X.; Ji, W. One-time rational secret sharing scheme based on bayesian game. Wuhan Univ. J. Nat. Sci. 2011, 16, 430–434. [Google Scholar] [CrossRef]
- Bonanno, G. Rational Play in Extensive-Form Games. Games 2022, 13, 72. [Google Scholar] [CrossRef]
- Fang, H.; Yi, P. Adaptive Decision-Making in Attack-Defense Games with Bayesian Inference of Rationality Level. IEEE Trans. Ind. Electron. 2024, 71, 16558–16567. [Google Scholar] [CrossRef]
- Wu, Y.; Feng, G.; Wang, N.; Liang, H. Game of information security investment: Impact of attack types and network vulnerability. Expert Syst. Appl. 2015, 42, 6132–6146. [Google Scholar] [CrossRef]
- Kremer, S.; Raskin, J.-F. Game analysis of abuse-free contract signing. In Proceedings of the 15th IEEE Computer Security Foundations Workshop, Cape Breton, NS, Canada, 24–26 June 2002; pp. 206–220. [Google Scholar]
- Heng, S.-H.; Tan, S.-Y. A survey on optimistic fair exchange protocol and its variants. In Proceedings of the 2017 5th International Conference on Information and Communication Technology, Melaka, Malaysia, 17–19 May 2017; pp. 1–6. [Google Scholar]
- Ouyang, Y.; Tavafoghi, H.; Teneketzis, D. Dynamic games with asymmetric information: Common information based perfect bayesian equilibria and sequential decomposition. IEEE Trans. Autom. Control 2016, 62, 222–237. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).