Complex Question Decomposition Based on Causal Reinforcement Learning
Abstract
1. Introduction
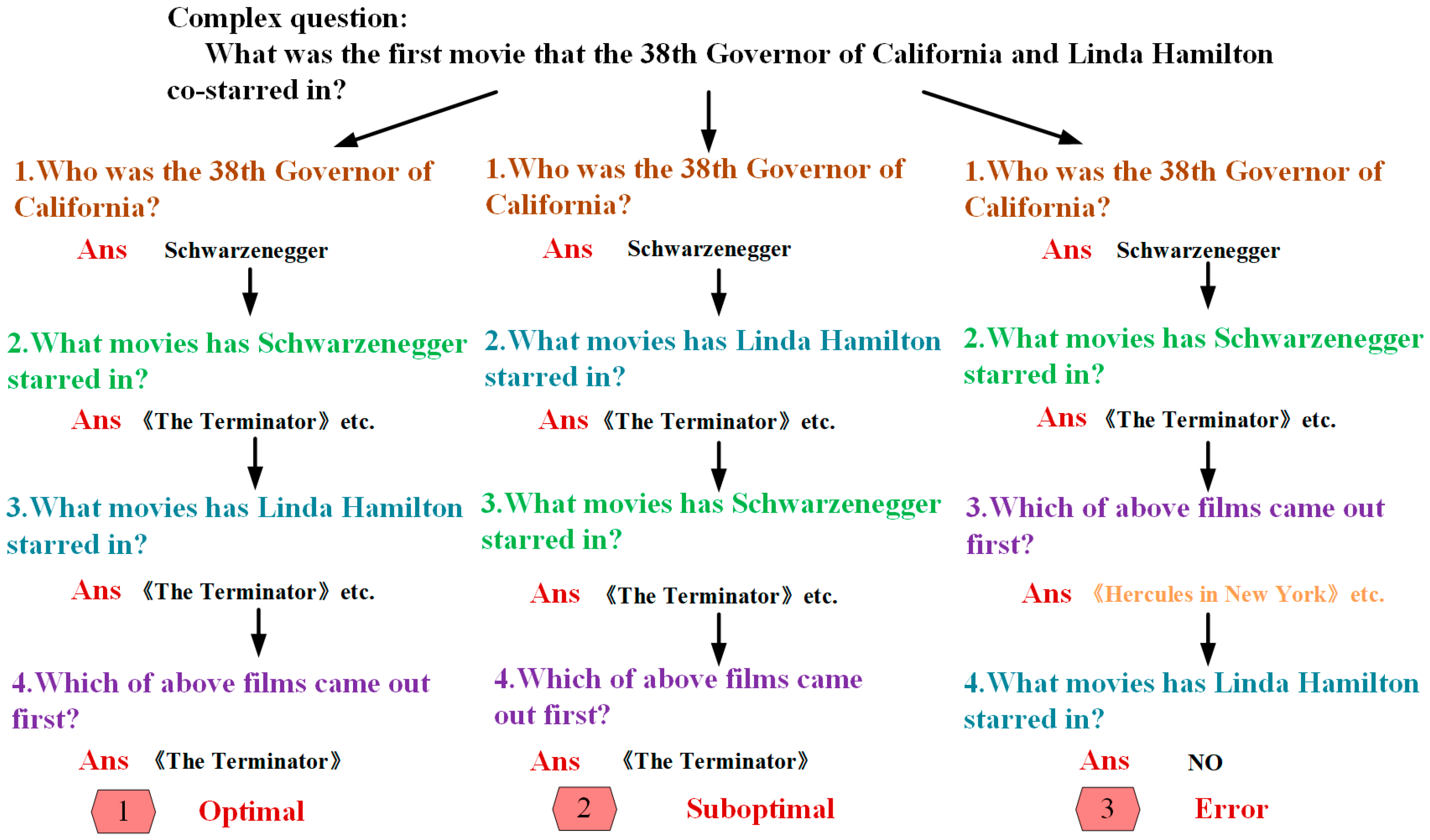
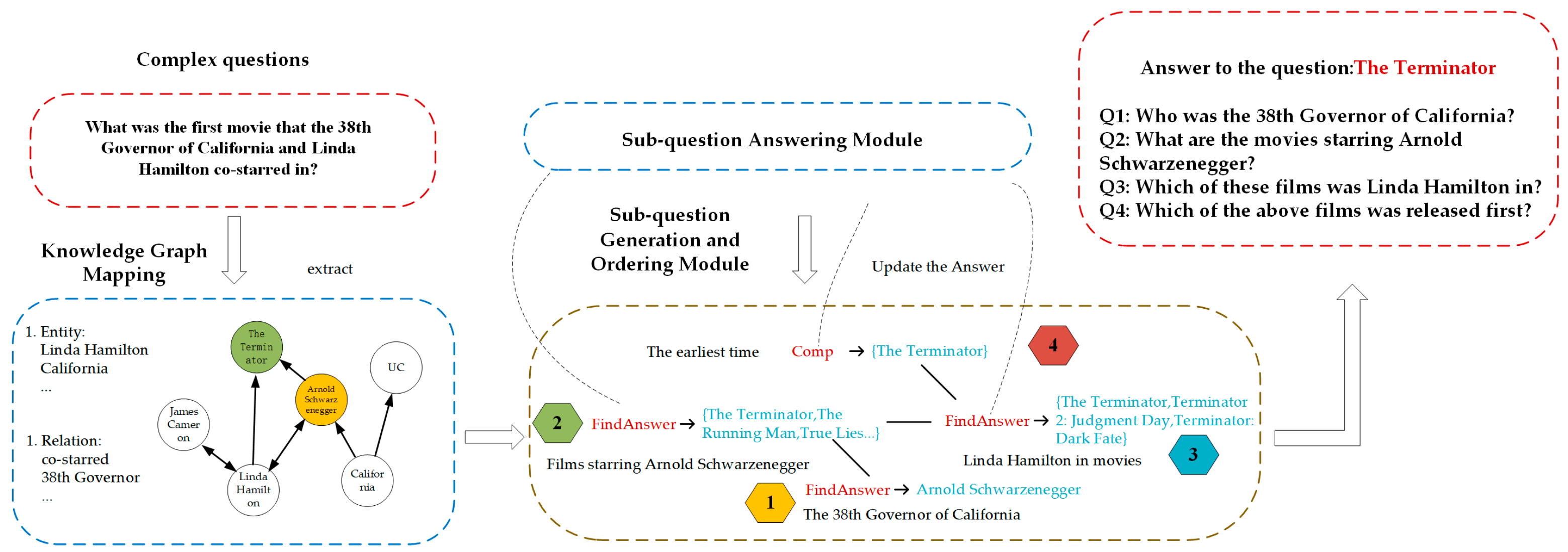
- Sub-question 1: “Who is the 38th Governor of California?”
- Sub-question 2: “What movies has Arnold Schwarzenegger been in?”
- Sub-question 3: “The Terminator” The Running Man “Predator” Terminator 2: Judgment Day “True Lies” The Expendables“ In films such as “Expendables” and “Terminator: Dark Fate” (due to space limitations, not all films starring Arnold Schwarzenegger are listed here), which ones did Linda Hamilton play?
- Sub-question 4: “Terminator The Terminator 2: Judgment Day Terminator 2: Judgment Day Terminator: Dark Fate Which of the three movies will be released first?”.
- (1)
- We propose a method to determine the difficulty of answering a question using causal inference, which aggregates the answers of each sub-question decomposed from a complex question, obtains the ratio of the number of the next-hop entities which enable the intelligent body to obtain the maximum reward in the iteration and the total number of all the next-hop entities selected by the intelligent body through the counterfactual method, and converts it into a weight value to provide support for the subsequent combination with the reinforcement learning framework.
- (2)
- We propose a complex question decomposition framework, including a knowledge graph embedding module, sub-question generation and ordering module, and a sub-question-answering module, among which the sub-question generation and ordering module is the focus of this paper.
- (3)
- We design the sub-question generation and ordering module based on causal inference and reinforcement learning, model the dependencies between the sub-questions through the multi-head attention mechanism, and determine the ordering of the sub-questions based on the weight value or the neural network.
- (4)
- Experiments demonstrate that the performance of our method is improved by 5–10% compared with the baseline method on Hits@n (n = 1, 3, 10), and the ablation experiments verify that the proposed model is effective compared with the pure reinforcement learning model.
2. Related Works
2.1. Reinforcement Learning
2.2. Causal Inference
2.3. Causal Reinforcement Learning
2.4. Complex Question Decomposition
3. Proposed Method
3.1. Problem Definition
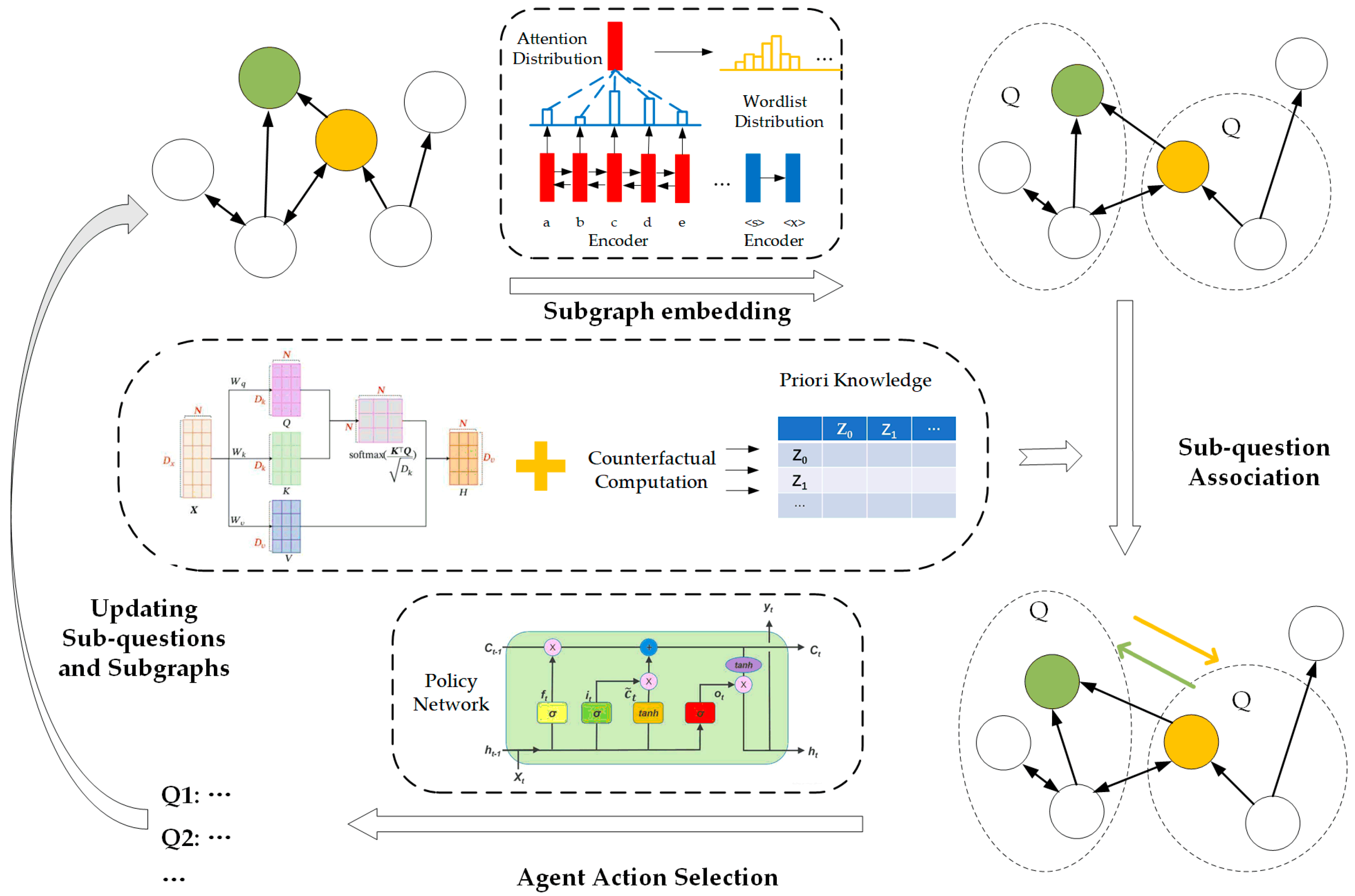
3.2. Overall Architecture
3.3. Causal Reinforcement Learning Model
3.3.1. Action Space
3.3.2. State Space
- Subgraph Representation
- 2.
- Subgraph Interaction
- 3.
- State Space Representation
3.3.3. Reward
- Positive Effect Reward Design
- 2.
- Negative Effect Reward Design
3.3.4. Target Function
3.3.5. Policy Network
4. Experiments
4.1. Datasets
4.2. Baseline Method
4.3. Evaluation Index
4.4. Model Training
4.5. Experimental Results and Analysis
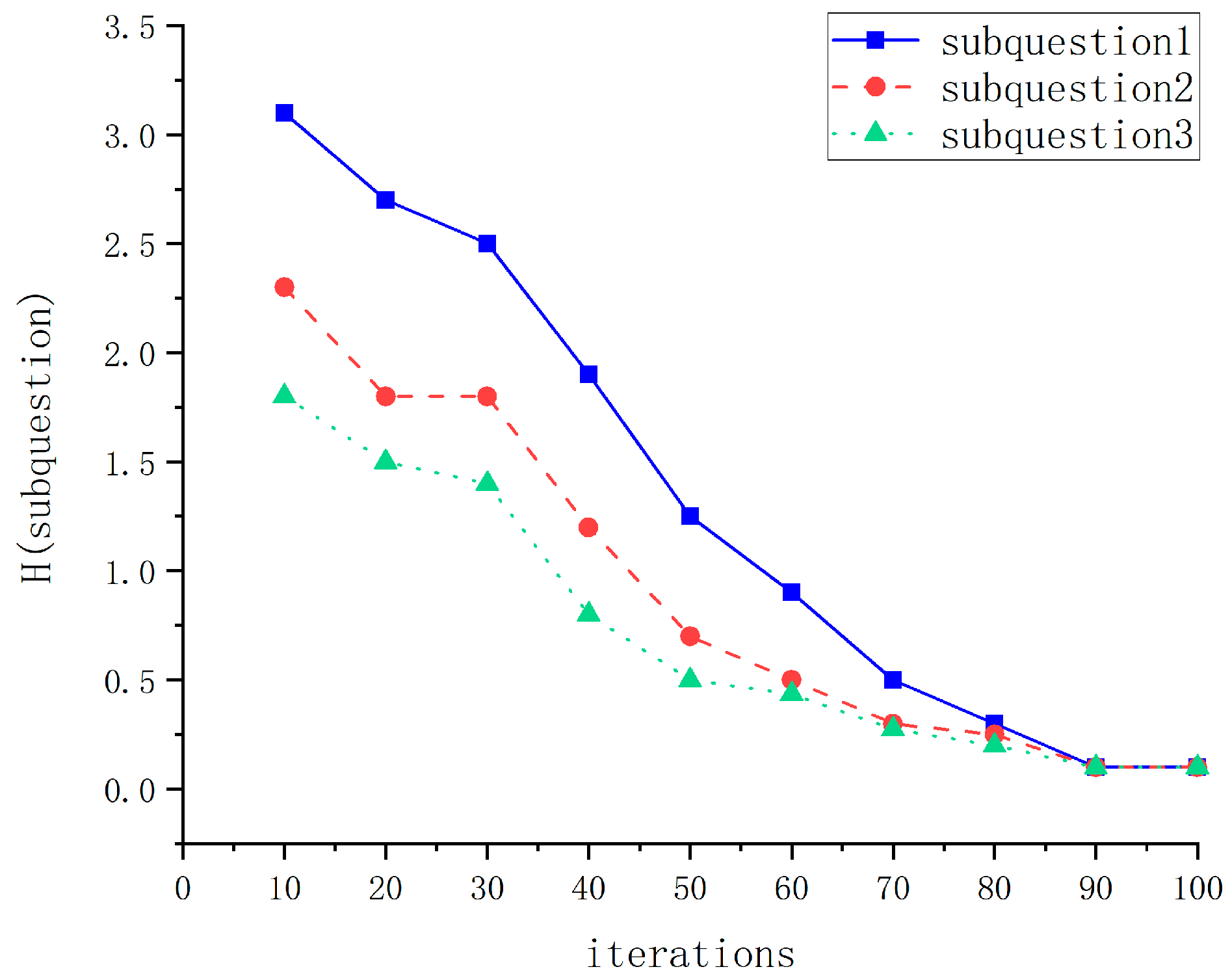
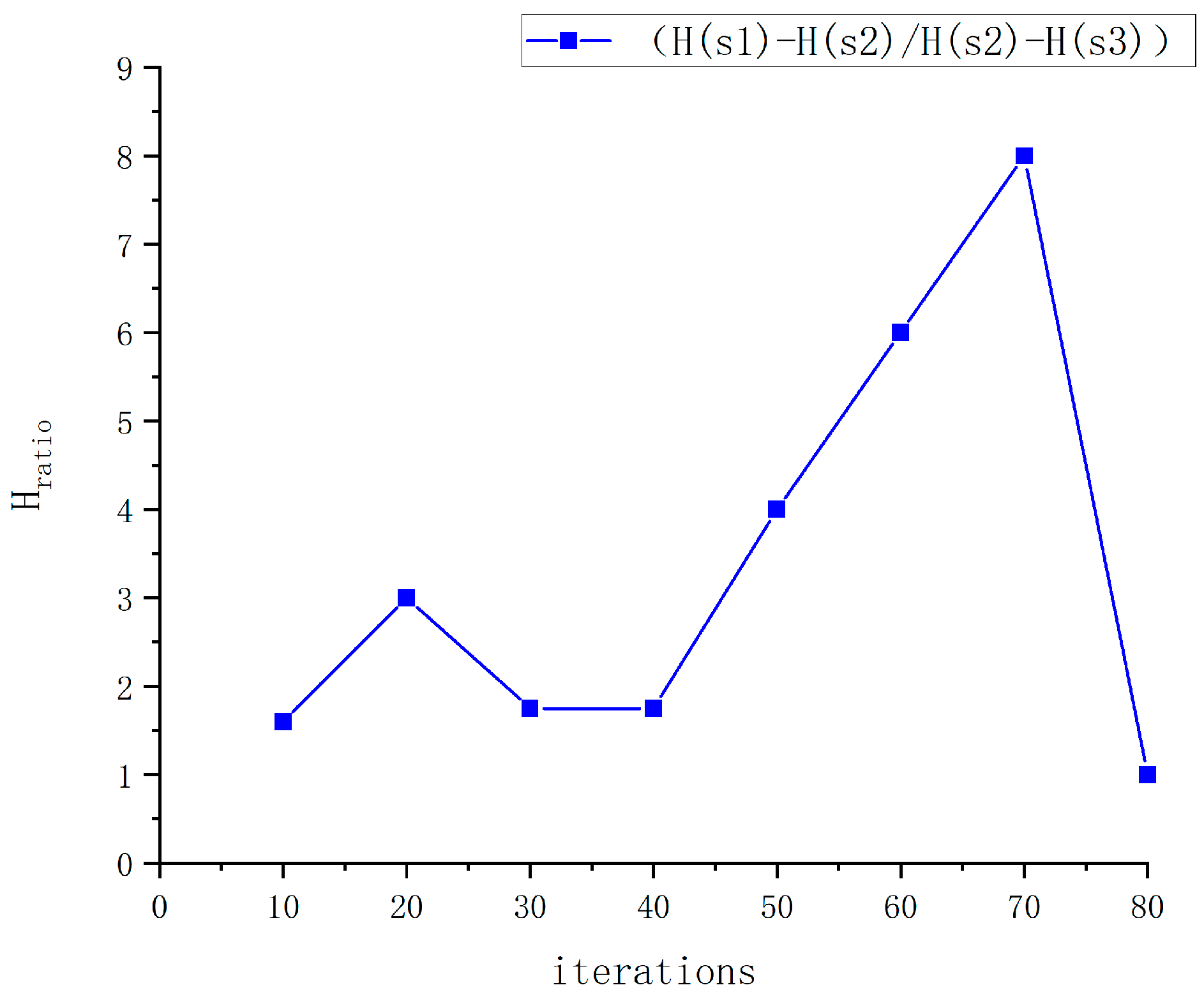
4.5.1. Error Rate and Entropy Analysis
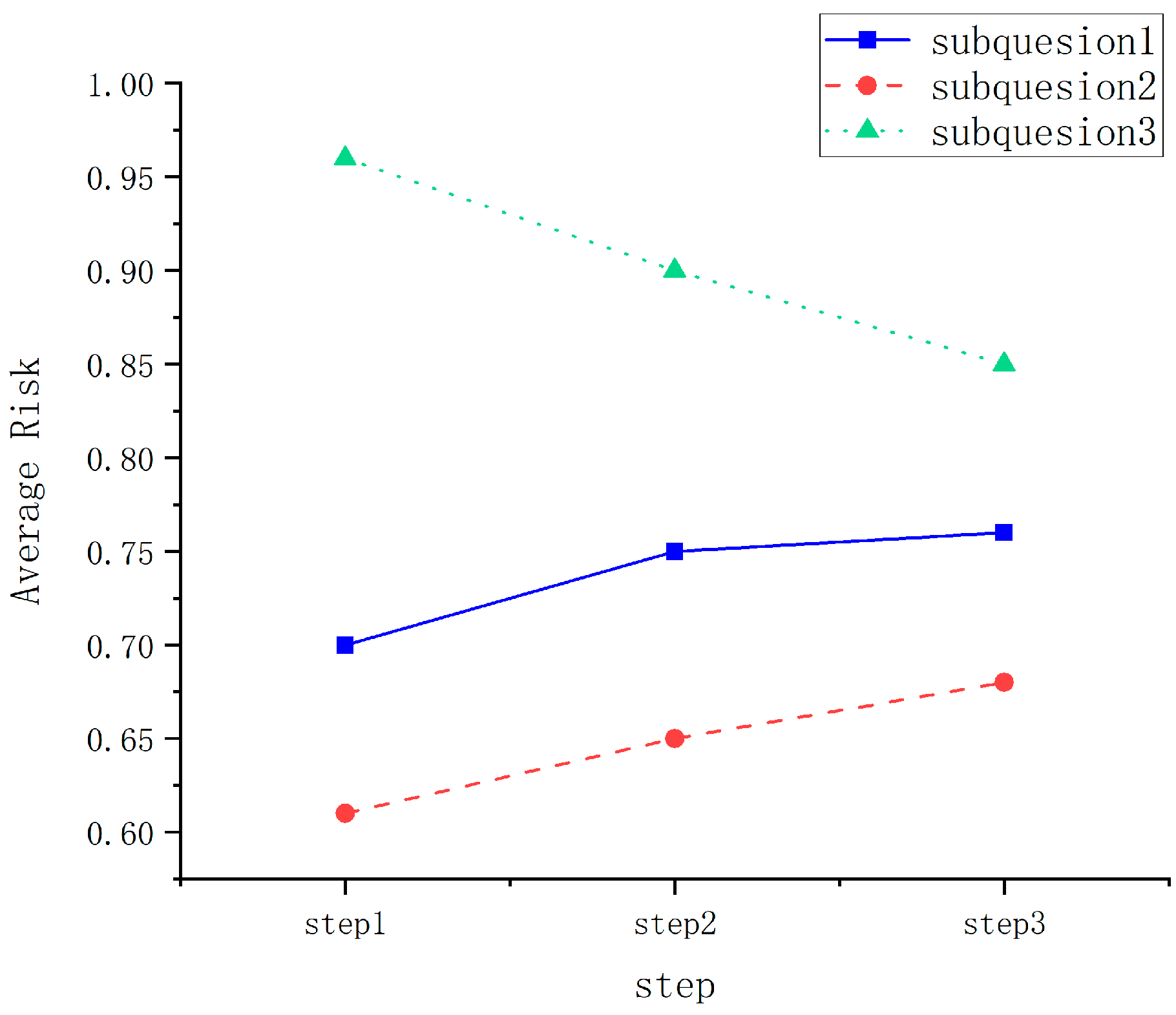
4.5.2. Risk Rate Analysis
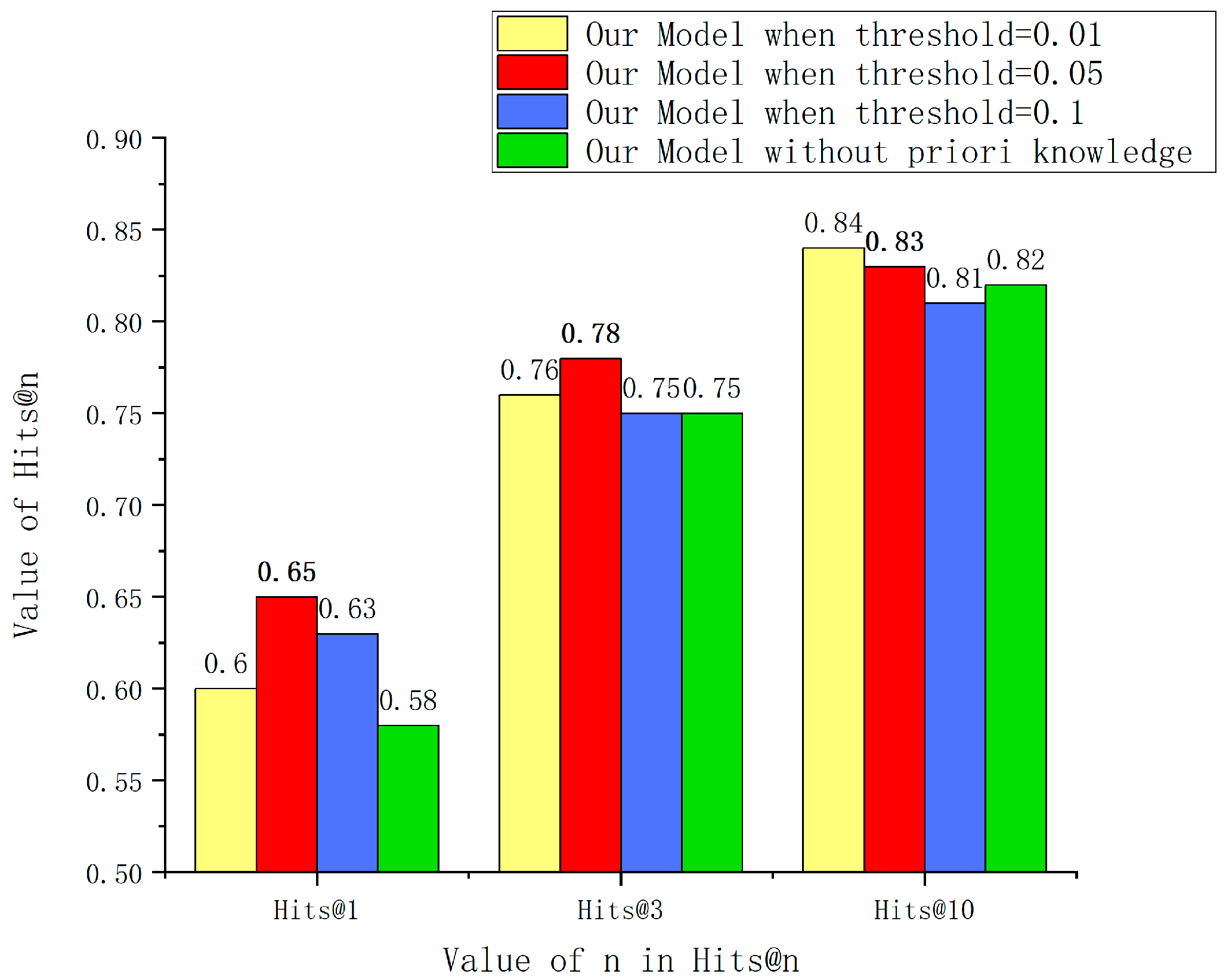
4.5.3. Threshold Setting and Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NLP | Natural language processing |
| TMN | Text modular network |
| RERC | Relation extractor–reader and comparator |
| GFCI | Greedy fast causal inference |
| GES | Greedy equivalence search |
| FCI | Fast causal inference |
| PC | Peter Clark |
| MCI | Momentary conditional independence |
| CGTST | Causality-gated time series transformer |
| SARSA | State Action Reward State Action |
| MDP | Markov Decision Process |
| IV | Instrumental Variables |
| CMDP-IV | Confounded Markov Decision Process–Instrumental Variables |
| ASRs | Action-Sufficient Representations |
| LSTM | Long Short-Term Memory |
References
- Jun, F.; Yan, L.; Ting, H.T. A survey of complex question decomposition methods in question answering system. Comput. Eng. Appl. 2022, 17, 22–33. [Google Scholar]
- Wei, S.Y.; Gong, C. Complex question answering Method of interpretable knowledge map based on graph matching network. J. Comput. Res. Dev. 2021, 12, 2673–2683. [Google Scholar]
- Bin, S.; Zhi, C.K.; Tao, L.S. Intelligent understanding of intention of complex questions for medical consultation. J. Chin. Inf. Process. 2023, 37, 112–120. [Google Scholar]
- Zhang, Y.N.; Cheng, X.; Zhang, Y.F. Learning to order sub-questions for complex question answering. arXiv 2019, arXiv:1911.04065. [Google Scholar]
- Fazili, B.; Goswami, K.; Modani, N. GenSco: Can Question Decomposition based Passage Alignment improve Question Answering? arXiv 2024, arXiv:2407.10245. [Google Scholar]
- Rosset, C.; Qin, G.; Feng, Z. Researchy Questions: A Dataset of Multi-Perspective, Decompositional Questions for LLM Web Agents. arXiv 2024, arXiv:2402.17896. [Google Scholar]
- Yi, F.; Fu, W.; Liang, H. Model-based reinforcement learning: A survey. In Proceedings of the 18th ICEB, Guilin, China, 2–6 December 2018. [Google Scholar]
- Wang, H.N.; Liu, N.; Zhang, Y.Y. Deep reinforcement learning: A survey. Front. Inf. Technol. Electron. Eng. 2020, 12, 1726–1744. [Google Scholar] [CrossRef]
- Moerland, T.M.; Broekens, J.; Plaat, A. Model-based reinforcement learning: A survey. Found. Trends Mach. Learn. 2023, 16, 101–118. [Google Scholar] [CrossRef]
- Yang, L.M.; Ke, X.; Qiang, S.Z. A review of research on multi-agent reinforcement learning algorithms. J. Front. Comput. Sci. Technol. 2024, 4, 1101–1123. [Google Scholar]
- Watkins, C.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Silver, D.; Graves, A. Playing Atari with deep reinforcement learning. arXiv 2013, arXiv:1312.09092. [Google Scholar]
- Singh, S.; Jaakkola, T.; Littman, M. Convergence results for single-step on-policy reinforcement-learning algorithms. Mach. Learn. 2000, 38, 287–308. [Google Scholar] [CrossRef]
- Fortunato, M.; Azar, M.; Piot, B. Noisy networks for exploration. In Proceedings of the 6th ICLR, Vancouver, BC, Canada, 1–4 May 2018. [Google Scholar]
- Gal, Y.; McAllister, R.; Rasmussen, C.E. Improving PILCO with bayesian neural network dynamics models. In Proceedings of the 33th ICML, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M. Asynchronous methods for deep reinforcement learning. In Proceedings of the 33th ICML, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Shen, X.P.; Ma, S.S.; Vemuri, P. Challenges and opportunities with causal discovery algorithms: Application to Alzheimer’s pathophysiology. Sci. Rep. 2020, 1, 2975–2982. [Google Scholar] [CrossRef]
- Guo, R.C.; Cheng, L.; Li, J.D. A survey of learning causality with data: Problems and methods. ACM Comput. Surv. 2020, 53, 3397269. [Google Scholar] [CrossRef]
- Nogueira, A.R.; Gama, J.; Ferreira, C.A. Causal discovery in machine learning: Theories and applications. J. Dyn. Games 2021, 3, 203–231. [Google Scholar] [CrossRef]
- Ogarrio, J.M.; Spirtes, P.; Ramsey, J. A hybrid causal search algorithm for latent variable models. In Proceedings of the 8th PGM, Lugano, Switzerland, 6–9 September 2016. [Google Scholar]
- Chickering, D.M. Optimal structure identification with greedy search. J. Mach. Learn. Res. 2003, 3, 507–554. [Google Scholar]
- Spirtes, P.L.; Meek, C.; Richardon, T.S. Causal inference in the presence of latent variables and selection bias. In Proceedings of the 11th UAI, Montreal, QC, Canada, 18–20 August 1995. [Google Scholar]
- Runge, J.; Nowack, P.; Kretschmer, M. Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 2019, 5, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Affeldt, S.; Isambert, H. Robust reconstruction of causal graphical models based on conditional 2-point and 3-point information. In Proceedings of the 31th UAI, Amsterdam, The Netherlands, 12–16 July 2015. [Google Scholar]
- Vansteelandt, S.; Daniel, R.M. On regression adjustment for the propensity score. Stat. Med. 2014, 23, 4053–4072. [Google Scholar] [CrossRef]
- Danilo, J.; Danihelka, I.; George, P. Causally correct partial models for reinforcement learning. arXiv 2020, arXiv:2020.02836v1. [Google Scholar]
- Zhi, H.D.; Jing, J.; Guo, D.L. Causal reinforcement learning: A survey. arXiv 2023, arXiv:2307.01452. [Google Scholar]
- Zeng, Y.; Rui, C.; Fu, S. A survey on causal reinforcement learning. arXiv 2023, arXiv:2302.05209. [Google Scholar] [CrossRef] [PubMed]
- Yue, S.; Wen, Z.; Chang, S. Causality in reinforcement learning control: The state of the art and prospects. Acta Autom. Sin. 2023, 49, 661–677. [Google Scholar]
- Liao, Z.; Fu, Z.; Yang, Y. Instrumental variable value iteration for causal offline reinforcement learning. arXiv 2021, arXiv:2102.09907. [Google Scholar]
- Subramanian, C.; Ravindran, B. Causal contextual bandits with targeted interventions. In Proceedings of the 10th ICLR, Online, 25–29 April 2022. [Google Scholar]
- Huang, B.; Lu, C.; Le, J. Action-sufficient state representation learning for control with structural constraints. In Proceedings of the 39th ICML, Baltimore, MD, USA, 17–23 July 2022. [Google Scholar]
- Bica, I.; Jarrett, D. Learning what if explanations for sequential decision-making. In Proceedings of the 9th ICLR, Online, 3–7 May 2021. [Google Scholar]
- Feng, S.X.; Ru, L.; Li, L.X. A span-based target-aware relation model for frame-semantic parsing. ACM Trans. Asian Low. Resour. Lang. Inf. Process. 2023, 22, 9001–9024. [Google Scholar]
- Kalyanpur, A.; Patwardhan, S.; Boguraev, B. Fact-based question decomposition for candidate answer re-ranking. In Proceedings of the 20th ACM CIKM, New York, NY, USA, 24–28 October 2011. [Google Scholar]
- Kalyanpur, A.; Patwardhan, S.; Boguraev, B. Fact-based question decomposition in DeepQA. IBM J. Res. Dev. 2012, 3, 133–145. [Google Scholar] [CrossRef]
- Kalyanpur, A.; Patwardhan, S.; Boguraev, B. Parallel and nested decomposition for factoid questions. In Proceedings of the 13th EACL, Philadelphia, PA, USA, 23–27 April 2012. [Google Scholar]
- Zheng, W.G.; Yu, J.X.; Zou, L. Question answering over knowledge graphs: Question understanding via template decomposition. Proc. VLDB Endow. 2018, 11, 1373–1386. [Google Scholar] [CrossRef]
- Min, S.; Zhong, V.; Zettlemoyer, L. Multi-hop reading comprehension through question decomposition and rescoring. In Proceedings of the 20th EACL, Florence, Italy, 3–5 July 2019. [Google Scholar]
- Yan, H.; Qiu, X.P.; Huang, X.J. A graph-based model for joint Chinese word segmentation and dependency parsing. Trans. Assoc. Comput. Linguist. 2020, 8, 78–92. [Google Scholar] [CrossRef]
- Wu, L.Z.; Zhang, M.S. Deep graph-based character-level Chinese dependency parsing. Inst. Electr. Electron. Eng. 2021, 29, 1329–1339. [Google Scholar] [CrossRef]
- Khot, T.; Khashabi, D.; Richardson, K. Text modular networks: Learning to decompose tasks in the language of existing models. In Proceedings of the 2021 NAACL, Online, 6–11 June 2021. [Google Scholar]
- Fu, R.L.; Wang, H.; Zhang, X.J. Decomposing complex questions makes multi- hop QA easier and more interpretable. In Proceedings of the 2021 EMNLP, Punta Cana, Dominican Republic, 7–11 November 2021. [Google Scholar]
- Shin, S.; Lee, K. Processing knowledge graph-based complex questions through question decomposition and recomposition. Inf. Sci. 2020, 523, 234–244. [Google Scholar] [CrossRef]
- Lin, X.V.; Socher, R.; Xiong, C. Multi-hop knowledge graph reasoning with reward shaping. In Proceedings of the 2018 EMNLP, Brussels, Belgium, 2–4 November 2018. [Google Scholar]
- Das, R. Go for a walk and arrive at the answer-reasoning over paths in knowledge bases using reinforcement learning. In Proceedings of the 6th ICLR, Vancouver, BC, Canada, 1–3 May 2018. [Google Scholar]
- Talmor, A.; Berant, J. The web as a knowledge-base for answering complex questions. In Proceedings of the 2018 NAACL-HLT, New Orleans, LA, USA, 1–6 June 2018. [Google Scholar]
- Yih, M.; Richardson, C.; Meek, M. The value of semantic parse labeling for knowledge base question answering. In Proceedings of the 2018 ACL, Berlin, Germany, 15–20 July 2018. [Google Scholar]
- Zhang, L.; Winn, J.M.; Tomioka, R. Gaussian attention model and its application to knowledge base embedding and question answering. arXiv 2016, arXiv:1611.02266. [Google Scholar]


| Training Triples | Test Triples | |
|---|---|---|
| CNQD | 7734 | 1475 |
| WC-2014-C | 6209 | 1881 |
| FB15K-C | 5000 | 1660 |
| CNQD | WC-2014-C | FB-15k-C | |
|---|---|---|---|
| Time (Hour) | 5.5 | 4.5 | 4 |
| Number of Iterations | 100 | 80 | 70 |
| Models | CNQD | WC-2014-C | FB-15k-C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Hits@1 | Hits@3 | Hits@10 | Hits@1 | Hits@3 | Hits@10 | Hits@1 | Hits@3 | Hits@10 | |
| Ours | 0.552 | 0.618 | 0.719 | 0.558 | 0.602 | 0.671 | 0.212 | 0.257 | 0.383 |
| RR | 0.479 | 0.525 | 0.628 | 0.418 | 0.531 | 0.615 | 0.179 | 0.238 | 0.266 |
| MINERVA | 0.496 | 0.558 | 0.667 | 0.441 | 0.552 | 0.639 | 0.191 | 0.242 | 0.287 |
| Index | Ours | Separate Reinforcement Learning | |
|---|---|---|---|
| Experimental times | 30 | 30 | 0 |
| Mean value of HITS@1 | 0.63 ± 0.02 | 0.58 ± 0.03 | 0.05 |
| Mean value of HITS@3 | 0.77 ± 0.03 | 0.75 ± 0.02 | 0.02 |
| Mean value of HITS@10 | 0.84 ± 0.03 | 0.82 ± 0.03 | 0.02 |
| t | - | - | 6.708 |
| p | - | - | 0.01 |
| 95% confidence interval | - | - | (0.021, 0.039) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Lu, Y.; Wu, J.; Zhou, W.; Zeng, G. Complex Question Decomposition Based on Causal Reinforcement Learning. Symmetry 2025, 17, 1022. https://doi.org/10.3390/sym17071022
Li D, Lu Y, Wu J, Zhou W, Zeng G. Complex Question Decomposition Based on Causal Reinforcement Learning. Symmetry. 2025; 17(7):1022. https://doi.org/10.3390/sym17071022
Chicago/Turabian StyleLi, Dezhi, Yunjun Lu, Jianping Wu, Wenlu Zhou, and Guangjun Zeng. 2025. "Complex Question Decomposition Based on Causal Reinforcement Learning" Symmetry 17, no. 7: 1022. https://doi.org/10.3390/sym17071022
APA StyleLi, D., Lu, Y., Wu, J., Zhou, W., & Zeng, G. (2025). Complex Question Decomposition Based on Causal Reinforcement Learning. Symmetry, 17(7), 1022. https://doi.org/10.3390/sym17071022





