Recent Advances in Chiral and Achiral Metasurfaces Under Symmetry Preservation and Breaking
Abstract
1. Introduction
2. Fundamental Principles of Chiral and Achiral Metasurfaces
2.1. Principles of Chiral Metasurfaces
2.2. Principles of Achiral Metasurfaces
3. Chiral Metasurfaces
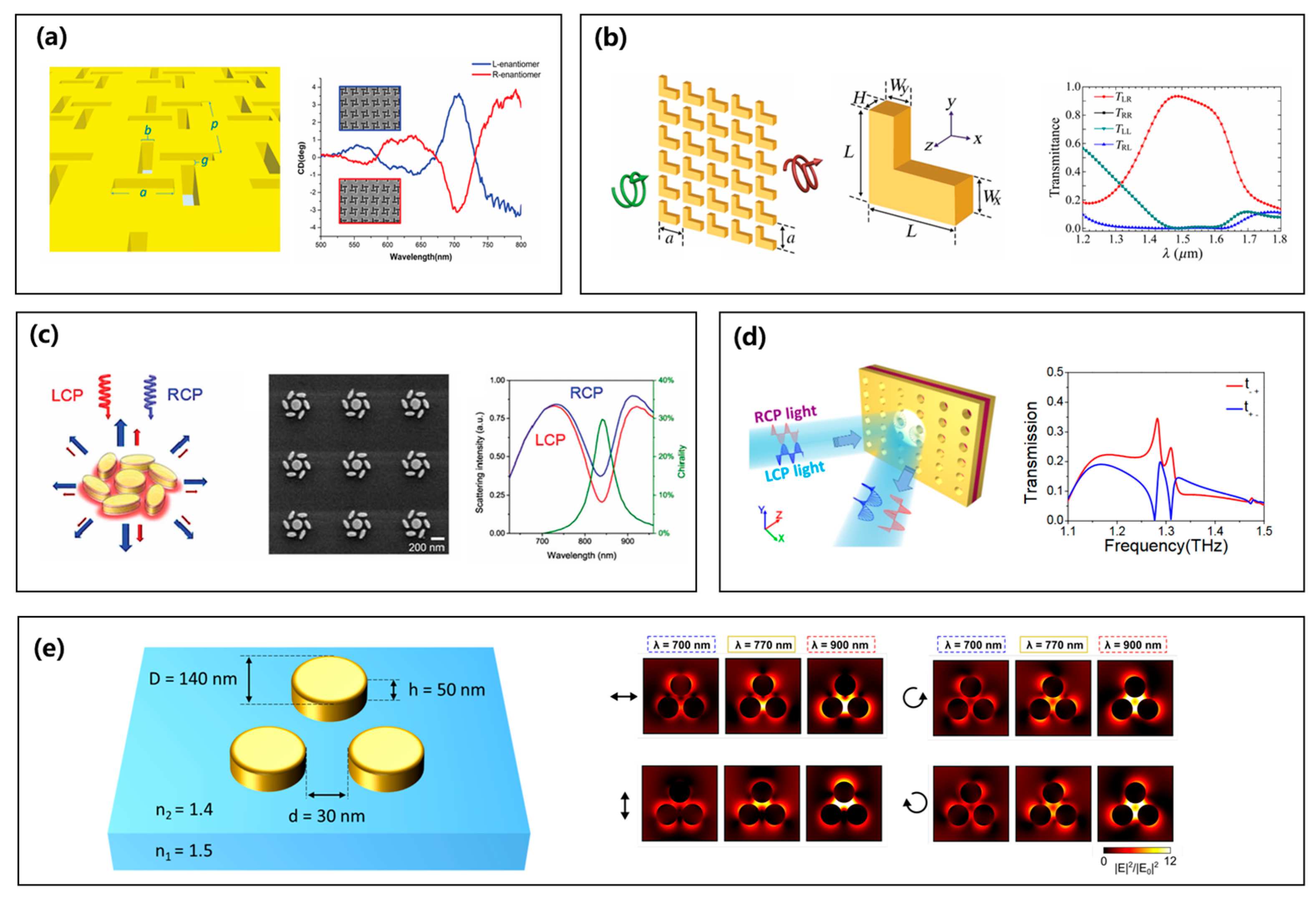
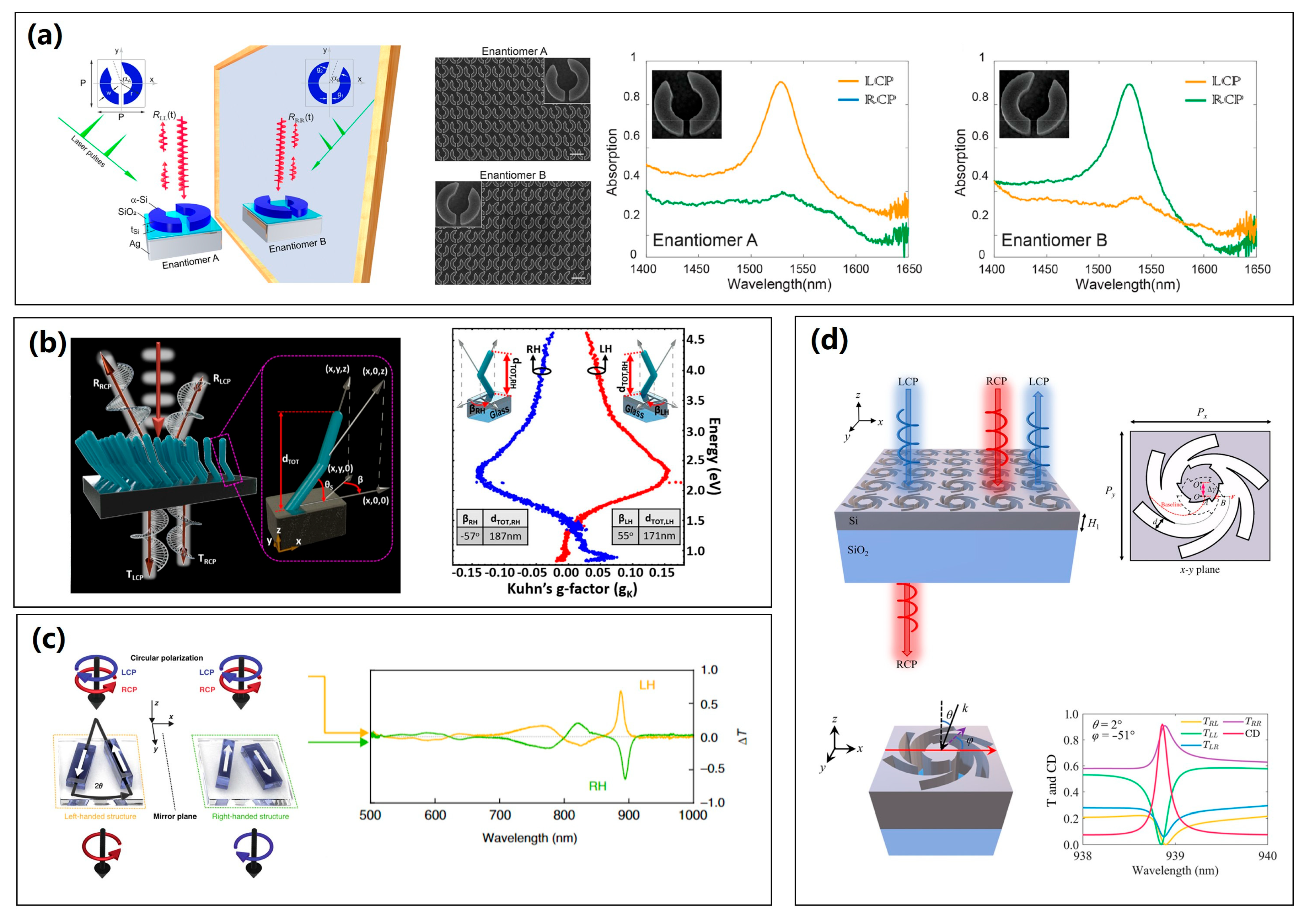
3.1. Metallic Chiral Metasurfaces
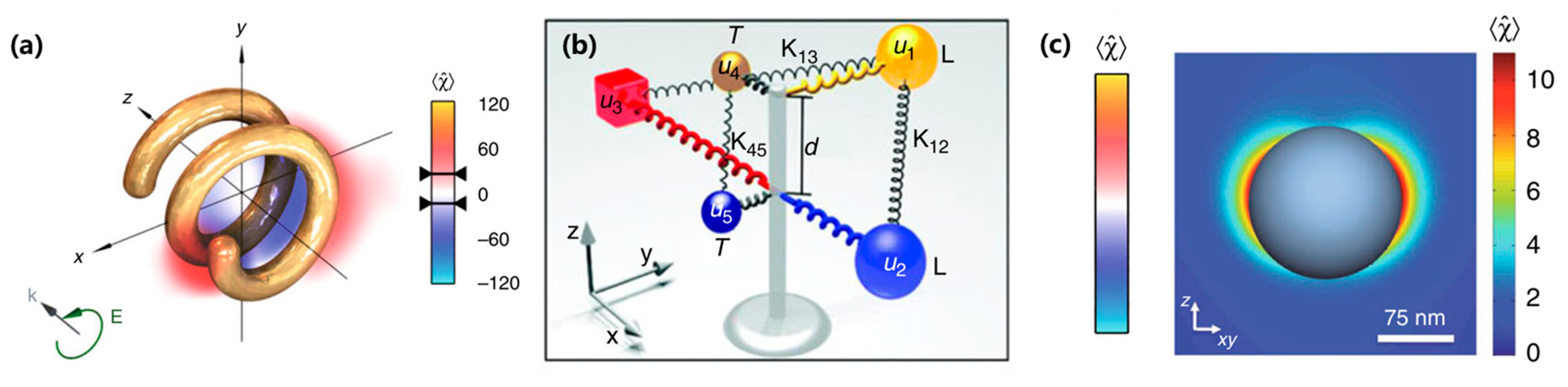
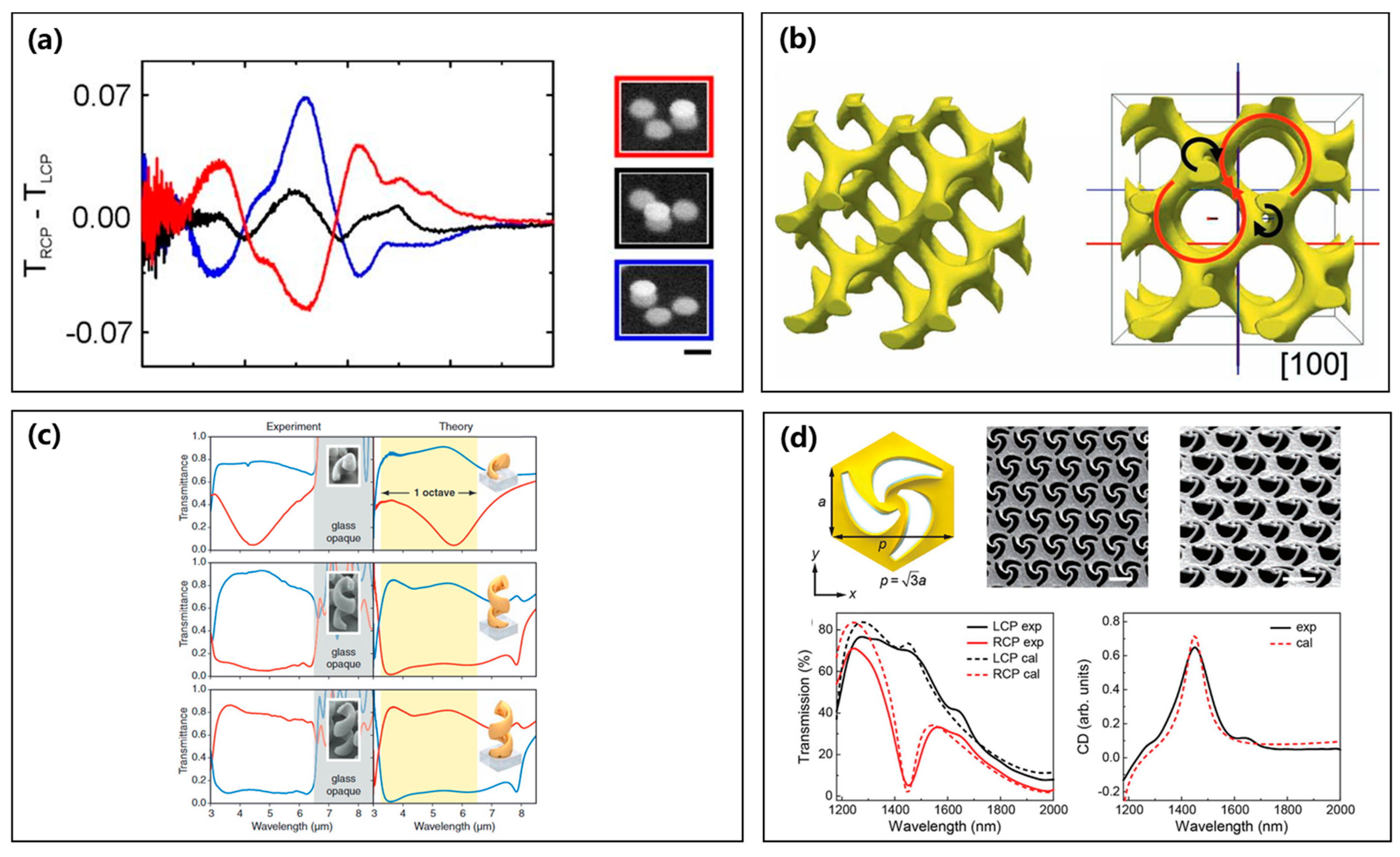
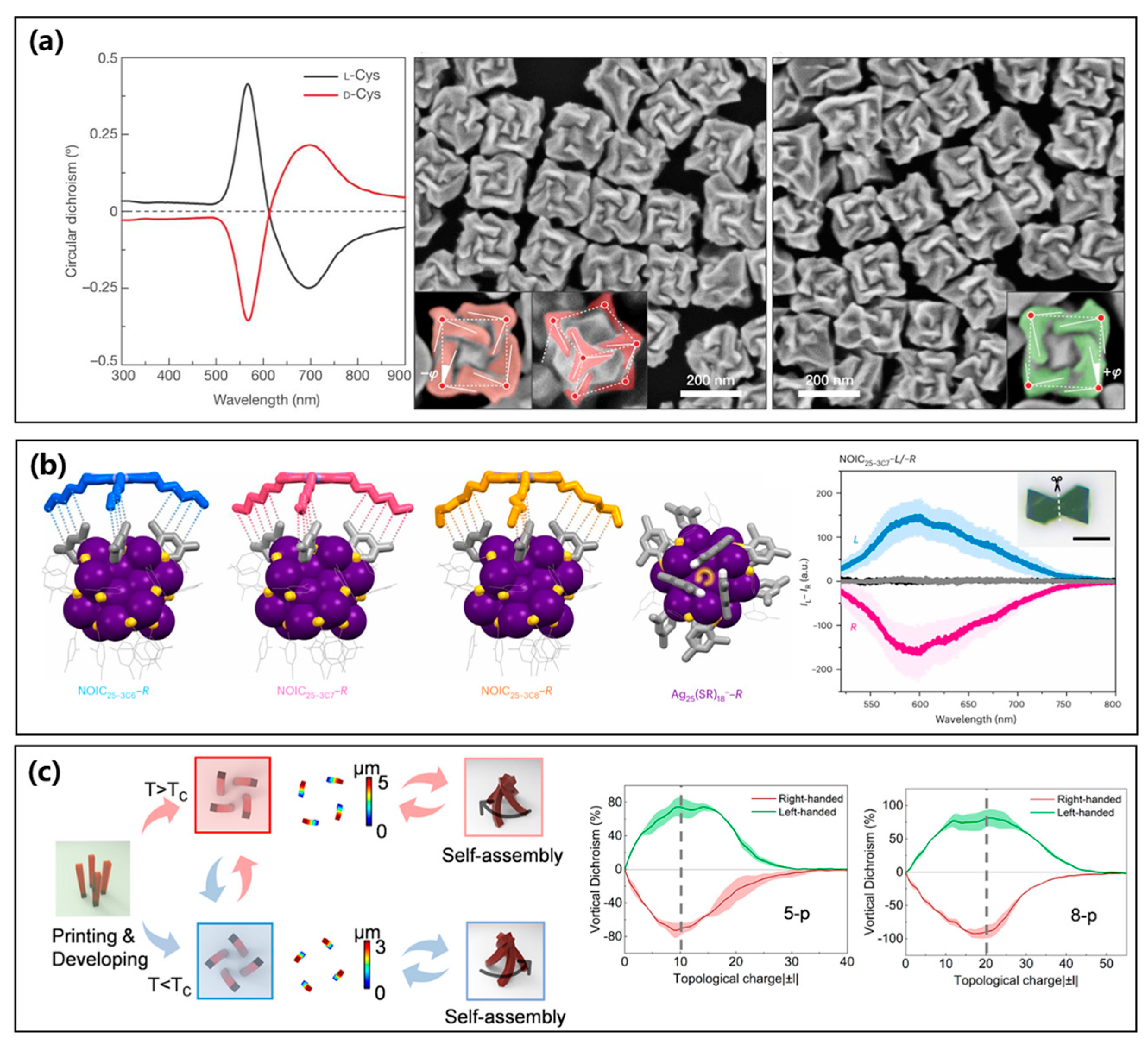
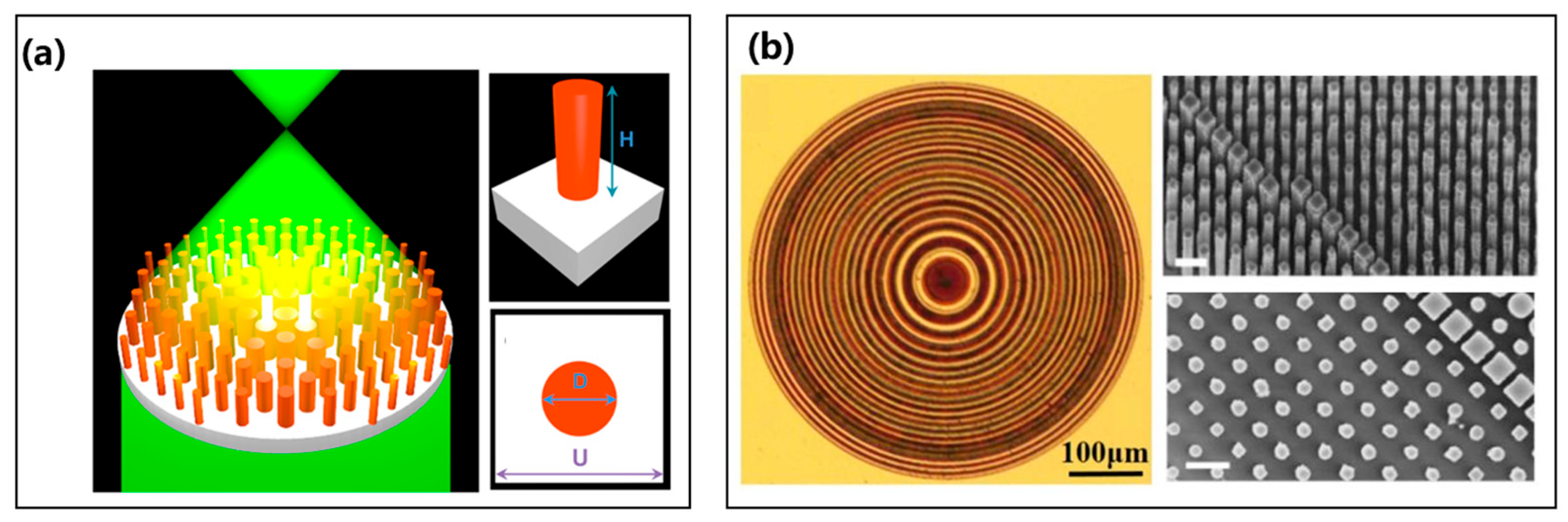
3.1.1. 3D Structures of Metallic Chiral Metasurfaces
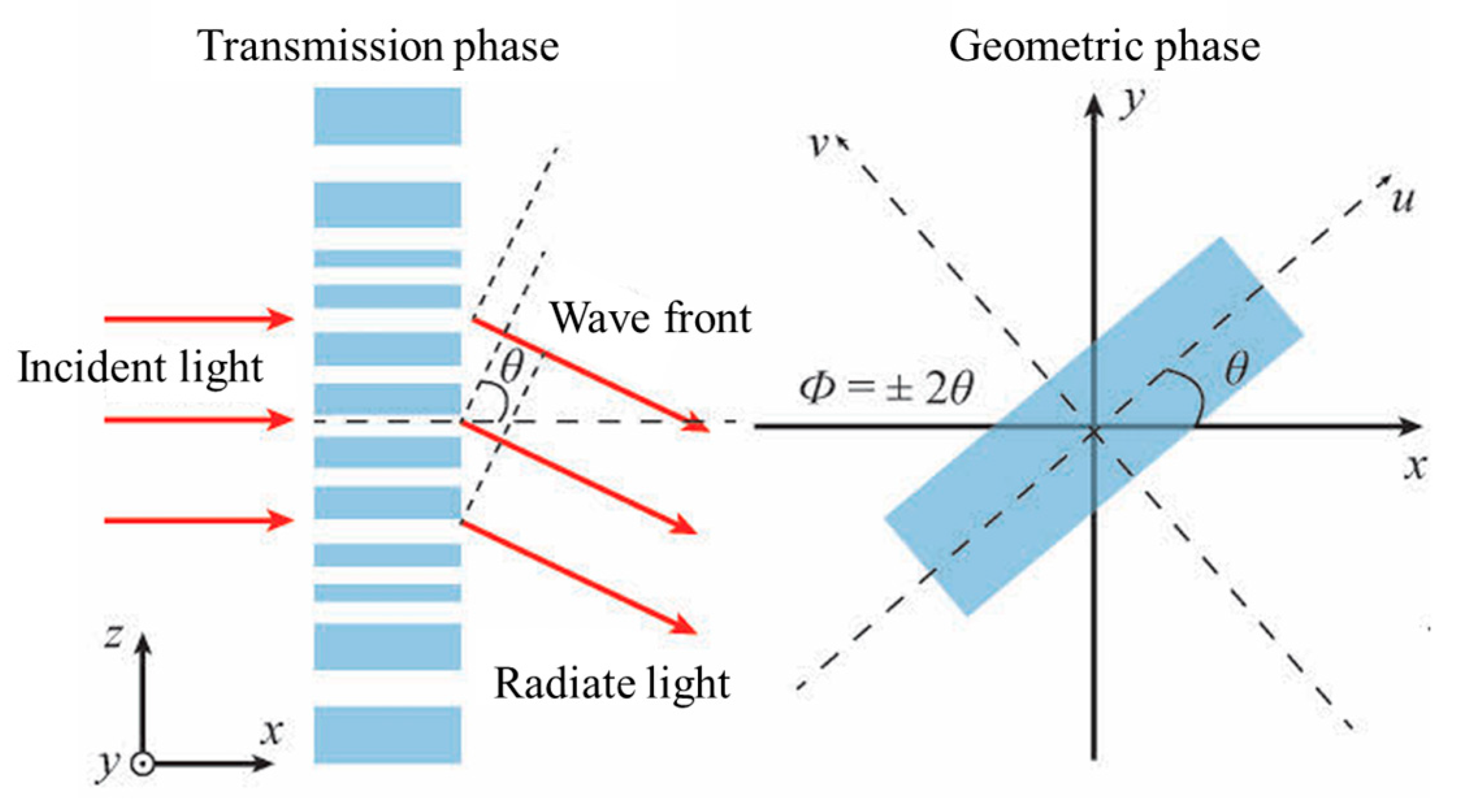
3.1.2. 2D Structures of Metallic Chiral Metasurfaces
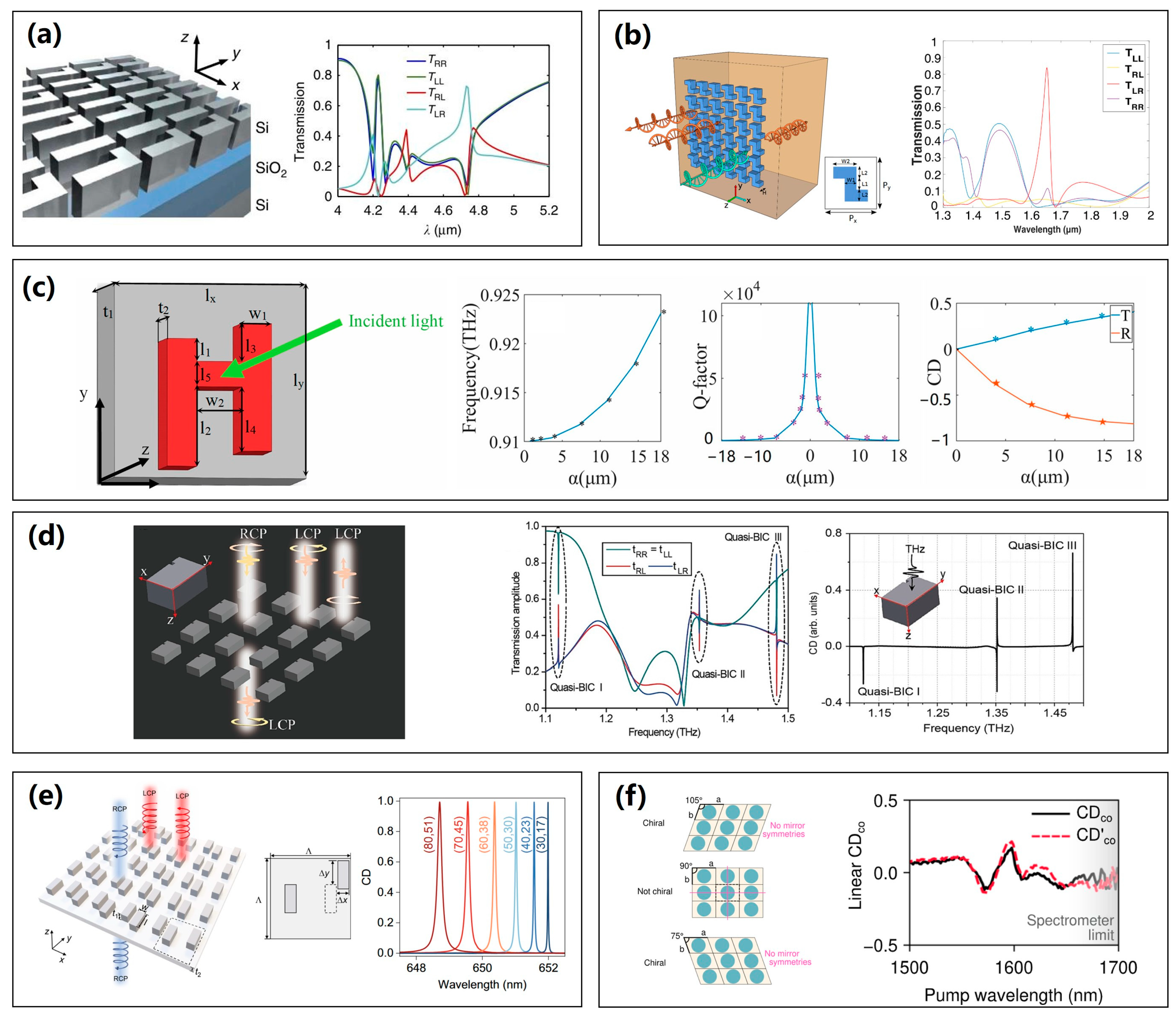
3.2. Dielectric Chiral Metasurfaces
3.2.1. 3D Structures of Dielectric Chiral Metasurfaces
3.2.2. 2D Structures of Dielectric Chiral Metasurfaces
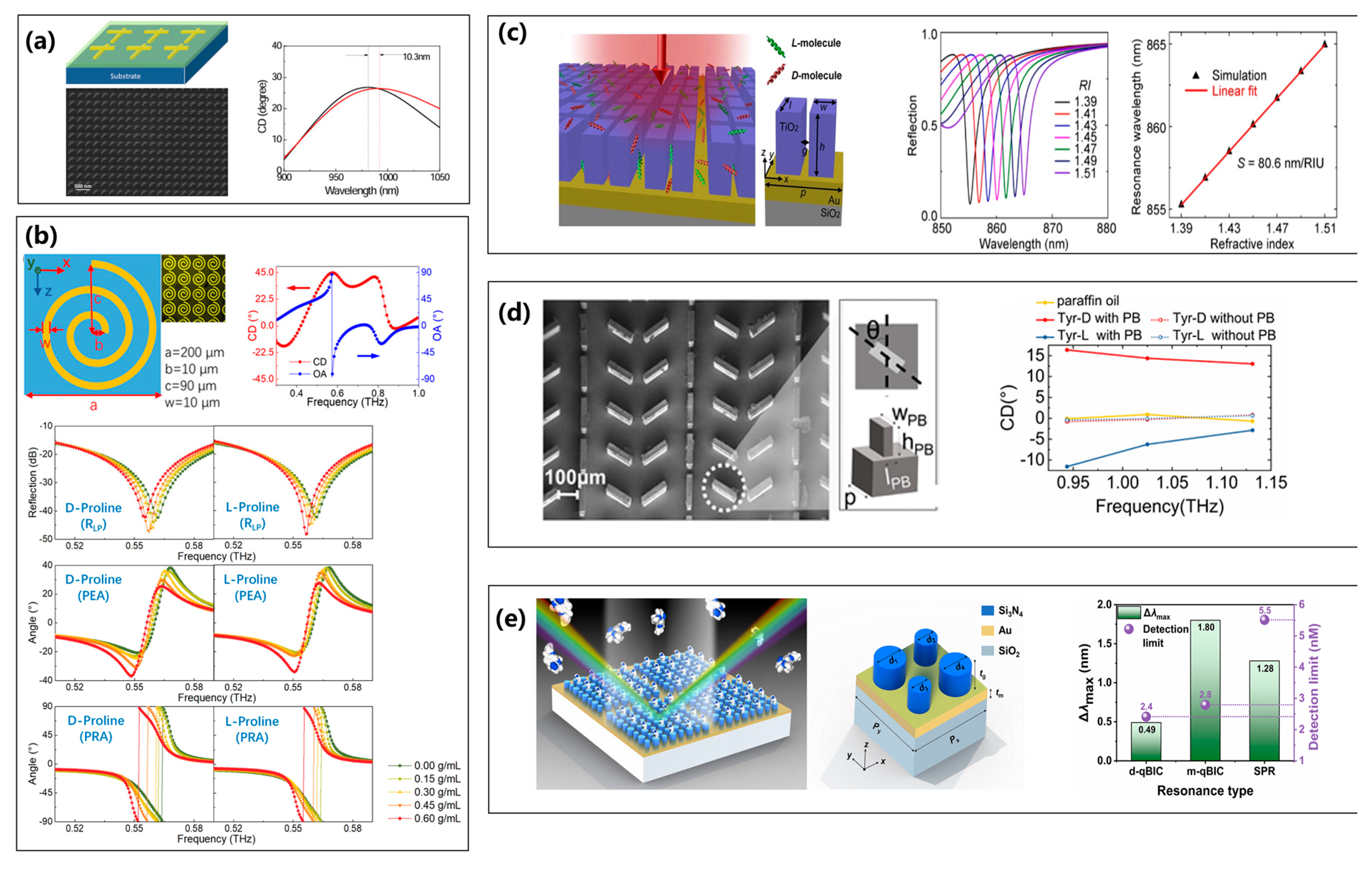
3.3. Applications of Chiral Metasurfaces
3.3.1. Chiral Sensing
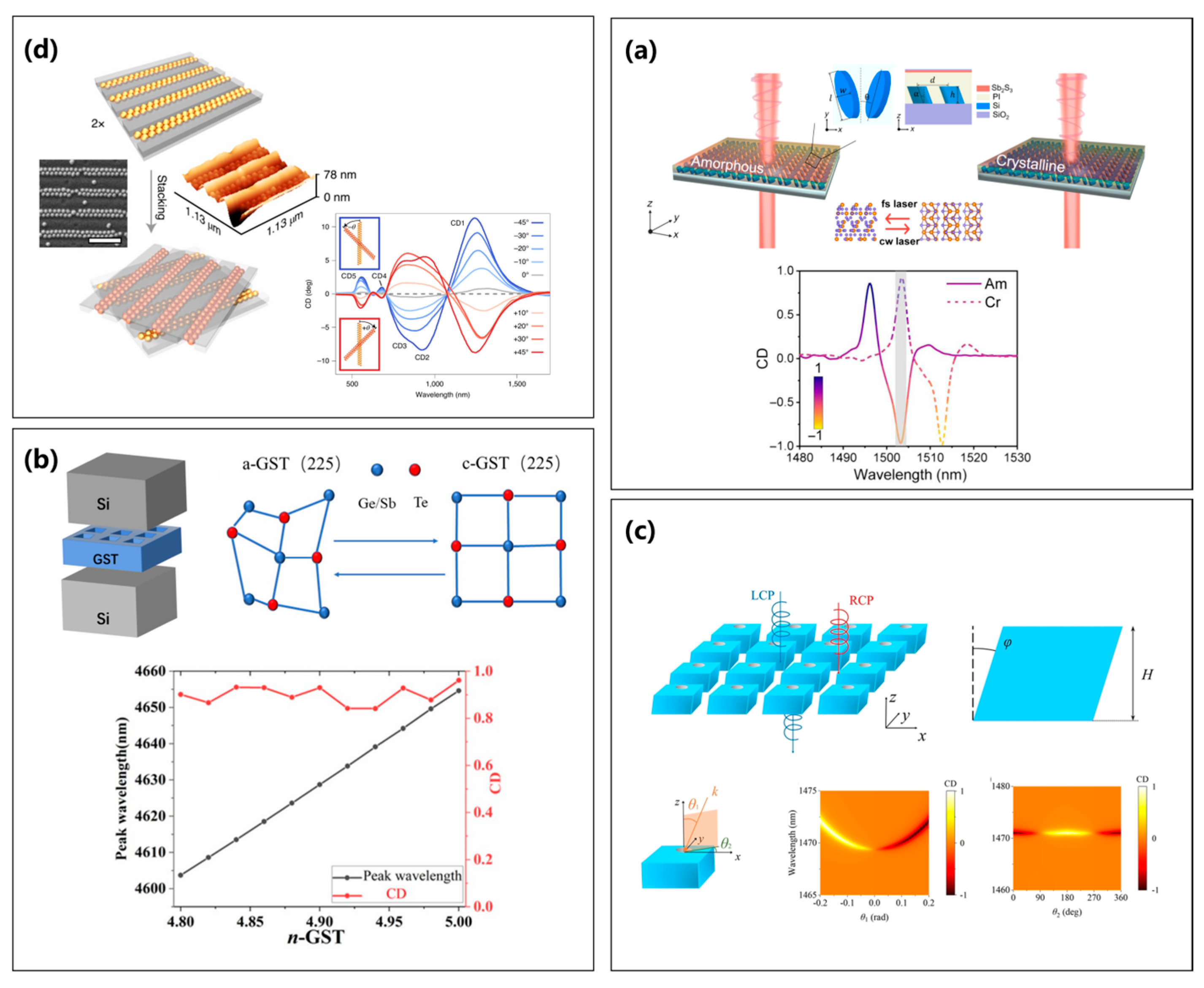
3.3.2. Dynamic Chirality Tuning
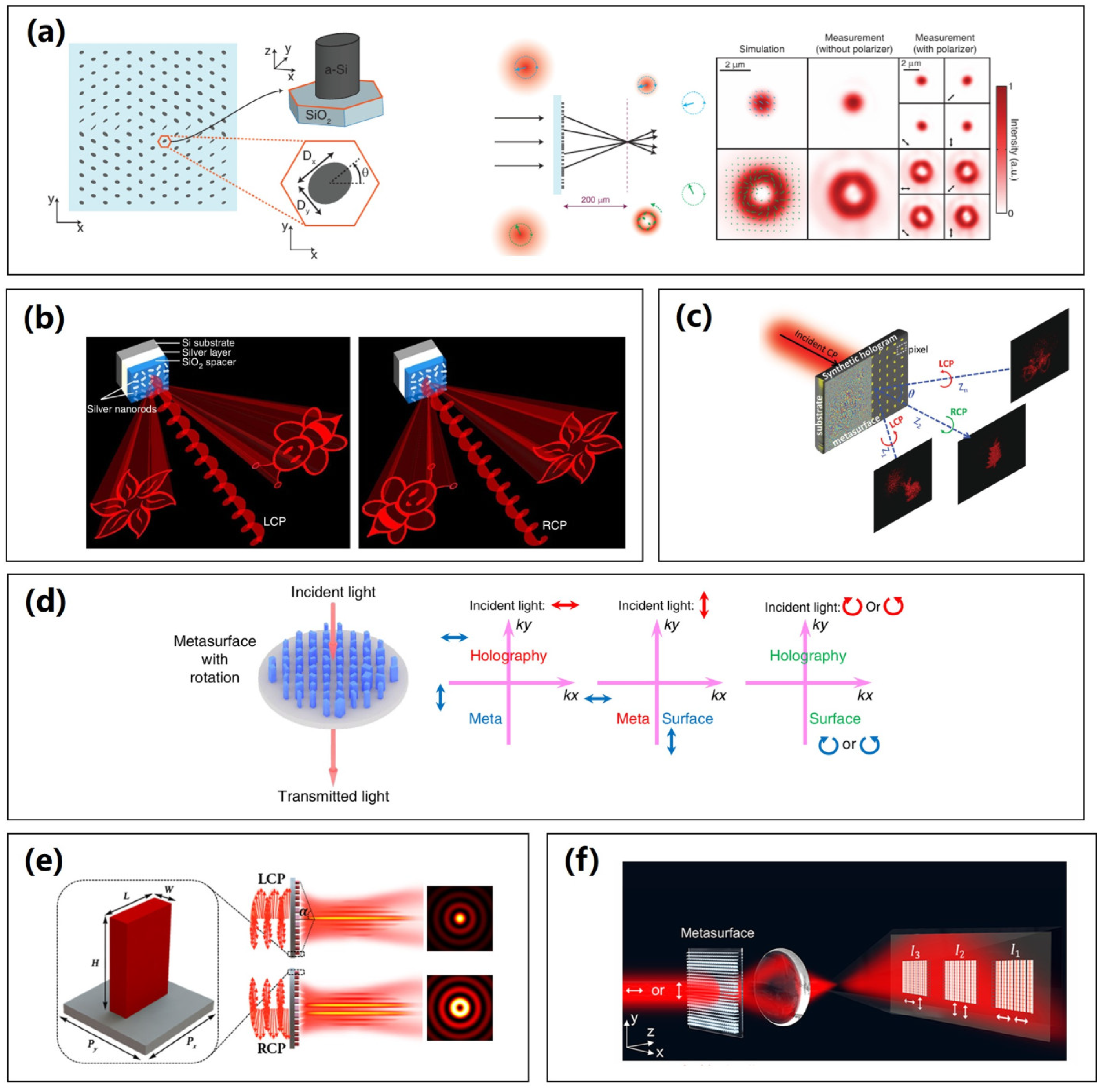
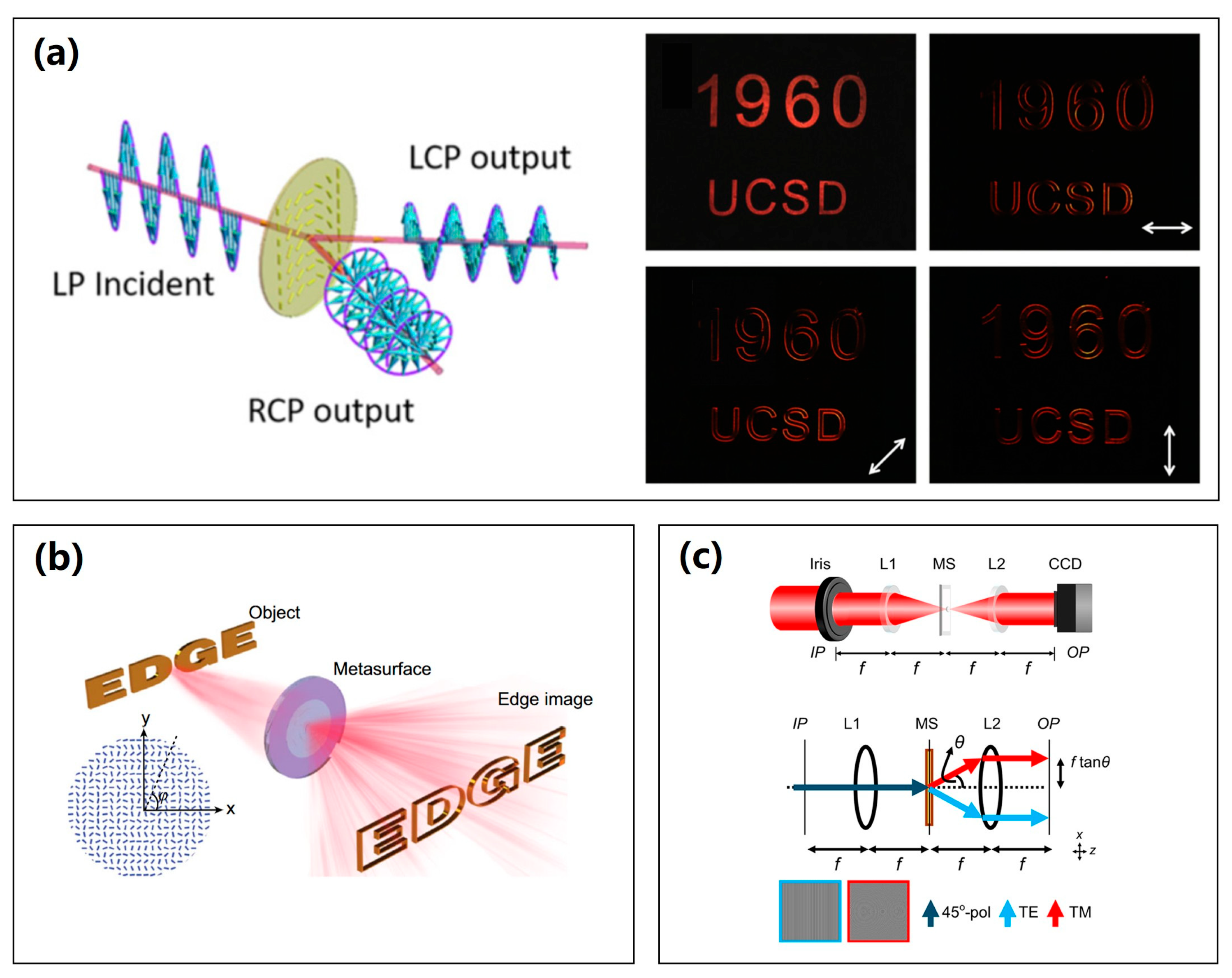
3.3.3. Chiral Imaging
3.4. Performance Comparison and Summary
4. Achiral Metasurfaces
4.1. Polarization Multiplexing
4.2. Phase Imaging
4.3. Polarization-Insensitive
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Andrews, D.L. Symmetry and quantum features in optical vortices. Symmetry 2021, 13, 1368. [Google Scholar] [CrossRef]
- Cong, L.; Xu, N.; Zhang, W.; Singh, R. Polarization control in terahertz metasurfaces with the lowest order rotational symmetry. Adv. Opt. Mater. 2015, 3, 1176–1183. [Google Scholar] [CrossRef]
- Damnjanović, M.; Milošević, I.; Vuković, T.; Sredanović, R. Full symmetry, optical activity, and potentials of single-wall and multiwall nanotubes. Phys. Rev. B 1999, 60, 2728. [Google Scholar] [CrossRef]
- Li, Y.; Ling, J.; Guo, J.; Li, Q.; Zhong, D.; Wang, X. Design of compact dielectric metalens visor for augmented reality using spin-dependent supercells. Photonics 2024, 11, 824. [Google Scholar] [CrossRef]
- Guo, J.-K.; Wang, H.; Chang, F.; Ling, J.; Yuan, Y.; Zhang, X.; Wang, X. Production and Reconfiguration of Double Emulsions by Temperature Control. Langmuir 2023, 39, 13296–13302. [Google Scholar] [CrossRef]
- Yang, J. Symmetry breaking of solitons in one-dimensional parity-time-symmetric optical potentials. Opt. Lett. 2014, 39, 5547–5550. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A. Nonlinear optics: Symmetry breaking in laser cavities. Nat. Photonics 2015, 9, 287. [Google Scholar] [CrossRef]
- Tang, W.; Chen, M.Z.; Dai, J.Y.; Zeng, Y.; Zhao, X.; Jin, S.; Cheng, Q.; Cui, T.J. Wireless communications with programmable metasurface: New paradigms, opportunities, and challenges on transceiver design. IEEE Wirel. Commun. 2020, 27, 180–187. [Google Scholar] [CrossRef]
- Zhang, X.G.; Jiang, W.X.; Jiang, H.L.; Wang, Q.; Tian, H.W.; Bai, L.; Luo, Z.J.; Sun, S.; Luo, Y.; Qiu, C.W.; et al. An optically driven digital metasurface for programming electromagnetic functions. Nat. Electron. 2020, 3, 165–171. [Google Scholar] [CrossRef]
- Sun, Y.L.; Zhang, X.G.; Yu, Q.; Jiang, W.X.; Cui, T.J. Infrared-controlled programmable metasurface. Sci. Bull. 2020, 65, 883–888. [Google Scholar] [CrossRef]
- Buijs, R.D.; Wolterink, T.A.W.; Gerini, G.; Verhagen, E.; Koenderink, A.F. Programming metasurface near-fields for nano-optical sensing. Adv. Opt. Mater. 2021, 9, 2100435. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Li, Z.; Cheng, H.; Tang, C.; Li, J.; Chen, S.; Tian, J. Energy-tailorable spin-selective multifunctional metasurfaces with full Fourier components. Adv. Mater. 2019, 31, 1901729. [Google Scholar] [CrossRef]
- Jafar-Zanjani, S.; Inampudi, S.; Mosallaei, H. Adaptive genetic algorithm for optical metasurfaces design. Sci. Rep. 2018, 8, 11040. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.K.; Gao, Y.; Ling, J.; Yuan, Y.; Wang, X.; Song, J.K. Laser processing of microdroplet structure of liquid crystal in 3D. Opt. Express 2022, 30, 26018–26026. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.F.; Zhu, A.Y.; Paniagua Domínguez, R.; Fu, Y.H.; Lukyanchuk, B.; Kuznetsov, A.I. High-transmission dielectric metasurface with 2π phase control at visible wavelengths. Laser Photonics Rev. 2015, 9, 412–418. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X.; Kenney, M.; Su, X.; Xu, N.; Ouyang, C.; Shi, Y.; Han, J.; Zhang, W.; Zhang, S. Broadband metasurfaces with simultaneous control of phase and amplitude. Adv. Mater. 2014, 26, 5031–5036. [Google Scholar] [CrossRef]
- Chen, S.; Li, Z.; Zhang, Y.; Cheng, H.; Tian, J. Phase manipulation of electromagnetic waves with metasurfaces and its applications in nanophotonics. Adv. Opt. Mater. 2018, 6, 1800104. [Google Scholar] [CrossRef]
- Ren, H.; Fang, X.; Jang, J.; Bürger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 2020, 15, 948–955. [Google Scholar] [CrossRef]
- Tang, Y.; Cohen, A.E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 2010, 104, 163901. [Google Scholar] [CrossRef]
- Dai, W.G.; He, D.N. Selective photoelectrochemical oxidation of chiral ibuprofen enantiomers. Acta Phys. Chim. Sin. 2017, 33, 960–967. [Google Scholar] [CrossRef]
- Ben Moshe, A.; Szwarcman, D.; Markovich, G. Size dependence of chiroptical activity in colloidal quantum dots. ACS Nano 2011, 5, 9034–9043. [Google Scholar] [CrossRef] [PubMed]
- Polavarapu, P.L. Volume 2: Applications in Stereochemical Analysis of Synthetic Compounds, Natural Products, and Biomolecules. In Comprehensive Chiroptical Spectroscopy; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tsukube, H.; Shinoda, S. Lanthanide complexes in molecular recognition and chirality sensing of biological substrates. Chem. Rev. 2002, 102, 2389–2404. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, F.; Winsor, T.; Liu, Y. Optical chiral metamaterials: A review of the fundamentals, fabrication methods and applications. Nanotechnology 2016, 27, 412001. [Google Scholar] [CrossRef]
- Guo, J.-K.; Sandaruwan, W.; Li, J.; Ling, J.; Yuan, Y.; Liu, X.; Li, Q.; Wang, X. Recent Progress in Droplet Structure Machining for Advanced Optics. Micromachines 2024, 15, 337. [Google Scholar] [CrossRef]
- Pan, C.C.; Bae, M.; Wang, H.; Lim, J.; Unnithan, R.R.; Yang, J.K.W.; Chung, H.; Kim, S. Inverse design of chiral structures for giant helical dichroism. Nanoscale Horiz. 2025, 10, 1077–1083. [Google Scholar] [CrossRef]
- Lin, L.; Lepeshov, S.; Krasnok, A.; Jiang, T.; Peng, X.; Korgel, B.A.; Alu, A.; Zheng, Y. All-optical reconfigurable chiral meta-molecules. Mater. Today 2019, 25, 10–20. [Google Scholar] [CrossRef]
- Oh, S.S.; Hess, O. Chiral metamaterials: Enhancement and control of optical activity and circular dichroism. Nano Converg. 2015, 2, 24. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Ding, G.; Hu, G.; Jin, Z.; Zhao, J.; Feng, Y.; Jiang, T.; Alu, A.; Qiu, C.W. Directional Janus metasurface. Adv. Mater. 2020, 32, 1906352. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Yue, Z.; Zheng, C.; Wang, G.; Liu, J.; Xu, H.; Song, C.; Yang, F.; Li, H.; et al. Structured vector field manipulation of terahertz wave along the propagation direction based on dielectric metasurfaces. Laser Photonics Rev. 2022, 16, 2200325. [Google Scholar] [CrossRef]
- Li, Z.; Kim, M.H.; Wang, C.; Han, Z.; Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Agarwal, A.M.; Lončar, M.; et al. Controlling propagation and coupling of waveguide modes using phase-gradient metasurfaces. Nat. Nanotechnol. 2017, 12, 675–683. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Feng, Y. A review of recent progress on directional metasurfaces: Concept, design, and application. J. Phys. D Appl. Phys. 2022, 55, 383001. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, W.; Park, C.I.; Oh, J.H. Elastic wave energy entrapment for reflectionless metasurface. Phys. Rev. Appl. 2020, 13, 054036. [Google Scholar] [CrossRef]
- Karimi, E.; Schulz, S.A.; De Leon, I.; Qassim, H.; Upham, J.; Boyd, R.W. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface. Light Sci. Appl. 2014, 3, e167. [Google Scholar] [CrossRef]
- Plum, E.; Liu, X.X.; Fedotov, V.A.; Chen, Y.; Tsai, D.P.; Zheludev, N.I. Metamaterials: Optical activity without chirality. Phys. Rev. Lett. 2009, 102, 113902. [Google Scholar] [CrossRef]
- Hong, Q.; Xu, W.; Zhang, J.; Zhu, Z.; Yuan, X.; Qin, S. Optical activity in monolayer black phosphorus due to extrinsic chirality. Opt. Lett. 2019, 44, 1774–1777. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Rubin, N.A.; Zaidi, A.; Tamagnone, M.; Capasso, F. Metasurface optics for on-demand polarization transformations along the optical path. Nat. Photonics 2021, 15, 287–296. [Google Scholar] [CrossRef]
- Xu, H.X.; Hu, G.; Wang, Y.; Wang, C.; Wang, M.; Wang, S.; Huang, Y.; Genevet, P.; Huang, W.; Qiu, C.W. Polarization-insensitive 3D conformal-skin metasurface cloak. Light Sci. Appl. 2021, 10, 75. [Google Scholar] [CrossRef]
- Jo, J.; Lee, S.; Bae, M.; Nelson, D.; Crozier, K.B.; Yu, N.; Chung, H.; Kim, S. Inverse designed ws2 planar chiral metasurface with geometric phase. J. Opt. 2024, 26, 085101. [Google Scholar] [CrossRef]
- Akram, M.R.; Mehmood, M.Q.; Tauqeer, T.; Rana, A.S.; Rukhlenko, I.D.; Zhu, W. Highly efficient generation of Bessel beams with polarization insensitive metasurfaces. Opt. Express 2019, 27, 9467–9480. [Google Scholar] [CrossRef]
- Cai, Y.; Huang, Y.; Zhu, K.; Wu, H. Symmetric metasurface with dual band polarization-independent high-Q resonances governed by symmetry-protected BIC. Opt. Lett. 2021, 46, 4049–4052. [Google Scholar] [CrossRef] [PubMed]
- Kruk, S.S.; Poddubny, A.N.; Powell, D.A.; Helgert, C.; Decker, M.; Pertsch, T.; Neshev, D.N.; Kivshar, Y.S. Polarization properties of optical metasurfaces of different symmetries. Phys. Rev. B 2015, 91, 195401. [Google Scholar] [CrossRef]
- Fasman, G.D. (Ed.) Circular Dichroism and the Conformational Analysis of Biomolecules; Springer: Boston, MA, USA, 2013. [Google Scholar]
- Genet, C. Chiral light–chiral matter interactions: An optical force perspective. ACS Photonics 2022, 9, 319–332. [Google Scholar] [CrossRef]
- García-Etxarri, A.; Dionne, J.A. Surface-enhanced circular dichroism spectroscopy mediated by nonchiral nanoantennas. Phys. Rev. B 2013, 87, 235409. [Google Scholar] [CrossRef]
- Solomon, M.L.; Hu, J.; Lawrence, M.; García-Etxarri, A.; Dionne, J.A.; Uehara, H. Enantiospecific optical enhancement of chiral sensing and separation with dielectric metasurfaces. ACS Photonics 2018, 6, 43–49. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Mun, J.; Kim, M.; Yang, Y.; Badloe, T.; Ni, J.; Chen, Y.; Qiu, C.W.; Rho, J. Electromagnetic chirality: From fundamentals to nontraditional chiroptical phenomena. Light Sci. Appl. 2020, 9, 139. [Google Scholar] [CrossRef] [PubMed]
- Kruk, S.; Kivshar, Y. Functional meta-optics and nanophotonics governed by Mie resonances. ACS Photonics 2017, 4, 2638–2649. [Google Scholar] [CrossRef]
- Jahani, S.; Jacob, Z. All-dielectric metamaterials. Nat. Nanotechnol. 2016, 11, 23–36. [Google Scholar] [CrossRef]
- Li, D.; Li, Y. An aberration-corrected single layer metasurface with large field of view. Opt. Commun. 2023, 530, 129195. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Y.; Zhang, C.; Yuan, Y.; Li, Q.; Wang, X. Design of short-focus near-eye optical system for virtual reality using polarization-insensitive metasurface. Phys. Scr. 2024, 99, 105540. [Google Scholar] [CrossRef]
- Hentschel, M.; Schäferling, M.; Weiss, T.; Liu, N.; Giessen, H. Three-dimensional chiral plasmonic oligomers. Nano Lett. 2012, 12, 2542–2547. [Google Scholar] [CrossRef]
- Oh, S.S.; Demetriadou, A.; Wuestner, S.; Hess, O. On the origin of chirality in nanoplasmonic gyroid metamaterials. Adv. Mater. 2012, 25, 612–617. [Google Scholar] [CrossRef] [PubMed]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; von Freymann, G.; Linden, S.; Wegener, M. Gold helix photonic metamaterial as broadband circular polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Liu, Z.; Deng, J.; Li, K.; Li, J.; Li, G. Nano-Kirigami metasurface with giant nonlinear optical circular dichroism. Laser Photonics Rev. 2020, 14, 2000085. [Google Scholar] [CrossRef]
- Lee, H.E.; Ahn, H.Y.; Mun, J.; Lee, Y.Y.; Kim, M.; Cho, N.H.; Chang, K.; Kim, W.S.; Rho, J.; Nam, K.T. Amino-acid- and peptide-directed synthesis of chiral plasmonic gold nanoparticles. Nature 2018, 556, 360–365. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Stec, G.J.; Kim, H.K.; Thapa, S.; Zheng, S.L.; McClelland, A.; Mason, J.A. Self-assembly of chiroptical ionic co-crystals from silver nanoclusters and organic macrocycles. Nat. Chem. 2025; in press. [Google Scholar] [CrossRef]
- Lao, Z.; Liu, X.; Qi, Q.; Zhao, Y. Bidirectionally symmetric self-assembly of switchable chiral microstructures based on angle compensation and pH regulation strategy for chiroptical metamaterials. Adv. Funct. Mater. 2025; in press. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Adamo, G.; Teh, B.H.; Wu, Q.Y.S.; Teng, J.; Sun, H.; Zhao, Y. A novel chiral metasurface with controllable circular dichroism induced by coupling localized and propagating modes. Sci. Rep. 2016, 6, 30309. [Google Scholar] [CrossRef]
- Ye, W.; Yuan, X.; Guo, C.; Zhang, J.; Yang, B.; Zhang, S. Large chiroptical effects in planar chiral metamaterials. Phys. Rev. Appl. 2017, 7, 054003. [Google Scholar] [CrossRef]
- Zu, S.; Bao, Y.; Fang, Z. Planar plasmonic chiral nanostructures. Nanoscale 2016, 8, 3900–3905. [Google Scholar] [CrossRef]
- Cao, T.; Wei, C.; Li, Y. Dual-band strong extrinsic 2D chirality in a highly symmetric metal-dielectric-metal achiral metasurface. Opt. Mater. Express 2016, 6, 303–311. [Google Scholar] [CrossRef]
- Horrer, A.; Zhang, Y.; Gérard, D.; Béal, J.; Kociak, M.; Plain, J.; Bachelot, R. Local optical chirality induced by near-field mode interference in achiral plasmonic metamolecules. Nano Lett. 2019, 20, 509–516. [Google Scholar] [CrossRef]
- Kang, L.; Wang, C.Y.; Guo, X.; Ni, X.; Liu, Z.; Werner, D.H. Nonlinear chiral meta-mirrors: Enabling technology for ultrafast switching of light polarization. Nano Lett. 2020, 20, 2047–2055. [Google Scholar] [CrossRef] [PubMed]
- Kilic, U.; Hilfiker, M.; Wimer, S.; Ruder, A.; Schubert, E.; Schubert, M.; Argyropoulos, C. Controlling the broadband enhanced light chirality with L-shaped dielectric metamaterials. Nat. Commun. 2024, 15, 3757. [Google Scholar] [CrossRef]
- Kühner, L.; Wendisch, F.J.; Antonov, A.A.; Bürger, J.; Hüttenhofer, L.; de S. Menezes, L.; Maier, S.A.; Gorkunov, M.V.; Kivshar, Y.; Tittl, A. Unlocking the out-of-plane dimension for photonic bound states in the continuum to achieve maximum optical chirality. Light Sci. Appl. 2023, 12, 250. [Google Scholar] [CrossRef]
- Li, J.; Duan, Q.; Dong, X.; Yang, Z.; Xie, Z.; Zhu, S.; Chen, H. Chiral quasi-bound states in the continuum for refractive-index sensing in metasurfaces. Phys. Rev. Appl. 2024, 22, 044035. [Google Scholar] [CrossRef]
- Wu, C.; Arju, N.; Kelp, G.; Fan, J.A.; Dominguez, J.; Gonzales, E.; Tutuc, E.; Brener, I.; Shvets, G. Spectrally selective chiral silicon metasurfaces based on infrared Fano resonances. Nat. Commun. 2014, 5, 3892. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Li, Y.; Li, Y.; Gong, Y.; Maier, S.A.; Hong, M. All-dielectric planar chiral metasurface with gradient geometric phase. Opt. Express 2018, 26, 6067–6078. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Xie, S.; Nan, H.; Sun, S.; Shen, W.; Yang, J.; Guan, X. Chiral quasi-bound states in the continuum of a dielectric metasurface for optical monitoring and temperature sensing. Photonics 2023, 10, 980. [Google Scholar] [CrossRef]
- Li, J.; Yue, Z.; Li, J.; Zheng, C.; Yang, D.; Wang, S.; Li, M.; Zhang, Y.; Yao, J. Ultra-narrowband terahertz circular dichroism driven by planar metasurface supporting chiral quasi bound states in continuum. Opt. Laser Technol. 2023, 161, 109173. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, T.; Lei, L.; Deng, W.; Wang, T.; Liao, Q.; Liu, W.; Xiao, S.; Yu, T. Tailoring intrinsic chirality in a two-dimensional planar waveguide grating via quasibound states in the continuum. Phys. Rev. B 2024, 109, 205403. [Google Scholar] [CrossRef]
- Toftul, I.; Tonkaev, P.; Koshelev, K.; Lai, F.; Song, Q.; Gorkunov, M.; Kivshar, Y. Chiral dichroism in resonant metasurfaces with monoclinic lattices. Phys. Rev. Lett. 2024, 133, 216901. [Google Scholar] [CrossRef]
- Zhao, Y.; Askarpour, A.N.; Sun, L.; Shi, J.; Li, X.; Alù, A. High-sensitivity chiral molecular sensing with optical metasurfaces. In Proceedings of the CLEO: QELS_Fundamental Science, San Jose, CA, USA, 8–13 June 2014. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhong, C.; Fan, F.; Liu, G.; Chang, S. Terahertz polarization and chirality sensing for amino acid solution based on chiral metasurface sensor. Sens. Actuators B Chem. 2021, 330, 129315. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, C.; Zhang, Y.; Qiu, C.W. Integrated molar chiral sensing based on high-Q metasurface. Nano Lett. 2020, 20, 8696–8703. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, T.; Tan, Z.; Cheng, J.; Chang, S.; Fan, F. Chiral enantiomer recognition of amino acids enhanced by terahertz spin beam separation based on a Pancharatnam–Berry metasurface. Opt. Lett. 2023, 48, 440–443. [Google Scholar] [CrossRef]
- Luo, M.; Zhou, Y.; Zhao, X.; Guo, Z.; Li, Y.; Wang, Q.; Liu, J.; Luo, W.; Shi, Y.; Liu, A.Q.; et al. High-sensitivity optical sensors empowered by quasi-bound states in the continuum in a hybrid metal–dielectric metasurface. ACS Nano 2024, 18, 6477–6486. [Google Scholar] [CrossRef]
- Probst, P.T.; Mayer, M.; Gupta, V.; Steiner, A.M.; Zhou, Z.; Auernhammer, G.K.; König, T.A.F.; Fery, A. Mechano-tunable chiral metasurfaces via colloidal assembly. Nat. Mater. 2021, 20, 1024–1028. [Google Scholar] [CrossRef] [PubMed]
- Sha, X.; Du, K.; Zeng, Y.; Lai, F.; Yin, J.; Zhang, H.; Song, B.; Han, J.; Xiao, S.; Kivshar, Y.; et al. Chirality tuning and reversing with resonant phase-change metasurfaces. Sci. Adv. 2024, 10, eadn9017. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, J.; Gu, L.; Hu, H.; Zhan, Q. Wavelength-tunable infrared metasurfaces with chiral bound states in the continuum. Sci. Rep. 2025, 15, 128. [Google Scholar] [CrossRef] [PubMed]
- Lv, S.; Hu, F.; Luo, W.; Xu, H.; An, L. Design of tunable selective light-absorbing metasurfaces driven by intrinsically chiral quasi-bound states in the continuum. Opt. Express 2024, 32, 30053–30064. [Google Scholar] [CrossRef]
- Zhang, F.; Pu, M.; Li, X.; Gao, P.; Li, X.; Ma, X.; Luo, X. All-dielectric metasurfaces for simultaneous giant circular asymmetric transmission and wavefront shaping based on asymmetric photonic spin–orbit interactions. Adv. Funct. Mater. 2017, 27, 1704295. [Google Scholar] [CrossRef]
- Zhang, J.C.; Chen, M.K.; Liang, Y.; Hong, X.; Wang, M.; Cheng, Y.; Liu, X.; Tsai, D.P.; Pang, S.W. Nanoimprint meta-device for chiral imaging. Adv. Funct. Mater. 2023, 33, 2306422. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhou, W.; Zhang, H.; Wang, Y.; Zong, H.; Wang, Y.; Dong, Y.; Burokur, S.N.; Zhang, K. Full-polarimetric synthesized holographic displaying empowered by chirality-assisted metasurface. Small Sci. 2024, 4, 2400138. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.; Wong, P.W.H.; Cheah, K.W.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef]
- Huang, L.; Mühlenbernd, H.; Li, X.; Song, X.; Bai, B.; Wang, Y.; Zentgraf, T. Broadband hybrid holographic multiplexing with geometric metasurfaces. Adv. Mater. 2015, 27, 6444–6449. [Google Scholar] [CrossRef]
- Zhao, R.; Sain, B.; Wei, Q.; Yang, J.; Zhang, X.; Cui, T.J.; Capasso, F.; Qiu, C.W. Multichannel vectorial holographic display and encryption. Light Sci. Appl. 2018, 7, 95. [Google Scholar] [CrossRef]
- Li, T.; Li, X.; Yan, S.; Xu, X.; Wang, S.; Yao, B.; Wang, Z.; Zhu, S. Generation and conversion dynamics of dual Bessel beams with a photonic spin-dependent dielectric metasurface. Phys. Rev. Appl. 2021, 15, 014059. [Google Scholar] [CrossRef]
- Zhou, Q.; Yang, C.; Lin, P.; Zhang, Y.; Zhao, A.; Zhang, H.; Ren, Y.; Long, Z.; Lu, Y.-Q.; Xu, T. Far-field phase-shifting structured light illumination enabled by polarization multiplexing metasurface for super-resolution imaging. Nano Lett. 2024, 24, 11036–11042. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, H.; Chen, C.F.; Zhao, G.; Li, G.; Wu, Q.; Luo, H.; Wen, S.; Liu, Z. Optical edge detection based on high-efficiency dielectric metasurface. Proc. Natl. Acad. Sci. USA 2019, 116, 11137–11140. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Qian, H.; Zhao, J.; Tang, M.; Wu, Q.; Lei, M.; Luo, H.; Wen, S.; Chen, S.; Liu, Z. Two-dimensional optical spatial differentiation and high-contrast imaging. Natl. Sci. Rev. 2021, 8, nwaa176. [Google Scholar] [CrossRef]
- Engay, E.; Huo, D.; Malureanu, R.; Bunea, A.I.; Lavrinenko, A. Polarization-dependent all-dielectric metasurface for single-shot quantitative phase imaging. Nano Lett. 2021, 21, 3820–3826. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-insensitive metalenses at visible wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Hu, J.; Ma, S.; Xu, F.; Wang, C. Polarization-insensitive achromatic metalens based on computational wavefront coding. Opt. Express 2021, 29, 31902–31914. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, Y.; Jiang, M.; Han, T.; Chi, C.; Lin, F.; Fang, Z.; Li, Y. Self-learning perfect optical chirality via a deep neural network. Phys. Rev. Lett. 2019, 123, 213902. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Cheng, F.; Xu, Y.; Wen, Q.; Liu, Y. Probabilistic representation and inverse design of metamaterials based on a deep generative model with semi-supervised learning strategy. Adv. Mater. 2019, 31, 1901111. [Google Scholar] [CrossRef]
- Hou, Z.; Zheng, C.; Li, J.; Zhang, P.; Li, S.; Zheng, S.; Shen, J.; Yao, J.; Li, C. On-demand design based on deep learning and phase manipulation of all-silicon terahertz chiral metasurfaces. Results Phys. 2022, 42, 106024. [Google Scholar] [CrossRef]


| Structure Type | Typical Materials | Resonance Mechanism | CD Value (Typical) | Q-Factor | Bandwidth | Fabrication Complexity | CMOS Compatibility | Surface Affinity |
|---|---|---|---|---|---|---|---|---|
| Metallic | Au, Ag, Al | LSPR | 0.1–0.6 | Low (10–50) | Narrow | Medium (etching, self-assembly) | Poor | Strong (near-field) |
| Dielectric | Si, Ge, TiO2, GaN | Mie, q-BIC | 0.6–0.85 | High (100–1000+) | Tunable/Wide | High (EBL, GLAD) | Good | Moderate (internal field) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Li, Y.; Wang, Y.; Li, Y.; Zhang, C. Recent Advances in Chiral and Achiral Metasurfaces Under Symmetry Preservation and Breaking. Symmetry 2025, 17, 1001. https://doi.org/10.3390/sym17071001
Wan X, Li Y, Wang Y, Li Y, Zhang C. Recent Advances in Chiral and Achiral Metasurfaces Under Symmetry Preservation and Breaking. Symmetry. 2025; 17(7):1001. https://doi.org/10.3390/sym17071001
Chicago/Turabian StyleWan, Xingcheng, Yangyang Li, Yixin Wang, Yifan Li, and Chao Zhang. 2025. "Recent Advances in Chiral and Achiral Metasurfaces Under Symmetry Preservation and Breaking" Symmetry 17, no. 7: 1001. https://doi.org/10.3390/sym17071001
APA StyleWan, X., Li, Y., Wang, Y., Li, Y., & Zhang, C. (2025). Recent Advances in Chiral and Achiral Metasurfaces Under Symmetry Preservation and Breaking. Symmetry, 17(7), 1001. https://doi.org/10.3390/sym17071001






