Symmetrical Learning and Transferring: Efficient Knowledge Distillation for Remote Sensing Image Classification
Abstract
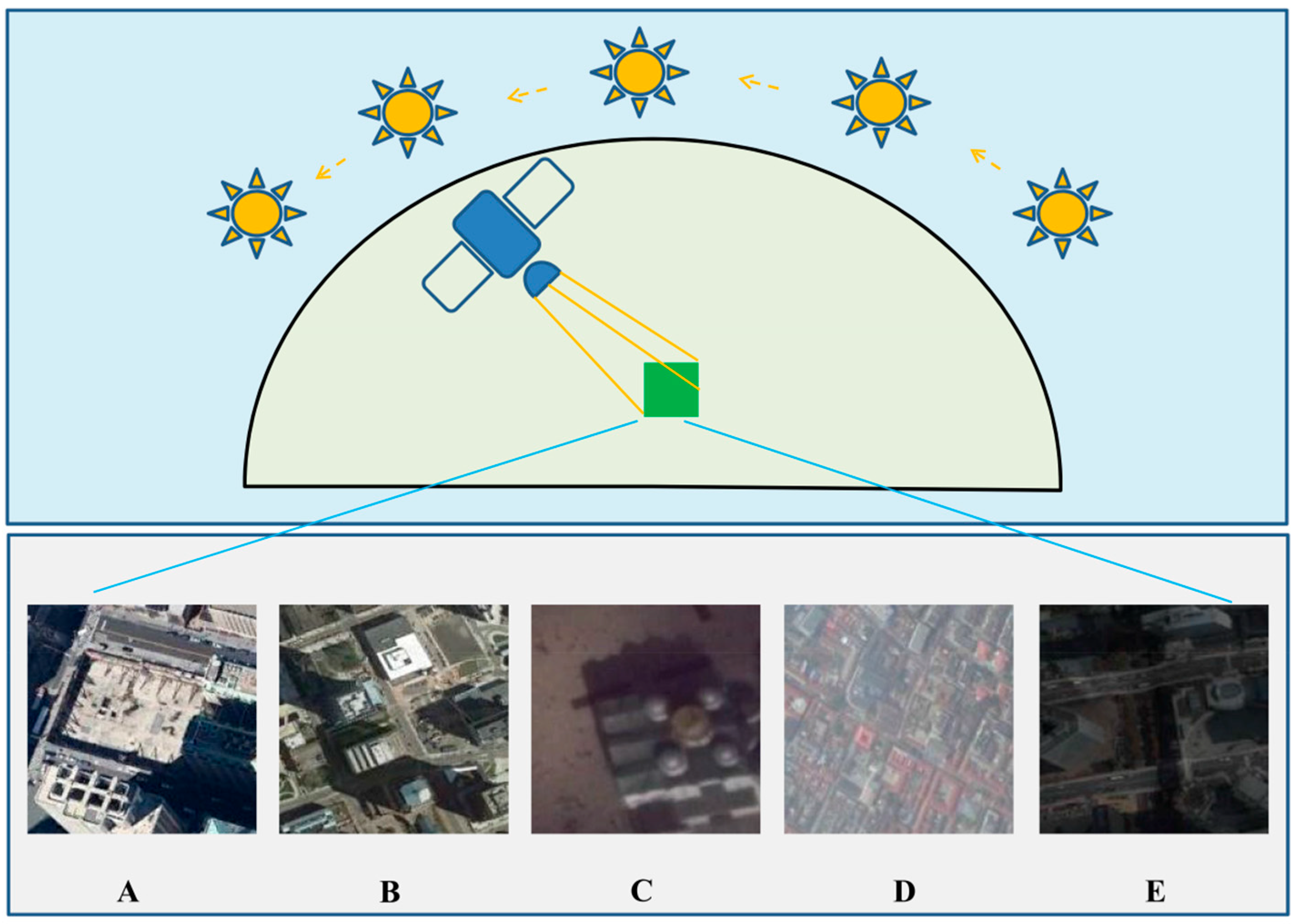
1. Introduction
- (1)
- Symmetry-aware KD: We propose the SLT strategy, which addresses the challenge of preserving symmetry in RSI samples during the KD process. By ensuring that augmented data maintains spatial and feature symmetry, our method enhances the alignment between the teacher and student models, leading to more accurate knowledge transfer and reduced accuracy discrepancies.
- (2)
- Improved KD-based approach for RSI classification: Our approach introduces a symmetry-aware KD method that outperforms previous techniques with accuracy improvements of up to 22.5%. The student model also excels over multi-model strategies by maintaining a consistent, symmetrical feature representation across both training and augmented data, achieving significant reductions in model size (up to 96%) and inference time (up to 88%).
- (3)
- Purely data-driven, symmetry-preserving solution: Our method is entirely data-driven, requiring no architectural changes, and provides a straightforward solution for developing lightweight and accurate RSI classifiers. By focusing on symmetry-preserving data augmentation, regularization, and feature alignment, we achieve high performance without the need for complex model adjustments.
2. Related Works
2.1. Classical Distillation Approaches
2.2. Self-Distillation Approaches
2.3. Lightweight CNN Approaches
2.4. Lightweight Transformer Approaches
2.5. Attention CNN Approaches
2.6. Customized Learning Approaches
2.7. Multiple Model Approaches
2.8. Comparative Summary of Related Approaches
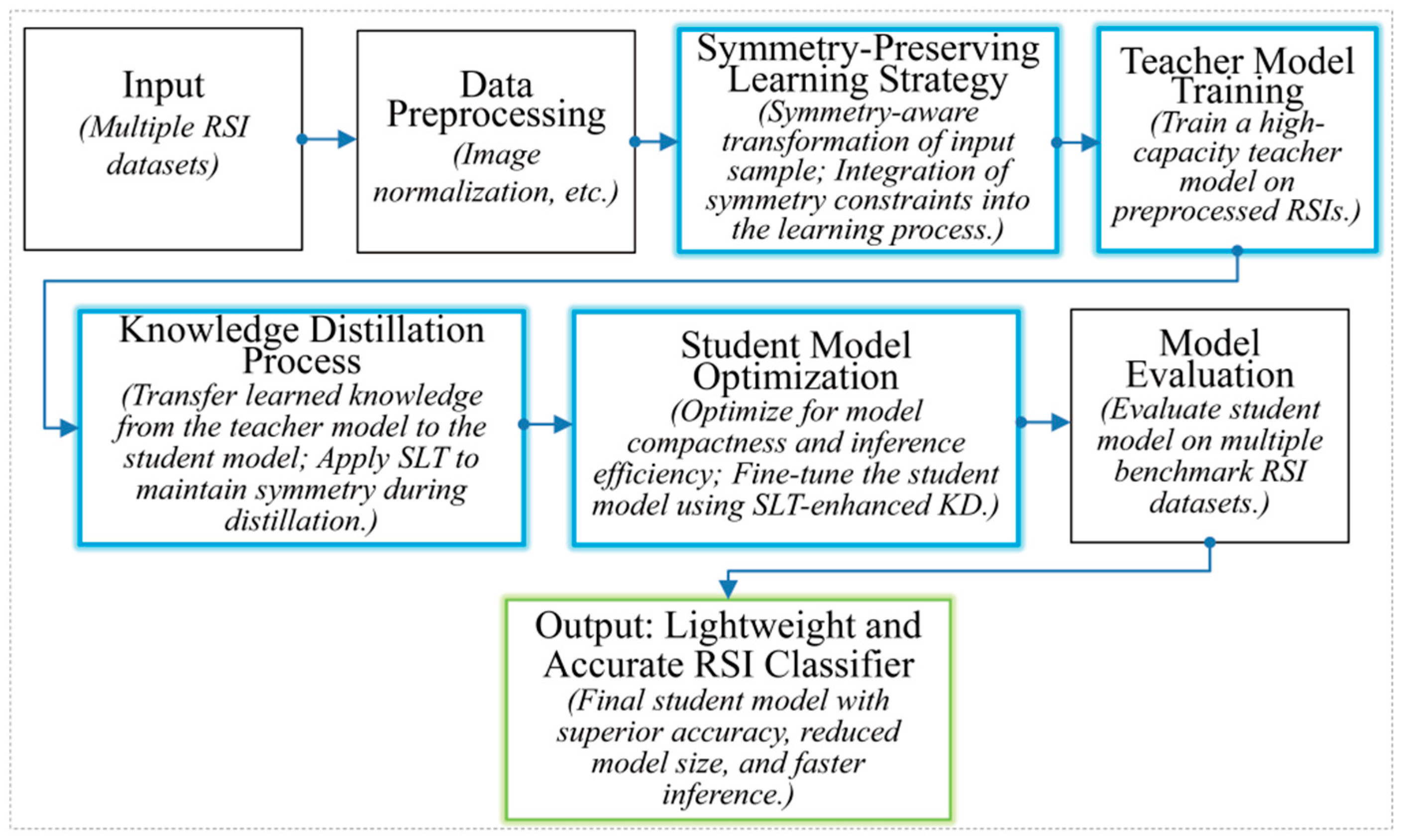
3. Methodologies
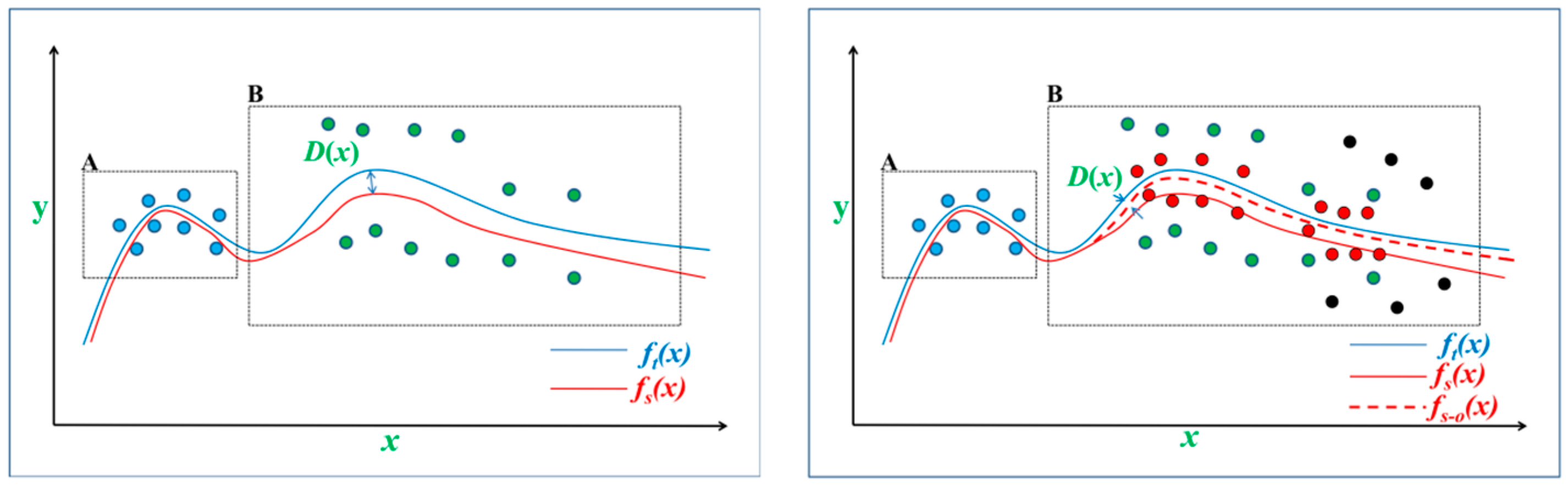
3.1. Qualitative Feature Alignment
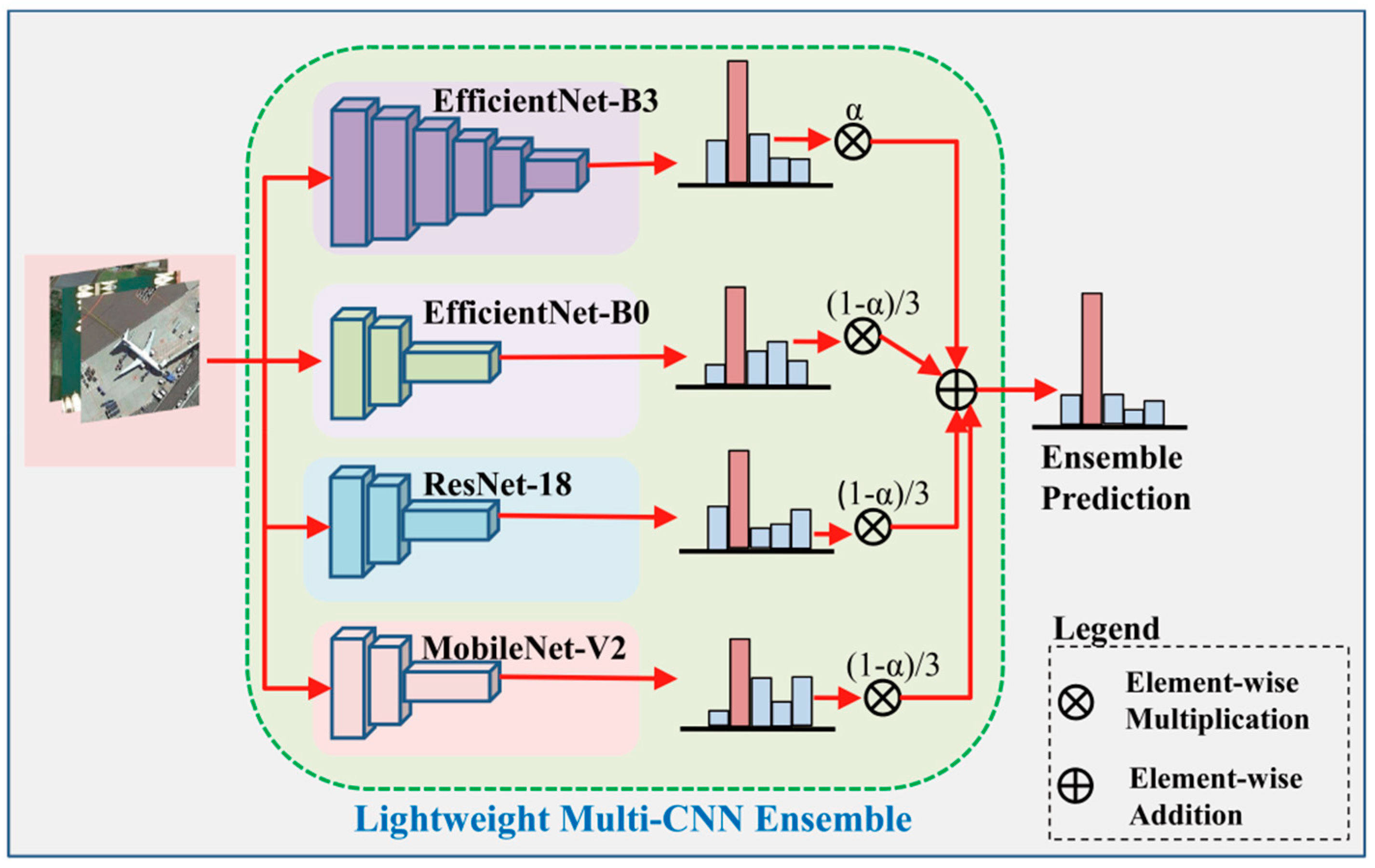
3.2. Architecture of the Teacher Ensemble
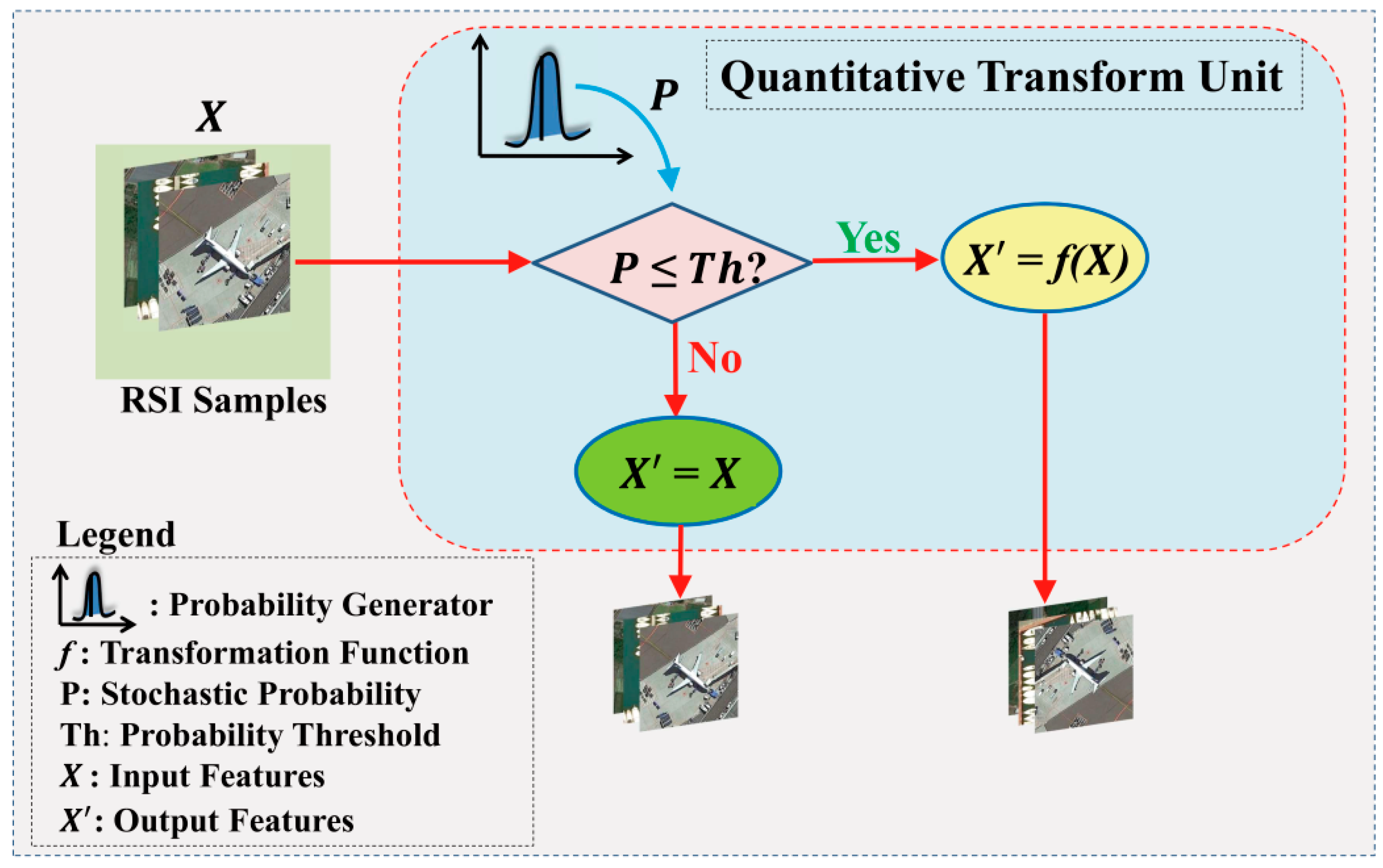
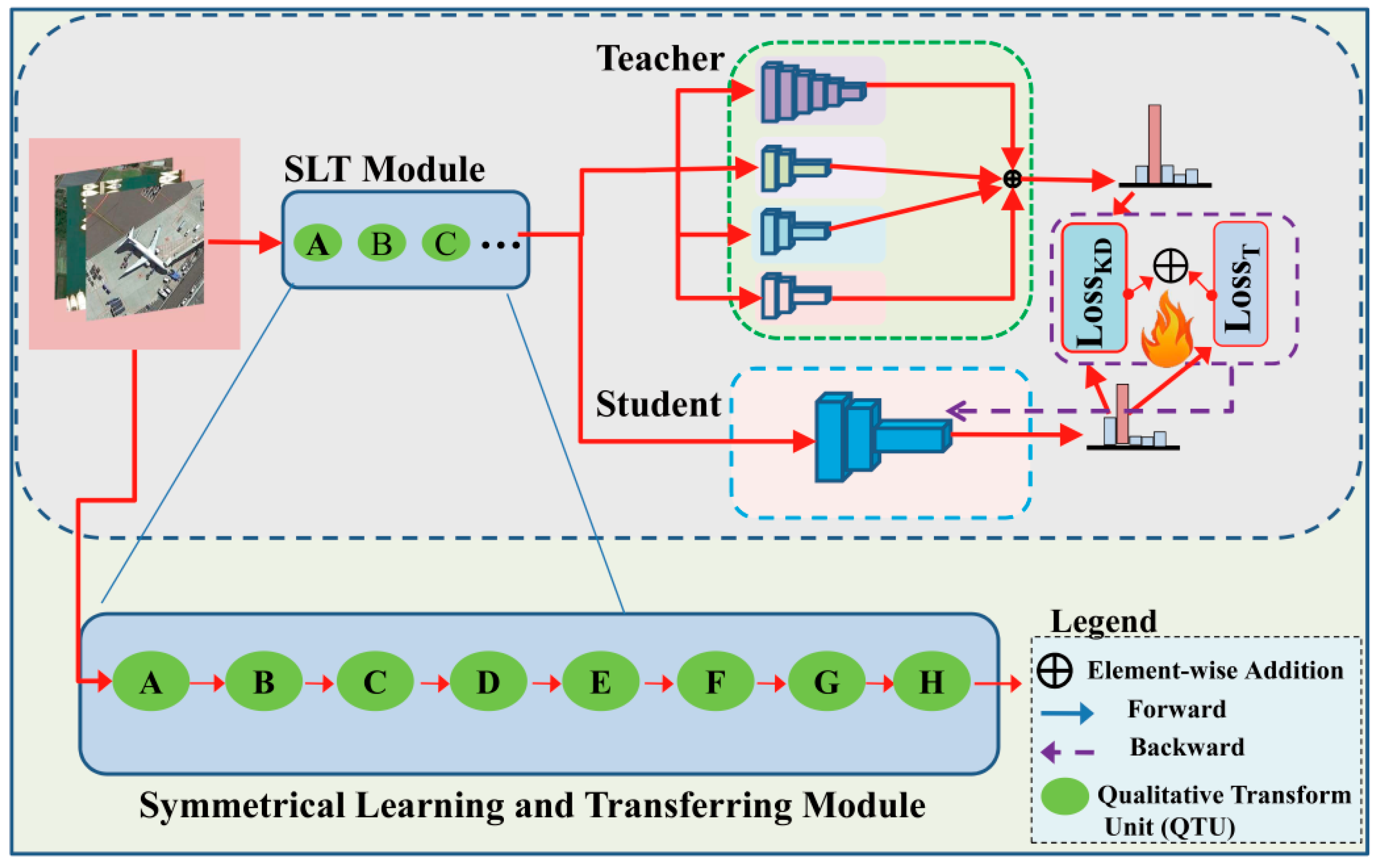
3.3. Symmetrical Learning and Transferring Framework
3.4. KD Loss
3.5. Algorithm for Generating the Teacher Ensemble
| Algorithm 1. Procedures for Generating the Teacher Ensemble (Pseudocode) | ||
| Definition: Let represent the testing dataset. Let , , , , , and represent the same definitions as those in Equation (2). | ||
| Input: images and labels from testing subsets. Output: the accuracy () results of the teacher ensemble. | ||
| Procedures: | ||
| 1: | Generate the teacher ensemble using Equation (3), where is alterable | |
| 2: | Initialize to 0.1. | |
| 3: | FOR i = 1 TO 9 DO | |
| 4: | Calculate the ensemble’s accuracy on using current . | |
| 5: | Increment by 0.1. | |
| 6: | END FOR | |
| 7: | Return the results along with the corresponding . | |
3.6. KD Algorithm
| Algorithm 2. Distillation procedures (Pseudocode) | |||
| Definitions: The training subset for RSI is denoted as , while a batch of samples is denoted as . The ensemble teacher model is represented by , and the student model is represented by . The SLT module is signified by , while and are the same as those in Equation (6). | |||
| Input: images and labels from training or testing subsets. Output: the accuracy () results of the student model. | |||
| Procedures: | |||
| 1 | FOR Epoch = 1 TO 1200 DO | ||
| 2 | FOR iteration = 1 TO DO | ||
| 3 | Sample a batch of samples from , and input them to the functions and , respectively. | ||
| 4 | Predict teacher probabilities using the equation: . | ||
| 5 | Predict student probabilities using the equation: . | ||
| 6 | Calculate the loss using Equation (13). | ||
| 7 | Update the student model’s parameters through back propagation. | ||
| 8 | End For | ||
| 9 | Calculate the student model’s accuracy and save this accuracy. | ||
| 10 | End For | ||
| 11 | Return the results | ||
3.7. CNN Models
3.8. Dataset and Division
3.9. Performance Evaluation Metrics
3.10. Experimental Settings
4. Experimental Results
4.1. OA Results of the Teacher Ensemble
Sensitivity Analysis of the Ensemble Configuration
4.2. OA Results of the Student Models
Analysis of Ensemble Configuration Sensitivity on KD Efficiency
4.3. Performance Comparison with Previous KD Methods
4.3.1. Performance Comparison with Previous Single-Model Methods
4.3.2. Performance Comparison with Previous Multi-Model Methods
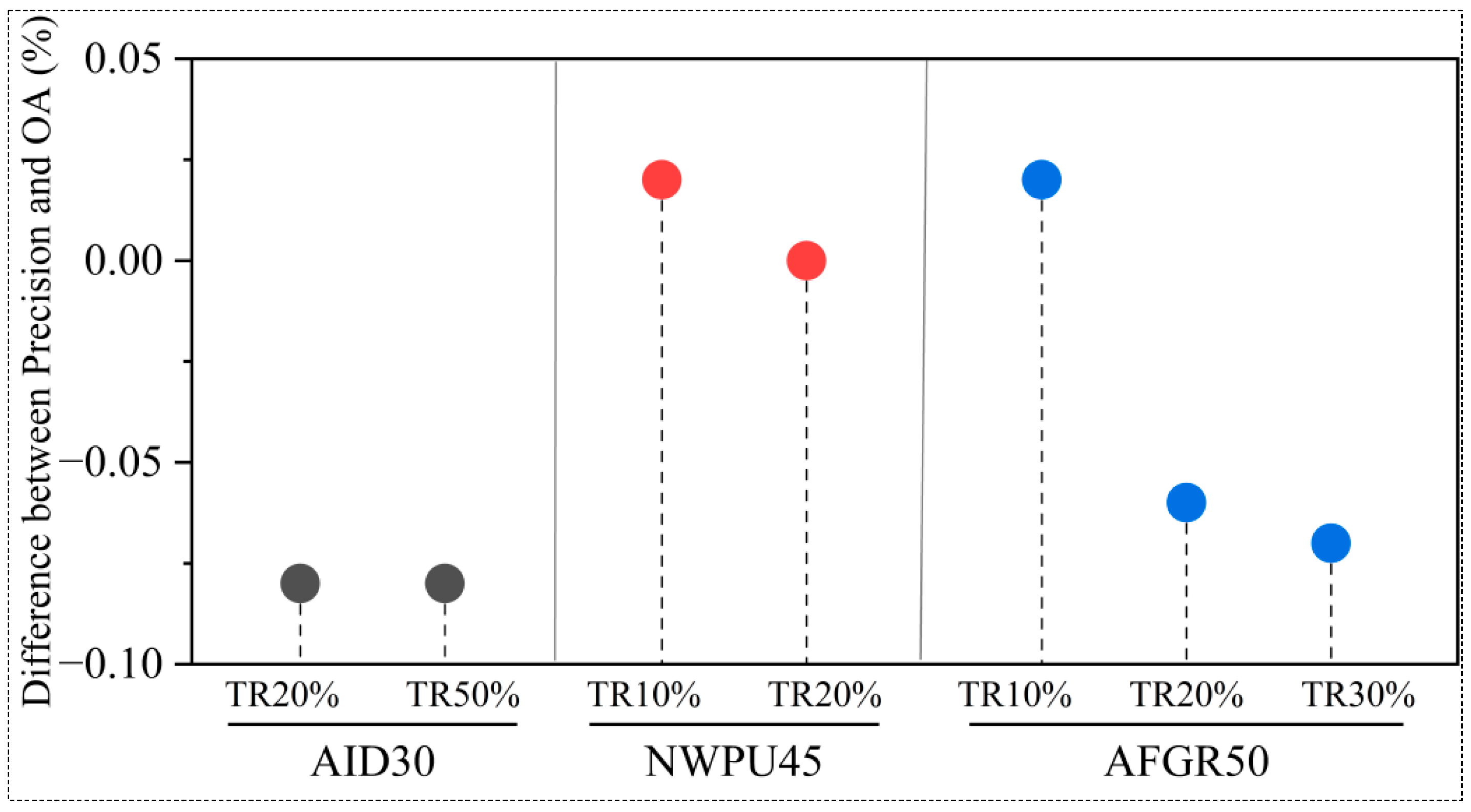
4.3.3. Model Precision Analysis
4.4. Ablation Experiments
4.4.1. Efficacy of Qualitative Feature Alignment
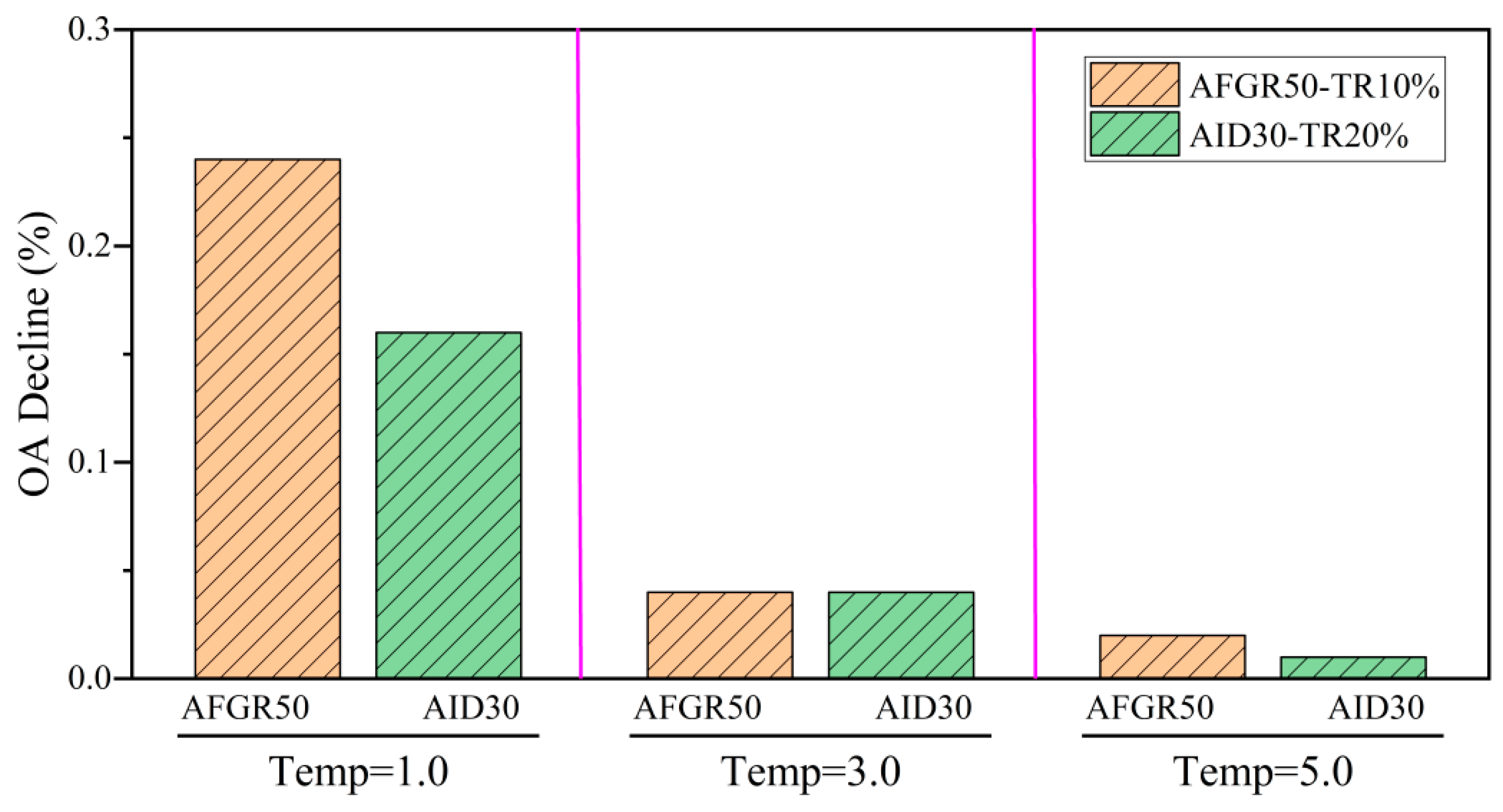
4.4.2. Sensitivity of Distillation Temperature
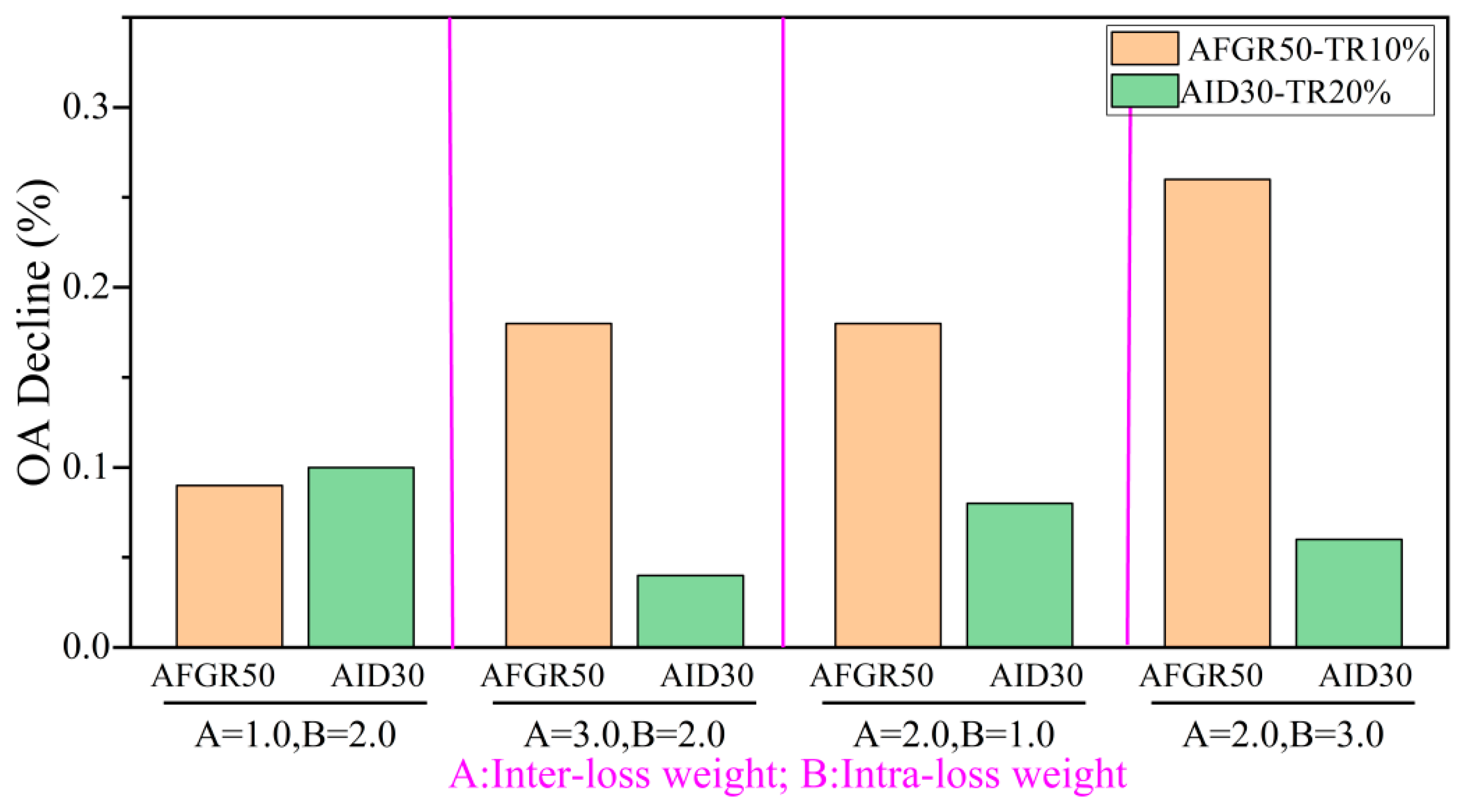
4.4.3. Sensitivity of Weights for Inter- and Intra-Loss
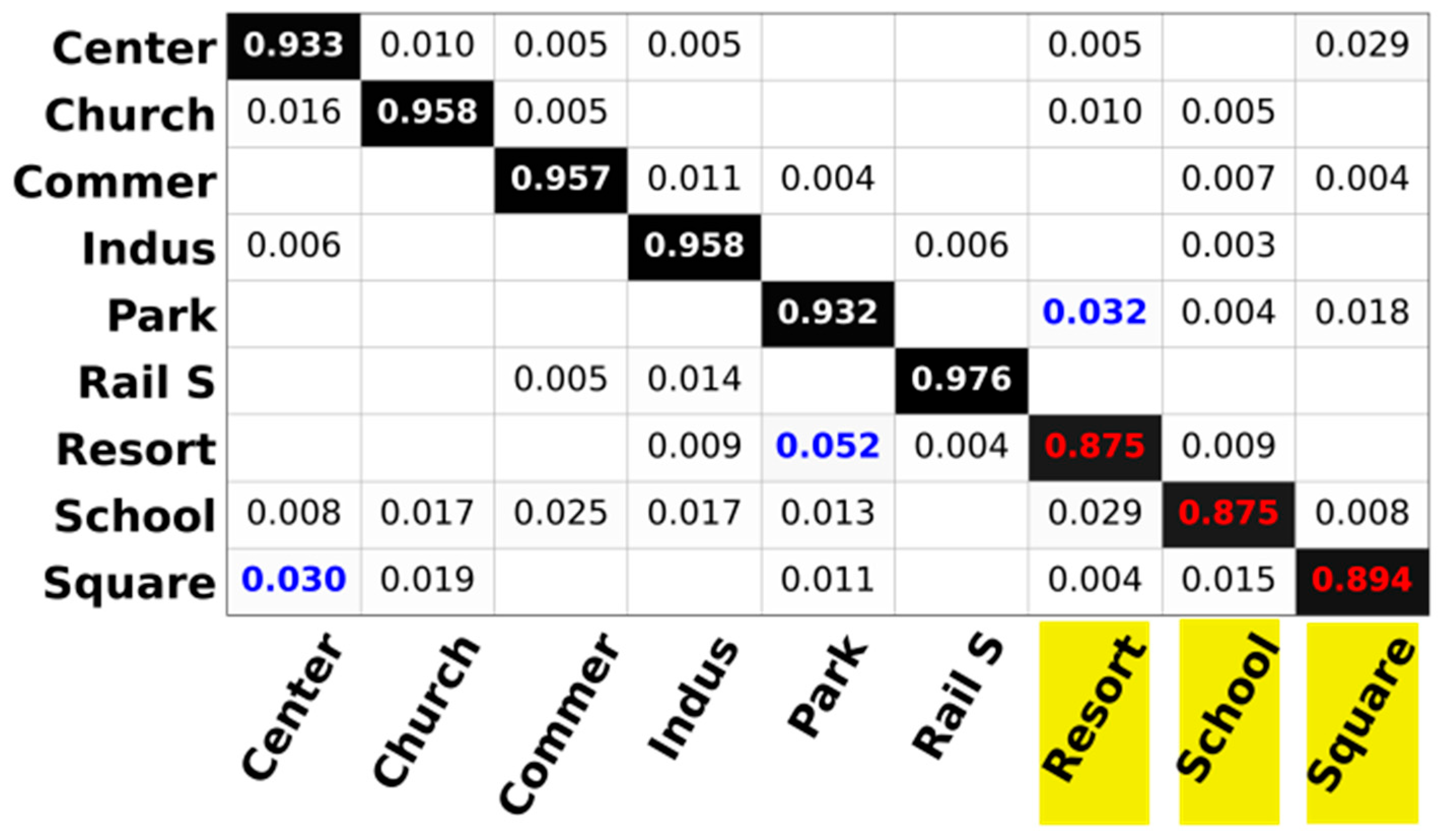
4.5. Confusion Matrix
4.6. Visualization and Analysis
4.7. Evaluation of Computational Efficiency
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Lenton, T.M.; Abrams, J.F.; Bartsch, A.; Bathiany, S.; Boulton, C.A.; Buxton, J.E.; Conversi, A.; Cunliffe, A.M.; Hebden, S.; Lavergne, T.; et al. Remotely sensing potential climate change tipping points across scales. Nat. Commun. 2024, 15, 343. [Google Scholar] [CrossRef] [PubMed]
- Lara-Alvarez, C.; Flores, J.J.; Rodriguez-Rangel, H.; Lopez-Farias, R. A literature review on satellite image time series forecasting: Methods and applications for remote sensing. WIREs Data Min. Knowl. Discov. 2024, 14, e1528. [Google Scholar] [CrossRef]
- Dong, X.; Cao, J.; Zhao, W. A review of research on remote sensing images shadow detection and application to building extraction. Eur. J. Remote Sens. 2024, 57, 2293163. [Google Scholar] [CrossRef]
- Vasquez, J.; Acevedo-Barrios, R.; Miranda-Castro, W.; Guerrero, M.; Meneses-Ospina, L. Determining Changes in Mangrove Cover Using Remote Sensing with Landsat Images: A Review. Water Air Soil Pollut. 2023, 235, 18. [Google Scholar] [CrossRef]
- Dutta, S.; Das, M. Remote sensing scene classification under scarcity of labelled samples—A survey of the state-of-the-arts. Comput. Geosci. 2023, 171, 105295. [Google Scholar] [CrossRef]
- Adegun, A.A.; Viriri, S.; Tapamo, J.-R. Review of deep learning methods for remote sensing satellite images classification: Experimental survey and comparative analysis. J. Big Data 2023, 10, 93. [Google Scholar] [CrossRef]
- Chong, Q.; Ni, M.; Huang, J.; Wei, G.; Li, Z.; Xu, J. Rethinking high-resolution remote sensing image segmentation not limited to technology: A review of segmentation methods and outlook on technical interpretability. Int. J. Remote Sens. 2024, 45, 3689–3716. [Google Scholar] [CrossRef]
- Zhao, H.; Morgenroth, J.; Pearse, G.; Schindler, J. A Systematic Review of Individual Tree Crown Detection and Delineation with Convolutional Neural Networks (CNN). Curr. For. Rep. 2023, 9, 149–170. [Google Scholar] [CrossRef]
- Xu, T.; Zhao, Z.; Wu, J. Breaking the ImageNet Pretraining Paradigm: A General Framework for Training Using Only Remote Sensing Scene Images. Appl. Sci. 2023, 13, 11374. [Google Scholar] [CrossRef]
- Ma, Y.; Meng, J.; Liu, B.; Sun, L.; Zhang, H.; Ren, P. Dictionary Learning for Few-Shot Remote Sensing Scene Classification. Remote Sens. 2023, 15, 773. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, S.; Wu, W.; Guo, W.; Li, X.; Xia, G.; Zhao, Z. NaSC-TG2: Natural Scene Classification with Tiangong-2 Remotely Sensed Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3228–3242. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A Survey on Vision Transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Kumari, M.; Kaul, A. Recent advances in the application of vision transformers to remote sensing image scene classification. Remote Sens. Lett. 2023, 14, 722–732. [Google Scholar] [CrossRef]
- Fayad, I.; Ciais, P.; Schwartz, M.; Wigneron, J.-P.; Baghdadi, N.; de Truchis, A.; D’ASpremont, A.; Frappart, F.; Saatchi, S.; Sean, E.; et al. Hy-TeC: A hybrid vision transformer model for high-resolution and large-scale mapping of canopy height. Remote Sens. Environ. 2024, 302, 113945. [Google Scholar] [CrossRef]
- Song, H. MBC-Net: Long-range enhanced feature fusion for classifying remote sensing images. Int. J. Intell. Comput. Cybern. 2024, 17, 181–209. [Google Scholar] [CrossRef]
- Song, H.; Yuan, Y.; Ouyang, Z.; Yang, Y.; Xiang, H. Quantitative regularization in robust vision transformer for remote sensing image classification. Photogramm. Rec. 2024, 39, 340–372. [Google Scholar] [CrossRef]
- Song, H.; Xia, H.; Wang, W.; Zhou, Y.; Liu, W.; Liu, Q.; Liu, J. QAGA-Net: Enhanced vision transformer-based object detection for remote sensing images. Int. J. Intell. Comput. Cybern. 2025, 18, 133–152. [Google Scholar] [CrossRef]
- Song, H.; Xie, J.; Wang, Y.; Fu, L.; Zhou, Y.; Zhou, X. Optimized Data Distribution Learning for Enhancing Vision Transformer-Based Object Detection in Remote Sensing Images. Photogramm. Rec. 2025, 40, e70004. [Google Scholar] [CrossRef]
- Cao, Z.; Kooistra, L.; Wang, W.; Guo, L.; Valente, J. Real-Time Object Detection Based on UAV Remote Sensing: A Systematic Literature Review. Drones 2023, 7, 620. [Google Scholar] [CrossRef]
- Tang, W.; He, F.; Bashir, A.K.; Shao, X.; Cheng, Y.; Yu, K. A remote sensing image rotation object detection approach for real-time environmental monitoring. Sustain. Energy Technol. Assess. 2023, 57, 103270. [Google Scholar] [CrossRef]
- Pal, M. Deep learning algorithms for hyperspectral remote sensing classifications: An applied review. Int. J. Remote Sens. 2024, 45, 451–491. [Google Scholar] [CrossRef]
- Wang, R.; Ma, L.; He, G.; Johnson, B.A.; Yan, Z.; Chang, M.; Liang, Y. Transformers for Remote Sensing: A Systematic Review and Analysis. Sensors 2024, 24, 3495. [Google Scholar] [CrossRef] [PubMed]
- Thapa, A.; Horanont, T.; Neupane, B.; Aryal, J. Deep Learning for Remote Sensing Image Scene Classification: A Review and Meta-Analysis. Remote Sens. 2023, 15, 4804. [Google Scholar] [CrossRef]
- Song, H.; Xie, H.; Duan, Y.; Xie, X.; Gan, F.; Wang, W.; Liu, J. Pure data correction enhancing remote sensing image classification with a lightweight ensemble model. Sci. Rep. 2025, 15, 5507. [Google Scholar] [CrossRef]
- Lee, G.Y.; Dam, T.; Ferdaus, M.M.; Poenar, D.P.; Duong, V.N. Unlocking the capabilities of explainable few-shot learning in remote sensing. Artif. Intell. Rev. 2024, 57, 169. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, C.; Zhang, B.; He, Y. Triplet Contrastive Learning Framework with Adversarial Hard-Negative Sample Generation for Multimodal Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5506015. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Li, T.; Li, T.; Li, W.; Wang, G.; Liu, X.; Yang, W.; Liu, Y. Towards constructing a DOE-based practical optical neural system for ship recognition in remote sensing images. Signal Process. 2024, 221, 109488. [Google Scholar] [CrossRef]
- Jin, E.; Du, J.; Bi, Y.; Wang, S.; Gao, X. Research on Classification of Grassland Degeneration Indicator Objects Based on UAV Hyperspectral Remote Sensing and 3D_RNet-O Model. Sensors 2024, 24, 1114. [Google Scholar] [CrossRef]
- Zhang, R.; Jin, S.; Zhang, Y.; Zang, J.; Wang, Y.; Li, Q.; Sun, Z.; Wang, X.; Zhou, Q.; Cai, J.; et al. PhenoNet: A two-stage lightweight deep learning framework for real-time wheat phenophase classification. ISPRS J. Photogramm. Remote Sens. 2024, 208, 136–157. [Google Scholar] [CrossRef]
- Zheng, Y.-J.; Chen, S.-B.; Ding, C.H.Q.; Luo, B. Model Compression Based on Differentiable Network Channel Pruning. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 10203–10212. [Google Scholar] [CrossRef]
- Rajpal, M.; Zhang, Y.; Low, B.K.H. Pruning during training by network efficacy modeling. Mach. Learn. 2023, 112, 2653–2684. [Google Scholar] [CrossRef]
- Yuan, M.; Lang, B.; Quan, F. Student-friendly knowledge distillation. Knowl.-Based Syst. 2024, 296, 111915. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, J.; Li, B.; Hu, W.; Ding, J.; Li, L.; Maybank, S. Cross-Architecture Knowledge Distillation. Int. J. Comput. Vis. 2024, 132, 2798–2824. [Google Scholar] [CrossRef]
- Song, H.; Yuan, Y.; Ouyang, Z.; Yang, Y.; Xiang, H. Efficient knowledge distillation for hybrid models: A vision transformer-convolutional neural network to convolutional neural network approach for classifying remote sensing images. IET Cyber-Syst. Robot. 2024, 6, e12120. [Google Scholar] [CrossRef]
- Yue, H.; Li, J.; Liu, H. Second-Order Unsupervised Feature Selection via Knowledge Contrastive Distillation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 15577–15587. [Google Scholar] [CrossRef]
- Zheng, Z.; Ye, R.; Hou, Q.; Ren, D.; Wang, P.; Zuo, W.; Cheng, M.-M. Localization Distillation for Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10070–10083. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Guo, Y.; Liang, P.; Ji, M.; Zhen, C.; Wang, H. Global key knowledge distillation framework. Comput. Vis. Image Underst. 2024, 239, 103902. [Google Scholar] [CrossRef]
- Tian, L.; Wang, Z.; He, B.; He, C.; Wang, D.; Li, D. Knowledge Distillation of Grassmann Manifold Network for Remote Sensing Scene Classification. Remote Sens. 2021, 13, 4537. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, X.; Gao, F.; Dong, J. Pair-Wise Similarity Knowledge Distillation for RSI Scene Classification. Remote Sens. 2022, 14, 2483. [Google Scholar] [CrossRef]
- Xu, K.; Deng, P.; Huang, H. Vision Transformer: An Excellent Teacher for Guiding Small Networks in Remote Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5618715. [Google Scholar] [CrossRef]
- Li, D.; Nan, Y.; Liu, Y. Remote Sensing Image Scene Classification Model Based on Dual Knowledge Distillation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4514305. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, G.; Wang, J.; Chen, H.; Liu, W.; Chen, L. All Adder Neural Networks for On-Board Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5607916. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Z.; Cheng, P.; Xu, G.; Sun, X. DCNNet: A Distributed Convolutional Neural Network for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5603618. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.; Yang, J.; Wu, Z. EMSCNet: Efficient Multisample Contrastive Network for Remote Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5605814. [Google Scholar] [CrossRef]
- Xing, S.; Xing, J.; Ju, J.; Hou, Q.; Ding, X. Collaborative Consistent Knowledge Distillation Framework for Remote Sensing Image Scene Classification Network. Remote Sens. 2022, 14, 5186. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, J.; Yan, Z.; Zhang, Z.; Zhang, Y.; Chen, Y.; Li, H. LaST: Label-Free Self-Distillation Contrastive Learning with Transformer Architecture for Remote Sensing Image Scene Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6512205. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, X.; Luo, X.; Han, J.; Cao, X.; Zhang, J. Variational Self-Distillation for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5627313. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, Y.; Lyu, S.; Chen, L. Embedded Self-Distillation in Compact Multibranch Ensemble Network for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4506415. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.; Yang, J.; Wu, Z. Remote Sensing Image Scene Classification via Self-Supervised Learning and Knowledge Distillation. Remote Sens. 2022, 14, 4813. [Google Scholar] [CrossRef]
- Shi, C.; Ding, M.; Wang, L.; Pan, H. Learn by Yourself: A Feature-Augmented Self-Distillation Convolutional Neural Network for Remote Sensing Scene Image Classification. Remote Sens. 2023, 15, 5620. [Google Scholar] [CrossRef]
- Wu, B.; Hao, S.; Wang, W. Class-Aware Self-Distillation for Remote Sensing Image Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 2173–2188. [Google Scholar] [CrossRef]
- Xie, W.; Fan, X.; Zhang, X.; Li, Y.; Sheng, M.; Fang, L. Co-Compression via Superior Gene for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5604112. [Google Scholar] [CrossRef]
- Alhichri, H.; Alswayed, A.S.; Bazi, Y.; Ammour, N.; Alajlan, N.A. Classification of Remote Sensing Images Using EfficientNet-B3 CNN Model with Attention. IEEE Access 2021, 9, 14078–14094. [Google Scholar] [CrossRef]
- Liang, L.; Wang, G. Efficient recurrent attention network for remote sensing scene classification. IET Image Process. 2021, 15, 1712–1721. [Google Scholar] [CrossRef]
- Yang, S.; Song, F.; Jeon, G.; Sun, R. Scene Changes Understanding Framework Based on Graph Convolutional Networks and Swin Transformer Blocks for Monitoring LCLU Using High-Resolution Remote Sensing Images. Remote Sens. 2022, 14, 3709. [Google Scholar] [CrossRef]
- Sinaga, K.B.M.; Yudistira, N.; Santoso, E. Efficient CNN for high-resolution remote sensing imagery understanding. Multimed. Tools Appl. 2023, 83, 61737–61759. [Google Scholar] [CrossRef]
- Alharbi, R.; Alhichri, H.; Ouni, R.; Bazi, Y.; Alsabaan, M. Improving remote sensing scene classification using quality-based data augmentation. Int. J. Remote Sens. 2023, 44, 1749–1765. [Google Scholar] [CrossRef]
- Zheng, F.; Lin, S.; Zhou, W.; Huang, H. A Lightweight Dual-Branch Swin Transformer for Remote Sensing Scene Classification. Remote Sens. 2023, 15, 2865. [Google Scholar] [CrossRef]
- Song, J.; Fan, Y.; Song, W.; Zhou, H.; Yang, L.; Huang, Q.; Jiang, Z.; Wang, C.; Liao, T. SwinHCST: A deep learning network architecture for scene classification of remote sensing images based on improved CNN and Transformer. Int. J. Remote Sens. 2023, 44, 7439–7463. [Google Scholar] [CrossRef]
- Chen, X.; Ma, M.; Li, Y.; Mei, S.; Han, Z.; Zhao, J.; Cheng, W. Hierarchical Feature Fusion of Transformer with Patch Dilating for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4410516. [Google Scholar] [CrossRef]
- Hao, S.; Li, N.; Ye, Y. Inductive Biased Swin-Transformer with Cyclic Regressor for Remote Sensing Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 6265–6278. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, N.; Liu, W.; Chen, H.; Xie, Y. MFST: A Multi-Level Fusion Network for Remote Sensing Scene Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6516005. [Google Scholar] [CrossRef]
- Zhou, M.; Zhou, Y.; Yang, D.; Song, K. Remote Sensing Image Classification Based on Canny Operator Enhanced Edge Features. Sensors 2024, 24, 3912. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.-E.; Yang, K.; Dang, L.; Liu, Y. Contextual Spatial-Channel Attention Network for Remote Sensing Scene Classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6008805. [Google Scholar] [CrossRef]
- Li, D.; Liu, R.; Tang, Y.; Liu, Y. PSCLI-TF: Position-Sensitive Cross-Layer Interactive Transformer Model for Remote Sensing Image Scene Classification. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5001305. [Google Scholar] [CrossRef]
- Sitaula, C.; Kc, S.; Aryal, J. Enhanced multi-level features for very high resolution remote sensing scene classification. Neural Comput. Appl. 2024, 36, 7071–7083. [Google Scholar] [CrossRef]
- Wang, W.; Sun, Y.; Li, J.; Wang, X. Frequency and spatial based multi-layer context network (FSCNet) for remote sensing scene classification. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103781. [Google Scholar] [CrossRef]
- Xia, J.; Zhou, Y.; Tan, L.; Ding, Y. MCAFNet: Multi-Channel Attention Fusion Network-Based CNN For Remote Sensing Scene Classification. Photogramm. Eng. Remote Sens. 2023, 89, 183–192. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, J.; Feng, Z.; Chen, L.; Li, L. BiShuffleNeXt: A lightweight bi-path network for remote sensing scene classification. Measurement 2023, 209, 112537. [Google Scholar] [CrossRef]
- Sagar, A.S.M.S.; Tanveer, J.; Chen, Y.; Dang, L.M.; Haider, A.; Song, H.-K.; Moon, H. BayesNet: Enhancing UAV-Based Remote Sensing Scene Understanding with Quantifiable Uncertainties. Remote Sens. 2024, 16, 925. [Google Scholar] [CrossRef]
- Albarakati, H.M.; Khan, M.A.; Hamza, A.; Khan, F.; Kraiem, N.; Jamel, L.; Almuqren, L.; Alroobaea, R. A Novel Deep Learning Architecture for Agriculture Land Cover and Land Use Classification from Remote Sensing Images Based on Network-Level Fusion of Self-Attention Architecture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 6338–6353. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, X.; Wang, L.; Jin, Z. A lightweight convolution neural network based on joint features for Remote Sensing scene image classification. Int. J. Remote Sens. 2023, 44, 6615–6641. [Google Scholar] [CrossRef]
- Shen, X.; Wang, H.; Wei, B.; Cao, J. Real-time scene classification of unmanned aerial vehicles remote sensing image based on Modified GhostNet. PLoS ONE 2023, 18, e0286873. [Google Scholar] [CrossRef]
- Bi, M.; Wang, M.; Li, Z.; Hong, D. Vision Transformer with Contrastive Learning for Remote Sensing Image Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 738–749. [Google Scholar] [CrossRef]
- Lu, W.; Chen, S.-B.; Tang, J.; Ding, C.H.Q.; Luo, B. A Robust Feature Downsampling Module for Remote-Sensing Visual Tasks. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4404312. [Google Scholar] [CrossRef]
- Zhao, M.; Meng, Q.; Zhang, L.; Hu, X.; Bruzzone, L. Local and Long-Range Collaborative Learning for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5606215. [Google Scholar] [CrossRef]
- Wang, G.; Chen, H.; Chen, L.; Zhuang, Y.; Zhang, S.; Zhang, T.; Dong, H.; Gao, P. P2FEViT: Plug-and-Play CNN Feature Embedded Hybrid Vision Transformer for Remote Sensing Image Classification. Remote Sens. 2023, 15, 1773. [Google Scholar] [CrossRef]
- Yue, H.; Qing, L.; Zhang, Z.; Wang, Z.; Guo, L.; Peng, Y. MSE-Net: A novel master–slave encoding network for remote sensing scene classification. Eng. Appl. Artif. Intell. 2024, 132, 107909. [Google Scholar] [CrossRef]
- Yang, Y.; Jiao, L.; Liu, F.; Liu, X.; Li, L.; Chen, P.; Yang, S. An Explainable Spatial–Frequency Multiscale Transformer for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5907515. [Google Scholar] [CrossRef]
- Siddiqui, M.I.; Khan, K.; Fazil, A.; Zakwan, M. Snapshot ensemble-based residual network (SnapEnsemResNet) for remote sensing image scene classification. Geoinformatica 2023, 27, 341–372. [Google Scholar] [CrossRef]
- Xiao, F.; Li, X.; Li, W.; Shi, J.; Zhang, N.; Gao, X. Integrating category-related key regions with a dual-stream network for remote sensing scene classification. J. Vis. Commun. Image Represent. 2024, 100, 104098. [Google Scholar] [CrossRef]
- Hao, S.; Wu, B.; Zhao, K.; Ye, Y.; Wang, W. Two-Stream Swin Transformer with Differentiable Sobel Operator for Remote Sensing Image Classification. Remote Sens. 2022, 14, 1507. [Google Scholar] [CrossRef]
- Stanton, S.; Izmailov, P.; Kirichenko, P.; Alemi, A.A.; Wilson, A.G. Does Knowledge Distillation Really Work? In Advances in Neural Information Processing Systems; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P.S., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; pp. 6906–6919. Available online: https://proceedings.neurips.cc/paper_files/paper/2021/file/376c6b9ff3bedbbea56751a84fffc10c-Paper.pdf (accessed on 1 March 2025).
- Huang, T.; You, S.; Wang, F.; Qian, C.; Xu, C. Knowledge Distillation from A Stronger Teacher. In Advances in Neural Information Processing Systems; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2022; pp. 33716–33727. Available online: https://proceedings.neurips.cc/paper_files/paper/2022/file/da669dfd3c36c93905a17ddba01eef06-Paper-Conference.pdf (accessed on 1 March 2025).
- Yun, S.; Han, D.; Chun, S.; Oh, S.J.; Yoo, Y.; Choe, J. CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6022–6031. [Google Scholar] [CrossRef]
- Beyer, L.; Zhai, X.; Royer, A.; Markeeva, L.; Anil, R.; Kolesnikov, A. Knowledge distillation: A good teacher is patient and consistent. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 10915–10924. [Google Scholar] [CrossRef]




| Approaches | Merits | Limitations |
|---|---|---|
| Classical Distillation [38,39,40,41,42,43] | Improves the accuracy of smaller student models for RSI classification | Student models generally exhibit suboptimal accuracy and insufficient model compactness |
| Self-Distillation [44,45,46,47,48,49,50,51] | Enhances backbone model accuracy through integrated functional modules | Backbone and student models typically fail to achieve superior accuracy; model size often increases |
| Lightweight CNN [52,53,54,55,56,57] | Employs EfficientNets with integrated attention mechanisms; moderate gains | Lack of ImageNet-1K retraining limits transfer learning benefits; overall accuracy remains limited |
| Lightweight Transformer [58,59,60,61,62,63] | Introduces functional modules to ViT models | Struggles to capture long-range dependencies in low-quality RSI data, leading to limited performance |
| Attention CNN [64,65,66,67,68,69] | Incorporates attention mechanisms, improving accuracy on baseline CNNs | Improvements are primarily demonstrated on less competitive architectures; superior accuracy is rare |
| Customized Learning [70,71,72,73,74,75] | Proposes innovative learning strategies for CNNs and ViTs | Techniques are still in developmental stages and generally lack high accuracy |
| Multiple Models [76,77,78,79,80,81,82] | Combines multiple models, occasionally achieving competitive performance | Fusion significantly increases model size with limited corresponding accuracy improvements |
| Our Proposed Method | Addresses RSI asymmetries with SLT strategy; achieves superior accuracy, reduced model size (up to 96%), and faster inference (up to 88%) without architectural modifications | Further exploration needed to verify generalization across broader datasets and real-world applications |
| Model | Accuracy (%) | Parameters (M) |
|---|---|---|
| EfficientNet-B3 | 82.0 | 12.2 |
| EfficientNet-B1 | 78.6 | 7.8 |
| EfficientNet-B0 | 77.6 | 6.3 |
| ResNet-50 | 76.1 | 25.6 |
| ResNet-18 | 69.7 | 11.7 |
| MobileNet-V2 | 72.1 | 3.5 |
| Dataset | Total Classes | Spatial Resolution | Total Images | Image Size | Samples per Class | Training Ratio |
|---|---|---|---|---|---|---|
| AID30 [6] | 30 | 0.5–8 m | 10,000 | 6002 pixels | 220–420 (varied) | 20%, 50% |
| NWPU45 [6] | 45 | 30~0.2 m | 31,500 | 2562 pixels | 700 (fixed) | 10%, 20% |
| AFGR50 [77] | 50 | 0.5–8 m | 12,500 | 1282 pixels | 250 (fixed) | 10%, 20%, 30% |
| Model | AID30 | NWPU45 | AFGR50 | ||||
|---|---|---|---|---|---|---|---|
| TR-20% | TR-50% | TR-10% | TR-20% | TR-10% | TR-20% | TR-30% | |
| EfficientNet-B3 | 97.30 ± 0.06 ↓0.31 | 98.28 ± 0.07 ↓0.11 | 94.66 ± 0.17 ↓0.50 | 96.20 ± 0.08 ↓0.37 | 93.15 ± 0.61 ↓0.57 | 96.52 ± 0.13 ↓0.42 | 97.53 ± 0.10 ↓0.23 |
| EfficientNet-B0 | 97.05 ± 0.20 ↓0.56 | 98.17 ± 0.07 ↓0.22 | 94.45 ± 0.12 ↓0.71 | 96.01 ± 0.01 ↓0.56 | 91.58 ± 0.30 ↓2.14 | 96.11 ± 0.32 ↓0.83 | 97.37 ± 0.12 ↓0.39 |
| ResNet-18 | 96.08 ± 0.12 ↓1.53 | 97.08 ± 0.21 ↓1.21 | 92.78 ± 0.10 ↓2.38 | 94.54 ± 0.01 ↓2.03 | 91.90 ± 0.21 ↓1.82 | 95.88 ± 0.20 ↓1.06 | 97.06 ± 0.05 ↓0.70 |
| MobileNet-V2 | 95.96 ± 0.12 ↓1.65 | 97.27 ± 0.12 ↓1.19 | 92.68 ± 0.05 ↓2.48 | 94.60 ± 0.05 ↓1.97 | 91.86 ± 0.26 ↓1.86 | 95.60 ± 0.18 ↓1.34 | 96.95 ± 0.03 ↓0.81 |
| Teacher Ensemble | 97.61 ± 0.04 | 98.39 ± 0.10 | 95.16 ± 0.19 | 96.57 ± 0.01 | 93.72 ± 0.40 | 96.94 ± 0.15 | 97.76 ± 0.04 |
| Model | AID30 | NWPU45 | AFGR50 | ||||
|---|---|---|---|---|---|---|---|
| TR-20% | TR-50% | TR-10% | TR-20% | TR-10% | TR-20% | TR-30% | |
| EfficientNet-B1 | 97.14 ± 0.11 ↑0.09 | 98.16 ± 0.07 ↓0.01 | 94.45 ± 0.12 ↑0.0 | 96.03 ± 0.01 ↑0.02 | 91.27 ± 0.34 ↓0.31 | 95.97 ± 0.18 ↓0.14 | 97.23 ± 0.05 ↓0.14 |
| ResNet-50 | 96.08 ± 0.12 ↑0.0 | 97.08 ± 0.21 ↑0.0 | 92.78 ± 0.10 ↑0.0 | 94.54 ± 0.01 ↑0.0 | 92.33 ± 0.32 ↑0.43 | 96.13 ± 0.22 ↑0.25 | 97.25 ± 0.14 ↑0.19 |
| Teacher Ensemble (heavy) | 97.63 ± 0.07 ↑0.02 | 98.39 ± 0.08 ↑0.0 | 95.08 ± 0.14 ↓0.08 | 96.58 ± 0.06 ↑0.01 | 93.96 ± 0.45 ↑0.24 | 96.89 ± 0.15 ↓0.05 | 97.73 ± 0.01 ↓0.03 |
| Model | Params (M) | AID30 | NWPU45 | AFGR50 | ||||
|---|---|---|---|---|---|---|---|---|
| TR-20% | TR-50% | TR-10% | TR-20% | TR-10% | TR-20% | TR-30% | ||
| Teacher Ensemble | 33.7 | 97.61 ± 0.04 | 98.39 ± 0.10 | 95.16 ± 0.19 | 96.57 ± 0.01 | 93.72 ± 0.40 | 96.94 ± 0.15 | 97.76 ± 0.04 |
| Student (MobileNet-V2) | 3.5 | 96.69 ± 0.06 ↓0.92 | 97.77 ± 0.09 ↓0.62 | 93.79 ± 0.03 ↓1.37 | 95.49 ± 0.07 ↓1.08 | 93.10 ± 0.30 ↓0.62 | 96.34 ± 0.24 ↓0.60 | 97.52 ± 0.04 ↓0.24 |
| Student (ResNet-18) | 11.7 | 96.55 ± 0.22 ↓1.06 | 97.45 ± 0.22 ↓0.94 | 93.70 ± 0.09 ↓1.46 | 95.35 ± 0.04 ↓1.22 | 93.13 ± 0.36 ↓0.59 | 96.32 ± 0.18 ↓0.62 | 97.50 ± 0.06 ↓0.26 |
| Student (EfficientNet-B0) | 6.3 | 97.32 ± 0.06 ↓0.29 | 98.24 ± 0.05 ↓0.15 | 94.70 ± 0.04 ↓0.46 | 96.34 ± 0.11 ↓0.23 | 93.15 ± 0.31 ↓0.57 | 96.55 ± 0.26 ↓0.39 | 97.79 ± 0.05 ↑0.03 |
| Student (EfficientNet-B1) | 7.8 | 97.44 ± 0.05 ↓0.17 | 98.34 ± 0.09 ↓0.05 | 94.97 ± 0.09 ↓0.19 | 96.43 ± 0.01 ↓0.14 | 93.29 ± 0.33 ↓0.43 | 96.64 ± 0.23 ↓0.30 | 97.73 ± 0.03 ↓0.03 |
| Model | Params (M) | AID30 | NWPU45 | AFGR50 | ||||
|---|---|---|---|---|---|---|---|---|
| TR-20% | TR-50% | TR-10% | TR-20% | TR-10% | TR-20% | TR-30% | ||
| Teacher Ensemble (heavy) | 33.7 | 97.63 ± 0.07 | 98.39 ± 0.08 | 95.08 ± 0.14 | 96.58 ± 0.06 | 93.96 ± 0.45 | 96.89 ± 0.15 | 97.73 ± 0.01 |
| Student (MobileNet-V2) | 3.5 | 96.56 ± 0.09 ↓1.07 | 97.66 ± 0.10 ↓0.73 | 93.66 ± 0.11 ↓1.42 | 95.33 ± 0.04 ↓1.25 | 93.04 ± 0.27 ↓0.92 | 96.24 ± 0.22 ↓0.65 | 97.49 ± 0.10 ↓0.24 |
| Student (ResNet-18) | 11.7 | 96.25 ± 0.10 ↓1.38 | 97.35 ± 0.09 ↓1.04 | 93.43 ± 0.04 ↓1.65 | 95.17 ± 0.04 ↓1.41 | 92.93 ± 0.43 ↓1.03 | 96.26 ± 0.20 ↓0.63 | 97.50 ± 0.09 ↓0.23 |
| Student (EfficientNet-B0) | 6.3 | 97.22 ± 0.06 ↓0.41 | 98.26 ± 0.08 ↓0.13 | 94.66 ± 0.10 ↓0.42 | 96.31 ± 0.05 ↓0.27 | 93.23 ± 0.34 ↓0.73 | 96.63 ± 0.18 ↓0.26 | 97.77 ± 0.02 ↑0.04 |
| Student (EfficientNet-B1) | 7.8 | 97.43 ± 0.12 ↓0.20 | 98.22 ± 0.13 ↓0.17 | 94.89 ± 0.04 ↓0.19 | 96.43 ± 0.02 ↓0.15 | 93.20 ± 0.26 ↓0.76 | 96.57 ± 0.16 ↓0.32 | 97.63 ± 0.02 ↓0.10 |
| Model | Tech. Approach | Pub. Year | Params (M) | AID30 | NWPU45 | ||
|---|---|---|---|---|---|---|---|
| TR-20% | TR-50% | TR-10% | TR-20% | ||||
| GeNet2B [38] | Logit- Based | 2021 | 1.7 | 80.97 ± 0.01 ↓16.46 | None | None | None |
| PWS-Net [39] | 2022 | 21.8 | 91.57 (TR equals 50%) ↓6.65 | 94.77 (TR equals 70%) ↓1.66 | |||
| ETGS-Net [40] | 2022 | 11.7 | 95.58 ± 0.18 ↓1.85 | 96.88 ± 0.19 ↓1.34 | 92.72 ± 0.28 ↓2.17 | 94.50 ± 0.18 ↓1.93 | |
| DKD-Net [41] | Feature- Based | 2022 | 4.4 | 95.09 ↓2.43 | 96.94 ↓1.28 | 93.72 ↓1.17 | 95.76 ↓0.67 |
| A2N-Net [42] | 2023 | >143.7 | 84.20 ± 0.39 ↓13.43 | None | None | None | |
| DCN-Net [43] | 2023 | None | 94.94 ± 0.16 ↓2.49 | 97.34 ± 0.18 ↓0.88 | 94.58 ± 0.18 ↓0.31 | 95.80 ± 0.12 ↓0.63 | |
| CKD-Net [45] | 2022 | >90.0 | None | None | None | 91.60 ↓4.83 | |
| EMSC-Net [44] | Contrastive Learning with KD | 2023 | 173.6 | 96.02 ± 0.18 ↓1.41 | 97.35 ± 0.17 ↓0.87 | 93.58 ± 0.22 ↓1.31 | 95.37 ± 0.07 ↓1.06 |
| LaST-Net [46] | Self- Distillation | 2022 | 28.3 | 83.23 ↓14.2 | 87.34 ↓10.88 | 72.58 ↓22.31 | 73.67 ↓22.76 |
| VSD-Net [47] | 2022 | >8.0 | 96.73 ± 0.15 ↓0.70 | 97.95 ± 0.10 ↓0.27 | 93.24 ± 0.11 ↓1.65 | 95.67 ± 0.11 ↓0.76 | |
| ESDMBE-Net [48] | 2022 | 92.5 | 96.00 ± 0.15 ↓1.43 | 98.54 ± 0.17 ↑0.32 | 94.32 ± 0.15 ↓0.57 | 95.58 ± 0.08 ↓0.85 | |
| SSKD-Net [49] | 2022 | 77.2 | 95.96 ± 0.12 ↓1.47 | 97.45 ± 0.19 ↓0.77 | 92.77 ± 0.05 ↓2.12 | 94.92 ± 0.12 ↓1.51 | |
| FASD-Net [50] | 2023 | 24.8 | 96.05 ± 0.13 ↓1.38 | 97.84 ± 0.12 ↓0.38 | 92.89 ± 0.13 ↓2.00 | 94.95 ± 0.12 ↓1.48 | |
| CASD-ViT [51] | 2024 | 86.0 | 96.18 ± 0.20 ↓1.25 | 97.64 ± 0.11 ↓0.58 | 93.12 ± 0.12 ↓1.77 | 95.52 ± 0.16 ↓0.91 | |
| Teacher Ensemble | Logit- Based | Ours | 33.7 | 97.63 ± 0.07 | 98.39 ± 0.08 | 95.08 ± 0.14 | 96.58 ± 0.06 |
| Student-B0 | 6.3 | 97.22 ± 0.06 | 98.26 ± 0.08 | 94.66 ± 0.10 | 96.31 ± 0.05 | ||
| Student-B1 | 7.8 | 97.43 ± 0.12 | 98.22 ± 0.13 | 94.89 ± 0.04 | 96.43 ± 0.02 | ||
| Model | Tech. Approach | Pub. Year | Params (M) | AID30 | NWPU45 | ||
|---|---|---|---|---|---|---|---|
| TR-20% | TR-50% | TR-10% | TR-20% | ||||
| B3Attn-Net [53] | EfficientNet Reinforcement | 2021 | >12.2 | 94.45 ± 0.76 | 96.56 ± 0.12 | None | None |
| ERA-Net [54] | 2021 | >6.3 | 95.93 ± 0.13 | 98.39 ± 0.16 ↑0.17 | 91.95 ± 0.19 | 95.12 ± 0.17 | |
| LSRL-Net [55] | 2022 | None | 96.44 ± 0.10 ↓0.99 | 97.36 ± 0.21 | 93.45 ± 0.16 | 94.27 ± 0.44 | |
| B7Mod-Net [56] | 2023 | 66.3 | 94.63 | 97.46 | None | None | |
| QSS-Net [57] | 2023 | 12.2 | 95.71 | None | 93.98 ↓0.91 | 94.71 ↓1.72 | |
| LDBST-Net [58] | Swin- Transformer Reinforcement | 2023 | 38.4 | 95.10 ± 0.09 | 96.84 ± 0.20 | 93.86 ± 0.18 | 94.36 ± 0.12 |
| SwinHCST [59] | 2023 | None | 93.60 (TR equals 70%) | 93.76 (TR equals 70%) | |||
| HFFT-Swin [60] | 2023 | 29.3 | 97.08 ± 0.53 | 97.91 ± 0.27 | 93.98 ± 0.43 | 95.98 ± 0.26 ↓0.45 | |
| IBSW-Net [61] | 2023 | 164.0 | 97.61 ± 0.12 ↑0.18 | 98.78 ± 0.09 ↑0.56 | 93.98 ± 0.24 ↓0.91 | 95.65 ± 0.11 | |
| MFST-Net [62] | 2022 | 30.8 | 96.23 ± 0.16 | 97.38 ± 0.08 | 92.64 ± 0.08 | 94.90 ± 0.06 | |
| CAF-Net [63] | 2024 | None | None | None | 94.12 (TR equals 80%) | ||
| CSCA-Net [64] | CNN Reinforcement | 2023 | >21.8 | 94.67 ± 0.20 | 96.83 ± 0.14 | 91.27 ± 0.11 | 93.72 ± 0.10 |
| PSCLI-Net [65] | 2024 | 26.6 | 96.28 | 97.52 | 92.92 | 94.86 | |
| EAM-Net [66] | 2024 | >25.6 | 93.14 | 95.39 | 90.38 | 93.04 | |
| FSC-Net [67] | 2024 | 28.8 | 95.56 ± 0.07 ↓1.87 | 97.51 ± 0.03 ↓0.71 | 93.03 ± 0.02 ↓1.86 | 94.76 ± 0.03 ↓1.67 | |
| MCAF-Net [68] | 2023 | None | 93.72 ± 0.28 | 96.06 ± 0.29 | 91.97 ± 0.24 | 93.86 ± 0.17 | |
| BSN-Net [69] | 2023 | None | 94.06 (TR equals 80%) | 95.93 (TR equals 80%) | |||
| Bayes-Net [70] | New CNN Architecture | 2024 | 949.9 | None | 97.57 | 96.44 (TR equals 50%) | |
| FSA-Net [71] | 2024 | 18.6 | None | None | 91.7 (TR equals 50%) | ||
| JF-Net [72] | 2023 | 5.0 | 93.05 ± 0.46 ↓4.38 | 96.65 ± 0.15 ↓1.57 | 91.36 ± 0.29 ↓3.53 | 93.25 ± 0.16 ↓3.18 | |
| MGhost-Net [73] | 2023 | 5.7 | 92.05 (TR equals 50%) | 91.73 (TR equals 50%) | |||
| ViT-CL [74] | ViT Reinforcement | 2023 | 86.6 | 95.60 ↓1.83 | 97.42 ↓0.90 | 92.85 ↓2.04 | 94.69 ↓1.74 |
| RFD-Net [75] | 2023 | 30.0 | None | None | 96.29 (TR equals 80%) | ||
| Teacher Ensemble | Logit- Based | Ours | 33.7 | 97.63 ± 0.07 | 98.39 ± 0.08 | 95.08 ± 0.14 | 96.58 ± 0.06 |
| Student-B0 | 6.3 | 97.22 ± 0.06 | 98.26 ± 0.08 | 94.66 ± 0.10 | 96.31 ± 0.05 | ||
| Student-B1 | 7.8 | 97.43 ± 0.12 | 98.22 ± 0.13 | 94.89 ± 0.04 | 96.43 ± 0.02 | ||
| Model | Pub. Year | Params (M) | AID30 | NWPU45 | AFGR50 | ||||
|---|---|---|---|---|---|---|---|---|---|
| TR-20% | TR-50% | TR-10% | TR-20% | TR-10% | TR-20% | TR-30% | |||
| MBC-Net [15] | 2024 | 17.3 | 97.39 ± 0.01 ↓0.04 | 98.35 ± 0.09 | 94.85 ± 0.04 | 96.40 ± 0.06 ↓0.03 | 91.01 ± 0.61 ↓2.28 | 96.13 ± 0.26 ↓0.51 | 97.28 ± 0.27 ↓0.45 |
| L2RCF-Net [76] | 2023 | 46.7 | 97.00 ± 0.17 | 97.80 ± 0.22 | 94.58 ± 0.16 | 95.60 ± 0.12 | None | None | None |
| P2FEViT [77] | 2023 | >112.2 | None | None | 94.97 ± 0.13 ↑0.08 | 95.74 ± 0.19 | 89.30 ± 0.07 | 94.78 ± 0.15 | 97.12 ± 0.09 |
| MSE-Net [78] | 2024 | 61.4 | 96.30 ± 0.10 | 97.00 ± 0.17 | 92.80 ± 0.17 | 94.70 ± 0.16 | None | None | None |
| SFMS-Former [79] | 2023 | 36.3 | 96.68 ± 0.64 | 98.57 ± 0.23 | 92.74 ± 0.23 | 94.85 ± 0.13 | None | None | None |
| SER-Net [80] | 2023 | None | None | None | 93.31 ± 0.16 | 95.40 ± 0.13 | None | None | None |
| CKRL-Net [81] | 2024 | >113.4 | 97.08 ± 0.12 | 98.16 ± 0.21 | 94.60 ± 0.10 | 95.88 ± 0.17 | None | None | None |
| TST-Net [82] | 2022 | 173.0 | 97.20 ± 0.22 | 98.70 ± 0.12 ↑0.48 | 94.08 ± 0.24 | 95.70 ± 0.10 | None | None | None |
| Teacher Ensemble | Ours | 33.7 | 97.63 ± 0.07 | 98.39 ± 0.08 | 95.08 ± 0.14 | 96.58 ± 0.06 | 93.72 ± 0.40 | 96.94 ± 0.15 | 97.76 ± 0.04 |
| Student-B0 | 6.3 | 97.22 ± 0.06 | 98.26 ± 0.08 | 94.66 ± 0.10 | 96.31 ± 0.05 | 93.15 ± 0.31 | 96.55 ± 0.26 | 97.79 ± 0.05 | |
| Student-B1 | 7.8 | 97.43 ± 0.12 | 98.22 ± 0.13 | 94.89 ± 0.04 | 96.43 ± 0.02 | 93.29 ± 0.33 | 96.64 ± 0.23 | 97.73 ± 0.03 | |
| Model | Parameter Settings (Operation Prob. = 1.0) | AID30 | NWPU45 | AFGR50 |
|---|---|---|---|---|
| TR-20% | TR-10% | TR-10% | ||
| EfficientNet-B3 | Color Jitter | 97.32 ± 0.12 ↑0.02 | 94.57 ± 0.07 ↓0.09 | 93.04 ± 0.73 ↓0.11 |
| Horizontal Flip | 97.26 ± 0.05 ↓0.04 | 94.64 ± 0.11 ↓0.02 | 92.78 ± 0.61 ↓0.37 | |
| Vertical Flip | 97.21 ± 0.02 ↓0.09 | 94.63 ± 0.21 ↓0.03 | 92.75 ± 0.35 ↓0.04 | |
| Random Rotation | 97.14 ± 0.11 ↓0.16 | 94.46 ± 0.12 ↓0.20 | 92.74 ± 0.36 ↓0.40 | |
| Random Grayscale | 17.50 ± 1.11 ↓79.8 | 47.93 ± 6.33 ↓46.7 | 43.31 ± 6.43 ↓0.04 | |
| Auto Contrast | 97.15 ± 0.11 ↓0.15 | 94.49 ± 0.12 ↓0.17 | 92.89 ± 0.43 ↓49.8 | |
| Gaussian blur | 97.29 ± 0.01 ↓0.01 | 94.55 ± 0.10 ↓0.11 | 92.81 ± 0.52 ↓0.04 | |
| CutMix | 97.25 ± 0.08 ↓0.05 | 94.51 ± 0.08 ↓0.15 | 92.77 ± 0.33 ↓0.34 | |
| Our SLT | 97.30 ± 0.06 | 94.66 ± 0.17 | 93.15 ± 0.61 |
| Model | Parameter Settings (Operation Prob. = 1.0) | AID30 | NWPU45 | AFGR50 |
|---|---|---|---|---|
| TR-20% | TR-10% | TR-10% | ||
| Student-B1 | Color Jitter | 97.47 ± 0.08 ↑0.03 | 94.88 ± 0.09 ↓0.09 | 93.19 ± 0.39 ↓0.20 |
| Horizontal Flip | 97.41 ± 0.03 ↓0.03 | 94.91 ± 0.05 ↓0.06 | 93.26 ± 0.32 ↓0.03 | |
| Vertical Flip | 97.42 ± 0.06 ↓0.02 | 94.86 ± 0.06 ↓0.11 | 93.22 ± 0.31 ↓0.07 | |
| Random Rotation | 97.29 ± 0.10 ↓0.15 | 94.80 ± 0.11 ↓0.17 | 93.04 ± 0.29 ↓0.25 | |
| Random Grayscale | 90.14 ± 3.92 ↓7.30 | 92.56 ± 0.38 ↓2.41 | 87.12 ± 0.40 ↓10.2 | |
| Auto Contrast | 97.36 ± 0.09 ↓0.08 | 94.83 ± 0.08 ↓0.14 | 93.16 ± 0.29 ↓0.13 | |
| Gaussian blur | 97.42 ± 0.03 ↓0.02 | 94.88 ± 0.09 ↓0.09 | 93.16 ± 0.27 ↓0.13 | |
| CutMix | 97.38 ± 0.11 ↓0.06 | 94.85 ± 0.08 ↓0.12 | 93.37 ± 0.32 ↑0.08 | |
| Our SLT | 97.44 ± 0.05 | 94.97 ± 0.09 | 93.29 ± 0.33 |
| Model | Parameter Settings (Operation Prob. = 1.0) | AID30 | NWPU45 | AFGR50 |
|---|---|---|---|---|
| TR-20% | TR-10% | TR-10% | ||
| Student-B1 | H-flip + V-flip | 96.43 ± 0.13 ↓1.01 | 93.61 ± 0.06 ↓1.36 | 84.63 ± 0.46 ↓8.66 |
| H-flip + V-flip + CutMix | 97.32 ± 0.11 ↓0.12 | 94.49 ± 0.08 ↓0.48 | 91.06 ± 0.05 ↓2.23 | |
| Our SLT | 97.44 ± 0.05 | 94.97 ± 0.09 | 93.29 ± 0.33 |
| Method | Params (M) | FLOPs (G) | Inferring Time (second) |
|---|---|---|---|
| P2FEViT [77] | >112.2 | >21.7 | 73.39 ± 0.21 |
| TST-Net [82] | 173.0 | 30.2 | 150.39 ± 0.04 |
| EfficientNet-B3 | 12.2 | 1.8 | 23.80 ± 0.02 |
| ResNet-50 | 25.2 | 4.1 | 23.78 ± 0.01 |
| Swin Transformer-tiny | 28.3 | 4.5 | 31.98 ± 0.23 |
| Swin Transformer-base | 87.8 | 20.3 | 75.64 ± 0.10 |
| Teacher Ensemble (heavy) | 48.7 | 6.9 | 71.85 ± 0.01 |
| Teacher Ensemble | 32.7 | 4.3 | 50.79 ± 0.07 |
| Student ResNet-18 | 11.7 | 1.8 | 11.63 ± 0.01 |
| Student MobileNet-V2 | 3.5 | 0.3 | 11.69 ± 0.01 |
| Student-B0 | 5.3 | 0.4 | 12.70 ± 0.07 |
| Student-B1 | 7.8 | 0.7 | 17.43 ± 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Xie, J.; Liang, L.; Su, Y.; Xiao, Y.; Zhang, X.; Ouyang, Y.; Li, X.; Chen, S.; Li, Y. Symmetrical Learning and Transferring: Efficient Knowledge Distillation for Remote Sensing Image Classification. Symmetry 2025, 17, 1002. https://doi.org/10.3390/sym17071002
Song H, Xie J, Liang L, Su Y, Xiao Y, Zhang X, Ouyang Y, Li X, Chen S, Li Y. Symmetrical Learning and Transferring: Efficient Knowledge Distillation for Remote Sensing Image Classification. Symmetry. 2025; 17(7):1002. https://doi.org/10.3390/sym17071002
Chicago/Turabian StyleSong, Huaxiang, Junping Xie, Liang Liang, Yan Su, Yao Xiao, Xinyuan Zhang, Yuqi Ouyang, Xinling Li, Siyi Chen, and Yucheng Li. 2025. "Symmetrical Learning and Transferring: Efficient Knowledge Distillation for Remote Sensing Image Classification" Symmetry 17, no. 7: 1002. https://doi.org/10.3390/sym17071002
APA StyleSong, H., Xie, J., Liang, L., Su, Y., Xiao, Y., Zhang, X., Ouyang, Y., Li, X., Chen, S., & Li, Y. (2025). Symmetrical Learning and Transferring: Efficient Knowledge Distillation for Remote Sensing Image Classification. Symmetry, 17(7), 1002. https://doi.org/10.3390/sym17071002





