A Metric Approach to Newtonian Cosmology and Its Applications to Gravitational Systems

Abstract

We explore a modified, including some relativistic effects, Newtonian formalism in cosmology, using a system of constituent equations that includes a modified first Friedmann equation—incorporating its homogeneous counterpart—alongside the classical Poisson equation. Furthermore, we include the dynamical equations arising from stress-energy tensor conservation. Within this framework, we examine stellar equilibrium under spherical symmetry. By specifying the equation of state, we derive the corresponding equilibrium configurations. Finally, we investigate gravitational collapse in this context.

1. Introduction

The study of cosmological dynamics has long been rooted in two foundational frameworks: Newtonian mechanics and General Relativity (GR), see the classical books [1,2,3]. While Newtonian theory provides an intuitive and mathematically tractable description of gravitational interactions, particularly in weak-field regimes, GR offers a comprehensive and relativistic description of gravity, essential for understanding phenomena on cosmic scales and in strong-field environments. Bridging these two frameworks has been a central challenge in theoretical cosmology, as it enables a deeper understanding of the interplay between local gravitational interactions and the large-scale structure of the universe.

In this article, we develop a metric-based approach to cosmology, building on a previously proposed metric within the broader class of metric gravity theories. This framework brings together essential elements of Newtonian mechanics and GR into a unified, consistent formulation. By incorporating stress-energy conservation and a modified, non-homogeneous Friedmann equation, our approach naturally connects the classical Poisson equation with the relativistic Hamiltonian constraint. This formulation not only recovers the standard homogeneous Friedmann equations but also agrees with GR at first order in perturbations, thereby remaining consistent with key observational tests such as Mercury’s perihelion precession and the bending of light (for further details, see [4]).

We further explore the implications of this framework in both static and dynamic scenarios. In the static case, our approach yields a conformastatic metric that reduces to the Newtonian potential at large distances while remaining consistent with relativistic predictions. In dynamic settings, we apply the framework to study equilibrium configurations of spherically symmetric stars and the gravitational collapse of pressureless spherical objects. By relating the collapse to the homogeneous Friedmann equations [5,6], we demonstrate the versatility of our approach in describing both local and cosmological phenomena.

Overall, this study establishes a robust and consistent bridge between Newtonian and relativistic descriptions of gravitational interactions, offering an intermediate perspective between Newtonian gravity and GR in the context of cosmological dynamics. By attempting to reconcile these two theoretical frameworks, our approach provides a unified description that captures essential aspects of both classical and relativistic gravity. This formulation not only enhances our understanding of gravitational phenomena across different scales but also offers a framework that remains analytically tractable while preserving key relativistic features.

Furthermore, by integrating elements of Newtonian mechanics with the fundamental principles of GR, our approach sheds light on the transition between weak-field and strong-field regimes, which is crucial for studying astrophysical systems such as galaxies, compact objects, and large-scale cosmic structures. The ability to recover the standard homogeneous Friedmann equations, while also accommodating perturbations consistent with GR, ensures that the model remains compatible with observational constraints, including planetary motion, gravitational lensing, and large-scale structure formation.

The work is organized as follows: In Section 2, we derive the homogeneous Friedmann equations using the principles of Newtonian mechanics. A key element in this derivation is the application of the shell theorem, which allows us to simplify the gravitational interactions in a homogeneous universe and obtain the well-known Friedmann equations. This section highlights the remarkable consistency between Newtonian mechanics and cosmological dynamics in the appropriate regime. In Section 3, we present the modified Newtonian dynamical equations within our proposed framework. These equations extend the Newtonian description by incorporating relativistic corrections, providing a more accurate representation of gravitational interactions in regimes where relativistic effects become significant. This section lays the foundation for bridging the gap between Newtonian and relativistic descriptions of cosmological dynamics. In Section 4, we calculate the metric generated by a point mass particle and demonstrate that our framework, like GR, successfully passes the classical tests of gravity for non-rotating bodies, such as the precession of the perihelion of Mercury and the deflection of light. Section 5 focuses on the application of our approach to a conformastat metric. We explore equilibrium configurations for spherically symmetric systems, showcasing the versatility of our approach in describing static gravitational fields. In Section 6, we investigate gravitational collapse within both Newtonian and modified Newtonian gravity. We analyze the collapse of a pressure-less spherical star, establishing a connection between this process and the homogeneous Friedmann equations. Furthermore, we extend this analysis to our Newtonian framework, examining how relativistic corrections influence the dynamics of collapse. This section underscores the applicability of our approach to both static and dynamic scenarios, providing a comprehensive understanding of gravitational phenomena across different regimes. We conclude this work in Section 7 with a concise overview of the entire study.

2. Newtonian Derivation of Friedmann Equations: A Review

As highlighted in several seminal works [7,8], Newtonian mechanics is entirely adequate for describing the dynamics of a homogeneous expanding universe. These studies argue that Newtonian theory correctly predicts the expansion dynamics in regimes where both GR and Newtonian mechanics are equally applicable.

In this section, we revisit the simple and intuitive derivation of the homogeneous Friedmann equations outlined in [9], relying exclusively on the principles of Newtonian mechanics, particularly the well-known shell theorem [10]. Following the approach in [9], we consider a homogeneous large ball with radius $\overline{R}$ in Euclidean space, using co-moving coordinates. Although we can also consider $\overline{R}=+\infty$, for finite radius, the total mass within the ball is finite and given by $\overline{M}={\displaystyle \frac{4\pi }{3}}\rho {\overline{R}}^3$, where $\rho$ is the mass density. We assume the ball expands radially. This means that if O is the center of the ball, a point P within the ball at time $t_0$ transforms into point $P_t$ at time t, and the distance from O to $P_t$ is given by $d_{O{P}_t}\equiv d_{OP}\left(t\right)=a\left(t\right)d_{OP}$, where $a\left(t\right)$ denotes the expansion scale factor of the Friedmann-Lemaître-Robertson-Walker (FLRW) universe given by $d{s}^2=-d{t}^2+a^2\left(t\right)\left[d{r}^2/(1-k{r}^2)+r^2\left(d{\theta }^2+{sin}^2\theta d{\varphi }^2\right)\right]$, with k corresponding to the spatial geometry of the universe) (for simplicity, we assume that the present-day value of the scale factor is unity, i.e., $a\left(t_0\right)=1$). Furthermore, at time $t_0$, we consider the triangle $\widehat{POQ}$, which transforms into the equivalent triangle $\widehat{P_{t}O{Q}_t}$ at time t. As $d_{O{P}_t}=a\left(t\right)d_{OP}$ and $d_{O{Q}_t}=a\left(t\right)d_{OQ}$, applying Thales’ theorem, we find that for any points P and Q within the ball, $d_{P_t{Q}_t}=a\left(t\right)d_{PQ}$. The relation shows that any ball, centered at a point P at time $t_0$, expands radially at the same rate as the original large ball. Furthermore, the relative velocity between $P_t$ and $Q_t$ follows the Hubble-Lemaître law:

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\left(d_{P_t{Q}_t}\right)=\dot{a}\left(t\right)d_{PQ}=H\left(t\right)d_{P_t{Q}_t}.\end{array}$$

(1)

The dynamical equation for the scale factor in Newtonian mechanics is formulated by utilizing the shell theorem [10]. This theorem states that the gravitational field inside a hollow sphere, produced by a homogeneous mass distribution, vanishes. Consequently, in a homogeneous universe, the gravitational force acting on a test particle can be determined by considering only a homogeneous solid sphere centered at the origin 0, where the test particle is located on its boundary. This simplification arises because the gravitational contributions from mass distributions outside this sphere cancel out, allowing the problem to be reduced to the dynamics of the sphere itself.

Then the radial force acting in the test particle is $\mathbf{F}\left(a\left(t\right)\mathbf{r}\right)=-{\displaystyle \frac{4\pi G}{3}}{\sigma }_{0}a\left(t\right)\mathbf{r}$, where ${\sigma }_0$ is the mass density and $\mathbf{r}$ is the co-moving vector from the origin to the test particle. As a result, the acceleration that a probe particle with mass m experiences at point Q due to the influence of the ball is calculated using Newton’s second law, which states the following:

$$\begin{array}{c}\hfill m{\displaystyle \frac{d^2}{d{t}^2}}\left(a\left(t\right)\mathbf{r}\right)=-{\displaystyle \frac{4\pi Gm}{3}}{\sigma }_{0}a\left(t\right)\mathbf{r},\end{array}$$

(2)

which after the elimination of the mass m, leads to the second Friedmann equation for a homogeneous dust field $(p_0=0)$:

$$\begin{array}{c}\hfill {\displaystyle \frac{\ddot{a}}{a}}=-{\displaystyle \frac{4\pi G}{3}}{\sigma }_0.\end{array}$$

(3)

This equation can be derived from the Lagrangian:

$$\begin{array}{c}\hfill L_N={\displaystyle \frac{R^2{\dot{a}}^2}{2}}+{\displaystyle \frac{GM}{aR}}={\displaystyle \frac{R^2{\dot{a}}^2}{2}}+{\displaystyle \frac{4\pi G}{3}}{R}^2{a}^2{\sigma }_0,\end{array}$$

(4)

where $M={\displaystyle \frac{4\pi }{3}}{a}^3{R}^3{\sigma }_0$ represents the mass inside the ball. Indeed, employing the Euler–Lagrange equation yields the following:

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L_N}{\partial \dot{a}}}\right)={\displaystyle \frac{\partial L_N}{\partial a}}⟹\ddot{a}={\displaystyle \frac{4\pi G}{3}}{\displaystyle \frac{\partial }{\partial a}}\left(a^2{\sigma }_0\right)=-{\displaystyle \frac{4\pi G}{3}}{\sigma }_{0}a,\end{array}$$

(5)

where we have utilized the mass conservation equation: ${\displaystyle \frac{\partial }{\partial a}}\left(a^3{\sigma }_0\right)=0⟹{\displaystyle \frac{\partial }{\partial a}}\left(a^2{\sigma }_0\right)=-a{\sigma }_0.$

We note that the radius R of the selected ball does not influence the dynamical equations. Therefore, we can set $R=1$ for simplicity. In order to derive the second Friedmann equation for a general fluid field, it is necessary to consider the energy related to the microscopic movements of the particles that constitute the fluid, along with the interactions among these particles. Consequently, we replace the mass density with the energy density, denoted as ${\rho }_0$, in the Newtonian Lagrangian (4) where $R=1$, leading to the results found in [11]:

$$\begin{array}{c}\hfill {\overline{L}}_N={\displaystyle \frac{{\dot{a}}^2}{2}}+{\displaystyle \frac{4\pi G}{3}}{a}^2{\rho }_0.\end{array}$$

(6)

Using the Euler–Lagrange equation and the first law of thermodynamics as described in [9,12], one derives the second Friedmann equation ${\displaystyle \frac{\ddot{a}}{a}}=-{\displaystyle \frac{4\pi G}{3}}({\rho }_0+3p_0)$ and the first one $H^2-{\displaystyle \frac{8\pi G}{3}}{\rho }_0=c_0/a^2$, where $c_0$ is the constant of integration. Setting $c_0$ to be equal to $-k$ which corresponds to the spatial geometry of the universe as in the FLRW metric, one obtains the first Friedmann equation. In conclusion, considering that the energy of a uniform ball with radius a is given by $E={\displaystyle \frac{4\pi }{3}}{a}^3{\rho }_0$, the Newtonian Lagrangian can be expressed as ${\overline{L}}_N=E_{\mathrm{kin}}-V$. Here, $E_{\mathrm{kin}}={\displaystyle \frac{{\dot{a}}^2}{2}}$ represents the kinetic energy per unit mass, while $V=-{\displaystyle \frac{GE}{a}}$ denotes the gravitational potential created by the ball with rest mass E.

3. Dynamical Equations in the Newtonian Approach

In this section, we present a framework for testing GR under specific assumptions. It is important to emphasize that Einstein’s field equations are fundamentally rooted in the Principle of Equivalence [13,14]. Notably, when this principle was applied to a freely falling observer in a homogeneous gravitational field, it led Einstein to recognize that gravity enters the theory through the metric [15]. However, as highlighted in the literature, the derivation of these equations involved a considerable degree of intuition and heuristic reasoning [4,16,17]. With this in mind, we assess the validity of GR through a modified approach: while retaining the conventional laws governing particle and photon motion within a given metric, we permit deviations in the metric itself from the one predicted by Einstein’s equations—which rely on general covariance and underpin the relativistic theory of gravity.

More specifically, following [18], we postulate the conservation of the stress-energy tensor, which is equivalent to the relativistic conservation law and the Euler equations. This assumption can be justified using the Principle of Covariance: since the stress-energy tensor is conserved in special relativity—particularly in a locally inertial frame—it must be conserved in all reference frames as the covariant derivative reduces to the partial derivative in a locally inertial frame, and tensor equations hold universally.

Remark 1.

It is important to recognize that, in his early work on gravitation, Einstein assumed that test particles follow geodesics and derived the conservation of the stress-energy tensor for dust matter. This conservation law played a guiding role in his formulation of the field equations. This progression is evident in his lectures at the Prussian Academy of Sciences in November 1915.

On November 11, Einstein presented the paper “On the General Theory of Relativity (Addendum)” (readers can find this in the following: Volume 6: The Berlin Years: Writings, 1914-1917 (English translation supplement) [19]), where he postulated the following field equations:

$$\begin{array}{c}\hfill R_{\mu \nu }=8\pi G{T}_{\mu \nu },\end{array}$$

(7)

assuming that matter could be described purely in terms of electrodynamic processes. Consequently, the trace of the stress-energy tensor vanished, ensuring compatibility with stress-energy conservation.

Later, on November 25, Einstein submitted the final version of general relativity in “The Field Equations of Gravitation” [20]. To maintain stress-energy conservation in the general case, he revised the field equations as follows:

$$\begin{array}{c}\hfill R_{\mu \nu }=8\pi G\left(T_{\mu \nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }T\right).\end{array}$$

(8)

Taking the trace of this equation yields $R=-8\pi GT$, allowing (8) to be rewritten in its more familiar form:

$$\begin{array}{c}\hfill R_{\mu \nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }R=8\pi G{T}_{\mu \nu }.\end{array}$$

(9)

From this, the contracted Bianchi identity ensures the covariant conservation of the stress-energy tensor. However, this does not imply that stress-energy conservation is merely a consequence of the field equations. Rather, as evidenced by Einstein’s November lectures, it was the requirement of stress-energy conservation that guided his derivation of the correct field equations.

Additionally, we consider extensions of the homogeneous first Friedmann equation. These extensions must not only incorporate the classical Poisson equation but also align, at the first order of perturbations, with the well-established Hamiltonian constraint in GR. The resulting constitutive equations derived within this framework represent an extension of the classical equations of motion. Although these equations are simpler than the full set of Einstein’s field equations—notably lacking general covariance—they retain key insights from GR and satisfy classical tests, as we will demonstrate. This approach enables us to examine the implications of modified metrics while preserving essential physical principles, offering a valuable perspective on the interplay between classical and relativistic descriptions of gravity.

Since Newtonian gravity can be understood as the weak-field approximation of General Relativity (GR), it is expected that Newtonian features naturally emerge as perturbations around the FLRW metric—or the Minkowski metric in the case of a static universe—within any metric theory. In this context, three distinct types of perturbations are typically considered:

• Scalar perturbations, which capture Newtonian behavior already at first order.
• Vector perturbations, linked to the shift vector in GR, which also appear at first order but diminish quickly due to the universe’s expansion (whereas in a static background, they arise only at second order).
• Tensor perturbations, whose effects become relevant only at second order in perturbation theory, and at third order in static scenarios.

Given that the classical tests of General Relativity are reproduced by first-order perturbations in a static setting, our study focuses exclusively on scalar perturbations to ensure consistency with these foundational observational results. To proceed, we adopt harmonic coordinates [21] and begin with the following line element in the weak-field approximation for a static gravitational field: $|{\Phi }_{\mathrm{N}}| \ll 1$ [1,3],

$$\begin{array}{c}\hfill d{s}^2=(1+2{\Phi }_{\mathrm{N}}\left(\mathbf{x}\right))d{t}^2-(1-2{\Phi }_{\mathrm{N}}\left(\mathbf{x}\right))d{\mathbf{x}}^2.\end{array}$$

(10)

In this context, $\mathbf{x}$ represents the physical coordinate. When we take into account the expansion of the universe, which is described by the scale factor, as well as the changes in the Newtonian potential, the line element (10) in co-moving coordinates $\mathbf{q}$, where $\mathbf{x}=a\mathbf{q}$, takes on the following form:

$$\begin{array}{c}\hfill d{s}^2=(1+2{\Phi }_{\mathrm{N}}(\mathbf{q},t))d{t}^2-a^2\left(t\right)(1-2{\Phi }_{\mathrm{N}}(\mathbf{q},t))d{\mathbf{q}}^2,\end{array}$$

(11)

which is the linear approximation, for a more general metric, namely $\mathfrak{g}$, of

$$\begin{array}{c}\hfill d{s}^2={\left({\displaystyle \frac{a\left(t\right)}{a_{\mathrm{N}}(\mathbf{q},t)}}\right)}^{2}d{t}^2-a_{\mathrm{N}}^2(\mathbf{q},t)d{\mathbf{q}}^2,\end{array}$$

(12)

where $a_{\mathrm{N}}(\mathbf{q},t)$ represents the perturbed scale factor. At first order in perturbation theory, it is approximately given by $a_{\mathrm{N}}(\mathbf{q},t)\cong a\left(t\right)(1-{\Phi }_{\mathrm{N}}(\mathbf{q},t))$. This expression is essential for analyzing the universe’s dynamical behavior. The following two important remarks are in order:

• As we will see, our approach falls within the framework of so-called metric theories of gravity, [18,22,23,24] where, in page 19 of [18], the authors assume that a metric theory of gravity must satisfy the following two postulates:

  (a)

  Spacetime is endowed by a metric $\mathfrak{g}$.

  (b)

  The conservation law of the stress–energy tensor $\mathrm{div}\left(\mathfrak{T}\right)=0.$

  or as in Ref. [24]

  (a)

  Spacetime is endowed by a metric $\mathfrak{g}$.

  (b)

  World lines of test bodies are geodesics.

  (c)

  In local freely falling frames, the non-gravitational laws of physics are those of special relativity.

  In this context, we choose the “prior metric” (12), for which the spatial slices are conformally flat, and the conservation of the stress-energy tensor is imposed. Consequently, in addition to the vanishing divergence of the stress-energy tensor, we require an equation to determine $a_{\mathrm{N}}$. As we will shortly demonstrate, this equation will generalize the first Friedmann equation.
• To have an intuitive idea about the choice of the metric (12), we apply the the Principle of Equivalence to a uniform gravitational field, namely ${\Phi }_{\mathrm{N}}=gz$, and we seek a metric that reproduces Newton’s second law:

  $$\begin{array}{c}\hfill F_i+F_g=0,\end{array}$$

  (13)

  being $F_i=-m{a}_c$ the inertial force and $F_g=-mg$ the gravitational one, where $a_c$ denotes the acceleration of the body, and we have used the equality of the inertial and gravitational mass. To achieve this, we consider the static line element:

  $$\begin{array}{c}\hfill d{s}^2=A\left(z\right)d{t}^2-B\left(z\right)(d{x}^2+d{y}^2+d{z}^2),\end{array}$$

  (14)

  and from the minimization of the action $\delta S=-m\delta \int ds=0$, we find the following:

  $$\begin{array}{c}\hfill m{\displaystyle \frac{d^{2}z}{d{s}^2}}=-{\displaystyle \frac{m}{2A\left(z\right)B\left(z\right)}}\left[{\partial }_{z}A+{\partial }_z\left(AB\right){\left({\displaystyle \frac{dz}{ds}}\right)}^2\right].\end{array}$$

  (15)

  In order to derive the Newtonian equation, it is necessary to impose the condition that the velocity term on the right-hand side vanishes. This condition is fulfilled when $A\left(z\right)B\left(z\right)=C$, where C is a constant. Without loss of generality, this constant can be set to unity through an appropriate rescaling of the coordinates. Accordingly, we obtain the following:

  $$\begin{array}{c}\hfill -m{\displaystyle \frac{d^{2}z}{d{s}^2}}-{\displaystyle \frac{m}{2}}{\partial }_{z}A=0,\end{array}$$

  (16)

  and comparing with (13) we find that

  $$\begin{array}{c}\hfill a_c={\displaystyle \frac{d^{2}z}{d{s}^2}}\mathrm{and}A\left(z\right)=b+2{\Phi }_{\mathrm{N}}\left(z\right),\end{array}$$

  (17)

  where b is a constant which must be equal to 1 in order to recover the Minkowski metric when the acceleration vanishes. This concludes that, for a uniform gravitational field described by ${\Phi }_{\mathrm{N}}\left(z\right)=gz$, the motion of a freely falling object follows Newton’s second law when the acceleration $a_c$ represents the particle’s proper acceleration. Moreover, we can say that the object does not feel its own weight, since the proper inertial force exactly cancels out the gravitational force as described by Newtonian mechanics.

A final remark is warranted regarding the coefficient $A\left(z\right)$. Its derivation is straightforward and was, in fact, obtained by Einstein as early as 1912. At that time, he approximated the relationship between an unaccelerated frame and a uniformly accelerated frame through the transformation [25]

$$\begin{array}{c}\hfill T=(1+az)t,Z=z+(1+az)a{\displaystyle \frac{t^2}{2}},X=x,Y=y,\end{array}$$

(18)

where a is the uniform acceleration. Applying this transformation to the Minkowski line element $d{s}^2=d{T}^2-d{X}^2-d{Y}^2-d{Z}^2$ yields $d{s}^2={(1+az)}^{2}d{t}^2-d{x}^2-d{y}^2-d{z}^2$.

Now, invoking the Equivalence Principle, Einstein concluded that in a uniform gravitational field, the metric takes the following form:

$$\begin{array}{c}\hfill d{s}^2={(1+gz)}^{2}d{t}^2-d{x}^2-d{y}^2-d{z}^2,\end{array}$$

(19)

where g is the gravitational acceleration. In the weak-field approximation $\left|gz\right|\ll 1$, this reduces to $d{s}^2=(1+2gz)d{t}^2-d{x}^2-d{y}^2-d{z}^2$, thereby yielding $A\left(z\right)\cong 1+2gz$. This calculation motivated Einstein to consider spatially flat metrics of the following form:

$$\begin{array}{c}\hfill d{s}^2=c^2(x,y,z)d{t}^2-d{x}^2-d{y}^2-d{z}^2,\end{array}$$

(20)

for describing general static gravitational fields. However, a critical issue arises: the coefficient $B\left(z\right)$ is absent in this formulation. This omission posed a significant challenge in Einstein’s quest for the correct field equations. Collaborating with Marcel Grossmann, Einstein analyzed the weak-field limit of the field equations:

$$\begin{array}{c}\hfill R_{\mu \nu }=8\pi G{T}_{\mu \nu },\end{array}$$

(21)

using the spatially flat metric (20). This approach, however, proved incompatible with the classical Poisson equation—a discrepancy that ultimately led Einstein to temporarily abandon general covariance and formulate the “hole argument” against it (see, for example [26]). Thus, one may conclude that while the derivation of $A\left(z\right)$ is indeed simple, the inclusion of the second coefficient $B\left(z\right)$-essential for a complete description of gravity was, however, far less obvious, at least in Einstein’s early investigations.

3.1. First Friedmann Equation

By expressing the energy density and pressure as, $\rho ={\rho }_0+\delta \rho$, $p=p_0+\delta p$, where $\delta$ denotes a small perturbation of the respective quantity, the classical Poisson equation can be rewritten as follows:

$$\begin{array}{c}\hfill {\Delta }_{\mathbf{x}}{\Phi }_{\mathrm{N}}=4\pi G\delta \rho ,\end{array}$$

(22)

which using the co-moving coordinates can be written as follows:

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{3}}{\Delta }_{\mathbf{q}}(-2a^2{\Phi }_{\mathrm{N}})={\displaystyle \frac{8\pi G{a}^4}{3}}\delta \rho .\end{array}$$

(23)

To reconcile the homogeneous first Friedmann equation $H^2={\displaystyle \frac{8\pi G}{3}}{\rho }_0$ with the classical Poisson one, we consider the time $d\overline{t}=a\left(t\right)dt$ and the line element becomes $d{s}^2=a_{\mathrm{N}}^{-2}d{\overline{t}}^2-a_{\mathrm{N}}^{2}d{\mathbf{q}}^2$. The normal time-like vector is ${\partial }_{\mathbf{t}}=a_{\mathrm{N}}{\partial }_{\overline{t}}$, and with the use of this vector, and taking into account that in the first order of perturbations, $a_{\mathrm{N}}\cong a(1-{\Phi }_{\mathrm{N}})$, first Friedmann equation, which aligns with the first-order field equations of General Relativity, can be expressed as follows [12]:

$$\begin{array}{c}\hfill H_{\mathrm{N}}^2-{\displaystyle \frac{1}{3a_{\mathrm{N}}^4}}{\Delta }_{\mathbf{q}}{a}_{\mathrm{N}}^2={\displaystyle \frac{8\pi G}{3}}\rho ,\end{array}$$

(24)

where the Hubble rate in cosmic time is defined as $H_{\mathrm{N}}\equiv {\displaystyle \frac{1}{a_{\mathrm{N}}}}{\partial }_{\mathbf{t}}{a}_{\mathrm{N}}$. This equation can be reformulated in a more geometric manner by taking into account the gradient of the scale factor $a_{\mathrm{N}}$:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{a_{\mathrm{N}}}}\mathrm{grad}\left(a_{\mathrm{N}}\right)=H_{\mathrm{N}}{\partial }_{\mathbf{t}}+{\mathbf{H}}_{\mathrm{N}},\end{array}$$

(25)

where we have introduced the Hubble vector ${\mathbf{H}}_{\mathrm{N}}\equiv -{\displaystyle \frac{1}{a_{\mathrm{N}}^2}}{\displaystyle \frac{{\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}}{a_{\mathrm{N}}}}$ with ${\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}={\partial }_j{a}_{\mathrm{N}}{\partial }_j$ representing the three dimensional gradient. Then, with this notation, in our framework the first Friedmann Equation (24) becomes the following:

$$\begin{array}{c}\hfill H_{\mathrm{N}}^2+{\displaystyle \frac{2}{3}}(4\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},{\mathbf{H}}_{\mathrm{N}})+{\nabla }_{\mathbf{q}}·{\mathbf{H}}_{\mathrm{N}})={\displaystyle \frac{8\pi G}{3}}\rho ,\end{array}$$

(26)

where $\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},{\mathbf{H}}_{\mathrm{N}})$ is the square modulus of the Hubble vector and ${\nabla }_{\mathbf{q}}·{\mathbf{H}}_{\mathrm{N}}$ is the Euclidean divergence of the Hubble vector. This last form of the perturbed Friedmann equation can be written in a more geometric form introducing the spacial three divergence of a vector $\mathbf{G}$, that is, ${\mathrm{div}}_{\left(3\right)}\mathbf{G}\equiv {\displaystyle \frac{1}{a_{\mathrm{N}}^3}}{\nabla }_{\mathbf{q}}·a_{\mathrm{N}}^3\mathbf{G}$ and the three gradient of a function f denoted by ${\mathrm{grad}}_{\left(3\right)}f={\displaystyle \frac{1}{a_{\mathrm{N}}^2}}{\partial }_{j}f{\partial }_j$. With this notation, one has ${\mathbf{H}}_{\mathrm{N}}=-{\displaystyle \frac{1}{a_{\mathrm{N}}}}{\mathrm{grad}}_{\left(3\right)}{a}_{\mathrm{N}}$, and taking into account that

$$\begin{array}{c}\hfill {\mathrm{div}}_{\left(3\right)}{\mathbf{H}}_{\mathrm{N}}=-{\displaystyle \frac{1}{2a_{\mathrm{N}}^4}}{\Delta }_{\mathbf{q}}{a}_{\mathrm{N}}^2-\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},{\mathbf{H}}_{\mathrm{N}}),\end{array}$$

(27)

Equation (24) becomes the following:

$$\begin{array}{c}\hfill H_{\mathrm{N}}^2+{\displaystyle \frac{2}{3}}\left({\mathrm{div}}_{\left(3\right)}{\mathbf{H}}_{\mathrm{N}}+\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},{\mathbf{H}}_{\mathrm{N}})\right)={\displaystyle \frac{8\pi G}{3}}\rho .\end{array}$$

(28)

On the other hand, note also that this equation contains the first homogeneous Friedmann equation and coincides, at the first order of perturbations, with the field equations of GR

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{a^2}}{\Delta }_{\mathbf{q}}{\Phi }_{\mathrm{N}}-3H({\partial }_t{\Phi }_{\mathrm{N}}+H{\Phi }_{\mathrm{N}})=4\pi G\delta \rho .\end{array}$$

(29)

Next we want to compare Equation (24) with its corresponding analogous in GR, which is the Hamiltonian constraint obtained from the variation of the lapse function in the Einstein–Hilbert action [27]:

$$\begin{array}{c}\hfill \mathcal{R}-\mathcal{I}=16\pi G\rho ,\end{array}$$

(30)

where $\mathcal{R}$ is the intrinsic curvature (the spatial Ricci scalar) and $\mathcal{I}$ the extrinsic one. For our metric (12) one has the following:

$$\begin{array}{c}\hfill \mathcal{I}=-6H_{\mathrm{N}}^2\mathrm{and}\mathcal{R}=-{\displaystyle \frac{1}{a_{\mathrm{N}}^4}}\left(2{\Delta }_{\mathbf{q}}{a}_{\mathrm{N}}^2-{\displaystyle \frac{3}{2a_{\mathrm{N}}^2}}{\left|{\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}^2\right|}^2\right),\end{array}$$

(31)

where $|{\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}^2{|}^2$ is the Euclidean square modulus of the vector ${\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}^2$. Thus, in GR, the Hamiltonian constraint is

$$\begin{array}{c}\hfill \begin{array}{cc}& H_{\mathrm{N}}^2-{\displaystyle \frac{1}{3a_{\mathrm{N}}^4}}{\Delta }_{\mathbf{q}}{a}_{\mathrm{N}}^2+{\displaystyle \frac{1}{4a_{\mathrm{N}}^6}}{\left|{\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}^2\right|}^2={\displaystyle \frac{8\pi G}{3}}\rho \hfill \\ & ⟺H_{\mathrm{N}}^2+{\displaystyle \frac{2}{3}}\left({\mathrm{div}}_{\left(3\right)}{\mathbf{H}}_{\mathrm{N}}-{\displaystyle \frac{1}{2}}\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},{\mathbf{H}}_{\mathrm{N}})\right)={\displaystyle \frac{8\pi G}{3}}\rho ,\hfill \end{array}\end{array}$$

(32)

that only differs from our Equation (24) in the term ${\displaystyle \frac{1}{4a_{\mathrm{N}}^6}}{\left|{\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}^2\right|}^2$, which in the Newtonian approximation $a_{\mathrm{N}}\cong a(1-{\Phi }_{\mathrm{N}})$, is of quadratic order $|{\nabla }_{\mathbf{q}}{\Phi }_{\mathrm{N}}{|}^2$, that is, smaller compared with the other two terms on the left hand side of (32).

Finally, we wish to emphasize that there exist several extensions of the first Friedmann equation, for example, $H_{\mathrm{N}}^2+{\displaystyle \frac{2}{3}}{\nabla }_{\mathbf{q}}·{\mathbf{H}}_{\mathrm{N}}={\displaystyle \frac{8\pi G}{3}}\rho$. These extensions incorporate both the homogeneous first Friedmann equation and the classical Poisson equation, and they align, to first order in perturbation theory, with the Hamiltonian constraint in GR. From our perspective, the simplest such extension is

$$\begin{array}{c}\hfill H_{\mathrm{N}}^2-{\displaystyle \frac{1}{3a^4}}{\Delta }_{\mathbf{q}}{a}_{\mathrm{N}}^2={\displaystyle \frac{8\pi G}{3}}\rho ⟺H_{\mathrm{N}}^2+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{a_{\mathrm{N}}}{a}}\right)}^4(4\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},{\mathbf{H}}_{\mathrm{N}})+{\nabla }_{\mathbf{q}}·{\mathbf{H}}_{\mathrm{N}})={\displaystyle \frac{8\pi G}{3}}\rho .\end{array}$$

(33)

3.2. Conservation Laws

Introducing the four-velocity $\mathbf{u}=u^{\mu }{\partial }_{\mu }=\left({\displaystyle \frac{d\overline{t}}{ds}},\mathbf{v}\right)$ where $\mathbf{v}={\displaystyle \frac{d\mathbf{q}}{ds}}$ is the space-like velocity, and its dual form, namely $\mathfrak{u}=u_{\mu }d{x}^{\mu }=g_{\mu \nu }{u}^{\nu }d{x}^{\mu }$, which in a more geometric form can be written in terms of the “flat” operator as $\mathfrak{u}={\mathbf{u}}^{♭}$ where for a given four-vector $\mathbf{w}$, one has ${\mathbf{u}}^{♭}\left(\mathbf{w}\right)\equiv \mathfrak{g}(\mathbf{u},\mathbf{w})$, we can write the stress tensor as follows:

$$\begin{array}{c}\hfill \mathfrak{T}=(\rho +p)\mathfrak{u}\otimes \mathfrak{u}-p\mathfrak{g}⟹T_{\mu \nu }=\mathfrak{T}({\partial }_{\mu },{\partial }_{\nu })=(\rho +p)u_{\mu }{u}_{\nu }-p{g}_{\mu \nu }.\end{array}$$

(34)

The conservation equation is

$$\begin{array}{c}\hfill \mathrm{div}\left(\mathfrak{T}\right)=0,\end{array}$$

(35)

which leads to the relativistic conservation and Euler equations:

$$\begin{array}{c}\hfill {\displaystyle \frac{D\rho }{ds}}=-(\rho +p)\mathrm{div}\left(\mathbf{u}\right),(\rho +p){\displaystyle \frac{D\mathbf{u}}{ds}}=\mathrm{grad}\left(p\right)-{\displaystyle \frac{Dp}{ds}}\mathbf{u},\end{array}$$

(36)

where we have introduced the covariant derivative of a vector ${\displaystyle \frac{D\mathbf{u}}{ds}}=u^{\mu }{\nabla }_{\mu }\mathbf{u}$, for an scalar ${\displaystyle \frac{Df}{ds}}=u^{\mu }{\partial }_{\mu }f$, the gradient of a function $\mathrm{grad}\left(f\right)=g^{\mu \nu }{\partial }_{\mu }f{\partial }_{\nu }$, and the divergence of a vector $\mathrm{div}\left(\mathbf{u}\right)={\displaystyle \frac{1}{\sqrt{-g}}}{\partial }_{\mu }\left(\sqrt{-g}{u}^{\mu }\right)$. A simple calculation shows the following:

• $$\begin{array}{c}\hfill {\displaystyle \frac{d\overline{t}}{ds}}=a_{\mathrm{N}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})},\end{array}$$

  (37)
  where $\mathfrak{g}({\mathbf{w}}_1,{\mathbf{w}}_2)=g_{\mu \nu }{w}_1^{\mu }{w}_2^{\nu }$ is the scalar product of the vectors ${\mathbf{w}}_1$ and ${\mathbf{w}}_2$.
• $$\begin{array}{c}\hfill {\displaystyle \frac{Df}{ds}}=\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}{\partial }_{\mathbf{t}}f+\mathbf{v}·{\nabla }_{\mathbf{q}}f.\end{array}$$

  (38)
• $$\begin{array}{c}\hfill \mathrm{div}\left(\mathbf{u}\right)=3H_{\mathrm{N}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}+{\partial }_{\mathbf{t}}\left(\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}\right)+{\nabla }_{\mathbf{q}}·\mathbf{v}+2\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},\mathbf{v}).\end{array}$$

  (39)
• $$\begin{array}{c}\hfill \mathrm{grad}\left(f\right)={\partial }_{\mathbf{t}}f{\partial }_{\mathbf{t}}-{\displaystyle \frac{1}{a_{\mathrm{N}}^2}}{\nabla }_{\mathbf{q}}f,\end{array}$$

  (40)

Therefore, the conservation equation becomes

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}{\partial }_{\mathbf{t}}\rho +\mathbf{v}·{\nabla }_{\mathbf{q}}\rho =-(\rho +p)[3H_{\mathrm{N}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}\\ \hfill +{\partial }_{\mathbf{t}}\left(\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}\right)+{\nabla }_{\mathbf{q}}·\mathbf{v}+2\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},\mathbf{v})].\end{array}\end{array}$$

(41)

The Euler equation, which we will obtain from ${\nabla }_{\mu }{T}_k^{\mu }=0$, is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\partial }_{\mathbf{t}}\left(a_{\mathrm{N}}^2\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}(\rho +p)\mathbf{v}\right)+(\rho +p)a_{\mathrm{N}}^2\left[3H_{\mathrm{N}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}\mathbf{v}+{\mathbf{H}}_{\mathrm{N}}(1-2\mathfrak{g}(\mathbf{v},\mathbf{v}))\right]\\ \hfill +{\nabla }_{\mathbf{q}}p+a_{\mathrm{N}}^2[(\rho +p)({\nabla }_{\mathbf{q}}·\mathbf{v})\mathbf{v}+\mathbf{v}·{\nabla }_{\mathbf{q}}\left((\rho +p)\mathbf{v}\right)+4\mathfrak{g}(\mathbf{v},{\mathbf{H}}_{\mathrm{N}})(\rho +p)\mathbf{v}]=0.\end{array}\end{array}$$

(42)

Summing up, in this approach and disregarding quadratic terms in the velocity $\mathbf{v}$, the constituent equations are (here we use Equation (33) as a first Friedmann equation) as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{H}_{\mathrm{N}}^2+{\displaystyle \frac{2}{3}}{\left({\displaystyle \frac{a_{\mathrm{N}}}{a}}\right)}^4(4\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},{\mathbf{H}}_{\mathrm{N}})+{\nabla }_{\mathbf{q}}·{\mathbf{H}}_{\mathrm{N}})& =& {\displaystyle \frac{8\pi G}{3}}\rho \\ & & \\ {\partial }_{\mathbf{t}}\rho +\mathbf{v}·{\nabla }_{\mathbf{q}}\rho +(\rho +p)\left[3H_{\mathrm{N}}+{\nabla }_{\mathbf{q}}·\mathbf{v}+2\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},\mathbf{v})\right]& =& 0\\ & & \\ {\partial }_{\mathbf{t}}\left(a_{\mathrm{N}}^2(\rho +p)\mathbf{v}\right)+(\rho +p)a_{\mathrm{N}}^2\left[3H_{\mathrm{N}}\mathbf{v}+{\mathbf{H}}_{\mathrm{N}}\right]+{\nabla }_{\mathbf{q}}p& =& 0,\end{array}\right.\end{array}$$

(43)

which at first order of perturbations become

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle \frac{1}{a^2}}{\Delta }_{\mathbf{q}}{\Phi }_{\mathrm{N}}-3\left(H^2{\Phi }_{\mathrm{N}}+H{\partial }_t{\Phi }_{\mathrm{N}}\right)& =& 4\pi G\delta \rho \\ & & \\ {\partial }_t\delta \rho +({\rho }_0+p_0)[{\nabla }_{\mathbf{q}}.\mathbf{v}-3{\partial }_t{\Phi }_{\mathrm{N}}]+3H(\delta \rho +\delta p)& =& 0\\ & & \\ {\partial }_t\left(({\rho }_0+p_0)a^2\mathbf{v}\right)+({\rho }_0+p_0)[3H{a}^2\mathbf{v}+{\nabla }_{\mathbf{q}}{\Phi }_{\mathrm{N}}]+{\nabla }_{\mathbf{q}}\delta p& =& 0,\end{array}\right.\end{array}$$

(44)

and, are equivalent to the perturbed equations of GR using the Newtonian Gauge (see for example, Equations (7.47)–(7.49) of [28]). Effectively, the first equation of (44) coincides with the Equation (7.47) of [28]. Next, the third equation of (44) tells us that $\mathbf{v}$ is a gradient, and thus, performing the temporal derivative of the first equation of (44) and comparing with the second one we find the perturbed version of the so-called diffeomorphism constraint or momentum constraint $4\pi G{a}^2({\rho }_0+p_0)\mathbf{v}=-{\nabla }_{\mathbf{q}}({\partial }_t{\Phi }_{\mathrm{N}}+H{\Phi }_{\mathrm{N}})$, which is the Equation (7.48) of [28] and also ${\partial }_{t^2}^2{\Phi }_{\mathrm{N}}+4H{\partial }_t{\Phi }_{\mathrm{N}}+(2\dot{H}+3H^2){\Phi }_{\mathrm{N}}=4\pi G\delta p$, which coincides with the Equation (7.49) of [28]. Note also that, inserting the diffeomorphism constraint into the third equation of (44) is another way to find the Equation (7.49) of [28].

Finally, we emphasize that Equation (41), arising from the conservation of the stress-energy tensor, can also be derived from the first law of thermodynamics in the case of constant pressure [12]. Specifically, this derivation relies on the following result:

$$\begin{array}{c}\hfill {\left[{\displaystyle \frac{d}{d\overline{t}}}{\int }_{{\phi }_{\overline{t}}\left(\mathrm{\Omega }\right)}f(\overline{t},\mathbf{q})d{q}_{1}d{q}_{2}d{q}_3\right]}_{\overline{t}={\overline{t}}_0}={\int }_{\Omega }{\left({\partial }_{\overline{t}}f+{\nabla }_{\mathbf{q}}·\left(f\mathbf{w}\right)\right)}_{\overline{t}={\overline{t}}_0}d{q}_{1}d{q}_{2}d{q}_3,\end{array}$$

(45)

where ${\phi }_{\overline{t}}$ is the flow of the fluid, that is, ${\displaystyle \frac{{\phi }_{\overline{t}}\left(\mathbf{q}\right)}{d\overline{t}}}=\mathbf{w}(t,{\phi }_{\overline{t}}\left(\mathbf{q}\right))$ being ${\phi }_{{\overline{t}}_0}$ the identity. Utilizing this result in the context of the first law of thermodynamics

$$\begin{array}{c}\hfill {\left[{\displaystyle \frac{d}{d\overline{t}}}{\int }_{{\phi }_{\overline{t}}(\Omega )}\rho (\overline{t},\mathbf{q})dV\right]}_{\overline{t}={\overline{t}}_0}=-p{\left[{\displaystyle \frac{d}{d\overline{t}}}{\int }_{{\phi }_{\overline{t}}(\Omega )}1dV\right]}_{\overline{t}={\overline{t}}_0},\end{array}$$

(46)

where the element of volume for our metric is $dV=a_{\mathrm{N}}^{3}d{q}_{1}d{q}_{2}d{q}_3$. Applying the previous result, and taking into account that $\mathbf{w}=\mathbf{v}{\displaystyle \frac{ds}{d\overline{t}}}=\mathbf{v}{\displaystyle \frac{1}{a_{\mathrm{N}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v}})}}$ and ${\partial }_{\mathbf{t}}=a_{\mathrm{N}}{\partial }_{\overline{t}}$, we find the following equation:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}{\partial }_{\mathbf{t}}\rho +\mathbf{v}·{\nabla }_{\mathbf{q}}\rho =-(\rho +p)[3H_{\mathrm{N}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}-\\ \hfill {\displaystyle \frac{\mathbf{v}·{\nabla }_{\mathbf{q}}\left(\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}\right)}{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}}+{\nabla }_{\mathbf{q}}·\mathbf{v}+2\mathfrak{g}({\mathbf{H}}_{\mathrm{N}},\mathbf{v})].\end{array}\end{array}$$

(47)

Next, recalling that

$$\begin{array}{c}\hfill {\displaystyle \frac{D\mathfrak{g}(\mathbf{v},\mathbf{v})}{d\overline{t}}}={\displaystyle \frac{ds}{d\overline{t}}}{\displaystyle \frac{D\mathfrak{g}(\mathbf{v},\mathbf{v})}{ds}}=2{\displaystyle \frac{ds}{d\overline{t}}}\mathfrak{g}\left({\displaystyle \frac{D\mathbf{v}}{ds}},\mathbf{v}\right)=0,\end{array}$$

(48)

because, when the pressure is constant, the flow follows geodesics, i.e., ${\displaystyle \frac{D\mathbf{v}}{ds}}=0$, we also have

$$\begin{array}{c}\hfill 0={\displaystyle \frac{D\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}}{d\overline{t}}}={\partial }_{\overline{t}}\left(\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}\right)+\mathbf{w}·{\nabla }_{\mathbf{q}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}⟹\\ \hfill {\partial }_{\mathbf{t}}\left(\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}\right)+{\displaystyle \frac{1}{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}}\mathbf{v}·{\nabla }_{\mathbf{q}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}=0,\end{array}$$

(49)

and thus, obtaining the conservation Equation (41).

4. Conformastat Metric: Classical Tests

4.1. Dynamical Equation of Test Particles

We want to find the dynamics of a test particle in the case of a static universe for the conformastat metric $d{s}^2=a_{\mathrm{N}}^{-2}\left(\mathbf{q}\right)d{t}^2-a_{\mathrm{N}}^2\left(\mathbf{q}\right)d{\mathbf{q}}^2$ (see [29] for details and properties of this metric). The action for a test particle is $S=-m\int ds=-m\int {\displaystyle \frac{d{s}^2}{d{s}^2}}ds=-m\int \mathcal{L}ds$, with

$$\begin{array}{c}\hfill \mathcal{L}=a_{\mathrm{N}}^{-2}{\dot{t}}^2+\mathfrak{g}(\mathbf{v},\mathbf{v})=1,\end{array}$$

(50)

where we have used the notation $\dot{t}={\displaystyle \frac{dt}{ds}}$ and $\mathbf{v}={\displaystyle \frac{d\mathbf{q}}{ds}}=\dot{\mathbf{q}}$. Performing the calculations we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\nabla }_{\mathbf{q}}\mathcal{L}=2{\mathbf{H}}_{\mathrm{N}}({\dot{t}}^2-a_{\mathrm{N}}^2\mathfrak{g}(\mathbf{v},\mathbf{v}))=2{\mathbf{H}}_{\mathrm{N}}{a}_{\mathrm{N}}^2(1-2\mathfrak{g}(\mathbf{v},\mathbf{v})),\\ \hfill {\displaystyle \frac{d}{ds}}\left({\nabla }_{\mathbf{v}}\mathcal{L}\right)=-4a_{\mathrm{N}}^2\mathfrak{g}(\mathbf{v},{\mathbf{H}}_{\mathrm{N}})\mathbf{v}-2a_{\mathrm{N}}^2\dot{\mathbf{v}},\end{array}\end{array}$$

(51)

and the Euler–Lagrange equation, after introducing the orthogonal rejection of ${\mathbf{H}}_{\mathrm{N}}$ onto $\mathbf{v}$, namely ${\mathbf{H}}_{\mathrm{N},\perp }={\mathbf{H}}_{\mathrm{N}}-{\displaystyle \frac{\mathfrak{g}(\mathbf{v},{\mathbf{H}}_{\mathrm{N}})}{\mathfrak{g}(\mathbf{v},\mathbf{v})}}\mathbf{v}$, or in terms of the Euclidean inner product ${\mathbf{H}}_{\mathrm{N},\perp }={\mathbf{H}}_{\mathrm{N}}-{\displaystyle \frac{\mathbf{v}·{\mathbf{H}}_{\mathrm{N}}}{{\left|\mathbf{v}\right|}^2}}\mathbf{v}$, becomes

$$\begin{array}{c}\hfill \dot{\mathbf{v}}=-{\mathbf{H}}_{\mathrm{N}}+2\mathfrak{g}(\mathbf{v},\mathbf{v}){\mathbf{H}}_{\mathrm{N},\perp },\end{array}$$

(52)

which for movements parallels to ${\mathbf{H}}_{\mathrm{N}}$, i.e., parallels to ${\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}$, leads to the simple dynamical equation $\dot{\mathbf{v}}=-{\mathbf{H}}_{\mathrm{N}}$. Recalling that in the weak approximation $g_{00}\cong 1+2{\Phi }_{\mathrm{N}}$, and the exact result obtained for a homogeneous potential (see Equation (17)), we can define the “exact” Newtonian potential, namely ${\mathrm{\Psi }}_{\mathrm{N}}$, as $1+2{\Psi }_{\mathrm{N}}=a^2\left(t\right)a_{\mathrm{N}}^{-2}⟹{\mathbf{H}}_{\mathrm{N}}={\displaystyle \frac{1}{a^2\left(t\right)}}{\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}}$, and thus, since we are dealing with an static universe ($a\left(t\right)=1$) and potential, the first Friedmann Equation (24), which in the static case is the generalization of the classical Poisson equation, and the geodesic equation becomes

$$\begin{array}{c}\hfill -4{\displaystyle \frac{|{\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}}{|}^2}{1+2{\Psi }_{\mathrm{N}}}}+{\Delta }_{\mathbf{q}}{\Psi }_{\mathrm{N}}=4\pi G\rho ,\dot{\mathbf{v}}=-{\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}}-2{\displaystyle \frac{{\left|\mathbf{v}\right|}^2}{1+2{\Psi }_{\mathrm{N}}}}{\nabla }_{\mathbf{q}}^{\perp }{\Psi }_{\mathrm{N}},\end{array}$$

(53)

where ${\nabla }_{\mathbf{q}}^{\perp }{\Psi }_{\mathrm{N}}={\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}}-{\displaystyle \frac{\mathbf{v}·{\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}}}{{\left|\mathbf{v}\right|}^2}}\mathbf{v}$ is the orthogonal rejection of ${\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}}$ onto $\mathbf{v}$. Using, once again, the Euclidean inner product, we find

$$\begin{array}{c}\hfill \dot{\mathbf{v}}·\mathbf{v}=-\mathbf{v}·{\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}},\end{array}$$

(54)

which leads to the conservation equation

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{ds}}\left({\displaystyle \frac{1}{2}}{\left|\mathbf{v}\right|}^2+{\Psi }_{\mathrm{N}}\right)=0⟹{\displaystyle \frac{1}{2}}{\left|\mathbf{v}\right|}^2+{\Psi }_{\mathrm{N}}=E.\end{array}$$

(55)

Finally, for small velocities we disregard the quadratic terms in (52), obtaining the following:

$$\begin{array}{c}\hfill \dot{\mathbf{v}}\cong -{\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}}⟹{\displaystyle \frac{d^2\mathbf{q}}{d{t}^2}}\cong -{\displaystyle \frac{1}{a_{\mathrm{N}}^2}}{\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}},\end{array}$$

(56)

where we have used that $\dot{t}=a_{\mathrm{N}}\sqrt{1-\mathfrak{g}(\mathbf{v},\mathbf{v})}\cong a_{\mathrm{N}}$. Taking into account that $a_{\mathrm{N}}^{-2}=1+2{\Psi }_{\mathrm{N}}$, and in the week field approximation $|{\Psi }_{\mathrm{N}}| \ll 1⟹{\Psi }_{\mathrm{N}}\cong {\Phi }_{\mathrm{N}}$, we can disregard the quadratic terms on the potential, we find the Newton’s law ${\displaystyle \frac{d^2\mathbf{q}}{d{t}^2}}\cong -{\nabla }_{\mathbf{q}}{\Psi }_{\mathrm{N}}\cong -{\nabla }_{\mathbf{q}}{\Phi }_{\mathrm{N}}$.

4.2. Metric Produced by a Point Mass Particle

We consider, in a static universe ($a\left(t\right)=1)$, the first Friedmann Equation (33) looking for the stationary spherical symmetric solution produced by a point particle of mass M situated at the origin of $\mathbf{q}$-coordinates. Then, we have to solve the following:

$$\begin{array}{c}\hfill -{\Delta }_{\mathbf{q}}{a}_{\mathrm{N}}^2=8\pi GM\delta \left(\mathbf{q}\right),\end{array}$$

(57)

where $\delta$ is the Dirac’s delta function. The well-known solution is this equation, which aligns with the Minkowski metric when $M=0$ is

$$\begin{array}{c}\hfill a_{\mathrm{N}}^2\left(\mathbf{q}\right)=1+{\displaystyle \frac{2MG}{q}},\end{array}$$

(58)

where $q=\left|\mathbf{q}\right|$ is the Euclidean modulus of $\mathbf{q}$. Then, from our definition of the “exact” Newtonian potential

$$\begin{array}{c}\hfill 1+2{\Psi }_{\mathrm{N}}\left(q\right)={\displaystyle \frac{1}{a_{\mathrm{N}}^2\left(q\right)}}={\displaystyle \frac{q}{q+2MG}}⟹{\Psi }_{\mathrm{N}}\left(q\right)=-{\displaystyle \frac{MG}{q+2MG}}.\end{array}$$

(59)

Finally, to find the relationship with the spherical coordinates, that is between q and the Euclidean distance r, we see that our metric is

$$\begin{array}{c}\hfill d{s}^2=a_{\mathrm{N}}^{-2}\left(q\right)d{t}^2-a_{\mathrm{N}}^2\left(q\right)(d{q}^2+q^{2}d\Omega ),\end{array}$$

(60)

with $d\Omega =d{\theta }^2+sin\theta d{\varphi }^2$. Since, as was pointed out by Hilbert in [30], the angular term in spherical coordinates is $r^{2}d\Omega$ (see also Equation (8.3.4) of [4]), one has the following:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill r^2=q^2{a}_{\mathrm{N}}^2⟹r^2=q^2+2MGq⟹q=-MG\\ \hfill +\sqrt{M^2{G}^2+r^2}⟹{\Psi }_{\mathrm{N}}\left(r\right)=-{\displaystyle \frac{MG}{\sqrt{r^2+M^2{G}^2}+MG}},\end{array}\end{array}$$

(61)

and, in spherical coordinates, the metric becomes

$$\begin{array}{c}\hfill d{s}^2=\left(1+2{\Psi }_{\mathrm{N}}\left(r\right)\right)d{t}^2-{\left(1+2{\Psi }_{\mathrm{N}}\left(r\right)\right)}^{-1}{\left(1+{\displaystyle \frac{M^2{G}^2}{r^2}}\right)}^{-1}d{r}^2-r^{2}d\Omega \\ \hfill ⟹d{s}^2={\displaystyle \frac{1}{1+\frac{M^2{G}^2}{r^2}}}{\left(1+{\displaystyle \frac{MG}{\sqrt{r^2+M^2{G}^2}}}\right)}^{-2}d{t}^2-{\left(1+{\displaystyle \frac{MG}{\sqrt{r^2+M^2{G}^2}}}\right)}^{2}d{r}^2-r^{2}d\Omega \\ \hfill ⟹d{s}^2\cong \left(1+2\left(-{\displaystyle \frac{MG}{r}}+{\displaystyle \frac{M^2{G}^2}{r^2}}\right)\right)d{t}^2-\left(1+{\displaystyle \frac{2MG}{r}}+{\displaystyle \frac{M^2{G}^2}{r^2}}\right)d{r}^2-r^{2}d\Omega ,\end{array}$$

(62)

which is only singular at $r=0$ ($g_{00}=0$ at $r=0$), not like GR, where in spherical coordinates, the metric is singular at the Schwarzschild radius $r=2MG$. Note also that, the last approximation of (62) coincides with the post-Newtonian approximation obtained in formula (9.4.25) of [4]. Note that, the geodesic of a radially free falling particle is (52):

$$\begin{array}{c}\hfill \ddot{q}={\displaystyle \frac{1}{a_{\mathrm{N}}^3}}{\partial }_q{a}_{\mathrm{N}}=-{\displaystyle \frac{1}{2}}{\partial }_q{a}_{\mathrm{N}}^{-2}\left(q\right)=-{\partial }_q{\Psi }_{\mathrm{N}}\left(q\right),\end{array}$$

(63)

which is the Newtonian law for our potential (59). On the other hand, in the approximation $MG/r\ll 1$, the metric becomes:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill d{s}^2\cong \left(1+2{\Psi }_{\mathrm{N}}\left(r\right)\right)d{t}^2-\left(1-2{\Psi }_{\mathrm{N}}\left(r\right)\right)d{r}^2-r^{2}d\Omega \mathrm{with}\\ \hfill {\Psi }_{\mathrm{N}}\left(r\right)\cong -{\displaystyle \frac{MG}{r}}\left(1-{\displaystyle \frac{MG}{r}}\right)\cong -{\displaystyle \frac{MG}{r}}={\Phi }_{\mathrm{N}}\left(r\right),\end{array}\end{array}$$

(64)

which, in this approximation, that is, when $|{\Psi }_{\mathrm{N}}| \ll 1$, coincides with the Schwarzschild metric:

$$\begin{array}{c}\hfill d{s}^2=\left(1+2{\Phi }_{\mathrm{N}}\left(r\right)\right)d{t}^2-{\left(1+2{\Phi }_{\mathrm{N}}\left(r\right)\right)}^{-1}d{r}^2-r^{2}d\Omega \mathrm{with}{\Phi }_{\mathrm{N}}\left(r\right)=-{\displaystyle \frac{MG}{r}}.\end{array}$$

(65)

Three important remarks are in order:

Remark 2.

It is worth noting that the metric (65), commonly referred to as the Schwarzschild metric, was independently derived by Droste [31] and Hilbert [30]. Droste obtained this solution from Einstein’s 1914 “Entwurf” equations [32] without any prior knowledge of Schwarzschild’s work. Hilbert later derived the same result a few months after Droste, approximately one year after Schwarzschild first discovered his family of spherically symmetric solutions to Einstein’s field equations. These solutions describe the gravitational field produced by a point mass located at the origin of the coordinate system.

Among these solutions, Schwarzschild selected the metric that exhibits a singularity solely at the origin. However, through an appropriate coordinate transformation, specifically, using spherical coordinates, this metric reduces to the well-known Schwarzschild form [33].

Remark 3.

The Hilbert-Droste metric can be written in isotropic coordinates as follows [34]:

$$\begin{array}{c}\hfill d{s}^2={\left({\displaystyle \frac{2q-MG}{2q+MG}}\right)}^{2}d{t}^2-{\left(1+{\displaystyle \frac{MG}{2q}}\right)}^4(d{q}^2+q^{2}d\Omega ),\end{array}$$

(66)

where $r=q{\left(1+{\displaystyle \frac{MG}{2q}}\right)}^2$. Disregarding quadratic terms on $MG/q$ we find:

$$\begin{array}{c}\hfill d{s}^2=\left(1-{\displaystyle \frac{2MG}{q}}\right)d{t}^2-\left(1+{\displaystyle \frac{2MG}{q}}\right)(d{q}^2+q^{2}d\Omega ).\end{array}$$

(67)

At this point, it is important to recognize that R is not the radius in spherical coordinates, although it is sometimes identified as such. If one makes this identification, as in [34], it becomes impossible to obtain the correct precession of Mercury’s perihelion. However, by considering the relation between r and q, and disregarding the quadratic terms, one has $r=q+MG$. Using the correct polar coordinates, we recover the metric (64), which, as we will soon demonstrate, successfully passes the classical test. This observation underscores the fact that it is the physics that guides the accurate interpretation of the coordinates. In other words, the coordinates have no intrinsic meaning independent of the metric solution. Each specific metric defines its own physical interpretation of the local coordinates, as illustrated by the Schwarzschild solution (for further discussion, see [35]).

Remark 4.

A significant outcome of our approach is the identification of the Schwarzschild radius’s origin. In General Relativity, when our metric (10) is employed and the Hamiltonian constraint is solved in vacuum, one obtains the Schwarzschild coefficient in isotropic coordinates: $a_{\mathrm{N}}^2\left(q\right)={\left(1+{\displaystyle \frac{MG}{2q}}\right)}^4$. This expression inherently contains the Schwarzschild radius due to the relation $r=q{a}_{\mathrm{N}}\left(q\right)$, from which it follows that ${\displaystyle \frac{dr}{dq}}=1-{\displaystyle \frac{M^2{G}^2}{4q^2}}$. This derivative vanishes when $q={\displaystyle \frac{MG}{2}}$, implying that the mapping between q and r is bijective only for $q>{\displaystyle \frac{MG}{2}}$, or equivalently, for $r>2MG$, thus revealing the presence of the Schwarzschild radius in the GR solution. In contrast, within our framework, the Schwarzschild radius does not emerge. Our earlier analysis of the static case revealed that the fundamental difference between our theory and General Relativity lies in the additional GR term ${\displaystyle \frac{1}{a_{\mathrm{N}}^6}}{\left|{\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}^2\right|}^2$, which, in the weak-field limit, involves the square modulus of the gradient of the Newtonian potential. We therefore conclude that this term is the key element responsible for the appearance of the Schwarzschild radius in General Relativity.

Precession of the Perihelion

We consider the movement in the plane $\theta =\pi /2$. Then, in spherical coordinates, the Lagrangian, using the metric (64), will be:

$$\begin{array}{c}\hfill \mathcal{L}=\left(1+2{\Phi }_{\mathrm{N}}\right){\dot{t}}^2-\left(1-2{\Phi }_{\mathrm{N}}\right){\dot{r}}^2-r^2{\dot{\varphi }}^2,\mathrm{with}\mathcal{L}=1.\end{array}$$

(68)

Since the Lagrangian is independent on t and $\varphi$, we have two conserved quantities:

$$\begin{array}{c}\hfill \left(1+2{\Phi }_{\mathrm{N}}\right)\dot{t}=\sqrt{2E+1}\mathrm{and}{r}^2\dot{\varphi }=L,\end{array}$$

(69)

together with the condition $\mathcal{L}=1$, leads to:

$$\begin{array}{c}\hfill {\dot{r}}^2\cong 2E-2{\Phi }_{\mathrm{N}}\left(r\right)-(1+2{\Phi }_{\mathrm{N}}\left(r\right)){\displaystyle \frac{L^2}{r^2}}.\end{array}$$

(70)

That is

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{dr}{r^{2}d\varphi }}\right)}^2\cong {\displaystyle \frac{2E}{L^2}}+{\displaystyle \frac{2MG}{L^{2}r}}-\left(1-{\displaystyle \frac{2MG}{r}}\right){\displaystyle \frac{1}{r^2}},\end{array}$$

(71)

and performing the change of variable $u=1/r$, we find:

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{du}{d\varphi }}\right)}^2\cong P\left(u\right),\end{array}$$

(72)

where

$$\begin{array}{c}\hfill P\left(u\right)=2MG{u}^3-u^2+{\displaystyle \frac{2MG}{L^2}}u+{\displaystyle \frac{2E}{L^2}}.\end{array}$$

(73)

Note that taking the derivative with respect $\varphi$, we obtain:

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{2}u}{d{\varphi }^2}}=3MG{u}^2-u+{\displaystyle \frac{MG}{L^2}},\end{array}$$

(74)

which disregarding the quadratic term on u, is the well-known equation in Newtonian theory, whose solution is the ellipse:

$$\begin{array}{c}\hfill u={\displaystyle \frac{MG}{L^2}}(1+ecos\varphi )⟹r={\displaystyle \frac{l}{1+ecos\varphi }},\end{array}$$

(75)

where $l={\displaystyle \frac{L^2}{GM}}$ is the semi latus rectum and e the eccentricity of the ellipse. Next, we introduce the perihelion distance $r_{-}$ and $r_{+}$ the aphelion distance. Defining $u_{\pm }=1/r_{\pm }$, we see that they are roots of the three-degree polynomial P, because the trajectory $u\left(\varphi \right)$ reaches its maximum and minimum at $u_{\pm }$. Then, denoting by $u_0$ the other root and following the fundamental theorem of algebra, we have:

$$\begin{array}{c}\hfill P\left(u\right)=2MG(u-u_{+})(u-u_{-})(u-u_0),\end{array}$$

(76)

where expanding it and comparing with the quadratic term of (73) we find $2MG(u_{+}+u_{-}+u_0)=1$, that is $u_0={\displaystyle \frac{1}{2MG}}-(u_{+}+u_{-})$. And we can write:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill P\left(u\right)=(u-u_{+})(u_{-}-u)(1-2MG(u+u_{+}+u_{-}))\\ \hfill ⟹{\displaystyle \frac{1}{P\left(u\right)}}\cong {\displaystyle \frac{1+2MG(u+u_{+}+u_{-})}{(u-u_{+})(u_{-}-u)}}.\end{array}\end{array}$$

(77)

Therefore, we have the key differential equation:

$$\begin{array}{c}\hfill {\displaystyle \frac{d\varphi }{du}}\cong {\displaystyle \frac{1+MG(u+u_{+}+u_{-})}{\sqrt{(u-u_{+})(u_{-}-u)}}},\end{array}$$

(78)

which coincides with the one obtained using the Schwarzschild solution [36]. To count the angles starting at the perihelion we have to calculate the integral:

$$\begin{array}{c}\hfill \varphi \left(u\right)\cong {\int }_{u_{-}}^u{\displaystyle \frac{1+MG(v+u_{+}+u_{-})}{\sqrt{(v-u_{+})(u_{-}-v)}}}dv.\end{array}$$

(79)

Performing the change of variable [4]

$$\begin{array}{c}\hfill v={\displaystyle \frac{1}{2}}(u_{-}+u_{+})+{\displaystyle \frac{1}{2}}(u_{-}-u_{+})cos\psi ,\end{array}$$

(80)

obtaining:

$$\begin{array}{c}\hfill \varphi \left(u\right)=\varphi \left(\psi \right)\cong {\int }_0^{\psi \left(u\right)}\left(1+{\displaystyle \frac{3MG}{2}}(u_{-}+u_{+})+{\displaystyle \frac{MG}{2}}(u_{-}-u_{+})cos\psi \right)d\psi .\end{array}$$

(81)

To obtain the angle $\varphi$ during a revolution we integrate with respect $\psi$ from 0 to $\pi$ (from the perihelion to the aphelion) and multiply by 2, obtaining:

$$\begin{array}{c}\hfill 2\varphi \left(\pi \right)\cong 2\pi +3MG(u_{-}+u_{+}),\end{array}$$

(82)

and thus, the precession of the perihelion per revolution is:

$$\begin{array}{c}\hfill \Delta \varphi ={\displaystyle \frac{6MG}{l}},\end{array}$$

(83)

where we have used the following relation $l={\displaystyle \frac{2}{u_{-}+u_{+}}}$ between the semi latus rectum and $u_{\pm }$.

Remark 5.

In the same way one can calculate the deflection of a beam of light, obtaining the well known result:

$$\begin{array}{c}\hfill \Delta \varphi ={\displaystyle \frac{4MG}{R_0}},\end{array}$$

(84)

where $R_0$ is the distance of closed approach to the origin.

Finally, we emphasize that our approach is consistent with experimental tests conducted in static frames using co-moving coordinates. However, when translational and rotational effects are relevant—such as in the case of gyroscopic precession in orbit around the Earth—an extension of our metric framework is necessary to account for these second-order perturbative effects. Specifically, one must introduce the shift vector ${\mathbf{N}}_{\mathrm{N}}=N^i{\partial }_i$, leading to a metric of the form:

$$\begin{array}{c}\hfill d{s}^2=a_{\mathrm{N}}^{-2}d{\overline{t}}^2-2{\mathbf{N}}_{\mathrm{N}}^{♭}·d\mathbf{q}d\overline{t}-a_{\mathrm{N}}^{2}d{\mathbf{q}}^2=a_{\mathrm{N}}^{-2}d{\overline{t}}^2-2N_{i}d{q}^{i}d\overline{t}-a_{\mathrm{N}}^{2}d{q}^{i}d{q}^j{\delta }_{ij}.\end{array}$$

(85)

Since the extended metric introduces three additional degrees of freedom, we require three supplementary equations to fully determine the system. In our framework, these equations can be derived by using the momentum constraint in General Relativity as a guiding principle [37]:

$$\begin{array}{c}\hfill {\nabla }_j{K}_i^j-{\nabla }_{i}K=8\pi G{p}_i,\end{array}$$

(86)

where, upon introducing the unit vector

$$\begin{array}{c}\hfill {\mathbf{n}}_{\mathrm{N}}\equiv {\displaystyle \frac{1}{\sqrt{1-a_{\mathrm{N}}^2\mathfrak{g}({\mathbf{N}}_{\mathrm{N}},{\mathbf{N}}_{\mathrm{N}})}}}({\partial }_{\mathbf{t}}+a_{\mathrm{N}}{\mathbf{N}}_{\mathrm{N}}),\end{array}$$

(87)

which is orthogonal to the spatial basis ${\left\{{\partial }_i\right\}}_{i=1,2,3}$, we have $p_i=\mathfrak{T}({\mathbf{n}}_{\mathrm{N}},{\partial }_i)$ represents the coordinates momentum density, $K_{ij}=\mathfrak{g}({\nabla }_i{\partial }_j,{\mathbf{n}}_{\mathrm{N}})=-g({\partial }_j,{\nabla }_i{\mathbf{n}}_{\mathrm{N}})$ are the entries of the second fundamental form, and $K=K_i^i$ denotes its trace.

In a more geometric language the momentum constraint can be written as:

$$\begin{array}{c}\hfill {\mathrm{div}}_{\left(3\right)}\left(\mathfrak{K}\right)-{\left({\mathrm{grad}}_{\left(3\right)}K\right)}^{♭}=8\pi G\mathfrak{p},\end{array}$$

(88)

where, given two vector fields ${\mathbf{w}}_1$ and ${\mathbf{w}}_2$, the second fundamental form is defined as $\mathfrak{K}({\mathbf{w}}_1,{\mathbf{w}}_2)=\mathfrak{g}({\nabla }_{{\mathbf{w}}_1}{\mathbf{w}}_2,{\mathbf{n}}_{\mathrm{N}})$ and $\mathfrak{p}\left(\mathbf{w}\right)=\mathfrak{T}({\mathbf{w}}_{\perp },{\mathbf{n}}_{\mathrm{N}})$, being ${\mathbf{w}}_{\perp }$ the orthogonal rejection of the vector $\mathbf{w}$ onto ${\mathbf{n}}_{\mathrm{N}}$. To gain insights into the shift vector, we can utilize some results obtained in the weak field approximation when the universe does not expand. For example, using our notation, in formula (117) of [1], Einstein derived that the contribution to the shift vector ${\mathbf{N}}_{\mathrm{N}}$ due to the translation of a dust fluid is

$$\begin{array}{c}\hfill -4G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)\mathbf{v}(\overline{\mathbf{q}},t)}{|\mathbf{q} - \overline{\mathbf{q}}|}}d\overline{V},\end{array}$$

(89)

where the element of volume is $d\overline{V}=d{\overline{q}}_{1}d{\overline{q}}_{2}d{\overline{q}}_3$.

On the other hand, considering a rotating point mass particle, in Section 104 of [3], the authors found that the contribution to the shift in spherical coordinates is

$$\begin{array}{c}\hfill {\displaystyle \frac{2G}{r^3}}(\mathbf{r}\times \mathbf{M}),\end{array}$$

(90)

where $\mathbf{M}$ is the angular momentum of the particle and its gravitational field. It seems natural to assume that this is proportional to $M\mathbf{v}\times \mathbf{r}$. Therefore, the contribution of a rotating dust fluid must be of the form:

$$\begin{array}{c}\hfill KG\int {\displaystyle \frac{\rho \left(\overline{\mathbf{q}},t\right)(\mathbf{q}-\overline{\mathbf{q}})\times (\mathbf{v}(\overline{\mathbf{q}},t)\times (\mathbf{q}-\overline{\mathbf{q}}))}{|\mathbf{q} - \overline{\mathbf{q}}{|}^3}}d\overline{V},\end{array}$$

(91)

where taking into account the vector identity ${\mathbf{w}}_1\times ({\mathbf{w}}_2\times {\mathbf{w}}_3)={\mathbf{w}}_2({\mathbf{w}}_1·{\mathbf{w}}_3)-{\mathbf{w}}_3({\mathbf{w}}_1·{\mathbf{w}}_2)$, this contribution becomes:

$$\begin{array}{c}\hfill KG\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)\mathbf{v}(\overline{\mathbf{q}},t)}{|\mathbf{q} - \overline{\mathbf{q}}|}}d\overline{V}-KG\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)(\mathbf{q}-\overline{\mathbf{q}})(\mathbf{v}(\overline{\mathbf{q}},t)·(\mathbf{q}-\overline{\mathbf{q}}))}{|\mathbf{q} - \overline{\mathbf{q}}{|}^3}}d\overline{V}.\end{array}$$

(92)

Thus, including both effects, the shift vector has the form:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathbf{N}}_{\mathrm{N}}(\mathbf{q},t)\cong -(4+K)G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)\mathbf{v}(\overline{\mathbf{q}},t)}{|\mathbf{q} - \overline{\mathbf{q}}|}}d\overline{V}\\ \hfill -KG\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)(\mathbf{q}-\overline{\mathbf{q}})(\mathbf{v}(\overline{\mathbf{q}},t)·(\mathbf{q}-\overline{\mathbf{q}}))}{|\mathbf{q} - \overline{\mathbf{q}}{|}^3}}d\overline{V},\end{array}\end{array}$$

(93)

which, for $K=-{\displaystyle \frac{1}{2}}$, coincides with the formula (4.48) of [24], obtained using the Parametrized Post-Newtonian formalism with $\gamma =1$ and all the other parameters vanishing.

Alternatively, for a dust fluid, we derive the momentum constraint up to second order in perturbations, which reads:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\partial }_j{\partial }^j{N}_i-{\partial }_i{\partial }^j{N}_j-4{\partial }_{ti}^2{a}_{\mathrm{N}}=16\pi G{v}_i⟺\\ \hfill {\Delta }_{\mathbf{q}}{\mathbf{N}}_{\mathrm{N}}-{\nabla }_{\mathbf{q}}({\nabla }_{\mathbf{q}}·{\mathbf{N}}_{\mathrm{N}})-4{\nabla }_{\mathbf{q}}{\partial }_t{a}_{\mathrm{N}}=-16\pi G\rho \mathbf{v},\end{array}\end{array}$$

(94)

At this point, it is important to recall that the field equations of General Relativity are constructed using the Ricci curvature tensor, which is invariant under diffeomorphisms. This invariance implies that each diffeomorphism generates a different representation (a different solution) of the same physical solution. In the early development of General Relativity, this property led Einstein to formulate the “Hole Argument” as a challenge to general covariance. Fortunately, he overcame this issue through the “point-coincidence” interpretation of physical events, which asserts that only coincidences of physical events—not the coordinate labels themselves—have physical meaning.

Therefore, Equation (94) has many different solutions, and thus, the way to fix a solution is choice an specific gauge. For example, choosing the well-known de Donder or Lorenz gauge, which in our notation, is ${\nabla }_{\mathbf{q}}·{\mathbf{N}}_{\mathrm{N}}+4{\partial }_t{a}_{\mathrm{N}}=0$, the momentum constraint will become ${\Delta }_{\mathbf{q}}{\mathbf{N}}_{\mathrm{N}}=-16\pi G\rho \mathbf{v}.$

Taking into account that, in the first order of approximation we have $a_{\mathrm{N}}=1-{\Phi }_{\mathrm{N}}$ with

$$\begin{array}{c}\hfill {\Phi }_{\mathrm{N}}(\mathbf{q},t)=-G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)}{|\mathbf{q} - \overline{\mathbf{q}}|}}d\overline{V},\end{array}$$

(95)

using the conservation Equation (41), and retaining only second-order terms for a dust fluid, that is, ${\partial }_t\rho +{\nabla }_{\mathbf{q}}·\left(\mathbf{v}\rho \right)=0$, we find

$$\begin{array}{c}\hfill {\partial }_t{\Phi }_{\mathrm{N}}=-G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)(\mathbf{v}(\overline{\mathbf{q}},t)·(\mathbf{q}-\overline{\mathbf{q}}))}{|\mathbf{q} - \overline{\mathbf{q}}{|}^3}}d\overline{V},\end{array}$$

(96)

then, the solution of the De Donder gauge and the momentum constraint agrees with Einstein’s result:

$$\begin{array}{c}\hfill {\mathbf{N}}_{\mathrm{N}}(\mathbf{q},t)=4G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)\mathbf{v}(\overline{\mathbf{q}},t)}{|\mathbf{q} - \overline{\mathbf{q}}|}}d\overline{V}.\end{array}$$

(97)

On the other hand, in [24], the author adopts the so-called Post-Newtonian gauge ${\nabla }_{\mathbf{q}}·\mathbf{N}+3{\partial }_t{a}_{\mathrm{N}}=0$, under which the momentum constraint becomes ${\Delta }_{\mathbf{q}}{\mathbf{N}}_{\mathrm{N}}-{\nabla }_{\mathbf{q}}{\partial }_t{a}_{\mathrm{N}}=-16\pi G\rho \mathbf{v}$. The solution that satisfies both, the gauge condition and the momentum constraint, is given by:

$$\begin{array}{c}\hfill {\mathbf{N}}_{\mathrm{N}}(\mathbf{q},t)={\displaystyle \frac{7}{2}}G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)\mathbf{v}(\overline{\mathbf{q}},t)}{|\mathbf{q} - \overline{\mathbf{q}}|}}d\overline{V}+{\displaystyle \frac{1}{2}}G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)(\mathbf{q}-\overline{\mathbf{q}})(\mathbf{v}(\overline{\mathbf{q}},t)·(\mathbf{q}-\overline{\mathbf{q}}))}{|\mathbf{q} - \overline{\mathbf{q}}{|}^3}}d\overline{V},\end{array}$$

(98)

which coincides with the result obtained in the Parametrized Post-Newtonian approximation. Note that, first of all, we have found the general solution of the gauge condition, and then we have imposed that it satisfies the momentum constraint. To do it, we have written the second term of (93) as:

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{2}}G\int \rho \left(\overline{\mathbf{q}}t\right)(\mathbf{v}(\overline{\mathbf{q}},t)·(\mathbf{q}-\overline{\mathbf{q}})){\nabla }_{\mathbf{q}}\left({\displaystyle \frac{1}{|\mathbf{q} - \overline{\mathbf{q}}|}}\right)d\overline{V},\end{array}$$

(99)

we have used the identity ${\Delta }_{\mathbf{q}}\left({\displaystyle \frac{1}{|\mathbf{q}-\overline{\mathbf{q}}|}}\right)=-4\pi \delta (\mathbf{q}-\overline{\mathbf{q}})$, and we have performed an integration by parts.

Next, we impose the generalized gauge condition ${\nabla }_{\mathbf{q}}·\mathbf{N}+C{\partial }_t{a}_{\mathrm{N}}=0$, which leads to the modified momentum constraint ${\Delta }_{\mathbf{q}}{\mathbf{N}}_{\mathrm{N}}-(4-C){\nabla }_{\mathbf{q}}{\partial }_t{a}_{\mathrm{N}}=-16\pi G\rho \mathbf{v}$. We then seek solutions of the form:

$$\begin{array}{c}\hfill {\mathbf{N}}_{\mathrm{N}}(\mathbf{q},t)=AG\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)\mathbf{v}(\overline{\mathbf{q}},t)}{|\mathbf{q} - \overline{\mathbf{q}}|}}d\overline{V}+BG\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)(\mathbf{q}-\overline{\mathbf{q}})(\mathbf{v}(\overline{\mathbf{q}},t)·(\mathbf{q}-\overline{\mathbf{q}}))}{|\mathbf{q} - \overline{\mathbf{q}}{|}^3}}d\overline{V}.\end{array}$$

(100)

By inserting this solution into the gauge condition, we obtain the following relationship among the parameters: $A-B=C$.

Substituting into the momentum constraint yields two additional equations: $A+B=4$ and $-2B+4-C=0$. This forms an overdetermined linear system of three equations in three unknowns, whose solution, expressed in terms of C, is:

$$\begin{array}{c}\hfill A={\displaystyle \frac{4+C}{2}}\mathrm{and}B={\displaystyle \frac{4-C}{2}}.\end{array}$$

(101)

It can be verified that for $C=4$ one recovers Einstein’s result, while for $C=3$, the solution aligns with the Parametrized Post-Newtonian approximation.

Ultimately, in the lowest-order approximation, that is, when $a_{\mathrm{N}}=1-{\Phi }_{\mathrm{N}}$, a one-parameter family of solutions to the momentum constraint (94) is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathbf{N}}_{\mathrm{N}}(\mathbf{q},t)={\displaystyle \frac{4+C}{2}}G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)\mathbf{v}(\overline{\mathbf{q}},t)}{|\mathbf{q} - \overline{\mathbf{q}}|}}d\overline{V}\\ \hfill +{\displaystyle \frac{4-C}{2}}G\int {\displaystyle \frac{\rho (\overline{\mathbf{q}},t)(\mathbf{q}-\overline{\mathbf{q}})(\mathbf{v}(\overline{\mathbf{q}},t)·(\mathbf{q}-\overline{\mathbf{q}}))}{|\mathbf{q} - \overline{\mathbf{q}}{|}^3}}d\overline{V},\end{array}\end{array}$$

(102)

being C the free dimensionless parameter.

Therefore, if we aim for our approach to be consistent with the PPN framework, we must impose that the equation governing the shift vector, in an expanding universe, takes the form:

$$\begin{array}{c}\hfill {\Delta }_{\mathbf{q}}{\mathbf{N}}_{\mathrm{N}}-{\nabla }_{\mathbf{q}}{\partial }_{\mathbf{t}}{a}_{\mathrm{N}}=-16\pi G\mathbf{p}{a}_{\mathrm{N}}^2⟺{\displaystyle \frac{1}{a_{\mathrm{N}}^2}}{\Delta }_{\mathbf{q}}{\mathbf{N}}_{\mathrm{N}}-{\displaystyle \frac{1}{a_{\mathrm{N}}}}{\nabla }_{\mathbf{q}}{H}_{\mathrm{N}}=-16\pi G\mathbf{p},\end{array}$$

(103)

where here, the momentum vector $\mathbf{p}$ is the sharp of the 1-form $\mathfrak{p}$, that is, $\mathbf{p}={\mathfrak{p}}^{♯}$. In differential geometry, for a given vector $\mathbf{w}$, the sharp operator is defined via the relation $\mathfrak{g}({\mathfrak{p}}^{♯},\mathbf{w})=\mathfrak{p}\left(\mathbf{w}\right)$. In simpler terms, the sharp operator raises the indices.

On the contrary, if one wishes to obtain the shift vector independently of the field equations of General Relativity, one may proceed as follows: Consider, in a non-expanding universe, a static reference frame $K^{\prime }$, whose metric under a static potential is given by:

$$d{s}^2=(1+2\Phi )d{t^{\prime }}^2-(1-2\Phi )d{{\mathbf{q}}^{\prime }}^{\mathbf{2}}.$$

(104)

Now, consider another frame K moving with velocity $-\mathbf{v}$ with respect to the frame $K^{\prime }$. Equivalently, $K^{\prime }$ moves with velocity $\mathbf{v}$ with respect to K.

Neglecting terms quadratic in the velocity, the Lorentz transformation takes the form:

$${\mathbf{q}}^{\prime }=\mathbf{q}-t\mathbf{v},t^{\prime }=t-\mathbf{v}·\mathbf{q},$$

(105)

and, retaining only terms linear in the velocity, the metric becomes:

$$\begin{array}{c}\hfill d{s}^2=(1+2\Phi )d{t}^2-(1-2\Phi )d{\mathbf{q}}^2-2N_{i}d{q}^{i}dt,\end{array}$$

(106)

where we have introduced the notation $N_i\equiv 4\Phi v^i\cong -4\Phi v_i$, making use of the relation $v_i=g_{\mu i}{v}^{\mu }=-(1-2\Phi )v^i\cong -v^i$.

Note that for a point particle moving along a world line $\mathbf{q}\left(t\right)$, the shift vector can be written as ${\mathbf{N}}_{\mathrm{N}}(t,\mathbf{q})=4G\int {\displaystyle \frac{\delta (\overline{\mathbf{q}}-\mathbf{q}\left(t\right))\mathbf{v}(t,\overline{\mathbf{q}})}{|\mathbf{q}-\overline{\mathbf{q}}|}}d\overline{V}$, which, for a general body, coincides with Einstein’s result given in Equation (89).

To summarize, our formulation posits eight fundamental equations governing the dynamical system.

• The non-homogeneous first Friedmann equation obtained in Section III A.
• The Newtonian formulation of the momentum constraint, which—if we aim to align with the PPN approach—leads us to adopt Equation (103), or, alternatively, if we seek a framework independent of the GR field equations, the Lorentz transformations indicate that Equation (89) should be chosen as the shift vector.
• The energy density conservation equation.
• The relativistic Euler equation.

These equations collectively determine the evolution of eight physical variables:

• The Newtonian scale factor $a_{\mathrm{N}}$.
• Components of the shift vector.
• Energy density $\rho$.
• Three-velocity components of the fluid
• Pressure (through the equation of state $p=p\left(\rho \right)$).

This complete set of equations provides a self-consistent framework for analyzing the system dynamics while maintaining proper accounting of both gravitational and matter degrees of freedom.

5. Conformastat Metric: Stellar Equilibrium

We will apply our framework to the static case, where the constituent equations become:

$$\begin{array}{c}\hfill {\Delta }_{\mathbf{q}}{a}_{\mathrm{N}}^2=-8\pi G\rho \mathrm{and}(\rho +p){\displaystyle \frac{{\nabla }_{\mathbf{q}}{a}_{\mathrm{N}}}{a_{\mathrm{N}}}}={\nabla }_{\mathbf{q}}p,\end{array}$$

(107)

where we have used the first Friedmann Equation (24), although the same results are obtained using (33). Assuming spherical symmetry, we have:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{q^2}}{\left(q^2{\left(a_{\mathrm{N}}^2\right)}^{\prime }\right)}^{\prime }=-8\pi G\rho \mathrm{and}(\rho +p){\displaystyle \frac{a_{\mathrm{N}}^{\prime }}{a_{\mathrm{N}}}}=p^{\prime }.\end{array}$$

(108)

Integrating the first equation we have

$$\begin{array}{c}\hfill {\left(a_{\mathrm{N}}^2\right)}^{\prime }=-{\displaystyle \frac{2GM\left(q\right)}{q^2}}\mathrm{with}M\left(q\right)=4\pi {\int }_0^q{\overline{q}}^2\rho \left(\overline{q}\right)d\overline{q},\end{array}$$

(109)

which after another integration and imposing that $a_{\mathrm{N}}^2=1$ at infinity, leads to

$$\begin{array}{c}\hfill a_{\mathrm{N}}^2\left(q\right)=\left\{\begin{array}{ccc}1+{\displaystyle \frac{2MG}{q_s}}+2G{\int }_q^{q_s}{\displaystyle \frac{M\left(\overline{q}\right)}{{\overline{q}}^2}}d\overline{q}& \mathrm{for}& q\le q_s\\ 1+{\displaystyle \frac{2MG}{q}}& \mathrm{for}& q\ge q_s,\end{array}\right.\end{array}$$

(110)

where $q_s$ is the radius of the star and it mass is $M=4\pi {\int }_0^{q_s}{q}^2\rho \left(q\right)dq$. Therefore, the exact Newtonian potential is:

$$\begin{array}{c}\hfill {\Psi }_{\mathrm{N}}\left(q\right)=\left\{\begin{array}{ccc}-{\displaystyle \frac{MG+G{q}_s{\int }_q^{q_s}\frac{M\left(\overline{q}\right)}{{\overline{q}}^2}d\overline{q}}{q_s+2MG+2G{q}_s{\int }_q^{q_s}\frac{M\left(\overline{q}\right)}{{\overline{q}}^2}d\overline{q}}}& \mathrm{for}& q\le q_s\\ -{\displaystyle \frac{MG}{q+2MG}}& \mathrm{for}& q\ge q_s.\end{array}\right.\end{array}$$

(111)

And, for a fixed energy density, the solution of the equation $(\rho +p){\displaystyle \frac{a_{\mathrm{N}}^{\prime }}{a_{\mathrm{N}}}}=p^{\prime }$, which can be written as ${\displaystyle \frac{1}{2}}(\rho +p){\displaystyle \frac{{\left(a_{\mathrm{N}}^2\right)}^{\prime }}{a_{\mathrm{N}}^2}}=p^{\prime }$, with initial condition $p\left(q_s\right)=0$ is:

$$\begin{array}{c}\hfill p\left(q\right)=a_{\mathrm{N}}\left(q\right){\int }_q^{q_s}\rho \left(\overline{q}\right){\displaystyle \frac{M\left(\overline{q}\right)G}{{\overline{q}}^2}}{\displaystyle \frac{1}{a_{\mathrm{N}}^3\left(\overline{q}\right)}}d\overline{q}\mathrm{for}q<q_s.\end{array}$$

(112)

For example, for a constant energy density $\rho \left(q\right)={\rho }_0$, one has

$$\begin{array}{c}\hfill a_{\mathrm{N}}^2\left(q\right)=\left\{\begin{array}{ccc}1+{\displaystyle \frac{MG}{q_s}}\left(3-{\left({\displaystyle \frac{q}{q_s}}\right)}^2\right)& \mathrm{for}& q\le q_s\\ 1+{\displaystyle \frac{2MG}{q}}& \mathrm{for}& q\ge q_s,\end{array}\right.\end{array}$$

(113)

and thus, the exact Newtonian potential is:

$$\begin{array}{c}\hfill {\Psi }_{\mathrm{N}}\left(q\right)=\left\{\begin{array}{ccc}-{\displaystyle \frac{\frac{MG}{2q_s}\left(3-{\left(\frac{q}{q_s}\right)}^2\right)}{1+\frac{MG}{q_s}\left(3-{\left(\frac{q}{q_s}\right)}^2\right)}}& \mathrm{for}& q\le q_s\\ -{\displaystyle \frac{MG}{q+2MG}}& \mathrm{for}& q\ge q_s,\end{array}\right.\end{array}$$

(114)

and the pressure is:

$$\begin{array}{c}\hfill p\left(q\right)={\rho }_0\left({\displaystyle \frac{a_{\mathrm{N}}\left(q\right)}{a_{\mathrm{N}}\left(q_s\right)}}-1\right)\mathrm{for}q\le q_s.\end{array}$$

(115)

5.1. Linear Equation of State

5.1.1. Exact Solution

We consider the linear EoS $p=w\rho$ (w denotes the barotropic EoS), given the energy density at the boundary, namely ${\rho }_s$, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{a_{\mathrm{N}}^{\prime }}{a_{\mathrm{N}}}}={\displaystyle \frac{w}{1+w}}{\displaystyle \frac{{\rho }^{\prime }}{\rho }}⟹a_{\mathrm{N}}\left(q\right)=a_{\mathrm{N}}\left(q_s\right){\left({\displaystyle \frac{\rho \left(q\right)}{{\rho }_s}}\right)}^n,\mathrm{with}n={\displaystyle \frac{w}{1+w}}.\end{array}$$

(116)

Inserting it into the first equation of (108), we find:

$$\begin{array}{c}\hfill 2n\overline{\rho }{\displaystyle \frac{1}{\xi }}{\displaystyle \frac{d\overline{\rho }}{d\xi }}+n(2n-1){\left({\displaystyle \frac{d\overline{\rho }}{d\xi }}\right)}^2+n\overline{\rho }{\displaystyle \frac{d^2\overline{\rho }}{d{\xi }^2}}+{\overline{\rho }}^{3-2n}=0,\end{array}$$

(117)

with boundary conditions ${\displaystyle \frac{d\overline{\rho }}{d\xi }}\left(0\right)=0$ and $\overline{\rho }\left({\xi }_s\right)=1$, where $\rho ={\rho }_s\overline{\rho }$ and $\xi ={\displaystyle \frac{q}{a_{\mathrm{N}}\left(q_s\right)}}\sqrt{4\pi G{\rho }_s}$.

The mass of the star is:

$$\begin{array}{c}\hfill M=4\pi {\int }_0^{q_s}{q}^2\rho \left(q\right)dq={\displaystyle \frac{b_s{a}_{\mathrm{N}}^3\left(q_s\right)}{G\sqrt{4\pi G{\rho }_s}}},\end{array}$$

(118)

where

$$\begin{array}{c}\hfill b_s\equiv {\int }_0^{{\xi }_s}{\xi }^2\overline{\rho }\left(\xi \right)d\xi ,\end{array}$$

(119)

which relates the energy density at the boundary with the mass, that is, given M and ${\xi }_s$, one has:

$$\begin{array}{c}\hfill {\rho }_s={\displaystyle \frac{b_s^2{a}_{\mathrm{N}}^3\left(q_s\right)}{4\pi }}{\displaystyle \frac{1}{M^2{G}^3}}.\end{array}$$

(120)

On the other hand,

$$\begin{array}{c}\hfill a_{\mathrm{N}}^2\left(q_s\right)=1+{\displaystyle \frac{2MG}{q_s}}=1+{\displaystyle \frac{2b_s}{{\xi }_s}}\sqrt{a_{\mathrm{N}}\left(q_s\right)}\end{array}$$

(121)

which fixes the value of $a_{\mathrm{N}}$ at the boundary. Effectively, defining $x\equiv \sqrt{a_{\mathrm{N}}\left(q_s\right)}$ one has $x^4-{\displaystyle \frac{2b_s}{{\xi }_s}}x-1=0$, and thus, the Descartes’ rule of signs combined with Bolzano’s theorem, tells us that this equation only has a positive solution, which fixes $a_{\mathrm{N}}\left(q_s\right)$. That is, choosing the value of ${\xi }_s$ and the mass of the star M, and solving Equation (117) one finds $b_s$, and thus, solving Equation (121), one obtains $a_{\mathrm{N}}\left(q_s\right)$ and also ${\rho }_s$. Figure 1 presents the numerical solutions of the differential Equation (117) considering $w=1/3$ and taking several values of ${\xi }_s$.

5.1.2. Analytic Solutions

Taking into account that $\rho \left(q\right)={\rho }_s{\left({\displaystyle \frac{a_{\mathrm{N}}\left(q\right)}{a_{\mathrm{N}}\left(q_s\right)}}\right)}^{1/n}$, the first equation of (108) becomes the Lane-Emden equation:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{{\xi }^2}}{\displaystyle \frac{d}{d\xi }}\left({\xi }^2{\displaystyle \frac{d\theta }{d\xi }}\right)+{\theta }^{{\displaystyle \frac{1}{2n}}}=0,\end{array}$$

(122)

with $\theta =a_{\mathrm{N}}^2$ and $\xi =q\sqrt{8\pi G{\rho }_s}{\theta }^{-{\displaystyle \frac{1}{2n}}}\left(q_s\right)$.

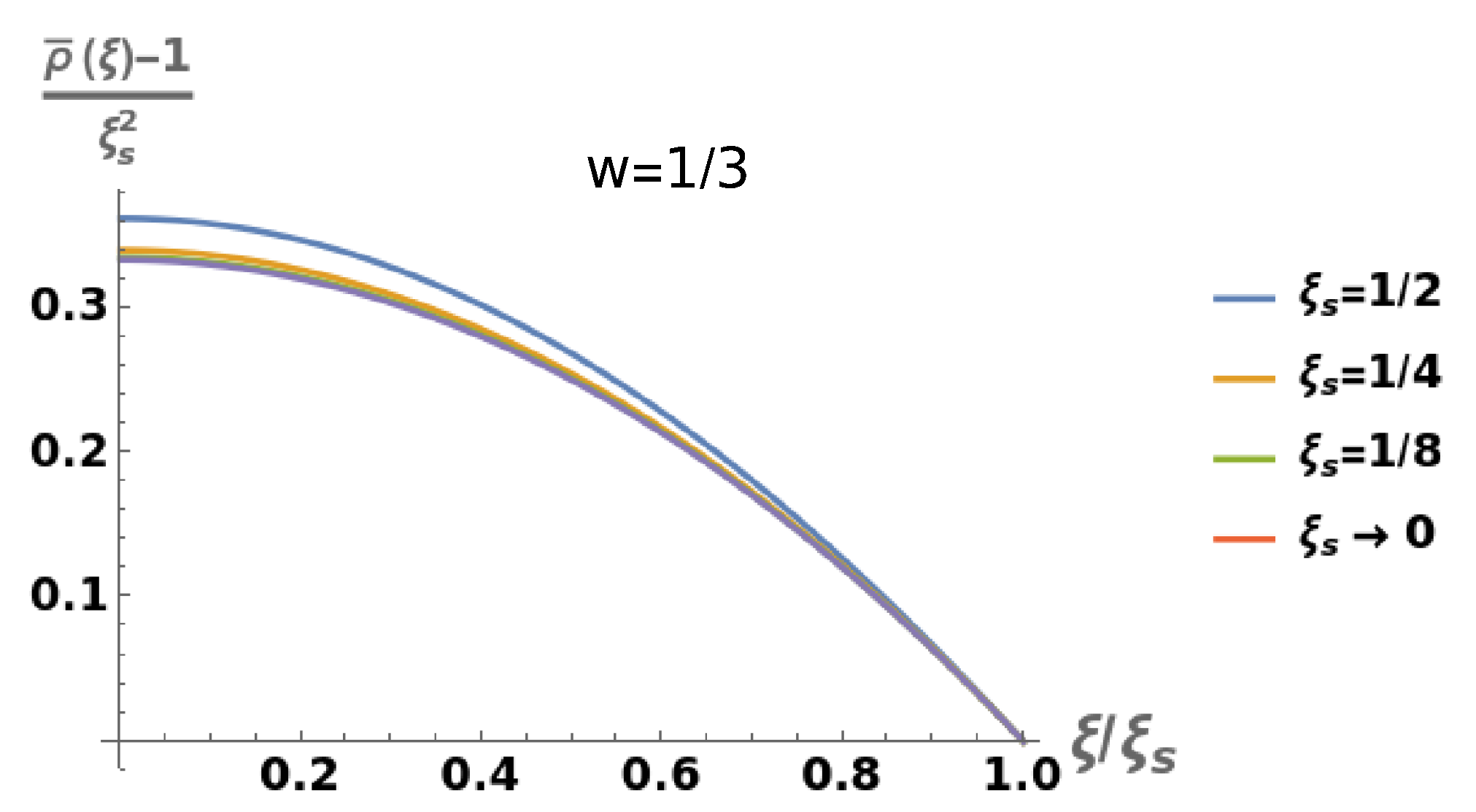
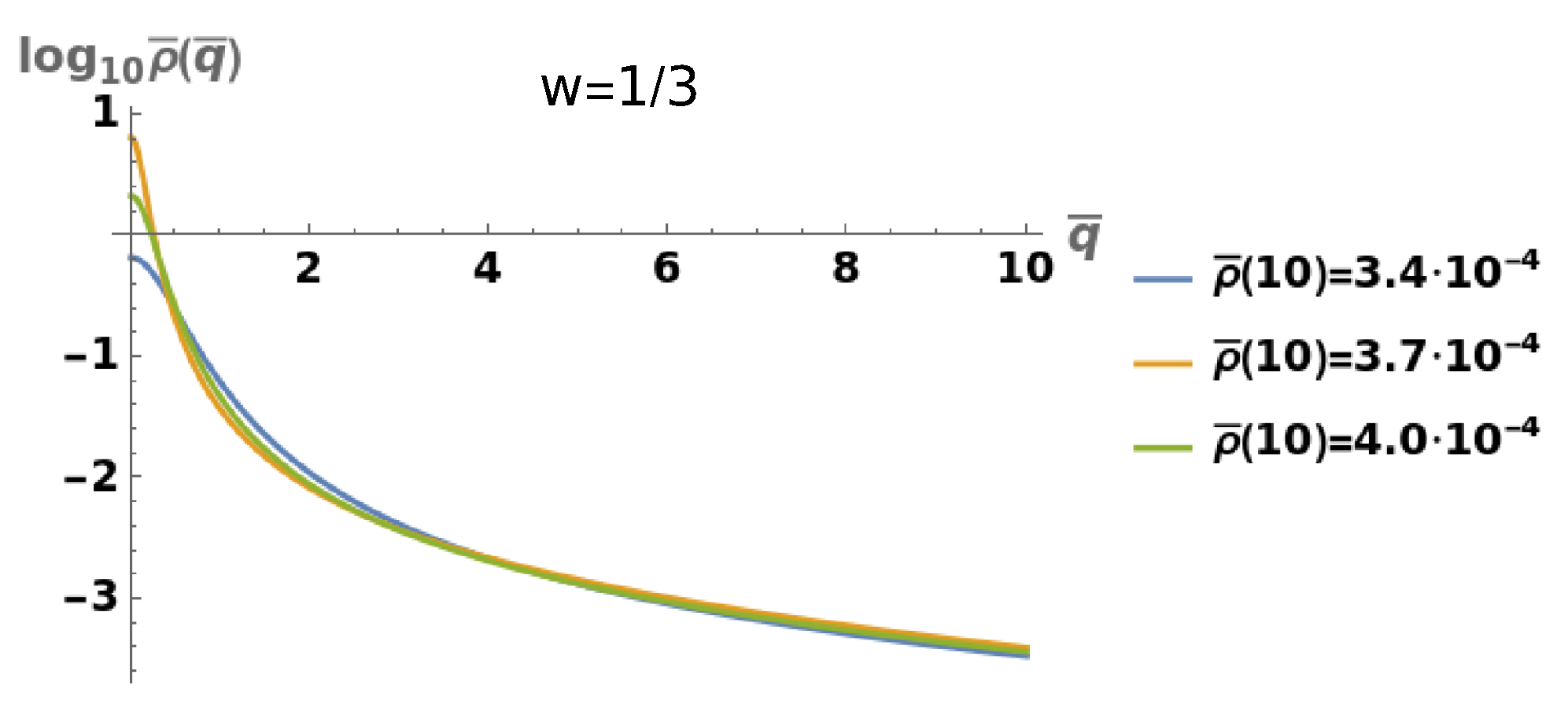
• $w=-1$. The Lane-Emden equation becomes

  $$\begin{array}{c}\hfill {\displaystyle \frac{1}{{\xi }^2}}{\displaystyle \frac{d}{d\xi }}\left({\xi }^2{\displaystyle \frac{d\theta }{d\xi }}\right)+1=0,\end{array}$$

  (123)

  whose solution is $\theta \left(\xi \right)=A-{\displaystyle \frac{{\xi }^2}{6}}$, where taking into account the boundary condition $\theta \left(q_s\right)=1+{\displaystyle \frac{2MG}{q_s}}$, one has:

  $$\begin{array}{c}\hfill A=1+{\displaystyle \frac{3MG}{q_s}}\mathrm{and}\rho \left(q\right)={\rho }_s.\end{array}$$

  (124)
  In terms of the q-coordinate:

  $$\begin{array}{c}\hfill a_{\mathrm{N}}^2\left(q\right)=1+{\displaystyle \frac{3MG}{q_s}}\left[1-{\displaystyle \frac{q^2}{q_s^2}}\right]\mathrm{for}q<q_s,\end{array}$$

  (125)

  which, of course, coincides with the case of a constant energy density, because $w=-1$ implies ${\rho }^{\prime }=0$.
• $w=1$. The Lane-Emden equation becomes

  $$\begin{array}{c}\hfill {\displaystyle \frac{1}{{\xi }^2}}{\displaystyle \frac{d}{d\xi }}\left({\xi }^2{\displaystyle \frac{d\theta }{d\xi }}\right)+\theta =0,\end{array}$$

  (126)

  whose solution is $\theta \left(\xi \right)=A{\displaystyle \frac{sin\xi }{\xi }}$ for $0<\xi \le {\xi }_s$, where ${\xi }_s$ is the radius of the star in the $\xi$-coordinate.
  The mass acquires the form:

  $$\begin{array}{c}\hfill \begin{array}{c}\hfill M=4\pi {\int }_0^{q_s}{q}^2\rho \left(q\right)dq={\displaystyle \frac{A^3}{2G\sqrt{8\pi G{\rho }_s}}}{\displaystyle \frac{{sin}^2{\xi }_s}{{\xi }_s^2}}\\ \hfill (sin{\xi }_s-{\xi }_{s}cos{\xi }_s)\mathrm{with}0<{\xi }_s\le \pi ,\end{array}\end{array}$$

  (127)

  and the relation at the boundary $\theta \left({\xi }_s\right)=1+{\displaystyle \frac{2MG}{q_s}}$, leads to:

  $$\begin{array}{c}\hfill A{\displaystyle \frac{sin{\xi }_s}{{\xi }_s}}=1+{\displaystyle \frac{2MG\sqrt{8\pi G{\rho }_s}}{Asin{\xi }_s}}.\end{array}$$

  (128)
  Combining both expressions, we find:

  $$\begin{array}{c}\hfill A^2{\displaystyle \frac{sin{\xi }_s}{{\xi }_s^2}}(sin{\xi }_s-{\xi }_{s}cos{\xi }_s)-A{\displaystyle \frac{sin{\xi }_s}{{\xi }_s}}+1=0,\end{array}$$

  (129)

  whose solution is:

  $$\begin{array}{c}\hfill A\left({\xi }_s\right)={\displaystyle \frac{{\xi }_s(1+\sqrt{4{\xi }_{s}cot{\xi }_s-3})}{2(sin{\xi }_s-{\xi }_{s}cos{\xi }_s)}}⟹\theta \left({\xi }_s\right)={\displaystyle \frac{1+\sqrt{4{\xi }_{s}cot{\xi }_s-3}}{2(sin{\xi }_s-{\xi }_{s}cos{\xi }_s)}}sin{\xi }_s,\end{array}$$

  (130)

  provided that, $tan\left({\xi }_s\right)\le {\displaystyle \frac{4{\xi }_s}{3}}⟹0<{\xi }_s\lesssim \pi /4$. Therefore, fixing ${\xi }_s\le \pi /4$ one finds the parameter $A\left({\xi }_s\right)$, and since

  $$\begin{array}{c}\hfill \sqrt{8\pi G{\rho }_s}={\displaystyle \frac{A^3\left({\xi }_s\right)}{2MG}}{\displaystyle \frac{{sin}^2{\xi }_s}{{\xi }_s^2}}(sin{\xi }_s-{\xi }_{s}cos{\xi }_s),\end{array}$$

  (131)

  we conclude that, fixing ${\xi }_s$ and the mass M, one finds the value of the parameters A, ${\rho }_s=\rho \left(q_s\right)$ and the radius of the star $q_s$.

5.1.3. Weak Field Approximation

Considering the EoS, $p=w\rho$, and taking into account that, in the linear approximation, ${\Phi }_{\mathrm{N}}^{\prime }={\displaystyle \frac{M\left(q\right)G}{q^2}}$, the equation $(\rho +p){\Phi }_{\mathrm{N}}^{\prime }=-p^{\prime }$, becomes:

$$\begin{array}{c}\hfill {\displaystyle \frac{q^2{\rho }^{\prime }}{\rho }}=-{\displaystyle \frac{1}{n}}M\left(q\right)G,\end{array}$$

(132)

and taking the derivative of this equation one gets:

$$\begin{array}{c}\hfill q\rho {\rho }^{\prime \prime }+2\rho {\rho }^{\prime }-q{\left({\rho }^{\prime }\right)}^2=-{\displaystyle \frac{4\pi G}{n}}q{\rho }^3.\end{array}$$

(133)

Introducing the dimensionless variables $\overline{q}={\displaystyle \frac{q}{MG}}$ and $\overline{\rho }=M^2{G}^3\rho$, the differential equation becomes:

$$\begin{array}{c}\hfill \overline{q}\overline{\rho }{\overline{\rho }}^{\prime \prime }+2\overline{\rho }{\overline{\rho }}^{\prime }-\overline{q}{\left({\overline{\rho }}^{\prime }\right)}^2=-{\displaystyle \frac{4\pi }{n}}\overline{q}{\overline{\rho }}^3,\end{array}$$

(134)

where now the derivative is with respect the dimensionless variable $\overline{q}$. We have to look for solutions satisfying ${\overline{\rho }}^{\prime }\left(0\right)=0$ and fixing the values of $q_s$ and $\overline{\rho }\left({\overline{q}}_s\right)$. Then, giving ${\overline{q}}_s$ and $\overline{\rho }\left({\overline{q}}_s\right)$, we find the energy density and the Newtonian potential in the interior of the star. In Figure 2 we have shown some solutions of the energy density for a fixed value of $w=1/3$.

6. Newtonian Gravitational Collapse

In this section we will deal with the gravitational collapse of a homogeneous pressure-less fluid with spherical symmetry in the framework of Newtonian gravity, showing its connection with the homogeneous Friedmann equations. The Newtonian equations for a pressure-less fluid are:

$$\begin{array}{c}\hfill {\Delta }_{\mathbf{q}}{\Phi }_{\mathrm{N}}=4\pi G\rho ,\end{array}$$

(135)

$$\begin{array}{c}\hfill {\partial }_t\rho +{\nabla }_{\mathbf{q}}·\left(\rho \mathbf{v}\right)=0,\end{array}$$

(136)

$$\begin{array}{c}\hfill {\partial }_t\mathbf{v}+\mathbf{v}·{\nabla }_{\mathbf{q}}\mathbf{v}=-{\nabla }_{\mathbf{q}}{\Phi }_{\mathrm{N}}.\end{array}$$

(137)

We look for spherical symmetric solutions. Then, the Newtonian potential has the form:

$$\begin{array}{c}\hfill {\Phi }_{\mathrm{N}}(q,t)={\int }_0^q{\displaystyle \frac{GM(\overline{q},t)}{{\overline{q}}^2}}d\overline{q}+C\left(t\right),\end{array}$$

(138)

where $M(q,t)=4\pi {\int }_0^q{u}^2\rho (u,t)du$ is the mass inside the solid sphere of radius q. Due to the spherical symmetry, we write the velocity as $\mathbf{v}=v{\partial }_q$, and the conservation equation becomes:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\partial }_t\rho +{\displaystyle \frac{1}{q^2}}{\partial }_q\left(q^2\rho v\right)=0⟹{\partial }_t\rho +{\partial }_q\left(\rho v\right)\\ \hfill +{\displaystyle \frac{2}{q}}\rho v=0\mathrm{with}\rho (q,t)=0\mathrm{when}q\ge q_s\left(t\right).\end{array}\end{array}$$

(139)

And the Euler’s equation, becomes:

$$\begin{array}{c}\hfill {\partial }_{t}v+v{\partial }_{q}v=-{\displaystyle \frac{GM(q,t)}{q^2}}.\end{array}$$

(140)

Considering the flux, namely, ${\phi }_t$, with ${\phi }_0=Id.$, we can perform the change of coordinates:

$$\begin{array}{c}\hfill {\phi }_t:[0,x_s]⟶[0,q_s\left(t\right)];x⟶q={\phi }_t\left(x\right),\end{array}$$

(141)

where $x_s=q_s$${\phi }_t\left(x_s\right)=q_s\left(t\right)$. And, taking into account that ${\partial }_t{\phi }_t\left(x\right)=v({\phi }_t\left(x\right),t)$, and defining $\overline{\rho }(x,t)=\rho ({\phi }_t\left(x\right),t)$, we have:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\partial }_t\overline{\rho }(x,t)={\partial }_t\rho ({\phi }_t\left(x\right),t)+v({\phi }_t\left(x\right),t){\partial }_q\rho ({\phi }_t\left(x\right),t),\\ \hfill {\partial }_x\overline{\rho }(x,t)={\partial }_x{\phi }_t\left(x\right){\partial }_q\rho ({\phi }_t\left(x\right),t).\end{array}\end{array}$$

(142)

We also define $\overline{v}(x,t)=v({\phi }_t\left(x\right),t)={\partial }_t{\phi }_t\left(x\right)\equiv {\dot{\phi }}_t\left(x\right)$, we obtain the following equations:

$$\begin{array}{c}\hfill {\partial }_t\overline{\rho }(x,t)+\left({\displaystyle \frac{{\partial }_x{\dot{\phi }}_t\left(x\right)}{{\partial }_x{\phi }_t\left(x\right)}}+{\displaystyle \frac{2{\dot{\phi }}_t\left(x\right)}{{\phi }_t\left(x\right)}}\right)\overline{\rho }(x,t)=0,\mathrm{with}x\in [0,x_s].\end{array}$$

(143)

And the Euler equation becomes:

$$\begin{array}{c}\hfill {\ddot{\phi }}_t\left(x\right)=-{\displaystyle \frac{GM({\phi }_t\left(x\right),t)}{{\phi }_t^2\left(x\right)}},\end{array}$$

(144)

which is the Newton’s law. The boundary condition is $\overline{\rho }(x_s,t)=0$, and the initial condition for the energy density is $\overline{\rho }(x,0)={\overline{\rho }}_0\left(x\right)$, for a fixed function ${\overline{\rho }}_0\left(x\right)$, satisfying ${\overline{\rho }}_0\left(x_s\right)=0$. For the flux ${\phi }_t\left(x\right)$, the initial conditions are ${\phi }_0\left(x\right)=0$ and ${\dot{\phi }}_0\left(x\right)={\overline{v}}_0\left(x\right)$, for a given function ${\overline{v}}_0\left(x\right)$. Dealing with the mass $M({\phi }_t\left(x\right),t)$, we have:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \overline{M}(x,t)\equiv M({\phi }_t\left(x\right),t)=4\pi {\int }_0^{{\phi }_t\left(x\right)}{u}^2\rho (u,t)du\\ \hfill =4\pi {\int }_0^x{\phi }_t^2\left(s\right)\overline{\rho }(s,t){\partial }_s{\phi }_t\left(s\right)ds={\displaystyle \frac{4\pi }{3}}{\int }_0^x\overline{\rho }(s,t){\partial }_s{\phi }_t^3\left(s\right)ds.\end{array}\end{array}$$

(145)

We deal with homogeneous energy densities of the form:

$$\begin{array}{c}\hfill \rho (q,t)=\left\{\begin{array}{ccc}\rho \left(t\right)& \mathrm{when}& 0\le q\le q_s\left(t\right)\\ 0& \mathrm{when}& q>q_s\left(t\right),\end{array}\right.\end{array}$$

(146)

that is:

$$\begin{array}{c}\hfill \overline{\rho }(x,t)=\left\{\begin{array}{ccc}\rho \left(t\right)& \mathrm{when}& 0\le x\le x_s\\ 0& \mathrm{when}& x>x_s.\end{array}\right.\end{array}$$

(147)

Then, considering, the evolution ${\phi }_t\left(x\right)=R\left(t\right)x$ as in an expanding or contracting homogeneous universe, the mass acquires the form:

$$\begin{array}{c}\hfill \overline{M}(x,t)={\displaystyle \frac{4\pi }{3}}\rho \left(t\right)R^3\left(t\right)x^3,\end{array}$$

(148)

and the Euler Equation (144) becomes:

$$\begin{array}{c}\hfill {\displaystyle \frac{\ddot{R}\left(t\right)}{R\left(t\right)}}=-{\displaystyle \frac{4\pi G}{3}}\rho \left(t\right),\end{array}$$

(149)

which is the homogeneous second Friedmann equation for a pressure-less fluid. The conservation Equation (143) becomes the usual conservation equation in a FLRW universe, that is:

$$\begin{array}{c}\hfill \dot{\rho }\left(t\right)+3{\displaystyle \frac{\dot{R}\left(t\right)}{R\left(t\right)}}\rho \left(t\right)=0.\end{array}$$

(150)

Combining both equations we also obtain the homogeneous first Friedmann equation:

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{\dot{R}\left(t\right)}{R\left(t\right)}}\right)}^2={\displaystyle \frac{8\pi G}{3}}\rho \left(t\right).\end{array}$$

(151)

The well-known solution is:

$$\begin{array}{c}\hfill R\left(t\right)=R\left(0\right){\left({\displaystyle \frac{3t\dot{R}\left(0\right)}{2R\left(0\right)}}+1\right)}^{2/3},\end{array}$$

(152)

where we have to choose $R\left(0\right)=1$, because ${\phi }_0\left(x\right)=x$, and $\dot{R}\left(0\right)<0$ to have contraction. That is, we have:

$$\begin{array}{c}\hfill R\left(t\right)={\left({\displaystyle \frac{3t\dot{R}\left(0\right)}{2}}+1\right)}^{2/3}.\end{array}$$

(153)

We see that the star collapses at the origin at time $\overline{t}=-{\displaystyle \frac{2}{3\dot{R}\left(0\right)}}>0$, and we also have:

$$\begin{array}{c}\hfill \rho \left(t\right)={\displaystyle \frac{3}{8\pi G}}{\displaystyle \frac{{\dot{R}}^2\left(0\right)}{{\left(\frac{3}{2}t\dot{R}\left(0\right)+1\right)}^2}}={\displaystyle \frac{3}{8\pi G}}{\displaystyle \frac{{\dot{R}}^2\left(0\right)}{R^3\left(t\right)}},\end{array}$$

(154)

and thus, the energy density is:

$$\begin{array}{c}\hfill \rho (q,t)=\left\{\begin{array}{ccc}{\displaystyle \frac{3}{8\pi G}}{\displaystyle \frac{{\dot{R}}^2\left(0\right)}{R^3\left(t\right)}}& \mathrm{when}& 0\le q\le R\left(t\right)q_s\\ 0& \mathrm{when}& q>R\left(t\right)q_s.\end{array}\right.\end{array}$$

(155)

We also have $\overline{M}(x,t)={\displaystyle \frac{1}{2G}}{\dot{R}}^2\left(0\right)x^3$ and

$$\begin{array}{c}\hfill M(q,t)=\overline{M}({\phi }_{-t}\left(q\right),t)={\displaystyle \frac{1}{2G}}{\dot{R}}^2\left(0\right){\phi }_{-t}^3\left(q\right)={\displaystyle \frac{1}{2G}}{\displaystyle \frac{{\dot{R}}^2\left(0\right)}{R^3\left(t\right)}}{q}^3.\end{array}$$

(156)

Finally, the Newtonian potential is given by:

$$\begin{array}{c}\hfill {\Phi }_{\mathrm{N}}(q,t)={\displaystyle \frac{1}{4}}{\displaystyle \frac{{\dot{R}}^2\left(0\right)}{R^3\left(t\right)}}{q}^2+C\left(t\right),\end{array}$$

(157)

and imposing at the boundary ${\Phi }_{\mathrm{N}}(R\left(t\right)q_s,t)=-{\displaystyle \frac{M(R\left(t\right)q_s,t)G}{R\left(t\right)q_s}}=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\dot{R}}^2\left(0\right)}{R\left(t\right)}}{q}_s^2$, we find:

$$\begin{array}{c}\hfill {\Phi }_{\mathrm{N}}(q,t)={\displaystyle \frac{1}{4}}{\displaystyle \frac{{\dot{R}}^2\left(0\right)}{R\left(t\right)}}\left({\displaystyle \frac{q^2}{R^2\left(t\right)}}-3q_s^2\right).\end{array}$$

(158)

In terms of the total mass $M\equiv M(R\left(t\right)q_s,t)={\displaystyle \frac{1}{2G}}{\dot{R}}^2\left(0\right)q_s^3$, we have:

$$\begin{array}{c}\hfill R\left(t\right)={\left({\displaystyle \frac{3}{2}}\sqrt{{\displaystyle \frac{2MG}{q_s}}}{\displaystyle \frac{t}{q_s}}+1\right)}^{2/3},\end{array}$$

(159)

$$\begin{array}{c}\hfill \rho (q,t)=\left\{\begin{array}{ccc}{\displaystyle \frac{3M}{4\pi R^3\left(t\right)q_s^3}}& \mathrm{when}& 0\le q\le R\left(t\right)q_s\\ & & \\ 0& \mathrm{when}& q\ge R\left(t\right)q_s,\end{array}\right.\end{array}$$

(160)

$$\begin{array}{c}\hfill {\Phi }_{\mathrm{N}}(q,t)=\left\{\begin{array}{ccc}-{\displaystyle \frac{MG}{2R\left(t\right)q_s}}\left[3-{\left({\displaystyle \frac{q}{R\left(t\right)q_s}}\right)}^2\right]& \mathrm{when}& 0\le q\le R\left(t\right)q_s\\ -{\displaystyle \frac{MG}{q}}& \mathrm{when}& q\ge R\left(t\right)q_s.\end{array}\right.\end{array}$$

(161)

Gravitational Collapse in a Conformastat Metric

We consider a spherical collapse, and we look, in our framework (see [38] for a discussion in the context of GR) for the geodesical evolution of the radius, which in this subsection we will denote by Q in q-coordinate, of the star. The exterior metric is given by

$$\begin{array}{c}\hfill d{s}^2=x_{\mathrm{N}}^{-1}\left(q\right)d{t}^2-x_{\mathrm{N}}\left(q\right)(d{q}^2+q^{2}d\Omega ),\end{array}$$

(162)

where $x_{\mathrm{N}}\left(q\right)=a_{\mathrm{N}}^2\left(q\right)=1+{\displaystyle \frac{2MG}{q}}$. Since the boundary moves radially, the Lagrangian is given by:

$$\begin{array}{c}\hfill \mathcal{L}=x_{\mathrm{N}}^{-1}{\dot{t}}^2-x_{\mathrm{N}}{\dot{q}}^2=1.\end{array}$$

(163)

Since the exterior metric is static we have the conservation law:

$$\begin{array}{c}\hfill {\partial }_{\dot{q}}\mathcal{L}=2x_{\mathrm{N}}^{-1}\dot{t}\equiv 2\sqrt{2E+1},\end{array}$$

(164)

where E is a dimensionless constant. To simplify the calculations we take $E=0$, obtaining $\dot{t}=x_{\mathrm{N}}$. Using the constraint $\mathcal{L}=1$, we find:

$$\begin{array}{c}\hfill {\dot{q}}^2=1-x_{\mathrm{N}}^{-1}\left(q\right)={\displaystyle \frac{2MG}{q+2MG}}⟹\dot{q}=-\sqrt{{\displaystyle \frac{2MG}{q+2MG}}},\end{array}$$

(165)

and the solution, as a function of the proper time, is given by:

$$\begin{array}{c}\hfill q\left(s\right)={\left({(Q+2MG)}^{3/2}-{\displaystyle \frac{3s}{2}}\sqrt{2MG}\right)}^{2/3}-2MG.\end{array}$$

(166)

And thus, we can solve $\dot{t}=x_{\mathrm{N}}\left(q\left(s\right)\right)$, obtaining:

$$\begin{array}{c}\hfill t\left(s\right)=s-4MG(f\left(s\right)-f\left(0\right))+{\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{\left(f\right(s)+1)\left(f\right(0)-1)}{\left(f\right(s)-1)\left(f\right(0)+1)}}\right),\end{array}$$

(167)

where

$$\begin{array}{c}\hfill f\left(s\right)=\sqrt{1+{\displaystyle \frac{q\left(s\right)}{2MG}}}.\end{array}$$

(168)

Note that the metric becomes singular when

$$\begin{array}{c}\hfill q\left(s\right)=0⟹s={\displaystyle \frac{4MG}{3}}\left[{\left(1+{\displaystyle \frac{Q}{2MG}}\right)}^{3/2}-1\right]⟹t=+\infty .\end{array}$$

(169)

This stands in stark contrast to the Newtonian case, where, from the perspective of an external observer, the singularity is reached within a finite time. Finally, it is important to note that when $E\ne 0$, analogous results can be derived, albeit with more complex analytical expressions. The underlying methodology remains consistent, but the increased complexity in the mathematical formulations necessitates a more intricate analysis. Effectively, when $E\ne 0$, the Equation (165) becomes:

$$\begin{array}{c}\hfill \dot{q}=-\sqrt{2E+{\displaystyle \frac{2mG}{q+2MG}}}⟹s=-\sqrt{{\displaystyle \frac{2}{E}}}{\displaystyle \frac{MG}{E}}{\int }_{x\left(Q\right)}^{x\left(q\right(s\left)\right)}{\displaystyle \frac{x^2}{\sqrt{1+x^2}}}dx,\end{array}$$

(170)

where we have performed the change of variable $q+2MG={\displaystyle \frac{MG}{E}}{x}^2$. Tanking into account that,

$$\begin{array}{c}\hfill \int {\displaystyle \frac{x^2}{\sqrt{1+x^2}}}dx={\displaystyle \frac{x\sqrt{x^2+1}}{2}}-{\displaystyle \frac{1}{2}}ln(x+\sqrt{1+x^2}),\end{array}$$

(171)

one finds an implicit expression of the form:

$$\begin{array}{c}\hfill s=F\left(q\right(s),Q,MG,E),\end{array}$$

(172)

where it is impossible to analytically isolate $q\left(s\right)$ as a function of the proper time.

7. Conclusions

In the present work, we have presented some metric theories of gravitation leading to an extended Newtonian approach to cosmology. This approach is based on a system of equations comprising the conservation of the stress-energy tensor and a non-homogeneous first Friedmann equation. This modified Friedmann equation incorporates both the standard homogeneous Friedmann equation and the classical Poisson equation. Furthermore, it aligns, to first order in perturbations, with the Hamiltonian constraint derived from the field equations in GR.

In the static case, our framework yields a conformastat metric. For a point mass particle located at the origin of the coordinate system, this metric exhibits a singularity solely at the origin and reduces to the Newtonian potential at large distances from the origin. Moreover, this metric reproduces the same predictions for the precession of the perihelion of Mercury and the deflection of light as those derived from GR. Thus, the framework maintains consistency with both Newtonian gravity in the weak-field limit and key observational tests of GR in static non-rotating systems.

We have also applied our framework to investigate equilibrium configurations of spherically symmetric stars. Additionally, we have examined the gravitational collapse of a pressure-less spherical star within the context of Newtonian theory, establishing a connection between this collapse and the homogeneous Friedmann equations. Furthermore, we have analyzed the collapse within our proposed approach, extending the analysis beyond the Newtonian framework to explore its implications in a more general setting.

In essence, we have demonstrated that our framework establishes a consistent and rigorous bridge between Newtonian and relativistic descriptions of cosmological dynamics. By unifying the key elements of Newtonian mechanics, such as, the Poisson equation, with the relativistic framework of GR, our approach captures the essential features of both theories. This is evident by its ability to reproduce the homogeneous Friedmann equations, aligned with the Hamiltonian constraint of GR to first order in perturbations, and correctly predict phenomena such as the precession of the perihelion of Mercury and the deflection of light. Additionally, the framework proves effective in addressing both static and dynamic situations—such as studying equilibrium configurations of stars and processes like gravitational collapse—highlighting its flexibility and strength. As a result, our work presents a unified and systematic approach for bridging the Newtonian and relativistic descriptions of gravity, shedding light on the relationship between these two fundamental perspectives.