An Analysis of Existing Hash-Based Post-Quantum Signature Schemes
Abstract
1. Introduction
2. Research Methodology
2.1. Research Questions
- RQ1:
- What are the fundamental principles and cryptographic properties of hash-based post-quantum signature schemes, and how do they compare in terms of security and efficiency?
- RQ2:
- What are the advantages and limitations of stateful and stateless hash-based signature schemes?
- RQ3:
- How do hash-based signature schemes compare in terms of key size, signature size, and computational cost?
- RQ4:
- What recent optimizations and improvements have been proposed for hash-based PQC signatures, and what limitations remain despite these advancements?
- RQ5:
- What are the real-world challenges in implementing hash-based PQC signatures?
- RQ6:
- Given the challenges of existing schemes, what alternative approaches, such as Verkle trees and vector commitments, offer improved scalability, security, and efficiency for post-quantum signatures?
2.2. Research Process
2.3. Exclusion and Inclusion Criteria
- Step 1: Abstract-Based Filtering—Articles that are irrelevant, based on their abstracts and keywords, are excluded. More precisely, only those that meet at least 50% of the relevance threshold are considered.
- Step 2: Full-Text Screening—Papers that address only a marginal aspect of the scope of this research, as determined by abstract and keywords, are excluded.
- Step 3: Quality Assessment—The remaining articles undergo an additional filtering step, where the exclusion applies if at least one of the following conditions is not met:
- –
- The paper provides a formal security analysis that includes resistance to quantum attacks.
- –
- The study includes experimental validation, benchmark comparisons, or practical implementation details.
- –
- The research aligns with NIST PQC standardization efforts or widely accepted cryptographic frameworks.
3. Overview of Existing Hash-Based Post-Quantum Signature Schemes and Their Importance in Cryptography
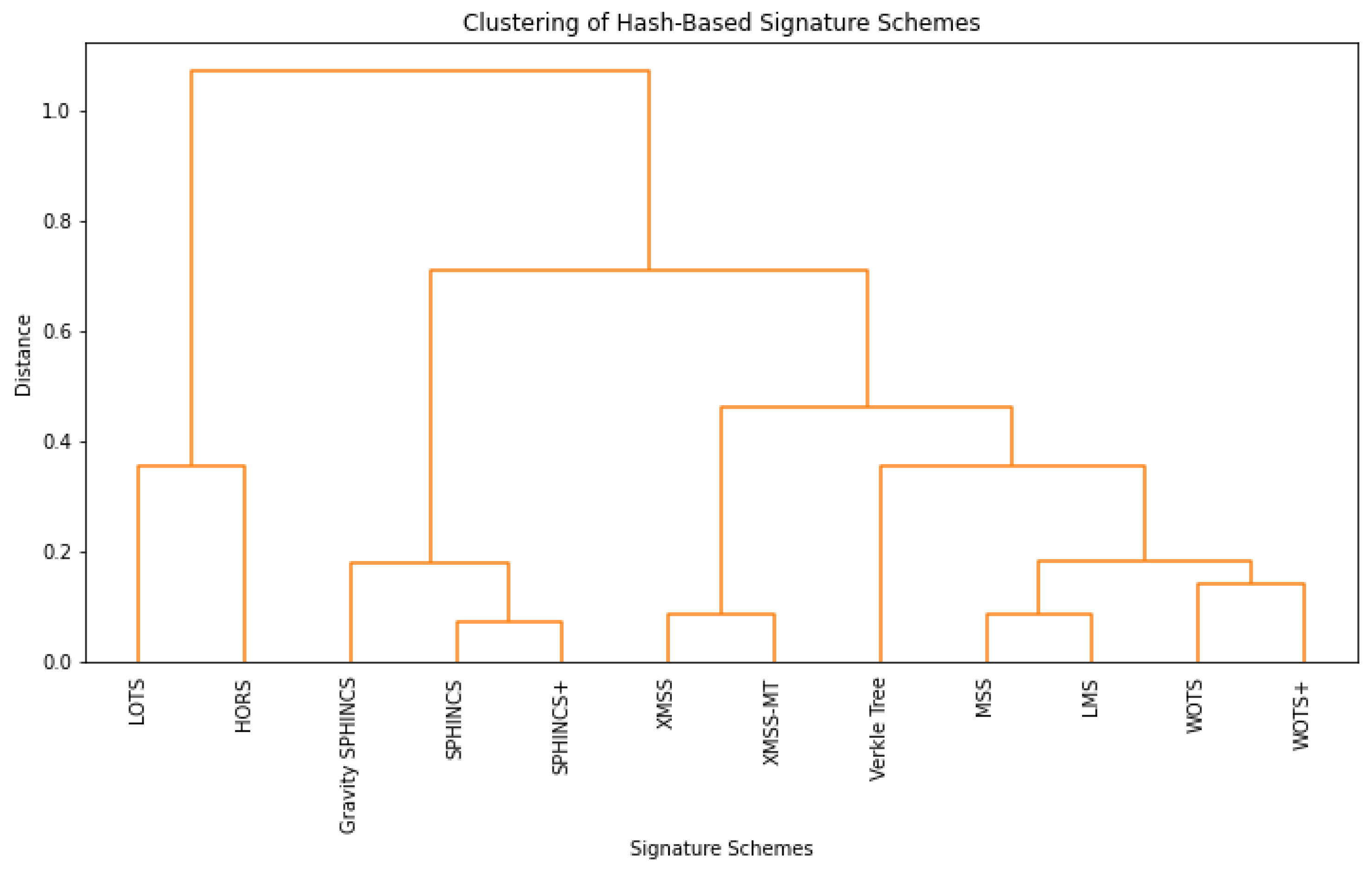
4. Classification of Identified Models
5. Motivation for Post-Quantum Security Due to Quantum Threats
- Reduced proof sizes—Verkle trees can achieve shorter authentication paths (significantly shorter than Merkle trees), thus decreasing the overall signature size.
- Enhanced scalability—Verkle trees are a more efficient data structure, making them better for handling larger datasets with lower storage and transmission requirements and particularly advantageous in resource-constrained environments.
- Improved verification efficiency—Verkle trees enable much faster signature verification, reducing the computational complexity associated with verifying long Merkle authentication paths, which is a crucial aspect for high-throughput applications and IoT devices.
6. Gaps and Open Questions in Identified Research
7. Comparative Analysis and Remarks
- -
- = key size (normalized between 0 and 1);
- -
- = signature size (normalized between 0 and 1);
- -
- = computational cost (normalized between 0 and 1);
- -
- = weights assigned to each factor.
- -
- Key size (KS): (important, since larger key sizes require more storage and transmission bandwidth but are manageable with modern storage capabilities);
- -
- Signature size (SS): (crucial for efficiency, as large signatures can lead to increased verification times and network overhead);
- -
- Computational cost (CC): (matters but depends on hardware).
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science (FOCS’94), Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; Miller, G.L., Ed.; ACM: New York, USA, 1996; pp. 212–219. [Google Scholar]
- Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef] [PubMed]
- Fathalla, E.; Azab, M. Beyond Classical Cryptography: A Systematic Review of Post-Quantum Hash-Based Signature Schemes, Security, and Optimizations. IEEE Access 2024, 12, 175969–175987. [Google Scholar] [CrossRef]
- Li, L.; Lu, X.; Wang, K. Hash-based signature revisited. Cybersecurity 2022, 5, 13. [Google Scholar] [CrossRef]
- Srivastava, V.; Baksi, A.; Debnath, S.K. An Overview of Hash-Based Signatures. Cryptology ePrint Archive. Paper 2023/411. 2023. Available online: https://eprint.iacr.org/2023/411 (accessed on 12 March 2025).
- Lamport, L. Constructing Digital Signatures from a One-Way Function; Technical Report SRI-CSL-98; SRI International: Menlo Park, CA, USA, 1979. [Google Scholar]
- Merkle, R.C. Secrecy, Authentication, and Public-Key Systems. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 1979. [Google Scholar]
- Merkle, R.C. A certified digital signature. In Advances in Cryptology—CRYPTO’89; Springer: New York, NY, USA, 1989; pp. 218–238. [Google Scholar]
- Buchmann, J.; Dahmen, E.; Hülsing, A. XMSS—A practical forward secure signature scheme based on minimal security assumptions. In Proceedings of the International Workshop on Post-Quantum Cryptography, Taipei, Taiwan, 29 November–2 December 2011; Volume 7071, pp. 117–129. [Google Scholar]
- Bernstein, D.J.; Hopwood, D.; Hülsing, A.; Lange, T.; Niederhagen, R.; Papachristodoulou, L.; Schneider, M.; Schwabe, P.; Wilcox-O’hearn, Z. SPHINCS: Practical Stateless Hash-Based Signatures. In Advances in Cryptology– EUROCRYPT 2015; Oswald, E., Fischlin, M., Eds.; Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2015; Volume 9056, pp. 368–397. [Google Scholar]
- Bernstein, D.J.; Hulsing, A.; Kolbl, S.; Niederhagen, R.; Rijneveld, J.; Schwabe, P. The sphincs+ signature framework. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 2129–2146. [Google Scholar]
- NIST. 2016. Submission Requirements and Evaluation Criteria for the PostQuantum Cryptography Standardization Process. Available online: https://csrc.nist.gov/pqc-standardization (accessed on 5 June 2025).
- Iavich, M.; Kuchukhidze, T. Digital Signature Design Using Verkle Tree. In Proceedings of the 28th International Conference on Information Society and University Studies (IVUS 2023), Kaunas, Lithuania, 12 May 2023; pp. 83–91. [Google Scholar]
- Catalano, D.; Fiore, D. Vector commitments and their applications. In Proceedings of the Public-Key Cryptography–PKC 2013: 16th International Conference on Practice and Theory in Public-Key Cryptography, Nara, Japan, 26 February–1 March 2013; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Iavich, M.; Kuchukhidze, T.; Bocu, R. A Post-Quantum Digital Signature Using Verkle Trees and Lattices. Symmetry 2023, 15, 2165. [Google Scholar] [CrossRef]
- Iavich, M.; Kapalova, N. Optimizing Post-Quantum Digital Signatures with Verkle Trees and Quantum Seed-Based Pseudo-Random Generators. Computers 2025, 14, 103. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Ann. Internal Med. 2009, 151, 264–269. [Google Scholar] [CrossRef] [PubMed]
- NIST Computer Security Division: Post-Quantum Cryptography Standardization—Call for Proposals Announcement. 2017. Available online: https://csrc.nist.gov/Projects/Post-Quantum-Cryptography/Post-Quantum-Cryptography-Standardization (accessed on 5 June 2025).
- Hülsing, A. W-OTS+—Shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa; Springer: Berlin/Heidelberg, Germany, 2013; pp. 173–188. [Google Scholar]
- Bernstein, D.J.; Dobraunig, C.; Eichlseder, M.; Fluhrer, S.; Gazdag, S.L.; Hülsing, A.; Kampanakis, P.; Kölbl, S.; Lange, T.; Lauridsen, M.; et al. SPHINCS+, A submission to the NIST Standardization Project on Post-Quantum Cryptography. Discrete MathematicsApplied and Provable SecurityCoding Theory and Cryptology. 2017. Available online: https://research.tue.nl/en/publications/sphincs-submission-to-the-nist-post-quantum-cryptography-project (accessed on 5 June 2025).
- Hulsing, A.; Kudinov, M.; Ronen, E.; Yogev, E. SPHINCS+C: Compressing SPHINCS+ with (Almost) No Cost. In Proceedings of the 2023 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 22–24 May 2023; pp. 1435–1453. [Google Scholar]
- Kuszmaul, J. Verkle Trees. 2019, pp. 1–12. Available online: https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf (accessed on 5 June 2025).
- Leighton, F.; Micali, S. Large Provably Fast and Secure Digital Signature Schemes Based on Secure Hash Functions. U.S. Patent 5,432,852, 11 July 1995. Available online: https://www.google.com/patents/US5432852 (accessed on 5 June 2025).
- Perrig, A. The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security, Philadelphia, PA, USA, 5–8 November 2001; pp. 28–37. [Google Scholar]
- Reyzin, L.; Reyzin, N. Better than BiBa: Short one-time signatures with fast signing and verifying. In Proceedings of the Australasian Conference on Information Security and Privacy, Perth, WA, Australia, 3–5 July 2002; Volume 2384, pp. 144–153. [Google Scholar]
- Buchmann, J.; García, L.C.C.; Dahmen, E.; Doring, M.; Klintsevich, E. CMSS—An improved Merkle signature scheme. In INDOCRYPT 2006; Barua, R., Lange, T., Eds.; Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2006; Volume 4329, pp. 349–363. [Google Scholar]
- Buchmann, J.; Dahmen, E.; Klintsevich, E.; Okeya, K.; Vuillaume, C. Merkle signatures with virtually unlimited signature capacity. In Applied Cryptography and Network Security; Springer: Berlin/Heidelberg, Germany, 2007; pp. 31–45. [Google Scholar]
- Lee, J.; Kim, S.; Cho, Y.; Chung, Y.; Park, Y. HORSIC: An efficient one-time signature scheme for wireless sensor networks. Inf. Process. Lett. 2012, 112, 783–787. [Google Scholar] [CrossRef]
- Hulsing, A.; Rausch, L.; Buchmann, J. Optimal parameters for XMSSMT. In Proceedings of the Security Engineering and Intelligence Informatics: CD-ARES 2013 Workshops: MoCrySEn and SeCIHD, Regensburg, Germany, 2–6 September 2013; Proceedings 8. Springer: Berlin/Heidelberg, Germany, 2013; pp. 194–208. [Google Scholar]
- Kolbl, S.; Lauridsen, M.; Mendel, F.; Rechberger, C. Haraka v2—Efficient Short-Input Hashing for Post-Quantum Applications; IACR Cryptology ePrint Archive: Report 2016/098; International Association for Cryptologic Research: Bellevue, WA, USA, 2016. [Google Scholar]
- Gueron, S.; Mouha, N. Simpira v2: A family of efficient permutations using the aes round function. In Proceedings of the Advances in Cryptology–ASIACRYPT 2016: 22nd International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 4–8 December 2016; Proceedings, Part I. Springer: New York, NY, USA, 2016; pp. 95–125. [Google Scholar]
- Gueron, S.; Mouha, N. Sphincs-simpira: Fast Stateless Hash-Based Signatures with Post-Quantum Security. Cryptology ePrint Archive. Paper 2017/645. Available online: https://eprint.iacr.org/2017/645 (accessed on 5 June 2025).
- Aumasson, J.P.; Endignoux, G. Gravity SPHINCS, A Submission to the NIST Standardization Project on Post-Quantum Cryptography. 2017. Available online: https://github.com/gravity-postquantum/gravity-sphincs (accessed on 5 June 2025).
- Aumasson, J.P.; Endignoux, G. Improving stateless hash-based signatures. In Cryptographers’ Track at the RSA Conference; Springer: Cham, Switzerland, 2018; pp. 219–242. [Google Scholar]
- Kiktenko, E.; Bulychev, A.; Karagodin, P.; Pozhar, N.; Anufriev, M.; Fedorov, A. Sphincs+ postquantum digital signature scheme with streebog hash function. AIP Conf. Proc. 2020, 2241, 020014. [Google Scholar]
- Lee, J.; Park, Y. HORSIC+: An Efficient Post-Quantum Few-Time Signature Scheme. Appl. Sci. 2021, 11, 7350. [Google Scholar] [CrossRef]
- Zhang, K.; Cui, H.; Yu, Y. Sphincs-α: A compact stateless hash-based signature scheme. Cryptol. Eprint Arch. 2022, 2022, 59. [Google Scholar]
- Sim, M.; Eum, S.; Song, G.; Kwon, H.; Jang, K.; Kim, H.; Kim, H.; Yang, Y.; Kim, W.; Lee, W.K.; et al. K-XMSS and K-SPHINCS+: Hash Based Signatures with Korean Cryptography Algorithms. Cryptology ePrint Archive. 2022. Paper 2022/152. Available online: https://eprint.iacr.org/2022/152 (accessed on 5 June 2025).
- Iavich, M.; Kuchukhidze, T.; Okhrimenko, T. Verkle Tree-based Post-Quantum Digital Signature Scheme using Stateless Updatable Vector Commitment. In Proceedings of the CPITS-2023-II: Cybersecurity Providing in Information and Telecommunication Systems, Kyiv, Ukraine, 26 October 2023; pp. 157–166. [Google Scholar]
- Ning, Y.; Dong, J.; Lin, J.; Zheng, F.; Fu, Y.; Dong, Z.; Xiao, F. GRASP: Accelerating Hash-Based PQC Performance on GPU Parallel Architecture. Cryptology ePrint Archive, Paper 2024/1030. 2024. Available online: https://eprint.iacr.org/2024/1030 (accessed on 5 June 2025).
- Algazy, K.; Sakan, K.; Nyssanbayeva, S.; Lizunov, O. Syrga2: Post-Quantum Hash-Based Signature Scheme. Computation 2024, 12, 125. [Google Scholar] [CrossRef]
- Sedghighadikolaei, K.; Yavuz, A.A.; Nouma, S.E. Signer-Optimal Multiple-Time Post-Quantum Hash-Based Signature for Heterogeneous IoT Systems. arXiv 2024, arXiv:2411.01380. [Google Scholar]
- McGrew, D.; Kampanakis, P.; Fluhrer, S.; Gazdag, S.L.; Butin, D.; Buchmann, J. State management for hash-based signatures. In Proceedings of the Security Standardisation Research: Third International Conference (SSR 2016), Gaithersburg, MD, USA, 5–6 December 2016; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2016; pp. 244–260. [Google Scholar]
- Cooper, D.; Apon, D.; Dang, Q.; Davidson, M.; Dworkin, M.; Miller, C. Recommendation for Stateful Hash-Based Signature Schemes; Draft NIST Special Publication SP 800–208; NIST: Gaithersburg, MD, USA, 2019. [Google Scholar]
- Bruinderink, L.G.; Hulsing, A. ‘Oops, I did it again’—Security of one-time signatures under two-message attacks. In Proceedings of the International Conference on Selected Areas in Cryptography, Ottawa, ON, Canada, 16–18 August 2017; Springer: Cham, Switzerland, 2017; pp. 299–322. [Google Scholar]
- NIST: FIPS 205 Stateless Hash-Based Digital Signature Standard. 2024. Available online: https://csrc.nist.gov/pubs/fips/205/final (accessed on 5 June 2025).
- Berger, R.M.; Tiepelt, M. On forging SPHINCS+-Haraka signatures on a fault-tolerant quantum computer. In Proceedings of the Progress in Cryptology—LATINCRYPT 2021: 7th International Conference on Cryptology and Information Security in Latin America, Bogotá, Colombia, 6–8 October 2021; Proceedings 7. Springer: Cham, Switzerland, 2021; pp. 44–63. [Google Scholar]
- Castelnovi, L.; Martinelli, A.; Prest, T. Grafting trees: A fault attack against the SPHINCS framework. In Proceedings of the International Conference on Post-Quantum Cryptography, Fort Lauderdale, FL, USA, 9–11 April 2018; Springer: Cham, Switzerland, 2018; pp. 165–184. [Google Scholar]
- Amiet, D.; Leuenberger, L.; Curiger, A.; Zbinden, P. FPGA-based SPHINCS+ implementations: Mind the Glitch. In Proceedings of the 2020 23rd Euromicro Conference on Digital System Design (DSD), Kranj, Slovenia, 26–28 August 2020; pp. 229–237. [Google Scholar]
- Genet, A. On Protecting SPHINCS+ Against Fault Attacks. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2023, 2023, 80–114. [Google Scholar] [CrossRef]
- Perlner, R.; Kelsey, J.; Cooper, D. Breaking category five SPHINCS+ with SHA-256. In Proceedings of the PQCrypto 2022: The Thirteenth International Conference on Post-Quantum Cryptography, Online, 28–30 September 2022; Springer: Cham, Switzerland, 2022; pp. 501–522. [Google Scholar]
| Type | Database/Search Engine | Motivation and Link |
|---|---|---|
| Digital Libraries (DL) | IEEE Xplore | High-impact cryptographic research, including PQC. https://ieeexplore.ieee.org |
| ACM Digital Library | Comprehensive computing and cryptography papers. https://dl.acm.org | |
| SpringerLink | Covers cryptographic security, mathematical foundations, and PQC research. https://link.springer.com | |
| ScienceDirect (Elsevier) | Publishes cryptographic algorithm research and theoretical advancements. https://www.sciencedirect.com | |
| Wiley Online Library | Contains highly cited cryptography and security research. https://onlinelibrary.wiley.com | |
| Academic Search Engines (SE) | Web of Science | Helps identify highly cited cryptography and PQC papers. https://www.webofscience.com |
| Google Scholar | Has the broadest academic coverage for recent and relevant research. https://scholar.google.com | |
| Scopus | High-quality indexing of cryptographic research with citation analysis. https://www.scopus.com | |
| DBLP | Specialized in computer science papers. https://dblp.uni-trier.de | |
| Semantic Scholar | AI-powered academic search engine with citation recommendations. https://www.semanticscholar.org | |
| Open-Access Repositories (OAR) | arXiv.org | Key source for cryptography preprints and emerging PQC research. https://arxiv.org |
| Cryptology ePrint Archive | Open-access preprints in cryptography, hosted by IACR. https://eprint.iacr.org | |
| HAL | French open-access repository, including cryptography and mathematics research. https://hal.archives-ouvertes.fr |
| ID | Inclusion Criterion |
|---|---|
| IC1 | Papers that focus on hash-based post-quantum signature schemes. |
| IC2 | Studies published in peer-reviewed journals, conferences, or high-impact cryptographic repositories (e.g., IACR, IEEE, ACM) and indexed in recognized academic databases such as Scopus or Web of Science. |
| IC3 | Research evaluating the security, efficiency, and feasibility of hash-based signatures in post-quantum cryptography. |
| IC4 | Papers discussing practical implementations, optimizations, or hybrid approaches for hash-based signatures. |
| IC5 | Studies comparing hash-based signatures with other post-quantum signature schemes (e.g., lattice-based, code-based). |
| IC6 | Papers proposing novel improvements to hash-based signature schemes or addressing their limitations. |
| IC7 | Papers that provide experimental or theoretical security analysis of hash-based signatures against quantum and classical attacks. |
| IC8 | Papers that have been cited frequently or have significant relevance in post-quantum cryptographic standardization efforts (e.g., NIST PQC). |
| ID | Exclusion Criterion |
|---|---|
| EC1 | Papers that do not focus on hash-based post-quantum signature schemes (e.g., RSA, ECC, or generic cryptography papers). |
| EC2 | Studies that lack technical or theoretical depth, such as opinion articles, editorials, or blog posts. |
| EC3 | Research that does not provide security or performance evaluations of hash-based signatures. |
| EC4 | Papers that discuss outdated or deprecated hash-based signature schemes with no relevance to modern post-quantum cryptography. |
| EC5 | Publications with insufficient experimental results, unverifiable claims, or a lack of mathematical proof for their proposed schemes. |
| EC6 | Non-English articles, unless they contain significant contributions and can be reliably translated. |
| EC7 | Preprints that lack peer review and show insufficient methodological rigor, clarity, or completeness based on objective assessment criteria. |
| EC8 | Duplicates of already included studies, unless they provide new experimental results or improvements. |
| Scheme | Year | Key Features | Limitations | Efficiency | Statefulness | Applicability in PQC |
|---|---|---|---|---|---|---|
| Lamport OTS (LOTS) [9] | 1979 | Simple, quantum-secure | Large key and signature size | Low (single-use key, size) | Stateless | Impractical due to size |
| Merkle Signature Scheme (MSS) [10] | 1979 | Tree-based OTS | Large signature sizes and expensive key generation | Improved compared to LOTS (reuses OTS keys) | Stateful | Basis for modern PQC schemes |
| Winternitz OTS (WOTS) [11] | 1989 | Smaller than Lamport | Slower signing process | More efficient verification (fewer hashes) | Stateless | Single-use limitation |
| Leighton–Micali Signatures (LMSs) [26] | 1995 | Variant of Merkle’s scheme supporting a multilevel structure for many signatures | Signature size and verification time increase with each additional level | Efficient (tree-based) | Stateful | NIST-approved alternative to XMSS; standardized for PQC (RFC 8554) |
| BiBa [27] | 2001 | Few-time scheme (FTS) with fast verification; efficient for broadcasts | Expensive signing, large public keys | Inefficient | Stateful | Not well suited for PQC |
| Hash to Obtain Random Subset (HORS) [28] | 2002 | Few-time signature scheme (FTS) with many public keys | Vulnerable to subset resilience attacks | Moderate | Stateless | Efficient but impractical when used alone |
| Compressed MSS (CMSS) [29] | 2006 | Hierarchical structure of multiple smaller Merkle trees; OTS | Limited signatures | Better than MSS but still computationally heavy | Stateful | More practical, not widely used |
| Generalized MSS (GMSS) [30] | 2006 | Variant of the Merkle OTS which allows signing cryptographically unlimited number of messages by using hyper-tree; generalization of CMSS | As secure as the collision resistance of the underlying hash function | Better than CMSS | Stateful | Secure for PQc |
| eXtended Merkle Signature Scheme (XMSS) [12] | 2011 | 25% smaller than previous best hash-based schemes; OTS | Computational cost and limited number of signatures per key pair | Efficient if hash functions are efficient | Stateful | Yes, post-quantum secure; standardized for PQC (RFC 8391) |
| Hash to Obtain Random Subset and Integer Composition (HORSIC) [31] | 2012 | One-time signature scheme with smaller signature and key size | Higher overhead in key generation and signature verification | Efficient | Stateless | Used for for broadcast authentication in wireless sensor networks |
| WOTS+ [22] | 2013 | Improves WOTS and reduces signature size | One-time use; requires additional authentication (e.g., Merkle trees) for key management | More efficient than WOTS | Stateless | Used in modern PQC schemes |
| Multitree XMSS (XMSS-MT) [32] | 2013 | Supports more signatures; better scalability than XMSS | Increases signature size | Higher than XMSS | Stateful | Improves performance for long-term keys; strong PQC candidate; NIST-recommended |
| SPHINCS [13] | 2015 | First stateless hash-based signature (hybrid approach using multiple layers of one-time signatures and Merkle trees, with HORST as a component) | Large signature sizes | Low efficiency | Stateless | Baseline stateless scheme; not standardized, but concept proven |
| Haraka [33] | 2016 | Short-Input Hashing | Not collision-resistant | Highly efficient in hardware | Stateless | Not a general-purpose PQC hash function, as it lacks collision resistance; used in SPHINCS+ |
| Forest of Random Subsets (FORS) [14,23] | 2017 | Improvement of HORS; FTS | Increased signature size | More efficient than HORS | Stateless | Used in SPHINCS+ |
| SPHINCS+ [14,23] | 2017 | Stateless, improved efficiency, flexible | Large (but improved) | Better than SPHINCS; uses tweakable hash (Haraka) and WOTS+ | Stateless | NIST PQC Round 3 winner |
| Sphincs-simpira [34,35] | 2017 | Security-similar original SPHINCS algorithm with faster key pair generation | Larger signature sizes compared to classical schemes | Improved performance | Stateless | Suitable for post-quantum applications requiring efficient hash-based signatures |
| PORS [36,37] | 2017 | Improved HORS; avoids weak messages | Requires a pseudorandom generator (PRG) for subset selection, adding computational overhead | Similar to HORS; slightly better | Stateless | Used for Gravity SPHINCS |
| Gravity SPHINCS [36,37] | 2017 | Improvement of SPHINCS based on PORS | Larger signature sizes and higher computational demands | Offers a balance between security and performance; optimized implementations available | Stateless | Submitted to NIST’s Post-Quantum Cryptography Project; relevant for post-quantum secure applications |
| Sphincs Streebog [38] | 2019 | Uses Streeborg hash-function | Depends on Streebog’s security assumptions | Dependent on Streebog’s performance characteristics | Stateless | Applicable in contexts where Streebog is a standard or preferred hash function |
| HORSIC+ (Hash to Obtain Random Subset and Integer Composition) [39] | 2021 | Improved HORSIC | Higher key storage requirements | More efficient than HORSIC | Stateless | Better candidate for PQC than HORSIC |
| SPHINCS- [40] | 2022 | Improvement performance using improved WOTS and improved FORS | Increased key size due to constant-sum encoding, impacting storage requirements | Improved signing and verification times over SPHINCS+ | Stateless | Enhances SPHINCS+; suitable for PQC applications |
| K-SPHINCS+ [41] | 2022 | Uses Korean hash functions such as LSH, CHAM, and LEA | Performance depends on the efficiency of the integrated hash functions | Comparable efficiency with potential for optimization using advanced techniques | Stateless | Relevant for regions or applications where Korean cryptographic standards are preferred |
| SPHINCS+C [24] | 2023 | Compresses SPHINCS+ signatures with minimal computational overhead | Potential tradeoffs between compression ratio and computational cost | Achieves smaller signature sizes with negligible impact on performance | Stateless | Suitable for applications requiring reduced signature sizes without sacrificing efficiency |
| Verkle tree and vector commitments [16,42] | 2023 | Use vector commitments to build the Merkle tree | New approach; use vector commitments | Efficient | Stateless | Not PQS-secure if based on RSA assumption [16]; PQS-secure if Verkle trees are used in signature procedures and lattices are used to create vector commitments [42] |
| Verkle tree with lattice-based vector commitments [18] | 2023 | Uses vector commitments to build the Merkle tree | New approach; requires further analysis | Aims to provide post-quantum security leveraging Verkle trees and lattice-based techniques | Stateless | Strong potential |
| GRASP (GPU-based paRallel Accelerated SPHINCS+) [43] | 2024 | Accelerates SPHINCS+ using GPU parallel architecture; significant throughput improvements | Requires specialized hardware (GPUs); implementation complexity | Surpasses NIST reference implementation by more then three orders of magnitude | Stateless | Enhances performance of SPHINCS+; applicable in PQC where high throughput is required |
| Syrga2 [44] | 2024 | Multiuse signatures with state retention | Larger key sizes; requires careful parameter selection | Efficient signing and verification | Stateful | Suitable for post-quantum cryptography |
| Maximum Utilization Multiple HORS (MUM-HORS) [45] | 2024 | Multiple-time usage, PQ security, compact key management | Requires careful implementation to avoid weak-message attacks | Fast signing; efficient for IoT devices | Stateless | Suitable for heterogeneous IoT systems |
| Verkle tree with lattice-based vector commitments and quantum seed-based pseudorandom generators [19] | 2025 | Verkle tree-based scheme improving efficiency, reducing memory requirements, enhancing security against quantum attacks | Complexity in implementation; requires quantum randomness sources | Faster verification, reduced memory use, efficient proof sizes | Stateless | Suitable for blockchain, IoT, and mobile security applications |
| Scheme | Security Assumptions | Performance Characteristics |
|---|---|---|
| LOTS | Collision resistance; second-preimage resistance of the hash function | Sign/Verify: n hash operations (one per message bit); Signature size: ; Public key size: |
| MSS | Collision resistance; secure Merkle tree authentication paths | Sign/Verify: hashes for authentication path; Signature size: ; KeyGen: LOTS key pairs |
| WOTS | One-wayness and collision resistance of hash functions | Sign/Verify: l chains of length w (total hashes); Signature size: , where |
| LMS | Collision and second-preimage resistance; Merkle tree assumptions | Sign/Verify: hash operations: Signature size: bits; KeyGen: bits |
| HORS | Subset resilience; preimage resistance; few-time use only | Sign/Verify: t hash operations per signature; Signature size: ; Public key size: |
| XMSS | Collision resistance; PRF security; second-preimage resistance | KeyGen: 0.5–2 s for ; Sign/Verify: 10 ms each (BDS-optimized) |
| WOTS+ | Collision and second-preimage resistance with chaining tweaks | Same as WOTS with chaining function enhancements |
| SPHINCS | Collision resistance; PRF security; multitarget second-preimage resistance | Sign ≈ ms; Verify ms; Sig size ≈ KB |
| SPHINCS+ | Tweakable hashes; strong collision and second-preimage resistance; PRF security | Sign ≈ ms; Verify ms; Sig size ≈ KB |
| Verkle Trees | Collision resistance of hash or lattice SIS hardness for vector commitment | Prove/Verify ≈ ms; Proof size ≈ B |
| Scheme | KS (0–1) | SS (0–1) | CC (0–1) |
|---|---|---|---|
| LOTS | 1.0 | 1.0 | 0.2 |
| MSS | 0.55 | 0.6 | 0.65 |
| WOTS | 0.6 | 0.6 | 0.5 |
| LMS | 0.5 | 0.55 | 0.6 |
| HORS | 0.75 | 0.85 | 0.4 |
| XMSS | 0.4 | 0.45 | 0.7 |
| WOTS+ | 0.5 | 0.5 | 0.5 |
| XMSS-MT | 0.35 | 0.4 | 0.75 |
| SPHINCS | 0.8 | 0.7 | 0.75 |
| SPHINCS+ | 0.75 | 0.65 | 0.75 |
| Gravity SPHINCS | 0.7 | 0.8 | 0.8 |
| Verkle Trees | 0.75 | 0.4 | 0.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacurar, C.M.; Bocu, R.; Iavich, M. An Analysis of Existing Hash-Based Post-Quantum Signature Schemes. Symmetry 2025, 17, 919. https://doi.org/10.3390/sym17060919
Pacurar CM, Bocu R, Iavich M. An Analysis of Existing Hash-Based Post-Quantum Signature Schemes. Symmetry. 2025; 17(6):919. https://doi.org/10.3390/sym17060919
Chicago/Turabian StylePacurar, Cristina Maria, Razvan Bocu, and Maksim Iavich. 2025. "An Analysis of Existing Hash-Based Post-Quantum Signature Schemes" Symmetry 17, no. 6: 919. https://doi.org/10.3390/sym17060919
APA StylePacurar, C. M., Bocu, R., & Iavich, M. (2025). An Analysis of Existing Hash-Based Post-Quantum Signature Schemes. Symmetry, 17(6), 919. https://doi.org/10.3390/sym17060919








