Abstract
In this paper, we propose a novel alternating direction method of multipliers based on acceleration technique involving two symmetrical inertial terms for a class of nonconvex optimization problems with a two-block structure. To address the nonconvex subproblem, we introduce a proximal term to reduce the difficulty of solving this subproblem. For the smooth subproblem, we employ a gradient descent method on the augmented Lagrangian function, which significantly reduces the computational complexity. Under appropriate assumptions, we prove subsequential convergence of the algorithm. Moreover, when the generated sequence is bounded and the auxiliary function satisfies Kurdyka–Łojasiewicz property, we establish global convergence of the algorithm. Finally, effectiveness and superior performance of the proposed algorithm are validated through numerical experiments in signal processing and smoothly clipped absolute deviation penalty problems.
Keywords:
convergence analysis; nonconvex optimization; alternating direction method of multipliers; symmetrical inertial term; Kurdyka–Łojasiewicz inequality MSC:
90C26; 65K05; 49K35; 41A25
1. Introduction
It is well known that recovering sparse signals from incomplete observations is an important and very significant research topic in practical applications. The core objective is to find the optimal sparse solution to a system of linear equations, which can be formulated as the following model [1]:
where is the measurement matrix, is the observed data, is a sparse signal, is a regularization parameter, and denotes the -norm. However, Chartrand and Staneva [2] pointed out that (1) represents a class of problems that are fundamentally difficult to solve. To overcome this challenge, Zeng et al. [3] proposed a relaxed objective function by replacing the regularization with the regularization; the model (1) is transformed into a more tractable nonconvex optimization problem. Therefore, adopting this modification becomes more reasonable in signal recovery problems, which leads to the following two-block nonconvex optimization problem:
where . Further, to mitigate feature compression and information loss in motor imagery decoding, Doostmohammadian et al. [4] proposed a Cauchy-based nonconvex sparse regularization model, which enhances feature extraction and noise reduction across datasets. In general, introducing an auxiliary variable such that in (2), we would consider reformulating the problem (2) as follows:
We notice that many scholars have investigated constrained nonconvex optimization problems of the form (3). In particular, Zeng et al. [3] pointed out that the iterative soft-thresholding algorithm can be used to solve the regularization problem, which was validated in the context of problem (3). Meanwhile, Chen and Selesnick [5] performed a performance validation of model (3) using an improved overlapping shrinkage algorithm. Further related works can be found in [6,7] and the references therein.
In order to solve (3), we will consider the general model of (3) in this paper. That is, in (3), extending the objective function, respectively, to a lower semicontinuous function and a differentiable function whose gradient is L-Lipschitz continuous with , and setting , the problem (3) is generalized as the following nonconvex optimization with linear constraints:
where A is the same as in (1). In recent years, nonconvex optimization problems of the form (4) have found widespread applications in science and engineering. For instance, based on a gradient tracking algorithm, Zhang et al. [8] investigated optimization of local nonconvex objective functions in time-varying networks. In addition, to ensure the effectiveness of image reconstruction, Tiddeman and Ghahremani [9] combined wavelet transforms with principal component analysis to propose a class of principal component waveform networks for solving linear inverse problems, and fully utilized the symmetry in wavelet transforms during the wavelet decomposition. For more related works, one can see [10,11,12] and the references therein.
In fact, variants of (4) have found applications in various fields, such as statistical learning [13,14,15], penalized zero-variance discriminant analysis [16] and image reconstruction [17,18]. Furthermore, if , for and in (4), then the nonconvex optimization degenerates to the following smoothly clipped absolute deviation (SCAD) penalty problem:
with the penalty function in the objective, we refer readers to (26) later. The SCAD penalty problem (5) proposed by scholars can be conceptually understood and it should be noted that in statistical optimization, certain penalty methods exhibit limitations, such as vulnerability to data circumvention and biased estimation of significant variables [19]. To address these questions, Fan and Li [20] proposed a SCAD penalty function, developed optimization algorithms to solve nonconcave penalized likelihood problems and demonstrated that this method possesses asymptotic oracle properties. Remarkably, with appropriate regularization parameter selection, the results can achieve nearly identical performance to the known true model.
It is well known that alternating direction method of multipliers (ADMM) has gained widespread attention due to its balance between performance and efficiency. When the subproblems are independent, ADMM exhibits a unique symmetry. In fact, with appropriately designed update steps, this symmetry ensures that the convergence of ADMM is independent of the order in which the subproblems are updated [21]. In recent years, as nonconvex optimization problems have gained increasing attention, convergence analysis of ADMM in nonconvex settings has become a research hotspot. Due to the lack of theoretical guarantees for ADMM in nonconvex problems, Hong et al. [22] not only established a convergence theory for ADMM in the nonconvex setting, but also overcame the limitation on the number of variable blocks. Wang et al. [23] demonstrated that incorporating the Bregman distance into ADMM can effectively simplify the computation of subproblems, emphasizing the feasibility of ADMM in nonconvex settings. Ding et al. [24] proposed a class of semi-proximal ADMM for solving low-rank matrix recovery problems. Furthermore, in the presence of noisy matrix data, by minimizing the nuclear norm, Ding et al. [24] effectively addressed the issues of Gaussian noise and related mixed noise. Guo et al. [25] provided insights into solving large-scale nonconvex optimization problems using ADMM. For more related work, readers may refer to [26,27,28,29] and the references therein.
The inertial acceleration technique, which is derived from the heavy-ball method, utilizes information from previous iterations to construct affine combinations [30]. Additionally, we observe that the inertial technique can employ different extrapolation strategies during the optimization process to enhance convergence speed. Using a general inertial proximal gradient method, Wu and Li [31] proposed two distinct extrapolation strategies to flexibly adjust convergence rate of the inertial proximal gradient method. Chao et al. [32] investigated an inertial proximal ADMM and established the global convergence of iterates under appropriate assumptions. Moreover, Wang et al. [33] considered a different inertial update scheme, which not only preserves the acceleration effect of inertia but also reduces the computational error caused by the inertial term.
Unfortunately, Wang et al. [33] only considered the inertial update step for x. We note that Chen et al. [34] also discovered that embedding the inertial term into the y-subproblem can significantly improve convergence speed of the presented algorithm. Inspired by the work in [33,34], we adopt the inertial update step for x proposed by Wang et al. [33], and additionally consider an inertial update step for y to further accelerate the convergence of the algorithm. Based on this, we propose a novel symmetrical inertial alternating direction method of multipliers with proximal term (NIP-ADMM) to solve (4) and two application problems (3) and (5). Our main contributions can be summarized as follows:
- (i)
- Building upon the inertial update step due to [33], we introduce an additional inertial update for y and incorporate into the x-subproblem update; this form of inertial update ensures that the primal variables are treated equally, and thereby we achieve faster acceleration. In addition, we introduce two distinct inertial parameters to avoid the differentiated feedback effect that a single inertial parameter may impose on different inertial terms.
- (ii)
- To simplify the computation of the subproblems, we introduce an approximation term in the x-subproblem, which under appropriate conditions, a closed-form solution can be obtained in practical applications.
- (iii)
- Under reasonable assumptions, we prove that any cluster point of the sequence generated by NIP-ADMM belongs to the set of critical points of the augmented Lagrangian function. Furthermore, under the condition that the auxiliary function satisfies Kurdyka–Łojasiewicz property (KLP), we further establish that the sequence generated by NIP-ADMM converges to a stationary point of the augmented Lagrangian function.
- (iv)
- Since function g in (4) is convex, this ensures that g is well-defined, and enables us to abandon the traditional ADMM update scheme and instead adopt a gradient descent approach. This method requires only the computation of gradients at each iteration, and significantly reduces computational complexity. Consequently, it offers substantial advantages when handling high-dimensional or large-scale datasets.
The structure of this paper is as follows. In Section 2, we review essential results required for further analysis. We present NIP-ADMM and analyze its convergence in Section 3. Numerical experiment and application to signal recovery model and SCAD penalty problem in Section 4 highlight the benefits of the majorization and inertial techniques. Lastly, in Section 5, we provide a conclusion.
2. Preliminaries
In this section, we introduce key notations and definitions that are essential for the results to be developed and are utilized in the subsequent sections.
Assume and for . If matrix S is a positive definite (semi-definite positive) matrix, then we have . Given any matrix and a vector , let be S-norm of x. For a matrix , we define and as the smallest and largest eigenvalues of , respectively. If we denote , then the domain of f is defined as .
Definition 1.
Let . Then the distance from point to Q is defined as . In particular, if , then .
Definition 2.
For a differentiable convex function , Bregman distance is defined by
Definition 3.
Assume is a proper lower semicontinuous function.
- (i)
- Frechet sub-differential of χ at is denoted by and defined as:Among others, we set when .
- (ii)
- The limiting sub-differential of χ at is written as and defined by
Definition 4.
We say the point is a critical point of the following augmented Lagrangian function associated with problem (4):
where λ denotes the augmented Lagrange multiplier, and is a penalty parameter, if it satisfies the following conditions:
Definition 5
([35]). (KLP) Let be a proper lower semicontinuous function with . For , if there exists , a neighborhood U of , and a function , where is the set of the concave function , then for any , the following inequality holds:
We say that χ has KLP at , and φ is the associate function of f with KLP.
Lemma 1
([36]). The sub-differential of a lower semicontinuous function possesses several fundamental and significant properties as follows:
- (i)
- From Definition 3, which implies that holds for all , and given that is a closed set, is also a closed set.
- (ii)
- Suppose that is a sequence that converges to , and converges to with . Then, by the definition of the sub-differential, we have .
- (iii)
- If is a local minimum of χ, then it follows that .
- (vi)
- Assuming that is a continuously differentiable function, we can derive:
Lemma 2
([35]). Assume , where and are both proper lower semicontinuous functions. Then, for any , we can obtain
Lemma 3
([37]). (Uniformized KLP) Let Ω be a compact set and be the same as in Definition 5. If a proper lower semicontinuous function is fixed at a point in Ω and satisfies the KLP at every point on Ω, and there exist , , and such that for any and , then the following inequality is satisfied:
Lemma 4
([38]). If the function is continuously differentiable, and is Lipschitz continuous with constant , then for any , the following result holds:
3. Novel Algorithm and Convergence Analysis
In this section, based on (6), we propose NIP-ADMM for solving the problem (4), which is outlined below:
| Algorithm 1 NIP-ADMM |
|
Remark 1.
(i) In Algorithm 1, S is a semi-definite matrix. Moreover, the parameters ϖ appearing in could be related to and .
- (ii)
- The update scheme in of Algorithm 1 for y-subproblem adopts the gradient descent method, where is the gradient of the function with respect to y, and γ is called the learning rate.
- (iii)
- The inertial structure adopted in Algorithm 1 employs a structurally balanced acceleration strategy. This update strategy is mathematically symmetric with the only distinction for the values of the parameters η and θ.
According to Algorithm 1, the optimality conditions for NIP-ADMM are obtained as
Before concluding this section, we present the following fundamental assumptions, which are essential for convergence analysis.
Assumption 1. (i) is a proper lower semicontinuous function. is continuously differentiable, and is Lipschitz continuous with a Lipschitz constant .
- (ii)
- S is a positive semidefinite matrix.
- (iii)
- For convenience, we introduce the following symbols:
- (iv)
- To analyze the monotonicity of , we set .
Lemma 5.
If conditions (i)-(iv) in Assumption 1 holds, then for any ,
where is the inertial parameter in Algorithm 1.
Proof.
According to the definition of the Lagrangian function, one gets
and we also can know that
Since is the optimal solution to the subproblem with respect to x in 2° of Algorithm 1, one knows that
Furthermore, we know
Combining the above two formulas yields (12); one can declare
Noticing Algorithm 1 and (7), one can see
Thus, it is natural to derive the following process:
According to Assumption 1 with and , the monotonic non-increasing property of the sequence is guaranteed.
Lemma 6.
If the sequence generated by Algorithm 1 is bounded, then we have
Proof.
Since is bounded, it is evident that is also bounded. Moreover, there exists an accumulation point; let us assume it to be , and there exists a subsequence of such that
which implies that is bounded from below. From the conclusion of Lemma 5 and the condition , it follows that
Now we give subsequential convergence analysis of NIP-ADMM.
Theorem 1.
(Subsequential Convergence) The sequence generated by NIP-ADMM is bounded, and assume M and are the sets of cluster points of and , respectively. Under the assumptions and the conditions of Lemma 5, we have the following conclusion:
- (i)
- M and are two non-empty compact sets. As , it follows that and .
- (ii)
- .
- (iii)
- .
- (iv)
- The sequence converges, and .
Proof.
Now let us draw conclusions (i)-(iv) in turn.
(i) Based on the definitions of M and , the conclusion can be satisfied.
(ii) Combining Lemma 5 with the definitions of and , we obtain the desired conclusion.
(iii) Letting , then one can obtain that a subsequence of can converge to . By Lemma 5, as , one has , which implies . On the one hand, noting that is the optimal solution to the x-subproblem in 2° of Algorithm 1, we have
From Lemma 6, we know that . And combining this with , we conclude that holds. On the other hand, since f is a lower semi-continuous function, we deduce that , and one gets
Moreover, given the closedness of and the continuity of , along with and the optimality condition of NIP-ADMM (7), we assert that
and is a critical point of .
(v) Let , and assume that there exists a subsequence of that converges to . Combining the relations (16), (19), and the continuity of g, we have
Considering that is monotonically non-increasing, it follows that is convergent. Consequently, for any , the relationship can be established as
□
By (6) and the semidefiniteness of the matrix S, the following can be defined with :
Then, the following result can be obtained.
Lemma 7.
Let be contained in . Then, there exists and such that
Proof.
By the definition of and , we can derive from Lemma 1 that
Combining the above expression with the optimality condition (7) of NIP-ADMM, it means
It is easy to see from Lemma 2 that . Moreover, since g has a Lipschitz continuous gradient with respect to L, we get
Thus, according to (20), there exists a positive real number such that
Furthermore, combining this with (15), we know that there exists and such that
Hence, by selecting and , we can further conclude that
This concludes the proof. □
Theorem 2.
(Global convergence) Suppose the sequence generated by NIP-ADMM is bounded, and the hypotheses (i)-(iv) in Assumption 1 hold. If is a KL function, then
Moreover, the sequence converges to a critical point of .
Proof.
From Theorem 1, we know that . For any , the proof process needs to consider the following two cases:
(Case I) For any and given that , it follows from Lemma 5 that there exists a constant such that
It is clear that . As a result, we have and . Combining (15) and (18), it follows that and . Finally, for any , we conclude that , and the result holds.
(Case II) Assume that for any , the inequality holds. Since
it follows that for any , there exists such that for all , we have:
Moreover, noting that
it implies that for any , there exists such that for all , the following inequality holds:
Hence, given and , when , we have
And, based on Lemma 3, it can be deduced that for all ,
Furthermore, using the concavity of , we derive the following:
Noting the fact that , together with the conclusion obtained in Lemma 7, one can infer that
where represents and represents Combining Lemma 5, we can rewrite (21) as follows:
which can be equivalently expressed as
By applying the Cauchy–Schwarz inequality and multiplying both sides by 6, we obtain
Then, by further applying the fundamental inequality for all , we can deduce that
Next, summing up (23) from to and rearranging the terms, one gets
Furthermore, as and , we can conclude that
which implies
Based on the relationship between (15) and (18), we can assert that
This demonstrates that forms a Cauchy sequence, which ensures its convergence. By applying Theorem 1, it follows that converges to a critical point of . □
4. Numerical Simulations
In this section, we demonstrate the application of NIP-ADMM to the signal recovery model (3) and SCAD penalty problem (5). To verify the effectiveness of Algorithm 1 (i.e., NIP-ADMM), we compare it with Bregman modification of ADMM (BADMM) proposed by Wang et al. [23] and inertial proximal ADMM (IPADMM) proposed by Chen et al. [34]. All codes were implemented in MATLAB 2024b and executed on a Windows 11 system equipped with an AMD Ryzen R9-9900X CPU.
4.1. Signal Recovery
In this subsection on signal recovery, we consider the previously mentioned model (3).
where , and ,, . In the context of the problem (24), Wang et al. [23] experimentally validated the effectiveness of BADMM. To further evaluate the efficiency of NIP-ADMM, numerical comparisons were conducted not only with BADMM by us, but also with IPADMM [34], to verify the rationality of the proposed inertial symmetric update scheme.
We construct the following framework to solve the problem (24). We set , where I denotes the identity matrix.
Here, H represents the half-shrinkage operator proposed by Xu et al. [39], which is defined as
where the function for is defined by
In this setup, the entries of matrix A are drawn from a standard normal distribution, with each column adjusted for normalization. The starting vector is initialized as a sparse vector, containing at least 100 non-zero components. The values are set initially to zero. To simulate the observation vector with added noise, we generate b using , where . For the regularization parameter c, we compute
Based on Assumption 1, the parameters are chosen as and . The error trend is depicted as
where log denotes the base-10 logarithm. At the -th iteration, the primal residual is expressed as while dual residual is represented as Termination occurs when both conditions are met:
During the experiments, to satisfy Assumption 1, we set . Table 1 shows that when , selecting the inertial parameter values and produces satisfactory results. Therefore, in subsequent experiments, we also adopt and . The metrics include the number of iterations (Iter), CPU running time (CPUT) and the objective function value (Obj). To better present the experimental results, we retain two decimal places for Obj and four decimal places for CPUT.

Table 1.
Numerical results of NIP-ADMM with different and .
The numerical results consistently demonstrate the superior performance of NIP-ADMM compared to BADMM and IPADMM (see Table 2). Due to the introduction of inertial and proximal terms, the proposed NIP-ADMM demonstrates accelerated convergence with respect to both objective value reduction and error diminution. For , NIP-ADMM shows faster convergence in terms of both objective value and error reduction (see Figure 1). For and , in comparison to BADMM and IPADMM, NIP-ADMM achieves a more significant reduction in the number of iterations and computational time (see Figure 2). For larger-scale models with , NIP-ADMM consistently outperforms both BADMM and IPADMM, further indicating its superior suitability for solving large-scale problems (see Figure 3). It is worth noting that the above results highlight the high efficiency of NIP-ADMM, which can be attributed to the proposed inertial update strategy.

Table 2.
Comparison of iteration effect between NIP-ADMM, IPADMM and BADMM.
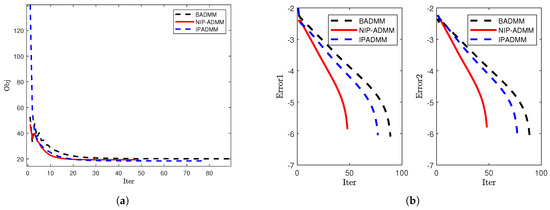
Figure 1.
Comparison of convergence when : (a) The objective value. (b) The error trends of Error1 and Error2.
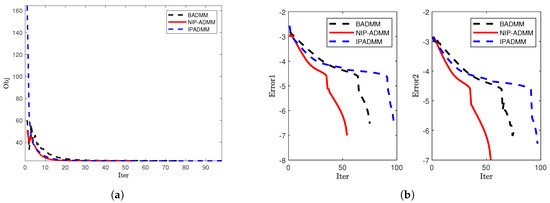
Figure 2.
Comparison of convergence when and : (a) The objective value. (b) The error trends of Error1 and Error2.
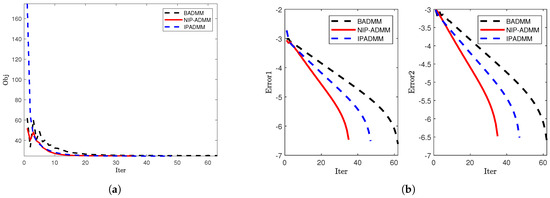
Figure 3.
Comparison of convergence when = 6000: (a) The objective value. (b) The error trends of Error1 and Error2.
4.2. SCAD Penalty Problem
We note that the SCAD penalty problem in statistics can be formulated as the following model [20,31]:
with ,, and the penalty function in the objective defined as
where and , being the knots of the quadratic spline function. In the reference signal recovery subsection, we similarly set and , where . For the problem (25), the x-subproblem corresponding to of Algorithm 1 can be expressed as
On the one hand, the x-subproblem can be equivalently formulated as:
On the other hand, under the condition that , we can update x using the following rule [31]:
where represents the positive part operator, which is defined as ; applying NIP-ADMM to solve the problem (25), one yields that
Similarly, the update scheme of BADMM can be represented by the following procedure:
Utilize IPADMM to address model (25) and derive the following iterative scheme:
In this experiment, we generate a random matrix A, and perform row and column normalization. Here, we choose to generate a vector z of dimension n with a sparsity ratio of . The vector b is represented as the sum of and a Gaussian noise vector with zero mean and variance . The initial variables , , and are set as zero vectors, serving as the starting point for optimization. To improve numerical efficiency, in this experiment, we set and . Under the condition that Assumption 1 is satisfied, we configure , , and for NIP-ADMM and other algorithms. The error trend is depicted as
and the stopping criterion for the updates is set as
In Table 3, we set . The results in the table support our choice of the inertial parameters and . Under these conditions, NIP-ADMM requires the fewest iterations and the least running time. Therefore, we selected the inertial parameters and for the experiments.

Table 3.
Numerical results of NIP-ADMM with different and .
To further evaluate the performance of NIP-ADMM, IPADMM, and BADMM in solving the SCAD penalized problem, we conducted numerical experiments under three different dimensional settings and compared the convergence behavior of the three algorithms. Figure 4, Figure 5 and Figure 6 illustrate the evolution of the objective function values (left) and iteration errors (right) with respect to the number of iterations for NIP-ADMM, IPADMM, and BADMM. As observed from the figures, although all three algorithms eventually converge, NIP-ADMM demonstrates superior performance in terms of convergence speed and error control. In addition, Table 4 presents the numerical performance of the three algorithms under different dimensional settings. Although there are slight differences in the objective function values among the three methods, NIP-ADMM exhibits a clear advantage in terms of iteration count (Iter) and computational time (CPUT). These results clearly demonstrate the acceleration effect brought by the incorporation of inertial and proximal terms in NIP-ADMM.
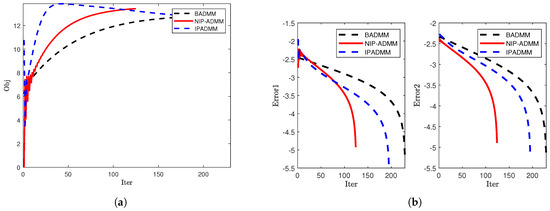
Figure 4.
Comparison of convergence when : (a) The objective value. (b) The error trends of Error1 and Error2.
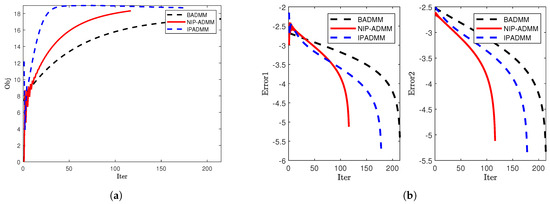
Figure 5.
Comparison of convergence when and : (a) The objective value. (b) The error trends of Error1 and Error2.
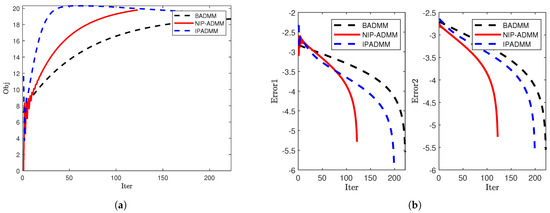
Figure 6.
Comparison of convergence when : (a) The objective value. (b) The error trends of Error1 and Error2.

Table 4.
Comparison of iteration effect between NIP-ADMM, IPADMM and BADMM.
5. Conclusions
In this paper, we studied a class of nonconvex optimization problems subject to linear constraints. By integrating a class of symmetrically structured inertial terms with a proximal ADMM framework, we proposed a novel symmetrical inertial alternating direction method of multipliers with a proximal term. Under some mild assumptions, we analyzed the subsequential convergence of the proposed NIP-ADMM. Furthermore, assuming that the associated auxiliary function satisfied Kurdyka–Łojasiewicz property, we established the global convergence of the algorithm, which provided theoretical support for the stability of the algorithm. Meanwhile, numerical simulations also validated the theoretical contributions. In both the signal recovery problem and SCAD-penalized problem, NIP-ADMM demonstrated faster convergence compared to IPADMM and BADMM. These results not only confirmed the theoretical advantages of the symmetric inertial term in accelerating convergence and the proximal term in simplifying subproblem computations, but also indicated that NIP-ADMM outperformed both non-inertial and traditional inertial methods in practical applications.
Furthermore, we believe that future work could explore whether the convergence of NIP-ADMM can be guaranteed when the objective function is non-separable. Additionally, it would be worthwhile to investigate whether introducing inertial terms into the y-subproblem and the multiplier could further accelerate the convergence speed of NIP-ADMM.
Author Contributions
Conceptualization, J.-H.L. and H.-Y.L.; methodology, J.-H.L.; software, J.-H.L. and S.-Y.L.; validation, J.-H.L. and H.-Y.L.; writing—original draft preparation, J.-H.L. and H.-Y.L.; writing—review and editing, J.-H.L. and H.-Y.L.; visualization, J.-H.L., H.-Y.L. and S.-Y.L.; supervision, H.-Y.L.; project administration, H.-Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Innovation Fund of Postgraduate, Sichuan University of Science & Engineering (Y2024340), the Scientific Research and Innovation Team Program of Sichuan University of Science and Engineering (SUSE652B002) and the Opening Project of Sichuan Province University Key Laboratory of Bridge Non-destruction Detecting and Engineering Computing (2023QZJ01).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors would appreciate the anonymous reviewers for their useful comments and advice.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kim, S.J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale ℓ1-regularized least Squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Chartrand, R.; Staneva, V. Restricted isometry properties and nonconvex compressive sensing. Inverse Probl. 2008, 24, 035020. [Google Scholar] [CrossRef]
- Zeng, J.S.; Lin, S.B.; Wang, Y.; Xu, Z.B. L1/2 regularization: Convergence of iterative half thresholding algorithm. IEEE Trans. Signal Process. 2014, 62, 2317–2329. [Google Scholar] [CrossRef]
- Doostmohammadian, M.; Gabidullina, Z.R.; Rabiee, H.R. Nonlinear perturbation-based non-convex optimization over time-varying networks. IEEE Trans. Netw. Sci. Eng. 2024, 11, 6461–6469. [Google Scholar] [CrossRef]
- Chen, P.Y.; Selesnick, I.W. Group-sparse signal denoising: Non-convex regularization, convex optimization. IEEE Trans. Signal Process. 2014, 62, 3464–3478. [Google Scholar] [CrossRef]
- Bai, Z.L. Sparse Bayesian learning for sparse signal recovery using ℓ1/2-norm. Appl. Acoust. 2023, 207, 109340. [Google Scholar] [CrossRef]
- Wang, C.; Yan, M.; Rahimi, Y.; Lou, Y.F. Accelerated schemes for the L1/L2 minimization. IEEE Trans. Signal Process. 2020, 68, 2660–2669. [Google Scholar] [CrossRef]
- Zhang, S.R.; Wang, Q.H.; Zhang, B.X.; Liang, Z.; Zhang, L.; Li, L.L.; Huang, G.; Zhang, Z.G.; Feng, B.; Yu, T.Y. Cauchy non-convex sparse feature selection method for the high-dimensional small-sample problem in motor imagery EEG decoding. Front. Neurosci. 2023, 17, 1292724. [Google Scholar] [CrossRef]
- Tiddeman, B.; Ghahremani, M. Principal component wavelet networks for solving linear inverse problems. Symmetry 2021, 13, 1083. [Google Scholar] [CrossRef]
- Xia, Z.C.; Liu, Y.; Hu, C.; Jiang, H.J. Distributed nonconvex optimization subject to globally coupled constraints via collaborative neurodynamic optimization. Neural Netw. 2025, 184, 107027. [Google Scholar] [CrossRef]
- Yu, G.; Fu, H.; Liu, Y.F. High-dimensional cost-constrained regression via nonconvex optimization. Technometrics 2021, 64, 52–64. [Google Scholar] [CrossRef] [PubMed]
- Merzbacher, C.; Mac Aodha, O.; Oyarzun, D.A. Bayesian optimization for design of multiscale biological circuits. ACS Synth. Biol. 2023, 12, 2073–2082. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.C.; Zhang, H.C.; Li, J.C. A parameterized proximal point algorithm for separable convex optimization. Optim. Lett. 2018, 12, 1589–1608. [Google Scholar] [CrossRef]
- Wen, F.; Liu, P.L.; Liu, Y.P.; Qiu, R.C.; Yu, W.X. Robust sparse recovery in impulsive noise via ℓp-ℓ1 optimization. IEEE Trans. Signal Process. 2017, 65, 105–118. [Google Scholar] [CrossRef]
- Zhang, H.M.; Gao, J.B.; Qian, J.J.; Yang, J.; Xu, C.Y.; Zhang, B. Linear regression problem relaxations solved by nonconvex ADMM with convergence analysis. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 828–838. [Google Scholar] [CrossRef]
- Ames, B.P.W.; Hong, M.Y. Alternating direction method of multipliers for penalized zero-variance discriminant analysis. Comput. Optim. Appl. 2016, 64, 725–754. [Google Scholar] [CrossRef]
- Zietlow, C.; Lindner, J.K.N. ADMM-TGV image restoration for scientific applications with unbiased parameter choice. Numer. Algorithms 2024, 97, 1481–1512. [Google Scholar] [CrossRef]
- Bian, F.M.; Liang, J.W.; Zhang, X.Q. A stochastic alternating direction method of multipliers for non-smooth and non-convex optimization. Inverse Probl. 2021, 37, 075009. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Fan, J.Q.; Li, R.Z. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Statist. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Parikh, N.; Boyd, S. Proximal Algorithms; Now Publishers: Braintree, MA, USA, 2014. [Google Scholar]
- Hong, M.Y.; Luo, Z.Q.; Razaviyayn, M. Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. SIAM J. Optim. 2016, 26, 337–364. [Google Scholar] [CrossRef]
- Wang, F.H.; Xu, Z.B.; Xu, H.K. Convergence of Bregman alternating direction method with multipliers for nonconvex composite problems. arXiv 2014, arXiv:1410.8625. [Google Scholar]
- Ding, W.; Shang, Y.; Jin, Z.; Fan, Y. Semi-proximal ADMM for primal and dual robust Low-Rank matrix restoration from corrupted observations. Symmetry 2024, 16, 303. [Google Scholar] [CrossRef]
- Guo, K.; Han, D.R.; Wu, T.T. Convergence of alternating direction method for minimizing sum of two nonconvex functions with linear constraints. Int. J. Comput. Math. 2016, 94, 1653–1669. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, W.T.; Zeng, J.S. Global convergence of ADMM in nonconvex nonsmooth optimization. J. Sci. Comput. 2019, 78, 29–63. [Google Scholar] [CrossRef]
- Wang, F.H.; Cao, W.F.; Xu, Z.B. Convergence of multi-block Bregman ADMM for nonconvex composite problems. Sci. China Inf. Sci. 2018, 61, 122101. [Google Scholar] [CrossRef]
- Barber, R.F.; Sidky, E.Y. Convergence for nonconvex ADMM, with applications to CT imaging. J. Mach. Learn. Res. 2024, 25, 1–46. [Google Scholar]
- Wang, X.F.; Yan, J.C.; Jin, B.; Li, W.H. Distributed and parallel ADMM for structured nonconvex optimization problem. IEEE Trans. Cybern. 2021, 51, 4540–4552. [Google Scholar] [CrossRef]
- Alvarez, F.; Attouch, H. An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 2001, 9, 3–11. [Google Scholar] [CrossRef]
- Wu, Z.M.; Li, M. General inertial proximal gradient method for a class of nonconvex nonsmooth optimization problems. Comput. Optim. Appl. 2019, 73, 129–158. [Google Scholar] [CrossRef]
- Chao, M.T.; Zhang, Y.; Jian, J.B. An inertial proximal alternating direction method of multipliers for nonconvex optimization. Int. J. Comput. Math. 2020, 98, 1199–1217. [Google Scholar] [CrossRef]
- Wang, X.Q.; Shao, H.; Liu, P.J.; Wu, T. An inertial proximal partially symmetric ADMM-based algorithm for linearly constrained multi-block nonconvex optimization problems with applications. J. Comput. Appl. Math. 2023, 420, 114821. [Google Scholar] [CrossRef]
- Chen, C.H.; Chan, R.H.; Ma, S.Q.; Yang, J.F. Inertial proximal ADMM for linearly constrained separable convex optimization. SIAM J. Imaging Sci. 2015, 8, 2239–2267. [Google Scholar] [CrossRef]
- Attouch, H.; Bolte, J.; Redont, P.; Soubeyran, A. Proximal alternating minimization and projection methods for nonconvex problems: An approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res. 2010, 35, 438–457. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Wets, R.J.B. Variational Analysis; Springer: Berlin, Germany, 1998. [Google Scholar]
- Bolte, J.; Sabach, S.; Teboulle, M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 2014, 146, 459–494. [Google Scholar] [CrossRef]
- Nesterov, Y. Introductory Lectures on Convex Optimization: A Basic Course; Springer: New York, NY, USA, 2004. [Google Scholar]
- Xu, Z.B.; Chang, X.Y.; Xu, F.M.; Zhang, H. L1/2 regularization: A thresholding representation theory and a fast solver. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1013–1027. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).