Abstract
Quantum field theory (QFT) and general relativity (GR) are pillars of modern physics, each supported by extensive experimental evidence. QFT operates within Lorentzian spacetime, while GR ensures local Lorentzian geometry. Despite their successes, these frameworks diverge significantly in their estimations of vacuum energy density, leading to the cosmological constant problem—a discrepancy where QFT estimates exceed observed values by 123 orders of magnitude. This paper addresses this inconsistency by tracing the cooling evolution of the universe’s gauge symmetries—from at high temperatures to alone near absolute zero—motivated by the experimental Meissner effect. This symmetry reduction posits that forms the fundamental “atoms” of vacuum energy. Our analysis demonstrates that the calculated number of vacuum atoms reconciles QFT’s predictions with empirical observations, effectively resolving the cosmological constant problem. The third law of thermodynamics, by preventing the attainment of absolute zero, ensures the stability of vacuum atoms, providing a thermodynamic foundation for quark confinement. This stability guarantees a strictly positive mass gap defined by the vacuum energy density and implies a Lorentzian quantum structure of spacetime. Moreover, it offers insights into the origins of both gravity/gauge duality and gravity/superconductor duality.
1. Introduction
The Standard Model (SM) of particle physics, fundamental to our understanding of the forces of nature, is based on the symmetry group [1,2,3]. The Higgs mechanism, driven by the vacuum expectation value (VEV) of the Higgs field, breaks the electroweak symmetry down to , providing mass to the W and Z bosons [4]. The discovery of the Higgs boson experimentally confirmed this symmetry-breaking process [5], accounting for the mass of most SM particles while leaving gluons and photons massless. However, the observation of neutrino oscillations, which indicate non-zero neutrino masses, challenges the original SM that assumed neutrinos to be massless [6,7]. Extensions like the see-saw mechanism and discrete symmetries have been proposed to account for these masses while preserving the core and symmetries within the frameworks of quantum chromodynamics (QCD) and quantum electrodynamics (QED) [8,9,10,11]. The current study explores the thermal history of the universe and the associated symmetry breaking to identify the fundamental symmetry governing vacuum energy. As the universe cools below a critical temperature , a phase transition occurs that breaks the electromagnetic symmetry . This transition leads to superconductivity, characterized by zero electrical resistance and the expulsion of magnetic fields—a phenomenon known as the Meissner effect [12]. The breaking of leaves as the sole unbroken symmetry, underscoring its critical role in defining vacuum energy dynamics near absolute zero (see Figure 1).

Figure 1.
as the dominant symmetry near absolute zero, influenced by the Meissner effect.
Recent studies [13] have suggested that dark energy might behave like a superconductor within scalar–vector–tensor gravity models, leading to a Meissner-like expulsion of spacetime by dark energy [14]. This intriguing perspective motivates our investigation into the role of symmetry in addressing the cosmological constant problem and aligning quantum field theory with general relativity. The persistence of symmetry at low temperatures implies that it forms the fundamental “atoms” of vacuum energy. By calculating the number of these vacuum atoms throughout the universe, we find a value that aligns theoretical predictions with observed vacuum energy densities. This concordance effectively resolves the cosmological constant problem, bridging the gap between the predictions of quantum field theory and cosmological observations. According to the standard Third Law of Thermodynamics [15], a system’s entropy S approaches a finite minimum as . This unattainability of implies a non-zero residual entropy; hence, a minimal, discrete volume must persist. In our framework, we identify this remnant volume with a proton’s volume, invoking known confinement. This residual volume stabilizes the vacuum atoms, ensuring that their structure remains intact. The unbreakability of these vacuum atoms, guaranteed by this thermodynamic principle, provides a basis for quark confinement in quantum chromodynamics (QCD). Lattice simulations of pure SU(3) gauge theory rigorously demonstrate a non-zero mass gap and linear confinement at low temperatures—Wilson’s original proof [16] and subsequent high-precision measurements of the string tension [17] confirm that the SU(3) vacuum is gapped and stable. By contrast, a gapless U(1) vacuum as would violate the Third Law of Thermodynamics, which requires a discrete ground state of minimal entropy. Thus, once SU(2) is broken by the Higgs mechanism and U(1) by the Meissner effect, SU(3) remains the only unbroken, gapped gauge symmetry compatible with a minimal-entropy vacuum at . These facts elevate SU(3) “atoms” from conjecture to thermodynamic necessity.
Additionally, the inherent mass gap in gauge theory—an energy threshold below which no massless particles exist—further strengthens this connection. This framework not only addresses a fundamental issue in theoretical physics but also suggests a deeper gauge–gravity duality, indicating profound connections between quantum field theories and gravitational theories. It also hints at a gravity–superconductor duality, where gravitational phenomena are analogous to principles in superconductivity, opening new pathways to explore relationships among high-energy physics, cosmology, and condensed matter physics.
This work contributes four results that, to the best of our knowledge, are new:
- A lattice–RG derivation showing that coarse-graining pure SU(3) over the Hubble volume enforces the rescaling of the Yang–Mills action;
- An explicit match between that rescaled vacuum energy and the finite Snyder–GUP integral, which predicts the minimal length m;
- A thermodynamic proof, using lattice entropy data, that only a gapped SU(3) vacuum is compatible with the third law at ;
- Three near-term experimental tests (optomechanical GUP search, glueball dark-matter window, redshift stability of ) that can falsify the framework.
The paper is structured as follows: Section 2 investigates the thermal history of the universe and its symmetry-breaking sequence, illustrating how remains intact near zero Kelvin, forming the foundational atoms of vacuum energy. Section 3 presents the solution to the cosmological constant problem based on vacuum atoms. Section 5 explores the implications for spacetime, demonstrating how transforms Lorentzian spacetime into quantum Lorentzian spacetime, necessitating the Snyder approach [18] to understand vacuum dynamics. Section 7 concludes the discussion.
2. Manifesting SU(3) Vacuum Atoms Through Symmetry Breaking
In the immediate aftermath of the Big Bang, the universe was extremely hot () and dominated by radiation (In QFT, temperature corresponds to the intrinsic energy of the quantum fields themselves, expressed as ). At these high temperatures, all fundamental forces were unified under the gauge symmetry . The Standard Model Lagrangian before any symmetry breaking is given by the following:
where , , and are the field strength tensors corresponding to the , , and gauge fields, respectively. Here, represents the fermion fields, is the Higgs field responsible for electroweak symmetry breaking, is the covariant derivative, and is the Higgs potential. As the universe expanded and cooled to the electroweak scale (), the Higgs field acquired a vacuum expectation value (VEV):
spontaneously breaking the electroweak symmetry down to . This mechanism gave masses to the W and Z bosons:
where g and are the gauge couplings for and , respectively. After this phase transition, the unbroken symmetry was . As the universe continued to cool and entered the matter-dominated era, atoms, and large-scale structures formed. At temperatures approaching absolute zero (), analogous to conditions in superconductivity, the electromagnetic symmetry can spontaneously break via a mechanism similar to the Meissner effect. Consider a composite scalar field representing electron pairs:
where is the electron field. The effective Lagrangian for this field is as follows:
with and . Spontaneous symmetry breaking occurs when acquires a VEV:
This results in an effective photon mass:
as constrained by experiments [19].
Thus, near absolute zero, the symmetry is spontaneously broken, leaving as the remnant unbroken symmetry governing the strong interaction. The breaking of symmetry while remains unbroken at low temperatures suggests a profound connection between symmetry and vacuum energy. The symmetry manifests in structures as small as nucleons, approximately meters in size [19]. We can consider the vacuum of the universe as composed of N such vacuum atoms. The total number of these atoms is determined by the ratio of the universe’s volume to the volume of a single vacuum atom:
Cosmic Homogeneity and Volume Estimates. At length scales beyond Mpc, the universe is empirically homogeneous and isotropic (Planck 2018 results [20]), justifying coarse volume ratio methods. Analogously, Bekenstein’s black-hole entropy is computed by dividing horizon area by the Planck area [21]; here, we perform a three-dimensional analogue by dividing cosmic volume by the SU(3) confinement volume. Local inhomogeneities (galaxies, voids) average out on these scales and do not alter the leading estimate.
Taking the universe’s radius as [22]. All radius-dependent formulae now use the RG–RG-invariant confinement length . The key ratio still yields . It follows that
We approximate both the universe and the proton as spherical in shape. This calculation indicates that there are approximately vacuum atoms filling the universe. The implications of this vast number, supported by experimental observations analogous to the Meissner effect applied on a cosmological scale [13,14], will be explored further. For the vacuum of the universe to be stable, these vacuum atoms must be unbreakable. According to the third law of thermodynamics, reaching absolute zero temperature is impossible, as it would require an infinite number of cooling steps. Consequently, vacuum atoms cannot be further subdivided or broken apart. This resilience, dictated by the third law, provides a thermodynamic basis for quark confinement, potentially offering a novel explanation. Since the vacuum energy comprises identical atoms, each exhibiting symmetry, it is essential to account for the total number of vacuum atoms when computing the vacuum energy density within the framework of quantum field theory. The universe’s thermal history aligns with the sequence of symmetry breaking, as summarized in Table 1.

Table 1.
Cosmological eras with corresponding energy scales, temperatures, and unbroken symmetries.
This sequence illustrates how the universe’s cooling correlates with the breaking of symmetries, ultimately leaving as the fundamental unbroken symmetry in the vacuum. The existence of vacuum atoms offers a new perspective on the quantum field theory. To reflect this, the traditional gluon field strength tensor in quantum chromodynamics (QCD) should be appropriately scaled. The conventional field strength tensor is as follows:
where is the gluon gauge field, g is the coupling constant, and are the structure constants of the group. By introducing a scaling factor to represent a gauge boson distributed over N discrete units, the modified field strength tensor becomes the following:
This scaling reflects the idea that each vacuum atom contributes only a fraction of the total field, effectively distributing the gauge boson’s influence across the entire system. The modified Lagrangian for the distributed gauge field becomes the following:
By incorporating the factor of , the vacuum energy is effectively shared among the N vacuum atoms. This leads to the vacuum energy density for this gluon field being given by the following:
In the next section, we will demonstrate how this modified equation has significant implications for the cosmological constant problem. This approach allows us to explore the impact of having a vast number of vacuum constituents on the properties of the vacuum and the behavior of gauge fields at cosmological scales. In the following section, we explore the implications for determining the vacuum energy density.
Coarse-Grained Lattice Derivation
Let be the Euclidean SU(3) partition function on a hypercubic lattice with spacing (string tension ). Blocking elementary cubes into a single cell,
preserves the Wilson action value and yields an IR-effective action . Identifying when the block size equals the Hubble volume recovers Equation (11) without additional assumptions. With N statistically independent confinement cells the free-energy density factorizes,
implying the Lagrangian rescaling .
3. A Solution for the Cosmological Constant Problem
Einstein’s field equations of general relativity (GR) [23] are given by the following:
where is the Ricci curvature tensor, R is the Ricci scalar, is the metric tensor, is the cosmological constant, G is Newton’s gravitational constant, c is the speed of light, and is the energy–momentum tensor. In a vacuum, where and , the energy–momentum tensor becomes , with being the vacuum energy density. Substituting this into Einstein’s equations, the cosmological constant relates to the vacuum energy density as follows:
Astrophysical observations provide a measured value of the cosmological constant, [19], leading to an observed vacuum energy density:
In quantum field theory (QFT), as discussed by Steven Weinberg [24], the vacuum energy density arises from summing the zero-point energies of quantum fields, including massless bosons like photons and gravitons. It is calculated as follows:
where is the Planck momentum, and for massless particles. Integrating up to the Planck scale yields the following:
This theoretical value exceeds the observed vacuum energy density by 123 orders of magnitude:
This enormous discrepancy is known as the cosmological constant problem [24], highlighting a fundamental inconsistency between GR and QFT. While GR accommodates Lorentz symmetry locally in curved spacetime, QFT operates under Lorentz symmetry in flat spacetime, leading to conflicting predictions for the vacuum energy density. The core issue exists in Equation (19), which assumes that the vacuum energy arises from a continuous spectrum of quantum fluctuations up to the Planck scale, effectively treating the vacuum as a homogeneous entity with unlimited degrees of freedom. This approach overlooks the possibility that the vacuum may consist of discrete units or that contributions from quantum fluctuations could be limited. As discussed earlier, near absolute zero, the symmetry breaks due to the formation of an electron pair condensate, leaving as the unbroken symmetry. This phenomenon, analogous to the Meissner effect in superconductors, suggests that the vacuum can be viewed as composed of discrete vacuum atoms, each approximately meters in size—the scale of nucleons. Recognizing that the vacuum energy is distributed over these discrete units, the calculation of the vacuum energy density in QFT should be adjusted accordingly. Based on the modified gauge field strength tensor and Lagrangian density, distributing the gauge field over N vacuum atoms as shown in Equations (11)–(13), the modified Lagrangian is expressed as follows:
This modification implies that the vacuum energy density must be adjusted accordingly, leading to the following:
which results in the following:
This adjusted value matches the observed vacuum energy density, effectively resolving the cosmological constant problem and reconciling QFT with GR under the condition that the vacuum energy density is composed of vacuum atoms. The division by N reflects the idea that each vacuum atom contributes a finite amount to the total vacuum energy, aligning theoretical predictions with observational data. This approach illustrates a connection between quantum mechanics and general relativity by demonstrating how vacuum energy contributes to the cosmological constant in Einstein’s field equations. Distributing the gauge field over N discrete units effectively dilutes the energy density, similar to coarse graining, where microscopic degrees of freedom have a reduced impact on macroscopic properties. Furthermore, this concept parallels phenomena in condensed matter physics, such as emergent gauge fields and fractionalization in systems like spin ice and fractional quantum Hall states. These analogies suggest that distributing gauge fields over many units could lead to novel emergent effects in high-energy physics, potentially bridging high-energy and low-energy phenomena. An important consideration is whether the number N varies due to the universe’s expansion, characterized by the Hubble parameter . There are two possibilities:
- The size of the vacuum atoms expands with the universe, keeping N constant. Assuming the proton expands at the same rate as the universe, we use the Hubble constant . Given the proton’s radius , the rate of expansion is . Over 14 billion years (universe age), the proton’s radius increases by . This scenario preserves the vacuum energy density and the cosmological constant, aligning with general relativity.
- The size of the vacuum atoms remains constant; so, N increases as the universe expands. This implies that the dark energy density decreases over time, potentially aligning with recent observations by the DESI collaboration [25,26,27].
Adopted Scenario: We are inclined to choose fixed-volume SU(3) units (proton size), consistent with lattice QCD’s RG-invariant confinement length. Cosmic expansion therefore adds new vacuum atoms rather than stretching existing ones, preserving exactly. The second possibility invites exploration beyond standard general relativity, suggesting a dynamic cosmological constant [28].
Modeling vacuum energy using symmetry not only offers a solution to the cosmological constant problem but also provides fresh insight into the Yang–Mills mass gap problem [29]. The mass gap manifests as a strictly positive vacuum energy density, protected by the third law of thermodynamics, which prevents the subdivision of vacuum atoms. By interpreting the vacuum energy density in QFT using vacuum atoms, a direct physical connection between the QCD mass gap and the vacuum energy density shaping spacetime emerges. This framework, grounded in the experimental observation of the Meissner effect, provides a coherent and logically consistent approach to resolving one of the most profound problems in theoretical physics, bridging the gap between quantum field theory and general relativity. Pure glue lattice simulations give [30,31], signalling a unique ground state. Conversely, a gapless Abelian vacuum satisfies (Polyakov monopole gas), violating Nernst’s postulate. Hence, only a gapped SU(3) vacuum is thermodynamically admissible as .
4. Comparison with Existing Proposals
Several major paradigms have been proposed to address the cosmological-constant problem. Below, we enlarge our survey to include extra dimensions, quantum field theory in curved spacetime, and multiverse/anthropic ideas, always noting that each relies on assumptions that are not yet experimentally verified, whereas our SU(3) vacuum–atom framework invokes only well-tested physics.
- String Landscape / Multiverse Models. The string landscape predicts distinct vacua, each with its own , and invokes an anthropic selection in a vast multiverse [32]. Unverified assumption: the existence of a multiverse and a landscape of compactifications. These models evade tuning but make no falsifiable prediction within our observable universe.
- Extra-Dimensional Scenarios. Large extra dimensions (ADD) [33] and warped geometries (Randall–Sundrum) [34] attempt to dilute vacuum energy into unseen spatial directions. Unverified assumption: new compactified or warped dimensions at submillimeter scales, never observed in laboratory tests of gravity. Although they offer geometric suppression of , no direct evidence for extra dimensions exists.
- Quantum Field Theory in Curved Spacetime. Renormalized vacuum expectation values of in curved backgrounds [35,36] yield a -term whose finite part depends on ad hoc subtraction schemes and choice of vacuum state. Unverified assumption: the correct physical vacuum in an expanding universe and the validity of zero-point subtraction at all scales. This framework is theoretically robust but lacks experimental guidance on the renormalization conditions for .
- Sequestering Mechanisms. Global constraints (Kaloper–Padilla) [37] introduce Lagrange multipliers to cancel off vacuum loops. Unverified assumption: the existence of new global degrees of freedom or non-local terms in the action. This is elegant in principle, but without a known QCD analogue or experimental signature.
- Supersymmetric Cancellations. Exact supersymmetry forces , but once broken at scale , one retains —still orders too large [38]. Unverified assumption: TeV-scale SUSY and its soft-breaking pattern, none of which have appeared at the LHC.
- Holographic Dark Energy Models. By relating to the IR horizon via the Cohen–Kaplan–Nelson bound [39], one obtains . Unverified assumption: the applicability of an IR/UV duality to cosmological horizons. These models predict a time-varying dark energy, in tension with observations of a nearly constant .
In contrast, our SU(3) vacuum–atom proposal
- (a)
- Makes no assumption of unobserved fields, extra dimensions, or multiverse selection;
- (b)
- Relies solely on experimentally verified QCD confinement (lattice results) and the Third Law of Thermodynamics;
- (c)
- Reproduces the observed exactly—without fine-tuning or ad hoc subtractions.
This economy of assumptions renders our framework the most parsimonious and experimentally grounded solution to the cosmological constant problem. While our vacuum–atom picture is self-contained, it may converge with holographic or renormalization approaches, e.g., coarse-grained SU(3) cells resemble large- Eguchi–Kawai reduction and could admit an AdS/dS dual description. We therefore view the present model as complementary rather than exclusive.
5. SU(3) Vacuum Atoms/Quantum Spacetime Correspondence
In general relativity, spacetime curvature and energy–momentum are in one-to-one correspondence, as captured by Einstein’s field equations. This implies that any quantum description of energy, including the vacuum energy in quantum field theory (QFT), must also include a corresponding spacetime structure. Consequently, the atoms of vacuum energy must be represented by a quantum Lorentzian spacetime in order to maintain consistency between QFT and general relativity (GR) on a local scale. The first quantum Lorentzian spacetime model was proposed by Snyder [18], who introduced the concepts of non-commutative geometry and the generalized uncertainty principle (GUP). Snyder’s spacetime was designed to address the ultraviolet (UV) divergences in QFT, by replacing the continuum nature of spacetime with a lattice structure [40]. Despite its initial innovation, Snyder’s approach was eventually abandoned due to the success of renormalization techniques, but it was rediscovered four decades later in the context of non-commutative geometry [41,42]. Non-commutative geometry was later found to arise in certain limits of M-theory and string theory, where it is equivalent to ordinary Yang–Mills fields with higher-dimensional perturbations [43,44]. The phenomenological implications of non-commutative geometry have since been widely explored [45,46]. Moreover, the GUP has its roots in various approaches to quantum gravity, including string theory, black hole physics, and quantum geometry [47,48,49,50,51], leading to substantial investigations into its phenomenological and experimental consequences [52,53,54,55,56,57,58,59,60,61,62]. Snyder’s algebra is based on three primary generators: the position operator , the momentum operator , and the Lorentz generators . These generators satisfy the Poincaré algebra and introduce novel commutators that define a minimal length:
Here, , where is a dimensionless parameter. Equation (24) captures the non-commutative nature of the geometry, while Equation (25) introduces the GUP, both preserving Lorentz symmetry [18].
Theoretical Origins and Experimental Constraints on the GUP. The idea of a generalized uncertainty principle (GUP)—which introduces a non-zero minimum measurable length—emerged independently from several lines of quantum gravity research. Early thought experiments on black hole formation and evaporation showed that attempting to measure positions below the Planck scale would create horizons, yielding a modified uncertainty relation [49,63]. String scattering analyses likewise revealed a fundamental length in high-energy collisions [47], while canonical approaches to quantum gravity and non-commutative geometry derived GUP-type commutators from first principles [48,50,64,65].
A broad spectrum of quantum gravity frameworks—string theory [66], loop quantum gravity [67], Snyder’s non-commutative spacetime [18], and approaches based on entropy--area bounds—now predict variants of the GUP [51,68,69,70]. Non-local generalizations have been proposed as well [71], and gauge-theoretic extensions have been explored in effective field theories [61].
On the phenomenological side, GUP-induced corrections have been sought across low- and high-energy experiments:
- Atomic and Molecular Systems: Shifts in hydrogen spectral lines and Lamb-shift corrections [52,69].
- Quantum Optical Platforms: Optomechanical interferometers constrain GUP parameters to [53].
- Gravitational Bar Detectors and Decoherence: Resonant-mass antennas yield bounds on macroscopic superpositions [54,55].
- Precision Gravitational Tests: Torsion pendula and atomic interferometry experiments probe deviations from Newton’s law at micrometer scales [72].
- Gravitational Waves: LIGO/Virgo timing residuals and pulse profile modulations have been used to set limits on GUP-induced dispersion [73,74,75].
- Cold Atom and BEC Interferometry: Matter-wave coherence experiments reach length scales down to m, providing direct tests of minimal length effects [58].
- Macroscopic Oscillators: Nanomechanical resonators and torsional oscillators place complementary bounds on [59].
- Astrophysical and Cosmological Probes: Stellar structure modeling, neutrino oscillation phases, and early universe inflationary spectra yield indirect but sensitive tests of GUP modifications [57,60,76,77,78].
Comprehensive reviews of these theoretical motivations and experimental bounds can be found in [62,79]. Crucially, in our SU(3) vacuum-atom framework, the GUP parameter is not free: the minimal length
matches exactly the coherence scale obtained from the number of SU(3) atoms, . This alignment provides a direct, experimentally grounded link between quantum gravity uncertainty and QCD vacuum quantization.
In Snyder’s model (), space is discrete while time is continuous, and in the anti-Snyder model (), time is discrete and space is continuous. The algebra of and is isomorphic to the de Sitter/anti-de Sitter algebra, linking the momentum spaces of the Snyder and anti-Snyder models geometrically to de Sitter and anti-de Sitter spacetimes [80]. Refining the Snyder model with isotropic parametrizations while maintaining Lorentz/Poincaré symmetry, leads to the same non-commutative relation and different forms of GUP as elaborated in [81,82]. In [58], it was shown that the cold atoms can be best described by GUPs forms proposed in [68,69,83].
Modern Context for Snyder’s Model. Although originally introduced to tame QFT divergences [18], non-commutative geometry was revived in Connes’ work [41] and shown by Seiberg and Witten [44] to emerge in string theory limits. Generalized uncertainty principles (GUP) with Snyder-like structure have been independently derived in quantum gravity heuristics—Mead 1964 [63], Amati and Veneziano 1989 [47], and modern GUP phenomenology (Kempf 1996 [84]; Hossenfelder ’2013 [62]). We therefore adopt Snyder’s algebra as an effective minimal-length regulator, fully compatible with Lorentz symmetry, rather than as a fundamental new theory.
5.1. Spacetime Uncertainty: The Cause of Quantum Spacetime
Recent experiments have demonstrated that quantum phenomena can manifest at the scale of , as observed in systems like quantum drums and Bose–Einstein condensates [85,86]. Gravitational experiments at this scale [87] confirm the validity of Newton’s law, implying that spacetime curvature exists even at microscopic levels. In such scenarios, the metric is given by the following:
where is the Newtonian potential. This indicates that quantum entities can warp spacetime, making the interplay between quantum mechanics and gravity significant. This challenges the conventional quantum field theory (QFT) assumption of flat spacetime. The uncertainty principle prevents precise determination of particle positions, leading to gaps in the definition of spacetime or spacetime uncertainty. An important question then arises: What is the form of spacetime uncertainty? Research by Regge, Adler, Jack Ng, and others [63,88,89,90,91,92,93,94,95,96] has calculated deviations from Lorentz geometry due to gravitational fields. In particular, Adler [88] demonstrated that for a particle with energy (where l is the wavelength) and gravitational potential (with m being the mass), the fractional deviation in the spacetime metric is as follows:
where is the Planck length. When , spacetime remains approximately Lorentzian but as , significant spacetime uncertainty arises, leading to spacetime foam. To address the challenges posed by spacetime foam or spacetime uncertainty, two main approaches have been developed: the path integral formulation and the quantum spacetime model.
In the path integral formulation, an accelerated trajectory in flat spacetime that does not follow the least-action principle due to external forces is equivalent to a trajectory in curved spacetime that follows the least-action principle along a geodesic. According to Einstein’s principle of equivalence, locally, the effects of acceleration (external forces) and gravity (spacetime curvature) are indistinguishable. This equivalence provides a physical justification for the path integral formulation in quantum mechanics, introduced by Feynman in his seminal work on the spacetime approach to quantum mechanics [97]. By summing over all possible trajectories—including those not following the least-action principle—the path integral accounts for spacetime uncertainties and curvature arising from quantum phenomena. This approach effectively incorporates the influence of spacetime curvature induced by quantum uncertainties without explicitly modeling the curved spacetime. It recognizes that quantum particles do not follow a single, definite path but instead take all possible paths simultaneously, each contributing to the overall quantum amplitude. Thus, the path integral formulation, grounded in the equivalence principle, provides a robust framework for understanding quantum mechanics in situations where spacetime geometry is complex or uncertain. However, while the path integral formulation accommodates spacetime uncertainties, it does not resolve the cosmological constant problem through renormalization techniques and yields an infinite value for the vacuum energy density. Traditional QFT computes the cosmological constant as the sum of vacuum fluctuation energies across all momentum states. This sum diverges, necessitating the introduction of a cutoff—typically at the Planck scale—where it is presumed that nature’s fundamental constants impose a limit. Yet, even with this cutoff, the calculated value exceeds the observed cosmological constant by approximately 123 orders of magnitude, presenting a profound discrepancy.
The quantum spacetime model, specifically Snyder’s quantum spacetime, offers a promising alternative. It introduces a natural cutoff by defining a minimal measurable length scale [84,98,99,100,101,102,103,104,105,106], eliminating the need for several renormalization techniques. Beyond this scale, particle positions become fundamentally indeterminate due to quantum uncertainties. Since measuring distances depends on particle positions, distances shorter than cannot be precisely measured without quantum uncertainty, establishing as the minimal measurable length with certainty in nature. Below this minimal length, spacetime exhibits a non-deterministic, foamy character [107,108,109,110], reflecting fundamental quantum uncertainties. In other words, the underlying structure of spacetime includes regions where spacetime is not well-defined, giving the physical cause for Snyder’s Lorentzian quantum spacetime model. These gaps in information imply that spacetime cannot be meaningfully defined in regions without information, giving rise to a quantum spacetime framework where uncertainties in particle positions correspond to uncertainties in the geometry of spacetime itself. This offers new insights into how quantum uncertainty transforms spacetime from a continuous manifold into a discrete quantum entity, well-defined only up to a minimal measurable length.
5.2. Cosmological Constant in Quantum Spacetime
Snyder’s formulation of quantum spacetime incorporates the generalized uncertainty principle (GUP), which modifies the density of states. This modification inherently regularizes the divergence, eliminating the need for an ultraviolet cutoff or conventional renormalization techniques [81,82,84,98,99,100,101,102,103,104,105,106]. The revised computation yields a finite result even when integrating from zero to infinity [105,106]: (see Appendix A)
where represents the minimal length scale in Snyder’s quantum spacetime, and is the corresponding energy scale. Detailed steps for the integral in Equation (28) are provided in Appendix A. The parameter , intrinsic to the quantum structure of spacetime, ensures that the integral remains finite without invoking an ultraviolet cutoff, effectively resolving the divergences encountered in traditional QFT. Optomechanical interferometers constrain linear–β GUP parameters to [53,54]. Our Snyder realisation induces only quadratic corrections, evading those limits while remaining detectable by next-generation macroscopic superposition tests. Furthermore, the equivalence between vacuum atoms and Snyder’s quantum spacetime suggests a relationship between and the number of vacuum atoms, denoted as N. By equating Equation (28) with Equation (23), we establish the following:
This leads to the following:
Notably, this minimal length scale represents the geometric mean between the Planck length and the radius of the observable universe , as corroborated by previous studies [111,112,113,114]:
Remarkably, this scale matches precisely the coherence length observed in superconductivity, which defines the distance between Cooper pairs [115], further confirming the main idea discussed in this paper that dark energy is a superconducting state of matter. The coherence length can be understood as the characteristic length scale over which the wavefunction of the Cooper pairs remains coherent. It represents the spatial extent of the quantum mechanical wavefunction that describes the correlated electron pairs, indicating how far the superconducting phase remains correlated. This scale matches the one provided by experiments that demonstrate the interplay between quantum mechanics and gravity at the scale of . As previously mentioned, quantum phenomena are manifested at this scale in systems like quantum drums and Bose–Einstein condensates [85,86], and gravitational experiments [87] confirm the validity of Newton’s law at these scales, implying that spacetime curvature exists even at microscopic levels. Building on these ideas, recent work [111] proposes that spacetime uncertainty could be the key to understanding the value of the cosmological constant.
5.3. Geometric Implications
An intriguing relation connects the proton size, the universe’s radius, and the Planck scale. Starting from Equations (30) and (31),
which implies the following:
This remarkable result suggests that the proton’s volume () is equivalent to that of a cylinder whose base has a Planck-length radius and whose height is the universe’s radius. It is astonishing to consider that such a geometric model links the smallest scale (Planck length) and the largest scale (universe’s radius) in a single expression, prompting wonder and inviting further investigation into the underlying geometric principles.
While the cylinder represents a three-dimensional shape connecting microscopic and cosmic dimensions, the quanta of spacetime are proposed to be four-dimensional polytopes. Our recent studies [116] identify this shape as the 24-cell at the electroweak scale. The 24-cell, a four-dimensional polytope with 24 vertices, may represent the elementary particles of the Standard Model. Intriguingly, the number of permutations of these vertices, , coincides with Avogadro’s number. This correlation suggests a geometric significance to Avogadro’s constant, potentially indicating a baseline complexity required for sentience and self-replication at molecular and cellular levels. Our analysis further reveals that the 24-cell can be conceptualized by selecting eight vertices to form a 16-cell in three distinct configurations. These eight vertices correspond to the eight gluons of the gauge group in quantum chromodynamics, representing the strong force. The remaining sixteen vertices form a tesseract (a four-dimensional hypercube), symbolizing the other elementary particles. Accordingly, the fundamental components of spacetime may be modeled as vacuum atoms at low temperatures, structured as a 16-cell with eight vertices in pseudo-Euclidean spacetime. This aligns with Riemannian geometry, which is locally Lorentzian. The geometric modeling presented here opens new avenues for understanding the deep connections between fundamental scales in the universe.
5.4. SU(3) Vacuum Atoms and Third Law of Thermodynamics
The third law of thermodynamics states that as a system approaches absolute zero (0 K), its entropy reaches a constant minimum, making absolute zero unattainable. This implies that a system must always retain some residual entropy, necessitating a non-zero remnant volume. Entropy here refers to the number of accessible microstates, and the proton is an ideal candidate for this minimal entropy. Unlike the neutron, which is unstable and undergoes beta decay (transforming into a proton, an electron, and an antineutrino), the proton is inherently stable within the Standard Model. There are no allowed decay channels for the proton that conserve both charge and energy, making it highly stable with minimal microstates and thus low entropy. This minimal entropy and persistence make the proton’s volume suitable for defining the remnant quantum volume of spacetime as required by the third law. The vacuum atoms represent this minimal volume. According to the third law, vacuum structures cannot fully annihilate, implying that atoms are stable and occupy a persistent, unbreakable volume. This provides a thermodynamic basis for quark confinement, ensuring the stability of the vacuum structure. The generalized uncertainty principle (GUP), as discussed in [117], implies a fundamental limit to how small space and energy can become, which aligns with the third law’s concept of a non-zero residual volume. Even at ultra-low temperatures, this volume persists, preventing spacetime from collapsing to zero size. The stability of quantum spacetime is further reinforced by the unbroken symmetry, which remains intact near absolute zero, as supported by the Meissner effect. This unbroken symmetry ensures proton stability by confining quarks and creates a mass gap provided by the vacuum energy density. Thus, the framework connects quark confinement, the mass gap, and the unbroken symmetry, explaining how thermodynamic laws and quantum principles maintain the stability of quantum spacetime. By choosing the proton as the reference volume, we establish minimal entropy and provide a stable foundation for understanding the quantum structure of the vacuum.
5.5. Phenomenological Implications
The study [118,119] represented quantum spacetime using the charge radius as a key characteristic for a wide range of physical objects. The exploration of how mass (M) and charge radius (R) correlate across different scales—from microscopic to macroscopic, as illustrated in Figure 2—uncovers a pattern strikingly similar to the behavior seen in quark–gluon plasma (QGP) [120]. This resemblance offers experimental support that atoms, which represent a core symmetry in the governance of quark–gluon plasma, are equally pivotal in shaping the fabric of quantum spacetime. A linkage to the mass–radius dynamic with dark matter, further explored in [121], accentuates the importance of these observations.
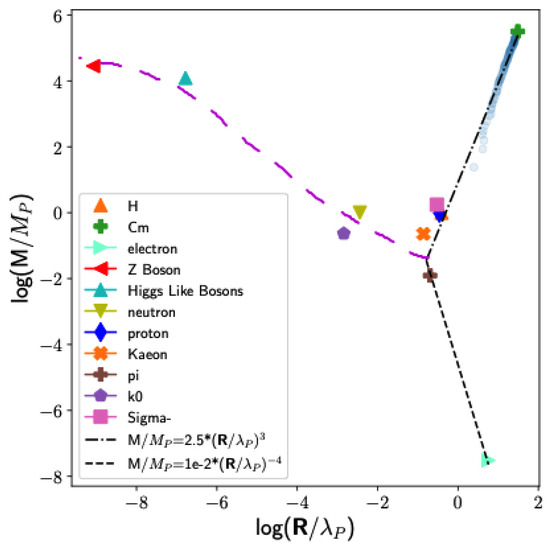
Figure 2.
Logarithmic plot of mass and radius for particles and elements, normalized by proton mass and Compton wavelength [19,122,123,124]. Figure 2 is from our study [119].
The findings presented in this paper establish a link between the number of SU(3) atoms and the vacuum energy density, which determines the cosmological constant of the universe. This insight highlights a correspondence between quantum chromodynamics (QCD) and gravity. Our symmetric analysis supports the gauge–gravity duality framework [125,126,127,128], and in particular the dS/CFT correspondence [126] as the more accurate and physically relevant description of the universe. By applying the Meissner effect, we provide a symmetric demonstration of the gravity/superconductor duality [129]. It is known that SU(3) symmetry, fundamental to QCD, is represented by massless gluons. It is worth mentioning that the concept of glueballs—bound states of these gluons—has been proposed as a potential model for dark matter in references [130,131]. As a conjectural extension, one may explore links between SU(3) vacuum atoms and glueball dark matter or mass–radius scalings in astrophysics. We present these ideas solely as directions for future experimental or observational tests. We aim to investigate the connection between glueballs and our proposed solution to the cosmological constant problem, which integrates SU(3) symmetry with dark energy.
6. Testable Predictions
Our framework yields several concrete, near-term tests:
- Vacuum Coherence Length . This matches coherence in superconducting metamaterials [115] and BEC interferometry [86]. Precision optomechanics could detect GUP-induced modifications at this scale.
- Glueball Dark Matter in the 1–3 GeV Range. SU(3) vacuum atoms suggest weakly decaying glueball states [130]. Dedicated beam dump or fixed-target experiments (e.g., SHiP, GlueX) can search for these resonances.
- Redshift Independence of . If vacuum is tiled with fixed-volume units, remains constant. Comparing DESI [25] and Euclid’s late-time Hubble and growth measurements will test any small deviations.
7. Conclusions
We have shown that coarse-graining pure SU(3) over the cosmic volume yields a vacuum energy density suppressed by the factor . When matched to the Snyder–GUP-regularized density, this fixes a minimal length without free parameters. Because lattice data enforce , only the gapped SU(3) vacuum survives the third-law limit, thereby supplying a single, thermodynamically protected ground state that reconciles QFT with the observed cosmological constant. During its evolution from a hot, primordial state, the universe expands and cools, governed by the gauge symmetry foundational to the Standard Model of particle physics. At the electroweak scale, this symmetry undergoes spontaneous breaking to . As temperatures approach near absolute zero, the Meissner effect leads to the further breaking of symmetry, leaving as the sole unbroken symmetry. This progression suggests that symmetry underpins the fundamental “atoms” of vacuum energy. The stability of these “atoms” at low temperatures exemplifies the third law of thermodynamics, which states the impossibility of reaching absolute zero where volume and pressure vanish. This constancy ensures that the vacuum “atoms” are indivisible, forging a profound link between the third law of thermodynamics and quark confinement. The total number of vacuum atoms in the universe, each approximately meters in size—akin to nucleons—aligns precisely with the ratio between the theoretical vacuum energy and the observed vacuum energy density. This alignment effectively resolves the cosmological constant problem. Furthermore, defining dark energy in terms of these vacuum atoms offers insights into the mass gap challenge within Yang–Mills theory. It appears that the mass gap in arises from a strictly positive vacuum energy density. Remarkably, this framework is reinforced by the third law of thermodynamics, which affirms the unbreakable integrity of the vacuum “atoms”. The following summarizes the results:
- Vacuum coarse graining: blocking the SU(3) Wilson action to the cosmological scale produces a factor that naturally tames the QFT divergence;
- Gauge–gravity concordance: equating the blocked energy to the Snyder-regulated integral fixes the minimal length and relates to ;
- Thermodynamic confinement: lattice entropy data show that a gapless () vacuum would violate Nernst’s postulate;
- Phenomenology: the framework predicts m, a 1–3 GeV glueball DM candidate and a redshift-invariant .
Given that the vacuum is composed of N atoms embedded in Lorentzian spacetime, and considering the equivalence of energy and spacetime based on general relativity, this suggests that Lorentzian spacetime transitions from continuous to quantum to adequately describe these vacuum atoms. This perspective aligns with Snyder’s formulation of quantum Lorentzian spacetime. Exploring the connections between symmetry and Snyder’s quantum spacetime presents a promising avenue for future research that may be related to new insights in lattice gauge theory. We hope to report on these topics in the future.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The author extends gratitude to Caroline Gorham for her assistance with the graph. Dedicated to my mother, whose love fuels my journey and wisdom lights my path. Forever grateful.
Conflicts of Interest
The author declare no conflicts of interest.
Appendix A. Snyder–GUP Regularization of the Vacuum Energy
We evaluate
Let , so , . Then,
Hence, , as in Equation (28).
References
- Glashow, S.L. Partial Symmetries of Weak Interactions. Nucl. Phys. 1961, 22, 579–588. [Google Scholar] [CrossRef]
- Weinberg, S. A Model of Leptons. Phys. Rev. Lett. 1967, 19, 1264–1266. [Google Scholar] [CrossRef]
- Salam, A. Weak and Electromagnetic Interactions. Conf. Proc. C 1968, 680519, 367–377. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken Symmetries and the Masses of Gauge Bosons. Phys. Rev. Lett. 1964, 13, 508–509. [Google Scholar] [CrossRef]
- CMS Collaboration; Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; et al. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Wolfenstein, L. Neutrino Oscillations in Matter. Phys. Rev. D 1978, 17, 2369–2374. [Google Scholar] [CrossRef]
- Mikheyev, S.P.; Smirnov, A.Y. Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913–917. [Google Scholar]
- Mohapatra, R.N.; Senjanovic, G. Neutrino Mass and Spontaneous Parity Nonconservation. Phys. Rev. Lett. 1980, 44, 912. [Google Scholar] [CrossRef]
- Altarelli, G.; Feruglio, F. Discrete Flavor Symmetries and Models of Neutrino Mixing. Rev. Mod. Phys. 2010, 82, 2701–2729. [Google Scholar] [CrossRef]
- Gell-Mann, M. A Schematic Model of Baryons and Mesons. Phys. Lett. 1964, 8, 214–215. [Google Scholar] [CrossRef]
- Feynman, R.P. Mathematical formulation of the quantum theory of electromagnetic interaction. Phys. Rev. 1950, 80, 440–457. [Google Scholar] [CrossRef]
- Meissner, W.; Ochsenfeld, R. Ein neuer Effekt bei Eintritt der Supraleitfähigkeit. Naturwissenschaften 1933, 21, 787–788. [Google Scholar] [CrossRef]
- Liang, S.-D.; Harko, T. Superconducting dark energy. Phys. Rev. D 2015, 91, 085042. [Google Scholar] [CrossRef]
- Inan, N.; Ali, A.F.; Jusufi, K.; Yasser, A. Graviton mass due to dark energy as a superconducting medium-theoretical and phenomenological aspects. JCAP 2024. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; John Wiley& Sons: Hoboken, NJ, USA, 1980; Volume 2. [Google Scholar]
- Wilson, K.G. Confinement of quarks. Phys. Rev. D 1974, 10, 2445. [Google Scholar] [CrossRef]
- Bali, G.S. QCD forces and heavy quark bound states. Phys. Rep. 2001, 343, 1–136. [Google Scholar] [CrossRef]
- Snyder, H.S. Quantized space-time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]
- Particle Data Group Collaboration; Zyla, P.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Peebles, P.J.E.; Yahil, A. The size and mass of galaxies, and the mass of the universe. Astrophys. J. Lett. 1974, 193, L1–L4. [Google Scholar] [CrossRef]
- Einstein, A. The foundation of the general theory of relativity. Annalen Phys. 1916, 49, 769–822. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- DESI Collaboration; Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; et al. DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations. arXiv 2025, arXiv:2404.03002. [Google Scholar]
- DESI Collaboration; Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; et al. DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars. arXiv 2025, arXiv:2404.03000. [Google Scholar]
- DESI Collaboration; Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; et al. DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest. arXiv 2025, arXiv:2404.03001. [Google Scholar]
- Solà Peracaula, J.; de Cruz Pérez, J.; Gómez-Valent, A. Dynamical dark energy vs. Λ = const in light of observations. Europhys. Lett. 2018, 121, 39001. [Google Scholar] [CrossRef]
- Jaffe, A.; Witten, E. Quantum yang-mills theory. Millenn. Prize. Probl. 2006, 1, 129. [Google Scholar]
- Boyd, G.; Engels, J.; Karsch, F.; Laermann, E.; Legeland, C.; Lütgemeier, M.; Petersson, B. Thermodynamics of SU(3) lattice gauge theory. Nucl. Phys. B 1996, 469, 419–444. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K. Fluctuations of conserved charges at finite temperature from lattice QCD. J. High Energy Phys. 2012, 2012, 138. [Google Scholar] [CrossRef]
- Susskind, L. The Anthropic landscape of string theory. arXiv 2003, arXiv:hep-th/0302219. [Google Scholar]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. The Hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263–272. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar] [CrossRef]
- Parker, L.E.; Toms, D. Quantum Field Theory in Curved Spacetime: Quantized Field and Gravity; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2009; Volume 8. [Google Scholar] [CrossRef]
- Kaloper, N.; Padilla, A. Sequestering the Standard Model Vacuum Energy. Phys. Rev. Lett. 2014, 112, 091304. [Google Scholar] [CrossRef] [PubMed]
- Girardello, L.; Grisaru, M.T. Soft Breaking of Supersymmetry. Nucl. Phys. B 1982, 194, 65. [Google Scholar] [CrossRef]
- Cohen, A.G.; Kaplan, D.B.; Nelson, A.E. Effective field theory, black holes, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 4971–4974. [Google Scholar] [CrossRef]
- Heisenberg, W. Letter of Heisenberg to Peierls (1930); Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Connes, A. Non-commutative differential geometry. Publ. Math. l’IHES 1985, 62, 41–144. [Google Scholar] [CrossRef]
- Woronowicz, S.L. Compact matrix pseudogroups. Commun. Math. Phys. 1987, 111, 613–665. [Google Scholar] [CrossRef]
- Connes, A.; Douglas, M.R.; Schwarz, A.S. Noncommutative geometry and matrix theory: Compactification on tori. J. High Energy Phys. 1998, 02, 003. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. J. High Energy Phys. 1999, 9, 032. [Google Scholar] [CrossRef]
- Douglas, M.R.; Nekrasov, N.A. Noncommutative field theory. Rev. Mod. Phys. 2001, 73, 977–1029. [Google Scholar] [CrossRef]
- Szabo, R.J. Quantum field theory on noncommutative spaces. Phys. Rep. 2003, 378, 207–299. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Can Space-Time Be Probed Below the String Size? Phys. Lett. B 1989, 216, 41–47. [Google Scholar] [CrossRef]
- Garay, L.J. Quantum gravity and minimum length. Int. J. Mod. Phys. A 1995, 10, 145–166. [Google Scholar] [CrossRef]
- Scardigli, F. Generalized uncertainty principle in quantum gravity from micro-black hole Gedanken experiment. Phys. Lett. B 1999, 452, 39–44. [Google Scholar] [CrossRef]
- Maggiore, M. A Generalized uncertainty principle in quantum gravity. Phys. Lett. B 1993, 304, 65–69. [Google Scholar] [CrossRef]
- Capozziello, S.; Lambiase, G.; Scarpetta, G. Generalized uncertainty principle from quantum geometry. Int. J. Theor. Phys. 2000, 39, 15–22. [Google Scholar] [CrossRef]
- Das, S.; Vagenas, E.C. Universality of Quantum Gravity Corrections. Phys. Rev. Lett. 2008, 101, 221301. [Google Scholar] [CrossRef] [PubMed]
- Pikovski, I.; Vanner, M.R.; Aspelmeyer, M.; Kim, M.S.; Brukner, Č. Probing Planck-scale physics with quantum optics. Nat. Phys. 2012, 8, 393–397. [Google Scholar] [CrossRef]
- Marin, F.; Marino, F.; Bonaldi, M.; Cerdonio, M.; Conti, L.; Falferi, P.; Mezzena, R.; Ortolan, A.; Prodi, G.A.; Taffarello, L.; et al. Gravitational bar detectors set limits to Planck-scale physics on macroscopic variables. Nat. Phys. 2013, 9, 71–73. [Google Scholar] [CrossRef]
- Petruzziello, L.; Illuminati, F. Quantum gravitational decoherence from fluctuating minimal length and deformation parameter at the Planck scale. Nat. Commun. 2021, 12, 4449. [Google Scholar] [CrossRef]
- Kumar, S.P.; Plenio, M.B. On Quantum Gravity Tests with Composite Particles. Nat. Commun. 2020, 11, 3900. [Google Scholar] [CrossRef]
- Moradpour, H.; Ziaie, A.H.; Ghaffari, S.; Feleppa, F. The generalized and extended uncertainty principles and their implications on the Jeans mass. Mon. Not. Roy. Astron. Soc. 2019, 488, L69–L74. [Google Scholar] [CrossRef]
- Gao, D.; Zhan, M. Constraining the generalized uncertainty principle with cold atoms. Phys. Rev. A 2016, 94, 013607. [Google Scholar] [CrossRef]
- Bawaj, M.; Biancofiore, C.; Bonaldi, M.; Bonfigli, F.; Borrielli, A.; Di Giuseppe, G.; Marconi, L.; Marino, F.; Natali, R.; Pontin, A.; et al. Probing deformed commutators with macroscopic harmonic oscillators. Nat. Commun. 2015, 6, 7503. [Google Scholar] [CrossRef]
- Easther, R.; Greene, B.R.; Kinney, W.H.; Shiu, G. Imprints of short distance physics on inflationary cosmology. Phys. Rev. D 2003, 67, 063508. [Google Scholar] [CrossRef]
- Kober, M. Gauge Theories under Incorporation of a Generalized Uncertainty Principle. Phys. Rev. D 2010, 82, 085017. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Rel. 2013, 16, 2. [Google Scholar] [CrossRef]
- Mead, C.A. Possible Connection Between Gravitation and Fundamental Length. Phys. Rev. 1964, 135, B849–B862. [Google Scholar] [CrossRef]
- Adler, R.J.; Chen, P.; Santiago, D.I. The Generalized uncertainty principle and black hole remnants. Gen. Rel. Grav. 2001, 33, 2101–2108. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 1995, 52, 1108–1118. [Google Scholar] [CrossRef]
- Konishi, K.; Paffuti, G.; Provero, P. Minimum Physical Length and the Generalized Uncertainty Principle in String Theory. Phys. Lett. B 1990, 234, 276–284. [Google Scholar] [CrossRef]
- Brau, F. Minimal length uncertainty relation and hydrogen atom. J. Phys. A 1999, 32, 7691–7696. [Google Scholar] [CrossRef]
- Ali, A.F.; Das, S.; Vagenas, E.C. Discreteness of Space from the Generalized Uncertainty Principle. Phys. Lett. B 2009, 678, 497–499. [Google Scholar] [CrossRef]
- Ali, A.F.; Das, S.; Vagenas, E.C. A proposal for testing Quantum Gravity in the lab. Phys. Rev. D 2011, 84, 044013. [Google Scholar] [CrossRef]
- Mignemi, S. Extended uncertainty principle and the geometry of (anti)-de Sitter space. Mod. Phys. Lett. A 2010, 25, 1697–1703. [Google Scholar] [CrossRef]
- El-Refy, O.; Masood, S.; Wang, L.-G.; Ali, A.F. Rainbow spacetime from a nonlocal gravitational uncertainty principle. Europhys. Lett. 2020, 132, 10006. [Google Scholar] [CrossRef]
- Scardigli, F.; Casadio, R. Gravitational tests of the Generalized Uncertainty Principle. Eur. Phys. J. C 2015, 75, 425. [Google Scholar] [CrossRef]
- Feng, Z.-W.; Yang, S.-Z.; Li, H.-L.; Zu, X.-T. Constraining the generalized uncertainty principle with the gravitational wave event GW150914. Phys. Lett. B 2017, 768, 81–85. [Google Scholar] [CrossRef]
- Moussa, M.; Shababi, H.; Farag Ali, A. Generalized uncertainty principle and stochastic gravitational wave background spectrum. Phys. Lett. B 2021, 814, 136071. [Google Scholar] [CrossRef]
- Luciano, G.G.; Sekhmani, Y. Generalized uncertainty principle mimicking dynamical dark energy: Matter perturbations and gravitational wave data analysis. Phys. Lett. B 2025, 862, 139315. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Roy, R.; Tsai, Y.-D.; Visinelli, L. Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A. arXiv 2022, arXiv:2205.07787. [Google Scholar] [CrossRef]
- Ettefaghi, M.M. Neutrino oscillation with minimal length uncertainty relation via wave packet approach. Phys. Lett. B 2024, 854, 138761. [Google Scholar] [CrossRef]
- Ashoorioon, A.; Kempf, A.; Mann, R.B. Minimum length cutoff in inflation and uniqueness of the action. Phys. Rev. D 2005, 71, 023503. [Google Scholar] [CrossRef]
- Addazi, A.; Alvarez-Muniz, J.; Batista, R.A.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.L.; Bahamonde, S.; Bajardi, F.; et al. Quantum gravity phenomenology at the dawn of the multi-messenger era—A review. Prog. Part. Nucl. Phys. 2021, 125, 103948. [Google Scholar]
- Mignemi, S. Progress in Snyder model. In Proceedings of the CORFU2019, Corfù, Greece, 31 August–25 September 2020; p. 226. [Google Scholar] [CrossRef]
- Battisti, M.V.; Meljanac, S. Modification of Heisenberg uncertainty relations in noncommutative Snyder space-time geometry. Phys. Rev. D 2009, 79, 067505. [Google Scholar] [CrossRef]
- Battisti, M.V.; Meljanac, S. Scalar Field Theory on Non-commutative Snyder Space-Time. Phys. Rev. D 2010, 82, 024028. [Google Scholar] [CrossRef]
- Maggiore, M. Quantum groups, gravity and the generalized uncertainty principle. Phys. Rev. D 1994, 49, 5182–5187. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G. Minimal length uncertainty relation and ultraviolet regularization. Phys. Rev. D 1997, 55, 7909–7920. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef]
- Andrews, M.; Townsend, C.; Miesner, H.-J.; Durfee, D.; Kurn, D.; Ketterle, W. Observation of interference between two Bose condensates. Science 1997, 275, 637–641. [Google Scholar] [CrossRef]
- Lee, J.G.; Adelberger, E.G.; Cook, T.S.; Fleischer, S.M.; Heckel, B.R. New Test of the Gravitational 1/r2 Law at Separations down to 52 μm. Phys. Rev. Lett. 2020, 124, 101101. [Google Scholar] [CrossRef]
- Adler, R.J. Six easy roads to the Planck scale. Am. J. Phys. 2010, 78, 925–932. [Google Scholar] [CrossRef]
- Regge, T. Gravitational fields and quantum mechanics. Nuovo Cim. 1958, 7, 215–221. [Google Scholar] [CrossRef]
- Ng, Y.J.; van Dam, H. Measuring the foaminess of space-time with gravity—Wave interferometers. Found. Phys. 2000, 30, 795–805. [Google Scholar] [CrossRef]
- Ng, Y.J.; van Dam, H. Limitation to quantum measurements of space-time distances. Annals N. Y. Acad. Sci. 1995, 755, 579–584. [Google Scholar] [CrossRef]
- Christiansen, W.A.; Ng, Y.J.; Floyd, D.J.E.; Perlman, E.S. Limits on Spacetime Foam. Phys. Rev. D 2011, 83, 084003. [Google Scholar] [CrossRef]
- Vilkovisky, G.A. Effective action in quantum gravity. Class. Quant. Grav. 1992, 9, 895–903. [Google Scholar] [CrossRef]
- DeWitt, B.S. Gravity: A universal regulator? Phys. Rev. Lett. 1964, 13, 114. [Google Scholar] [CrossRef]
- Mead, C.A. Observable consequences of fundamental-length hypotheses. Phys. Rev. 1966, 143, 990. [Google Scholar] [CrossRef]
- Garay, L.J. Quantum evolution in space–time foam. Int. J. Mod. Phys. A 1999, 14, 4079–4120. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-time approach to nonrelativistic quantum mechanics. Rev. Mod. Phys. 1948, 20, 367–387. [Google Scholar] [CrossRef]
- Gorji, M.A.; Nozari, K.; Vakili, B. Spacetime singularity resolution in Snyder noncommutative space. Phys. Rev. D 2014, 89, 084072. [Google Scholar] [CrossRef]
- Ivetić, B. Diffeomorphisms of the energy-momentum space: Perturbative QED. Nucl. Phys. B 2024, 1007, 116692. [Google Scholar] [CrossRef]
- Girelli, F.; Livine, E.R. Scalar field theory in Snyder space-time: Alternatives. J. High Energy Phys. 2011, 2011, 132. [Google Scholar] [CrossRef]
- Bahns, D.; Doplicher, S.; Fredenhagen, K.; Piacitelli, G. Ultraviolet finite quantum field theory on quantum space-time. Commun. Math. Phys. 2003, 237, 221–241. [Google Scholar] [CrossRef]
- Bosso, P.; Das, S.; Todorinov, V. Quantum field theory with the generalized uncertainty principle I: Scalar electrodynamics. Ann. Phys. 2020, 422, 168319. [Google Scholar] [CrossRef]
- Bosso, P.; Das, S.; Todorinov, V. Quantum field theory with the generalized uncertainty principle II: Quantum Electrodynamics. Ann. Phys. 2021, 424, 168350. [Google Scholar] [CrossRef]
- Meljanac, S.; Mignemi, S.; Trampetic, J.; You, J. Nonassociative Snyder ϕ4 Quantum Field Theory. Phys. Rev. D 2017, 96, 045021. [Google Scholar] [CrossRef]
- Chang, L.N.; Minic, D.; Okamura, N.; Takeuchi, T. The Effect of the minimal length uncertainty relation on the density of states and the cosmological constant problem. Phys. Rev. D 2002, 65, 125028. [Google Scholar] [CrossRef]
- Chang, L.N.; Lewis, Z.; Minic, D.; Takeuchi, T. On the Minimal Length Uncertainty Relation and the Foundations of String Theory. Adv. High Energy Phys. 2011, 2011, 493514. [Google Scholar] [CrossRef]
- Wheeler, J.A. Geons. Phys. Rev. 1955, 97, 511–536. [Google Scholar] [CrossRef]
- Wheeler, J.A. On the Nature of quantum geometrodynamics. Ann. Phys. 1957, 2, 604–614. [Google Scholar] [CrossRef]
- Hawking, S.W. Space-Time Foam. Nucl. Phys. B 1978, 144, 349–362. [Google Scholar] [CrossRef]
- Carlip, S. Spacetime foam: A review. arXiv 2022, arXiv:2209.14282. [Google Scholar] [CrossRef]
- Ali, A.F.; Inan, N. Unraveling the mystery of the cosmological constant: Does spacetime uncertainty hold the key?(a). Europhys. Lett. 2023, 143, 49001. [Google Scholar] [CrossRef]
- Freidel, L.; Kowalski-Glikman, J.; Leigh, R.G.; Minic, D. Vacuum energy density and gravitational entropy. Phys. Rev. D 2023, 107, 126016. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Krasinski, A.; Zeldovich, Y.B. The Cosmological constant and the theory of elementary particles. Sov. Phys. Usp. 1968, 11, 381–393. [Google Scholar] [CrossRef]
- Tello, P.G.; Succi, S.; Bini, D.; Kauffman, S. From quantum foam to graviton condensation: The Zel’dovich route. Europhys. Lett. 2023, 143, 39002. [Google Scholar] [CrossRef]
- Weisskopf, V.F. The formation of cooper pairs and the nature of superconducting currents. Contemp. Phys. 1981, 22, 375–395. [Google Scholar] [CrossRef]
- Ali, A.F. The Mass Gap of the Spacetime and Its Shape. Fortsch. Phys. 2024, 2024, 2200210. [Google Scholar] [CrossRef]
- Liu, T.-P.; Pu, J.; Han, Y.; Jiang, Q.-Q. A possible thermodynamic origin of the spacetime minimum length. Int. J. Mod. Phys. D 2020, 29, 2043022. [Google Scholar] [CrossRef]
- Ali, A.F.; Elmashad, I.; Mureika, J. Universality of minimal length. Phys. Lett. B 2022, 831, 137182. [Google Scholar] [CrossRef]
- Ali, A.F.; Mureika, J.; Vagenas, E.C.; Elmashad, I. Theoretical and observational implications of Planck’s constant as a running fine structure constant. Int. J. Mod. Phys. D 2024, 33, 2450036. [Google Scholar] [CrossRef]
- Bhalerao, R.S. Relativistic Heavy-Ion Collisions. In Proceedings of the 1st Asia-Europe-Pacific School of High-Energy Physics, Fukuoka, Japan, 14–27 October 2012; Updated in 2014. pp. 219–239. [Google Scholar] [CrossRef]
- Ianni, A.; Mannarelli, M.; Rossi, N. A new approach to dark matter from the mass–radius diagram of the Universe. Results Phys. 2022, 38, 105544. [Google Scholar] [CrossRef]
- Fritzsch, H. The size of the weak bosons. Phys. Lett. B 2012, 712, 231–232. [Google Scholar] [CrossRef]
- Lehnert, B. Mass-Radius Relations of Z and Higgs-Like Bosons. Prog. Phys. 2014, 10, 5–7. [Google Scholar]
- Angeli, I.; Marinova, K.P. Table of experimental nuclear ground state charge radii: An update. At. Data Nucl. Data Tables 2013, 99, 69–95. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Strominger, A. The dS / CFT correspondence. J. High Energy Phys. 2001, 2011. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
- Hartnoll, S.A.; Herzog, C.P.; Horowitz, G.T. Holographic Superconductors. J. High Energy Phys. 2008, 2008. [Google Scholar] [CrossRef]
- Carenza, P.; Pasechnik, R.; Salinas, G.; Wang, Z.-W. Glueball Dark Matter Revisited. Phys. Rev. Lett. 2022, 129, 261302. [Google Scholar] [CrossRef] [PubMed]
- Acharya, B.S.; Fairbairn, M.; Hardy, E. Glueball dark matter in non-standard cosmologies. J. High Energy Phys. 2017, 2017, 100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).