Abstract
Current improvements in quantum computing present a substantial challenge to classical cryptographic systems, which typically rely on problems that can be solved in polynomial time using quantum algorithms. Consequently, post-quantum cryptography (PQC) has emerged as a promising solution to emerging quantum-based cryptographic challenges. The greatest threat is public-key cryptosystems, which are primarily responsible for key exchanges. In PQC, key encapsulation mechanisms (KEMs) are crucial for securing key exchange protocols, particularly in Internet communication, virtual private networks (VPNs), and secure messaging applications. CRYSTALS-Kyber and NTRU are two well-known PQC KEMs offering robust security in the quantum world. However, even when quantum computers are functional, they are not easily accessible. IoT devices will not be able to utilize them directly, so there will still be a requirement to protect IoT devices from quantum attacks. Concerns such as limited computational power, energy efficiency, and memory constraints in devices such as those used in IoTs, embedded systems, and smart cards limit the use of these techniques in constrained environments. These concerns always arise there. To address this issue, this study conducts a broad comparative analysis of Kyber and NTRU, with special focus on their security, performance, and implementation efficiency in such environments (IOT/constrained environments). In addition, a case study was conducted by applying KEMs to a low-power embedded device to analyze their performance in real-world scenarios. These results offer an important comparison for cyber security engineers and cryptographers who are involved in integrating post-quantum cryptography into resource-constrained devices.
1. Introduction
Quantum computing is evolving at a remarkable pace, imposing significant challenges on the usual methods of cryptography, as discussed by Aumasson [1]. Many of the current cryptographic methods, such as RSA, DSA, and ECC, use complex mathematical techniques; however, quantum computers can break them in a matter of seconds. Complex mathematics forms the basis of recent cryptography protocols, such as integer factorization and discrete logarithms, which Shor’s algorithm can easily solve. An overview was provided by Ugwuishiwu et al. [2]. If a crypto-system becomes vulnerable, it can lead to the exposure of sensitive data, resulting in severe cyber security threats, as explored by Mavroeidis et al. [3]. To address these risks, researchers, including Dam et al. [4], formulated post-quantum cryptography (PQC), whose advanced algorithms are designed to withstand quantum attacks. One important and well-known technique among PQC methods is lattice-based cryptography, for which a comprehensive survey was provided by Wang et al. [5].
CRYSTALS-Kyber and NTRU are two salient lattice-based key encapsulation mechanisms (KEMs). CRYSTALS-Kyber is based on the module learning with errors (MLWE) problem, which was explored by Bos et al. [6], whereas NTRU employs polynomial rings and ideal lattices, which in turn enable quick and efficient cipher texts and robust security assurances, as presented by Wu et al. [7]. These cryptosystems were selected from the NIST Post-Quantum Cryptography Standardization Initiative. The Status Report on the Third Round of the NIST Post-quantum Cryptography Standardization Process [8] provides a comprehensive overview of the current progress in post-quantum cryptography standardization, and enables the establishment of future standards for secure encryption.
The PQC methods were designed to protect our data from hackers who use quantum computers. Essentially, PQC methods were initiated using KEM to securely exchange a secret key between two parties, based on complex mathematical problems assumed to be secure against quantum computer attacks, as described by Richter et al. [9]. Therefore, if an eavesdropper intercepts the communication, it cannot decrypt the key. Once both the receiver and sender have the key, a symmetric algorithm, such as AES, can be employed to encrypt and decrypt the data. In summary, KEM is employed to deliver a secure key in a quantum-resistant manner and AES handles the main task of encrypting the message. This hybrid scheme, often known as a hybrid cryptosystem or KEM-DEM, as explored by Panja et al. [10], combines the robust security of the PQC key exchange with the efficiency of AES for data encryption.
Shor and Grover’s algorithms help to highlight the shortcomings of the system and demonstrate the superiority of quantum computers over classical ones. Shor’s algorithm allows quantum computers to factorize large numbers very efficiently compared to present techniques. The security of public key systems relies on the difficulty of factoring large numbers. In contrast, Grover’s algorithm employs a brute-force search to find the key, performing only the square root of the total possible key sets, as examined by Mina-Zicu and Simion [11], which makes it faster. For instance, a 128-bit key that would require approximately 2128 operations to break using classical methods would only require approximately 264 operations on a quantum computer utilizing Grover’s algorithm. Although this represents notable acceleration, it is less impactful than the exponential enhancement provided by Shor’s algorithm.
With the realization that conventional key-exchange protocols are susceptible to quantum threats, post-quantum cryptography has introduced key encapsulation mechanisms to securely establish shared secrets between parties, as explored by Farooq et al. [12], even when faced with quantum adversaries. The KEMs functions in three main steps:
Key generation: A public–private key pair is produced using an algorithm. The public key is openly distributed, whereas the private key is kept secret.
Encapsulation: The sender uses the recipient’s public key to generate a random symmetric key, which is then encapsulated in cipher text and sent to the recipient.
Decapsulation: The recipient uses their private key to retrieve the symmetric key from the received cipher text.
This symmetric key is then used for efficient symmetric data encryption. This scheme ensures that communication remains confidential and intact, even with enhanced quantum computing. By implementing KEMs, cryptography systems can be protected from potential quantum threats, thereby guaranteeing secure communication. This study highlights key exchange algorithms and emphasizes the need for quantum-resistant solutions.
Literature Review
Most studies on PQC focus on theoretical security and computational efficiency in high-performance environments, such as desktop computers or cloud servers, as evaluated by Sabani et al. [13]. However, real-world cryptographic deployments often require encryption schemes that can operate under strict hardware limitations, particularly in IoT devices, embedded systems, and low-power networks, reviewed by Singh et al. [14]. Many IoT devices operate on low-power microcontrollers with a minimal processing capacity. Devices, such as smart sensors, medical implants, and industrial controllers, often have limited RAM and storage. Battery-powered devices such as wearables and smart home appliances require encryption schemes that consume minimal energy. Secure communication in 5G, satellite networks, and IoT mesh systems must be bandwidth-efficient to reduce data transmission overhead. Therefore, cryptographic algorithms must be optimized for these environments to ensure secure communication without excessive computational overhead. In the race to secure resource-constrained IoT devices against quantum attack, several novel 2-KEMs have emerged. QP-KEM leverages the lightweight Q-problem, as discussed by Kara et al. [15], where RLizard builds on Ring-LWE/Ring-LWR to secure IOTs, as analyzed by Jeon et al. [16].
Side-channel attacks: SCAs can be carried out by examining one of the numerous physical leak devices created during the implementation of cryptographic schemes. These leaks indicate a weakness that an attacker can use to examine and compromise the security of a cryptographic algorithm. The PQC is no exception to such attacks, as detailed in the analysis presented by Delgado-Vargas et al. [17]
This study aimed to evaluate and compare the performance of Kyber and NTRU, two of the most promising post-quantum key encapsulation schemes, by implementing them on devices with extremely limited resources, such as those in IoT networks. We begin by measuring how long each algorithm takes to produce its keys and encrypt and decrypt them, providing us with a clear understanding of their speed in real-world settings. Then, we check how much memory (RAM) each scheme requires at most and on average, so we can compare which fits best into small embedded spaces. We also connect our test devices to accurate power-measurement equipment to determine the amount of energy required for each operation, which directly affects battery life in portable devices. Finally, we determine the size of the public keys, cipher texts, and any additional data generated by each technique and determine their communication overhead on restricted networks. By performing all these tests on the same machine and under the same security settings, we provide a balanced comparison of the results that emphasize the strengths and limitations of each algorithm on four key metrics: speed of operation, memory usage, energy consumption, and bandwidth efficiency. These results provide real-world advice for engineers and scientists deciding between Kyber and NTRU in designing safe, forward-looking systems in situations where each millisecond of computation, each kilobyte of memory, each joule of power, and each byte on the wire genuinely matter.
The remainder of this paper is organized as follows. Section 2 provides an in-depth explanation of Kyber, NTRU, and their variants, mathematical foundations, and security guarantees. Section 3 describes the test setup, benchmarking tools, and experimental design. Section 4 presents the experimental findings, including graphs of speed, memory usage, and power consumption. Finally, Section 5 presents our conclusions and recommendations for future research.
2. Cryptographic Foundation
2.1. Lattice-Based Cryptography
Lattice-based cryptography has emerged as one of the most promising approaches to secure communication in the post-quantum era, as discussed by Micciancio and Regev [18]. It is built on mathematical problems that remain difficult to solve, even with quantum computers. Unlike RSA and ECC, which can be efficiently broken by Shor’s algorithm, as examined by Gitonga [19], lattice problems have no known quantum algorithms that can solve them efficiently. A lattice can be considered as a set of all integer combinations of a fixed set of basis vectors, and as the dimension increases, the complexity of its structure grows exponentially. This creates certain computational problems, such as the Shortest Vector Problem (SVP), explored by Micciancio and Goldwasser [20], and the Learning with Errors (LWE) problem by Regev [21], which are extraordinarily difficult to solve even with advanced quantum algorithms. These problems are used in constructing cryptographic schemes, such as KEM digital signatures and homomorphic encryption, which is a comprehensive survey provided by Acar et al. [22]. Kyber and NTRU are lattice-based KEMs designed to replace the classical key exchange protocols. However, they differ significantly in their mathematical structures, implementation complexities, and efficiency.
2.2. Overview of Kyber and Its Variants
CRYSTALS-Kyber is based on the Module Learning With Errors (Module LWE) problem, as discussed by Boudgoust et al. [23]. It relies on efficient polynomial arithmetic in a special type of mathematical ring, where polynomials are reduced using a structured rule that ensures efficient operation, as analyzed by Ding et al. [24]. This ring uses a small prime number (commonly 3329) as the modulus and operates with polynomials that have 256 terms. The scheme uses a small module dimension, which helps to keep the key and cipher text sizes compact. Kyber has multiple variants with different security levels: Kyber512, designed for Level 1 security, and Kyber768 and Kyber1024, which provide stronger security (equivalent to AES-192 and AES-256, respectively) and have larger key and cipher text sizes. Kyber is designed for efficiency by using fast polynomial multiplication (via the number theoretic transform (NTT)) and controlled noise distributions, which help to balance security and computational speed.
2.3. Overview of NTRU and Its Variants
Originally introduced in 1996, the NTRU cryptosystem is among the earliest lattice-based encryption schemes. Over time, they evolved into multiple variants. The two main families are as follows.
NTRU HPS: In this version, the secret and related polynomials are sampled using a fixed-weight distribution. This implies that each secret polynomial contains a specific number of non-zero values chosen from a small set of possible numbers. Fixed-weight sampling guarantees consistent properties, resulting in a secure decryption. The parameter set NTRU HPS 509 (officially ntruhps2048509) employs polynomials of 509 terms and a modulus of 2048. The public key size is approximately 699 bytes, and both the cipher text and secret key sizes are small, making it ideal for environments with storage and bandwidth constraints.
NTRU HRSS: In this implementation, each coefficient is sampled independently without limiting the number of non-zero terms. This approach adds more randomness, which makes some security analyses easier but potentially changes the key sizes and performance slightly.
In the second round of NIST’s post-quantum cryptography project, the NTRU group combined these two methods into a single NTRU submission update, provided by Moody [25]. This merger allows implementers to choose between different parameter sets: one that prioritizes speed (NTRU-HPS), and another that offers extra security against side-channel attacks (NTRU-HRSS). Thus, this merged submission provides a flexible solution that meets diverse needs while ensuring strong security against both classical and quantum threats, as conducted by Paradise and Sugeng [26].
Although this study focuses on the broader domain of post-quantum cryptography, our experimental study deliberately focuses on Level 1 algorithms, specifically Kyber512 and NTRU HPS 2048 509. For ease of reference, we refer to the NTRU HPS 2048 509 variant NTRU509 throughout this study (where n = 509 denotes the degree of the polynomial ring, and q = 2048 is the modulus parameter). We chose these Level 1 variants because they offer an optimal balance between security and efficiency, making them especially suitable for resource-constrained environments such as IoT devices and embedded systems. At Level 1, both schemes are intended to offer approximately 128-bit classical security, which is sufficient for several existing applications. This is both pragmatic and future-proof. Implementing the latest post-quantum cryptography algorithms is feasible with the existing computer power in many IoT devices. Additionally, as processing power increases over time, these systems can be upgraded to greater security levels without requiring redesign, thereby providing seamless migration towards future-proof security.
Table 1 compares Kyber-512 and NTRU-509, focusing on their security bases, encryption methods, and key structures [24,25]. Kyber-512 uses Learning with Errors (LWE) and structured lattices, whereas NTRU-509 uses the Shortest Vector Problem (SVP) and ideal lattices.

Table 1.
Comparison of Kyber-512 and NTRU-509.
3. Methodology
This study analyzed the performance of Kyber512 and NTRU509 under various settings, such as real-world IoT restrictions, common computing platforms, and virtualized testing environments. The primary goals involved measuring the encryption rate, decryption rate, memory requirements, and power and bandwidth usage. The goal is to determine an algorithm that performs better in IoT applications, embedded systems, low-power systems, and general computing platforms. Benchmarking tests should be performed on various platforms to ensure a thorough analysis of Kyber512 and NTRU509.
- Google Colab/Virtual Machine (VM): Used for algorithm testing, performance simulation, and baseline benchmarking
- Raspberry Pi/Low-Power ARM Processor: A simulation of a real-world IoT environment to assess real-world feasibility under limited conditions.
- Windows Laptop/PC with Limited Resources: A typical computing device with artificially limited CPU and memory settings to test performance under limited conditions.
Each platform has controlled resource limitations to examine how well Kyber512 and NTRU509 perform in different computing environments, including in low-power and memory-constrained settings. These constraints help to replicate real-world conditions in which devices may operate with minimal processing power, restricted memory, and limited battery life. This study specifically compared the impact of these constraints on Kyber512 and NTRU509 to determine which is more efficient in resource-limited environments (see Table 2).

Table 2.
Tools used for benchmarking.
4. Results and Analysis
4.1. Introduction to Results
We conducted benchmarking tests across four key performance metrics to evaluate the performance of the candidate KEMs in resource-constrained environments. These experiments were executed on three representative platforms: a high-performance cloud environment (Google Colab, with an effective 2.3 GHz clock), a high-performance Windows laptop (1.8 GHz), and a resource-constrained IoT device (a Raspberry Pi). The following sections detail our observations and present corresponding graphical comparisons.
4.2. Execution Speed
This metric measures the total time required to perform key generation, encapsulation, and decapsulation. Although the raw operation times (from optimized implementations) are very short (of the order of tens of microseconds), when integrated into a full TLS, the effective encryption and decryption times can be measured in milliseconds.
The results in Figure 1 show the calculation of key generation, encryption, and decryption in microseconds using Google Colab, which shows that NTRU509 requires a significantly longer key generation time than Kyber512, whereas the time spent on encryption and decryption are relatively close for both schemes. This means that Kyber512 can be more useful in applications with high-frequency key generation, although both schemes are close in encryption and decryption.

Figure 1.
Execution time on Google Colab.
Figure 2 shows the execution times (in microseconds) of Kyber512 and NTRU 509 key encapsulation mechanisms (KEMs) on a Windows platform. The outcome shows that NTRU509 has a much higher key generation time than Kyber512, indicating that Kyber512 is more efficient in key generation. However, both schemes showed similar execution times for encryption and decryption, with minor differences. The results show that although NTRU509 might take more time in key generation, its encryption and decryption performance is still on par with that of Kyber512 on Windows platforms.
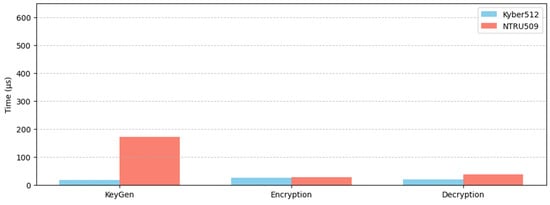
Figure 2.
Execution time on windows.
The graph in Figure 3 displays the execution time (in microseconds) of NTRU-HPS-2048-509 and Kyber512 on Raspberry Pi, representing the performance of the IoT. The values show that NTRU509 displays a significantly higher key generation time of more than 600 µs compared with Kyber512, which is less than 100 µs. This indicates that NTRU509 displays a huge computational overhead while creating keys for resource-constrained IoT devices. However, the encryption times of both schemes are relatively close to each other, with NTRU509 having a slightly longer decryption time than Kyber512.

Figure 3.
Execution time on Raspberry Pi (IOT).
Execution Speed Comparison
The graph in Figure 4 also shows that, as each operation phase is completed, the total time for Kyber512 increases at a significantly slower rate than that for NTRU509. This visual representation indicates that Kyber512 consistently maintains a lower cumulative execution time across all phases, which is crucial for low-power real-time IoT applications. At the same time, the graph gently acknowledges that, although NTRU509’s operations are slower, they still occur in microseconds, which might be acceptable in certain contexts where network or bandwidth constraints are the dominant factors.
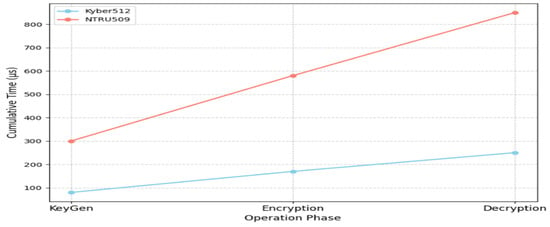
Figure 4.
Cumulative execution time per operation phase (Iot device).
4.3. Memory Usage
This metric evaluates the total RAM required during cryptographic operations. A lower memory consumption is critical for IoT devices and other systems with limited resources.
In Figure 5, the memory usage graph is illustrated with grouped bar charts showing the peak RAM consumption during cryptographic operations. In high-performance systems, such as Google Colab and Windows laptops, Kyber512 uses approximately 18,500 bytes (18.5 KB) of RAM, whereas NTRU509 uses approximately 18,100 bytes (18.1 KB). On Raspberry Pi, Kyber512’s memory footprint is reduced to approximately 2800 bytes (2.8 KB), and that of NTRU509 is approximately 3200 bytes (3.2 KB). This graph highlights that although both algorithms perform similarly on desktops, Kyber512 has a slight advantage in memory efficiency in IoT environments. Given that IoT devices often have severe RAM limitations, this reduction in memory usage (a difference of approximately 400 bytes) can be significant, whereas NTRU509 still maintains an acceptable performance in this domain.

Figure 5.
Memory usage comparison for Kyber512 vs. NTRU509.
4.4. Power Consumption
This metric measures the additional power (energy) generated during the complete KEM operation. A lower power consumption is especially important for battery-operated and energy-constrained IoT devices.
In Figure 6, the power consumption graph uses grouped bar charts to compare the additional power required to complete the full cryptographic operation for each algorithm. On high-performance platforms, Kyber512 draws approximately 2.0 to 2.1 Watts and NTRU509 approximately 2.3 2.4 Watts. In IoT devices, where energy efficiency is critical, these differences become even more important. For instance, on a Raspberry Pi, Kyber512’s operation consumes about 0.5 Watts, while NTRU509 consumes roughly 0.6 Watts. Although the difference in absolute power consumption on IoT devices is just about 0.1 Watts, over time, this translates into a substantial energy saving. In a battery-powered scenario, such as a small 1000 mAh battery, these differences directly impact the number of operations that can be performed before recharge is necessary. The graph, therefore, emphasizes that Kyber512 is more energy efficient and better suited for low-power, battery-operated IoT devices, while still recognizing that NTRU509’s power usage remains within an acceptable range.
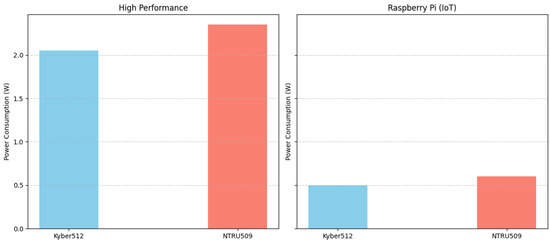
Figure 6.
Power consumption comparison for Kyber512 vs. NTRU509.
4.5. Bandwidth Efficiency (Ciphertext and Key Sizes)
This metric evaluates the size of the data transmitted over the network (public keys and ciphertexts). Smaller sizes result in a lower bandwidth usage and shorter transmission delays.
In Figure 7, the bandwidth efficiency graph is a dual-axis chart that simultaneously shows the sizes of the public key and cipher text (in bytes) and the corresponding estimated transmission time (in milliseconds) over a fixed network bandwidth (assumed to be 10 Mbps). According to these specifications, Kyber512 produces a public key of approximately 800 bytes and a cipher text of 768 bytes, totaling to approximately 1568 bytes. This results in an estimated transmission delay of approximately 1.25 milliseconds. By contrast, NTRU509 generates a smaller amount of data with both the public key and cipher text of approximately 699 bytes each, totaling approximately 1398 bytes, leading to an estimated delay of roughly 1.12 milliseconds. Although these transmission times are nearly identical on all platforms (because they depend only on the data size and network speed), the graph highlights that NTRU509 offers a slight advantage in terms of bandwidth efficiency owing to its smaller total transmission size. This efficiency is especially valuable in scenarios in which the network bandwidth is at a premium. However, the difference in transmission time is relatively small, and the graph shows that this advantage must be weighed against the computational efficiency benefits offered by Kyber512.
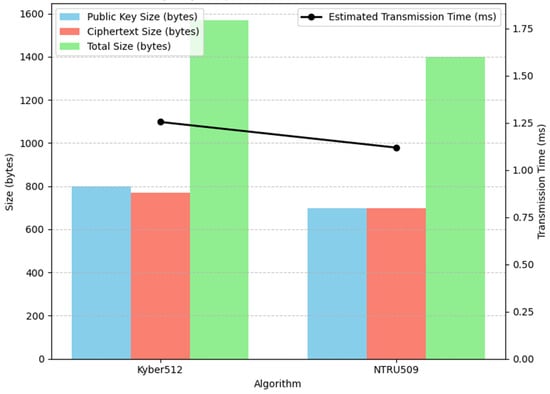
Figure 7.
Bandwidth efficiency: key and cipher text sizes and estimated transmission time.
4.6. Overall Performance Comparison
The performance chart in Figure 8 provides a holistic scorecard that combines all four key metrics—execution speed, memory usage, power consumption, and bandwidth efficiency—into a single normalized view, specifically for IoT devices. In this chart, each metric is normalized such that the best (lowest) observed value is 1.0. For the execution speed, with the best value of 250 μs, Kyber512 scored 1.0, and NTRU509 scored approximately 0.294 (with a value of 850 μs). For memory usage, the best value is 2800 bytes, giving Kyber512 a perfect score (1.0) and NTRU509 a score of approximately 0.875. In terms of power consumption, the Kyber512 (0.5 W) score was 1.0 compared to the NTRU509 score of 0.833 (0.5/0.6). Finally, for bandwidth efficiency, where the best transmission time is 1.12 ms, NTRU 509 scores 1.0 while Kyber512 scores about 0.896 (1.12/1.25). The chart gently conveys that while Kyber512 leads to the most critical metrics for IoT, namely execution speed, memory usage, and power consumption, NTRU509 has a slight edge in bandwidth efficiency.
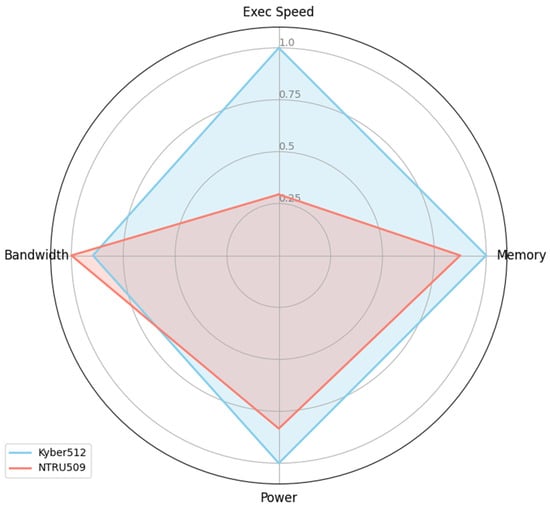
Figure 8.
Normalized performance comparison on IoT device.
5. Conclusions
In this study, the performance of Kyber512 and NTRU509 is assessed in the context of their appropriateness in different applications. Based on this discussion, it is concluded that Kyber512 is a better option than NTRU509 when considering the IoT and embedded systems in most cases. Computational efficiency, low energy consumption, and memory efficiency served as the benchmark criteria. The following are some important remarks.
- TLS 1.3, Virtual Private Networks (VPNs), and 5G security can benefit from these findings.
- Battery-operated devices, such as wearables, smart sensors, and edge-computing platforms that require continuous operation with limited power may also use Kyber512 with more efficiency.
- Kyber512’s streamlined encryption/decryption processes result in smaller time delays, and environments with energy constraints and limited computational resources may be seen to benefit, such as IoT devices in our case.
- NTRU509 excels in circumstances where decreasing the size of transmitted data is priority.
- NTRU509 is a better option in scenarios with limited bandwidth, such as satellite communications and remote sensor networks.
- NTRU509 has a slower processing speed and higher energy consumption, which restricts its use in energy-sensitive applications; in this case, IoT devices that emphasize battery efficiency.
- Ultimately, the selection among these cryptographic algorithms should be guided by the specific requirements of the deployment environment to ensure that performance, energy consumption, and data transmission needs are adequately addressed.
Post-quantum cryptography promises much in the protection of future communication systems, especially in use cases such as IoT device-secure firmware updates, 5G network privacy-preserving protocols, and robust VPNs securing critical infrastructure. However, similar to cryptographic innovations, there is a risk of abuse. Cyber attackers might exploit powerful post-quantum cryptography to scramble command-and-control traffic, hide criminal activities, or prevent digital forensics. To counter these issues, proactive approaches such as controlled deployment policies, strong key management, and anomaly-based traffic monitoring can be employed to detect or prevent abuse. By recognizing both the technical benefits and ethical considerations, this study supports a balanced and responsible response towards the use of post-quantum cryptographic technologies.
Limitations and Future Work
Although our study provides valuable insights into the performance of each KEM, it is important to acknowledge several limitations. Our experiments were carried out in virtualized settings and simulated scenarios rather than on dedicated IoT hardware, which might result in minor discrepancies compared to real-world performance. In addition, we evaluated only one security level, and exploring other parameter sets could reveal further trade-offs. Finally, although we thoroughly assessed the processing speed, memory usage, power consumption, and bandwidth efficiency, our study did not include in-depth measurements of resistance to side-channel attacks, which is a crucial aspect for secure deployment. Future work should involve real-world hardware tests, the exploration of multiple security levels, and comprehensive side-channel analyses.
Author Contributions
Conceptualization, M.A.E. and W.A.; methodology, M.A.E. and A.U.R.; software, M.A.E.; validation, A.U.R.; W.u.H. and A.Z.; formal analysis, A.Z.; investigation, M.A.E.; resources, W.A.; data curation, M.A.E.; writing—original draft preparation, M.A.E. and A.U.R.; writing—review and editing, A.Z.; visualization, W.u.H.; supervision, A.Z.; project administration, W.u.H.; funding acquisition, W.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Princess Nourah Bint Abdulrahman University Researchers Supporting Project Number PNURSP2025R500, Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
Data will be available on request.
Acknowledgments
The authors would like to acknowledge Princess Nourah bint Abdulrahman University Researchers Supporting Project Number PNURSP2025R500, and Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia, for supporting this project.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aumasson, J.-P. The impact of quantum computing on cryptography. Comput. Fraud Secur. 2017, 2017, 8–11. [Google Scholar] [CrossRef]
- Ugwuishiwu, C.H.; Orji, U.E.; Ugwu, C.I.; Asogwa, C.N. An overview of quantum cryptography and Shor’s algorithm. Int. J. Adv. Trends Comput. Sci. Eng 2020, 9, 7487–7495. [Google Scholar]
- Mavroeidis, V.; Vishi, K.; Zych, M.D.; Jøsang, A. The impact of quantum computing on present cryptography. arXiv 2018, arXiv:1804.00200. [Google Scholar] [CrossRef]
- Dam, D.T.; Tran, T.H.; Hoang, V.P.; Pham, C.K.; Hoang, T.T. A survey of post-quantum cryptography: Start of a new race. Cryptography 2023, 7, 40. [Google Scholar] [CrossRef]
- Wang, X.; Xu, G.; Yu, Y. Lattice-Based Cryptography: A Survey. Chin. Ann. Math. Ser. B 2023, 44, 945–960. [Google Scholar] [CrossRef]
- Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehle, D. CRYSTALS-Kyber: A CCA-Secure Module-Lattice-Based KEM. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 353–367. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, J.; Li, Z. Generalized NTRU Algorithms on Algebraic Rings. Electronics 2024, 13, 4293. [Google Scholar] [CrossRef]
- Status Report on the Third Round of NIST Post-Quantum Cryptography Standardization Process, IR 8413. Available online: https://csrc.nist.gov/ (accessed on 1 April 2025).
- Richter, M.; Bertram, M.; Seidensticker, J.; Tschache, A. A Mathematical Perspective on Post-Quantum Cryptography. Mathematics 2022, 10, 2579. [Google Scholar] [CrossRef]
- Panja, S.; Sharifian, S.; Jiang, S.; Safavi-Naini, R. CCA-Secure Hybrid Encryption in Correlated Randomness Model and KEM Combiners. arXiv 2024, arXiv:2401.00983. [Google Scholar]
- Mina-Zicu, M.; Simion, E. Threats to Modern Cryptography: Grover’s Algorithm. 2020. Available online: https://www.preprints.org/manuscript/202009.0677/v1/download (accessed on 1 April 2025).
- Farooq, S.; Altaf, A.; Iqbal, F.; Thompson, E.B.; Vargas, D.L.R.; Díez, I.T.; Ashraf, I. Resilience Optimization of Post-Quantum Cryptography Key Encapsulation Algorithms. Sensors 2023, 23, 5379. [Google Scholar] [CrossRef] [PubMed]
- Sabani, M.E.; Savvas, I.K.; Poulakis, D.; Garani, G.; Makris, G.C. Evaluation and Comparison of Lattice-Based Cryptosystems for a Secure Quantum Computing Era. Electronics 2023, 12, 2643. [Google Scholar] [CrossRef]
- Singh, S.; Sharma, P.K.; Moon, S.Y.; Park, J.H. Advanced Lightweight Encryption Algorithms for IoT Devices: Survey, Challenges and Solutions. J. Ambient Intell. Humaniz. Comput. 2024, 15, 1625–1642. [Google Scholar] [CrossRef]
- Kara, M.; Karampidis, K.; Panagiotakis, S.; Hammoudeh, M.; Felemban, M.; Papadourakis, G. Lightweight and Efficient Post Quantum Key Encapsulation Mechanism Based on Q-Problem. Electronics 2025, 14, 728. [Google Scholar] [CrossRef]
- Jeon, J.K.; Hwang, I.W.; Lee, H.J.; Lee, Y. Improving the Performance of RLizard on Memory-Constraint IoT Devices with 8-Bit ATmega MCU. Electronics 2020, 9, 1549. [Google Scholar] [CrossRef]
- Delgado-Vargas, K.A.; Mancillas-López, C.; Gallegos-García, G. A Look at Side Channel Attacks on Post-quantum Cryptography. Comput. Sistemas 2024, 28, 1879–1896. [Google Scholar] [CrossRef]
- Micciancio, D.; Regev, O. Lattice-Based Cryptography. In Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 147–191. [Google Scholar]
- Gitonga, C.K. The Impact of Quantum Computing on Cryptographic Systems: Urgency of Quantum-Resistant Algorithms and Practical Applications in Cryptography. Eur. J. Inf. Technol. Comput. Sci. 2025, 5, 1–10. [Google Scholar] [CrossRef]
- Micciancio, D.; Goldwasser, S. Shortest Vector Problem. In Complexity of Lattice Problems: A Cryptographic Perspective; Springer: Boston, MA, USA, 2002; pp. 69–90. [Google Scholar]
- Regev, O. The Learning with Errors Problem. In Proceedings of the 25th Annual IEEE Conference on Computational Complexity, CCC 2010, Cambridge, MA, USA, 9–11 June 2011. [Google Scholar]
- Acar, A.; Aksu, H.; Uluagac, A.S.; Conti, M. A Survey on Homomorphic Encryption Schemes: Theory and Implementation. ACM Comput. Surv. 2019, 51, 1–35. [Google Scholar] [CrossRef]
- Boudgoust, K.; Jeudy, C.; Roux-Langlois, A.; Wen, W. On the Hardness of Module Learning with Errors with Short Distributions. J. Cryptol. 2023, 36, 1. [Google Scholar] [CrossRef]
- Ding, X.; Esgin, M.F.; Sakzad, A.; Steinfeld, R. An Injectivity Analysis of CRYSTALS-Kyber and Implications on Quantum Security. In Australasian Conference on Information Security and Privacy; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Moody, D. NIST Status Update on the 3rd Round; Cryptography Technology Group, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2021. [Google Scholar]
- Paradise, F.; Sugeng, K. Algebraic Cryptanalysis on NTRU-HPS and NTRU-HRSS. Barekeng J. Math. App. 2023, 17, 2187–2196. [Google Scholar] [CrossRef]
- Avanzi, R.; Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-Kyber Algorithm Specifications and Supporting Documentation. NIST PQC Round 2019, 2, 1–43. [Google Scholar]
- Lyubashevsky, V.; Seiler, G. NTTRU: Truly Fast NTRU Using NTT. Cryptol. ePrint Arch. 2019. Available online: https://eprint.iacr.org/2019/058 (accessed on 20 January 2025). [CrossRef]
- PQClean. PQClean: Clean, Portable, Tested Implementations of Post-Quantum Cryptography. GitHub Repository. Available online: https://github.com/PQClean/PQClean (accessed on 20 January 2025).
- NTRU Library. Available online: https://github.com/jschanck/ntru (accessed on 20 January 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).