Dynamics of a Symmetric Seasonal Influenza Model with Variable Recovery, Treatment, and Fear Effects
Abstract
1. Introduction
2. The Transmission Model
3. Uniqueness, Non-Negativeness, and Boundedness of Solutions
- The solutions , and are guaranteed to exist uniquely.
- The solutions remain non-negative for all .
- The compact set Ψ, defined bywhere () are the solutions of the model (Equations (9)–(13)) with initial conditions (), forms a positively invariant domain.
4. Basic Reproduction Number
5. The Existence and Classification of Equilibria
5.1. Model’s Equilibria
- It can have a maximum of four non-trivial equilibria;
- It has only the disease-free equilibrium if and whenever case 1 is satisfied;
- It has a unique non-trivial equilibrium if and whenever cases 2, 4, 8, 16, and 32 are satisfied;
- It can have more than one non-trivial equilibrium for the other cases.
5.2. Local Stability of the Disease-Free Solution
- If , the disease-free equilibrium is always unstable.
- If , the disease-free equilibrium is stable if .
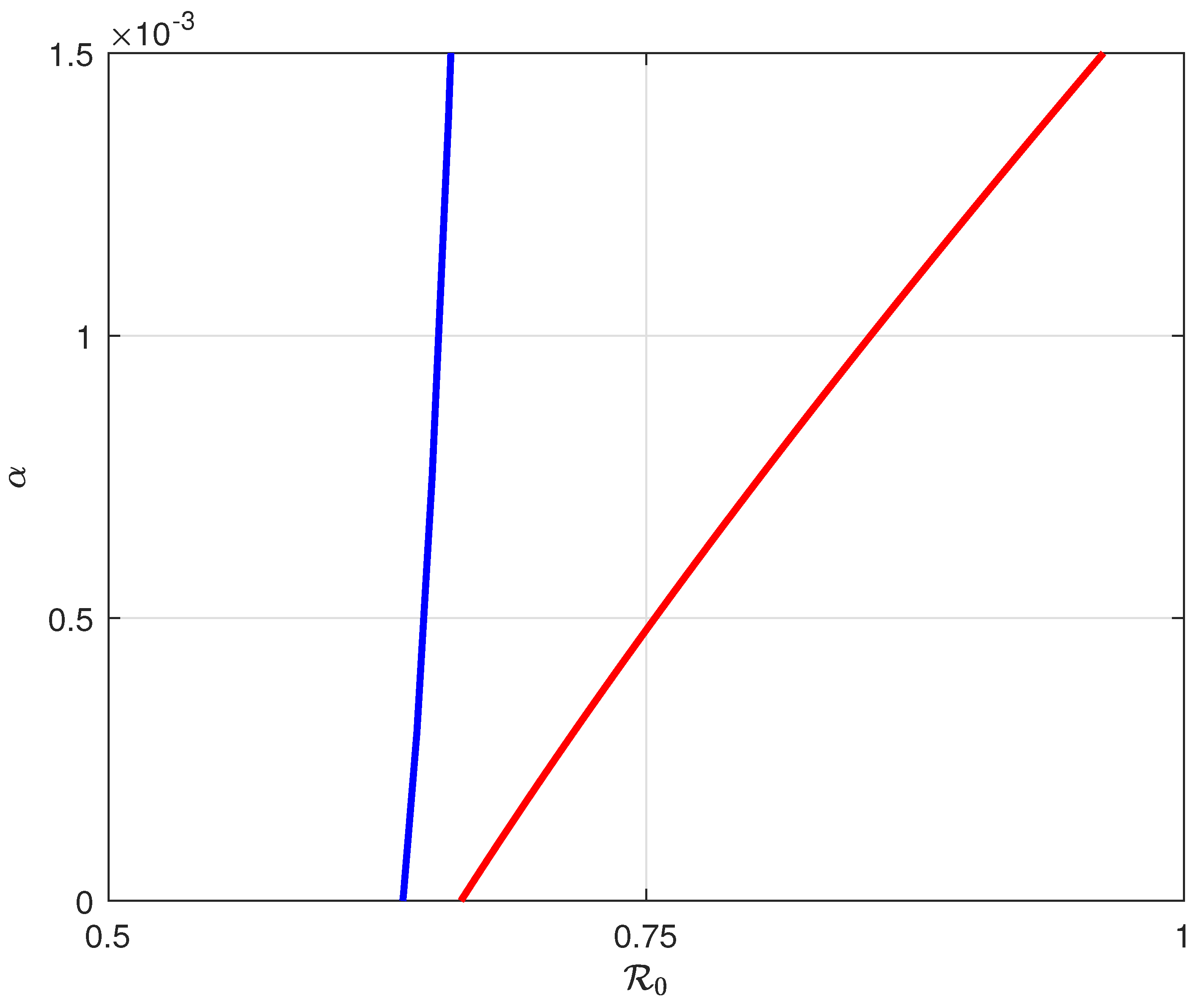
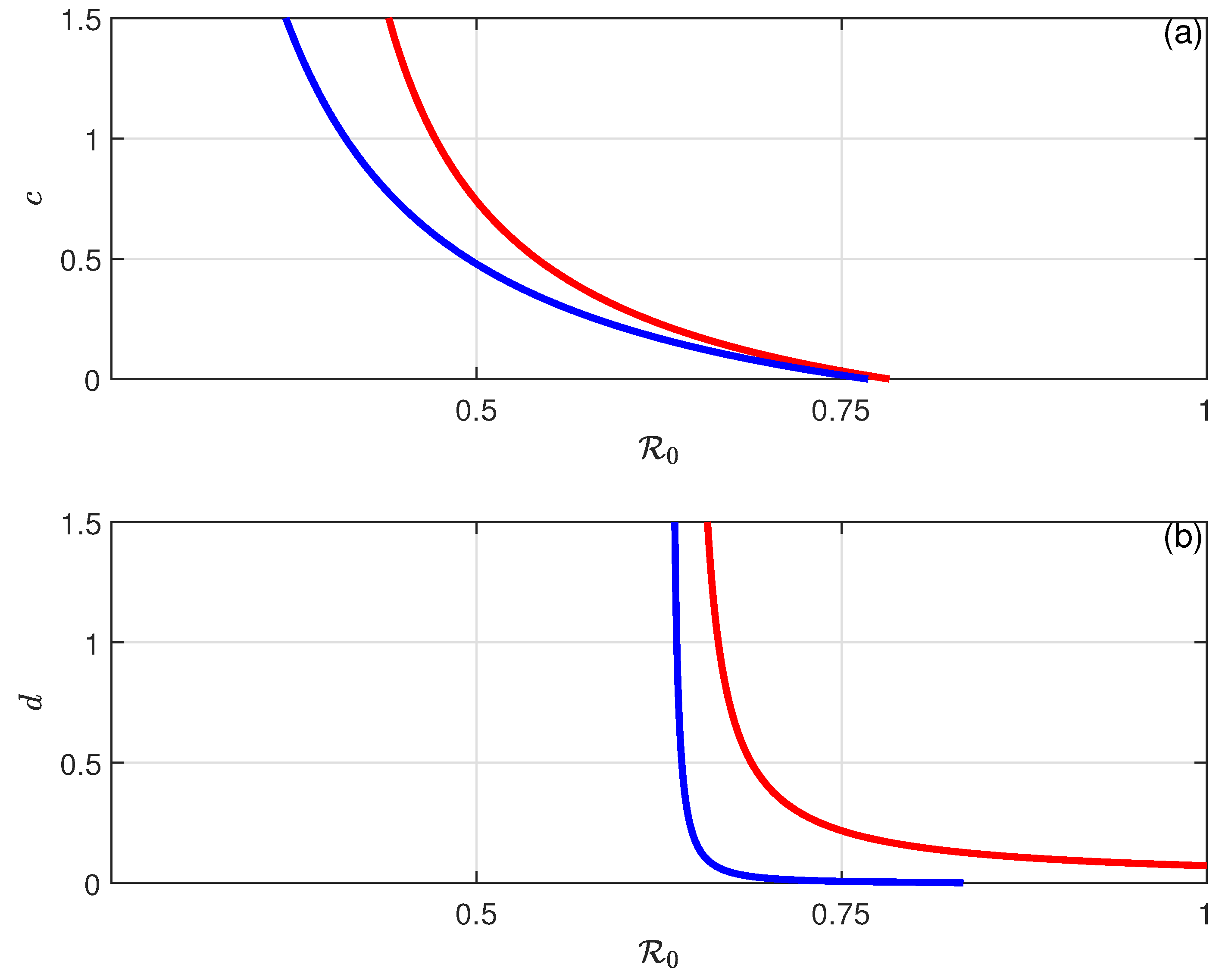
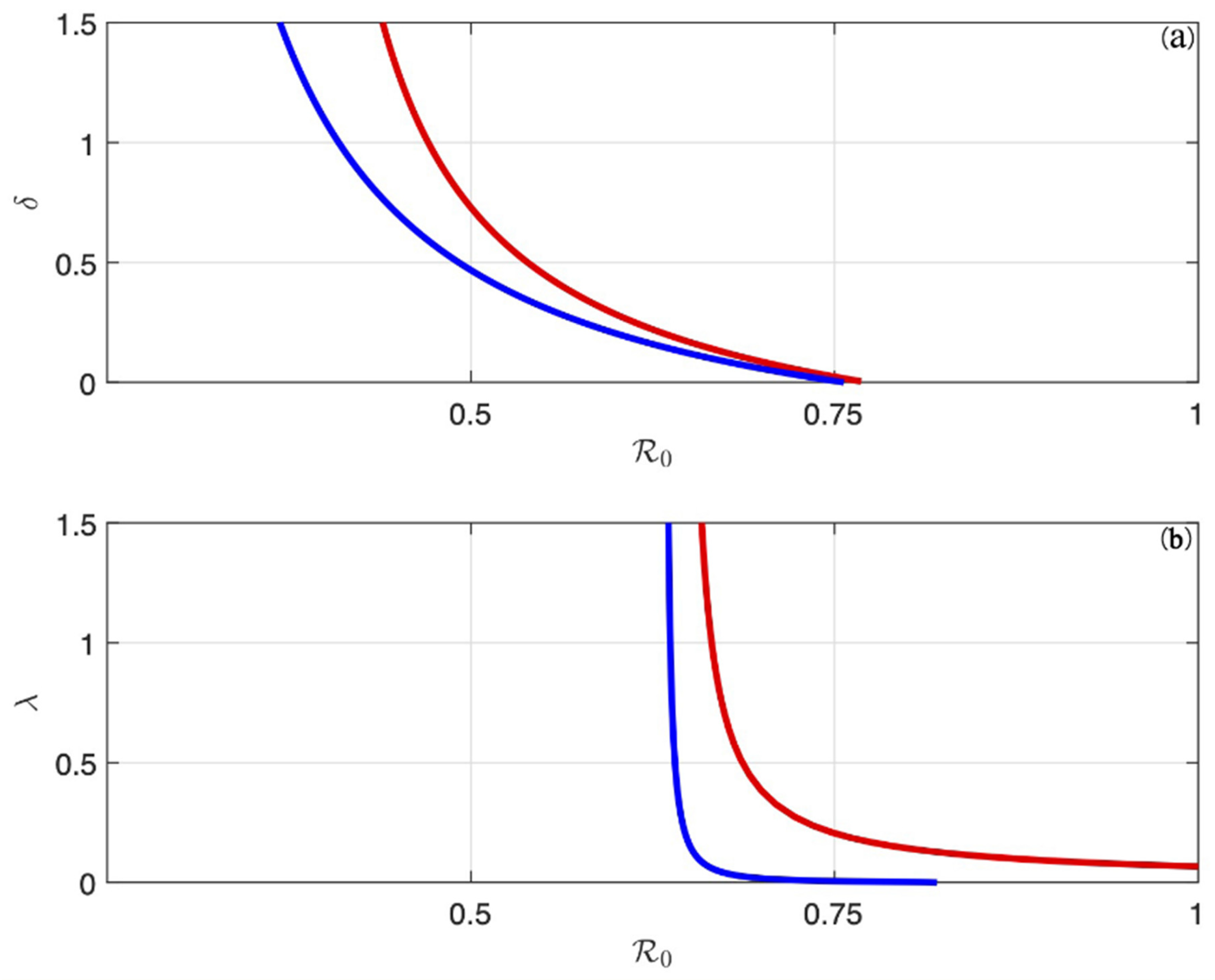
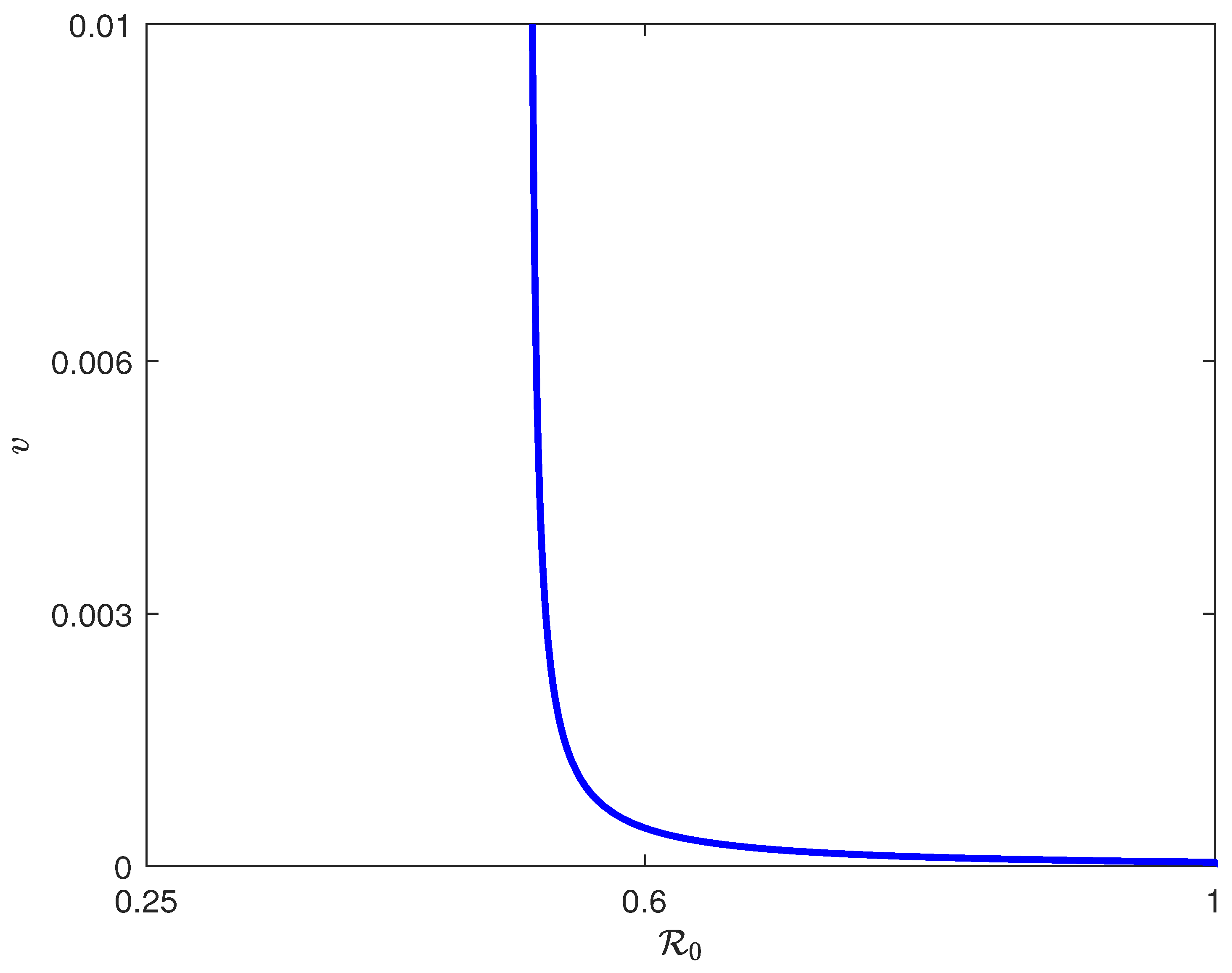
6. Backward Bifurcation
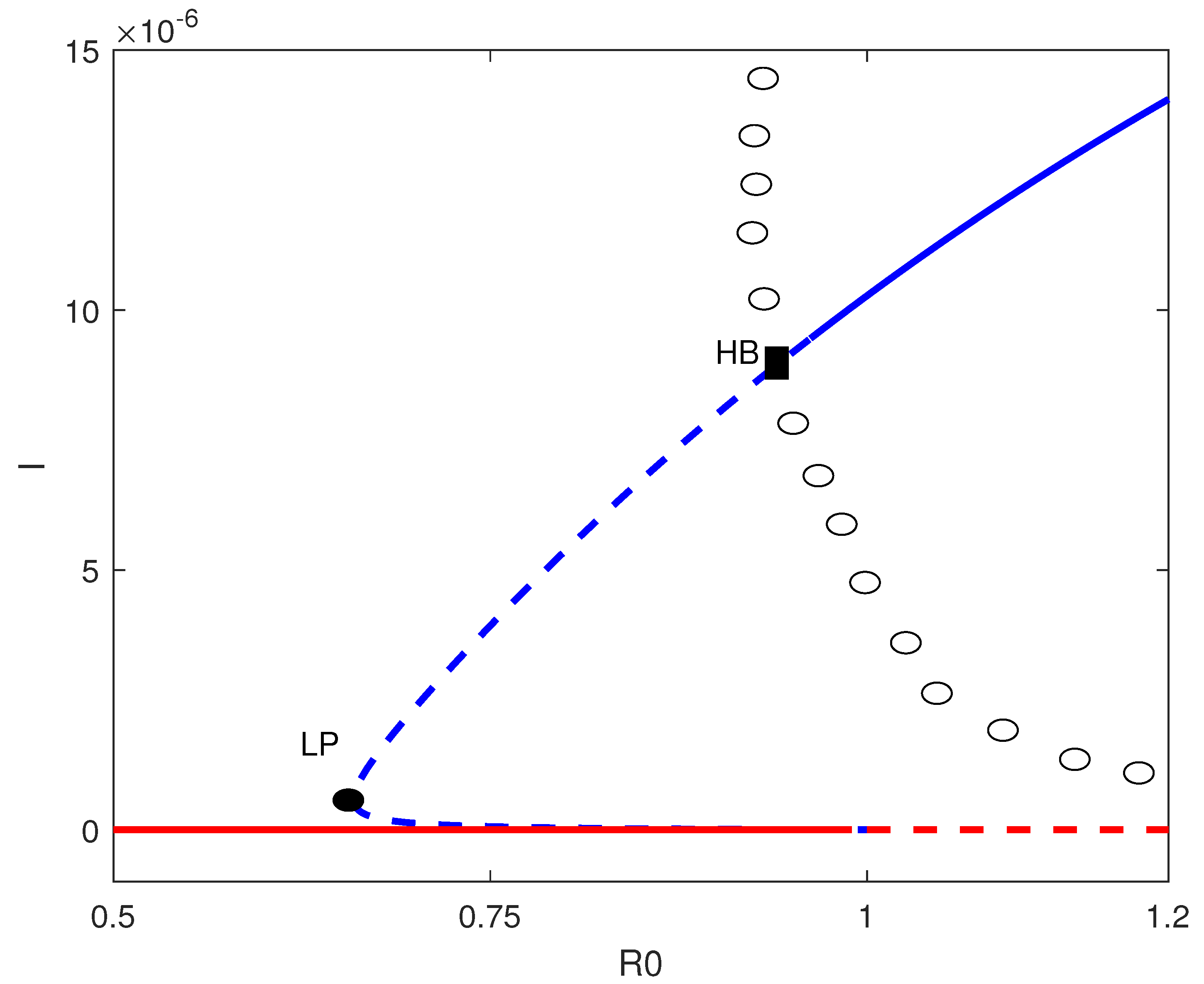
7. Existence of Hopf Points
8. Numerical Simulation
8.1. Model Parameters’ Baseline Values
8.2. Simulation Results
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Appendix A
- Existence and uniqueness: The right-hand side of the system (Equations (9)–(12)) is continuous and differentiable on and hence locally Lipschitzian. Therefore, the solution of the model with initial conditions exists and it is unique. We can write Equation (9) as follows:whereUsing the integrating factor method, integrating Equations (A1) and (A2) yieldsThus, is positive for all t.For the proofs that and are positive, we divide this issue into four cases:
- . From Equations (10) and (11), we can see for all .
- and . Since is continuous at and since , we conclude that and for all . If this is not true, then we can chooseIf , then since for , we conclude thatwhich contradicts the assumption that .If, on the other hand, , then there exists such that and on . Equation (11) implies, since and , thatThis giveswhich also contradicts the assumption that . The same analysis can be carried out for the other cases: and . We conclude, therefore, that and are positive for all .Next, since we showed that and , we can deduce from Equation (12) thatThis yieldsThis proves that .
- Boundedness The compact set , defined bywhere () are the solutions of the model (Equations (9)–(13)) with initial conditions (), is a positively invariant region. Let us denote that . We then have from Equations (9)–(13) thatTherefore,Integrating Equation (A11) yieldswhere is the initial condition of . Therefore, as t goes to and for . This shows that is positively invariant.
Appendix B
References
- World Health Organization. Available online: https://www.who.int/ (accessed on 10 April 2025).
- Iuliano, A.D.; Roguski, K.M.; Chang, H.H.; Muscatello, D.J.; Palekar, R.; Tempia, S.; Cohen, C.; Gran, J.M.; Schanzer, D.; Cowling, B.J.; et al. Estimates of global seasonal influenza-associated respiratory mortality: A modelling study. Lancet 2018, 391, 1285. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Chauhan, A. Fighting the flu: A brief review on anti-influenza agents. Biotechnol. Genet. Eng. Rev. 2023, 40, 858. [Google Scholar] [CrossRef]
- Gao, Y.; Guyatt, G.; Uyeki, T.M.; Liu, M.; Chen, Y.; Zhao, Y.; Shen, Y.; Xu, J.; Zheng, Q.; Li, Z.; et al. Antivirals for treatment of severe influenza: A systematic review and network meta-analysis of randomised controlled trials. Lancet 2024, 404, 753. [Google Scholar] [CrossRef]
- Quirouette, C.; Younis, N.P.; Reddy, M.B.; Beauchemin, C.A. A mathematical model describing the localization and spread of influenza A virus infection within the human respiratory tract. PLoS Comput. Biol. 2020, 16, e1007705. [Google Scholar]
- Zhao, Z.; Zhai, M.; Li, G.; Gao, X.; Song, W.; Wang, X.; Ren, H.; Cui, Y.; Qiao, Y.; Ren, J.; et al. Study on the prediction effect of a combined model of SARIMA and LSTM based on SSA for influenza in Shanxi Province, China. BMC Infect. Dis. 2023, 23, 71. [Google Scholar] [CrossRef]
- Modnak, C.; Wang, J. Optimal treatment strategy of an avian influenza model with latency. Int. J. Biomath. 2017, 10, 1750066. [Google Scholar] [CrossRef]
- Shi, W.W.; Tan, Y.S. Transmission dynamics and optimal control of an influenza model with quarantine and treatment. Int. J. Biomath. 2012, 5, 1260011. [Google Scholar] [CrossRef]
- Baba, I.A.; Ahmad, H.; Alsulami, M.D.; Abualnaja, K.M.; Altanji, M. A mathematical model to study resistance and non-resistance strains of influenza. Results Phys. 2021, 26, 104390. [Google Scholar] [CrossRef]
- Mathur, K.S.; Narayan, P. Dynamics of an SVEIRS epidemic model with vaccination and saturated incidence rate. Int. J. Appl. Comput. Math. 2018, 4, 118. [Google Scholar] [CrossRef]
- Mohammad, K.M.; Akhi, A.A.; Kamrujjaman, M. Bifurcation analysis of an influenza A (H1N1) model with treatment and vaccination. PLoS ONE 2025, 20, e0315280. [Google Scholar] [CrossRef]
- Osthus, D.; Hickmann, K.S.; Caragea, P.C.; Higdon, D.; Del Valle, S.Y. Forecasting seasonal influenza with a state-space SIR model. Forecasting seasonal influenza with a state-space SIR model. Ann. Appl. Stat. 2017, 11, 202. [Google Scholar] [CrossRef] [PubMed]
- Sabir, Z.; Said, S.B.; Al-Mdallal, Q. A fractional order numerical study for the influenza disease mathematical model. Alex. Eng. J. 2023, 65, 615. [Google Scholar] [CrossRef]
- Evirgen, F.; Uçar, E.; Uçar, S.; Özdemir, N. Modelling Influenza A disease dynamics under Caputo-Fabrizio fractional derivative with distinct contact rates. Math. Model. Numer. Simul. Appl. 2023, 3, 58. [Google Scholar] [CrossRef]
- Alzahrani, S.M.; Saadeh, R.; Abdoon, M.A.; Qazza, A.; EL Guma, F.; Berir, M. Numerical simulation of an influenza epidemic: Prediction with fractional SEIR and the ARIMA model. Appl. Math. Inf. Sci. 2024, 18, 1. [Google Scholar]
- Chen, Y.; Zhang, J.; Jin, Z. Optimal control of an influenza model with mixed cross-infection by age group. Math. Comput. Simul. 2023, 206, 410. [Google Scholar] [CrossRef]
- Samanta, G.P. Global dynamics of a nonautonomous SIRC model for influenza A with distributed time delay. Differ. Equ. Dyn. Syst. 2010, 18, 341. [Google Scholar] [CrossRef]
- Sabir, Z.; Botmart, T.; Raja, M.A.Z.; Sadat, R.; Ali, M.R.; Alsulami, A.A.; Alghamdi, A. Artificial neural network scheme to solve the nonlinear influenza disease model. Biomed. Signal Process. Control 2022, 75, 103594. [Google Scholar] [CrossRef]
- Epstein, J.M.; Parker, J.; Cummings, D.; Hammond, R.A. Coupled contagion dynamics of fear and disease: Mathematical and computational explorations. PLoS ONE 2008, 3, e3955. [Google Scholar] [CrossRef] [PubMed]
- Valle, S.; Mniszewski, S.; Hyman, J. Modeling the impact of behavior changes on the spread of pandemic influenza. In Modeling the Interplay Between Human Behavior and the Spread of Infectious Diseases; Manfredi, P., d’Onofrio, A., Eds.; Springer Science Business Media: New York, NY, USA, 2012; pp. 59–77. [Google Scholar]
- Mpeshe, S.C.; Nyerere, N. Modeling the dynamics of coronavirus disease pandemic coupled with fear epidemics. Comput. Math. Methods Med. 2021, 2021, 6647425. [Google Scholar] [CrossRef]
- Maji, C. Impact of media-induced fear on the control of COVID-19 outbreak: A mathematical study. Int. J. Differ. Equ. 2021, 2021, 2129490. [Google Scholar] [CrossRef]
- Thirthar, A.A.; Abboubakar, H.; Khan, A.; Abdeljawad, T. Mathematical modeling of the COVID-19 epidemic with fear impact. J. AIMS Math. 2023, 8, 6447. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X. Backward bifurcation of an epidemic model with saturated treatment. J. Math. Anal. Appl. 2008, 348, 433. [Google Scholar] [CrossRef]
- Chan, C.; Zhu, H. Bifurcations and complex dynamics of an SIR model with the impact of the number of hospital beds. J. Diff. Equ. 2014, 257, 1662. [Google Scholar]
- Wang, W. Backward bifurcation of an epidemic model with treatment. Math. Biosci. 2006, 201, 58. [Google Scholar] [CrossRef]
- Candelli, M.; Pignataro, G.; Torelli, E.; Gullì, A.; Nista, E.C.; Petrucci, M.; Saviano, A.; Marchesini, D.; Covino, M.; Ojetti, V.; et al. Effect of influenza vaccine on COVID-19 mortality: A retrospective study. Intern. Emerg. Med. 2021, 16, 1849. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361. [Google Scholar] [CrossRef]
- General Authority for Statistics in Saudi Arabia. Statistics Library. Available online: https://www.stats.gov.sa/en/statistics?index=119025 (accessed on 10 April 2025).
- Alshahrani, A.M.; Okmi, E.; Sullivan, S.G.; Tempia, S.; Barakat, A.; Naja, H.A.E.; Aman, A.; Hamedelneil, O.; Mohamed, M.; Basheer, S.F.; et al. Uncovering the burden of influenza-associated illness across levels of severity in the kingdom of Saudi Arabia across three seasons. J. Epidemiol. Glob. Health 2025, 15, 47. [Google Scholar] [CrossRef]
- Carcione, J.M.; Santos, J.E.; Bagaini, C.; Ba, J. A Simulation of a COVID-19 Epidemic Based on a Deterministic SEIR Model. Front. Public Health 2020, 8, 230. [Google Scholar] [CrossRef]
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A.; Meijer, H.G.E.; Sautois, B. New features of the software MatCont for bifurcation analysis of dynamical systems. Math. Comput. Model. Dyn. Syst. 2008, 14, 147. [Google Scholar] [CrossRef]
- MATLAB. Version 9.4.0 (R2018a); The MathWorks Inc.: Natick, MA, USA, 2018. [Google Scholar]
| Case | Number of Sign Changes | Number of Positive Roots | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 0 | 0 | |
| 2 | −1 | −1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | |
| 3 | −1 | −1 | −1 | −1 | −1 | 1 | −1 | 2 | 2, 0 | |
| 4 | −1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | |
| 5 | −1 | −1 | −1 | −1 | 1 | −1 | −1 | 2 | 2, 0 | |
| 6 | −1 | −1 | −1 | −1 | 1 | −1 | 1 | 3 | 3, 1 | |
| 7 | −1 | −1 | −1 | −1 | 1 | 1 | −1 | 2 | 2, 0 | |
| 8 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 1 | |
| 9 | −1 | −1 | −1 | 1 | −1 | −1 | −1 | 2 | 2, 0 | |
| 10 | −1 | −1 | −1 | 1 | −1 | −1 | 1 | 3 | 3, 1 | |
| 11 | −1 | −1 | −1 | 1 | −1 | 1 | −1 | 4 | 4, 2, 0 | |
| 12 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | 3 | 3, 1 | |
| 13 | −1 | −1 | −1 | 1 | 1 | −1 | −1 | 2 | 2, 0 | |
| 14 | −1 | −1 | −1 | 1 | 1 | −1 | 1 | 3 | 3, 1 | |
| 15 | −1 | −1 | −1 | 1 | 1 | 1 | −1 | 2 | 2, 0 | |
| 16 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 17 | −1 | −1 | 1 | −1 | −1 | −1 | −1 | 2 | 2, 0 | |
| 18 | −1 | −1 | 1 | −1 | −1 | −1 | 1 | 3 | 3, 1 | |
| 19 | −1 | −1 | 1 | −1 | −1 | 1 | −1 | 4 | 4, 2, 0 | |
| 20 | −1 | −1 | 1 | −1 | −1 | 1 | 1 | 3 | 3,1 | |
| 21 | −1 | −1 | 1 | −1 | 1 | −1 | −1 | 4 | 4, 2, 0 | |
| 22 | −1 | −1 | 1 | −1 | 1 | −1 | 1 | 4 | 4, 2, 0 | |
| 23 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 4 | 4, 2, 0 | |
| 24 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | 3 | 3, 1 | |
| 25 | −1 | −1 | 1 | 1 | −1 | −1 | −1 | 2 | 2, 0 | |
| 26 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 3 | 3, 1 | |
| 27 | −1 | −1 | 1 | 1 | −1 | 1 | −1 | 4 | 4, 2, 0 | |
| 28 | −1 | −1 | 1 | 1 | −1 | 1 | 1 | 2 | 2, 0 | |
| 29 | −1 | −1 | 1 | 1 | 1 | −1 | −1 | 2 | 2, 0 | |
| 30 | −1 | −1 | 1 | 1 | 1 | −1 | 1 | 3 | 3, 1 | |
| 31 | −1 | −1 | 1 | 1 | 1 | 1 | −1 | 2 | 2, 0 | |
| 32 | −1 | −1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqahtani, R.T.; Ajbar, A.; Alqhtani, M. Dynamics of a Symmetric Seasonal Influenza Model with Variable Recovery, Treatment, and Fear Effects. Symmetry 2025, 17, 803. https://doi.org/10.3390/sym17060803
Alqahtani RT, Ajbar A, Alqhtani M. Dynamics of a Symmetric Seasonal Influenza Model with Variable Recovery, Treatment, and Fear Effects. Symmetry. 2025; 17(6):803. https://doi.org/10.3390/sym17060803
Chicago/Turabian StyleAlqahtani, Rubayyi T., Abdelhamid Ajbar, and Manal Alqhtani. 2025. "Dynamics of a Symmetric Seasonal Influenza Model with Variable Recovery, Treatment, and Fear Effects" Symmetry 17, no. 6: 803. https://doi.org/10.3390/sym17060803
APA StyleAlqahtani, R. T., Ajbar, A., & Alqhtani, M. (2025). Dynamics of a Symmetric Seasonal Influenza Model with Variable Recovery, Treatment, and Fear Effects. Symmetry, 17(6), 803. https://doi.org/10.3390/sym17060803




