FedOPCS: An Optimized Poisoning Countermeasure for Non-IID Federated Learning with Privacy-Preserving Stability
Abstract
1. Introduction
- Novel weight constraints and metric criteria: We propose a new set of weight constraints and metrics for evaluating and ensuring the security and robustness of models in FL environments. The dynamic weight adjustment mechanism ensures symmetric contributions from clients by penalizing malicious updates and rewarding trustworthy ones, thus maintaining equilibrium in the aggregation process.
- Conditional Generative Adversarial Network (CGAN) data generation method to enhance model robustness: Our CGAN-based data augmentation restores symmetry in local data distributions by generating synthetic samples that align with the global data profile, mitigating the skewness caused by non-IID conditions. This method allows us to provide a more accurate view of the data for the FL system while protecting data privacy, thereby effectively guiding the adjustment of client model aggregation weights.
- Model aggregation method using adaptive weighting and homomorphic encryption (HE) techniques: We propose an innovative client model aggregation framework that combines adaptive weighting and homomorphic encryption techniques. The adaptive weighting mechanism dynamically adjusts the weight of models in the global model based on their performance and trustworthiness to optimize the aggregation process and resist model poisoning attacks. Homomorphic encryption ensures the security of the entire aggregation process, preventing potential man-in-the-middle attacks and model leakage risks.
2. Related Work
2.1. Security and Defence Mechanisms in Federated Learning
2.2. Handling Non-IID Data in Federated Learning
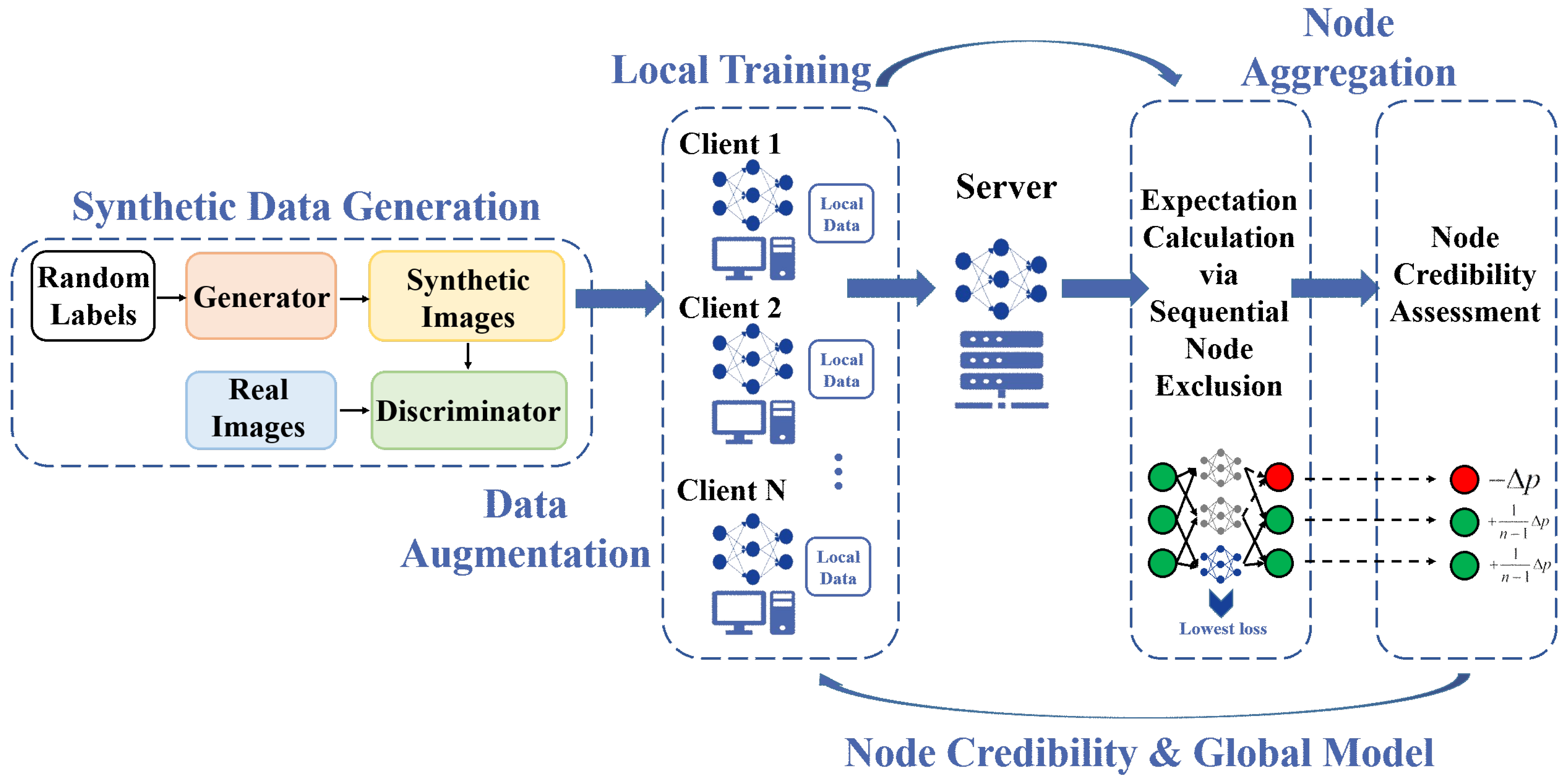
3. System Model
4. Node Credibility Assessment in Federated Learning Based on CGAN Data Augmentation
4.1. Optimal Aggregation with Node Credibility Assessment
| Algorithm 1 Aggregation Based on Inner Product Metrics |
|
4.2. Data Augmentation with Conditional GANs
| Algorithm 2 Node Selection with Data Augmentation |
|
5. Experiment
5.1. Experimental Setup
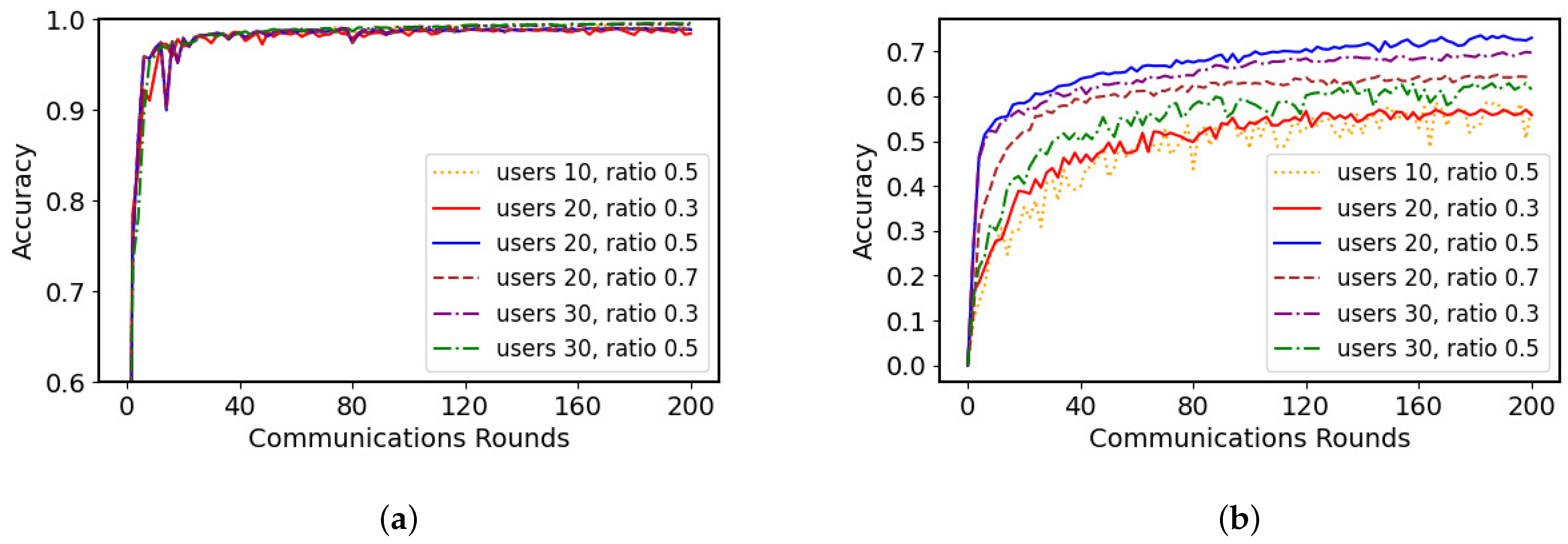
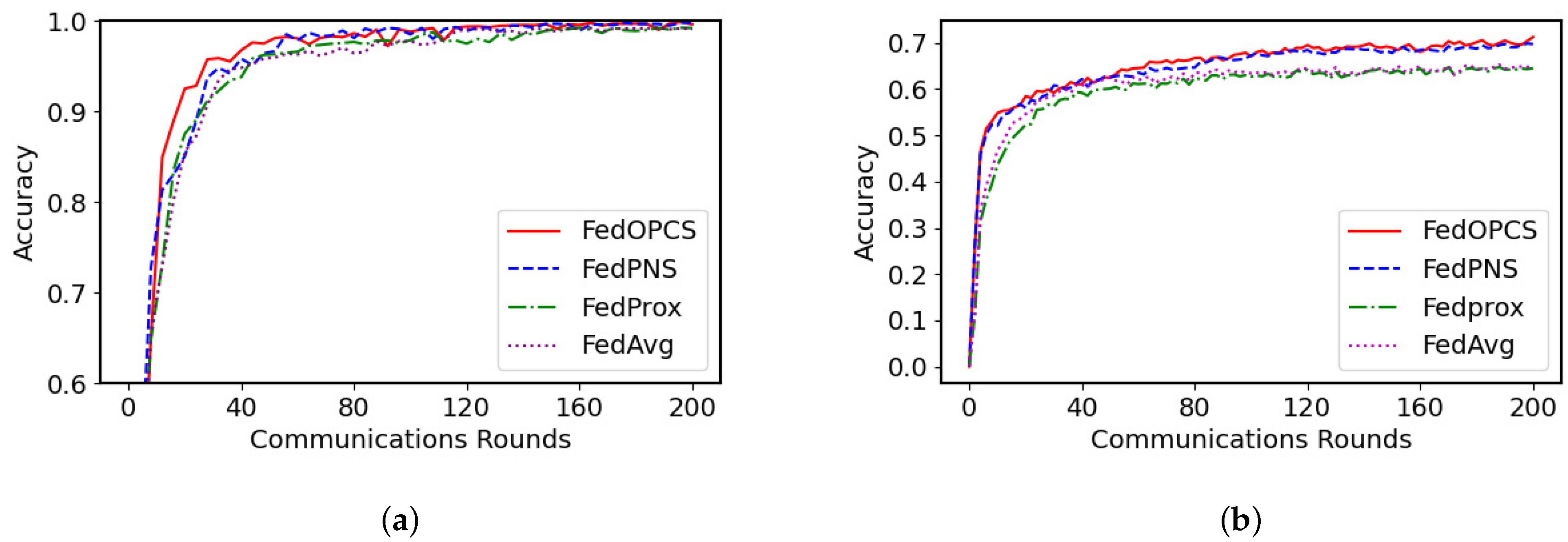
5.2. Experimental Results and Analysis
5.2.1. Model Performance Evaluation
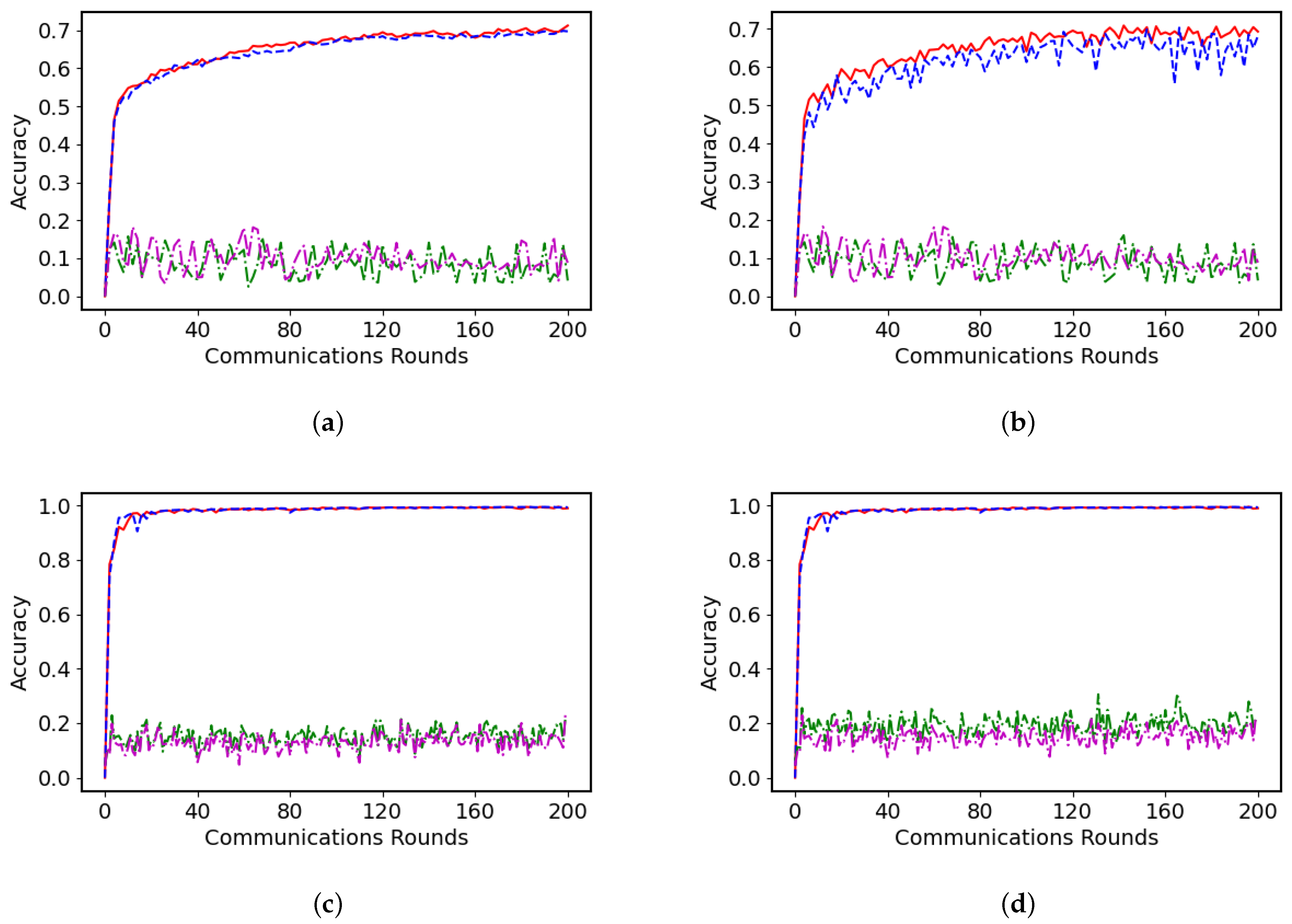
5.2.2. Robustness Testing Against Adversarial Attacks
5.2.3. Analysis of the Impact of the Poisoning Ratio
5.2.4. Time Consumption and Rationale for Paillier HE
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wiedemann, S.; Müller, K.R.; Samek, W. Compact and computationally efficient representation of deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 772–785. [Google Scholar] [CrossRef]
- Wiedemann, S.; Marban, A.; Müller, K.R.; Samek, W. Entropy-constrained training of deep neural networks. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics. PMLR, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Shen, S.; Tople, S.; Saxena, P. Auror: Defending against poisoning attacks in collaborative deep learning systems. In Proceedings of the 32nd Annual Conference on Computer Security Applications, Los Angeles, CA, USA, 5–8 December 2016; pp. 508–519. [Google Scholar]
- Ek, S.; Portet, F.; Lalanda, P.; Vega, G. Evaluation of federated learning aggregation algorithms: Application to human activity recognition. In Proceedings of the Adjunct Proceedings of the 2020 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2020 ACM International Symposium on Wearable Computers, Virtual, 12–17 September 2020; pp. 638–643. [Google Scholar]
- Lam, M.; Wei, G.Y.; Brooks, D.; Reddi, V.J.; Mitzenmacher, M. Gradient disaggregation: Breaking privacy in federated learning by reconstructing the user participant matrix. In Proceedings of the International Conference on Machine Learning. PMLR, Online, 18–24 July 2021; pp. 5959–5968. [Google Scholar]
- Zhang, C.; Li, S.; Xia, J.; Wang, W.; Yan, F.; Liu, Y. {BatchCrypt}: Efficient homomorphic encryption for {Cross-Silo} federated learning. In Proceedings of the 2020 USENIX Annual Technical Conference (USENIX ATC 20), Online, 15–17 July 2020; pp. 493–506. [Google Scholar]
- Kaur, H.; Rani, V.; Kumar, M.; Sachdeva, M.; Mittal, A.; Kumar, K. Federated learning: A comprehensive review of recent advances and applications. Multimed. Tools Appl. 2024, 83, 54165–54188. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl.-Based Syst. 2021, 216, 106775. [Google Scholar] [CrossRef]
- Cetinkaya, A.E.; Akin, M.; Sagiroglu, S. Improving performance of federated learning based medical image analysis in non-IID settings using image augmentation. In Proceedings of the 2021 International Conference on Information Security and Cryptology (ISCTURKEY), Ankara, Turkey, 2–3 December 2021; pp. 69–74. [Google Scholar]
- Duan, M.; Liu, D.; Chen, X.; Liu, R.; Tan, Y.; Liang, L. Self-balancing federated learning with global imbalanced data in mobile systems. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 59–71. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Y.; Miao, Y.; Xu, G.; Liu, X.; Ma, J.; Deng, R.H. FLGAN: GAN-Based Unbiased FederatedLearning under non-IID Settings. IEEE Trans. Knowl. Data Eng. 2023, 36, 1566–1581. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Wu, H.; Wang, P. Node selection toward faster convergence for federated learning on non-iid data. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3099–3111. [Google Scholar] [CrossRef]
- Blanchard, P.; El Mhamdi, E.M.; Guerraoui, R.; Stainer, J. Machine learning with adversaries: Byzantine tolerant gradient descent. Adv. Neural Inf. Process. Syst. 2017, 30, 118–128. [Google Scholar]
- Xie, C.; Koyejo, S.; Gupta, I. Zeno: Distributed stochastic gradient descent with suspicion-based fault-tolerance. In Proceedings of the International Conference on Machine Learning. PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6893–6901. [Google Scholar]
- Guerraoui, R.; Rouault, S. The hidden vulnerability of distributed learning in byzantium. In Proceedings of the International Conference on Machine Learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 3521–3530. [Google Scholar]
- Cao, X.; Fang, M.; Liu, J.; Gong, N.Z. Fltrust: Byzantine-robust federated learning via trust bootstrapping. arXiv 2020, arXiv:2012.13995. [Google Scholar]
- Mo, F.; Shamsabadi, A.S.; Katevas, K.; Demetriou, S.; Leontiadis, I.; Cavallaro, A.; Haddadi, H. Darknetz: Towards model privacy at the edge using trusted execution environments. In Proceedings of the 18th International Conference on Mobile Systems, Applications, and Services, Helsinki, Finland, 15–19 June 2020; pp. 161–174. [Google Scholar]
- Tomsett, R.; Chan, K.; Chakraborty, S. Model poisoning attacks against distributed machine learning systems. In Proceedings of the Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications, Baltimore, MD, USA, 14–18 April 2019; Volume 11006, pp. 481–489. [Google Scholar]
- Ma, Z.; Ma, J.; Miao, Y.; Li, Y.; Deng, R.H. ShieldFL: Mitigating model poisoning attacks in privacy-preserving federated learning. IEEE Trans. Inf. Forensics Secur. 2022, 17, 1639–1654. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, H.; Xie, Q.; Ma, C.; Wang, S.; Xing, G. Lancelot: Towards efficient and privacy-preserving byzantine-robust federated learning within fully homomorphic encryption. arXiv 2024, arXiv:2408.06197. [Google Scholar]
- Mai, P.; Yan, R.; Pang, Y. Rflpa: A robust federated learning framework against poisoning attacks with secure aggregation. Adv. Neural Inf. Process. Syst. 2024, 37, 104329–104356. [Google Scholar]
- Sun, H.; Zhang, Y.; Zhuang, H.; Li, J.; Xu, Z.; Wu, L. PEAR: Privacy-preserving and effective aggregation for byzantine-robust federated learning in real-world scenarios. Comput. J. 2025, 2025, bxae086. [Google Scholar] [CrossRef]
- Cao, X.; Gong, N.Z. Mpaf: Model poisoning attacks to federated learning based on fake clients. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 3396–3404. [Google Scholar]
- Sun, J.; Li, A.; DiValentin, L.; Hassanzadeh, A.; Chen, Y.; Li, H. Fl-wbc: Enhancing robustness against model poisoning attacks in federated learning from a client perspective. Adv. Neural Inf. Process. Syst. 2021, 34, 12613–12624. [Google Scholar]
- Zhang, J.; Chen, B.; Cheng, X.; Binh, H.T.T.; Yu, S. PoisonGAN: Generative poisoning attacks against federated learning in edge computing systems. IEEE Internet Things J. 2020, 8, 3310–3322. [Google Scholar] [CrossRef]
- Li, X.; Qu, Z.; Zhao, S.; Tang, B.; Lu, Z.; Liu, Y. Lomar: A local defense against poisoning attack on federated learning. IEEE Trans. Dependable Secur. Comput. 2021, 20, 437–450. [Google Scholar] [CrossRef]
- Awan, S.; Luo, B.; Li, F. Contra: Defending against poisoning attacks in federated learning. In Proceedings of the Computer Security–ESORICS 2021: 26th European Symposium on Research in Computer Security, Darmstadt, Germany, 4–8 October 2021; Proceedings, Part I 26. Springer: Berlin/Heidelberg, Germany, 2021; pp. 455–475. [Google Scholar]
- Wang, H.; Kaplan, Z.; Niu, D.; Li, B. Optimizing federated learning on non-IID data with reinforcement learning. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Online, 6–9 July 2020; pp. 1698–1707. [Google Scholar]
- Sattler, F.; Wiedemann, S.; Müller, K.R.; Samek, W. Robust and communication-efficient federated learning from non-IID data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3400–3413. [Google Scholar] [CrossRef]
- Li, Q.; Diao, Y.; Chen, Q.; He, B. Federated learning on non-IID data silos: An experimental study. In Proceedings of the 2022 IEEE 38th International Conference on Data Engineering (ICDE), Kuala Lumpur, Malaysia, 9–12 May 2022; pp. 965–978. [Google Scholar]
- Briggs, C.; Fan, Z.; Andras, P. Federated learning with hierarchical clustering of local updates to improve training on non-IID data. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–9. [Google Scholar]
- Sery, T.; Shlezinger, N.; Cohen, K.; Eldar, Y.C. Over-the-air federated learning from heterogeneous data. IEEE Trans. Signal Process. 2021, 69, 3796–3811. [Google Scholar] [CrossRef]
- Qu, L.; Zhou, Y.; Liang, P.P.; Xia, Y.; Wang, F.; Adeli, E.; Fei-Fei, L.; Rubin, D. Rethinking architecture design for tackling data heterogeneity in federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10061–10071. [Google Scholar]
- Mendieta, M.; Yang, T.; Wang, P.; Lee, M.; Ding, Z.; Chen, C. Local learning matters: Rethinking data heterogeneity in federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8397–8406. [Google Scholar]
- Wang, S.; Lee, M.; Hosseinalipour, S.; Morabito, R.; Chiang, M.; Brinton, C.G. Device sampling for heterogeneous federated learning: Theory, algorithms, and implementation. In Proceedings of the IEEE INFOCOM 2021-IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar]
- Balakrishnan, R.; Li, T.; Zhou, T.; Himayat, N.; Smith, V.; Bilmes, J. Diverse client selection for federated learning: Submodularity and convergence analysis. In Proceedings of the ICML 2021 International Workshop on Federated Learning for User Privacy and Data Confidentiality, Online, 24 July 2021; Volume 3. [Google Scholar]
- Zhang, Z.; Yang, Y.; Yao, Z.; Yan, Y.; Gonzalez, J.E.; Ramchandran, K.; Mahoney, M.W. Improving semi-supervised federated learning by reducing the gradient diversity of models. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Orlando, FL, USA, 15–18 December 2021; pp. 1214–1225. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- Hu, R.; Guo, Y.; Gong, Y. Federated learning with sparsified model perturbation: Improving accuracy under client-level differential privacy. IEEE Trans. Mob. Comput. 2023, 23, 8242–8255. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Fan, J.; Vercauteren, F. Somewhat practical fully homomorphic encryption. Cryptol. ePrint Arch. 2012. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Proceedings of the Advances in Cryptology—ASIACRYPT 2017: 23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Volume 23, pp. 409–437. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Jhunjhunwala, D.; Sharma, P.; Nagarkatti, A.; Joshi, G. Fedvarp: Tackling the variance due to partial client participation in federated learning. In Uncertainty in Artificial Intelligence; MLResearchPress: Cambridge, MA, USA, 2022; Volume 180, pp. 906–916. [Google Scholar]
- Cho, Y.J.; Sharma, P.; Joshi, G.; Xu, Z.; Kale, S.; Zhang, T. On the convergence of federated averaging with cyclic client participation. In International Conference on Machine Learning; MLResearchPress: Cambridge, MA, USA, 2023; Volume 202, pp. 5677–5721. [Google Scholar]
- Chen, S.; Tavallaie, O.; Hambali, M.H.; Zandavi, S.M.; Haddadi, H.; Lane, N.; Guo, S.; Zomaya, A.Y. Optimization of federated learning’s client selection for non-iid data based on grey relational analysis. arXiv 2023, arXiv:2310.08147. [Google Scholar]
- Seol, M.; Kim, T. Performance enhancement in federated learning by reducing class imbalance of non-iid data. Sensors 2023, 23, 1152. [Google Scholar] [CrossRef]

| Method | Ratio = 0.2 | Ratio = 0.5 | ||
|---|---|---|---|---|
| Min | Max | Min | Max | |
| FedAVG | 34.3 | 41.6 | 30.9 | 33.8 |
| Fedprox | 36.5 | 42.7 | 31.7 | 35.6 |
| FedPNS | 68.3 | 68.5 | 60.1 | 60.2 |
| Ours | 72.7 | 72.8 | 71.4 | 71.6 |
| Method | Ratio = 0.2 | Ratio = 0.5 | ||
|---|---|---|---|---|
| Min | Max | Min | Max | |
| FedAVG | 43.1 | 44.7 | 40.2 | 41.8 |
| Fedprox | 45.0 | 46.9 | 43.3 | 44.6 |
| FedPNS | 58.4 | 58.5 | 55.6 | 55.7 |
| Ours | 61.6 | 61.8 | 60.3 | 60.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, F.; Zhao, Y.; Shen, T.; Zeng, K.; Zhang, X.; Zhang, C. FedOPCS: An Optimized Poisoning Countermeasure for Non-IID Federated Learning with Privacy-Preserving Stability. Symmetry 2025, 17, 782. https://doi.org/10.3390/sym17050782
Bai F, Zhao Y, Shen T, Zeng K, Zhang X, Zhang C. FedOPCS: An Optimized Poisoning Countermeasure for Non-IID Federated Learning with Privacy-Preserving Stability. Symmetry. 2025; 17(5):782. https://doi.org/10.3390/sym17050782
Chicago/Turabian StyleBai, Fenhua, Yinqi Zhao, Tao Shen, Kai Zeng, Xiaohui Zhang, and Chi Zhang. 2025. "FedOPCS: An Optimized Poisoning Countermeasure for Non-IID Federated Learning with Privacy-Preserving Stability" Symmetry 17, no. 5: 782. https://doi.org/10.3390/sym17050782
APA StyleBai, F., Zhao, Y., Shen, T., Zeng, K., Zhang, X., & Zhang, C. (2025). FedOPCS: An Optimized Poisoning Countermeasure for Non-IID Federated Learning with Privacy-Preserving Stability. Symmetry, 17(5), 782. https://doi.org/10.3390/sym17050782






