Abstract
The Dynamic response of two cavities, an elliptical inclusion and a linear crack near anisotropic bi-material interface, was explored analytically by incident out-plane waves in the current work. Firstly, the media is divided into two half spaces (an elastic anisotropic half space with a circular cavity and a linear crack, and an elastic isotropic half space containing an elliptical cavity and an elliptical inclusion). With the help of the image principle, the complex function method is then used to derive the wave fields in each half space. Combined with Green’s functions approach, the relevant Green’s functions developed in the “crack creation” and “conjunction of two half spaces” procedures are derived sequentially. Subsequently, based on the “conjunction” technique, undetermined anti-plane forces are applied to the horizontal surfaces of two half spaces to maintain the continuity criteria of the interface. A series of Fredholm integral equations isobtained and then solved by utilizing the direct discrete technique. Dynamic stress concentration of two elliptical cavities and an elliptical inclusion is mainly considered graphically to discuss the interaction between two half spaces. Finally, a parametric study on the dynamic stress concentration factor (DSCF) was given to show the influence of different parameters on the interaction.
1. Introduction
The investigation of wave propagation in complex media and wave scattering by complex structures constitutes a classical and fundamental problem in elastodynamics. Since practical engineering materials, whether natural or artificial, frequently exhibit defects such as cracks, cavities or inclusions in stratified structures, the phenomenon of elastic wave scattering caused by such defects within a continuous medium has broad applications across multiple engineering fields, including non-destructive testing (NDT), material science, mechanical engineering, geophysics, earthquake engineering, and others.
Firstly, we will provide an overview of recent studies addressing the issue of wave scattering induced by the intricate combination of structures and crack faults in an isotropic medium. Liu et al. [1] were the first to apply the complex variable technique to analyze the static stress concentration phenomenon around a cavity in an elastic space with high accuracy. Subsequently, Liu et al. expanded this approach mathematically to explore the dynamic response of cavities interacted by bi-material interface [2]. Building upon this computational framework, numerous studies into SH-wave scattering problems have been documented [3,4,5,6,7,8,9,10,11,12,13]. Sheikhhassani et al. [14] also examined the dynamic response of multiple multilayered inclusions subjected to SH waves combined with hypersingular integrals. Using linear elastic fracture mechanics theory, the dynamic behavior of multiple interfacial cracks in bonded dissimilar nonhomogeneous half-planes was successfully assessed [15]. Additionally, we reviewed the interaction between an elastic cylindrical inclusion and a crack in a half space [16], and the dynamic response of complex defects interacted by a bi-material interface [17]. To address this general issue, several numerical techniques have been employed, including elastodynamic reciprocity theorem [18], the traction boundary integral equation method [19], multiple expansion method [20], direct boundary element method [21,22], direct boundary integral equation method [23], isogeometric boundary element method [24], and singular integral equation method [25].
The analytical and numerical solutions derived from the aforementioned studies primarily emphasize the isotropic medium model, which holds substantial importance in modern acoustics, petroleum geophysics, explosive mechanics, and material mechanical property investigations. However, in earthquake engineering, geotechnical characteristics are often represented with models of an anisotropic medium. An anisotropic medium involves numerous independent constants, leading to highly complex scattering fields when elastic waves propagate through structures with defects or complex geometries. As a result, only a limited number of studies [26,27,28,29,30,31,32,33,34,35,36,37,38] have explored this area. Among these, the complex variables computational methodology was widely adopted. For instance, Liu and Chen et al. [26,27,28,29] applied this approach to analyze the dynamic stress concentration of cavities and the ground motion of semi-cylindrical alluvial valleys scattered by SH-wave incidence. Combined with Green’s function approach, Xu et al. further developed it to report the dynamic response of a circular cavity and crack in anisotropic elastic halfspace [30] and two cavities and a linear crack located within bonded isotropic and anisotropic half spaces [31]. Regarding crack dynamics in anisotropic media under elastic wave excitation, exact solutions were obtained using Fourier and Hubert transforms, stiffness matrix formulations, and nonlocal theory [32,33,34,35,36]. Based on a model of two semi-infinite anisotropic magnetoelastic media, Kumar et al. [37] also established precise solutions for SH-wave reflection and transmission. Additionally, the dispersion of longitudinal and transverse elastic waves in composites was investigated by modeling an anisotropic matrix with anisotropic interface layers, where the final composite consisted of an isotropic matrix containing spherical inclusions [38].
The interfaces between water and rocks, oil and rocks, or sand and rocks on the seabed can be modeled as an analytical model of anisotropic bi-material interfaces containing flaws. Presently, there is limited research on wave scattering caused by defects in bonded isotropic and anisotropic halfspaces, particularly regarding the complex analytical modeling of combined structures (such as cavities and inclusions) and defects (such as several linear or non-linear cracks)(work on DSCFs around the structure and DSIFs at the defect), for theoretical monitoring in engineering contexts. Under incident SH waves, the dynamic response of two cavities, an inclusion and a linear crack, interacted by anisotropic bi-material interface, was analyzed by developing the technique of complex variables and Green’s function in this work. According to the idea of “Conjunction”, anisotropic bi-material space is divided into an elastic anisotropic half space comprising a circular cavity and an elastic half space including an elliptical cavity and an elliptical inclusion. For the anisotropic half space, a sort of transformation is used to convert the complex plane into the plane. Simultaneously, the method of “conformal mapping” in complex variables is applied to map the outland of the elliptical boundary of the cavity and inclusion in the Z-plane to one of the unit circle boundary in -plane for the elastic half space.
2. Analytical Model
Figure 1 gives the analytical model of two cavities and an inclusion and a crack in the vicinity of a bi-material interface under incident SHwaves. As Figure 1 depicts, the medium I is anisotropic while the medium II is isotropic. Hence, the elastic constants of medium I are ρ1, c44, c45, and c55, while in medium II are ρ2 and μ2. In the medium I, the buried depth of the circular cavity and the linear crack are h and h1, respectively, and the distance between the crack and the center of the circular cavity is h2. The included angle between the crack and the horizontal direction is β, and the length of the crack is l = 2A. The origin of coordinates xoy and x1oy1 coincide with the center of the cylindrical cavity, and the axis coincides with the bonded interface of two half spaces. An elliptical cavity and an inclusion are buried in medium II, and the distance between the cavity and the interface of two half spaces is h3. The distance between the elliptical cavity and the inclusion is b. Considering a complicated condition of wave propagation, a pair of symmetrical incident waves and propagate with angle α in two half spaces, respectively.
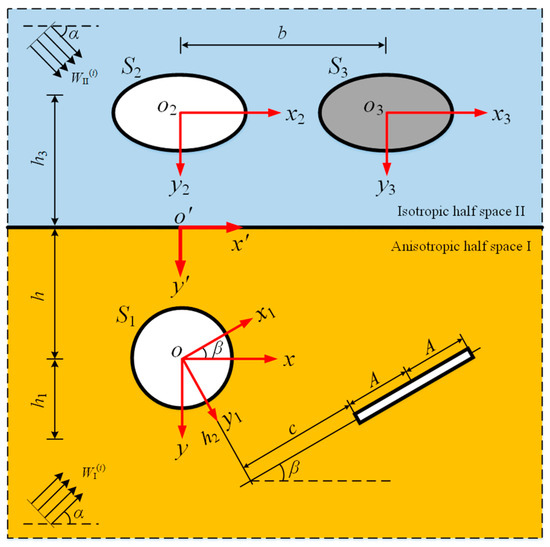
Figure 1.
Scattering model in the bonded half spaces under incident SH wave.
According to the relation of each coordinate, some useful relations can be deduced:
and a supplementary equation can also be obtained:
3. Governing Equation
As stated in ref. [1], assuming a harmonic anti-plane response and neglecting the body force, the equation of motion can be written as follows:
Furthermore, on the strength of the generalized Hooke’s law, the constitutive relations in both isotropic and anisotropic media are written as
where , , and should obey , and .
By inserting Equation (4) or (5) into Equation (3), the governing equations for SH wave propagation can be derived:
Upon solving the governing equations, the wave field expressions in the two halfspaces can be determined. By taking into account the material properties of the bonded halfspaces, Equation (6) is suitable for medium II, while Equation (7) corresponds to medium I. Clearly, compared to Equation (7), Equation (6) is easier to solve. In medium II, according to complex function theory, we introduce a pair of complex variables and and (t is the time), the governing Equation (3) is then converted into
where indicates the wave number in the isotropic medium, the circular frequency, the shear wave velocity in the medium II, and the shear modulus and density of the isotropic half space, respectively.
Equation (8) is a typical Helmholtz equation, so it can be solved analytically. Hence, it is evident that scatter fields in medium II can be derived directly through solving Equation (8). Utilizing the following constitutive relation, the stress components can be deduced:
In order to study the scattering problem related to the elliptical cavity, radial stress and hoop stress in polar coordinates are essential to be given:
Furthermore, to facilitate the investigation of the scattering problem generated by an elliptical cavity and inclusion, the conformal mapping method is employed to transform the elliptical outland to be a unit circle boundary (in Figure 2). Inspired by the complex function method, we introduce the conformal mapping function:
where , .
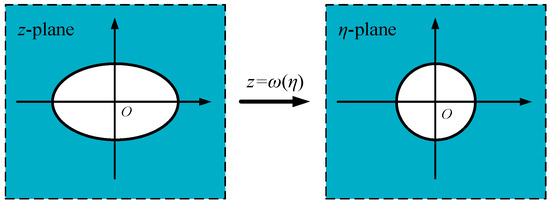
Figure 2.
“Conformal mapping” of ellipse.
Consequently, governing Equation (8) becomes
Equivalently, the conversion of polar angle and the corresponding stresses turn into
and
Upon examining the solution of displacement fields and stress components in medium II, the governing equation applicable to an anisotropic halfspace (medium I) can also be addressed by employing the complex function method. Introducing and in Equation (7), it becomes
Introducing the subsequent transformation expressions
where , .
The governing Equation (15) can be transformed into
as derived theoretically by Liu [26], where , represents the circular frequency, , .
Accordingly, the associated stresses in coordinates are
where
4. The Scattering Waves Around the Cavities and the Inclusion
4.1. The Scattering Wave Around the Circular Cavity in Medium I
The scattering waves and () motivated by the cavities and the inclusion should obey the governing Equation (17) and the radiation condition for infinite distance, except for the stress-free condition on the horizontal interface, take the form of
where ; and (i =1, 2) indicates the unknown coefficients that will be determined using the boundary condition of the cavities and the inclusion; , represents the propagation velocity of the shear wave along ; the th order Hankel function of the first kind.
Inserting the expressions above into Equations (14) and (18), respectively, the relevant stresses can be obtained.
4.2. The Standing Wave in Medium III
In medium III, there exists a standing wave, which can be written as
where is the undetermined coefficient to be solved using the boundary conditions.
5. Green’s Function
Since both the “conjunction” and “crack division” methods will be employed to join two halfspaces at the interface and to form the linear crack within the anisotropic halfspace; it is necessary to construct certain fundamental Green’s functions beforehand.
5.1. Green’s Function G1
As shown in Figure 3, the first Green’s function G1 represents the displacement discipline excited by an out-plane load that impacts the surface of an anisotropic half space only containing a cylindrical cavity. G1 should satisfy Equation (17) and the boundary condition as follows:
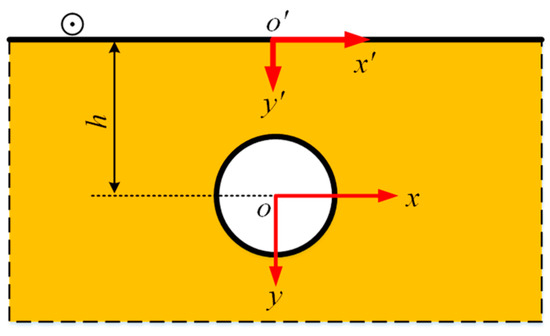
Figure 3.
Illustration of source load at anisotropic half space of G1.
Assume that the out-of-plane source load is applied at a specific point , the source load can be denoted as . In the anisotropically elastic half space, G1 can be regarded as the incident wave, which takes the form of
where represents the 0th order Hankel function of the first kind, while is the image point of in the plane.
The form of the scattering wave motivated by the circular cavity in the half space is identical to Equation (19).
At this point, the total wave fields can be obtained:
Substituting Equation (24) into Equation (18), the related stress fields are deduced and then inserted into the first equation of the boundary condition Equation (22), we have
where
Hence, the unknown coefficients can be figured out by employing the least squares method:
where indicates conjugate variables of .
5.2. Green’s Function G2
Figure 4 plotted is the analytical model for the second Green’s function G2. The boundary condition is identical to Equation (22). In a full elastic halfspace, the incident displacement field motivated by the source load in the half space and the reflected wave generated by the horizontal surface have the form of
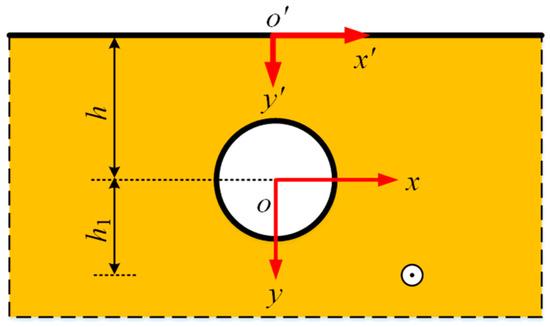
Figure 4.
Illustration of source load in anisotropic half space of G2.
Evidently, the scattering wave motivated by the cavity is also uniform with Equation (19), andafter substitution of Equations (27) and (28) into Equation (18), we can obtain the related stresses: , , , and . Thus far, the entire wave field can be formulated as
5.3. Green’s Function G3
The Green’s function G3 presents the wave field excited by a source load impacting at the surface of the anisotropic half space, as shown in Figure 5. In Section 5.1, we have obtained the wave field without a crack and the corresponding stresses, and . In order to describe the influence of the crack, the “crack division” technique is applied. At the position of the crack, a series of stresses which is equal to the hoop stresses at the same point of the half space but contrary in course is exerted; therefore, the ultimate stress will be zero, and then the linear crack can be created.
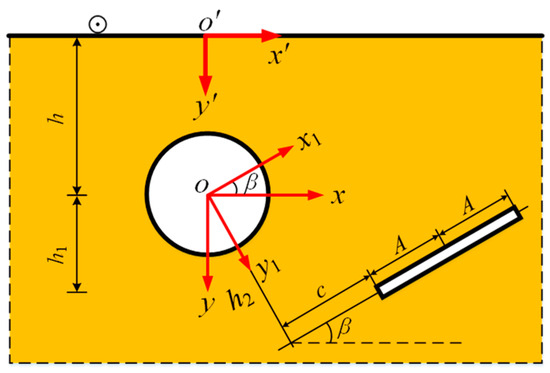
Figure 5.
Illustration of source load at anisotropic half space of G3.
Consequently, utilizing given in Section 5.1, the displacement fields of the created crack stimulated by anti-plane loads can be expressed as
where is the stress fields corresponding to G1.
Finally, the expression of the Green’s function G3 is
5.4. Green’s FunctionG4
The displacement field for an isotropic half space containing an elliptical cavity and an elliptical inclusion (in Figure 6) is defined as the 4th Green’s function G4. Based on the governing Equation (14), the incident wave and the scattering wave take the forms of
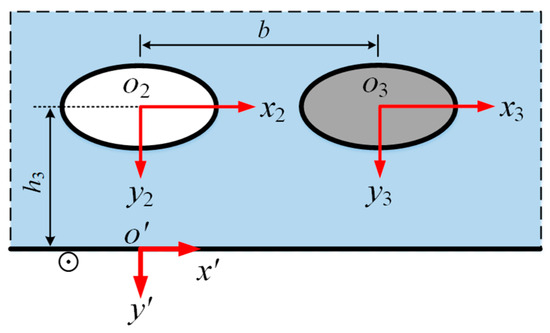
Figure 6.
Illustration of source load at isotropic half space of G4.
Thus, we obtain the form of the Green’s function G4 as
6. Plane SH Wave Incidence in Two Half Spaces
6.1. Wave Fields in Anisotropic Half Space
Considering the anisotropic half space separately, the plane SH wave with incident angle α, and the reflected wave induced by the interface of the anisotropic half space, can be formulated as
herein, W0 indicates the amplitude of the incident wave, the incident wave number. refers to the wave velocity along with the direction of the incident wave, , , and . is the reflected wave number and the reflected wave’s propagation velocity. For , , , and . Meanwhile, the velocity of the reflected wave obeys ; when , , , , and .
The scattering wave in the anisotropic halfspace caused by the cavity takes the same form as Equation (20). By incorporating the wave fields into the constitutive relation given in Equation (14), the stress components within medium I can be derived. Consequently, the wave and stress fields can be expressed as follows:
As discussed in Section 5.3, in the anisotropic half space, the linear crack strongly influences the wave fields. After utilizing the “crack division” technique, the linear crack is created, and the wave field , excited by the antiplane loads, takes the form of
and the entire wave field in the anisotropic half space becomes
Since the radius of the cylindrical cavity is , the boundary condition of the cavity in an anisotropic half space, which determines the unknown coefficient , can be written as
6.2. Wave Fields in Isotropic Half Space
In the isotropic halfspace (medium II), independently, the SH wave is assumed to have symmetric incidence relative to the wave in medium I. The reflected wave is motivated by the interface of the isotropic medium. By taking into account the governing Equation (8), the incident wave, reflected wave, and scattering wave can be represented as follows:
The associated stresses of the above wave fields can also be derived by using Equation (14). Consequently, the total wave and stress fields are
Considering the long and short half axes are a and b, respectively, the boundary condition at the elliptical cavity and inclusion in the isotropic half space can be formulated by applying the conformal mapping method:
Hence, the undetermined coefficients (i = 1, 2) and can be solved.
7. Definite Integral Equations
Given that the wave and stress fields in the two halfspaces are examined separately in Section 4, the “conjunction” technique must be employed to unify the two halfspaces. Nonetheless, according to the derivations obtained for the two halfspaces, the wave fields and stress components at the interface are free.
Based on the “conjunction” technique, a sequence of external forces and are applied at the horizontal surfaces of two half spaces (in Figure 7). Hence, the continuous conditions of displacements and stresses can be maintained at the interface of two half spaces. As a result, the total wave and stress fields at the interface of two bonded half spaces become
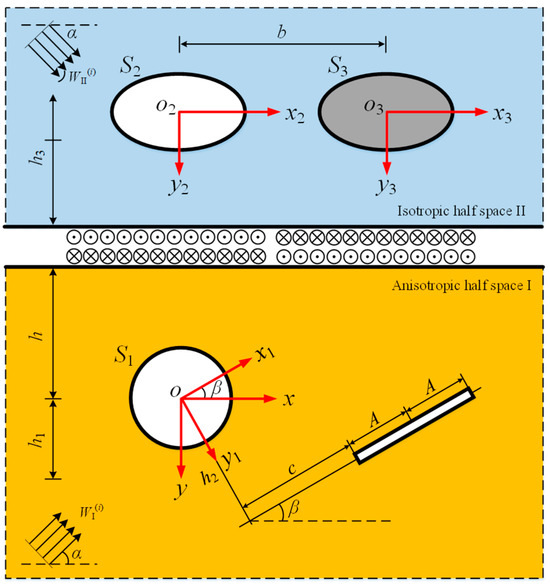
Figure 7.
Illustration of the “conjunction” of two half spaces.
Herein, and have been defined by Equations (31) and (34), respectively.
Then, according to the continuous conditions of displacements and stresses at the interface, we have
Equations (54) and (55) are a group of integral equations, and the equations are a group of Fredholm equations with weak singularity. The external forces F1 and F2 can be solved by linearizing the integral equations. The derivation can be concluded with the following flowchart shown as Figure 8:
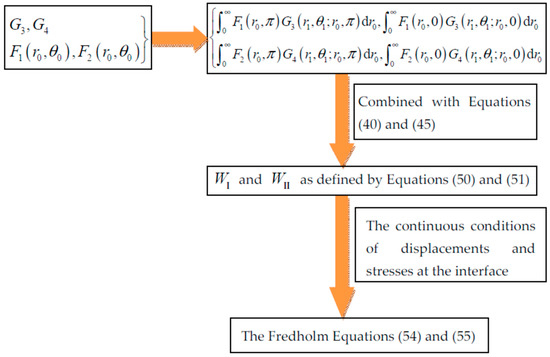
Figure 8.
The flowchart of derivation of Fredholm equations.
8. Dynamic Stress Concentration Factor (DSCF) at the Cavity
The current work primarily focuses on the dynamic stress distribution in two halfspaces, it is necessary to examine the dynamic stress concentration at two cavities and an inclusion scattered by the incident SH wave. To this end, the dynamic stress concentration factor (DSCF) for the cavities and the inclusion is explored to characterize the degree of dynamic stress concentration. Based on the definition of the dynamic stress concentration factor, the expression is given as follows:
where represents the stress around the outer of the cavity and the inclusion, and represents the maximum stress caused by the incident wave. In the anisotropic half space (medium I), . While in medium II, .
9. Numerical Results and Discussion
The dynamic stress concentration factor (DSCF) around the outer of two cavities and an inclusion iscomputed based on theoretical analysis. A substantial number of examples are given to discuss the impact of two dimensionless anisotropic parameters and and dimensionless incident wave number , incidence angle , ratios associated with cavities or inclusion geometry (, , and ), as well as the wave number ratio and the shear modulus ratio between matrix and inclusion, are discussed. Equation (57) provides the expression of . Three cases of contrast ratio between matrix and inclusion properties are considered: = 0.25 and stand for relatively rigid inclusion compared to the matrix; = 4.0 and representcomparatively soft inclusion; = 16.0 and signify softer inclusion. The distribution curves of the dynamic stress concentration factor around the cavities and the inclusion under SH wave incidence are illustrated in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28 with varying parameters.
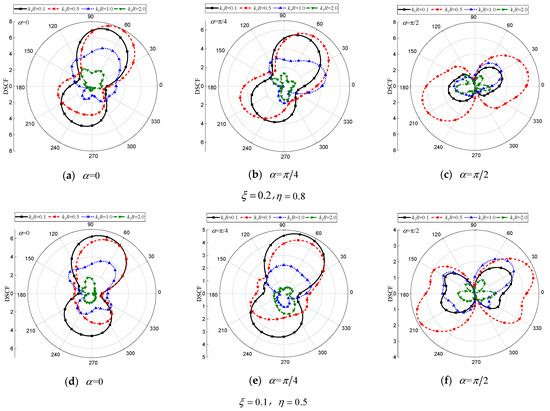
Figure 9.
DSCF of the circular cavity with different . (, , , , , , , , , , , , , , , 0.5).
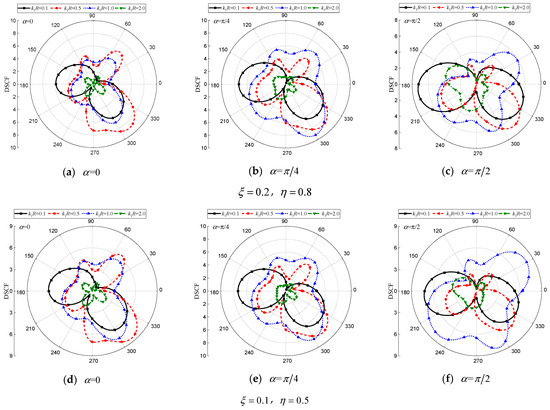
Figure 10.
DSCF of the elliptical cavity with different . (, , , , , , , , , , , , , , , 0.5).
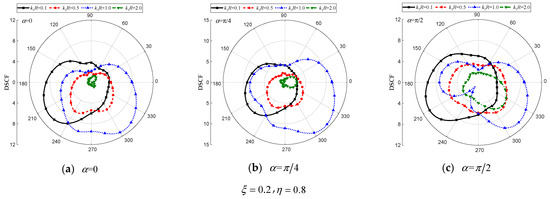
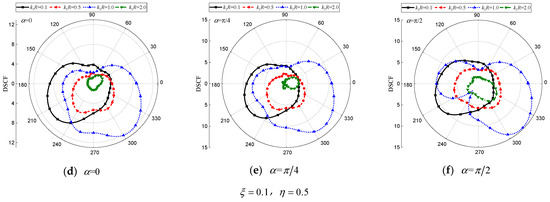
Figure 11.
DSCF of the elliptical inclusion with different . (, , , , , , , , , , , , , , , 0.5).
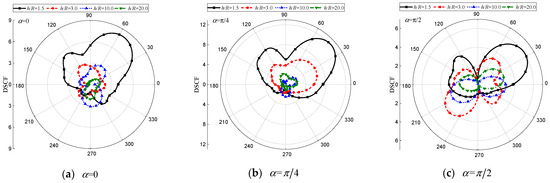
Figure 12.
DSCF of the circular cavity with different . (, , , , , , , , , , , , , , , , , 0.5).
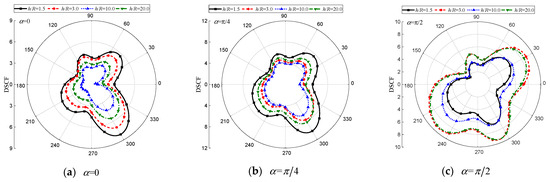
Figure 13.
DSCF of the elliptical cavity with different . (, , , , , , , , , , , , , , , , , 0.5).
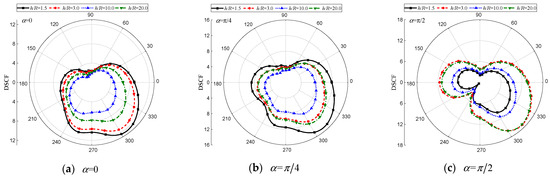
Figure 14.
DSCF of the elliptical inclusion with different . (, , , , , , , , , , , , , , , , , 0.5).
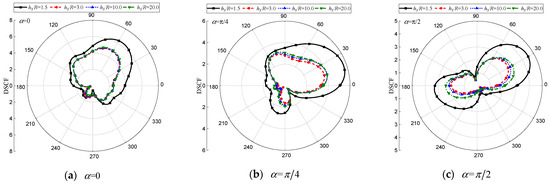
Figure 15.
DSCF of the circular cavity with different . (, , , , , , , , , , , , , , , , , 0.5).
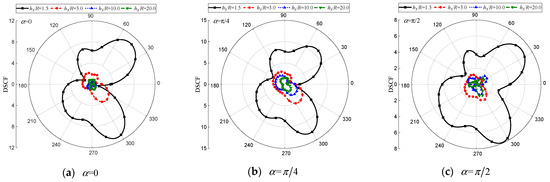
Figure 16.
DSCF of the elliptical cavity with different . (, , , , , , , , , , , , , , , , , 0.5).
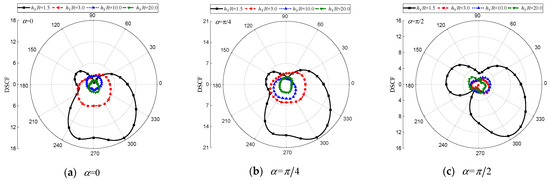
Figure 17.
DSCF of the elliptical inclusion with different . (, , , , , , , , , , , , , , , , , 0.5).
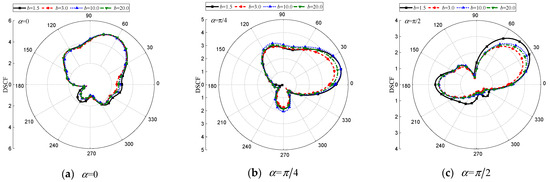
Figure 18.
DSCF of the circular cavity with different . (, , , , , , , , , , , , , , , , , 0.5).
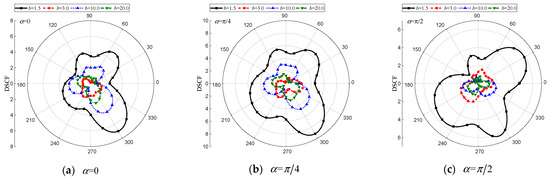
Figure 19.
DSCF of the elliptical cavity with different . (, , , , , , , , , , , , , , , , , 0.5).
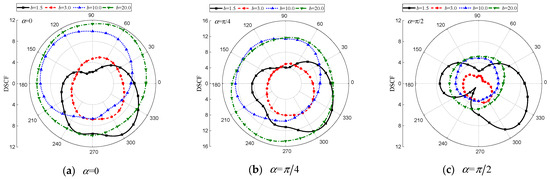
Figure 20.
DSCF of the elliptical inclusion with different . (, , , , , , , , , , , , , , , , , 0.5).
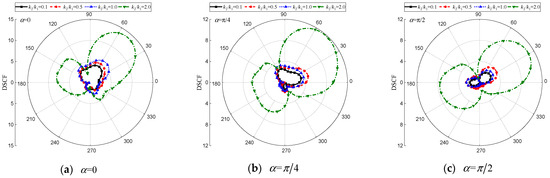
Figure 21.
DSCF of the circular cavity with different . (, , , , , , , , , , , , , , , , , 0.5).
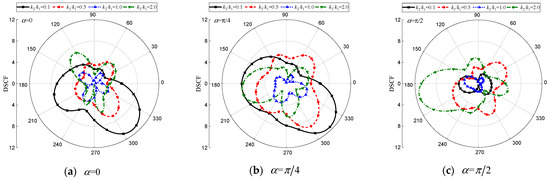
Figure 22.
DSCF of the elliptical cavity with different . (, , , , , , , , , , , , , , , , , 0.5).
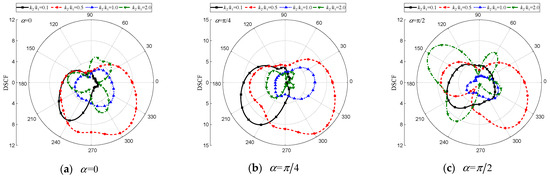
Figure 23.
DSCF of the elliptical inclusion with different . (, , , , , , , , , , , , , , , , , 0.5).
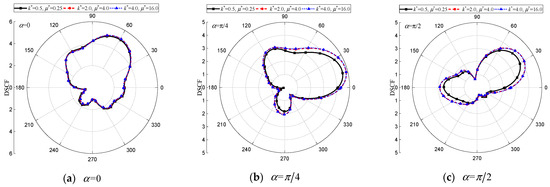
Figure 24.
DSCF of the circular cavity with and . (, , , , , , , , , , , , , , , , 0.5).
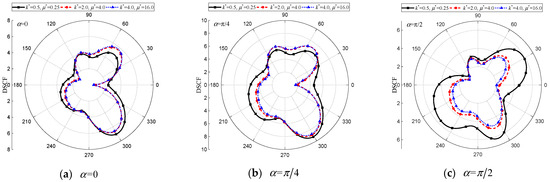
Figure 25.
DSCF of the elliptical cavity with and . (, , , , , , , , , , , , , , , , 0.5).
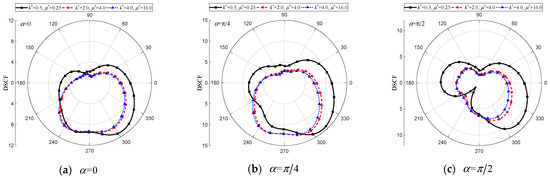
Figure 26.
DSCF of the elliptical inclusion with and . (, , , , , , , , , , , , , , , , 0.5).
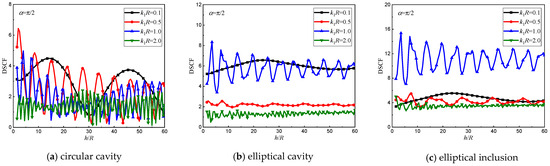
Figure 27.
DSCF at with different . (, , , , , , , , , , , , , , , , , 0.5).
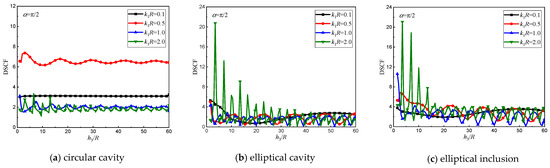
Figure 28.
DSCF at with different . (, , , , , , , , , , , , , , , , , 0.5).
Figure 9, Figure 10 and Figure 11 illustrate that the oscillation characteristics of the distribution curve become more pronounced as the incident wave number . increases. When SH waves incident horizontally or obliquely, a higher intensity of dynamic stress concentration occurs near the interface. This can be attributed to the generation of a more complex scattered wave field between the circular hole and the interface when the circular hole is shallowly buried. Moreover, in an orthogonal anisotropic medium, the propagation of incident waves exhibits directional disparities. Under vertical incidence, there is a deflection in the distribution curve around the circular cavity due to the coupling of medium characteristics of the orthogonal anisotropic medium in the and -axis for , as shown in Figure 9c,f. For the circular hole with = 0.5 and for the inclusion with = 1.0, the values of are larger compared to the other three cases.
Figure 11 shows the values of around the inclusion are significantly higher than those around the circular and elliptical cavities. Upon comparing Figure 11e,f, it can be concluded that under and , the value is considerably larger compared to the case of and for vertical incidence and = 1.0. The maximum value for the two cases can reach 10.81 and 14.74, respectively.
Figure 12, Figure 13 and Figure 14 reveal the strong influence of the buried depth of the circular cavity on around the cavities and the inclusion. It can be observed that a shallower buried depth results in a more severe dynamic stress concentration near the interface, indicating that a closer distance between the circular cavity and the interface leads to a more complex scattered wave field. Additionally, variations in incidence angle also have a substantial impact on the distribution of . As depicted in Figure 12a,b, Figure 13a,b, and Figure 14a,b, greater values are observed with shallower buried depths under and . Conversely, larger values are obtained with greater buried depths under vertical incidence (see Figure 12c, Figure 13c, and Figure 14c).
Figure 15, Figure 16 and Figure 17 show that variations in (representing the distance between the elliptical cavity and inclusion and the interface) have a significant influence on around the cavities and the inclusion. Specifically, for = 1.5, the value of is notably higher compared to the other three cases. Moreover, the change curves of are proximate for = 3.0, 10.0, and 20.0, considering the circular cavity, but for =10.0 and 20.0, considering the elliptical hole and the inclusion. Besides, the values of are generally larger due to increased complexity in scattered wave field interactions between the complex structure (elliptical cavity and elliptical inclusion) and the interface, leading to more pronounced dynamic responses. Figure 16b exemplifies this conclusion where max reaches 20.3 at = 1.5.
The impact of the distance between the elliptical hole and the inclusion on around the cavities and the inclusion is discussed in Figure 18, Figure 19 and Figure 20. As illustrated in Figure 18, it can be observed that has little influenceon around the circular hole but relatively a lot for the elliptical hole and inclusion.
The dynamic stress concentration around the elliptical hole is significantly more severe and exhibits larger values when = 1.5, as illustrated in Figure 19. Conversely, for the cases of = 3.0, 10.0, and 20.0, similar levels of dynamic stress concentration are observed with a weaker impact on the vicinity of the elliptical hole. Furthermore, Figure 20 shows that the relationship between the increasing incidence angle and dynamic stress concentration around an elliptical inclusion is complex. When = 10.0 and 20.0, the magnitude of around the elliptic inclusion tends to be greater for horizontal and oblique incidence of SH waves, while it decreases for vertical incidence of SH waves. However, when = 1.5, the value of shows a significant increase, with a maximum value reaching up to 10.81.
Similar to the model without inclusion [31], the variation in medium wave-number ratio significantly impacts the distribution of around the cavities and inclusion, as illustrated in Figure 21. In anisotropic media, when comparing = 2.0 with the other three cases, a considerably higher value of around the circular hole is observed under SH wave horizontal incidence ( = 13.93 at ). Conversely, for the remaining three cases, exhibits similar distribution curves but lower values and the respective maximum values are 5.99 ( = 1.0), 5.05 ( = 0.5), and 4.30 ( = 0.1), as shown in Figure 21a.
Comparison of Figure 22 and Figure 23 with Figure 21 shows that the influence of on dynamic stress concentration for the elliptical cavity and the elliptical inclusion differs significantly from that of the circular cavity. As shown in Figure 22a,b for , when the SH wave is incident either horizontally or obliquely, significant dynamic stress concentration occurs around the elliptical cavity. In contrast, this dynamic stress concentration diminishes with vertical incidence. At , a significant dynamic stress concentration occurs at the left part of the ellipse hole with a maximum value of 11.38. Analysis of Figure 23 reveals a more pronounced dynamic stress concentration around for the elliptical inclusion compared to the other three cases when , with larger values obtained as well. Furthermore, different incidence angles of SH waves also exert substantial influence on the curve depicting the dynamic stress concentration coefficient against .
It can be observed in Figure 24, Figure 25 and Figure 26 that the change in matrix–inclusion ratio ( and ) has minimal impact on around the circular cavity (refer to Figure 24), but significantly influences the distribution of around the elliptical cavity and inclusion, particularly under vertically incidence (as shown in Figure 25 and Figure 26). When and , indicating a harder inclusion compared to the matrix, a more severe dynamic stress concentration occurs around the elliptical cavity and inclusion. Conversely, when the inclusion and matrix are relatively soft or softer, values become much smaller with similar distribution curves. Considering for Figure 25c, max = 6.26, 5.09, and 4.80 for three different matrix–inclusion ratios. For Figure 26c, approximate values of max = 10.81, 7.97, and 7.38, at .
The distribution curves of of two cavities and an inclusion at with varying buried depth of the circular cavity are illustrated in Figure 27 under vertical incidence of the SH wave. Upon analysis of these graphs, it is evident that as the incident wave number increases, the curve representing against exhibits more pronounced oscillation characteristics and gradually decays into periodic changes. By comparison of Figure 27a with Figure 27b,c, it can be concluded that, for circular cavity, exerts a greater influence on the dynamic stress concentration around it than the cases for the elliptical cavity and elliptical inclusion. Besides, as continues to increase, its value initially rises sharply and then decreases again. Ultimately, the distribution curve tends to exhibit periodic changes with diminishing amplitude. For elliptical inclusion, when , its corresponding value is significantly larger than the other three cases (as depicted in Figure 27c).
The influence of at on the distance from the elliptic cavity and inclusion to the interface is illustrated in Figure 28. It can be observed intuitively from Figure 28a that at has minimal impact on its variation with respect to , particularly when , namely, quasi-static, where remains almost unchanged. As depicted in Figure 28b,c, variations in significantly affect of both the elliptical cavity and inclusion at . With an increase in , the change curve of initially exhibits sharp periodic increments, followed by decay until it eventually reaches a stable periodic pattern. Moreover, higher incident wave numbers result in more intense distribution curves. For values of 0.1, 0.5, and 1.0, respectively, vibration amplitudes are approximately equal around 2.60 for the elliptical cavity and about 3.80 for the elliptical inclusion.
Finally, by comparing the numerical results obtained in this study to the model without the elliptical inclusion as reported in ref. [31], it is demonstrated that the presence of the elliptical inclusion exerts a relatively minor influence on the distribution of around the circular cavity in anisotropic media, but the values are much lower. In contrast, the elliptical inclusion significantly impacts the distribution rules of around the elliptical cavity in isotropic media with different parameters, which markedly differ from those observed in ref. [31]. It is most likely due to the fact that, in the same medium, the scattered wave field by the elliptical cavity and the inclusion interactsmore intensely with the interface, and consequently, dynamic stress concentrates more severely.
10. Discussion and Conclusions
The mechanical models for analyzing the behavior of two cavities, an inclusion and a linear crack near an orthogonal anisotropic bi-material interface, are established, followed by a comprehensive numerical investigation. Various parameters influencing the dynamic stress concentration around the cavities and inclusion are thoroughly examined. Consequently, the following conclusions can be drawn:
- With the rise in frequency of incident waves, the scattering field surrounding the cavities becomes more noticeable. When SH waves propagate through anisotropic media at horizontal or diagonal angles, they display distinct propagation characteristics and unique instructions. Moreover, the scattering field produced by the interaction between the complex structure (two cavities and an inclusion) and the bi-material interface is highly complex, especially when the complex structure is shallowly buried. Thus, dynamic stress concentration around the complex structure will be more pronounced when the cavities are located near the interface. Additionally, the distance between the elliptical cavity and the elliptical inclusion , wave-number ratio and shear modulus ratio of isotropic medium to inclusion influence slightly on DSCFs around the circular cavity within anisotropic medium, but a lot on dynamic response of the elliptical cavity and inclusion while exhibiting distinct variations with changing incidence angles of SH waves. Besides, the research presented in this article also demonstrates that wave-number ratio and shear modulus ratio between two halfspaces also significantly affect dynamic stress concentration around the cavities and inclusion, which should be focused on consideration in engineering design involving interface problems.
- The research conducted in this project has yielded valuable mechanical principles that can serve as a valuable reference for engineering practice. These principles have wide-ranging applications in fields such as mining engineering, seismic engineering, earth exploration, oil and gas exploration and development of underground structures, environmental engineering exploration, and quantitative non-destructive testing. The theoretical guidance provided in the presented paper is essential for investigating engineering problems involving formations with inclusions, holes, or cracks. By expanding the scope of this project’s research, we can further explore models of anisotropic bimaterials and multilayer media that incorporate irregular holes and inclusions as well as multiple defects incident by SHwave, Pwave, or SVwave. This endeavor is expected to generate additional significant research literature with immense practical value.
Author Contributions
Conceptualization, H.X.; methodology, H.X. and F.Q.; software, H.X. and C.Y.; validation, Y.W. and G.L.; formal analysis, H.X. and F.Q.; investigation, G.L.; resources, C.Y.; data curation, C.Y.; writing—original draft preparation, H.X. and G.L.; writing—review and editing, H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the NATURAL SCIENCE FUNDOF FUJIAN PROVINCE, grant number 2023J01958, and the NATIONAL SCIENCE FOUNDATION OF CHINA, grant number 12002143.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
Author Faqiang Qiu was employed by Jian Yan Test Group Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interes.
References
- Liu, D.K.; Gai, B.Z.; Tao, G.Y. Applications of the method of complex variables to dynamic stress concentrations. Wave Motion 1982, 4, 293–304. [Google Scholar] [CrossRef]
- Liu, D.K.; Lin, H. Scattering of SH-waves by circular cavities near biomaterial interface. Acta Mech. Solida Sin. 2003, 24, 197–204. [Google Scholar]
- Chen, T.Y.; Wang, H. Dynamic analysis of upright incident of SH-waves at semi-cylindrical interface with a circular lining structure. J. Tianjin Univ. 2006, 39, 1305–1309. [Google Scholar]
- Wang, G.Q.; Liu, D.K. Scattering of SH-wave by multiple circular cavities in half space. Earthq. Eng. Eng. Vib. 2002, 1, 36–44. [Google Scholar] [CrossRef]
- Xu, P.; Tie, Y.; Xia, T.D. Scattering of plane SH Waves by two separated circular tunnel linings. Northwest Seism. J. 2008, 30, 145–149. [Google Scholar]
- Wang, Y.S.; Qiu, Z.Y.; Yu, G.L. Scattering of SH waves from a partially debonded rigid elliptic cylinder. Soil. Dyn. Earthq. Eng. 2001, 21, 139–149. [Google Scholar] [CrossRef]
- Qi, H.; Yang, J. Dynamic analysis for circular inclusions of arbitrary positions near interfacial crack impacted by SH-wave in half-space. Eur. J. Mech. A Solids 2012, 36, 18–24. [Google Scholar] [CrossRef]
- Lu, J.F.; Wang, Y.S.; Cai, L. Scattering of SH wave by a crack terminating at the interface of bi-material. Chin. J. Theor. Appl. Mech. 2003, 35, 432–436. [Google Scholar]
- Yang, J.; Qi, H. Analysis of dynamic stress intensity factors for interfacial crack near shallow circular inclusion in bi-material half-space to SH wave. Acta Mech. 2016, 227, 3703–3714. [Google Scholar] [CrossRef]
- Bian, J.L.; Yang, Z.L.; Jiang, G.X.X.; Yang, Y.; Sun, M. Analytical solution to the SH wave scattering problem caused by a circular cavity in a half space with inhomogeneous modulus. Meccanica 2021, 56, 705–709. [Google Scholar] [CrossRef]
- Li, M.H.; Yang, Z.L.; Bian, J.L.; Yang, Y. Theoretical modeling and dynamic analysis of designable grillages for repairing material surface defect. Mech. Adv. Mater. Struct. 2024, 31, 12504–12511. [Google Scholar] [CrossRef]
- Yang, J.; Liu, S.; Yang, B.; Liu, Y. Scattering of SH waves in a bi-material half space with a circular hole and periodic type III interfacial cracks. Mech. Adv. Mater. Struct. 2023, 30, 2863–2871. [Google Scholar] [CrossRef]
- An, N.; Song, T.S.; Hou, G. Dynamic interaction between complex defect and crack in functionally graded magnetic-electro-elastic bi-materials. Mech. Adv. Mater. Struct. 2022, 30, 2748–2764. [Google Scholar] [CrossRef]
- Sheikhhassani, R.; Dravinski, M. Dynamic stress concentration for multiple multilayered inclusions embedded in an elastic half-space subjected to SH-waves. Wave Motion 2016, 62, 20–40. [Google Scholar] [CrossRef]
- Bagheri, R.; Monfared, M.M. In-plane transient analysis of two dissimilar nonhomogeneous half-planes containing several interface cracks. Acta Mech. 2020, 231, 3779–3797. [Google Scholar] [CrossRef]
- Yang, Z.L.; Yan, P.L.; Liu, D.K. Scattering of SH-waves and ground motion by an elastic cylindrical inclusion and a crack in half space. Chin. J. Theor. Appl. Mech. 2009, 41, 229–235. [Google Scholar]
- Xu, H.N.; Yang, Z.L.; Wang, S.S. Dynamics Response of Complex Defects near Bimaterials Interface by Incident Out-plane Waves. Acta Mech. 2016, 227, 1251–1264. [Google Scholar] [CrossRef]
- Wang, C.Y.; Balogunc, O.; Achenbach, J.D. Application of the reciprocity theorem to scattering of surface waves by an inclined subsurface crack. Int. J. Solids Struct. 2020, 207, 82–88. [Google Scholar] [CrossRef]
- Sung, J.C.; Wong, D.C. Effect of an inclusion on the interaction of elastic waves with a crack. Eng. Fract. Mech. 1995, 51, 679–695. [Google Scholar] [CrossRef]
- Ghafarollahi, A.; Shodja, H.M. Scattering of SH-waves by an elliptic cavity/crack beneath the interface between functionally graded and homogeneous half-spaces via multipole expansion method. J. Sound Vib. 2018, 435, 372–389. [Google Scholar] [CrossRef]
- Dravinski, M.; Sheikhhassani, R. Scattering of a plane harmonic SH wave by a rough multilayered inclusion of arbitrary shape. Wave Motion 2013, 50, 836–851. [Google Scholar] [CrossRef]
- Sonia, P.; Petia, D.; George, D.M. Elastic wave fields in a half-plane with free-surface relief, tunnels and multiple buried inclusions. Acta Mech. 2014, 225, 1843–1865. [Google Scholar] [CrossRef]
- Yu, C.W.; Dravinski, M. Scattering of plane harmonic P, SV and Rayleigh waves by a completely embedded corrugated elastic inclusion. Wave Motion 2010, 47, 156–167. [Google Scholar] [CrossRef]
- Andrade, H.C.; Trevelyan, J.; Leonel, E.D. Direct evaluation of stress intensity factors and T-stress for biomaterial interface cracks using the extended isogeometric boundary element method. Theor. Appl. Fract. Mech. 2023, 127, 104091. [Google Scholar] [CrossRef]
- Wei, P.J.; Zhang, Z.M. Scattering of inhomogeneous wave by viscoelastic interface crack. Acta Mech. 2002, 158, 215–225. [Google Scholar] [CrossRef]
- Liu, D.K.; Han, F. Scattering of plane SH wave by noncircular cavity in anisotropic media. J. Appl. Mech. Trans. ASME 1993, 60, 769–772. [Google Scholar] [CrossRef]
- Liu, D.K. Dynamic stress concentration around a circular cavity by SH wave in an anisotropic media. Acta Mech. Sin. 1988, 20, 443–452. [Google Scholar]
- Chen, Z.G. Dynamic stress concentration around shallow cylindrical cavity by SH wave in anisotropically elastic half-space. Roc. Soi Mech. 2012, 33, 899–905. [Google Scholar] [CrossRef]
- Chen, Z.G. Scattering of an orthotropic semi-cylindrical alluvial valley by SH waves. Earthq. Eng. Eng. Vib. 2016, 1, 68–74. [Google Scholar]
- Xu, H.N.; Zhang, J.W.; Yang, Z.L.; Lan, G.G.; Huang, Q.Y. Dynamic response of circular cavity and crack in anisotropic elastic half-space by out-plane waves. Mech. Res. Commun. 2018, 91, 100–106. [Google Scholar] [CrossRef]
- Lan, G.G.; Jiang, G.X.X.; Xu, H.N.; Qiu, F.Q.; Yang, Z.L. Analytical analysis of the interaction between cavities and a crack in bonded isotropic and anisotropic half spaces under SH wave. Mech. Adv. Mater. Struct. 2025, 32, 1518–1533. [Google Scholar] [CrossRef]
- Eslami, H.; Gatmiria, B. Two formulations for dynamic response of a cylindrical cavity in crossanisotropic porous media. Int. J. Numer. Anal. Meth. Geomech. 2010, 34, 331–356. [Google Scholar] [CrossRef]
- Sarkar, J.; Mandal, S.C.; Ghosh, M.L. Interaction of elastic waves with two coplanar griffith cracks in an orthotropic medium. Eng. Fract. Mech. 1994, 49, 411–423. [Google Scholar] [CrossRef]
- Shen, S.P.; Kuang, Z.B. Wave scattering from an interface crack in laminated anisotropic media. Mech. Res. Commun. 1998, 25, 509–517. [Google Scholar] [CrossRef]
- Zhou, Z.G.; Wu, L.Z.; Wang, B. The scattering of harmonic elastic anti-plane shear waves by two collinear cracks in anisotropic material plane by using the non-local theory. Meccanica 2006, 41, 591–598. [Google Scholar] [CrossRef]
- Boström, A.; Grahn, T.; Niklasson, A.J. Scattering of elastic waves by a rectangular crack in an anisotropic half-space. Wave Motion 2003, 38, 91–107. [Google Scholar] [CrossRef]
- Kumar, S.; Majhi, S.; Pal, P.C. Reflection and transmission of plane SH-waves in two semi-infinite anisotropic magnetoelastic media. Meccanica 2015, 50, 2431–2440. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Maleki, M. Effect of Interface anisotropy on elastic wave propagation in particulate composites. J. Mech. 2013, 29, 7–26. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).