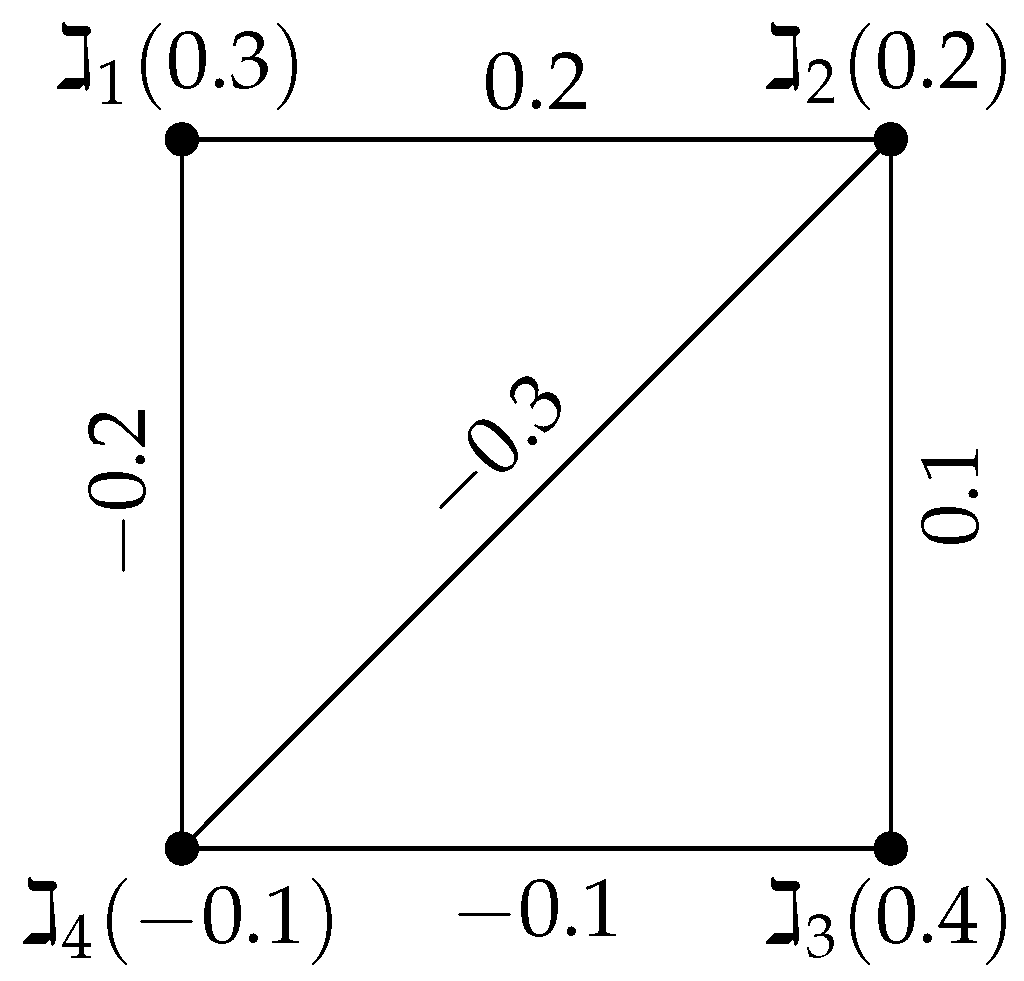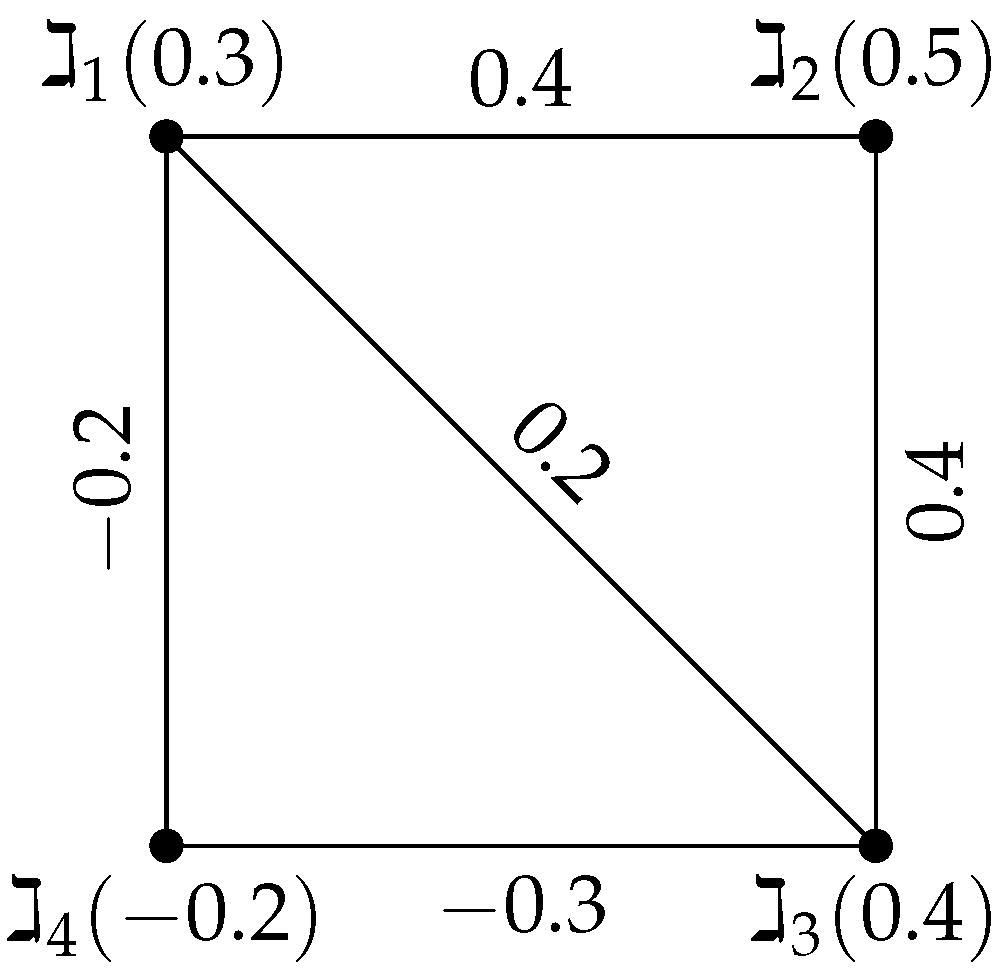Analyzing Network Stability via Symmetric Structures and Domination Integrity in Signed Fuzzy Graphs

Abstract

The concept of domination is introduced within the context of signed fuzzy graphs (signed-FGs), along with examples, as a novel metric to evaluate graph stability under varying conditions. This metric particularly focuses on dominant sets and integrity measures, providing a well-rounded approach to assessing the structural stability of signed- FGs. The necessity of fulfilling the domination integrity condition in evaluating the performance of signed-FGs is highlighted through a discussion on its formulation and an analysis of its upper and lower bounds. An algorithm for identifying strong arcs and classifying them is presented, along with an algorithm for identifying signed fuzzy trees. Furthermore, the role of symmetry in signed-FGs is explored, revealing that symmetrical structures often correspond to higher domination integrity, thus contributing to the improved stability and predictability of the graphs. The paper also establishes important connections with classical graph varieties, such as complete graphs and their variations, demonstrating that changes in domination integrity increase with certain parameters. Additionally, real-life scenarios where these concepts are applicable serve to complement the theoretical results. The case study findings illustrate the significance of domination integrity in practical contexts by emphasizing various instances where it can be determined and utilized. Such instances include identifying independent dominant sets in path and cycle diagrams, as well as estimating the lower bounds of domination integrity in these structures. The estimation of domination integrity using block graph methods is underscored as crucial for enhancing the efficiency of signed-FG applications.

1. Introduction

It has long been known that graphs are useful tools for relationship modeling because they provide a simple way to depict connections between items. This framework uses vertices to represent things and edges to represent their relationships. While traditional graph models are valuable in many contexts, they typically rely on binary relationships, where edges either exist or do not. However, real-world scenarios often involve uncertainty or ambiguity in defining objects, their relationships, or both. Examples include the strength of friendships in social networks, the reliability of transportation routes, or the accuracy of sensor data in environmental monitoring, all of which can be variable and unpredictable when modeled using binary edges.

Fuzzy graphs provide a more flexible framework by enabling more precise relationship modeling through the assignment of membership values to vertices and edges. Yet, they lack the ability to represent the binary nature of relationships, which can be either positive (supportive) or negative (antagonistic). This limitation is critical in applications where relationships are not only uncertain but also polarized, such as conflict and cooperation analysis, ecosystems, or wireless sensor networks. For example, communication networks may entail trust and interference, ecosystems may involve symbiosis and predation, and social or political connections may involve cooperation and rivalry.

Fuzzy graphs are expanded upon by signed-FGs, which add polarity to their edges. Each edge in a signed-FG is identified by a sign that indicates whether the relationship is positive or negative, as well as a relationship value that indicates the strength of the link. In systems where both uncertainty and the type of interaction are important, signed-FGs can capture small fluctuations thanks to this dual representation. The addition of polarity to interactions in signed-FGs provides a thorough framework for investigation. Moreover, the concept of symmetry plays a critical role in signed-FGs, where symmetrical structures are often associated with more stable and resilient networks, leading to enhanced domination integrity and balanced interaction dynamics. These models operate together to offer a cohesive and reliable method for researching intricate communication systems in a variety of fields, such as wireless communication, social networks, and environmental monitoring.

A graph [1] on a nonempty set ℑ can be regarded as a binary relation. The foundation of fuzzy graphs is the notion of fuzzy relations and fuzzy sets, which Zadeh initially introduced in 1965 [2]. Rosenfeld extended this concept in 1975 [3], establishing the connection between fuzzy sets and graph theory, enabling research on fuzzy trees, blocks, bridges, and cut nodes. In his seminal paper [3], Rosenfeld explored the ideas of blocks, cut nodes, fuzzy trees, and bridges in FGs. Yeh [4] introduced several connection notions in FGs at the same period. Fuzzy analogues of classic graph theory notions, such as automorphisms of FGs [5], cycles and cocycles in FGs [6], fuzzy interval graphs [7,8], fuzzy trees [4,9], and fuzzy line graphs [10], have been developed by several scholars since these fundamental works.

In [4], Yeh defined fuzzy trees compatible with cut-level representations and developed concepts like connectedness and acyclicity degrees for fuzzy trees. By defining boundaries, computing domination numbers for different fuzzy graph sets, and extending the concepts of dominance and absolute domination in fuzzy graphs, Somasundaram [11,12] advanced the topic even further. Furthermore, Somasundaram [13] identified the prevailing parameters of operations on fuzzy graphs, such as union, join, composition, and Cartesian products. Moderson [9] made a contribution by researching FGs with different levels of connectedness.

It has been demonstrated that operational research problems can be successfully addressed by the structural properties of finite fuzzy graphs. The characteristics of cut nodes, bridges, trees, and fuzzy cycles in fuzzy graphs have all been studied. To show how fuzzy graphs are interconnected, Nagoor Gani [14] examined the connections between degree, order, and size. Fuzzy end nodes were first proposed by Bhutani [15], who demonstrated that no node could be both a cut node and a fuzzy end node at the same time. Bhutani also described fuzzy cycles without fuzzy end nodes or cut nodes and investigated the characteristics of fuzzy end nodes in fuzzy trees.

In [16], the notions of strong arcs and strong paths in fuzzy graphs were initially presented. According to the study, a fuzzy bridge is always strong, while a powerful arc is not always a fuzzy bridge. The authors also defined fuzzy trees using strong paths and explained the use of strong arcs in fuzzy trees. Applications of fuzzy optimal cut edges and vertices are discussed in [17]. Matroid perspectives were used to expand the fuzzy graph to Plithogenic fuzzy sets in TOPSIS applications [18] and to analyze single-valued neutrosophic fuzzy graphs in [19].

External stability, external dominance, and their combinations into FGs were among the ideas that Assia Alaoui [20] added to the theory. Likewise, Sameena and Sunitha investigated strong arcs in maximum spanning trees [21] and their use in neural networks [22,23]. Database theory, group structure analysis, and chemical systems and applications are just a few of the many domains where fuzzy graphs have been proven useful [24,25,26].

Saravanan [27] identified vulnerabilities in a 2015 study that concentrated on the integrity features of edges and vertices in fuzzy graphs. Vertex and edge integrity in fuzzy graphs were extensively studied in [28], with examples and mathematical theorems illustrating their importance in assessing network vulnerability and connectedness. A significant advancement in the field was made in [29] by studying dominance integrity in graphs with the goal of placing Phasor Measurement Units in electric power networks as optimally as possible to guarantee system stability and observability. Furthermore, the concept of integrity in fuzzy graphs was clarified and examined in more detail, as well as its mathematical properties and consequences for network vulnerability and stability. The notion of domination integrity in fuzzy graphs was presented in [30,31,32], along with its definitions, features, and real-world applications, in order to evaluate the efficacy and stability of network topologies. The span integrity of fuzzy graphs has been used in brain network investigations in [33], and it has shown potential for improving neural network communication and identifying functional issues. Concepts of signed-FG [34], mathematical modeling are pertinent to the analysis of vulnerability parameters in these graphs and integrity in vertex connectivity within supply chain networks. According to [35], edge integrity, applications in agriculture supply chains, and how they handle decision-making issues are facilitated by incorporating membership values and signs to reflect positive and negative consequences.

1.1. Preliminary Concepts

A simple graph ${\sum }^{\ast }=(\Im ,\xi )$ consists of a nonempty set of nodes ℑ and edges $\xi$. This basic terminology was extended to fuzzy graphs by Rosenfield. A fuzzy graph $\sum =(\eta ,\phi )$ is defined as a pair of functions, where $\eta :\Im \to [0,1]$ and $\phi :\Im \times \Im \to [0,1]$. For all ${\gimel }_1,{\gimel }_2\in \Im$, $\phi ({\gimel }_1,{\gimel }_2)\le \eta \left({\gimel }_1\right)\wedge \eta \left({\gimel }_2\right)$. A subgraph of $\sum =(\eta ,\phi )$ is a fuzzy graph $\eta =(\tau ,\nu )$ if $\nu (\gimel )\ge \tau (\gimel )$ and $\xi ({\gimel }_1,{\gimel }_2)\ge \nu ({\gimel }_1,{\gimel }_2)$ for all ${\gimel }_1,{\gimel }_2\in \Im$, and ∑ has a spanning subgraph $\Gamma$ if both fuzzy graphs have the same nodes. A sequence of distinct nodes ${\gimel }_0,{\gimel }_1,\cdots ,{\gimel }_n$ such that $\phi ({\gimel }_i,{\gimel }_{i+1})>0$ for all i constitutes a path ${\gimel }_n$ in ∑ of length n. The minimum membership value of the edges in a path determines its strength. $\Gamma$ is a connected fuzzy graph if there exists at least one path between every two vertices of the fuzzy graph. The maximum strengths of all paths define the connectedness of the two nodes ${\gimel }_1$ and ${\gimel }_2$, indicated by $CON{N}_{\sum }({\gimel }_1,{\gimel }_2)$. In a fuzzy graph, if $\phi ({\gimel }_1,{\gimel }_2)=\eta \left({\gimel }_1\right)\wedge \eta \left({\gimel }_2\right)$ for all $({\gimel }_1,{\gimel }_2)\in \xi$, then it is a strong fuzzy graph. In a complete fuzzy graph, $\forall {\gimel }_1,{\gimel }_2\in \Im$, $\phi ({\gimel }_1,{\gimel }_2)=\eta \left({\gimel }_1\right)\wedge \eta \left({\gimel }_2\right)$. The order and size of a fuzzy graph are ${\displaystyle \sum _{{\gimel }_1\in \Im }\eta \left({\gimel }_1\right)}$ and ${\displaystyle \sum _{({\gimel }_1,{\gimel }_2)\in \xi }\phi ({\gimel }_1,{\gimel }_2)}$, respectively. The complement of a fuzzy graph $\sum =(\eta ,\phi )$ is ${\displaystyle \overline{\sum }}=(\overline{\eta },\overline{\phi })$, where $\overline{\eta }=\eta$ and $\overline{\phi }({\gimel }_1,{\gimel }_2)=\eta \left({\gimel }_1\right)\wedge \eta \left({\gimel }_2\right)-\phi ({\gimel }_1,{\gimel }_2)$ for all ${\gimel }_1,{\gimel }_2\in \Im$.

Definition 1

([34]). The definition of vertex integrity in signed-FG is $I_{\pm }\left({\sum }_{\pm }\right)=min\left\{\right|S|+m({\sum }_{\pm }-S)\}$, where ${\displaystyle \left|S\right|=\sum _{S\subseteq \Im }\eta (\gimel )}$ and the largest ${\sum }_{\pm }-S$ component’s order is ${\displaystyle m\left({\sum }_{\pm }-S\right)=\sum _{\gimel \in \left({\sum }_{\pm }-S\right)}\eta (\gimel )}$.

Definition 2

([34]). The definition of edge integrity in signed-FG is ${\displaystyle I_{\pm }^{\prime }\left({\sum }_{\pm }\right)=\underset{S\subset \xi }{min}\left\{\right|S|+m\left({\Sigma }_{\pm }-S\right)\}}$, where ${\displaystyle \left|S\right|=\sum _{e\in \xi }\phi \left(e\right)}$ and the largest ${\sum }_{\pm }-S$ component’s order is ${\displaystyle m\left({\sum }_{\pm }-S\right)=\sum _{\gimel \in \left({\sum }_{\pm }-S\right)}\eta (\gimel )}$.

A fuzzy graph whose vertex and edge minimum values include either a positive or negative sign is referred to as a signed-FG (signed-FG). It is formally defined as follows: the signed-FG ${\sum }_{\pm }=\left(\eta ,\phi \right)$ is a pair of functions defined such that $\eta :\Im \to [-1,+1]$ and $\phi :\Im \times \Im \to [-1,+1]$, where $\phi ({\gimel }_1,{\gimel }_2)\le \eta \left({\gimel }_1\right)\wedge \eta \left({\gimel }_2\right)$ for all $({\gimel }_1,{\gimel }_2)\in \Im \times \Im$.

Definition 3.

In a signed-FG ${\sum }_{\pm }=(\eta ,\phi )$, if $\phi ({\gimel }_1,{\gimel }_2)=\eta \left({\gimel }_1\right)\wedge \eta \left({\gimel }_2\right)$ for $({\gimel }_1,{\gimel }_2)\in \xi$, this means it is an effective arc.

Definition 4.

In a signed-FG ${\sum }_{\pm }=(\eta ,\phi )$, if all arcs are effective, then it is a complete signed-FG.

Definition 5.

An edge $\left({\gimel }_1,{\gimel }_2\right)$ in a signed-FG ${\sum }_{\pm }=(\eta ,\phi )$ is

• α-strong if $\Im ({\gimel }_1,{\gimel }_2)>CON{N}_{{\sum }_{\pm }-({\gimel }_1,{\gimel }_2)}({\gimel }_1,{\gimel }_2)$.
• β-strong if $\Im ({\gimel }_1,{\gimel }_2)=CON{N}_{{\sum }_{\pm }-({\gimel }_1,{\gimel }_2)}({\gimel }_1,{\gimel }_2)$.
• δ-arc if $\Im ({\gimel }_1,{\gimel }_2)<CON{N}_{{\sum }_{\pm }-({\gimel }_1,{\gimel }_2)}({\gimel }_1,{\gimel }_2)$.

1.2. Motivation

Domination in signed-FGs is being investigated to express complex, dynamic, and uncertain real-world interactions. A more flexible approach is required because traditional graph models frequently fall short in capturing the nuances of relationships, such as cooperation and rivalry. By combining both positive and negative associations, signed-FGs fill this gap and allow for a more thorough examination of the connectivity and strength of interactions between vertices. This approach is especially useful in fields like healthcare, because knowing connection integrity can help improve patient care in emergency situations. Furthermore, a key indicator for assessing network resilience is domination integrity (DI). This study provides useful tools to assist practitioners in overcoming operational issues by expanding upon theoretical underpinnings.

1.3. Organization of the Paper

An introduction and a review of the literature are given in Section 1. In Section 2, “Domination in signed-FGs”, the fundamental ideas of domination in signed-FGs are examined, with an emphasis on how they might be used to evaluate the resilience and capacity of networks. The novel concept of domination integrity (DI), which examines the connection and stability of hierarchical organizations, particularly in healthcare systems, is introduced. Effective arcs, definitions, and findings pertaining to standard signed-FGs are covered in Section 3. The relationships between the several nodes that represent healthcare facilities and how they affect the overall connectivity of the network are highlighted in Section 4. Domination integrity’s practical applications are explored in Section 5, with a focus on how they contribute to efficient resource management and team-based response tactics in actual circumstances like emergencies or public health crises. Finally, important new information about the dynamics of signed-FGs and their consequences for network stability and management is presented.

2. Algorithm for Classifying Strong Arcs in Signed Fuzzy Graphs and Identifying Signed Fuzzy Trees

Analyzing the structural characteristics of signed-FGs, especially in identifying strong edges and tree topologies, depends heavily on graph connectivity. In this work, we provide basic matrix representations for signed-FGs, including the adjacency matrix, the upper triangular adjacency matrix, and the strength of connectivity matrix. These matrices offer a systematic approach to categorizing strong arcs, measuring connectivity between vertices, and identifying signed fuzzy trees in a signed-FG.

By encoding connection values between vertex pairs, the adjacency matrix, an upper triangular representation, efficiently eliminates redundancy in edge representation. By keeping only important connectivity values that match actual edges in the graph, we are able to refine the adjacency matrix using the connectedness adjacency matrix. The process of classifying strong edges involves determining the highest connectivity values in the connectedness adjacency matrix.

Definition 6.

The adjacency matrix of a signed-FG is an $n\times n$ matrix that represents the membership values of edges connecting the vertices. The adjacency matrix $A\left({\Sigma }_{\pm }\right)$ is defined as follows:

$$A{\left({\Sigma }_{\pm }\right)}_{ij}=\left\{\begin{array}{cc}\phi (v_i,v_j),\hfill & \mathit{if}{v}_i\mathit{and}{v}_j\mathit{are}\mathit{connected}\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

Definition 7.

The upper triangular adjacency matrix retains only the upper triangular part of the adjacency matrix to avoid redundancy in an undirected signed-FG.

$$A^U{\left({\Sigma }_{\pm }\right)}_{ij}=\left\{\begin{array}{cc}\phi (v_i,v_j),\hfill & \mathit{if}i<j\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

Definition 8.

The strength of connectedness between two vertices is defined as the strongest weakest link in any path between them as follows:

$$C_s(v_i,v_j)=\underset{\wp }{max}\left(\underset{e\in \wp }{min}\phi \left(e\right)\right)$$

where ℘ represents the set of all paths between $v_i$ and $v_j$.

2.1. Pseudocode for the Classification of Arcs

Input: Simple signed-FG.

Output: Classification of arcs.

Step 1: The adjacency matrix of the given simple graph.

Step 2: The upper triangular adjacency matrix.

Step 3: The strength of connectedness between two vertices is defined as the strongest weakest link in any path between the vertices.

Step 4: Compare the upper triangular adjacency matrix $A^U\left({\Sigma }_{\pm }\right)$ with the strength of connectedness upper triangular adjacency matrix $C_s^U\left({\Sigma }_{\pm }\right)$. If $A^U{\left({\Sigma }_{\pm }\right)}_{ij}=C_s^U{\left(G\right)}_{ij}$, retain the value. Otherwise, mark the entry as ‘-’.

Classify Strong Arcs as α-Strong or β-Strong:

An arc $(v_i,v_j)$ in the strong upper triangular adjacency matrix is classified as follows:

• $\alpha$-strong if its membership value is the maximum in its row or column in $A\left({\Sigma }_{\pm }\right)$.
• $\beta$-strong otherwise.

2.2. Time Complexity

The time complexity of the pseudocode is $O\left(n^3\right)$. Step 1, reading the adjacency matrix, and Step 2, extracting the upper triangular matrix, each take $O\left(n^2\right)$. Step 3, computing the strength of connectedness, and Step 4, classifying strong arcs, dominate with $O\left(n^3\right)$, as they involve graph traversal and checking each element for connectivity or maximum values. Thus, the overall complexity is $O\left(n^3\right)$.

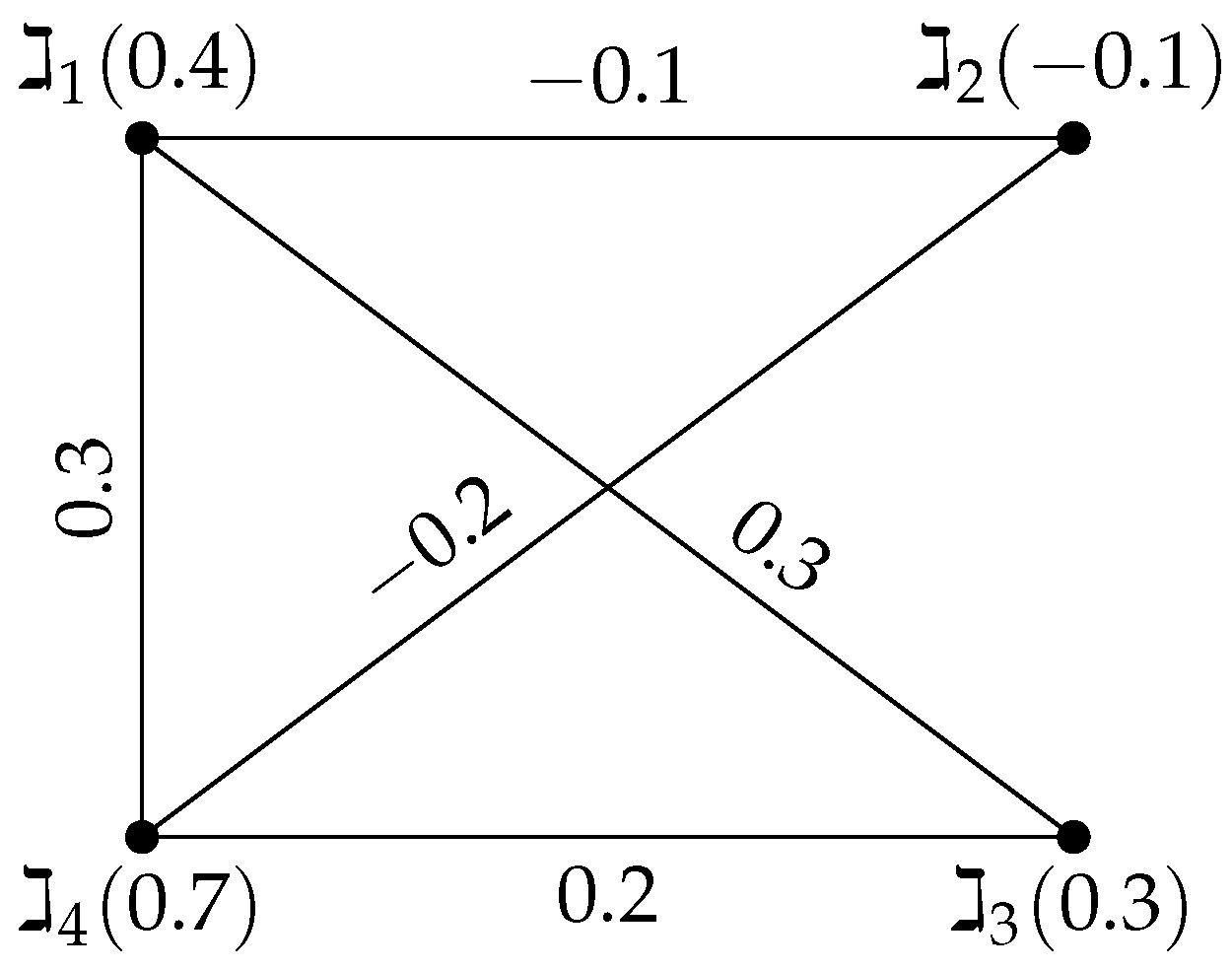
Example 1.

Consider a signed-FG with the vertex set $\Im =\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3,{\gimel }_4,{\gimel }_5\right\}$, ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$, and edge set $\Im \times \Im =\left\{({\gimel }_1,{\gimel }_2),({\gimel }_2,{\gimel }_3),({\gimel }_2,{\gimel }_4),({\gimel }_4,{\gimel }_5),({\gimel }_1,{\gimel }_5),({\gimel }_3,{\gimel }_4)\right\}$ with the vertex values listed below $\eta \left({\gimel }_1\right)=0.4,\eta \left({\gimel }_2\right)=0.2,\eta \left({\gimel }_3\right)=0.3,\eta \left({\gimel }_4\right)=0.4$, and $\eta \left({\gimel }_5\right)=-0.3$. According to Figure 1, the edge values are $\phi ({\gimel }_1,{\gimel }_2)=0.1,\phi ({\gimel }_1,{\gimel }_5)=-0.3,\phi ({\gimel }_2,{\gimel }_4)=0.2,\phi ({\gimel }_2,{\gimel }_3)=0.2,\phi ({\gimel }_3,{\gimel }_4)=0.3$, and $\phi ({\gimel }_4,{\gimel }_5)=-0.4$. Using Algorithm 1, we now discuss this example.

Step 1: The adjacency matrix is expressed as follows:

$$A\left({\mathsf{\Sigma }}_{\pm }\right)=\begin{array}{c}\hfill & \begin{array}{ccccc}{\gimel }_1& {\gimel }_2& {\gimel }_3& {\gimel }_4& {\gimel }_5\end{array}\\ \begin{array}{c}{\gimel }_1\\ {\gimel }_2\\ {\gimel }_3\\ {\gimel }_4\\ {\gimel }_5\end{array}& \left[\begin{array}{ccccc}-& 0.1& -& -& -0.3\\ 0.1& -& 0.2& 0.2& -\\ -& 0.2& -& 0.3& -\\ -& 0.2& 0.3& -& -0.4\\ -0.3& -& -& -0.4& -\end{array}\right]\end{array}$$

Step 2: The upper triangular adjacency matrix

$$A^U\left({\mathsf{\Sigma }}_{\pm }\right)=\begin{array}{c}\hfill & \begin{array}{ccccc}{\gimel }_1& {\gimel }_2& {\gimel }_3& {\gimel }_4& {\gimel }_5\end{array}\\ \begin{array}{c}{\gimel }_1\\ {\gimel }_2\\ {\gimel }_3\\ {\gimel }_4\end{array}& \left[\begin{array}{ccccc}-& 0.1& -& -& -0.3\\ -& -& 0.2& 0.2& -\\ -& -& -& 0.3& -\\ -& -& -& -& -0.4\end{array}\right]\end{array}$$

Step 3: The strength of connectedness between two vertices is defined as the strongest weakest link in any path between them as follows:

$$C_s^U\left({\mathsf{\Sigma }}_{\pm }\right)=\begin{array}{c}\hfill & \begin{array}{ccccc}{\gimel }_1& {\gimel }_2& {\gimel }_3& {\gimel }_4& {\gimel }_5\end{array}\\ \begin{array}{c}{\gimel }_1\\ {\gimel }_2\\ {\gimel }_3\\ {\gimel }_4\end{array}& \left[\begin{array}{ccccc}-& 0.1& -& -& -0.3\\ -& -& 0.2& 0.2& -\\ -& -& -& 0.3& -\\ -& -& -& -& -0.3\end{array}\right]\end{array}$$

Step 4: Compare the upper triangular adjacency matrix $A^U\left({\Sigma }_{\pm }\right)$ and the strength of the connectedness of the upper triangular adjacency matrix $C_s^U\left({\Sigma }_{\pm }\right)$. If $A^U{\left({\Sigma }_{\pm }\right)}_{ij}=C_s^U{\left(G\right)}_{ij}$; retain the value. Otherwise, mark the entry as ‘-’.

$$S^U\left({\mathsf{\Sigma }}_{\pm }\right)=\begin{array}{c}\hfill & \begin{array}{ccccc}{\gimel }_1& {\gimel }_2& {\gimel }_3& {\gimel }_4& {\gimel }_5\end{array}\\ \begin{array}{c}{\gimel }_1\\ {\gimel }_2\\ {\gimel }_3\\ {\gimel }_4\end{array}& \left[\begin{array}{ccccc}-& 0.1& -& -& -0.3\\ -& -& 0.2& 0.2& -\\ -& -& -& 0.3& -\\ -& -& -& -& -\end{array}\right]\end{array}$$

Classify strong arcs as $\alpha$-strong or $\beta$-strong

An arc $(v_i,v_j)$ in the strong upper triangular adjacency matrix is classified as follows: $\alpha$-strong if its membership value is the maximum in its row or column in $A\left({\Sigma }_{\pm }\right)$ and $\beta$-strong otherwise.

For matrix $S^U\left({\Sigma }_{\pm }\right)$, the following hold:

• $({\gimel }_1,{\gimel }_2)=0.1$ is $\alpha$-strong (unique maximum in row/column).
• $({\gimel }_1,{\gimel }_5)=-0.3$ is $\alpha$-strong (unique maximum in row/column).
• $({\gimel }_2,{\gimel }_3)=0.2$ is $\beta$-strong.
• $({\gimel }_2,{\gimel }_4)=0.2$ is $\beta$-strong.
• $({\gimel }_3,{\gimel }_4)=0.3$ is $\alpha$-strong (unique maximum in row/column).

Final Summary

• Construct the adjacency matrix for a signed-FG.
• Convert it into the upper triangular adjacency matrix.
• Compute the strength of connectedness upper triangular matrix.
• Compare matrices and construct the strong upper triangular adjacency matrix.
• Classify strong arcs as $\alpha$-strong or $\beta$-strong.

This process helps analyze connectivity strength and classification of strong arcs in signed-FG-based applications.

Algorithm 1 Classification of arcs.

1: Input: Adjacency matrix $A\left({\Sigma }_{\pm }\right)$ of a signed-FG 2: Output: Strong upper triangular adjacency matrix $S^U\left({\Sigma }_{\pm }\right)$ and classification of strong arcs 3: Step 1: Construct the Upper Triangular Adjacency Matrix $A^U\left({\Sigma }_{\pm }\right)$ 4: for $i=1$ to n do 5:     for $j=i+1$ to n do 6:         $A^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]\leftarrow A\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]$ 7:     end for 8: end for 9: Step 2: Compute the Strength of Connectedness Matrix $C_s^U\left({\Sigma }_{\pm }\right)$ 10: for each pair of vertices $(i,j)$ do 11:     if $(i,j)$ is directly connected then 12:         $C_s^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]\leftarrow A^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]$ 13:     else 14:         Find all paths from i to j 15:         Determine max(min(edge weights along paths from i to j)) 16:         $C_s^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]\leftarrow$ computed value 17:     end if 18: end for 19: Step 3: Construct Strong Upper Triangular Matrix $S^U\left({\Sigma }_{\pm }\right)$ 20: for $i=1$ to n do 21:     for $j=i+1$ to n do 22:         if $A^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]=C_s^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]$ then 23:            $S^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]\leftarrow A^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]$ 24:         else 25:            $S^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]{\leftarrow }^{\prime }{-}^{\prime }$ 26:         end if 27:     end for 28: end for 29: Step 4: Classify Strong Arcs as α-Strong or β-Strong 30: for each nonzero element $(i,j)$ in $S^U\left({\Sigma }_{\pm }\right)$ do 31:     Find unique maximum in row and column of $A\left({\Sigma }_{\pm }\right)$ 32:     if $A\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]$ is unique maximum in its row or column then 33:         Mark $(i,j)$ as $\alpha$-strong arc 34:     else 35:         Mark $(i,j)$ as $\beta$-strong arc 36:     end if 37: end for

Definition 9.

A connected signed-FG ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ has a signed fuzzy spanning subgraph $F_{\pm }=\left(\Im ,\tau ,\nu \right)$ such that $\mu ({\gimel }_1,{\gimel }_2)<CONN({\gimel }_1,{\gimel }_2)$ for all arcs $({\gimel }_1,{\gimel }_2)$ not in $F_{\pm }=\left(\Im ,\tau ,\nu \right)$. Then, ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ is a signed fuzzy tree.

Thus, ${\Sigma }_{\pm }$ can be classified as a signed fuzzy tree if all edges not in $F_{\pm }$ have lower fuzzy membership values than the connectivity function, ensuring that $F_{\pm }$ alone sufficiently represents the strongest connected structure of ${\Sigma }_{\pm }$.

2.3. Pseudocode for Checking Whether a Signed-FG Is a Signed Fuzzy Tree or Not

Input: Simple signed-FG.

Output: Whether it is a signed fuzzy tree or not.

• Construct the upper triangular adjacency matrix.
• Check for unique maximum values in each row and column as follows:
  • If each row and each column has a unique maximum value, then the signed fuzzy graph is a signed fuzzy tree.
  • Otherwise, it is not a signed fuzzy tree.

2.4. Time Complexity

The time complexity for checking whether a signed-FG is a signed fuzzy tree is $O\left(n^2\right)$, where n is the number of vertices in the graph. Constructing the upper triangular adjacency matrix requires comparing each pair of vertices, resulting in a time complexity of $O\left(n^2\right)$. After constructing the matrix, checking for the unique maximum value in each row and column also takes $O\left(n^2\right)$ time, as each row and column must be scanned individually. Since both steps individually require $O\left(n^2\right)$ operations, the overall time complexity of the pseudocode remains $O\left(n^2\right)$.

Example 2.

Consider a signed-FG with the vertex set $\Im =\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3,{\gimel }_4,{\gimel }_5\right\}$, and ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ and edge set $\Im \times \Im =\left\{({\gimel }_1,{\gimel }_2),({\gimel }_2,{\gimel }_3),({\gimel }_2,{\gimel }_4),({\gimel }_4,{\gimel }_5),({\gimel }_1,{\gimel }_4),({\gimel }_1,{\gimel }_5)\right\}$ with the vertex values listed below $\eta \left({\gimel }_1\right)=0.5,\eta \left({\gimel }_2\right)=0.4,\eta \left({\gimel }_3\right)=-0.3,\eta \left({\gimel }_4\right)=0.3$, and $\eta \left({\gimel }_5\right)=0.4$. According to Figure 2, the edge values are $\phi ({\gimel }_1,{\gimel }_2)=0.3,\phi ({\gimel }_1,{\gimel }_5)=0.4,\phi ({\gimel }_2,{\gimel }_3)=-0.3,\phi ({\gimel }_2,{\gimel }_4)=0.2,\phi ({\gimel }_3,{\gimel }_4)=-0.4,\phi ({\gimel }_1,{\gimel }_4)=0.1$ and $\phi ({\gimel }_4,{\gimel }_5)=0.2$. Using Algorithm 2, we now discuss this example.

Step 1: The upper triangular adjacency matrix

$$A^U\left({\mathsf{\Sigma }}_{\pm }\right)=\begin{array}{c}\hfill & \begin{array}{ccccc}{\gimel }_1& {\gimel }_2& {\gimel }_3& {\gimel }_4& {\gimel }_5\end{array}\\ \begin{array}{c}{\gimel }_1\\ {\gimel }_2\\ {\gimel }_3\\ {\gimel }_4\end{array}& \left[\begin{array}{ccccc}-& 0.3& -& 0.1& 0.4\\ -& -& -0.3& 0.2& -\\ -& -& -& -0.4& -\\ -& -& -& -& 0.2\end{array}\right]\end{array}$$

Step 2: Checking the unique maximum values in each row and column as follows:

• Row 1: Max = $0.4$ (Unique).
• Row 2: Max = $0.2$ (Unique).
• Row 3: Max = $-0.4$ (Unique).
• Row 4: Max = $0.2$ (Unique).

• Column 2: Max = $0.3$ (Unique).
• Column 3: Max = $-0.3$ (Unique).
• Column 4: Max = $0.2$ (Unique).
• Column 5: Max = $0.4$ (Unique).

Since each row and each column has a unique maximum, the signed-FG is a signed fuzzy tree.

Example 3.

Consider a signed-FG with the vertex set $\Im =\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3,{\gimel }_4\right\}$, ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$, and edge set $\Im \times \Im =\left\{({\gimel }_1,{\gimel }_2),({\gimel }_2,{\gimel }_4),({\gimel }_3,{\gimel }_4),({\gimel }_1,{\gimel }_4),({\gimel }_1,{\gimel }_3)\right\}$, with the vertex values listed below—$\eta \left({\gimel }_1\right)=0.4,\eta \left({\gimel }_2\right)=-0.1,\eta \left({\gimel }_3\right)=0.3$, and $\eta \left({\gimel }_4\right)=0.7$. According to Figure 3, the edge values are $\phi ({\gimel }_1,{\gimel }_2)=-0.1,\phi ({\gimel }_1,{\gimel }_3)=0.3,\phi ({\gimel }_1,{\gimel }_4)=0.3,\phi ({\gimel }_2,{\gimel }_4)=-0.2$, and $\phi ({\gimel }_3,{\gimel }_4)=0.2$.

Algorithm 2 Check if a signed-FG is a signed fuzzy tree.

Input: Adjacency matrix $A\left({\Sigma }_{\pm }\right)$ of a signed-FG with n vertices 2: Output: “Signed Fuzzy Tree” if valid, otherwise “Not a Signed Fuzzy Tree” Step 1: Construct the Upper Triangular Adjacency Matrix $A^U\left({\Sigma }_{\pm }\right)$ 4: for $i=1$ to n do     for $j=i+1$ to n do 6:         $A^U\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]\leftarrow A\left({\Sigma }_{\pm }\right)\left[i\right]\left[j\right]$     end for 8: end for Step 2: Check Row Maximum and Row Minimum 10: for each row i in $A^U\left({\Sigma }_{\pm }\right)$ do     Extract all nonzero values in row i 12:     if row has at least one nonzero value then         max_value $\leftarrow max\left(\mathrm{nonzero}\mathrm{elements}\mathrm{in}\mathrm{row}i\right)$ 14:         min_value $\leftarrow min\left(\mathrm{nonzero}\mathrm{elements}\mathrm{in}\mathrm{row}i\right)$         if max_value or min_value does not exist then 16:            return “Not a Signed Fuzzy Tree”         end if 18:     end if end for 20: Step 3: If all valid rows have both max and min values return “Signed Fuzzy Tree”

Step 1: The upper triangular adjacency matrix

$$A^U\left({\mathsf{\Sigma }}_{\pm }\right)=\begin{array}{c}\hfill & \begin{array}{cccc}{\gimel }_1& {\gimel }_2& {\gimel }_3& {\gimel }_4\end{array}\\ \begin{array}{c}{\gimel }_1\\ {\gimel }_2\\ {\gimel }_3\end{array}& \left[\begin{array}{cccc}-& -0.1& 0.3& 0.3\\ -& -& -& -0.2\\ -& -& -& 0.2\end{array}\right]\end{array}$$

Step 2: Checking the unique maximum values in each row and column as follows:

• Row 1: No unique max.
• Row 2: Max = $-0.2$ (Unique).
• Row 3: Max = $0.2$ (Unique).

• Column 2: Max = $-0.1$ (Unique).
• Column 3: Max = $0.3$ (Unique).
• Column 4: Max = $0.3$ (Unique).

Since the first row does not have a unique maximum, the signed-FG is not a signed fuzzy tree.

3. The Concept of Domination Integrity in Signed-FGs

In this section, domination in signed-FGs and domination integrity are presented with examples. Two distinct parameters, domination and integrity, describe a graph’s stability under various conditions. A new parameter, domination integrity, is developed, and its upper and lower bounds are established using the strong arc concept. The domination integrity of standard signed-FGs, including paths, cycles, and complete signed-FGs, is investigated in this section.

Definition 10.

Let ${\gimel }_1$ and ${\gimel }_2$ be members of ℑ, and let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ be a signed-FG. If $({\gimel }_1,{\gimel }_2)$ is a strong arc, then ${\gimel }_1$ dominates ${\gimel }_2$ in ${\sum }_{\pm }$. A subset $\mathfrak{D}$ of ℑ is referred to as a domination set of ${\sum }_{\pm }$ if, for each ${\gimel }_2\notin \mathfrak{D}$, there is a ${\gimel }_1$ that dominates ${\gimel }_2$.

Definition 11.

A domination set $\mathfrak{D}$ is referred to as a minimum domination set if none of its smaller subsets are also a domination set, and ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ is a signed-FG. The domination number, represented by $\gamma \left({\sum }_{\pm }\right)$, is the minimum size of any domination set in a graph ${\sum }_{\pm }$. A $\mathfrak{D}$ domination set in a signed-FG has a size of $\left|\mathfrak{D}\right|=\gamma \left({\sum }_{\pm }\right)$. One term for a minimum domination set is ${\sum }_{\pm }$.

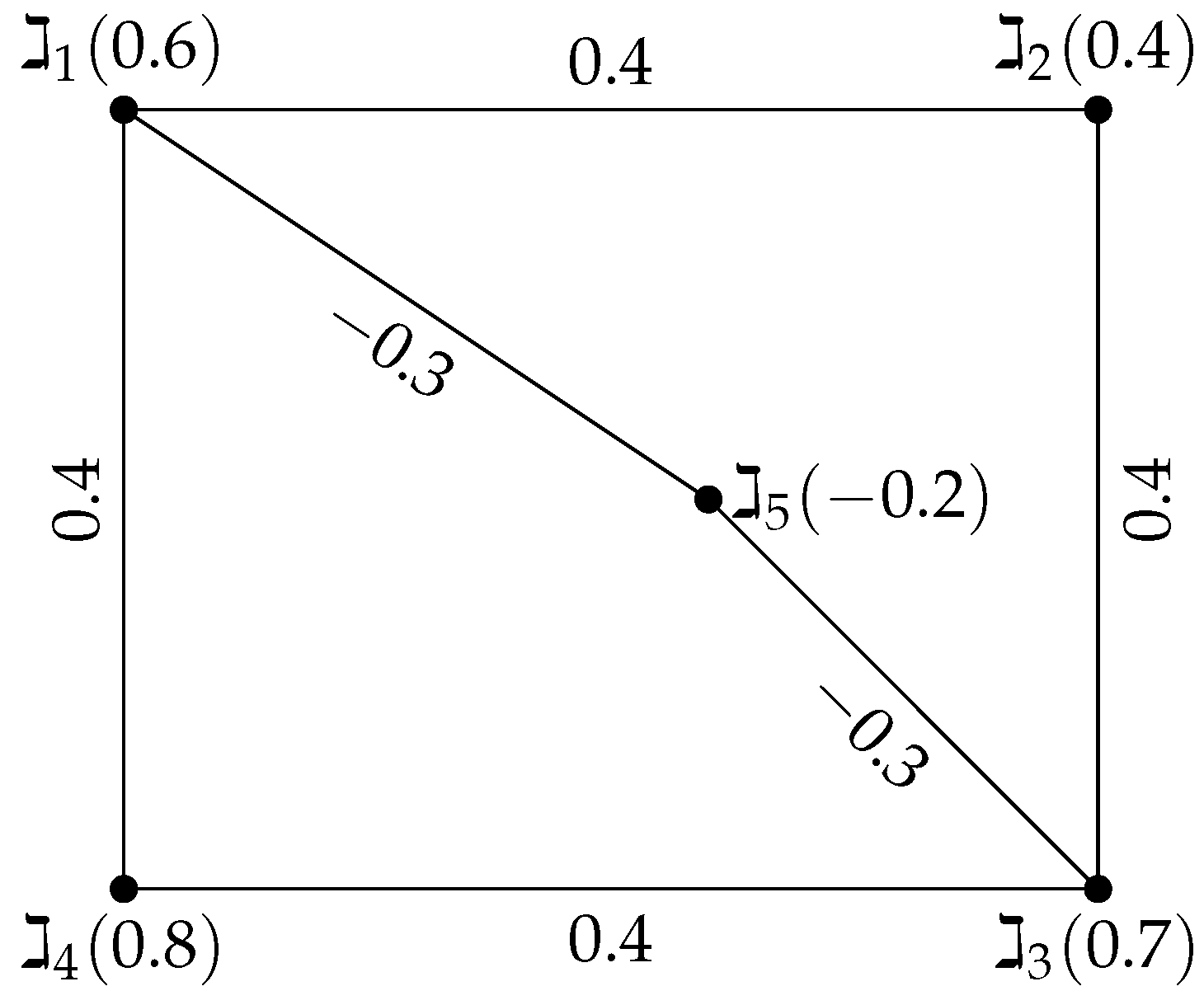
Example 4.

Consider a signed-FG with the vertex set $\Im =\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3,{\gimel }_4,{\gimel }_5\right\}$, ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$, and edge set $\Im \times \Im =\left\{({\gimel }_1,{\gimel }_2),({\gimel }_2,{\gimel }_5),({\gimel }_2,{\gimel }_3),({\gimel }_2,{\gimel }_4),({\gimel }_4,{\gimel }_5),({\gimel }_1,{\gimel }_5)\right\}$, with the vertex values listed below, $\eta \left({\gimel }_1\right)=-0.3,\eta \left({\gimel }_2\right)=0.4,\eta \left({\gimel }_3\right)=-0.3,\eta \left({\gimel }_4\right)=0.5$, and $\eta \left({\gimel }_5\right)=0.2$. According to Figure 4, the edge values are $\phi ({\gimel }_1,{\gimel }_2)=-0.4,\phi ({\gimel }_1,{\gimel }_5)=-0.3,\phi ({\gimel }_2,{\gimel }_5)=0.2,\phi ({\gimel }_2,{\gimel }_4)=0.4,\phi ({\gimel }_2,{\gimel }_3)=-0.3$, and $\phi ({\gimel }_4,{\gimel }_5)=0.1$. $({\gimel }_1,{\gimel }_5),({\gimel }_2,{\gimel }_5),({\gimel }_2,{\gimel }_4)$, and $({\gimel }_2,{\gimel }_3)$ are the strong arcs. The sets that could be dominating are $\left\{{\gimel }_1,{\gimel }_2\right\}$, $\left\{{\gimel }_5,{\gimel }_2\right\}$, $\left\{{\gimel }_1,{\gimel }_3,{\gimel }_4\right\}$, and $\left\{{\gimel }_3,{\gimel }_4,{\gimel }_5\right\}$. The dominating number of ${\sum }_{\pm }$ is the minimal cardinality, taken across all domination sets. The minimum domination set is $\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3\right\}$, and the domination number is $\gamma \left({\sum }_{\pm }\right)=-0.1$.

Definition 12.

Let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ be a signed-FG. $DI\left({\sum }_{\pm }\right)=min\left\{\right|S|+m\left({\sum }_{\pm }-S\right)/S\mathrm{is}\mathrm{the}\mathrm{dominating}\mathrm{set}\mathrm{of}{\sum }_{\pm }\}$ is the definition of the domination integrity of a signed-FG, where $\left|S\right|$ denotes the vertex cardinality of S and $m\left({\sum }_{\pm }-S\right)$ is the maximum order of ${\sum }_{\pm }-S$. For a signed-FG, $DI\left({\sum }_{\pm }\right)=\left\{\left|S\right|+m({\sum }_{\pm }-S)\right\}$ is the minimal domination integrity set.

Example 5.

Let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ be a signed-FG, where the vertex set is $\Im =\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3,{\gimel }_4\right\}$ and edge set $\Im \times \Im =\left\{({\gimel }_1,{\gimel }_2),({\gimel }_1,{\gimel }_4),({\gimel }_2,{\gimel }_4),({\gimel }_2,{\gimel }_3),({\gimel }_3,{\gimel }_4)\right\}$ have the following vertex values $\eta \left({\gimel }_1\right)=0.3,\eta \left({\gimel }_2\right)=0.2,\eta \left({\gimel }_3\right)=0.4$, and $\eta \left({\gimel }_4\right)=-0.1$. The edge values are $\phi ({\gimel }_1,{\gimel }_2)=0.2,\phi ({\gimel }_1,{\gimel }_4)=-0.2,\phi ({\gimel }_2,{\gimel }_4)=-0.3,\phi ({\gimel }_2,{\gimel }_3)=0.1$, and $\phi ({\gimel }_4,{\gimel }_3)=-0.1$. As shown in Figure 5, the strong arcs are $({\gimel }_1,{\gimel }_2),({\gimel }_2,{\gimel }_3)$, and $({\gimel }_3,{\gimel }_4)$. The domination sets are $\left\{{\gimel }_2,{\gimel }_4\right\},\left\{{\gimel }_1,{\gimel }_4\right\}$, and $\left\{{\gimel }_2,{\gimel }_3\right\}$. The domination integrity is calculated in

Table 1. Domination integrity is calculated for a signed-FG in Figure 5 such that $DI\left({\sum }_{\pm }\right)=min\left\{\left|S\right|+m\left({\sum }_{\pm }-S\right)\right\}=0.5$.

S	$\left|\mathit{S}\right|$	$\mathit{m}\left({\sum }_{\pm }-\mathit{S}\right)$	$\left|\mathit{S}\right|+\mathit{m}\left({\sum }_{\pm }-\mathit{S}\right)$
$\left\{{\gimel }_2,{\gimel }_4\right\}$	0.1	0.4	0.5
$\left\{{\gimel }_1,{\gimel }_4\right\}$	0.7	0.1	0.8
$\left\{{\gimel }_2,{\gimel }_3\right\}$	0.6	0.2	0.8

and is given by: $DI\left({\sum }_{\pm }\right)=min\left\{\left|S\right|+m\left({\sum }_{\pm }-S\right)\right\}=0.5$.

Theorem 1.

For any signed-FG ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$, $\gamma \left({\sum }_{\pm }\right)\le DI\left({\sum }_{\pm }\right)$.

Proof. 

The domination number of a signed-FG is determined by the cardinality of the dominating set. The dominating integrity number is determined by the greatest order of the component of ${\sum }_{\pm }-S$ that belongs to the dominating set S, implying that $\gamma \left({\sum }_{\pm }\right)<DI\left({\sum }_{\pm }\right)$. Equality holds if the vertices in the signed-FG are isolated. Since the full set of vertices is the only dominating set in a signed-FG with isolated vertices and $m({\sum }_{\pm }-S)=0$, it follows that $\gamma \left({\sum }_{\pm }\right)=DI\left({\sum }_{\pm }\right)$. Thus, we have $\gamma \left({\sum }_{\pm }\right)\le DI\left({\sum }_{\pm }\right)$. □

Corollary 1.

If ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ is a trivial signed-FG, then $\gamma \left({\sum }_{\pm }\right)=DI\left({\sum }_{\pm }\right)$.

Proof. 

A trivial signed-FG is a signed-FG that consists of a single vertex and no edges or multiple vertices, with all edge membership values equal to zero.

Case 1. Trivial signed-FG with one vertex

If the signed-FG has only one vertex, say ${\eta }_1=k$, then the domination number will be k. Similarly, the domination integrity is also k because the integrity set consists of only itself. Since there are no other vertices, the domination integrity is k. Hence, $\gamma \left({\sum }_{\pm }\right)=DI\left({\sum }_{\pm }\right)$.

Case 2. Trivial signed-FG with Multiple Isolated Vertices

If ${\sum }_{\pm }$ has multiple vertices but no edges $(\phi ({\gimel }_1,{\gimel }_2)=0,\forall {\gimel }_1,{\gimel }_2\in \Im ,{\gimel }_1\ne {\gimel }_2)$, then the following holds:

Each vertex is an isolated vertex, meaning each vertex must be chosen individually to dominate itself. The domination number $\gamma \left({\sum }_{\pm }\right)$ is the total number of vertices, since no vertex can dominate another. The $DI\left({\sum }_{\pm }\right)$ is also the total number of vertices, as all vertices are independent (no two are adjacent). Hence, $\gamma \left({\sum }_{\pm }\right)=DI\left({\sum }_{\pm }\right)$.

Therefore, it can be concluded from both scenarios that ${\sum }_{\pm }$ is a trivial signed-FG. □

Theorem 2.

In a signed-FG ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$, the domination integrity parameter increases monotonically.

Proof. 

Let ${\sum }_{\pm }$ be a signed-FG and let $N_{\pm }$ be a subgraph of ${\sum }_{\pm }$. We aim to show that $DI\left(N_{\pm }\right)\le DI\left({\sum }_{\pm }\right)$

By the Definition 12, for any signed-FG, $DI$ depends on the following two aspects: the size of a minimum dominating set and the structure of the components formed when this set is removed.

Since $N_{\pm }$ is a subgraph of ${\sum }_{\pm }$, the vertex set and the strong arc set of $N_{\pm }$ are subsets of those of ${\sum }_{\pm }$. Therefore, any dominating set in ${\sum }_{\pm }$ will dominate at least as many vertices and arcs as in $N_{\pm }$.

Now, we apply induction on the number of vertices. For graphs with one or two vertices, the domination integrity is trivially satisfied since the subgraph would either be identical or a smaller version, and thus, $DI\left(N_{\pm }\right)\le DI\left({\sum }_{\pm }\right)$. WE assume that for all signed-FGs with n vertices, the inequality holds. We consider a signed-FG ${\sum }_{\pm }$ with $n+1$ vertices, and a subgraph $N_{\pm }$ obtained by removing one or more vertices and the associated arcs. Since removing vertices cannot increase the number of connections, and dominating sets must cover fewer vertices or require fewer strong arcs to dominate, it follows that the domination integrity of $N_{\pm }$ is less than or equal to that of ${\sum }_{\pm }$.

Case 1. The equality holds if and only if the subgraph $N_{\pm }$ has the same vertex set and strong arc set as ${\sum }_{\pm }$, meaning no actual reduction has occurred.

Case 2. In all other cases, when either vertices or arcs are removed, $DI\left(N_{\pm }\right)$ will be strictly less than $DI\left({\sum }_{\pm }\right)$.

Hence, by the principle of induction, the domination integrity parameter increases monotonically with respect to subgraphs in signed fuzzy graphs. □

Theorem 3.

A complete signed-FG or the complement of a complete signed-FG is ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$. Then, $DI\left({\sum }_{\pm }\right)=$ order of signed-FG.

Proof. 

Assume that ${\sum }_{\pm }$ is a complete signed-FG. Subsets of ℑ are then all sets that dominate ${\sum }_{\pm }$. The graph is reduced to a single component, consisting of all remaining vertices, when any subset of ℑ is eliminated. Therefore, the order of ${\sum }_{\pm }$ equals the dominating integrity of ${\sum }_{\pm }$. Assume that ${\displaystyle \overline{{\sum }_{\pm }}}$ is the signed-FG complement ${\sum }_{\pm }$. Then, the vertices of ${\displaystyle \overline{{\sum }_{\pm }}}$ are isolated. For all ℷ in ${\displaystyle \overline{{\sum }_{\pm }}}$, $N(\gimel )=\varphi ,\forall \gimel$. The complete vertex set is the only dominating set in ${\sum }_{\pm }$. Because S is the dominating set, $m({\sum }_{\pm }-S)$ is zero. Consequently, order ${\sum }_{\pm }$ is the dominating integrity of ${\sum }_{\pm }$. As a result, ℑ is the only dominating set. The order of ${\sum }_{\pm }$ is thus $\gamma \left({\sum }_{\pm }\right)=DI\left({\sum }_{\pm }\right)$.

Conversely, suppose that the dominating integrity number equals the order of ${\sum }_{\pm }$. Suppose that the dominating set in ${\sum }_{\pm }$ is S. If ${\sum }_{\pm }-S$ contains more than one component, the sum of the cardinality of S and $m({\sum }_{\pm }-S)$ must be less than the order of ${\sum }_{\pm }$. ${\sum }_{\pm }-S$ must therefore be a single connected component. This is true for all dominating sets, but is particularly true for sets that contain a singleton vertex. Consequently, this singleton vertex set is inferior to all other vertices in ${\sum }_{\pm }$. This implies that ${\sum }_{\pm }$ is a signed-FG that is complete. □

Theorem 4.

Let the complete bipartite signed-FG ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$. $DI\left({\sum }_{\pm }\right)=min\left\{\right|{\Im }_1|+max\left({\eta }_2\left(\Im \right)\right),|{\Im }_2|+max\left({\eta }_1\left(\Im \right)\right)\}$, if $K_{{\eta }_1,{\eta }_2}$.

Proof. 

Let the complete bipartite signed-FG be ${\sum }_{\pm }$, whose bipartitions are ${\Im }_1$ and ${\Im }_2$. One vertex from ${\Im }_1$ and another from ${\Im }_2$, or one vertex from ${\Im }_2$ and another from ${\Im }_1$, constitute the dominating set S of ${\sum }_{\pm }$. ${\sum }_{\pm }-S$ is a single linked component if S is one node from ${\Im }_1$ and another from ${\Im }_2$, or one node from ${\Im }_2$ and another from ${\Im }_1$. $m({\sum }_{\pm }-S)=max\left\{{\eta }_1\left(\Im \right)\right\}$ if S is ${\Im }_1$. $m({\sum }_{\pm }-S)=max\left\{{\eta }_2\left(\Im \right)\right\}$ if S is ${\Im }_2$. Hence, $DI\left({\sum }_{\pm }\right)=min\left\{|{\Im }_1|+max\left({\eta }_2\left(\Im \right)\right),\left|{\Im }_2\right|+max\left({\eta }_1\left(\Im \right)\right)\right\}$. □

Theorem 5.

Let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ be a signed-FG, and assume that the underlying crisp path graph is ${\wp }_n,n\ge 2$, where every edge functions as an effective edge. There is then at least one independent dominant set with $\lceil {\displaystyle \frac{n}{3}}\rceil$ vertices.

Proof. 

Let ${\sum }_{\pm }$ be a signed-FG. whose underlying network is m vertices and a path ${\wp }_n$. The edges in ${\sum }_{\pm }$ are all effective edges. In order to dominate ${\sum }_{\pm }$, we want at least $\lceil {\displaystyle \frac{n}{3}}\rceil$ edges. The following represents a way to construct the independent dominant set: When $n\equiv 0(mod3)$, the vetex set ${\Im }_2,{\Im }_5,{\Im }_8,\cdots ,{\Im }_{n-1}$ forms the independent dominant set. When $n\equiv 1(mod3)$, the vetex set ${\Im }_2,{\Im }_4,{\Im }_7,\cdots ,{\Im }_m$ forms the independent dominant set. When $n\equiv 2(mod3)$, the vetex set ${\Im }_2,{\Im }_4,{\Im }_7,\cdots ,{\Im }_{n-1}$ forms the independent dominant set. The nodes of $\lceil {\displaystyle \frac{n}{3}}\rceil$ are not next to each other. Clearly, they are not related to one other. Consequently, a dominating set with $\lceil {\displaystyle \frac{n}{3}}\rceil$ nodes is independent. □

Theorem 6.

Let a signed-FG be ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$, and let $C_n,n\ge 3$ be the crisp cycle graph underneath, with all arcs functioning as effective arcs. There is then at least one independent dominant set with $\lceil {\displaystyle \frac{n}{3}}\rceil$ vertices.

Proof. 

Suppose that ${\sum }_{\pm }$ is a signed-FG. We use an underlying network $C_n$ and n vertices. Every edge in ${\sum }_{\pm }$ is an effective edge. At least $\lceil {\displaystyle \frac{n}{3}}\rceil$ edges are required in order to dominate ${\sum }_{\pm }$. Vertex ${\wp }_1$ is isolated by definition [24] if $\phi ({\wp }_1,{\wp }_2)<\eta \left({\wp }_1\right)\wedge \eta \left({\wp }_2\right),\forall {\wp }_2\in \Im -\left\{{\wp }_2\right\}$. For any ${\wp }_1,{\wp }_2\in S$, a set is said to be independent $\phi ({\wp }_1,{\wp }_2)<\eta \left({\wp }_1\right)\wedge \eta \left({\wp }_2\right)$. A set is considered independent if there are no adjacencies between any of its vertices. $\left\{{\Im }_1,{\Im }_2,\cdots ,{\Im }_n\right\}$ should be the vertices of $C_n$. The independent dominant set can be constructed as follows: If $n\equiv 0(mod3)$, then the vetex set ${\Im }_1,{\Im }_4,{\Im }_7,\cdots ,{\Im }_{n-2}$ forms the independent dominant set. If $n\equiv 1(mod3)$, then the vetex set ${\Im }_1,{\Im }_4,{\Im }_7,\cdots ,{\Im }_{n-3},{\Im }_{n-1}$ forms the independent dominant set. If $n\equiv 2(mod3)$, then the vetex set ${\Im }_1,{\Im }_4,{\Im }_7,\cdots ,{\Im }_{n-1}$ forms the independent dominant set. A dominant set with $\lceil {\displaystyle \frac{n}{3}}\rceil$ vertices is independent as all of the arcs in ${\sum }_{\pm }$ are effective arcs. □

Theorem 7.

Assume that ${\sum }_{\pm }$ is a connected signed-FG. A distinct strong path between any two nodes in ${\sum }_{\pm }$ is necessary for ${\sum }_{\pm }$ to be classified as a signed fuzzy tree. A path that has the greatest strength between two points, ${\gimel }_1$ and ${\gimel }_2$, for any ${\gimel }_1,{\gimel }_2\in \Im$, is also considered strong.

Theorem 8.

Let the connected signed-FG be ${\sum }_{\pm }$. It is a signed fuzzy tree if and only if ${\sum }_{\pm }$ has a distinct maximum spanning tree.

Theorem 9.

If $F_{\pm }$ is the maximum spanning tree and ${\sum }_{\pm }$ is a signed fuzzy tree, then $DI\left({\sum }_{\pm }\right)=DI\left(F_{\pm }\right)$.

Proof. 

Let $F_{\pm }$ be a maximum spanning tree and ${\sum }_{\pm }$ be a signed fuzzy tree. Theorem 7 states that every arc in $F_{\pm }$ is strong. $F_{\pm }$ is unique according to the Theorem 8. Consequently, the ${\sum }_{\pm }$ strong edge set and vertex set are the same as $F_{\pm }$’s edge set and vertex set. $DI\left({\sum }_{\pm }\right)=DI\left(F_{\pm }\right)$ follows as a result. □

4. Efficient Signed-FGs

Each crisp graph clearly belongs to a distinct class of signed-FGs. If the values of $\eta$ and $\phi$ for every node and arcs are equal to 1, the signed-FG is considered crisp. Interestingly, the signed-FG may not match the dominant sets of the underlying crisp graph. Consequently, we develop a new type of signed-FG, the efficient signed-FG.

Definition 13.

Any signed-FG, where ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ has the same domination set as its crisp graph, except for ℑ, is regarded as an efficient signed-FG.

Example 6.

Let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ be a signed-FG, where the vertex set $\Im =\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3,{\gimel }_4\right\}$ and edge set $\Im \times \Im =\left\{({\gimel }_1,{\gimel }_2),({\gimel }_1,{\gimel }_4),({\gimel }_1,{\gimel }_3),({\gimel }_2,{\gimel }_3),({\gimel }_4,{\gimel }_3)\right\}$ have the following vertex values $\eta \left({\gimel }_1\right)=0.3,\eta \left({\gimel }_2\right)=0.5,\eta \left({\gimel }_3\right)=0.4$ and $\eta \left({\gimel }_4\right)=-0.2$. The edge values are $\phi ({\gimel }_1,{\gimel }_2)=0.4,\phi ({\gimel }_1,{\gimel }_4)=-0.2,\phi ({\gimel }_1,{\gimel }_3)=0.2,\phi ({\gimel }_2,{\gimel }_3)=0.4$, and $\phi ({\gimel }_4,{\gimel }_3)=-0.3$, as shown in Figure 6. The strong arcs are $({\gimel }_1,{\gimel }_2),({\gimel }_2,{\gimel }_3)$, and $({\gimel }_1,{\gimel }_4)$. The domination sets are $\left\{{\gimel }_1\right\},\left\{{\gimel }_3,{\gimel }_4\right\}$, and $\left\{{\gimel }_2,{\gimel }_4\right\}$

Example 7.

Let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ be a signed-FG, where the vertex set $\Im =\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3,{\gimel }_4,{\gimel }_5\right\}$ and edge set $\Im \times \Im =\left\{({\gimel }_1,{\gimel }_2),({\gimel }_1,{\gimel }_5),({\gimel }_1,{\gimel }_4),({\gimel }_2,{\gimel }_3),({\gimel }_4,{\gimel }_3),({\gimel }_3,{\gimel }_5)\right\}$ have the following vertex values $\eta \left({\gimel }_1\right)=0.6,\eta \left({\gimel }_2\right)=0.4,\eta \left({\gimel }_3\right)=0.7,\eta \left({\gimel }_4\right)=0.8$ and $\eta \left({\gimel }_5\right)=-0.2$. The edge values are $\phi ({\gimel }_1,{\gimel }_2)=0.4,\phi ({\gimel }_1,{\gimel }_4)=0.4,\phi ({\gimel }_1,{\gimel }_5)=-0.3,\phi ({\gimel }_2,{\gimel }_3)=0.4,\phi ({\gimel }_3,{\gimel }_5)=-0.3$, and $\phi ({\gimel }_4,{\gimel }_3)=0.4$, as shown in Figure 7. The strong arcs are $({\gimel }_1,{\gimel }_2),({\gimel }_1,{\gimel }_5),({\gimel }_1,{\gimel }_4),({\gimel }_2,{\gimel }_3),({\gimel }_3,{\gimel }_5)$, and $({\gimel }_3,{\gimel }_4)$. The domination sets for crisp graph ${\sum }^{\ast }$ and ${\sum }_{\pm }$ are identical. As a result, the signed-FG is efficient.

Theorem 10.

Let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ represent a signed-FG and the underlying crisp graph ${\sum }_{\pm }$ be path ${\wp }_n$. Then, ${\sum }_{\pm }$ is an efficient signed-FG.

Proof. 

Let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ be a signed-FG and assume that ${\sum }_{\pm }$ represents a path. The vertex and edge sets of ${\sum }_{\pm }$ and its underlying crisp graph ${\sum }^{\ast }$ are identical if every arc is effective. Consequently, they share the same dominating set, making ${\sum }_{\pm }$ a productive signed-FG. Now, suppose that every arc is inefficient. It must be shown that each inefficient arc is also a strong arc. Since there is exactly one path in ${\wp }_n$ connecting any two vertices, removing an edge disconnects the graph, thereby reducing the connectivity between neighboring vertices. Hence, such an edge must be a strong edge. Therefore, in ${\wp }_n$, all inefficient edges are strong edges. As a result, ${\sum }_{\pm }$ is an efficient signed-FG. □

Theorem 11.

A signed-FG ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ is considered efficient if it is complete.

Proof. 

Each set of vertices in a complete signed-FG is a dominant set of ${\sum }_{\pm }$. Since the supplied signed-FG ${\sum }_{\pm }$ is a complete signed-FG, each edge is a strong arc. Thus, ${\sum }_{\pm }$ and ${\sum }^{\ast }$ have the same vertex set and edge. As a consequence, they have the same dominating set. Thus, any complete signed-FG is likewise an efficient signed-FG. □

Theorem 12.

An efficient signed-FG ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ is any signed-FG that has a constant $\phi$ value.

Proof. 

When all of the arc values are equal, the arc is said to be strong. The arcs are regarded as $\beta$-strong arcs in this instance. Each arc has become stronger as a result. As a result, each vertex in the fuzzy and crisp graphs ${\sum }_{\pm }$ has the same closed neighborhood set. As a result, ${\sum }_{\pm }$ is an effective signed-FG since it has the same dominating set as ${\sum }_{\pm }^c$. □

Theorem 13.

All efficient signed-FG ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ is a strong signed-FG.

Proof. 

In a strong signed-FG, every arc is an effective edge. Any effective edge is a strong edge. But not every powerful arc qualifies as an effective one. In this case, every edge is an effective edge. Every edge is therefore a powerful edge. This implies that the dominating sets of the signed-FG and its underlying fuzzy graph are the same since the neighborhood set of each vertex is the same for both. Consequently, every strong signed-FG is likewise an efficient signed-FG. □

5. Applications of Integrity in Domination for Signed-FGs

In healthcare systems, hospitals, clinics, and medical personnel are considered nodes, while patient referrals, medical supply chains, and information flows are treated as edges. In real-world healthcare networks, the dependability of these connections can vary depending on whether the interactions are competitive (negative) or cooperative (positive).

During a pandemic like COVID-19, when major hospitals and other critical nodes become overwhelmed, dominance integrity can be used to quantitatively evaluate the resilience of a healthcare network. It measures how well the network can adapt by shifting patients to secondary hospitals, reallocating resources, or strengthening alternative care pathways.

Its application is illustrated through the following real-world examples:

• In a mass casualty event, dominance integrity can determine whether the healthcare system maintains patient care by dynamically adjusting patient referrals and resource sharing across institutions.
• If major referral hospitals are compromised, the model assesses whether other healthcare centers can sustain the flow and quality of care.
• When supply chains fail (e.g., ventilator shortages), the integrity score reflects how effectively alternative sourcing and distribution routes compensate for disruptions.

Thus, dominance integrity serves as a resilience metric, helping administrators design healthcare systems that can withstand shocks, reallocate resources efficiently, and maintain operational effectiveness under pressure. In this context, symmetry within healthcare network structures emerges as a crucial factor, as more symmetrical networks tend to exhibit higher domination integrity, thereby enhancing the system’s robustness and adaptability during crises.

Although this study primarily establishes the theoretical foundation, future work is planned to validate these concepts using real-world healthcare network data, particularly from pandemic response efforts and crisis management scenarios.

Graph Representation for Domination Integrity in Signed-FGs

A signed-FG’s nodes and edges can be used to depict the relationships and interactions among healthcare organizations in a network, ${\sum }_{\pm }$. Domination integrity $DI\left({\sum }_{\pm }\right)$ measures the resilience of the network in the event that important components (nodes) are lost or corrupted. The integrity of dominion is provided by the following: At $DI\left({\sum }_{\pm }\right)$, the minimum of $\left\{\left|\mathcal{D}\right|+max({\sum }_{\pm }-\mathcal{D})\right\}$ is the minimum and $max({\sum }_{\pm }-\mathcal{D})$ is the maximum order of the components of ${\sum }_{\pm }-\mathcal{D}$. The nodes that dominate the network are represented by $\mathcal{D}$, which is a subset of all nodes.The total of the set’s membership values is $\left|\mathcal{D}\right|$. When $\mathcal{D}$ is subtracted from ${\sum }_{\pm }$, the remaining network is ${\sum }_{\pm }-\mathcal{D}$.

Nodes represent various healthcare facilities such as clinics, hospitals, pharmacies, and emergency rooms. Each node is assigned attributes, including a signed fuzzy membership value ranging from $-1$ to 1. This value reflects the facility’s capacity, reliability, and relevance within the network. For instance, a large hospital with a membership value close to 1 indicates high importance, whereas a small community clinic may have a lower membership value, signifying a more limited role in the network.

Margin represents the relationships or interactions between hospitals. Among these could be patient referrals, which allow one hospital to send patients to another. In order to offer medical staff or equipment between hospitals, shared services collaborate. Planning for emergency response or medical aid is facilitated by communication. Positive dynamics include encounters that are constructive, including successful patient transitions or successful corporate outcomes. Negativity is a symbol for negative interactions, such as site competitiveness or communication breakdowns. The degree or level of confidence in these relationships can be indicated by the signed fuzzy membership.

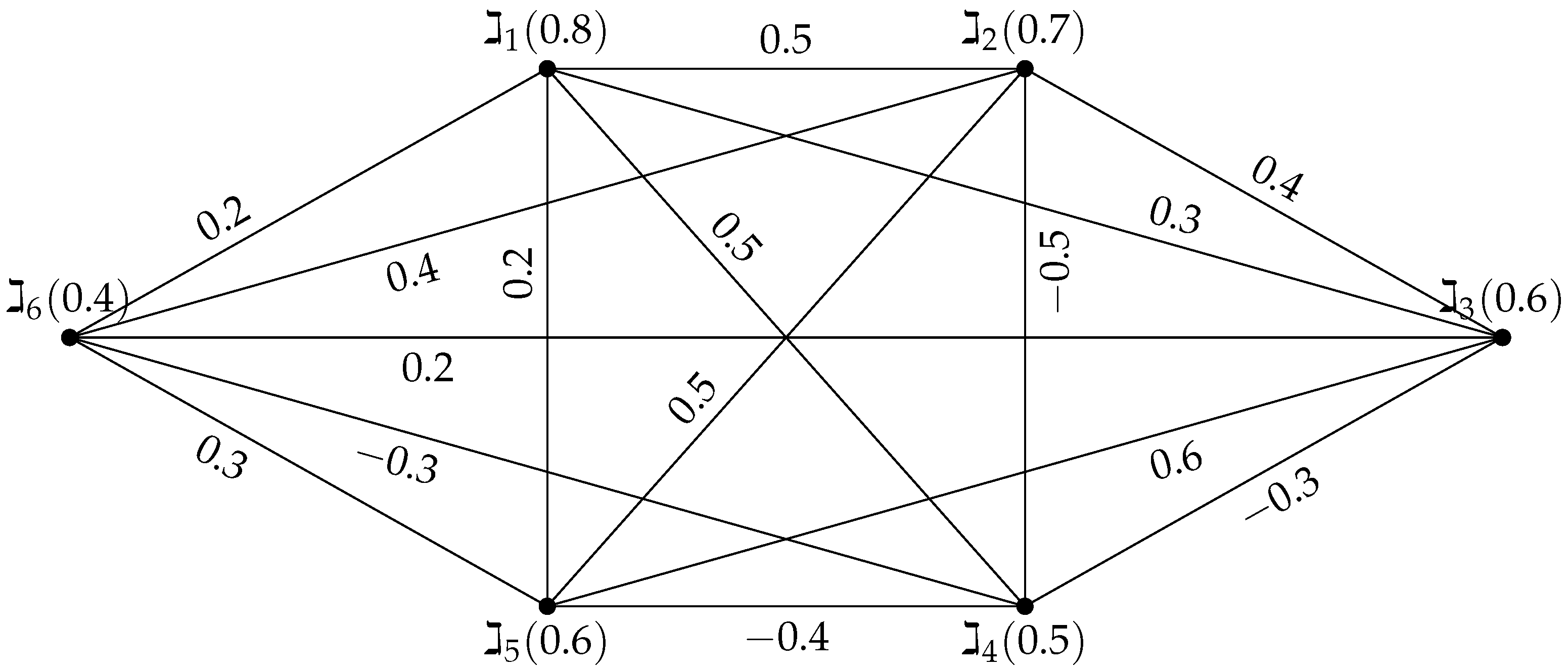
Suppose we have a signed-FG representing a healthcare network with six nodes as follows: ${\gimel }_1$ denotes a large hospital with a membership value of $0.9$, ${\gimel }_2$ denotes a clinic with a membership value of $0.8$, ${\gimel }_3$ denotes a specialty care facility with a membership value of $0.6$, ${\gimel }_4$ denotes a pharmacy with a membership value of $0.7$, ${\gimel }_5$ denotes a rehabilitation facility with a membership value of $0.6$, and ${\gimel }_6$ denotes an emergency care facility with a membership value of $0.4$. The connections between these facilities are depicted as edges, including supply chains, patient referrals, and casework collaboration. With a signed fuzzy membership value (ranging from $-1$ to 1) and a sign (positive or negative), each edge indicates the reliability and strength of the connection.

Let ${\sum }_{\pm }=\left(\Im ,\eta ,\phi \right)$ be a signed-FG, where the vertex set $\Im =\left\{{\gimel }_1,{\gimel }_2,{\gimel }_3,{\gimel }_4,{\gimel }_5,{\gimel }_6\right\}$ and edge set $\Im \times \Im =\{({\gimel }_1,{\gimel }_2),({\gimel }_1,{\gimel }_3),({\gimel }_1,{\gimel }_4),({\gimel }_1,{\gimel }_5),({\gimel }_2,{\gimel }_3),({\gimel }_2,{\gimel }_4),({\gimel }_2,{\gimel }_5),({\gimel }_3,{\gimel }_4),({\gimel }_3,{\gimel }_5),({\gimel }_3,{\gimel }_5)\}$ with the following vertex values: $\eta \left({\gimel }_1\right)=0.8,\eta \left({\gimel }_2\right)=0.7,\eta \left({\gimel }_3\right)=0.5,\eta \left({\gimel }_4\right)=0.6$, $\eta \left({\gimel }_5\right)=0.5$, and $\eta \left({\gimel }_6\right)=0.3$. The edge values are $\phi ({\gimel }_1,{\gimel }_2)=0.4,\phi ({\gimel }_1,{\gimel }_3)=0.2,\phi ({\gimel }_1,{\gimel }_4)=0.4,\phi ({\gimel }_1,{\gimel }_5)=0.2,\phi ({\gimel }_2,{\gimel }_3)=0.3,\phi ({\gimel }_2,{\gimel }_4)=-0.4,\phi ({\gimel }_2,{\gimel }_5)=0.4,\phi ({\gimel }_2,{\gimel }_6)=0.3,$ $\phi ({\gimel }_3,{\gimel }_4)=-0.4,\phi ({\gimel }_3,{\gimel }_5)=0.5,\phi ({\gimel }_3,{\gimel }_6)=0.1,\phi ({\gimel }_3,{\gimel }_6)=-0.2,\phi ({\gimel }_4,{\gimel }_5)=-0.3$, and $\phi ({\gimel }_5,{\gimel }_6)=0.2$, as shown in Figure 8. The strong arcs are $({\gimel }_1,{\gimel }_2),({\gimel }_1,{\gimel }_4),({\gimel }_2,{\gimel }_5),({\gimel }_3,{\gimel }_5)$, and $({\gimel }_3,{\gimel }_5)$. The possible dominating sets are $\left\{{\gimel }_1,{\gimel }_4\right\}$, $\left\{{\gimel }_2,{\gimel }_3\right\}$, $\left\{{\gimel }_2,{\gimel }_4\right\}$, and $\left\{{\gimel }_1,{\gimel }_3\right\}$. The domination integrity is $min\left\{\left|S\right|+m\left({\sum }_{\pm }-S\right)\right\}=1.4$.

Using the above formula, healthcare administrators can apply the concept of dominance integrity $DI\left({\sum }_{\pm }\right)$ in healthcare networks to quantitatively assess and optimize the resilience of their networks. The lowest value of $DI\left({\sum }_{\pm }\right)$ denotes the optimal configuration of key facilities to ensure minimal disruption to network operations, guiding strategic decisions to maintain a dependable and effective healthcare delivery system.

6. Conclusions

Signed fuzzy domination integrity is examined in this paper as a metric for graph stability and domination characteristics. For a variety of signed-FGs, such as routes, cycles, and complete bipartite graphs, the study calculates the domination integrity to shed light on their structural properties. Additionally, the new idea of efficient signed-FGs is presented in this paper, according to which the domination set of the signed-FG is the same as that of the underlying crisp graph. Efficiency in signed-FGs is defined and made explicit through basic theorems and examples, providing a fresh viewpoint on signed-FG research.