An Enhanced Fuzzy Time Series Forecasting Model Integrating Fuzzy C-Means Clustering, the Principle of Justifiable Granularity, and Particle Swarm Optimization
Abstract
1. Introduction
2. Preliminaries
2.1. Fuzzy Time Series Model
2.2. Fuzzy C-Means Clustering
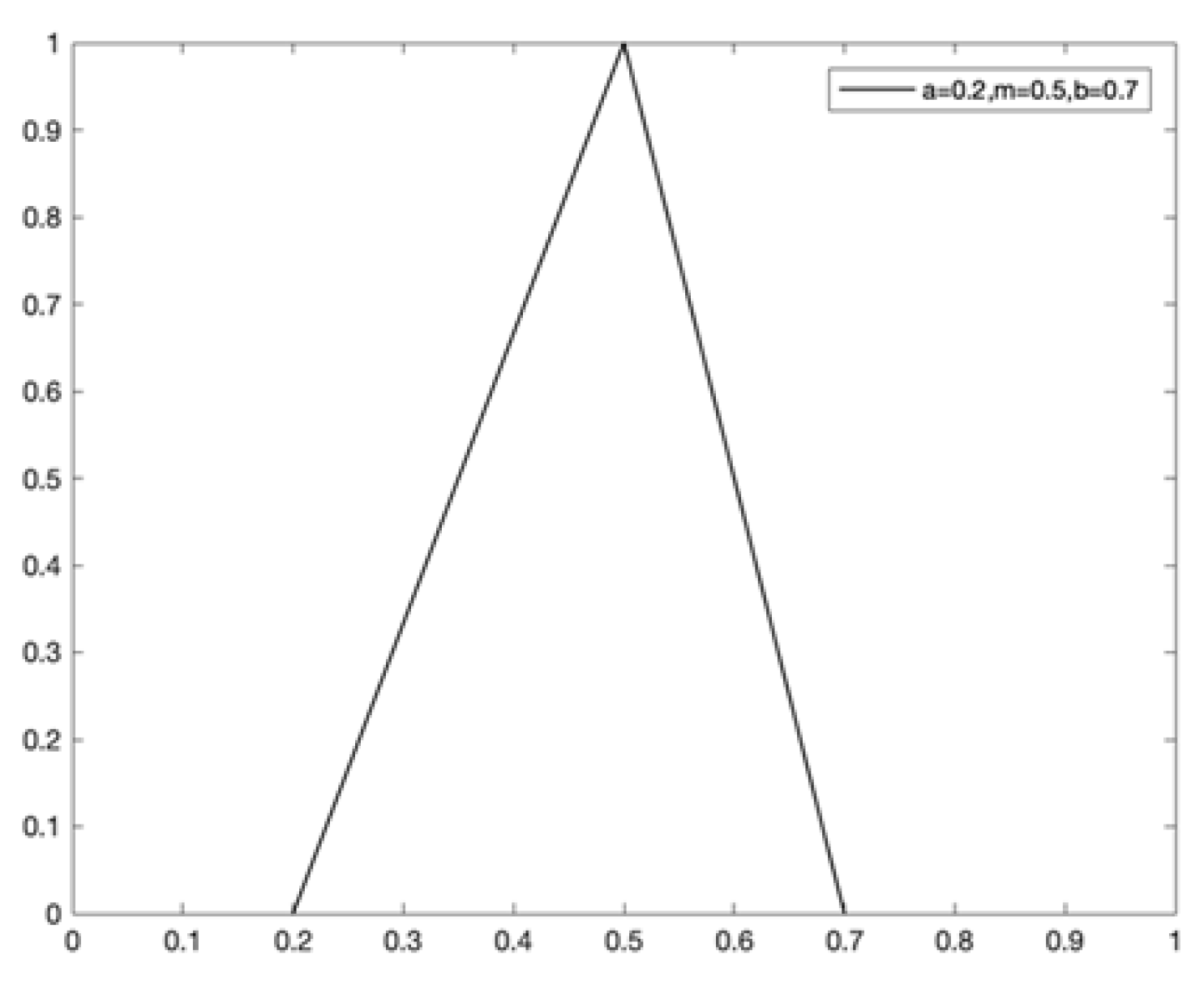
2.3. Triangular Fuzzy Information Granules
2.4. Principle of Justifiable Granularity
2.5. Particle Swarm Optimization Algorithm
3. Partition of the Universe of Discourse Based on FCM, PJG, and PSO
3.1. Initial Partition of the Universe of Discourse Based on FCM
3.2. Optimized Partition of the Universe of Discourse Based on PJG and PSO
| Algorithm 1: Partition of the Universe of Discourse Based on FCM, PJG, and PSO |
| Input: Time series and the number of partition intervals p Output: The optimal partition intervals of the universe of discourse |
| 1. Utilize the FCM clustering method to divide the universe of discourse into p clusters, obtain the clustering centers, then sort the clustering centers in ascending order, and calculate the initial partition subintervals of the universe of discourse according to Formula (19). 2. For the initial partition subintervals, use triangular fuzzy sets to construct information granules , and solve the parameters of TFIGs according to PJG. 3. For the TFIGs, use the PSO algorithm to solve it according to Formulas (21) and (22) to obtain the final optimal partition intervals of the universe of discourse. |
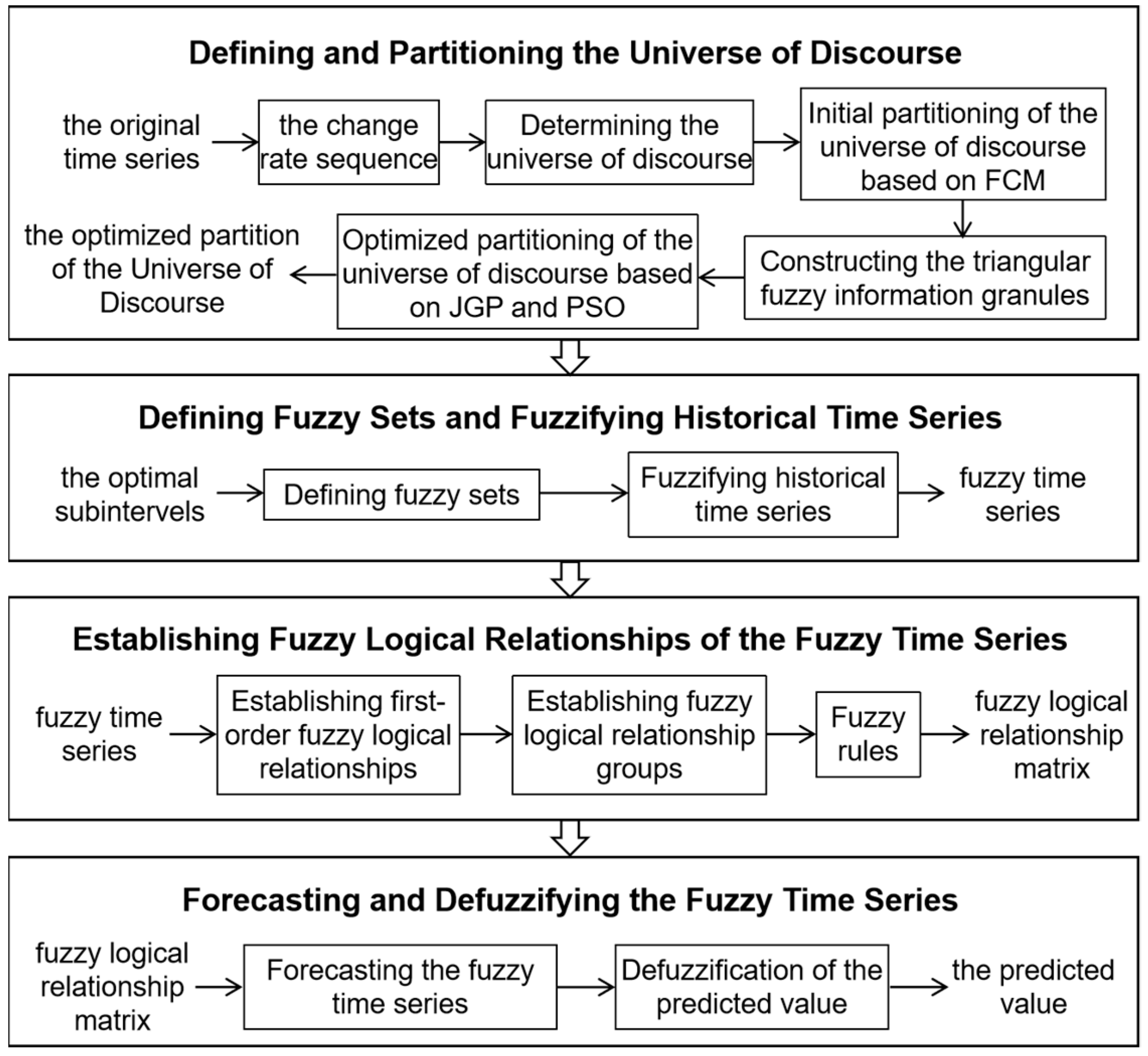
4. Fuzzy Time Series Forecasting Based on the Novel Partition of the Universe of Discourse
4.1. Defining and Partitioning the Universe of Discourse
4.2. Defining Fuzzy Sets and Fuzzifying Historical Time Series
4.3. Establishing Fuzzy Logical Relationships
4.4. Forecasting and Defuzzification
| Algorithm 2: Fuzzy Time Series Forecasting Based on the Novel Partition of the Universe of Discourse |
| Input: Time series and the subintervals p Output: Predicted value x(t) |
| 1. Define and partition the universe of discourse. Convert the original time series X into a rate of change series R, and define the universe of discourse of R is , then use Algorithm 1 to divide U into p subintervals. 2. Define fuzzy sets and fuzzify historical time series. Based on the subintervals, define a fuzzy set for each subinterval, and fuzzify the historical data to obtain the fuzzy time series. 3. Establish fuzzy logical relationships. Based on the fuzzified data, establish fuzzy logical relationships. Combine the FLRs with the same antecedents into the same group to construct fuzzy logical relationship groups, thereby obtaining fuzzy logic rules and building the fuzzy logical relationship matrix. 4. Perform forecasting and defuzzification. For the fuzzy logical relationship matrix, calculate the fuzzy predicted values according to Formula (25), and perform defuzzification according to Formula (26) to derive the final predicted value x(t). |
5. Experiments
5.1. Evaluation Metrics
5.1.1. Evaluation Metric of Prediction Accuracy
5.1.2. Evaluation Metric of Predicted Linguistic Accuracy
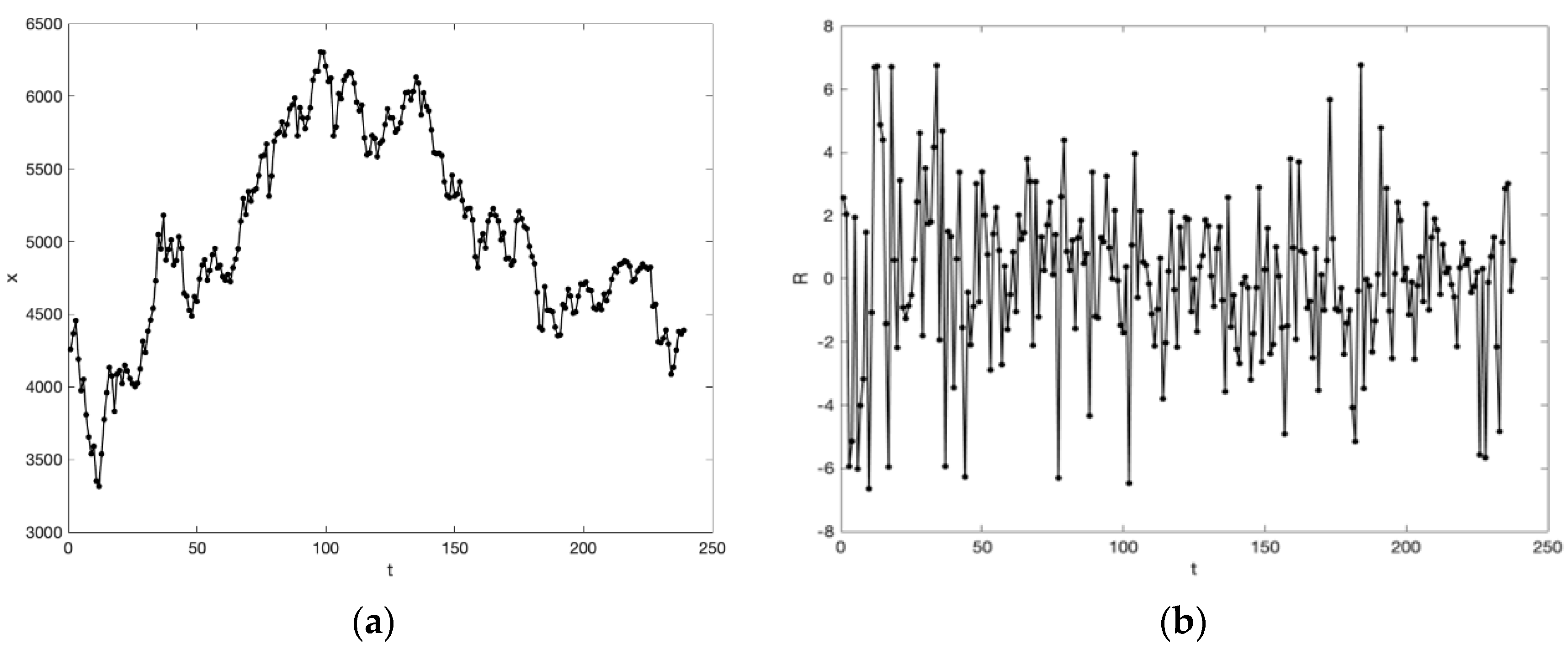
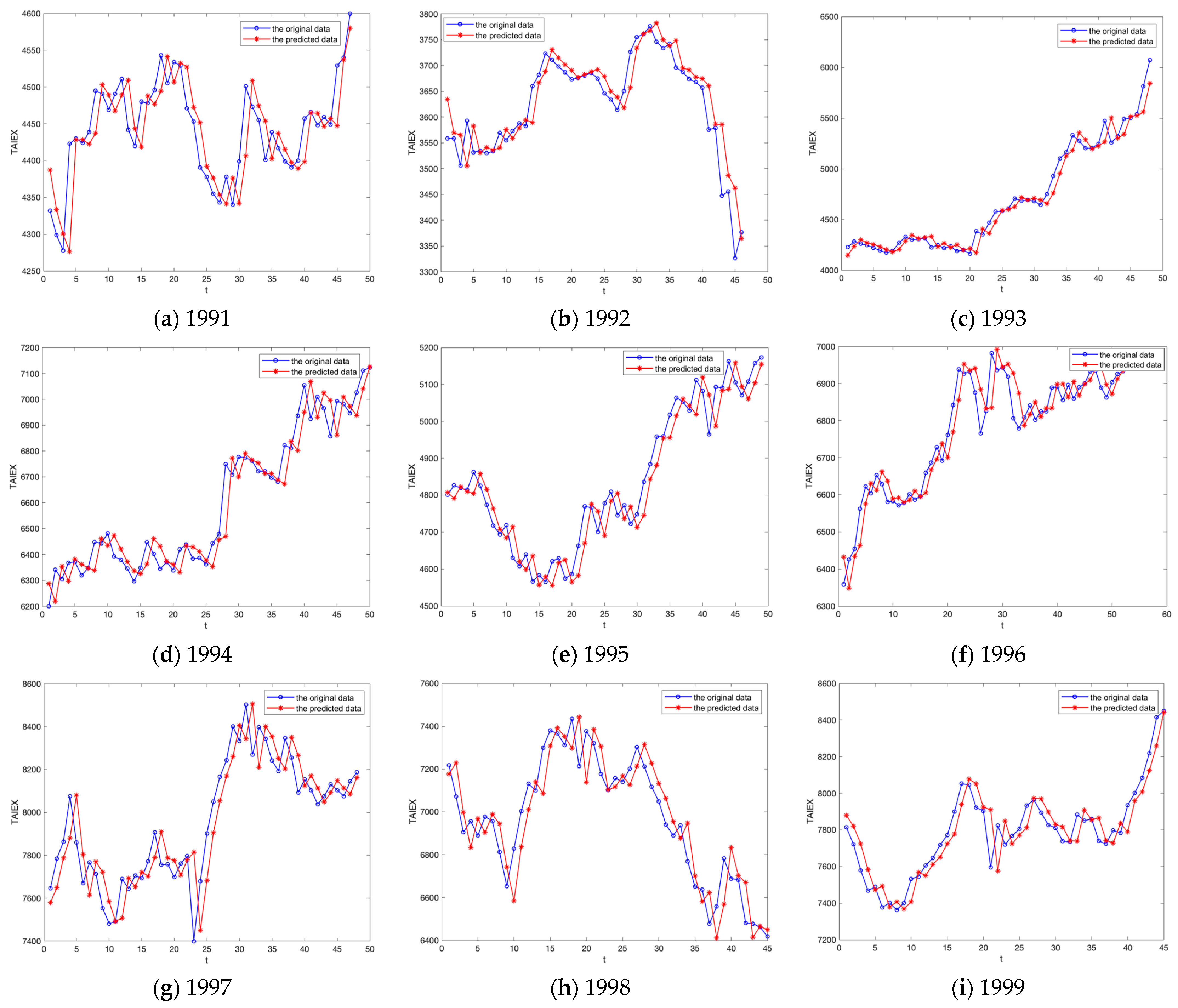
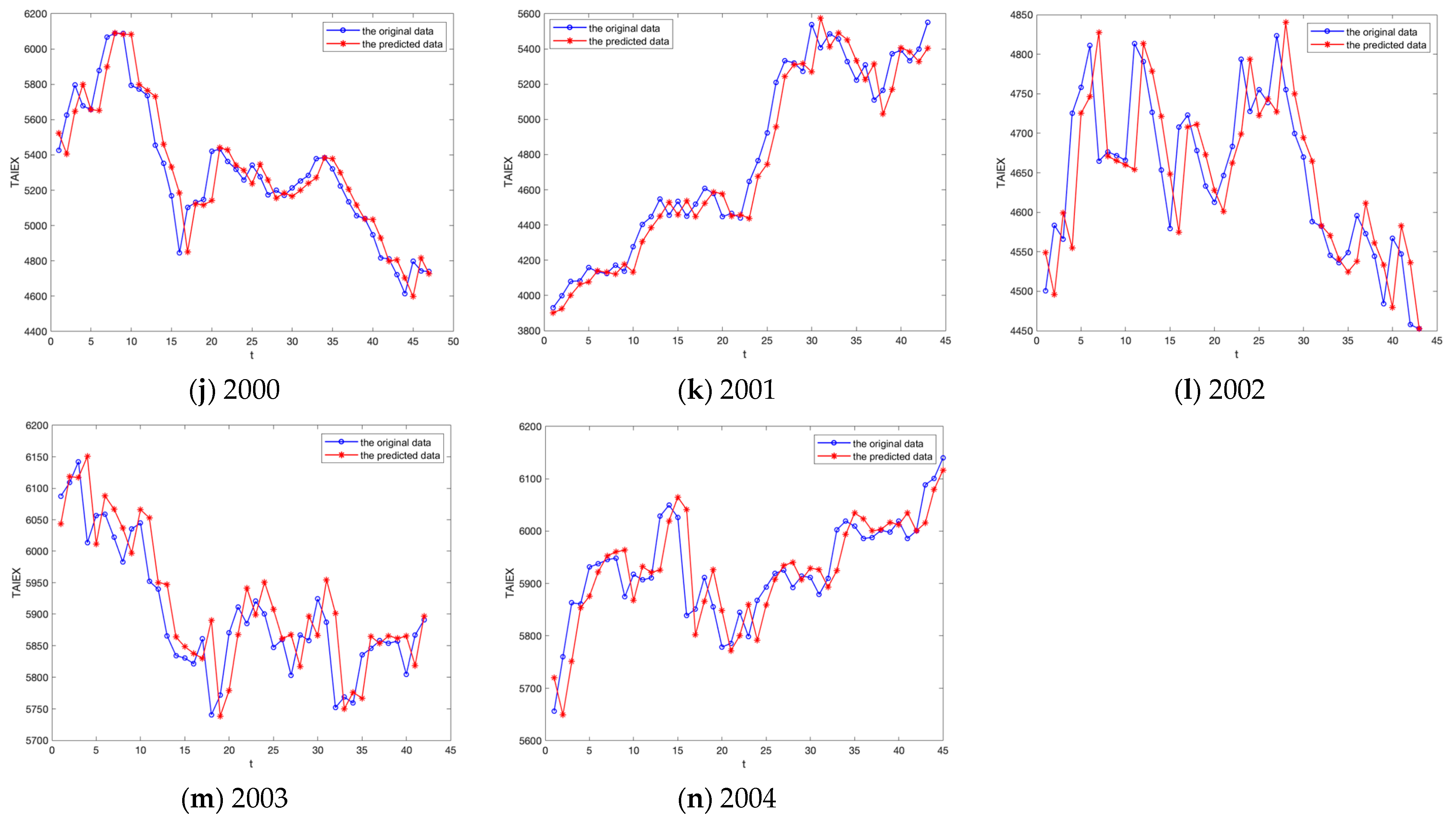
5.2. Experiment A: TAIEX Forecasting
5.3. Experiment B: SHCI Forecasting
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, Y.; Zhang, Z.Y.; Zhao, Y. Stock index forecasting based on multivariate empirical mode decomposition and temporal convolutional networks. Appl. Soft Comput. 2023, 142, 110356. [Google Scholar] [CrossRef]
- Palash, W.; Akanda, A.S.; Islam, S. A data-driven global flood forecasting system for medium to large rivers. Sci. Rep. 2024, 14, 8979. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.; Liu, C.; Wu, W.-Z. A novel fractional grey system model with non-singular exponential kernel for forecasting enrollments. Expert Syst. Appl. 2023, 219, 119652. [Google Scholar] [CrossRef]
- Meng, X.; Zhao, H.; Shu, T.; Zhao, J.H.; Wan, Q.L. Machine learning-based spatial downscaling and bias-correction framework for high-resolution temperature forecasting. Appl. Intell. 2024, 54, 8399–8414. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1990. [Google Scholar]
- Aasim, S.N.; Singh, A. Mohapatra, Data driven day-ahead electrical load forecasting through repeated wavelet transform assisted SVM model. Appl. Soft Comput. 2021, 111, 107730. [Google Scholar] [CrossRef]
- Wei, X.K.; Li, Y.H.; Zhang, P.; Lu, J.M. Analysis and applications of time series forecasting model via support vector machines. Syst. Eng. Electron. 2005, 27, 529–532. (In Chinese) [Google Scholar]
- Wibawa, A.P.; Utama, A.B.P.; Elmunsyah, H.; Pujianto, U.; Dwiyanto, F.A.; Hernandez, L. Time-series analysis with smoothed Convolutional Neural Network. J. Big Data 2022, 9, 44. [Google Scholar] [CrossRef]
- Kirisci, M.; Cagcag Yolcu, O. A new CNN-based model for financial time series: TAIEX and FTSE stocks forecasting. Neural Process. Lett. 2022, 54, 3357–3374. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data, Los Angeles, CA, USA, 9–12 December 2019. [Google Scholar]
- Zhou, F.; Huang, Z.; Zhang, C. Carbon price forecasting based on CEEMDAN and LSTM. Appl. Energy 2022, 311, 118601. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and its Applications to Modeling and Control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series—Part I. Fuzzy Sets Syst. 1993, 54, 1–9. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series—Part II. Fuzzy Sets Syst. 1994, 62, 1–8. [Google Scholar] [CrossRef]
- Chen, S.M.; Wang, J.R. A Novel Fuzzy Time Series Forecasting Model Based on Optimal Partitioning of the Universe of Discourse. Fuzzy Sets Syst. 2000, 114, 159–175. [Google Scholar]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Huarng, K. Effective Lengths of Intervals to Improve Forecasting in Fuzzy Time Series. Fuzzy Sets Syst. 2001, 123, 387–394. [Google Scholar] [CrossRef]
- Huarng, K.; Yu, H.K. Ratio-Based Lengths of Intervals to Improve Fuzzy Time Series Forecasting. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2006, 36, 328–340. [Google Scholar] [CrossRef]
- Chen, S.M.; Hsu, C.C. A New Method to Forecast Enrollments Using Fuzzy Time Series. Int. J. Appl. Sci. Eng. 2004, 2, 234–244. [Google Scholar]
- Chen, M.Y.; Chen, B.T. A Hybrid Fuzzy Time Series Model Based on Granular Computing for Stock Price Forecasting. Inf. Sci. 2015, 294, 227–241. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Pedrycz, W. Effective Intervals Determined by Information Granules to Improve Forecasting in Fuzzy Time Series. Expert Syst. Appl. 2013, 40, 5673–5679. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Pedrycz, W.; Shao, Y.Y. Determination of Temporal Information Granules to Improve Forecasting in Fuzzy Time Series. Expert Syst. Appl. 2014, 41, 3134–3142. [Google Scholar] [CrossRef]
- Yin, Y.; Sheng, Y.; Qin, J. Interval type-2 fuzzy C-means forecasting model for fuzzy time series. Appl. Soft Comput. 2022, 129, 109574. [Google Scholar] [CrossRef]
- Pedrycz, W.; Wang, X.M. Designing fuzzy sets with the use of the parametric principle of justifiable granularity. IEEE Trans. Fuzzy Syst. 2016, 24, 489–496. [Google Scholar] [CrossRef]
- Moreno, J.E.; Sanchez, M.A.; Mendoza, O.; Rodríguez-Díaz, A.; Castillo, O.; Melin, P.; Castro, J.R. Design of an interval Type-2 fuzzy model with justifiable uncertainty. Inf. Sci. 2020, 513, 206–221. [Google Scholar] [CrossRef]
- Zhang, B.; Pedrycz, W.; Wang, X.; Gacek, A. Design of Interval Type-2 Information Granules Based on the Principle of Justifiable Granularity. IEEE Trans. Fuzzy Syst. 2021, 29, 3456–3469. [Google Scholar] [CrossRef]
- Castillo, O.; Castro, J.R.; Melin, P. A Methodology for Building of Interval and General Type-2 Fuzzy Systems Based on the Principle of Justifiable Granularity. J. Mult. Valued Log. Soft Comput. 2023, 40, 253–284. [Google Scholar]
- Aladag, C.H.; Basaran, M.A.; Egrioglu, E.; Yolcu, U.; Uslu, V.R. Forecasting in High Order Fuzzy Times Series by Using Neural Networks to Define Fuzzy Relations. Expert Syst. Appl. 2009, 36, 4228–4231. [Google Scholar] [CrossRef]
- Aladag, C.H.; Yolcu, U.; Egrioglu, E. A High Order Fuzzy Time Series Forecasting Model Based on Adaptive Expectation and Artificial Neural Networks. Math. Comput. Simul. 2010, 81, 875–882. [Google Scholar] [CrossRef]
- Egrioglu, E.; Aladag, C.H.; Yolcu, U.; Uslu, V.R.; Basaran, M.A. Finding an Optimal Interval Length in High Order Fuzzy Time Series. Expert Syst. Appl. 2010, 37, 5052–5055. [Google Scholar] [CrossRef]
- Kuo, I.H.; Horng, S.J.; Chen, Y.H.; Run, R.S.; Kao, T.W.; Chen, R.J.; Lai, J.L.; Lin, T.L. Forecasting TAIFEX Based on Fuzzy Time Series and Particle Swarm Optimization. Expert Syst. Appl. 2010, 37, 1494–1502. [Google Scholar] [CrossRef]
- Huang, Y.L.; Horng, S.J.; He, M.; Fan, P.; Kao, T.W.; Khan, M.K.; Lai, J.L.; Kuo, I.H. A Hybrid Forecasting Model for Enrollments Based on Aggregated Fuzzy Time Series and Particle Swarm Optimization. Expert Syst. Appl. 2011, 38, 8014–8023. [Google Scholar] [CrossRef]
- Pant, M.; Kumar, S. Fuzzy time series forecasting based on hesitant fuzzy sets, particle swarm optimization and support vector machine-based hybrid method. Granul. Comput. 2022, 7, 861–879. [Google Scholar] [CrossRef]
- Didugu, G.; Gandhudi, M.; Alphonse, P.J.A.; Gangadharan, G.R. VWFTS-PSO: A novel method for time series forecasting using variational weighted fuzzy time series and particle swarm optimization. Int. J. Gen. Syst. 2024, 54, 540–559. [Google Scholar] [CrossRef]
- Xian, S.; Zhang, J.; Xiao, Y.; Pang, J. A novel fuzzy time series forecasting method based on the improved artificial fish swarm optimization algorithm. Soft Comput. 2018, 22, 3907–3917. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy C-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Pedrycz, W.; Vukovich, G. Abstraction and specialization of information granules. IEEE Trans. Syst. Man Cybern. B Cybern. 2001, 31, 106–111. [Google Scholar] [CrossRef]
- Pedrycz, W.; Homenda, W. Building the fundamentals of granular computing: A principle of justifiable granularity. Appl. Soft Comput. 2013, 13, 4209–4218. [Google Scholar] [CrossRef]
- Geng, G.; He, Y.; Zhang, J.; Qin, T.; Yang, B. Short-Term Power Load Forecasting Based on PSO-Optimized VMD-TCN-Attention Mechanism. Energies 2023, 16, 4616. [Google Scholar] [CrossRef]
- Lu, W. Time Series Analysis and Modeling Method Research Based on Granular Computing; Dalian University of Technology: Dalian, China, 2015. (In Chinese) [Google Scholar]
- Shao, G.H. Modeling and Forecasting Based on Multivariate Granular Time Series; Dalian University of Technology: Dalian, China, 2017. (In Chinese) [Google Scholar]
- Zhou, W. Modeling Methods for Interval-Valued Time Series Based on Granular Computing; Dalian University of Technology: Dalian, China, 2019. (In Chinese) [Google Scholar]
- Sullivan, J.; Woodall, W.H. A Comparison of Fuzzy Forecasting and Markov Modeling. Fuzzy Sets Syst. 1994, 64, 279–293. [Google Scholar] [CrossRef]
- Chen, S.M. Forecasting Enrollments Based on Fuzzy Time Series. Fuzzy Sets Syst. 1996, 81, 311–319. [Google Scholar] [CrossRef]
- Huarng, K. Heuristic Models of Fuzzy Time Series for Forecasting. Fuzzy Sets Syst. 2001, 123, 369–386. [Google Scholar] [CrossRef]
- Yu, T. Weighted Fuzzy Time Series Model for TAIEX Forecasting. Physica A 2005, 349, 609–624. [Google Scholar] [CrossRef]
- Huarng, K.; Yu, T.H.K. The Application of Neural Networks to Forecast Fuzzy Time Series. Phys. A Stat. Mech. Appl. 2006, 363, 481–491. [Google Scholar] [CrossRef]
- Chen, S.M.; Wang, N.Y. Fuzzy Forecasting Based on Fuzzy-trend Logical Relationship Groups. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2010, 40, 10594–10605. [Google Scholar]
- Chen, S.M.; Chen, C.D. TAIEX Forecasting Based on Fuzzy Time Series and Fuzzy Variation Groups. IEEE Trans. Fuzzy Syst. 2011, 19, 1–12. [Google Scholar] [CrossRef]
- Wang, X. A hybrid forecasting model based on automatic clustering, axiomatic fuzzy set classification, and autoregressive integrated moving average (ARIMA) for stock market trends. Expert Syst. Appl. 2016, 55, 1–10. [Google Scholar] [CrossRef]
- Huarng, K.H.; Yu, T.H.K.; Hsu, Y.W. A Multivariate Heuristic Model for Fuzzy Time-Series Forecasting. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2007, 37, 836–846. [Google Scholar] [CrossRef]
- Yu, T.H.K.; Huarng, K.H. A Bivariate Fuzzy Time Series Model to Forecast the TAIEX. Expert Syst. Appl. 2008, 34, 2945–2952. [Google Scholar] [CrossRef]
- Chen, S.M.; Chang, Y.C. Multi-Variable Fuzzy Forecasting Based on Fuzzy Clustering and Fuzzy Rule Interpolation Techniques. Inf. Sci. 2010, 180, 4772–4783. [Google Scholar] [CrossRef]
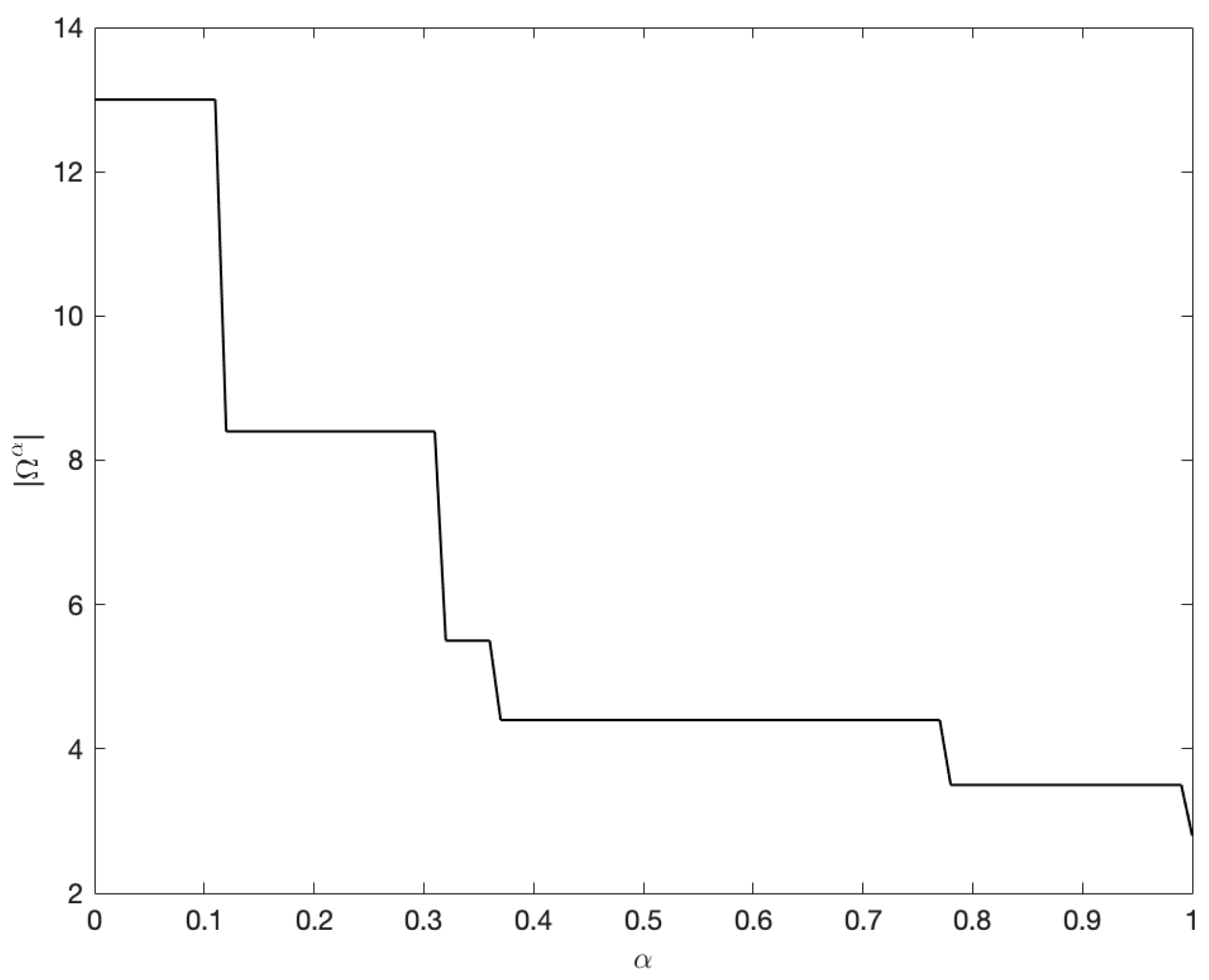
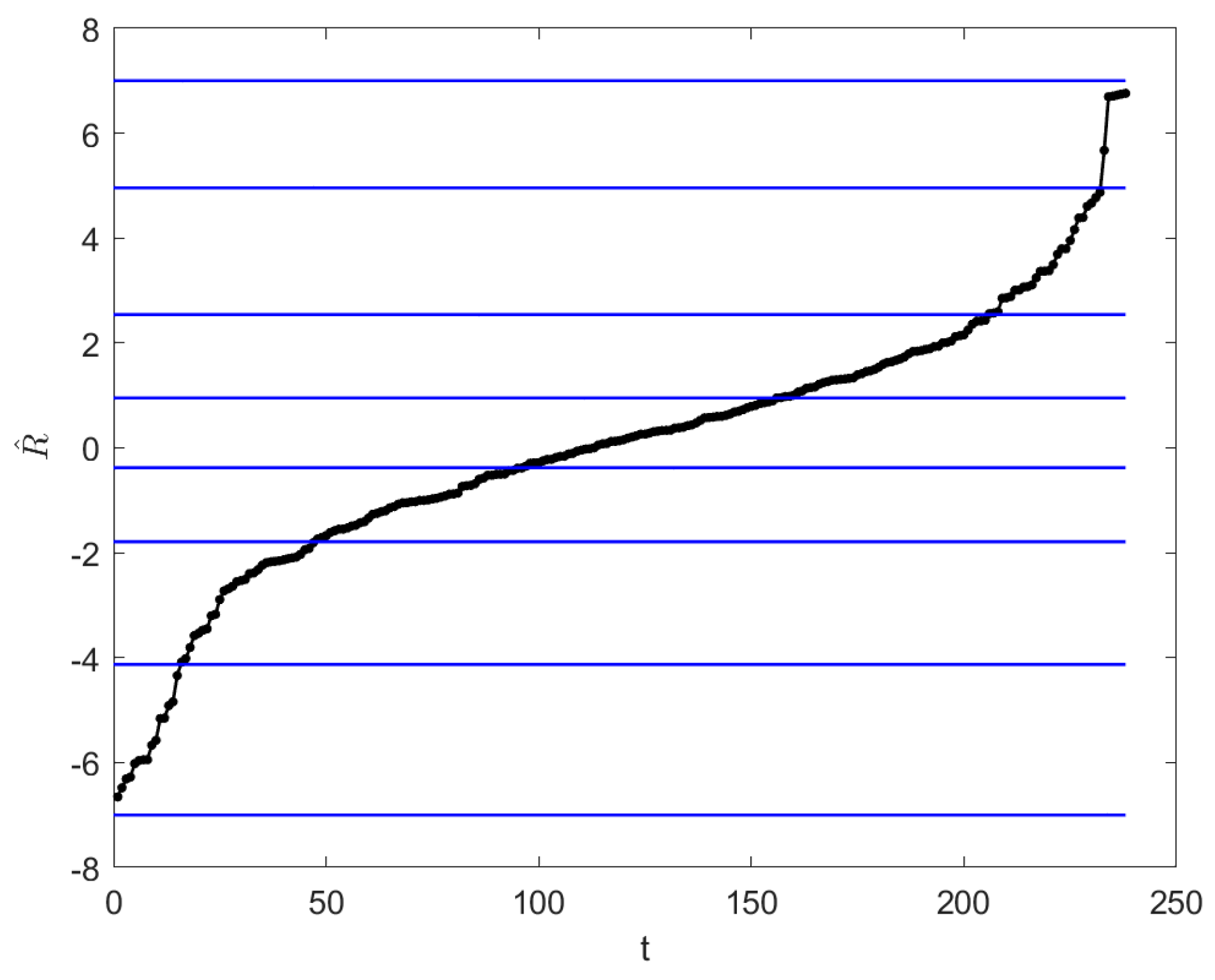

| α | Ωα | α | Ωα |
|---|---|---|---|
| 0 | [−8,5] | 0.6 | [−2.3,2.1] |
| 0.1 | [−8,5] | 0.7 | [−2.3,2.1] |
| 0.2 | [−3.4,5] | 0.8 | [−2.3,1.2] |
| 0.3 | [−3.4,5] | 0.9 | [−2.3,1.2] |
| 0.4 | [−2.3,2.1] | 1 | [−1.6,1.2] |
| 0.5 | [−2.3,2.1] |
| Time | The Original Data | The Rate of Change (%) | Time | The Original Data | The Rate of Change (%) |
|---|---|---|---|---|---|
| 03/01/1991 | 4258 | - | 02/07/1991 | 5613 | −2.69 |
| 04/01/1991 | 4367 | 2.56 | 03/07/1991 | 5604 | −0.16 |
| 05/01/1991 | 4456 | 2.04 | 04/07/1991 | 5607 | 0.05 |
| 07/01/1991 | 4191 | −5.95 | 05/07/1991 | 5591 | −0.29 |
| 08/01/1991 | 3975 | −5.15 | 06/07/1991 | 5412 | −3.20 |
| 25/06/1991 | 5872 | −3.58 | 23/10/1991 | 4135 | 1.15 |
| 26/06/1991 | 6023 | 2.57 | 24/10/1991 | 4253 | 2.85 |
| 27/06/1991 | 5931 | −1.53 | 28/10/1991 | 4381 | 3.01 |
| 28/06/1991 | 5900 | −0.52 | 29/10/1991 | 4364 | −0.39 |
| 29/06/1991 | 5768 | −2.24 | 30/10/1991 | 4389 | 0.57 |
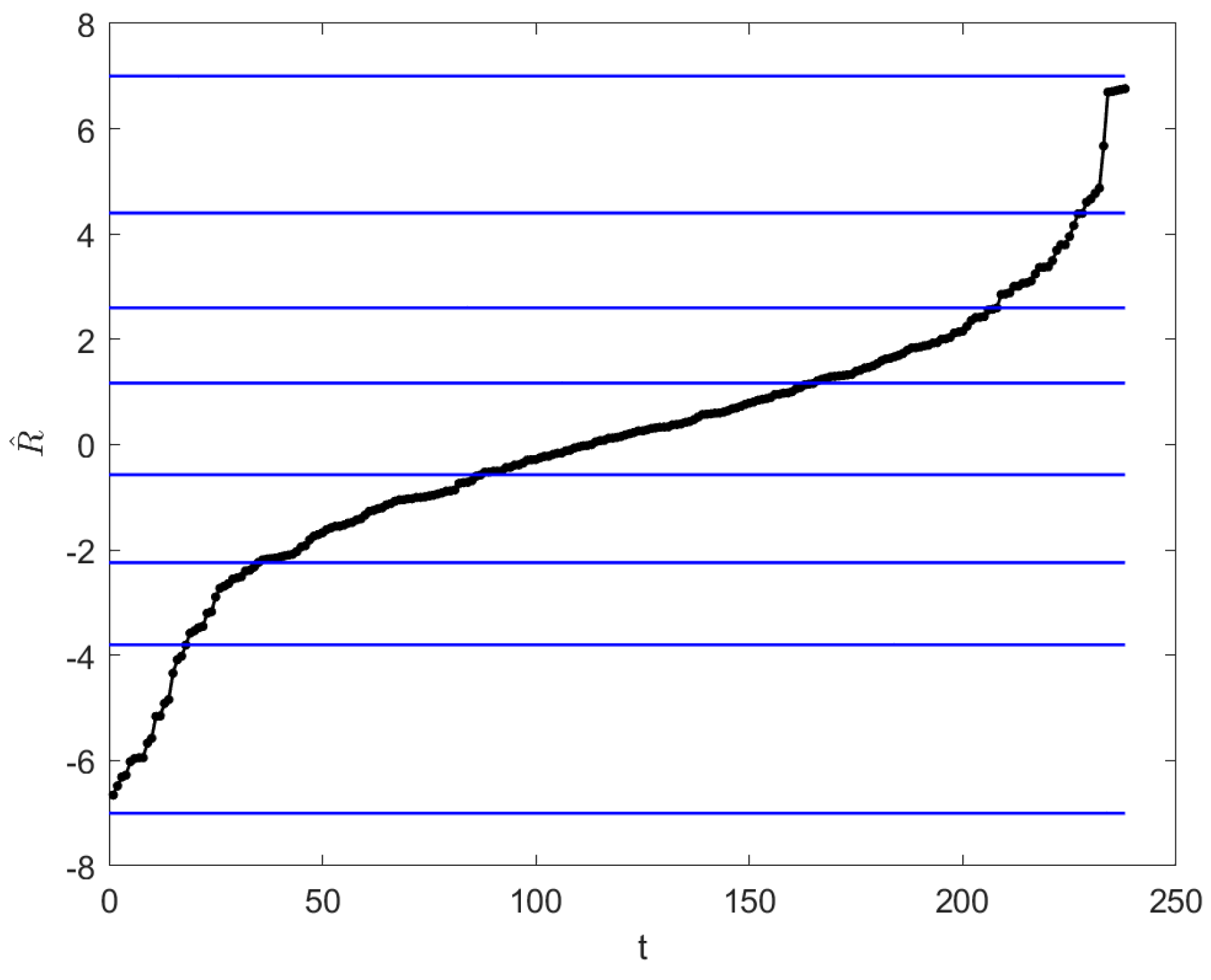
| Subinterval | Fuzzy Set | Semantic Value |
|---|---|---|
| [−7.00, −3.80) | A1 | Sharp decrease |
| [−3.80, −2.24) | A2 | Decrease |
| [−2.24, −0.57) | A3 | Slight decrease |
| [−0.57, 1.17) | A4 | No change |
| [1.17, 2.60) | A5 | Slight increase |
| [2.60, 4.40) | A6 | Increase |
| [4.40, 7.00] | A7 | Sharp increase |
| Time | The Rate of Change (%) | Fuzzy Value | Time | The Rate of Change (%) | Fuzzy Value |
|---|---|---|---|---|---|
| 03/01/1991 | - | - | 02/07/1991 | −2.69 | A2 |
| 04/01/1991 | 2.56 | A5 | 03/07/1991 | −0.16 | A4 |
| 05/01/1991 | 2.04 | A5 | 04/07/1991 | 0.05 | A4 |
| 07/01/1991 | −5.95 | A1 | 05/07/1991 | −0.29 | A4 |
| 08/01/1991 | −5.15 | A1 | 06/07/1991 | −3.20 | A2 |
| 25/06/1991 | −3.58 | A2 | 23/10/1991 | 1.15 | A4 |
| 26/06/1991 | 2.57 | A5 | 24/10/1991 | 2.85 | A6 |
| 27/06/1991 | −1.53 | A3 | 28/10/1991 | 3.01 | A6 |
| 28/06/1991 | −0.52 | A4 | 29/10/1991 | −0.39 | A4 |
| 29/06/1991 | −2.24 | A3 | 30/10/1991 | 0.57 | A4 |
| Time | Fuzzy Value | First-Order FLR | Time | Fuzzy Value | First-Order FLR |
|---|---|---|---|---|---|
| 03/01/1991 | - | - | 02/07/1991 | A2 | A3 → A2 |
| 04/01/1991 | A5 | - | 03/07/1991 | A4 | A2 → A4 |
| 05/01/1991 | A5 | A5 → A5 | 04/07/1991 | A4 | A4 → A4 |
| 07/01/1991 | A1 | A5 → A1 | 05/07/1991 | A4 | A4 → A4 |
| 08/01/1991 | A1 | A1 → A1 | 06/07/1991 | A2 | A4 → A2 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 25/06/1991 | A2 | A3 → A2 | 23/10/1991 | A4 | A1 → A4 |
| 26/06/1991 | A5 | A2 → A5 | 24/10/1991 | A6 | A4 → A6 |
| 27/06/1991 | A3 | A5 → A3 | 28/10/1991 | A6 | A6 → A6 |
| 28/06/1991 | A4 | A3 → A4 | 29/10/1991 | A4 | A6 → A4 |
| 29/06/1991 | A3 | A4 → A3 | 30/10/1991 | A4 | A4 → A4 |
| FLRGs | ||
|---|---|---|
| Ft−1 | Ft | ||||||
|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | |
| A1 | 3 | 1 | 3 | 6 | 3 | 1 | 1 |
| A2 | 0 | 0 | 4 | 9 | 3 | 0 | 0 |
| A3 | 5 | 4 | 11 | 16 | 8 | 7 | 2 |
| A4 | 5 | 7 | 17 | 27 | 12 | 6 | 3 |
| A5 | 4 | 2 | 7 | 13 | 13 | 3 | 1 |
| A6 | 0 | 1 | 9 | 5 | 2 | 2 | 1 |
| A7 | 1 | 1 | 2 | 2 | 1 | 1 | 2 |
| Ft−1 | Ft | ||||||
|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | |
| A1 | 0.17 | 0.05 | 0.17 | 0.34 | 0.17 | 0.05 | 0.05 |
| A2 | 0 | 0 | 0.25 | 0.56 | 0.19 | 0 | 0 |
| A3 | 0.09 | 0.08 | 0.21 | 0.30 | 0.15 | 0.13 | 0.04 |
| A4 | 0.06 | 0.09 | 0.22 | 0.35 | 0.16 | 0.08 | 0.04 |
| A5 | 0.09 | 0.05 | 0.16 | 0.30 | 0.30 | 0.08 | 0.02 |
| A6 | 0 | 0.05 | 0.45 | 0.25 | 0.10 | 0.10 | 0.05 |
| A7 | 0.10 | 0.10 | 0.20 | 0.20 | 0.10 | 0.10 | 0.20 |
| Year | Size | Training Set | Size of Training Set | Test Set | Size of Test Set |
|---|---|---|---|---|---|
| 1991 | 286 | 1/3~10/30 | 239 | 11/1~12/28 | 47 |
| 1992 | 284 | 1/4~10/30 | 238 | 11/2~12/29 | 46 |
| 1993 | 291 | 1/5~10/30 | 243 | 11/2~12/31 | 48 |
| 1994 | 286 | 1/5~10/29 | 236 | 11/1~12/31 | 50 |
| 1995 | 286 | 1/5~10/30 | 237 | 11/1~12/30 | 49 |
| 1996 | 288 | 1/4~10/30 | 236 | 11/1~12/31 | 52 |
| 1997 | 286 | 1/4~10/30 | 238 | 11/3~12/31 | 48 |
| 1998 | 271 | 1/3~10/31 | 226 | 11/2~12/31 | 45 |
| 1999 | 266 | 1/5~10/30 | 221 | 11/1~12/28 | 45 |
| 2000 | 271 | 1/4~10/31 | 224 | 11/1~12/30 | 47 |
| 2001 | 244 | 1/2~10/31 | 201 | 11/1~12/31 | 43 |
| 2002 | 248 | 1/2~10/31 | 205 | 11/1~12/31 | 43 |
| 2003 | 248 | 1/2~10/31 | 206 | 11/3~12/31 | 42 |
| 2004 | 250 | 1/2~10/29 | 205 | 11/1~12/31 | 45 |
| Parameters | Value |
|---|---|
| Particle swarm size | 150 |
| Number of iterations | 1000 |
| Inertia weight coefficient | 0.8 |
| Cognitive coefficient | 1.5 |
| Social coefficient | 1.5 |
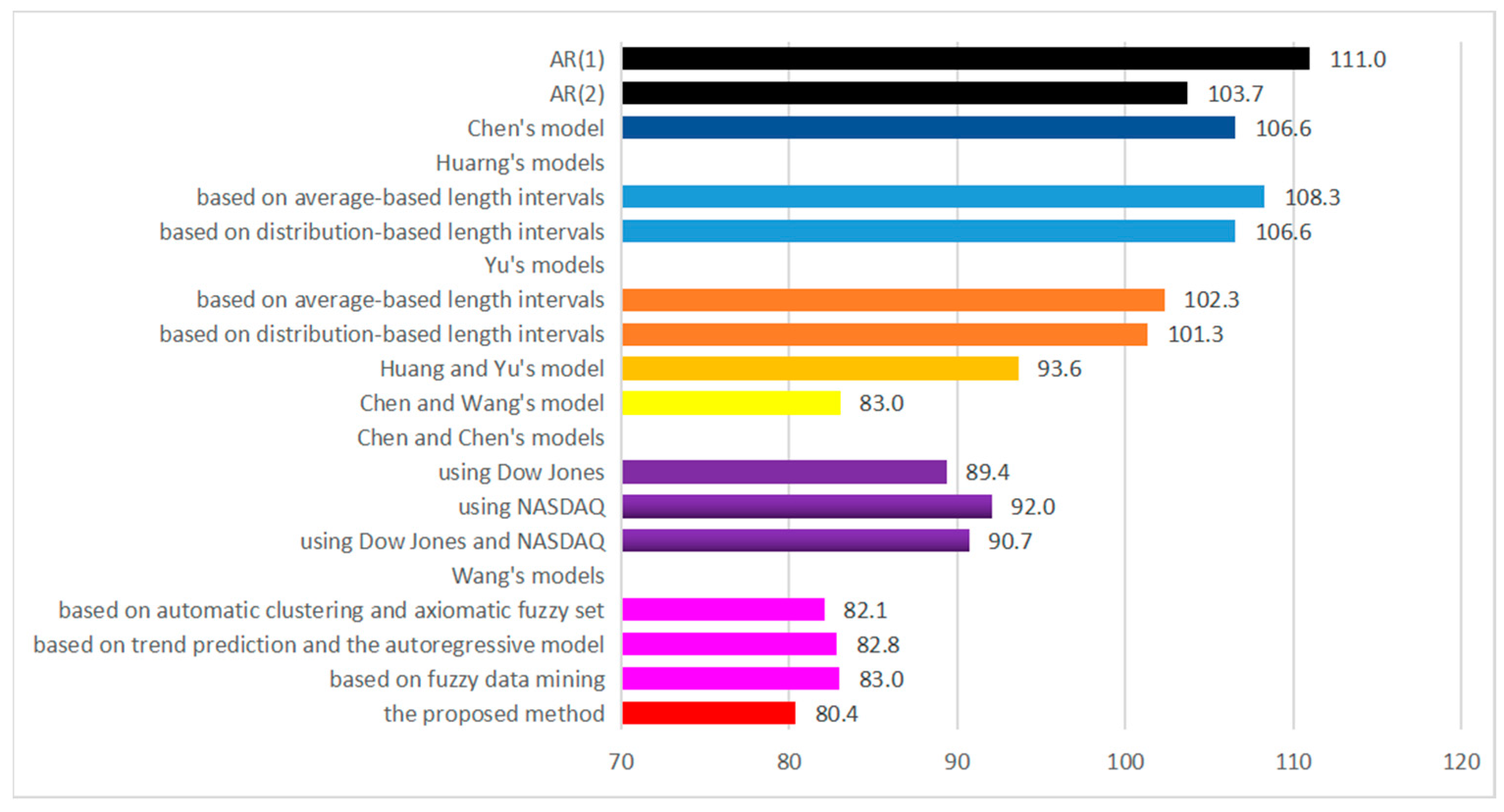
| Models | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
|---|---|---|---|---|---|---|---|---|---|
| AR(1) [44] | 87.1 | 95.8 | 103.6 | 111.7 | 90.3 | 86 | 153.3 | 149.2 | 121.9 |
| AR(2) [44] | 59.2 | 76.9 | 110.9 | 111.1 | 69.2 | 62.9 | 175.3 | 137 | 130.9 |
| Chen [45] | 80 | 60 | 110 | 112 | 79 | 54 | 148 | 167 | 149 |
| Huarng [46] | |||||||||
| based on average-based length intervals | 79.4 | 59.9 | 105.2 | 132.4 | 78.6 | 52.1 | 148.8 | 159.3 | 159.1 |
| based on distribution-based length intervals | 80.2 | 60.3 | 110 | 111.7 | 78.6 | 54.2 | 148.0 | 167.3 | 148.7 |
| Yu [47] | |||||||||
| based on average-based length intervals | 61 | 67 | 105 | 135 | 70 | 54 | 133 | 151 | 145 |
| based on distribution-based length intervals | 67 | 56 | 105 | 114 | 70 | 52 | 152 | 154 | 142 |
| Huang and Yu [48] | 54.7 | 61.1 | 117.9 | 88.7 | 64.1 | 52.1 | 135.9 | 136.2 | 131.9 |
| Chen and Wang [49] | 42.9 | 43.5 | 103.4 | 89.8 | 52.2 | 52.8 | 140.8 | 116.9 | 104.9 |
| Chen and Chen [50] | |||||||||
| using Dow Jones | 72.9 | 43.4 | 103.2 | 78.6 | 66.7 | 59.8 | 139.7 | 124.4 | 115.5 |
| using NASDAQ | 66.1 | 49.6 | 104.8 | 75.7 | 67.0 | 60.9 | 140.9 | 144.1 | 119.3 |
| using Dow Jones and NASDAQ | 74.9 | 43.8 | 101.4 | 78.1 | 68.1 | 61.3 | 139.3 | 132.9 | 116.6 |
| Wang [51] | |||||||||
| based on automatic clustering and axiomatic fuzzy set | 43.6 | 41.4 | 102.4 | 89.0 | 55.0 | 49.4 | 139.0 | 118.2 | 100.9 |
| based on trend prediction and the autoregressive model | 42.5 | 44.0 | 101.0 | 93.1 | 52.9 | 50.5 | 145.1 | 115.1 | 101.3 |
| based on fuzzy data mining | 43.5 | 43.3 | 102.2 | 87.6 | 57.1 | 50.6 | 139.5 | 120.4 | 102.9 |
| The proposed method | 43.5 | 42.3 | 98.2 | 80.1 | 53.4 | 52.0 | 132.5 | 120.3 | 101.2 |
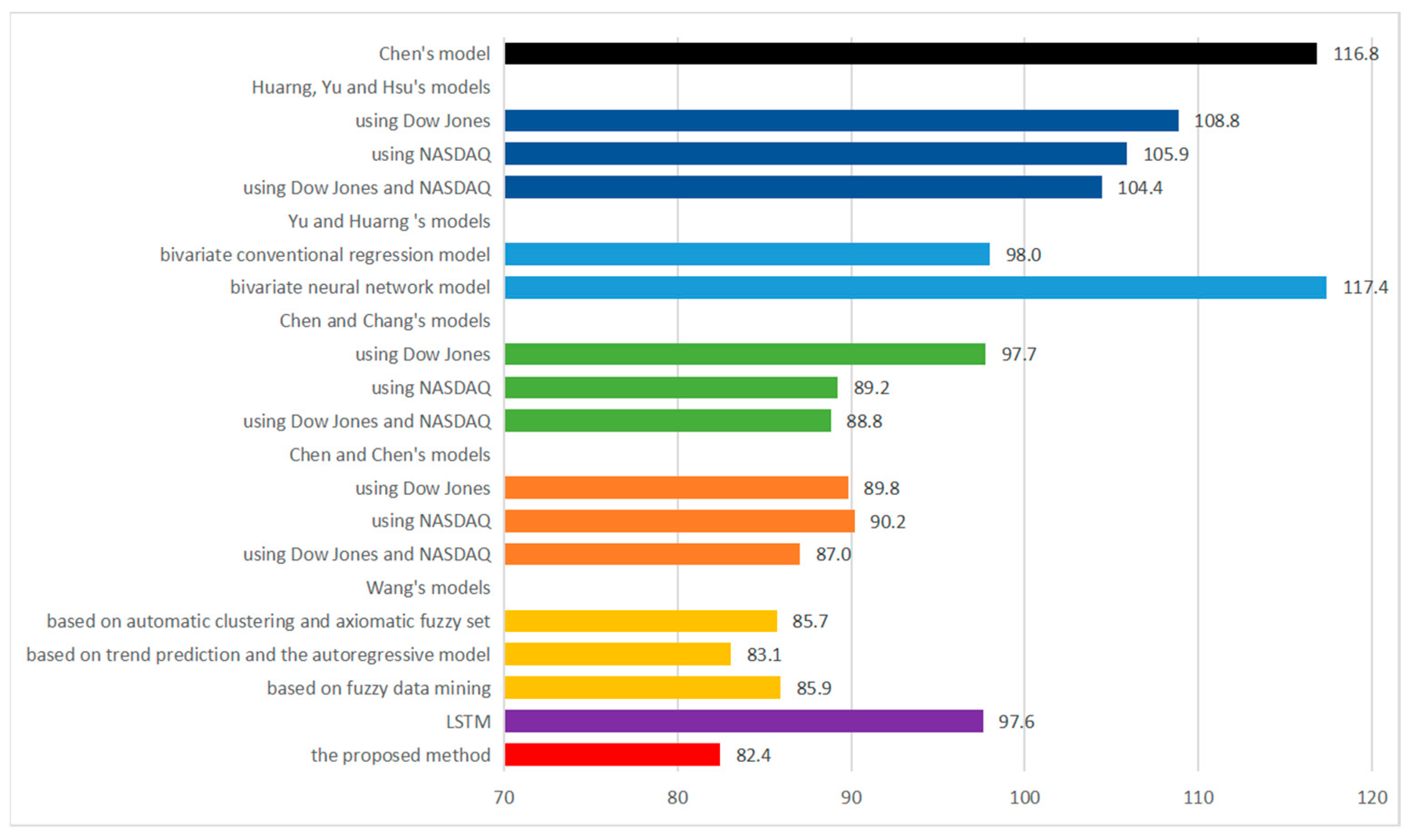
| Models | 2000 | 2001 | 2002 | 2003 | 2004 |
|---|---|---|---|---|---|
| Chen [45] | 176.3 | 147.8 | 101.2 | 74.5 | 84.3 |
| Huarng, Yu and Hsu [52] | |||||
| using Dow Jones | 165.8 | 138.25 | 93.73 | 72.95 | 73.49 |
| using NASDAQ | 158.7 | 136.49 | 95.15 | 65.51 | 73.57 |
| using Dow Jones and NASDAQ | 157.64 | 131.98 | 93.48 | 65.51 | 73.49 |
| Yu and Huarng [53] | |||||
| bivariate conventional regression model | 154 | 120 | 77 | 54 | 85 |
| bivariate neural network model | 274 | 131 | 69 | 52 | 61 |
| Chen and Chang [54] | |||||
| using Dow Jones | 148.8 | 113.7 | 79.8 | 64.08 | 82.32 |
| using NASDAQ | 131.1 | 115.1 | 73.1 | 66.4 | 60.5 |
| using Dow Jones and NASDAQ | 130.1 | 113.3 | 72.3 | 60.3 | 68.1 |
| Chen and Chen [50] | |||||
| using Dow Jones | 127.5 | 122.0 | 74.7 | 66.0 | 58.9 |
| using NASDAQ | 129.9 | 123.1 | 71.0 | 65.1 | 61.9 |
| using Dow Jones and NASDAQ | 123.6 | 123.9 | 71.9 | 58.1 | 57.7 |
| Wang [51] | |||||
| based on automatic clustering and axiomatic fuzzy set classification | 138.0 | 113.8 | 65.0 | 56.5 | 55.3 |
| based on trend prediction and the autoregressive model | 132.0 | 111.5 | 65.3 | 52.4 | 54.2 |
| based on fuzzy data mining | 131.6 | 113.6 | 68.5 | 59.3 | 56.7 |
| LSTM [9] | 136 | 101 | 89 | 92 | 70 |
| The proposed method | 121.2 | 112.7 | 65.5 | 57.6 | 55.2 |
| Year | Size | Training Set | Size of Training Set | Test Set | Size of Test Set |
|---|---|---|---|---|---|
| 2011 | 244 | 1/4~10/31 | 200 | 11/1~12/30 | 44 |
| 2012 | 243 | 1/4~10/31 | 200 | 11/1~12/31 | 43 |
| 2013 | 238 | 1/4~10/31 | 195 | 11/1~12/31 | 43 |
| 2014 | 245 | 1/2~10/31 | 202 | 11/3~12/31 | 43 |
| 2015 | 244 | 1/5~10/30 | 200 | 11/2~12/31 | 44 |
| 2016 | 244 | 1/4~10/31 | 200 | 11/1~12/30 | 44 |
| 2017 | 244 | 1/3~10/31 | 201 | 11/1~12/29 | 43 |
| 2018 | 243 | 1/2~10/31 | 201 | 11/1~12/28 | 42 |
| 2019 | 244 | 1/2~10/31 | 201 | 11/1~12/31 | 43 |
| Parameters | Value |
|---|---|
| Particle swarm size | 150 |
| Number of iterations | 1000 |
| Inertia weight coefficient | 0.8 |
| Cognitive coefficient | 1.5 |
| Social coefficient | 1.5 |
| Year | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
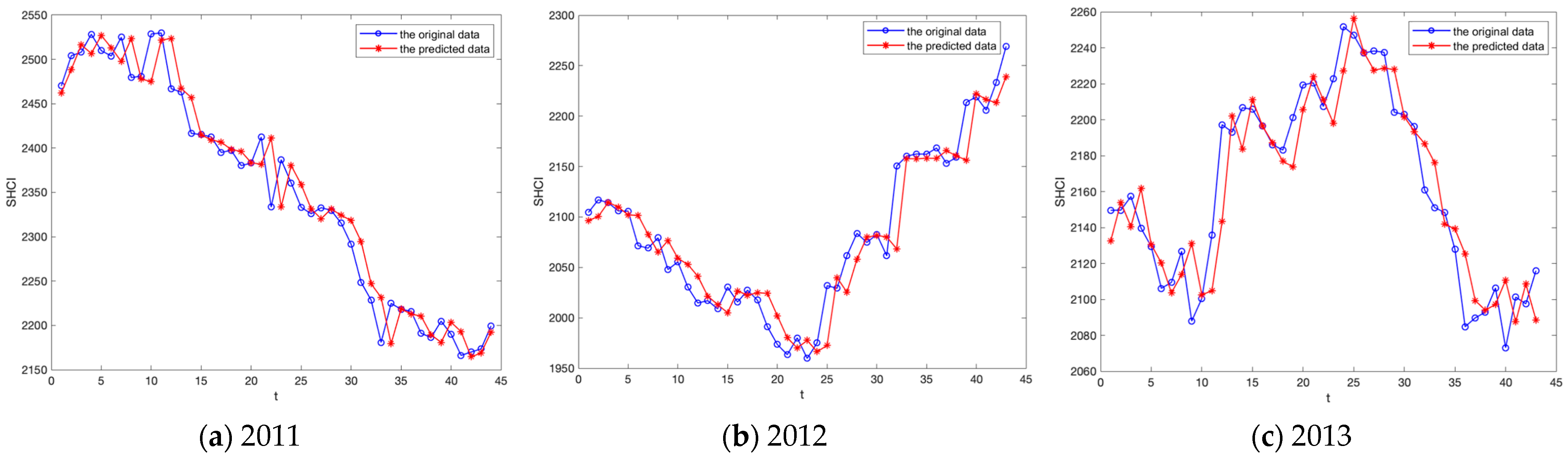
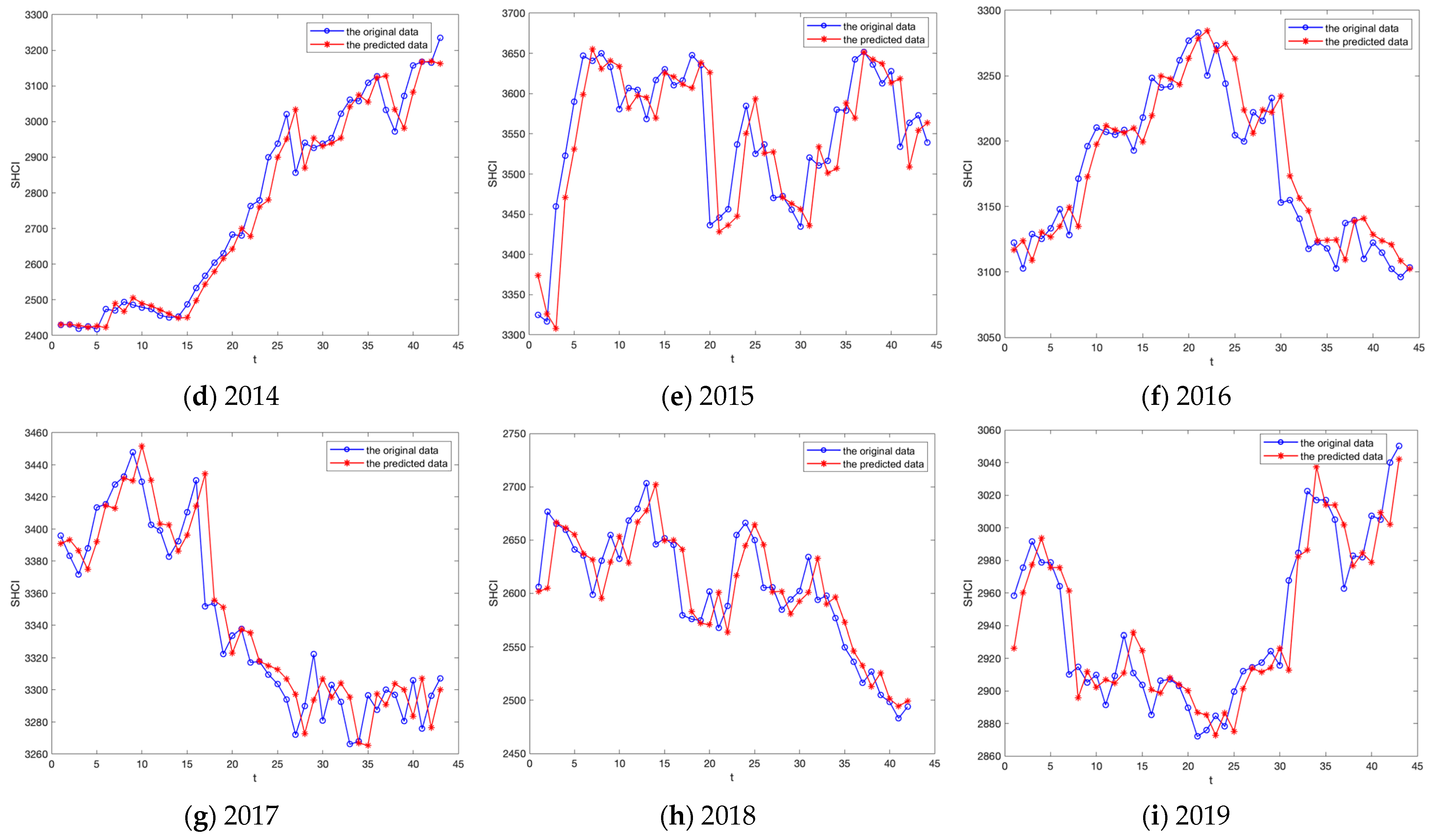
| RMSE | 27.40 | 24.13 | 19.69 | 52.05 | 54.00 | 22.06 | 21.05 | 26.75 | 20.12 |
| Year | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| LA(%) | 70.45 | 58.14 | 72.09 | 60.47 | 75.00 | 75.00 | 72.09 | 97.62 | 76.74 |
| p | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RMSE | 37.29 | 20.43 | 20.22 | 20.96 | 20.12 | 21.69 | 21.61 | 23.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Gao, X.; Wu, Q. An Enhanced Fuzzy Time Series Forecasting Model Integrating Fuzzy C-Means Clustering, the Principle of Justifiable Granularity, and Particle Swarm Optimization. Symmetry 2025, 17, 753. https://doi.org/10.3390/sym17050753
Chen H, Gao X, Wu Q. An Enhanced Fuzzy Time Series Forecasting Model Integrating Fuzzy C-Means Clustering, the Principle of Justifiable Granularity, and Particle Swarm Optimization. Symmetry. 2025; 17(5):753. https://doi.org/10.3390/sym17050753
Chicago/Turabian StyleChen, Hailan, Xuedong Gao, and Qi Wu. 2025. "An Enhanced Fuzzy Time Series Forecasting Model Integrating Fuzzy C-Means Clustering, the Principle of Justifiable Granularity, and Particle Swarm Optimization" Symmetry 17, no. 5: 753. https://doi.org/10.3390/sym17050753
APA StyleChen, H., Gao, X., & Wu, Q. (2025). An Enhanced Fuzzy Time Series Forecasting Model Integrating Fuzzy C-Means Clustering, the Principle of Justifiable Granularity, and Particle Swarm Optimization. Symmetry, 17(5), 753. https://doi.org/10.3390/sym17050753




