Insights into Freezeout Dynamics in Symmetric Heavy Ion Collisions with Changing Event Centrality
Abstract
1. Introduction
2. The Method and Formalism
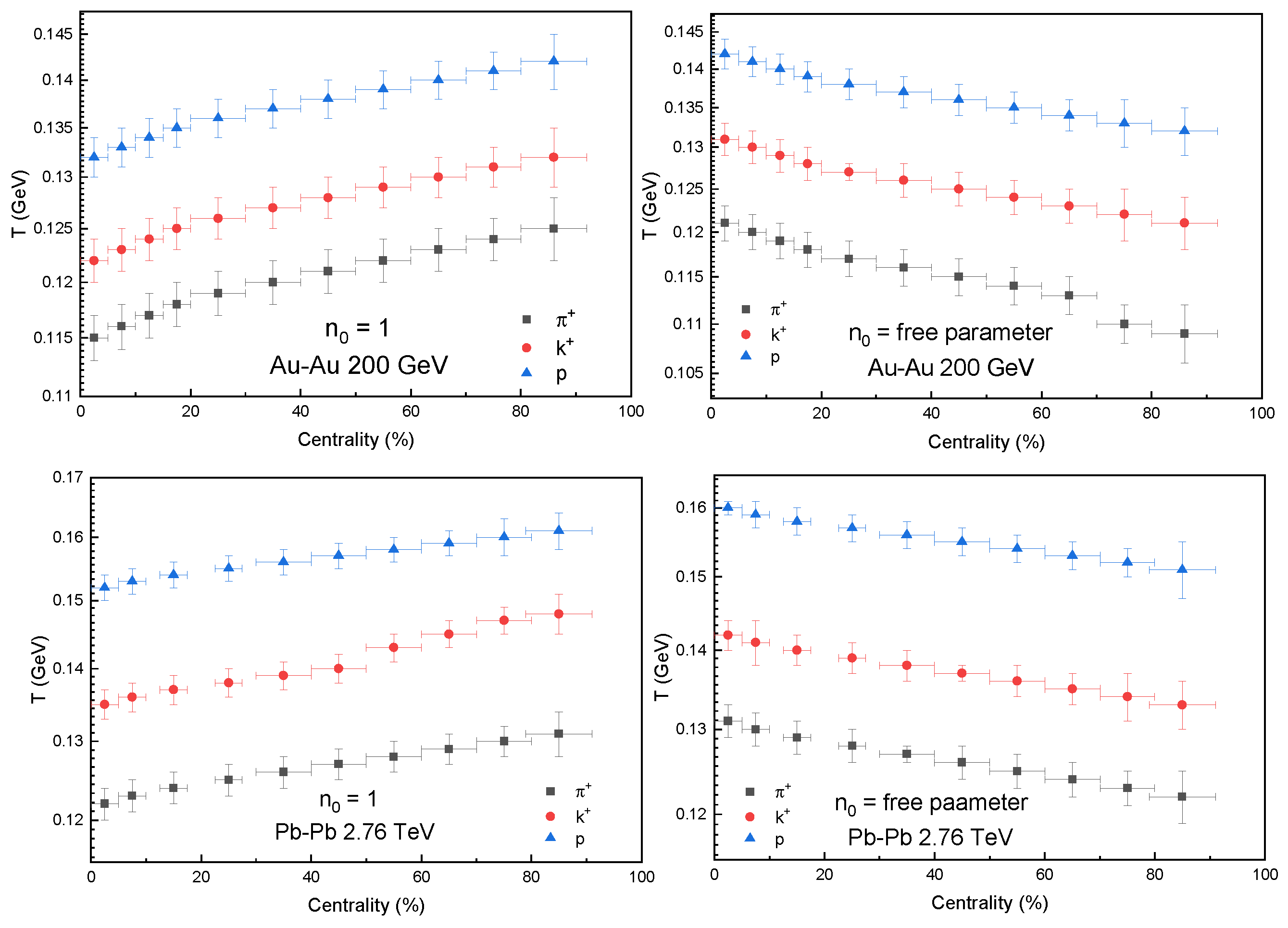
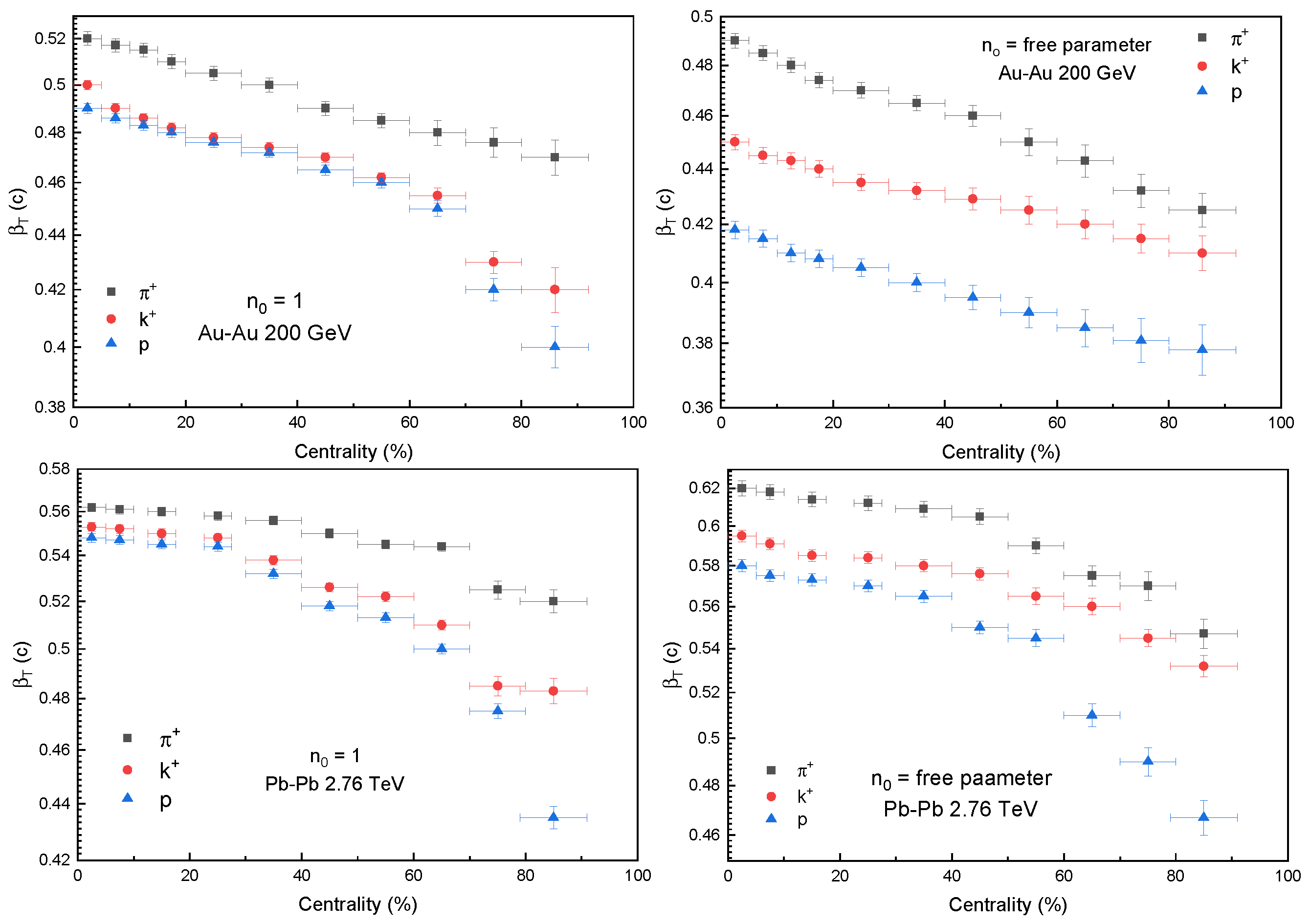
3. Results and Discussion
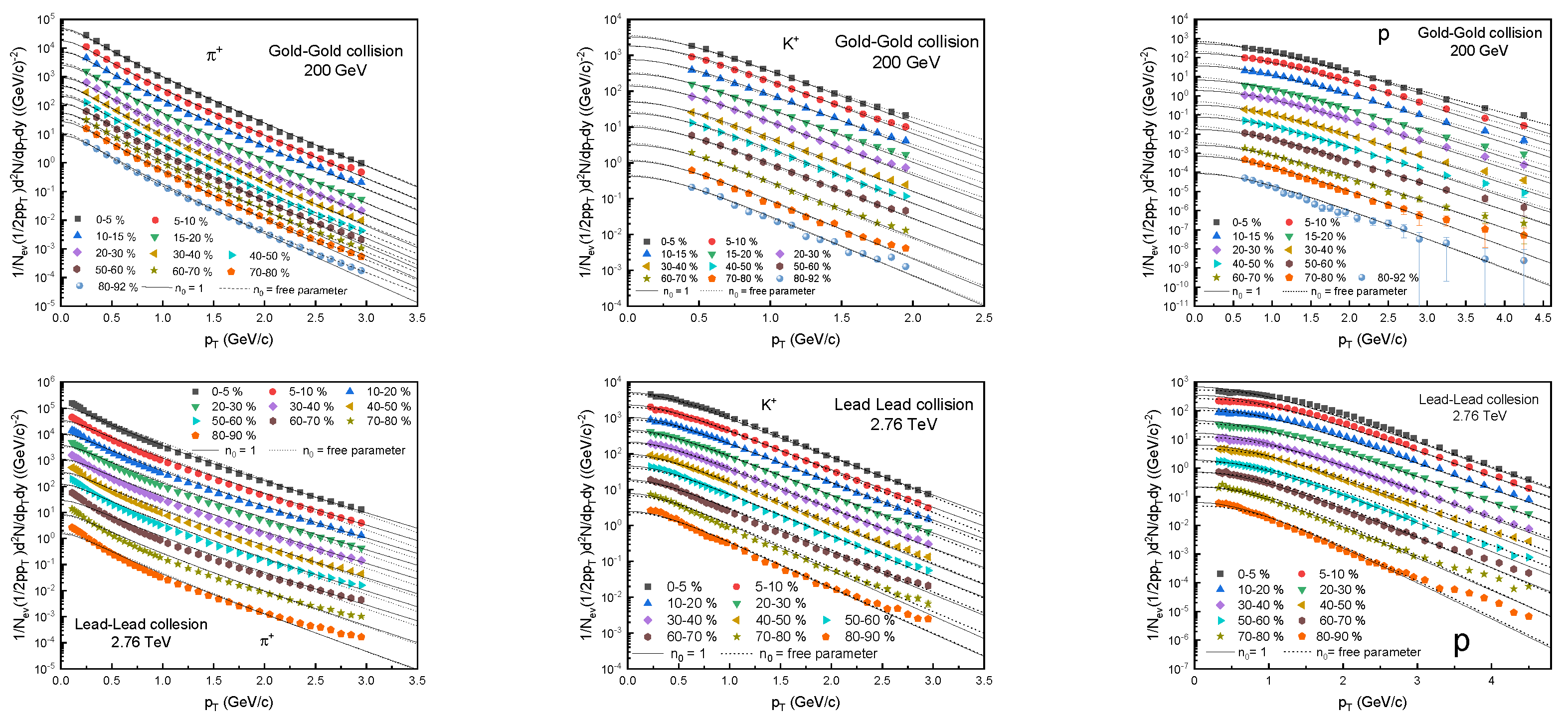
- (1)
- Anomalous centrality dependence of T (deviating from smooth participant scaling);
- (2)
- Correlated fluctuations in other observables (e.g., particle ratios, flow patterns);
- (3)
- Non-trivial system-size dependence.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jeon, S.; Koch, V. 2004 Review for Quark-Gluon Plasma 3; Hwa, R.C., Wang, X.-N., Eds.; World Scientific: Singapore, 2004. [Google Scholar]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291. [Google Scholar] [CrossRef]
- Ivanenko, D.D.; Kurdgelaidze, D.F. Hypothesis concerning quark stars. Astrophysics 1965, 1, 251. [Google Scholar] [CrossRef]
- Lee, T.D.; Wick, G.C. Vacuum Stability and Vacuum Excitation in a Spin 0 Field Theory. Phys. Rev. D 1974, 9, 2291. [Google Scholar] [CrossRef]
- Greiner, W.; Schafer, A. Quantum Chromodynamics; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; Christ, N.H.; DeTar, C.; Ejiri, S.; Gottlieb, S.; Gupta, R.; Heller, U.M.; Huebner, K.; et al. Equation of state and QCD transition at finite temperature. Phys. Rev. D 2009, 80, 014504. [Google Scholar] [CrossRef]
- Fodor, Z.; Katz, S.D. The Phase diagram of quantum chromodynamics. arXiv 2009, arXiv:0908.3341. [Google Scholar] [CrossRef]
- Borsanyi, S.; Endrodi, G.; Fodor, Z.; Jakovac, A.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. The QCD equation of state with dynamical quarks. JHEP 2010, 11, 077. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabo, K.K. Full result for the QCD equation of state with 2+1 flavors. Phys. Lett. B 2014, 730, 99. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; HotQCD Collaboration. Equation of state in (2+1)-flavor QCD. Phys. Rev. D 2014, 90, 094503. [Google Scholar] [CrossRef]
- Puglisi, A.; Sarracino, A.; Vulpiani, A. Temperature in and out of equilibrium: A review of concepts, tools and attempts. Phys. Rep. 2017, 709–710, 1–60. [Google Scholar] [CrossRef]
- Vogt, R. Ultrarelativistic Heavy-Ion Collisions; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Chatterjee, S.; Das, S.; Kumar, L.; Mishra, D.; Mohanty, B.; Sahoo, R.; Sharma, N. Freeze-Out Parameters in Heavy-Ion Collisions at AGS, SPS, RHIC, and LHC Energies. Adv. High Energy Phys. 2015, 2015, 349013. [Google Scholar] [CrossRef]
- Waqas, M.; Liu, F.H. Initial, effective, and kinetic freeze-out temperatures from transverse momentum spectra in high-energy proton(deuteron)–nucleus and nucleus–nucleus collisions. Eur. Phys. J. Plus 2020, 135, 147. [Google Scholar] [CrossRef]
- Waqas, M.; Li, B.C. Kinetic freeze-out temperature and transverse flow velocity in Au-Au collisions at RHIC-BES energies. Adv. High Energy Phys. 2020, 2020, 1787183. [Google Scholar] [CrossRef]
- Tang, Z.; Xu, Y.; Ruan, L.; Buren, V.G.; Wang, F.; Xu, Z. Spectra and radial flow at RHIC with Tsallis statistics in a Blast-Wave description. Phys. Rev. C 2009, 79, 051901. [Google Scholar] [CrossRef]
- Thakur, D.; Tripathy, S.; Garg, P.; Sahoo, R.; Cleymans, J. Indication of a Differential Freeze-out in Proton-Proton and Heavy-Ion Collisions at RHIC and LHC energies. Adv. High Energy Phys. 2016, 2016, 4149352. [Google Scholar] [CrossRef]
- Chatterjee, S.; Mohanty, B. Production of Light Nuclei in Heavy Ion Collisions Within Multiple Freezeout Scenario. Phys. Rev. C 2014, 90, 034908. [Google Scholar] [CrossRef]
- Waqas, M.; Liu, F.H.; Wang, R.Q.; Siddique, I. Energy scan/dependence of kinetic freeze-out scenarios of multi-strange and other identified particles in central nucleus-nucleus collisions. Eur. Phys. J. A 2020, 56, 188. [Google Scholar] [CrossRef]
- Chatterjee, S.; Mohanty, B.; Singh, R. Freezeout hypersurface at energies available at the CERN Large Hadron Collider from particle spectra: Flavor and centrality dependence. Phys. Rev. C 2015, 92, 024917. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitan, N.N.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; STAR Collaboration. Bulk Properties of the Medium Produced in Relativistic Heavy-Ion Collisions from the Beam Energy Scan Program. Phys. Rev. C 2017, 96, 044904. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X. Study of Proton, Deuteron, and Triton at 54.4 GeV. Adv. High Energy Phys. 2021, 2021, 6674470. [Google Scholar] [CrossRef]
- Chen, J.Y.; Duan, M.Y.; Liu, F.H.; Olimov, K.K. Extracting Kinetic Freeze-Out Properties in High-Energy Collisions Using a Multisource Thermal Model. Adv. High Energy Phys. 2024, 2024, 9938669. [Google Scholar] [CrossRef]
- Olimov, K.K.; Lebedev, I.A.; Fedosimova, A.I.; Liu, F.H.; Kanokova, S.Z.; Shodmonov, M.Z.; Tukhtaev, B.J. Simultaneous Analysis of Midrapidity pT Spectra of Identified Particle Species in Pb + Pb Collisions at = 2.76 TeV Using Tsallis Distribution with Transverse Flow. Universe 2022, 8, 655. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X.; Ajaz, M.; Ismail, A.H.; Dawi, E.A. Analyses of the collective properties of hadronic matter in Au-Au collisions at 54.4 GeV. Phys. Rev. D 2022, 106, 075009. [Google Scholar] [CrossRef]
- Schnedermann, E.; Sollfrank, J.; Heinz, U.W. Thermal phenomenology of hadrons from 200-A/GeV S+S collisions. Phys. Rev. C 1993, 48, 2462–2475. [Google Scholar] [CrossRef]
- Adam, J.; Adamova, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmed, I.; Ahn, S.U.; ALICE Collaboration. Production of light nuclei and anti-nuclei in pp and Pb-Pb collisions at energies available at the CERN Large Hadron Collider. Phys. Rev. C 2016, 93, 024917. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Anderson, D.M.; STAR Collaboration. Beam energy dependence of (anti-)deuteron production in Au + Au collisions at the BNL Relativistic Heavy Ion Collider. Phys. Rev. C 2019, 99, 064905. [Google Scholar] [CrossRef]
- Schnedermann, E.; Heinz, U.W. A Hydrodynamical assessment of 200-A/GeV collisions. Phys. Rev. C 1994, 50, 1675–1683. [Google Scholar] [CrossRef]
- Ristea, O.; Jipa, A.; Ristea, C.; Esanu, T.; Calin, M.; Barzu, A.; Scurtu, A.; Abu-Quoad, I. Study of the freeze-out process in heavy ion collisions at relativistic energies. J. Phys. Conf. Ser. 2013, 420, 012041. [Google Scholar] [CrossRef]
- Biyajima, M.; Mizoguchi, T.; Suzuki, N. Analyses of whole transverse momentum distributions in and pp collisions by using a modified version of Hagedorn’s formula. Int. J. Mod. Phys. A 2017, 32, 1750057. [Google Scholar] [CrossRef]
- Odorico, R. Does a Transverse Energy Trigger Actually Trigger on Large P(T) Jets? Phys. Lett. B 1982, 118, 151–154. [Google Scholar] [CrossRef]
- Arnison, G.; Astbury, A.; Aubert, B.; Bacci, C.; Bernabei, R.; Bézaguet, A.; Böck, R.; Bowcock, T.J.V.; Calvetti, M.; Carroll, T.; et al. Transverse Momentum Spectra for Charged Particles at the CERN Proton anti-Proton Collider. Phys. Lett. B 1982, 118, 167–172. [Google Scholar] [CrossRef]
- Hagedorn, R. Multiplicities, pT Distributions and the Expected Hadron → Quark - Gluon Phase Transition. Riv. Nuovo Cim. 1983, 6N10, 1–50. [Google Scholar] [CrossRef]
- De Falco, A. Vector meson production in pp collisions at = 7 TeV, measured with the ALICE detector. J. Phys. G 2011, 38, 124083. [Google Scholar] [CrossRef]
- Aamodt, K.; Abel, N.; Abeysekara, U.; Abrahantes Quintana, A.; Abramyan, A.; Adamová, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; Aguilar Salazar, S.; et al. Transverse momentum spectra of charged particles in proton-proton collisions at = 900 GeV with ALICE at the LHC. Phys. Lett. B 2010, 693, 53–68. [Google Scholar] [CrossRef]
- Abelev, B.; Quintana, A.A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; Ahammed, Z.; et al. Light vector meson production in pp collisions at = 7 TeV. Phys. Lett. B 2012, 710, 557–568. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; Agostinelli, A.; Aguilar Salazar, S.; Ahammed, Z.; et al. Heavy flavour decay muon production at forward rapidity in proton–proton collisions at = 7 TeV. Phys. Lett. B 2012, 708, 265–275. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; Agostinelli, A.; Aguilar Salazar, S.; Ahammed, Z.; et al. Inclusive J/ψ production in pp collisions at = 2.76 TeV. Phys. Lett. B 2012, 718, 295–306, Erratum in Phys. Lett. B 2015, 748, 472–473. [Google Scholar] [CrossRef]
- Lakomov, I. Event activity dependence of inclusive J/ψ production in p-Pb collisions at = 5.02 TeV with ALICE at the LHC. Nucl. Phys. A 2014, 931, 1179–1183. [Google Scholar] [CrossRef][Green Version]
- Waqas, M.; Peng, G.X.; Ajaz, M.; Haj, A.A.I.; Wazir, Z.; Li, L.L. Extraction of different temperatures and kinetic freeze-out volume in high energy collisions. J. Phys. G 2022, 49, 095102. [Google Scholar] [CrossRef]
- Lao, H.L.; Wei, H.R.; Liu, F.H.; Lacey, R.A. An evidence of mass-dependent differential kinetic freeze-out scenario observed in Pb-Pb collisions at 2.76 TeV. Eur. Phys. J. A 2016, 52, 203. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X.; Liu, F.H. An evidence of triple kinetic freezeout scenario observed in all centrality intervals in Cu–Cu, Au–Au and Pb–Pb collisions at high energies. J. Phys. G 2021, 48, 075108. [Google Scholar] [CrossRef]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitan, N.N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.H.; PHENIX Collaboration. Identified charged particle spectra and yields in Au+Au collisions at S(NN)**1/2 = 200-GeV. Phys. Rev. C 2004, 69, 034909. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; ALICE Collaboration. Centrality dependence of π, K, p production in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar] [CrossRef]
- Sahoo, R. Possible Formation of QGP-droplets in Proton-Proton Collisions at the CERN Large Hadron Collider. Assoc. Asia Pac. Phys. Soc. Bull. 2019, 29, 16. [Google Scholar]
- Badshah, M.; Alrebdi, H.I.; Waqas, M.; Ajaz, M.; Ammar, M.B. Centrality-dependent analysis of hadrons and light nuclei for phase transition insights in intermediate-energy Au–Au collisions. Eur. Phys. J. A 2024, 60, 139. [Google Scholar] [CrossRef]
- Li, L.L.; Liu, F.H.; Olimov, K.K. Excitation Functions of Tsallis-Like Parameters in High-Energy Nucleus–Nucleus Collisions. Entropy 2021, 23, 478. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.-P.; Abdelkader, A.; Galal Amin, L.; Bilal Hussain, H.M.; Salem, O.; Salouci, M. Insights into Freezeout Dynamics in Symmetric Heavy Ion Collisions with Changing Event Centrality. Symmetry 2025, 17, 744. https://doi.org/10.3390/sym17050744
Yang P-P, Abdelkader A, Galal Amin L, Bilal Hussain HM, Salem O, Salouci M. Insights into Freezeout Dynamics in Symmetric Heavy Ion Collisions with Changing Event Centrality. Symmetry. 2025; 17(5):744. https://doi.org/10.3390/sym17050744
Chicago/Turabian StyleYang, Pei-Pin, Atef Abdelkader, Lamiaa Galal Amin, Haji Muhammad Bilal Hussain, Ouazir Salem, and Moustafa Salouci. 2025. "Insights into Freezeout Dynamics in Symmetric Heavy Ion Collisions with Changing Event Centrality" Symmetry 17, no. 5: 744. https://doi.org/10.3390/sym17050744
APA StyleYang, P.-P., Abdelkader, A., Galal Amin, L., Bilal Hussain, H. M., Salem, O., & Salouci, M. (2025). Insights into Freezeout Dynamics in Symmetric Heavy Ion Collisions with Changing Event Centrality. Symmetry, 17(5), 744. https://doi.org/10.3390/sym17050744






