Multi-Objective Cauchy Particle Swarm Optimization for Energy-Aware Virtual Machine Placement in Cloud Datacenters

Abstract

With the continuous expansion of application scenarios for cloud computing, large-scale service deployments in cloud data centers are accompanied by a significant increase in resource consumption. Virtual machines (VMs) in data centers are allocated to physical machines (PMs) and require the resources provided by PMs to run various services. Apparently, a simple solution to minimize energy consumption is to allocate VMs as compactly as possible. However, the above virtual machine placement (VMP) strategy may lead to system performance degradation and service failures due to imbalanced resource load, thereby reducing the robustness of the cloud data center. Therefore, an effective VMP solution that comprehensively considers both energy consumption and other performance metrics in data centers is urgently needed. In this paper, we first construct a multi-objective VMP model aiming to simultaneously optimize energy consumption, resource utilization, load balancing, and system robustness, and we then build a joint optimization function with resource constraints. Subsequently, a novel energy-aware Cauchy particle swarm optimization (EA-CPSO) algorithm is proposed, which implements particle asymmetric disturbances and an energy-efficient population iteration strategy, aiming to minimize the value of the joint optimization function. Finally, our extensive experiments demonstrated that EA-CPSO outperforms existing methods.

1. Introduction

1.1. Background

Recent years have witnessed the rapid development of cloud computing, which has been a hot topic in academia and industry [1,2]. A large number of cloud services bring incremental wide-area applications and economies of scale computing models [3], and more and more applications are deployed in cloud data centers [4]. The average size of data centers has also continued to expand. A cloud data center usually runs thousands of PMs with hardware resources such as CPU, bandwidth, and memory that are shared through virtualization technology to achieve scalable and resilient computing capabilities [5]. VMs operate independently on PMs, enabling efficient utilization and flexible management of physical resources. The VMP problem aims to allocate VMs to appropriate PMs based on established objectives and constraints [6]. An efficient VMP strategy can ensure the stable and efficient operation of data centers [7] and has become a key research focus in the field of cloud computing.

1.2. Motivation

The issue of energy consumption in data centers is becoming increasingly severe. As early as 2010, data centers worldwide consumed as much as 201.8 terawatt-hours of electricity, an amount sufficient to power 19 million average U.S. households for a year, and this figure has continued to grow since then [8]. In addition, in order to meet user demands for quality of services (QoS) and cope with the dynamics and uncertainty of VM resource requirements [9], cloud service providers often adopt an over-provisioning strategy to ensure the stability and reliability of services [10]. However, this approach also brings problems of excess resources and energy waste. Moreover, energy consumption is directly linked to carbon emissions [11], and the increase in carbon emissions will have a significant negative impact on the global environment. Consequently, reducing the energy consumption of cloud data centers while ensuring system performance has become an urgent and essential task [4].

Beyond energy conservation, cloud providers must also pay attention to resource utilization and load balancing among PMs to ensure the performance of customer VMs [12], thereby enhancing overall user experience, market competitiveness, and operational efficiency. Additionally, the dynamic and stochastic characteristics of VM demand in cloud environments calls for robust VMP strategies that can maintain system performance and QoS even under load fluctuations, unexpected resource demands, or hardware failures [13]. As a result, designing more robust VMP strategies has become an increasing focus for cloud providers. Nevertheless, most existing research [13,14] on VMP problems primarily targets energy efficiency and resource utilization, with limited consideration given to the robustness of VM layout schemes.

1.3. Author’s Contribution

Based on the aforementioned analysis, comprehensively considering those optimization objectives that are really concerned about practical applications and seeking the optimal solution for VMP is of great significance for service cluster deployment and cloud computing development. This study models the VMP problem as a constrained multi-objective optimization problem, taking into account the various resources within cloud data centers. To address this problem, we establish a novel multi-objective VMP optimization model and design a joint objective optimization function. We also propose the EA-CPSO algorithm to efficiently solve this optimization problem.

In summary, the contributions of this paper are as follows:

• Driven by practical application scenarios and in response to the diversity and complexity of resources within cloud data centers, we construct a multi-dimensional optimization model that is applicable to various cloud data centers. This model focuses on four optimization directions: firstly, reducing energy consumption through global VM regulation; secondly, achieving optimal load balancing by optimizing resource allocation and deployment strategies; thirdly, enhancing resource utilization efficiency based on resource consumption tracking during allocation processes; lastly, strengthening the robustness of the system to cope with various uncertainties and dynamic changes.
• Based on the existing PSO, EA-CPSO is proposed to have the ability to solve discrete optimization problems. The EA-CPSO algorithm implements a Cauchy mutation operation and an elite solution preservation operation to ensure that iterative individuals tend to high-quality solutions while preventing the algorithm from converging to the local optimal. A Cauchy mutation leverages its heavy-tailed distribution property, allowing particles to have a higher probability of making large jumps, thereby increasing the likelihood of asymmetric transitions. The elite solution preservation mechanism retains the historically best solutions in each generation, preventing high-quality solutions from being disrupted or degraded by random perturbations or mutation operations during the population evolution process. Additionally, EA-CPSO demonstrates an ability to perceive changes in energy and resource allocation within the system, minimizing the value of the optimization function while ensuring all constraints are met.
• We developed a simulation platform for data center resource scheduling and designed a series of comparative experiments. The experimental results demonstrate that EA-CPSO outperforms existing approaches in solving multi-objective VM deployment optimization problems, while also validating the rationality and effectiveness of the proposed model in practical application scenarios.

1.4. Organization of the Paper

The structure of this paper is as follows: Section 2 reviews the related work. Section 3 describes the system model and problem statement. Section 4 focuses on the development of the algorithm, while Section 5 presents and analyzes the experimental results. Lastly, Section 6 concludes the paper with a summary.

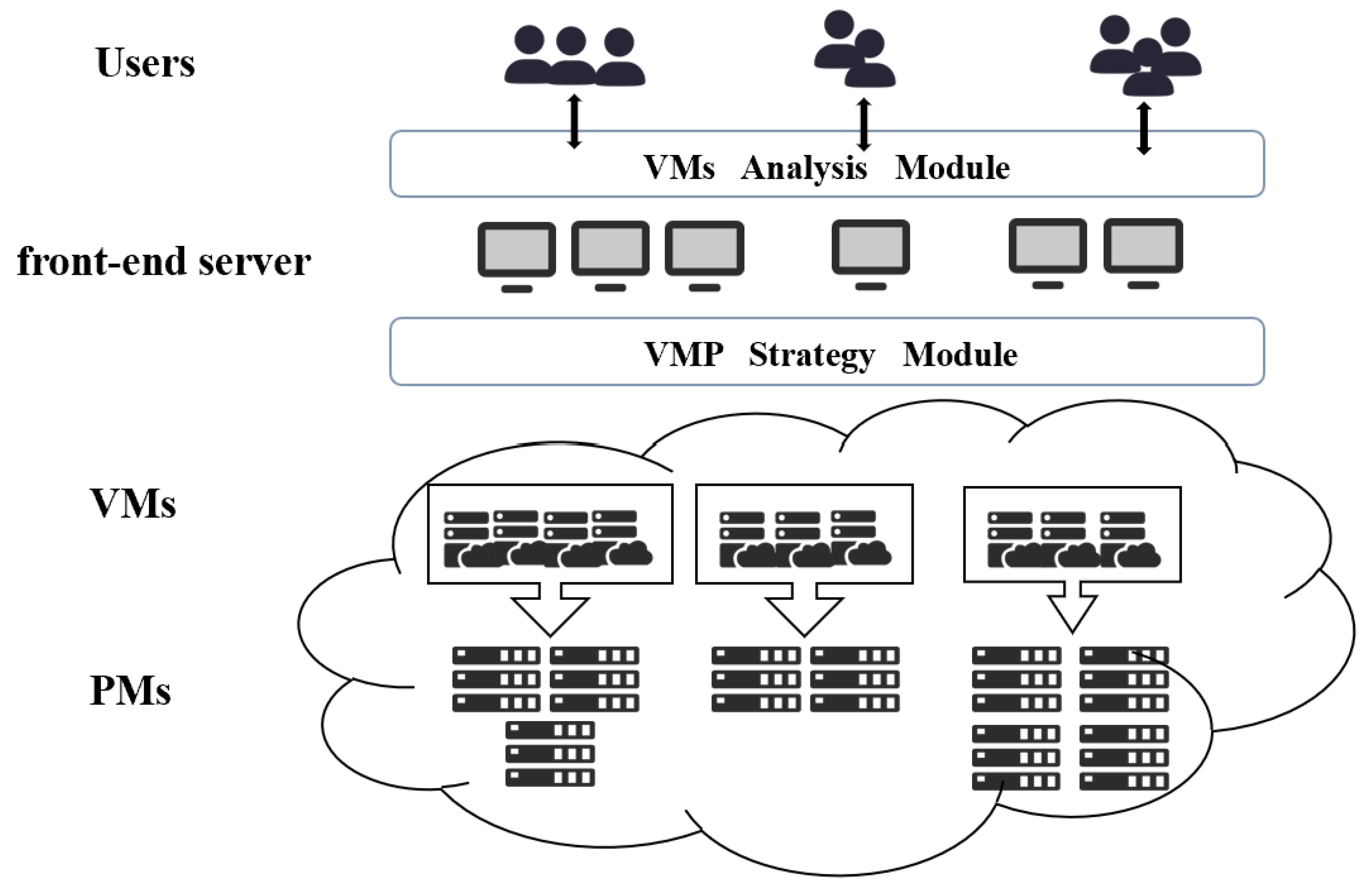
2. Related Works

VMP is a research problem with various optimization objectives and has garnered significant attention in both industrial and academic fields. Numerous optimization algorithms have been developed to address this problem, aiming to find effective solutions. The following provides an overview of relevant research achievements in this field.

High-level comprehensive surveys on VMP problems have been discussed in [2,7]. The research conducted by Alashaikh et al. [2] emphasized the pivotal role of preferences in VMP decisions. They demonstrated how preferences influence the solutions to the VMP problem by conducting a detailed analysis of the specific applications of preferences in various scenarios, such as considering communication costs between VMs, resource utilization, and the specific needs of users or administrators. Study [7] conducted a comprehensive review and in-depth exploration of optimization methods for VMP and migration. This work encompassed approaches based on various optimization objectives such as cost, QoS, and energy efficiency, and discussed VMs management strategies in distributed and decentralized architectures.

Study [15] addressed the issues of task scheduling and load balancing in cloud computing by proposing two hybrid scheduling strategies based on genetic algorithms, one combining the genetic algorithm with First-Come-First-Serve, and the other with Round Robin. By integrating classical scheduling policies, the proposed approach enhances the quality of the initial population and accelerates the convergence of the genetic algorithm. Using real-world asymmetric workload traces, simulation experiments demonstrated the superiority of the proposed methods in terms of scheduling efficiency, resource utilization, and system throughput.

The work of [16] emphasized load balancing within cloud data centers, aiming to evenly allocate tasks and resources across all PMs to prevent any node from becoming overloaded or underutilized. It solved the problem of insufficient efficiency in reducing response time, energy consumption, and execution cost in existing load-balancing methods. This study proposed a load balancing model and used a hybrid optimization algorithm to solve it.

Study [17] primarily focused on the issue of energy consumption optimization in VM allocation within cloud data centers, particularly addressing the demands of Internet of Things (IoT) applications. It proposed a novel framework called AFED-EF, which classifies servers into five types by setting four thresholds and dynamically adjusts VM allocation and migration strategies based on these categories, aiming to jointly tackle the challenges of load fluctuations in VM configurations and enhance energy efficiency.

In their latest study [18], Hasanein D. Rjeib and Gabor Kecskemeti focused on optimizing energy consumption and minimizing resource wastage through reducing active PMs. They proposed models for energy consumption and resource wastage, defining PM energy usage as linearly proportional to CPU utilization. Additionally, they quantified the potential cost of unused resources within the servers and defined SLA violations as instances where the host fails to provide services to VMs during specific resource-request periods.

The research in [19] modeled the VMP problem as a multi-dimensional bin-packing task. Considering resources like CPU, memory, and disk, it designed a novel fitness function to optimize load balancing, resource utilization, and active PMs. The constraint of this problem ensures that the resource demands of VMs assigned to each PM remain within the PM’s capacity limits.

The study in [20] addressed the VMP problems by formulating a multi-objective VMP model aimed at minimizing energy consumption while maximizing load balancing, resource utilization, and robustness. To tackle these challenges, the study proposed an improved algorithm named energy-efficient KnEA, which builds on the Knee point-driven evolutionary algorithm (KnEA) and incorporates a population initialization strategy focused on energy efficiency.

Ma et al. [21] proposed a PSO-based algorithm for joint network selection and service deployment, called PSO-JNSSP. In this algorithm, the network selection and service deployment of each particle are treated as potential solutions, and the speed and position of the particles are iteratively updated to converge to the optimal solution. Firstly, this study addressed the contradiction between the continuous updates of particle positions and the discrete nature of base station locations by introducing a transition probability mechanism, where a transition probability is defined based on the distance between the particle’s calculated continuous pseudo-position and each base station as well as the current queue length of each base station, comprehensively considering both distance and load. Secondly, the fitness function was also improved by not simply optimizing delay or energy consumption alone but by combining both through weighted summation, allowing particles to balance task execution delay and energy consumption during the search process.

Study [22] proposed an innovative algorithm based on Quantum PSO to optimize service placement. The goal was to achieve optimal service placement while improving system throughput, energy consumption, delay, and load. Specifically, this paper improved particle representation by introducing the concept of quantum particles where each particle can represent multiple potential solutions simultaneously through quantum superposition, thereby enhancing the coverage of the search space. This paper also designed a double hashing technique to ensure that the encoding observed from the quantum state can be uniformly and effectively mapped to the actual edge node identifiers.

In [23], the service placement problem for IoT applications on fog resources was formulated as an optimization problem, with a hierarchical structure consisting of fog cells and fog orchestration control nodes. Additionally, the study introduced a heuristic approach based on the genetic algorithm (GA) to address the service deployment problem, and it evaluated the performance of the GA, the exact optimization method, and the greedy algorithm on the service deployment problem.

Study [24] proposed an Availability-aware Virtual Cluster Allocation algorithm based on Biogeography-based Optimization. In this study, the calculation methods for risk cost and total bandwidth usage were defined, and a joint optimization function was constructed for evaluating the performance of various virtual cluster allocation schemes.

Unlike previous works, we aimed to achieve the joint optimization of energy consumption, resource utilization, load balancing, and robustness in the VMP problem, addressing the limitations of most existing research that considers fewer than three objectives, which is often insufficient for many practical applications. Moreover, we improved existing models and used real-world test data as much as possible to ensure that the experimental results are more applicable to real scenarios. In terms of algorithm design, the proposed EA-CPSO algorithm effectively handles constrained multi-objective optimization problems and enhances population optimization through energy-aware Cauchy mutation.

3. System Models and Problem Formulation

In this section, we formulate the VMP problem as an NP-hard multi-objective optimization problem. Then, we construct branch models for the four optimization objectives mentioned earlier, precisely expressing these objectives through mathematical formulas. Based on this, we establish a multi-objective VMP optimization model designed to optimize all the set objectives simultaneously. For clarity in understanding the formulations in subsequent sections,

Table 1. Notations.

Symbol	Meaning
P, $P_j$	PMs and PM j
V, $V_i$	VMs and VM i
n	number of VMs
m	number of PMs in the data center
X	allocation scheme and X is a $m\times n$ binary matrix
$x_{ij}$	if the VM i is allocated in the PM j, and $x_{ij}\in \{0,1\}$
$C_j^k$	resource k capacity of PM j, $k\in$ {CPU, mem, band}
$D_i^k$	resource k demand of VM i, $k\in$ {CPU, mem, band}
S	virtual machine placement scheme
$U_j^k$	resource k utilization of the sum hosted VMs, $k\in$ {CPU, mem, band}
$\overline{U^k}$	resource k average utilization
U	overall resource utilization ratio of S
$E\left(D_i^k\right)$	expectation of resource k demand
$\sigma \left(D_i^k\right)$	standard deviations of resource k demand
$P^{\prime }$	the set of PMs already used in S
$m^{\prime }$	number of PMs in the set $P^{\prime }$
E	whole energy consumption of all PMs in the data center
$E_j$	energy consumption of the PM j
$U_j^{cpu}\left(t\right)$	CPU utilization as a function of time
${RE}_j^k$	reserved resource k of PM j
$W_j^k$	weight of reserved resource space on PM j
$R_j$	total robustness measure of PM j
R	average of the robustness measures of all PMs
	(the robustness measure of S)
L	all PMs’ resource load imbalance degree
f	optimization objective
${\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4$	variable weight coefficient
F	joint optimization objective (fitness function)

provides explanations for all the mathematical notations:

3.1. Problem Description

In cloud architecture, numerous PMs are interconnected through the network [25] and virtualized into multiple independent VM instances, each capable of running different applications or services [16]. The model of the VM placement problem, as illustrated in Figure 1, revolves around the rational allocation of VMs with varying resource requirements to their corresponding PMs. The objectives of this allocation include minimizing energy consumption and maximizing resource utilization, load balance, and robustness. PMs are equipped with multiple types of resources [16], which are requested by VMs based on their operational needs. Specifically, the main modules include the following:

• Users and frontend server: Cloud users submit requests to the frontend, which is the frontend server that handles these requests. The frontend server, used for processing client requests and providing user interfaces and services, plays a bridge role in connecting users and cloud services in cloud computing.
• VMs analysis module: This module determines the million instructions per second (MI/s) and memory for each VM request and calculates the number of active VMs during each time interval based on the frontend server.
• VMP strategy module: The role of this module is to determine the optimal strategy for deploying VMs in a cloud computing environment. It relies on a set of algorithms, rules, and policies to make decisions in order to meet user requirements, maximize resource utilization, and achieve high performance goals.
• VMs: The workload is deployed and executed on VMs. Based on the workload and resource requirements, VMs are optimally placed and allocated to PMs through placement algorithms.
• PMs: The infrastructure provides hardware support for provisioning virtualized resources to fulfill user requests.

3.1.1. Physical Machine

The set of PMs is represented as P, and P can be represented as $P=\left\{P_1,P_2,\dots ,P_m\right\}$, m being the number of available PMs. Each PM $P_j\left(P_j\in P\right)$ has a resource capacity vector $C_j^k=〈C_j^{cpu},C_j^{mem},C_j^{band}〉$, $j=1,2,...m$, where $C_j^{cpu}$, $C_j^{mem}$, and $C_j^{band}$ denote the CPU, memory, and bandwidth capacities of $P_j$, respectively.

3.1.2. Virtual Machine

The set of VMs is represented as V, and V can be represented as $V=\left\{V_1,V_2,\dots ,V_n\right\}$, n representing the number of VMs. Each VM $V_i\left(V_i\in V\right)$ is characterized by its resource demand vector $D_i^k=〈D_i^{cpu},D_i^{mem},D_i^{band}〉$, $i=1,2,...n$, where $D_i^{cpu}$, $D_i^{mem}$, and $D_i^{band}$ indicate the resource requirements for the CPU, memory, and bandwidth of $V_i$, respectively.

Subsequently, the constraint on the PM’s resource capacity (i.e., the demands $D^k$ of the hosted VMs for each resource type should not exceed the resource capacity $C^k$ of the host PM) is formulated as follows:

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n{D}_i^k{x}_{ij}\le C_j^k,}\\ \forall i\in \left\{1,\dots ,n\right\},\forall k\in \left\{cpu,mem,band\right\}\end{array}$$

(1)

3.1.3. Placement Relationship

The placement relationship between VMs and PMs can be depicted by a two-dimensional matrix X of size $m\times n$, as shown by Formulas (2) and (3):

$$X=\left(\begin{array}{cccc}{x}_{11}& x_{12}& \dots & x_{1n}\\ x_{21}& x_{22}& \dots & x_{2n}\\ \dots & \dots & \dots & \dots \\ x_{m1}& x_{m2}& \dots & x_{mn}\end{array}\right)$$

(2)

$$x_{ij}=\left\{\begin{array}{cc}1& \mathrm{if}{V}_i\mathrm{is}\mathrm{placed}\mathrm{in}{P}_j\\ 0& \mathrm{otherwise}\end{array}\right.$$

(3)

where $a_{ij}$ is a binary variable; $x_{ij}=1$ indicates that $V_i$ is allocated to $P_j$, whereas $x_{ij}=0$ signifies that $V_i$ is not allocated to $P_j$. The following condition ensures that each VM is assigned to no more than one PM:

$${\displaystyle \sum _j^m{x}_{ij}\le 1,\forall i\in \left\{1,\dots ,n\right\}}$$

(4)

Optimizing resource utilization reduces resource wastage and lowers the number of required PMs [26], thereby directly decreasing energy consumption and operating costs in data centers. According to [27], overall resource utilization is defined as the average utilization across different resource types, and the resource utilization vector $U_j^k=〈U_j^{cpu},U_j^{mem},U_j^{band}〉$ of $P_j$ is computed as follows:

$$U_j^{cpu}={\displaystyle \frac{{\displaystyle \sum _i^n{D}_i^{cpu}·x_{ij}}}{C_j^{cpu}}}$$

(5)

$$U_j^{mem}={\displaystyle \frac{{\displaystyle \sum _i^n{D}_i^{mem}·x_{ij}}}{C_j^{mem}}}$$

(6)

$$U_j^{band}={\displaystyle \frac{{\displaystyle \sum _i^n{D}_i^{band}·x_{ij}}}{C_j^{band}}}$$

(7)

where $U_j^{cpu}$, $U_j^{mem}$, and $U_j^{band}$ denote the utilization ratios of the CPU, memory, and bandwidth for $P_j$. The average utilization ratio of each resource across all PMs can be calculated from the utilization ratio of each resource for every PM. The resource utilization of scheme S is then obtained, as illustrated in (8)–(11):

$${\displaystyle \overline{U^{cpu}}=\frac{1}{m^{\prime }}\sum _{j\in P^{\prime }}{U}_j^{cpu}}$$

(8)

$${\displaystyle \overline{U^{mem}}=\frac{1}{m^{\prime }}\sum _{j\in P^{\prime }}{U}_j^{mem}}$$

(9)

$${\displaystyle \overline{U^{band}}=\frac{1}{m^{\prime }}\sum _{j\in P^{\prime }}{U}_j^{band}}$$

(10)

$$U=\left(\overline{U_{cpu}}+\overline{U_{mem}}+\overline{U_{band}}\right)/3$$

(11)

In scheme S, the set $P^{\prime }$ denotes the utilized PMs and $m^{\prime }$ indicates the number of PMs within $P^{\prime }$. The average utilization ratios of the CPU, memory, and bandwidth are represented by $\overline{U^{cpu}}$, $\overline{U^{mem}}$, and $\overline{U^{band}}$, respectively. Additionally, U denotes the overall resource utilization ratio for S.

3.2. Energy Consumption Model

According to most research [28], the CPU is the primary energy drain when compared to the other components. Consequently, the energy consumption of a PM is often represented by the CPU workload. The energy consumption of PM $Pj$ is represented by $Ej$, while the total energy consumption of all PMs is denoted as E. We drew upon empirical data derived from SPECpower benchmarking [29] to inform our analysis.

Table A1. Energy consumption in watts at varying CPU utilization levels.

Server	$0\%$	$10\%$	$20\%$	$30\%$	$40\%$	$50\%$	$60\%$	$70\%$	$80\%$	$90\%$	$100\%$
G4	86	89.4	92.6	96	99.5	102	106	108	112	114	117
G5	93.7	97	101	105	110	116	121	125	129	133	135

shows the energy consumption of the HP ProLiant G4 and G5 servers under varying workload levels.

3.3. Robustness Measure

In data centers, different types of applications run on VMs. Given the inherent differences among these applications and the varying times and frequencies of user access, the requirements for computing resources, storage resources, and network resources by VMs show significant diversity and variability [25]. This dynamic and random nature of demand implies that the resource load of VMs will change dynamically accordingly [30].

In practical applications [31], deploying VMs based on peak-hour load conditions often leads to a significant underutilization of resources during off-peak hours, which leads to problems such as resource waste, cost escalation, and energy consumption increase. On the contrary, deploying VMs according to average load can reduce resource idleness but the performance requirements may not be met during specific periods, thereby compromising QoS and user experience [20]. Therefore, there is an urgent need for an efficient and robust VMP strategy that can flexibly address the dynamic fluctuations in resource load, ensuring a balance among effective cost and energy control, maintenance of high-level QoS, and user satisfaction.

Regarding the dynamic workload of VMs, we can calculate the expectation and standard deviation of a VM load based on historical log data. The expectation represents the average level of demand for a certain type of resource when the VM requests resources from the cloud data center. In contrast, the standard deviation reveals the degree of fluctuation in the VM’s load around this average value, essentially quantifying the uncertainty of the load. Therefore, to enhance the robustness of VM placement strategies, we take the expected resource demand of VMs as the baseline while thoroughly considering the variation in their load levels [16]. This approach ensures that sufficient buffer space is allocated during planning to maintain system stability, even under conditions of significant load fluctuations, thereby averting resource shortages or overload scenarios.

Furthermore, the likelihood of PM overload is related to both the reserved space on the PMs and the standard deviation of the resource loads of the VMs assigned to them [20]. Specifically, a larger reserved resource space corresponds to a reduced risk of PM overload, albeit potentially at the cost of decreased resource utilization efficiency. Conversely, inadequate reserved resource space, coupled with significant fluctuations in the resource loads of the VMs hosted, renders the PMs more susceptible to reaching an overloaded state. In summary, to accurately evaluate the robustness of a PM, it is necessary to comprehensively consider its reserved resource space and assign an appropriate weighting factor to it.

Based on the aforementioned concept, the robustness metrics for VMP schemes are constructed as follows:

$${\displaystyle {RE}_j^{cpu}=C_j^{cpu}-\sum _{i}E\left({D_i}^{cpu}\right)x_{ij},j=1,2,\dots ,m}$$

(12)

$${\displaystyle {RE}_j^{mem}=C_j^{mem}-\sum _{i}E\left({D_i}^{mem}\right)x_{ij},j=1,2,\dots ,m}$$

(13)

$${\displaystyle {RE}_j^{band}=C_j^{band}-\sum _{i}E\left({D_i}^{band}\right)x_{ij},j=1,2,\dots ,m}$$

(14)

where $RE{j}^{cpu}$, $RE{j}^{mem}$, and $RE{j}^{band}$ denote the reserved resources for CPU, memory, and bandwidth, respectively. Let $\sigma \left(D{i}^{cpu}\right)$, $\sigma \left(D{i}^{mem}\right)$, and $\sigma \left(D{i}^{band}\right)$ represent the standard deviations of the resource demands for $Vi$. The weight of the reserved resource on $Pj$ is then defined by Formulas (15)–(17):

$$W_j^{cpu}={\displaystyle \frac{{\displaystyle \sum _i^n\sigma \left(D_i^{cpu}\right)x_{ij}}}{{\displaystyle \sum _i^n\sigma \left(D_i^{cpu}\right)}}}$$

(15)

$$W_j^{mem}={\displaystyle \frac{{\displaystyle \sum _i^n\sigma \left(D_i^{mem}\right)x_{ij}}}{{\displaystyle \sum _i^n\sigma \left(D_i^{mem}\right)}}}$$

(16)

$$W_j^{band}={\displaystyle \frac{{\displaystyle \sum _i^n\sigma \left(D_i^{band}\right)x_{ij}}}{{\displaystyle \sum _i^n\sigma \left(D_i^{band}\right)}}}$$

(17)

Furthermore, the robustness measure for CPU, memory, and bandwidth can be defined as follows:

$$R_j^{cpu}=W_j^{cpu}·{RE}_j^{cpu}={\displaystyle \frac{{\displaystyle \sum _i^n\sigma \left(D_i^{cpu}\right)x_{ij}}}{{\displaystyle \sum _i^n\sigma \left(D_i^{cpu}\right)}}}\left({\displaystyle C_j^{cpu}-\sum _{i=1}^{n}E\left({D_i}^{cpu}\right)x_{ij}}\right)$$

(18)

$$R_j^{mem}=W_j^{mem}·{RE}_j^{mem}={\displaystyle \frac{{\displaystyle \sum _i^n\sigma \left(D_i^{mem}\right)x_{ij}}}{{\displaystyle \sum _i^n\sigma \left(D_i^{mem}\right)}}}\left({\displaystyle C_j^{mem}-\sum _{i=1}^{n}E\left({D_i}^{mem}\right)x_{ij}}\right)$$

(19)

$$R_j^{band}=W_j^{band}·{RE}_j^{band}={\displaystyle \frac{{\displaystyle \sum _i^n\sigma \left(D_i^{band}\right)x_{ij}}}{{\displaystyle \sum _i^n\sigma \left(D_i^{band}\right)}}}\left({\displaystyle C_j^{band}-\sum _{i=1}^{n}E\left({D_i}^{band}\right)x_{ij}}\right)$$

(20)

The total robustness measure of $P_j$ is defined in (21). The robustness measure of S is represented by the average of the robustness measures across all the PMs, as shown in (22):

$$R_j=R_j^{cpu}·R_j^{mem}·R_j^{band}$$

(21)

$${\displaystyle R=\frac{1}{m^{\prime }}\sum _{j\in P^{\prime }}{R}_j}$$

(22)

3.4. Load Balance

Load balancing aims to ensure fair utilization and effective allocation of PM resources, thereby meeting the QoS requirements of users [9]. Considering CPU, memory, and bandwidth resources, we use L in this paper to measure the degree of resource load imbalance for PM $P_i$, as shown in formula (23):

$$L=\left(\sqrt{{\displaystyle \sum _{j\in P^{\prime }}{\left(U_j^{cpu}-\overline{U^{cpu}}\right)}^2}}+\sqrt{{\displaystyle \sum _{j\in P^{\prime }}{\left(U_j^{mem}-\overline{U^{mem}}\right)}^2}}+\sqrt{{\displaystyle \sum _{j\in P^{\prime }}{\left(U_j^{band}-\overline{U^{band}}\right)}^2}}\right)/3$$

(23)

3.5. VMP Problem Model

Based on the above analysis, we model the optimization model of the VMP problem as follows:

$$min:f_1\left(X\right)=E$$

(24)

$$min:f_2\left(X\right)=c-R$$

(25)

$$min:f_3\left(X\right)=1-U$$

(26)

$$min:f_4\left(X\right)=L$$

(27)

Expressions (24)–(27) define four optimization objectives, including minimizing the energy consumption of physical machines, achieving optimal robustness, maximizing resource utilization, and minimizing load variance. Specifically, in Expression (25), the symbol c introduced represents a constant term. Notably, for the purpose of normalizing the model, a fixed constant is subtracted from robustness and resource utilization, shifting their optimization direction towards minimization. Since there is a trade-off between the above four optimization objectives, we measure a combined metric called $F\left(X\right)$, as the formula of (28) and (29) shows, where ${\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4$ are the variable weight coefficient:

$$min:F\left(X\right)={\gamma }_1{f}_1+{\gamma }_2{f}_2+{\gamma }_3{f}_3+{\gamma }_4{f}_4$$

(28)

$$s.t.Constraints\left(1\right)–(4)$$

(29)

4. Algorithm

In this section, we propose an improved algorithm based on PSO, namely EA-CPSO. The improvements focus on two aspects. Firstly, an efficient particle encoding method is designed based on the characteristics of the VMP problem. Secondly, an energy-saving-oriented particle mutation and population iteration strategy is proposed.

Table 2. Notations.

Symbol	Meaning
X	position of particle
V	velocity of particle
i	currently accessed particle
k	current iteration number
$\omega$	inertia weight
${\xi }_1,{\xi }_2,\xi$	random variables lie in $\left(0,1\right)$
$C_1$	individual cognitive factor
$C_2$	social cognitive factor
$pbest$	individual historical optimal solution
$gbest$	global optimal solution
${\omega }_{max}$	maximum inertia weight
${\omega }_{min}$	minimum inertia weight
K	maximum number of iterations
I	number of particles
p	a probability of particle mutation
$\eta$	tunable weight
$\mathcal{C}$	standard Cauchy-distributed random value
$X_{max}$	upper bound of the particle’s position
$X_{min}$	lower bound of the particle’s position

complements related notations about the algorithm description:

4.1. Particle Swarm Optimization

Particle swarm optimization (PSO) [21] is a swarm intelligence-based optimization algorithm, which simulates the behavior of biological organisms in nature that collaborate within a group to locate food. Each particle’s position represents a solution, and its velocity determines its direction and speed of movement within the search space. The particles iteratively adjust their velocities and positions to seek out more optimal solutions. At the k iteration, the velocity of particle i is given by $v_i^k$ and the position is denoted by $x_i^k$. The position update is formulated as shown in Formula (30), while the velocity update is given by Formula (31):

$$X_i^{k+1}=X_i^k+V_i^k$$

(30)

$$V_i^{k+1}=\omega V_i^k+c_1·{\xi }_1({pbest}_i^k-X_i^k)+c_2·{\xi }_2({gbest}^k-X_i^k)$$

(31)

where $x_i^{k+1}$ is the position of particle i of the $k+1$ iteration, and where $V_i^{k+1}$ is the velocity of particle i of the $k+1$ iteration. is a local optimal solution; ${pbest}_i^k$ represents the individual historical optimal solution of particle i up to the k iteration, while ${gbest}^k$ represents the global optimal solution of the population up to the k iteration; $c_1$ represents the individual cognitive factor, while $c_2$ represents the social cognitive factor; ${\xi }_1$, ${\xi }_2$ represent random variables that lie in $\left(0,1\right)$. Specifically, $\omega$ is the inertia weight used to control the detection capabilities of the algorithm. The expression for $\omega$ is shown in Formula (32). Here, ${\omega }_{max}$ denotes the maximum inertia weight, ${\omega }_{min}$ represents the minimum inertia weight, and K signifies the maximum number of iterations.

$$\omega ={\omega }_{max}-\left({\omega }_{max}-{\omega }_{min}\right){\displaystyle \frac{k}{K}}$$

(32)

Given the importance of the inertia weight, we aim for particles to exhibit differentiated search characteristics at various stages of the algorithm. Therefore, we employ a linearly decreasing inertia weight throughout the iterations. Specifically, as the number of iterations increases, $\omega$ gradually decreases. This design allows the population to maintain strong global exploration capabilities during the initial stages, which helps it to avoid becoming trapped in the local optimal. In the later stages of iterations, the particles’ local exploitation abilities are enhanced, facilitating more refined searches and thereby improving the convergence rate of the algorithm.

4.2. Cauchy Mutation

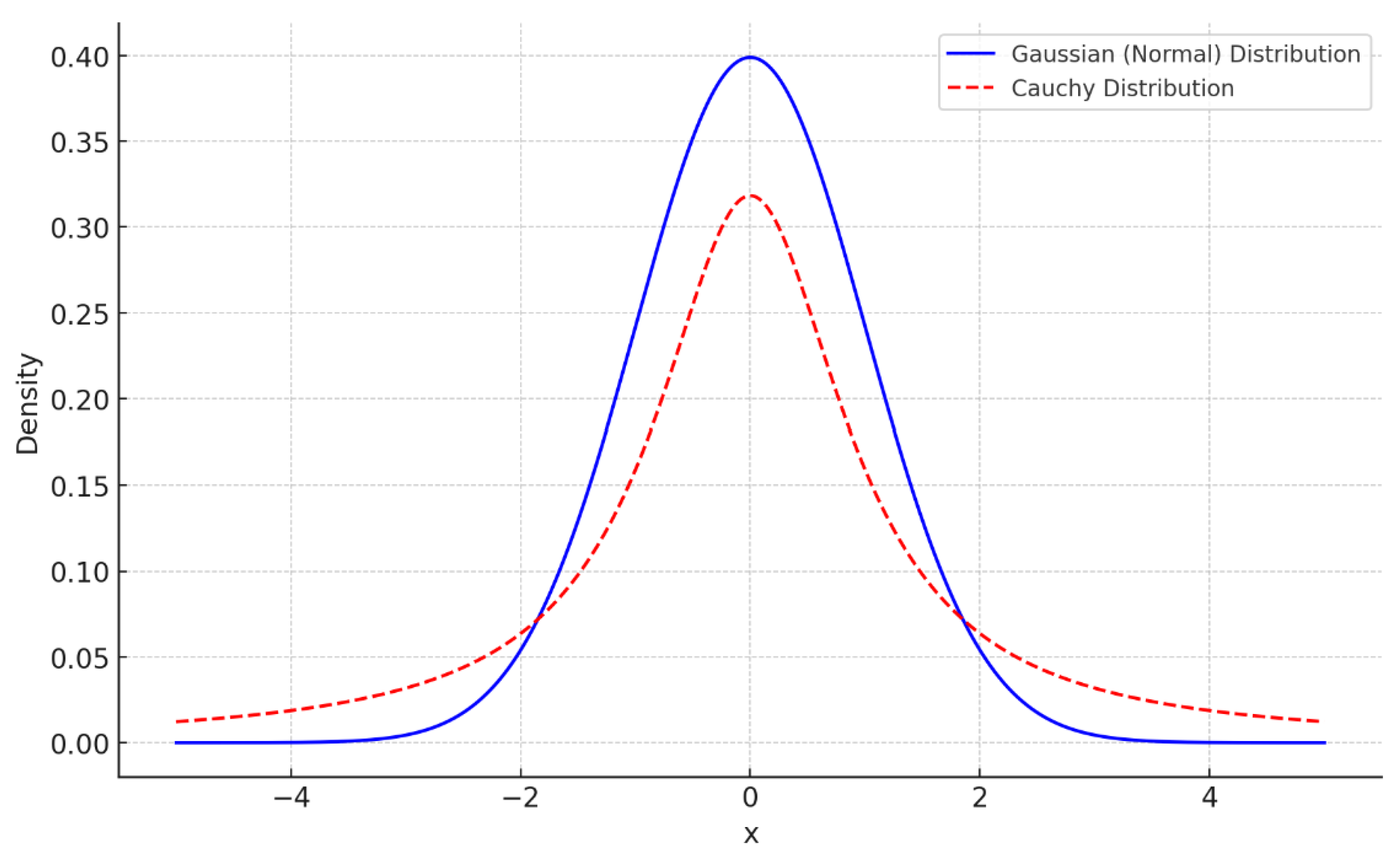
It is difficult to solve complex optimization problems effectively using standard PSO algorithms. To overcome this limitation, many researchers have incorporated mutation strategies into the standard PSO [21,22], with Gaussian and Cauchy mutations being the primary mutation operators introduced. Figure 2 illustrates the comparison between Gaussian and Cauchy density functions [32]. It can be observed that the Gaussian distribution exhibits a characteristic bell-shaped curve with a narrow peak and rapid decay. In contrast, although the Cauchy distribution also has a high peak near the center, its tails decay more slowly, resulting in a broader distribution range. More importantly, whereas the Gaussian distribution introduces symmetric disturbances, the Cauchy distribution introduces asymmetric disturbances through its long tail, thereby increasing the probability of particles undergoing asymmetric transitions. Consequently, particles mutated with the Cauchy distribution possess stronger exploration capabilities.

We propose the EA-CPSO algorithm, which applies the Cauchy mutation to selected particles with a certain probability p. This approach aims to enhance the diversity of the swarm and reduce the risk of premature convergence to the local optimal. The Cauchy mutation process for $X_i$ is implemented as follows:

$$X_i=X_i\left(1+\eta ·\mathcal{C}\right)$$

(33)

$$\mathcal{C}=tan\left(\left(\xi -0.5\right)·\pi \right)$$

(34)

$$X_i=\left\{\begin{array}{cc}{X}_{max}& X_i>X_{max}\\ X_i& X_{main}<X_i<X_{max}\\ X_{min}& X_i<X_{min}\end{array}\right.$$

(35)

where $\eta$ is the tunable weight and $\xi$ is a random value between 0 and 1. $\mathcal{C}$ represents a random perturbation value drawn from a standard Cauchy distribution with a location parameter of 0 and a scale parameter of 1; while max and min signify the upper and lower bounds, respectively, for the particle position variable.

4.3. Implementation Scheme of EA-CPSO Algorithm

In Section 3, the objective of the VMP optimization is identifying an optimized placement solution S. Consequently, each particle retains a set of solutions during each iteration, and VMP subsequently determines the optimal mapping of VMs to PMs through comparison. Furthermore, in practical scenarios, cloud service providers offer a limited number of VM types [10]. Inspired by this, the particle encoding proposed in this chapter solely considers the mapping of VM types (rather than VM instances) to PMs. The VM scheduling sequence is illustrated in Figure 3. In the figure, each black rectangle within the solid box on the left represents a PM, while each white rectangle within the dashed box on the right represents a VM. The number in the bottom-right corner of each rectangle indicates the ID of the corresponding PM or VM. The arrows in the figure represent the mapping relationships between VMs and PMs. Taking the topmost arrow as an example, the PM with ID 1 is associated with VMs with ID 3 and ID 5, meaning that VMs $V_3$ and $V_5$ are allocated to $P_1$:

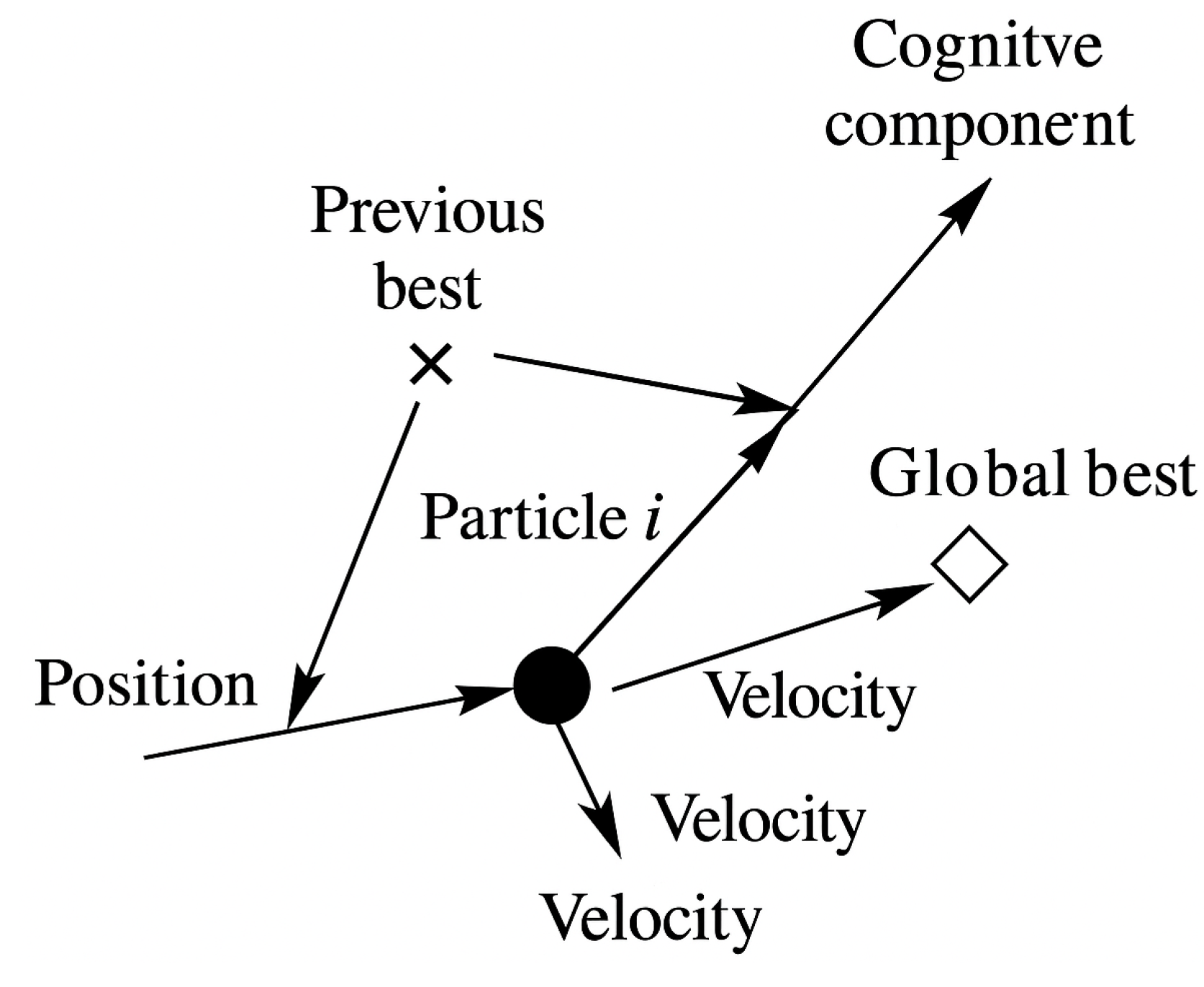
Figure 4 illustrates the search mechanism of the PSO algorithm. Each particle represents a potential solution, and its movement is guided by both its own search history and the collective experience of the swarm. The position of a particle is updated according to three components: the inertia component, which maintains its previous motion direction; the cognitive component, which drives it toward its personal best position; and the social component, which directs it toward the global best position. By combining these three driving forces, particles achieve a balance between exploration and exploitation within the search space, continuously updating their positions based on individual and global experiences and gradually approaching the optimal solution.

As shown in Algorithm 1, we present the implementation scheme of the VMP approach using EA-CPSO. Lines 1 to 2 are initialization; we define K as the maximum number of iterations, and we define I as the number of particles; then, the optimization loop begins. During iteration, the velocity and position of each particle are updated based on its $pbest$ and $gbest$ values. Particles are sorted according to their fitness, and a subset is selected for Cauchy mutation, aiming to enhance diversity and avoid getting trapped in the local optimal. After each iteration, the global optimal solution is updated, and, ultimately, the algorithm returns the optimal position and fitness value.

Algorithm 2 elaborates on the VM allocation process within Algorithm 1. For each particle in Algorithm 1, Algorithm 2 handles the assignment of VMs to PMs by evaluating available resources and updating the allocation scheme. Specifically, for each VM, it checks if a PM has sufficient resources; if not, it performs a linear search for a suitable PM and assigns the VM accordingly. Essentially, Algorithm 2 serves as the resource allocation mechanism invoked by Algorithm 1 for each particle, ensuring feasible and optimized VM-to-PM allocation within the EA-CPSO framework.

Algorithm 1 VMP approach with EA-CPSO

1:   Initialize particles with random X and V 2:   Initialize F, $pbest$, $gbest$, and other parameters 3:   for $k=1$ to K do 4:      for $i=1$ to I do 5:        Update $V_i$ based on pbest and gbest by the Formula (31) 6:        Update $X_i$ based on the $V_i$ by the Formula (30) 7:        Compute $F\left(X_i\right)$ of particle by Formulas (24) and (29) 8:        if $F\left(X_i\right)<F\left(pbes{t}_i\right)$ then 9:           Set $pbes{t}_i$ to a copy of $X_i$ 10:      end if 11:    end for 12:    Sort particles by F, select particles with probability p 13:    for each selected particle do 14:      Apply Cauchy mutation by Formulas (33)–(35) 15:      update X 16:    end for 17:    update $gbest$ 18: end for 19: return gbest and F(gbest)

Algorithm 2 VM allocation

1:   Initialize PMs and V 2:   Initialize particles, scheme S, and other parameters 3:   for each particle do 4:     update S based on available resources by Formulas (1) and (4) 5:     for each VM in VMs do 6:        if PM resources are insufficient then 7:           perform linear search for an available PM 8:        end if 9:        Assign VM to PM 10:   end for 11: end for 12: return S

5. Experimental Evaluations

5.1. Experiment Settings

In all our experiments, the following scenarios were used. Forty PMs were provided for the placement of 50 VMs. Typically, cloud data centers offer a variety of PMs to meet diverse requirements [29]. Meanwhile, the standard deviation of the VM resource requests was randomly set to reflect their diversity. Each host had a capacity of two CPU cores with MIPS values of either 1880 or 2660, 4 GB of RAM, and 1 TB of storage space. Power models were used from either the HP ProLiant ML110 G4 or HP ProLiant ML110 G5, and these models indicated the energy consumption of the hosts at various utilization rates, as shown in Table A1. For the VMs configurations [33], we considered four types of VMs with MIPS ratings of 250, 500, 1000, and 1250, with the number of each type being randomly generated. Detailed specifications for both the hosts and the VMs can be found in

Table 3. Host/VM types and capacity.

Name	CPU (MIPS)	Cores	Memory	Bandwidth	Storage
PM Type 1	1.86 GHz	4	4 GB	1 Bbit/s	1 TB
PM Type 2	2.66 GHz	4	4 GB	1 Bbit/s	1 TB
VM Type 1	1.25 GHz	1	0.6 GB	100 MBbit/s	1 GB
VM Type 2	1.0 GHz	1	1.7 GB	200 MBbit/s	1 GB
VM Type 3	0.5 GHz	1	3.75 GB	100 MBbit/s	1 GB
VM Type 4	0.25 GHz	1	0.85 GB	200 MBbit/s	1 GB

:

The parameter values of the EA-CPSO algorithm are as follows: the population size is 40; the number of iterations is 60 or 120; the Cauchy mutation probability is 0.2; the individual cognitive factor is 1.8; and the social cognitive factor is 2.2. The stopping criterion of the algorithm is reaching the predefined maximum number of iterations. We used a weighted summation method to calculate the joint optimization objective function [21], as shown in Formula (28). The weight coefficients for each indicator were set as follows: ${\gamma }_1=0.0004$, ${\gamma }_2=0.02$, ${\gamma }_3=1$, ${\gamma }_4=0.5$. The design of the weight coefficients aimed to normalize the value ranges of each optimization indicator to the $\left[0,1\right]$ interval, thereby avoiding bias due to dimensional differences and ensuring the comparability of the objectives during the optimization process.

To assess the effectiveness of our approach, we performed experiments comparing the EA-CPSO algorithm with these alternative methods.

• RFF [24]: The RFF (random first-fit) algorithm is a typical greedy algorithm. Its core idea is to randomly select a VM and attempt to assign it to the first PM that satisfies the constraints.
• MGGA [23]: The MGGA (multi-objective grouping genetic) algorithm is an optimization method based on the GA. It utilizes the global search capability of the GA, combined with the characteristics of grouping problems, to gradually approach the Pareto optimal solution set through population evolution.
• PSO [21]: a heuristic optimization algorithm based on population intelligence, which has been introduced in Section 4.1.

5.2. Experimental Results and Evaluation

5.2.1. Comparison of Joint Optimization Result

In this paper, we define the optimization objective as $F\left(X\right)$ (as shown in Equations (28) and (29)). The fitness function $F\left(X\right)$ comprehensively considers four objectives: robustness, resource utilization, energy consumption, and load balancing. By employing a weighted summation method, the multi-objective optimization problem is converted into a single-objective optimization problem. This approach improves computational efficiency and provides a unified evaluation standard for comparing different algorithms.

Figure 5 illustrates the joint optimization results of four algorithms (PSO, RFF, MGGA, and EA-CPSO) under 60 and 120 iterations. It is evident that EA-CPSO demonstrated superior optimization performance under both conditions. Specifically, its joint optimization result was approximately 2.90 after 60 iterations and further reduced to 2.87 after 120 iterations, showcasing the algorithm’s efficiency in handling joint optimization problems. Taking the 60-iteration case as an example, EA-CPSO outperformed PSO by 14.66%, RFF by 33.82%, and MGGA by 16.18%.

The results indicate that EA-CPSO performs consistently well in both fewer and more iterations, making it highly suitable for efficiently solving complex optimization problems. MGGA exhibited notable improvement with increased iterations, indicating it to be more suitable for scenarios requiring higher computational resources. In contrast, PSO and RFF showed relatively lower optimization capabilities, with RFF, in particular, demonstrating limitations in addressing such problems effectively.

The experimental data have been summarized in Appendix A. In addition to the three comparison experiments discussed above, we also included the artificial bee colony (ABC) algorithm, the tree seed algorithm (TSA), and the knee point-driven evolutionary algorithm (KnEA) for further comparison, in order to more comprehensively validate the effectiveness of the proposed method. Among them, ABC simulates the foraging behavior of bees; STA models the seed dispersal mechanism of trees for both local and global search; and KnEA addresses multi-objective optimization by identifying knee points on the Pareto front.

5.2.2. Comparison of Convergence

To verify the convergence performance of different algorithms during the optimization process, this study plotted the convergence curves of EA-CPSO and other alternative algorithms within 60 iterations, as shown in Figure 6. We highlighted the convergence points in red to better illustrate the convergence behavior of the algorithm. Specifically, since the RFF algorithm does not have the concepts of population size and iteration, its values were directly used for comparison:

The curves show that EA-CPSO demonstrated significant advantages in both optimization efficiency and final results. It exhibited a rapid convergence trend in the early stages of iteration, with the optimization value significantly decreasing within the first 20 iterations and stabilizing after about 30 iterations. The Cauchy mutation significantly enhanced EA-CPSO’s jumping ability in the global search phase, effectively overcoming the limitation of PSO, which tends to get trapped in the local optimal.

In contrast, the other algorithms showed certain limitations. While MGGA gradually converged to a better result in the later stages of optimization, its convergence speed in the early iterations was noticeably slower than that of EA-CPSO, leading to lower optimization efficiency. PSO showed a fast decline in optimization value during the initial iterations, but due to the lack of an effective global search mechanism it eventually became stuck in the local optimal. RFF, as a classic greedy approximation algorithm, was mainly used as a reference in this experiment, and its optimization performance was relatively weak.

5.2.3. Comparison of Different Algorithms for Each Objective

To further compare the performance of different algorithms in multi-objective optimization, this paper conducted a quantitative analysis of the optimization values for each objective in the different algorithms and presents the results in the bar charts shown in Figure 7:

Firstly, evaluated for energy consumption and robustness, EA-CPSO significantly outperformed the other algorithms, demonstrating its advantages in global optimization and resource allocation balance. However, EA-CPSO did not excel in the objective of load balancing. On the one hand, EA-CPSO achieved greater optimization for the other objectives but sacrificed the adequate optimization of load balancing. On the other hand, this was related to the diversity and imbalance in the resource demands of the VMs and the resource capacities of the PMs in the experimental environment. Additionally, although RFF performed well for certain individual objectives, its lack of global search capability led to notable shortcomings in multi-objective trade-offs.

6. Conclusions

In this paper, we focused on the VMP problem in data centers and proposed a multi-objective placement model that comprehensively considers energy consumption, resource utilization, load balancing, and robustness. Based on this model, a joint optimization objective function was constructed, and a population-based heuristic algorithm, EA-CPSO, was developed to efficiently address the problem. By incorporating an energy-aware Cauchy mutation strategy, EA-CPSO significantly enhances the global search capability of the population. Subsequently, EA-CPSO was compared with existing algorithms, and our experimental results demonstrate that it outperforms other methods, achieving better trade-offs among all optimization objectives.

EA-CPSO achieves a dynamic balance between exploration and exploitation within the search space by integrating the inertia component, the cognitive component, and the social component, while introducing a mutation mechanism. This makes it suitable for solving complex problems such as multi-objective optimization and constrained optimization. The mutation mechanism leverages the heavy-tailed property of the Cauchy distribution, enabling particles to perform large-scale jumps with a higher probability and thereby enhancing the global search capability. The elite solution preservation mechanism ensures that the best solutions in each generation are retained, improving the overall optimization performance. However, EA-CPSO exhibits sensitivity to parameter settings in practical applications. To address this issue, future research will consider incorporating an adaptive parameter control mechanism to further enhance the robustness and optimization performance of EA-CPSO across different application scenarios.