Performance Prediction of Store and Forward Telemedicine Using Graph Theoretic Approach of Symmetry Queueing Network
Abstract
1. Introduction
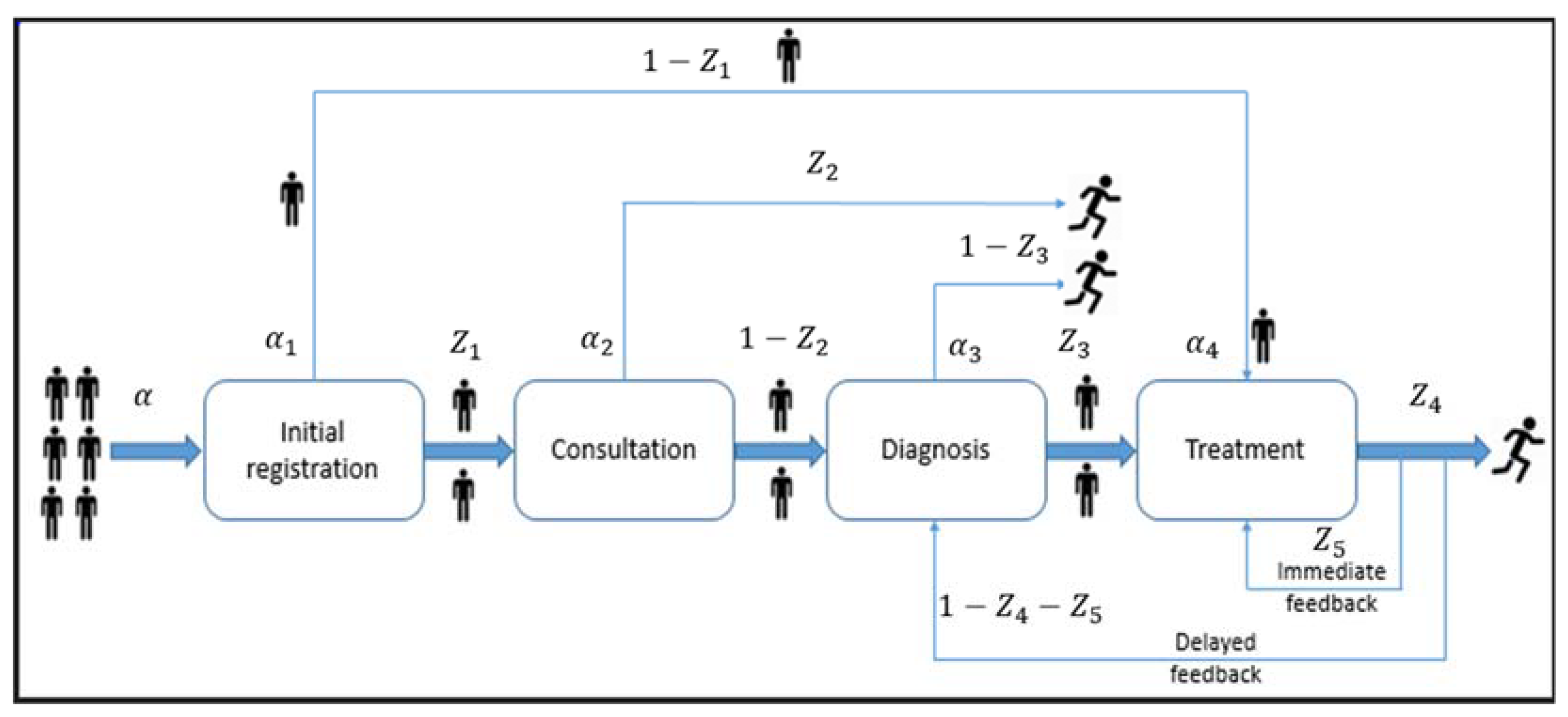
2. Models and Methods
- Single server at each node.
- Poisson Arrival process, exponential service time, open queueing network, fixed routing probabilities, feedback mechanisms, and symmetry in system behavior.
2.1. Notations
2.2. Balance Equation
- = total arrival rate at node i;
- = routing probabilities at specific transitions between nodes.
2.3. Measuring Network Performance
2.3.1. Average Visit Count to Nodes
2.3.2. Average Number of Patients in the System
2.3.3. Average Waiting Time of a Patient at Each Node
3. Results
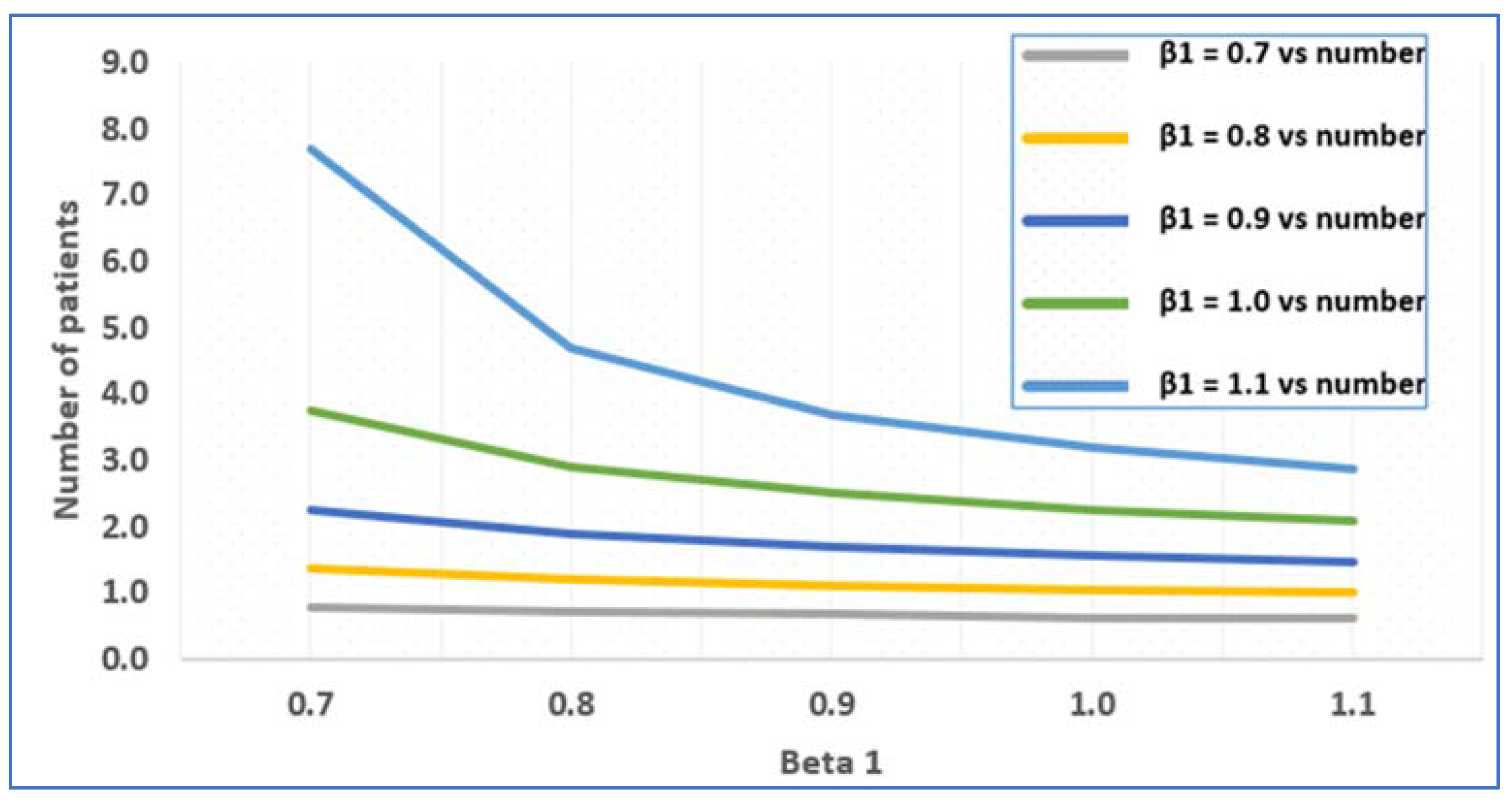
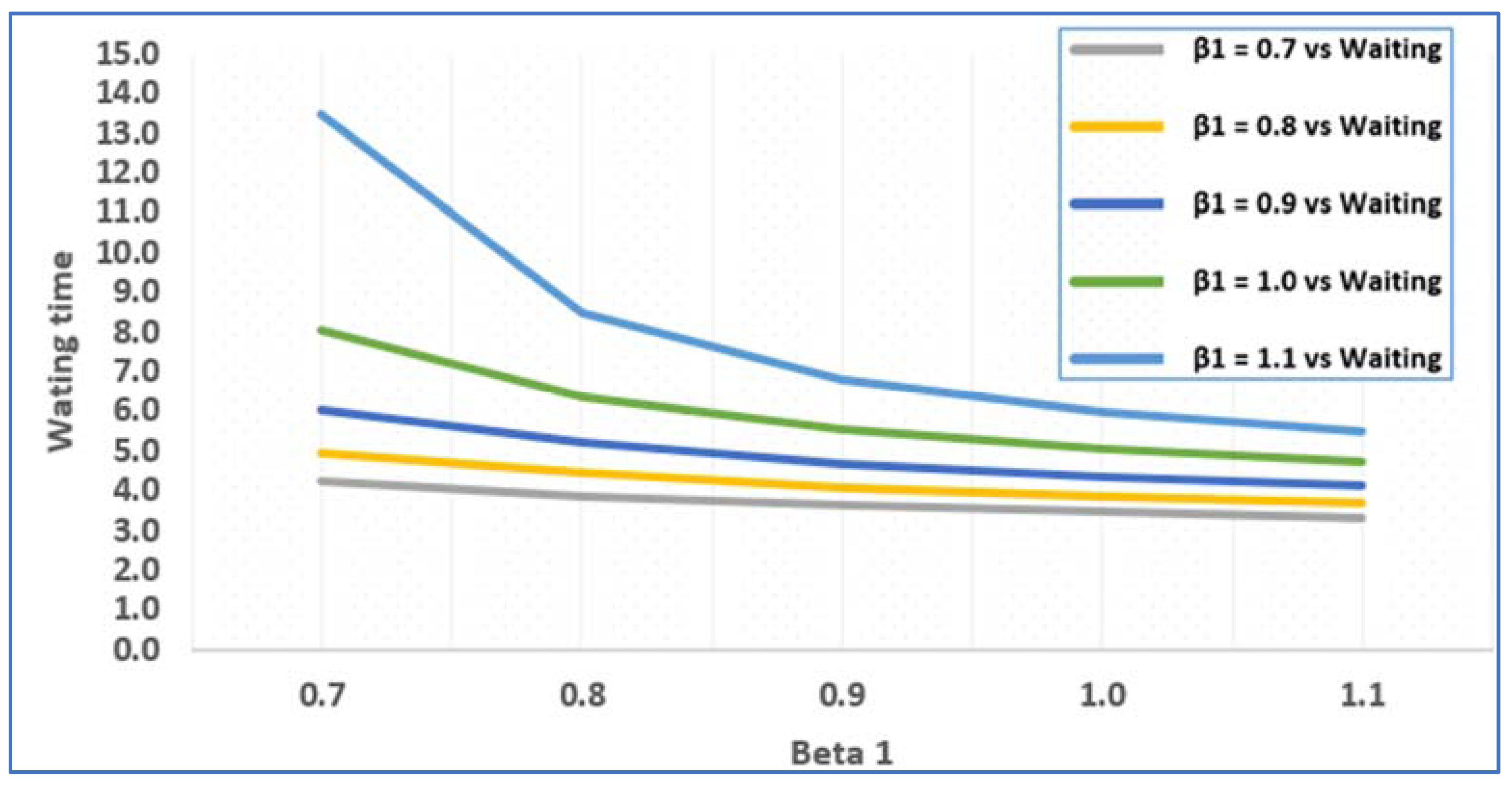
3.1. Numerical Illustration
- Case 1:
- Case 2:
3.2. Graph-Theoretic Approach of Queueing Network
3.2.1. Description of the Model
3.2.2. Graph Representation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sreekala, M.S. Study on Queueing Networks and Their Applications; Department of Statistics, University of Calicut: Malappuram, India, 2016. [Google Scholar]
- Pandian, P.S.; Safeer, K.P.; Shakunthala, D.T.I.; Gopal, P.; Padaki, V.C. Store and Forward Applications in Telemedicine for Wireless IP Based Networks. J. Netw. 2007, 2, 58–65. [Google Scholar] [CrossRef]
- Alenany, E.; Adel El-Baz, M. Modelling a hospital as a queueing network: Analysis for improving performance. Int. J. Ind. Manuf. Eng. 2017, 11, 1181–1187. [Google Scholar]
- Smith, J.M. Introduction to Queueing Networks: Theory Practice; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Gupta, R.; Gamad, R.S.; Bansod, P. Telemedicine: A brief analysis. Cogent Eng. 2014, 1, 966459. [Google Scholar] [CrossRef]
- Gross, D.; Shortie, J.F.; Thompson, J.M.; Harris, C.M. Fundamentals of Queueing Theory, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Thangaraj, V.; Vanitha, S. On the analysis of M/M/1 feedback queue with Catastrophes using continued fractions. Int. J. Pure Appl. Math. 2009, 53, 133–151. [Google Scholar]
- Gaston, E.A. Telemedicne—Is Ben Boon. JAMA—J. Am. Med. Assoc. 1964, 188, 329. [Google Scholar] [CrossRef]
- Bird, K.T.; Murphy, R.L.H.; Cohen, G.L. Telemedicine and Future of Pulmonary Disease. Dis. Chest 1969, 56, 242. [Google Scholar]
- Dean, N.; Kelmans, A.K.; Lih, K.; Massey, W.A. The Spanning Tree Enumeration Problem for Digraphs; Princeton University: Princeton, NJ, USA, 1999. [Google Scholar]
- Brown, F.W. Rural telepsychiatry. Psychiatr. Serv. 1998, 49, 963–964. [Google Scholar] [CrossRef]
- Holzer, W.H. Telemedicine—New Application of Communications Technology. IEEE Transac. Commun. 1974, 22, 685–688. [Google Scholar] [CrossRef]
- Clifford, M.H. One-UPMANSHIP in Telemedicine. IEEE Trans. Aerosp. Electron. Syst. 1973, AES9(5), 805–806. [Google Scholar]
- Park, B.; Bashshur, R. Some Implication of Telemedicine. J. Commun. 1975, 25, 161–166. [Google Scholar] [CrossRef]
- Grundly, B.L. Telemedicine in Critical Care—Preliminary Report. Crit. Care Med. 1976, 4, 104–105. [Google Scholar] [CrossRef]
- Allan, R. Medical Electronics Coming—Era of Telemedicine. IEEE Spectr. 1976, 13, 30–35. [Google Scholar]
- Scholl, J.; Lambrinos, L.; Lindgren, A. Rural telemedicine networks using store-and-forward Voice-over-IP. Stud. Health Technol. Inform. 2009, 150, 448–452. [Google Scholar]
- Berge, C. Graphs and Hypergraph, 2nd ed.; North-Holland: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Gabow, H.N.; Myers, W.W. Finding all spanning trees of directed and undirected graphs. SIAM J. Comput. 1978, 7, 280–287. [Google Scholar] [CrossRef]
- Pandian, P.S. An Overview of Telemedicine Technologies for Healthcare Applications. Int. J. Biomed. Clin. Eng. 2016, 5, 29–52. [Google Scholar] [CrossRef]
- Chen, H.; Yao, D.D. Fundamentals of Queueing Networks: Performance, Asymptotics, and Optimization; Springer: New York, NY, USA, 2001. [Google Scholar]
- Yue, W.; Takahashi, Y.; Takagi, H. (Eds.) Advances in Queueing Theory and Network Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Simonetta, B.; Marin, A. Queueing networks. In Formal Methods for Performance Evaluation, Proceedings of the 7th International School on Formal Methods for the Design of Computer, Communication and Software Systems, Bertinoro, Italy, 8 May–2 June 2007; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sharma, V.S.; Iyer, P.S.K. Markov Chains and Queueing Networks; CS 797 Independent Study Report. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=14048110bd19779aa0ab32d0158521f7d3706382 (accessed on 31 March 2025).
- Cohen, J.W. The Single Server Queue, 2nd ed.; North-Holland Publishing Company: Amsterdam, The Netherlands; London, UK, 1982. [Google Scholar]
- Boucherie, R.J.; van Dijk, N.M. Queueing Networks—A Fundamental Approach; International Series in Operations Research and Management Science; Springer: New York, NY, USA, 2011. [Google Scholar]
- Abraham, I.; Chechik, S.; Elkin, M.; Filtser, A.; Neiman, O. Ramsey spanning trees and their applications. ACM Trans. Algorithms 2020, 16, 19. [Google Scholar] [CrossRef]
- Davignon, G.R.; Disney, R.L. Single server queues with state dependent feedback. INFORS Inf. Syst. Oper. Res. 1976, 14, 71–85. [Google Scholar] [CrossRef]
- Foley, R.D.; Disney, R.L. Queues with delayed feedback. Adv. Appl. Probab. 1983, 15, 162–182. [Google Scholar] [CrossRef]
- Narmadha, V.; Rajendran, P. A Literature Review on Development of Queueing Networks. Reliab. Theory Appl. 2024, 19, 696–702. [Google Scholar]
- Sreekala, M.S.; Manoharan, M. An Application of Restricted Open Queueing Networks to Healthcare System. Int. J. Latest Trends Eng. Technol. 2016, 7, 103–113. [Google Scholar]
- Cheng, B.; Wang, D.; Fan, J. Independent spanning trees in networks: A survey. ACM Comput. Surv. 2023, 55, 335. [Google Scholar] [CrossRef]
- Deng, L.; Poole, M.S. Learning through telemedicine networks. In Proceedings of the 36th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 6–9 January 2003. [Google Scholar]
- Ghasemi, S.; Taghipour, F.; Aghsami, A.; Jolai, F.; Jolai, S. A novel mathematical model to minimize the total cost of the hospital and COVID-19 outbreak concerning waiting time of patients using Jackson queueing networks, a case study. Sci. Iran. 2023. [Google Scholar] [CrossRef]
- Shortle, J.F.; Thompson, J.M.; Gross, D.; Harris, C. Fundamentals of Queueing Theory; John Wiley & Sons: Hoboken, NJ, USA, 2018; Volume 339. [Google Scholar]
- Vass, H.; Szabo, Z.K. Application of queuing model to patient flow in emergency department. Case study. Procedia Econ. Financ. 2015, 32, 479–487. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, Y.; Dong, Y.; Xie, X.; Xing, F. CAT-Net: Cascaded Attention Transformer Network for Medical Image Segmentation. IEEE Trans. Med. Imaging 2023, 42, 123–136. [Google Scholar]
- Wang, L.; Huang, R.; Zhang, J.; Li, Z.; Wu, Y. CVANet: Cascaded Visual Attention Network for Fine-Grained Visual Recognition. Pattern Recognit. 2023, 139, 109425. [Google Scholar] [CrossRef]
- Graham, R.L.; Hell, P. On the history of the minimum spanning tree problem. Ann. Hist. Comput. 1985, 7, 43–57. [Google Scholar] [CrossRef]
- Putri, A.H.M.; Endrayanto, I. On the Application of the Open Jackson Queuing Network in Hospital. In Proceedings of the 2nd International Seminar on Science and Technology (ISSTEC 2019), Yogyakarta, Indonesia, 25 November 2019; Atlantis Press: Dordrecht, The Netherlands, 2020. [Google Scholar]
- Youngberry, K.; Swinfen, R.; Swinfen, P.; Wootton, R. Store-and-forward telemedicine. In Telepediatrics: Telemedicine and Child Health; CRC Press: Boca Raton, FL, USA, 2024; pp. 199–210. [Google Scholar]



| Symbol | Description |
|---|---|
| External Arrival rate to the system (Poisson arrival rate) | |
| α1, α2, α3, α4 | Arrival Rate at node 1, node 2, node 3, node 4. |
| β1, β2, β3, β4 | Service Rate at node 1, node 2, node 3, node 4. |
| γ1, γ2, γ3, γ4 | Traffic intensity (utilization factor) at nodes 1, 2, 3, 4. |
| Routing probabilities and immediate feedback | |
| Number of patients at nodes 1, 2, 3, 4. | |
| Average visit counts at nodes 1, 2, 3, 4. | |
| Average number of patients at nodes 1, 2, 3, 4. | |
| Average waiting time of customers at nodes 1, 2, 3, 4. | |
| Joint probability of having patients x1, x2, x3, x4 at nodes 1, 2, 3, 4, respectively. | |
| X | Total average number of customers in the system calculated as X = X1 + X2 + X3 + X4. |
| Total average waiting time for patients in the system S = S1 + S2 + S3 + S4. |
| 1 | 0.3 | 1.82 | 1.97 |
| 0.667 | 0.0937 | 1.542 | 0.9559 | 3.2586 |
| 3.335 | 0.4685 | 7.71 | 4.816 | 16.3295 |
| (0 0 0 0) | 0.36206 | 0.0000003 | |
| 0.01448 | 0.000001 | ||
| 0.00579 | 0.0000004 | ||
| 0.00232 | 0.0000002 | ||
| 0.00093 | 0.00000007 | ||
| 0.00310 | 0.00000002 | ||
| 0.00124 | 0.011354 | ||
| 0.00050 | 0.004542 | ||
| 0.00019 | 0.001816 | ||
| 0.000079 | 0.00073 | ||
| 0.00027 | 0.00029 | ||
| 0.00014 | 0.000973 | ||
| 0.000042 | 0.00038 | ||
| 0.000017 | 0.00015 | ||
| 0.0000068 | 0.000062 | ||
| 0.0000228 | 0.000025 | ||
| 0.0000091 | 0.000083 | ||
| 0.0000036 | 0.000033 | ||
| 1.4592 × 10−6 | 0.000013 | ||
| 5.8368 × 10−7 | 0.000005 | ||
| 1.954 × 10−6 | 2.13555 × 10−6 | ||
| 7.817 × 10−7 | 7.15015 × 10−6 | ||
| 3.1269 × 10−7 | 0.000973 | ||
| 1.2505 × 10−7 | 1.1445 × 10−6 | ||
| 5.003 × 10−8 | 4.57615 × 10−7 | ||
| 0.02027 | 1.83045 × 10−7 | ||
| 0.00811 | 2.61395 × 10−8 | ||
| 0.00324 | 1.04555 × 10−8 | ||
| 0.00129 | 4.18225 × 10−9 | ||
| 0.000520 | 1.38865 × 10−7 | ||
| 0.000175 | 5.55445 × 10−8 | ||
| 0.00070 | 2.22185 × 10−8 | ||
| 0.00028 | 8.88715 × 10−9 | ||
| 0.00011 | 3.55485 × 10−9 | ||
| 4.4495 × 10−5 | 1.18035 × 10−7 | ||
| 0.000148 | 4.72135 × 10−8 | ||
| 5.95845 × 10−5 | 1.88855 × 10−8 | ||
| 2.38345 × 10−5 | 7.5545 × 10−9 | ||
| 9.53355 × 10−6 | 3.02165 × 10−9 | ||
| 3.81345 × 10−6 | 1.00335 × 10−7 | ||
| 1.27685 × 10−5 | 4.01315 × 10−8 | ||
| 5.1075 × 10−6 | 1.60525 × 10−8 | ||
| 2.04295 × 10−6 | 6.42095 × 10−9 | ||
| 8.17165 × 10−7 | 2.56845 × 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niranjan, S.P.; Aswini, K.; Vlase, S.; Scutaru, M.L. Performance Prediction of Store and Forward Telemedicine Using Graph Theoretic Approach of Symmetry Queueing Network. Symmetry 2025, 17, 741. https://doi.org/10.3390/sym17050741
Niranjan SP, Aswini K, Vlase S, Scutaru ML. Performance Prediction of Store and Forward Telemedicine Using Graph Theoretic Approach of Symmetry Queueing Network. Symmetry. 2025; 17(5):741. https://doi.org/10.3390/sym17050741
Chicago/Turabian StyleNiranjan, Subramani Palani, Kumar Aswini, Sorin Vlase, and Maria Luminita Scutaru. 2025. "Performance Prediction of Store and Forward Telemedicine Using Graph Theoretic Approach of Symmetry Queueing Network" Symmetry 17, no. 5: 741. https://doi.org/10.3390/sym17050741
APA StyleNiranjan, S. P., Aswini, K., Vlase, S., & Scutaru, M. L. (2025). Performance Prediction of Store and Forward Telemedicine Using Graph Theoretic Approach of Symmetry Queueing Network. Symmetry, 17(5), 741. https://doi.org/10.3390/sym17050741









