Analysis of Main Roof Mechanical State in Inclined Coal Seams with Roof Cutting and Gob-Side Entry Retaining
Abstract
1. Introduction
2. General Situation of No. 3131 Haulage Roadway Roof Cutting and Retaining Engineering
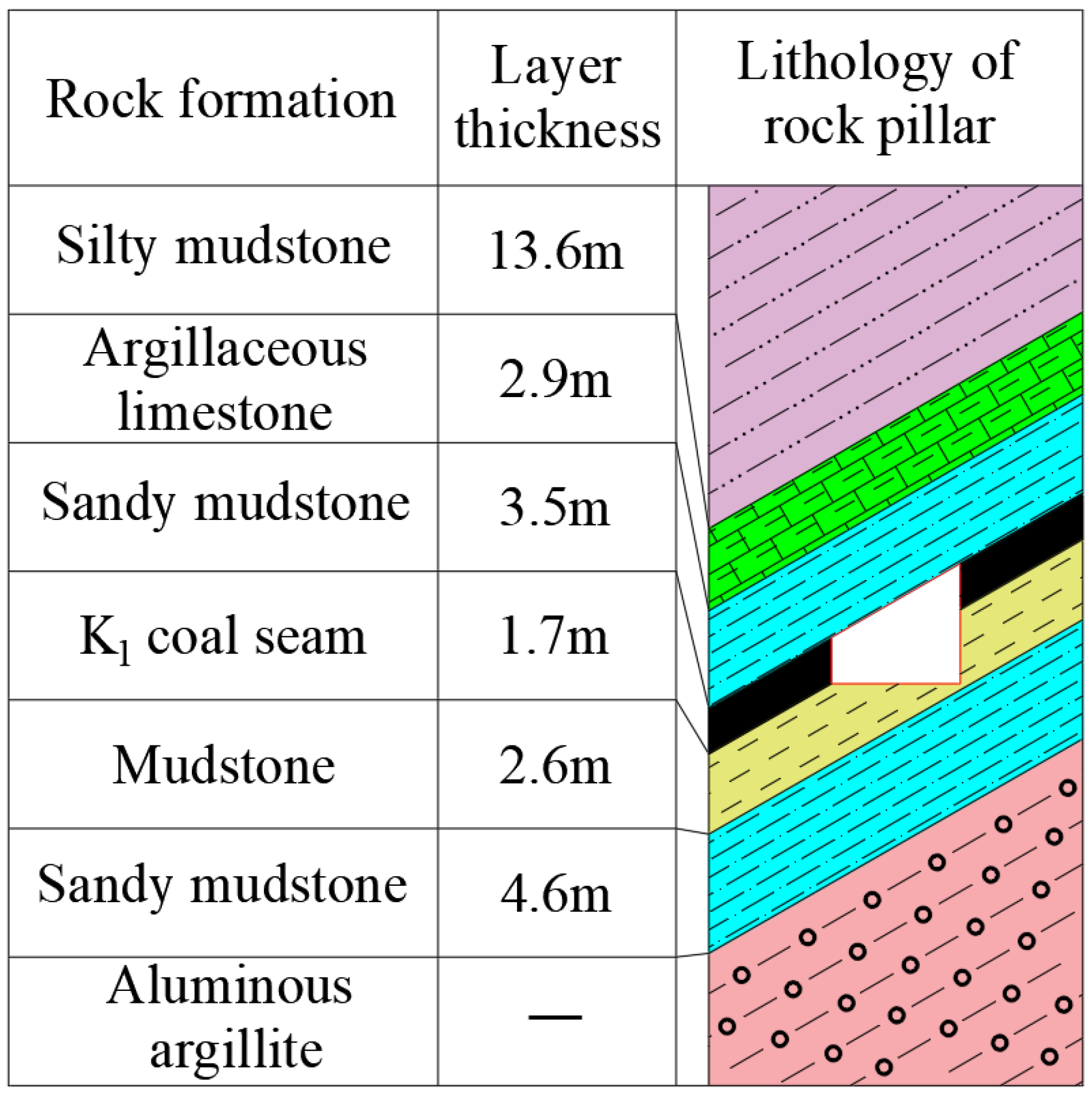
2.1. Overview of Production Geology
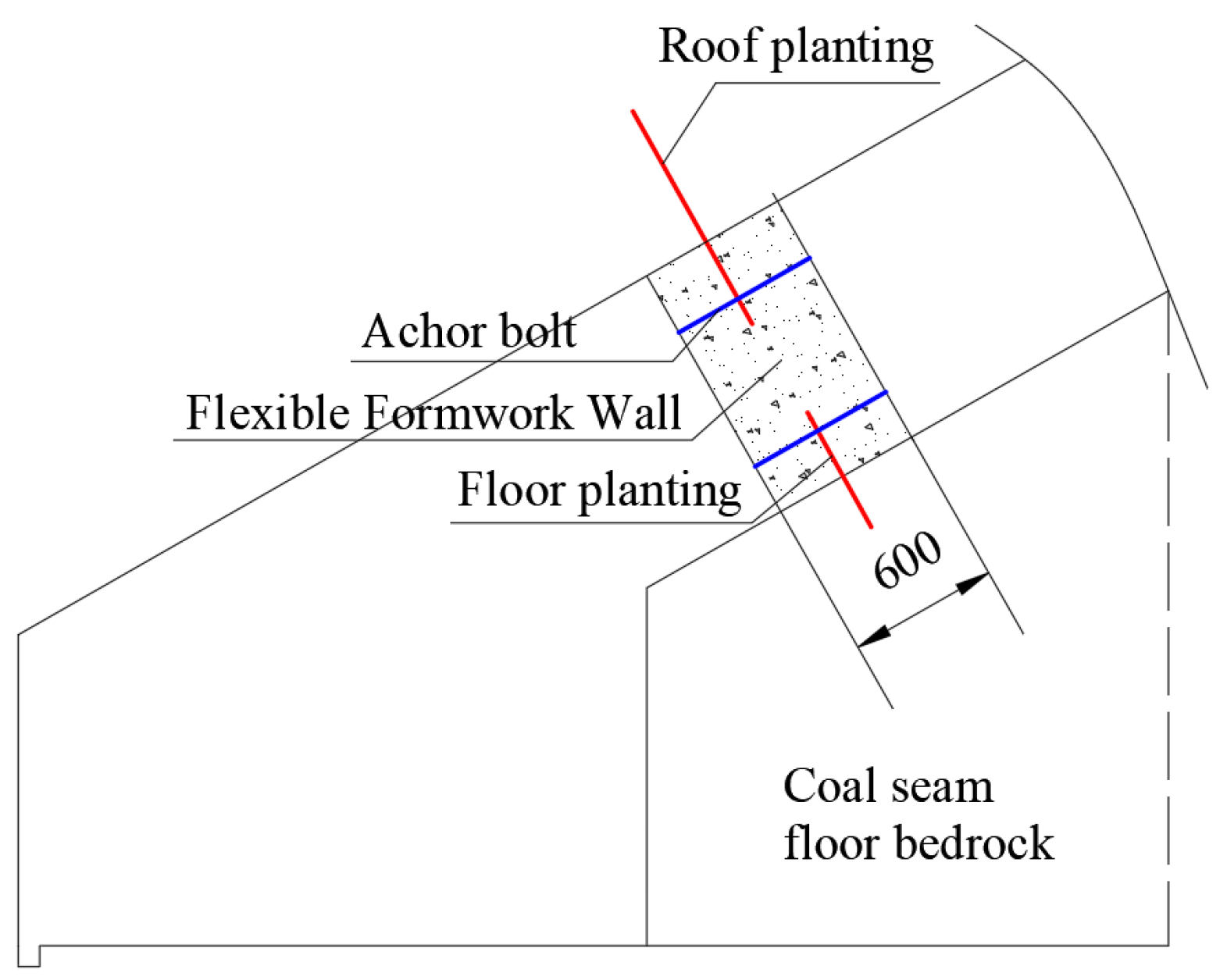
2.2. Engineering Parameters of Gob-Side Entry Retaining with Roof Cutting
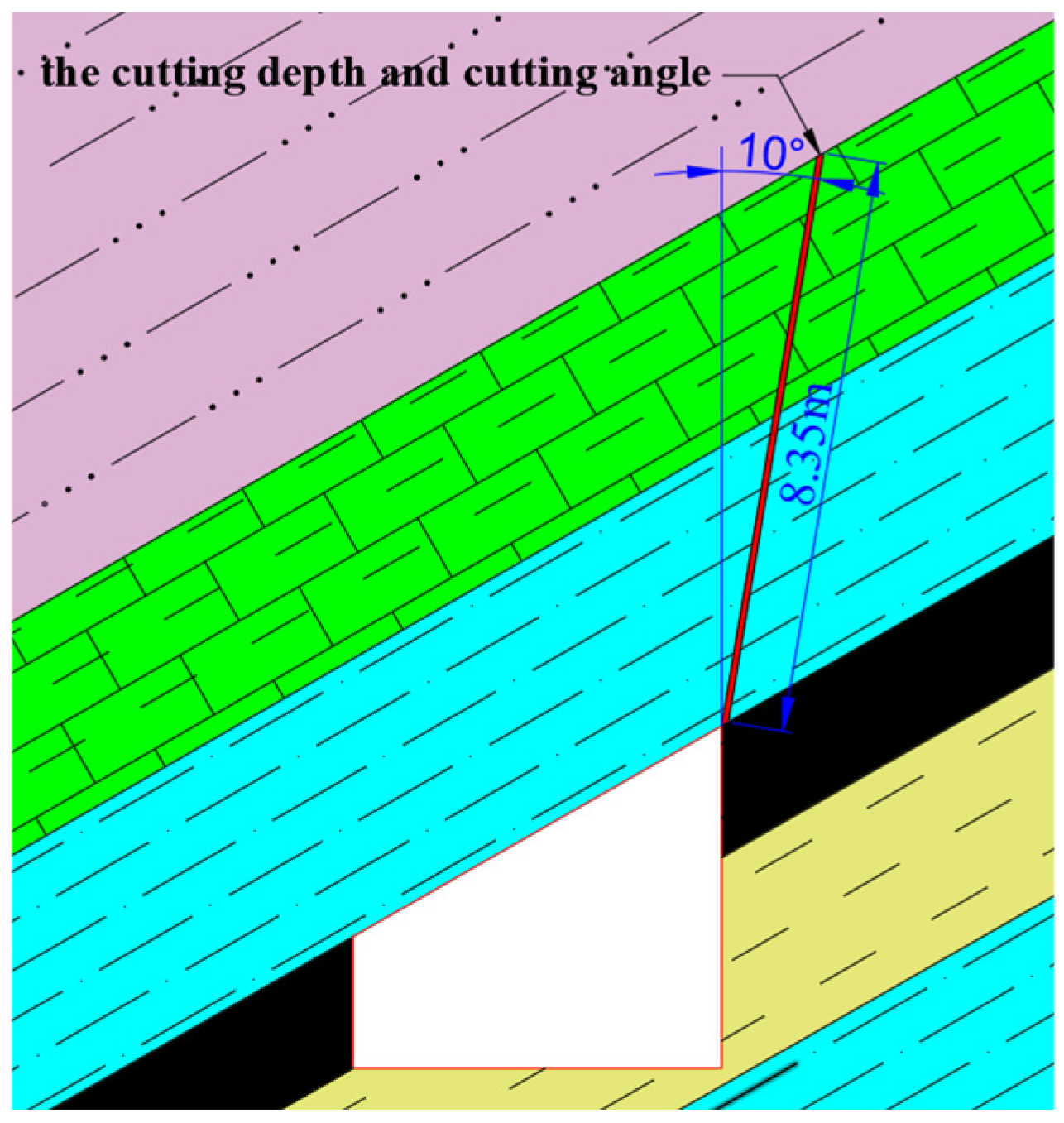
- (1)
- Roof-cutting depth
- (2)
- Roof-cutting angle
- (3)
- Spacing between blasting boreholes
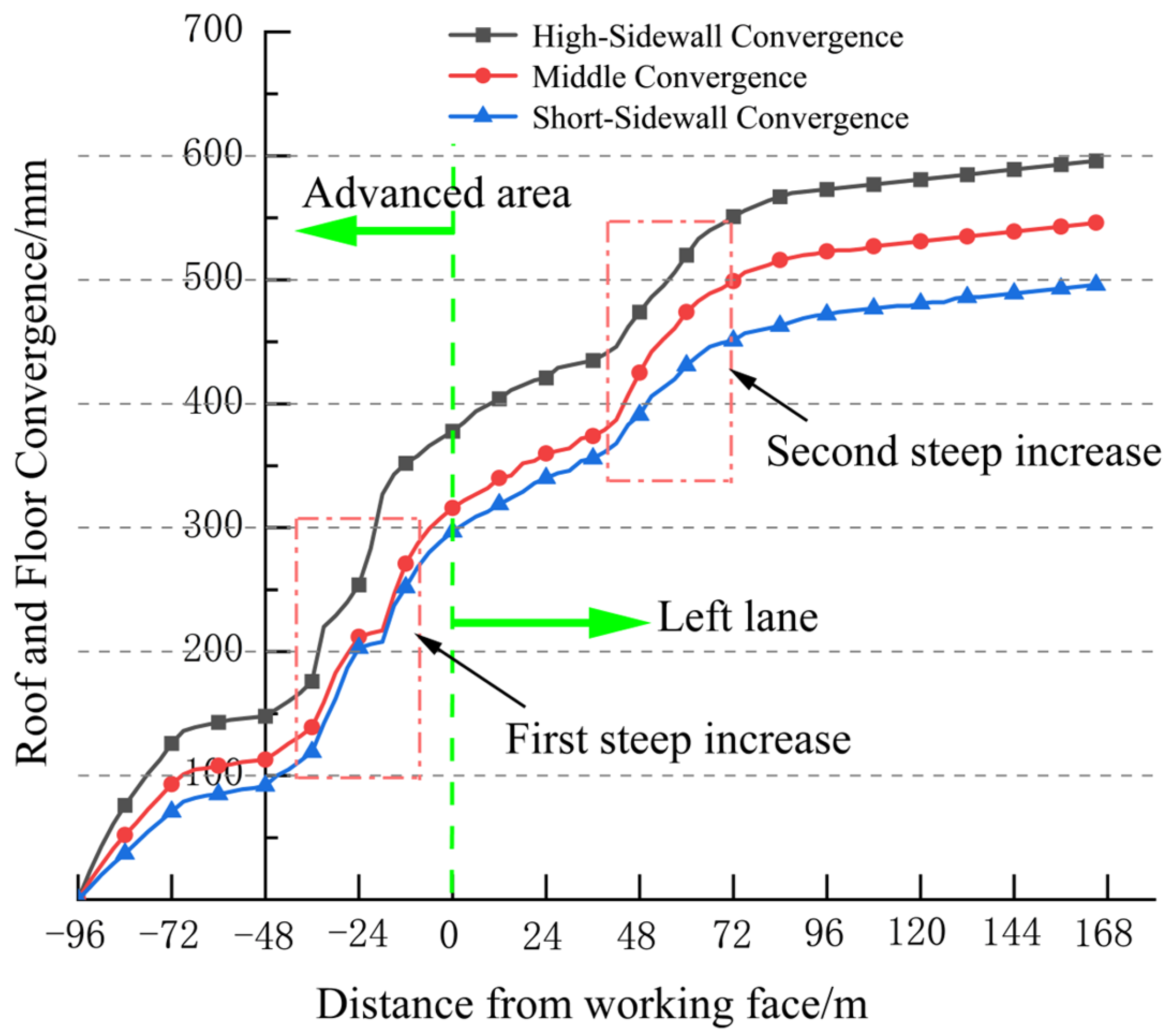
3. Deformation Characteristics of Surrounding Rock in 3131 Transport Roadway
4. Mechanical Analysis of Roof Structure of Gob-Side Entry Retaining with Roof Cutting
4.1. Analysis of Evolution Characteristics of Roof Structure
4.2. Analysis on Mechanical State of Basic Roof of Gob-Side Entry Retaining with Roof Cutting
4.2.1. Analysis of Mechanical State of Basic Roof in Roadway Excavation Period
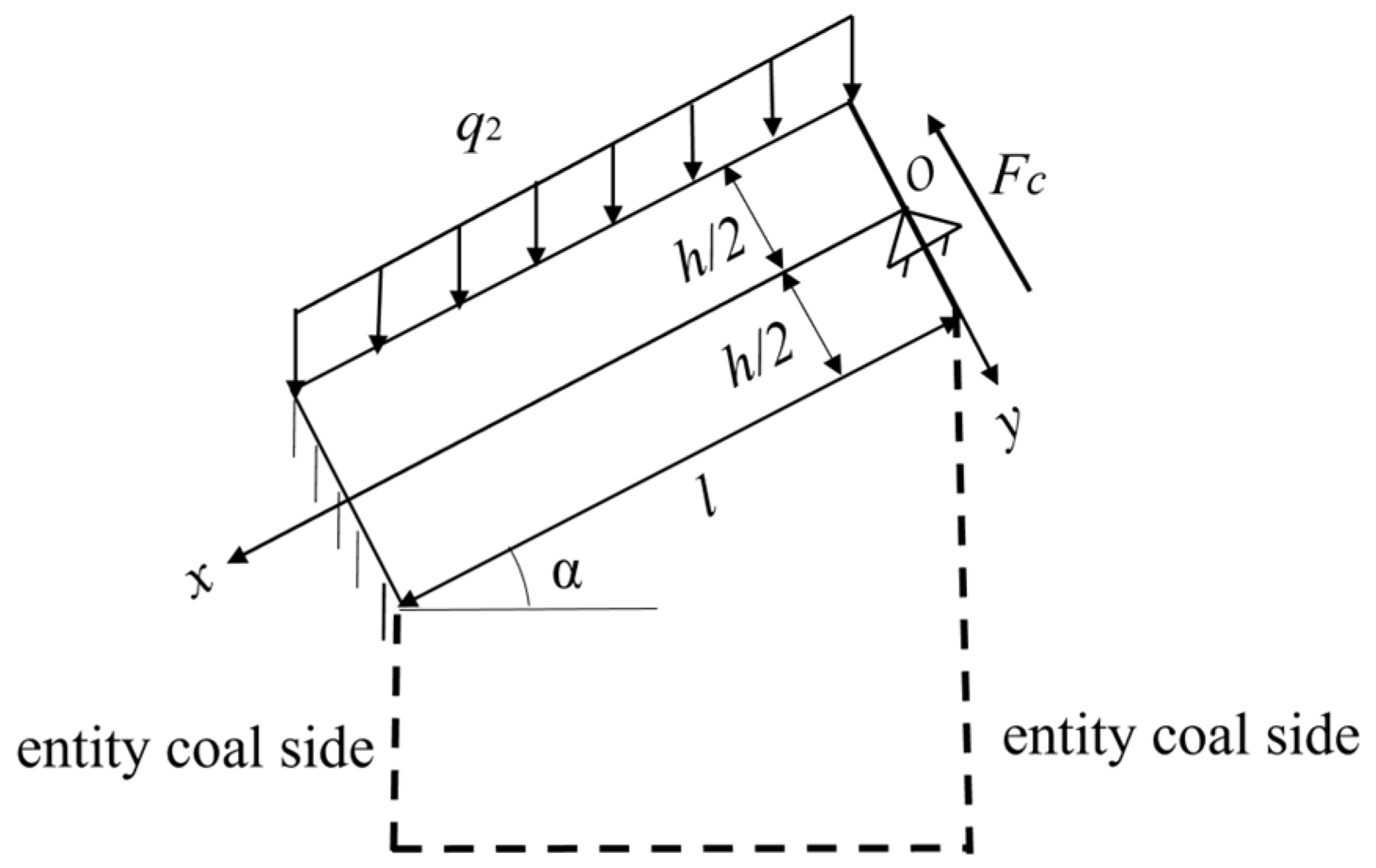
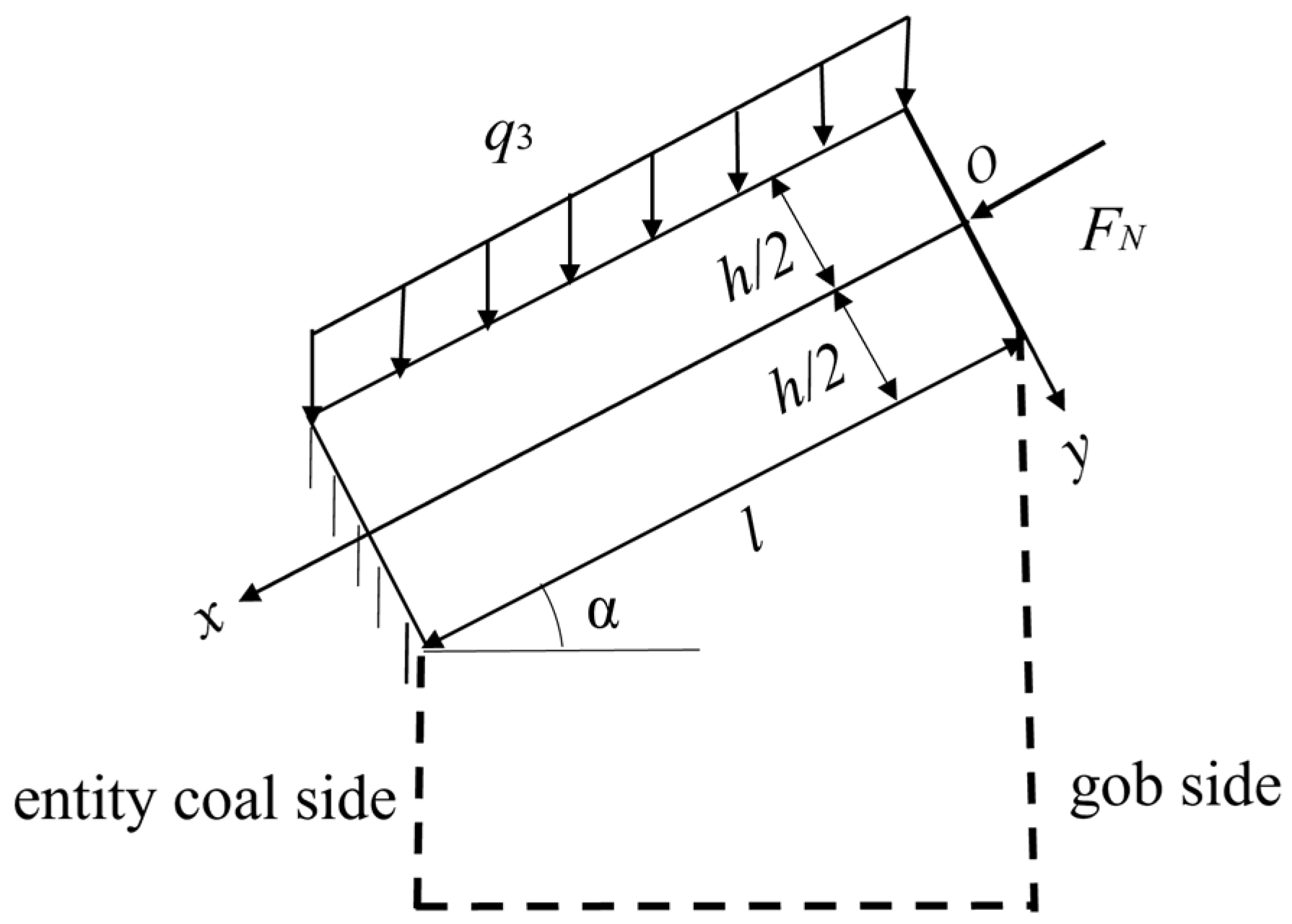
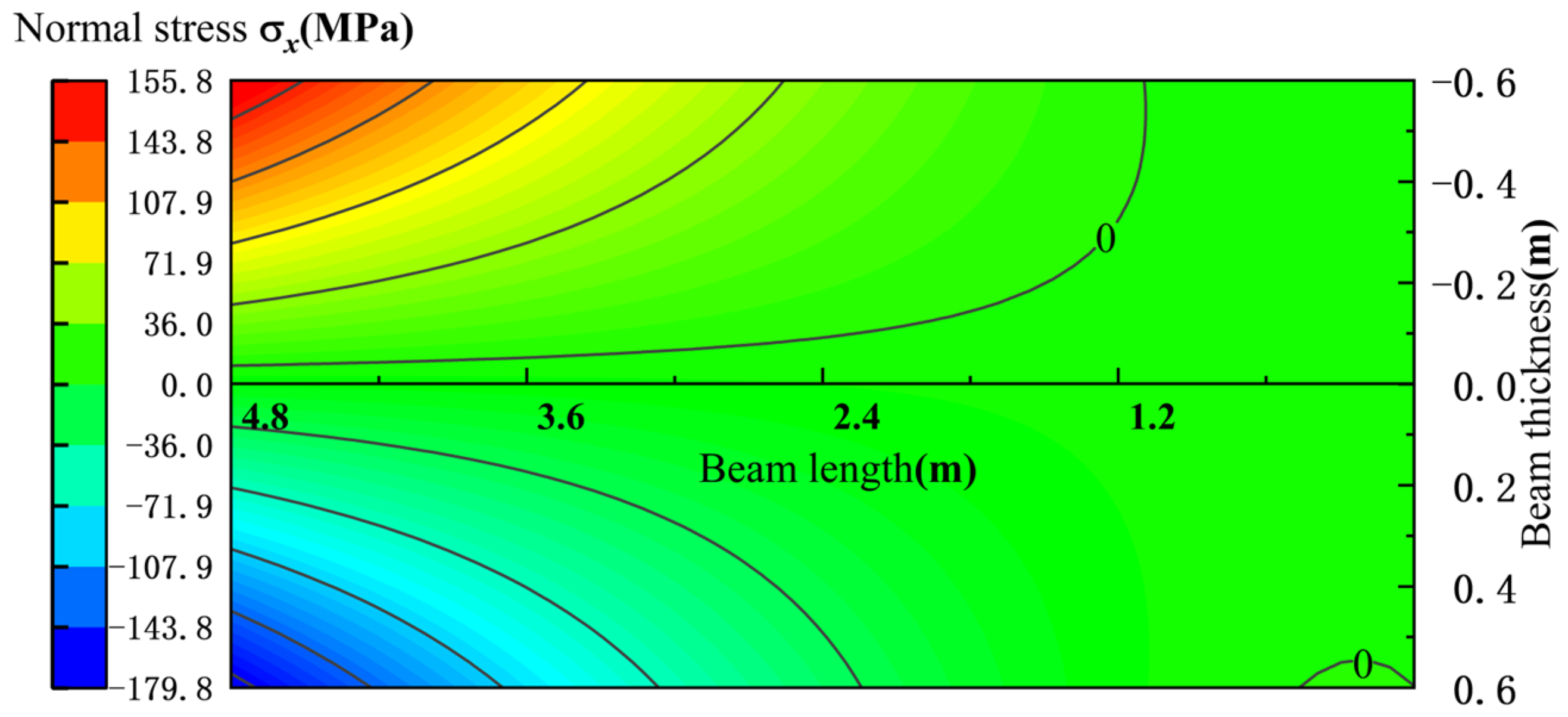
4.2.2. Analysis of Mechanical State of Main Roof in Advanced Influence Period of Primary Mining
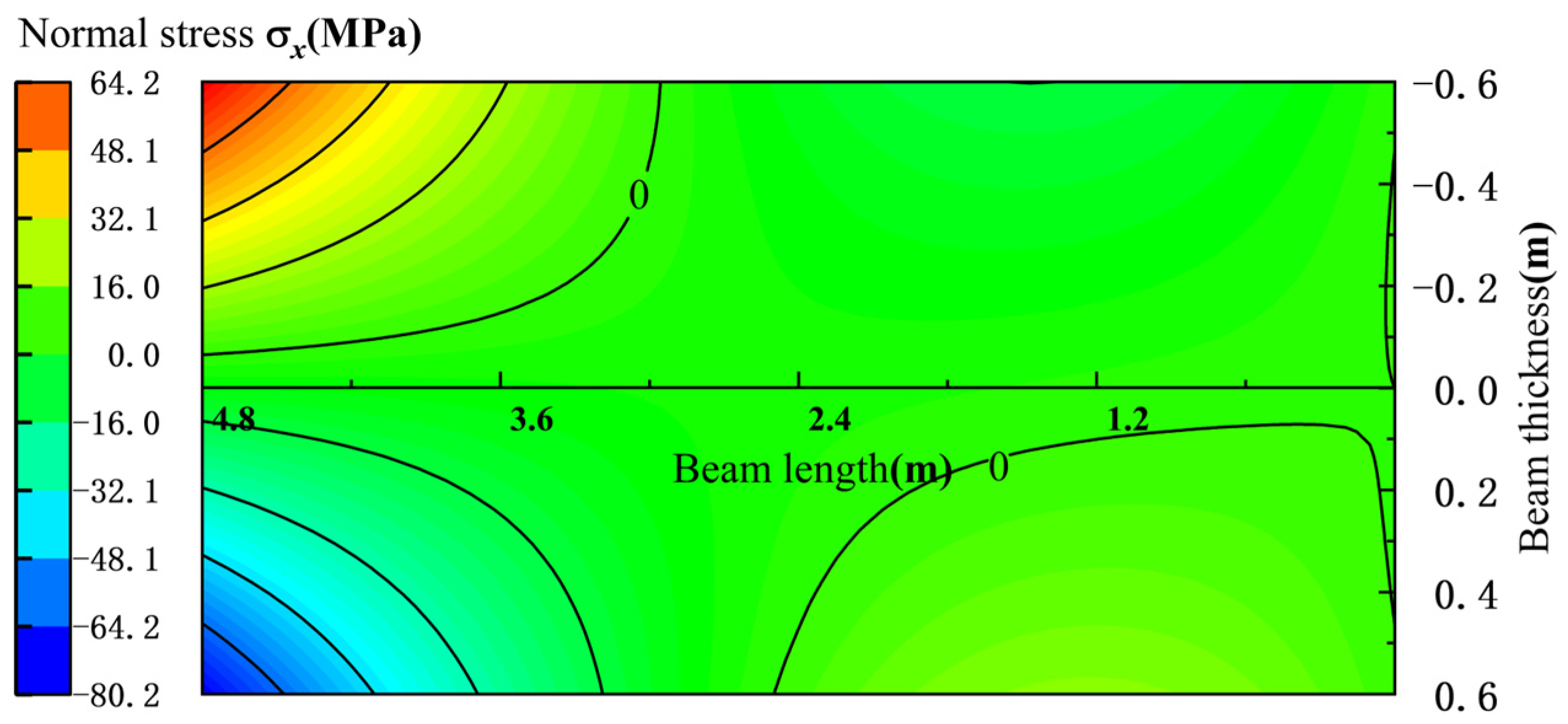
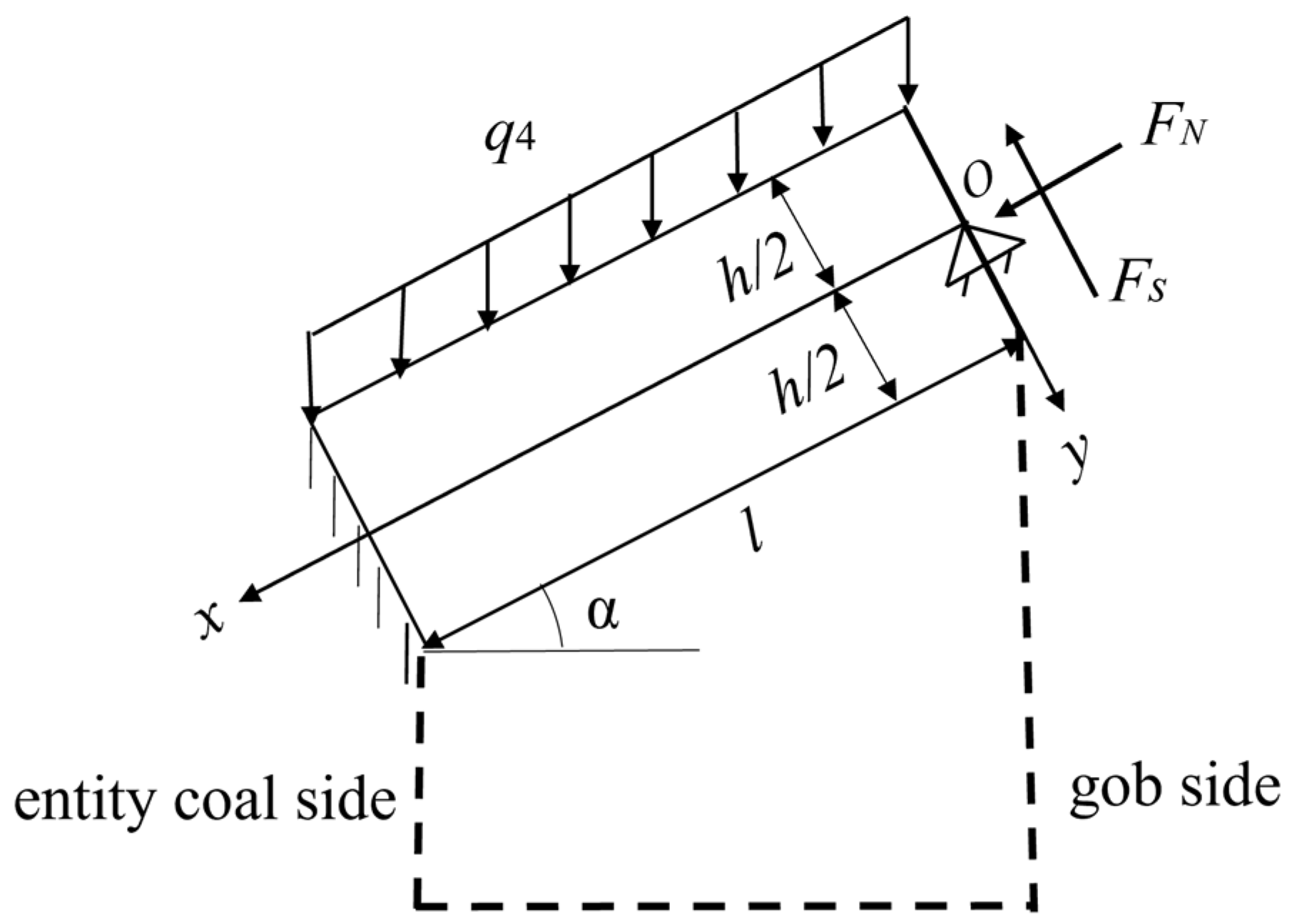
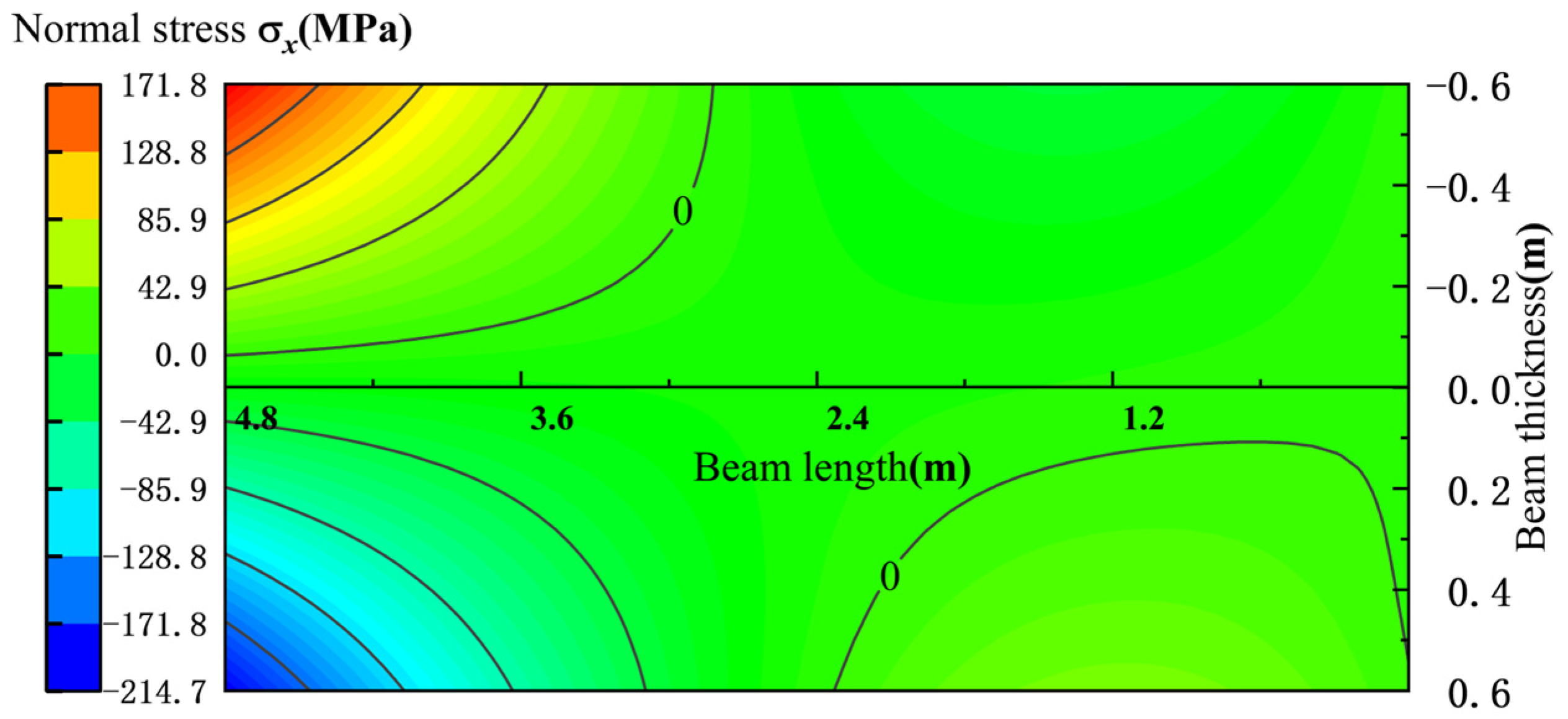
4.2.3. Analysis of Mechanical State of Basic Roof in Roadway Retaining Period
4.2.4. Analysis of Mechanical State of Main Roof in Advanced Influence Period of Secondary Mining
4.3. Design of Roadside Support Resistance
5. The Influence of Coal Seam Dip Angle on the Stability of Main Roof Rock Beam of Gob-Side Entry Retaining in Inclined Coal Seam
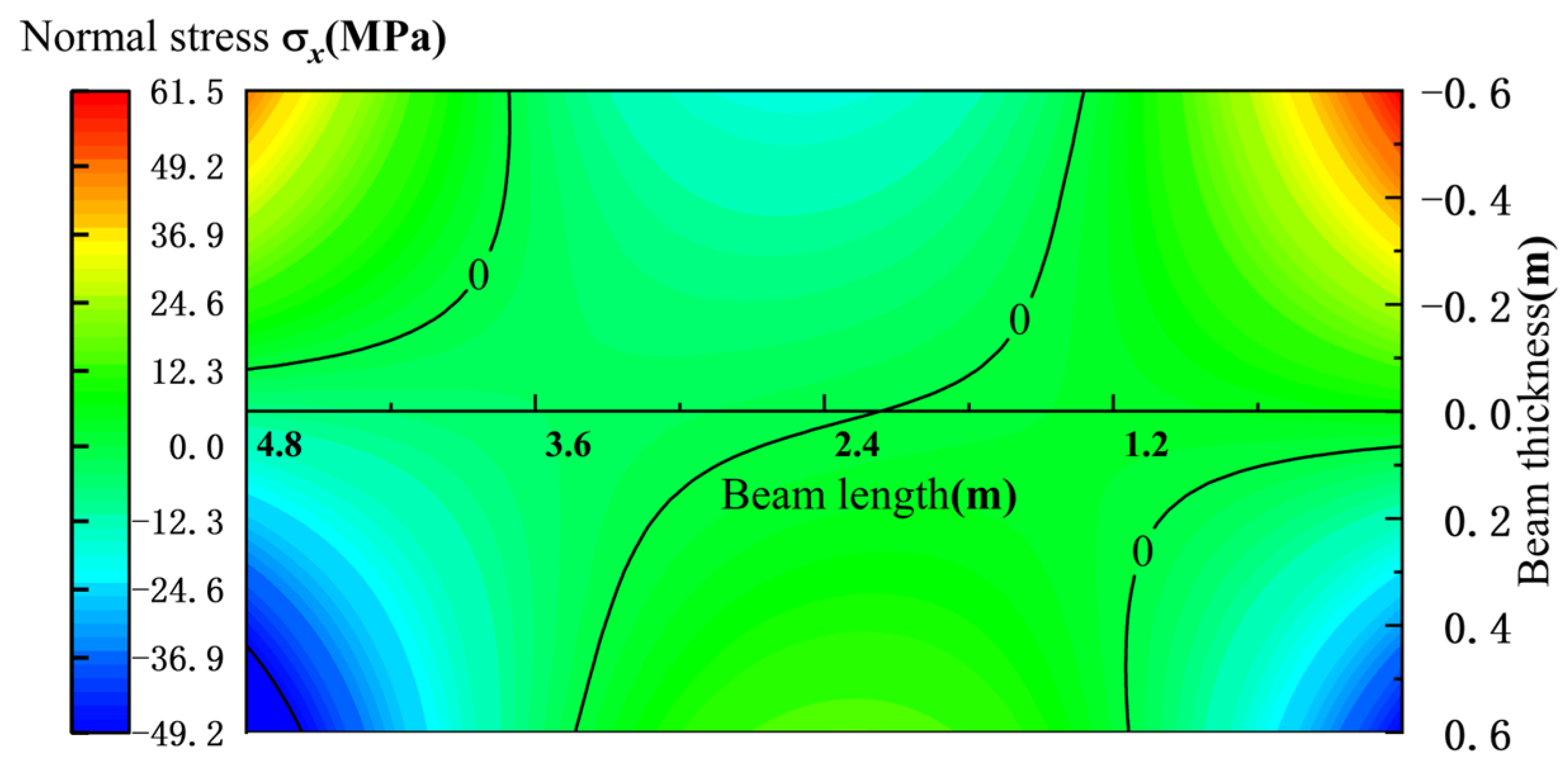
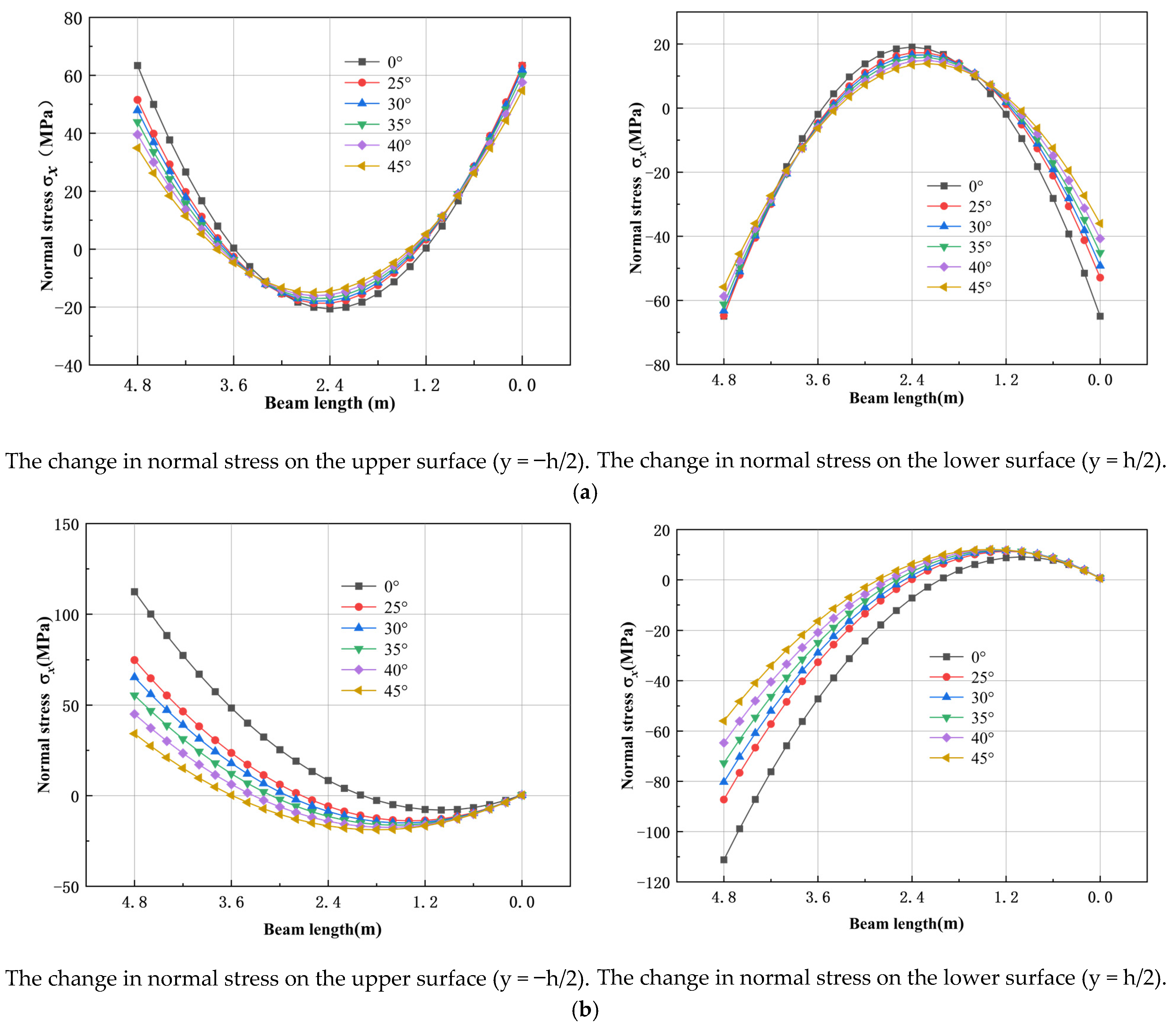
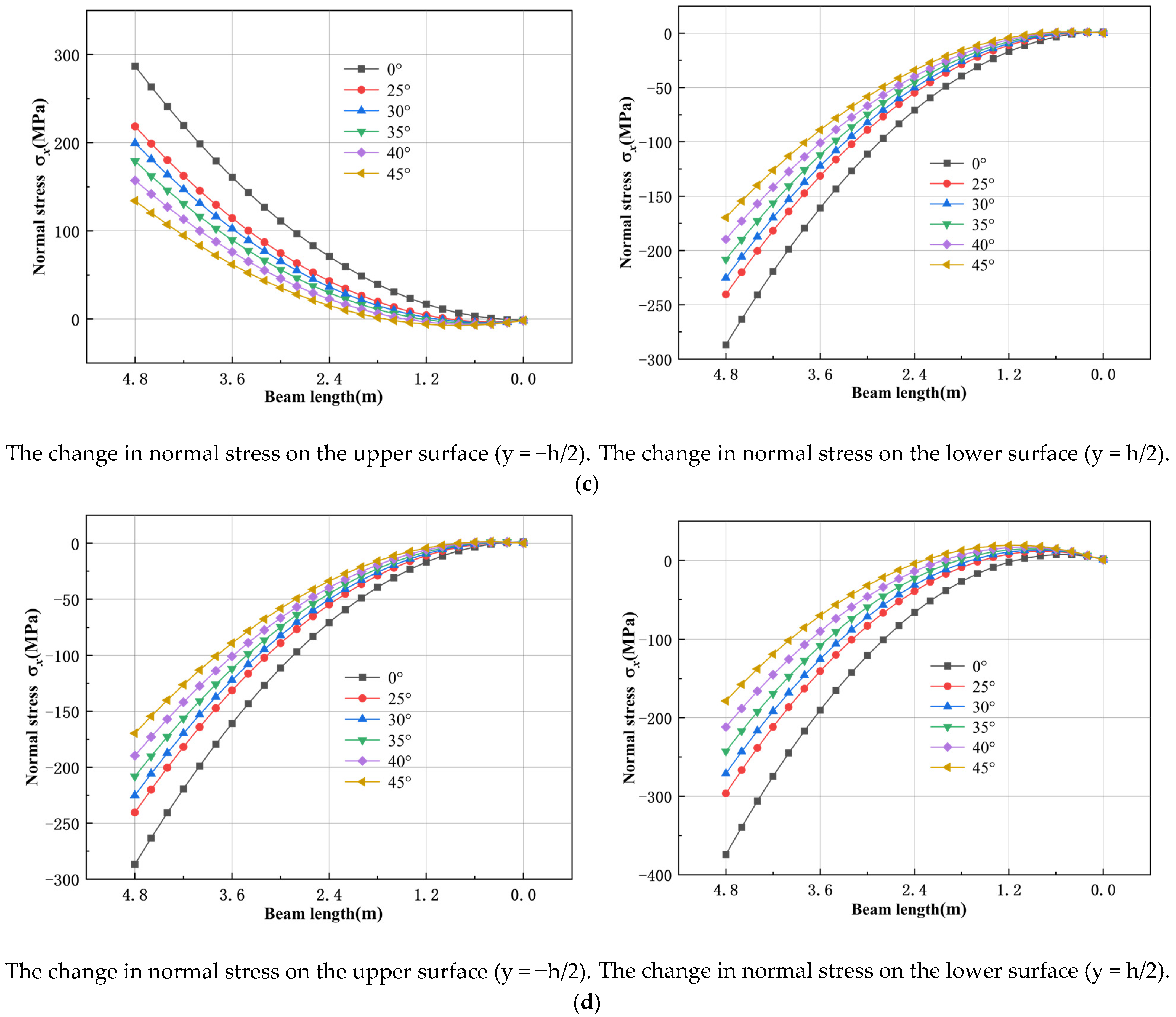
5.1. Influence of Dip Angle of Coal Seam on Stress State of Main Roof
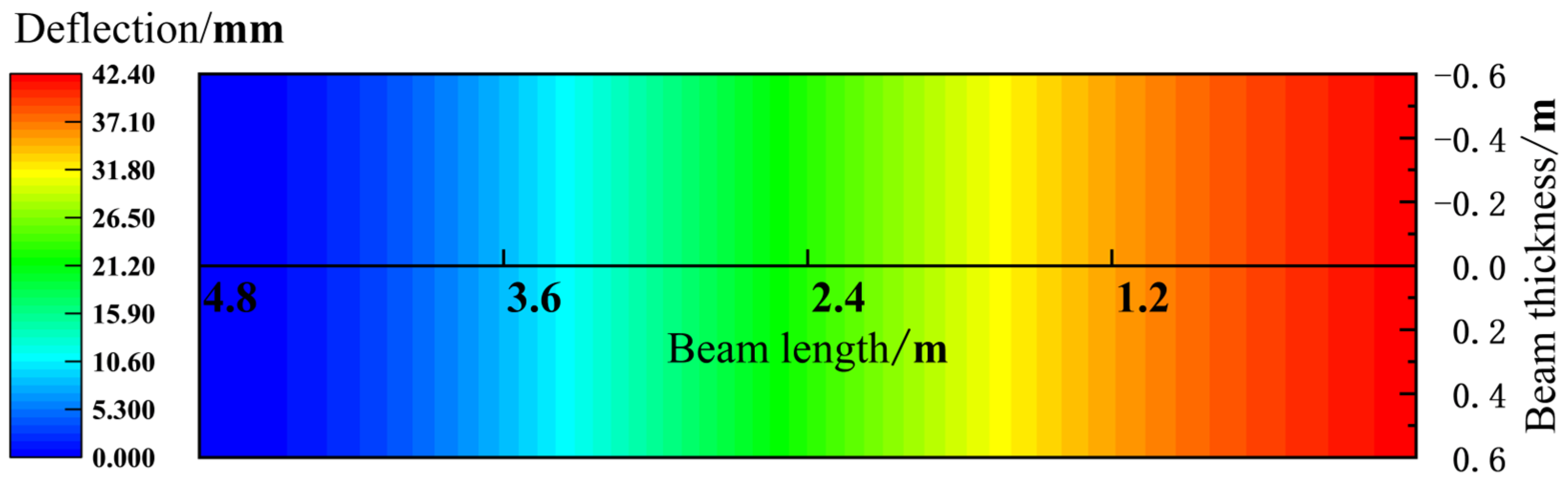
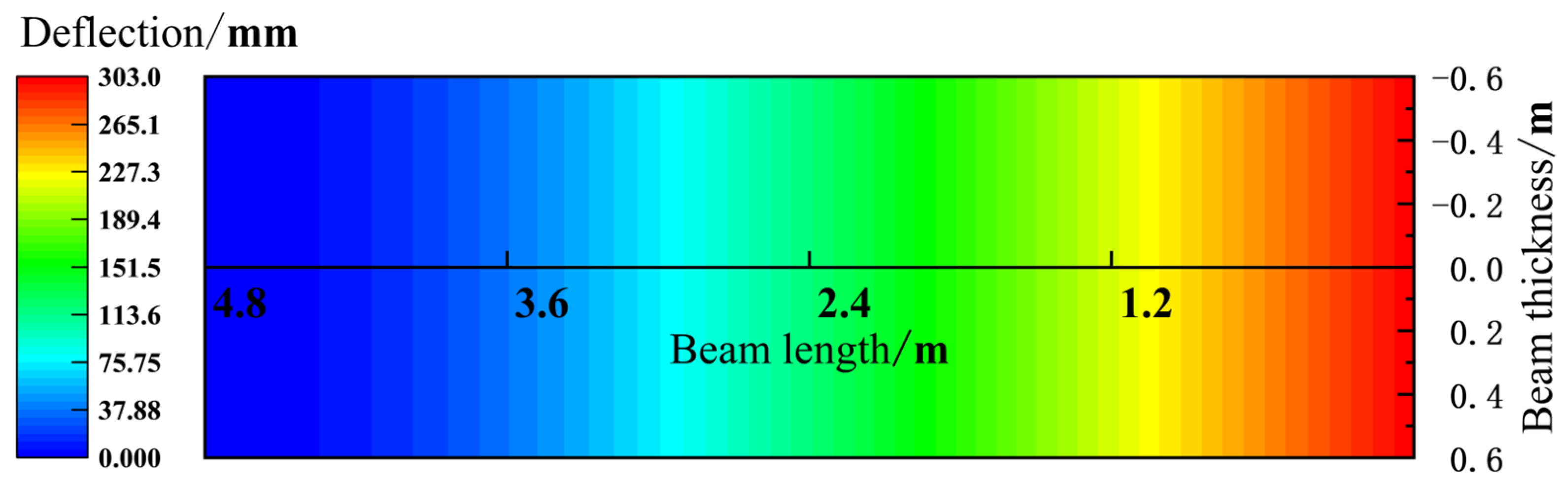
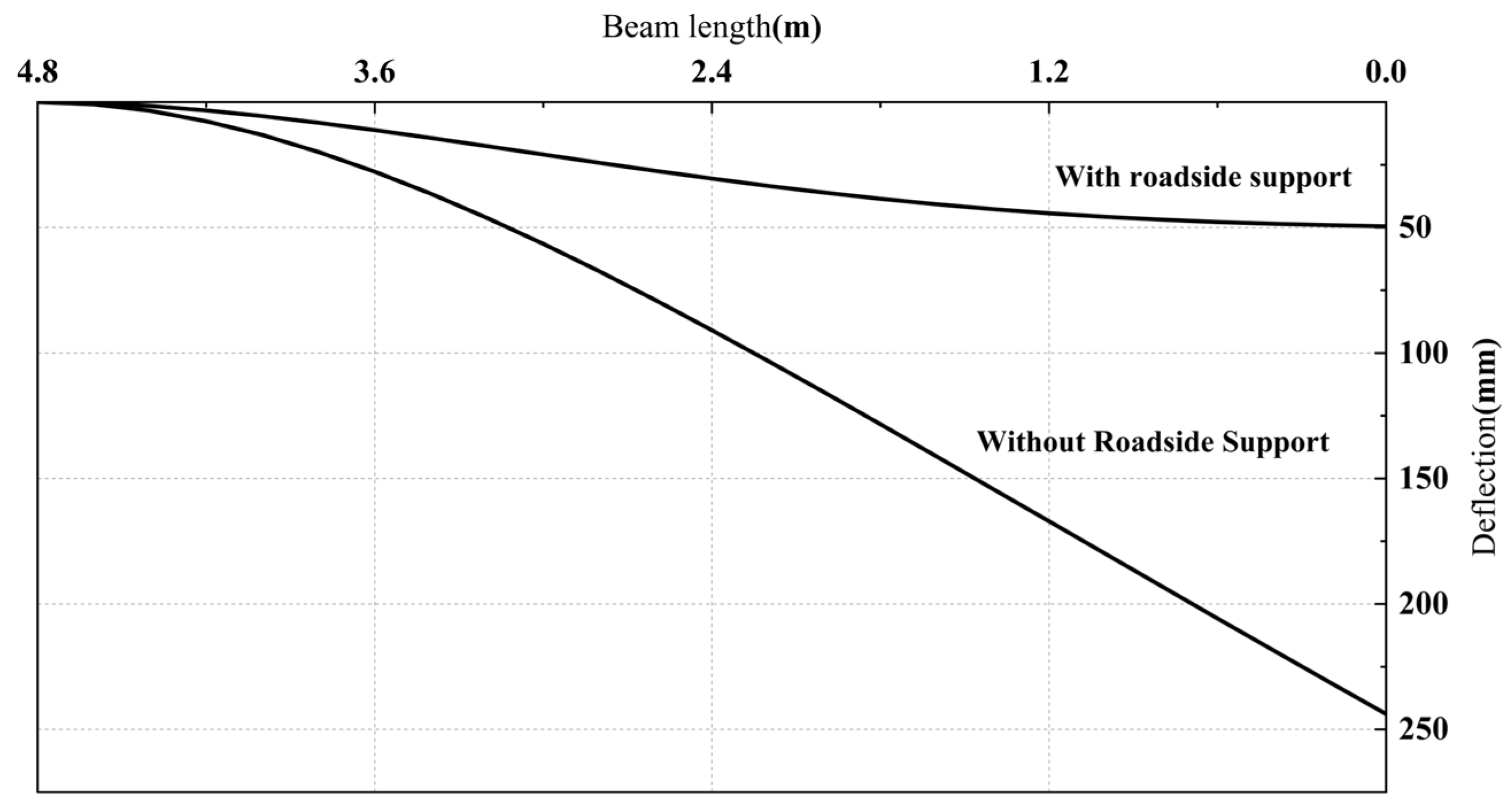
5.2. Influence of Dip Angle of Coal Seam on Deflection Change of Main Roof
6. Engineering Practice
6.1. Design of Roadside Support for the No. 3131 Haulage Roadway
6.2. On-Site Deformation Monitoring of Surrounding Rock
7. Conclusions
- (1)
- In the case where there is no roadside support in the No. 3131 haulage roadway, the main roof deflection is the smallest during the roadway excavation period. From the advanced influence period of the first mining activity, the roadway retaining period to the advanced influence period of the second mining activity, the deflection on the high-sidewall side shows the most significant growth, while the degree of deflection increase in the central area is relatively slight.
- (2)
- During the roadway excavation period, the normal stress σx of the main roof under the (nearly) horizontal coal seam shows a symmetrical distribution. As the coal seam dip angle increases, the maximum compressive stress in the middle of the upper surface shifts to the short-sidewall side, the maximum tensile stress in the middle of the lower surface shifts to the high-sidewall side, and the stress on the short-sidewall side decreases.
- (3)
- During the advanced influence period of the first mining activity and the advanced influence period of the second mining activity, the increase in the coal seam dip angle causes the compressive stress area on the upper surface of the main roof to expand from the high-sidewall side to the short-sidewall side, and the tensile stress area to decrease. The situation on the lower surface is the opposite, but the stress value is larger during the advanced influence period of the second mining activity.
- (4)
- During the roadway retaining period, the upper surface of the main roof is in tension, and the lower surface is under compression. The stress value increases slowly from the high-sidewall side to the middle, but sharply from the middle to the short-sidewall side.
- (5)
- Under the inclined coal seam, as the dip angle of the coal and rock strata increases, the load component perpendicular to the main roof direction decreases, resulting in a decrease in the roof deflection and the roadside support resistance. The roadside backfill walls can be engineered based on the computational formulas for roadside support resistance, with specific design parameters calibrated according to in situ geological and operational conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Wang, M.; Liu, J. Management of national planned coal mining areas and discrimination with coal mining areas. Coal Geol. Explor. 2019, 47, 219–222. [Google Scholar]
- Han, K.; Wang, Y. Developing trend and expectation of energy consume in China. J. China Univ. Min. Technol. 2004, 4–8. [Google Scholar] [CrossRef]
- Sun, H.; Zhao, B. Theory and Practice of Gob-Side Entry Retaining; Coal Industry Press: Beijing, China, 1993. [Google Scholar]
- Hua, X.; Li, C.; Liu, X.; Guo, Y.; Qi, Y.; Chen, D. Current situation of gob-side entry retaining and suggestions for its improvement in China. Coal Sci. Technol. 2023, 51, 128–145. [Google Scholar] [CrossRef]
- Yu, G.; Wang, J.; Ren, J.; Hu, J.; Pan, Z.; Wang, D.; Ming, W. Study on Surrounding Rock Structure Evolution Characteristics and Roof Control Techniques of the Retained Roadway Formed by Roof Cutting in Inclined Coal Seams. Shock Vib. 2021, 2021, 7491887. [Google Scholar] [CrossRef]
- Zhen, E.; Gao, Y. Application of Roof-Cutting and Pressure-Release Entry Retaining in Inclined Coal Seams: A Case Study. Geotech. Geol. Eng. 2020, 38, 2559–2572. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, J.; Zang, C.; Wang, S. An Innovative Approach for Gob-Side Entry Retaining by Roof Cutting in Steeply Pitching Seam Longwall Mining with Hard Roof: A Case Study. Min. Metall. Explor. 2020, 37, 1079–1091. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, P.; Wang, M. Numerical study on the stability of surrounding rock of gob-side entry retaining along the fully mechanized working face in inclined seam. China Sci. Pap. 2015, 10, 2568–2573. [Google Scholar]
- Shi, W.; Li, Z.; Liu, C.; Lv, Y.; Zhang, H.; Yang, T. Study on optimization of key parameters of thick hard roof cutting and retaining roadway in inclined coal seam. Coal Sci. Technol. 2024, 52, 11–24. [Google Scholar]
- Zhu, Y.; Ren, H.; Wang, P.; Li, P.; Wang, X.; Wei, M. Stability control of gob-side entry retention under the condition of inclined thick layer and hard roof. J. Cent. South Univ. Sci. Technol. 2023, 54, 956–966. [Google Scholar]
- Cao, S.; Wang, Y.; Zou, D. Mechanical model analysis of roadway along the roadway in inclined coal seam. J. Chongqing Univ. Nat. Sci. Ed. 2013, 36, 143–150. [Google Scholar]
- Zhang, L.; Zhao, J.; Wang, S. Research on the roof structure evolution and control technology of gob-side entry retaining with cutting the roof in steeply dipping seam. J. Min. Sci. Technol. 2020, 5, 169–178. [Google Scholar] [CrossRef]
- Yang, J.; Fu, Q.; Gao, Y.; Cheng, Y.; Zhang, J. Research on roof deformation laws and mechanism in a non-pillar mining method with entry automatically formed during the whole cycle. J. China Coal Soc. 2020, 45, 87–98. [Google Scholar] [CrossRef]
- Yang, J.; Wei, Q.; Wang, Y.; Gao, Y.; Hou, S.; Qiao, B. Roof deformation mechanism and control measures of pillarless mining with gob-side entry retaining by roof cutting and pressure relief. Rock Soil Mech. 2020, 41, 989–998. [Google Scholar] [CrossRef]
- Yang, H.; Li, Y.; Liu, Y.; Cao, S.; Pan, R.; Wang, H.; Wang, B.; Chen, X.; Zhao, X. Structure evolution and stability control mechanism of hard-roof cutting for roadway retaining. J. Min. Saf. Eng. 2021, 38, 766–773. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, K.; Yuan, H. Control Technology and Its Application of Roadway Side Wall Formed by Gangue in Gob-Side Entry Retaining Formed by Roof Cutting and Pressure Releasing. Coal Sci. Technol. 2018, 46, 25–32. [Google Scholar] [CrossRef]
- Zhu, Z.; Yuan, H.; Zhang, K.; Gao, Y. Analysis and control technology of roof subsidence in non-pillar gob-side entry retaining formed by roof cutting and pressure release. Coal Sci. Technol. 2018, 46, 1–7. [Google Scholar] [CrossRef]
- Liu, X.; Hua, X.; Yang, P.; Huang, Z. A Study of the Mechanical Structure of the Direct Roof during the Whole Process of Non-Pillar Gob-Side Entry Retaining by Roof Cutting. Energy Explor. Exploit. 2020, 38, 1706–1724. [Google Scholar] [CrossRef]
- Hu, J.; Ma, Z.; Guo, P.; Hu, Y. Fracture Evolution of the Main Roof in Gob-Side Entry Retaining by Roof Cutting of an Inclined Coal Seam. Energy Explor. Exploit. 2023, 41, 1396–1414. [Google Scholar] [CrossRef]
- He, M.; Ma, Z.; Guo, Z.; Chen, S. Key parameters of the gob-side entry retaining formed by roof cutting and pressure release in deep medium-thickness coal seams. J. China Univ. Min. Technol. 2018, 47, 468–477. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, F.; Wang, H.; Yuan, G.; Guo, Z.; Yang, J. Determination of key parameters of gob-side entry retaining by cutting roof and its application to a deep mine. Rock Soil Mech. 2019, 40, 332–342+350. [Google Scholar] [CrossRef]
- Gao, Y.; Guo, Z.; Yang, J.; Wang, J.; Wang, Y. Steady analysis of gob-side entry retaining formed by roof fracturing and control techniques by optimizing mine pressure. J. China Coal Soc. 2017, 42, 1672–1681. [Google Scholar] [CrossRef]
- Huo, X. Evolution Characteristics of Surrounding Rock Deformation and Its Control Technology of Gob-Side Entry Retaining by Roof; Shandong University of Science and Technology: Qingdao, China, 2021. [Google Scholar]
- Xu, Z. A Concise Course in Elasticity; Higher Education Press: Beijing, China, 2018; ISBN 978-7-04-049871-4. [Google Scholar]

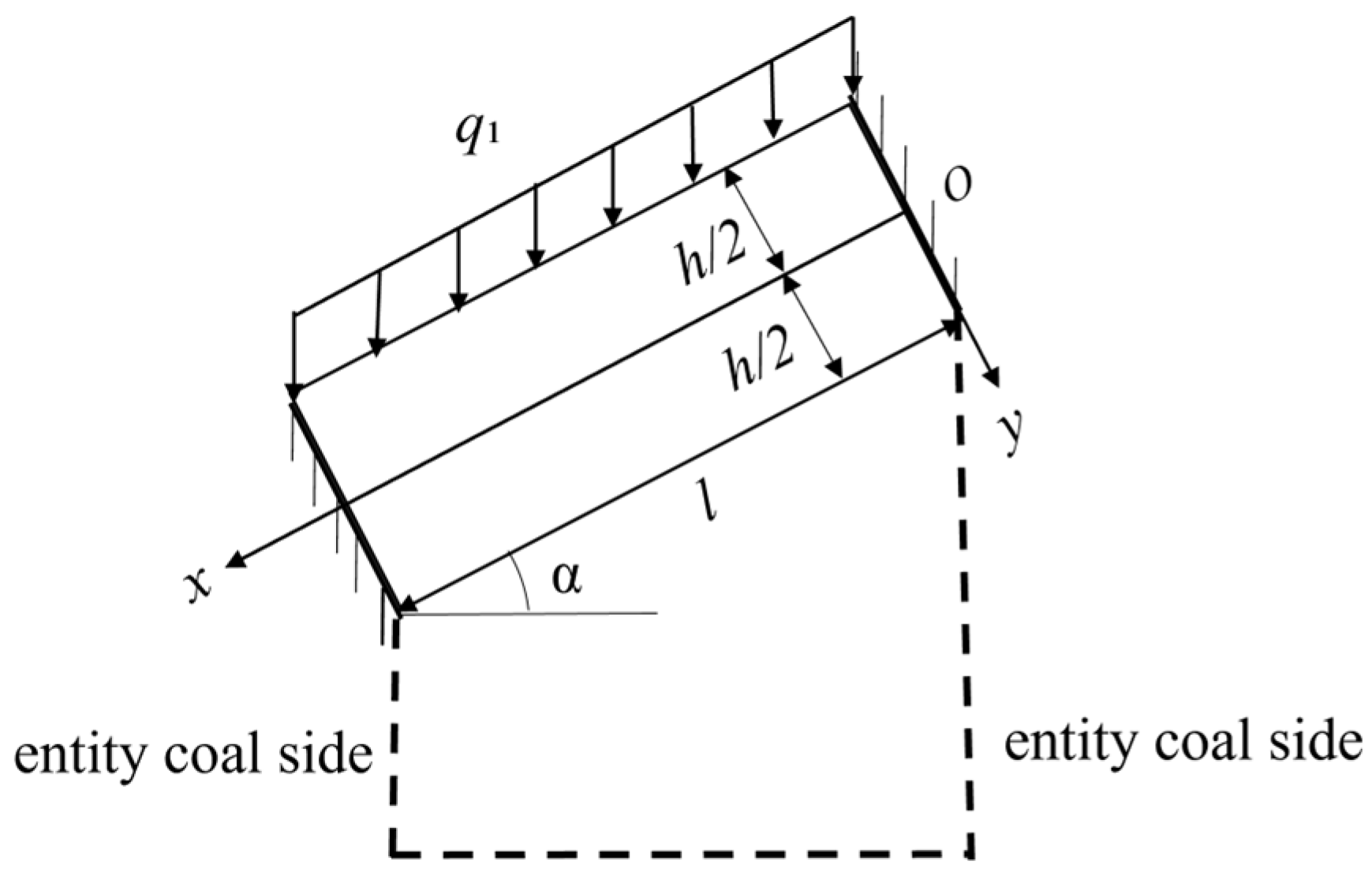






| Load | Boundary Conditions | Support Assumptions |
|---|---|---|
| Uniform overburden load q1 perpendicular to the horizontal | The main boundary conditions on the upper and lower sides and the small boundary conditions on the left and right sides | Fixed supports at both ends (solid coal ribs) |
| Load | Boundary Conditions | Support Assumptions |
|---|---|---|
| Uniform load q2 and lateral force Fc from adjacent coal | The main boundary conditions on the upper and lower sides and the small boundary conditions on the left and right sides | Fixed support at low-sidewall coal, simple support at high-sidewall coal |
| Load | Boundary Conditions | Support Assumptions |
|---|---|---|
| Uniform load q3 and lateral force FN from collapsed rock block B | The main boundary conditions on the upper and lower sides and the small boundary conditions on the left and right sides | Fixed support at low-sidewall coal, free end over goaf |
| Load | Boundary Conditions | Support Assumptions |
|---|---|---|
| Uniform load q4, lateral force FN, and goaf support Fs | The main boundary conditions on the upper and lower sides and the small boundary conditions on the left and right sides | Fixed support at low-sidewall coal, simple support from compacted goaf |
| Stress Maximum/MPa | Deflection Peak/mm | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 25° | 30° | 35° | 40° | 45° | 0° | 25° | 30° | 35° | 40° | 45° | |
| Roadway excavation period | 63.38 | 63.36 | 61.8 | 59.9 | 57.5 | 54.7 | 9.1 | 8.2 | 8.0 | 7.4 | 6.9 | 6.4 |
| The advanced influence period of the first mining activity | 112.4 | 74.8 | 65.3 | 55.3 | 45.0 | 34.2 | 96.9 | 48.0 | 42.2 | 31.6 | 20.6 | 9.6 |
| Roadway retaining period | 286.8 | 218.5 | 199.5 | 179.0 | 157.1 | 134.0 | 353.8 | 267.8 | 243.8 | 218.1 | 190.6 | 161.7 |
| The advanced influence period of the second mining activity | 374.3 | 256.9 | 225.2 | 191.1 | 154.6 | 116.2 | 485.4 | 342.1 | 302.2 | 259.2 | 213.5 | 165.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yan, B.; Dong, J.; Qiang, X.; Chen, C.; Zhou, G.; Zheng, Y. Analysis of Main Roof Mechanical State in Inclined Coal Seams with Roof Cutting and Gob-Side Entry Retaining. Symmetry 2025, 17, 723. https://doi.org/10.3390/sym17050723
Li J, Yan B, Dong J, Qiang X, Chen C, Zhou G, Zheng Y. Analysis of Main Roof Mechanical State in Inclined Coal Seams with Roof Cutting and Gob-Side Entry Retaining. Symmetry. 2025; 17(5):723. https://doi.org/10.3390/sym17050723
Chicago/Turabian StyleLi, Ji, Bo Yan, Jihui Dong, Xubo Qiang, Chaosen Chen, Guangyong Zhou, and Yingjian Zheng. 2025. "Analysis of Main Roof Mechanical State in Inclined Coal Seams with Roof Cutting and Gob-Side Entry Retaining" Symmetry 17, no. 5: 723. https://doi.org/10.3390/sym17050723
APA StyleLi, J., Yan, B., Dong, J., Qiang, X., Chen, C., Zhou, G., & Zheng, Y. (2025). Analysis of Main Roof Mechanical State in Inclined Coal Seams with Roof Cutting and Gob-Side Entry Retaining. Symmetry, 17(5), 723. https://doi.org/10.3390/sym17050723





