A Symmetry-Based Computational Framework for Motor Skill Optimization: Integrating Screw Theory and Ecological Perception

Abstract

This study introduces a computational framework for understanding the symmetry and asymmetry of human movement by integrating Laban Movement Analysis (LMA). By conceptualizing movement refinement as a structured computational process, we model the golf swing as a series of state transitions where perceptual invariants guide biomechanical optimization. The golf club’s motion is analyzed using the instantaneous screw axis (ISA) and inertia tensor revealing how expert golfers dynamically adjust movement by detecting and responding to invariant biomechanical structures. This approach extends Gibson’s ecological theory by proposing that movement execution follows an iterative optimization process analogous to a Turing machine updating its states. Furthermore, we explore the role of symmetry in motor control by aligning Laban’s X-scale with structured computational transitions, demonstrating how movement coordination emerges from dynamically balanced affordance–action couplings. This insight gained from the study suggests that AI-driven sports training and rehabilitation can leverage symmetry-based computational principles to enhance motion learning and real-time adaptation in virtual and physical environments.

1. Introduction

1.1. Symmetry and Reciprocity in Human Movement: A Framework for Motor Learning

The study of symmetry in human movement offers crucial insights into how the body organizes complex motion efficiently. In biomechanics, symmetry is often associated with coordinated patterns that enhance energy transfer and minimize redundancy, while asymmetry can indicate adaptive compensation or inefficiency. These ideas are particularly relevant in tasks like the golf swing where fine-tuned temporal and spatial coordination defines performance.

Building on this foundation, we propose a novel interpretation of motor control using symmetry principles from screw theory. Rather than framing the golf swing in terms of isolated kinematic segments or simplified control feedback loops, we adopt a holistic perspective grounded in the duality and reciprocity of movement and force. Duality describes the relationship between twists (angular–linear displacements) and wrenches (force–torque inputs) where one acts as the complement of the other. This dual structure forms the basis of symmetry: motion and force are not opposing phenomena but co-constructive, with their alignment producing efficient action.

We further extend this idea using harmonic screws, a concept in screw theory that models the convergence of kinetic and potential effects. In this context, we define symmetry not just as mirrored movement, but as the structural alignment between perception, intention, and mechanical outcome. Skilled performance, as observed in expert golfers, reflects this alignment through what Laban termed “free flow”—a seamless integration of internal and external forces. Conversely, asymmetry emerges when this integration breaks down, manifesting as “bound flow”, constrained by inefficient perception–action coupling.

Through this framework, we reinterpret motor learning as the progressive refinement of these symmetry relationships [1]. By modeling the golf swing as a structured sequence of interactions between the body’s inertia and environmental affordances (e.g., ground reaction forces, club dynamics), we shift the analysis from command-based control to ecological computation. This sets the stage for a new class of bioengineering applications in motion capture, virtual coaching [2], and neurorehabilitation [3], centered not on correcting deviations from a fixed trajectory but on restoring the symmetry of action potentials across the movement system.

1.2. A Computational Perspective on Golf Swing Dynamics

Golf performance emerges from a complex interplay of biomechanical coordination, perceptual adaptation, and strategic execution. The golf swing, in particular, represents a sequential movement process, requiring precise timing, controlled force distribution, and dynamic postural regulation to maximize efficiency. Among the various phases of the swing, the downswing is particularly crucial as it involves the conversion of stored potential energy into clubhead acceleration, directly influencing ball trajectory, impact force, and overall shot precision.

Traditional research in golf biomechanics has primarily focused on kinematic and kinetic analyses, examining joint articulations, torque production, and external force dynamics to quantify movement efficiency [4,5]. Studies have explored the relative contributions of anatomical structures in power generation, control, and swing optimization [6,7,8,9,10,11]. While these approaches provide valuable insights, they tend to discretize movement into isolated biomechanical components, overlooking the sequential refinement and structured flow of motion that distinguish expert performance. The absence of a formal computational framework in traditional biomechanical studies limits the ability to capture how perception and action dynamically evolve in skilled movement execution.

A pioneering proposition made by Wells (2002) was the formalization of Gibson’s ecological theory of affordances through Turing’s computational framework [12]. Wells demonstrated that Turing’s model of computation offers a structured, sequential approach to understanding how affordances dynamically shape motor learning and execution [13]. This insight bridges the gap between computational models and ecological perception, allowing affordance-based actions to be interpreted as state transitions within a computationally structured system. Wells further emphasized that effectivities, which are necessary to complement affordances in action execution, can be understood within Turing’s finite-state transition model, offering a precise way to analyze how movement adapts in response to environmental constraints.

Building on Wells’ framework, this study applies Turing’s computational principles to golf swing refinement, viewing each movement phase as an iterative, computationally governed adjustment. The golfer interacts with external affordances such as club inertia and ground reaction forces, dynamically updating movement execution through perception–action coupling. By conceptualizing the golf swing as a structured sequence of affordance-based adjustments, we align biomechanical execution with computational optimization, reinforcing Wells’ proposition that Turing’s formalism enriches the study of ecological perception and motor control. This approach not only provides a theoretical basis for understanding skilled movement but also offers a structured methodology for analyzing expertise in sports biomechanics.

This perspective integrates Turing’s principles of sequential computation with Gibson’s ecological psychology [14] and Laban movement analysis [15], forming a multi-dimensional model that encapsulates both biomechanical execution and perceptual adaptation. The golf club, much like Turing’s computational pencil, inscribes motion trajectories onto the external environment, dynamically adjusting to inertial cues, environmental affordances, and proprioceptive inputs. This computational paradigm enables us to quantify skill acquisition, optimize movement refinement, and design AI-driven training methodologies [16] that extend beyond traditional kinematic approaches.

Thus, this study presents a novel intersection between Turing’s machine theory, affordance-based motor control, and sports biomechanics, providing a structured computational framework for understanding how expert golfers refine their swing through iterative perception–action cycles.

1.3. Laban Movement Analysis (LMA) and Motion Coordination

Laban Movement Analysis (LMA) [17] provides a structured framework for understanding human motion, integrating principles of space, effort, shape, and body awareness. The kinesphere concept, central to LMA, defines the spatial reach and organization of movement, making it a valuable tool for analyzing golf swing mechanics. By mapping motion trajectories, movement qualities, and spatial organization, LMA enables a qualitative understanding of movement efficiency and coordination in sports.

The Laban/Bartenieff Movement System (LBMS) offers a comprehensive theoretical framework for understanding human movement through three aspects: Doing (embodying), Seeing (observing), and Writing (notating or motifing). This system, developed by Rudolf Laban and his colleagues, describes body movements in terms of Body, Effort, Space, and Shape (BESS) [18].

Remarkably, Laban’s work was referenced by James Gibson in his influential book, The Senses Considered as Perceptual Systems (1966), where he acknowledges the precision of movement analysis in ballet and highlights efforts by choreographers to establish a formal notation system for human movement [19]. Gibson specifically notes that “Some choreographers have analyzed the movements and pauses of the human body in the effort to establish a dance notation”, referring to the intricate systems developed to capture the nuances of human motion, such as Labanotation. This recognition of Laban’s work in a text primarily concerned with ecological psychology underscores the relevance of Laban’s insights into the embodied nature of movement within an environmental context.

In this study, the integration of Laban Movement Analysis with computational models, such as Turing’s machine theory, provides a structured approach to understanding sequential movement refinement. The A-Scale from Laban’s choreutics serves as a state transition framework, guiding how golfers navigate key movement phases, akin to how a Turing machine processes discrete states.

1.4. Distinguishing Control Theory from Gibson’s Perceptual Systems in Motor Learning

Traditional control theory has made significant contributions to the understanding of motor control by modeling movement as a combination of feedforward planning and feedback correction [20]. In these frameworks, internal models are used to predict and initiate movement, while feedback mechanisms provide real-time adjustments in response to sensory discrepancies. This integrated approach has been empirically validated in numerous studies, including recent work by Kim and colleagues [21], who demonstrated that both mechanisms are critical for compensating age-related deficits in a 3D visuomotor tracking task.

We acknowledge the value of these contributions and the maturity of control theory as a tool for understanding motor adaptation. However, our goal in this paper is not to dismiss control theory but to contrast it with an alternative framework grounded in Gibson’s ecological approach, which fundamentally redefines the architecture of movement regulation.

While control theory assumes an input–output architecture where movement arises from internally generated commands and is modulated via feedback, Gibson’s ecological theory argues that movement is guided directly by information available in the environment, particularly invariants that specify the dynamics of the actor–environment relationship [22]. For example, touch and posture are not merely outputs of a feedback loop but constitute a covariant perceptual stream that informs ongoing movement without the need for internal error computation.

In this framework, the golf swing is not a correction-based task but a perception–action system that tunes itself to environmental affordances (e.g., club inertia, ground reaction forces). This view is aligned with Turing’s model of computation, where each movement phase is a sequentially structured refinement step, not an output of real-time feedback loops. We further integrate Bellman’s dynamic programming to illustrate how skilled performance emerges through recursive state optimization rather than continuous error correction.

In summary, our approach diverges from classical control theory, not out of oversight but as a deliberate reconceptualization of motor learning. We advocate for a computational–perceptual model that emphasizes structured environmental interaction over internal feedback regulation. This framework offers complementary insights to control theory and opens new avenues for interpreting movement as a self-organizing, symmetry-seeking process guided by perceptual information.

1.5. Turing’s Machine Theory and Algorithmic Motion Learning

Alan Turing’s universal machine theory describes how sequential state transitions can generate complex patterns and adaptive learning processes [13]. In the context of motor learning, the human nervous system refines movement execution through an iterative process, updating motion patterns based on perceptual invariants, much like a Turing machine updates its computational states. By applying Turing’s computational principles to Laban-based motion learning, we propose that the golf swing follows a structured refinement process where each motion phase transitions into the next through kinematic affordance adjustment.

An affordance in golf biomechanics is best understood as a dynamic interaction between the golfer and the environment where the club, ground, and ball provide structured information that guides movement. Gibson (1979) [14] conceptualized affordances as opportunities for action arising from environmental and bodily properties, emphasizing their relational nature. Shaw and Turvey elaborated on this by introducing effectivities [23], which define the golfer’s capacity to act upon these affordances.

Alan Turing’s theoretical work on computation provides an effective framework for modeling how golfers refine their swings. Rather than viewing computation as an abstract mental process, Turing originally described it in terms of a human interacting with a structured environment, where a person writes on paper with a pencil, following stepwise rules. By reinterpreting this model, we can replace the pencil with the golf club, the paper with the ball and playing field, and the human computer with the golfer [12].

1.6. Integrating Computational Perception with Ecological Psychology

James Gibson’s ecological approach to perception emphasizes that motor actions are guided by perceptual invariants in the environment. The concept of dynamic touch suggests that golfers perceive the club’s inertial properties and adjust their motion accordingly. By integrating Gibson’s perceptual invariants with Turing’s computational model, we can better understand how golfers adapt to real-time biomechanical constraints and refine their perception–action coupling during the swing.

This integration of computational perception and ecological psychology [12] enables a formalized understanding of how movement refinement emerges from structured sensory–motor interactions. In the context of Turing’s machine theory, the golfer’s perception of club inertia, ground reaction forces, and spatial constraints functions as an input stream that informs the next biomechanical state in the swing sequence. Each phase of the swing represents a computational transition where information pickup from previous states determines the upcoming motor adjustment, similar to how a Turing machine processes symbols and updates configurations accordingly. By framing motor learning as an iterative computational process, we can quantify how affordance detection, proprioceptive adaptation, and biomechanical constraints collectively shape expert performance [24]. This approach not only reinforces the perception–action loop [22] in ecological psychology but also introduces a predictive computational model for understanding skill acquisition and adaptive motor control in complex athletic movements.

1.7. Objectives of the Study

This study aims to:

• Integrate Laban’s kinesphere framework with Turing’s sequential computation model to establish a computational motion learning paradigm for the golf swing.
• Analyze instantaneous screw axis (ISA) [24] and inertia tensor [25] within a structured motion refinement framework, demonstrating how skilled golfers adapt dynamically.
• Investigate how perception–action coupling and motor sequence optimization contribute to swing efficiency using Gibson’s ecological perception theory.
• Provide a computationally structured methodology for improving golf training, skill acquisition, and motion learning in sports science [1].

This study offers a new paradigm for motion optimization, integrating computational, biomechanical, and perceptual principles to enhance our understanding of golf swing dynamics. The following sections will present the methodology, computational framework, experimental validation, and results supporting this approach.

2. Materials and Methods

Although biomechanical models offer detailed accounts of motion and force, they often lack integration with qualitative descriptors that capture the nuanced characteristics of movement efficiency and skill differentiation. Incorporating principles from Laban Movement Analysis (LMA), particularly the Effort category, provides an opportunity to bridge this divide. Assessing swing performance through Effort dynamics—such as whether the Flow quality is characterized by freedom or constraint—can yield insights into the coordination and timing strategies employed by golfers. These qualitative features may show meaningful alignment with established biomechanical metrics like the instantaneous screw axis (ISA), which encapsulates both rotational and translational behavior of body segments [26]. The ISA has been employed in prior work as a concise representation of club dynamics during motion [27,28].

Building on this foundation, James Gibson’s theory of ecological psychology introduces the concept of dynamic touch, which emphasizes the perception of an object’s inertial properties—such as mass distribution and resistance to movement—through active manipulation [19,29]. Dynamic touch involves the integration of sensory inputs from the skin, muscles, tendons, and joints, allowing an individual to perceive the inertia of an object by wielding it. This process directly relates to the inertia tensor, a mathematical representation of how mass is distributed within an object and how this distribution influences the object’s resistance to rotational and translational forces.

In the context of a golf swing, the perception of the club’s inertial properties through dynamic touch is crucial for achieving a powerful and efficient swing. The golfer’s ability to sense and respond to the club’s inertia, as encapsulated by the inertia tensor, plays a vital role in the coordination and execution of the swing. This interaction between perception and action, as described by Gibson, is fundamental to understanding the dynamics of the golf swing.

The current research aims to bridge this gap by applying LMA’s Effort theory specifically to the biomechanical context of golf swings. By focusing on how the physical forces generated by the golf club (e.g., mass moment of inertia) are managed and utilized by the golfer, this study seeks to uncover the underlying dynamics that contribute to more efficient and powerful swings, particularly during the critical phase of the downswing [10]. This novel approach not only promises to enhance our understanding of the biomechanical aspects of golf swings but also opens the door for broader applications in sports science and rehabilitation.

The hypothesis of this study is that integrating Laban Movement Analysis (LMA) with biomechanical principles and Gibson’s concept of dynamic touch will create a comprehensive framework that enhances the analysis of golf swing dynamics. This approach is expected to provide a deeper understanding of how different skill levels can be distinguished through qualitative descriptors, such as Effort factors, spatial configurations, and the perception of inertial properties through dynamic touch. By bridging these qualitative elements with traditional biomechanical data, the study hypothesizes that more precise insights can be gained, leading to improved performance metrics and potentially informing better training methodologies for golfers at various skill levels.

2.1. Integrating Laban’s Icosahedron with Embodied Cognition in the Golf Swing

In the study of human movement, Laban’s icosahedron offers a profound model for understanding the embodied cognition of personal space, especially in dynamic activities such as the golf swing. Laban’s icosahedron, characterized by its geometric structure, encapsulates the spatial dimensions and axes that a golfer navigates during a swing (Figure 1 and Figure 2). This model is not merely a theoretical construct; it represents the tangible, perceptible space within which movement occurs, serving as a framework for understanding how a golfer engages with their environment.

James Gibson’s ecological psychology asserts that completely empty space is unperceivable because it lacks the surfaces and environmental cues necessary to define orientation and movement. The dimensions or axes of empty space become meaningful only when they are embodied within a solid environment—this is vividly illustrated by the inherent north–south, east–west, and up–down orientations in the physical world.

In the context of a golfer, Laban’s icosahedron can be seen as the embodied structure through which the golfer perceives and interacts with their personal space. The golf swing, with its intricate coordination of body movements, is not simply an action performed in a vacuum but is deeply rooted in the golfer’s perception of the surrounding environment, as organized by the icosahedron. This geometric framework allows the golfer to orient themselves within their kinesphere, enabling them to perceive and respond to the inertial forces of the club as they move through the defined axes of space.

This integration of Laban’s Icosahedron into the understanding of the golf swing provides new insights into the embodied cognition involved in athletic performance. By recognizing the significance of this geometric model, we can explore how it enhances spatial awareness and performance in golf and other sports, offering a more holistic approach to training and movement analysis.

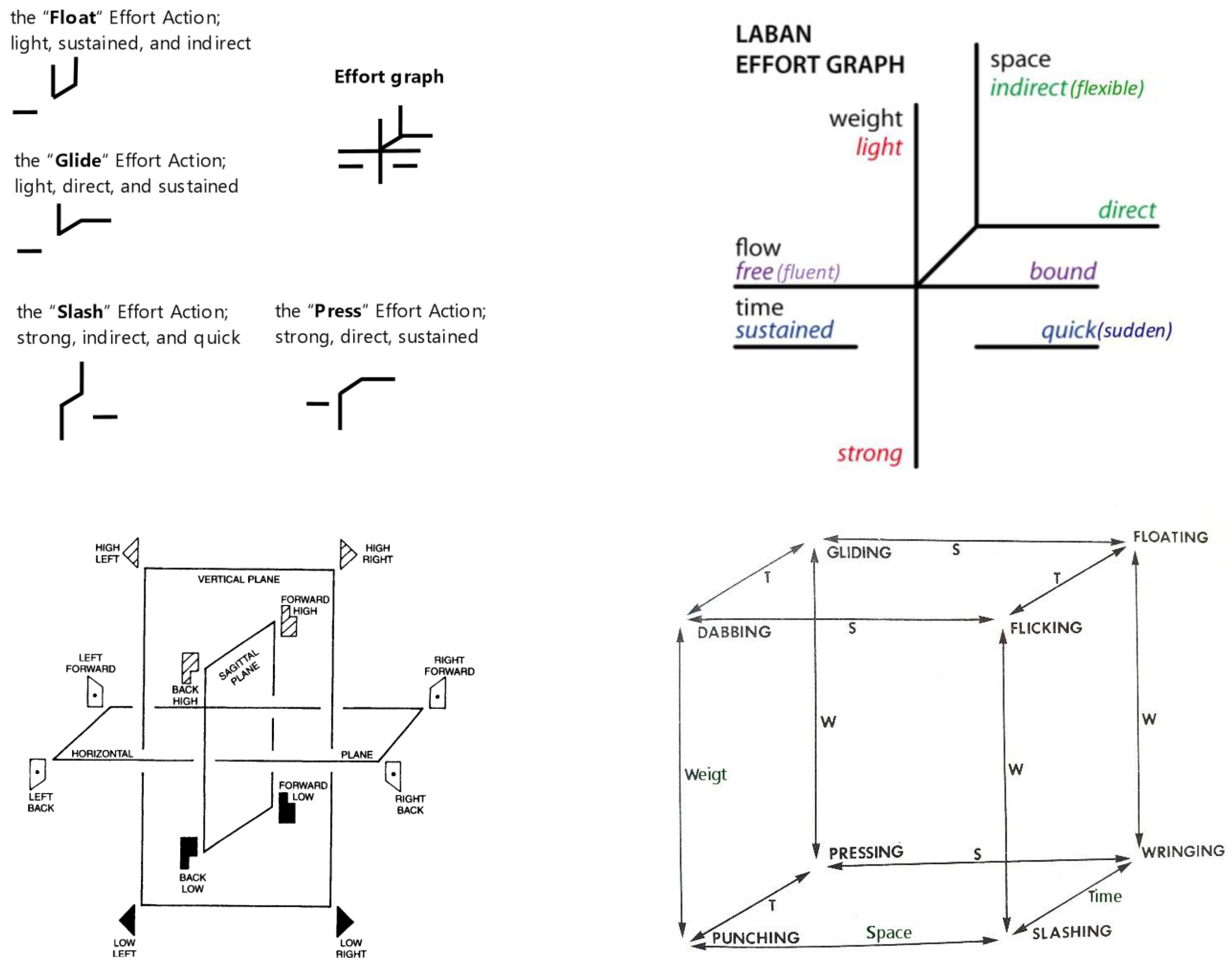
Laban’s Eight Effort Actions, also known as Laban Effort Drives, are a key part of Rudolf Laban’s system for understanding and notating dance and movement, known as Laban Movement Analysis (LMA) [30,31]. These Effort Actions are used to describe the quality of movement and are organized according to Laban’s Effort–Shape theory, which considers both the inner intention and the outer shape of the movement. The eight Effort Actions are categorized into four pairs of opposite qualities, with each pair representing one of the factors of motion: Weight, Time, Space, and Flow (Figure 1). The graph shows how these polarities interact to create various movement qualities, such as gliding (light, sustained, direct), Flicking (light, sudden, indirect), Pressing (Strong, sustained, direct), and wringing (strong, sustained, indirect). Each combination represents a unique effort and intention in movement. (Adapted from Laban’s original work on movement analysis).

This Effort graph was created by Laban to delineate his organization of inner intent or motivation behind a movement. Light and strong are the two polarities of the Weight Effort; sustained and sudden are the two polarities of the Time Effort; direct and indirect are the two polarities of the Space Effort; and free and bound are the two polarities of the Flow Effort. In refining the understanding of the golf swing, this study applies Rudolf Laban’s Eight Effort Actions, part of the Laban Movement Analysis (LMA), which characterizes movement through dynamic qualities. Each of these actions corresponds to a combination of Effort elements—Weight, Time, Space, and Flow—depicting how movement can be experienced and executed with varying intensities and intentions [30].

The golf swing, as a complex biomechanical sequence, reflects a range of Laban Effort qualities throughout its execution. It typically starts with a setup phase where the golfer establishes alignment with the intended target, proceeds through the backswing, and culminates in the rapid, forceful action of the downswing. These distinct phases can be meaningfully interpreted using Laban’s Effort Actions, providing a qualitative framework for examining how energy, intention, and spatial orientation are managed during the swing (see Figure 2). The icosahedrons in the figure are rendered from different vantage points to illustrate how movement pathways shift in space. From a front-facing perspective, the left-hand view displays “A4” on the left and “A7” on the right; from a rear view, these positions are reversed. This dual perspective emphasizes the spatial orientation of movement and enhances the clarity of analysis across multiple planes.

Laban’s concept of Space Harmony offers valuable insight into golf swing mechanics, particularly through the structural lens of the icosahedron and the A-scale. As visualized in Figure 2, the A-scale outlines a directional movement sequence that is symmetrical across two parts, beginning with the right arm as the lead and expressed through volute phrasing [32]. Originally developed for fencing analysis, this structure can be repurposed to interpret the spatial and temporal coordination required in an effective golf swing:

• A-Scale Framework

• The A-scale comprises 12 directional movement patterns, organized into two sequences of six.
• The latter six patterns serve as a reflective counterpart to the initial six, creating a sense of spatial and dynamic balance across the full sequence.

2.

Volute Phrasing

• The term volute conveys a spiral or screw-like motion, characterized by a continuous, cyclic flow that eventually resolves at its origin.
• In the context of the A-scale, each volute encompasses six movements, emphasizing fluid progression through three-dimensional space.

3.

Mapping to the Golf Swing

• The first six movements correspond to the backswing and initial transition into the downswing phase.
• The second six capture the completion of the downswing and the follow-through, highlighting continuity and energy release.

4.

Directional and Spatial Flow

• Each inclination represents a defined spatial trajectory, involving directionality and verticality.
• The sequence ensures a coordinated flow, allowing smooth transitions between spatial pulls and directional shifts.

5.

Integration with Body Mechanics

• In golf-specific terms, the initial inclination of each volute often involves leg motion on the active side, enhancing balance and kinetic loading.
• A subsequent movement might include a step toward the target, aligning the body with the intended shot direction.

6.

Symmetry and Motion Efficiency

• The A-scale encourages symmetrical, flowing coordination between limbs on the same side of the body, fostering consistency in movement traces.
• Though this study emphasizes the right-side sequence for right-handed golfers, the left-side mirror sequence is equally valid and valuable for holistic training.

7.

Three-Dimensional Coordination in Golf

• The A-scale reveals the swing as a multi-planar action, rather than a simple linear path.
• It shows how body segments interact across space to generate both control and power.

8.

Coaching and Analytical Potential

• Aligning swing positions with A-scale movements allows coaches and players to evaluate spatial alignment and flow.
• This comparison can reveal deviations from optimal trajectories, offering practical guidance for correction and improvement.

Remember, the A-scale does not represent the entire golf swing, but rather provides a framework for understanding and potentially improving the spatial aspects of the swing. It is a tool that can offer insights into the complex spatial relationships involved in this athletic movement.

The lower-left quadrant of Figure 1 illustrates a set of authentic three-dimensional movement directions. These are conceptually aligned with the icosahedron structure shown in Figure 2, which serves as a spatial mapping tool in Laban Movement Analysis. The icosahedron defines what is termed “Ai” directions, essential for analyzing the geometric dynamics of human motion in space. This visual connection aids in illustrating how a mover’s orientation shifts as they transition through varying spatial planes and directional flows.

While it is not required to utilize all 6 + 6 “Ai” movements in every analysis, incorporating them can be highly beneficial for golfers aiming to enhance proprioception and spatial control. These directional patterns, categorized under Laban’s choreutic or spatial harmony forms, reflect underlying energetic structures projected around and through the body. They are arranged on a 27-directional grid, segmented into:

• Six primary cardinal directions (high/low, right/left, forward/backward);
• Eight high and low corner diagonals;
• Twelve intermediate orientations across horizontal, vertical (door), and sagittal (wheel) planes.

Engaging with these 6 + 6 movement sequences supports balanced yet dynamic coordination. They naturally elicit shifts in body weight, rotations, and tilting motions. Practicing these patterns enhances the golfer’s ability to maintain postural control and execute smoother transitions—both of which are crucial for a precise and powerful swing.

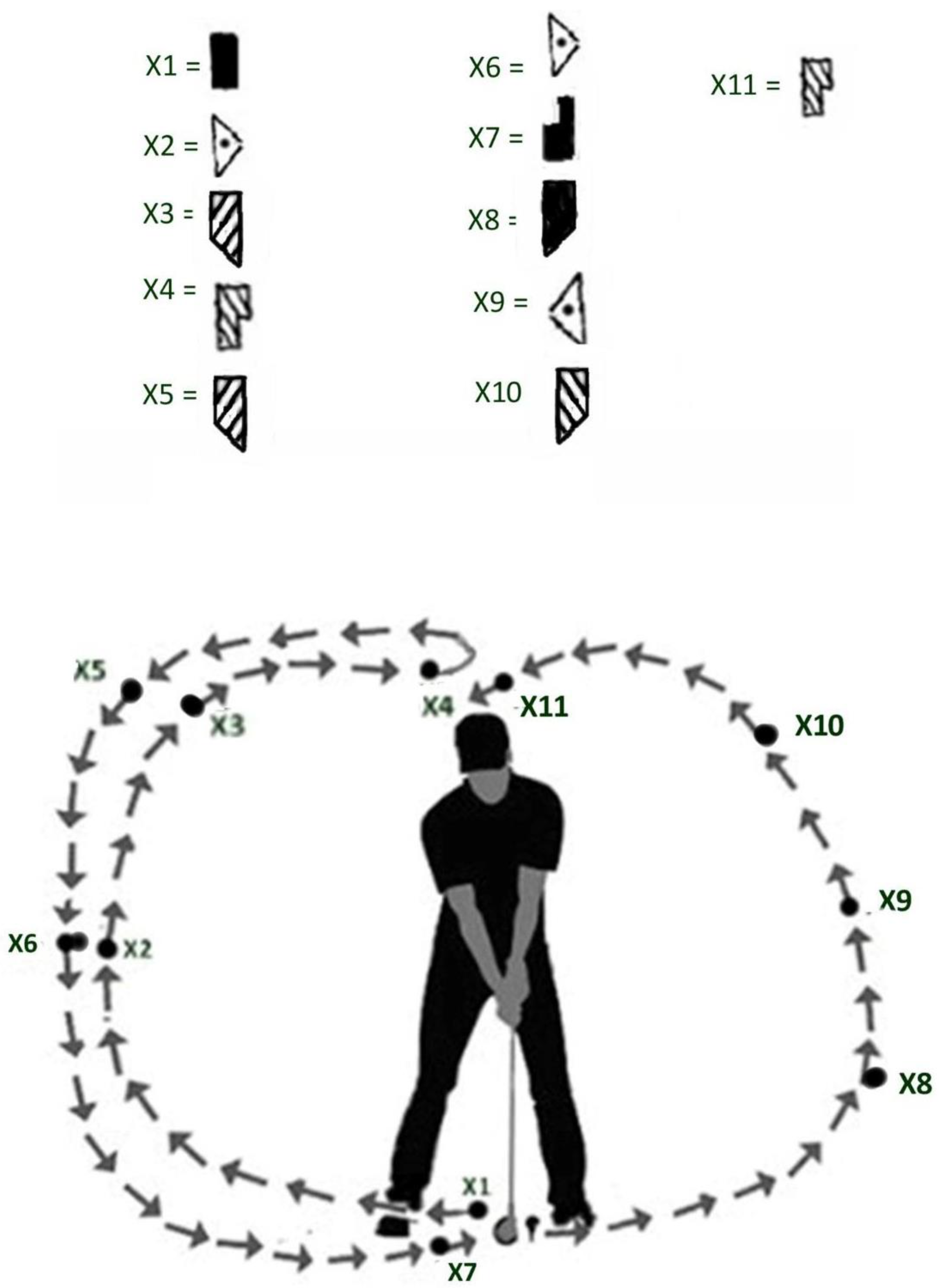
Building on these spatial harmony principles, we introduce the “X-scale”—a structured set of key postural positions that describe the movement phases of a golf swing, as depicted in Figure 3. While not a conventional term in Laban Movement Analysis, we use “X-scale” to refer to a context-specific model tailored to golf performance. It provides a practical framework to describe how the golfer’s body and club interact with space throughout the swing cycle. Through regular engagement with these positions, players may deepen their kinesthetic awareness, refine their spatial control, and cultivate a more integrated swing.

Summary of X-Scale Positions

• X1—Start position: Club positioned downward in front of the torso, establishing baseline alignment and stability.
• X2—Right sideward middle (door plane): The swing begins by moving the club rightward in a vertical path—initiation of backswing.
• X3—Right backward high (table plane): Club ascends backward and laterally, aligning with shoulder and hip rotation; weight transitions rightward.
• X4—Top of backswing (wheel plane): Club reaches its peak directly behind the golfer; maximum coiling and potential energy storage.
• X5—Right backward high (table plane): Reaffirmation of horizontal rotation trajectory at the top of the backswing.
• X6—Right sideward middle (door plane): Beginning of the downswing; uncoiling with vertical drop and lateral return.
• X7—Forward low (wheel plane): Acceleration zone; the club drops low and forward toward impact.
• X8—Left backward low (table plane): Early follow-through; club arcs leftward and back with energy release.
• X9—Left middle (door plane): Swing passes through left vertical midline, ensuring balance recovery.
• X10—Left backward high (table plane): Completion of follow-through; high finish to the left with continued rotation.
• X11—Backward high (wheel plane): Club settles behind the body, reflecting complete extension and closure of the swing cycle.

This X-scale acts as a bridge between biomechanical precision and Laban’s spatial logic, enabling more intentional and refined training for golfers. Its integration with the A-scale and spatial harmony offers a comprehensive lens through which movement fluency and performance quality can be both understood and enhanced.

X1: Start position, club down in front of the golfer.

X2: Right sideward middle (door plane, vertical).

X3: Right backward high (table plane, horizontal).

X4: Top of backswing, backward high (wheel plane, sagittal).

X5: Right backward high (table plane, horizontal).

X6: Right sideward middle (door plane, vertical).

X7: Forward low (wheel plane, sagittal).

X8: Left forward low (table plane, horizontal).

X9: Left middle (door plane, vertical).

X10: Left backward high (table plane, horizontal).

X11: Follow-through, backward high (wheel plane, sagittal).

+

The X-scale provides a structured approach to analyzing the spatial and directional aspects of the golf swing, aiding in the development of spatial awareness and flow in the golfer’s movement.

2.2. Golf Swing as a Turing Machine Process: A State-Driven Computational Model

In both Turing’s computational model and Laban’s X-scale framework for golf biomechanics, the functional states of an agent are treated as finite and structured, disregarding subjective or emotional influences. In Turing’s analogy of the hapless prisoner (HP), the internal states of the prisoner are constrained to a finite set of functional states necessary to execute the computational task [12]. This abstraction deliberately ignores subjective experiences such as boredom, frustration, or fatigue, focusing solely on the mechanical execution of the sequence. The finiteness of the model is crucial—it ensures that each computational step is well defined and does not depend on external, uncontrolled variables such as emotional fluctuations.

Similarly, in golf biomechanics, the golfer’s state is modeled through the finite X-scale positions (X1–X11), which structure movement within a computationally tractable framework. Golfers must focus their attention on key biomechanical constraints, such as keeping the lead arm straight, maintaining head position, and fixing visual focus on the ball. These constraints function as practical limitations of cognitive load and memory, shaping movement sequences in a way that aligns with affordance-based execution rather than emotional or psychological variables.

By defining the golf swing as a sequence of finite state transitions in the X-scale, this model abstracts away subjective states and psychological distractions, treating the golfer much like a computational system processing biomechanical inputs and executing structured movement commands. This ensures that swing optimization is a controlled, repeatable process, much like a Turing machine executes a finite set of rule-based operations.

In the context of Turing’s machine framework, the golf swing can be conceptualized as a state-driven computational process where each functional state (q1, q2, q3, q4) (Figure 4) corresponds to distinct biomechanical adjustments rather than a sequential trajectory. The machine’s tape, which in Turing’s model represents an interactive external environment, aligns with the golf club’s inertia and environmental constraints—both dynamically shaping the execution of movement.

As shown in Figure 4, the Turing machine operates through a finite set of functional states (q1–q4), each governing specific interactions with the tape (analogous to the golfer’s perception of club inertia, ball position, and proprioceptive information pickup). The golfer’s posture, instantaneous screw axis (ISA), and muscular adjustments serve as internal computational states, which adapt iteratively in response to environmental affordances. Just as the machine processes symbols on the tape and updates its state accordingly, the golfer continuously refines swing mechanics based on external sensory input (e.g., club inertia, ground reaction forces).

Crucially, q1, q2, q3, and q4 are not sequential movement phases but represent distinct control states in response to different affordances, mirroring how the golfer’s internal control mechanisms dynamically adjust at critical points of the swing. This computational framework highlights that golf performance is not merely a linear kinematic sequence but an adaptive system governed by structured state transitions, enabling real-time biomechanical optimization and skill refinement.

Figure 4. The diagram illustrates the HP Turing machine’s state transition system:

Figure 4. The diagram illustrates the HP Turing machine’s state transition system:

States (q1–q4):

-

q1 (Initial): Begins new segments

-

q2 (Scanning): Detects and marks 1 s with X

-

q3 (Copying): Copies marked numbers

-

q4 (Completing): Finalizes segments

Key Affordances:

• State–symbol pairs: each combination of state (q1–q4) and symbol (#,0,1,X) forms a configuration.
• Transitions: show how configurations lead to actions (write symbol, move, change state).
• Movement: R/L arrows indicate tape navigation.
• Marking: X symbols temporarily mark processed 1 s.

2.3. Structured Refinement in Golf Swing: A Computational Analogy to Turing Machines and Laban’s X-Scale

Turing machines operate by systematically building sequences through scanning, marking, copying, and completing operations, ensuring that each computational step refines the next in an iterative and structured manner. This concept can be directly applied to Laban’s X-scale framework in golf biomechanics where movement refinement follows an ordered yet continuous process (

Table 1. Computational and biomechanical parallels.

Turing Machine Concept	Laban X-Scale Concept
0 (Zero) functions as a boundary marker between segments.	X1, X2, X3, etc. function as structured but non-stopping reference points.
Each segment contains key evolving numerical data.	Each X-scale movement phase encodes critical biomechanical transitions.
The sequence of segments is continuous but analyzed in steps.	The swing is a continuous motion but analyzed through X-scale sequences.
Important information is carried between segment transitions.	Kinematic adjustments occur dynamically between X-scale markers.

).

In the Turing machine framework, computational steps are structured into overlapping segments, where:

• Each segment is bounded by zeroes (0), acting as markers that define computational boundaries.
• The in-between numerical sequence (1, 2, … ones) carries structured information, evolving iteratively from one segment to the next.
• Despite these discrete boundaries, the computational process remains continuous, ensuring that meaningful patterns are preserved across transitions.

For example, in the sequence 0010110111…, each computational segment follows an incremental evolution:

• Segment 1: 00
• Segment 2: 010
• Segment 3: 0110

Here, the zeroes function as boundaries, separating key information, yet the computational process itself flows continuously through structured refinement.

In Laban Movement Analysis (LMA), particularly in the X-scale framework, the golf swing follows a continuous motion, but structural markers (X1 → X12) segment the movement into analyzable states:

• Each X-scale position (X1, X2, X3, …, X12) functions like the zeroes in Turing’s sequence, marking reference points within a continuous biomechanical process.
• The swing itself does not stop at each X-scale position, just as computation does not halt at each segment boundary.
• The critical information in Turing’s model (numerical evolution) corresponds to biomechanical adjustments in X-scale positions, encoding how the golfer dynamically refines movement through inertia, balance, and posture.

By interpreting golf swing mechanics through the lens of computational refinement, we can observe that expert performance emerges from structured sequential optimization:

• A novice golfer lacks structured refinement, much like an inefficient computational system struggling with unnecessary state transitions.
• A skilled golfer exhibits an efficient, adaptive flow of movement, processing external affordances (club inertia, ground reaction forces) in real-time, akin to an optimized Turing machine iterating toward an ideal output.

This framework not only bridges computational models with sports biomechanics but also provides a systematic approach for training methodologies, where movement refinement can be optimized through structured, algorithmic learning.

2.4. Iterative Optimization: The Swing as Computational Refinement

At each stage of the swing, the golfer perceives affordances (e.g., club position, ball trajectory) and executes effectivities (e.g., grip adjustments, swing speed) in a manner analogous to a Turing machine processing inputs and updating states sequentially. This process can be visualized in the attached figure, which illustrates the step-by-step transitions of a Turing machine (t0 → t6) as it processes symbols on a tape.

Just as the Turing machine’s head moves left or right to read and write symbols (e.g., 0, 1, #, X) based on its current state (q1 → q4), the golfer’s body and club transition through phases of the swing (e.g., backswing, downswing, follow-through) based on sensory input and motor commands. The golfer’s adjustments occur in real time, enabling biomechanical optimization through affordance-driven adaptation [19,29].

This computational analogy highlights how the golf swing can be modeled as a dynamic, state-based process where affordances and effectivities drive real-time optimization. The attached figure serves as a visual aid to bridge the abstract concepts of Turing’s theory with the practical dynamics of the golf swing.

This framework highlights motor learning in golf as a structured computational process, integrating Turing’s machine theory, Laban’s X-scale sequences, and ecological psychology. The golfer refines movement through sequential interactions with the club and environment, reinforcing the idea that swing optimization is an iterative and computationally structured process.

In this section of our study, we build upon the foundational understanding of Laban Movement Analysis (LMA), where we explore the golfer’s dynamic interaction with the three-dimensional kinesphere [32]. Moving beyond the basic interactions, we delve deeper into the nuanced concept of “shaping”, a critical aspect of movement form within LMA that enables the golfer to adapt to the plastic character of the inertia surface of the golf club.

Laban’s movement theory, which emphasizes the spatial engagement of the human body, proposes that a person can project intention and energy into surrounding space without necessarily changing physical position—a concept we refer to here as the “stance” [32] This framework is especially pertinent when analyzing how golfers adapt their body movements in response to the inertial behavior of the club throughout different phases of the swing. Whereas earlier sections introduced the broader spatial constructs of movement, this part focuses on how shaping actions—intentional changes in body configuration—are modulated in accordance with the geometry and resistance characteristics of the club’s inertia in motion.

Figure 3 plays a key role in visualizing the interplay between the golfer’s movement patterns and the inertial characteristics of the club. It depicts not only directional zones within the kinesphere but, more significantly, how those spatial regions are actively shaped in response to the club’s dynamic resistance. The “Xi” labels shown in the figure serve as more than abstract representations of Effort—they are used here to demonstrate how the golfer’s posture and spatial orientation evolve in coordination with the mechanical demands of the swing. The marked three-dimensional axes further clarify how these transformations unfold across movement planes.

2.5. Screw Theory as a Framework for Golf Swing Analysis

While Laban’s concept of spatial harmony has offered meaningful ways to describe human movement, its traditional reliance on Cartesian frameworks limits its ability to represent the full complexity of spatial transformations. To address this, we incorporate screw theory—a mathematical model that unifies rotational and translational motion into a single representation.

The downswing phase of the golf swing is a prime example of what Laban termed volute phrasing [32], which describes a coordinated sequence of three non-equivalent directional pulls that shift in a continuous, spiral-like pattern. This phrasing can be interpreted as a dynamic three-dimensional helix in which sagittal, vertical, and horizontal components evolve proportionally and fluidly over time.

By combining screw theory with Laban’s qualitative descriptors, we establish a robust analytical model capable of capturing the dynamic symmetry and spatial complexity of the swing. This framework enables us to measure and visualize the graded interactions of spatial pulls, offering a precise interpretation of how movement efficiency and control emerge across different skill levels.

Human movement is governed by the complex interplay between rotational and translational dynamics. In skillful actions such as the golf swing, these components are not independent but are structured along a common axis—what screw theory [33] defines as the instantaneous screw axis (ISA). Unlike standard coordinate-based methods that rely on position derivatives, screw theory allows motion to be characterized using kinematical variables—quantities that describe velocities independently of specific displacement paths [34]. This becomes particularly relevant in contexts where the axis of motion evolves over time, such as in the downswing phase of a golf swing.

The ISA, in such cases, represents the collective effect of rotational and translational motions resulting from all contributing joints and body segments. Since the axis is not fixed during the movement, the angular displacement cannot be described as the differential of an angle. Instead, the angular velocity must be treated as an infinitesimal rotation about a moving axis—a scenario ideally suited for analysis through screw theory [35].

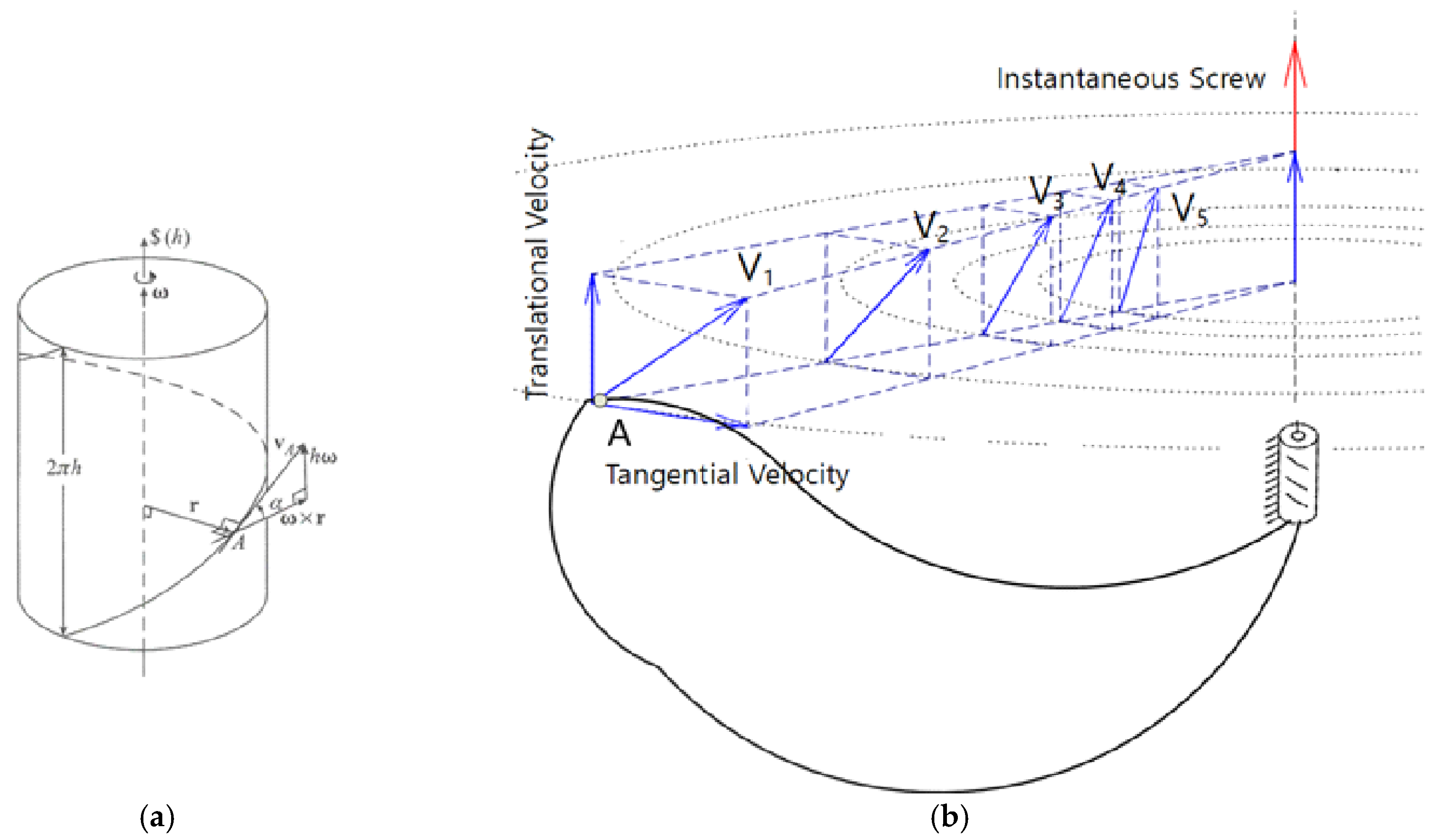
Figure 5 provides an intuitive geometric interpretation of this framework. In Figure 5a, a rigid body undergoing screw motion has each point’s velocity vector tangential to a helical path, forming what is known as a helicoidal velocity field. The motion is completely characterized by a twist with a given pitch about the instantaneous screw axis. Figure 5b further breaks this down: the velocity at each point consists of two components—a translational component parallel to the ISA and a tangential component due to rotation about the ISA. This helical field of linear velocity demonstrates how the combination of these elements defines the rigid body’s instantaneous motion.

In screw theory, a 6D twist screw $ = $\left[v\omega \right]$ includes:

• v: linear velocity
• ω: angular velocity

The pitch h of the twist (i.e., the screw) is defined as:

$$h={\displaystyle \frac{v\cdot \omega }{{\parallel \omega \parallel }^2}}$$

(1)

This gives the translation per unit rotation—the classical screw pitch.

Specifically, we used the homogeneous screw coordinates $ = (L, M, N, P, Q, R), as defined by Davidson and Hunt (1990) where (L, M, N) represent the direction of the axis and (P, Q, R) define the moment of the line about the origin [36]. These coordinates describe the axis of the screw motion in its simplest form and allow for the localization of the instantaneous axis of kinematics (IAK) through the ISA [37].

The pitch of the screw, h, which quantifies the ratio of translational to rotational motion along the ISA, was computed using Equation (2).

$$\begin{gathered} {\mathrm{P}}^{*}=\mathrm{P}+\mathrm{hL},{\mathrm{Q}}^{*}=\mathrm{Q}+\mathrm{hM}.{\mathrm{R}}^{*}=\mathrm{R}+\mathrm{hN} \\ \mathrm{h}={\displaystyle \frac{{LP}^{*}+{MQ}^{*}+{NR}^{*}}{L^2+M^2+N^2}} \end{gathered}$$

(2)

We employ Plücker coordinates [38] to mathematically represent the instantaneous screw axes (ISAs) of the golf club during motion. This formulation captures both the direction of the axis and the associated moment, effectively modeling the combined rotational and translational behavior of the club. This screw-based representation offers a more complete depiction of the dynamic interaction between the golfer and the club, which is essential for performance assessment and technique refinement.

To further characterize the club’s dynamic properties, we utilize the spatial inertia tensor [25], a core concept in rigid body dynamics. This tensor facilitates the mapping between the kinesphere-based spatial acceleration space—conceptualized via the icosahedron—and the corresponding force domain, here expressed through the Effort Cube. Much like an error covariance matrix in estimation theory, the spatial inertia tensor encodes the club’s mass distribution and resistance to motion relative to the wrist joint, offering insights into how golfers perceive and regulate the club during various swing phases.

Through decomposition of this tensor into geometric and physical components, we solve eigenvalue problems that reveal how different inertia modes contribute to the swing’s dynamic structure. This approach enables an analysis of how biomechanical inputs from the golfer translate into mechanical outcomes through the club.

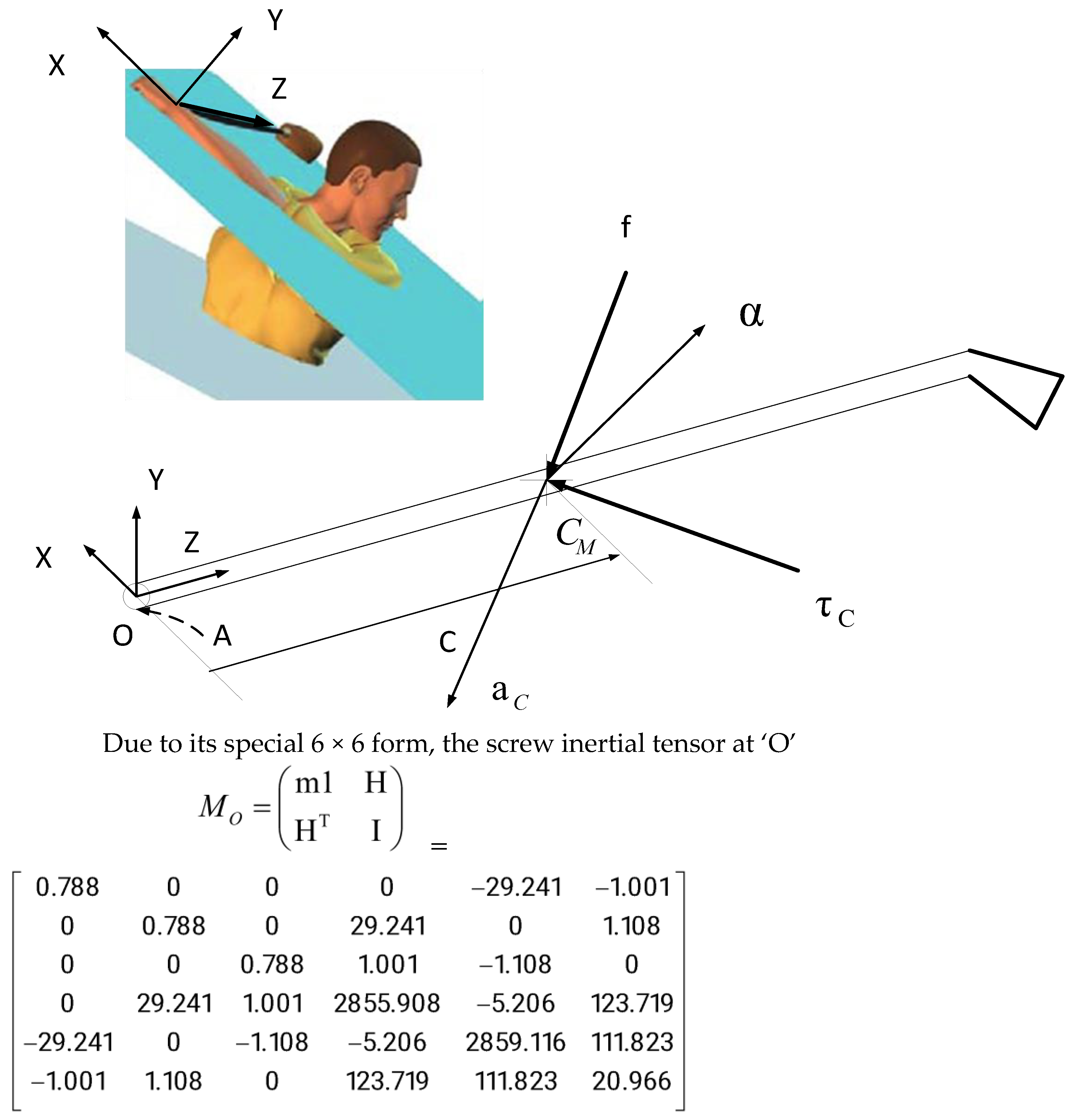
Accordingly, this section introduces a free-vector decomposition method for the rigid-body spatial inertia tensor. The linear mapping from acceleration twists to wrenches is defined by this tensor whose structure is naturally suited to be expressed via principal screws of inertia [25]. In the configuration shown in Figure 6, the club (mass m) has its center of mass (CM) located at vector position C; and the inertia tensor about its center of mass is J. The club is at rest, and experiences a force, f, acting along a line passing through the center of mass, and a couple, τ_C. The resulting acceleration is determined by an angular acceleration, α, along an axis passing through the center of mass (C_M), and the linear acceleration, a_C, on C_M.

To estimate the inertia tensor used in our model, we did not rely on direct physical measurements. Instead, we began with reference data from a club produced by the same manufacturer. We then applied a geometric scaling technique to adapt these values to our experimental club. This process was grounded in principles outlined by Zatsiorsky (1998), where segment moments of inertia scale with mass and the square of a characteristic length [39].

In a subsequent refinement step, we adjusted mass, center of mass, and inertial properties using parameter-tuning procedures informed by the work of MacKenzie and Sprigings (2009) [7]. These adjustments ensured that our estimated tensor accurately reflected the physical properties of the specific club tested [7].

The inertia matrix shown in Figure 6 thus reflects a rigorously derived estimate based on validated scaling methodologies and domain-specific tuning, ensuring fidelity to the physical characteristics of our experimental setup (units in kg∙cm²). The matrix presented is entirely original, created using these established procedures.

The motion dynamics are formulated as a linear mapping from screw-form accelerations—expressed as twists—to corresponding wrenches in force space, following the framework described by (Kim, Veloso et al., 2013 [40]).

$$\left[\begin{array}{c}f\\ {\tau }_c\end{array}\right]=\left[\begin{array}{cc}m1& 0\\ 0& J\end{array}\right]\left[\begin{array}{c}{a}_c\\ \alpha \end{array}\right]$$

(3)

where $m1=\left[\begin{array}{ccc}m& & \\ & m& \\ & & m\end{array}\right]$= M, and 1 is the 3 × 3 identity matrix.

Because all spatial variables are initially referenced relative to the center of mass, the translational and rotational dynamics are effectively decoupled, with linear acceleration resulting solely from applied force and angular acceleration driven by the applied moment. To express Equation (1) from the perspective of the joint axis origin (as shown in Figure 6), we apply a transformation that repositions the spatial inertia tensor accordingly.

$$\left[\begin{array}{c}f\\ {\tau }_0\end{array}\right]=\left[\begin{array}{cc}m1& H\\ H^T& I\end{array}\right]\left[\begin{array}{c}{a}_0\\ \alpha \end{array}\right]$$

(4)

where H = C × M, I = J + C × MC × ^T, and C× is the anti-symmetric skew matrix corresponding to C.

$$C\times =\left[\begin{array}{ccc}0& -C_z& C_y\\ C_z& 0& {-C}_x\\ {-C}_y& C_x& 0\end{array}\right]$$

(5)

Due to its special 6 × 6 form, the spatial inertial tensor is as follows:

$$M_0=\left[\begin{array}{cc}m1& H\\ H^T& I\end{array}\right]$$

(6)

is expected to have special eigenstructures.

The spatial inertia tensor M₀ represented at the origin is a symmetric, positive definite tensor and transforms to any point ‘A’ by the spatial Jacobian, Φ, according to the following:

$$M_A=\left[\begin{array}{cc}1& 0\\ -r_{A/0}\times & 1\end{array}\right]M_0{\left[\begin{array}{cc}1& 0\\ -r_{A/0}\times & 1\end{array}\right]}^T$$

(7)

where $r_{A/0}=\overrightarrow{OA}$ and $\mathsf{\Phi }={\left[\begin{array}{cc}1& 0\\ -r_{A/0}\times & 1\end{array}\right]}^T$.

The eigenvalue problem provides a unique decomposition of M₀ as follows:

$$\left[\begin{array}{cc}m1& H\\ H^T& I\end{array}\right]=M_0=\left[\begin{array}{cc}f& 0\\ \tau & \gamma \end{array}\right]\left[\begin{array}{cc}{m}_f& 0\\ 0& m_{\gamma }\end{array}\right]{\left[\begin{array}{cc}f& 0\\ \tau & \gamma \end{array}\right]}^T$$

(8)

where m_f and m_γ are representing the eigen values of mass and mass moment of inertia, respectively (following the common notational tactics for the principal axes of inertia, we use $e_1,e_2,e_3$ for the corresponding eigenvectors to m_γ and, to the corresponding principal moment of inertia, ${\mathit{I}}_1\le {\mathit{I}}_2\le {\mathit{I}}_3$ for γ). We state that I₃ is the largest principal moment of inertia, representing the mass distribution along the longitudinal axis of the golf club. The e₃ eigenvector, known as the principal axis of inertia, is aligned perpendicular to the longitudinal axis and passes through the mass center of the golf club. This alignment contributes to the perceptual simplifications obtained by using it as the axis of reference and is critical for understanding the dynamics of the golf swing.

One might wonder whether the decomposition based on the solution for the free-vector eigenvalue problem would be different at another point A. We apply the transformation rule (Equation (7)) to the above decomposition (Equation (8)) as follows:

$$=\left[\begin{array}{cc}1& 0\\ -r_{A/0}\times & 1\end{array}\right]\left[\begin{array}{cc}f& 0\\ {\tau }_0& \gamma \end{array}\right]\left[\begin{array}{cc}{m}_f& 0\\ 0& m_{\gamma }\end{array}\right]{\left[\begin{array}{cc}f& 0\\ {\tau }_0& \gamma \end{array}\right]}^T{\left[\begin{array}{cc}1& 0\\ -r_{A/0}\times & 1\end{array}\right]}^T$$

(9)

$$=\left[\begin{array}{cc}f& 0\\ {\tau }_0-r_{A/0}\times f& \gamma \end{array}\right]\left[\begin{array}{cc}{m}_f& 0\\ 0& m_{\gamma }\end{array}\right]{\left[\begin{array}{cc}f& 0\\ {\tau }_0-r_{A/0}\times f& \gamma \end{array}\right]}^T$$

(10)

$$=\left[\begin{array}{cc}f& 0\\ {\tau }_A& \gamma \end{array}\right]\left[\begin{array}{cc}{m}_f& 0\\ 0& m_{\gamma }\end{array}\right]{\left[\begin{array}{cc}f& 0\\ {\tau }_A& \gamma \end{array}\right]}^T$$

(11)

which shows that M_A is decomposed by the same eigenscrews in the same manner, just represented at B. That is, no matter where the problem is posed, the same eigenscrews form the basis of the decomposition.

2.6. Inertia Tensor and Dynamic Touch

To relate the concept of the inertia tensor with Gibson’s idea of dynamic touch as described in “The Senses Considered as Perceptual Systems [19]”, we can delve into how the perception of an object’s inertial properties is intimately connected to the way it is wielded and experienced through dynamic touch. Here’s how these ideas connect:

James Gibson’s concept of dynamic touch emphasizes that the perception of an object’s mass and inertial properties arises not merely from passive touch but from actively wielding the object. When an object is lifted, shaken, or manipulated, the information about its weight and resistance—its inertia—is derived from the interaction of sensory inputs from muscles, tendons, and joints.

This interaction aligns with the notion of the inertia tensor, which mathematically represents how mass is distributed relative to an axis of rotation. The inertia tensor determines how an object resists changes to its motion when force is applied, and thus, it encapsulates the very properties that Gibson argues are perceived through dynamic touch.

Gibson suggests that when an object is wielded—tossed, shaken, or moved—our perception filters out the transient sensations, focusing instead on the invariants, such as the object’s resistance to motion, which are directly linked to its inertial properties. The inertia tensor, which describes how different parts of an object contribute to its overall resistance to rotational and translational forces, is essentially the physical correlate of these perceptual invariants.

As a golfer swings a club, for instance, the golfer perceives the club’s inertial properties—how it resists acceleration and rotation—through dynamic touch. This perception is mediated by the inertia tensor, which encapsulates the distribution of mass within the club and how that distribution influences the club’s behavior during the swing.

2.7. The Golf Swing as a Universal Computational Process: Integrating Material Substance, Inertia, and Cognitive Performance

Gibson’s concept of dynamic touch—the perception of an object’s heaviness, resistance, and inertia through sensory information from the skin, muscles, and joints—can be reinterpreted through the lens of Turing’s universal machine theory. Just as a Turing machine processes input symbols on a tape to produce an output, the golfer’s sensory system processes tactile and proprioceptive inputs to compute the object’s inertial properties.

The inertia tensor, which mathematically models an object’s mass distribution and resistance to motion, can be likened to the transition rules of a Turing machine. These rules dictate how the machine updates its state based on input, analogous to how the golfer’s brain updates its understanding of the club’s inertia based on sensory feedback. For example, when wielding a golf club, the golfer perceives the club’s resistance to motion (its inertia) through the forces required to initiate and control its movement. This perception is akin to the Turing machine reading and interpreting symbols on its tape, with each sensory input (e.g., muscle tension, joint angle) serving as a symbol that informs the next state of the system.

Gibson emphasizes that dynamic touch is not merely perceptual but also deeply intertwined with performance. This integration can be modeled as a computational process, where the golfer’s brain acts as a Turing machine that integrates sensory inputs (affordances) with motor outputs (effectivities) to optimize performance. In a golf swing, the golfer’s brain computes the club’s inertia tensor—its mass distribution and resistance to rotation—and uses this information to guide motor actions. This process mirrors the way a Turing machine processes input symbols to produce an output. For instance, the golfer’s perception of the club’s inertia (input) informs the precise application of muscular effort (output), enabling an efficient and powerful swing. This cognitive integration is a form of real-time computation where the golfer’s sensory-motor system continuously updates its state based on feedback, much like a Turing machine transitions between states based on its transition rules.

The inertia tensor serves as the mathematical foundation for understanding how humans perceive and interact with objects’ mass and resistance through movement. In the context of Turing’s universal machine theory, the inertia tensor can be viewed as the set of rules that govern the golfer’s sensory–motor system. When a golfer wields a club, the perception of its inertial properties is a direct manifestation of the information encapsulated by the inertia tensor, guiding the swing and optimizing performance. This blend of perception and performance, as described by Gibson, can be understood as a deeply embodied computational process. The golfer’s sensory–motor system acts as a Turing machine, processing inputs (sensory feedback) and producing outputs (motor actions) in real time. This computational analogy highlights the elegance of human–environment interaction where the perception of inertial properties is seamlessly integrated with motor control to achieve optimal performance [41].

2.8. Instrumentation and Data Analysis

This study drew upon an existing dataset originally collected to examine the golf swing mechanics of two female golfers with differing skill levels (see

Table 2. Participant demographics and golfing background. This table summarizes the personal and performance-related characteristics of the two female participants included in the study. Key variables include age, height, body mass, golf handicap, years of playing experience, and the average number of rounds played annually. These contextual details help interpret inter-individual differences observed in swing mechanics and biomechanical performance measures.

Participant	Age	Height	Mass	Handicap	Experience	Rounds
	(years)	(cm)	(kg)		(years)	(per year)
A	17	167	54	32	1	10
B	51	165	55	8	15	110

) (Kim, Veloso et al., 2013 [40]). The decision to reuse this dataset was guided by its comprehensive biomechanical scope, which includes high-resolution motion capture and synchronized ground reaction force (GRF) data. This made it well-suited for advanced kinematic modeling, including screw-theoretic analysis.

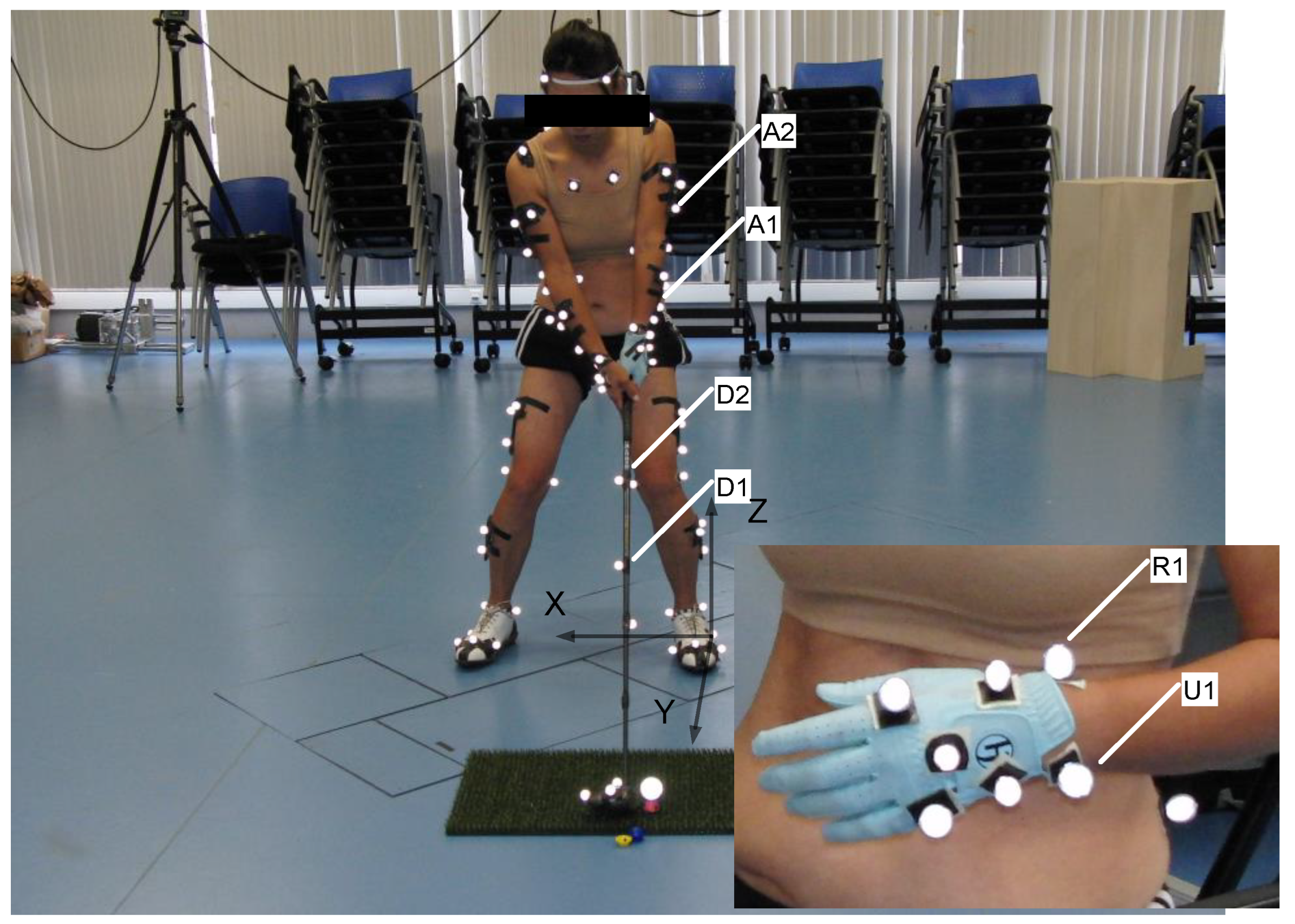
The motion data were acquired using a 12-camera Qualisys optoelectronic system (type: Oqus-300, Qualisys AB, Göteborg, Sweden), operating at 300 Hz. A total of twenty-four reflective markers, along with four marker clusters, were placed on anatomical landmarks in accordance with ISAK (International Society for the Advancement of Kinanthropometry) standards. These markers enabled the 3D reconstruction of twelve key body segments, including the head, trunk, limbs, pelvis, and feet, as well as precise tracking of the golf club. Ground reaction forces were captured via a Kistler force plate, enabling the integration of kinetic and kinematic data during analysis.

Figure 7 illustrates the marker configuration at the address position, including detailed placements on the wrist and club, which are essential for evaluating grip dynamics and force transmission. The global coordinate origin was aligned with the initial center of pressure (COP) beneath the lead foot, ensuring consistent spatial reference across all measurements.

The dataset captured the full swing cycle, but this study focused on the downswing phase, beginning at the initiation of forward motion and ending just before club–ball impact. Using the original anatomical coordinate systems, we calculated the instantaneous screw axes (ISAs) and analyzed their evolution over time. This allowed us to assess how effectively each golfer synchronized their movement patterns with the inertial properties of the club.

The reuse of this previously validated dataset allowed for a focused, resource-efficient investigation, eliminating inter-trial variability while preserving ecological relevance. This analytical approach provided a reliable foundation for exploring how dynamic interaction between the golfer and the club unfolds during performance-critical moments of the swing.

3. Results

3.1. Free Flow vs. Bound Flow: A Computational Perspective on Golf Swing Dynamics

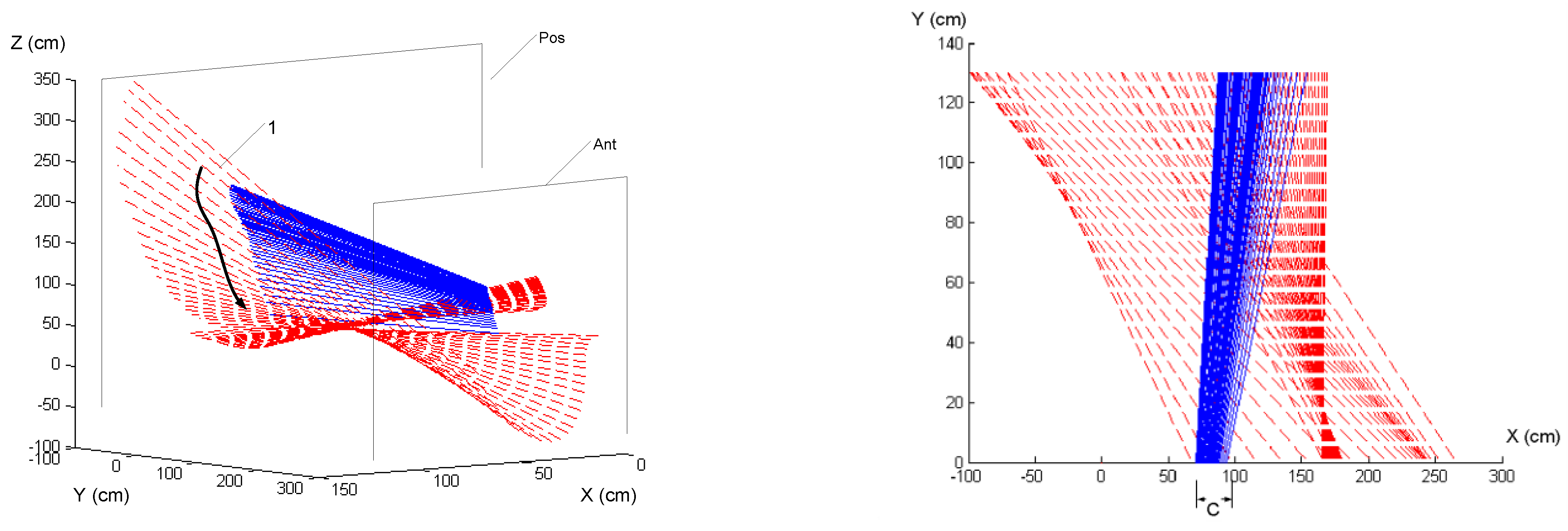
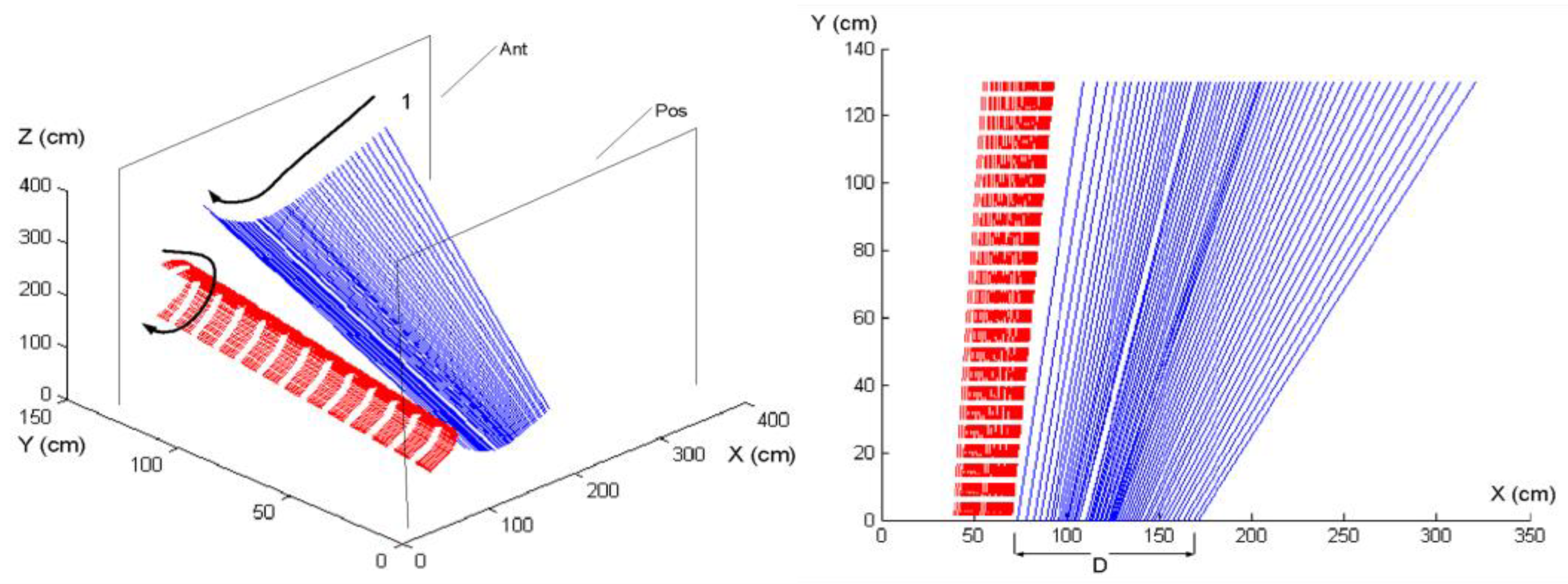
In the context of Turing’s computational framework, movement execution in golf can be analyzed as a process where information is perceived by interacting with the environment rather than modifying the golfer’s internal functional states. A skilled golfer operates within a free-flow dynamic where the forces of club inertia and environmental affordances are directly perceived and seamlessly integrated into movement execution. In contrast, a novice golfer exhibits a bound flow where the perception of inertia is restricted, leading to conscious movement control that disrupts natural swing efficiency.

Figure 8 and Figure 9 illustrate this distinction, adapted from our prior research [40]. Figure 8 (Novice Golfer) demonstrates disjointed and inefficient ISA paths, where the golfer struggles to process and respond to external affordances such as club inertia and ground reaction forces (GRF). This inefficiency is further reflected in Figure 10b where the novice golfer exhibits lower and more variable GRF peaks in the vertical directions, indicating poor timing, balance, and inefficient force application. The lack of continuous kinematic affordance adjustment results in abrupt trajectory shifts and inconsistent movement execution. This corresponds to a Turing machine that inefficiently modifies its internal state rather than leveraging environmental interaction for optimized performance.

In contrast, Figure 8 (proficient golfer) showcases fluid, self-organizing ISA paths, indicating a well-structured perception–action cycle where the golfer effectively integrates club inertia and GRF into their motion execution. This is confirmed by the GRF profiles in Figure 11b, where the proficient golfer demonstrates higher, sharper, and more consistent peaks, reflecting optimal force application, better balance, and greater efficiency in energy transfer. The smooth and controlled force application in the proficient golfer’s GRF pattern aligns with a Turing machine optimizing computational efficiency by leveraging external affordances rather than relying on excessive internal state modifications.

This comparison highlights that expert movement refinement in golf emerges from structured interaction with external forces rather than excessive internal corrections, reinforcing the importance of computational models in analyzing motor learning and performance optimization. Accordingly, Figure 9 (skilled golfer) presents an optimized perception–action coupling, where the ISA paths remain aligned with the club’s inertia forces. The skilled golfer does not resist external forces but rather exploits them, allowing inertia to naturally guide movement execution. This is analogous to a Turing machine that efficiently interacts with the environment to store and process information dynamically, reducing the need for unnecessary internal state modifications.

3.2. Turing’s Computational Model and Swing Flow

A novice golfer (Figure 8), constrained by the bound flow, attempts to manually regulate each swing phase, much like a Turing machine struggling with excessive state transitions. The lack of synchronization between club inertia and biomechanical adjustments forces the novice to overcompensate with internal modifications, resulting in inefficiencies and inconsistent swing execution.

A skilled golfer (Figure 9) operates within the free flow, where information is efficiently processed through interaction with the club and environmental affordances rather than through rigid internal control. The golfer’s motor adjustments emerge naturally from kinematic affordance adjustment, minimizing unnecessary cognitive interference. This mirrors a Turing machine optimizing computational efficiency by leveraging external input rather than overloading internal state modifications.

The spatiotemporal representation of the swings in Figure 8 and Figure 9 further underscores this computational distinction, drawing parallels with Conway’s Game of Life [42] where emergent self-organizing patterns arise from simple iterative rules. Skilled golfers exhibit fluid, self-organizing patterns where ISA paths and inertia forces remain consistently aligned, allowing them to efficiently process biomechanical information in real time, much like how stable structures emerge in Conway’s Game of Life through iterative state transitions. In this context, the golfer’s swing refinement mirrors a computationally optimized system where each movement phase builds upon previous states, adapting dynamically to affordances such as club inertia and ground reaction forces (GRF).

In contrast, novice golfers struggle to establish sequentially structured refinement, akin to an unstable computational system in the Game of Life that fails to reach stable oscillators or gliders. Their disruptive ISA paths and inefficient force application introduce instability, increasing energy dissipation and preventing efficient movement execution. This comparison reinforces the idea that skilled motor control, like computational systems, thrives on structured yet adaptable self-organization, with optimal movement efficiency emerging from coordinated perception–action cycles rather than excessive internal corrections.

These findings highlight that expert golf performance emerges from the ability to store and process biomechanical information externally, rather than relying on rigid internal modifications. The ability to access and utilize external force dynamics is a hallmark of proficiency, reinforcing Turing’s computational principle that effective information storage relies on environmental interaction rather than excessive internal state changes. This computational perspective bridges biomechanics, ecological psychology, and machine learning, offering a novel framework for sports training, AI-driven motor learning, and performance optimization.

3.3. A ‘Free’ Flow Versus a ‘Bound’ Flow Based on Laban’s Effort Theory

This misalignment suggests that the golfer fails to utilize external force dynamics effectively, instead attempting to regulate movement through internal control modifications, characteristic of the bound flow. In Turing’s computational framework, this corresponds to a system that modifies its internal state rather than leveraging environmental interaction for information storage. The arrows mark the sequential migration of axes at 0.0333-s intervals (units in cm), illustrating disruptions in movement execution due to inconsistent processing of external affordances.

3.4. Pitch Invariance Reveals Skill-Specific Coordination in Human Movement

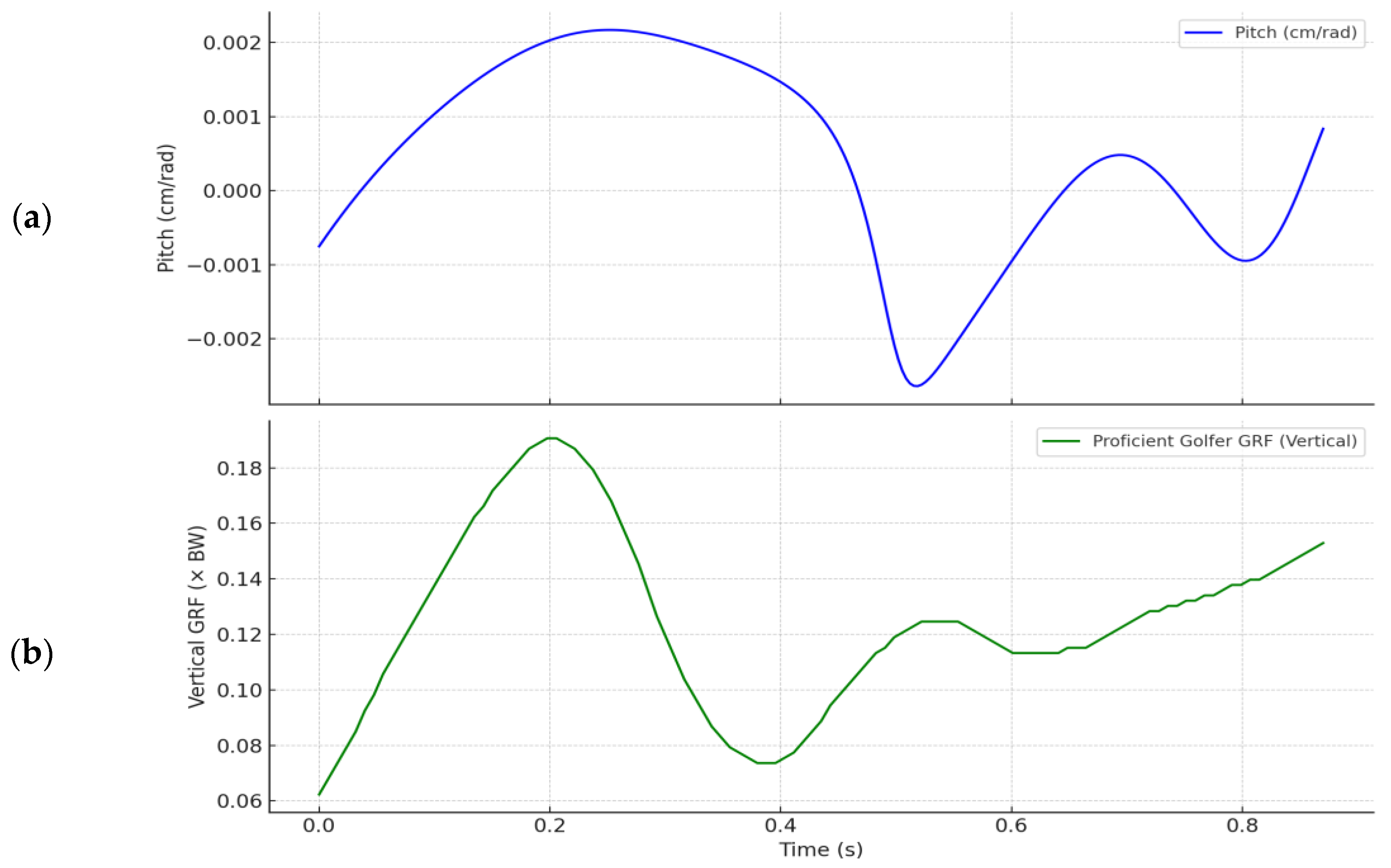
In this study, we focus on pitch, defined as the translational displacement per unit of angular rotation along the instantaneous screw axis (ISA), as a biomechanical invariant reflecting skilled motor coordination. Because both pitch and ground reaction force (GRF) are scalar quantities, they can be easily compared, enabling a straightforward assessment of how rotational and translational dynamics are integrated during performance. We analyze pitch in conjunction with GRF data during the golf swing to evaluate how skilled movement aligns internal biomechanics with external force production. The goal is to demonstrate that pitch serves as a compact and informative descriptor of biomechanical efficiency and perceptual–motor integration.

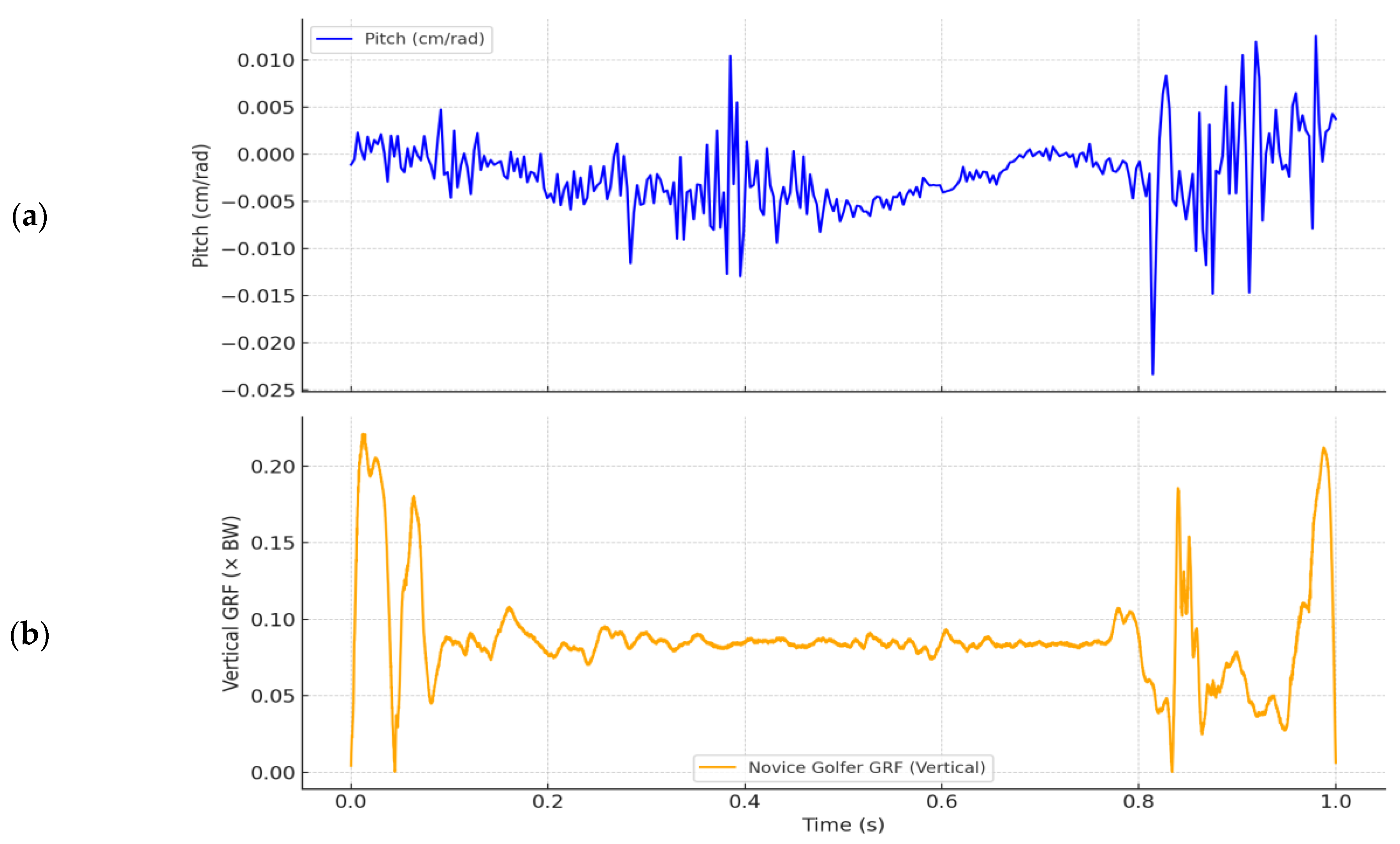
Figure 10a and Figure 11a present the pitch variation during the downswing phase of a novice (A) and proficient (B) golfer, respectively. Pitch, defined as the translational displacement per unit of rotation along the instantaneous screw axis (ISA), is expressed in centimeters per radian (cm/rad). This measure captures the geometric coordination of motion and offers a biomechanical indicator of the rotational–translational coupling within the swing.

The proficient golfer (Figure 11a) demonstrates a narrow range of pitch values between −0.0025 and 0.0025 cm/rad. The consistent oscillation near zero reflects a stable integration of rotational and translational components. This smooth profile indicates effective control of motion along the screw axis and suggests optimized energy transfer.

In contrast, the novice golfer (Figure 10a) exhibits a much broader and more erratic pitch profile, ranging from −0.025 to 0.01 cm/rad. Frequent fluctuations and direction changes signal instability in motion coordination. The variability in pitch highlights the absence of controlled coupling between rotation and translation during the downswing.

Vertical ground reaction force (GRF) data complement the pitch findings. Figure 11b shows the GRF pattern for the proficient golfer. A single, well-defined peak (approximately 0.19 × body weight) is observed, distributed smoothly across the 0.87-s interval. This force signature supports the presence of synchronized lower-limb dynamics and precise timing in energy application.

Figure 10b shows the novice golfer’s GRF profile over the same duration. The data exhibit irregular force magnitudes, multiple local peaks, and abrupt discontinuities. These features align with the erratic pitch profile, indicating uncoordinated lower-limb control and inefficient force transmission during the downswing.

As shown in

Table 3. Biomechanical comparison between a novice and a proficient golfer based on pitch variation, vertical ground reaction force (GRF) profiles, and their temporal alignment. The proficient golfer exhibits synchronized, stable coordination between pitch and GRF, while the novice shows disorganized patterns indicative of inefficient motor control.

Participant	Pitch Pattern	GRF Profile	Temporal Alignment	Interpretation
A (Novice)	Erratic, irregular swings with high variability	Multiple force spikes and unstable fluctuations	No alignment between pitch stability and GRF peaks	Breakdown in rotation-translation coupling; inefficient force timing
B (Proficient)	Smooth, narrow oscillation near zero	Single, sharp, well-timed peak	Peak GRF aligns with minimal pitch deviation	Efficient motor control and energy transfer

, the proficient golfer demonstrates a close temporal alignment between pitch stability and peak GRF, unlike the novice golfer.

The proficient golfer’s GRF and pitch are phase-aligned, converging at a moment where energy is channeled optimally. In contrast, the novice golfer exhibits asynchronous patterns, showing that the timing of force and motion direction is uncoordinated—a hallmark of underdeveloped motor strategies. This confirms the value of pitch as a diagnostic invariant and suggests that synchronized pitch-GRF analysis can be a powerful tool in coaching, rehab, and performance science.

3.5. Golf Swing as a Computationally Structured Process

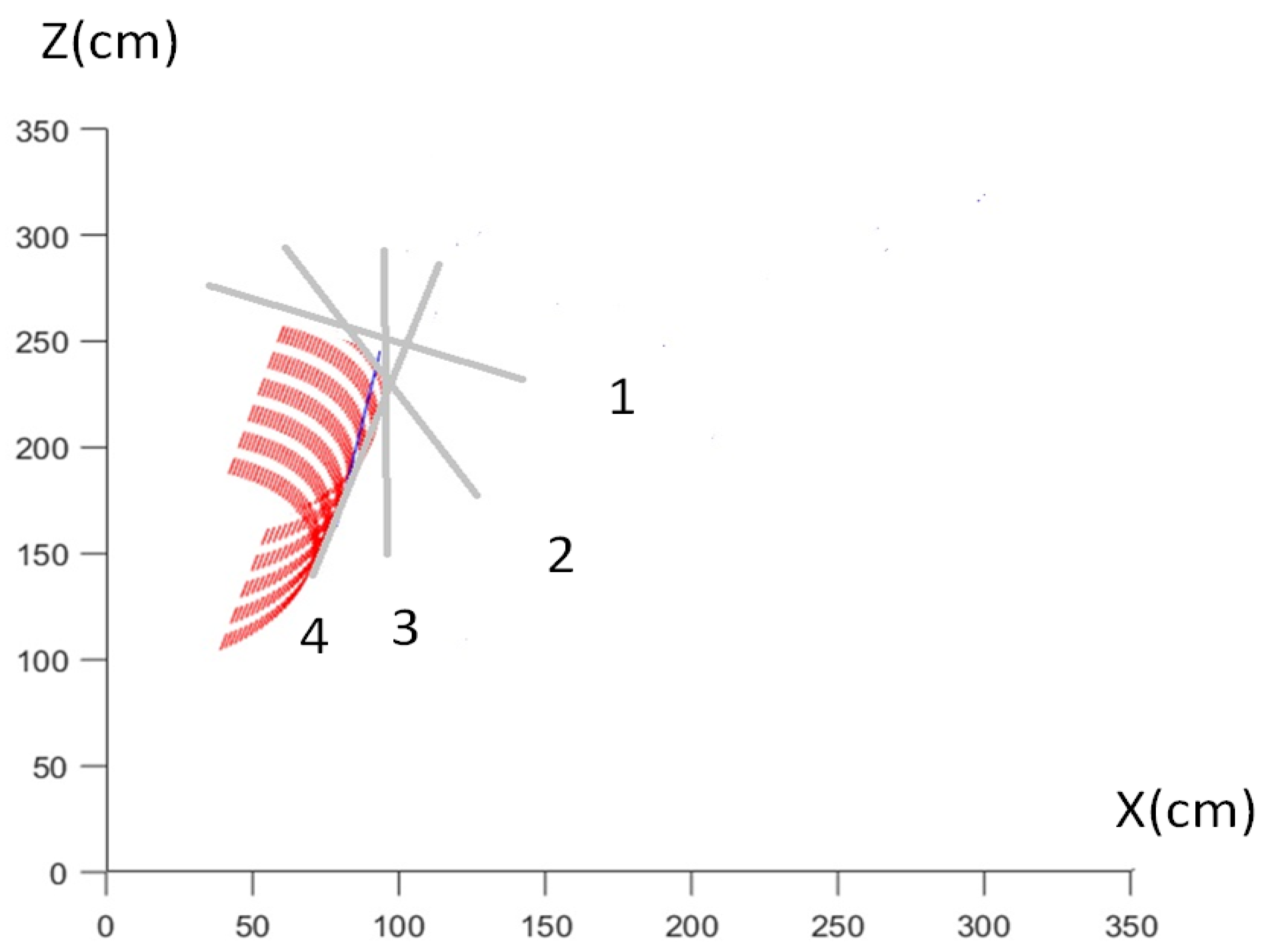
Figure 12 vividly illustrates the shaping dynamics of the golf swing through the lens of gathering and scattering, a movement quality reminiscent of Dell’s metaphor of molding space like a sculptor working with pliable material [30]. The progression from phase 1 to phase 4 in the downswing depicts how the golfer actively adapts and refines the club’s trajectory in response to evolving force vectors and spatial demands.

When considered alongside Figure 5, which presents the helicoidal velocity field generated by screw motion, the club’s longitudinal axis can be understood as enveloping a spiral path with a constant pitch—a screw-like trajectory that underlies the club’s translation and rotation throughout the swing. This helix not only defines the club’s motion in space but also affords the golfer a reference axis for coordinating hip rotation, enabling precise timing and energy transfer at the moment of impact, the most decisive point in the entire swing cycle.

Together, Figure 5 and Figure 12 metaphorically and mathematically converge: while one models the screw-theoretic underpinnings of the swing, the other visualizes its embodied expression. The result is a comprehensive representation of how spatial geometry, pitch invariance, and perceptual shaping coalesce to support efficient, high-performance movement in expert golfers.

This image can be interpreted using Turing’s machine framework by drawing an analogy between the golf club and the computational pencil, and the club’s inertia trajectories and the Turing machine’s tape. The gray lines represent the golf club’s orientation at different moments in the swing, analogous to the movement of a pencil recording computational states in Turing’s framework.

The red curves depict the trajectories of the club’s inertia, which can be seen as the tape on which the club inscribes movement patterns, much like a Turing machine writes states onto its tape. The numbered points (1–4) denote key transition states in the swing, corresponding to how a Turing machine updates its configuration iteratively based on previous inputs.

Just as a Turing machine follows deterministic rules to update symbols on a tape, the golfer’s swing is continuously refined by adjusting posture, force application, and rotational alignment in response to club inertia. This conceptualization aligns with the perception–action cycle in ecological psychology, where the club’s inertial cues serve as an external affordance that dynamically shapes movement execution. The instantaneous screw axes (ISA) represent how these affordances are perceived and acted upon, forming a structured sequence of computationally driven biomechanical adaptations.

Turing’s original framework conceptualized the human as a computer, using paper as a structured environment and a pencil as an agent of inscription. In the golf swing, the club functions analogously to the pencil, while the club’s trajectories represent the evolving computations inscribed onto the environment (the ball, ground, and air resistances). The golfer’s internal configurations—defined by postural alignments, instantaneous screw axes (ISA), and torque production—parallel the finite states of a Turing machine.

As the golfer moves through the X-scale sequence (X1–X11), each phase corresponds to a computational state transition where new affordances emerge and effectivities are executed. The golfer, like a Turing machine, follows an iterative process of reading environmental cues (e.g., ground reaction forces, club inertia) and adapting internal states based on movement constraints and affordances. This process can be formally described as a mapping of configurations (q, a) onto actions (b, p, k), where:

q represents the golfer’s internal biomechanical state (e.g., torque, balance, posture);

a represents external affordances (e.g., ball position, wind, ground slope);

b represents the movement behavior (e.g., backswing, downswing, follow-through);

p represents the updated functional state of the golfer;

k represents the trajectory of the swing.

This framing bridges biomechanics, perceptual psychology, and computational modeling, offering a novel way to analyze and enhance movement execution in sports training.

As the golfer progresses through the X-scale sequence (X1–X11), each phase represents a computational state transition, where new affordances emerge and effectivities are executed. This iterative adjustment process mirrors the Markov decision process (MDP), in which actions (movement behaviors) are sequentially optimized based on the Principle of Optimality in Dynamic Programming (DP) [37,43]. The golfer, much like a Turing machine solving a computational task, continuously reads environmental cues (e.g., ground reaction forces, club inertia) and updates internal states accordingly.

A crucial characteristic of Dynamic Programming (DP) is its backward induction process where optimal solutions are determined by first evaluating the end state and working backward to refine preceding steps [44]. This principle is directly observed in the backswing phase (X1 to X4) where the club moves backward, creating a structured sequence of movement refinements. DP solves problems recursively by considering the final goal (X4) first, ensuring that each preceding decision contributes optimally to the overall outcome.

Similarly, in golf swing mechanics, the optimal movement strategy is determined not just by the initial motion (X1) but by the biomechanical constraints and affordances at the peak of the backswing (X4). The golfer must account for the end goal (X4) first—where the club’s inertia, body torque, and balance are maximized—before refining the preceding movements (X3, X2, X1).

This characteristic of backward induction in DP is evident in expert golfers, who adjust their backswing trajectory dynamically to ensure an efficient transition into the downswing. By contrast, novice golfers often fail to optimize the backswing structure, leading to inefficient force application in subsequent phases.

Thus, the backswing follows a computationally structured process where each movement phase (X1 → X4) is optimized by considering the final goal (X4) first, mirroring the recursive nature of Bellman’s Dynamic Programming in solving complex, sequential decision-making tasks.

4. Discussion

4.1. Symmetry and Asymmetry in Skilled Manipulation

The comparison between proficient and novice golfers reveals that a pitch variation provides a concise and meaningful biomechanical signature of skilled performance. In the proficient swing, low pitch variability corresponds with a coherent screw motion and symmetrical force application. The close alignment of rotational and translational dynamics along the ISA reflects biomechanical efficiency.

In contrast, the novice golfer’s higher pitch variability and irregular GRF behavior highlight poor motor integration. Disruption in the coordination of joint torques and segmental motion results in unstable energy transfer and mechanical asymmetry.

These results support the utility of pitch as an invariant descriptor of motion coordination, grounded in screw theory. As a compact measure of the covariance between translation and rotation, pitch enables the evaluation of movement quality using physically interpretable principles. This approach may be extended beyond golf to any domain involving dynamic manipulation, offering a practical framework for assessing biomechanical performance in sport and rehabilitation contexts.

4.2. Nested Affordance Structures and Adaptive Motor Learning in Golf Swing Optimization

Motor learning in the golf swing can be further understood through the lens of Gibson’s ecological psychology, particularly his concept of recurrences and nesting of events. In Gibson’s ecological theory, movements are not isolated but embedded within a hierarchical structure of affordance-driven interactions, where lower-order movement adjustments contribute to higher-order skill refinement. This aligns with Bellman’s Dynamic Programming (DP) framework, in which movement optimization occurs through recursively solving subproblems that refine an overall control strategy.

In the case of golf swing optimization, expert golfers exhibit a nested structure of recurrent movement adaptations where each refinement builds upon previous affordance-based interactions. For example, the backswing (X1–X4) serves as a preparatory state, guiding the transition into downswing acceleration (X4–X7) and culminating in impact and follow-through (X8–X11). Novice golfers, by contrast, fail to establish these nested affordance–action sequences, leading to inefficient energy transfer and poor perception–action coupling.

This hierarchical structuring of movement recurrences resembles approximation in policy space, where motor learning progresses iteratively toward an optimal swing. The golfer’s adaptive control system updates its state transitions based on real-time computational refinement, similar to how Bellman’s DP refines decision-making by dynamically approximating an optimal policy over time. This perspective reinforces that expert motor control is not a rigidly preprogrammed sequence but an emergent, self-optimizing process, where movements evolve through layered, recurrent affordance interactions rather than discrete biomechanical corrections.

By integrating Gibson’s event nesting with Bellman’s DP framework, we present a unified perspective on skill acquisition, where recurrent perceptual-motor interactions drive adaptive refinement. This insight is particularly relevant for AI-driven sports training and reinforcement learning models where motor learning can be structured through progressive affordance tuning and computationally guided movement optimizations.

4.3. Contributions to Sports Science and Motor Learning Computational Model of Affordance-Based Action

We introduce Turing’s machine as a conceptual model for analyzing the sequential nature of motor learning in golf. The golf club acts as a computational instrument, inscribing motion trajectories onto the environment, analogous to Turing’s paper-and-pencil framework.

By aligning Laban’s X-scale with Turing’s state transitions, we provide a structured model of affordance perception and movement control. The club’s moment of inertia serves as an affordance, guiding the golfer’s execution through biomechanical effectivities.

Real-time motion tracking could leverage this framework, enabling AI-driven computational refinement systems that optimize affordance detection and action refinement.

VR and augmented reality (AR) could implement computational affordance-based training models where golfers interact with adaptive virtual environments that simulate Turing-like input–output cycles for skill acquisition.

5. Conclusions

We quantified affordance–effectivity dynamics in sports using machine learning models trained on Turing-inspired motion data and developed AI-enhanced training tools that incorporate real-time affordance perception and state-action reinforcement learning.

We also explored the role of virtual environments in refining affordance-based action for rehabilitation and motor skill acquisition. In conclusion, Turing’s machine theory provides a compelling computational framework for understanding motor learning. By extending Gibson’s affordance theory and Laban Movement Analysis, we present a novel paradigm for analyzing, coaching, and enhancing sports performance through computationally structured affordance detection and biomechanical adaptation.