Abstract
This study sought to deepen our understanding of the dynamical properties of the newly extended -dimensional integrable Kadomtsev–Petviashvili (KP) equation, which models the behavior of ion acoustic waves in plasmas and nonlinear optics. This paper aimed to perform Lie symmetry analysis and derive lump, breather, and soliton solutions using the extended hyperbolic function method and the generalized logistic equation method. It also analyzed the dynamical system using chaos detection techniques such as the Lyapunov exponent, return maps, and the fractal dimension. Initially, we focused on constructing lump and breather soliton solutions by employing Hirota’s bilinear method. Secondly, employing Lie symmetry analysis, symmetry generators were utilized to satisfy the Lie invariance conditions. This approach revealed a seven-dimensional Lie algebra for the extended -dimensional integrable KP equation, incorporating translational symmetry (including dilation or scaling) as well as translations in space and time, which were linked to the conservation of energy. The analysis demonstrated that this formed an optimal sub-algebraic system via similarity reductions. Subsequently, a wave transformation method was applied to reduce the governing system to ordinary differential equations, yielding a wide array of exact solitary wave solutions. The extended hyperbolic function method and the generalized logistic equation method were employed to solve the ordinary differential equations and explore closed-form analytical solitary wave solutions for the diffusive system under consideration. Among the results obtained were various soliton solutions. When plotting the results of all the solutions, we obtained bright, dark, kink, anti-kink, peak, and periodic wave structures. The outcomes are illustrated using 2D, 3D, and contour plots. Finally, upon introducing the perturbation term, the system’s behavior was analyzed using chaos detection techniques such as the Lyapunov exponent, return maps, and the fractal dimension. The results contribute to a deeper understanding of the dynamic properties of the extended KP equation in fluid mechanics.
1. Introduction
The investigation of nonlinear partial differential equations (NLPDEs) remains a dynamic and crucial area of research. Developing both analytical and numerical techniques to solve these equations poses significant challenges but is essential across numerous scientific disciplines. Nonlinear PDEs hold substantial value in various fields due to their ability to model a wide array of physical and natural processes exhibiting nonlinear characteristics. Their applications span across physics, engineering, biology, computer science, and image processing, among other areas [1,2,3]. These equations are used to describe complex phenomena such as fluid dynamics, theoretical quantum mechanics, thermal transfer, mechanical structures, electromagnetic radiation, electronic control systems, population dynamics, cardiac electrophysiology, disease transmission, artificial intelligence, and graphic design. Many reliable and successful techniques for tackling nonlinear partial differential equations have been established recently. These approaches include the multivariate generalized exponential rational integral function method [4], the generalized arnous approach [5], the ansatz method [6], the generalized logistic equation approach [7], the Hirota bilinear method [8], the extended hyperbolic function method [9], the Kumar–Malik method [10], and the Jacobi elliptic function method [11]. We emphasize that the Hirota bilinear method is a straightforward and effective approach in soliton theory, offering certain advantages over more complex techniques like the Inverse Scattering Transform [12] and the Darboux Transformation [13], which are commonly employed to derive families of exact solutions for nonlinear evolution equations. Lump and breather solutions derived via the Hirota bilinear method play a crucial role in capturing localized wave phenomena in nonlinear systems. Lump solutions model fully localized structures, while breather solutions represent oscillatory, quasi-periodic behaviors. These solutions have applications in fluid dynamics, plasma physics, and optical fiber communication.
The Kadomtsev–Petviashvili (KP) equation is typically expressed in the following standard form [14]:
The KP model, characterized by the nonlinear term and the weak dispersion term , is fundamental in fluid mechanics. The analysis of its soliton dynamics provides insights into wave structures and system behavior, making it a focus of extensive research on nonlinear wave theory and its applications [15,16,17].
A more recent development introduced an extended form of the KP equation [18]:
The extended KP equation includes the terms and , where is a smooth function and and are nonzero constants. This model describes surface and internal waves in channels. Though non-integrable, it admits analytic multi-soliton and mixed breather–soliton solutions [19].
An additional term, , has been incorporated into Equation (2), which introduces enhanced dispersion effects compared to those of the extended KP equation. Building on this formulation, a new integrable -dimensional KP-type equation has been proposed by adding the term to the MWL equation, which leads to the following expression:
Here, is a smooth function dependent on the spatial variables and and the time , while and are nonzero arbitrary constants. This equation extends the standard KP model in Equation (1) by incorporating four additional second-order derivatives, introducing new dispersive effects, especially in the and directions, when compared to Equation (4). In [20], the authors performed the Painlevé test and confirmed the integrability of Equation (4) under specific conditions of the parameters. Notably, the phase shift behavior of this model deviates from that of the classical KP equation, highlighting a unique wave structure. More recently, Li et al. [21] have proposed a novel (3 + 1)-dimensional integrable KP-type equation:
The temporal variable is denoted by , and the spatial variables are and . Equation (5) arises from fluid dynamics, nonlinear optics, plasma physics, and shallow water wave models. It extends the traditional KP equation by incorporating more spatial dimensions and higher-order effects, covering ion acoustic waves, pulse propagation in nonlinear optics, and capillary–gravity wave interactions. Its solutions reveal complex wave structures, such as rational and semi-rational solitons. Lingefei Li et al. [21] studied Equation (5), deriving N-soliton and O-type solitary solutions. Naila Nasreen [22] analyzed bifurcation and chaos in Equation (5) alongside soliton solutions using the Riccati equation method. In this work, we explored Lie point symmetries, group analysis, and certain interaction solutions of Equation (5) which have not been addressed in the literature. Additionally, we obtained soliton solutions using two distinct methods. Furthermore, we transformed the nonlinear ordinary differential equation into a dynamical system using Galilean transformation and analyzed chaotic behavior using Lyapunov exponent, return map, and the fractal dimension.
Lie symmetry analysis is a powerful tool for deriving exact solutions to complex NPDEs, offering a systematic approach widely discussed in textbooks and applied across engineering and physical sciences [23]. Jiwari et al. [24] analyzed a nonlinear regularized long-wave system using the Lie group method. Almusawa et al. [25] applied Lie symmetry analysis to investigate the microtubule equation. Kumar et al. [26] employed it to derive bright and dark soliton solutions within a nonlinear regularized long-wave framework.
Complex systems theory extends dynamical system analysis to models involving many variables. Unlike traditional approaches focused on few-variable systems, it is essential in fields like robotics, engineering, and science. For example, the trajectory modeling of human demonstrations and hybrid electric vehicle dynamics involve complex interactions requiring such a theory. This study explored the behavior of a perturbed nonlinear system representing physical phenomena. Chaos describes the sustained, non-repetitive behavior of nonlinear dynamical systems governed by deterministic rules [27]. Though seemingly random, such behavior arises from simple systems and is highly sensitive to the initial conditions, making long-term predictions extremely challenging. In continuous-time systems, chaos typically requires at least three nonlinear, independent variables. A system is considered chaotic if it responds unpredictably to slight changes in the initial states. Numerous methods exist to detect chaos, including the Lyapunov exponent, return maps, the fractal dimension, Poincaré maps, time series analysis, and phase portraits. These techniques effectively distinguish chaotic, quasi-periodic, and periodic dynamics in physical models. Naila Nasreen [22] conducted chaos analysis using time series analysis, phase portraits, and Poincaré maps. In the present study, we analyzed chaotic behavior using the Lyapunov exponent, return maps, and the fractal dimension.
The extended hyperbolic function method [9] is particularly advantageous due to its capacity to address a diverse array of nonlinear equations, yielding either exact or approximate solutions. Its inherent flexibility facilitates its application to intricate systems, including wave propagation phenomena, soliton equations, and reaction–diffusion frameworks. Furthermore, the method proves to be efficacious in the derivation of multi-soliton solutions, which hold significant relevance in the examination of nonlinear wave dynamics across disciplines such as fluid dynamics, plasma physics, and optics. Its proficiency in accurately modeling both periodic and solitary wave solutions underscores its utility in addressing practical challenges within the realm of nonlinear science. Additionally, the method demonstrates robustness in managing boundary conditions and can be adapted to accommodate systems characterized by various forms of nonlinearities, thereby augmenting its general applicability. Conversely, the generalized logistic equation method [7] presents numerous advantages, particularly due to its uncomplicated mathematical formulation, rendering it a cogent option for the resolution of nonlinear growth models. Its extensive applicability to real-world phenomena, such as population dynamics, epidemic modeling, and market saturation, is evident, as the behavior of solutions is frequently influenced by external constraints e.g., the carrying capacity. This methodology facilitates the straightforward examination of equilibrium points and stability, which is imperative for comprehending long-term dynamics across various systems. Its inherent simplicity and transparency render it a formidable instrument for both analytical and numerical analyses, affording us profound insights into the characteristics of solutions, particularly in systems that exhibit bistability or multistability. Furthermore, the generalized logistic equation proves advantageous for modeling processes characterized by thresholds and feedback mechanisms, which are prevalent in biological, ecological, and economic contexts.
This paper is structured as follows: Section 2 outlines the methodology. In Section 3, we analyze lump wave and breather solutions to assess their effectiveness. Section 4 presents the Lie point symmetry infinitesimals, while Section 5 details the similarity reduction process. The extended hyperbolic function technique and generalized logistic equation methodology are applied in Section 6, followed by the presentation of graphical representations in Section 7. Section 8 explores the chaotic behavior of the perturbed system. Finally, conclusions are provided in Section 9. Figure 1 presents a schematic diagram illustrating the structure of the article.
Figure 1.
A schematic representation illustrating the structural layout of this paper.
2. Synthesis of Methodologies
In this part, we summarize the key steps involved in the integrated schemes.
Stage 1: The process starts with the assumption of an NPDE expressed in the following form:
Stage 2: By applying the transformations and , we transform Equation (6) into the following ODE:
where generally represents the wave speed in solitary wave transformations, and represent spatial variables, and denotes the time variable, while the coefficients typically correspond to spatial scaling factors or wave propagation directions.
Stage 3: The following represents the initial solution for these approaches:
is the balancing number and represents stochastic constants that must be identified.
2.1. An Overview of the Extended Hyperbolic Function Method
The extended hyperbolic function method is discussed in detail in Ref. [9].
Stage 1a: The function used in this technique is derived from the following auxiliary equation:
Stage 1b: The balancing principle is employed to calculate . By substituting Equation (8) into Equation (7) and utilizing Equation (9), we derive a system of algebraic equations. Solving it yields the following set of solutions:
Family 1: When and ,
Family 2: When and ,
Family 3: When and ,
Family 4: When and ,
Family 5: When and ,
Family 6: When and ,
Family 7: When and ,
Family 8: When and ,
2.2. A Description of the Generalized Logistic Equation Methodology
The generalized logistic equation method is discussed in detail in Ref. [7].
Stage 2a: The function in this technique is derived from the following auxiliary equation:
Stage 2b: To find , we use the balancing principle. Substituting Equation (8) into Equation (7) and then using Equation (9) produces a system of algebraic equations, which, when solved, provides the following set of solutions:
3. Hirota’s Bilinear Approach
In this section, we present the breather and lump wave solutions to Equation (5). To do so, we first transform Equation (5) into its bilinear form. Considering the transformation
Equation (5) can be converted into the corresponding bilinear form as follows:
As a result, the Hirota bilinear form of Equation (5) is expressed as:
In this case, D stands for the Hirota bilinear operator, which is defined as
The variables , and are considered to be positive integers in this case:
Set 1:
Substituting the values from Equation (16) into Equation (25), we obtain
Substituting Equation (17) into Equation (12), we obtain the following solution to Equation (5):
Set 2:
Substituting the values from Equation (19) into Equation (25), we obtain
Substituting Equation (20) into Equation (12), we obtain the following solution to Equation (5):
Set 3:
Substitutingthe values from Equation (22) into Equation (25), we obtain
Substituting Equation (23) into Equation (12), we obtain the following solution to Equation (5):
3.1. Lump Solitons of Equation (5)
To explore the quadratic function solutions of the (3 + 1)-dimensional integrable KP equation given in Equation (5), we start with [28]
where , , and (; ) are free parameters to be determined later. We substitute Equation (25) into Equation (13) and collect the coefficients of various polynomial terms, including , , , , , , , , , , , , , , and their combinations. By solving the resulting system of equations, we obtain the following solution.
3.2. Breather Wave Solutions of Equation (5)
To construct the breather wave solutions of Equation (5), we consider the following test function as a solution for the bilinear equation Equation (13):
where , and are arbitrary constants. Substituting Equation (32) into Equation (13) and equating all the coefficients of , , and as equal to zero, we obtain a set of algebraic equations. By solving this system, we derive the following sets of solutions:
4. Lie Group Analysis Applied to Equation (5)
To derive the symmetries for Equation (5), consider the following one-parameter Lie group of transformations [29]:
where , and represent infinitesimals, which are also functions of . The corresponding infinitesimal generator for Equation (37) is given by [30]:
and the associated fourth-order prolongation formula is expressed as:
As per the invariance criteria, Equation (5) must meet the specified condition:
Applying the fourth prolongation to Equation (5) results in the following Lie point symmetries:
Theorem 1.
The seven-dimensional Lie algebra in Equation (5) is formed by seven generators.
Proof.
By incorporating Theorem 1, the corresponding five ordinary differential equations, and the initial conditions,
Utilizing , we obtain specific one-parameter groups,
As If is a solution to Equation (5), then another solution can be given by
□
Theorem 2.
Equation (5) represents a seven-dimensional commutative algebra.
Proof.
According to the definition of the Lie bracket, , the commutators are given by
Other commutator relations are zero. Equation (44) confirms the anti-symmetric nature of the structure with zero diagonal elements. The commutator table allows for the easy analysis of the structure constants and the verification of Jacobi’s identity. □
5. Reduction Techniques and Precise Solutions
In this section, we apply reduction techniques to convert the PDE into an ODE using each symmetry and their combinations.
5.1. Reduction via Translation Symmetry:
The characteristic equation corresponding to takes the following form:
Solving the characteristic Equation (45) yields the following defined variables:
Here, , , , and represent the similarity variables of Equation (5). Substituting the similarity variables from Equation (46) into Equation (5) results in the following reduced form of a (2 + 1)-dimensional NPDE:
Applying the similarity transformation method (STM) to Equation (47) yields the following new set of Lie point symmetries:
For , the characteristic equation is expressed as follows:
The defined variables are obtained by solving the characteristic Equation (49):
Here, , , and represent the similarity variables of Equation (48). Substituting the similarity variables from Equation (50) into Equation (47) results in the following reduced form of a (1 + 1)-dimensional NPDE:
The solution for Equation (5) is derived as follows:
5.2. Translation Symmetry-Based Reduction:
The following form represents the characteristic equation for :
From the solution of the characteristic Equation (45), the following variables are determined:
Here, , , , and represent the similarity variables of Equation (5). Substituting the similarity variables from Equation (54) into Equation (5) results in the following reduced form of a (2 + 1)-dimensional NPDE [31]:
Applying the STM to Equation (47) yields the following new set of Lie point symmetries:
For , the characteristic equation is expressed as follows:
The defined variables are obtained by solving the characteristic Equation (57):
Here, , , and represent the similarity variables of Equation (58). Substituting the similarity variables from Equation (58) into Equation (55) results in the following reduced form of a (1 + 1)-dimensional NPDE:
5.3. Applying Translation Symmetry Reduction:
The characteristic equation related to the generator takes the form
From the solution of the characteristic Equation (60), the following variables are determined:
The similarity variables of Equation (5) are , , , and . By applying the similarity variables from Equation (61) to Equation (5), we obtain the following -dimensional reduced form [32]:
The Lie point symmetries of Equation (62) are
The characteristic equation corresponding to is
The similarity variables of Equation (5) are , , and . By applying the similarity variables from Equation (64) to Equation (62), we obtain the following -dimensional reduced form:
5.4. Applying Translation Symmetry Reduction:
The characteristic equation related to the generator takes the form
From the solution of the characteristic Equation (66), the following variables are determined:
The similarity variables of Equation (5) are , , , and . By applying the similarity variables from Equation (67) to Equation (5), we obtain the following -dimensional reduced form:
5.5. Applying Translation Symmetry Reduction:
The characteristic equation related to the generator takes the form
From the solution of the characteristic Equation (69), the following variables are determined:
The similarity variables of Equation (5) are , , , and . By applying the similarity variables from Equation (70) to Equation (5), we obtain the following -dimensional reduced form:
5.6. Applying Translation Symmetry Reduction:
The characteristic equation related to the generator takes the form
From the solution of the characteristic Equation (72), the following variables are determined:
The similarity variables of Equation (5) are , , , and . By applying the similarity variables from Equation (73) to Equation (5), we obtain the following -dimensional reduced form:
5.7. Symmetry-Based Reduction via Transformation
The characteristic equation corresponding to is given by
with its solution yielding
Applying the similarity variables from Equation (87) to Equation (5) allows for the derivation of its reduced form:
This represents an alternative 3-dimensional reduction of the (2 + 1)-dimensional governing equation.
5.8. Reduction Through a Combination of Translational Symmetries,
The form of the characteristic equation associated with is
and the obtained solution gives
By introducing the similarity variables defined in Equation (79) into Equation (5), the corresponding reduced form can be obtained:
It also serves as another 3D reduced version of the (2 + 1)-dimensional governing equation.
5.9. Applying Symmetry for System Reduction
The characteristic equation derived from takes the following structure:
and the corresponding solution gives
Substituting the similarity variables from Equation (82) into Equation (5) yields its reduced representation:
This provides another possible 3D reduced representation of the (2 + 1)-dimensional governing equation.
5.10. Reduction Through Merging Translational Asymmetries
5.11. Utilizing for Symmetric System Reduction
5.12. Transformation-Induced Reduction Using Symmetries
The characteristic equation related to follows this form:
whose solution results in
Through the application of similarity variables from Equation (96) to Equation (5), it can be rewritten in its reduced form:
This constitutes an additional 3-dimensional reduced form of the (2 + 1)-dimensional governing equation.
5.13. Reduction via a Combination of Translation Symmetries:
6. Solitary Wave Solutions of Equation (5)
In this section, we investigate the solitary wave solutions of Equation (5) using the extended hyperbolic function technique and the generalized logistic equation approach. Let us introduce the following transformation:
In Equation (96), generally represents the wave speed in solitary wave transformations, while the coefficients and typically correspond to spatial scaling factors or wave propagation directions. Inserting Equation (96) into Equation (5) results in the following ODE:
Performing two successive integrations on Equation (97) results in
The index is found by comparing the highest-order nonlinear term and the highest-order linear term in Equation (98), leading to . Our next objective is to compute the soliton solutions for Equation (98).
6.1. The Implementation of the Extended Hyperbolic Function Technique
This section is dedicated to applying the extended hyperbolic function technique for obtaining analytical solutions. The initial solution in this scenario is
By inserting Equations (99) and (9) into Equation (98) and solving for , and , the resulting solution is as follows.
After inserting the aforementioned values into Equation (99), the solutions for Equation (5) are derived as follows:
Family 1: When and ,
Family 2: When and ,
Family 3: When and ,
Family 4: When and ,
Family 5: When and ,
Family 6: When and ,
Family 7: When and ,
6.2. The Adoption of the Generalized Logistic Equation Approach
7. The Visual Interpretation of the Solutions
Graphical representation plays a vital role in comprehending the dynamics of physical systems and assessing the influence of various parameters. In this study, we examined specific solutions of Equation (5) to gain deeper insights into its behavior. This section presents the graphical interpretation of lump, breather, and other solutions derived using the extended hyperbolic function method and the generalized logistic equation method for Equation (5). By visualizing these solutions in different planes, we examine their properties and significance, emphasizing their broad relevance across multiple scientific disciplines. The solutions are illustrated using 3D, 2D, and contour plots generated in Mathematica. While 3D visualizations provide a holistic perspective by depicting the solution in three dimensions, 2D graphs allow for a more detailed analysis of particular cross-sections or projections. Such visual tools are widely utilized for exploring PDE solutions, offering a clearer understanding of their properties and behavior. Depending on the equation’s complexity and the solution’s characteristics, one or both visualization methods may be employed to enhance the analysis. First, I will examine the interaction solutions of Equation (5) using various methods regarding its bilinear form.
- The lump–periodic soliton characterized by the parameters , , , and is shown for various values of within the domain in Figure 2.
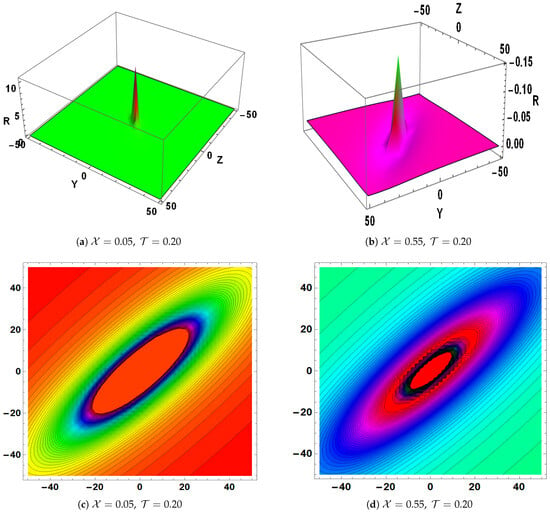 Figure 2. Visualization of the lump–periodic soliton , as defined in Equation (28).
Figure 2. Visualization of the lump–periodic soliton , as defined in Equation (28). - The lump–periodic soliton characterized by the parameters , , , and is shown for various values of and within the domain in Figure 3.
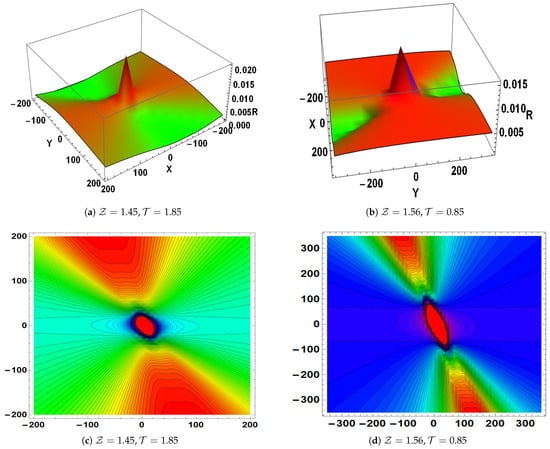 Figure 3. Visualization of the lump–periodic soliton , as defined in Equation (31).
Figure 3. Visualization of the lump–periodic soliton , as defined in Equation (31). - The breather soliton characterized by the parameters , , , and is shown for various values of and within the domain in Figure 4.
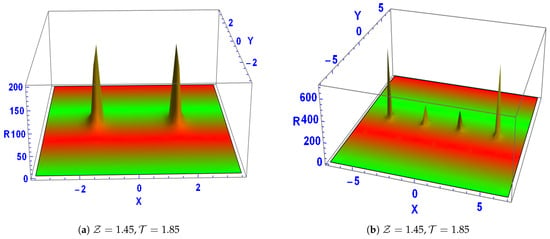
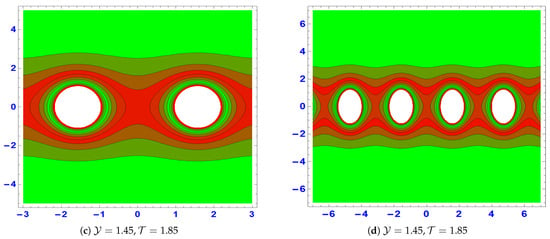 Figure 4. The breather soliton solution for Equation (34).
Figure 4. The breather soliton solution for Equation (34). - The breather soliton characterized by the parameters , , , and is shown for various values of and within the domain in Figure 5.
 Figure 5. The breather soliton solution for Equation (36).
Figure 5. The breather soliton solution for Equation (36). - In the study of PDEs, especially in nonlinear wave dynamics, lump and breather solutions are important. Lump solutions are important for modeling stable, non-dispersive waveforms in fluid dynamics, plasma physics, and optical fiber communications because they are localized, logically decaying structures that explain solitonic behaviors without singularities. Conversely, breather solutions are essential for characterizing wave propagation in nonlinear lattices, Bose–Einstein condensates, and mechanical systems because they describe periodic or localized oscillatory waves with concentrated energy. They can be used to comprehend nonlinear interactions in complicated media, create rogue waves, and create optical solitons.
Secondly, we analyze the visual representation of the solutions obtained using the extended hyperbolic function method.
- Figure 6: This graph illustrates that the proposed model exhibits a trigonometric solution, as described by Equation (101). When the parameters are set to , , , , , and , with a positive wave speed of 3, the solution forms a family of periodic singular solitons as shown in Figure 6a–c. The solution is defined over the domain . When modeling intricate wave patterns in nonlinear systems, periodic singular solitons are essential because they provide information on stability transitions and bifurcations. They are useful in fields where the comprehension of wave behavior is crucial, such as fluid dynamics, plasma physics, and optical fiber communications. These solitons aid in the mathematical study of partial differential equations’ compatibility, chaos, and multistability. In many branches of science and technology, the evaluation of them aids in the prediction and management of nonlinear wave occurrences [33,34].
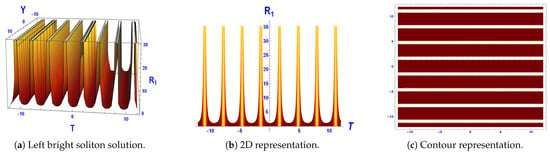 Figure 6. Visual representations of the solution for , as detailed in Equation (101).
Figure 6. Visual representations of the solution for , as detailed in Equation (101). - Figure 7: This plot illustrates that the model possesses a hyperbolic solution, as given by Equation (102). With the parameter values of , , , , , and and a wave speed of 2, a leftward-moving bright soliton solution emerges within the domain , as shown in Figure 7a–c. If the wave speed is changed to −2, the bright soliton reverses direction, moving rightward instead as shown in Figure 7d–f. Moreover, as the domain range expands, the bright soliton transitions into a singular soliton solution. Bright soliton solutions that move left and right are essential for comprehending the transmission of waves and energy transport in nonlinear media. They are extensively used in the study of fluid dynamics, plasma waves, and optical fiber interactions, where directional wave movement affects interactions and stability. Signal processing and information transfer in optical and quantum systems depend on the capacity to control the soliton direction by varying the wave speed. Furthermore, their domain expansion-induced transition into single solitons provides insights into turbulence, rogue waves, and wave collapse [35,36].
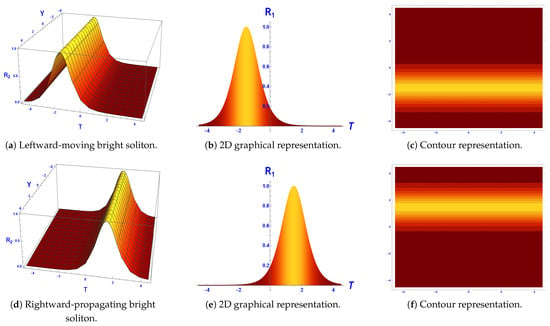 Figure 7. Illustrations of the solution for , as described in Equation (102).
Figure 7. Illustrations of the solution for , as described in Equation (102).
Lastly, we analyze the visual representation of the solutions obtained using the generalized logistic equation method.
- Figure 7: This graph illustrates that the model possesses an exponential solution, as given by Equation (110). With the parameter values of , , , , , , , and and a wave speed of 1.23, a kink soliton solution emerges within the domain , as shown in Figure 8a–c. If the wave speed is changed to −1.23, the anti-kink soliton reverses direction, moving rightward instead as shown in Figure 8d–f. The phase shifts, domain borders, and energy transfer in nonlinear systems—especially in condensed matter physics and field theory—are all described by kink soliton solutions. In fields like optical fibers and plasma physics, where information transfer depends on steady wave propagation, they are essential. In complicated nonlinear media, anti-kink brilliant soliton solutions aid in the analysis of stability, collision dynamics, and wave collisions. They are used to describe shock waves, brain impulses, and early universe structures in cosmological theory, organisms, and fluid motion.
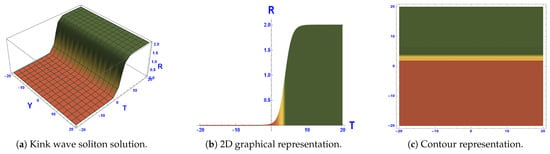
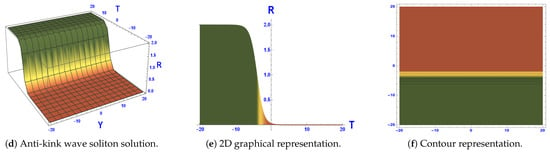 Figure 8. Solution of , as outlined in Equation (110).
Figure 8. Solution of , as outlined in Equation (110).
We now compare our results with those of Naila Nasreen et al. [22], who obtained solutions for Equation (14) using the Riccati equation method. Nasreen et al. [22] presented only two types of wave solutions, namely bright and dark solitons, by considering different wave speeds. Our approach yields a broader class of exact solutions, including kink, anti-kink, lump, periodic, bright, and dark wave solutions, among others. The extended solution set offers greater flexibility for modeling complex nonlinear wave behaviors in real-world systems.
8. Chaotic Behavior
This section employs perturbed terms to explore the chaotic behavior of the resulting dynamical system [37]. The use of dynamical analysis to investigate chaotic behavior using return maps, the fractal dimension, the power spectrum, and the Lyapunov exponent has not been explored in the existing literature. The system under consideration is obtained from Equation (98) by substituting :
We incorporate the perturbation term into the planar dynamical system (111), leading to the following perturbed formulation [38]:
The perturbed phase of the aforementioned system (112) is governed by the parameters and , representing the amplitude and frequency of the external force, respectively. The influence of such external forces can lead to irregular and chaotic dynamics within the system. We now turn our attention to the tools used for identifying chaotic behavior. Nasreen et al. [22] investigated chaotic behavior using 2D phase portraits, 3D phase portraits, time series analysis, and Poincare maps.
8.1. Lyapunov Exponent
Lyapunov exponents quantitatively evaluate the mean rates of divergence or convergence among proximate trajectories. A positive maximum Lyapunov exponent serves as a robust indicator of chaotic behavior, illustrating the system’s sensitivity to the initial conditions. The concept of Lyapunov exponents was introduced by Aleksandr Lyapunov in the 19th century as a means to characterize the stability of dynamical systems [39]. In the present analysis, we calculated the Lyapunov exponents for system (112) using the Wolf algorithm, which relies on Gram–Schmidt orthogonalization. The chaotic behavior of system (112) was validated using the Lyapunov exponent with the parameters , , , , , , , , and under different initial conditions, as illustrated in Figure 9. As shown in Figure 9a, the computed Lyapunov exponents , , and for the initial condition confirm the presence of chaotic behavior in the system. Similarly, Figure 9b shows the Lyapunov exponents , , and for the initial condition , again indicating chaotic dynamics.
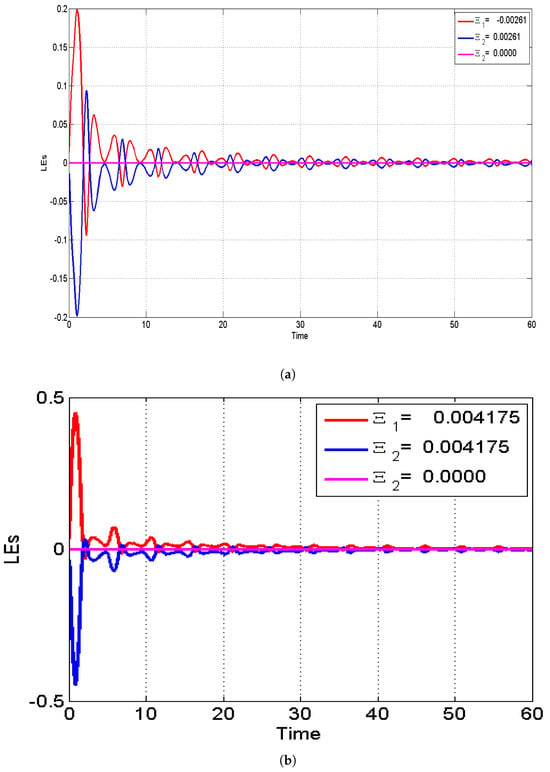
Figure 9.
The chaotic behavior of system (112) was validated using the Lyapunov exponent with the parameters , , , , , , , , and for the initial conditions (a) and (b) .
8.2. Return Maps
Return maps serve as a fundamental approach for analyzing the behavior of dynamical systems influenced by time delays. Figure 10 presents the return maps of system (112) under various delay conditions [40]. In these plots, the horizontal axis corresponds to , while the vertical axis represents , where denotes a small time shift or decay. This technique is instrumental in uncovering underlying structures such as fixed points, limit cycles, or strange attractors. Figure 10 shows the return maps for varying values of the bump function and the emergence and evolution of chaotic behavior. The plot for has irregular loops and scattered points, which indicate low-dimensional chaos, as shown in Figure 10a. It appears that the structure became denser and more intricate for , implying greater or higher-dimensional chaos, as shown in Figure 10b. This confirms that a fixed parameter system becomes more sensitive and complex with an increase in .
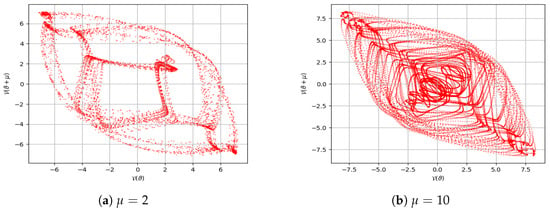
Figure 10.
The chaotic behavior of system (112) was validated through return map analysis using the parameters , , , , , , , , and .
8.3. Fractal Dimension
The fractal dimension quantitatively characterizes the geometric intricacy of an attractor. It assesses how the granularity of the system’s phase space scales with the resolution, thereby effectively differentiating between linear and chaotic dynamics [40,41]. The fractal dimension was approximately 0.26, indicating a low-dimensional attractor, as shown in Figure 11. This non-integer value confirms the presence of fractal geometry in the system. System (112) likely exhibits weak chaos or intermittent behavior.
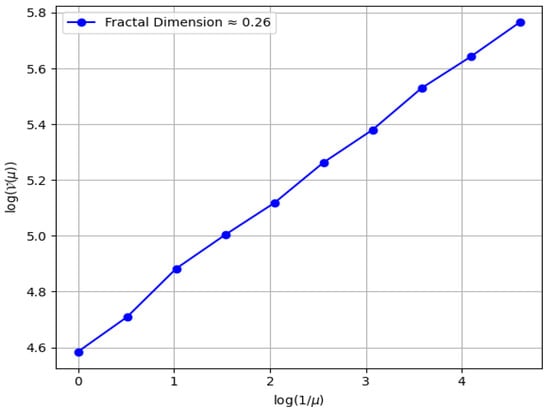
Figure 11.
The chaotic behavior of the system was validated through fractal dimension analysis using the parameters , , , , , , , , and .
9. Conclusions
This study investigated the qualitative dynamics of and derived novel soliton solutions for the newly extended -dimensional integrable KP equation. Initially, we analyzed the bilinear form of Equation (5) using Hirota’s bilinear method, through which lump and breather solutions for Equation (5) were obtained. This comprehensive approach offered significant insights into the complex behaviors of the extended -dimensional integrable KP model, particularly regarding the influence of the dispersion parameters, as shown in Figure 2, Figure 3, Figure 4 and Figure 5. The identification of various solitary wave structures and their interactions deepened our understanding of nonlinear wave propagation. Subsequently, the analysis utilized Lie symmetry reduction, the optimal system method, the extended hyperbolic function method, and the generalized logistic equation method to construct the Lie algebra and identify an optimal system of sub-algebras. The extended -dimensional integrable KP equation admitted translational and scaling symmetries linked to energy conservation. A broad class of exact solitary wave solutions was derived using the extended hyperbolic function method and the generalized logistic equation method, enriching the spectrum of soliton solutions. The propagation of solitary waves was shown to be influenced by the soliton wave number. To interpret the graphical representation of wave propagation phenomena, appropriate values for the free parameters were selected based on the computed analytical solutions. Our approach yielded a broader class of exact solutions, including kink, anti-kink, lump, periodic, bright, and dark wave solutions, among others, as shown in Figure 6, Figure 7 and Figure 8. The results contribute to a deeper understanding of the dynamic properties of the extended KP equation in the context of fluid mechanics. Thirdly, the planar dynamical structure of the given equation was developed via a Galilean transformation. Using the method, we also computed trajectories exhibiting chaotic behavior, as illustrated in Figure 9 and Figure 10, through the analysis of Lyapunov exponents, return maps, and the fractal dimension. Future research may delve into conservation laws using different techniques, neural network-based approaches, fractional derivatives, and other analytical techniques for investigating soliton solutions.
Author Contributions
Conceptualization, B. and M.S.; methodology, B. and M.S.; validation, B., M.S. and F.S.A.; formal analysis, B. and M.S.; investigation, M.S., B. and F.S.A.; writing—original draft, B. and M.S.; writing—review and editing, F.S.A.; supervision, M.S.; funding acquisition, F.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2503).
Data Availability Statement
The data are contained within the article.
Acknowledgments
Fehaid Salem Alshammari is grateful for the financial support provided by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2503).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KP | Kadomtsev–Petviashvili |
| NLPDEs | Nonlinear partial differential equations |
References
- Treves, F. Applications of distributions to PDE theory. Am. Math. Mon. 1970, 77, 241–248. [Google Scholar] [CrossRef]
- Kazdan, J.L. Applications of partial differential equations to problems in geometry. Grad. Texts Math. 1983. Available online: https://www2.math.upenn.edu/~kazdan/japan/japan.pdf (accessed on 28 April 2025).
- Faridi, W.A.; Bakar, M.A.; Akgül, A.; Abd El-Rahman, M.; El Din, S.M. Exact fractional soliton solutions of thin-film ferroelectric material equation by analytical approaches. Alex. Eng. J. 2023, 78, 483–497. [Google Scholar] [CrossRef]
- Niwas, M.; Kumar, S.; Rajput, R.; Chadha, D. Exploring localized waves and different dynamics of solitons in (2+1)-dimensional Hirota bilinear equation: A multivariate generalized exponential rational integral function approach. Nonlinear Dyn. 2024, 112, 9431–9444. [Google Scholar] [CrossRef]
- Younas, U.; Hussain, E.; Muhammad, J.; Sharaf, M.; Meligy, M.E. Chaotic Structure, Sensitivity Analysis and Dynamics of Solitons to the Nonlinear Fractional Longitudinal Wave Equation. Int. J. Theor. Phys. 2025, 64, 42. [Google Scholar] [CrossRef]
- Dong, S.H. A new approach to the relativistic Schrödinger equation with central potential: Ansatz method. Int. J. Theor. Phys. 2001, 40, 559–567. [Google Scholar] [CrossRef]
- Riaz, M.B.; Jhangeer, A.; Martinovic, J.; Kazmi, S.S. Bifurcation and chaos: Unraveling soliton solutions in a couple fractional-order nonlinear evolution equation. Nonlinear Eng. 2024, 13, 20240024. [Google Scholar] [CrossRef]
- Hirota, R. Direct methods in soliton theory. In Solitons; Springer: Berlin/Heidelberg, Germany, 1980; pp. 157–176. [Google Scholar]
- Shang, Y.; Huang, Y.; Yuan, W. The extended hyperbolic functions method and new exact solutions to the Zakharov equations. Appl. Math. Comput. 2008, 200, 110–122. [Google Scholar] [CrossRef]
- Farooq, K.; Hussain, E.; Younas, U.; Mukalazi, H.; Khalaf, T.M.; Mutlib, A.; Shah, S.A.A. Exploring the wave’s structures to the nonlinear coupled system arising in surface geometry. Sci. Rep. 2025, 15, 11624. [Google Scholar] [CrossRef]
- Sait, A.; Altunay, R. Abundant travelling wave solutions of (3 + 1) dimensional Boussinesq equation with dual dispersion. Rev. Mex. Física E 2022, 19, 0202031. [Google Scholar]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991; Volume 149. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer Series in Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Liu, J.G.; Yang, X.J.; Feng, Y.Y. Characteristic of the algebraic solitary wave solutions for two extended (2 + 1)-dimensional Kadomtsev–Petviashvili equations. Mod. Phys. Lett. A 2020, 35, 2050028. [Google Scholar] [CrossRef]
- Xu, Y.; Zheng, X.; Xin, J. New explicit and exact solitary wave solutions of (3 + 1)-dimensional KP equation. Math. Found. Comput. 2021, 4, 105–115. [Google Scholar] [CrossRef]
- Liu, J.G.; Yang, X.J.; Feng, Y.Y.; Cui, P. Nonlinear dynamic behaviors of the generalized (3 + 1)-dimensional KP equation. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. 2022, 102, e202000168. [Google Scholar] [CrossRef]
- Ozisik, M.; Secer, A.; Bayram, M.; Yusuf, A.; Sulaiman, T.A. Soliton solutions of the (2 + 1)-dimensional Kadomtsev–Petviashvili equation via two different integration schemes. Int. J. Mod. Phys. B 2023, 37, 2350212. [Google Scholar] [CrossRef]
- Manukure, S.; Zhou, Y.; Ma, W.X. Lump solutions to a (2 + 1)-dimensional extended KP equation. Comput. Math. Appl. 2018, 75, 2414–2419. [Google Scholar] [CrossRef]
- Guo, J.; He, J.; Li, M.; Mihalache, D. Exact solutions with elastic interactions for the (2 + 1)-dimensional extended Kadomtsev–Petviashvili equation. Nonlinear Dyn. 2020, 101, 2413–2422. [Google Scholar] [CrossRef]
- Ma, Y.L.; Wazwaz, A.M.; Li, B.Q. New extended Kadomtsev–Petviashvili equation: Multiple soliton solutions, breather, lump and interaction solutions. Nonlinear Dyn. 2021, 104, 1581–1594. [Google Scholar] [CrossRef]
- Li, L.; Yan, Y.; Xie, Y. Dynamical analysis of rational and semi-rational solution for a new extended (3 + 1)-dimensional Kadomtsev-Petviashvili equation. Math. Methods Appl. Sci. 2023, 46, 1772–1788. [Google Scholar] [CrossRef]
- Nasreen, N.; Yadav, A.; Malik, S.; Hussain, E.; Alsubaie, A.S.; Alsharif, F. Phase trajectories, chaotic behavior, and solitary wave solutions for (3 + 1)-dimensional integrable Kadomtsev–Petviashvili equation in fluid dynamics. Chaos Solitons Fractals 2024, 188, 115588. [Google Scholar] [CrossRef]
- Luo, A.C.; Gazizov, R.K. Symmetries and Applications of Differential Equations; Springer: Singapore, 2021. [Google Scholar]
- Jiwari, R.; Kumar, V.; Karan, R.; Alshomrani, A.S. Haar wavelet quasilinearization approach for MHD Falkner–Skan flow over permeable wall via Lie group method. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 1332–1350. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Kumar, S.; Jiwari, R.; Mittal, R.C.; Awrejcewicz, J. Dark and bright soliton solutions and computational modeling of nonlinear regularized long wave model. Nonlinear Dyn. 2021, 104, 661–682. [Google Scholar] [CrossRef]
- Baker, G.L.; Gollub, J.P. Chaotic Dynamics: An Introduction; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- El-Shorbagy, M.A.; Akram, S.; ur Rahman, M. Investigation of lump, breather and multi solitonic wave solutions to fractional nonlinear dynamical model with stability analysis. Partial Differ. Equ. Appl. Math. 2024, 12, 100955. [Google Scholar] [CrossRef]
- Jafari, M.; Zaeim, A.; Gandom, M. On similarity reductions and conservation laws of the two non-linearity term Benjamin-Bona-Mahoney equation. J. Math. Ext. 2023, 17, 1–22. [Google Scholar]
- Jafari, M.; Mahdion, S.; Akgül, A.; Eldin, S.M. New conservation laws of the Boussinesq and generalized Kadomtsev–Petviashvili equations via homotopy operator. Results Phys. 2023, 47, 106369. [Google Scholar] [CrossRef]
- Jafari, M.; Zaeim, A.; Tanhaeivash, A. Symmetry group analysis and conservation laws of the potential modified KdV equation using the scaling method. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250098. [Google Scholar] [CrossRef]
- Jafari, M.; Mahdion, S. Non-classical symmetry and new exact solutions of the Kudryashov-Sinelshchikov and modified KdV-ZK equations. AUT J. Math. Comput. 2023, 4, 195–203. [Google Scholar]
- Li, B.; Liang, H.; He, Q. Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos Solitons Fractals 2021, 146, 110856. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, X.; He, Q. Multi-scale systemic risk and spillover networks of commodity markets in the bullish and bearish regimes. N. Am. J. Econ. Financ. 2022, 62, 101766. [Google Scholar] [CrossRef]
- Zhu, X.; Xia, P.; He, Q.; Ni, Z.; Ni, L. Coke price prediction approach based on dense GRU and opposition-based learning salp swarm algorithm. Int. J. Bio-Inspired Comput. 2023, 21, 106–121. [Google Scholar] [CrossRef]
- Eskandari, Z.; Avazzadeh, Z.; Khoshsiar Ghaziani, R.; Li, B. Dynamics and bifurcations of a discrete-time Lotka–Volterra model using nonstandard finite difference discretization method. Math. Methods Appl. Sci. 2022, 48, 7197–7212. [Google Scholar] [CrossRef]
- Mahmood, T.; Alhawael, G.; Akram, S.; ur Rahman, M. Exploring the Lie symmetries, conservation laws, bifurcation analysis and dynamical waveform patterns of diverse exact solution to the Klein–Gordan equation. Opt. Quantum Electron. 2024, 56, 1978. [Google Scholar] [CrossRef]
- Muhammad, J.; Younas, U.; Hussain, E.; Ali, Q.; Sediqmal, M.; Kedzia, K.; Jan, A.Z. Solitary wave solutions and sensitivity analysis to the space-time β-fractional Pochhammer–Chree equation in elastic medium. Sci. Rep. 2024, 14, 28383. [Google Scholar] [CrossRef] [PubMed]
- Barreira, L. Lyapunov Exponents; Springer International Publishing: Cham, Switzerland, 2017; Volume 1002. [Google Scholar]
- Almheidat, M.; Alqudah, M.; Alderremy, A.A.; Elamin, M.; Mahmoud, E.E.; Ahmad, S. Lie-bäcklund symmetry, soliton solutions, chaotic structure and its characteristics of the extended (3 + 1) dimensional Kairat-II model. Nonlinear Dyn. 2025, 113, 2635–2651. [Google Scholar] [CrossRef]
- Theiler, J. Estimating fractal dimension. J. Opt. Soc. Am. A 1990, 7, 1055–1073. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).