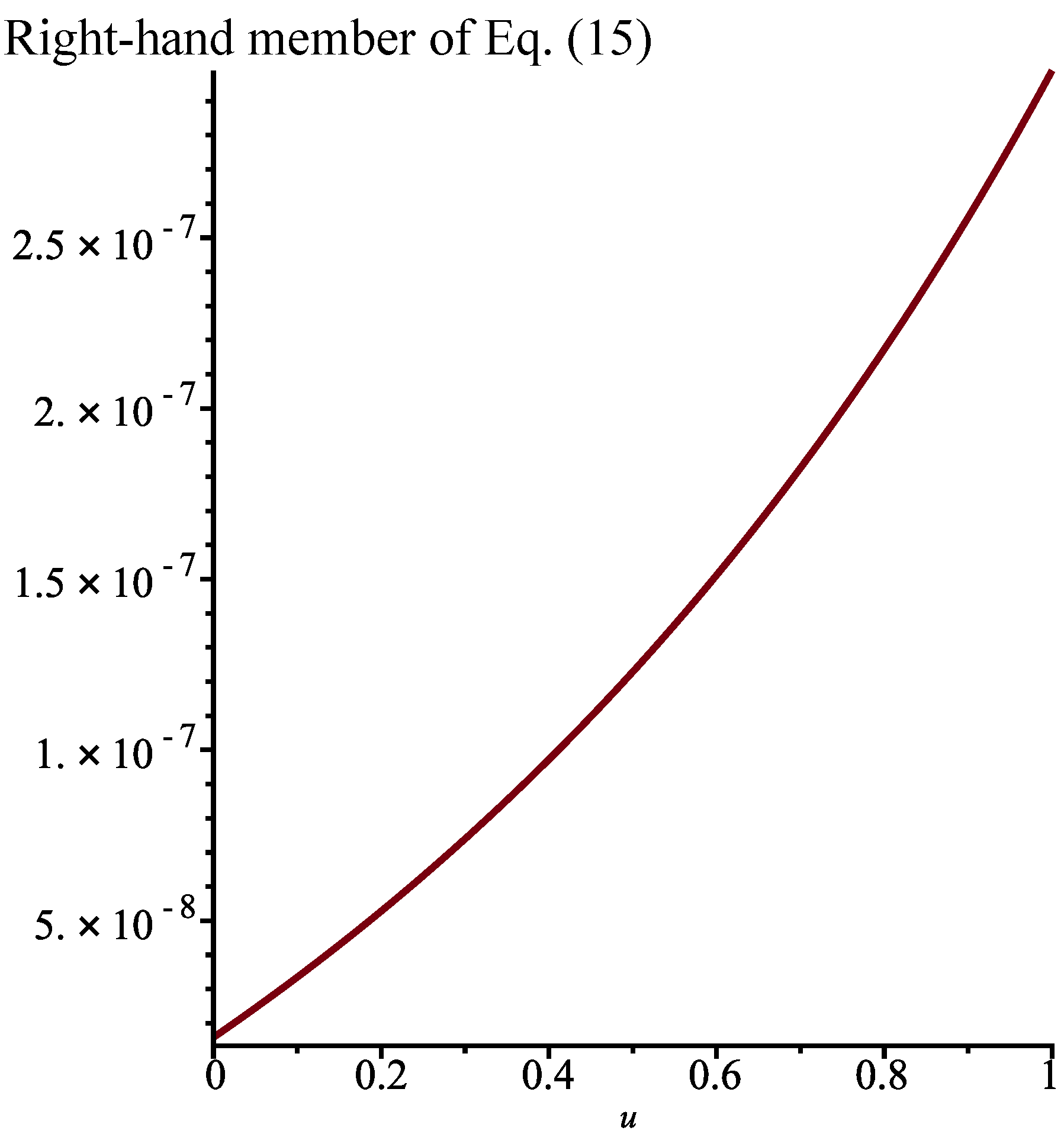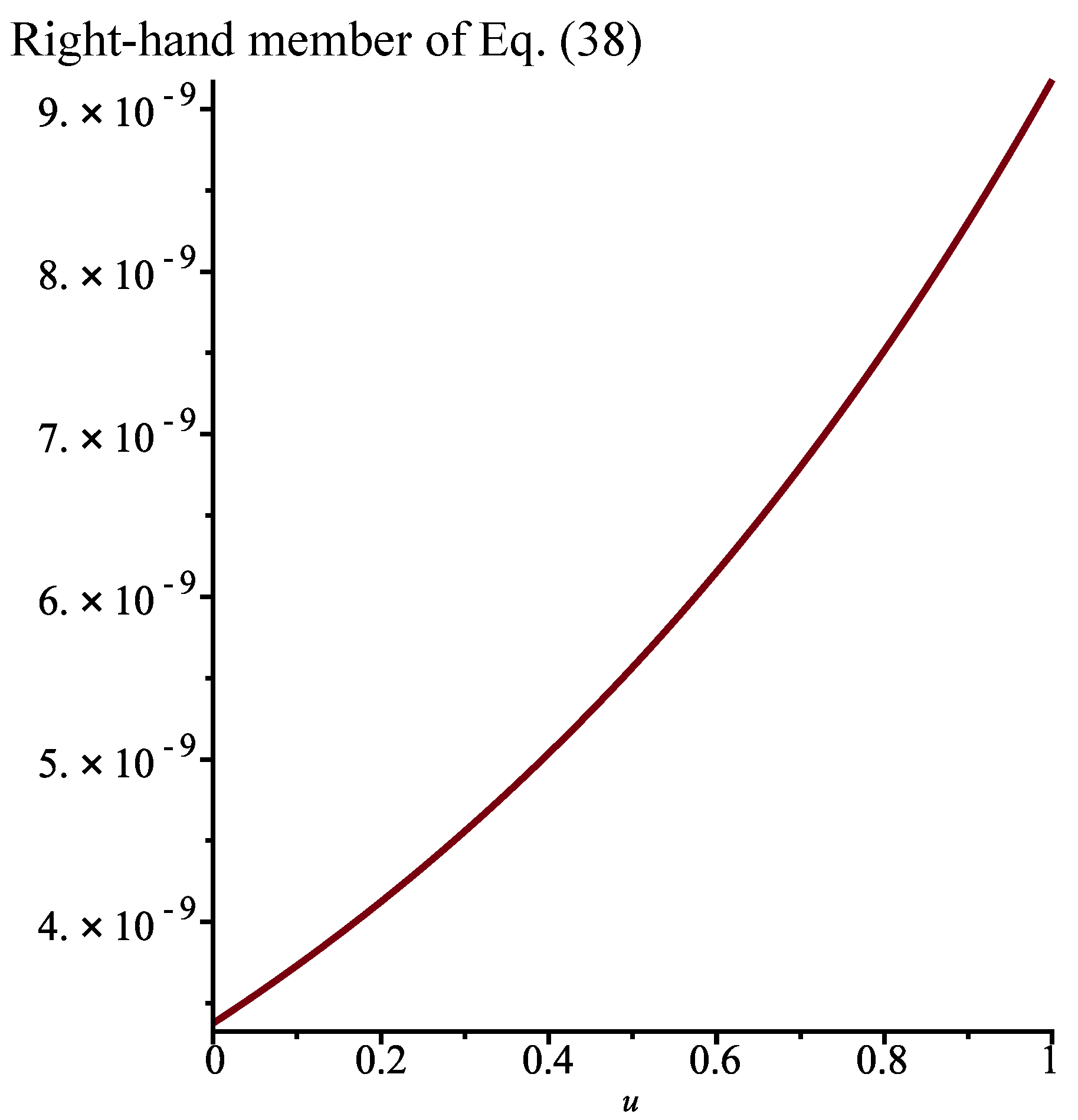1. Introduction
Let
be a one-dimensional standard Brownian motion starting at zero for
, and let
be a Poisson process with rate
. The three stochastic processes are assumed to be independent. We define
where
are independent random variables that are distributed as the continuous random variable
Z with the probability density function
and are independent of the Poisson process. The functions
,
and
,
, are such that
is a two-dimensional jump-diffusion process.
If
and
is a non-negative or non-positive deterministic function, then
could serve as a model for the wear or the remaining lifetime, respectively, of a device. The model would be a generalization of the one proposed by Rishel [
1] and considered by Lefebvre in various papers (see, for instance, [
2]).
Suppose that
, and let
be the
first-exit time defined by
Generalizing the results in [
3,
4] (see also [
5]), we can state that the moment-generating function
of
, where
, satisfies the partial differential–integral equation (PDIE)
In this paper, we assume that
Z has an exponential distribution with parameter
. It follows that Equation (
5) becomes
Since the jumps are positive, the boundary conditions are
if
or
.
Similarly, the mean
of
satisfies the PDIE
and is such that
if
or
.
Finally, let
This function, which is the probability of first exit at
, is a solution of the PDIE
The boundary conditions are
if
and
if
.
In one dimension, and when there are no jumps, obtaining exact analytical expressions for the functions corresponding to
,
, and
is generally rather straightforward. When jumps are added to the model, the problem becomes much more difficult. Papers on problems of this type have been written by Abundo (see [
6,
7,
8,
9]). In [
8], the first-passage area of one-dimensional jump-diffusion processes was computed. In addition to his papers on jump-diffusion processes, Lefebvre has also considered stochastic control problems for these processes. Jump-diffusion processes are especially important in financial mathematics; see the seminal paper by Merton [
10], as well as [
11]. Other papers on this subject are those by Cai [
12], Peng and Liu [
13], Yin et al. [
14], Zhou and Wu [
15], Gapeev and Stoev [
16], Herrmann and Zucca [
17], Song [
18], and Ai et al. [
19].
In the next section, we will compute the function
explicitly and exactly in three particular cases. First, taking advantage of the symmetry in the problems considered, we will make use of the method of similarity solutions to reduce Equation (
9) to an integro-differential equation (IDE). Then, we will transform the IDE into an ordinary differential equation (ODE) of the third order. In
Section 3, the problem of computing the mean
and the moment-generating function
of
will be studied. We will end this paper with a few remarks in
Section 4.
2. Computation of the Probability
Case I. The first particular case that we consider is the following:
where
c,
, and
are positive constants. Then,
is an Ornstein–Uhlenbeck process with Poissonian jumps. Moreover, if we let
decrease to zero, then
is an integrated Ornstein–Uhlenbeck process, which is multiplied by the constant
c.
Now, based on the definition of the first-exit time
, we will look for a solution of the form
where
. This is an application of the method of similarity solutions to solve partial differential equations, and
u is the similarity variable. For the method to work, we must be able to express (after simplification) all elements of Equation (
12) in terms of
u, as well as the boundary conditions. Here, the boundary conditions reduce to
Furthermore, Equation (
12) can be rewritten as follows:
Next, differentiating the above equation with respect to
u, we deduce from the Leibniz integral rule that
Moreover, from Equation (
15), we have
Substituting this expression into Equation (
16), we find that
Notice that this is a second-order linear ODE with constant coefficients for
. Its general solution is
where
is an arbitrary constant for
, and
For the sake of simplicity, let us take
,
, and
. Then,
The unique solution of Equation (
18) that satisfies the conditions
,
, and
is given by
where
If we substitute the above function into Equation (
15), we find that this equation is satisfied if we take
. Indeed, as can be seen in
Figure 1, the right-hand member of Equation (
15) is then practically equal to 0.
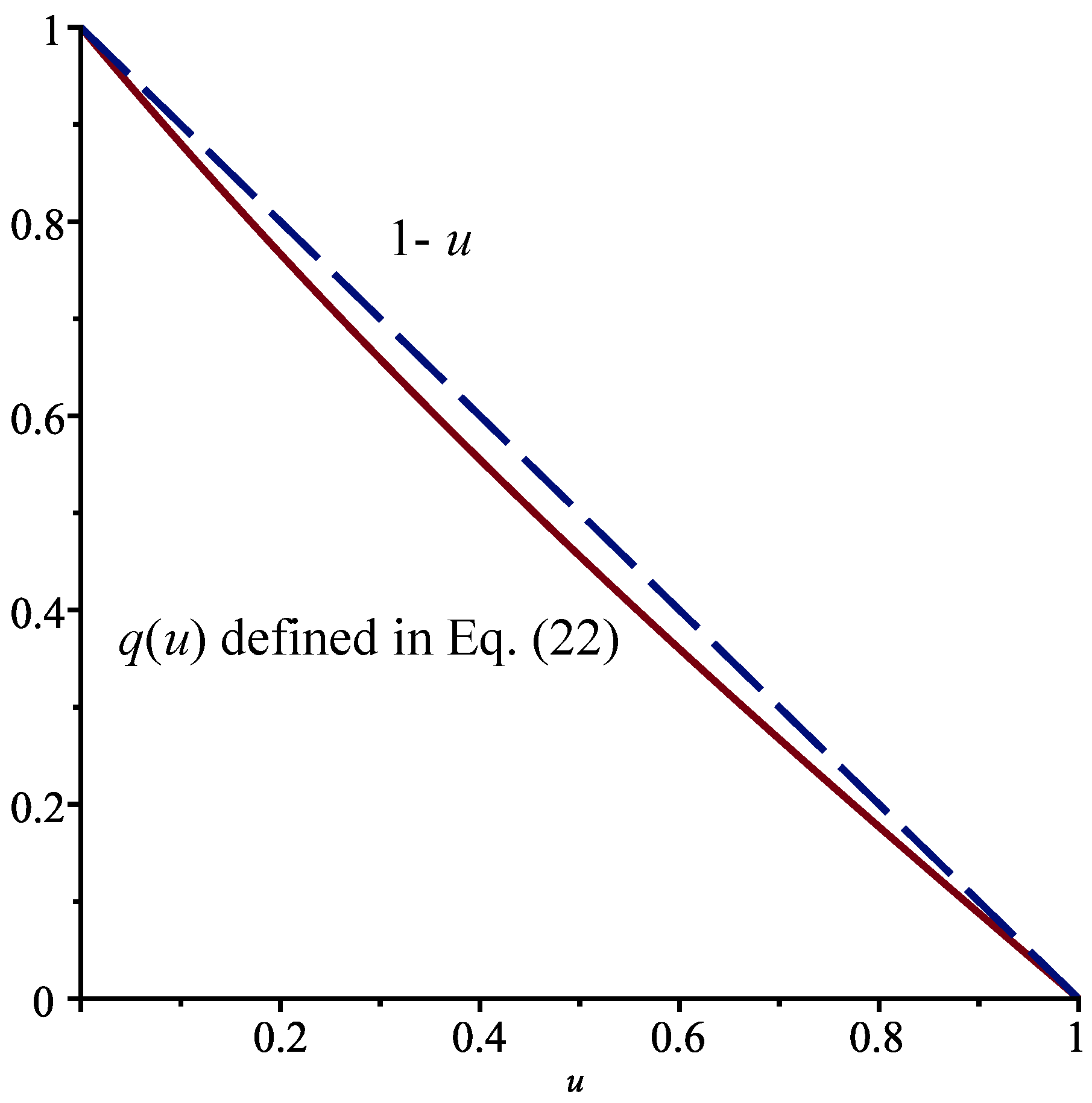
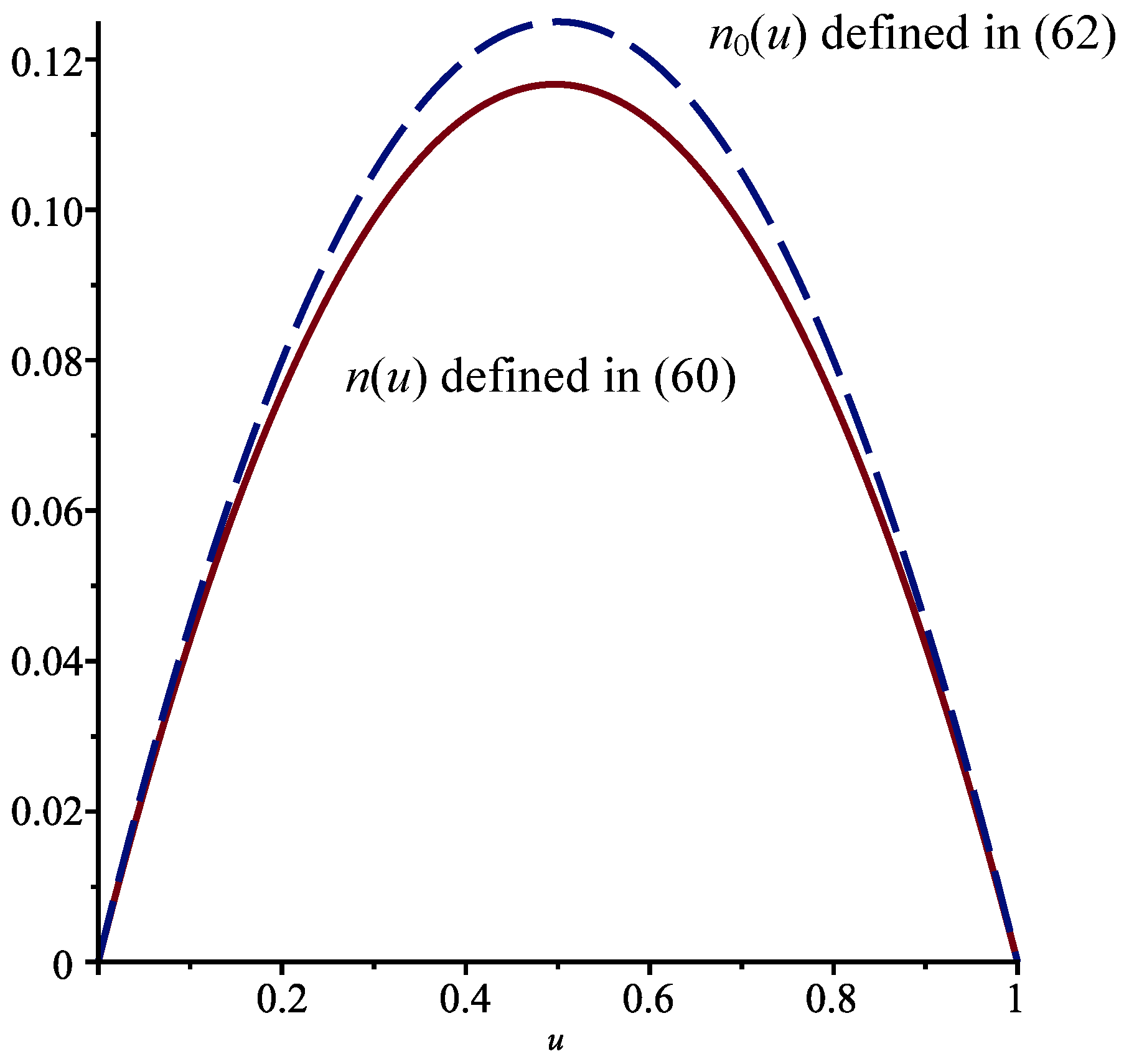
Proposition 1. When , , and , the probability is given by , where is defined in Equation (22) and . We havefor . Remark 1. We can calculate the function for any admissible values of the parameters γ, σ, λ, and θ, as well as for any constants and . However, the general solution is rather cumbersome. Moreover, to determine the value of the constant r, it is almost mandatory to choose particular values for all the quantities mentioned above.
When
so that there are no jumps, the function
that corresponds to
can be written as
, where
satisfies the elementary ODE
The solution that satisfies the boundary conditions
and
is
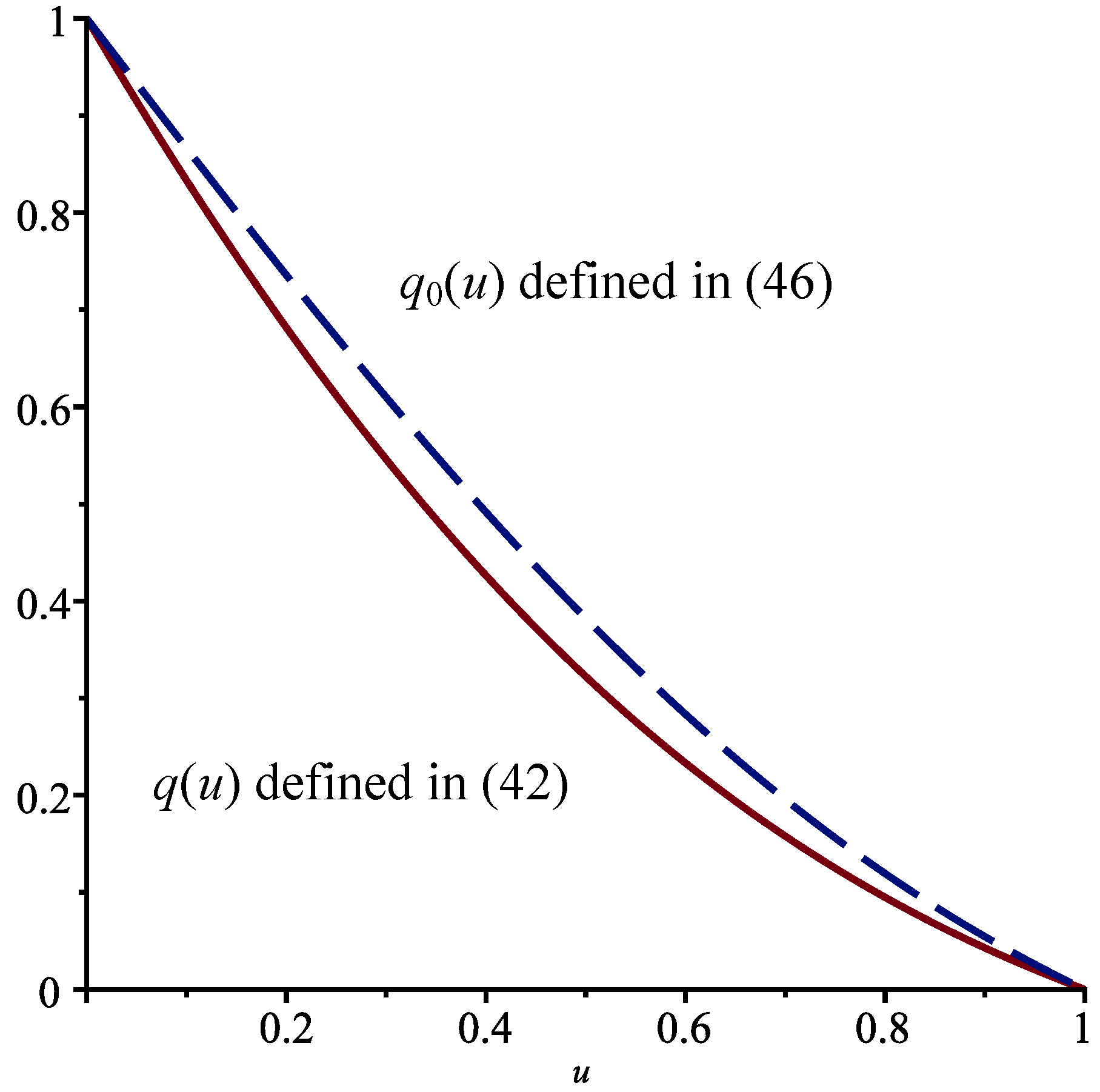
. In
Figure 2, the functions
and
are shown in the interval
. Notice the effect of the jumps on the probability of absorption at
. The effect would be more pronounced if we increased the value of the parameter
and/or decreased
.
Case II. Next, we consider the case when
where
. This time,
is a jump-diffusion process whose continuous part is a geometric Brownian motion, which is used extensively in financial mathematics.
We need to solve the following PDIE (see (
9)):
As in Case I, we set
, where
. The boundary conditions are the same as those in Equation (
14), and the PDIE becomes the IDE
Proceeding as above, we find that Equation (
29) is transformed into
which is again a second-order linear ODE for
but with non-constant coefficients. When
, the general solution of (
30) can be written as follows:
where
is an
exponential integral. The function
is defined by
We take
and
. The solution for
,
, and
is
In order for the function defined in Equation (
33) to satisfy the PDIE (
29), we must take
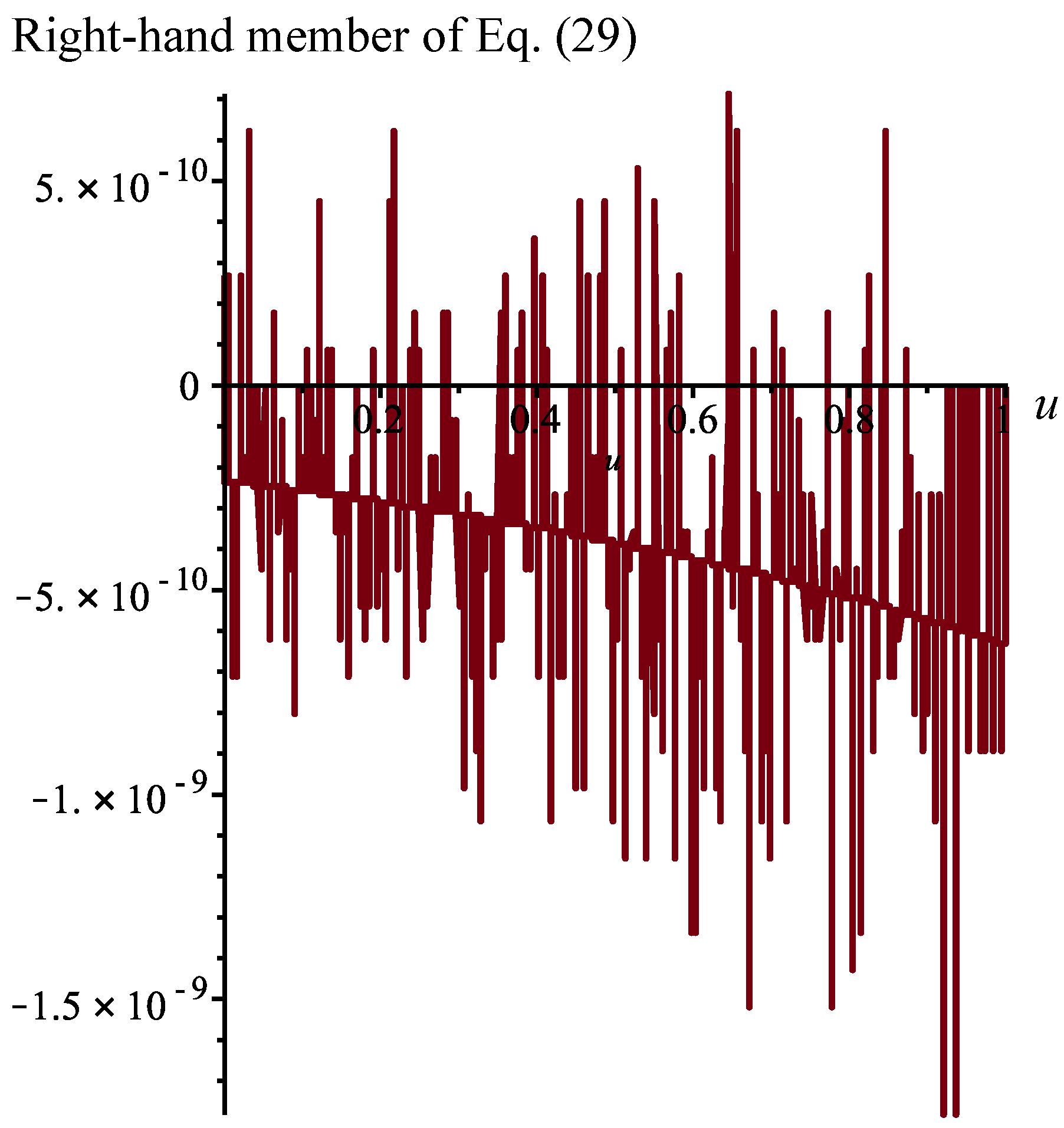
. In
Figure 3, we present the value of the right-hand member of Equation (
29) that we obtain with the function
.
We can state the following proposition.
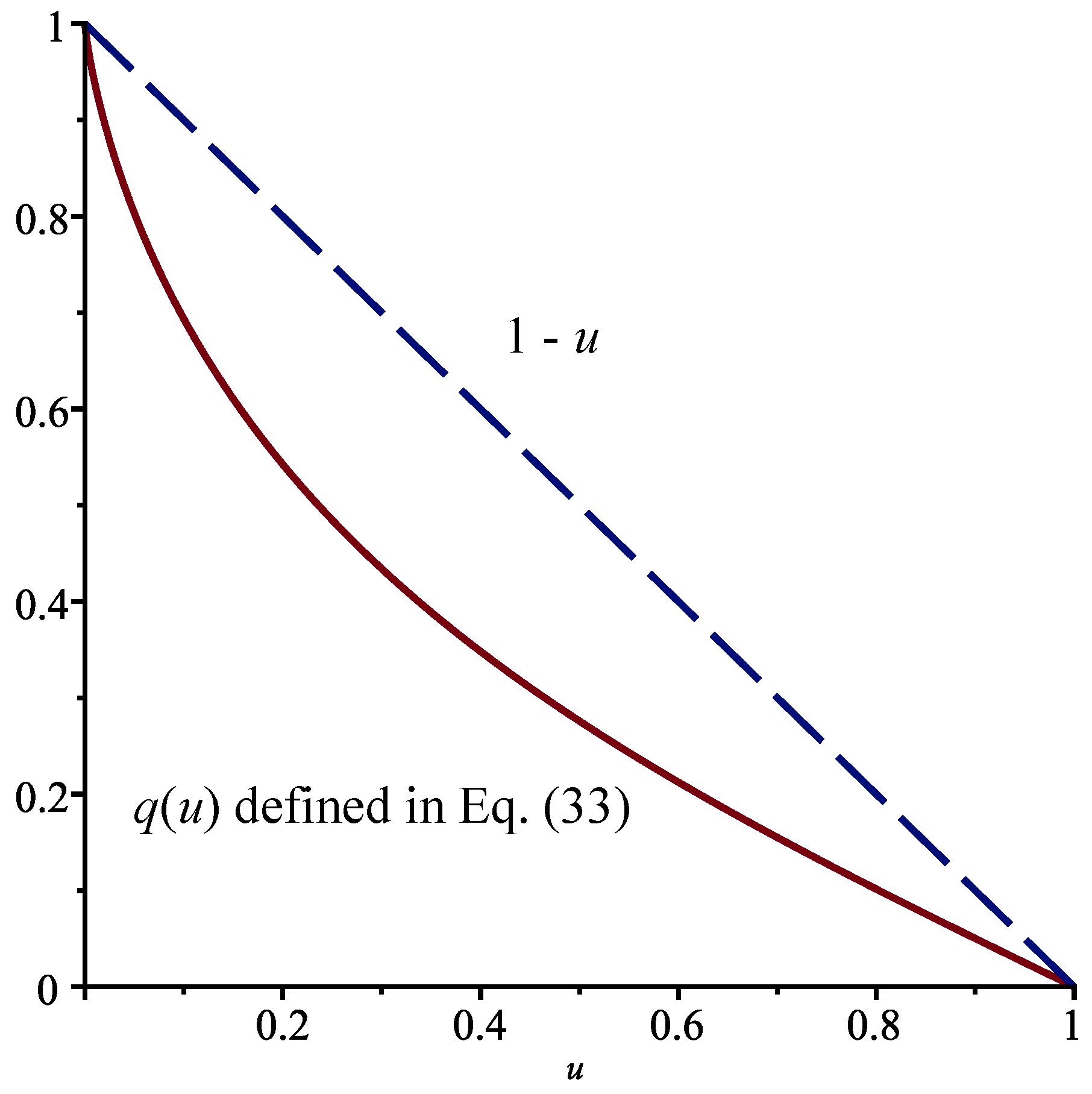
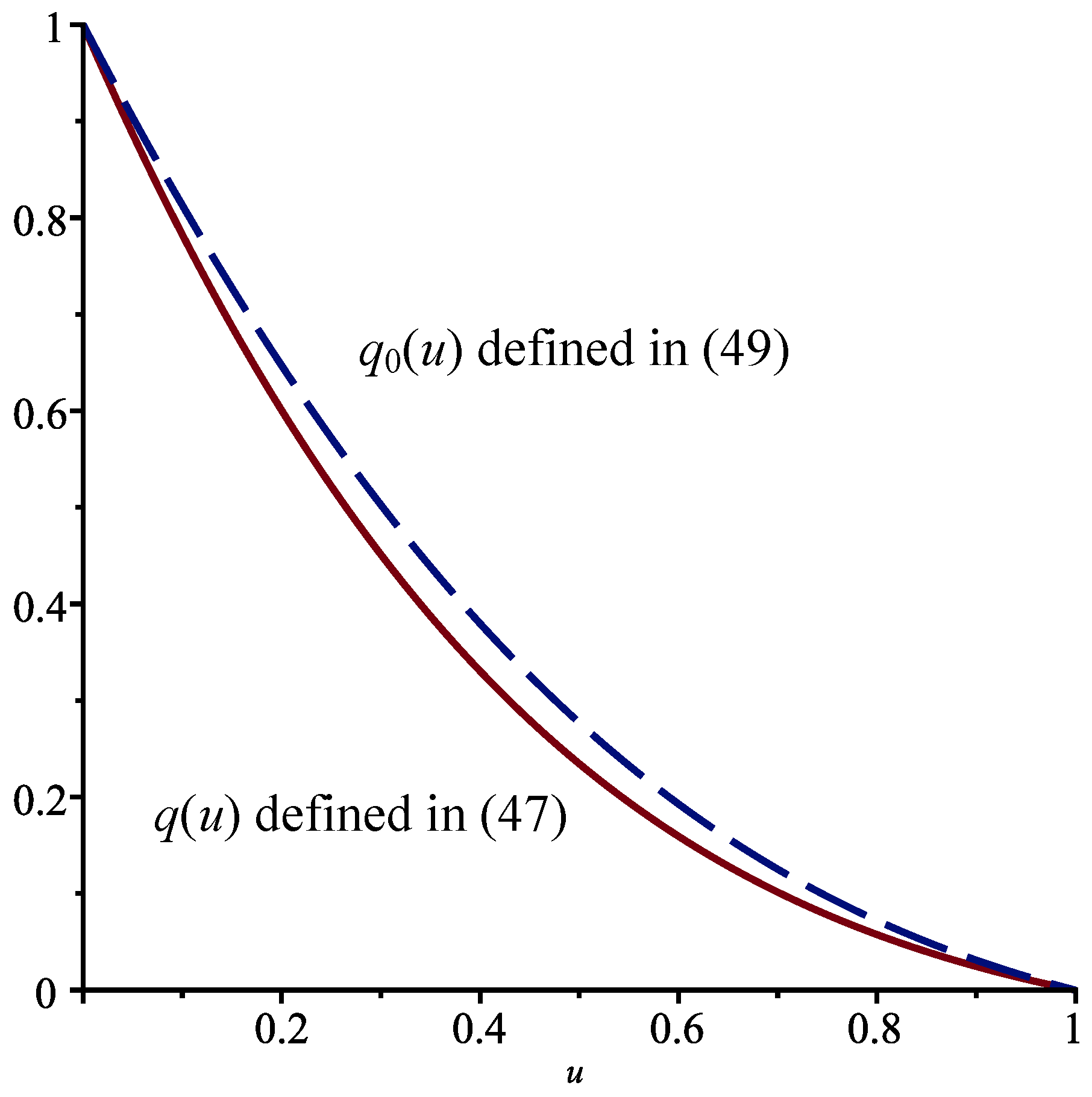
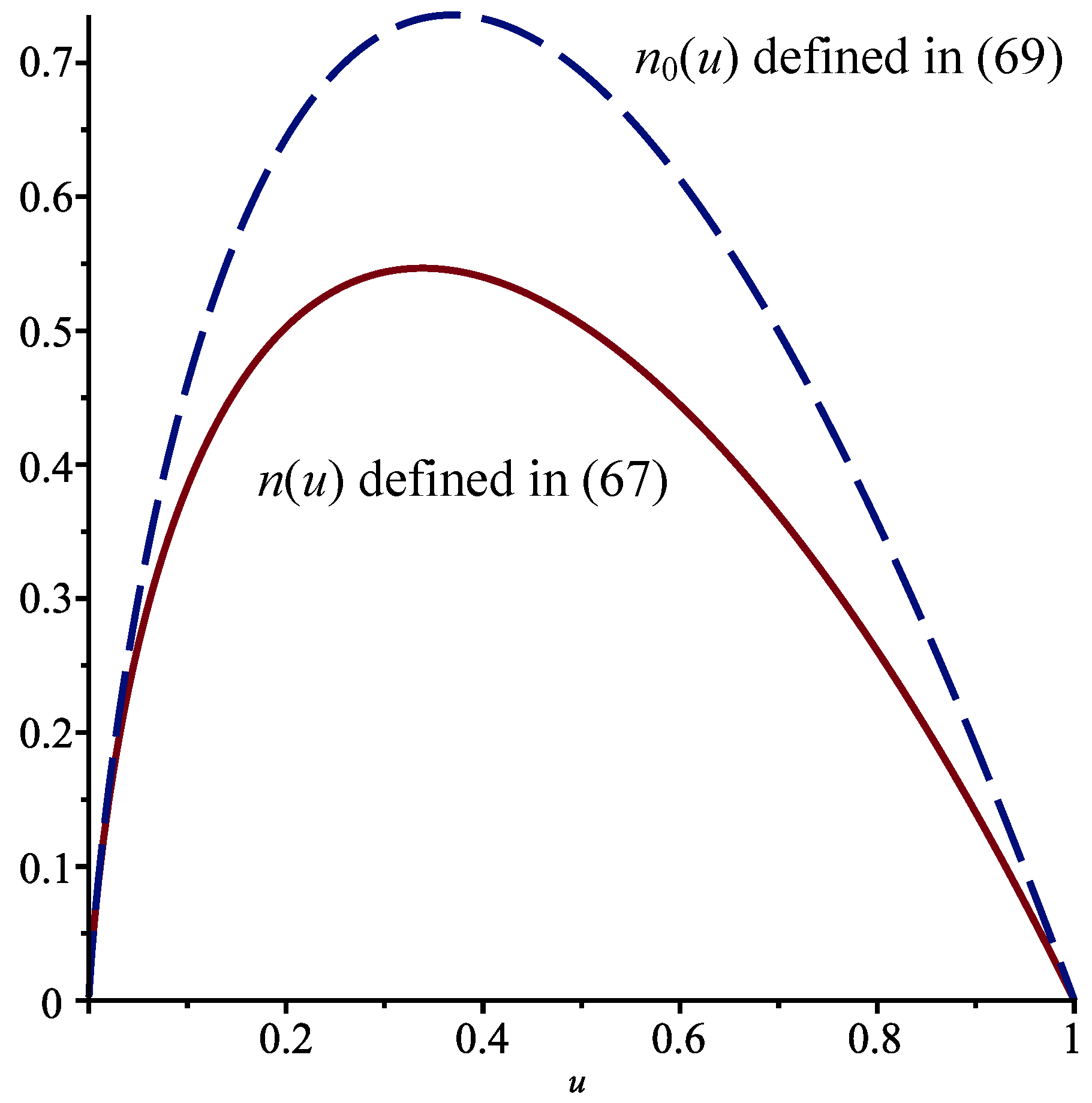
Proposition 2. When , , and , the function is equal to , where is defined in Equation (33) and . We computefor . When there are no jumps, the function
is equal to
, as in Case I, so that
. The functions
and
are displayed in
Figure 4 for
. The effect of the jumps is more pronounced than in Case I.
Case III. Finally, we define
The continuous part of the process
is a Wiener process (or Brownian motion) with drift
and dispersion parameter
, which is the basic diffusion process. Note that there is a single Brownian motion in the above system so that
is a degenerate two-dimensional jump-diffusion process. Moreover, as mentioned in Case I, this type of process is important in reliability theory to model the wear or remaining lifetime of devices.
We deduce from Equation (
9) that the function
satisfies the PDIE
Assuming that
, with
, the above equation reduces to
As in the previous cases, the boundary conditions are those in Equation (
14).
With
, we obtain the ODE
The general solution of this ODE is
where
is the
error function, which is defined by
When
,
, and
, we find that the solution such that
,
, and
is
where
Proceeding as in the previous cases, we find that if
, then the above function satisfies the PDIE in (
38). The right-hand member of Equation (
38) obtained with this function is shown in
Figure 5.
Proposition 3. When , , , and , we have , where is defined in Equation (42) with . We can write thatfor . Without the jumps, we consider the function
, which satisfies the ODE
Making use of the boundary conditions
and
, we find that
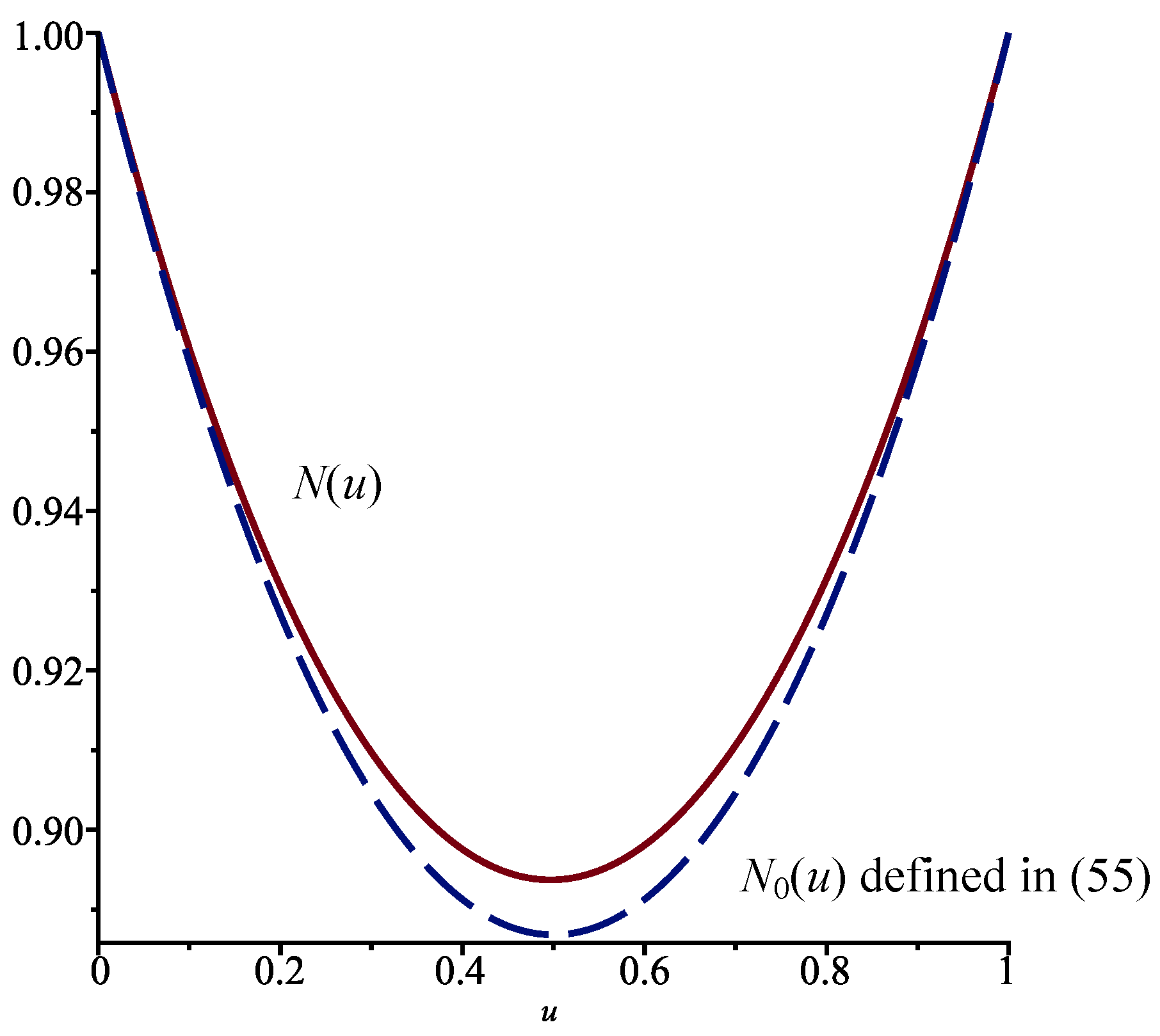
See
Figure 6.
Finally, with
, we obtain that
and
The function
is the unique solution of the ODE
such that
and
. We have
The functions
and
are presented in
Figure 7.
3. Computation of the Mean and the Moment-Generating Function
In this section, we will first compute the functions
and
for the process considered in Case I of
Section 2. Because the coefficients of the equations that we need to solve are constants, the task is much easier than when these coefficients depend on
, as in Cases II and III. We will also obtain the function
in Case II.
First, the PDIE satisfied by the function
in Case I is (see Equation (
6))
subject to the boundary conditions
if
or
.
We look for a solution of the form
, with
. This leads to the following equation:
Differentiating the above equation with respect to
u, we obtain (after some work) that
satisfies the linear third-order ODE
Let us take
so that
We can find the general solution of the above equation. We choose
and
, and we seek the unique solution for which
and
. Proceeding as in
Section 2, we are able to find the value of the constant
r. The resulting expression for the function
is rather long and will not be reproduced here.
With
, the function
that corresponds to
is a solution of the simple ODE
The unique solution such that
is
The functions
and
are shown in
Figure 8.
Next, in the case of the function
, the PDIE is (see Equation (
7))
and we must have
if
or
. We define
, which yields the following ODE:
Letting
, the above equation simplifies to the ODE
whose general solution is
As previously, we can first find the constants
,
, such that
and
, and then the constant
r for which the PDIE is satisfied. The constant is
and
The corresponding function
is the unique solution of
such that
. We easily find that
See
Figure 9.
Finally, in Case II, the PDIE that we need to solve to obtain
is
This equation is transformed into the ODE
Choosing
, we obtain
With the help of the software program
Maple, we find that the general solution of the above equation is
Once again, we impose the conditions
and
. We find that we must take
. We have
In the absence of jumps, we compute the function
. It satisfies the ODE
With the conditions
, we find that
Figure 10 presents the functions
and
, which are quite different.
4. Discussion
In several fields, notably, financial mathematics, many authors are now proposing diffusion processes with jumps as models. Moreover, random variables known as first-hitting times are important in various applications. In two or more dimensions, when there are no jumps, to obtain the quantities of interest, such as the mean of these random variables, we need to solve partial differential equations. These equations become partial differential–integral equations when continuous jumps are added.
In this paper, we have considered problems of this type. Owing to the symmetry in these problems, we were able to reduce the PDIEs to (ordinary) integro-differential equations. For the distribution of the random jumps that we used, we succeeded in transforming the IDEs into ODEs.
We have obtained exact analytical solutions to problems involving important diffusion processes. In cases where it is not possible to find analytical solutions, numerical methods can be used to obtain solutions to problems for fixed values of the various parameters in the models.
To generalize the results obtained in this paper, we could add random jumps to the stochastic process as well. Furthermore, other distributions for the random jumps could be used. For discrete distributions, the equations to be solved would be partial differential–difference equations.
Finally, we could try to solve optimal control problems for these jump-diffusion processes in two or more dimensions. To find the optimal control, in the case of random jumps with a continuous distribution, we generally need to obtain the value function, which would then satisfy a nonlinear PDIE.