Shape Transition and Coexistence in 66Se Studied with Phenomenological and Microscopic Models
Abstract
1. Introduction
2. Theoretical Models
2.1. Covariant Density Functional Theory with Meson-Exchange Model
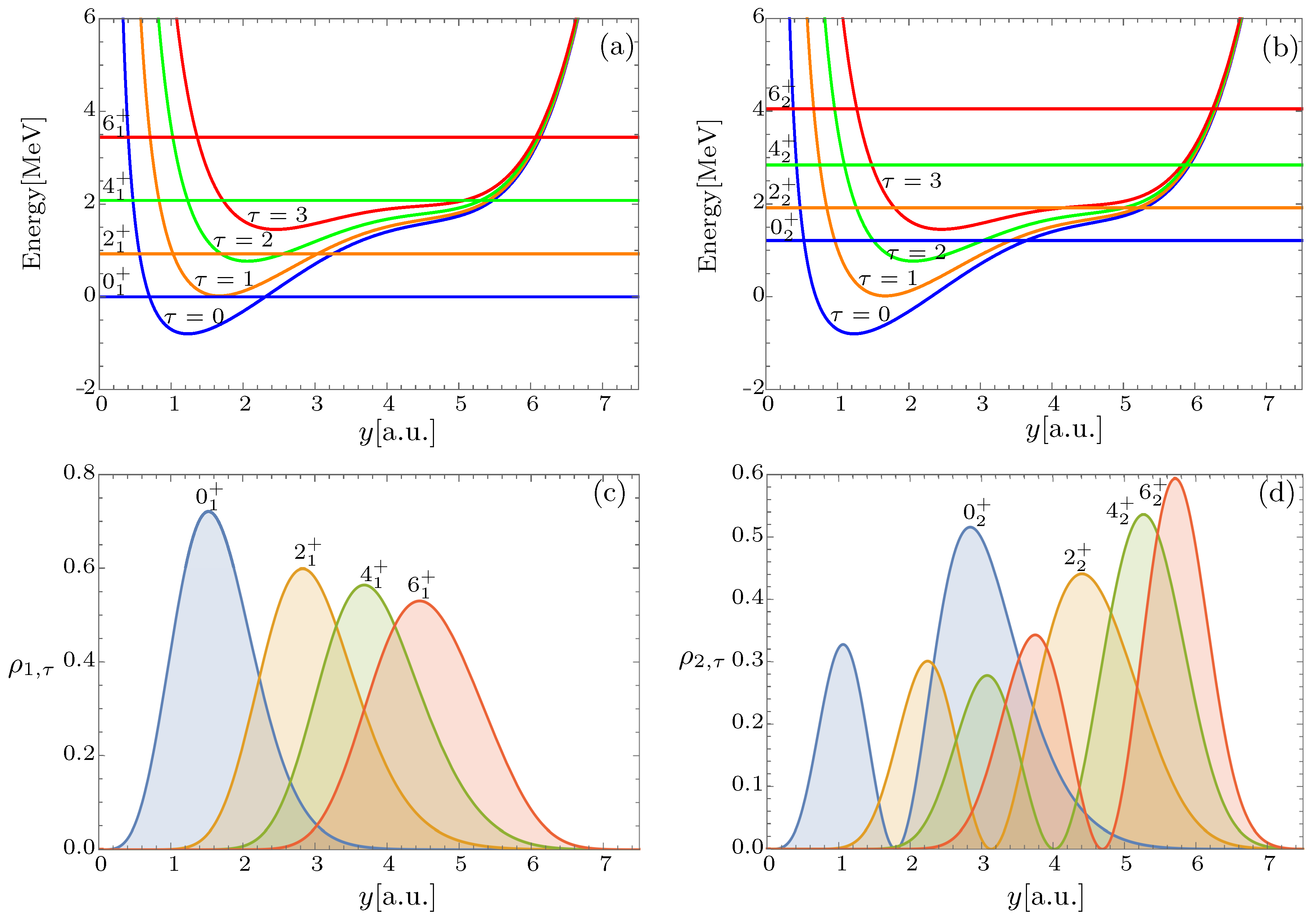
2.2. Bohr Hamiltonian with Sextic Oscillator Potential
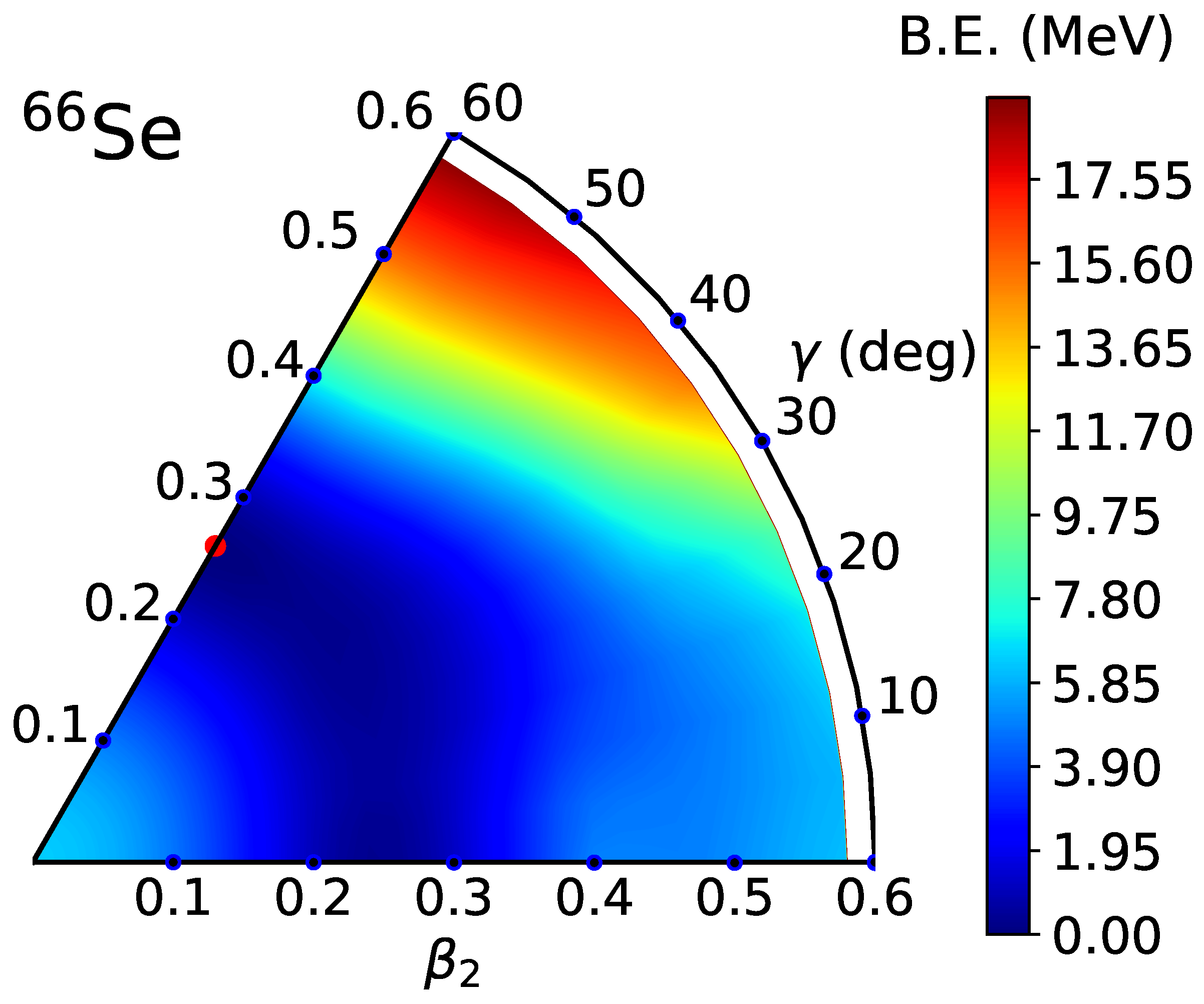
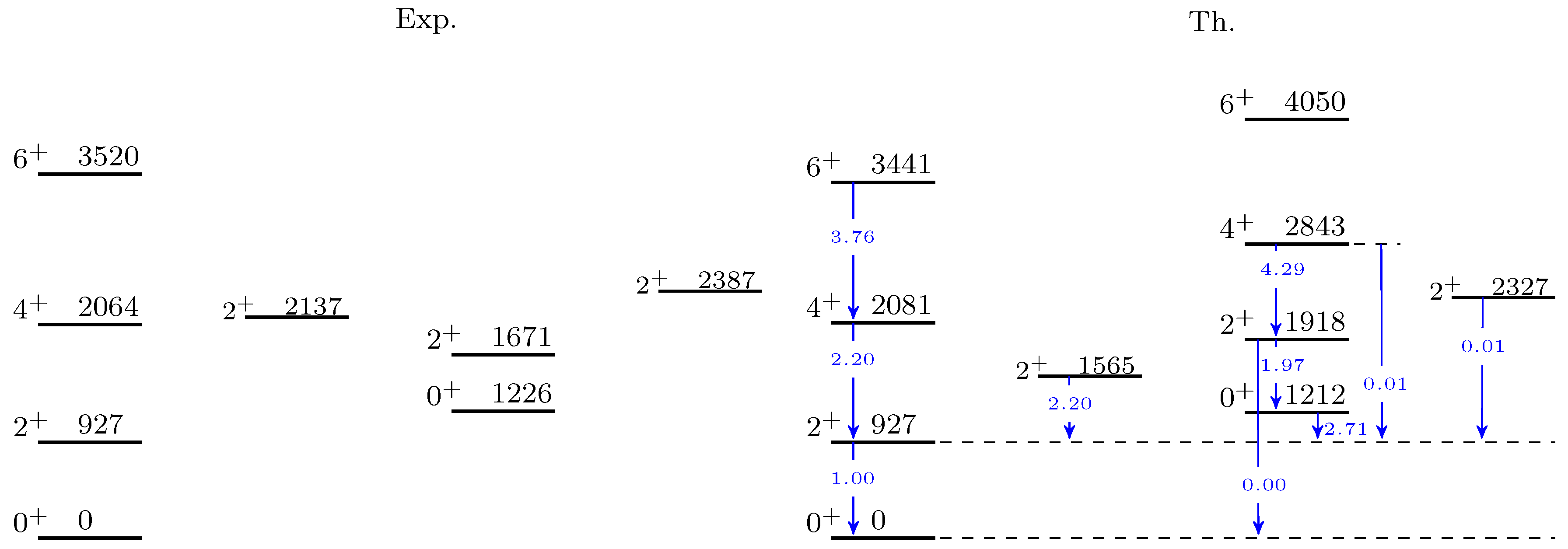
3. Numerical Applications
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morinaga, H. Interpretation of some of the excited states of 4n self-conjugate nuclei. Phys. Rev. 1956, 101, 254. [Google Scholar]
- Heyde, K.; Isacker, P.V.; Waroquier, M.; Wood, J.L.; Mayer, R.A. Coexistence in odd-mass nuclei. Phys. Rep. 1983, 102, 291. [Google Scholar]
- Wood, J.L.; Heyde, K.; Nazarewicz, W.; Huyse, M.; van Duppen, P. Coexistence in even-mass nuclei. Phys. Rep. 1992, 215, 101. [Google Scholar] [CrossRef]
- Wood, J.L.; Zganjar, E.F.; Coster, C.D.; Heyde, K. Electric monopole transitions from low energy excitations in nuclei. Nucl. Phys. A 1999, 651, 323. [Google Scholar]
- Heyde, K.; Wood, J.L. Shape coexistence in atomic nuclei. Rev. Mod. Phys. 2011, 83, 1467. [Google Scholar]
- Wood, J.L.; Heyde, K. A focus on shape coexistence in nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 020402. [Google Scholar]
- Obertelli, A.; Baugher, T.; Bazin, D.; Boissinot, S.; Delaroche, J.P.; Dijon, A.; Flavigny, F.; Gade, A.; Girod, M.; Glasmacher, T.; et al. First spectroscopy of 66Se and 65As: Investigating shape coexistence beyond the N=Z line. Phys. Lett. B 2011, 701, 417. [Google Scholar] [CrossRef]
- Ruotsalainen, P.; Jenkins, D.G.; Bentley, M.A.; Wadsworth, R.; Scholey, C.; Aura-nen, K.; Davies, P.J.; Grahn, T.; Greenlees, P.T.; Henderson, J.; et al. Spectroscopy of proton-rich 66Se up to Jπ = 6+: Isospin-breaking effect in the A = 66 isobaric triplet. Phys. Rev. C 2013, 88, 041308. [Google Scholar]
- Elekes, Z.; Panin, V.; Rodríguez, T.R.; Sieja, K.; Ahn, D.S.; Al-Adili, A.; Baba, H.; Stefanescu, A.I.; Cook, K.J.; Dósa, C.; et al. Shape coexistence in 66Se. Phys. Lett. B 2023, 844, 138072. [Google Scholar]
- Nikšić, T.; Paar, N.; Vretenar, D.; Ring, P. DIRHB-A relativistic self-consistent mean-field framework for atomic nuclei. Comput. Phys. Commun. 2014, 185, 1808. [Google Scholar]
- Nikšić, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Adjusting parameters to biding energies. Phys. Rev. C 2008, 78, 034318. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Viñas, X.; Centelles, M.; Ring, P.; Schuck, P. Relativistic mean-field interaction with density-dependent meson-nucleon vertices based on microscopical calculations. Phys. Rev. C 2011, 84, 054309, Erratum in Phys. Rev. C 2016, 93, 069905. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R. Nuclear Structure, Vol. II: Nuclear Deformations; W.A. Benjamin: Reading, MA, USA, 1975. [Google Scholar]
- Budaca, R.; Buganu, P.; Budaca, A.I. Bohr model description of the critical point for the first order shape phase transition. Phys. Lett. B 2018, 776, 26. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I.; Buganu, P. Application of the Bohr Hamiltonian with a double-well sextic potential to collective states of Mo isotopes. J. Phys. G Nucl. Part. Phys. 2019, 46, 125102. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Finelli, P.; Ring, P. Relativistic Hartree-Bogoliubov model with density-dependent meson-nucleon couplings. Phys. Rev. C 2002, 66, 024306. [Google Scholar] [CrossRef]
- Meng, J.; Zhou, S.G. Halos in medium-heavy nuclei with covariant density functional theory in continuum. J. Phys. G Nucl. Part. Phys. 2015, 42, 093101. [Google Scholar] [CrossRef]
- Matev, M.; Afanasjev, A.V.; Dobaczewski, J.; Lalazissis, G.A.; Nazarewicz, W. Additivity of effective quadrupole moments and angular momentum alignments in A∼130 nuclei. Phys. Rev. C 2007, 76, 034304. [Google Scholar] [CrossRef]
- Afanasjev, A.V. Band terminations in density functional theory. Phys. Rev. C 2008, 78, 054303. [Google Scholar] [CrossRef]
- Agbemava, S.E.; Afanasjev, A.V.; Nakatsukasa, T.; Ring, P. Covariant density functional theory: Reexamining the structure of superheavy nuclei. Phys. Rev. C 2015, 92, 054310. [Google Scholar] [CrossRef]
- Agbemava, S.E.; Afanasjev, A.V.; Ray, D.; Ring, P. Assessing theoretical uncertainties in fission barriers of superheavy nuclei. Phys. Rev. C 2017, 95, 054324. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Karatzikos, S.; Fossion, R.; Arteaga, D.P.; Afanasjev, A.V.; Ring, P. The effective force NL3 revisited. Phys. Lett. B 2009, 671, 36. [Google Scholar] [CrossRef]
- Gambhir, Y.K.; Ring, P.; Thimet, A. Relativistic mean field theory for finite nuclei. Ann. Phys. 1990, 198, 132. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, Z.Y.; Ring, P. A finite range pairing force for density functional theory in superfluid nuclei. Phys. Lett. B 2009, 676, 44. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Bohr, A. The coupling of nuclear surface oscillations to the motion of individual nucleons. Mat.-Fyz. Medd. K. Dan. Vidensk. Selsk. 1952, 26, 14. [Google Scholar]
- Wilets, L.; Jean, M. Surface oscillations in even-even nuclei. Phys. Rev. 1956, 102, 788. [Google Scholar] [CrossRef]
- Bès, D.R. The γ-dependent part of the wave functions representing γ-unstable surface vibrations. Nucl. Phys. 1959, 10, 373. [Google Scholar] [CrossRef]
- Rakavy, G. The classification of states of surface vibration. Nucl. Phys. 1957, 4, 289. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I. Coexistence, mixing and fluctuation of nuclear shapes. EPL 2018, 123, 42001. [Google Scholar] [CrossRef]
- Budaca, R.; Buganu, P.; Budaca, A.I. Geometrical model description of shape coexistence in Se isotopes. Nucl. Phys. A 2019, 990, 137. [Google Scholar] [CrossRef]
- Mennana, A.A.B.; Benjedi, R.; Budaca, R.; Buganu, P.; Bassem, Y.E.; Lahbas, A.; Oulne, M. Mixing of the coexisting shapes in the ground states of 74Ge and 74Kr. Phys. Scr. 2021, 96, 125306. [Google Scholar] [CrossRef]
- Benjedi, R.; Budaca, R.; Buganu, P.; Bassem, Y.E.L.; Lahbas, A.; Oulne, M. Shapes and structure for the lowest states of the 42,44Ca isotopes. Phys. Scr. 2024, 99, 055307. [Google Scholar] [CrossRef]
- Buganu, P.; Budaca, R. Analytical solution for the Davydov-Chaban Hamiltonian with a sextic oscillator potential for γ = 30o. Phys. Rev. C 2015, 91, 014306. [Google Scholar] [CrossRef]
- Iachello, F. Dynamic symmetries at the critical point. Phys. Rev. Lett. 2000, 85, 3580. [Google Scholar] [CrossRef]
- Caprio, M.A.; Iachello, F. Analytic descriptions for transitional nuclei near the critical point. Nucl. Phys. A 2007, 781, 26. [Google Scholar] [CrossRef]
- Wigner, E.P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra; Griffin, J.J., Translator; Academic Press Inc.: New York, NY, USA; London, UK, 1959. [Google Scholar]
- Rowe, D.J.; Turner, P.S.; Repka, J. Spherical harmonics and basic coupling coefficients for the group SO(5) in an SO(3) basis. J. Math. Phys. 2004, 45, 2761. [Google Scholar] [CrossRef]
- Rowe, D.J. An algebraic approach to problems with polynomial Hamiltonians on Euclidean spaces. J. Phys. A Math. Gen. 2005, 38, 10181. [Google Scholar] [CrossRef]
- Rowe, D.J.; Turner, P.S. The algebraic collective model. Nucl. Phys. A 2005, 753, 94. [Google Scholar] [CrossRef]
- Fortunato, L. Solutions of the Bohr Hamiltonian, a compendium. Eur. Phys. J. A-Hadrons Nucl. 2005, 26, 1–30. [Google Scholar] [CrossRef]
- Wang, T. A collective description of the unusually low ratio B4/2 = B(E2; → )/B(E2; → ). EPL 2020, 129, 52001. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.-W.; Karlsson, D.; Qi, C.; Pan, F.; Draayer, J.P. A theoretical interpretation of the anomalous reduced E2 transition probabilities along the yrast line of neutron-deficient nuclei. Phys. Lett. B 2022, 834, 137443. [Google Scholar] [CrossRef]
- Wang, T.; He, B.-C.; Li, D.-K.; Zhou, C.-X. Prolate-oblate asymmetric shape phase transition in the interacting boson model with SU(3) higher-order interactions. Phys. Rev. C 2023, 107, 064322. [Google Scholar] [CrossRef]
- Pan, F.; Zhang, Y.; Wu, Y.; Dai, L.; Draayer, J.P. B(E2) anomaly along the yrast line in neutron-deficient A ≈ 170 even-even nuclei induced by a triaxial rotor term. Phys. Rev. C 2024, 110, 054324. [Google Scholar] [CrossRef]
- Zhang, Y.; Teng, W. B(E2) anomaly and triaxial deformation in the interacting boson model. Phys. Rev. C 2025, 111, 014324. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, Y.X.; Li, D.K.; Kang, X.S.; Jin, S.C.; Wang, T.; Zhang, Z.Q.; Zhang, C.G.; Zhang, Z.X. Level-anticrossing in B(E2) anomaly (I). arXiv 2025, arXiv:2503.22100v2. [Google Scholar]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Mennana, A.A.B.; Benjedi, R.; Budaca, R.; Buganu, P.; Bassem, Y.E.; Lahbas, A.; Oulne, M. Shape and structure for the low-lying states of the 80Ge nucleus. Phys. Rev. C 2022, 105, 034347. [Google Scholar] [CrossRef]
| Parameter | DD-ME2 |
|---|---|
| m | 939 |
| 550.1238 | |
| 783.000 | |
| 763.000 | |
| 10.5396 | |
| 13.0189 | |
| 3.6836 | |
| 1.3881 | |
| 1.0943 | |
| 1.7057 | |
| 0.4421 | |
| 1.3892 | |
| 0.9240 | |
| 1.4620 | |
| 0.4775 | |
| 0.5647 |
| Nucleus | d | [keV] | ||||
|---|---|---|---|---|---|---|
| −0.0434384787 | 0.0006814582 | 0.084722 | 7.500 | 434.94 | 0.278 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buganu, P.; Chafik, S.; Lahbas, A.; Oulne, M. Shape Transition and Coexistence in 66Se Studied with Phenomenological and Microscopic Models. Symmetry 2025, 17, 687. https://doi.org/10.3390/sym17050687
Buganu P, Chafik S, Lahbas A, Oulne M. Shape Transition and Coexistence in 66Se Studied with Phenomenological and Microscopic Models. Symmetry. 2025; 17(5):687. https://doi.org/10.3390/sym17050687
Chicago/Turabian StyleBuganu, Petricǎ, Sara Chafik, Alaaeddine Lahbas, and Mustapha Oulne. 2025. "Shape Transition and Coexistence in 66Se Studied with Phenomenological and Microscopic Models" Symmetry 17, no. 5: 687. https://doi.org/10.3390/sym17050687
APA StyleBuganu, P., Chafik, S., Lahbas, A., & Oulne, M. (2025). Shape Transition and Coexistence in 66Se Studied with Phenomenological and Microscopic Models. Symmetry, 17(5), 687. https://doi.org/10.3390/sym17050687





