Multivariate Time-Series Missing Data Imputation with Convolutional Transformer Model
Abstract
1. Introduction
2. Literature Review
3. Preliminary
3.1. Point Energy Monitoring System
3.2. Problem Formulation
4. The Convolutional Transformer Imputation Model
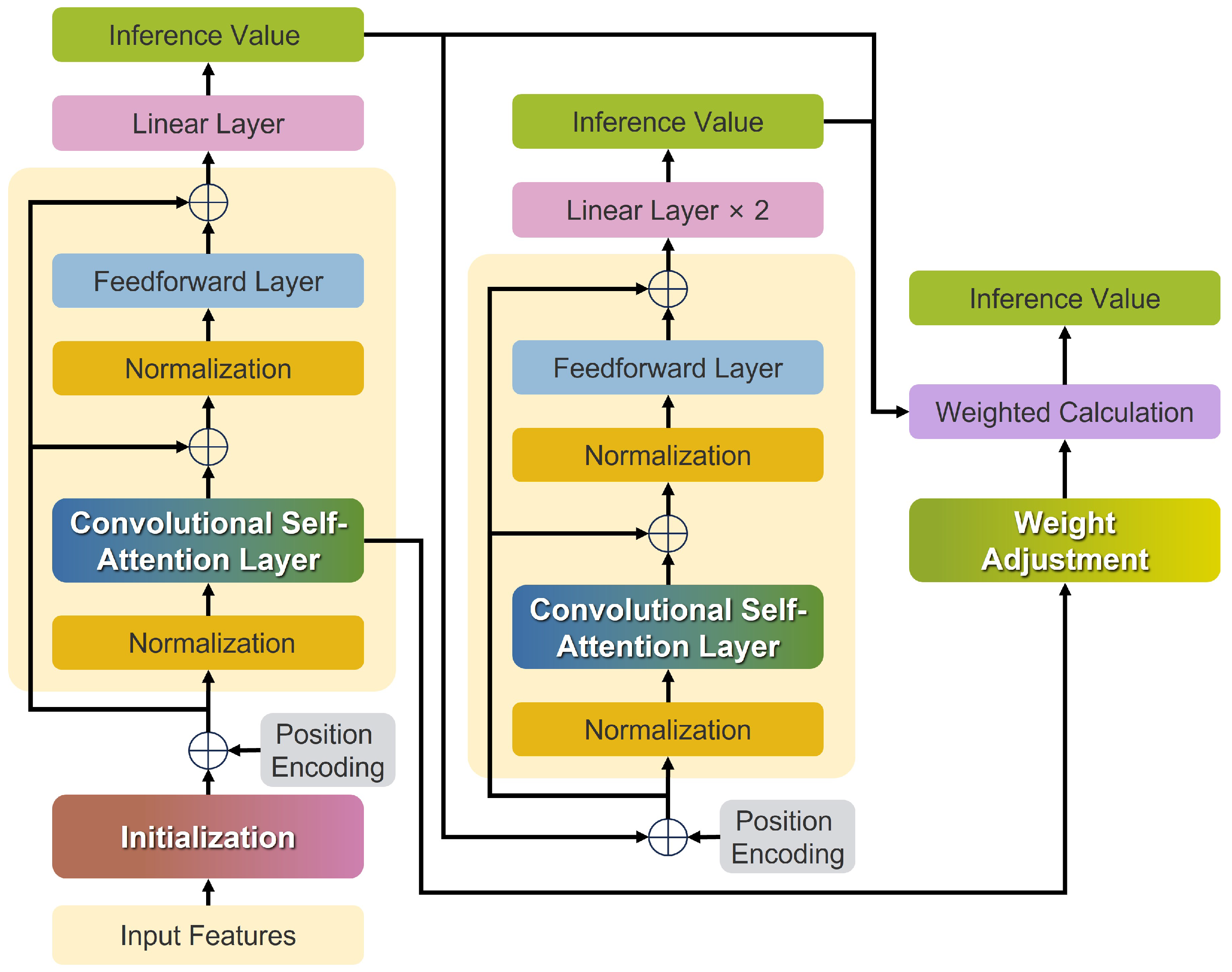
4.1. The Overall Architecture of the CTIM
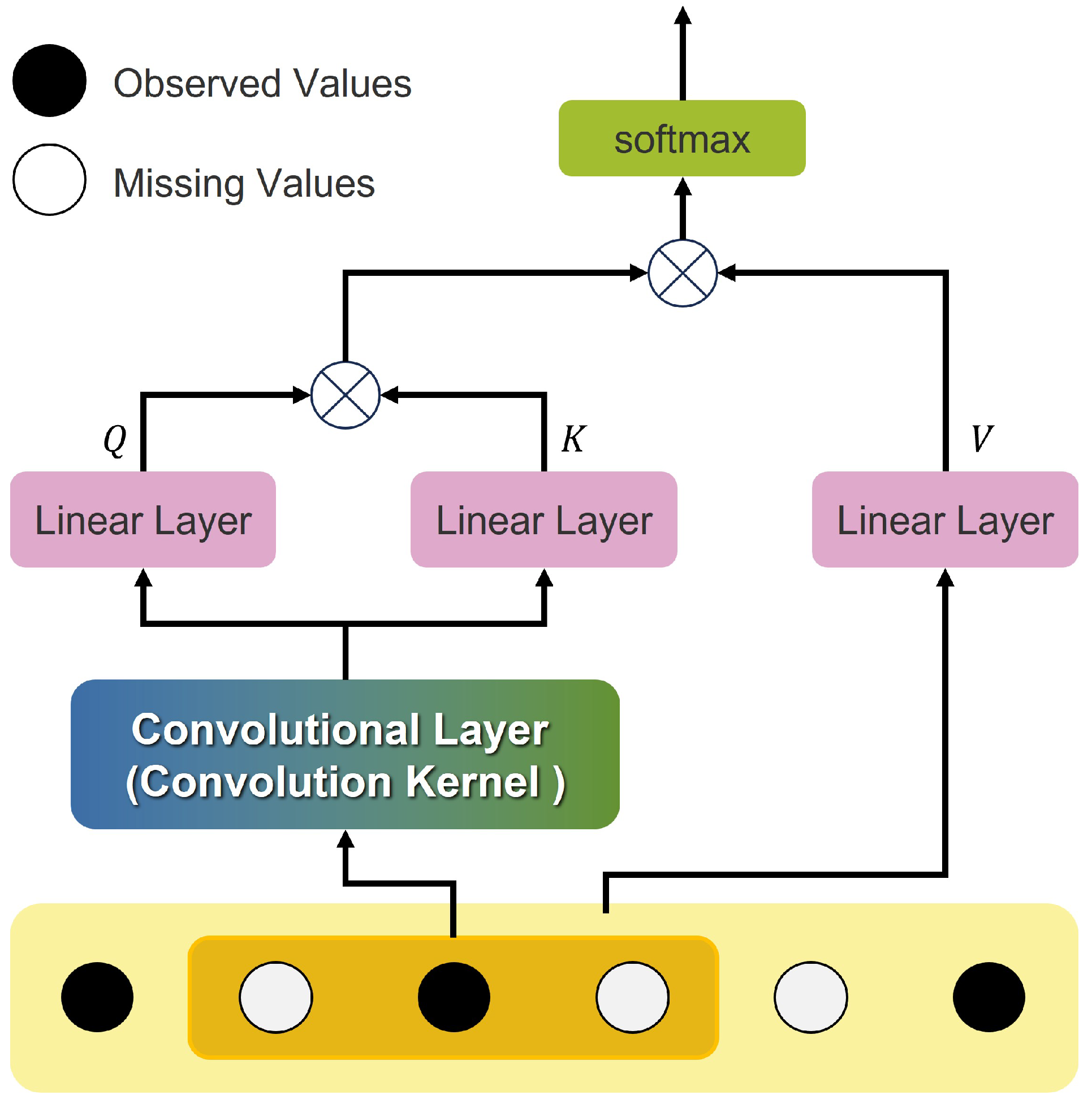
4.2. The Convolutional Self-Attention Layer
4.3. Position Encoding
4.4. The Loss Function
4.5. Training and Testing Process
5. Experimental Implementation
5.1. Industrial Data Set
5.2. Experimental Setup
5.3. Hyperparameter Configuration
6. Experiment Results and Discussion
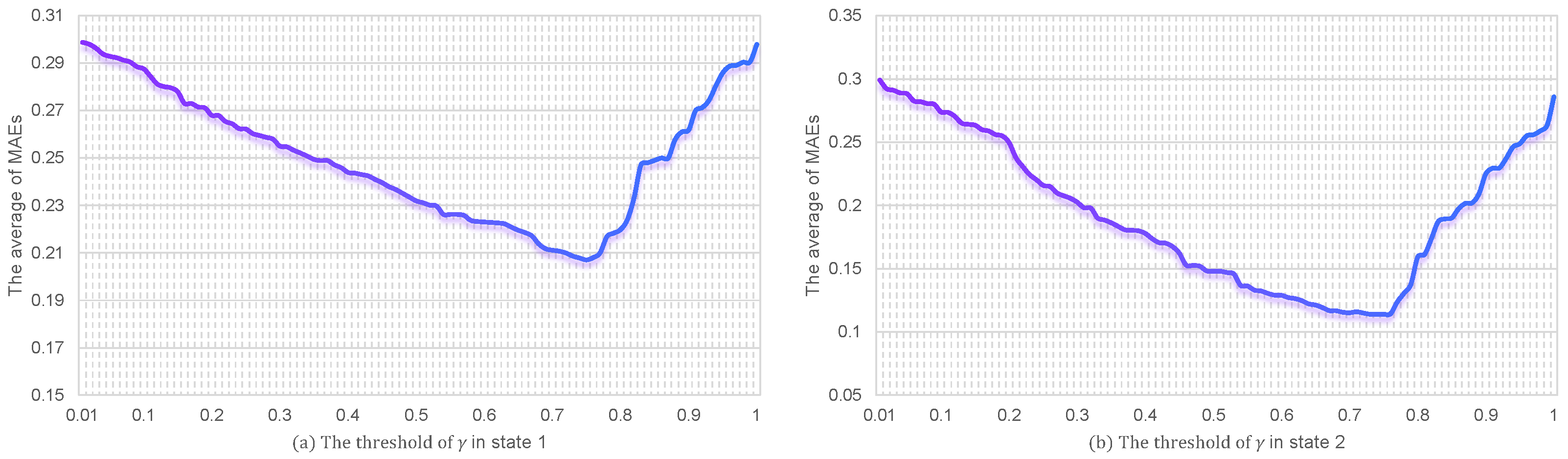
6.1. The Weight Threshold
6.2. Computational Complexity
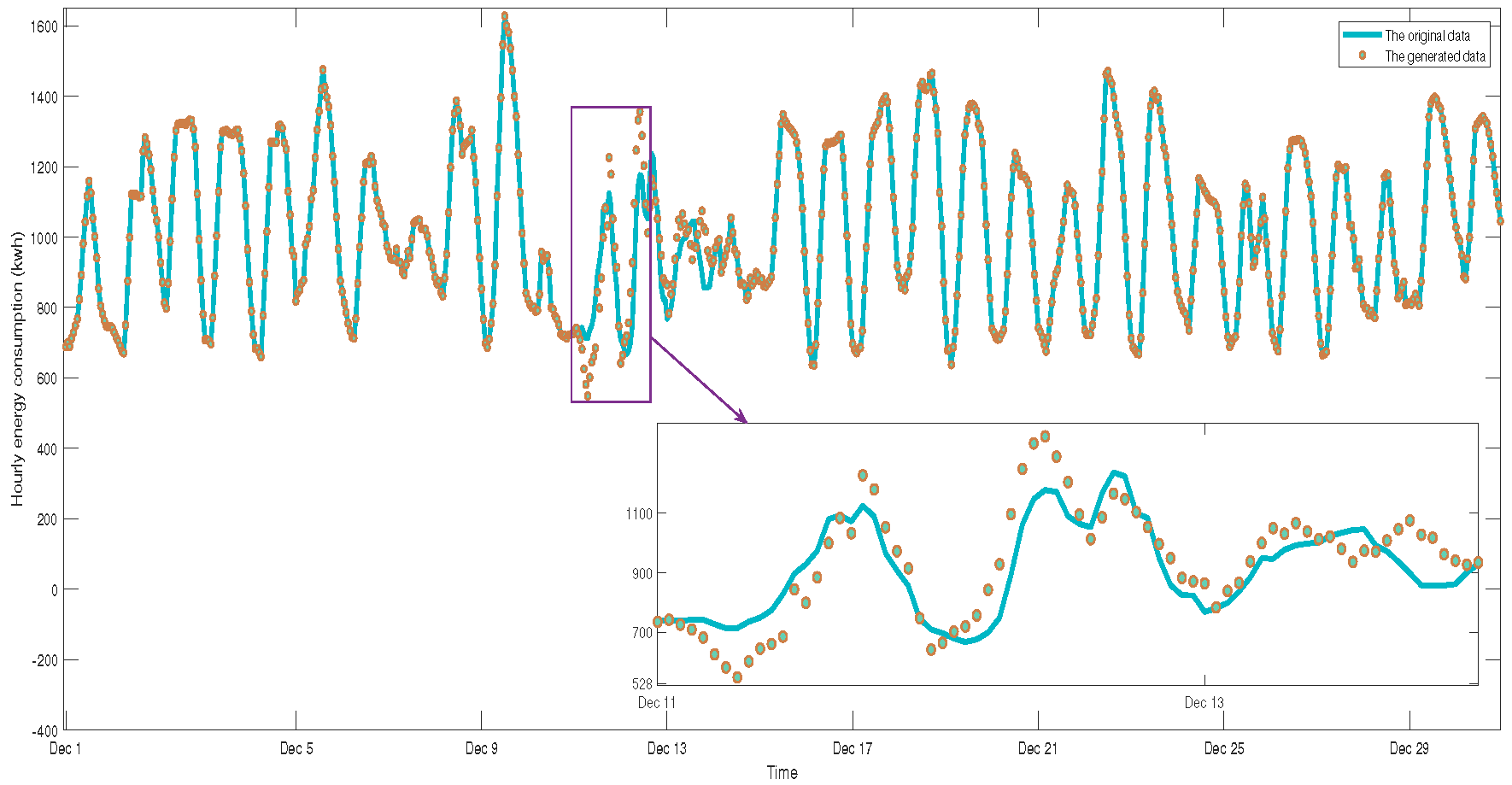
6.3. Continuous Missing vs. Random Missing
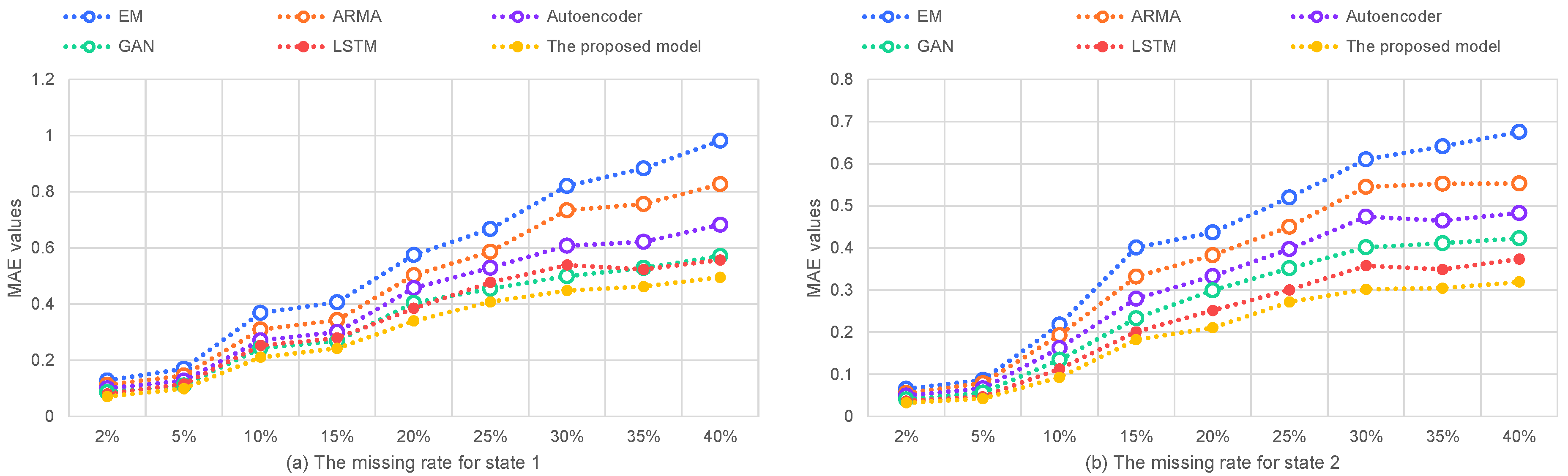
6.4. Effects of Different Missing Data Ratios
6.5. Bias Analysis and Mitigation Strategies
6.6. Robustness Analysis of CTIM Model
6.7. Online Adaptation and Model Extension
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schafer, J.L.; Olsen, M.K. Multiple imputation for multivariate missing-data problems: A data analyst’s perspective. Multivar. Behav. Res. 1998, 33, 545–571. [Google Scholar] [CrossRef] [PubMed]
- Reinsel, G.C. Elements of Multivariate Time Series Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Li, J.; Izakian, H.; Pedrycz, W.; Jamal, I. Clustering-based anomaly detection in multivariate time series data. Appl. Soft Comput. 2021, 100, 106919. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Wang, Y.; Ran, B. Missing value imputation for traffic-related time series data based on a multi-view learning method. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2933–2943. [Google Scholar] [CrossRef]
- Wu, R.; Hamshaw, S.D.; Yang, L.; Kincaid, D.W.; Etheridge, R.; Ghasemkhani, A. Data imputation for multivariate time series sensor data with large gaps of missing data. IEEE Sensors J. 2022, 22, 10671–10683. [Google Scholar] [CrossRef]
- Park, J.; Müller, J.; Arora, B.; Faybishenko, B.; Pastorello, G.; Varadharajan, C.; Sahu, R.; Agarwal, D. Long-term missing value imputation for time series data using deep neural networks. Neural Comput. Appl. 2023, 35, 9071–9091. [Google Scholar] [CrossRef]
- Wang, T.; Ke, H.; Jolfaei, A.; Wen, S.; Haghighi, M.S.; Huang, S. Missing value filling based on the collaboration of cloud and edge in artificial intelligence of things. IEEE Trans. Ind. Inform. 2021, 18, 5394–5402. [Google Scholar] [CrossRef]
- Luo, Y.; Cai, X.; Zhang, Y.; Xu, J. Multivariate time series imputation with generative adversarial networks. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Zhao, J.; Rong, C.; Lin, C.; Dang, X. Multivariate time series data imputation using attention-based mechanism. Neurocomputing 2023, 542, 126238. [Google Scholar] [CrossRef]
- Cismondi, F.; Fialho, A.S.; Vieira, S.M.; Reti, S.R.; Sousa, J.M.; Finkelstein, S.N. Missing data in medical databases: Impute, delete or classify? Artif. Intell. Med. 2013, 58, 63–72. [Google Scholar] [CrossRef]
- King, G.; Honaker, J.; Joseph, A.; Scheve, K. List-wise deletion is evil: What to do about missing data in political science. In Proceedings of the Annual Meeting of the American Political Science Association, Boston, MA, USA, 3–6 September 1998; Volume 52. [Google Scholar]
- Zhang, H.; Yue, D.; Dou, C.; Xie, X.; Li, K.; Hancke, G.P. Resilient optimal defensive strategy of TSK fuzzy-model-based microgrids’ system via a novel reinforcement learning approach. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 1921–1931. [Google Scholar] [CrossRef]
- Abu Alfeilat, H.A.; Hassanat, A.B.; Lasassmeh, O.; Tarawneh, A.S.; Alhasanat, M.B.; Eyal Salman, H.S.; Prasath, V.S. Effects of distance measure choice on k-nearest neighbor classifier performance: A review. Big Data 2019, 7, 221–248. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Zhang, S.; Deng, Z.; Zhu, Y.; Zong, M. k NN algorithm with data-driven k value. In Proceedings of the Advanced Data Mining and Applications: 10th International Conference, ADMA 2014, Guilin, China, 19–21 December 2014; Proceedings 10. Springer: Berlin/Heidelberg, Germany, 2014; pp. 499–512. [Google Scholar]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Cheng, D. Learning k for knn classification. ACM Trans. Intell. Syst. Technol. (TIST) 2017, 8, 43. [Google Scholar] [CrossRef]
- Moon, T.K. The expectation-maximization algorithm. IEEE Signal Process. Mag. 1996, 13, 47–60. [Google Scholar] [CrossRef]
- Fessler, J.A.; Hero, A.O. Space-alternating generalized expectation-maximization algorithm. IEEE Trans. Signal Process. 1994, 42, 2664–2677. [Google Scholar] [CrossRef]
- Zhang, K.; Gonzalez, R.; Huang, B.; Ji, G. Expectation–maximization approach to fault diagnosis with missing data. IEEE Trans. Ind. Electron. 2014, 62, 1231–1240. [Google Scholar] [CrossRef]
- Chen, L.; Wu, Z.; Cao, J.; Zhu, G.; Ge, Y. Travel recommendation via fusing multi-auxiliary information into matrix factorization. ACM Trans. Intell. Syst. Technol. (TIST) 2020, 11, 1–24. [Google Scholar] [CrossRef]
- He, X.; Tang, J.; Du, X.; Hong, R.; Ren, T.; Chua, T.S. Fast matrix factorization with nonuniform weights on missing data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2791–2804. [Google Scholar] [CrossRef]
- Wu, P.; Pei, M.; Wang, T.; Liu, Y.; Liu, Z.; Zhong, L. A Low-Rank Bayesian Temporal Matrix Factorization for the Transfer Time Prediction Between Metro and Bus Systems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7206–7222. [Google Scholar] [CrossRef]
- Žitnik, M.; Zupan, B. Data fusion by matrix factorization. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 41–53. [Google Scholar] [CrossRef]
- Zhang, H.; Yue, D.; Yue, W.; Li, K.; Yin, M. MOEA/D-based probabilistic PBI approach for risk-based optimal operation of hybrid energy system with intermittent power uncertainty. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 51, 2080–2090. [Google Scholar] [CrossRef]
- Batista, G.E.; Monard, M.C. An analysis of four missing data treatment methods for supervised learning. Appl. Artif. Intell. 2003, 17, 519–533. [Google Scholar] [CrossRef]
- Gómez, V.; Maravall, A.; Peña, D. Missing observations in ARIMA models: Skipping approach versus additive outlier approach. J. Econom. 1999, 88, 341–363. [Google Scholar] [CrossRef]
- Abiri, N.; Linse, B.; Edén, P.; Ohlsson, M. Establishing strong imputation performance of a denoising autoencoder in a wide range of missing data problems. Neurocomputing 2019, 365, 137–146. [Google Scholar] [CrossRef]
- Kang, M.; Zhu, R.; Chen, D.; Liu, X.; Yu, W. CM-GAN: A cross-modal generative adversarial network for imputing completely missing data in digital industry. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 2917–2926. [Google Scholar] [CrossRef]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [PubMed]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Bianchi, F.M.; Livi, L.; Mikalsen, K.Ø.; Kampffmeyer, M.; Jenssen, R. Learning representations of multivariate time series with missing data. Pattern Recognit. 2019, 96, 106973. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.; Jiang, F.; Chen, W.; Wang, M.; Zhai, C. A bi-directional missing data imputation scheme based on LSTM and transfer learning for building energy data. Energy Build. 2020, 216, 109941. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, K.; Li, J.; Lin, X.; Yang, B. LSTM-based traffic flow prediction with missing data. Neurocomputing 2018, 318, 297–305. [Google Scholar] [CrossRef]
- Tang, B.; Matteson, D.S. Probabilistic transformer for time series analysis. Adv. Neural Inf. Process. Syst. 2021, 34, 23592–23608. [Google Scholar]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A transformer-based framework for multivariate time series representation learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual, 14–18 August 2021; pp. 2114–2124. [Google Scholar]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef]
- Liu, J.; Pasumarthi, S.; Duffy, B.; Gong, E.; Datta, K.; Zaharchuk, G. One model to synthesize them all: Multi-contrast multi-scale transformer for missing data imputation. IEEE Trans. Med. Imaging 2023, 42, 2577–2591. [Google Scholar] [CrossRef] [PubMed]
- Kline, J.; Kline, C. Power modeling for an industrial installation. In Proceedings of the Cement Industry Technical Conference, 2017 IEEE-IAS/PCA, Calgary, AB, Canada, 21–25 May 2017; pp. 1–10. [Google Scholar]
- Wang, H.; Ma, S.; Dong, L.; Huang, S.; Zhang, D.; Wei, F. Deepnet: Scaling transformers to 1000 layers. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 6761–6774. [Google Scholar] [CrossRef]
- Kazemnejad, A.; Padhi, I.; Natesan Ramamurthy, K.; Das, P.; Reddy, S. The impact of positional encoding on length generalization in transformers. Adv. Neural Inf. Process. Syst. 2023, 36, 24892–24928. [Google Scholar]
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. Discuss. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, J.; Li, B.; Lu, J. Normalization and solvability of dynamic-algebraic Boolean networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3301–3306. [Google Scholar] [CrossRef]
- Zahari, F.Z.; Khalid, K.; Roslan, R.; Sufahani, S.; Mohamad, M.; Rusiman, M.S.; Ali, M. Forecasting natural rubber price in Malaysia using ARIMA. J. Physics: Conf. Ser. 2018, 995, 012013. [Google Scholar] [CrossRef]
- Wahbah, M.; El-Fouly, T.H.; Zahawi, B.; Feng, S. Hybrid beta-KDE model for solar irradiance probability density estimation. IEEE Trans. Sustain. Energy 2019, 11, 1110–1113. [Google Scholar] [CrossRef]
- Mesleh, R.; Ikki, S.S.; Aggoune, H.M. Quadrature spatial modulation. IEEE Trans. Veh. Technol. 2015, 64, 2738–2742. [Google Scholar] [CrossRef]





| Dataset | Attribution | Time | Initial Length |
|---|---|---|---|
| Electricity | 10 | 31 days | 744 |
| Heat | 14 | 31 days | 744 |
| Model | Training Time (s/epoch) | Memory Usage (GB) |
|---|---|---|
| Traditional SA | 145 | 3.2 |
| The proposed model | 82 | 1.8 |
| Reduction | 43.4% | 43.8% |
| Methods | State 1 (Continuous Missing) | State 2 (Random Missing) | ||||||
|---|---|---|---|---|---|---|---|---|
| In(Mean) | Sensitivity | 95% CI of MAE | In(Mean) | Sensitivity | 95% CI of MAE | |||
| EM | 0.2382 | 0.05% | 0.0032 | 0.278 ± 0.022 | 0.1643 | 0.01% | 0.0013 | 0.191 ± 0.015 |
| ARIMA | 0.2061 | 2.19% | 0.0100 | 0.241 ± 0.019 | 0.1402 | 40.59% | 0.0370 | 0.163 ± 0.013 |
| Autoencoder | 0.1790 | 13.38% | 0.0162 | 0.209 ± 0.016 | 0.1177 | 34.99% | 0.0275 | 0.137 ± 0.011 |
| GAN | 0.1581 | 20.09% | 0.0150 | 0.185 ± 0.014 | 0.1018 | 29.67% | 0.0245 | 0.119 ± 0.010 |
| LSTM | 0.1610 | 18.42% | 0.0149 | 0.188 ± 0.014 | 0.1014 | 31.82% | 0.0244 | 0.118 ± 0.009 |
| The proposed model | 0.1351 | 11.10% | 0.0096 | 0.158 ± 0.012 | 0.0875 | 14.85% | 0.0218 | 0.102 ± 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ding, H.; Li, H. Multivariate Time-Series Missing Data Imputation with Convolutional Transformer Model. Symmetry 2025, 17, 686. https://doi.org/10.3390/sym17050686
Wang Y, Ding H, Li H. Multivariate Time-Series Missing Data Imputation with Convolutional Transformer Model. Symmetry. 2025; 17(5):686. https://doi.org/10.3390/sym17050686
Chicago/Turabian StyleWang, Yanxia, He Ding, and Hongdun Li. 2025. "Multivariate Time-Series Missing Data Imputation with Convolutional Transformer Model" Symmetry 17, no. 5: 686. https://doi.org/10.3390/sym17050686
APA StyleWang, Y., Ding, H., & Li, H. (2025). Multivariate Time-Series Missing Data Imputation with Convolutional Transformer Model. Symmetry, 17(5), 686. https://doi.org/10.3390/sym17050686





