Electroweak Form Factors of Baryons in Dense Nuclear Matter
Abstract
1. Introduction
2. Octet Baryon Electromagnetic and Axial Form Factors
2.1. Electromagnetic Transitions
2.2. Weak Transitions and Axial Form Factors
3. Covariant Quark Model for the Free Space and Nuclear Medium
3.1. Model for the Valence Quark Contributions
3.1.1. Radial Wave Functions
3.1.2. Electromagnetic Interaction with Quarks
3.1.3. Weak Interaction with Quarks
3.1.4. Extension of the Model to the Lattice QCD Regime
3.2. Meson Cloud Contributions
3.2.1. Electromagnetic Transitions
- the octet baryon magnetic moments of the , , , , and [149];
3.2.2. Axial Transitions
3.3. Extension of the Model to the Nuclear Medium
3.4. Summary of the Formalism
4. Electroweak Form Factors in Nuclear Medium
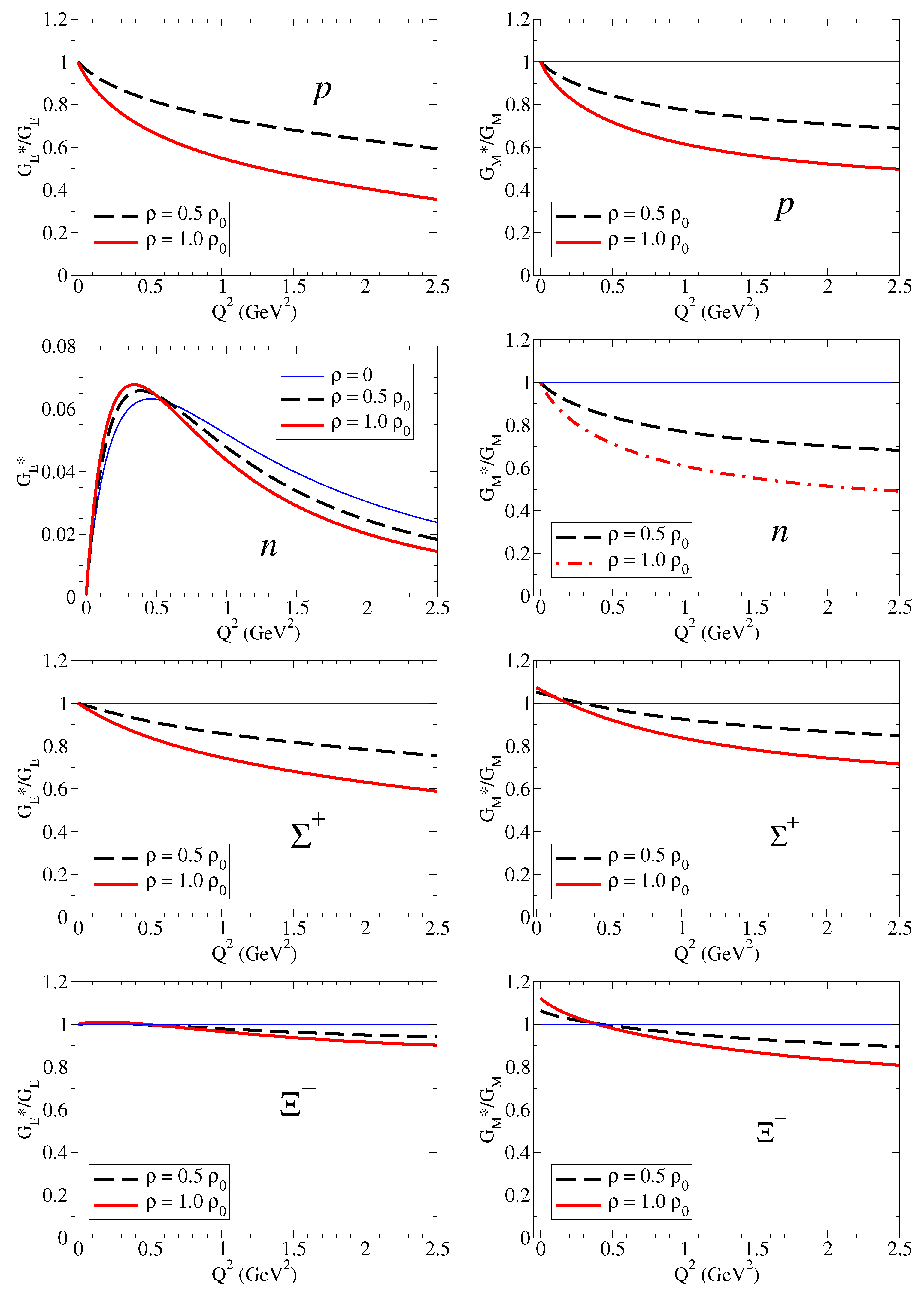
4.1. Electromagnetic Form Factors
4.1.1. Electromagnetic Ratios and
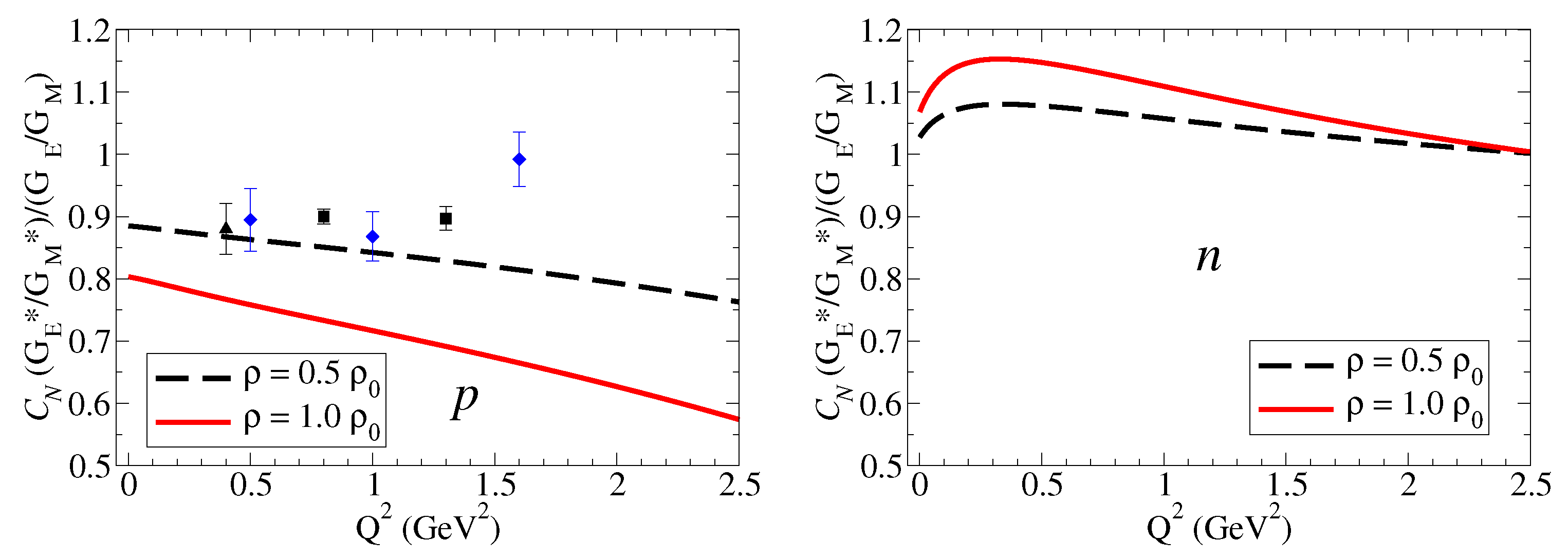
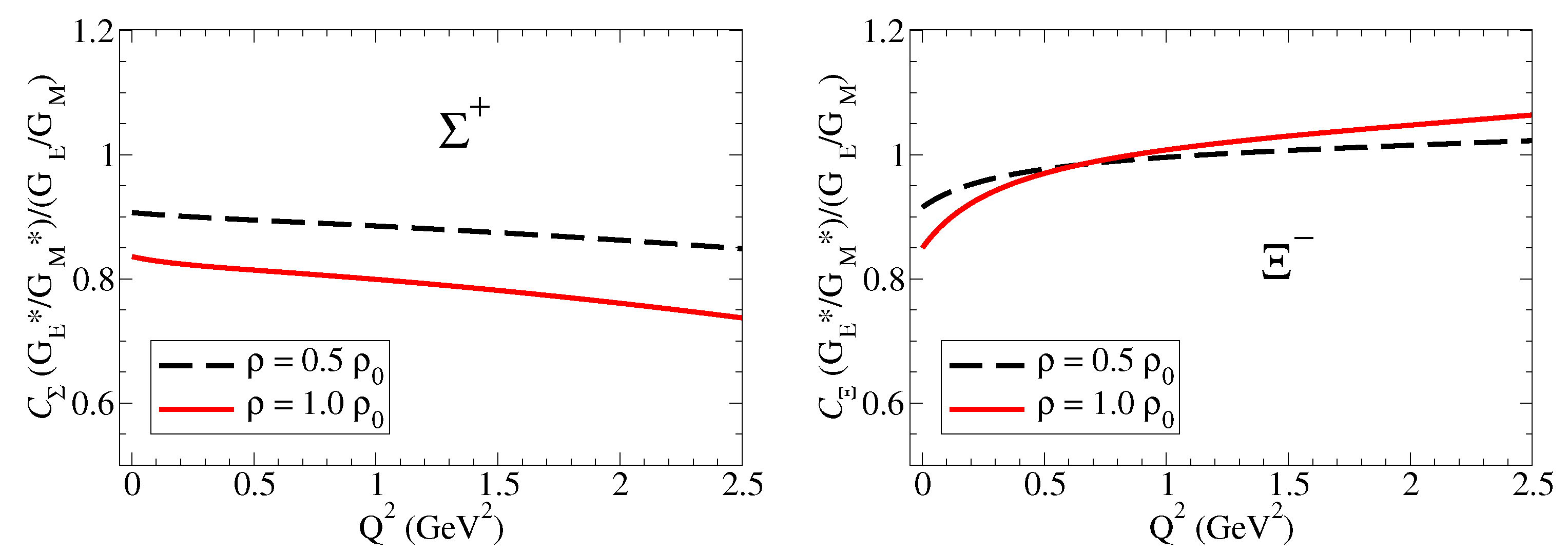
4.1.2. Electromagnetic Double Ratios of Octet Baryons
4.2. Axial Form Factors
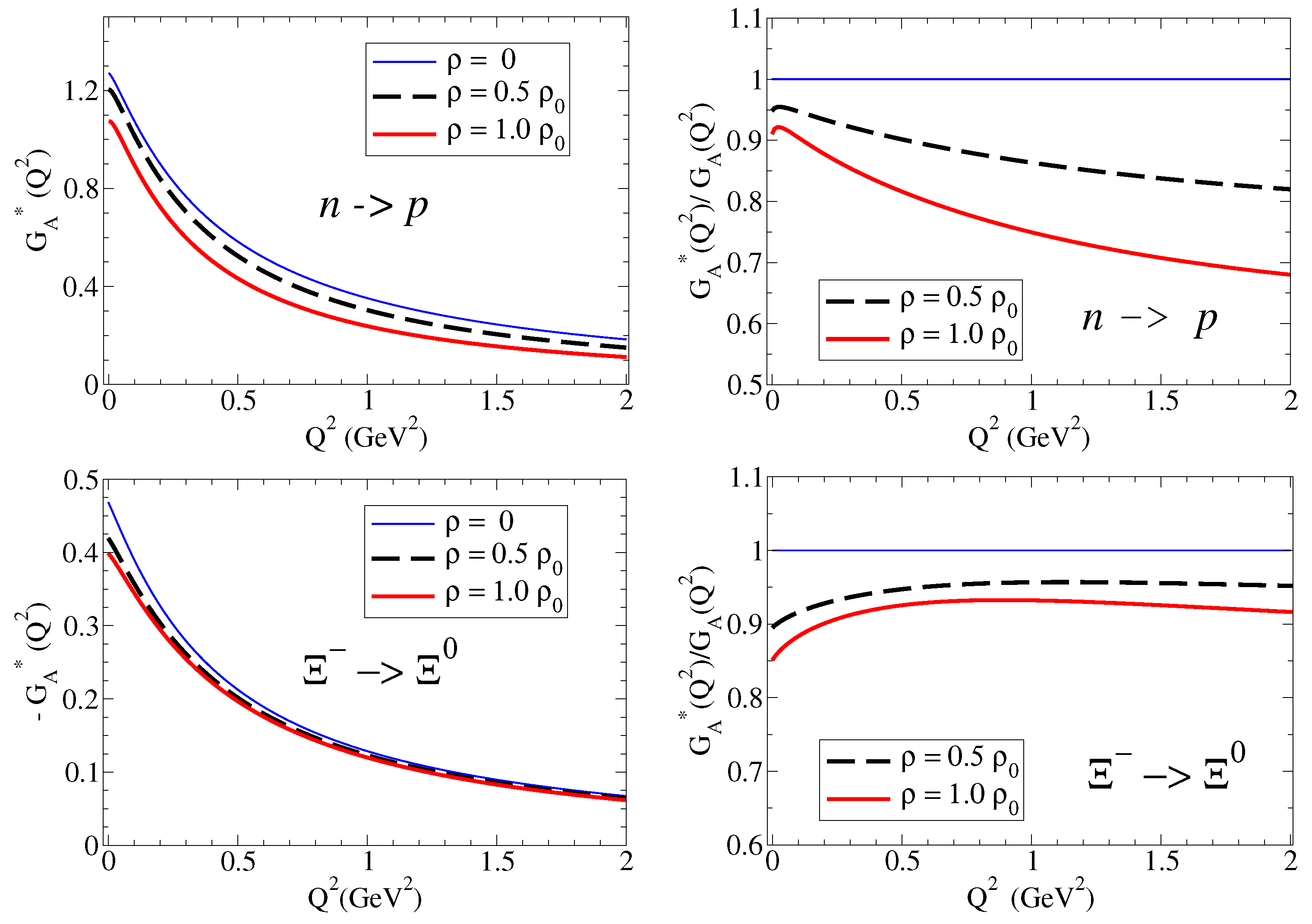
4.2.1. Axial-Vector Form Factor
4.2.2. Induced Pseudoscalar Form Factor
5. Applications
5.1. Nucleon Bound to a Nucleus
5.2. Hyperons in Dense Nuclear Matter
6. Discussion
7. Outlook and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Gell–Mann Matrices
Appendix B. Information About the Valence Quark Contributions
| B | ||
|---|---|---|
| p | ||
| n | ||
Appendix B.1. Quark Electromagnetic Form Factors
| B | ||
|---|---|---|
| p | ||
| n | ||
| B | |
|---|---|
| p | |
| n | |
Appendix B.2. Quark Axial Form Factors
| 1 | |||||
| 0 | |||||
| 0 | |||||
| 0 | |||||
| 0 | |||||
| 1 | |||||
| , | |||||
| 0 |
Appendix C. Information About the Meson Cloud Contributions
Appendix C.1. Electromagnetic Transitions
| (0) | (0) | (0) | (0) | (GeV2) | (GeV2) | |
|---|---|---|---|---|---|---|
| 0.0510 | 0.216 | 0.00286 | 0.0821 | 0.618 | 1.281 |
Appendix C.2. Axial Transitions
References
- Brown, G.E.; Rho, M. Scaling effective Lagrangians in a dense medium. Phys. Rev. Lett. 1991, 66, 2720. [Google Scholar] [CrossRef] [PubMed]
- Brooks, W.K.; Strauch, S.; Tsushima, K. Medium Modifications of Hadron Properties and Partonic Processes. J. Phys. Conf. Ser. 2011, 299, 012011. [Google Scholar] [CrossRef]
- Saito, K.; Tsushima, K.; Thomas, A.W. Nucleon and hadron structure changes in the nuclear medium and impact on observables. Prog. Part. Nucl. Phys. 2007, 58, 1–167. [Google Scholar] [CrossRef]
- Miyatsu, T.; Cheoun, M.K.; Saito, K. Equation of State for Neutron Stars with Hyperons and Quarks in the Relativistic Hartree–fock Approximation. Astrophys. J. 2015, 813, 135. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K.; Cheoun, M.K. Weak interaction axial form factors of the octet baryons in nuclear medium. Phys. Rev. D 2025, 111, 013002. [Google Scholar] [CrossRef]
- Aubert, J.J.; Bassompierre, G.; Becks, K.H.; Best, C.; Bohm, E.; de Bouard, X.; Brasse, F.W.; Broll, C.; Brown, S.; Carr, J.; et al. The ratio of the nucleon structure functions F2n for iron and deuterium. Phys. Lett. B 1983, 123, 275. [Google Scholar] [CrossRef]
- Arnold, R.G.; Bosted, P.E.; Chang, C.C.; Gomez, J.; Katramatou, A.T.; Petratos, G.; Rahbar, A.A.; Rock, S.; Sill, A.F.; Szalata, Z.M.; et al. Measurements of the a-Dependence of Deep Inelastic electron Scattering from Nuclei. Phys. Rev. Lett. 1984, 52, 727. [Google Scholar] [CrossRef]
- Hen, O.; Miller, G.A.; Piasetzky, E.; Weinstein, L.B. Nucleon-Nucleon Correlations, Short-lived Excitations, and the Quarks Within. Rev. Mod. Phys. 2017, 89, 045002. [Google Scholar] [CrossRef]
- Dieterich, S.; Bartsch, P.; Baumann, D.; Bermuth, J.; Bohinc, K.; Bohm, R.; Bosnar, D.; Derber, S.; Ding, M.; Distler, M.; et al. Polarization transfer in the 4He(e→,e′p→)3H reaction. Phys. Lett. 2001, B500, 47. [Google Scholar] [CrossRef]
- Strauch, S.; Dieterich, S.; Aniol, K.A.; Ann, J.R.; Baker, O.K.; Bertozzi, W.; Boswell, M.; Brash, E.J.; Chai, Z.; Chen, J.P.; et al. Polarization transfer in the 4He(e→,e′p→)3H reaction up to Q2= 2.6 (GeV/c)2. Phys. Rev. Lett. 2003, 91, 052301. [Google Scholar] [CrossRef]
- Strauch, S. [E93-049 Collaboration]. Medium modification of the proton form-factor. Eur. Phys. J. A 2004, 19, 153. [Google Scholar] [CrossRef]
- Paolone, M.; Malace, S.P.; Strauch, S.; Albayrak, I.; Arrington, J.; Berman, B.L.; Brash, E.J.; Briscoe, B.; Camsonne, A.; Chen, J.P.; et al. Polarization Transfer in the 4He(e,e′p)3H at Q2=0.8 and 1.3 (GeV/c)2. Phys. Rev. Lett. 2010, 105, 072001. [Google Scholar] [CrossRef] [PubMed]
- Malace, S.P.; Paolone, M.; Strauch, S.; Albayrak, I.; Arrington, J.; Berman, B.L.; Brash, E.J.; Briscoe, W.J.; Camsonne, A.; Chen, J.P.; et al. A precise extraction of the induced polarization in the 4He(e,e′p)3H reaction. Phys. Rev. Lett. 2011, 106, 052501. [Google Scholar] [CrossRef]
- Malov, S.; Wijesooriya, K.; Baker, F.T.; Bimbot, L.; Brash, E.J.; Chang, C.C.; Finn, J.M.; Fissum, K.G.; Gao, J.; Gilman, R.; et al. Polarization transfer in the 16O(e→,e′p→)15N reaction. Phys. Rev. C 2000, 62, 057302. [Google Scholar] [CrossRef]
- Izraeli, D.; Brecelj, T.; Achenbach, P.; Ashkenazi, A.; Böhm, R.; Cohen, E.O.; Distler, M.O.; Esser, A.; Gilman, R.; Kolar, T.; et al. Measurement of polarization-transfer to bound protons in carbon and its virtuality dependence. Phys. Lett. B 2018, 781, 95–98. [Google Scholar] [CrossRef]
- Kolar, T.; Achenbach, P.; Christmann, M.; Distler, M.O.; Doria, L.; Eckert, P.; Esser, A.; Giusti, C.; Geimer, C.; Gülker, P.; et al. Measurement of polarization transfer in the quasi-elastic 40Ca(e→,e′p→) process. Phys. Lett. B 2023, 847, 138309. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K.; Thomas, A.W. Octet Baryon Electromagnetic form Factors in Nuclear Medium. J. Phys. G 2013, 40, 015102. [Google Scholar] [CrossRef]
- Ramalho, G.; de Melo, J.P.B.C.; Tsushima, K. Octet baryon electromagnetic form factor double ratios (GE*/GM*)/(GE/GM) in a nuclear medium. Phys. Rev. D 2019, 100, 014030. [Google Scholar] [CrossRef]
- Frank, M.R.; Jennings, B.K.; Miller, G.A. The Role of color neutrality in nuclear physics: Modifications of nucleonic wave functions. Phys. Rev. C 1996, 54, 920. [Google Scholar] [CrossRef]
- Lu, D.H.; Tsushima, K.; Thomas, A.W.; Williams, A.G.; Saito, K. Electromagnetic form-factors of the bound nucleon. Phys. Rev. C 1999, 60, 068201. [Google Scholar] [CrossRef]
- Smith, J.R.; Miller, G.A. Chiral solitons in nuclei: Electromagnetic form-factors. Phys. Rev. C 2004, 70, 065205. [Google Scholar] [CrossRef]
- Cloet, I.C.; Miller, G.A.; Piasetzky, E.; Ron, G. Neutron Properties in the Medium. Phys. Rev. Lett. 2009, 103, 082301. [Google Scholar] [CrossRef]
- De Araújo, W.R.B.; de Melo, J.P.B.C.; Tsushima, K. Study of the in-medium nucleon electromagnetic form factors using a light-front nucleon wave function combined with the quark-meson coupling model. Nucl. Phys. A 2018, 970, 325. [Google Scholar] [CrossRef]
- Miller, G.A. Light front cloudy bag model: Nucleon electromagnetic form-factors. Phys. Rev. C 2002, 66, 032201. [Google Scholar] [CrossRef]
- Yakhshiev, U.T.; Meissner, U.G.; Wirzba, A. Electromagnetic form-factors of bound nucleons revisited. Eur. Phys. J. A 2003, 16, 569. [Google Scholar] [CrossRef]
- Lu, D.H.; Thomas, A.W.; Tsushima, K.; Williams, A.G.; Saito, K. In-medium electron-nucleon scattering. Phys. Lett. B 1998, 417, 217. [Google Scholar] [CrossRef]
- Lu, D.H.; Tsushima, K.; Thomas, A.W.; Williams, A.G.; Saito, K. The Neutron charge form-factor in helium-3. Phys. Lett. B 1998, 441, 27. [Google Scholar] [CrossRef]
- Tsushima, K.; Kim, H.; Saito, K. Effect of the bound nucleon form-factors on charged current neutrino nucleus scattering. Phys. Rev. C 2004, 70, 038501. [Google Scholar] [CrossRef]
- Christov, C.V.; Gorski, A.Z.; Goeke, K.; Pobylitsa, P.V. Electromagnetic form-factors of the nucleon in the chiral quark soliton model. Nucl. Phys. A 1995, 592, 513. [Google Scholar] [CrossRef]
- Letter of Intent to JLab PAC 35. In Neutron Properties in the Nuclear Medium Studied by Polarization Measurements; Gilman, R.; Higinbotham, D.W.; Lichtenstadt, J.; Ron, G.; Strauch, S., Eds. Available online: https://hallaweb.jlab.org/collab/PAC/PAC35/LOI-10-007-Neutron-Modification.pdf (accessed on 1 March 2025).
- Brown, B.A.; Wildenthal, B.H. Experimental and Theoretical Gamow-Teller Beta-Decay Observables for the sd-Shell Nuclei. Atom. Data Nucl. Data Tabl. 1985, 33, 347. [Google Scholar] [CrossRef]
- Gysbers, P.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Morris, T.D.; Navrátil, P.; Papenbrock, T.; Quaglioni, S.; Schwenk, A.; Stroberg, S.R.; et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat. Phys. 2019, 15, 428. [Google Scholar] [CrossRef]
- Thomas, A.W. Chiral Symmetry And The Bag Model: A New Starting Point For Nuclear Physics. Adv. Nucl. Phys. 1984, 13, 1–137. [Google Scholar]
- Lu, D.H.; Thomas, A.W.; Tsushima, K. Medium modification of the nucleon axial form-factor. arXiv 2001, arXiv:nucl-th/0112001. [Google Scholar]
- Christov, C.V.; Blotz, A.; Kim, H.-C.; Pobylitsa, P.; Watabe, T.; Meissner, T.; Arriola, E.R.; Goeke, K. Baryons as non-topological chiral solitons. Prog. Part. Nucl. Phys. 1996, 37, 91–191. [Google Scholar] [CrossRef]
- Rakhimov, A.M.; Khanna, F.C.; Yakhshiev, U.T.; Musakhanov, M.M. Density dependence of meson nucleon vertices in nuclear matter. Nucl. Phys. A 1998, 643, 383. [Google Scholar] [CrossRef]
- Meier, F.; Walliser, H. Quantum corrections to baryon properties in chiral soliton models. Phys. Rept. 1997, 289, 383. [Google Scholar] [CrossRef]
- Meissner, U.G.; Kaiser, N.; Weise, W. Nucleons as Skyrme Solitons with Vector Mesons: Electromagnetic and Axial Properties. Nucl. Phys. A 1987, 466, 685. [Google Scholar] [CrossRef]
- Meissner, U.G. Chiral Symmetry and Medium Modifications of Nucleon Properties. Phys. Lett. B 1989, 220, 1. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. Electromagnetic transition form factors of baryon resonances. Prog. Part. Nucl. Phys. 2024, 136, 104097. [Google Scholar] [CrossRef]
- Aznauryan, I.G.; Bashir, A.; Braun, V.; Brodsky, S.J.; Burkert, V.D.; Chang, L.; Chen, C.h.; El-Bennich, B.; Cloet, I.C.; Cole, P.L.; et al. Studies of Nucleon Resonance Structure in Exclusive Meson Electroproduction. Int. J. Mod. Phys. E 2013, 22, 1330015. [Google Scholar] [CrossRef]
- Aznauryan, I.G.; Burkert, V.D. Electroexcitation of nucleon resonances. Prog. Part. Nucl. Phys. 2012, 67, 1. [Google Scholar] [CrossRef]
- Eichmann, G.; Ramalho, G. Nucleon resonances in Compton scattering. Phys. Rev. D 2018, 98, 093007. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. Axial form factors of the octet baryons in a covariant quark model. Phys. Rev. D 2016, 94, 014001. [Google Scholar] [CrossRef]
- Gaillard, J.M.; Sauvage, G. Hyperon Beta Decays. Ann. Rev. Nucl. Part. Sci. 1984, 34, 351. [Google Scholar] [CrossRef]
- Bernard, V.; Elouadrhiri, L.; Meissner, U.G. Axial structure of the nucleon: Topical Review. J. Phys. G 2002, 28, R1. [Google Scholar] [CrossRef]
- Gorringe, T.; Fearing, H.W. Induced pseudoscalar coupling of the proton weak interaction. Rev. Mod. Phys. 2004, 76, 31. [Google Scholar] [CrossRef]
- Schindler, M.R.; Scherer, S. Nucleon Form Factors of the Isovector Axial-Vector Current: Situation of Experiments and Theory. Eur. Phys. J. A 2007, 32, 429. [Google Scholar] [CrossRef]
- Ramalho, G. N* Form Factors based on a Covariant Quark Model. Few Body Syst. 2018, 59, 92. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T.; Gross, F. D-state effects in the electromagnetic NΔ transition. Phys. Rev. D 2008, 78, 114017. [Google Scholar] [CrossRef]
- Gross, F.; Ramalho, G.; Peña, M.T. A Pure S-wave covariant model for the nucleon. Phys. Rev. C 2008, 77, 015202. [Google Scholar] [CrossRef]
- Gross, F.; Ramalho, G.; Peña, M.T. Covariant nucleon wave function with S, D, and P-state components. Phys. Rev. D 2012, 85, 093005. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K.; Gross, F. A Relativistic quark model for the Ω− electromagnetic form factors. Phys. Rev. D 2009, 80, 033004. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. Octet baryon electromagnetic form factors in a relativistic quark model. Phys. Rev. D 2011, 84, 054014. [Google Scholar] [CrossRef]
- Gross, F.; Ramalho, G.; Tsushima, K. Using baryon octet magnetic moments and masses to fix the pion cloud contribution. Phys. Lett. B 2010, 690, 183. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. Octet to decuplet electromagnetic transition in a relativistic quark model. Phys. Rev. D 2013, 87, 093011. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. Electromagnetic form factors of the Delta in a S-wave approach. J. Phys. G 2009, 36, 085004. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T.; Gross, F. Electromagnetic form factors of the Delta with D-waves. Phys. Rev. D 2010, 81, 113011. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T.; Gross, F. Electric quadrupole and magnetic octupole moments of the Delta. Phys. Lett. B 2009, 678, 355. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. Extracting the Ω− electric quadrupole moment from lattice QCD data. Phys. Rev. D 2011, 83, 054011. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T.; Stadler, A. The shape of the Δ baryon in a covariant spectator quark model. Phys. Rev. D 2012, 86, 093022. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. Covariant spectator quark model description of the γ*Λ→Σ0 transition. Phys. Rev. D 2012, 86, 114030. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. What is the role of the meson cloud in the Σ*0→γΛ and Σ*→γΣ decays? Phys. Rev. D 2013, 88, 053002. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T.; Tsushima, K. Hyperon electromagnetic timelike elastic form factors at large q2. Phys. Rev. D 2020, 101, 014014. [Google Scholar] [CrossRef]
- Ramalho, G. Electromagnetic form factors of the Ω− baryon in the spacelike and timelike regions. Phys. Rev. D 2021, 103, 074018. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T.; Tsushima, K.; Cheoun, M.K. Electromagnetic |GE/GM| ratios of hyperons at large timelike q2. Phys. Lett. B 2024, 858, 139060. [Google Scholar] [CrossRef]
- Ramalho, G. Ovariant model for Dalitz decays of decuplet baryons to octet baryons. Phys. Rev. D 2020, 102, 054016. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. Meson cloud contributions to the Dalitz decays of decuplet to octet baryons. Phys. Rev. D 2023, 108, 074019. [Google Scholar] [CrossRef]
- Saito, K.; Tsushima, K.; Thomas, A.W. Selfconsistent description of finite nuclei based on a relativistic quark model. Nucl. Phys. A 1996, 609, 339. [Google Scholar] [CrossRef]
- Lu, D.H.; Yang, S.N.; Thomas, A.W. On the role of the pion cloud in nucleon electromagnetic form-factors. Nucl. Phys. A 2001, 684, 296. [Google Scholar] [CrossRef]
- Theberge, S.; Thomas, A.W. Magnetic Moments Of The Nucleon Octet Calculated In The Cloudy Bag Model. Nucl. Phys. A 1983, 393, 252. [Google Scholar] [CrossRef]
- Lu, D.H.; Thomas, A.W.; Williams, A.G. Electromagnetic form-factors of the nucleon in an improved quark model. Phys. Rev. C 1998, 57, 2628–2637. [Google Scholar] [CrossRef]
- Kubodera, K.; Kohyama, Y.; Oikawa, K.; Kim, C.W. Weak Interactions Form-factors of the Octet Baryons in the Cloudy Bag Model. Nucl. Phys. A 1985, 439, 695. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Tsushima, K.; Kohyama, Y.; Kubodera, K. Semileptonic Beta Decay Form-factors and Magnetic Moments of Octet Baryons: Recoil Effects and Center-of-mass Corrections in the Cloudy Bag Model Including Gluonic Effects. Nucl. Phys. A 1989, 500, 429. [Google Scholar]
- Tsushima, K.; Yamaguchi, T.; Kohyama, Y.; Kubodera, K. Weak Interaction Form-factors and Magnetic Moments of Octet Baryons: Chiral Bag Model with Gluonic Effects. Nucl. Phys. A 1988, 489, 557. [Google Scholar] [CrossRef]
- Eichmann, G.; Sanchis-Alepuz, H.; Williams, R.; Alkofer, R.; Fischer, C.S. Baryons as relativistic three-quark bound states. Prog. Part. Nucl. Phys. 2016, 91, 100. [Google Scholar] [CrossRef]
- Cloet, I.C.; Roberts, C.D. Explanation and Prediction of Observables using Continuum Strong QCD. Prog. Part. Nucl. Phys. 2014, 77, 1. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D. Dyson-Schwinger equations: A Tool for hadron physics. Int. J. Mod. Phys. E 2003, 12, 297. [Google Scholar] [CrossRef]
- Bernard, V.; Fearing, H.W.; Hemmert, T.R.; Meissner, U.G. The form-factors of the nucleon at small momentum transfer. Nucl. Phys. A 1998, 635, 121, Erratum in Nucl. Phys. A 1998, 642, 563.. [Google Scholar] [CrossRef]
- Hammer, H.W.; Drechsel, D.; Meissner, U.G. On the pion cloud of the nucleon. Phys. Lett. B 2004, 586, 291. [Google Scholar] [CrossRef]
- Meissner, U.G. The Pion cloud of the nucleon: Facts and popular fantasies. AIP Conf. Proc. 2007, 904, 142. [Google Scholar]
- Ronchen, D.; Doring, M.; Huang, F.; Haberzettl, H.; Haidenbauer, J.; Hanhart, C.; Krewald, S.; Meissner, U.G.; Nakayama, K. Coupled-channel dynamics in the reactions πN→πN, ηN, KΛ, KΣ. Eur. Phys. J. A 2013, 49, 44. [Google Scholar] [CrossRef]
- Pascalutsa, V.; Vanderhaeghen, M.; Yang, S.N. Electromagnetic excitation of the Δ(1232)-resonance. Phys. Rept. 2007, 437, 125. [Google Scholar] [CrossRef]
- Alexandrou, C.; Koutsou, G.; Neff, H.; Negele, J.W.; Schroers, W.; Tsapalis, A. Nucleon to delta electromagnetic transition form factors in lattice QCD. Phys. Rev. D 2008, 77, 085012. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T.; Gross, F. A Covariant model for the nucleon and the Delta. Eur. Phys. J. A 2008, 36, 329. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. Valence quark contribution for the γN→Δ quadrupole transition extracted from lattice QCD. Phys. Rev. D 2009, 80, 013008. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. Nucleon and γN→Δ lattice form factors in a constituent quark model. J. Phys. G 2009, 36, 115011. [Google Scholar] [CrossRef]
- Ramalho, G. Parametrizations of the γ*N→Δ(1232) quadrupole form factors and Siegert’s theorem. Phys. Rev. D 2016, 94, 114001. [Google Scholar] [CrossRef]
- Ramalho, G. New low-Q2 measurements of the γ*N→Δ(1232) Coulomb quadrupole form factor, pion cloud parametrizations and Siegert’s theorem. Eur. Phys. J. A 2018, 54, 75. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. Valence quark contributions for the γN→P11(1440) form factors. Phys. Rev. D 2010, 81, 074020. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. γ*N→N(1710) transition at high momentum transfer. Phys. Rev. D 2014, 89, 073010. [Google Scholar] [CrossRef]
- Ramalho, G. Semirelativistic approximation to the γ*N→N(1520) and γ*N→N(1535) transition form factors. Phys. Rev. D 2017, 95, 054008. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. A covariant model for the γN→N(1535) transition at high momentum transfer. Phys. Rev. D 2011, 84, 033007. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. A simple relation between the γN→N(1535) helicity amplitudes. Phys. Rev. D 2011, 84, 051301. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. γ*N→N*(1520) form factors in the spacelike region. Phys. Rev. D 2014, 89, 094016. [Google Scholar] [CrossRef]
- Ramalho, G. Using the Single Quark Transition Model to predict nucleon resonance amplitudes. Phys. Rev. D 2014, 90, 033010. [Google Scholar] [CrossRef]
- Ramalho, G.; Jido, D.; Tsushima, K. Valence quark and meson cloud contributions for the γ*Λ→Λ* and γ*Σ0→Λ* reactions. Phys. Rev. D 2012, 85, 093014. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K. A Model for the Δ(1600) resonance and γN→Δ(1600) transition. Phys. Rev. D 2010, 82, 073007. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. Covariant model for the Dalitz decay of the N(1535) resonance. Phys. Rev. D 2020, 101, 114008. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. γ*N→N*(1520) form factors in the timelike regime. Phys. Rev. D 2017, 95, 014003. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T.; Weil, J.; van Hees, H.; Mosel, U. Role of the pion electromagnetic form factor in the Δ(1232)→γ*N timelike transition. Phys. Rev. D 2016, 93, 033004. [Google Scholar] [CrossRef]
- Ramalho, G.; Peña, M.T. Timelike γ*N→Δ form factors and Delta Dalitz decay. Phys. Rev. D 2012, 85, 113014. [Google Scholar] [CrossRef]
- Gross, F.; Ramalho, G.; Peña, M.T. Spin and angular momentum in the nucleon. Phys. Rev. D 2012, 85, 093006. [Google Scholar] [CrossRef]
- Gross, F. Three-Dimensional Covariant Integral Equations For Low-Energy Systems. Phys. Rev. 1969, 186, 1448. [Google Scholar] [CrossRef]
- Stadler, A.; Gross, F.; Frank, M. Covariant equations for the three-body bound state. Phys. Rev. C 1997, 56, 2396. [Google Scholar] [CrossRef]
- Gross, F.; Ramalho, G.; Peña, M.T. Fixed-axis polarization states: Covariance and comparisons. Phys. Rev. C 2008, 77, 035203. [Google Scholar] [CrossRef]
- Savkli, C.; Gross, F. Quark-antiquark bound states in the relativistic spectator formalism. Phys. Rev. C 2001, 63, 035208. [Google Scholar] [CrossRef]
- Gross, F.; Agbakpe, P. The Shape of the nucleon. Phys. Rev. C 2006, 73, 015203. [Google Scholar] [CrossRef]
- Lin, H.W.; Orginos, K. Strange Baryon Electromagnetic Form Factors and SU(3) Flavor Symmetry Breaking. Phys. Rev. D 2009, 79, 074507. [Google Scholar] [CrossRef]
- Alexandrou, C.; Brinet, M.; Carbonell, J.; Constantinou, M.; Harraud, P.A.; Guichon, P.; Jansen, K.; Korzec, T.; Papinutto, M. Axial Nucleon form factors from lattice QCD. Phys. Rev. D 2011, 83, 045010. [Google Scholar] [CrossRef]
- Alexandrou, C.; Constantinou, M.; Dinter, S.; Drach, V.; Jansen, K.; Kallidonis, C.; Koutsou, G. Nucleon form factors and moments of generalized parton distributions using Nf = 2 + 1 + 1 twisted mass fermions. Phys. Rev. D 2013, 88, 014509. [Google Scholar] [CrossRef]
- Abdel-Rehim, A.; Alexandrou, C.; Constantinou, M.; Dimopoulos, P.; Frezzotti, R.; Hadjiyiannakou, K.; Jansen, K.; Kallidonis, C.; Kostrzewa, B.; Koutsou, G.; et al. Nucleon and pion structure with lattice QCD simulations at physical value of the pion mass. Phys. Rev. D 2015, 92, 114513, Erratum in Phys. Rev. D 2016, 93, 039904. [Google Scholar] [CrossRef]
- Jang, Y.C.; Gupta, R.; Yoon, B.; Bhattacharya, T. Axial Vector Form Factors from Lattice QCD that Satisfy the PCAC Relation. Phys. Rev. Lett. 2020, 124, 072002. [Google Scholar] [CrossRef] [PubMed]
- Djukanovic, D.; von Hippel, G.; Koponen, J.; Meyer, H.B.; Ottnad, K.; Schulz, T.; Wittig, H. Isovector axial form factor of the nucleon from lattice QCD. Phys. Rev. D 2022, 106, 074503. [Google Scholar] [CrossRef]
- Bali, G.S.; Collins, S.; Heybrock, S.; Löffler, M.; Rödl, R.; Söldner, W.; Weishäupl, S. Octet baryon isovector charges from Nf=2+1 lattice QCD. Phys. Rev. D 2023, 108, 034512. [Google Scholar] [CrossRef]
- Chang, C.C.; Nicholson, A.N.; Rinaldi, E.; Berkowitz, E.; Garron, N.; Brantley, D.A.; Monge-Camacho, H.; Monahan, C.J.; Bouchard, C.; Clark, M.A.; et al. A per-cent-level determination of the nucleon axial coupling from quantum chromodynamics. Nature 2018, 558, 91. [Google Scholar] [CrossRef]
- Meyer, A.S.; Walker-Loud, A.; Wilkinson, C. Status of Lattice QCD Determination of Nucleon Form Factors and their Relevance for the Few-GeV Neutrino Program. Ann. Rev. Nucl. Part. Sci. 2022, 72, 205. [Google Scholar] [CrossRef]
- Ramalho, G. Holographic estimate of the meson cloud contribution to nucleon axial form factor. Phys. Rev. D 2018, 97, 073002. [Google Scholar] [CrossRef]
- Jenkins, E.E.; Luke, M.E.; Manohar, A.V.; Savage, M.J. Chiral perturbation theory analysis of the baryon magnetic moments. Phys. Lett. B 1993, 302, 482. [Google Scholar] [CrossRef]
- Meissner, U.G.; Steininger, S. Baryon magnetic moments in chiral perturbation theory. Nucl. Phys. B 1997, 499, 349. [Google Scholar] [CrossRef]
- Kubis, B.; Hemmert, T.R.; Meissner, U.G. Baryon form-factors. Phys. Lett. B 1999, 456, 240. [Google Scholar] [CrossRef]
- Franklin, J. Phenomenological quark model for baryon magnetic moments and beta decay ratios (GA/GV). Phys. Rev. D 2002, 66, 033010. [Google Scholar] [CrossRef]
- Cheedket, S.; Lyubovitskij, V.E.; Gutsche, T.; Faessler, A.; Pumsa-ard, K.; Yan, Y. Electromagnetic form factors of the baryon octet in the perturbative chiral quark modeluark model. Eur. Phys. J. A 2004, 20, 317. [Google Scholar] [CrossRef][Green Version]
- Leinweber, D.B.; Boinepalli, S.; Cloet, I.C.; Thomas, A.W.; Williams, A.G.; Young, R.D.; Zanotti, J.M.; Zhang, J.B. Precise determination of the strangeness magnetic moment of the nucleon. Phys. Rev. Lett. 2005, 94, 212001. [Google Scholar] [CrossRef]
- Boinepalli, S.; Leinweber, D.B.; Williams, A.G.; Zanotti, J.M.; Zhang, J.B. Precision electromagnetic structure of octet baryons in the chiral regime. Phys. Rev. D 2006, 74, 093005. [Google Scholar] [CrossRef]
- Wang, P.; Leinweber, D.B.; Thomas, A.W.; Young, R.D. Chiral extrapolation of octet-baryon charge radii. Phys. Rev. D 2009, 79, 094001. [Google Scholar] [CrossRef]
- Bernard, V.; Kaiser, N.; Meissner, U.G. Chiral dynamics in nucleons and nuclei. Int. J. Mod. Phys. E 1995, 4, 193. [Google Scholar] [CrossRef]
- Perdrisat, C.F.; Punjabi, V.; Vanderhaeghen, M. Nucleon Electromagnetic Form Factors. Prog. Part. Nucl. Phys. 2007, 59, 694. [Google Scholar] [CrossRef]
- Jones, M.K.; Aniol, K.A.; Baker, F.T.; Berthot, J.; Bertin, P.Y.; Bertozzi, W.; Besson, A.; Bimbot, L.; Boeglin, W.U.; Brash, E.J.; et al. GEp/GMp ratio by polarization transfer in e→p→ep→. Phys. Rev. Lett. 2000, 84, 1398–1402. [Google Scholar] [CrossRef]
- Gayou, O.; Benmokhtar, F.; Bertozzi, W.; Bimbot, L.; Brash, E.J.; Calarco, J.R.; Cavata, C.; Chai, Z.; Chang, C.C.; Chang, T.; et al. Measurement of GEp/GMp in e→p→ep→ to Q2=5.6 GeV2. Phys. Rev. Lett. 2002, 88, 092301. [Google Scholar] [CrossRef]
- Puckett, A.J.R.; Brash, E.J.; Jones, M.K.; Luo, W.; Meziane, M.; Pentchev, L.; Perdrisat, C.F.; Punjabi, V.; Wesselmann, F.R. and Ahmidouch, A.; et al. Recoil Polarization Measurements of the Proton Electromagnetic Form Factor Ratio to Q2 = 8.5 GeV2. Phys. Rev. Lett. 2010, 104, 242301. [Google Scholar] [CrossRef]
- Zhan, X.; Allada, K.; Armstrong, D.S.; Arrington, J.; Bertozzi, W.; Boeglin, W.; Chen, J.-P.; Chirapatpimol, K.; Choi, S.; Chudakov, E.; et al. High Precision Measurement of the Proton Elastic Form Factor Ratio μpGE/GM at low Q2. Phys. Lett. B 2011, 705, 59. [Google Scholar] [CrossRef]
- Arrington, J.; Melnitchouk, W.; Tjon, J.A. Global analysis of proton elastic form factor data with two-photon exchange corrections. Phys. Rev. C 2007, 76, 035205. [Google Scholar] [CrossRef]
- Ostrick, M.; Herberg, C.; Andresen, H.G.; Annand, J.R.M.; Aulenbacher, K.; Becker, J.; Drescher, P.; Eyl, D.; Frey, A.; Grabmayr, P.; et al. Measurement of the neutron electric form factor GE,n in the quasifree 2H(e→,e′p→)p reaction. Phys. Rev. Lett. 1999, 83, 276. [Google Scholar] [CrossRef]
- Herberg, C.; Ostrick, M.; Andresen, H.G.; Annand, J.R.M.; Aulenbacher, K.; Becker, J.; Drescher, P.; Eyl, D.; Frey, A.; Grabmayr, P.; et al. Determination of the neutron electric form factor in the D(e,e′n)p reaction and the influence of nuclear binding. Eur. Phys. J. A 1999, 5, 131. [Google Scholar] [CrossRef]
- Glazier, D.I.; Seimetz, M.; Annand, J.R.M.; Arenhövel, H.; Antelo, M.A.; Ayerbe, C.; Bartsch, P.; Baumann, D.; Bermuth, J.; Böhm, R.; et al. Measurement of the Electric Form Factor of the Neutron at Q2=0.3–0.8 (GeV/c)2. Eur. Phys. J. A 2005, 24, 101. [Google Scholar] [CrossRef]
- Passchier, I.; Alarcon, R.; Bauer, T.S.; Boersma, D.; Brand, J.F.J.v.; Buuren, L.D.v.; Bulten, H.J.; Ferro-Luzzi, M.; Heimberg, P.; Higinbotham, D.W.; et al. The charge form factor of the neutron from the reaction 2H(e→,e′n)p. Phys. Rev. Lett. 1999, 82, 4988. [Google Scholar] [CrossRef]
- Eden, T.; Madey, R.; Zhang, W.-M.; Anderson, B.D.; Arenhövel, H.; Baldwin, A.R.; Barkhuff, D.; Beard, K.B.; Bertozzi, W.; Cameron, J.M.; et al. Electric form-factor of the neutron from the 2H(e→,e′n)1H reaction at Q2=0.255 (GeV/c)2. Phys. Rev. C 1994, 50, 1749. [Google Scholar] [CrossRef]
- Zhu, H.; Ahmidouch, A.; Anklin, H.; Arenhövel, H.; Armstrong, C.; Bernet, C.; Boeglin, W.; Breuer, H.; Brindza, P.; Brown, D.; et al. A measurement of the electric form-factor of the neutron through d(e→,e′n)p at Q2=0.5 (GeV/c)2. Phys. Rev. Lett. 2001, 87, 081801. [Google Scholar] [CrossRef]
- Warren, G.; Wesselmann, F.; Zhu, H.; McKee, P.; Savvinov, N.; Zeier, M.; Aghalaryan, A.; Ahmidouch, A.; Arenhövel, H.; Asaturyan, R.; et al. Measurement of the electric form factor of the neutron Q2=0.5 (GeV/c)2 and 1.0 (GeV/c)2. Phys. Rev. Lett. 2004, 92, 042301. [Google Scholar] [CrossRef]
- Madey, R.; Semenov, A.Y.; Taylor, S.; Plaster, B. Measurements of GEn/GMn from 2H(e→,e′n)1H reaction to Q2=1.45 (GeV/c)2. Phys. Rev. Lett. 2003, 91, 122002. [Google Scholar] [CrossRef]
- Beck, A.; Beck, S.M.-T.; Puckett, A.J.R.; Qiang, Y.; Sirca, S.; Zhu, X. Measurements of the Electric Form Factor of the Neutron up to Q2=3.4 GeV2 using the Reaction 3He(e→,e′n)pp. Phys. Rev. Lett. 2010, 105, 262302. [Google Scholar]
- Schiavilla, R.; Sick, I. Neutron charge form factor at large q2. Phys. Rev. C 2001, 64, 041002. [Google Scholar] [CrossRef]
- Bosted, P.E. An Empirical fit to the nucleon electromagnetic form-factors. Phys. Rev. C 1995, 51, 409. [Google Scholar] [CrossRef]
- Kubon, G.; Anklin, H.; Bartsch, P.; Baumann, D.; Boeglin, W.U.; Bohinc, K.; Böhm, R.; Distler, M.O.; Ewald, I.; Friedrich, J.; et al. Precise neutron magnetic form factors. Phys. Lett. B 2002, 524, 26. [Google Scholar] [CrossRef]
- Anklin, H.; deBever, L.J.; Blomqvist, K.I.; Boeglin, W.U.; Böhm, R.; Distler, M.; Edelhoff, R.; Friedrich, J.; Fritschi, D.; Geiges, R.; et al. Precise measurements of the neutron magnetic form factor. Phys. Lett. B 1998, 428, 248. [Google Scholar] [CrossRef]
- Anklin, H.; Bruins, E.E.W.; Day, D.; Fritschi, D.; Groft, B.; Joosse, F.C.P.; Jourdan, J.; Lichtenstadt, J.; Loppacher, M.; Masson, G.; et al. Precision measurement of the neutron magnetic form-factor. Phys. Lett. B 1994, 336, 313. [Google Scholar] [CrossRef]
- Lachniet, J. et al. [CLAS Collaboration] A Precise Measurement of the Neutron Magnetic Form Factor GMn in the Few-GeV2 Region. Phys. Rev. Lett. 2009, 102, 192001. [Google Scholar] [CrossRef]
- Nakamura, K.; Particle Data Group. Review of particle physics. J. Phys. G 2010, 37, 075021. [Google Scholar] [CrossRef]
- Eschrich, I.; Krüger, H.; Simon, J.; Vorwalter, K.; Alkhazov, G.; Atamantchouk, A.G.; Balatz, M.Y.; Bondar, N.F.; Cooper, P.S.; Dauwe, L.J.; et al. Measurement of the Σ− charge radius by Σ− electron elastic scattering. Phys. Lett. B 2001, 522, 233. [Google Scholar] [CrossRef]
- Park, K.; Gothe, R.W.; Adhikari, K.P.; Adikaram, D.; Anghinolfi, M.; Baghdasaryan, H.; Ball, J.; Battaglieri, M.; Batourine, V.; Bedlinskiy, I.; et al. Measurement of the generalized form factors near threshold via γ*p→nπ+ at high Q2. Phys. Rev. C 2012, 85, 035208. [Google Scholar] [CrossRef]
- Particle Data Group; Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar]
- Choi, S.; Duval, M.A.; Elouadrhiri, L.; Estenne, V.; Bardin, G.; Berthot, J.; Bertin, P.Y.; Botton, N.D.; Didelez, J.P.; Fonvieille, H.; et al. Axial and pseudoscalar nucleon form-factors from low-energy pion electroproduction. Phys. Rev. Lett. 1993, 71, 3927. [Google Scholar] [CrossRef]
- Tsushima, K. Magnetic moments of the octet, decuplet, low-lying charm, and low-lying bottom baryons in a nuclear medium. Prog. Theor. Exp. Phys. 2022, 2022, 043D02. [Google Scholar] [CrossRef]
- Cobos-Martínez, J.J.; Tsushima, K.; Krein, G.; Thomas, A.W. ϕ meson mass and decay width in nuclear matter and nuclei. Phys. Lett. B 2017, 771, 113. [Google Scholar] [CrossRef]
- Goldberger, M.L.; Treiman, S.B. Decay of the pi meson. Phys. Rev. 1958, 110, 1178. [Google Scholar] [CrossRef]
- Kirchbach, M.; Wirzba, A. In-medium chiral perturbation theory and pion weak decay in the presence of background matter. Nucl. Phys. A 1997, 616, 648. [Google Scholar] [CrossRef]
- Christy, M.E.; Ahmidouch, M.E.; Armstrong, C.S.; Arrington, J.; Asaturyan, R.; Avery, S.; Baker, O.K.; Beck, D.H.; Blok, H.P.; Bochna, C.W.; et al. Measurements of electron proton elastic cross-sections for 0.4<Q2<5.5 (GeV/c)2. Phys. Rev. C 2004, 70, 015206. [Google Scholar]
- Punjabi, V.; Perdrisat, C.F.; Aniol, K.A.; Baker, F.T.; Berthot, J.; Bertin, P.Y.; Bertozzi, W.; Besson, A.; Bimbot, L.; Boeglin, W.U.; et al. Proton elastic form-factor ratios to Q2=3.5 GeV2 by polarization transfer. Phys. Rev. C 2005, 71, 055202, Erratum in Phys. Rev. C 2005, 71, 069902.. [Google Scholar] [CrossRef]
- Puckett, A.J.R.; Brash, E.J.; Gayou, O.; Jones, M.K.; Pentchev, L.; Perdrisat, C.F.; Punjabi, V.; Aniol, K.A.; Averett, T.; Benmokhtar, F.; et al. Final Analysis of Proton Form Factor Ratio Data at Q2=4.0, 4.8 and 5.6 GeV2. Phys. Rev. C 2012, 85, 045203. [Google Scholar] [CrossRef]
- Puckett, A.J.R.; Brash, E.J.; Jones, M.K.; Luo, W.; Meziane, M.; Pentchev, L.; Perdrisat, C.F.; Punjabi, V.; Wesselmann, F.R.; Afanasev, A.; et al. Polarization Transfer Observables in Elastic Electron Proton Scattering at Q2=2.5, 5.2, 6.8, and 8.5 GeV2. Phys. Rev. C 2017, 96, 055203, Erratum in Phys. Rev. C 2018, 98, 019907.. [Google Scholar] [CrossRef]
- Cheoun, M.K.; Choi, K.S.; Kim, K.S.; Saito, K.; Kajino, T.; Tsushima, K.; Maruyama, T. Effects of the density-dependent weak form factors on the neutrino reaction via neutral current for the nucleon in nuclear medium and 12C. Phys. Rev. C 2013, 87, 065502. [Google Scholar] [CrossRef]
- Cheoun, M.K.; Choi, K.; Kim, K.S.; Saito, K.; Kajino, T.; Tsushima, K.; Maruyama, T. Asymmetry in the neutrino and anti-neutrino reactions in a nuclear medium. Phys. Lett. B 2013, 723, 464. [Google Scholar] [CrossRef][Green Version]
- Cai, T.; Moore, M.L.; Olivier, A.; Akhter, S.; Dar, Z.A.; Ansari, V.; Ascencio, M.V.; Bashyal, A.; Bercellie, A.; Betancourt, M.; et al. Measurement of the axial vector form factor from antineutrino-proton scattering. Nature 2023, 614, 48. [Google Scholar] [CrossRef] [PubMed]
- The DUNE Collaboration; Abud, A.A.; Abi, B.; Acciarri, R.; Acero, M.A.; Adames, M.R.; Adamov, G.; Adams, D.; Adinolfi, M.; Aduszkiewicz, A.; et al. Searching for solar KDAR with DUNE. J. Cosmol. Astropart. Phys. 2021, 10, 065. [Google Scholar] [CrossRef]
- Alberico, W.M.; Bilenky, S.M.; Maieron, C. Strangeness in the nucleon: Neutrino-nucleon and polarized electron-nucleon scattering. Phys. Rept. 2002, 358, 227. [Google Scholar] [CrossRef]
- Ahrens, L.A.; Aronson, S.H.; Connolly, P.L.; Gibbard, B.G.; Murtagh, M.J.; Murtagh, S.J.; Terada, S.; White, D.H.; Callas, J.L.; Cutts, D.; et al. Measurement of Neutrino—Proton and anti-neutrino-Proton Elastic Scattering. Phys. Rev. D 1987, 35, 785. [Google Scholar] [CrossRef]
- Athar, M.S.; Fatima, A.; Singh, S.K. Neutrinos and their interactions with matter. Prog. Part. Nucl. Phys. 2023, 129, 104019. [Google Scholar] [CrossRef]
- Ruso, L.A.; Ankowski, A.M.; Bacca, S.; Balantekin, A.B.; Carlson, J.; Gardiner, S.; González-Jiménez, R.; Gupta, R.; Hobbs, T.J.; Hoferichter, M.; et al. Theoretical tools for neutrino scattering: Interplay between lattice QCD, EFTs, nuclear physics, phenomenology, and neutrino event generators. arXiv 2022, arXiv:2203.09030. [Google Scholar]
- Akimov, D.; Alawabdeh, S.; An, P.; Awe, C.; Barbeau, P.S.; Barry, C.; Becker, B.; Belov, V.; Bernardi, I.; Bock, C.; et al. The COHERENT Experimental Program. arXiv 2022, arXiv:2204.04575. [Google Scholar]
- Simons, D.; Steinberg, N.; Lovato, A.; Meurice, Y.; Rocco, N.; Wagman, M. Form factor and model dependence in neutrino-nucleus cross section predictions. arXiv 2022, arXiv:2210.02455. [Google Scholar]
- Hoferichter, M.; Menéndez, J.; Schwenk, A. Coherent elastic neutrino-nucleus scattering: EFT analysis and nuclear responses. Phys. Rev. D 2020, 102, 074018. [Google Scholar] [CrossRef]
- Abdullah, M.; Aristizabal Sierra, D.; Dutta, B.; Strigari, L.E. Coherent Elastic Neutrino-Nucleus Scattering with directional detectors. Phys. Rev. D 2020, 102, 015009. [Google Scholar] [CrossRef]
- Cadeddu, M.; Dordei, F.; Giunti, C. A view of coherent elastic neutrino-nucleus scattering. Europhys. Lett. 2023, 143, 34001. [Google Scholar] [CrossRef]
- Gondolo, P. Recoil momentum spectrum in directional dark matter detectors. Phys. Rev. D 2002, 66, 103513. [Google Scholar] [CrossRef]
- Ramalho, G.; Tsushima, K.; Cheoun, M.K. Soongsil University, Seoul 06978, Republic of Korea, 2025; (manuscript in preparation; to be submitted).
- Hutauruk, P.T.P.; Oh, Y.; Tsushima, K. Impact of medium modifications of the nucleon weak and electromagnetic form factors on the neutrino mean free path in dense matter. Phys. Rev. D 2018, 98, 013009. [Google Scholar] [CrossRef]
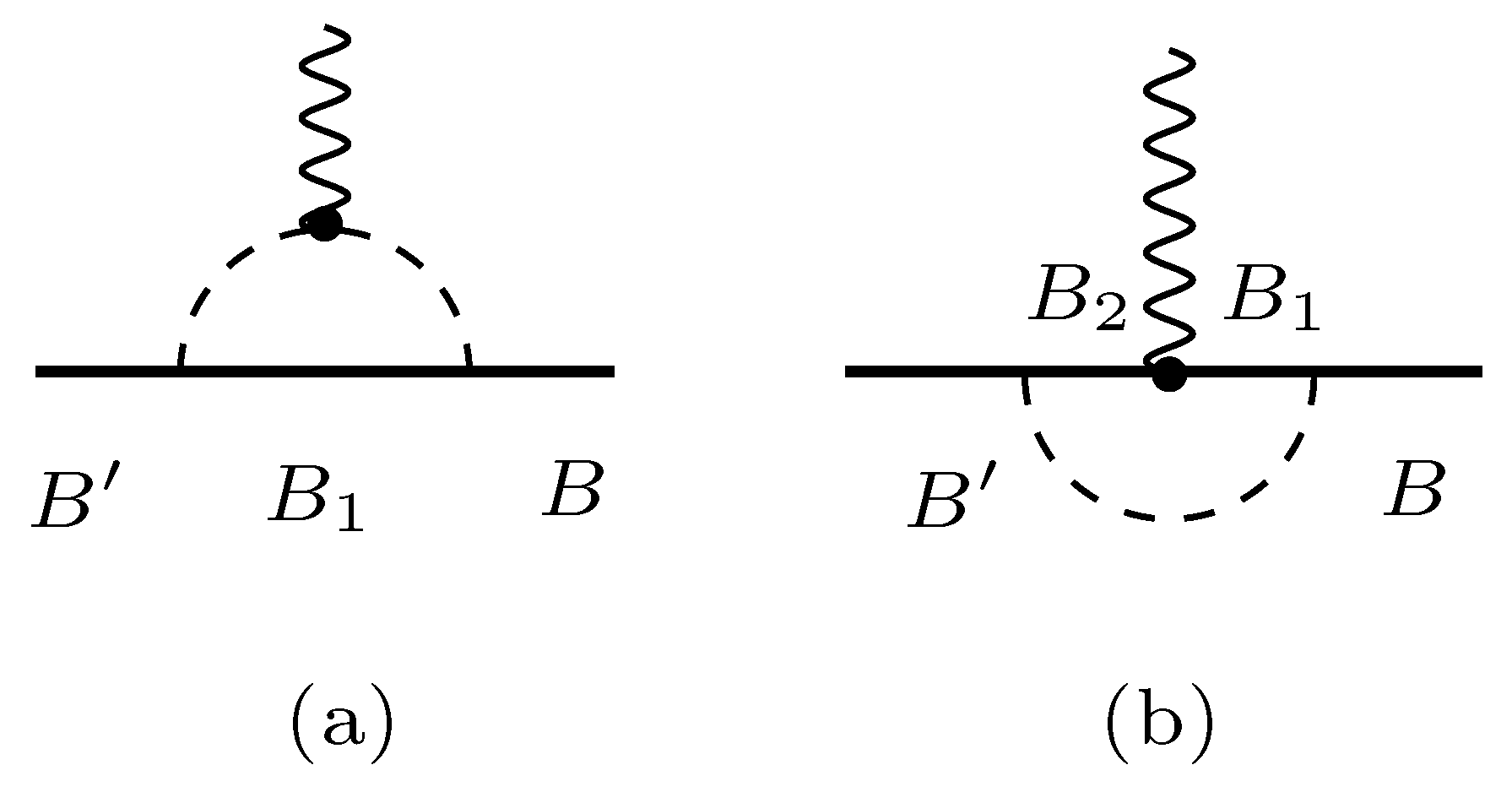

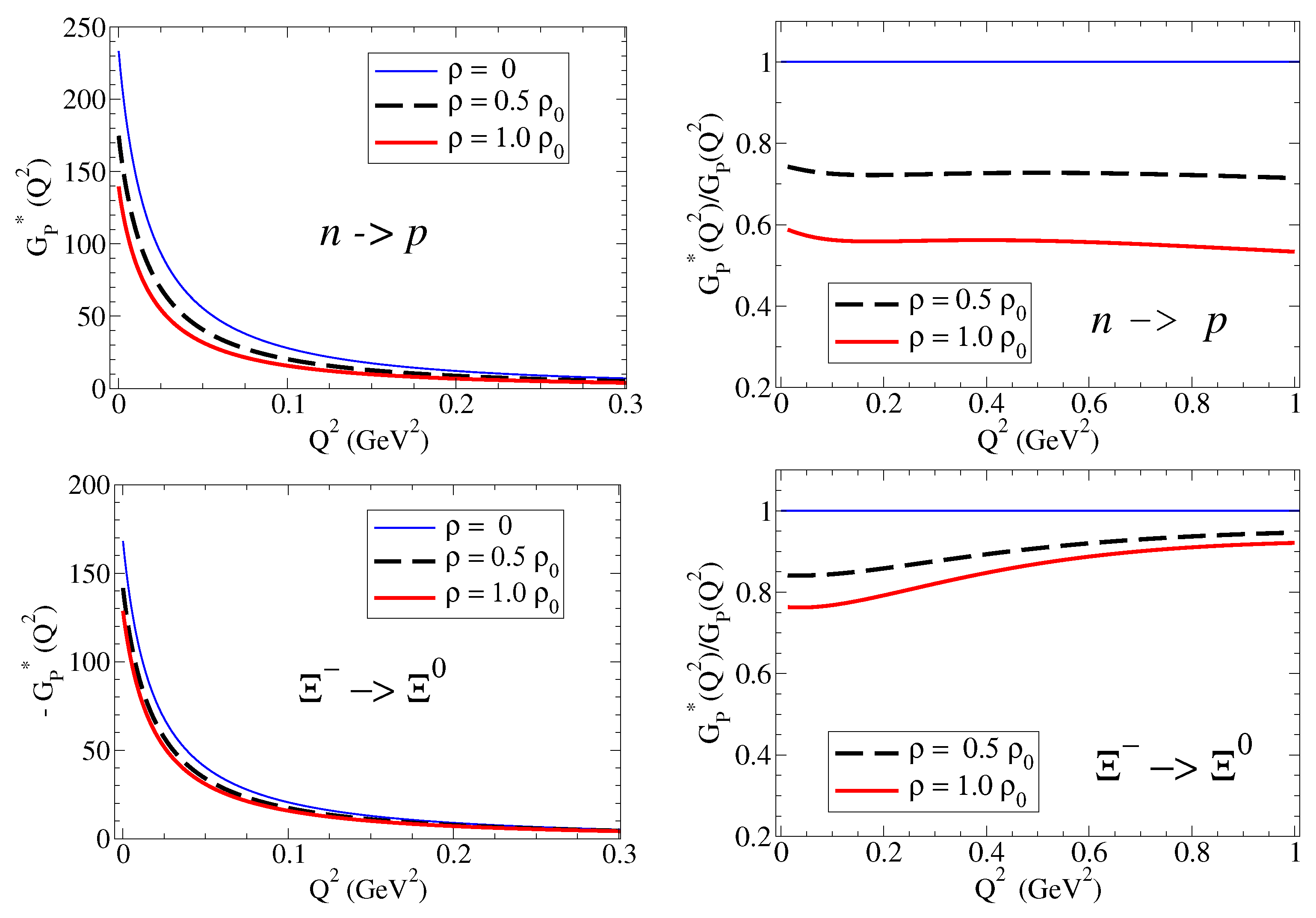

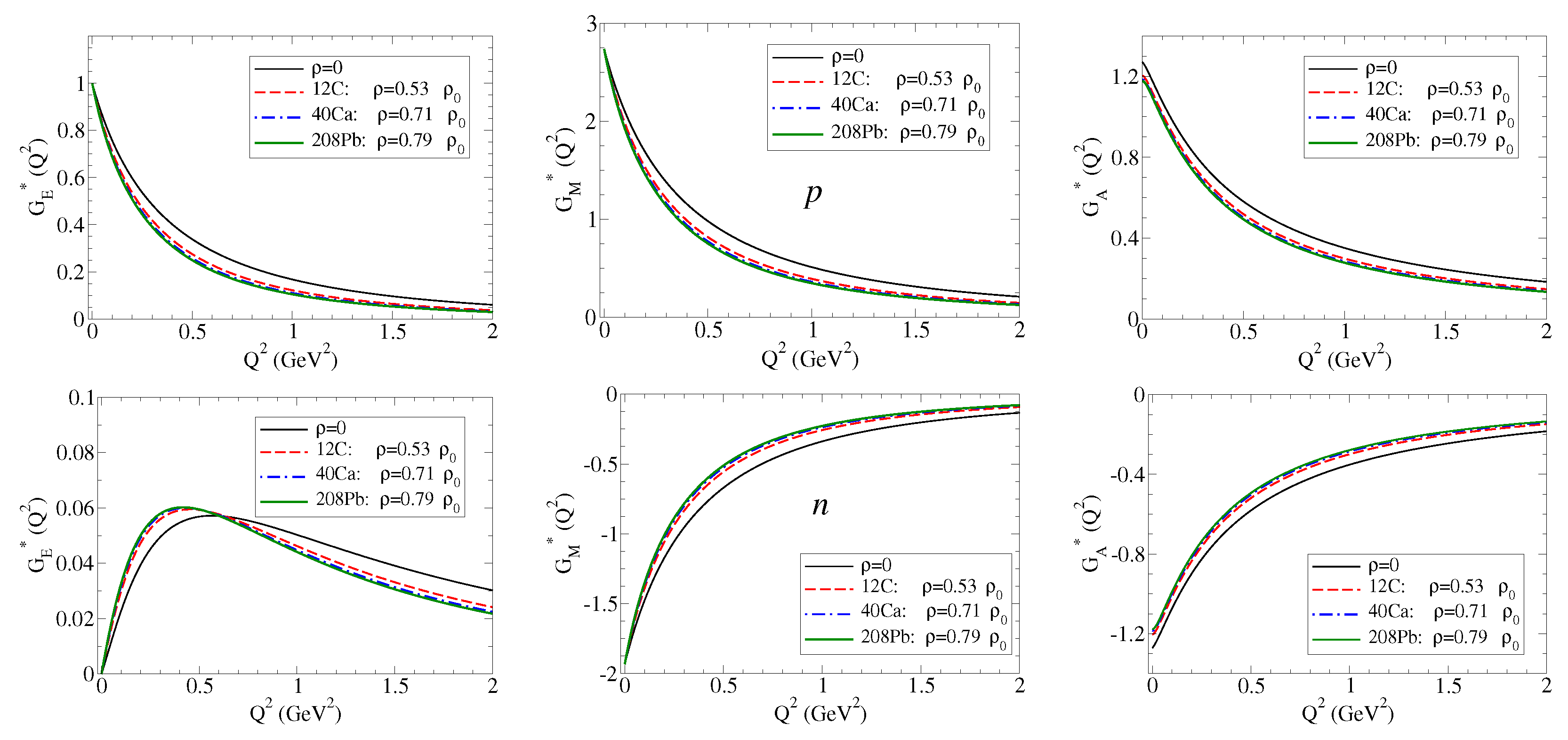
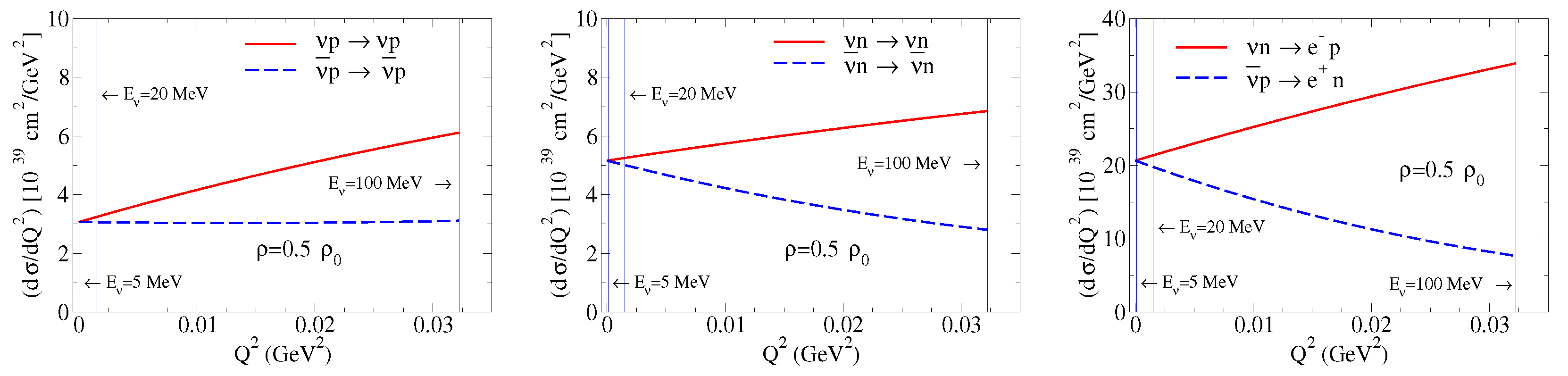
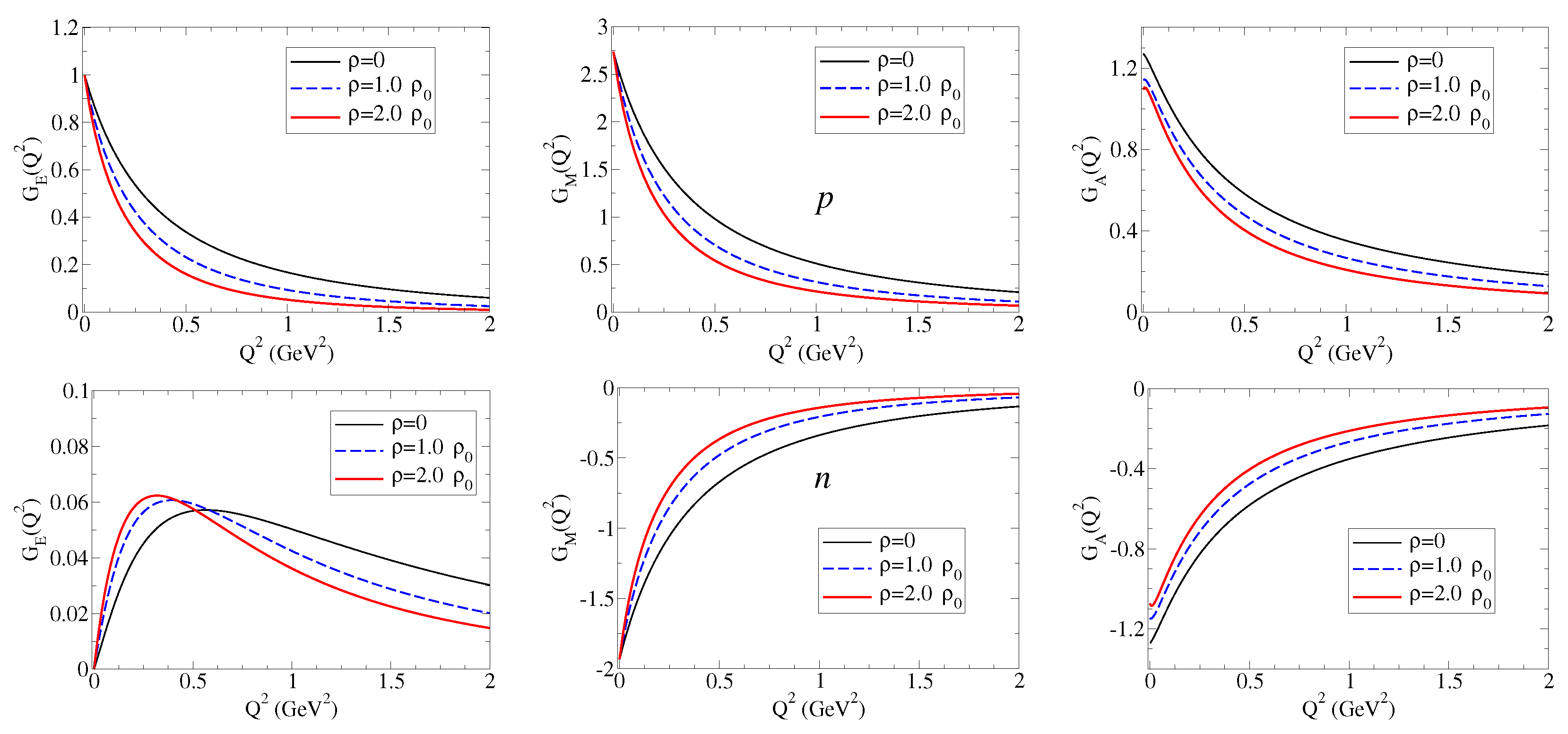
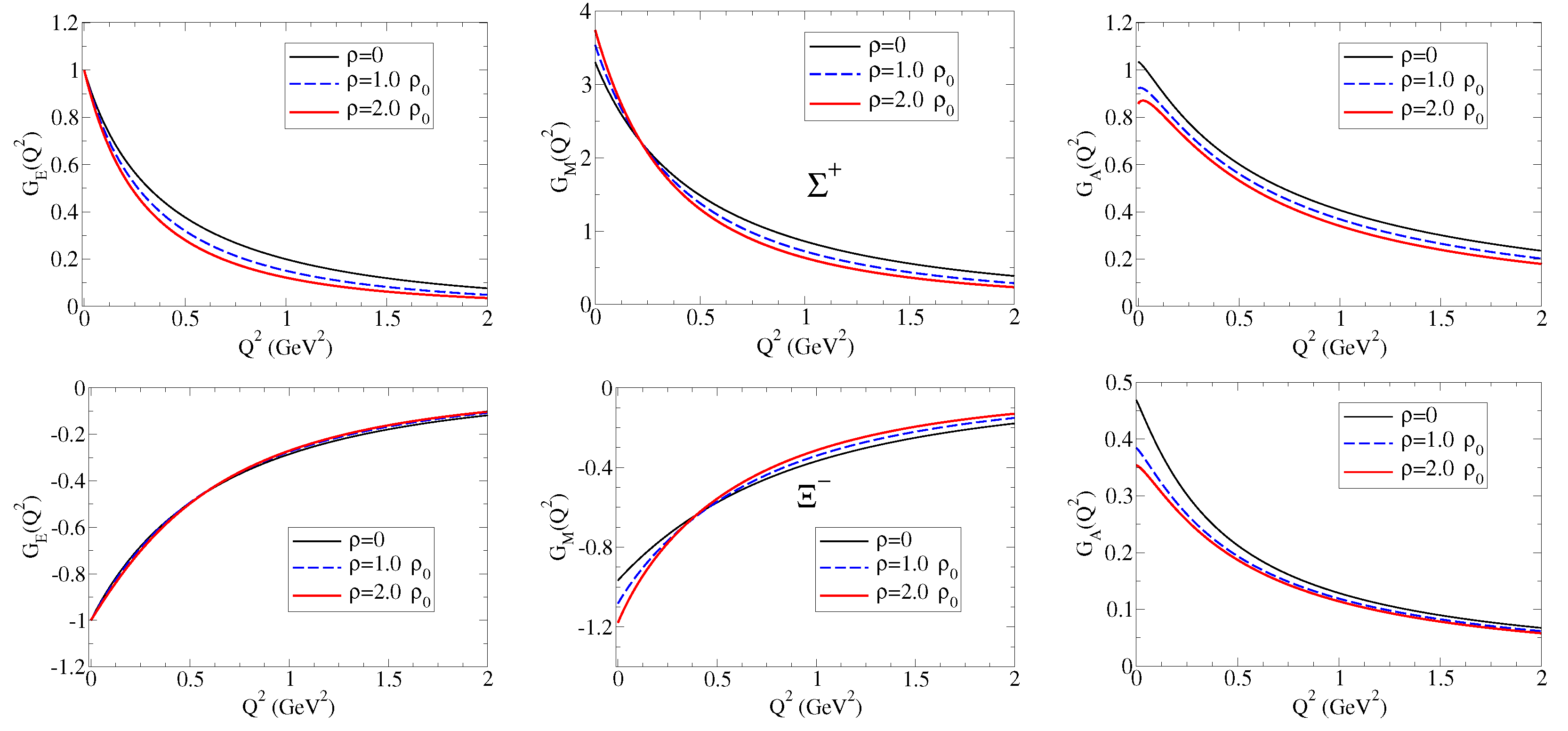
| X | ||
|---|---|---|
| 0.0 | 0.138 | 0.7753 | 1.0195 | 0.4937 | 0.9390 | 1.1157 | 1.1931 | 1.3181 |
| 0.5 | 0.138 | 0.7031 | 1.0080 | 0.4573 | 0.8311 | 1.0438 | 1.1213 | 1.2822 |
| 1.0 | 0.138 | 0.6516 | 1.0010 | 0.4305 | 0.7544 | 0.9929 | 1.0707 | 1.2568 |
| 0.0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 0.5 | 0.9404 | 0.9180 | 0.9067 | 0.9584 | 0.9628 | 0.9965 |
| 1.0 | 0.8920 | 0.8279 | 0.8656 | 0.9588 | 0.9669 | 1.0273 |
| Nucleus | |
|---|---|
| 12C | 0.533 |
| 16O | 0.612 |
| 40Ca | 0.711 |
| 90Zr | 0.767 |
| 97Au | 0.783 |
| 208Pb | 0.786 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramalho, G.; Tsushima, K.; Cheoun, M.-K. Electroweak Form Factors of Baryons in Dense Nuclear Matter. Symmetry 2025, 17, 681. https://doi.org/10.3390/sym17050681
Ramalho G, Tsushima K, Cheoun M-K. Electroweak Form Factors of Baryons in Dense Nuclear Matter. Symmetry. 2025; 17(5):681. https://doi.org/10.3390/sym17050681
Chicago/Turabian StyleRamalho, G., K. Tsushima, and Myung-Ki Cheoun. 2025. "Electroweak Form Factors of Baryons in Dense Nuclear Matter" Symmetry 17, no. 5: 681. https://doi.org/10.3390/sym17050681
APA StyleRamalho, G., Tsushima, K., & Cheoun, M.-K. (2025). Electroweak Form Factors of Baryons in Dense Nuclear Matter. Symmetry, 17(5), 681. https://doi.org/10.3390/sym17050681








