Some New Results Connected with Symmetric Random Variables: Generating Skew Distributions

Abstract

We combine two well-known statements of results in the statistical and mathematical literature, one related to symmetric continuous distributions and the other to the integration of functions, to obtain some new results regarding symmetric distributions and involving the value at risk and the tail value at risk, well-known tools used in actuarial and financial statistics, among others. Generalizations of the skew normal distribution in its univariate and multivariate versions obtained from one of the results are also shown, and a new method is proposed for generating families of skewed continuous distributions.

1. Introduction

Symmetric distributions ($f\left(x\right)=f(-x)$, $F\left(x\right)=1-F(-x)$, $x\in \mathbb{R}$, where f and F represent the probability density function and cumulative distribution function of the random variable X, respectively) play a prominent role in theoretical and applied statistics. The most obvious example is the normal distribution with zero mean, the starting point for numerous applications, especially in many scientific fields. Apart from the normal distribution, other distributions that can be symmetric about zero and are referred to in multiple studies include the Cauchy distribution and the logistic distribution, among others. Undoubtedly, the normal distribution with zero mean is the primary reference when symmetric continuous distributions are being discussed—distinguished researchers such as F. Y. Edgeworth and Chas. H. Kummel, Arthur L. Bowley, and Morgan W. Crofton, among many others, have slightly modified the normal distribution to obtain proposed distributions that are similar but, at the same time, capable of explaining empirical data that present asymmetry that cannot be explained using the normal distribution. Good references include [1,2].

In this work, we use the method of [3] to obtain some results that extended the conclusion of Theorem 1 in [3]. Specifically, we reintroducea well-known result of [3] as the starting point to obtain new results (at least to our knowledge) that are simple and easy, but that could well have applications in the fields of theoretical and applied statistics. Generalizations of this earlier result are also proposed, connecting it to the inverse of the distribution function of a symmetric distribution and to risk measures commonly used in actuarial statistics and financial economics. The aim is to find adequate provisions and capital requirements to prevent the insolvency of an insurance company or a business. These risk results could be beneficial for determining the amount of risk an investment could incur.

The rest of the paper is organized as follows. Section 2 provides the main results of this work. Some results are connected to the inverse distribution function of a symmetric distribution, and others are connected to risk measures usually used in actuarial and financial research, such as the value at risk (VaR) and the tail value at risk (TVaR). Based on these results, a generalization of the skew-normal distribution (and related distributions) is developed in Section 3. The paper ends with the summary and conclusions in the last section.

2. Main Results

We recall the following Theorem, which appears in [3] and is required for the development of this work; the same result also appears in [4]. This result, although well known and simple, has a greater scope than it was intended for.

Theorem 1

([3]). Let $G_X\left(x\right)$ be the cumulative distribution function (CDF) of a random variable X that is symmetric about zero. Then,

$$\begin{array}{c}\hfill {\int }_{-a}^a{G}_X\left(z\right)dz=a,\forall a\in {\mathbb{R}}^{+}.\end{array}$$

(1)

Expression (2) in [5] also establishes this assertion. To obtain the strong relation that is provided in Theorem 1, we will use the following Lemma, which is well known in the statistical literature.

Lemma 1

([6]). Let X be a symmetric random variable, and let $y=h\left(x\right)$ be an odd real-valued function. Then, the random variable $Y=h\left(X\right)$ is also symmetric.

Now, using this Lemma, a more general result than provided in Theorem 1 can be established.

Theorem 2.

Let $G_X\left(x\right)$ be the CDF of a random variable X that is symmetric about zero, $h\left(x\right)$ be an odd real-valued function, and $\lambda \in \mathbb{R}$. Then,

$$\begin{array}{c}\hfill {\int }_{-a}^a{G}_X\left(\lambda h\left(z\right)\right)dz=a,\forall a\in {\mathbb{R}}^{+}.\end{array}$$

(2)

Note that when $\lambda =1$, the expression given in (2) reduces to (1). In fact, the relation given in (2) is also valid when we replace $h\left(z\right)$ with any of the following:

• $h\left(z\right)\eta \left(\mu z\right)$, where $\eta \left(z\right)$ is an even function and $\mu \in \mathbb{R}$;
• $\eta \left(\mu z\right)/h\left(z\right)$, where $\eta \left(z\right)$ is an even function, $h\left(z\right)\ne 0$, $z\in (-a,a)$, and $\mu \in \mathbb{R}$;
• $h\left(z\right)/\eta \left(\mu z\right)$, where $\eta \left(z\right)$ is an even function $\eta \left(z\right)\ne 0$, $z\in (-a,a)$, and $\mu \in \mathbb{R}$;
• $(d/dz)\eta \left(\mu z\right)$, where $\eta \left(z\right)$ is an even function and $\mu \in \mathbb{R}$.

It is simple to see that for ${\overline{G}}_X\left(x\right)=1-G_X\left(x\right)$, it holds that

$$\begin{array}{c}\hfill {\int }_{-a}^a{\overline{G}}_X\left(\lambda h\left(z\right)\right)dz=a,\forall a\in {\mathbb{R}}^{+}.\end{array}$$

(3)

Then, from (2) and (3), we can infer that

$$\begin{array}{c}\hfill {\int }_{-a}^a[2G_X\left(\lambda h\left(z\right)\right)-1]dz=0.\end{array}$$

The following result will be used later.

Proposition 1.

Let $\zeta \left(x\right)$ be a real-valued function with an inverse. Then, it holds that

$$\begin{array}{c}\hfill {\int }_a^b{\left[{\zeta }^{-1}\left(x\right)\right]}^{k}dx=b{\left[{\zeta }^{-1}\left(b\right)\right]}^k-a{\left[{\zeta }^{-1}\left(a\right)\right]}^k-k{\int }_{{\zeta }^{-1}\left(a\right)}^{{\zeta }^{-1}\left(b\right)}{y}^{k-1}\zeta \left(y\right)dy.\end{array}$$

(4)

Proof. 

The result is obtained straightforwardly after integrating by parts. □

When we replace k with one in (4), we obtain the result provided in [7], which relates the integration of a function $\varsigma =\zeta \left(x\right)$ to the integration of the inverse of this function in the following form:

$$\begin{array}{c}\hfill {\int }_a^b{\zeta }^{-1}\left(x\right)dx=b{\zeta }^{-1}\left(b\right)-a{\zeta }^{-1}\left(a\right)-{\int }_{{\zeta }^{-1}\left(a\right)}^{{\zeta }^{-1}\left(b\right)}\zeta \left(y\right)dy.\end{array}$$

(5)

It is well known that for a symmetric distribution about zero, it holds true that $G_X\left(a\right)=1-G_X(-a)$. A counterpart for the inverse of the distribution $G_X$ exists and will be established later. For that, we need the following result first.

Theorem 3.

Let $G_X(·)$ be the CDF of an arbitrary distribution that is symmetric about zero. Then, it holds that

$$\begin{array}{c}\hfill {\int }_0^p{G}_X^{-1}\left(z\right)dz={\int }_0^{1-p}{G}_X^{-1}\left(z\right)dz,\forall p\in [0,1],\end{array}$$

(6)

where $G^{-1}\left(t\right)=inf\{x:G\left(x\right)\ge t\}$, $t\in (0,1]$.

Proof. 

Using (1) together with (5), it is simple to see that

$$\begin{array}{c}\hfill a={\int }_{-a}^a{G}_X\left(z\right)dz=a{G}_X\left(a\right)+a{G}_X(-a)-{\int }_{G_X(-a)}^{G_X\left(a\right)}{G}_X^{-1}\left(z\right)dz=a-{\int }_{G_X(-a)}^{G_X\left(a\right)}{G}_X^{-1}\left(z\right)dz,\end{array}$$

where we have used the fact that $G_X(-a)=1-G_X\left(a\right)$ because $G_X$ is the CDF of a symmetric random variable.

Now, we can write

$$\begin{array}{ccc}\hfill {\int }_{G_X(-a)}^{G_X\left(a\right)}{G}_X^{-1}\left(z\right)dz& =& {\int }_0^{G_X\left(a\right)}{G}_X^{-1}\left(z\right)dz+{\int }_{G_X(-a)}^0{G}_X^{-1}\left(z\right)dz\hfill \\ & =& {\int }_0^{G_X\left(a\right)}{G}_X^{-1}\left(z\right)dz-{\int }_0^{G_X(-a)}{G}_X^{-1}\left(z\right)dz,\hfill \end{array}$$

then take $p=G_X\left(a\right)\in (0,1)$, and we directly obtain the result. □

Corollary 1.

Let $G_X(·)$ be the CDF of an arbitrary distribution that is symmetric about zero. Then, it holds that

$$\begin{array}{c}\hfill G_X^{-1}\left(p\right)+G_X^{-1}(1-p)=0,p\in (0,1).\end{array}$$

(7)

Proof. 

The result follows from (6) by taking the derivative on both sides of the equality concerning p and applying the Fundamental Theorem of Calculus. (This theorem can be stated as follows: Let f be a continuous real-valued function defined on a closed interval $[a,b]$. Additionally, let F be a function defined for all $x\in [a,b]$ by $F\left(x\right)={\int }_a^{x}f\left(t\right)dt$. Then F is uniformly continuous on $[a,b]$ and differentiable on $(a,b)$ and $F^{\prime }\left(x\right)=f\left(x\right)$ for all $x\in (a,b)$). □

The result given now is more general than the one provided in (6).

Corollary 2.

It holds that

$$\begin{array}{c}\hfill {\int }_0^{p/\lambda }{G}_X^{-1}\left(\lambda z\right)dz={\int }_0^{(1-p)/\lambda }{G}_X^{-1}\left(\lambda z\right)dz,\forall p\in [0,1],\lambda \in \mathbb{R}-\left\{0\right\}.\end{array}$$

Proof. 

It is directly obtained from (6) by making the variable substitution $Z=\lambda Y$. □

Furthermore, a generalization of the result given in Theorem 3, although only valid for the odd powers of the inverse of the CDF, is given next.

Theorem 4.

Let $G_X(·)$ be the CDF of an arbitrary distribution that is symmetric about zero. Then, it holds that

$$\begin{array}{c}\hfill {\int }_0^p{\left[G_X^{-1}\left(z\right)\right]}^{k}dz={\int }_0^{1-p}{\left[G_X^{-1}\left(z\right)\right]}^{k}dz,\forall p\in [0,1],k=1,3,5,\dots \end{array}$$

(8)

where $G^{-1}\left(t\right)=inf\{x:G\left(x\right)\ge t\}$ for $t\in (0,1]$.

Proof. 

Using (7), we have

$$\begin{array}{c}\hfill G_X^{-1}\left(z\right)=-G_X^{-1}(1-z),0<z<1.\end{array}$$

Thus, ${\left[G_X^{-1}\left(z\right)\right]}^k={(-1)}^k{\left[G_X^{-1}(1-z)\right]}^k$, and therefore,

$$\begin{array}{c}\hfill {\int }_0^p{\left[G_X^{-1}\left(z\right)\right]}^{k}dz={(-1)}^k{\int }_0^p{\left[G_X^{-1}(1-z)\right]}^{k}dz={(-1)}^{k+1}{\int }_0^{1-p}{\left[G_X^{-1}\left(t\right)\right]}^{k}dt.\end{array}$$

Therefore, k should be an odd integer value to ensure that the integral at the left is non-negative. □

Again, from (8), by deriving on both sides of the equality concerning p and applying the Fundamental Theorem of Calculus, we arrive at

$$\begin{array}{c}\hfill {\left[G_X^{-1}\left(p\right)\right]}^k+{\left[G_X^{-1}(1-p)\right]}^k=0,\forall p\in [0,1],k=1,3,5,\dots \end{array}$$

From (8), and again by making the variable substitution $Z=\lambda Y$, we obtain

$$\begin{array}{c}\hfill {\int }_0^{p/\lambda }{\left[G_X^{-1}\left(\lambda z\right)\right]}^{k}dz={\int }_0^{(1-p)/\lambda }{\left[G_X^{-1}\left(\lambda z\right)\right]}^{k}dz,\forall p\in [0,1],\lambda \in \mathbb{R}-\left\{0\right\},k=1,3,\dots .\end{array}$$

A well-known result concerning the odd moments of a symmetric random variable is now obtained using the result provided in (8). That is, let X be a random variable that is symmetric about zero and has a CDF of $G_X\left(x\right)$; then, it holds that

$$\begin{array}{c}\hfill {\mathbb{E}}_X\left(X^k\right)=0,k=1,3,5,\dots ,\end{array}$$

which is obtained directly from ${\mathbb{E}}_X\left(X^k\right)={\int }_0^1{\left[G_X^{-1}\left(x\right)\right]}^{k}dx$ and by taking $p=1$ (or $p=0$) in (8).

The following result generalizes the one provided in Theorem 1.

Theorem 5.

Let $G_X\left(x\right)$ be the cumulative distribution function (CDF) of a random variable X that is symmetric about zero. Then,

$$\begin{array}{c}\hfill {\int }_{-a}^a{\left[G_X\left(z\right)\right]}^{k}dz=a[p^k+{(1-p)}^k]-k{\int }_{1-p}^p{z}^{k-1}{G}_X^{-1}\left(z\right)dz,\forall a\in {\mathbb{R}}^{+},\end{array}$$

(9)

where $p=G_X\left(a\right)$ and $k>0$.

Proof. 

By using (4), we can show that

$$\begin{array}{ccc}\hfill {\int }_{-a}^a{\left[G_X\left(z\right)\right]}^{k}dz& =& a\left\{{\left[G_X\left(a\right)\right]}^k+{\left[G_X(-a)\right]}^k\right\}-k{\int }_{G_X(-a)}^{G_X\left(a\right)}{y}^{k-1}{G}_X^{-1}\left(y\right)dy\hfill \\ & =& a\left\{{\left[G_X\left(a\right)\right]}^k+{\left[G_X(-a)\right]}^k\right\}-k\left[{\int }_0^{G_X\left(a\right)}{y}^{k-1}{G}_X^{-1}\left(y\right)dy\right.\hfill \\ & & \left.-{\int }_0^{G_X(-a)}{y}^{k-1}{G}_X^{-1}\left(y\right)dy\right].\hfill \end{array}$$

Now, we take $p=G_X\left(a\right)$, $p\in (0,1)$, and we obtain the result after simple algebra. □

Note that if $k=1$, then, by taking into account (6), the expression given in (9) reduces to expression (1).

Proposition 2.

Let $G_X\left(x\right)$ be the CDF of a random variable X that is symmetric about zero. Then, it holds that

$$\begin{array}{c}\hfill {\int }_{-a}^a{\displaystyle \frac{dz}{1-G_X\left(z\right)}}={\displaystyle \frac{a}{G_X\left(a\right)G_X(-a)}}-{\int }_{G_X(-a)}^{G_X\left(a\right)}{\displaystyle \frac{G_X^{-1}\left(z\right)}{{(1-z)}^2}}dz,a\in {\mathbb{R}}^{+}.\end{array}$$

Proof. 

Assume that $k\in \mathbb{N}=\{0,1,\dots \}$. Then, the result follows after simple algebra by taking the sum on both sides of expression (9). □

Risk Measures in the Tail of the Distribution

In insurance and financial risk management, risk measures are used to determine provisions and adequate capital requirements to avoid insolvency and to calculate insurance premiums. Since risks are usually considered non-negative and continuous random variables, measuring risk involves establishing a correspondence between the space of random variables and ${\mathbb{R}}^{+}$. Generally, a positive real number (i.e., the premium) is the price that policyholders periodically pay to the insurance company to cover their risk. In this work, we will pay special attention to risk measures that make it possible to measure the upper extremes of the distribution functions associated with risk, since the greater the risk, the higher the risk measure should be. Among the different risk measures, coherent measures have traditionally been used in actuarial science because they have interesting properties. In this regard, see [8,9,10,11], among others. In actuarial statistics and financial economics, there are various ways to describe risk, and each measurement method may encompass specific characteristics. A traditional way of describing risk is through a coherent measure, which is a function that considers translational invariance, monotonicity, homogeneity, and subadditivity. Most experienced investors and actuaries have used a coherent measure daily. Measures that have these mathematical properties can be beneficial in determining the level of risk that an investment could assume.

Definition 1.

Let X denote a random variable representing loss. The value at risk of X at the 100$p\%$ level, denoted by ${VaR}_p\left(X\right)$, is the 100p percentile (or quantile) of the distribution of X, i.e., ${VaR}_p\left(X\right)=inf\{x\in \mathbb{R}:G_X\left(x\right)\ge p\}$.

For a continuous distribution with CDF $G_X(·)$, we can simply write the value at risk as the quantity ${\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right)$ satisfying

$$\begin{array}{c}\hfill Pr\left[X>{\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right)\right]=1-G_X\left({\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right)\right)=1-p,p\in (0,1).\end{array}$$

Thus, we know that ${\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right)=G_X^{-1}\left(p\right)$, $p\in (0,1)$, i.e., the value at risk is a quantile risk measure. From (7), we can show that when $G_X(·)$ is the CDF of an arbitrary distribution that is symmetric about zero, it holds that ${\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right)=-{\mathrm{V}\mathrm{a}\mathrm{R}}_{1-p}\left(X\right)$.

The VaR as a risk measure corresponds to the percentile premium principle usually considered in actuarial statistics (see [12]).

Definition 2.

Suppose that X is the random variable that models losses. The tail value at risk of X at the 100$p\%$ security level, denoted ${TVaR}_p\left(X\right)$, is the expected loss given that the loss exceeds the 100p percentile (or quantile) of the distribution of X.

This measure is also called the average value at risk, since it can be viewed as the mean of the VaR of X from p. From Definition 2, it is simple to see that the tail value at risk can be written as

$$\begin{array}{c}\hfill {\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right)=\mathbb{E}\left[X|X>{\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right)\right]={\displaystyle \frac{1}{1-p}}{\int }_p^1{\mathrm{V}\mathrm{a}\mathrm{R}}_z\left(X\right)dz,\end{array}$$

(10)

where p is the confidence level.

Some simple expressions connecting the tail value at risk for two complementary confidence level values are now given.

Corollary 3.

Let X be a random variable with a symmetric distribution function $G_X\left(x\right)$. Then,

$$\begin{array}{c}\hfill (1-p){TVaR}_p\left(X\right)=p{TVaR}_{1-p}\left(X\right),p\in (0,1).\end{array}$$

(11)

Proof. 

From (10), we can show that

$$\begin{array}{ccc}\hfill {\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right)& =& {\displaystyle \frac{1}{1-p}}{\int }_p^1{\mathrm{V}\mathrm{a}\mathrm{R}}_z\left(X\right)dz\hfill \\ & =& {\displaystyle \frac{1}{1-p}}\left[{\int }_0^{1-p}{G}_X^{-1}\left(z\right)dz-{\int }_0^p{G}_X^{-1}\left(z\right)dz+{\int }_{1-p}^1{G}_X^{-1}\left(z\right)dz\right]\hfill \\ & =& {\displaystyle \frac{1}{1-p}}{\int }_{1-p}^1{G}_X^{-1}\left(z\right)dz={\displaystyle \frac{p}{1-p}}{\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_{1-p}\left(X\right),\hfill \end{array}$$

where we have used (6) to obtain the last equality. Now, the result can be obtained directly. □

Equation (11) connects the attitude of the decision-maker toward the TVaR risk measure in terms of the value of the confidence level p. That is, if the decision-maker is unsure whether to use p or $1-p$, then the relation between them is established in this equation.

From (11), it is simple to see that

$$\begin{array}{c}\hfill (1-p){\mathrm{V}\mathrm{a}\mathrm{R}}_X\left(p\right)+\mathbb{E}\left[S_X\left(p\right)\right]=p{\mathrm{V}\mathrm{a}\mathrm{R}}_X(1-p)+\mathbb{E}\left[S_X(1-p)\right],\end{array}$$

where

$$\begin{array}{c}\hfill \mathbb{E}\left[S_X\left(p\right)\right]=\mathbb{E}\left[{(X-{\mathrm{V}\mathrm{a}\mathrm{R}}_X\left(p\right))}_{+}\right]\end{array}$$

is the expected shortfall of X at a confidence level p, where ${\left(x\right)}_{+}=max\{x,0\}$. See [13] for details.

If X and Y are random variables with symmetric distribution functions, not necessarily the same, it is simple to see from (11) that

$$\begin{array}{c}\hfill {\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(X\right){\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_{1-p}\left(Y\right)={\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_{1-p}\left(X\right){\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_p\left(Y\right).\end{array}$$

(12)

Now, if the decision must be made by a decision-maker who is not sure whether to use p or $1-p$ but also is not sure which of two different distribution functions to use (symmetric), Equation (12) connects the different TVaRs involved.

Note that the expression given in (11) can be generalized to obtain

$$\begin{array}{c}\hfill \sum _{i=1}^k(1-p_i){\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_{p_i}\left(X\right)=\sum _{i=1}^k{p}_i{\mathrm{T}\mathrm{V}\mathrm{a}\mathrm{R}}_{1-p_i}\left(X\right),p_i\in (0,1),\sum _{i=1}^k{p}_i=1,\end{array}$$

which can be verified straightforwardly by induction.

3. Beyond Azzalini’s Scheme

In this section, we will see that expression (1) can be used to obtain a family of skew distributions, which includes the skew normal distribution. There are many mechanisms in the statistical literature for obtaining an expanded version of a symmetric distribution that can be asymmetrical from a symmetric distribution. Two of the several existing mechanisms are those proposed by [14,15]. However, in this work, we will focus on the proposal by [16], which has achieved considerable popularity and has generated numerous works on the subject. These works include [16,17,18,19,20,21,22,23,24,25], among others. Let g and G be the probability density function (PDF) and the cumulative distribution function (CDF) of a symmetric distribution. A random variable Y is said to have an asymmetric distribution if its PDF is given by

$$\begin{array}{c}\hfill f_Y\left(y\right)=2g\left(y\right)G\left(\lambda y\right),y\in \mathbb{R},\lambda \in \mathbb{R}.\end{array}$$

(13)

In particular, when $G\left(x\right)=\Phi \left(x\right)$ and $g\left(x\right)=\varphi \left(x\right)$, the expression given in (13) is the skew normal distribution proposed and studied in [16].

3.1. First Proposal

In this subsection, we present a series of results that were proposed in [20] and that we reproduce for the most part with the aim of making this work self-sufficient. We begin with the following result, which is built from (1) and generalizes (13).

Theorem 6

([20]). Let X and Y be two random variables with symmetric CDFs $G_X\left(x\right)$ and $G_Y\left(y\right)$ and PDFs $g_X\left(x\right)$ and $g_Y\left(y\right)$, respectively. Then,

$$\begin{array}{c}\hfill f_Y(y;\lambda ,a)={\displaystyle \frac{g_Y\left(y\right)}{a}}{\int }_{-a}^a{G}_X(z+\lambda y)dz\end{array}$$

(14)

represents a genuine PDF for $a\in \mathbb{R}-\left\{0\right\}$ and $\lambda \in \mathbb{R}$.

Note that

$$\begin{array}{c}\hfill s_Y(y;\lambda ,a)={\displaystyle \frac{g_Y\left(y\right)}{a}}{\int }_{-a}^a{\overline{G}}_X(z+\lambda y)dz\end{array}$$

also represents a genuine PDF for $a\in \mathbb{R}-\left\{0\right\}$ and $\lambda \in \mathbb{R}$, and it holds that $f_Y(y;\lambda ,a)=s_Y(y;-\lambda ,a)$.

Note that the expression (14) can be viewed as an infinite mixture construction. Let $G_X(\xi +\lambda y)$, $\lambda \in \mathbb{R}$, $\xi \in \mathbb{R}$, and $y\in \mathbb{R}$ be the cumulative distribution functions (CDFs) of a symmetric distribution with support in $\mathbb{R}$. Now, assume that $\xi$ is a random variable following a uniform distribution on the interval $[-a,a]$; then,

$$\begin{array}{c}\hfill H_X(y;\lambda ,a)={\displaystyle \frac{1}{2a}}{\int }_{-a}^{a}G(\xi +\lambda y)d\xi \end{array}$$

is also a genuine CDF symmetric around zero. That is, $H_X\left(y\right)=1-H_X(-y)$. Now, (14) is derived by taking into account the fact that $2g_Y\left(y\right)H_X\left(y\right)$ is a genuine PDF. Another elegant way to see that (14) defines a genuine PDF is to consider the argument given in Lemma 1 in [19]. That is, let $S(\lambda ,a)={\int }_{-\infty }^{\infty }{f}_Y(y;\lambda ,a)dy$. Now, we can see that $S(0,a)={\int }_{-\infty }^{\infty }{g}_Y\left(y\right)dy=1$. and since

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial \lambda }}S(\lambda ,a)={\int }_{-\infty }^{\infty }{\displaystyle \frac{y{g}_Y\left(y\right)}{a}}\left[G_X(a+\lambda y)-G_X(-a+\lambda y)\right]dy=0,\end{array}$$

we can see that $S(\lambda ,a)=1$.

Figure 1 shows the PDF (14) for different values of the parameters $\lambda$ and a, assuming $g_Y\left(y\right)=\varphi \left(y\right)$ and $G_X\left(x\right)=\Phi \left(x\right)$, where $\Phi (·)$ and $\Phi (·)$ represent the PDF and CDF of the standard normal distributions, respectively.

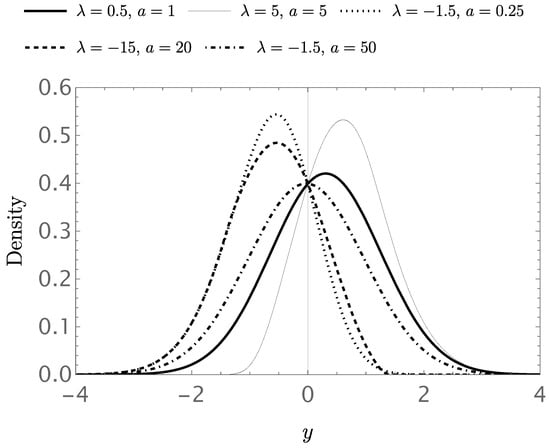
Figure 1. Graphs of the density (14) for various parameter values, assuming $g_Y\left(y\right)=\varphi \left(y\right)$ and $G_X\left(x\right)=\Phi \left(x\right)$.

A more flexible family of distributions than the one provided in (14) is given by

$$\begin{array}{c}\hfill f_Y(y;\lambda ,a)={\displaystyle \frac{g_Y\left(y\right)}{a}}{\int }_{-a}^a{G}_X(z+\lambda h\left(y\right))dz,\end{array}$$

(15)

where $h\left(x\right)$ is an odd real-valued function. Examples of this PDF for $h\left(x\right)=x^3$ are now shown in Figure 2. As we can see, the PDF is now more versatile and can be bimodal for appropriate parameter values. There exist many examples showing empirical bimodal data. For example, it is well known that when measuring the weight of adult animals, an empirical distribution with two peaks (modes) is observed. The bimodality is due to the average weights of males and females. This data type should be analyzed with probability distributions that allow the two modes to be detected. Another example of bimodal data is the well-known Old Faithful geyser data set. This data set consists of measurements of the numerical eruption time in minutes and the waiting time for the next eruption (also in minutes). This popular dataset has been studied widely in the statistical literature. See [26], among others. Specifically, the $\lambda$ parameter acts by modifying the skewness of the distribution. On the other hand, keeping the $\lambda$ value fixed, large values of a lead the distribution to take on a normal-like appearance, while small values of a, essentially between zero and one, result in a distribution with two modal values.

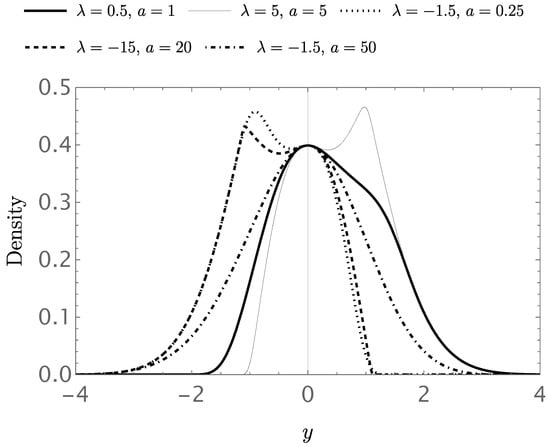
Figure 2. Graphs of the density (15) for various parameter values, assuming $g_Y\left(y\right)=\varphi \left(y\right)$; $G_X\left(x\right)=\Phi \left(x\right)$; and $h\left(x\right)=x^3$, an odd function.

Observe that (14) can be written as

$$\begin{array}{c}\hfill f_Y(y;\lambda ,a)={\displaystyle \frac{g_Y\left(y\right)}{a}}{\int }_{\lambda y-a}^{\lambda y+a}{G}_X\left(u\right)du,\end{array}$$

(16)

which is obtained after making the variable substitution $u=z+\lambda y$ in (14). Note that the family of asymmetric distributions proposed by [16] appears, as a special case, from (16) onward by applying the first mean value theorem to the integral that appears in (15) in the interval $[\lambda y-a,\lambda y+a]$. To achieve this, we take $c=\lambda y$ in the well-known formula ${\int }_s^{r}f\left(x\right)dx=f\left(c\right)(r-s)$, $c\in [s,r]$, to obtain $f_Y(y;\lambda )=2g_Y\left(y\right)G_X\left(\lambda y\right)$.

We present another family of skew distributions in connection with the latter. This new family is derived from (15) by integrating on both sides of the equality, taking the derivative concerning a, and applying the Fundamental Theorem of Calculus.

Theorem 7

([20]). If $g_Y\left(y\right)$ is a density function that is symmetric about zero and $G_X$ is a CDF that is also symmetric about zero, then

$$\begin{array}{c}\hfill f_Y(y;\lambda ,a)=g_Y\left(y\right)\left[G_X(\lambda y+a)+G_X(\lambda y-a)\right]\end{array}$$

(17)

is a valid PDF for $a\in \mathbb{R}$ and $\lambda \in \mathbb{R}$.

Obviously, $f_Y(y;\lambda ,0)=2g_Y\left(y\right)G_X\left(y\right)$, $f_Y(y;\lambda ,\infty )=g_Y\left(y\right)$, while $f_Y(y;0,a)=g_Y\left(y\right)$. Figure 3 shows the probability density function (17) for different values of the parameters $\lambda$ and a. Again, the parameter $\lambda$ controls the skewness of the distribution, while the parameter a controls the kurtosis. Thus, small values of the parameter a produce a distribution with lower kurtosis than larger values. In the latter case, the distribution generates data that are dispersed and far from the center and, therefore, at the tail of the distribution.

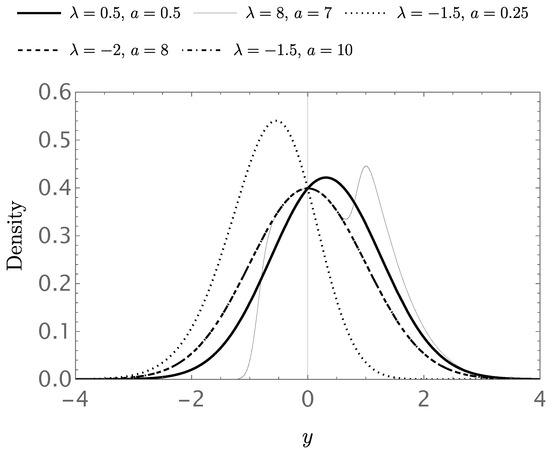
Figure 3. Graphs of the density (17) for various parameter values, assuming $g_Y\left(y\right)=\varphi \left(y\right)$ and $G_X\left(y\right)=\Phi \left(y\right)$.

Note that the two proposed families, (14) and (17), are different, and the only element they have in common is the density $g_Y\left(y\right)$. On the other hand, the most significant difference between the two families is that the parameter a is not allowed to take the value zero in the first case, which is permitted in the second.

Since $G_X\left(a\right)=1-G_X(-a)$, we can obtain from (17) that, when $\lambda =0$, $f_Y\left(y\right)=g_Y\left(y\right)$, while for $a=0$, we obtain the family of skewed distributions proposed in [16]. Again, it can be verified that $f_Y(y;\lambda ,a)=f_Y(y;\lambda ,-a)$ for the family given in (17).

We will now show a result that is more general than the one provided in [16,27,28] for a symmetric random variable.

Proposition 3

([20]). If U is a random variable that is symmetric about zero with a CDF of $G\left(u\right)$ and a PDF of $g\left(u\right)$, and if λ and α are two real numbers, then

$$\begin{array}{c}\hfill \mathbb{E}\left[G\right(\lambda U+a\left)\right]=1-\mathbb{E}\left[G\right(\lambda U-a\left)\right].\end{array}$$

(18)

When U follows a standard normal distribution, (18) reduces to

$$\begin{array}{c}\hfill \mathbb{E}[\Phi (\lambda U+a)]=1-\mathbb{E}[\Phi (\lambda U-a)]=\Phi \left({\displaystyle \frac{a}{\sqrt{1+{\lambda }^2}}}\right),\end{array}$$

a result that is well known in the statistical literature (see [16,27,28]).

Multivariate extensions of the univariate distributions given in Theorem 6 arise easily, as seen in the next result.

Theorem 8

([20]). Let X and $\underline{Y}$ be two random variables where $X\sim N(0,1)$ and $\underline{Y}\sim N^{\left(m\right)}(\underline{0},\mathsf{\Sigma })$. Then,

$$\begin{array}{c}\hfill f(\underline{y};\underline{\lambda },a)={\displaystyle \frac{f_{\underline{Y}}\left(\underline{y}\right)}{\alpha }}{\int }_{-a}^a{F}_X(z+{\underline{\lambda }}^T\underline{y})dz\end{array}$$

represents a genuine PDF for $a\in \mathbb{R}-\left\{0\right\}$ and $\underline{\lambda }\in {\mathbb{R}}^m$.

Note that the two proposed families, (14) and (17), are It is important to note that the only requirement for the distributions of $\underline{Y}$ and X is that they be symmetric about zero. This requirement applies to the previous theorem as well as the following one.

Theorem 9

([20]). Let X and $\underline{Y}$ be two random variables where $X\sim N(0,1)$ and $\underline{Y}\sim N^{\left(m\right)}(\underline{0},\mathsf{\Sigma })$. Then,

$$\begin{array}{c}\hfill f(\underline{y};\underline{\lambda },a)=f_{\underline{Y}}\left(\underline{y}\right)\left[F_X({\underline{\lambda }}^T\underline{y}+a)+F_X({\underline{\lambda }}^T\underline{y}-a)\right]\end{array}$$

(19)

is a valid PDF for $a\in \mathbb{R}$ and $\underline{\lambda }\in {\mathbb{R}}^m$.

Note that if we set $\alpha =0$ in (19), we obtain

$$f(\underline{y};\underline{\lambda })=2f_{\underline{Y}}\left(\underline{y}\right)F_X\left({\underline{\lambda }}^T\underline{y}\right),$$

which was one of the first multivariate skew normal models to appear in the literature. See [17,18], for instance.

Applications and properties of these distributions (the univariate and multivariate expressions) are provided in [20].

3.2. Second Proposal to Be Studied

Recent works ([21,22]) propose generalizations of symmetric continuous distributions, paying special attention to the case of the normal distribution. In particular, and building on the idea in the following result, which, in turn, is based on an idea taken from [21,29], a very flexible family of antinormal distributions can be obtained.

Theorem 10

([21]). Let $f\left(x\right)$ be a PDF symmetric about zero, and consider the function $f\left(\omega \right(x;\beta \left)\right)$, with $\omega (x;\beta )=x-\beta /x$, where $\omega (x;\beta )\ge 0$. Then, if $df\left(\omega \right(x;\beta \left)\right)/\left(d\beta \right)$ is also a symmetric function, we can infer that ${\int }_{-\infty }^{\infty }f\left(\omega (x;\beta )\right)dx=1$.

Based on the use of Theorem 10, we can build a family of PDFs by taking

$$g(x;\beta )=\left\{\begin{array}{cc}f\left(\omega \right(x;\beta \left)\right),& x\ne 0,\\ f\left(0\right),& x=0,\end{array}\right.$$

(20)

where $\beta \ge 0$, which is a two-part piecewise PDF.

We now pay attention to a simple family of distributions obtained by substituting (20) into (17) after taking $f\left(\omega \right(x;\beta \left)\right)=\Phi \left(\omega \right(x;\beta \left)\right)$ and $G_X(·)={\Phi }_X(·)$. Its PDF is

$$\begin{array}{c}\hfill f(x;\lambda ,a,\beta )=\varphi \left(\omega (x;\beta )\right)\left[\Phi (\lambda x+a)+\Phi (\lambda x-a)\right],x\in \mathbb{R}-\left\{0\right\}\end{array}$$

(21)

and $g(0;\beta )=\varphi \left(0\right)$.

The case $a=0$ provides a family of distributions that are symmetric about zero. The case $a=\beta =0$ gives the skew normal distribution studied in [2,16].

Figure 4 shows the probability density function (21) for different values of the parameters $\lambda$, $\alpha$, and $\beta$. In this case, the $\beta$ parameter acts similarly to a scale parameter. The $\alpha$ parameter, together with the $\lambda$ parameter, controls the unimodality or bimodality of the distribution, although there does not appear to be a pattern that can generally describe the shape of the distribution.

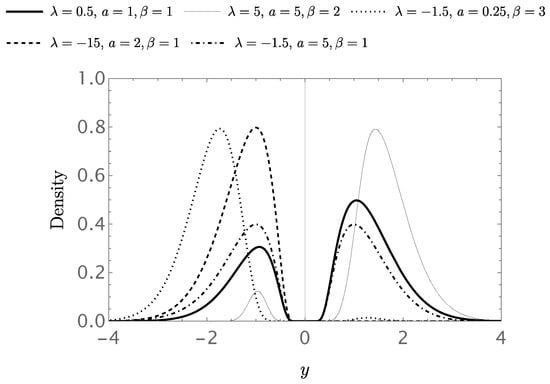
Figure 4. Graphs of the density (21) for various parameter values.

Of course, for the purpose of application, it is convenient to consider the introduction of location-scale generalization of the proposed distributions, defined as the distribution of $Z=\mu +\sigma X$, where $\mu \in \mathbb{R}$ and $\sigma >0$.

A later study will present the derivation of properties and parametric estimators for this family. Further studies of the application of this family of distributions will also be performed. Thus, this family will be confronted with actual data to provide a justification for this work.

4. Summary and Conclusions

This paper has shown how, by starting from a simple result provided by [3] more than two decades ago and generalizing it, a whole range of results related to a symmetrical distribution function and its inverse can be obtained. The usefulness of these contributions is in financial and actuarial statistics, mainly in the area of risk measures in the tail of the distribution, such as the VaR and the TVaR, among others. In addition, this result has served as a launchpad to obtain a generalization of the Azzalini scheme (see [16]) that is useful for constructing skew distributions starting from a distribution that is symmetrical and therefore not skewed.

One aspect that undoubtedly merits detailed study, particularly for the last family of proposed distributions, is the estimation of its parameters, which will be carried out in subsequent work currently under development. Additional studies will also be conducted on this family, its application to real data, and its comparison with traditional models used in the applied statistics literature.

Other aspects to be considered include changing the support of the distributions to obtain generalizations of the log-normal distributions, which can be helpful in fitting empirical positive data with long tails.