Probabilistic Analysis of Distributed Fractional-Order Stochastic Systems Driven by Fractional Brownian Motion: Existence, Uniqueness, and Transportation Inequalities
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Brownian Motion and Wick Product
2.2. Malliavin Derivative
- (H1) and on for some and .
- (H2) There exists such that for ,
- (H3) There exists such that for all , ,
3. Existence and Uniqueness
- (1)
- Structural Picard sequence:
- (2)
- Prove that the sequence converges uniformly: Then, for any , we obtain by mathematical induction thatby observing that the series defined on the right-hand side of the equation converges to (8). At first, let , , ,Secondly, we obtain
- (3)
- Verify that the limit function is a solution: According to the Borel–Cantelli lemma, converges uniformly on [0,T] to , taking the limit for (9):So, is the solution of Equation (4). So the proof of existence is complete.
4. Transportation Inequalities for (4)
- (1)
- Construct the measure transformation.
- (2)
- Define a new noise process.
- (3)
- Rewrite the original equation.
- (4)
- Construct coupling equation.
- (5)
- (Control Wasserstein distance.
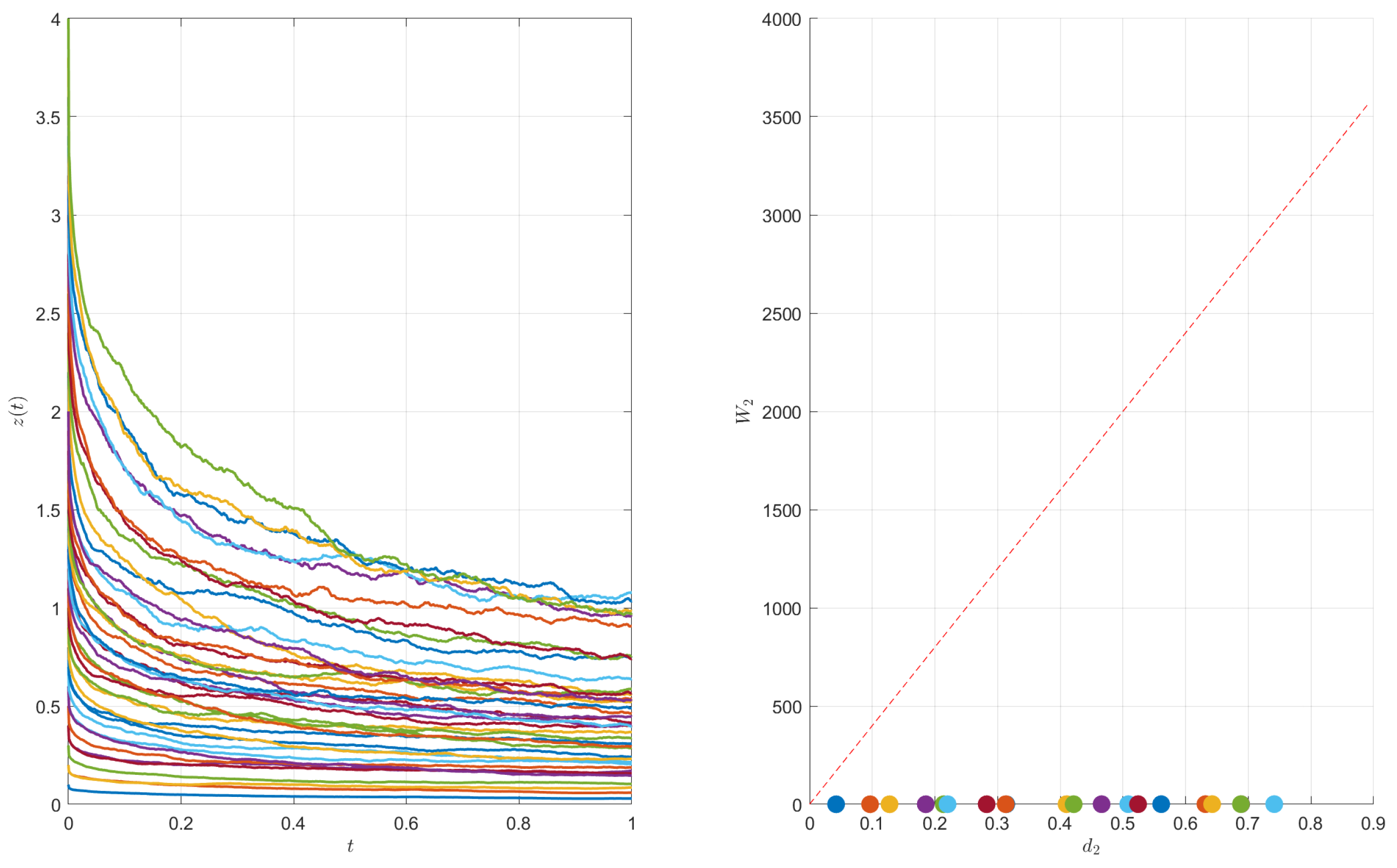
5. Example
- (1)
- When is a probability density function, defineHere, we choose and . Obviously, satisfies (H1), that is, on and
- (2)
- When , define . Obviously, satisfies (H2), that is, for all ,
- (3)
- (When , define . Obviously, satisfies (H3), that is, for all ,
- (4)
- with .
- (5)
- is a fractional Brownian motion with .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Z.; Zheng, X.; Wang, H. A variably distributed-order time-fractional diffusion equation: Analysis and approximation. Comput. Methods Appl. Mech. Eng. 2020, 367, 113118. [Google Scholar] [CrossRef]
- Bao, H.; Park, J.H.; Cao, J. Adaptive synchronization of fractional-order output-coupling neural networks via quantized output control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3230–3239. [Google Scholar] [CrossRef] [PubMed]
- Diethelm, K. The Analysis of Fractional Differential Equations. An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Li, C.; Li, Z. The finite-time blow-up for semilinear fractional diffusion equations with time ψ-Caputo derivative. J. Nonlinear Sci. 2022, 32, 1–42. [Google Scholar] [CrossRef]
- Ahmadova, A.; Mahmudov, N. Existence and uniqueness results for a class of fractional stochastic neutral differential equations. Chaos Solitons Fractals 2020, 139, 110253. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Publishers: London, UK, 1993. [Google Scholar]
- Xu, L.; Li, Z. Stochastic fractional evolution equations with fractional brownian motion and infinite delay. Appl. Math. Comput. 2018, 336, 36–46. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H. Strong convergence of a Euler-Maruyama scheme to a variable-order fractional stochastic differential equation driven by a multiplicative white noise. Chaos Solitons Fractals 2021, 142, 110392. [Google Scholar] [CrossRef]
- Dong, J.; Du, N.; Yang, Z. A distributed-order fractional stochastic differential equation driven by Lévy noise: Existence, uniqueness, and a fast EM scheme. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 023109. [Google Scholar] [CrossRef]
- Lorenzo, C.; Hartley, T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Chen, Y. Variable-order fractional differential operators in anomalous diffusion modeling. Phys. A Stat. Mech. Its Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Zhang, Y. A review on variable-order fractional differential equations: Mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N. Numerical analysis for distributed-order differential equations. J. Comput. Appl. Math. 2009, 225, 96–104. [Google Scholar] [CrossRef]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Some aspects of fractional diffusion equations of single and distributed order. Appl. Math. Comput. 2007, 187, 295–305. [Google Scholar]
- Boufoussi, B.; Hajji, S. Neutral stochastic functional differential equations driven by a fractional Brownian motion in a Hilbert space. Stat. Probab. Lett. 2012, 82, 1549–1558. [Google Scholar] [CrossRef]
- Caraballo, T.; Garrido-Atienza, M.; Taniguchi, T. The existence and exponential behavior of solutions to stochastic delay evolution equations with a fractional Brownian motion. Nonlinear Anal. Theory Methods Appl. 2011, 74, 3671–3684. [Google Scholar] [CrossRef]
- Li, Z. Shift Harnack inequality and integration by parts formula for functional SDEs driven by fractional Brownian motion. Proc. Am. Math. Soc. 2016, 144, 2651–2659. [Google Scholar] [CrossRef]
- Li, Z.; Yan, L. Stochastic averaging for two-time-scale stochastic partial differential equations with fractional Brownian motion. Nonlinear Anal. Hybrid Syst. 2019, 31, 317–333. [Google Scholar] [CrossRef]
- Li, Z.; Xu, L.; Zhou, J. Viability for coupled SDEs driven by fractional Brownian motion. Appl. Math. Optim. 2021, 84, 55–98. [Google Scholar] [CrossRef]
- Shen, G.; Xiang, J.; Wu, J. Averaging principle for distribution dependent stochastic differential equations driven by fractional Brownian motion and standard Brownian motion. J. Differ. Equ. 2022, 321, 381–414. [Google Scholar] [CrossRef]
- Xu, J.; Lian, Q.; Wu, J. A strong averaging principle rate for two-time-scale coupled forward–backward stochastic differential equations driven by fractional Brownian motion. Appl. Math. Optim. 2023, 88, 32. [Google Scholar] [CrossRef]
- Xu, J.; Sun, Y.; Ren, J. A support theorem for stochastic differential equations driven by a fractional Brownian motion. J. Theor. Probab. 2022, 36, 728–761. [Google Scholar] [CrossRef]
- Djellout, H.; Guillin, A.; Wu, L. Transportation cost-information inequalities and applications to random dynamical systems and diffusions. Ann. Probablity 2004, 32, 2702–2732. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Z. Talagrand’s T2-transportation inequality w.r.t. a uniform metric for diffusions. Acta Math. Appl. Sin. 2004, 20, 357–364. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Z. Talagrand’s T2-transportation inequality and log-sobolev inequality for dissipative SPDEs and applications to reaction-diffusion equations. Chin. Ann. Math. Ser. B 2006, 27, 243–262. [Google Scholar] [CrossRef]
- Ma, Y. Transportation inequalities for stochastic differential equations with jumps. Stoch. Processes Their Appl. 2010, 120, 2–21. [Google Scholar] [CrossRef]
- Wu, L. Transportation inequalities for stochastic differential equations of pure jumps. Ann. l’IHP Probab. Stat. 2010, 46, 465–479. [Google Scholar] [CrossRef]
- Pal, S. Concentration for multidimensional diffusions and their boundary local times. Probab. Theory Relat. Fields 2012, 154, 225–254. [Google Scholar] [CrossRef]
- Saussereau, B. Transportation inequalities for stochastic differential equations driven by a fractional Brownian motion. Bernoulli 2012, 18, 1–23. [Google Scholar] [CrossRef]
- Li, Z.; Luo, J. Transportation inequalities for stochastic delay evolution equations driven by fractional Brownian motion. Front. Math. China 2015, 10, 303–321. [Google Scholar] [CrossRef]
- Boufoussi, B.; Hajji, S. Transportation inequalities for neutral stochastic differential equations driven by fractional Brownian motion with Hurst parameter less than 1/2. Mediterr. J. Math. 2017, 14, 192. [Google Scholar] [CrossRef]
- Mishura, Y.; Mishura, I. Stochastic Calculus for Fractional Brownian Motion and Related Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 1929. [Google Scholar]
- Hu, Y.; Øksendal, B. Fractional white noise calculus and applications to finance. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 2003, 6, 1–32. [Google Scholar] [CrossRef]
- Biagini, F.; Hu, Y.; Øksendal, B.; Zhang, T. Stochastic Calculus for Fractional Brownian Motion and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Alos, E.; Mazet, O.; Nualart, D. Stochastic calculus with respect to Gaussian processes. Ann. Probab. 2001, 29, 766–801. [Google Scholar] [CrossRef]
- Rascanu, A. Differential equations driven by fractional Brownian motion. Collect. Math. 2002, 53, 55–81. [Google Scholar]
- Holden, H.; Øksendal, B.; Ubøe, J.; Zhang, T.; Holden, H. Stochastic Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Karatzas, I.; Shreve, S. Brownian Motion and Stochastic Calculus; Springer: Berlin/Heidelberg, Germany, 2014; Volume 113. [Google Scholar]
- Xu, Y.; Pei, B.; Wu, J. Stochastic averaging principle for differential equations with non-Lipschitz coefficients driven by fractional Brownian motion. Stochastics Dyn. 2017, 17, 1750013. [Google Scholar] [CrossRef]
- Prato, G.; Zabczyk, J. Stochastic Equations in Infinite Dimensions; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, G.; Xu, L.; Li, Z. Probabilistic Analysis of Distributed Fractional-Order Stochastic Systems Driven by Fractional Brownian Motion: Existence, Uniqueness, and Transportation Inequalities. Symmetry 2025, 17, 650. https://doi.org/10.3390/sym17050650
Xia G, Xu L, Li Z. Probabilistic Analysis of Distributed Fractional-Order Stochastic Systems Driven by Fractional Brownian Motion: Existence, Uniqueness, and Transportation Inequalities. Symmetry. 2025; 17(5):650. https://doi.org/10.3390/sym17050650
Chicago/Turabian StyleXia, Guangyue, Liping Xu, and Zhi Li. 2025. "Probabilistic Analysis of Distributed Fractional-Order Stochastic Systems Driven by Fractional Brownian Motion: Existence, Uniqueness, and Transportation Inequalities" Symmetry 17, no. 5: 650. https://doi.org/10.3390/sym17050650
APA StyleXia, G., Xu, L., & Li, Z. (2025). Probabilistic Analysis of Distributed Fractional-Order Stochastic Systems Driven by Fractional Brownian Motion: Existence, Uniqueness, and Transportation Inequalities. Symmetry, 17(5), 650. https://doi.org/10.3390/sym17050650





