The Effect of Graphene Nanofiller on Electromagnetic-Related Primary Resonance of an Axially Moving Nanocomposite Beam
Abstract
1. Introduction
2. Theory
2.1. Theoretical Modeling of Graphene Nanocomposites
2.1.1. Theoretical Framework of Effective Medium Theory
2.1.2. Interface, Agglomeration and Percolation Effects
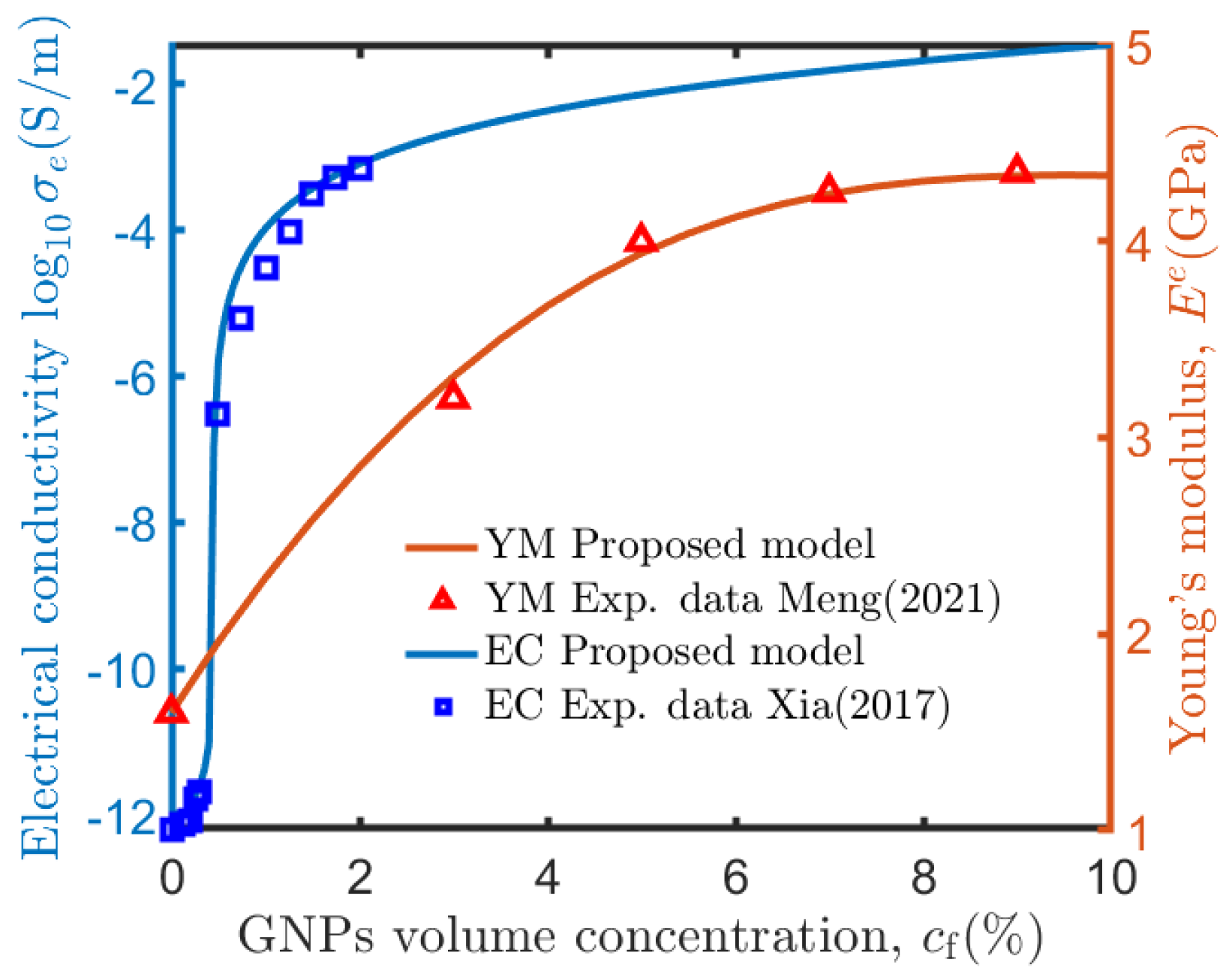
2.1.3. Model Verification
2.2. Primary Resonance
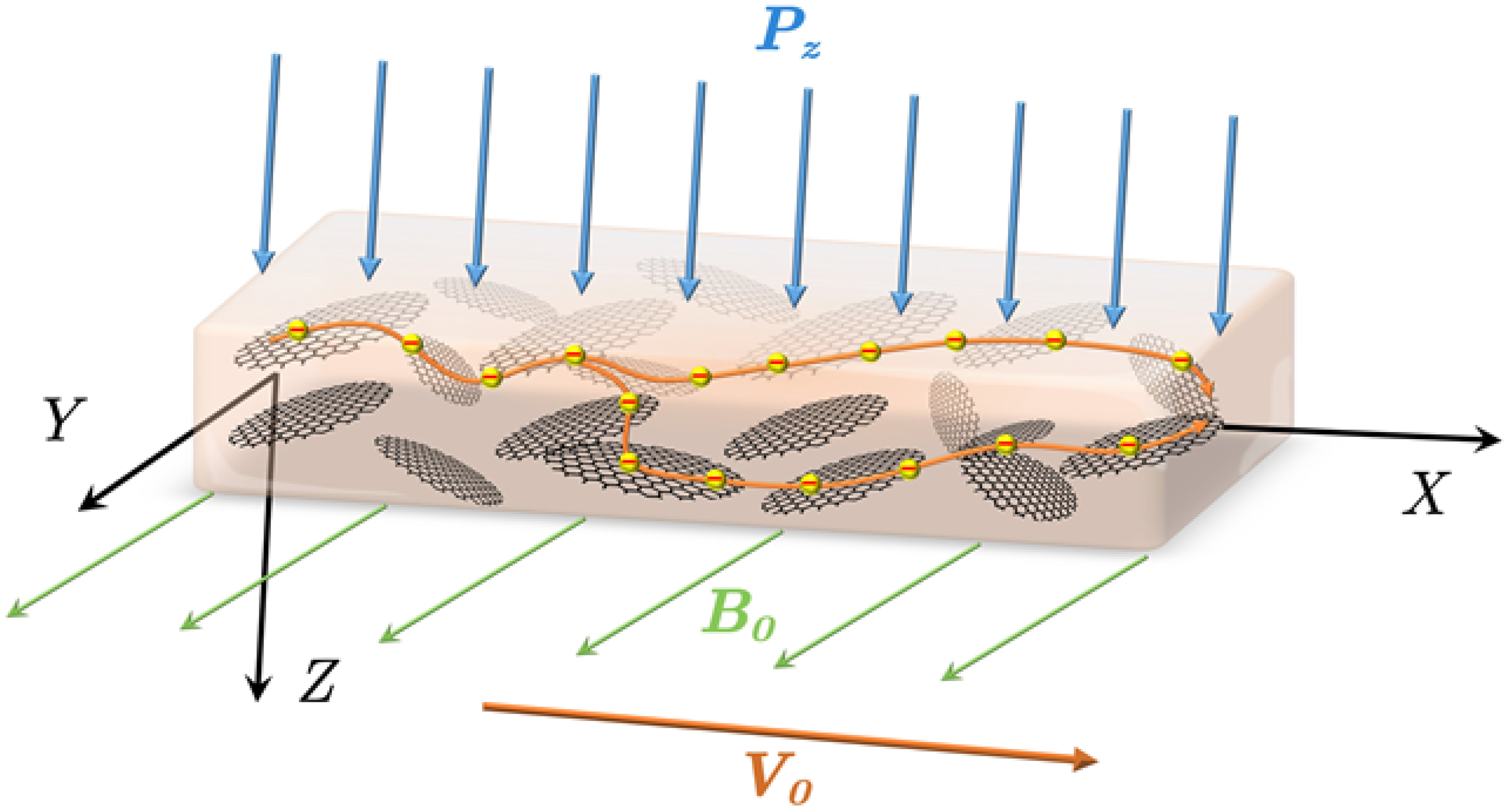
2.2.1. Model Setup and Vibration Equation
2.2.2. Model Verification
3. Numerical Calculation and Discussion
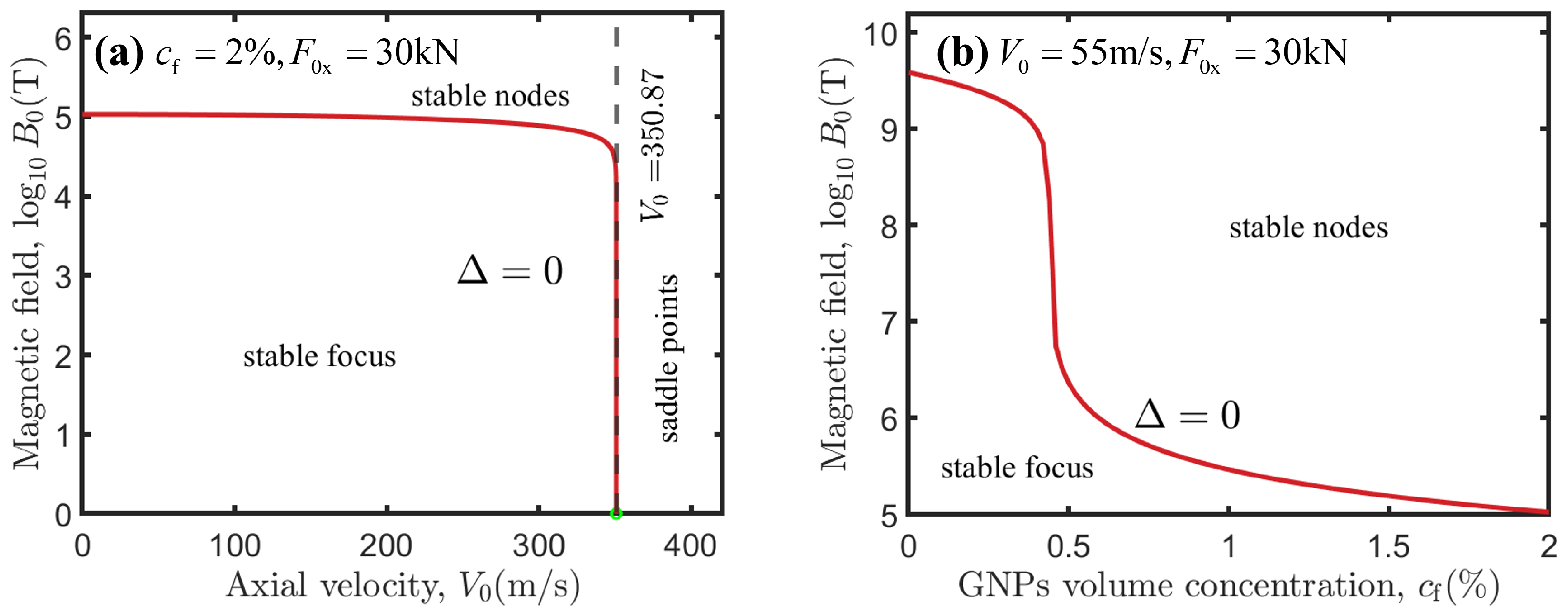
3.1. Stability Analysis
3.2. Primary Resonance
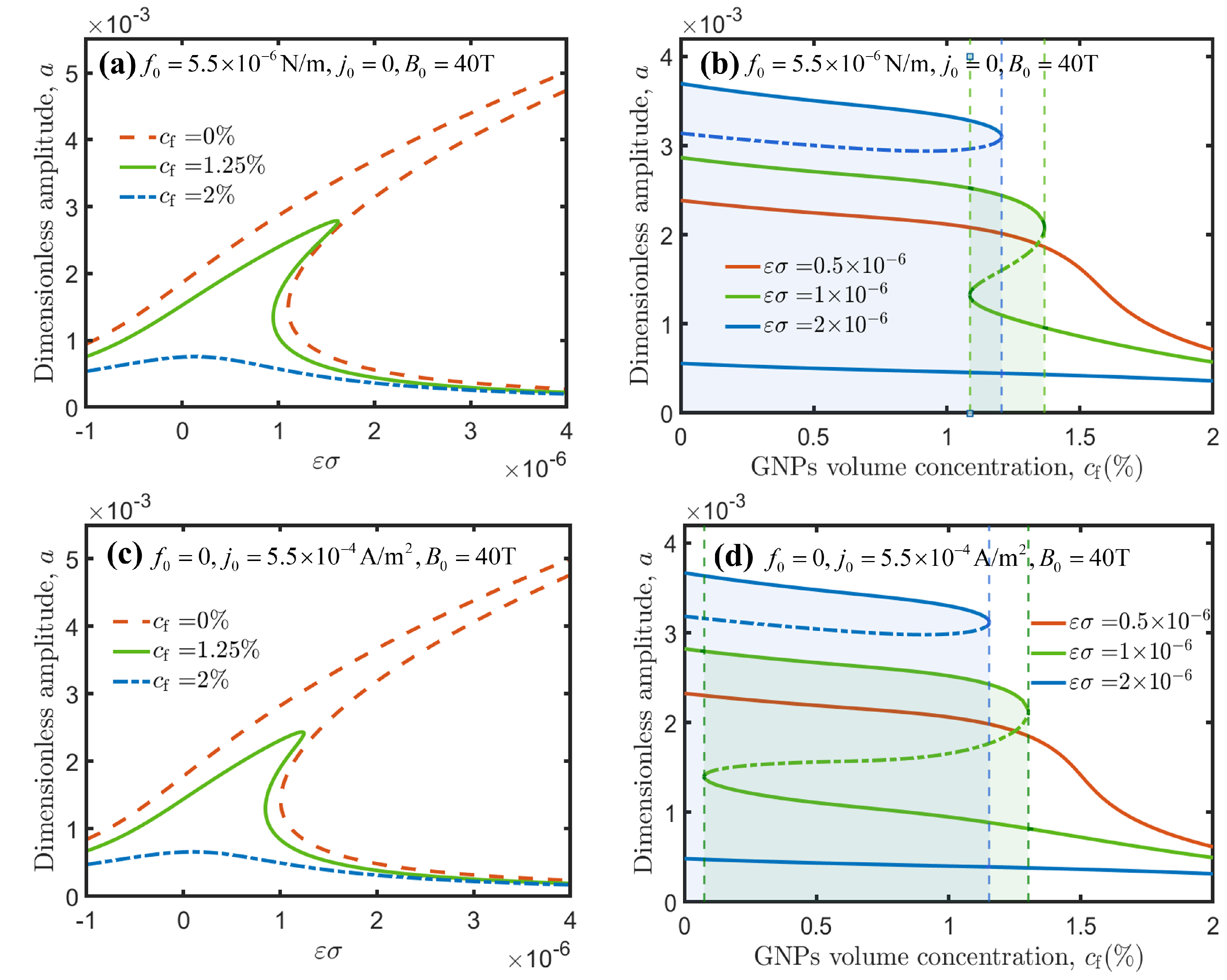
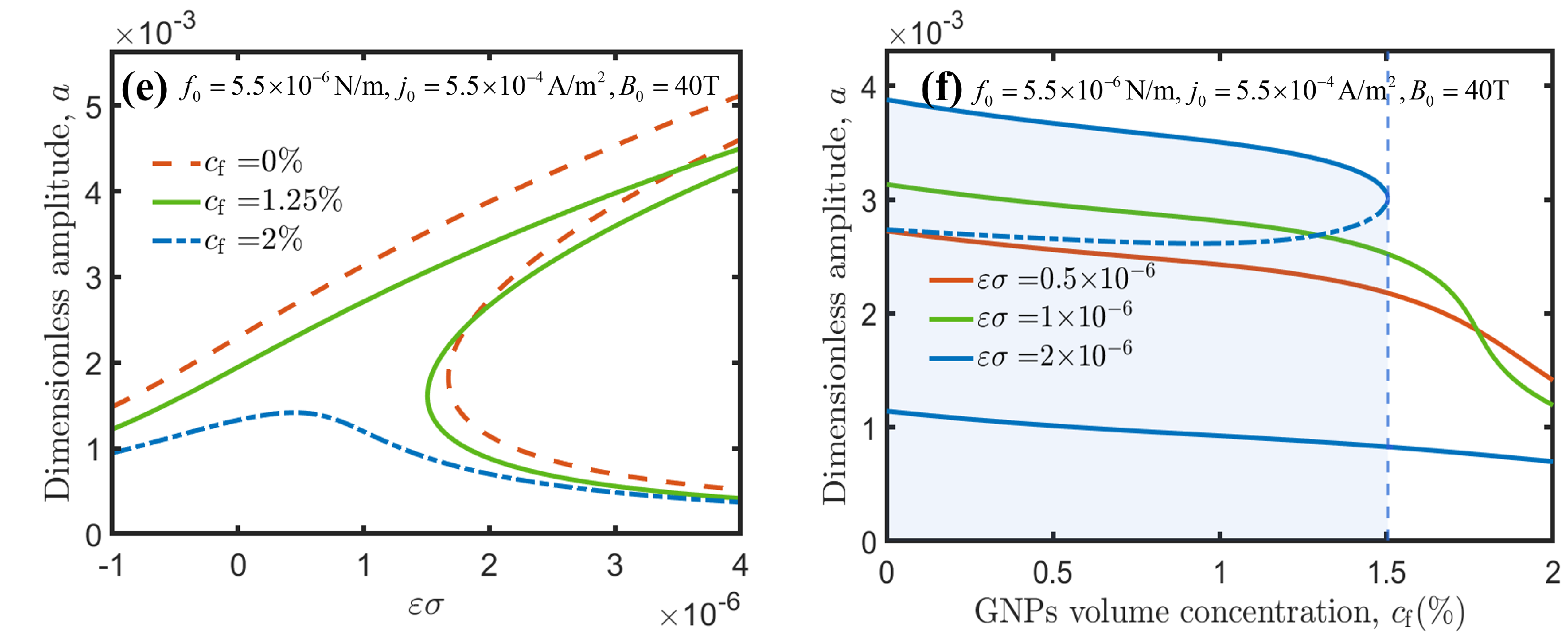
3.2.1. Amplitude-Frequency Response
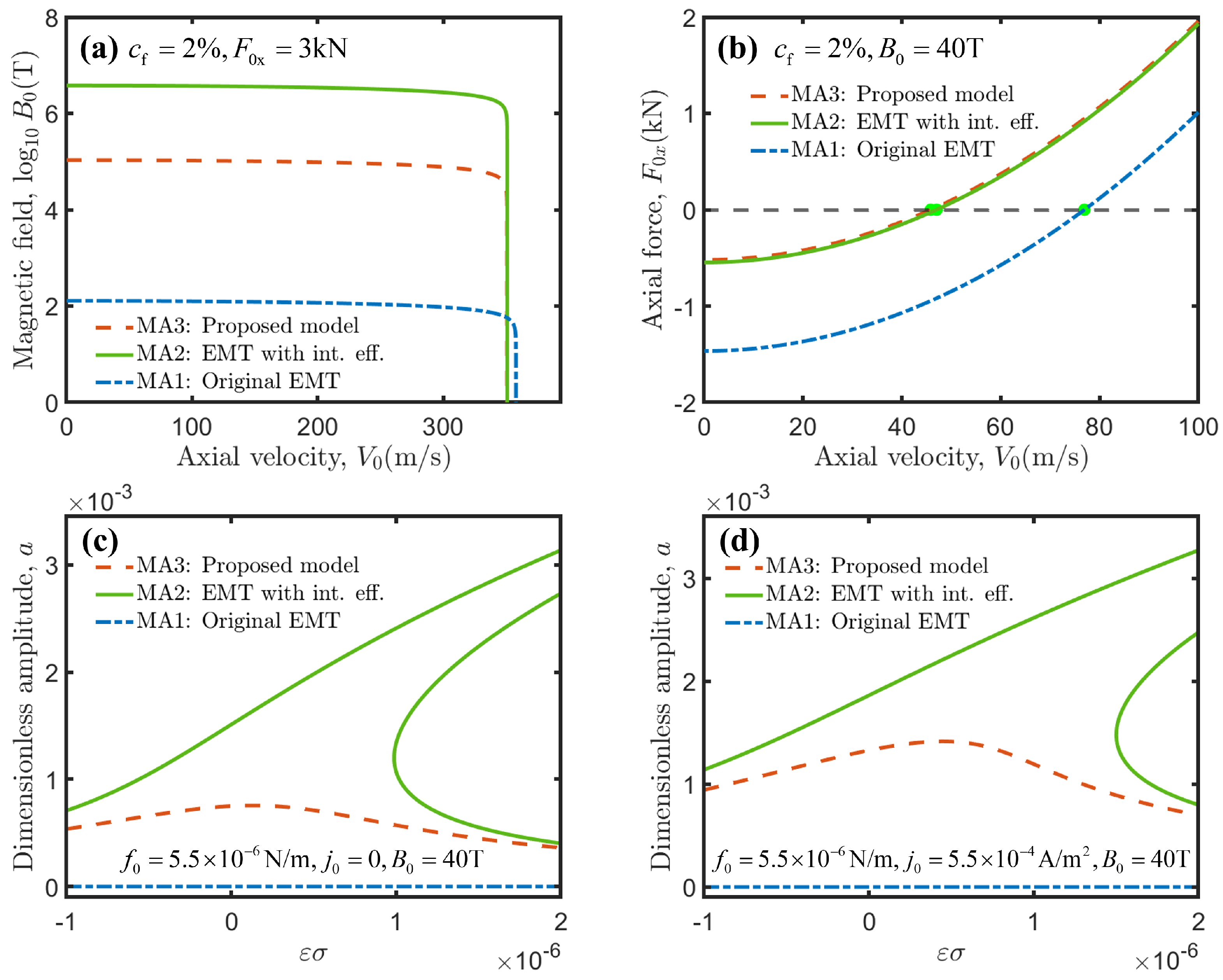
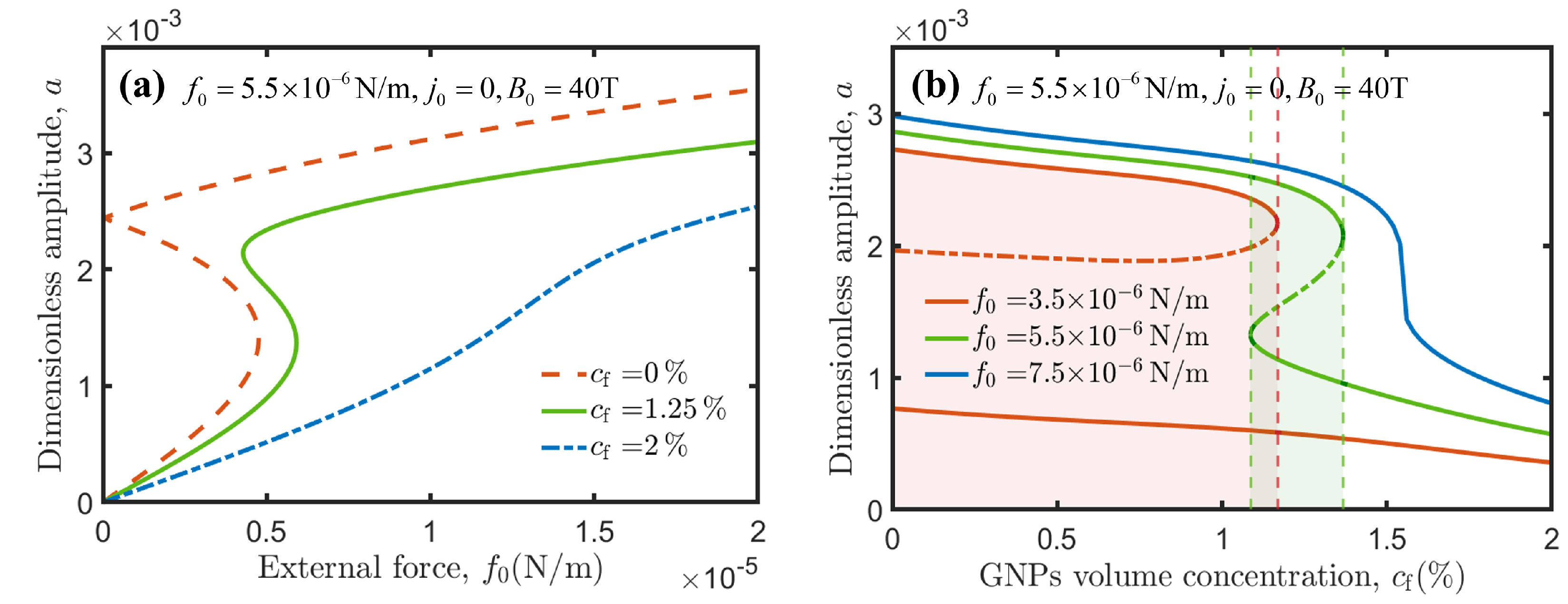
3.2.2. Amplitude-External Load Response
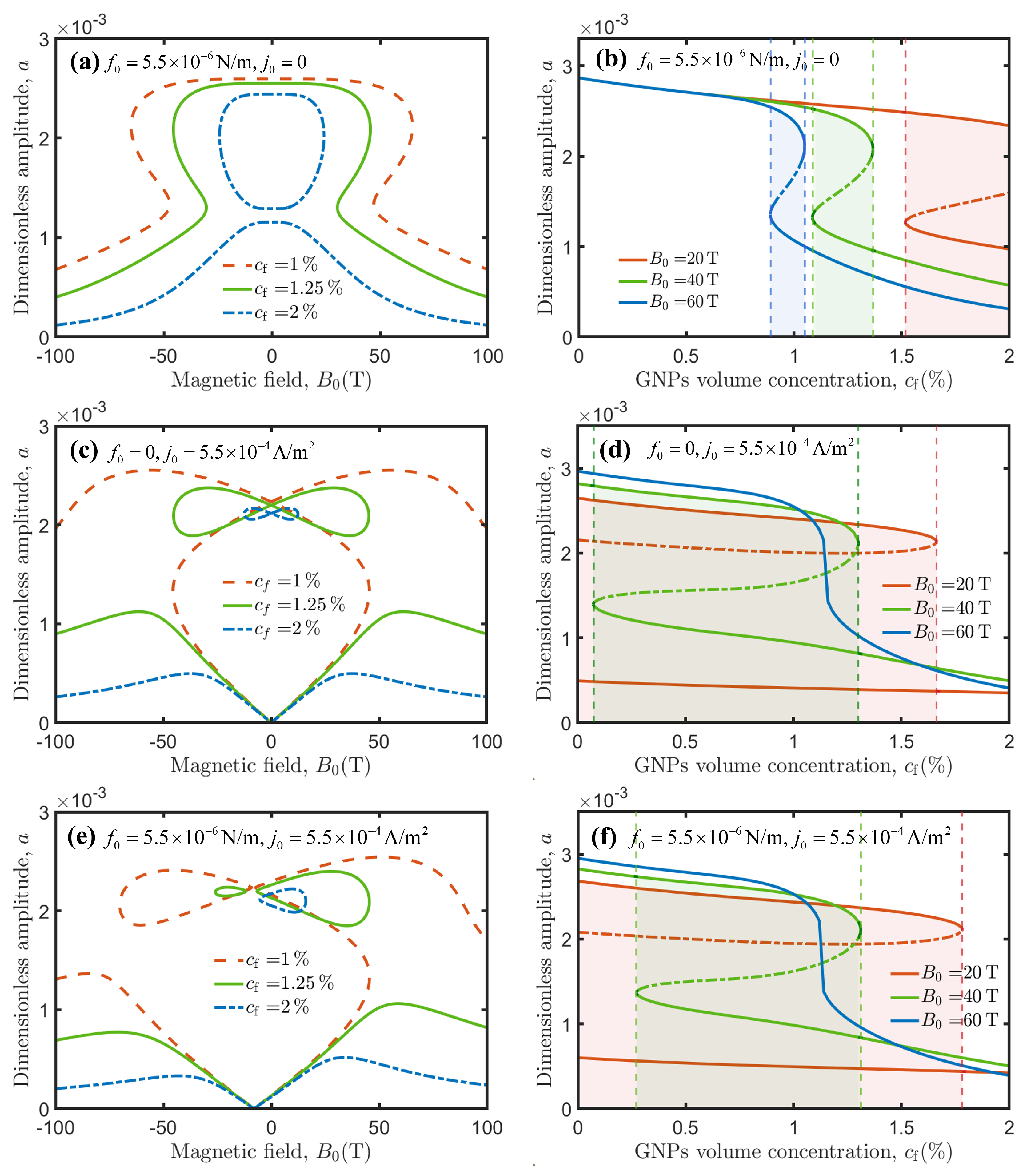
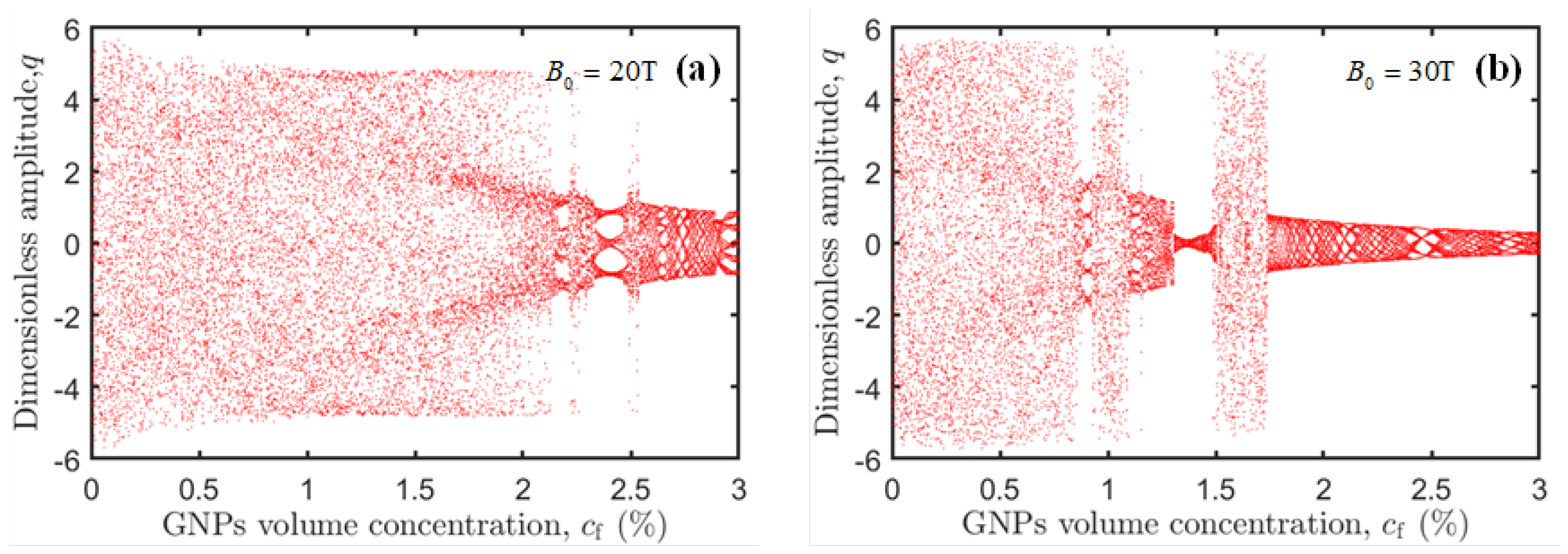
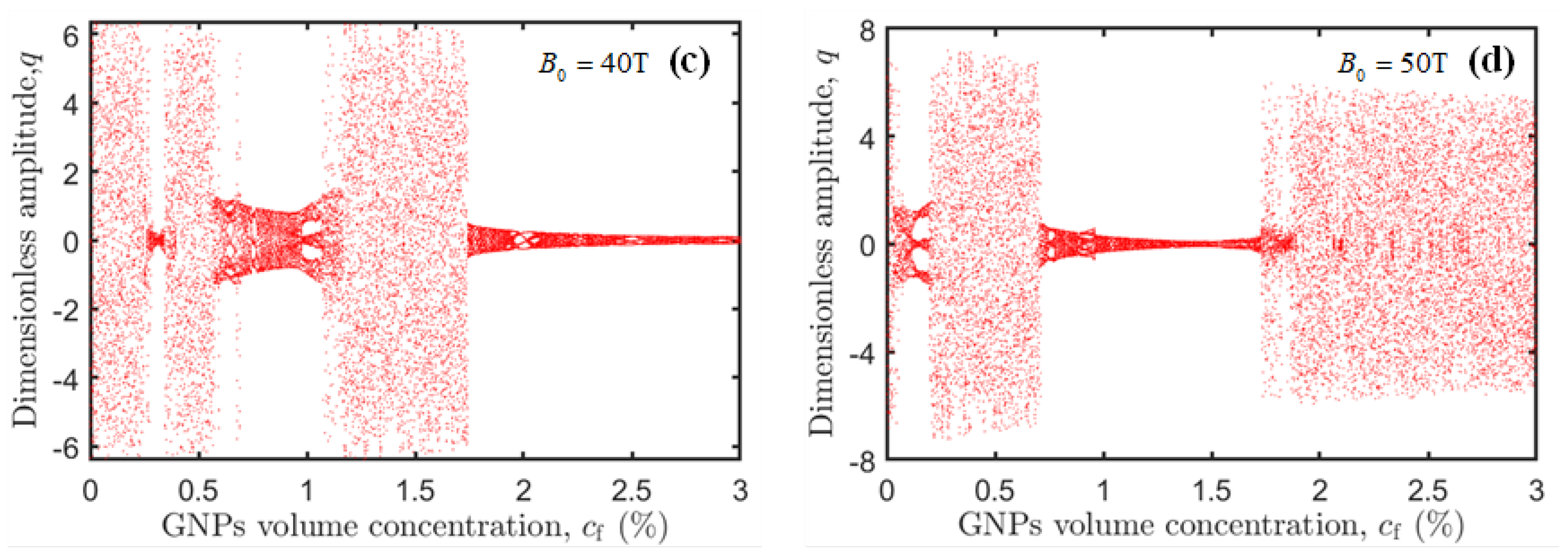
3.2.3. Amplitude-Magnetic Field Response
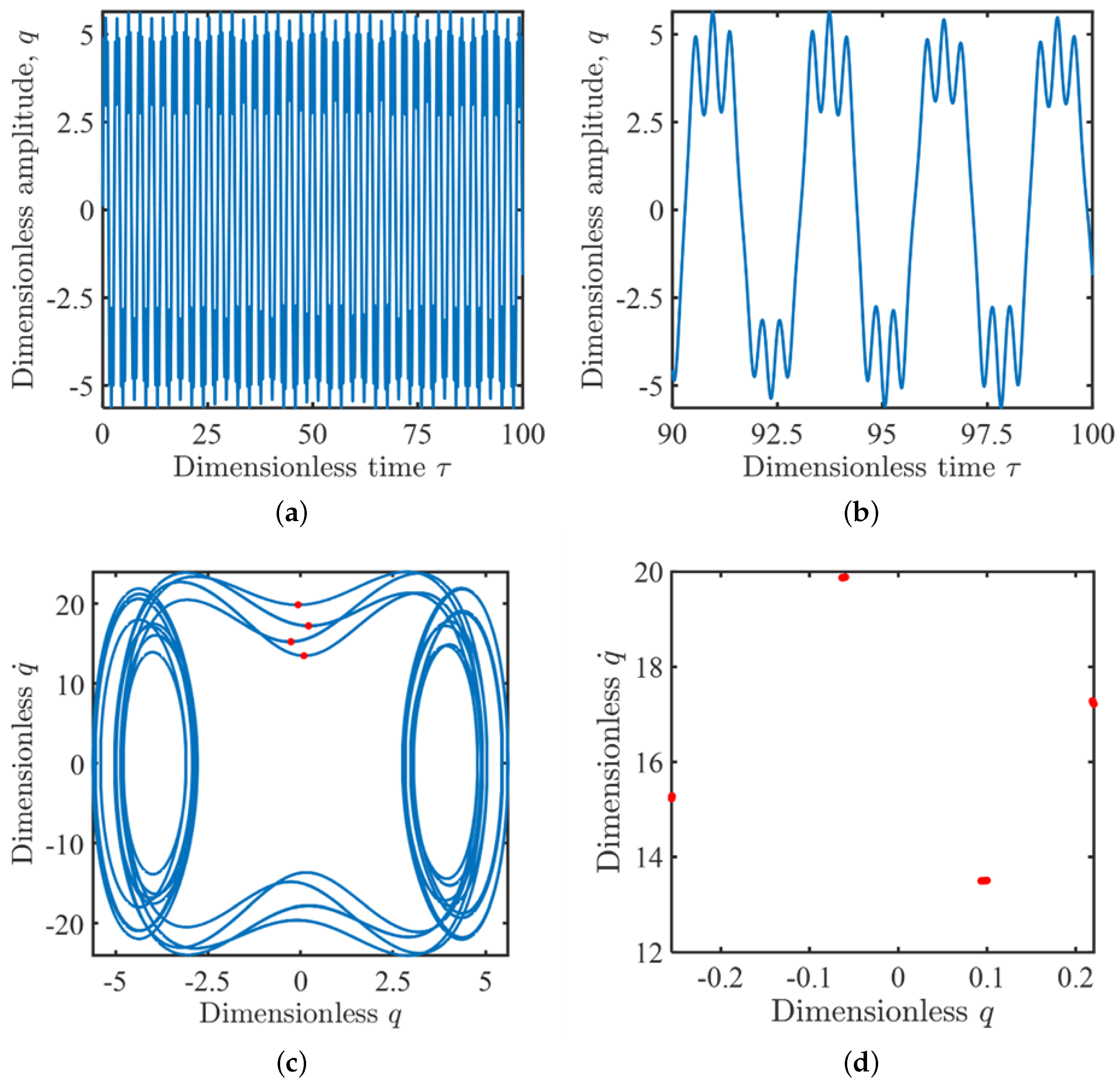
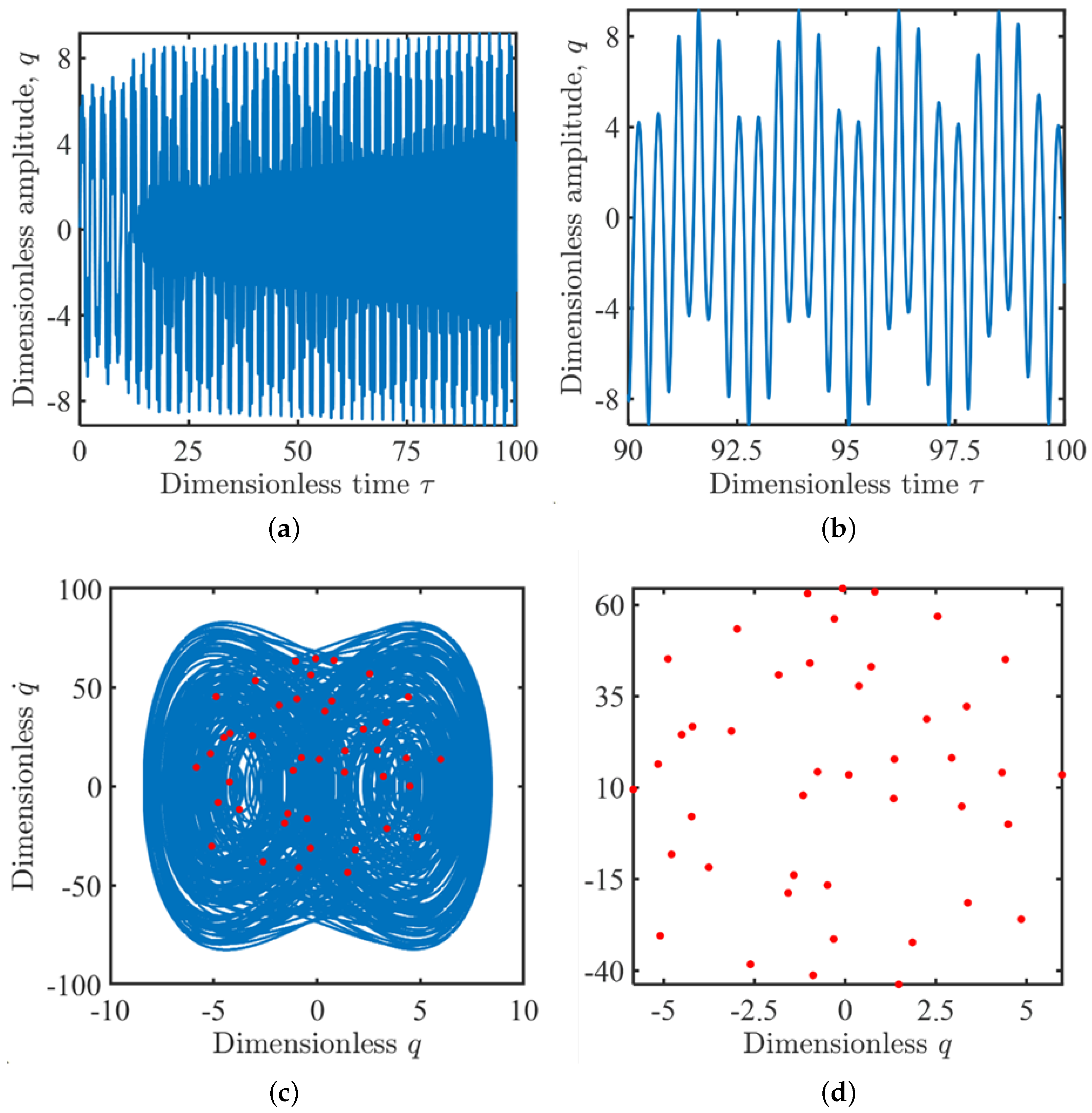
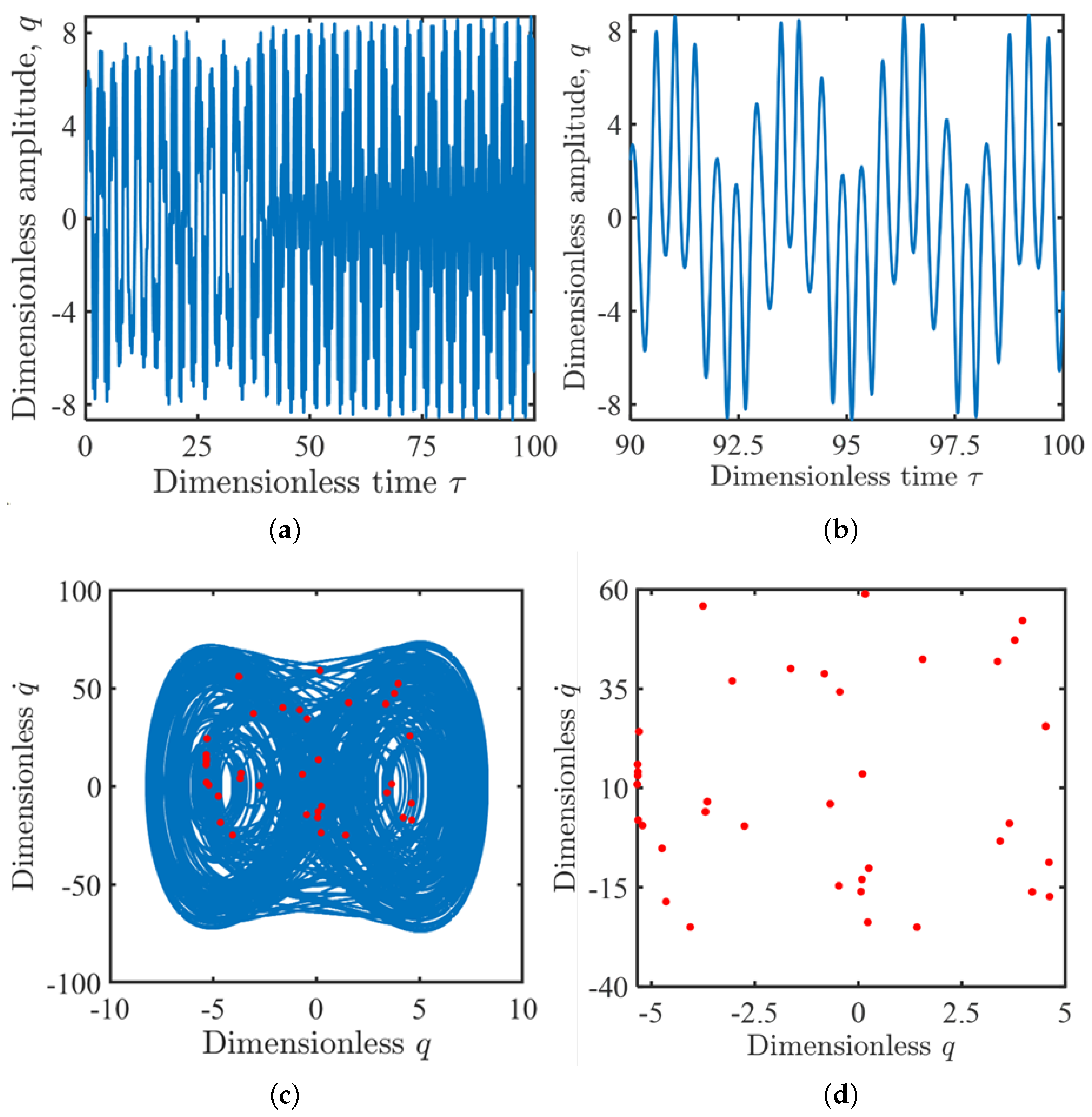
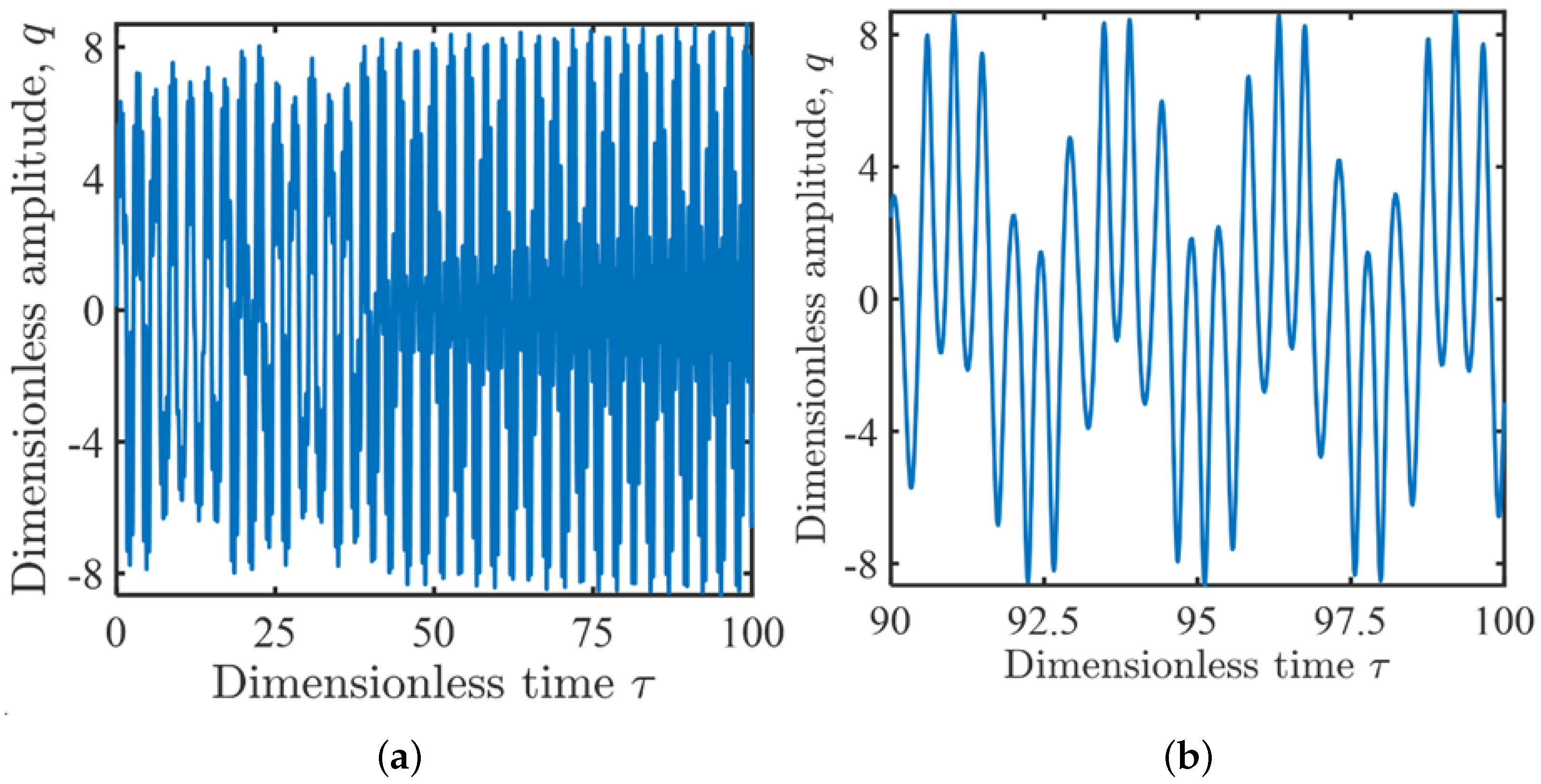
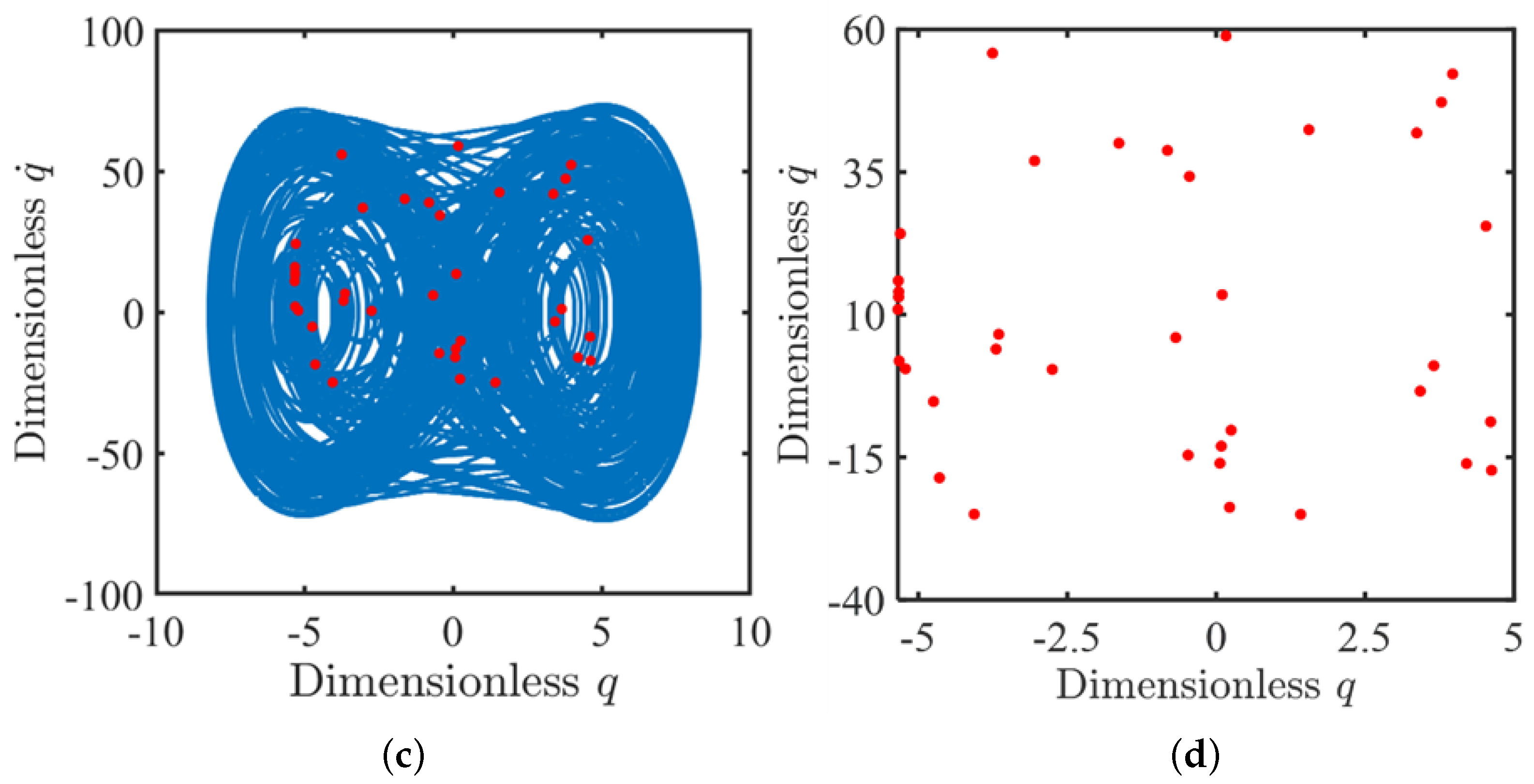
3.2.4. Period-Doubling and Chaotic Motion
3.3. Bifurcation and Chaos Behaviors
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kopperger, E.; List, J.; Madhira, S.; Rothfischer, F.; Lamb, D.C.; Simmel, F.C. A self-assembled nanoscale robotic arm controlled by electric fields. Science 2018, 359, 296–301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Teng, Z.; Zhao, L.; Liu, Z.; Yu, X.; Zhu, X.; Peng, S.; Wang, T.; Qiu, J.; Wang, Q.; et al. Multi-Dimensional Mechanical Mapping Sensor Based on Flexoelectric-Like and Optical Signals. Adv. Sci. 2023, 10, 2301214. [Google Scholar] [CrossRef]
- Islam, M.H.; Afroj, S.; Uddin, M.A.; Andreeva, D.V.; Novoselov, K.S.; Karim, N. Graphene and CNT-based smart fiber-reinforced composites: A review. Adv. Funct. Mater. 2022, 32, 2205723. [Google Scholar] [CrossRef]
- Sun, X.; Huang, C.; Wang, L.; Liang, L.; Cheng, Y.; Fei, W.; Li, Y. Recent progress in graphene/polymer nanocomposites. Adv. Mater. 2021, 33, 2001105. [Google Scholar] [CrossRef]
- Lava Kumar, P.; Lombardi, A.; Byczynski, G.; Narayana Murty, S.V.S.; Murty, B.S.; Bichler, L. Recent advances in aluminium matrix composites reinforced with graphene-based nanomaterial: A critical review. Prog. Mater. Sci. 2022, 128, 100948. [Google Scholar] [CrossRef]
- Meng, Q.; Araby, S.; Oh, J.A.; Chand, A.; Zhang, X.; Kenelak, V.; Ma, J.; Liu, T.; Ma, J. Accurate self-damage detection by electrically conductive epoxy/graphene nanocomposite film. J. Appl. Polym. Sci. 2021, 138, 50452. [Google Scholar] [CrossRef]
- Xia, X.; Hao, J.; Wang, Y.; Zhong, Z.; Weng, G.J. Theory of electrical conductivity and dielectric permittivity of highly aligned graphene-based nanocomposites. J. Phys. Condens. Matter 2017, 29, 205702. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, D.G.; Kinloch, I.A.; Young, R.J. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- Young, R.J.; Liu, M.; Kinloch, I.A.; Li, S.; Zhao, X.; Vallés, C.; Papageorgiou, D.G. The mechanics of reinforcement of polymers by graphene nanoplatelets. Compos. Sci. Technol. 2018, 154, 110–116. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Li, Z.; Liu, M.; Kinloch, I.A.; Young, R.J. Mechanisms of mechanical reinforcement by graphene and carbon nanotubes in polymer nanocomposites. Nanoscale 2020, 12, 2228–2267. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. Vibration analysis of multi-scale hybrid nanocomposite plates based on a Halpin-Tsai homogenization model. Compos. Part B Eng. 2019, 173, 106955. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Pan, H.G.; Yuan, H.Q.; Yang, J. Free vibration analysis of a functionally graded graphene nanoplatelet reinforced disk-shaft assembly with whirl motion. Int. J. Mech. Sci. 2021, 197, 106335. [Google Scholar] [CrossRef]
- Weng, G.J. Some elastic properties of reinforced solids, with special reference to isotropic ones containing spherical inclusions. Int. J. Eng. Sci. 1984, 22, 845–856. [Google Scholar] [CrossRef]
- Sadeghpour, E.; Guo, Y.; Chua, D.; Shim, V.P.W. A modified Mori–Tanaka approach incorporating filler-matrix interface failure to model graphene/polymer nanocomposites. Int. J. Mech. Sci. 2020, 180, 105699. [Google Scholar] [CrossRef]
- Fedotov, A.F. Mori-Tanaka experimental-analytical model for predicting engineering elastic moduli of composite materials. Compos. Part B Eng. 2022, 232, 109635. [Google Scholar] [CrossRef]
- Weng, G.J. The theoretical connection between Mori-Tanaka’s theory and the Hashin-Shtrikman-Walpole bounds. Int. J. Eng. Sci. 1990, 28, 1111–1120. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, K.X.; Chandra, A. Several variations of the generalized self-consistent method for hybrid composites. Compos. Sci. Technol. 1994, 52, 19–27. [Google Scholar] [CrossRef]
- Weng, G.J. A dynamical theory for the Mori–Tanaka and Ponte Castañeda–Willis estimates. Mech. Mater. 2010, 42, 886–893. [Google Scholar] [CrossRef]
- Nan, C.W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.J.; Weng, G.J. Theory of thermal conductivity of graphene-polymer nanocomposites with interfacial Kapitza resistance and graphene-graphene contact resistance. Carbon 2018, 137, 222–233. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Wang, X.; Zhao, Z.; Romero, C.S.; Yang, J. Nonlinear free vibration of graphene platelets (GPLs)/polymer dielectric beam. Smart Mater. Struct. 2019, 28, 055013. [Google Scholar] [CrossRef]
- Li, X.; Song, M.; Yang, J.; Kitipornchai, S. Primary and secondary resonances of functionally graded graphene platelet-reinforced nanocomposite beams. Nonlinear Dyn. 2019, 95, 1807–1826. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. Nonlinear harmonically excited vibration of third-order shear deformable functionally graded graphene platelet-reinforced composite rectangular plates. Eng. Struct. 2018, 156, 197–209. [Google Scholar] [CrossRef]
- Song, M.; Gong, Y.; Yang, J.; Zhu, W.; Kitipornchai, S. Free vibration and buckling analyses of edge-cracked functionally graded multilayer graphene nanoplatelet-reinforced composite beams resting on an elastic foundation. J. Sound Vib. 2019, 458, 89–108. [Google Scholar] [CrossRef]
- Song, M.; Gong, Y.; Yang, J.; Zhu, W.; Kitipornchai, S. Nonlinear free vibration of cracked functionally graded graphene platelet-reinforced nanocomposite beams in thermal environments. J. Sound Vib. 2020, 468, 115115. [Google Scholar] [CrossRef]
- Wei, D.; Nurakhmetov, D.; Aniyarov, A.; Zhang, D.; Spitas, C. Lumped-parameter model for dynamic monolayer graphene sheets. J. Sound Vib. 2022, 534, 117062. [Google Scholar] [CrossRef]
- Vila, J.; Fernández-Sáez, J.; Zaera, R. Reproducing the nonlinear dynamic behavior of a structured beam with a generalized continuum model. J. Sound Vib. 2018, 420, 296–314. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Thai, H.T.; Civaek, Ö. On viscoelastic transient response of magnetically imperfect functionally graded nanobeams. Int. J. Eng. Sci. 2022, 172, 103629. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar]
- Wang, J.; Li, J.J.; Weng, G.J.; Su, Y. The effects of temperature and alignment state of nanofillers on the thermal conductivity of both metal and nonmetal based graphene nanocomposites. Acta Mater. 2020, 185, 461–473. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Li, J.; Weng, G.J.; Su, Y. A multiscale study of the filler-size and temperature dependence of the thermal conductivity of graphene-polymer nanocomposites. Carbon 2021, 175, 259–270. [Google Scholar] [CrossRef]
- Gong, L.; Kinloch, I.A.; Young, R.J.; Riaz, I.; Jalil, R.; Novoselov, K.S. Interfacial stress transfer in a graphene monolayer nanocomposite. arXiv 2010, arXiv:1007.1953. [Google Scholar] [CrossRef]
- Wang, J.; Gong, L.; Xi, S.; Li, C.; Su, Y.; Yang, L. Synergistic effect of interface and agglomeration on Young’s modulus of graphene-polymer nanocomposites. Int. J. Solids Struct. 2024, 292, 112716. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Su, Y. A dual-role theory of the aspect ratio of the nanofillers for the thermal conductivity of graphene-polymer nanocomposites. Int. J. Eng. Sci. 2021, 160, 103453. [Google Scholar] [CrossRef]
- Wang, Y.; Weng, G.J.; Meguid, S.A.; Hamouda, A.M. A continuum model with a percolation threshold and tunneling-assisted interfacial conductivity for carbon nanotube-based nanocomposites. J. Appl. Phys. 2014, 115, 193706. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Zhang, M.; Gong, L. Magneto-elastic vibration of axially moving graphene nanocomposite current-carrying beam with variable speed and axial force. Acta Mech. 2024, 235, 5747–5763. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J. Principal-internal resonance of an axially moving current-carrying beam in magnetic field. Nonlinear Dyn. 2017, 90, 683–695. [Google Scholar] [CrossRef]
- Beskin, V.S.; Balogh, A.; Falanga, M.; Treumann, R.A. Magnetic Fields at Largest Universal Strengths: Overview. Space Sci. Rev. 2015, 191, 1–12. [Google Scholar] [CrossRef]
- Hahn, S.; Kim, K.; Kim, K.; Hu, X.; Painter, T.; Dixon, I.; Kim, S.; Bhattarai, K.R.; Noguchi, S.; Jaroszynski, J.; et al. 45.5-tesla direct-current magnetic field generated with a high-temperature superconducting magnet. Nature 2019, 570, 496–499. [Google Scholar] [CrossRef]
- Ji, J.C.; Zhang, N. Suppression of the primary resonance vibrations of a forced nonlinear system using a dynamic vibration absorber. J. Sound Vib. 2010, 329, 2044–2056. [Google Scholar] [CrossRef]
- Chen, G.; Moiola, J.L. An overview of bifurcation, chaos and nonlinear dynamics in control systems. J. Frankl. Inst. 1994, 331, 819–858. [Google Scholar] [CrossRef]
- Luo, A.C.J. Bifurcation and Stability in Nonlinear Dynamical Systems; Springer: Cham, Switzerland, 2019. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wang, J.; Hu, J.; Pu, X.; Gong, L. The Effect of Graphene Nanofiller on Electromagnetic-Related Primary Resonance of an Axially Moving Nanocomposite Beam. Symmetry 2025, 17, 651. https://doi.org/10.3390/sym17050651
Wang L, Wang J, Hu J, Pu X, Gong L. The Effect of Graphene Nanofiller on Electromagnetic-Related Primary Resonance of an Axially Moving Nanocomposite Beam. Symmetry. 2025; 17(5):651. https://doi.org/10.3390/sym17050651
Chicago/Turabian StyleWang, Liwen, Jie Wang, Jinyuan Hu, Xiaomalong Pu, and Liangfei Gong. 2025. "The Effect of Graphene Nanofiller on Electromagnetic-Related Primary Resonance of an Axially Moving Nanocomposite Beam" Symmetry 17, no. 5: 651. https://doi.org/10.3390/sym17050651
APA StyleWang, L., Wang, J., Hu, J., Pu, X., & Gong, L. (2025). The Effect of Graphene Nanofiller on Electromagnetic-Related Primary Resonance of an Axially Moving Nanocomposite Beam. Symmetry, 17(5), 651. https://doi.org/10.3390/sym17050651





