Abstract
A force-finding analysis is crucial for a single-layer cable net glass curtain structure. In engineering applications, the boundary for such a cable net glass curtain structure exhibits limited rigidity, which frequently causes prestress loss and differential changes in the reaction force of the supports at both ends during the construction process. Here, we propose a nonlinear force-finding method based on the inherent symmetry and nonlinear structural stiffness of these large-scale cable net curtain wall structures. Our method utilizes undirected subgraphs to preprocess and analyze the cable net curtain structures. The subgraphs and their graph products are introduced to effectively compute the overall configuration of the cable net structure. According to the preprocessing results and the boundary conditions of the cable net structure, a nonlinear force-finding method based on the stiffness of the overall structure is presented. Finally, the feasibility of the proposed method could be verified by combining it with actual engineering applications. It took approximately 12 min for a large-scale cable net structure with more than 2000 nodes and members. The obtained prestresses agreed well with the target forces, whereas the computation accuracy was less than 5%. This method provides an important reference for further engineering applications of these cable net glass curtain structures.
1. Introduction
Single-layer cable net glass curtain structures are composed of prestressed cables and surrounding structures. Because of their beautiful appearance, high transparency, and overall simplicity, these structures have been widely used in exhibition centers, high-rise buildings, airport terminals, and other buildings.
Compared with conventional engineering structures, a single-layer cable net glass curtain structure is basically flexible. The structural rigidity and bearing capacity of the structure are mainly provided by being prestressed, and the cable net has significant geometric nonlinear behavior [1]. In other words, there is necessarily strong coupling between the structural configuration (i.e., form) and the initial prestresses (i.e., force). During the construction process (i.e., prestressing), the overall configuration, cable forces, and structural stiffness change with prestressing [2]. Therefore, it is necessary to carry out a nonlinear force-finding (or form-finding) analysis of single-layer cable net glass curtain structures. At present, the common force-finding methods for cable net structures and prestressed cable-strut structures include the force density method, dynamic relaxation method, and nonlinear finite element method [3]. In addition, some optimization algorithms have been applied to force-finding, such as particle swarm optimization [4], the simulated annealing algorithm [5], and the genetic algorithm [6,7].
The force density method was first proposed by Linkwitz and Schek [8,9]. This method is primarily applicable to cable net structures and membrane structures. It adopts the force density of a specified cable segment to solve the equilibrium equation of the nodes to obtain the coordinates of the free nodes [10]. The advantage of the force density method is that the coordinates of the nodes can only be obtained by solving linear equations [11]. Aboul-Nasr and Mourad [12] adopted the assumed cable force density distribution to perform a linear analysis to obtain the initial shape of a prestressed cable net. This method simplifies the design process of a cable network. Subsequently, Maurin and Motro [13] introduced the force density method to solve the problem of force-finding for membrane and/or prestressed cable-strut structures. Hayashi et al. [14] proposed a force density method that could simultaneously optimize the topology and geometry of truss structures. Then, to tailor the mentioned force density method to single-layer cable net glass curtain structures, Luo et al. [15] combined the classical force density method with the finite element method, and proposed an improved force-finding method for a mixed structure with steel tubular trusses coupled to spatial cable networks. This method could obtain an optimal solution without constraining the node positions. Recently, on the basis of group theory and the force density method, Chen et al. [16] proposed an effective symmetry method for a force-finding analysis of tensegrity and cable net structures. In addition, using the force density theory, Zhang et al. [17] proposed an extended force-finding method for single-layer cable net structures. Their method was capable of considering the interaction effect between the cable net and the boundary truss structure. Ye et al. [18] improved the force density method by utilizing the internal forces of the cables and membranes as initial conditions and utilizing the unbalanced forces at the nodes to control the error. This method overcomes the inefficiency of the force density method in structural force-finding. On the basis of the updated force density method, Zhao et al. [19] proposed a force-finding method suitable for prestressable grid structures with branching columns.
The dynamic relaxation method is a discrete numerical method that has been introduced into civil engineering since the last century [20]. This method linearizes the differential equations of Newton’s first law by an explicit scheme of numerical integration and is suitable for flexible structures with large displacements [21]. Collins et al. [22] adopted the dynamic relaxation method to study the effect of different joint models and bracing systems on the stiffness of a lattice shell. Wang et al. [23] proposed a dynamic relaxation method for cable net structures in space engineering. Their method has high calculation efficiency and does not require a real stiffness matrix. Barnes [24] conducted a force-finding analysis of long-span cable net structures based on a dynamic relaxation method with dynamic damping. During the force-finding process, dynamic damping was adopted to ensure the stability, topology, geometry, and specified prestress distribution. Utilizing the dynamic relaxation method, Rezaiee-Pajand et al. [25] evaluated six different stiffness matrices of cable elements to determine the most efficient method. Li et al. [26] proposed a detailed process for surface construction and optimization based on the dynamic relaxation method. Their method adopted the equilibrium of cable nets (or tension membranes) combined with a geometric analysis and mechanical property optimization. Tu et al. [27] proposed a force-finding method based on the dynamic relaxation of branching structures. It overcame the problem of huge and repeated manual adjustments due to the possible slackness of cables during force-finding. This method balances slack cables that are not present in the branching model. Bagrianski et al. [28] proposed prescriptive dynamic relaxation to solve the problem of the limited application of the dynamic relaxation method in the force-finding of compressive structures. Bessini et al. [29] developed a dynamic relaxation procedure suitable for bending-active structures and cable net structures.
On the other hand, the nonlinear finite element method was first proposed by Haug and Powell [30]. This method adopts nonlinear equations combined with boundary conditions for iterative calculations to determine the structural configuration. Wan et al. [31] proposed a force-finding method for air-supported structures by using the finite element method, which could generate the design results in real time. Chen et al. [32] proposed a novel method to apply the backward algorithm to the simulation of the tensioning process. It combines the inherent vector finite element method and force-finding method. Zhu et al. [33] proposed a force-finding method based on Euler’s nonlinear finite element method, which is suitable for the force-finding of cable structures under specific loads. Arcaro and Adeli [34] studied mathematical models based on special strut elements and unconstrained nonlinear programming. Subsequently, the force-finding analysis of tensegrity structures was extended to hyperelastic tensegrity structures. Argyris et al. [35] applied the finite element method to a force-finding analysis of the cable roof of the Munich Olympic Stadium. In addition, Lu et al. [36] utilized the singular value decomposition of the equilibrium matrix to perform a force-finding analysis of semi-regular tensegrity structures. Chen et al. [37,38] extended the ant colony algorithm to the force-finding of prestressed cable-strut structures. Kabasi et al. [39] carried out a force-finding of membrane structures using machine learning. Compared with traditional force-finding methods, the reported machine-learning-based method was not affected by mesh distortion, stability, or convergence.
Ideally, for most force-finding and form-finding problems, the boundary condition is assumed to be rigid, and then the target force/forms can successfully be applied. However, in engineering applications, the boundary of a cable net glass curtain structure exhibits limited rigidity, which frequently causes prestress loss and differential changes in the reaction force of the supports at both ends during the construction process. Here, inspired by a symmetry analysis and nonlinear structural stiffness, we propose a computational force-finding analysis method for cable net glass curtain structures. Utilizing this method, the force-finding analysis of large-scale cable net glass curtain structures with nonlinear structural stiffness and flexible boundary conditions was carried out. First, the cable net grid was expressed by subgraphs and their graph products. The force-finding analysis could be carried out according to the results of the preprocessing. The influence of the actual boundary conditions on the force-finding results of the cable net structure was considered. Finally, using the above-mentioned force-finding method, a large-scale cable net structure for the landside hall of the Chongqing Jiangbei International Airport Terminal T3A in China was analyzed.
2. Method
2.1. Geometric and Symmetry Representations of Cable Nets Described by Graph Products
A single-layer cable net glass curtain structure shows certain regularity and symmetry. Thus, it can be regarded as the Cartesian graph product of two subgraphs. By adopting the inherent symmetry of the structure and combining graph theory with group theory, the analysis of the original structures can be transformed into an efficient analysis of the structures involved with subgraphs. This method greatly reduces the difficulty and computational cost of solving the initial prestress distribution and structural force-finding [40].
In this section, we show a simple single-layer cable net structure denoted by cyclic symmetry and a graph product representation. The single-layer cable net structure is cyclically symmetric around a two-fold rotation axis (i.e., denoted by C2v symmetry using group theory [16,41]), as shown in Figure 1. It consists of 191 pin joints and 310 cables, of which 48 boundary nodes are constrained in three directions. Its geometry is derived from the Cartesian product of two sub-paths, illustrated by the paths P15 and P13 for the corresponding straight lines in Figure 1, and removes 4 trivial boundary nodes and 52 redundant members.
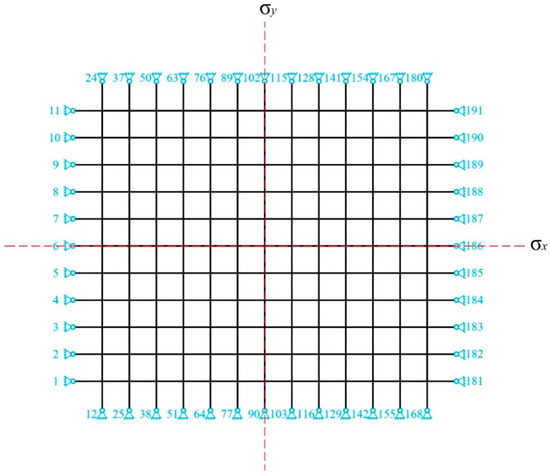
Figure 1.
A two-fold C2v symmetric cable net structure under two mirror operations, symmetry operation and operation .
Notably, only the unshifted nodes and members for subgraphs P15 and P13 should be evaluated, rather than those of the entire structure, as shown in Figure 2. As the subgraph is also C2v symmetric around its symmetry axis (i.e., or ), the equivalence is maintained when performing the identity operation (i.e., E) and the mirror operation (i.e., or ).
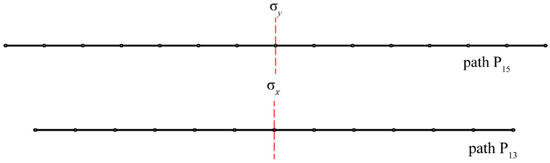
Figure 2.
Subgraphs P15 and P13 under their specific mirror operations.
It can be noticed from Figure 2 that, under the identity operation E, all nodes and members of the subgraphs remain unchanged. Under the mirror operation, only the node located along the mirror line remains unchanged, whereas all the members have shifted. Therefore, the matrix representations of the subgraphs under symmetry operations (i.e., E and σ) are represented as follows.
The matrix representation for the unshifted nodes of subgraph P15 is
and the matrix representation for the unshifted members of subgraph P15 is
The matrix representation for the unshifted nodes of subgraph P13 is
and the matrix representation for the unshifted members of subgraph P13 is
Then, using graph theory [40], the representations and for the whole structure associated with the Cartesian product of subgraphs P15 and P13 are
Using the symmetry extension of the Maxwell rule [16,41], we find that
where is the symmetry representation of the internal mechanism mode; is the symmetry representation of self-stress state; is the representation of the rigid body translation; and are the representations of the unshifted nodes and unshifted members under different symmetry operations, respectively; and is the symmetry representation of the kinematic constraint. For freestanding structures, , where is the representations of rigid body rotation.
Using Equations (5) and (6), the matrix representations of the joints and the members of the whole structure can be effectively evaluated from those of the graph products, given by
and
Moreover, through the boundary condition described in Figure 1, the matrix representation for the invariant kinematic constraints is
Using Equations (7)–(10), the symmetry-extended mobility of the C2v symmetric cable net is
In Equation (11), the symbols E, σx, σy, and C2, respectively, denote four different symmetry operations for a C2v symmetry group. A detailed evaluation of the C2v symmetric cable net is listed in Table 1, where E, σx, σy, and C2 in the first row show all four independent symmetry operations. Thus, based on group theory and the symmetry-extended Maxwell rule [16,41], the symmetry representation of the relative mobility is given by
where A1, A2, B1, and B2 indicate the first, second, third, and fourth irreducible representations, and A1 denotes full symmetry in the C2v group. Equation (12) reveals that this cable net structure has more than 127 mechanism modes and 31 of them are integral mechanisms associated with full symmetry [41].

Table 1.
Symmetry-extended mobility evaluation of the C2v symmetric cable net.
2.2. Nonlinear Force-Finding Analysis Based on Overall Structural Stiffness
Notably, a single-layer cable net glass curtain structure is generally a flexible structure and its boundary should be taken to be a flexible boundary. When prestress is actively applied to a cable net glass curtain structure during construction, the overall configuration and cable forces of the structure necessarily change and the rigidity of the structure changes accordingly. To consider such cases, this section proposes a numerical force-finding method for single-layer cable net glass curtain structures, i.e., a nonlinear force-finding method based on the structural stiffness of the overall structure.
The nonlinear force-finding analysis introduces an iterative method to solve nonlinear equations. Importantly, the nonlinear equilibrium equations and the nodal coordinates are iteratively evaluated step by step until the evaluated cable forces and/or structural configuration meet the accuracy requirement (in this study, the relative error between the actual cable forces and the target cable forces should be less than 5%).
The involved structural stiffness matrix for the nonlinear analysis is as follows [42,43]:
where is the current and global stiffness matrix and is the current elastic stiffness matrix, which refers to the stiffness matrix determined by the updated structural configuration and material of the structure during each iteration step, given by
where H is the updated equilibrium matrix, which describes the relationship between the internal forces of the members and the external loads on the updated locations for the nodes, and is the diagonal matrix, including the updated and modified axial stiffness of the members [44,45]. In Equation (13), is the geometric stiffness matrix, which refers to the stiffness matrix contributed by the evaluated prestresses, given by
In Equation (15), is the identity matrix, is the Kronecker product, the diagonal matrix indicates the prestress level per unit length, and C is a topological matrix that describes the geometric topology: if a member k connects nodes i and j, then the corresponding i-th and j-th entries along the k-th row are 1 and −1. Then, a nonlinear iterative solution is provided according to the updated tangent stiffness matrix , expressed as
where is the nodal displacement vector, is the external load vector, and is the equivalent nodal load vector.
In this study, the “cooling method” was adopted to simulate the prestressing process for the cables. The relationship between the cable length and temperature change is
where is the temperature change, is the length change of a cable, is the coefficient of linear expansion, and is the original length of the cable. Equation (17) shows that temperature changes change the cable length. As the temperature decreases, the cable length contracts, leading to an increase in cable force. Therefore, when the temperature of the member changes, the internal force and cable length change.
Notably, the above-mentioned force-finding process can be generally described by using the following six iteration steps: (1) adopt certain and proper sub-paths based on the boundary conditions and input information, and utilize the obtained graph product to represent the structure according to the inherent symmetry of the structure; (2) establish a cable net curtain model by combining the graph products and the finite element method; (3) utilize the mentioned “cooling method” to apply the target prestress forces to the structure; (4) adopt a geometric nonlinear analysis to calculate the exact nodal coordinates by considering the unbalanced forces of the structure and the flexible boundary condition; (5) obtain the updated prestresses of the members according to the updated nodal coordinates; and (6) compare the evaluated cable forces with the target cable forces and compare the configuration with the target configuration to determine whether the computational accuracy is satisfied. If the accuracy is satisfied, the iteration ends; otherwise, the procedure should return to Step (3) and, thus, the iteration continues. All the involved force-finding process steps were successfully implemented by combining SAP2000 v15 and MATLAB R2018b, and the force-finding flowchart is shown in Figure 3.
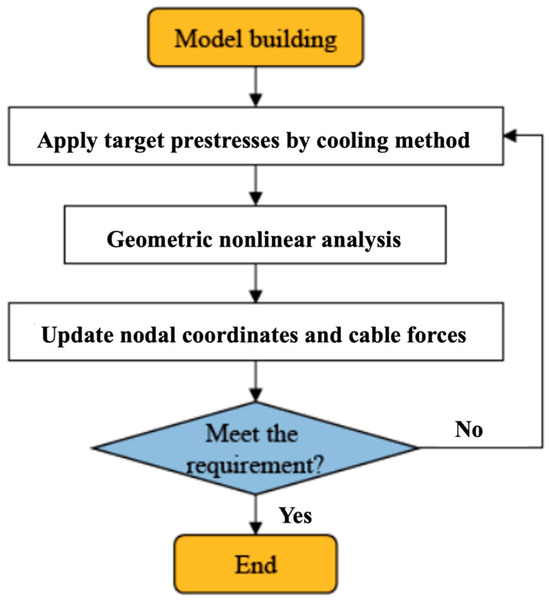
Figure 3.
Brief flowchart for nonlinear force-finding of cable net structures.
2.3. Flexible Boundary Conditions
It is important to note that conventional force-finding analyses and structural designs for cable net curtain structures typically use pin-jointed or rigid supports for boundary conditions. However, in actual engineering, the boundary condition of the cable net structure is frequently a flexible boundary. Thus, flexible boundary conditions should be considered. At the same time, asymmetry of stiffness often occurs at the support and the boundary displacements along different directions are frequently coupled to each other. In the prestressing process, such behavior causes a change in elongation and the loss of prestress, which increases the difficulty of the force-finding analysis. Asymmetry of the support stiffness causes different changes in the reaction force at both ends of the support. Thus, when modeling the overall structure, it is necessary to consider the influence of real boundary conditions on the deformation of a cable net.
The nonlinear iterative method is suitable for flexible boundary conditions [46,47,48,49]. Thus, the geometric stiffness matrix expressed in Equation (16) and contributed into Equation (17) should be rewritten as
where is the stress stiffness matrix determined by the prestresses of the structure (see Equation (15)). is the large displacement stiffness matrix, which describes the contributions of the flexible boundary and the involved prestress loss [48,49,50,51]. Consequently, the nonlinear equilibrium Equation (16) during iteration should be rewritten as
3. Engineering Example
3.1. Engineering Background
This example shows the landside hall of the T3A terminal of Chongqing Jiangbei International Airport, located in Yubei District, Chongqing, China. The terminal building is divided into the main building E; the four corridors A, B, C, and D; and the landside hall. The overall configuration adopts an H-shaped configuration, with lengths of 750 m from east to west and 1060 m from north to south. The highest node of the roof is 49 m.
In order to make effective utilization of natural light, the terminal building adopts a single-layer cable net glass curtain structure for the landside hall. The single-layer cable net glass curtain structure is a flexible structure and, therefore, a large deformation and P-∆ effect need to be considered. The load combination does not satisfy the simple linear superposition method and the nonlinear analysis method is utilized. This example adopts the nonlinear force-finding method for large-scale cable net glass curtain structures. The model of the curtain structure of the landside hall is shown in Figure 4.
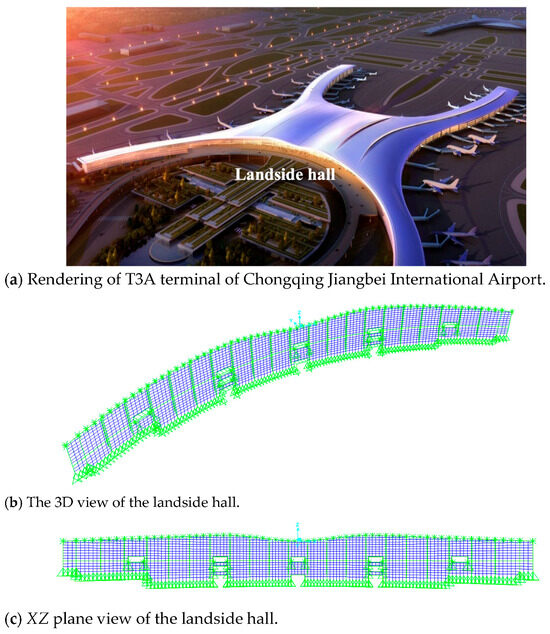
Figure 4.
Cable net curtain structure model of the landside hall of the T3A terminal of Chongqing Jiangbei International Airport.
In the cable net curtain structure of the landside hall, the vertical cables are made of stainless steel cables, with a cross-section of ∅40 (cross-sectional area of 945.07 mm2), and the horizontal cables are made of stainless steel cables with a cross-section of ∅42 (cross-sectional area of 1041.94 mm2). The remaining members are made of Q345 steel. The specific material parameters are shown in Table 2.

Table 2.
Material parameters.
The model is connected to the ground at the bottom of the truss columns, wind-resistant columns, vertical cables, gantry columns, and certain horizontal cables. There are lateral support constraints on the top of the wind-resistant columns and the top of the door frame columns, and the direction is along the direction of the wind load and perpendicular to the axis of the box girder. An upper box girder with lateral supports is provided every 6 m.
As the cable net curtain structure for the landside hall exhibits cyclic symmetry and regularity, all the tension members—with 20 types of horizontal cables and 107 types of vertical cables—can be neatly represented by the graph product of two sub-paths, P21 and P107. Specific nodal positions are involved in the points of the sub-paths and certain unnecessary members have been removed according to the structural configuration. Then, according to the force-finding process provided in Section 2, the obtained model and its nodal coordinates and connectivity patterns could be utilized to establish the computational models implemented in SAP2000 and MATLAB.
Based on the “cooling method” mentioned for Step 3 in Section 2.2, prestressing forces were iteratively applied to the horizontal and vertical cables. The proper prestress force for each cable should be about 15% to 25% of the minimum breaking force, whereas the minimum breaking forces of the horizontal and vertical cables were 1314.41 kN and 1192.21 kN. Thus, the target forces for the horizontal and vertical cables were taken to be 220 kN and 200 kN.
After implementing more than 165 iteration steps (approximately 12 min) for the proposed nonlinear force-finding process, we observed that all the updated prestresses of the tension members agreed well with the target prestresses. The computational accuracy was less than 5%, whereas the evaluated forces for the horizontal cables were 210.5–230 kN and those of the vertical cables were 195.3–205.2 kN. On the other hand, the obtained configuration did not show significant deformation as the maximum nodal displacement was less than 1/85 of the involved span of the curtain structure. Thus, the structural configuration obtained by the proposed force-finding process was verified to be feasible, and it could be considered as a reference model for the following structural analysis.
3.2. Structural Analysis Results
3.2.1. Modal Analysis
The single-layer cable net glass curtain structure adopted a nonlinear analysis method, considering the large deformation and P-∆ effect. For horizontal cables and vertical cables, initial prestresses were applied using the “cooling method” (see Equation (17)). Given the target cable force and target configuration, the iterative procedure described above was utilized to obtain the temperature value required by the cable. We ensured that the absolute value of the difference between the actual cable force and the target cable force of each cable did not exceed 5% of the target cable force value. In order to consider the flexible boundary conditions, a local coordinate system was established for the constrained nodes. The displacement constraining direction was along the wind load direction and perpendicular to the axis of the box girder.
3.2.2. Lower-Order Natural Frequencies and Vibration Modes
Under the action of prestress, a modal analysis of the single-layer cable net glass curtain structure of the landside hall was carried out. Then, the low-order natural frequency and the corresponding vibration mode shapes were effectively extracted. Figure 5 shows the main natural vibration shapes associated with the first fifteen modes of the curtain structure of the landside hall.
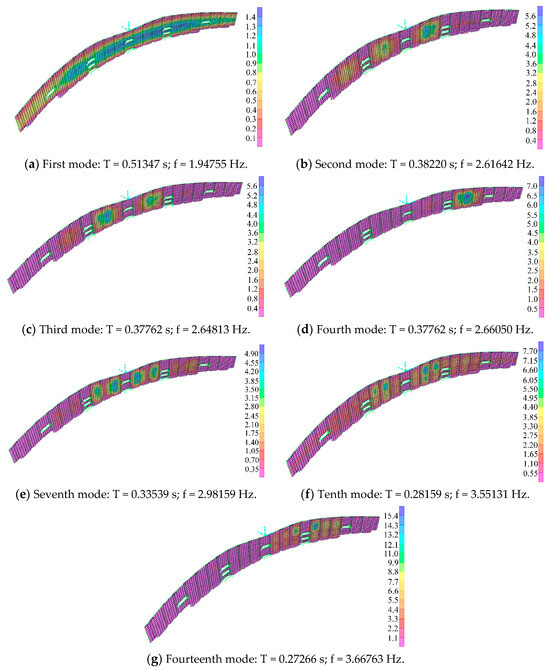
Figure 5.
Lower-order natural vibration modes for the curtain structure (scale factor of 5).
3.2.3. Deformation Behavior
After initial prestresses were introduced into the curtain structure and the structural stiffness was improved, different load patterns were applied to the involved FEM model. During the structural analysis, the load condition of the FEM model considered the combination of dead loads, positive wind pressure, negative wind pressure, prestresses, and temperature action. As the “cooling method” was utilized to simulate the cable prestress, the temperature effect was considered in accordance with a temperature rise of 30 °C and a temperature drop of 25 °C. When the cables were tensioned, the ambient temperature was considered to be 15 °C. More importantly, the envelope combinations of various load combinations in the ultimate load-bearing capacity limit state and the normal service limit state were separately considered.
The most unfavorable displacement is shown in Figure 6, and the maximum displacement was 336 mm. Importantly, the displacement results met the design requirements (here, each nodal displacement was less than 1/50 of the involved span of the cable net glass curtain structure). However, it can be noticed in Figure 6 that the nodal displacement of the upper cable net and the side columns on both sides of the central hall were relatively large. In order to enhance the safety and design requirements, a prestressing process could be considered to further reduce the unfavorable displacement caused by the prestresses on the components. During the construction process, measures such as pre-imposed reverse displacement on the top of the side column and pre-arch of the upper box girder could be adopted.
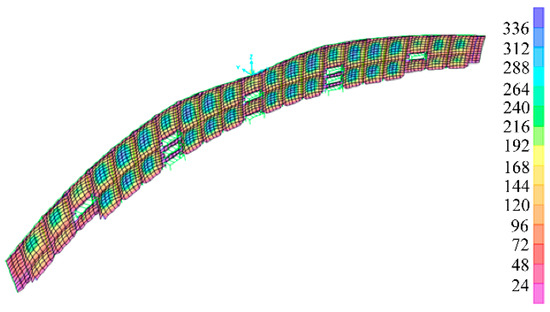
Figure 6.
Most unfavorable displacement cloud map for the cable net curtain structure (dimension: mm).
3.3. Flexible Boundaries and Supports
As the boundary condition of a cable net curtain is a flexible boundary condition, force-finding and structural mechanic analyses of a cable net structure are related to the deformation of the boundary structure. When designing a cable net structure, it is necessary to consider the influence of flexible boundary conditions and assemble an entire model. There was reaction force transmission among the cable net curtain structure, the upper steel roof structure, and the lower concrete structure. Table 3 lists the most unfavorable values of the reaction force under different combinations of load-bearing capacity limit states. In the global coordinate system, the x direction is the tangent direction of the curtain plane from left to right, the y direction is from south to north, and the z direction is vertical upward. In Table 3, for the boundary joints, Fx, Fy, and Fz describe the obtained reaction forces involved in the global coordinate system. Table 3 shows that the structure was mainly subjected to forces along the x and z directions.

Table 3.
Reaction forces for the boundary joints of the cable net curtain structure.
3.4. Initial Geometric Defects
Initial geometric defects are one of the influencing factors of the nonlinear behavior of a structure and they have an impact on the overall stability of the structure. Therefore, in order to consider the influence of initial geometric defects on the overall stability of our structure, initial geometric defects were applied to the nonlinear structural analysis. The values of the initial defects were L/1000 and L/300, respectively, where L is the maximum length of the wind-resistant columns. In this example, L = 34.4 m. The buckling mode shown in Figure 7 was taken to be the overall buckling mode. It can be observed from this figure that the inner and outer chords of the wind-resistant columns in this example exhibited obvious overall buckling.
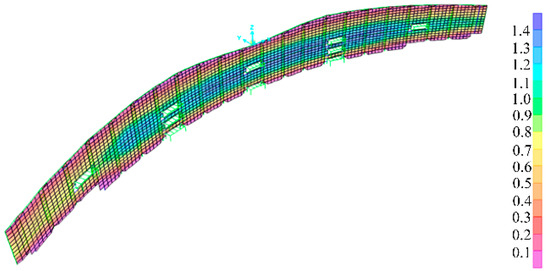
Figure 7.
Buckling mode for the cable net curtain structure.
Using the involved structural analysis of the structures with and without initial defects, different cable forces and structural behaviors of the landside hall were evaluated and are shown in Table 4, where Dmax is the maximum displacement of the cable net structure, Ftop is the maximum reaction force at the top of the columns, Fi is the initial cable force, and Fu is the cable force under the most unfavorable working conditions. From Table 4, it can be found that the maximum displacement of the cable net, the maximum reaction force at the top of the column, the initial cable force, and the cable force under the most unfavorable conditions were not significantly affected by the geometric defects. In other words, the overall stability of such a cable net structure was reliable.

Table 4.
Cable forces affected by different initial defects.
4. Discussion
The proposed force-finding method provides an important reference for further engineering applications of these cable net glass curtain structures. It can be applied not only to novel design and construction processes but also to performance improvement, demolition, and reconstruction phases. Moreover, it can be extended from traditional cable net structures to large-span cable structures and bridges.
Admittedly, the proposed force-finding method cannot be applied to certain form-finding problems with the precise and dual control of both internal forces and structural configurations. It has not yet been able to integrate shape control subjected to complicated load patterns such as wind loads and dynamic action. For high-precision (no more than 10−5) or large-scale structures with a huge number of nodes, the involved force-finding process would be computationally expensive. However, with the rapid development of AI, our method could be further improved by incorporating machine learning or deep learning techniques to optimize these complicated force-finding/form-finding problems in real time.
5. Conclusions
This study proposes a force-finding method for large-scale cable net glass curtain structures with nonlinear structural stiffness. On the basis of graph products and graph theory, our force-finding method requires a geometric nonlinear analysis of a structure, and then the nodal coordinates and cable forces can be calculated according to the corresponding unbalanced forces at the free nodes. The node coordinates are utilized and updated until the accuracy requirements are met, where the final configuration and cable forces of cable net curtain structures during prestressing can be obtained.
Before the force-finding analysis, the cable net curtain structures need to be preprocessed using graph products. Each cable net structure can be neatly represented by using undirected subgraphs. The force-finding analysis could be carried out according to the preprocessing results. During the force-finding process, special attention should be paid to the influence of the actual boundary conditions of the cable net curtain structures. Finally, the force-finding process of large-scale cable net glass curtain structures with nonlinear structural stiffness can be demonstrated using a numerical example, and the feasibility of the force-finding process described in this paper can be confirmed.
Author Contributions
Conceptualization: Y.L. and Y.C.; methodology: L.F., Y.L., Y.C. and J.F.; software: L.F. and Y.L.; validation: Y.L., J.G. and X.C.; formal analysis: Y.L.; investigation: L.F. and X.F.; resources: Y.C. and J.F.; data curation: X.F.; writing—original draft preparation: L.F. and Y.L.; writing—review and editing: L.F., Y.L., Y.C., J.G., X.C. and J.F.; visualization: L.F. and Y.L.; supervision: Y.C. and J.F.; project administration: Y.C. and J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 22KJB560027), the Qing Lan Project of Jiangsu Province, and the Natural Science Foundation of Jiangsu Province for Distinguished Young Scientists (Grant No. BK20231517).
Data Availability Statement
Due to privacy concerns, the data presented in this study are only available on request from the corresponding author.
Acknowledgments
We appreciate the information about the case building provided by its engineers. We are grateful to the editors and anonymous reviewers for their professional comments and valuable suggestions for improving the quality of the paper.
Conflicts of Interest
Jiangjun Gao and Xingwang Cao were employed by China Construction Fifth Engineering Bureau Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The sponsors also had no role in the design, execution, interpretation, or writing of the study.
References
- Xiang, Y.; Luo, Y.; Guo, X.; Xiong, Z.; Shen, Z. A linearized approach for the seismic response analysis of flexible cable net structures. Soil. Dyn. Earthq. Eng. 2016, 88, 92–108. [Google Scholar] [CrossRef]
- Nie, R.; He, B.; Hodges, D.H.; Ma, X. Form finding and design optimization of cable network structures with flexible frames. Comput. Struct. 2019, 220, 81–91. [Google Scholar] [CrossRef]
- Tang, Y.; Li, T.; Hao, L.; Ma, X. Extended nonlinear force density method for form-finding of cable-membrane structures. J. Aerosp. Eng. 2017, 30, 04016101. [Google Scholar] [CrossRef]
- Dutta, S.; Ghosh, S. Form-finding of frame-supported tensile membrane structures using stochastic optimisation. Structures 2021, 32, 2211–2221. [Google Scholar] [CrossRef]
- Xian, X.; Luo, Y. Force finding of tensegrity systems using simulated annealing algorithm. J. Struct. Eng. 2010, 136, 1027–1031. [Google Scholar]
- Yamamoto, M.; Gan, B.S.; Fujita, K.; Kurokawa, J. A genetic algorithm based form-finding for tensegrity structure. Procedia Eng. 2011, 14, 2949–2956. [Google Scholar] [CrossRef]
- Koohestani, K. Form-finding of tensegrity structures via genetic algorithm. Int. J. Solids Struct. 2012, 49, 739–747. [Google Scholar] [CrossRef]
- Linkwitz, K.; Schek, H.J. Einige bemerkungen zur berechnung von vorgespannten seilnetzkonstruktionen. Ing.-Arch. 1971, 40, 145–158. [Google Scholar] [CrossRef]
- Schek, H.J. The force density method for form finding and computation of general networks. Comput. Methods Appl. Mech. Eng. 1974, 3, 115–134. [Google Scholar] [CrossRef]
- Liew, A. Constrained force density method optimisation for compression-only shell structures. Structures 2020, 28, 1845–1856. [Google Scholar] [CrossRef]
- Zhao, Z.; Yu, D.; Zhang, T.; Cai, Q. Intelligent design algorithm for branching structures based on updated force density method. J. Build. Eng. 2022, 57, 104858. [Google Scholar] [CrossRef]
- Aboul-Nasr, G.; Mourad, S.A. An extended force density method for form finding of constrained cable nets. Case Stud. Struct. Eng. 2015, 3, 19–32. [Google Scholar] [CrossRef]
- Maurin, B.; Motro, R. The surface stress density method as a form-finding tool for tensile membranes. Eng. Struct. 1998, 20, 712–719. [Google Scholar] [CrossRef]
- Hayashi, K.; Ohsaki, M. FDMopt: Force density method for optimal geometry and topology of trusses. Adv. Eng. Softw. 2019, 133, 12–19. [Google Scholar] [CrossRef]
- Luo, X.Q.; Zhang, Q.L.; Chen, L. Form-finding of a mixed structure with cable nets and tubular trusses. J. Constr. Steel Res. 2012, 72, 192–202. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Q.; Feng, J. Improved form-finding of tensegrity structures using blocks of symmetry-adapted force density matrix. J. Struct. Eng. 2018, 144, 04018174. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Zhang, Y.; Ye, J. Force density sensitivity form-finding design method for cable-mesh reflector antennas considering interactive effects between cable network and supporting truss. Eng. Struct. 2021, 244, 112722. [Google Scholar] [CrossRef]
- Ye, J.; Feng, R.; Zhou, S.; Tian, J. The modified force-density method for form-finding of membrane structures. Int. J. Steel Struct. 2012, 12, 299–310. [Google Scholar] [CrossRef]
- Zhao, Z.; Yu, D.; Zhang, T.; Gao, H. Form-finding and optimization for free form grid structures supported by branching columns based on updated force density method. Structures 2022, 44, 1190–1203. [Google Scholar] [CrossRef]
- Otter, J.R.H. Computations for prestressed concrete reactor pressure vessels using dynamic relaxation. Nucl. Struct. Eng. 1965, 1, 61–75. [Google Scholar] [CrossRef]
- Boulaud, R.; Douthe, C.; Sab, K. Modelling of curtain effect in rockfall barrier with the dynamic relaxation. Int. J. Solids Struct. 2020, 200–201, 297–312. [Google Scholar] [CrossRef]
- Collins, M.; Cosgrove, T. Dynamic relaxation modelling of braced bending active gridshells with rectangular sections. Eng. Struct. 2019, 187, 16–24. [Google Scholar] [CrossRef]
- Wang, X.; Cai, J.; Yang, R.; Feng, J. Form-finding of deployable mesh reflectors using dynamic relaxation method. Acta Astronaut. 2018, 151, 380–388. [Google Scholar] [CrossRef]
- Barnes, M.R. Form-finding and analysis of prestressed nets and membranes. Comput. Struct. 1988, 30, 685–695. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Mohammadi-Khatami, M. Nonlinear analysis of cable structures using the dynamic relaxation method. Front. Struct. Civ. Eng. 2021, 15, 253–274. [Google Scholar] [CrossRef]
- Li, N.; Zong, W.; Fan, Y.; Lu, J. Form-finding optimization methods for free-form reticulated shells: Reverse realization and numerical simulation. Adv. Mech. Eng. 2017, 9, 1687814017737256. [Google Scholar] [CrossRef]
- Tu, G.; Chen, C.; Gong, Z.; Wang, Y. A form-finding method for branching structures based on dynamic relaxation. Appl. Sci. 2021, 11, 7165. [Google Scholar] [CrossRef]
- Bagrianski, S.; Halpern, A.B. Form-finding of compressive structures using Prescriptive Dynamic Relaxation. Comput. Struct. 2014, 132, 65–74. [Google Scholar] [CrossRef]
- Bessini, J.; Lázaro, C.; Monleón, S. A form-finding method based on the geometrically exact rod model for bending-active structures. Eng. Struct. 2017, 152, 549–558. [Google Scholar] [CrossRef]
- Haug, E.; De Kermel, P.; Gawenat, B.; Michalski, A. Industrial design and analysis of structural membranes. Int. J. Space Struct. 2009, 24, 191–204. [Google Scholar] [CrossRef]
- Wan, Z.; Ohlbrock, P.O.; D’Acunto, P.; Cao, Z.; Fan, F.; Schwartz, J. A form-finding approach for the conceptual design of air-supported structures using 3D graphic statics. Comput. Struct. 2021, 243, 106401. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, Y.; Qian, H.; Wang, H.; Jin, X. Numerical approach for simulating the tensioning process of complex prestressed cable-net structures. J. Civ. Eng. Manag. 2021, 27, 571–578. [Google Scholar] [CrossRef]
- Zhu, W.; Ge, Y.; Fang, G.; Cao, J. A novel shape finding method for the main cable of suspension bridge using nonlinear finite element approach. Appl. Sci. 2021, 11, 4644. [Google Scholar] [CrossRef]
- Arcaro, V.; Adeli, H. Form-finding and analysis of hyperelastic tensegrity structures using unconstrained nonlinear programming. Eng. Struct. 2019, 191, 439–446. [Google Scholar] [CrossRef]
- Argyris, J.H.; Angelopoulos, T.; Bichat, B. A general method for the shape finding of lightweight tension structures. Comput. Methods Appl. Mech. Eng. 1974, 3, 135–149. [Google Scholar] [CrossRef]
- Lu, J.; Dong, X.; Zhao, X.; Wu, X.; Shu, G. Form-finding analysis for a new type of cable-strut tensile structures generated by semi-regular tensegrity. Adv. Struct. Eng. 2017, 20, 772–783. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Wu, Y. Novel form-finding of tensegrity structures using ant colony systems. J. Mech. Robot. 2012, 4, 031001. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Wu, Y. Prestress stability of pin-jointed assemblies using ant colony systems. Mech. Res. Commun. 2012, 41, 30–36. [Google Scholar] [CrossRef]
- Kabasi, S.; Marbaniang, A.L.; Ghosh, S. Physics-informed neural networks for the form-finding of tensile membranes by solving the Euler–Lagrange equation of minimal surfaces. Thin Walled Struct. 2023, 182, 110309. [Google Scholar] [CrossRef]
- Sareh, P. The least symmetric crystallographic derivative of the developable double corrugation surface: Computational design using underlying conic and cubic curves. Mater. Des. 2019, 183, 108128. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Ma, R.; Zhang, Y. Efficient symmetry method for calculating integral prestress modes of statically indeterminate cable-strut structures. J. Struct. Eng. 2015, 141, 04014240. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, J.; Sareh, P.; Feng, J. Feasible prestress modes for cable-strut structures with multiple self-stress states using particle swarm optimization. J. Comput. Civ. Eng. 2020, 34, 04020003. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Li, Y.; Cao, Y.P.; Feng, X.Q. Stiffness matrix based form-finding method of tensegrity structures. Eng. Struct. 2014, 58, 36–48. [Google Scholar] [CrossRef]
- Fan, L.; Xu, R.; Shi, P.; Feng, X.; Chen, Y. Simplified form-finding for tensegrity structures through reference joints of symmetry orbits. Structures 2023, 49, 1157–1167. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Guest, S.D.; Ohsaki, M. Symmetric prismatic tensegrity structures. Part I: Configuration and stability. Int. J. Solids Struct. 2009, 46, 1–14. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, W.; Yuan, H.; Zhu, J.; Zheng, J. Modified double-control form-finding analysis for suspendomes considering the construction process and the friction of cable-strut joints. Eng. Struct. 2016, 120, 75–81. [Google Scholar] [CrossRef]
- Wallin, M.; Ristinmaa, M. Topology optimization utilizing inverse motion based form finding. Comput. Methods Appl. Mech. Eng. 2015, 289, 316–331. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, H.; Gao, J.; Shen, Z.; Xie, T.; Sareh, P. Accurate force evaluation in prestressed cable-strut structures: A robust sparse bayesian learning method with feedback-driven error optimization. Eng. Struct. 2025, 330, 119878. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ohsaki, M. Force identification of prestressed pin-jointed structures. Comput. Struct. 2011, 89, 2361–2368. [Google Scholar] [CrossRef]
- Quagliaroli, M.; Malerba, P.G.; Albertin, A.; Pollini, N. The role of prestress and its optimization in cable domes design. Comput. Struct. 2015, 161, 17–30. [Google Scholar] [CrossRef]
- Serra, M.; Shahbazian, A.; Da Silva, L.S.; Marques, L.; Rebelo, C.; Vellasco, P.C.G.d.S. A full scale experimental study of prestressed stayed columns. Eng. Struct. 2015, 100, 490–510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).