Multi-Ship Collision Avoidance in Inland Waterways Using Actor–Critic Learning with Intrinsic and Extrinsic Rewards
Abstract
1. Introduction
1.1. Traditional Approaches
1.2. Intelligent Methodologies
2. Preliminaries
2.1. Ship Encounter Situations
- The vessels should stay as close to the outer limit of the channel on their starboard side as is safe and practical (rule 8).
- Under any circumstances, ferries navigating the main channel of the Yangtze River must yield to vessels traveling downstream or navigating the channel (rule 9).
- Crossing vessels must yield to vessels traveling downstream or navigating the channel and must not suddenly or forcefully cross in front of vessels that are proceeding downstream (rule 12).
- In a head-on situation (two power-driven vessels are meeting on reciprocal or nearly reciprocal courses) with a risk of collision, both vessels should turn to starboard to pass port side to port side (rule 10).
- If one vessel plans to overtake another one, in which the vessel approaches another vessel from a direction more than 22.5 degrees abaft the beam, it must not impede the movement of the vessel being overtaken (rule 11).
- When two vessels are crossing and a collision risk exists, the vessel with the other on its starboard side should give way and avoid crossing ahead of the other vessel (rule 12).
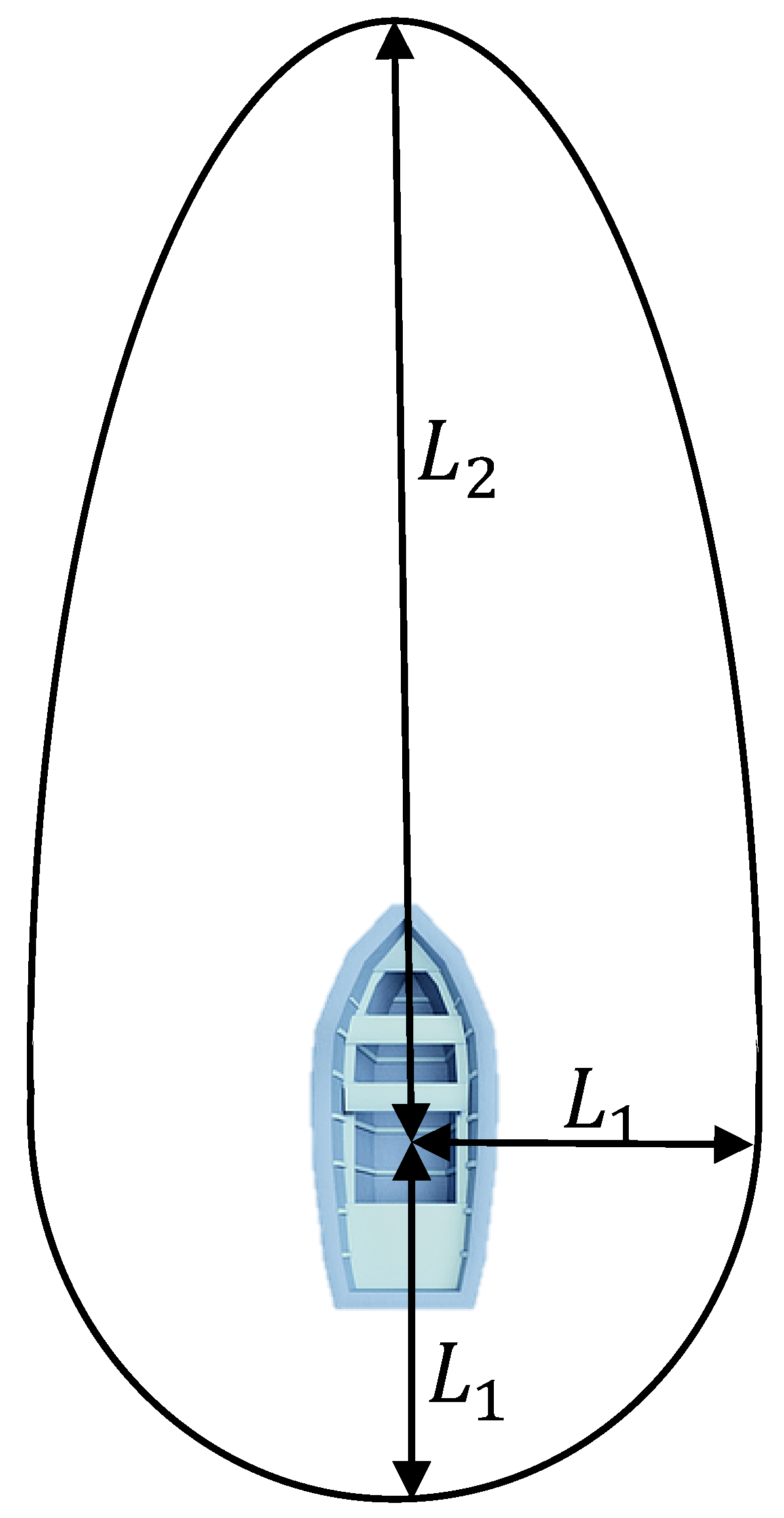
2.2. Collision Diameter
- •
- Taking-over ();
- •
- Crossing ();
- •
- Head-on ().

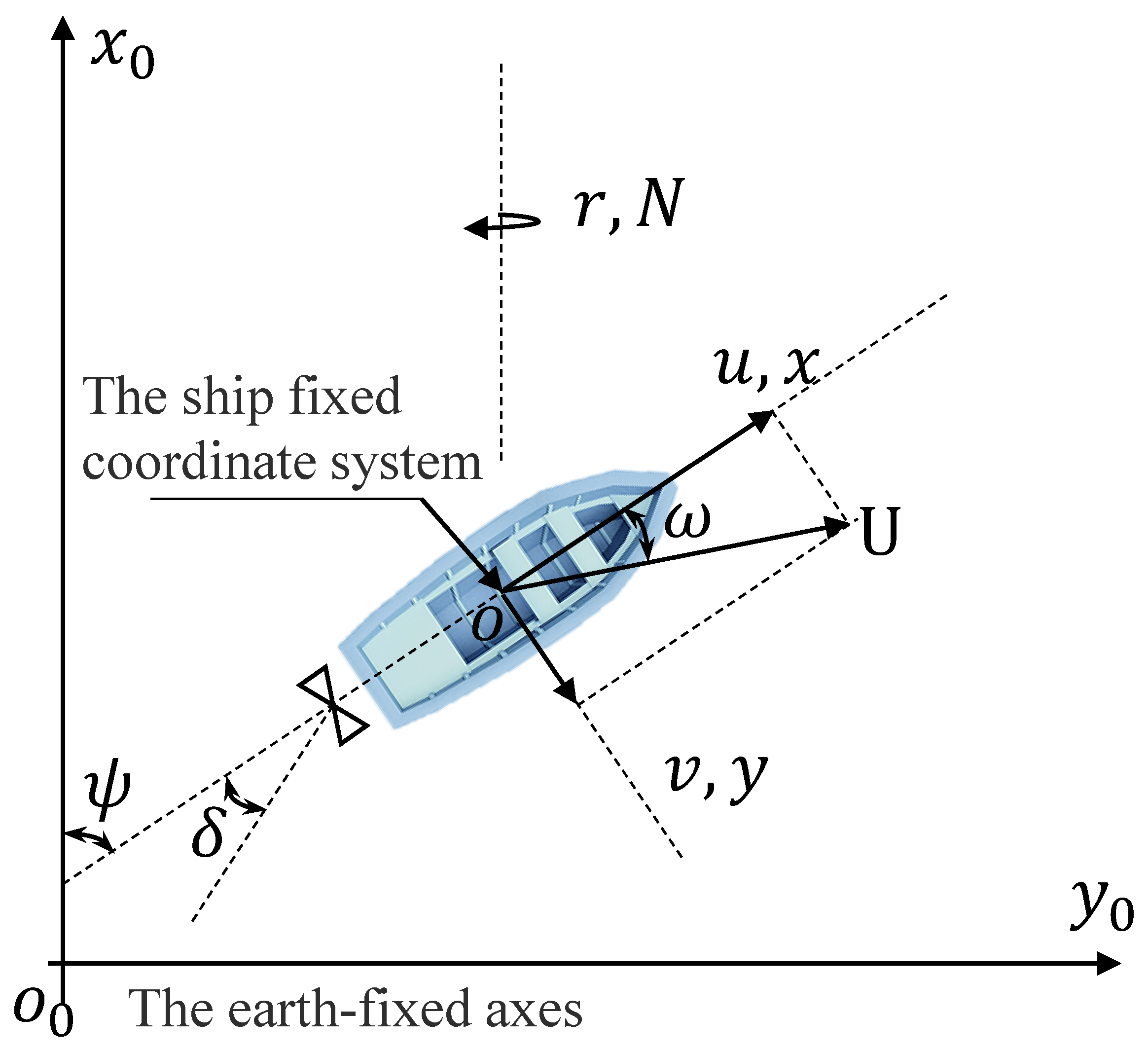
2.3. Ship Motion Model with Environmental Disturbances
3. Multi-Agent Reinforcement Learning for Collision Avoidance
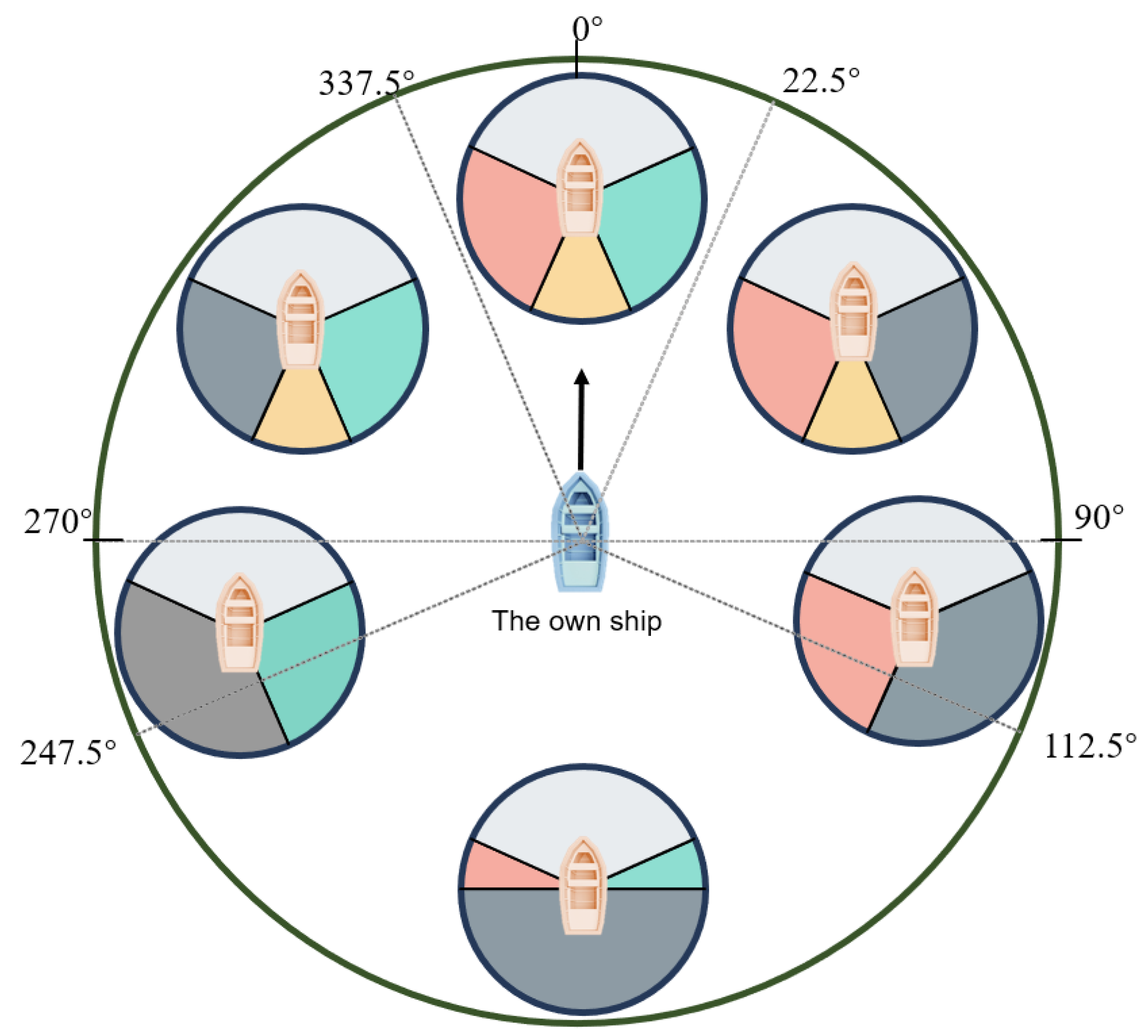
3.1. Grid Mesh Discretization
3.2. Definitions of Collision Avoidance Model
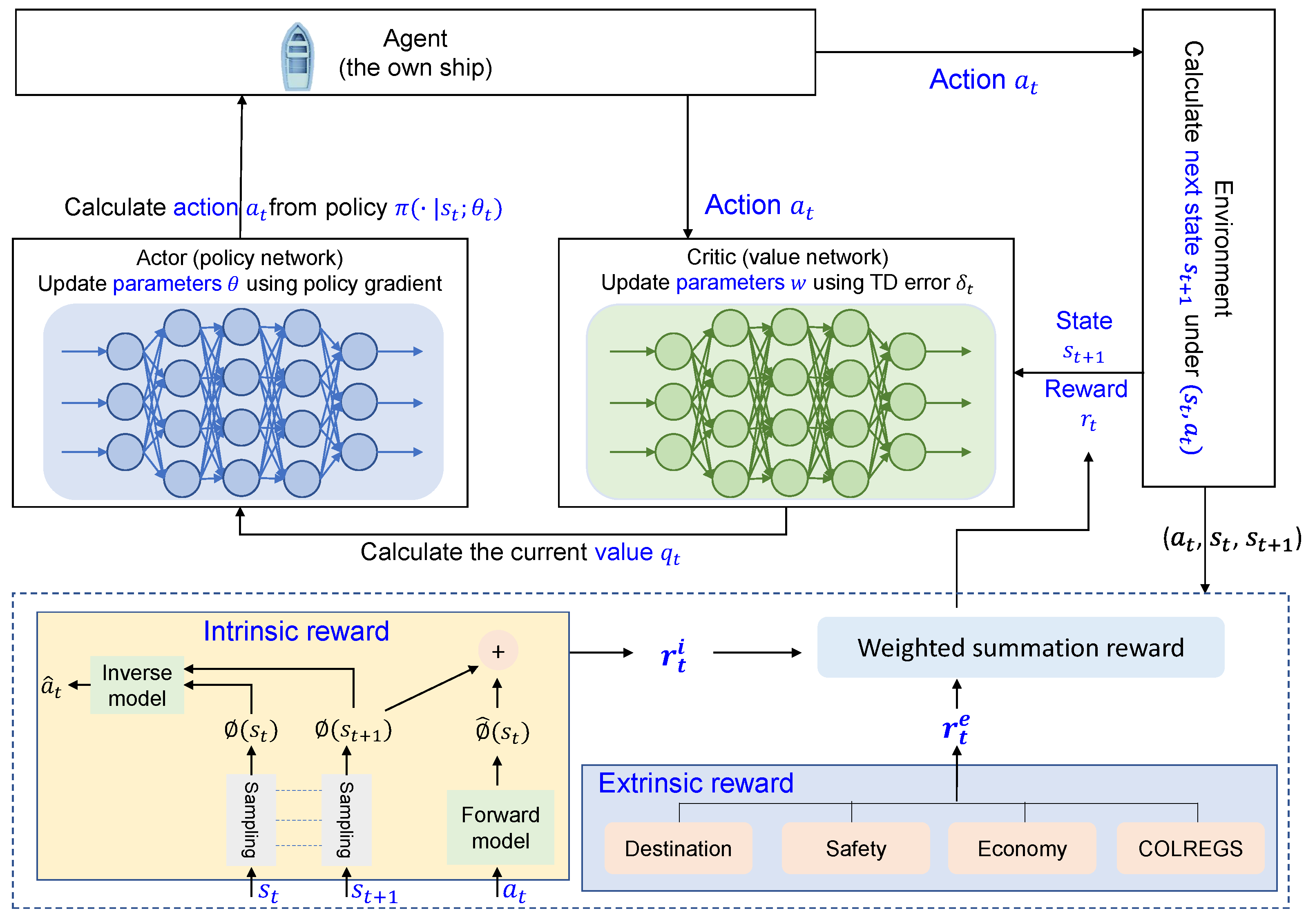
3.3. Reward Design
3.3.1. Intrinsic Reward
3.3.2. Extrinsic Reward
3.4. Actor–Critic Collision Avoidance Method
4. Experimental Data and Baseline Algorithms
4.1. AIS Dataset Characteristics
4.2. Comparable Algorithms
5. Simulation Design
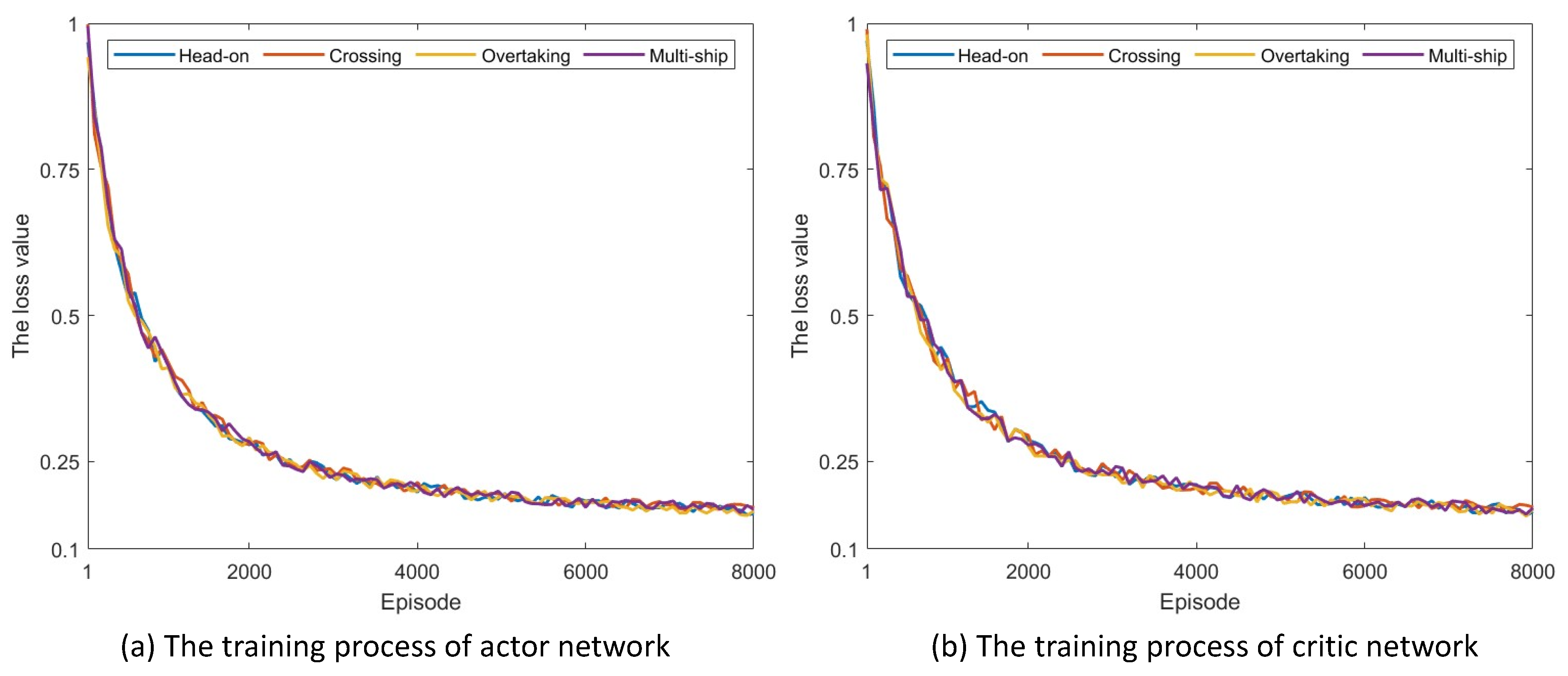
5.1. Training Process
5.2. Parameter Settings
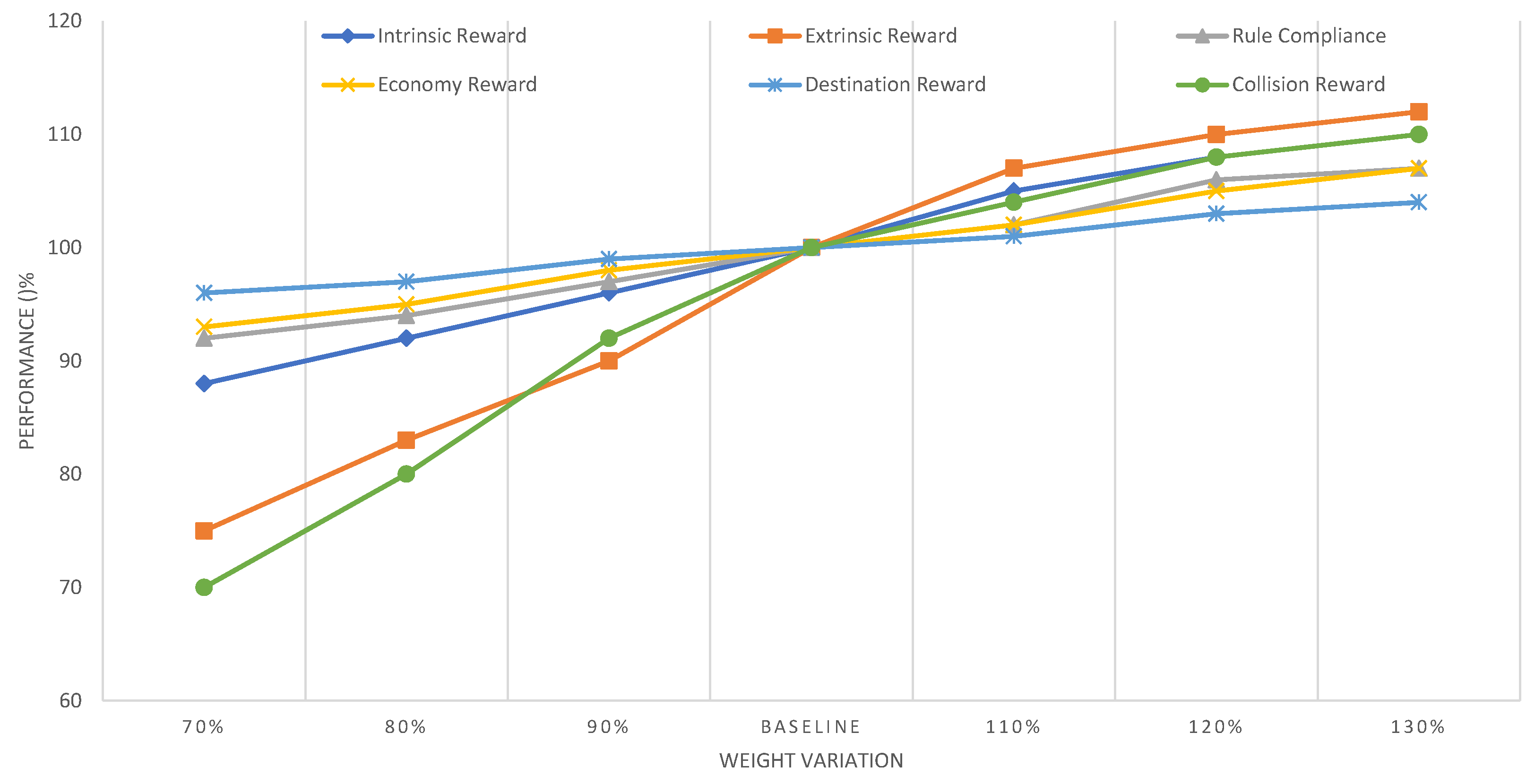
5.3. Reward Weighting Analysis
6. Analysis of Experimental Results
6.1. Comparative Performance Analysis
6.2. The Influence of Ship Density
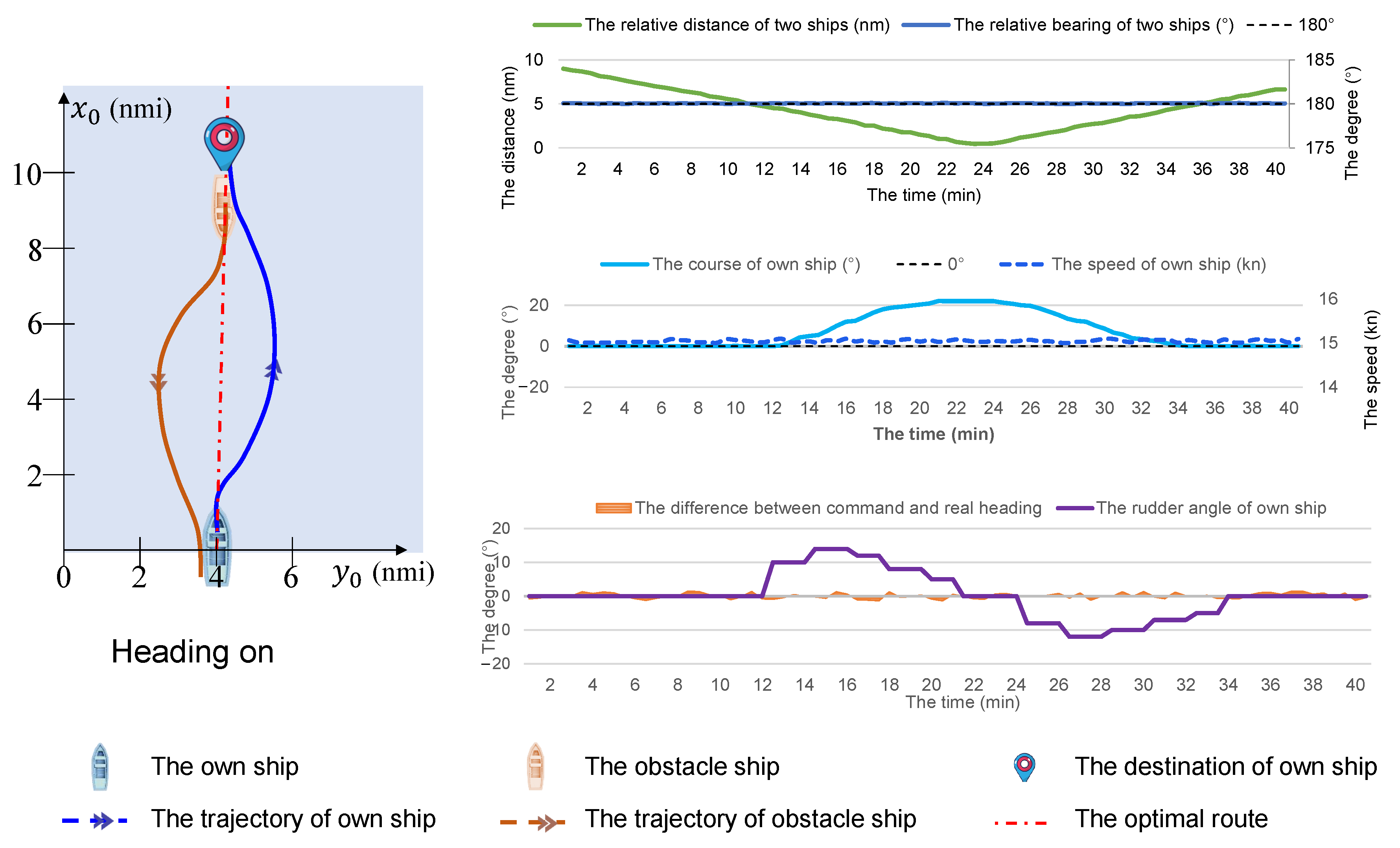
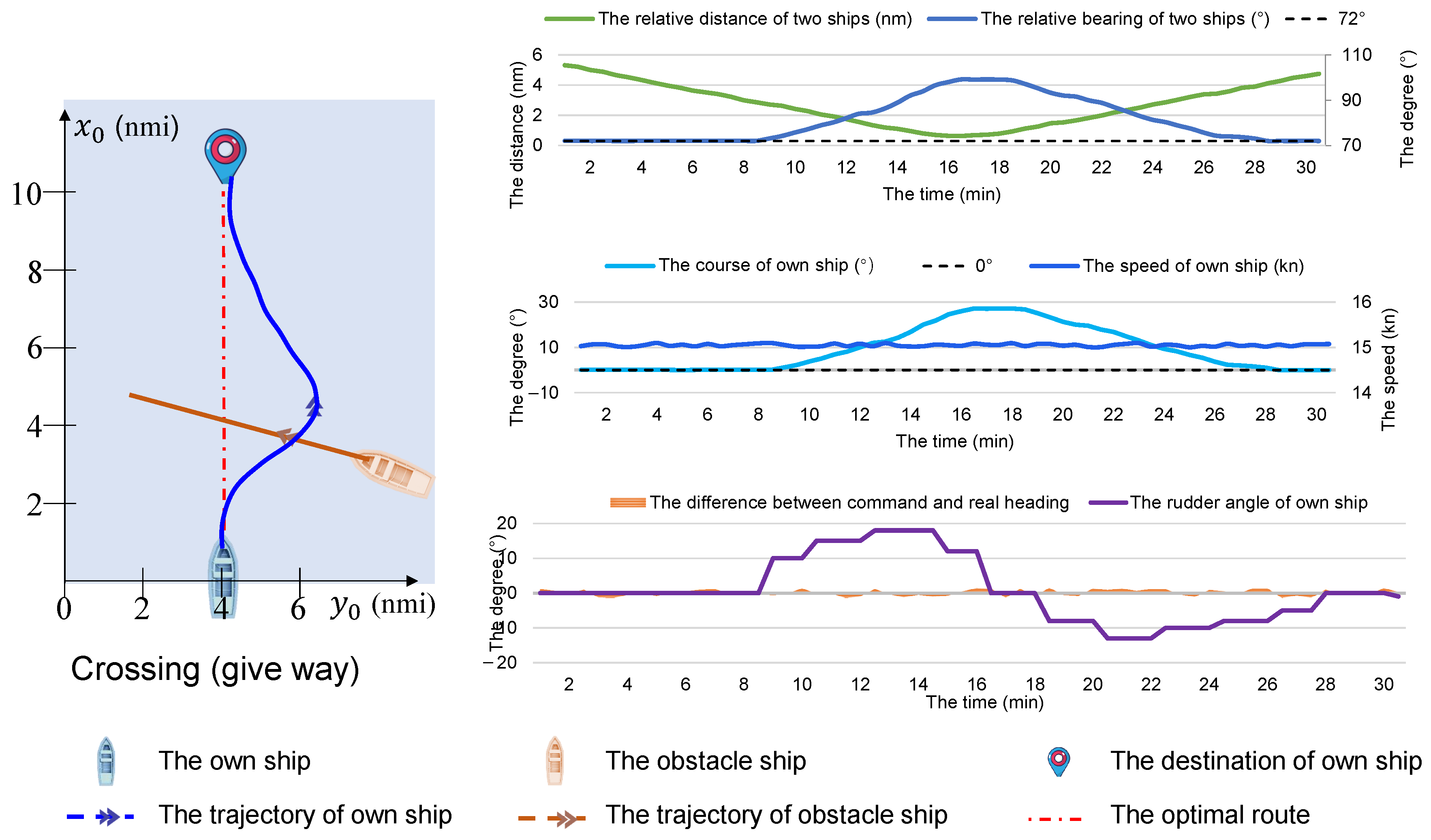
6.3. Typical Two-Ship Encounter Situation
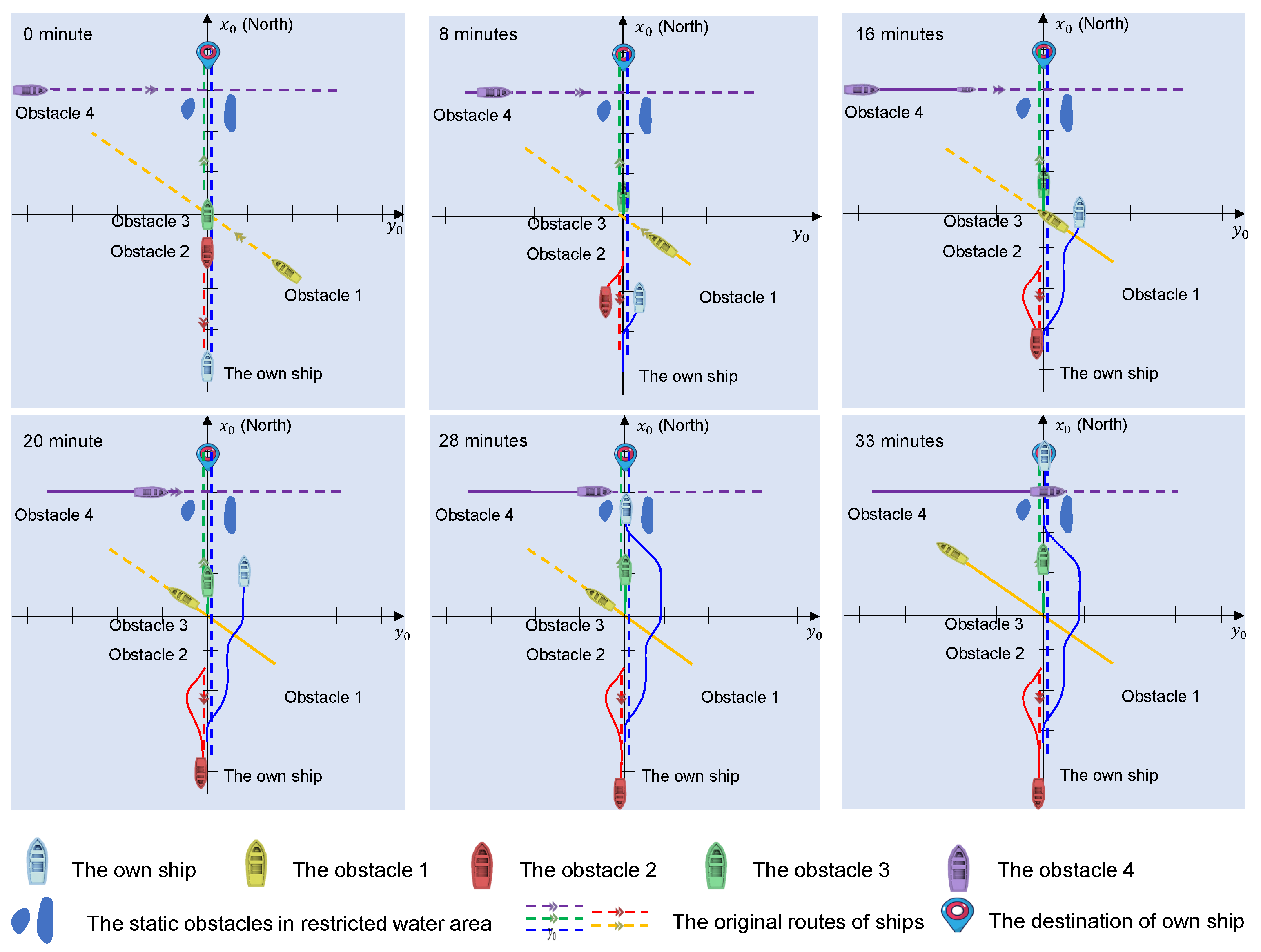
6.4. Multi-Ship Encounter Scenario
6.5. Limitations and Implementation Challenges
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aritua, B.; Cheng, L.; van Liere, R.; de Leijer, H. Blue Routes for a New Era: Developing Inland Waterways Transportation in China; World Bank Publications; World Bank Group: Washington, DC, USA, 2021. [Google Scholar]
- Chaal, M.; Ren, X.; BahooToroody, A.; Basnet, S.; Bolbot, V.; Banda, O.A.V.; Van Gelder, P. Research on risk, safety, and reliability of autonomous ships: A bibliometric review. Saf. Sci. 2023, 167, 106256. [Google Scholar] [CrossRef]
- Namgung, H.; Kim, J.S. Collision risk inference system for maritime autonomous surface ships using COLREGs rules compliant collision avoidance. IEEE Access 2021, 9, 7823–7835. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, L.; Chen, P.; Negenborn, R.R.; Van Gelder, P. Ship collision avoidance methods: State-of-the-art. Saf. Sci. 2020, 121, 451–473. [Google Scholar] [CrossRef]
- Vagale, A.; Oucheikh, R.; Bye, R.T.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles I: A review. J. Mar. Sci. Technol. 2021, 26, 1292–1306. [Google Scholar] [CrossRef]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Eng. 2018, 169, 187–201. [Google Scholar] [CrossRef]
- Xue, Y.; Clelland, D.; Lee, B.; Han, D. Automatic simulation of ship navigation. Ocean Eng. 2011, 38, 2290–2305. [Google Scholar] [CrossRef]
- Liu, C.; Mao, Q.; Chu, X.; Xie, S. An improved A-star algorithm considering water current, traffic separation and berthing for vessel path planning. Appl. Sci. 2019, 9, 1057. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, J.; Zheng, G.; Liang, Y. HAS: Hierarchical A-Star algorithm for big map navigation in special areas. In Proceedings of the 2014 5th International Conference on Digital Home, Guangzhou, China, 28–30 November 2014; IEEE: New York, NY, USA, 2014; pp. 222–225. [Google Scholar]
- Kouzuki, A.; Hasegawa, K. Automatic collision avoidance system for ships using fuzzy control. J. Kansai Soc. Nav. Arch. Jpn. 1987, 205, 1–10. [Google Scholar]
- Denker, C.; Baldauf, M.; Fischer, S.; Hahn, A.; Ziebold, R.; Gehrmann, E.; Semann, M. E-Navigation based cooperative collision avoidance at sea: The MTCAS approach. In Proceedings of the 2016 European Navigation Conference (ENC), Helsinki, Finland, 30 May–2 June 2016; IEEE: New York, NY, USA, 2016; pp. 1–8. [Google Scholar]
- Zhao, Y.; Li, W.; Shi, P. A real-time collision avoidance learning system for Unmanned Surface Vessels. Neurocomputing 2016, 182, 255–266. [Google Scholar] [CrossRef]
- Chen, P.; Huang, Y.; Mou, J.; Van Gelder, P. Probabilistic risk analysis for ship-ship collision: State-of-the-art. Saf. Sci. 2019, 117, 108–122. [Google Scholar] [CrossRef]
- Degre, T.; Lefevre, X. A collision avoidance system. J. Navig. 1981, 34, 294–302. [Google Scholar] [CrossRef]
- Bareiss, D.; Van den Berg, J. Generalized reciprocal collision avoidance. Int. J. Robot. Res. 2015, 34, 1501–1514. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, L.; Van Gelder, P. Generalized velocity obstacle algorithm for preventing ship collisions at sea. Ocean Eng. 2019, 173, 142–156. [Google Scholar] [CrossRef]
- Wilson, P.; Harris, C.; Hong, X. A line of sight counteraction navigation algorithm for ship encounter collision avoidance. J. Navig. 2003, 56, 111–121. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Gohl, P.; Watson, S.; Siegwart, R.; Beardsley, P. Shared control of autonomous vehicles based on velocity space optimization. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; IEEE: New York, NY, USA, 2014; pp. 1639–1645. [Google Scholar]
- Fujii, Y.; Shiobara, R. The analysis of traffic accidents. J. Navig. 1971, 24, 534–543. [Google Scholar] [CrossRef]
- Goodwin, E.M. A statistical study of ship domains. J. Navig. 1975, 28, 328–344. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Szlapczynska, J. Review of ship safety domains: Models and applications. Ocean Eng. 2017, 145, 277–289. [Google Scholar] [CrossRef]
- Shinar, J.; Steinberg, D. Analysis of optimal evasive maneuvers based on a linearized two-dimensional kinematic model. J. Aircr. 1977, 14, 795–802. [Google Scholar] [CrossRef]
- Coldwell, T. Marine traffic behaviour in restricted waters. J. Navig. 1983, 36, 430–444. [Google Scholar] [CrossRef]
- Xu, P.; Lan, D.; Yang, H.; Zhang, S.; Kim, H.; Shin, I. Ship formation and route optimization design based on improved PSO and DP algorithm. IEEE Access 2025, 13, 15529–15546. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, L.; Ding, S.; Li, F. Numerical simulation of moored ships in level ice considering dynamic behavior of mooring cable. Mar. Struct. 2025, 99, 103716. [Google Scholar] [CrossRef]
- Statheros, T.; Howells, G.; Maier, K.M. Autonomous ship collision avoidance navigation concepts, technologies and techniques. J. Navig. 2008, 61, 129–142. [Google Scholar] [CrossRef]
- Tsou, M.C.; Hsueh, C.K. The study of ship collision avoidance route planning by ant colony algorithm. J. Mar. Sci. Technol. 2010, 18, 16. [Google Scholar] [CrossRef]
- Cho, Y.; Han, J.; Kim, J. Efficient COLREG-compliant collision avoidance in multi-ship encounter situations. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1899–1911. [Google Scholar] [CrossRef]
- He, Z.; Liu, C.; Chu, X.; Negenborn, R.R.; Wu, Q. Dynamic anti-collision A-star algorithm for multi-ship encounter situations. Appl. Ocean Res. 2022, 118, 102995. [Google Scholar] [CrossRef]
- Karbowska-Chilinska, J.; Koszelew, J.; Ostrowski, K.; Kuczynski, P.; Kulbiej, E.; Wolejsza, P. Beam search Algorithm for ship anti-collision trajectory planning. Sensors 2019, 19, 5338. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q. Collision avoidance strategy optimization based on danger immune algorithm. Comput. Ind. Eng. 2014, 76, 268–279. [Google Scholar] [CrossRef]
- Sawada, R.; Sato, K.; Majima, T. Automatic ship collision avoidance using deep reinforcement learning with LSTM in continuous action spaces. J. Mar. Sci. Technol. 2021, 26, 509–524. [Google Scholar] [CrossRef]
- Chun, D.H.; Roh, M.I.; Lee, H.W.; Ha, J.; Yu, D. Deep reinforcement learning-based collision avoidance for an autonomous ship. Ocean Eng. 2021, 234, 109216. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Feng, H.; He, J.; Yang, H.; Li, F.; Yang, Z. Deep reinforcement learning based collision avoidance system for autonomous ships. Ocean Eng. 2024, 292, 116527. [Google Scholar] [CrossRef]
- Xie, S.; Chu, X.; Zheng, M.; Liu, C. A composite learning method for multi-ship collision avoidance based on reinforcement learning and inverse control. Neurocomputing 2020, 411, 375–392. [Google Scholar] [CrossRef]
- Rongcai, Z.; Hongwei, X.; Kexin, Y. Autonomous collision avoidance system in a multi-ship environment based on proximal policy optimization method. Ocean Eng. 2023, 272, 113779. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.; Wang, C.; Zhang, M.; Cui, H. A partially observable multi-ship collision avoidance decision-making model based on deep reinforcement learning. Ocean Coast. Manag. 2023, 242, 106689. [Google Scholar] [CrossRef]
- Yang, X.; Han, Q. Improved reinforcement learning for collision-free local path planning of dynamic obstacle. Ocean Eng. 2023, 283, 115040. [Google Scholar] [CrossRef]
- Yang, L.; Li, L.; Liu, Q.; Ma, Y.; Liao, J. Influence of physiological, psychological and environmental factors on passenger ship seafarer fatigue in real navigation environment. Saf. Sci. 2023, 168, 106293. [Google Scholar] [CrossRef]
- Sui, Z.; Wen, Y.; Huang, Y.; Song, R.; Piera, M.A. Maritime accidents in the Yangtze River: A time series analysis for 2011–2020. Accid. Anal. Prev. 2023, 180, 106901. [Google Scholar] [CrossRef]
- Tam, C.; Bucknall, R. Collision risk assessment for ships. J. Mar. Sci. Technol. 2010, 15, 257–270. [Google Scholar] [CrossRef]
- Davis, P.; Dove, M.; Stockel, C. A computer simulation of marine traffic using domains and arenas. J. Navig. 1980, 33, 215–222. [Google Scholar] [CrossRef]
- Pedersen, P.T. Collision and grounding mechanics. Proc. WEMT 1995, 95, 125–157. [Google Scholar]
- Friis-Hansen, P.; Ravn, E.; Engberg, P. Basic modelling principles for prediction of collision and grounding frequencies. In IWRAP Mark II Working Document; Technical University of Denmark: Kongens Lyngby, Denmark, 2008; pp. 1–59. [Google Scholar]
- Altan, Y.C. Collision diameter for maritime accidents considering the drifting of vessels. Ocean Eng. 2019, 187, 106158. [Google Scholar] [CrossRef]
- Pedersen, P.T.; Zhang, S. Collision analysis for MS Dextra. In Proceedings of the SAFER EURORO Spring Meeting, Nantes, France, 28 April 1999; Citeseer: Princeton, NJ, USA, 1999; Volume 28, pp. 1–33. [Google Scholar]
- Yoshimura, Y. Mathematical model for the manoeuvring ship motion in shallow water (2nd Report)-mathematical model at slow forward speed. J. Kansai Soc. Nav. Archit. 1988, 210, 77–84. [Google Scholar]
- Ogawa, A.; Koyama, T.; Kijima, K. MMG report-I, on the mathematical model of ship manoeuvring. Bull. Soc. Nav. Arch. Jpn. 1977, 575, 22–28. [Google Scholar]
- Miele, A.; Wang, T.; Chao, C.; Dabney, J. Optimal control of a ship for collision avoidance maneuvers. J. Optim. Theory Appl. 1999, 103, 495–519. [Google Scholar] [CrossRef]
- Debnath, A.K.; Chin, H.C. Navigational traffic conflict technique: A proactive approach to quantitative measurement of collision risks in port waters. J. Navig. 2010, 63, 137–152. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, Q. Probabilistic ship domain with applications to ship collision risk assessment. Ocean Eng. 2019, 186, 106130. [Google Scholar] [CrossRef]
- Qu, X.; Meng, Q.; Suyi, L. Ship collision risk assessment for the Singapore Strait. Accid. Anal. Prev. 2011, 43, 2030–2036. [Google Scholar] [CrossRef]
- Yoshimura, Y. Mathematical model for manoeuvring ship motion (MMG Model). In Proceedings of the Workshop on Mathematical Models for Operations involving Ship-Ship Interaction, Tokyo, Japan, 4 August 2005; pp. 1–6. [Google Scholar]





| Training: Update the Parameters of Actor and Critic Networks |
|---|
| 1. Observe the state ; |
| 2. Randomly sample action according to ; |
| 3. Perform and observe the new state and reward ; |
| 4. Update parameters in the critic network using the TD error; |
| 5. Update parameters in the actor network using the policy gradient method. |
| Parameter | Value |
|---|---|
| Discount rate | 0.9 |
| Max episodes | 8000 |
| Max steps | 500 |
| Batch size | 64 |
| Sampling time | 30 s |
| Learning rate of actor network | 2 × 10−3 |
| Learning rate of critic network | 1 × 10−3 |
| Scenarios | Episodes to Converge | Actor Final Loss | Critic Final Loss | Time to Converge (h) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A3C | PPO | DDPG | Proposed Model | A3C | PPO | DDPG | Proposed Model | A3C | PPO | DDPG | Proposed Model | A3C | PPO | DDPG | Proposed Model | |
| Head-on | 4500 | 6000 | 7000 | 5000 | 0.21 | 0.18 | 0.2 | 0.15 | 0.18 | 0.16 | 0.19 | 0.13 | 12.5 | 16.7 | 19.4 | 13.9 |
| Crossing | 4600 | 6100 | 7000 | 4900 | 0.2 | 0.19 | 0.21 | 0.16 | 0.19 | 0.17 | 0.2 | 0.14 | 12.8 | 16.9 | 19.4 | 13.6 |
| Overtaking | 4500 | 6000 | 6800 | 5000 | 0.23 | 0.18 | 0.2 | 0.15 | 0.18 | 0.15 | 0.19 | 0.15 | 12.5 | 16.7 | 18.9 | 13.9 |
| Multi-ship | 5000 | 6300 | 7500 | 5200 | 0.23 | 0.2 | 0.22 | 0.16 | 0.22 | 0.19 | 0.21 | 0.17 | 13.9 | 17.5 | 20.8 | 14.4 |
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|
| −0.0196 | 0.3979 | 0.0992 | 0.709 | ||||
| −0.0082 | 0.0918 | −0.0579 | 0.28 | ||||
| −0.1446 | 1.6016 | 0.1439 | −0.377 | ||||
| 0.0125 | −0.2953 | −0.3574 | 0.73 | ||||
| 0.3190 | 0.4140 | 0.0183 | 2.5 m | ||||
| −0.0055 | −0.0496 | −0.0207 | 1025 kg/m3 |
| Method | Success Rate (%) | Avg. Min. Distance (nmi) | Computational Time (ms) |
|---|---|---|---|
| Proposed model | 97.6 | 0.648 | 410 |
| PPO | 93.2 | 0.572 | 438 |
| A3C | 91.8 | 0.591 | 392 |
| DDPG | 89.5 | 0.484 | 425 |
| Velocity obstacle | 91.3 | 0.517 | 335 |
| AIS trajectory | - | 0.515 | - |
| Ship Count | Success Rate (%) | Avg. Comput. Time (ms) | Min. Dist. (nmi) |
|---|---|---|---|
| 2 | 99.2 | 410 | 0.698 |
| 4 | 97.8 | 428 | 0.654 |
| 6 | 95.4 | 455 | 0.633 |
| 8 | 93.1 | 486 | 0.591 |
| 10 | 90.5 | 524 | 0.534 |
| Ships | Length (m) | Width (m) | Initial Course (°) | Initial Speed (kts) | Initial Position (nmi) | Target Position (nmi) | Encounter Situations |
|---|---|---|---|---|---|---|---|
| Own ship | 66 | 11 | 0 | 15 | (0, 4) | (10, 4) | - |
| Ship 1 | 66 | 11 | 180 | 10 | (9, 4) | (0, 3.8) | Head-on |
| Ship 2 | 66 | 11 | 280 | 15.5 | (3.5, 8) | (6.2, 0) | Crossing |
| Ship 3 | 66 | 11 | 0 | 7 | (1.5, 4) | (10, 4) | Overtaking |
| Ships | Length (m) | Width (m) | Initial Course (°) | Initial Speed (kts) | Initial Position (nmi) | Target Position (nmi) |
|---|---|---|---|---|---|---|
| Own ship | 66 | 11 | 0 | 15 | (−4, 0) | (4, 0) |
| Ship 1 | 66 | 11 | 315 | 10.6 | (−2, 2) | (2, −2) |
| Ship 2 | 66 | 11 | 180 | 9 | (−1, 0) | (−5, 0) |
| Ship 3 | 66 | 11 | 0 | 3 | (0, 0) | (4, 0) |
| Ship 4 | 66 | 11 | 90 | 8.6 | (3, −4) | (3, 3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, S.; Zhang, Z.; Wang, Y.; Wang, D. Multi-Ship Collision Avoidance in Inland Waterways Using Actor–Critic Learning with Intrinsic and Extrinsic Rewards. Symmetry 2025, 17, 613. https://doi.org/10.3390/sym17040613
Gan S, Zhang Z, Wang Y, Wang D. Multi-Ship Collision Avoidance in Inland Waterways Using Actor–Critic Learning with Intrinsic and Extrinsic Rewards. Symmetry. 2025; 17(4):613. https://doi.org/10.3390/sym17040613
Chicago/Turabian StyleGan, Shaojun, Ziqi Zhang, Yanxia Wang, and Dejun Wang. 2025. "Multi-Ship Collision Avoidance in Inland Waterways Using Actor–Critic Learning with Intrinsic and Extrinsic Rewards" Symmetry 17, no. 4: 613. https://doi.org/10.3390/sym17040613
APA StyleGan, S., Zhang, Z., Wang, Y., & Wang, D. (2025). Multi-Ship Collision Avoidance in Inland Waterways Using Actor–Critic Learning with Intrinsic and Extrinsic Rewards. Symmetry, 17(4), 613. https://doi.org/10.3390/sym17040613





