Lie Group Intrinsic Mean Feature Detectors for Real-Time Industrial Surface Defect Detection
Abstract
1. Introduction
- The data collected by IoT devices have the characteristics of high dimensionality and large capacity, which not only poses a challenge to intelligent devices with limited resources but also makes defects difficult to detect [9].
- The data are usually in a streaming format (such as visual data or environmental data), which increases the difficulty of data labeling. Therefore, real-time detection of surface defects should be efficient, scalable, and have a certain sensitivity to anomalies and defects [10].
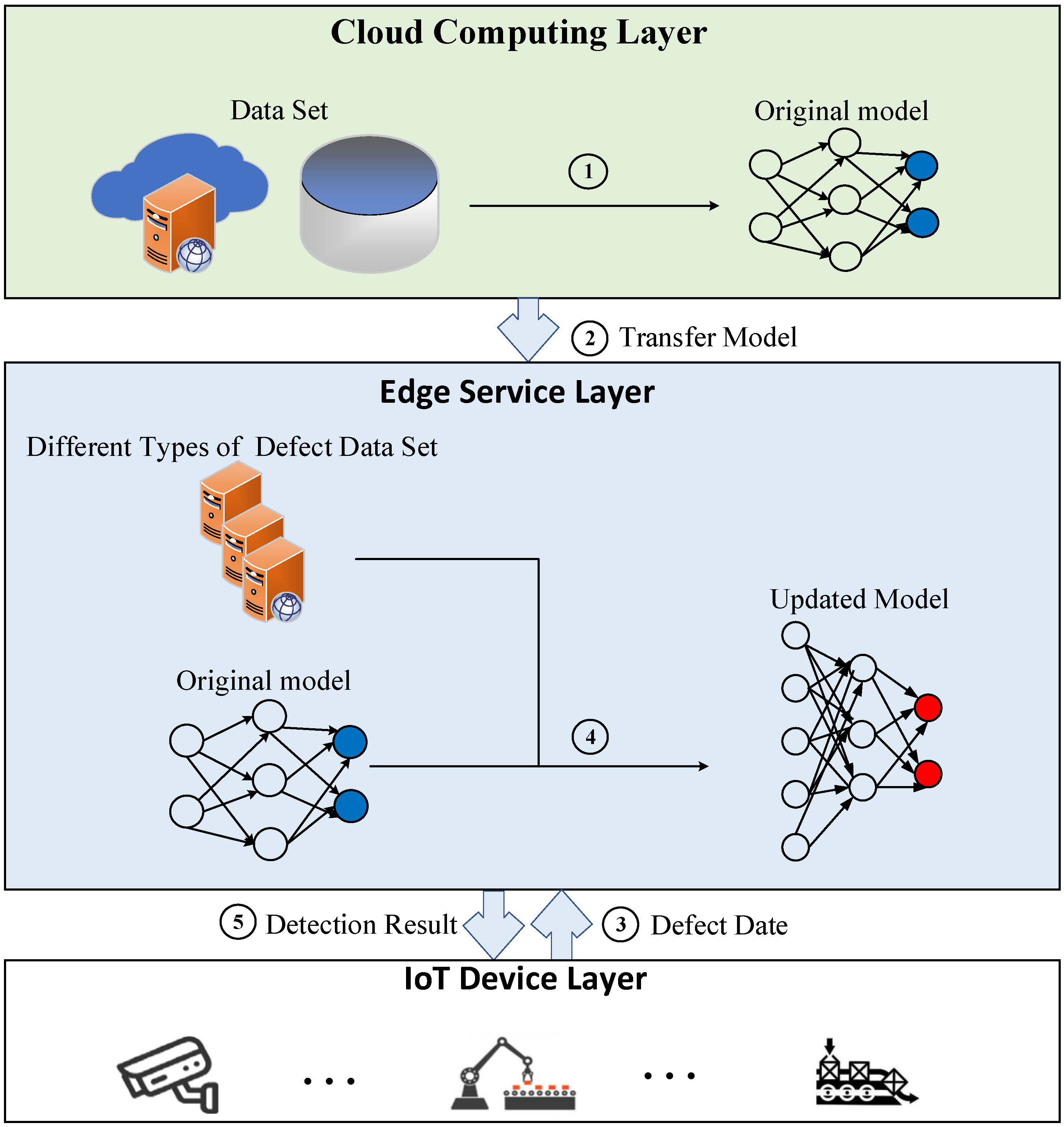
- To improve the speed and quality of SSD, we propose a three-layer structure model of MEC. In this model, the universal detection model trained on the cloud server is deployed to the edge server in advance and then updated according to the new data samples captured by IoT devices, so that the updated detection model shows better performance. The model can reduce the training time and improve the performance of tiny detection with limited data samples.
- To satisfy the real-time and efficiency of SSD, we propose an attention mechanism based on the intrinsic mean in the Lie Group manifold space. This mechanism utilizes the Lie Group manifold space calculation method instead of traditional operations such as pooling and convolution, which can efficiently locate the crucial features of tiny surfaces, effectively reduce the number of parameters of the model, avoid the selection and fine-tuning of hyperparameters, and better achieve the trade-off between detection accuracy and real-time performance.
- To verify the feasibility and performance of our proposed model through detailed experimental comparison. The experimental results show that our proposed model can effectively reduce the load on the edge server and satisfy the high-quality performance requirements of real-time detection; that is, our model is competitive with other state-of-the-art models in terms of improving the accuracy and speed of surface detection and reducing the detection delay.
2. Related Work
2.1. Defect Detection Based on Edge-Cloud Computing
2.2. Defect Detection Based on Deep Learning
2.3. Defect Detection Based on Attention Mechanism
3. Proposed Method
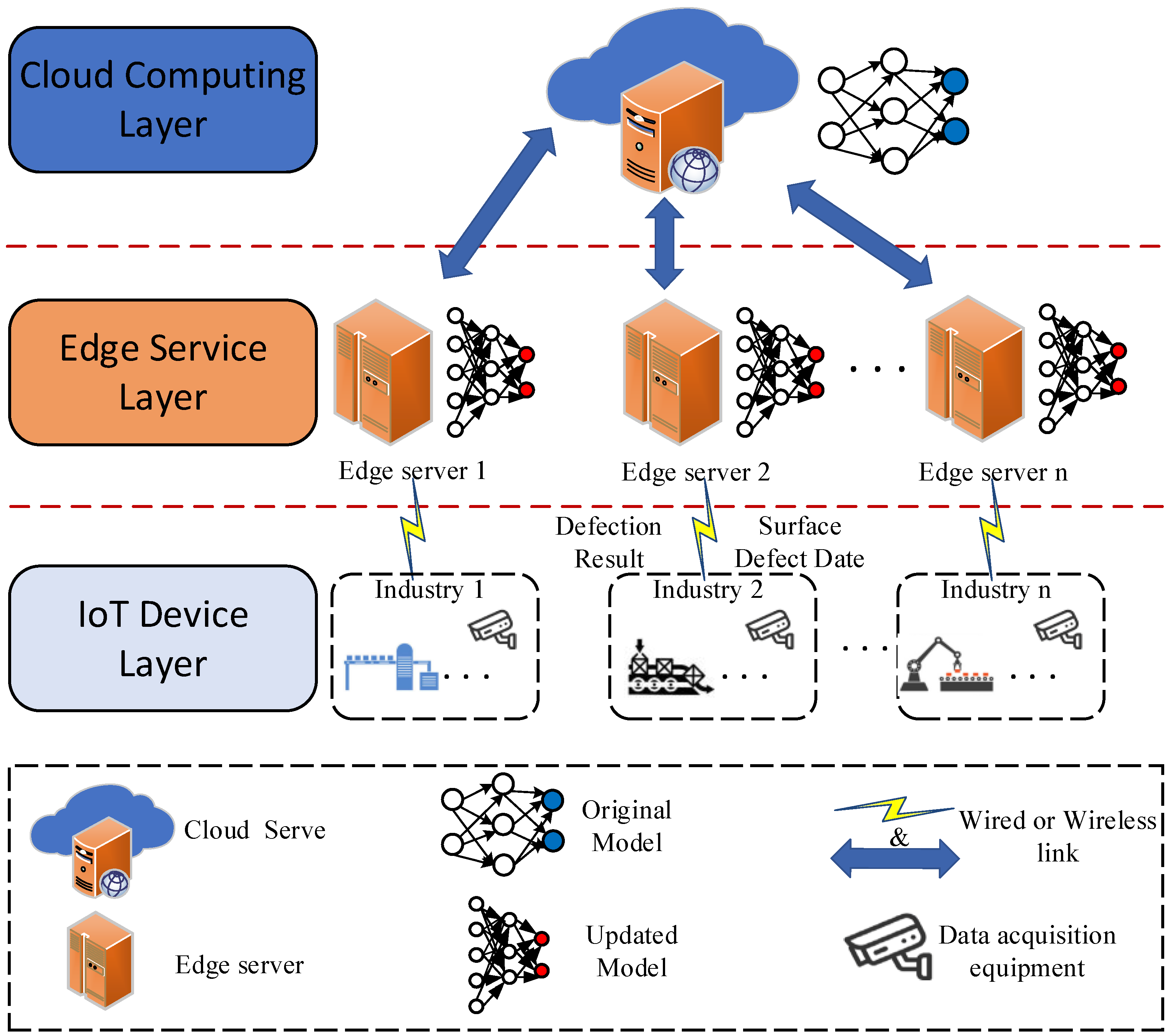
3.1. Overall Architecture
3.1.1. IoT Device Layer
3.1.2. Edge Service Layer
3.1.3. Cloud Computing Layer
3.2. Detection Process
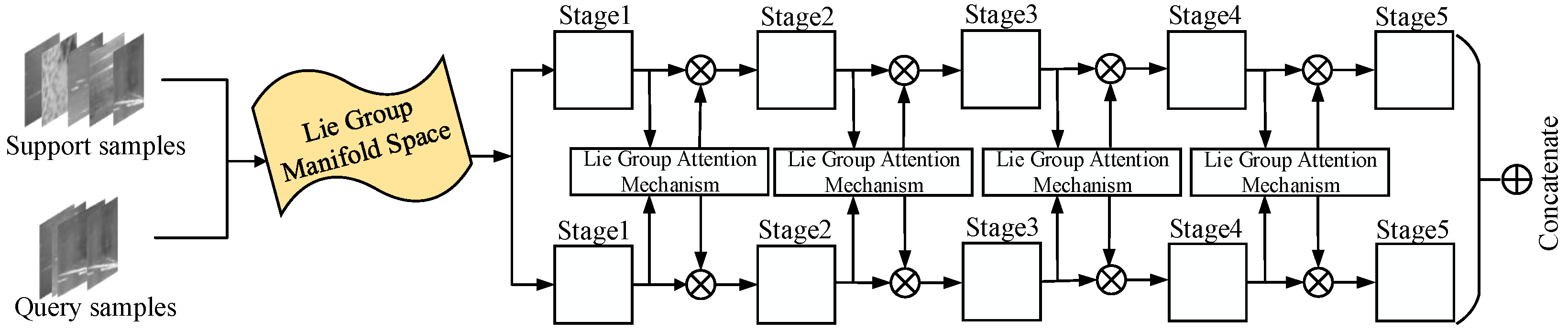
3.3. Detection Framework
3.3.1. Backbone Network Model
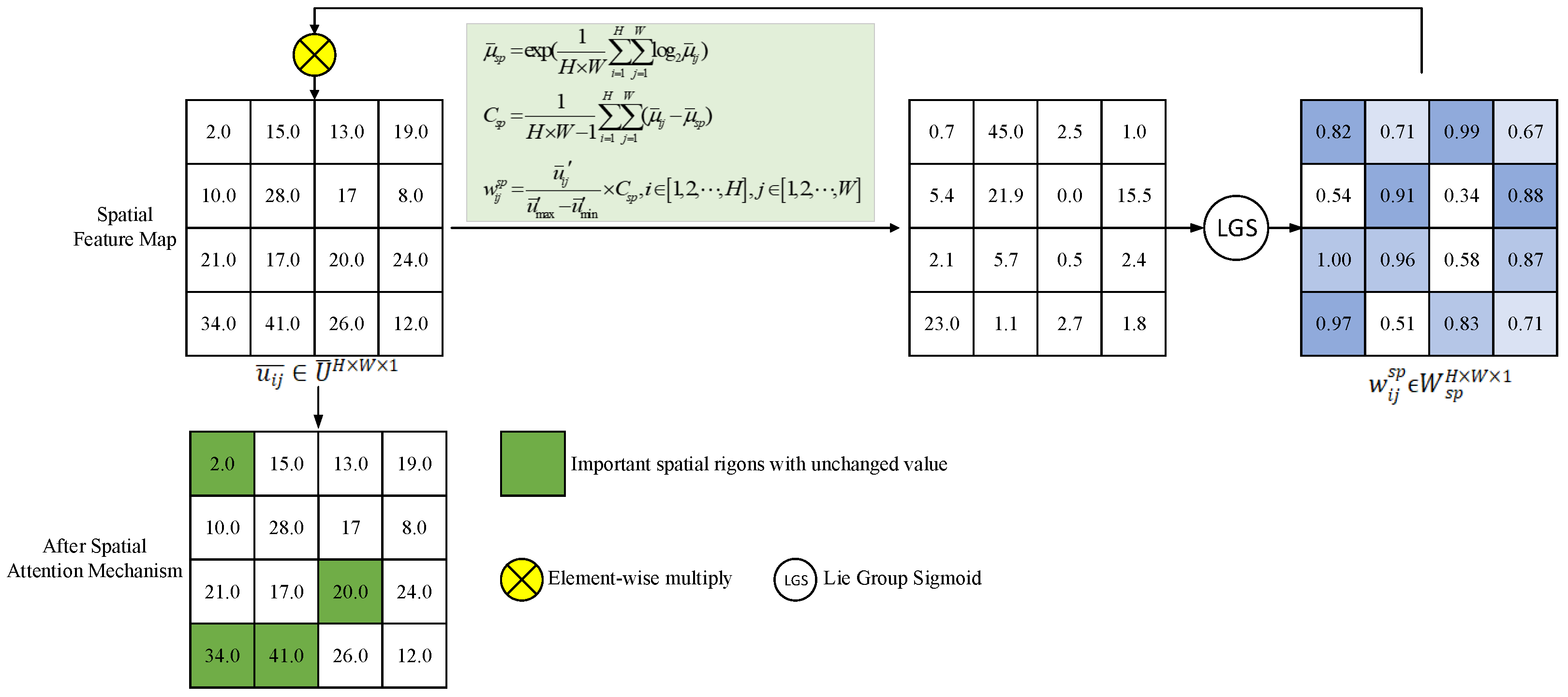
3.3.2. Attention Mechanism Based on Intrinsic Mean in Lie Group Manifold Space
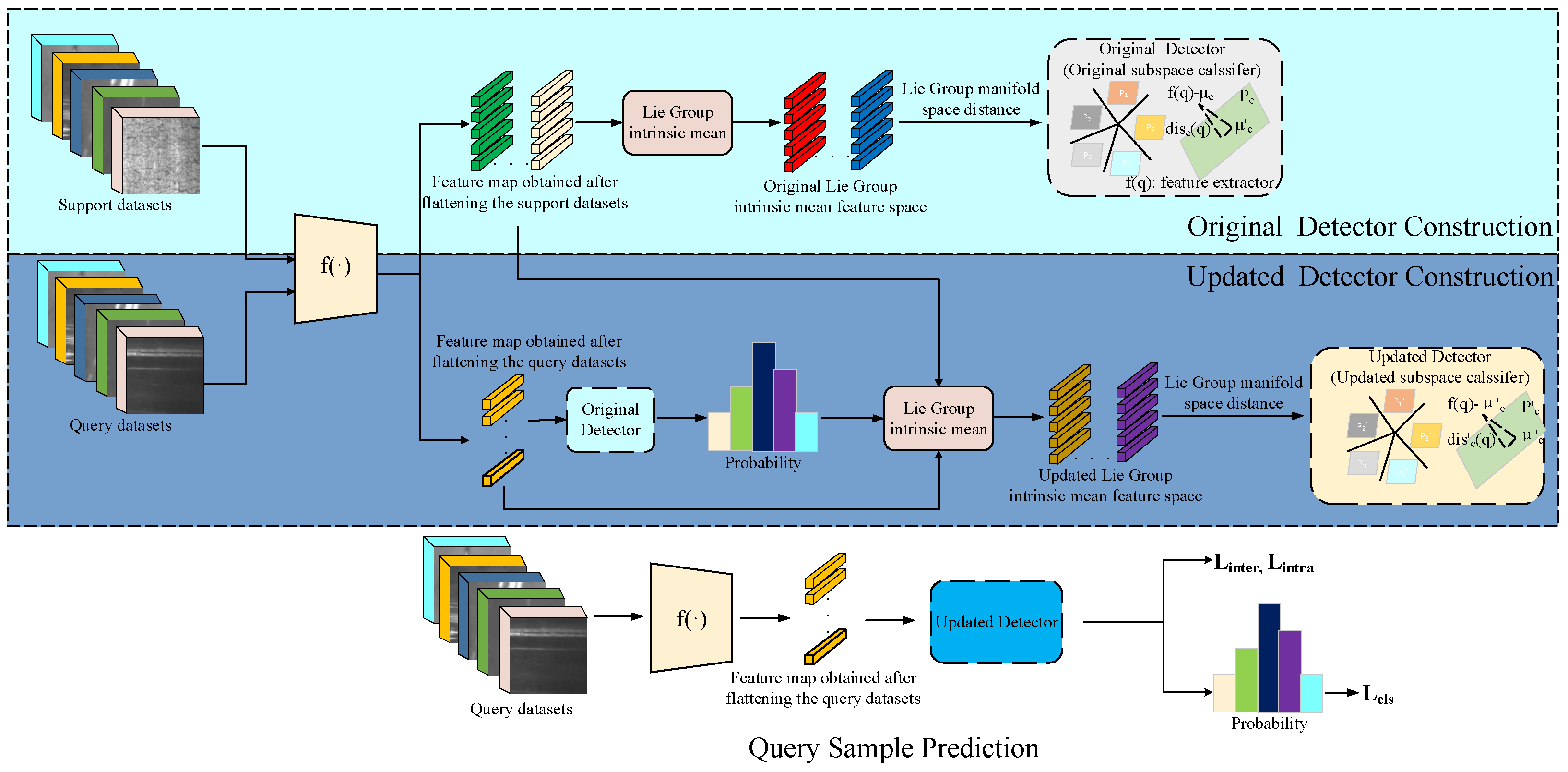
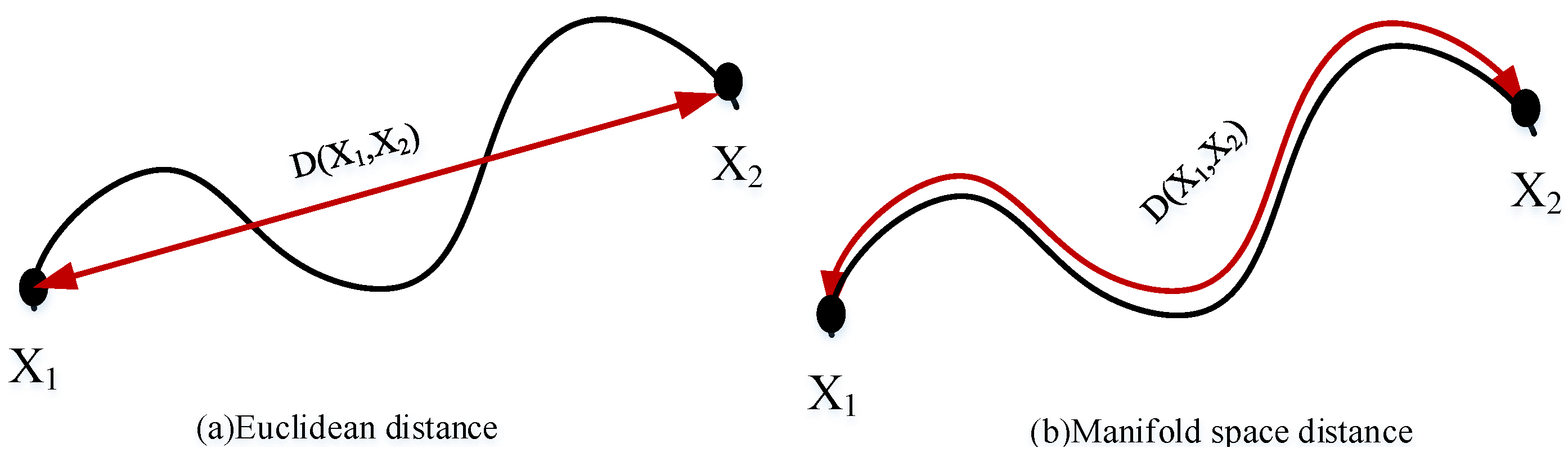
3.4. Intrinsic Mean Feature Detector in Lie Group Manifold Space
3.4.1. Methodology Overview
3.4.2. Problem Definition
3.4.3. Original Lie Group Manifold Space Intrinsic Mean Feature Detector
3.4.4. Updated Lie Group Manifold Space Intrinsic Mean Feature Detector
3.4.5. Loss Function
4. Experiments
4.1. Datasets and Implementation Details
4.2. Experimental Results and Comparison
4.2.1. Results and Comparison of Steel Surface Defect Dataset
- Under the same training ratio, our proposed model significantly improves the accuracy of defect detection compared to other models. Specifically, our model improves 17.1%, 16.32%, and 3.62% (89.87% vs 72.77%, 89.87% vs 73.55%, and 89.87% vs 86.25%) compared to CenterNet + HFAM [3], Faster R-CNN + CBAM [3], and YOLO v9S [59]. (The core improvement of YOLO v9S lies in dynamic parameter adjustment and hardware adaptation optimization, which improves the adaptability and deployment efficiency of the model in complex scenarios by flexibly controlling the number of channels, module depth, and memory alignment), respectively. Some models (such as CenterNet [3] and Faster R-CNN [3]) are detected by combining attention mechanism, and experimental results show that these models have higher detection accuracy compared to other models. In contrast, we adopt multi-scale fusion features, which can extract finer feature maps.
- Our proposed model adopts the attention mechanism based on the intrinsic mean in the Lie Group manifold space and achieves the highest detection accuracy under the same training ratio. Specifically, compared to the CBAM attention mechanism, our model improves 16.32%.
- In terms of the number of parameters and FLOPs, our model has certain advantages over other models. For example, compared to YOLO v5S [3], our model parameters have decreased by . From the experimental results, we can find that our model has better computational performance and fewer parameters. Compared with other models, it can better satisfy actual production needs.
4.2.2. Results and Comparison of Railway Tracks Dataset
- We utilize multi-scale feature fusion to enhance the feature representation ability of the model at different scales. With the training ratio of 50%, the detection accuracy reaches 92.41%, which is 15.09%, 17.15%, and 19.59% higher than the baseline models CenterNet [3], Faster R-CNN [3], and SSD [3] without attention mechanism, respectively. Compared with CenteNet + HFAM [3], YOLO v9C [59], and RTMEC [3], the proposed algorith/ov9, and RTMEC [3], the proposed algorithm improves the detection accuracy by 14.49%, 2.66%, and 1.18%, respectively.
- We find that in most cases, the detection accuracy of the model with attention mechanism is higher than that of the model without attention mechanism. For example, the detection accuracy of Faster R-CNN + HFAM [3] is improved by 0.53% compared to Faster R-CNN [3]. However, in some cases, the introduction of the attention mechanism even reduces the model detection accuracy, indicating that the attention mechanism damages the performance of the model, such as Faster R-CNN + SimAM [3].
- In terms of F1 and Recall, our model improves 0.2% and 0.14%, respectively, compared with RTMEC [3]. The experimental results once again reflect the comprehensiveness of our model. Similar to the HFAM and SimAM attention mechanisms, our proposed attention mechanism based on the intrinsic mean in the Lie Group manifold space does not increase the number of parameters of the model. It should be noted that, compared with other attention mechanisms (such as CBAM and SimAM), we do not utilize hyperparameters, which is more conducive to the deployment of the model in actual production.
4.2.3. Results and Comparison of the NEU-DET Dataset
- Our model performs the best, consistent with the experimental results of the two datasets mentioned above. Specifically, our model achieves a defect detection accuracy of 82.69%, which is superior to other models. Compared with YOLO v5S [3], Faster R-CNN + HFAM [3], and RTMEC [3], the detection accuracy has been improved by 3.37%, 8.13%, and 0.93%, respectively. In addition to the advantage in detection accuracy, our model also demonstrates certain advantages in F1 and Recall metrics.
- The experimental results show that in the case of the same training ratio of data samples, compared with other attention mechanisms, our proposed attention mechanism based on the intrinsic mean in the Lie Group manifold space can help the model improve detection accuracy without increasing the number of model parameters and computational complexity. This is crucial for deployment in real production environments.
- In terms of the number of model parameters and computational performance, the experimental results further verify the superiority of our proposed model. From the experimental results, we find that in SimAM, HFAM, and our attention mechanism, the number of parameters of the model is not increased. In addition, we have advantages in detection accuracy and the number of parameters, and our method, like HFAM, does not require extensive experimentation to identify hyperparameters, which is a significant advantage for deploying the model on the edge server.
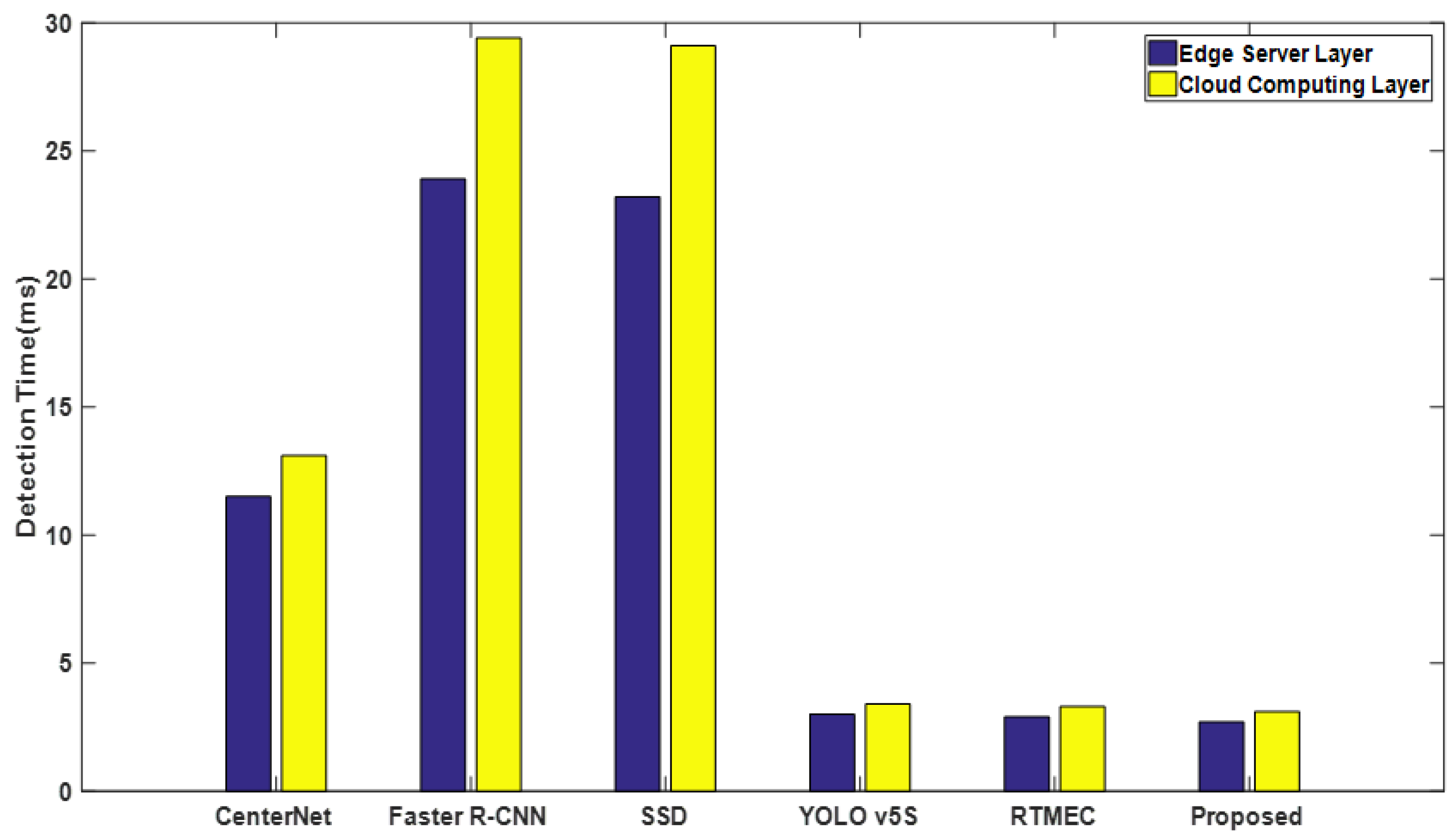
4.2.4. Comparison of Real-Time Performance of Different Detection Models
- Edge servers have significantly lower detection delay compared to the cloud computing layer. For example, Faster R-CNN [3] has a detection delay of ms on the edge servers and ms on the cloud computing layers, saving ms in detection delay. The detection delay of our model on the edge server is reduced by ms compared to the cloud computing layer. This is mainly because it takes more time and costs for the defect data samples to be transmitted from the IoT device layer to the cloud computing layer than to the edge service layer; that is, the transmission delay is caused by the longer transmission link, network bandwidth, force majeure, and other factors.
- Considering that in the actual production process, as the number of data sets collected by IoT devices continues to increase, the number of datasets sent to the cloud computing layer will also increase; the network may be congested, and the bandwidth of the network may be one of the bottleneck factors leading to low efficiency of defect detection. Therefore, from the above experimental results, it can be found that our model can effectively cope with the real-time requirements of tiny SSD.
4.3. Ablation Experiment
4.3.1. Impact of Different Modules on the Model
4.3.2. Impact of Inserting Attention Mechanism at Different Stages on the Model
4.3.3. Impact of the Loss Function on the Model
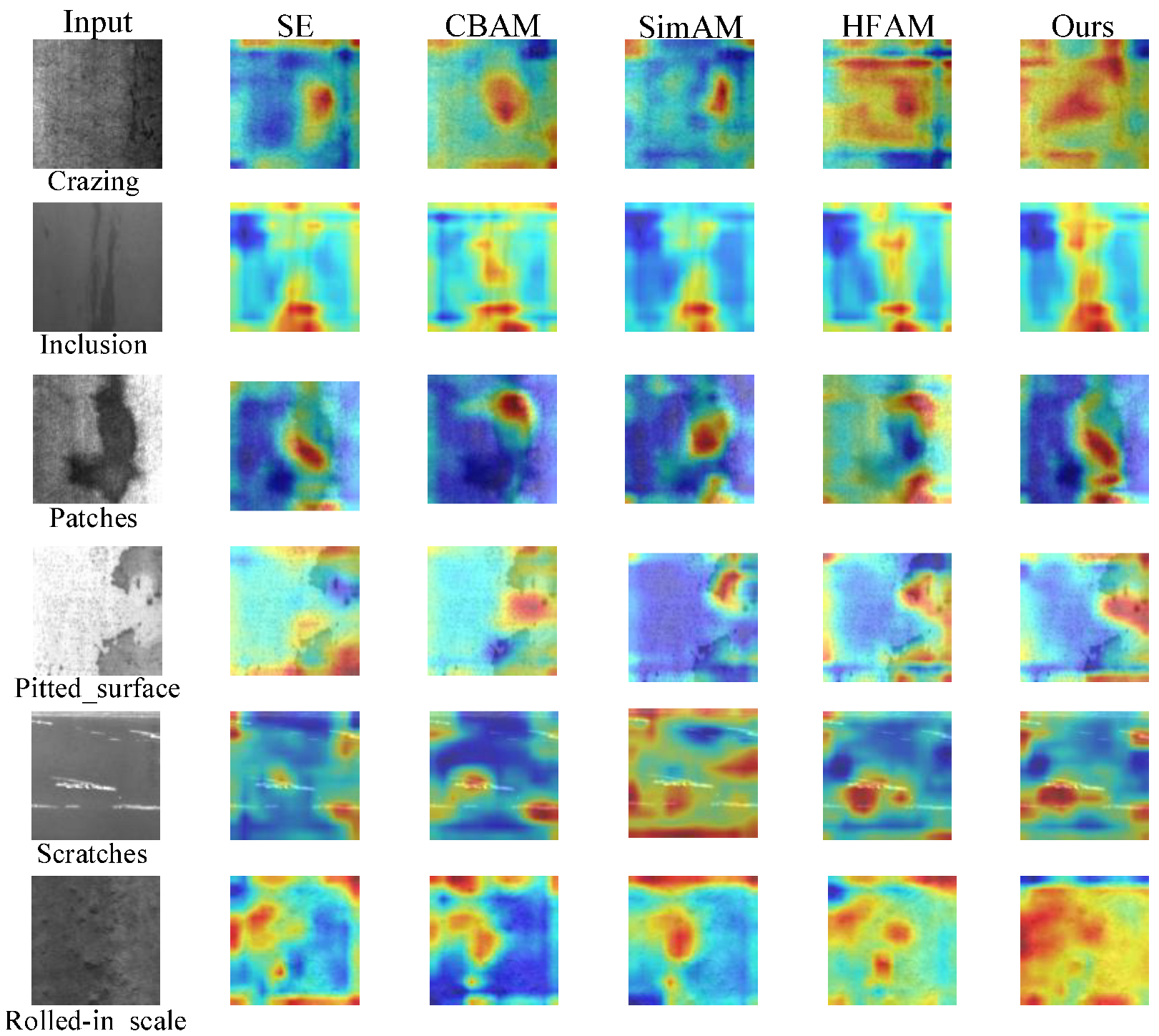
4.3.4. Visual Inspection of the Lie Group Manifold Space Attention Mechanism
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACC | Accuracy |
| AI | Artificial Intelligence |
| BN | Batch Normalization |
| CV | Computer Vision |
| FLOPs | Floating Point operations |
| IoT | Internet of Things |
| MEC | Multi-access Edge-cloud Computing |
| NLP | Natural Language Processing |
| PDConv | Parallel Dilated Convolution |
| SSD | Surface Defect Detection |
| YOLO | You Only Look Once |
References
- Zhao, Z.; Zhang, H.; Wang, L.; Huang, H. A Multimodel Edge Computing Offloading Framework for Deep-Learning Application Based on Bayesian Optimization. IEEE Internet Things J. 2023, 10, 18387–18399. [Google Scholar] [CrossRef]
- Al-Sarawi, S.; Anbar, M.; Abdullah, R.; Al Hawari, A.B. Internet of things market analysis forecasts, 2020–2030. In Proceedings of the 2020 Fourth World Conference on Smart Trends in Systems, Security and Sustainability (WorldS4), London, UK, 15–17 July 2020; pp. 449–453. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Fan, Q.; Xiong, Q.; Wang, X.; Leung, V.C.M. Transfer learning for real-time surface defect detection with multi-access edge-cloud computing networks. IEEE Trans. Netw. Serv. Manag. 2024, 21, 310–323. [Google Scholar] [CrossRef]
- Li, Z.; Duan, M.; Xiao, B.; Yang, S. A novel anomaly detection method for digital twin data using deconvolution operation with attention mechanism. IEEE Trans. Ind. Inform. 2022, 19, 7278–7286. [Google Scholar] [CrossRef]
- Wan, S.; Ding, S.; Chen, C. Edge computing enabled video segmentation for real-time traffic monitoring in internet of vehicles. Pattern Recognit. 2022, 121, 108146. [Google Scholar] [CrossRef]
- Niu, M.; Song, K.; Huang, L.; Wang, Q.; Yan, Y.; Meng, Q. Unsupervised saliency detection of rail surface defects using stereoscopic images. IEEE Trans. Ind. Inform. 2020, 17, 2271–2281. [Google Scholar] [CrossRef]
- Rakhmonov, A.A.U.; Subramanian, B.; Olimov, B.; Kim, J. Extensive knowledge distillation model: An end-to-end effective anomaly detection model for real-time industrial applications. IEEE Access 2023, 11, 69750–69761. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, L. Multi-system fusion based on deep neural network and cloud edge computing and its application in intelligent manufacturing. Neural Comput. Appl. 2022, 34, 3411–3420. [Google Scholar] [CrossRef]
- Erfani, S.M.; Rajasegarar, S.; Karunasekera, S.; Leckie, C. High-dimensional and large-scale anomaly detection using a linear one-class SVM with deep learning. Pattern Recognit. 2016, 58, 121–134. [Google Scholar] [CrossRef]
- Qiao, Y.; Wu, K.; Jin, P. Efficient anomaly detection for high-dimensional sensing data with one-class support vector machine. IEEE Trans. Knowl. Data Eng. 2021, 35, 404–417. [Google Scholar] [CrossRef]
- Mihai, S.; Yaqoob, M.; Hung, D.V.; Davis, W.; Towakel, P.; Raza, M.; Karamanoglu, M.; Barn, B.; Shetve, D.; Prasad, R.V. Digital twins: A survey on enabling technologies, challenges, trends and future prospects. IEEE Commun. Surv. Tuts. 2022, 24, 2255–2291. [Google Scholar] [CrossRef]
- Mohammed, A.S.; Venkatachalam, K.; Hubálovskỳ, S.; Trojovskỳ, P.; Prabu, P. Smart edge computing for 5G/6G satellite IoT for reducing inter transmission delay. Mob. Netw. Appl. 2022, 27, 1050–1059. [Google Scholar] [CrossRef]
- Ali, Z.; Abbas, Z.H.; Abbas, G.; Numani, A.; Bilal, M. Smart computational offloading for mobile edge computing in next-generation Internet of Things networks. Comput. Netw. 2021, 198, 108356. [Google Scholar] [CrossRef]
- Tahirkheli, A.I.; Shiraz, M.; Hayat, B.; Idrees, M.; Sajid, A.; Ullah, R.; Ayub, N.; Kim, K.-I. A survey on modern cloud computing security over smart city networks: Threats, vulnerabilities, consequences, countermeasures, and challenges. Electronics 2021, 10, 1811. [Google Scholar] [CrossRef]
- Mehedi, S.T.; Anwar, A.; Rahman, Z.; Ahmed, K.; Islam, R. Dependable intrusion detection system for IoT: A deep transfer learning based approach. IEEE Trans. Ind. Inform. 2022, 19, 1006–1017. [Google Scholar] [CrossRef]
- Singh, Y.; Biswas, A. Robustness of musical features on deep learning models for music genre classification. Expert Syst. Appl. 2022, 199, 116879. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, P.; Wang, P.; Lee, W.-J. Transfer learning featured short-term combining forecasting model for residential loads with small sample sets. IEEE Trans. Ind. Appl. 2022, 58, 4279–4288. [Google Scholar] [CrossRef]
- Ni, X.; Liu, H.; Ma, Z.; Wang, C.; Liu, J. Detection for rail surface defects via partitioned edge feature. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5806–5822. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly accurate machine fault diagnosis using deep transfer learning. IEEE Trans. Ind. Inform. 2018, 15, 2446–2455. [Google Scholar] [CrossRef]
- Li, W.; Huang, R.; Li, J.; Liao, Y.; Chen, Z.; He, G.; Yan, R.; Gryllias, K. A perspective survey on deep transfer learning for fault diagnosis in industrial scenarios: Theories, applications and challenges. Mech. Syst. Signal Process. 2022, 167, 108487. [Google Scholar] [CrossRef]
- Zhang, Q.; Han, R.; Xin, G.; Liu, C.H.; Wang, G.; Chen, L.Y. Lightweight and accurate DNN-based anomaly detection at edge. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 2927–2942. [Google Scholar] [CrossRef]
- Tang, Q.; Xie, R.; Yu, F.R.; Huang, T.; Liu, Y. Decentralized computation offloading in IoT fog computing system with energy harvesting: A Dec-POMDP approach. IEEE Internet Things J. 2020, 7, 4898–4911. [Google Scholar] [CrossRef]
- Zhu, Z.; Han, G.; Jia, G.; Shu, L. Modified densenet for automatic fabric defect detection with edge computing for minimizing latency. IEEE Internet Things J. 2020, 7, 9623–9636. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G. Intelligent manufacturing lie group machine learning: Real-time and efficient inspection system based on fog computing. J. Intell. Manuf. 2021, 32, 237–249. [Google Scholar] [CrossRef]
- Liang, S.; Wu, H.; Zhen, L.; Hua, Q.; Garg, S.; Kaddoum, G.; Hassan, M.M.; Yu, K. Edge YOLO: Real-time intelligent object detection system based on edge-cloud cooperation in autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25345–25360. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, J.; Zhang, J.; Bao, J.; Zhong, R. Edge-cloud collaborative fabric defect detection based on industrial internet architecture. In Proceedings of the 2020 IEEE 18th International Conference on Industrial Informatics (INDIN), Vienna, Austria, 28–30 July 2020; Volume 1, pp. 483–487. [Google Scholar] [CrossRef]
- Tang, W.; Yang, Q.; Hu, X.; Yan, W. Edge intelligence for smart EL images defects detection of PV plants in the IoT-based inspection system. IEEE Internet Things J. 2022, 10, 3047–3056. [Google Scholar] [CrossRef]
- Wu, H.; Wolter, K.; Jiao, P.; Deng, Y.; Zhao, Y.; Xu, M. EEDTO: An energy-efficient dynamic task offloading algorithm for blockchain-enabled IoT-edge-cloud orchestrated computing. IEEE Internet Things J. 2020, 8, 2163–2176. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef]
- Nuanmeesri, S. Enhanced hybrid attention deep learning for avocado ripeness classification on resource constrained devices. Sci. Rep. 2025, 15, 3719. [Google Scholar] [CrossRef]
- Nuanmeesri, S. Spectrum-based hybrid deep learning for intact prediction of postharvest avocado ripeness. IT Prof. 2025, 26, 55–61. [Google Scholar] [CrossRef]
- Nuanmeesri, S.; Tharasawatpipat, C.; Poomhiran, L. Transfer Learning Artificial Neural Network-based Ensemble Voting of Water Quality Classification for Different Types of Farming. Eng. Technol. Appl. Sci. Res. 2024, 14, 15384–15392. [Google Scholar] [CrossRef]
- Aboelwafa, M.M.N.; Seddik, K.G.; Eldefrawy, M.H.; Gadallah, Y.; Gidlund, M. A machine-learning-based technique for false data injection attacks detection in industrial IoT. IEEE Internet Things J. 2020, 7, 8462–8471. [Google Scholar] [CrossRef]
- Chalapathy, R.; Menon, A.K.; Chawla, S. Anomaly detection using one-class neural networks. arXiv 2018, arXiv:1802.06360. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef]
- Liu, W.; Ren, G.; Yu, R.; Guo, S.; Zhu, J.; Zhang, L. Image-adaptive YOLO for object detection in adverse weather conditions. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 22–27 February 2022; Volume 36, pp. 1792–1800. [Google Scholar] [CrossRef]
- Li, G.; Ji, Z.; Qu, X.; Zhou, R.; Cao, D. Cross-domain object detection for autonomous driving: A stepwise domain adaptative YOLO approach. IEEE Trans. Intell. Veh. 2022, 7, 603–615. [Google Scholar] [CrossRef]
- Chen, B.; Wang, X.; Bao, Q.; Jia, B.; Li, X.; Wang, Y. An unsafe behavior detection method based on improved YOLO framework. Electronics 2022, 11, 1912. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Huang, S.; Liu, Y.; Fung, C.; He, R.; Zhao, Y.; Yang, H.; Luan, Z. Hitanomaly: Hierarchical transformers for anomaly detection in system log. IEEE Trans. Netw. Serv. Manag. 2020, 17, 2064–2076. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Zhang, H.; Zhang, H.; Han, P. Log sequence anomaly detection based on local information extraction and globally sparse transformer model. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4119–4133. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y.; Zhang, X.; Cheng, W.; Chen, H.; Xiong, H. Cat: Beyond efficient transformer for content-aware anomaly detection in event sequences. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 4541–4550. [Google Scholar] [CrossRef]
- Li, S.; Liu, F.; Jiao, L. Self-training multi-sequence learning with transformer for weakly supervised video anomaly detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 22–27 February 2022; Volume 36, pp. 1395–1403. [Google Scholar] [CrossRef]
- Tuli, S.; Casale, G.; Jennings, N.R. Tranad: Deep transformer networks for anomaly detection in multivariate time series data. Proc. VLDB Endow. 2022, 15, 3373–3386. [Google Scholar] [CrossRef]
- Xu, J.; Wu, H.; Wang, J.; Long, M. Anomaly transformer: Time series anomaly detection with association discrepancy. In Proceedings of the 10th International Conference on Learning Representations (ICLR), Virtual Event, 3–7 May 2021. [Google Scholar]
- Xu, C.; Zhu, G.; Shu, J. A combination of lie group machine learning and deep learning for remote sensing scene classification using multi-layer heterogeneous feature extraction and fusion. Remote Sens. 2022, 14, 1445. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. Lie Group spatial attention mechanism model for remote sensing scene classification. Int. J. Remote Sens. 2022, 43, 2461–2474. [Google Scholar] [CrossRef]
- Xu, C.; Shu, J.; Zhu, G. Adversarial Remote Sensing Scene Classification Based on Lie Group Feature Learning. Remote Sens. 2023, 15, 914. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Cao, Y.; Shen, Y.; Tao, D. Towards data-efficient detection transformers. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 88–105. [Google Scholar] [CrossRef]
- Wan, Q.; Xiao, Z.; Yu, Y.; Liu, Z.; Wang, K.; Li, D. A hyperparameter-free attention module based on feature map mathematical calculation for remote-sensing image scene classification. IEEE Trans. Geosci. Remote Sens. 2023, 62, 5600318. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. Robust joint representation of intrinsic mean and kernel function of lie group for remote sensing scene classification. IEEE Geosci. Remote Sens. Lett. 2020, 18, 796–800. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. A lightweight intrinsic mean for remote sensing classification with lie group kernel function. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1741–1745. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Z.; Xu, H.; Darrell, T.; Wang, X. Meta-baseline: Exploring simple meta-learning for few-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 9062–9071. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. A lightweight and robust lie group-convolutional neural networks joint representation for remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5501415. [Google Scholar] [CrossRef]
- Baker, A. Matrix Groups: An Introduction to Lie Group Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Yu, H.; Li, Q.; Tan, Y.; Gan, J.; Wang, J.; Geng, Y.-a.; Jia, L. A coarse-to-fine model for rail surface defect detection. IEEE Trans. Instrum. Meas. 2018, 68, 656–666. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Yeh, I.-H.; Liao, H.-Y.M. Yolov9: Learning what you want to learn using programmable gradient information. arXiv 2024, arXiv:2402.13616. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar] [CrossRef]
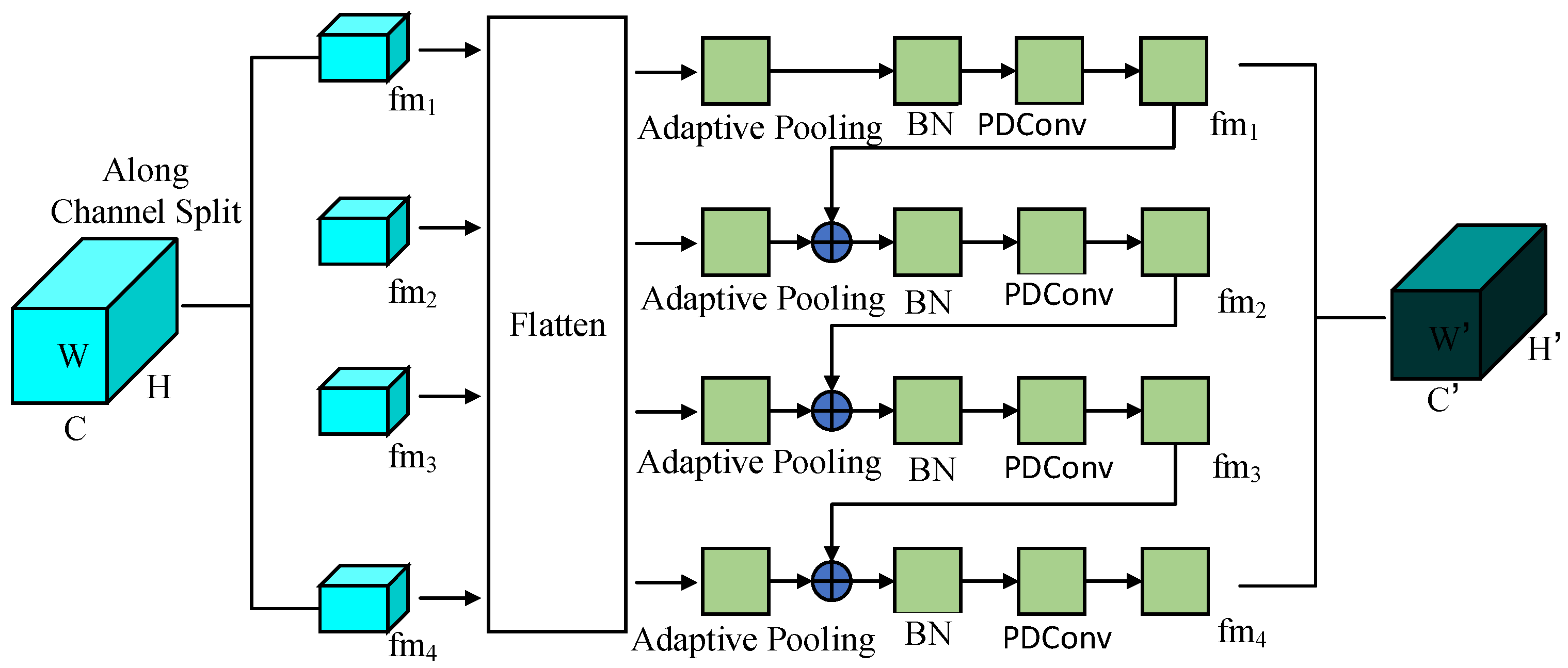

| Convolution | Kernel Size | Input Channel | Output Channel | Layer | Parameters | Total (M) |
|---|---|---|---|---|---|---|
| Traditional | 512 | 512 | Conv1 | 2,359,296 | 7,077,888 | |
| Conv2 | 2,359,296 | |||||
| Conv3 | 2,359,296 | |||||
| 512 | 512 | Conv1 | 6,553,600 | 19,600,800 | ||
| Conv2 | 6,553,600 | |||||
| Conv3 | 6,553,600 | |||||
| Parallel | 512 | 512 | Conv1 | 6,553,600 | 6,553,600 | |
| Conv2 | ||||||
| Conv3 |
| Datasets | Class | Image Number | Image per-Class | Training Ratio and Validation Ratio |
|---|---|---|---|---|
| Steel surface | 10 | 2294 | 100∼300 | 50%, 30% |
| Railway tracks | 2 | 195 | 85∼100 | 50%, 30% |
| NEU-DET | 6 | 1800 | 300 | 50%, 30% |
| Item | Content |
|---|---|
| Processor | Intel Core i7-4700 CPU with 2.70 GHz (Santa Clara, CA, USA) |
| Memory | 32 GB (Kingston: Fountain Valley, CA, USA—Headquarters) |
| Operating system | Windows 7 Pro (Microsoft: Redmond, DC, USA) |
| Hard disk | 1 T (Western Digital: San Jose, CA, USA—Headquarters) |
| Software | Matlab 2019a (MathWorks, Netik, MA, USA) |
| GPU | Nvidia Titan-X (NVIDIA, Santa Clara, CA, USA) |
| PyTorch | v1.1 (Meta AI, Menlo Park, CA, USA) |
| Batch size | 120 |
| Learning rate | 0.00326∼0.15 |
| Momentum | 0.863 |
| Weight decay | 0.000386 |
| Antenna gain | 5 dBi |
| Noise power | W |
| Transmission power | 1.0∼1.5 W |
| Wireless bandwidth | 20 Mhz |
| Methods | Param (M) | FLOPs (G) | Acc (%) | F1 (%) | Prec (%) | Recall (%) |
|---|---|---|---|---|---|---|
| CenterNet [3] | ||||||
| CenterNet + SE [3] | ||||||
| CenterNet + CBAM [3] | ||||||
| CenterNet + SimAM [3] | ||||||
| CenterNet + HFAM [3] | ||||||
| Faster R-CNN [3] | ||||||
| Faster R-CNN + SE [3] | ||||||
| Faster R-CNN + CBAM [3] | ||||||
| Faster R-CNN + SimAM [3] | ||||||
| Faster R-CNN + HFAM [3] | ||||||
| SSD [3] | ||||||
| YOLO v5S [3] | ||||||
| YOLO v9S [59] | ||||||
| YOLO v9M [59] | ||||||
| YOLO v9C [59] | ||||||
| YOLO v9E [59] | ||||||
| RTMEC [3] | ||||||
| Proposed |
| Methods | Param (M) | FLOPs (G) | Acc (%) | F1 (%) | Prec (%) | Recall (%) |
|---|---|---|---|---|---|---|
| CenterNet [3] | ||||||
| CenterNet + SE [3] | ||||||
| CenterNet + CBAM [3] | ||||||
| CenterNet + SimAM [3] | ||||||
| CenterNet + HFAM [3] | ||||||
| Faster R-CNN [3] | ||||||
| Faster R-CNN + SE [3] | ||||||
| Faster R-CNN + CBAM [3] | ||||||
| Faster R-CNN + SimAM [3] | ||||||
| Faster R-CNN + HFAM [3] | ||||||
| SSD [3] | ||||||
| YOLO v5S [3] | ||||||
| YOLO v9S [59] | ||||||
| YOLO v9M [59] | ||||||
| YOLO v9C [59] | ||||||
| YOLO v9E [59] | ||||||
| RTMEC [3] | ||||||
| Proposed |
| Methods | Param (M) | FLOPs (G) | Acc (%) | F1 (%) | Prec (%) | Recall (%) |
|---|---|---|---|---|---|---|
| CenterNet [3] | ||||||
| CenterNet + SE [3] | ||||||
| CenterNet + CBAM [3] | ||||||
| CenterNet + SimAM [3] | ||||||
| CenterNet + HFAM [3] | ||||||
| Faster R-CNN [3] | ||||||
| Faster R-CNN + SE [3] | ||||||
| Faster R-CNN + CBAM [3] | ||||||
| Faster R-CNN + SimAM [3] | ||||||
| Faster R-CNN + HFAM [3] | ||||||
| SSD [3] | ||||||
| YOLO v5S [3] | ||||||
| YOLO v9S [59] | ||||||
| YOLO v9M [59] | ||||||
| YOLO v9C [59] | ||||||
| YOLO v9E [59] | ||||||
| RTMEC [3] | ||||||
| Proposed |
| Item | GeForce RTX 3090 | GeForce RTX 2080 Ti |
|---|---|---|
| CUDA Cores | 8704 | 2944 |
| GPU Memory | 24 GB | 12 GB |
| Anacoda Version | ||
| CentOS Linux | ||
| CUDA Version | ||
| CuDNN Version | ||
| Driver Version | ||
| Enforced Power Limit | 320 W | 215 W |
| Model | Railway Racks | NEU-DET | ||||||
|---|---|---|---|---|---|---|---|---|
|
Detection Times on GPU 2080Ti (ms) |
Detection Times on GPU 3090 (ms) |
FPS on GPU 2080Ti (Hz) |
FPS on GPU 3090 (Hz) |
Detection Times on GPU 2080Ti (ms) |
Detection Times on GPU 3090 (ms) |
FPS on GPU 2080Ti (Hz) |
FPS on GPU 3090 (Hz) | |
| CenterNet [3] | 11.7 | 10.4 | 89.3 | 96.2 | 13.1 | 11.5 | 71.37 | 79.76 |
| Faster R-CNN [3] | 27.5 | 23.8 | 37.7 | 46.6 | 29.4 | 23.9 | 11.8 | 14.9 |
| SSD [3] | 26.8 | 22.4 | 43.86 | 44.6 | 29.1 | 23.2 | 59.72 | 66.87 |
| YOLO v5S [3] | 2.7 | 2.4 | 384.6 | 416.7 | 3.4 | 3.0 | 133.7 | 148.2 |
| RTMEC [3] | 3.2 | 2.8 | 312.5 | 357.1 | 3.3 | 2.9 | 118.4 | 131.5 |
| Proposed | 2.5 | 2.1 | 387.2 | 419.2 | 3.1 | 2.7 | 119.7 | 151.6 |
| Component | Acc (%) | F1 (%) | Prec (%) | Recall (%) |
|---|---|---|---|---|
| Feature Extraction | 77.23 | 53.27 | 61.17 | 53.67 |
| Lie Group intrinsic mean attention mechanism | 79.63 | 65.26 | 65.11 | 65.52 |
| Lie Group spatial space | 80.75 | 67.31 | 69.35 | 65.53 |
| Original Model | 80.93 | 69.67 | 72.35 | 68.37 |
| Updated Model | 82.69 | 78.61 | 79.97 | 78.76 |
| Methods | Stage1 | Stage2 | Stage3 | Stage4 | Stage5 | ACC (%) | F1 (%) | Prec (%) | Recall (%) |
|---|---|---|---|---|---|---|---|---|---|
| Ours | ✓ | 78.15 | 66.36 | 63.28 | 62.78 | ||||
| ✓ | ✓ | 79.33 | 68.47 | 69.86 | 67.62 | ||||
| ✓ | ✓ | ✓ | 80.46 | 70.52 | 68.16 | 66.73 | |||
| ✓ | ✓ | ✓ | ✓ | 81.52 | 72.76 | 71.97 | 70.82 | ||
| ✓ | ✓ | ✓ | ✓ | ✓ | 82.69 | 78.61 | 79.91 | 78.76 |
| Loss Function | Railway Racks | NEU-DET | ||||||
|---|---|---|---|---|---|---|---|---|
| Acc (%) | F1 (%) | Prec (%) | Recall (%) | Acc (%) | F1 (%) | Prec (%) | Recall (%) | |
| Cross-Entopy Loss | 90.36 | 78.39 | 78.68 | 76.41 | 80.97 | 77.39 | 77.67 | 76.82 |
| Our Proposed Loss | 92.41 | 78.57 | 79.77 | 77.65 | 82.69 | 78.61 | 79.91 | 78.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Shu, J.; Wang, Z.; Wang, J. Lie Group Intrinsic Mean Feature Detectors for Real-Time Industrial Surface Defect Detection. Symmetry 2025, 17, 612. https://doi.org/10.3390/sym17040612
Xu C, Shu J, Wang Z, Wang J. Lie Group Intrinsic Mean Feature Detectors for Real-Time Industrial Surface Defect Detection. Symmetry. 2025; 17(4):612. https://doi.org/10.3390/sym17040612
Chicago/Turabian StyleXu, Chengjun, Jingqian Shu, Zhenghan Wang, and Jialin Wang. 2025. "Lie Group Intrinsic Mean Feature Detectors for Real-Time Industrial Surface Defect Detection" Symmetry 17, no. 4: 612. https://doi.org/10.3390/sym17040612
APA StyleXu, C., Shu, J., Wang, Z., & Wang, J. (2025). Lie Group Intrinsic Mean Feature Detectors for Real-Time Industrial Surface Defect Detection. Symmetry, 17(4), 612. https://doi.org/10.3390/sym17040612





