Modeling the Digestion Process by a Distributed Delay Differential System
Abstract
1. Introduction
2. Model Formulation
- (A1)
- , ;
- (A2)
- for , ;
- (A3)
- For each fixed k, there is a positive real number , which is related to k, such that
3. Global Stability of and
4. Permanence
5. Stability of
5.1. The Weak Kernel
5.2. The Strong Kernel
5.3. The Delta Kernel
5.4. The Uniform Distribution
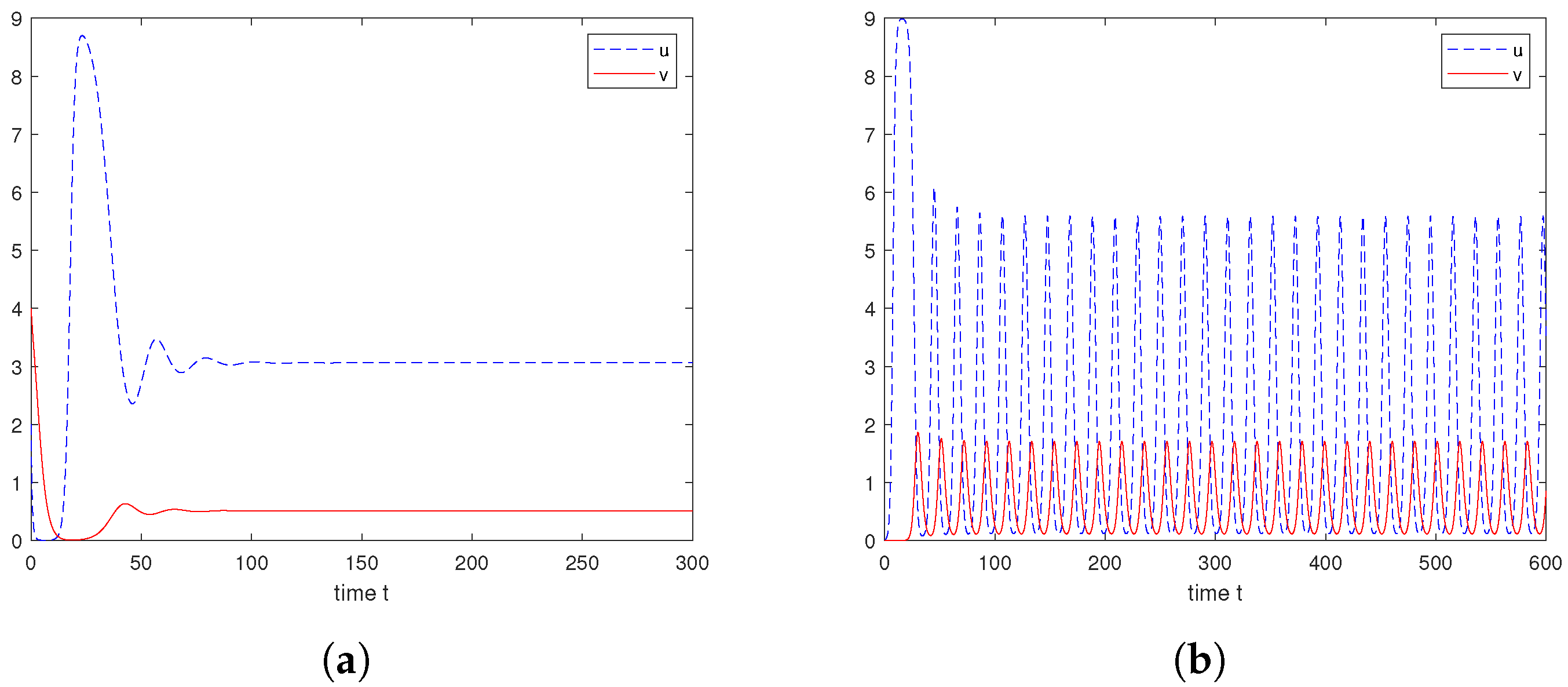
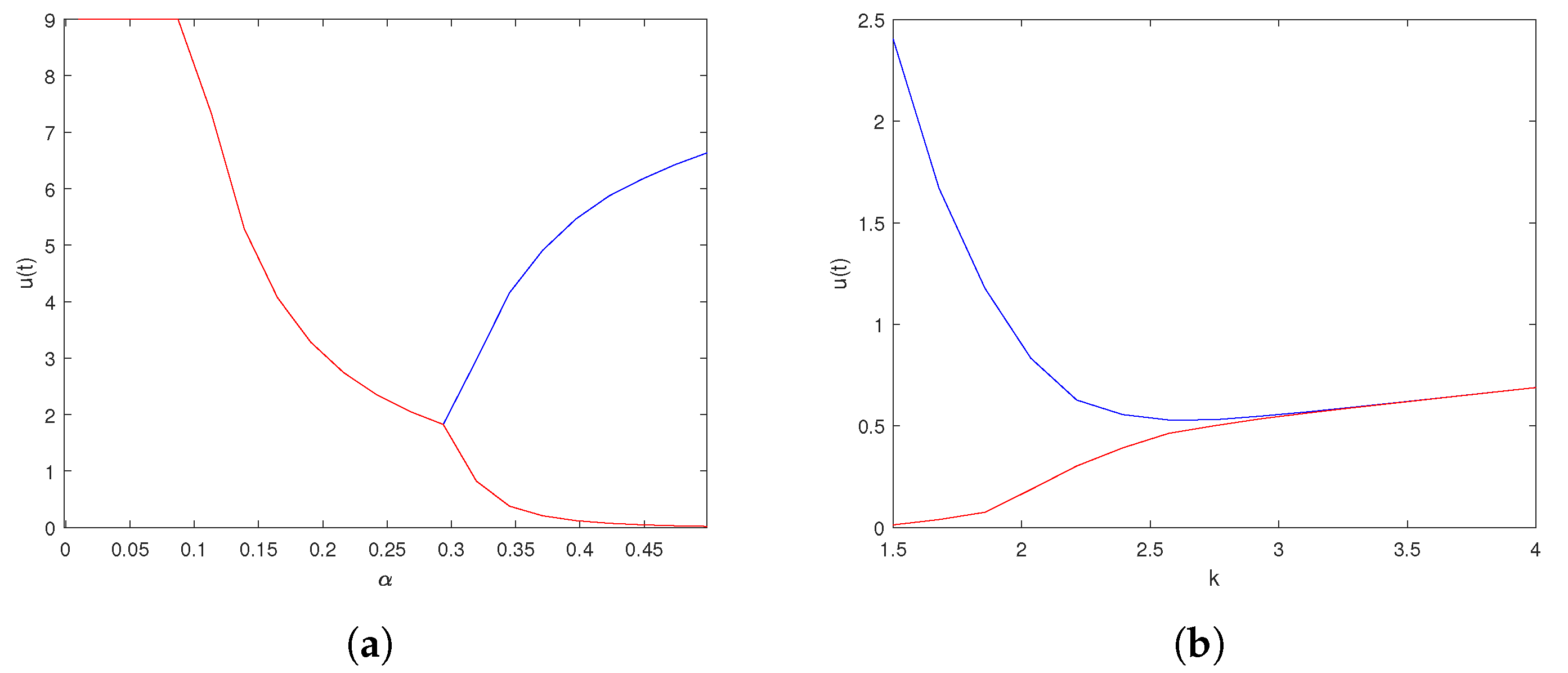
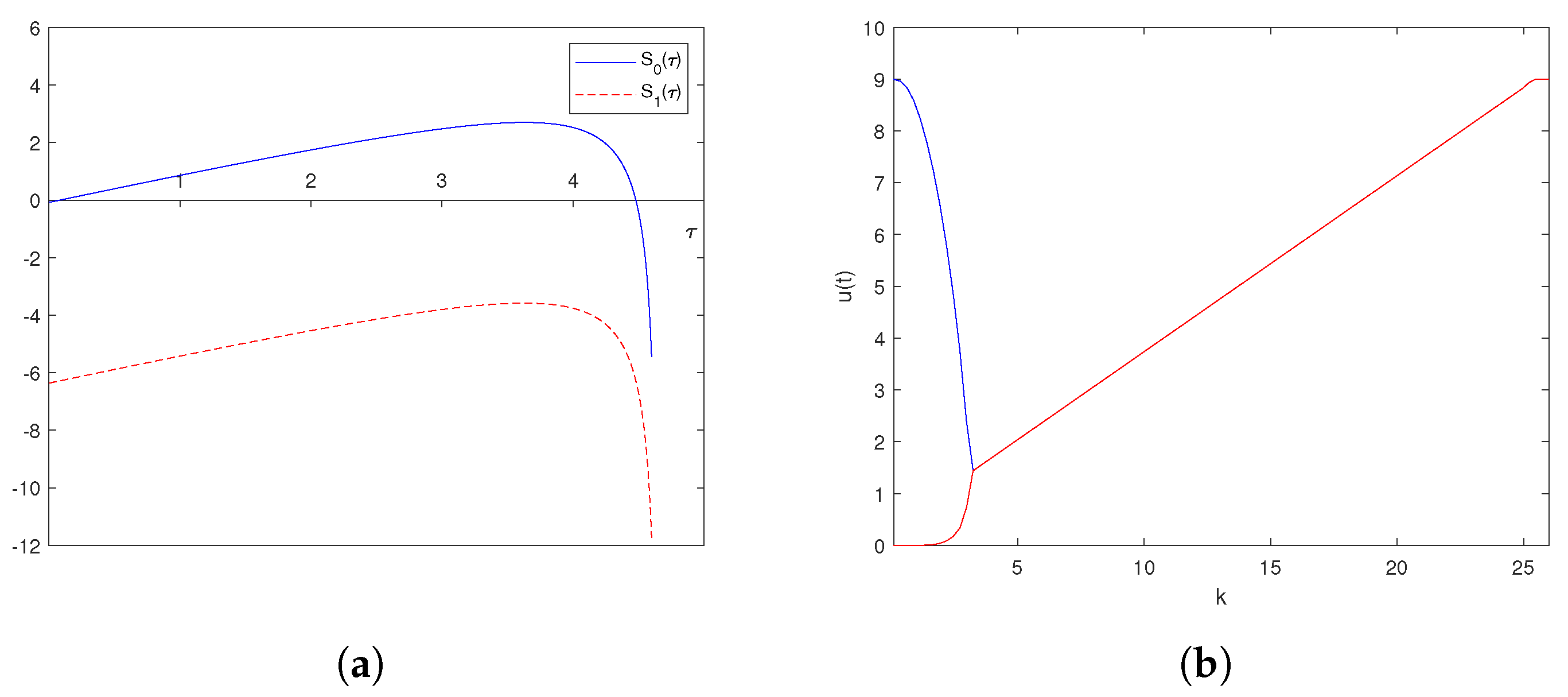
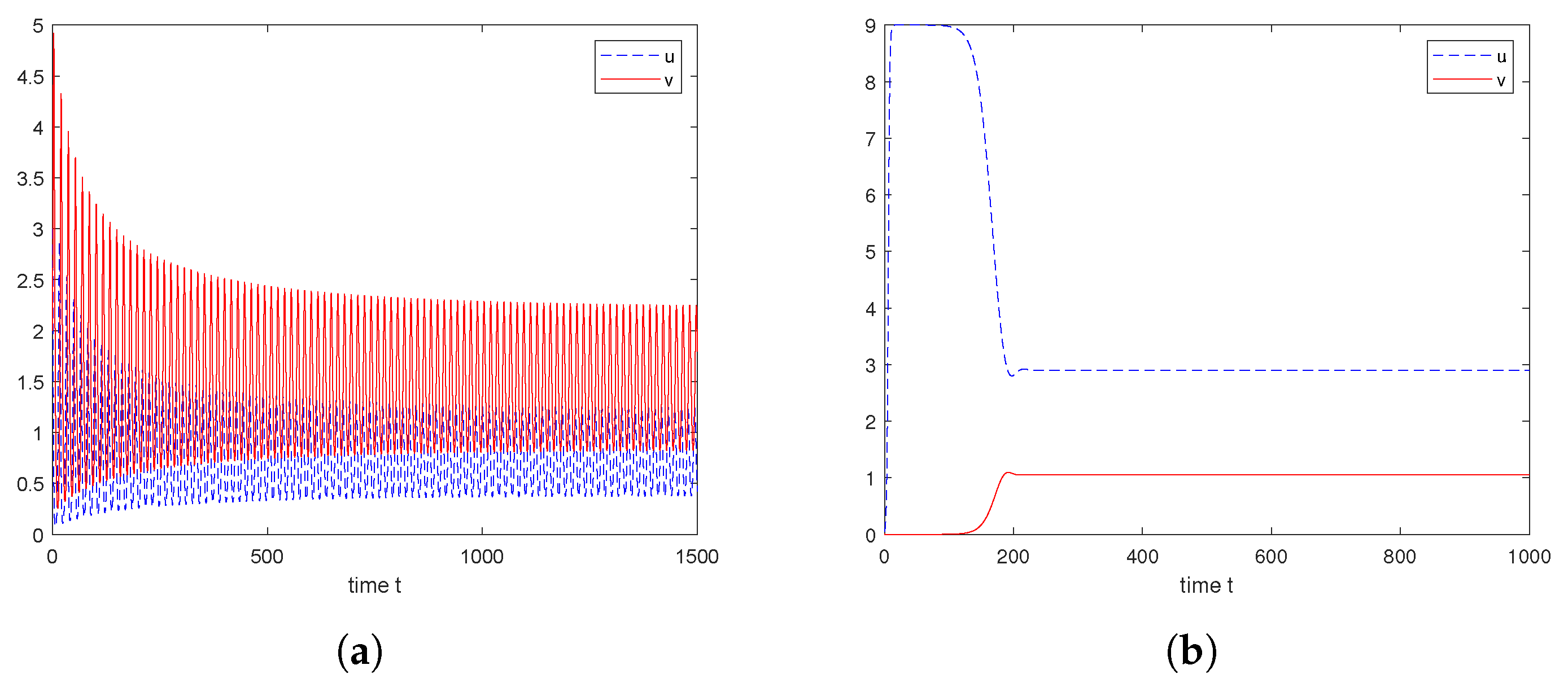
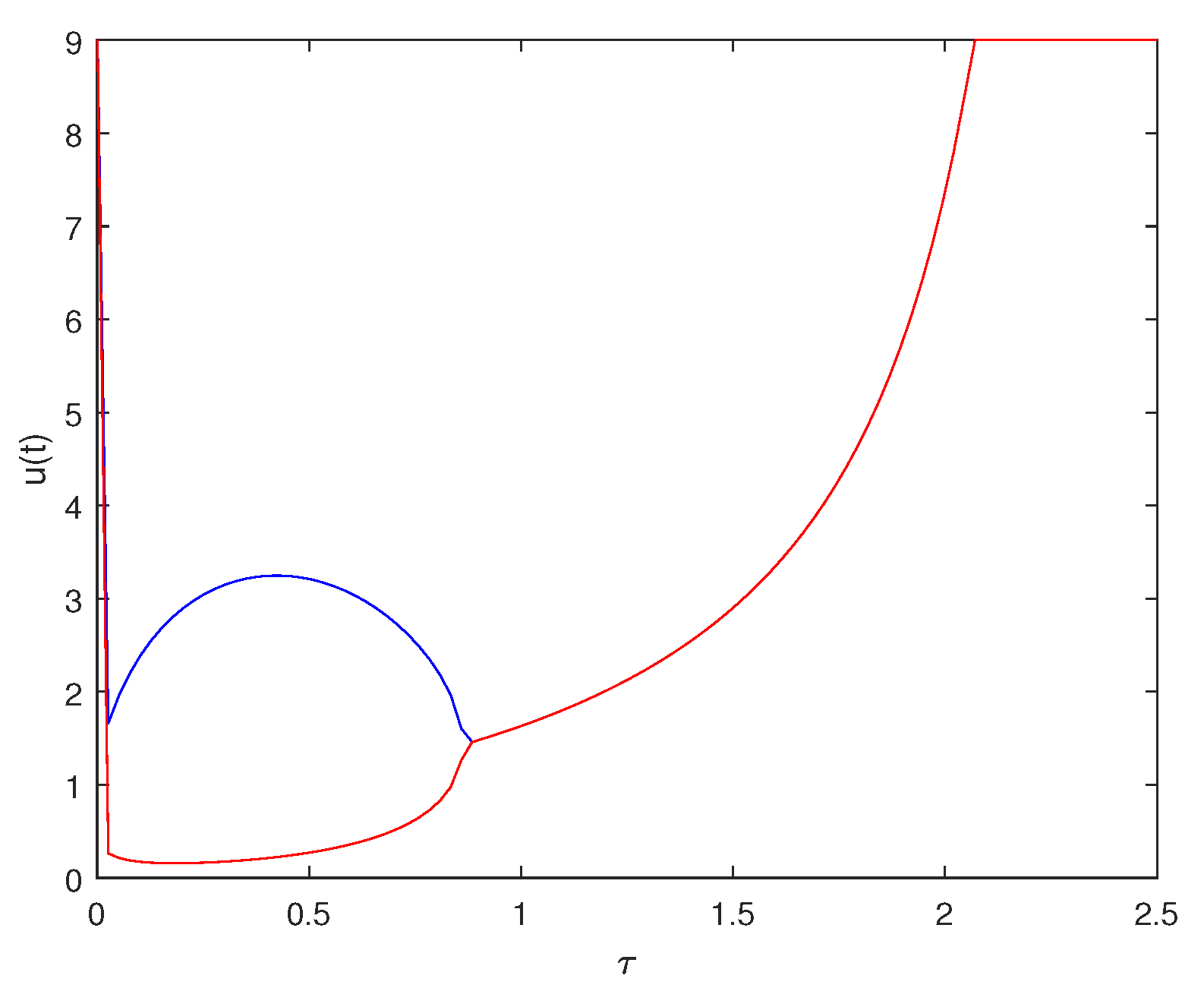
6. Numerical Explorations
7. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Creel, S.; Christianson, D.; Liley, S.; Winnie, J.A., Jr. Predation risk affects reproductive physiology and demography of elk. Science 2007, 315, 960. [Google Scholar] [CrossRef] [PubMed]
- Suraci, J.P.; Clinchy, M.; Dill, L.M.; Roberts, D.; Zanette, L.Y. Fear of large carnivores causes a trophic cascade. Nat. Commun. 2016, 7, 10698. [Google Scholar] [CrossRef]
- Zanette, L.Y.; White, A.F.; Allen, M.C.; Clinchy, M. Perceived predation risk reduces the number of offspring songbirds produce per year. Science 2011, 334, 1398–1401. [Google Scholar] [CrossRef]
- Wang, X.; Zanette, L.; Zou, X. Modelling the fear effect in predator-prey interactions. J. Math. Biol. 2016, 73, 1179–1204. [Google Scholar] [CrossRef]
- Holling, C.S. The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Ent. Soc. Can. 1965, 97, 1–60. [Google Scholar] [CrossRef]
- Wang, X.; Zou, X. Modeling the fear effect in predator-prey interactions with adaptive avoidance of predators. Bull. Math. Biol. 2017, 79, 1325–1359. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zou, X. On a predator-prey system with digestion delay and anti-predation strategy. J. Nonlinear Sci. 2020, 30, 1579–1605. [Google Scholar] [CrossRef]
- Sasmal, S.K.; Takeuchi, Y. Dynamics of a predator-prey system with fear and group defense. J. Math. Anal. Appl. 2020, 481, 123471. [Google Scholar] [CrossRef]
- Hossain, M.; Pal, N.; Samanta, S. Impact of fear on an eco-epidemiological model. Chaos Solitons Fractals 2020, 134, 109718. [Google Scholar] [CrossRef]
- Mishra, S.; Upadhyay, R.K. Strategies for the existence of spatial patterns in predator-prey communities generated by cross-diffusion. Nonlinear Anal. Real World Appl. 2020, 51, 103018. [Google Scholar] [CrossRef]
- Ma, T.; Meng, X. Global analysis and Hopf-bifurcation in a cross-diffusion prey-predator system with fear effect and predator cannibalism. Math. Biosic. Eng. 2022, 19, 6040–6071. [Google Scholar] [CrossRef]
- Li, Y. Global steady-state bifurcation of a diffusive Leslie-Gower model with both-density-dependent fear effect. Commun. Nonlinear Sci. Numer. Simulat. 2025, 141, 108477. [Google Scholar] [CrossRef]
- Cong, P.; Fan, M.; Zou, X. Dynamics of a three-species food chain model with fear effect. Commun. Nonlinear Sci. Numer. Simulat. 2021, 99, 105809. [Google Scholar] [CrossRef]
- Li, A.; Zou, X. Evolution and adaptation of anti-predation response of prey in a two-patchy environment. Bull. Math. Biol. 2021, 83, 59. [Google Scholar] [CrossRef]
- Panday, P.; Pal, N.; Samanta, S.; Tryjanowski, P.; Chattopadhyay, J. Dynamics of a stage-structured predator-prey model: Cost and benefit of fear-induced group defense. J. Theor. Biol. 2021, 528, 110846. [Google Scholar] [CrossRef]
- Liu, C.; Chen, Y.; Yu, Y.; Wang, Z. Bifurcation and stability analysis of a new fractional-order prey-predator model with fear effects in toxic injections. Mathematics 2023, 11, 4367. [Google Scholar] [CrossRef]
- Li, Y.; He, M.; Li, Z. Dynamics of a ratio-dependent Leslie-Gower predator-prey model with Allee effect and fear effect. Math. Comput. Simul. 2022, 201, 417–439. [Google Scholar] [CrossRef]
- Teslya, A.; Wolkowicz, G.S.K. Dynamics of a predator-prey model with distributed delay to represent the conversion process or maturation. Differ. Equat. Dyn. Sys. 2023, 31, 613–649. [Google Scholar] [CrossRef]
- Driver, R.D. Existence and stability of solutions of a delay-differential system. Arch. Ration. Mech. Anal. 1962, 10, 401–426. [Google Scholar] [CrossRef]
- Lin, C.J.; Wang, L.; Wolkowicz, G.S.K. An alternative formulation for a distributed delayed logistic equation. Bull. Math. Biol. 2018, 80, 1713–1735. [Google Scholar] [CrossRef]
- Yuan, Y.; Blair, J. Threshold dynamics in an SEIRS model with latency and temporary immunity. J. Math. Biol. 2014, 69, 875–904. [Google Scholar] [CrossRef] [PubMed]
- Wolkowicz, G.S.K.; Xia, H.; Wu, J. Global dynamics of a chemostat competition model with distributed delay. J. Math. Biol. 1999, 38, 285–316. [Google Scholar] [CrossRef]
- Gourley, S.A.; Ruan, S. Spatio-temporal delays in a nutrient-plankton model on a finite domain: Linear stability and bifurcations. Appl. Math. Comput. 2003, 145, 391–412. [Google Scholar] [CrossRef]
- Deng, J.; Shu, H.; Wang, L.; Wang, X.S. Viral dynamics with immune responses: Effects of distributed delays and Filippov antiretroviral therapy. J. Math. Biol. 2023, 86, 37. [Google Scholar] [CrossRef] [PubMed]
- Shu, H.; Chen, Y.; Wang, L. Impacts of the cell-free and cell-to-cell infection modes on viral dynamics. J. Dyn. Diff. Equat. 2018, 30, 1817–1836. [Google Scholar] [CrossRef]
- Beretta, E.; Kuang, Y. Geometric stability switch criteria in delay differential systems with delay dependent parameters. SIAM J. Math. Anal. 2002, 33, 1144–1165. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Guo, Z.; Guo, H. Modeling the Digestion Process by a Distributed Delay Differential System. Symmetry 2025, 17, 604. https://doi.org/10.3390/sym17040604
Liu J, Guo Z, Guo H. Modeling the Digestion Process by a Distributed Delay Differential System. Symmetry. 2025; 17(4):604. https://doi.org/10.3390/sym17040604
Chicago/Turabian StyleLiu, Junli, Zhenghua Guo, and Hui Guo. 2025. "Modeling the Digestion Process by a Distributed Delay Differential System" Symmetry 17, no. 4: 604. https://doi.org/10.3390/sym17040604
APA StyleLiu, J., Guo, Z., & Guo, H. (2025). Modeling the Digestion Process by a Distributed Delay Differential System. Symmetry, 17(4), 604. https://doi.org/10.3390/sym17040604




