Abstract
In the dynamically evolving field of collective computational optimization, modern approaches increasingly incorporate bio-inspired techniques, such as Smell Agent Optimization (SAO), to address complex, high-dimensional problems inherent to contemporary scientific and industrial applications. While these methods are distinguished by their dynamic convergence and heuristic ability to explore vast solution spaces, their growing computational complexity hinders their application in real-world, large-scale scenarios where simultaneous speed and precision are critical. To overcome this challenge, the present research advances a pioneering parallel implementation of SAO, which transcends simple workload distribution by integrating dynamic collaboration mechanisms and intelligent information dispersal among autonomous subpopulations. Concurrently, the method is enriched with innovative rules for exchanging optimal solutions between subpopulations. These rules not only prevent premature convergence to local minima but also establish a continuous flow of information that accelerates the global exploration of the solution space. Experimental validation of the proposed method demonstrated that, through optimized parameterization of the diffusion mechanisms, SAO’s efficiency can exceed 50%, achieving simultaneous reductions in both the number of objective function evaluations and total execution time. This outcome holds particular significance in high-dimensional problems, where balancing computational cost and accuracy is a decisive factor. These findings not only underscore the potential of parallel SAO to deliver sustainable solutions to real-world challenges but also open new horizons in the theory and practice of collective optimization. The implications extend to domains such as large-scale data analysis, autonomous systems, and adaptive resource management, where rapid and precise optimization is paramount.
1. Introduction
The core objective of global optimization is to identify the global minimum of a continuous and differentiable function , where S is a compact subset of . Mathematically, this task is defined as finding the point that satisfies
where represents the unique global minimizer of f over the domain S. The feasible region S is explicitly defined as an n-dimensional hyperrectangle, constructed by the Cartesian product of closed intervals in each dimension:
Here, and denote the lower and upper bounds, respectively, of the i-th variable , ensuring S is a closed and bounded set.
Global optimization constitutes a fundamental component of science and technology, providing essential tools for solving complex problems and improving systems across a wide range of scientific disciplines. It plays a pivotal role in numerous fields: in mathematics, it is used to find solutions to complex functions [1,2]; in physics, it helps identify the ground state of systems [3,4]; in chemistry, it supports the design of new molecules and chemical processes [5,6]; in medicine, it advances therapeutic methods [7,8]; in biology, it enables the application of artificial intelligence models and optimization algorithms in plant cell and tissue culture [9,10]; in agriculture, it facilitates the use of advanced computational methods to optimize the movement of agricultural machinery, for example, in sugarcane production [11,12]; and in economics, it contributes to comprehensive techno-economic Analyses such as the optimization of compressed air energy storage (CAES) systems [13,14].
The methods used for global optimization are generally categorized into two main classes: deterministic and stochastic approaches. Deterministic methods rely on strict mathematical models and aim to find the optimal solution with guaranteed accuracy. These include techniques such as interval methods [15,16] and algorithms based on branch-and-bound theory [17,18]. While theoretically powerful, such approaches often become computationally impractical for large-scale or highly complex problems due to their exponential computational cost. In contrast, stochastic methods are based on random processes and are often inspired by natural, biological [19,20], or social phenomena. This category includes a wide variety of algorithms such as Genetic Algorithms (GAs) [21,22], Differential Evolution (DE) [23,24], Controlled Random Search methods [25,26], Simulated Annealing (SA) [27,28], methods based on the Multistart technique [29,30], Particle Swarm Optimization (PSO) [31,32] and the Fish Swarm Algorithm [33,34], as well as more recent heuristics inspired by the behavior of living organisms. Examples include the Dolphin Swarm Algorithm (DSA) [35,36], Whale Optimization Algorithm (WOA) [37,38], Ant Colony Optimization [39,40], Aquila Optimizer [41,42,43], Arithmetic Optimization Algorithm (AOA) [44,45,46] and the Smell Agent Optimization (SAO) [47,48,49]. Stochastic methods offer greater flexibility and are particularly well suited for nonlinear, high-dimensional, or noisy objective functions where deterministic techniques often fail to perform adequately. The SAO belongs to the class of swarm intelligence algorithms [50,51], drawing inspiration from the way organisms detect and follow odor trails in their environment. The search process is performed by agents that move within the solution space, guided by the “intensity of smell”, which corresponds to the quality of the solution. SAO has already demonstrated effectiveness across various application domains, including microgrid energy management [52], vehicle routing [53], medical imaging [54], and machine learning [55]. The proposed parallel variant of SAO incorporates parallelization techniques by distributing the computational workload across multiple processing units. The core principle involves dividing the population into sub-populations, which operate independently and periodically collaborate through solution-sharing strategies. This cooperative approach aims to maintain diversity and enhance global exploration without sacrificing local exploitation. The optimization process continues until the termination criterion is satisfied.
- The proposed stop rule is based on his work Charilogis and Tsoulos [56], giving excellent results when applied to a number of well-known optimization problems. However, the proposed termination technique Section 2.4 is modified to be suitable for parallel computing environments, thus optimizing computing performance.
- Finally, a local search refinement step is implemented. In the current work, a variant of BFGS [57] was used as a local search procedure. The integration of the BFGS variant into the SAO algorithm serves as a localized exploitation mechanism, which is activated at selected points in time or for specific agents that are close to promising solutions. The use of BFGS can accelerate convergence toward local optima by providing faster improvement in regions where the stochastic search has already identified high-quality candidates. However, its coexistence with the stochastic phases of SAO requires careful balancing. If triggered too early or too frequently, there is a risk of overfitting to local optima and a reduction in population diversity, which may lead to premature convergence. To prevent this, it is advisable to apply BFGS only when specific stability or solution quality criteria are met and to accompany its use with mechanisms that maintain active exploration of the search space, ensuring a balance between exploitation and exploration.
Modern metaheuristic algorithms like the Musical Chairs Algorithm (MCA) [58] and Nested Particle Swarm Optimization (NESTPSO) [59] offer complementary approaches to parallel SAO. MCA introduces a dynamic competitive mechanism that forces solution diversification through systematic exclusion from promising regions, making it particularly effective for problems with complex local optima, though at increased computational cost in high-dimensional spaces. Conversely, NESTPSO implements a hierarchical search structure enabling gradual solution refinement by combining broad exploration with detailed exploitation. While superior for problems with convergence traps, its added complexity may limit scalability for large-scale problems. Compared to these, parallel SAO maintains key advantages in implementation simplicity and scalability through autonomous subpopulations. However, its specific weaknesses in certain problem types highlight opportunities for enhancement. Promising directions include incorporating MCA-inspired competitive elements to strengthen exploration and adopting NESTPSO-like hierarchical mechanisms to improve exploitation. These developments reflect the field’s ongoing evolution toward flexible, adaptive algorithms capable of addressing real-world optimization complexity. The strategic integration of these approaches’ strengths could yield next-generation metaheuristics with superior performance and versatility across diverse problem domains.
The remainder of this paper is divided as follows: in Section 2, the original Differential Evolution algorithm, the proposed method, and the flowchart with detailed description are presented; in Section 3, the test functions used in the experiments, as well as the related experiments, are presented; in Section 4, there is a brief discussion of the results obtained from the experiments; and in Section 5, some conclusions and directions for future improvements are discussed.
2. Materials and Methods
2.1. The Original SAO
The above pseudocode Algorithm 1 describes the operation of the SAO algorithm. The process begins with parameter initialization, including the iteration counter , the number of molecules (m), the maximum allowed iterations , the local search rate (), the stopping rule (Section 2.4) method based on the similarity of the optimal solution, and the integer parameter defining the maximum similarity count for . Initially, the positions of the molecules () are uniformly distributed in the search space , and the best () and worst () positions are determined based on the objective function . During the iterative process (while or is active), each molecule updates its velocity () and position () via the Sniffing Mode for each problem dimension. The fitness of the molecules is then re-evaluated, updating the best and worst positions if improved performance is observed. This is followed by the Trailing Mode, where the molecules’ positions are updated with stochastic modifications, and fitness is re-evaluated. If no improvement is detected, the molecules enter the Random Mode, where their positions are randomly perturbed to avoid stagnation. In this phase, a random number is generated. If , a local search procedure using the BFGS variant of Powell’s method is applied to refine the current position. The iterative process continues until the termination criteria (e.g., maximum iterations or solution homogeneity) are met, at which point the globally optimal solution is returned. The algorithm combines three modes (Sniffing, Trailing, Random) to balance exploration and exploitation of the search space, while the integration of stochastic and deterministic optimizations (e.g., BFGS) enhances convergence efficiency.
2.2. The Parallel Algorithm of SAO
The parallel pseudocode (Algorithm 2) of the SAO algorithm describes the distribution of the algorithm across N subpopulations that operate in parallel. Initially, all agents are initialized within the search space S, with parameters such as the number of subpopulations (N), the propagation method (), the propagation rate (), the number of agents involved in propagation (), and the termination criterion ().
Each subpopulation independently executes the core steps of the basic algorithm (Sniffing, Trailing, and Random Modes). At regular intervals (every iterations), the propagation strategy is applied, where agents exchange optimal solutions between randomly selected subpopulations. This enhances solution diversity and prevents convergence to local optima.
The process repeats until the termination criterion is satisfied (e.g., when a specific number of subpopulations have converged). Finally, a local search procedure (e.g., BFGS) is applied to the globally optimal solution () for further refinement.
The flowchart in Figure 1 analyzes the operation of a parallel implementation of the SAO algorithm, which utilizes multiple processing units (PUs) to accelerate the discovery of optimal solutions for complex problems. The process begins with the systematic initialization of controlled parameters, including population size, number of subpopulations, convergence coefficients, etc. Subsequently, the main population is partitioned into N distinct subpopulations, assigned to independent PUs. This decentralized architecture enables the simultaneous exploration of multiple search subspaces, aiming to maximize solution diversity and minimize the risk of entrapment in local optima. Each PU independently executes a sequence of computational steps in every iteration. First, a fitness array is calculated, quantifying the performance of each candidate solution based on the problem’s objective function. Next, the positions of the solutions are updated through three distinct operational modes:
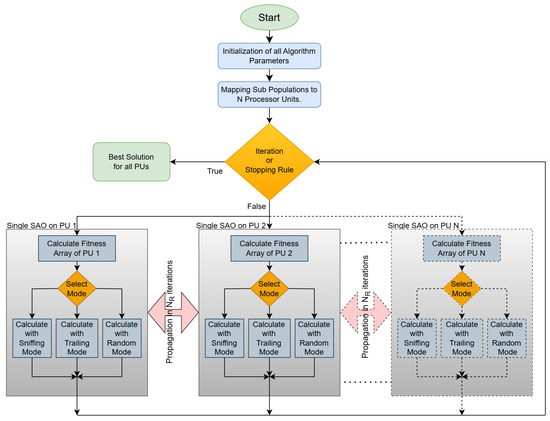
Figure 1.
Flowchart of parallel SAO.
- Sniffing Mode: Simulates an “information-gathering” process from neighboring solutions, intensifying exploitation around high-fitness regions.
- Trailing Mode: Applies stochastic variations to solutions, ensuring exploration of new areas in the search space.
- Random Mode: Introduces random perturbations to solution positions, preventing stagnation and enhancing population diversity.
Furthermore, within the parallel architecture, a periodic propagation mechanism for optimal solutions between subpopulations is implemented. This strategy, explained in Section 2.3, is based on collaboration rules that regulate the frequency and extent of information exchange. For instance, at regular intervals, PUs may exchange their locally optimal solutions, forming a dynamic communication network that strengthens global convergence. The choice of the optimal propagation strategy depends on the problem’s nature and the balance requirements between computational cost and accuracy. The iterative process concludes with the evaluation of predefined termination criteria, such as the maximum number of iterations or the homogeneity of the optimal solution. If none of these criteria are met, the algorithm repeats the process; otherwise, it returns the globally optimal solution.
| Algorithm 1 The base algorithm of SAO |
|
| Algorithm 2 The parallel algorithm of SAO |
Initialization.
Main Step For k = 1, …, N do in Parallel
If iter mod = 0, apply the propagation scheme with agents to the subpopulations.
Apply local search procedure to . |
The image in Figure 2 illustrates the parallelization of the SAO method and the information dissemination strategies among subpopulations. Each thread (Thread 1, 2, …, N) corresponds to an independent PU managing a subpopulation (SubCluster 1, 2, …, N). Each subpopulation operates in parallel, exploring distinct regions of the search space, while simultaneously exchanging information with other subpopulations via predefined strategies, as explained in Section 2.3. A core dissemination strategy is 1to1 (one-to-one), where a randomly selected subpopulation sends a specific number of optimal solutions (e.g., locally optimal positions) to another randomly chosen subpopulation. This exchange occurs periodically or under predefined conditions to enhance solution diversity and avoid convergence to local optima. For instance, if SubCluster 1 discovers a high-quality solution, transmitting it to SubCluster 3 could accelerate global convergence. Beyond 1to1, other strategies may be applied, such as NtoN (all-to-all), where all subpopulations exchange information simultaneously. In all cases, the dissemination of optimal solutions serves as a cooperative optimization mechanism. Even if a subpopulation becomes trapped in a local optimum, the introduction of external solutions through dissemination can “free” it. Additionally, the randomization in subpopulation selection (as in 1to1) ensures the process remains dynamic and adaptable. This combination of parallel execution and strategic information sharing improves the SAO method’s efficiency, particularly in large-scale or non-linear optimization problems by balancing exploration and exploitation while mitigating computational stagnation.
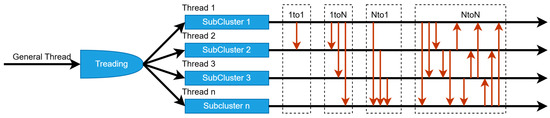
Figure 2.
Thread creation diagram and propagation methods.
The SAO algorithm is based on the idea of a population of agents that move through the search space according to specific rules and adjust their behavior based on their experience and the information they receive from the environment or other agents. The operation of SAO involves two main phases: exploration and exploitation. In the exploration phase, the agents move with the goal of covering as much of the search space as possible, testing different regions and increasing the diversity of solutions. Movement in this phase is based on large steps and a high degree of stochasticity, aiming to avoid premature convergence. In the exploitation phase, the agents’ movement focuses on promising regions, with smaller and more targeted steps, to accurately locate local or global optima. The transition from the exploration phase to the exploitation phase is implemented via a control mechanism that monitors the stagnation of solutions or the rate of improvement in the objective function’s value. For example, if no improvement beyond a predefined threshold is observed for a number of consecutive steps, the exploitation phase is activated. Alternatively, the transition can be based on a gradual change in parameters, such as reducing the variance of a stochastic movement term. The movement of agents within the search space is determined by a combination of stochastic and directed components. Specifically, each agent tends to move toward the best-known solution up to that point, while also maintaining a degree of randomness in its path. This randomness allows it to continue exploring new regions of the space and avoid premature trapping in local optima. The intensity with which it follows the best-known solution, as well as the amount of randomness incorporated into its movement, is automatically adjusted during the process. Thus, when an agent performs well, its tendency to move toward improved solutions is reinforced, while in cases of low performance, the degree of exploration is increased to identify alternative regions that may contain better solutions. In this way, the movement is dynamic and self-adjusting based on each agent’s experience, contributing to the overall effectiveness of the algorithm. Information propagation among agents occurs through a mechanism that exchanges the best solution found either by the agent itself or by its neighbors, depending on the communication topology used. In a fully connected network, all agents are immediately updated with the population’s best solution, which accelerates convergence but may limit diversity. The frequency of propagation can be per step or periodic, depending on the design, while advanced implementations may apply filters to assess the usefulness of information before broadcasting it. Regarding the parallel execution of the algorithm, each agent or group of agents can run on a separate thread or processor. The computations for evaluating the objective function are entirely independent and can be parallelized without synchronization. Synchronization is only required during information propagation, either for updating the shared best solution or for exchanging parameters among agents. In synchronized implementations, all threads wait for the slowest one before proceeding to the next step. However, this can cause delays, especially when execution times vary significantly. To address this issue, asynchronous schemes can be used, where each agent updates based on the most recently available information without requiring global synchronization. Such a scheme allows faster execution and better resource utilization in heterogeneous environments.
2.3. The Propagation Mechanism
During the propagation mechanism, the best values identified by each subpopulation are shared with the others, replacing their worst values. The goal of this process is to ensure that the subpopulations exchange their optimal findings, thereby enhancing the overall evolutionary process. The following four scenarios describe how propagation can take place:
- One-to-One (1to1): In this case, a randomly selected subpopulation sends its best values to another subpopulation, also chosen at random.
- One-to-All (1toN): Here, a random subpopulation shares its best values with all other subpopulations.
- All-to-One (Nto1): All subpopulations send their best values to a single subpopulation, which is chosen at random.
- All-to-All (NtoN): Each subpopulation communicates its best values to every other subpopulation.
This mechanism facilitates information exchange among subpopulations, increasing the likelihood of discovering optimal solutions through collaboration and communication. The choice of propagation strategies is driven by empirical motivations and the need to strike a balance between exploration and exploitation within the parallel SAO framework. These simple strategies offer a controllable and scalable way to exchange information among subpopulations without imposing significant computational overhead or requiring complex communication architectures. Although they do not incorporate adaptive topologies like those found in certain PSO variants, they provide a stable framework for evaluating the impact of cooperation on the algorithm’s behavior. In the context of this work, the use of such strategies allows for a focused study on the role of information propagation, without introducing external sources of complexity.
2.4. The Termination Rule
The proposed termination rule is based on a straightforward criterion, which is evaluated independently for each subpopulation. Specifically, for a given subpopulation k, the difference
is computed during each iteration , where represents the best function value identified in subpopulation k at iteration . If the difference is less than or equal to a predefined threshold for at least consecutive iterations, it is considered that subpopulation k has reached a state of stability and can terminate its population evolution.
Within the overall method, the algorithm terminates if the above condition is satisfied for more than N subpopulations. This rule ensures that the process concludes once the majority of subpopulations have stabilized their solutions, thereby optimizing computational efficiency.
3. Results
This section begins with a description of the functions that will be used in the experiments and then presents in detail the experiments that were performed, in which the parameters available in the proposed algorithm were studied, in order to study its reliability and adequacy. The following is the Table 1 with the relevant parameter settings of the method.

Table 1.
Parameters and settings.
3.1. Test Functions

Table 2.
The benchmark functions used in the experiments conducted.
3.2. Experimental Results
A series of experiments was conducted for the aforementioned functions, which were executed on a computer equipped with an Linux machine with 128 GB RAM. Each experiment was repeated 30 times, with different random numbers each time, and the averages were recorded. The software used in the experiments was coded in ANSI C++ using the freely available GLOBALOPTIMUS optimization environment, which can be downloaded from https://github.com/itsoulos/GlobalOptimus (accessed on 10 April 2025). The values of the experimental parameters for the proposed method are presented in Table 1.
In the following tables displaying the experimental results, the numbers in the cells represent the average number of function calls, as measured over 30 independent runs. The numbers in parentheses indicate the percentage of executions where the method successfully identified the global minimum. If this number is absent, it signifies that the method successfully located the global minimum in all runs (100% success rate).
Table 3 presents the experimental results of the SAO method, evaluating its performance across various functions with different numbers of subpopulations while keeping the total population size constant. The measurements are expressed in terms of objective function calls, where lower values indicate reduced computational cost and, consequently, higher efficiency. The values in parentheses denote the success rate of the method in finding the global minimum. The experimental measurements were carried out according to the parameter values listed in Table 1, but without allowing propagation between subpopulations. For the ACKLEY function, significant improvement is observed as the number of subpopulations increases, with function calls decreasing from 9080 for one subpopulation to 7863 for 20 subpopulations. This improvement is most notable between 10 and 20 subpopulations, suggesting that the method benefits from parallelization. The BF1 function, on the other hand, shows minimal change, with function calls remaining nearly constant, from 7936 to 7779, indicating that this function does not benefit significantly from parallelization. Similarly, the BF2 function demonstrates a smaller but noticeable decrease from 7411 to 7237 calls. The CAMEL function shows a steady downward trend, with calls decreasing from 5554 to 5276, while the CM function exhibits a reduction from 4141 to 4061, with the most significant drop observed between one and two subpopulations. For the DIFFPOWER functions, which are analyzed in versions of varying complexity, there is a systematic reduction in calls as the number of subpopulations increases. In DIFFPOWER2, calls decrease from 11,928 to 11,239, while in DIFFPOWER10, a reduction from 40,094 to 38,284 is noted, demonstrating that the method performs effectively even in complex search landscapes. Conversely, for the BRANIN function, only a slight reduction is observed, from 5077 to 5003 calls, indicating limited improvement. The GRIEWANK functions, however, show more pronounced improvements. GRIEWANK2 decreases from 8511 to 6394 calls, highlighting significant adaptability to parallelization, whereas GRIEWANK10 shows a more modest reduction. The RASTRIGIN function exhibits exceptional performance, with calls decreasing from 4505 to 3653 while maintaining a 97% success rate. This behavior underscores the method’s strength in handling highly challenging search landscapes. Similar behavior is observed for the SINUSOIDAL16 function, where calls drop from 8529 to 7235, with the success rate remaining consistently high. Conversely, for functions like BRANIN and HANSEN, the improvements are more limited, suggesting that the method may not be ideally suited for these problems. Overall, the total number of calls decreases from 398,004 for one subpopulation to 371,910 for 20 subpopulations. This overall reduction is significant, while the success rate remains consistently high, ranging between 95.3% and 95.9%. This indicates that parallelization in the SAO method not only reduces computational cost but also maintains its reliability in finding optimal solutions. However, performance varies across functions, highlighting that the effectiveness of parallelization is influenced by the nature of each function.

Table 3.
Comparison of the function calls of parallel SAO with different numbers of subpopulations.
Some test functions, such as F13 and GKLS350, have shocking convergence failure rates (3% and 67%). This is because the F13 function is known for having numerous local minima and narrow convergence regions, making the discovery of the global minimum particularly challenging even for advanced optimization methods. Similarly, GKLS350 belongs to a family of functions deliberately designed with “traps” that test an algorithm’s ability to avoid premature convergence to suboptimal solutions. The fact that parallel SAO manages to achieve even partial success on these functions (e.g., 67% for GKLS350) is considered significant, given that many other methods fail completely in similar tests. The focus is placed on the overall improvement in the algorithm’s performance rather than isolated failures, which can be attributed to the inherent difficulties of these specific benchmark problems.
In Figure 3, the statistical results from the comparison of different numbers of subpopulations for the critical parameter p, which represents levels of statistical significance, indicate significant differences between the groups. Specifically, the comparison between one subpopulation (1 Cluster) and two subpopulations (2 Clusters) yielded a p-value of 0.037, which is below the conventional significance threshold of 0.05, demonstrating statistically significant differences. The differences intensify as the number of subpopulations increases: for 5 subpopulations, the p-value is 0.00023, for 10 subpopulations, p = 0.0024, and for 20 subpopulations, p = 2.3 . This progressive reduction in p-values reveals that increasing the number of subpopulations correlates with a significant increase in statistical significance, suggesting stronger differences in the parameter p as more subpopulations are involved. These findings support the idea that using multiple subpopulations significantly impacts the results, with the effect becoming more pronounced as their number grows. This could indicate that parallel processing or managing more subpopulations enhances performance or drastically alters the behavior of the method under study.
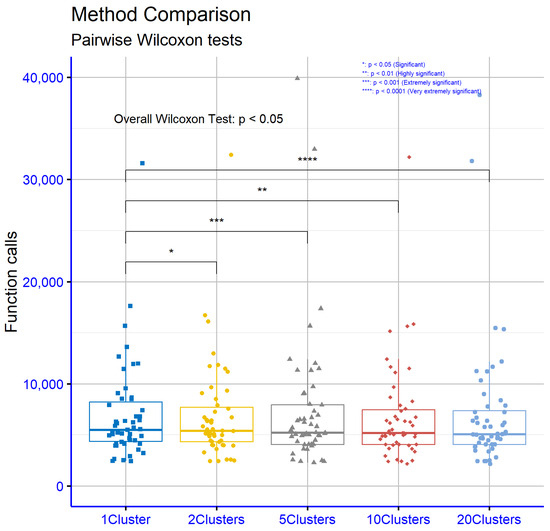
Figure 3.
Statistical comparison of function calls of parallel SAO with different numbers of subpopulations.
Table 4 presents the experimental results of the SAO method, evaluating its performance across different agent propagation strategies: 1to1, 1toN, Nto1, and NtoN, applied to a range of benchmark functions. The reported values represent the number of objective function evaluations required, with lower values indicating better computational efficiency. Values in parentheses denote the success rate in finding the global minimum. The experimental measurements were carried out according to the parameter values listed in Table 1 ( and ). For the ACKLEY function, the Nto1 strategy demonstrates the best performance, requiring 8495 evaluations, slightly outperforming the 1to1 strategy (8517) and significantly outperforming the NtoN strategy (11,242). The 1toN approach exhibits intermediate performance with 9106 evaluations. This indicates that the computational efficiency of the method varies significantly depending on the propagation strategy. The BF1 function shows an inverse trend, with the NtoN strategy requiring the fewest evaluations (7361), representing a substantial improvement compared to the other strategies, which hover around 7900 evaluations. Similarly, for the BF2 function, the Nto1 strategy shows superior performance with only 5477 evaluations, followed by NtoN at 6733, while 1to1 and 1toN remain close to 7300 evaluations. The DIFFPOWER functions reveal significant differences among strategies. For DIFFPOWER2, the NtoN strategy dramatically reduces the number of evaluations to 7633, compared to values exceeding 11,600 for the other methods. For more complex cases, such as DIFFPOWER10, the NtoN strategy exhibits even greater efficiency, reducing evaluations to 19,706 compared to over 42,000 for the 1to1 strategy. This underscores the robustness of the NtoN strategy for highcomplexity problems. The ELP functions further highlight the advantage of the NtoN strategy, especially in higher dimensions. For ELP10, evaluations decrease from approximately 5800 to 5080 with NtoN. The performance gap widens with increased complexity, as ELP30 requires only 7198 evaluations under the NtoN strategy, compared to over 11,400 for the 1to1 and 1toN strategies. The RASTRIGIN function shows a slight advantage for the Nto1 strategy, with 3737 evaluations and a 97% success rate. However, the NtoN strategy, despite having slightly higher evaluations (5224), maintains a high success rate (83%), demonstrating that Nto1 is marginally more efficient in this case while maintaining reliability. The results for the ROSENBROCK functions are particularly impressive, with NtoN outperforming all other strategies by a wide margin. For ROSENBROCK8, evaluations decrease to 7922 with NtoN, compared to over 11,800 for other approaches. Similarly, for ROSENBROCK16, the reduction is even more pronounced, with evaluations dropping to 9300 for NtoN, highlighting its superiority. For the HARTMAN and SHEKEL functions, the NtoN strategy consistently requires fewer evaluations than alternatives. For HARTMAN6, evaluations drop to 3144 with NtoN, compared to over 4200 for other strategies. Similar trends are observed for the SHEKEL functions, with SHEKEL10, for instance, showing a reduction to 5088 evaluations for NtoN, compared to over 6200 for the 1to1 strategy. In contrast, the GKLS250 and GKLS350 functions show mixed results, with marginal differences among strategies. Nonetheless, NtoN remains competitive, especially in GKLS350, where success rates remain relatively stable. The final row of the table provides an aggregate view of the results, confirming the superiority of the NtoN strategy in terms of computational efficiency. The total number of evaluations for NtoN is 295,761, a significant reduction compared to 387,465 for 1to1, 382,127 for 1toN, and 376,633 for Nto1. Success rates remain competitive, with the NtoN strategy achieving strong performance across various functions. Overall, the analysis highlights the effectiveness of the NtoN strategy in reducing computational cost while maintaining high success rates across a wide range of benchmark functions. While some functions exhibit marginal differences among strategies, NtoN consistently proves to be the most reliable and efficient approach within the parallel SAO framework.

Table 4.
Comparison of function calls with 10 subpopulations, using propagation every 4 iterations () and 5 agents propagated per event ().
In Figure 4, the statistical results from the comparison of information propagation strategies among subpopulations, based on the critical parameter p (levels of statistical significance), reveal significant differences in the effectiveness of the methods. The comparison between the 1to1 and 1toN strategies yielded p = 0.36, a value exceeding the conventional significance threshold of 0.05, suggesting that these two approaches do not differ statistically significantly. However, the remaining comparisons show marked differences. For example, the comparison of 1to1 vs. Nto1 (p = 0.00086) and 1to1 vs. NtoN (p = 7.3 ) demonstrate very high statistical significance, meaning the Nto1 and NtoN strategies differ dramatically from 1to1. The comparisons 1toN vs. Nto1 (p = 7.3 ) and 1toN vs. NtoN (p = 2.6 ) confirm that strategies involving multiple subpopulations (Nto1, NtoN) are statistically superior to 1toN. Finally, the comparison Nto1 vs. NtoN (p = 2.1 ) indicates that even between these two strategies, there is a significant difference, with NtoN standing out as the most distinct method.
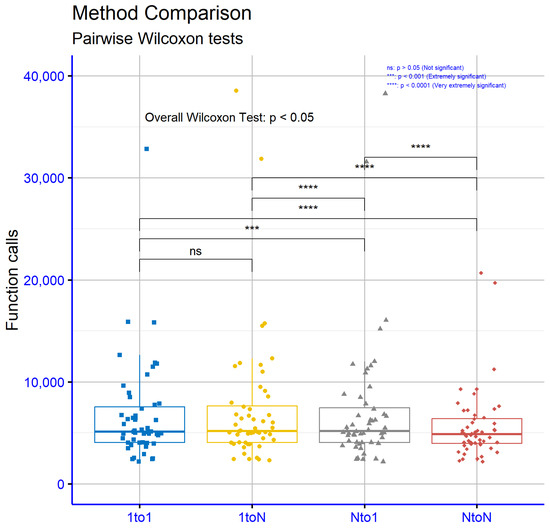
Figure 4.
Statistical comparison of function calls with 10 subpopulations, using propagation every 4 iterations () and 5 agents propagated per event ().
The experimental results presented in Table 5 illustrate the performance of the SAO method in parallel optimization scenarios, focusing on execution times (in seconds) for four propagation strategies: 1to1, 1toN, Nto1, and NtoN. The results reflect the average times taken per iteration of the algorithm across all subpopulations. The first row of the table categorizes different propagation strategies and provides their respective execution times. The last row aggregates these times to provide totals and averages, enabling a comprehensive comparison of the computational efficiency of each method. The experimental measurements were carried out according to the parameter values listed in Table 1 ( and ). Analyzing the table, it is evident that the NtoN strategy consistently achieves the lowest execution times across the majority of test functions. For example, in the ACKLEY function, the execution time for NtoN is 0.26 s, which is slightly higher than the 1to1 and Nto1 strategies (0.2 s each) but still competitive. However, as the complexity of the functions increases, the advantage of the NtoN strategy becomes more pronounced. For the DIFFPOWER10 function, the NtoN strategy records an execution time of 3.48 s, which is significantly lower than the 7.33 s required by the 1to1 strategy and the 6.7 s for the 1toN approach. In cases of simpler functions such as CAMEL and BRANIN, all strategies perform similarly, with execution times stabilizing around 0.17 s. However, for more computationally demanding functions like ELP30, the NtoN strategy outperforms the others, requiring only 1.67 s compared to over 2.4 s for the other approaches. Similarly, for POTENTIAL10, the NtoN strategy achieves a time of 4.02 s, while the 1to1 and 1toN strategies exceed 6.5 s. Another noteworthy observation is the performance of the NtoN strategy in high-dimensional or complex functions. For example, in ROSENBROCK16, the execution time of the NtoN strategy is 0.96 s, significantly lower than the approximately 1.4 s required by the other methods. In SINUSOIDAL16, the NtoN strategy records 1.5 s, far outperforming the next best approach, Nto1, which requires 2.17 s. Similar trends are observed in SHEKEL10, where the NtoN strategy achieves 0.34 s compared to 0.41 s for the 1to1 and Nto1 strategies. The NtoN strategy’s effectiveness is further emphasized in the total times reported in the last row of the table. The total execution time for the NtoN strategy is 29.13 seconds, which is significantly lower than the totals for the other strategies: 40.29 s for 1to1, 39.51 s for 1toN, and 39.99 seconds for Nto1. This substantial reduction in overall execution time underscores the computational efficiency and scalability of the NtoN strategy in parallel optimization contexts. In conclusion, the statistical analysis of the results demonstrates that the NtoN strategy consistently outperforms the other propagation methods in terms of execution time, particularly for complex and high-dimensional functions. While the differences among strategies are negligible for simpler functions, the NtoN approach exhibits clear superiority in reducing computational overhead for more demanding scenarios. This makes it the most efficient and reliable strategy for parallel SAO.

Table 5.
Comparison of times (seconds) with 10 subpopulations, using propagation every 4 iterations () and 5 agents propagated per event ().
In Figure 5, the statistical results from the comparison of propagation strategies among subpopulations, based on the critical parameter p, reveal variations in the significance of differences. The comparison between 1to1 and 1toN yielded p = 0.53, a value above the 0.05 significance threshold, suggesting no statistically significant difference between these strategies. Similarly, the comparisons 1to1 vs. Nto1 (p = 0.097) and 1toN vs. Nto1 (p = 0.16) show values above 0.05, though close to the threshold, without confirming statistical significance. However, the comparison of 1to1 vs. NtoN resulted in p = 0.04, a value below 0.05, indicating a statistically significant difference between these strategies. Additionally, the comparison of Nto1 vs. NtoN (p = 0.05) lies exactly at the significance threshold, which could be interpreted as suggestive of a difference. The comparison of 1toN vs. NtoN (p = 0.066) approaches the threshold but does not exceed it. These findings suggest that the NtoN (all-to-all) strategy appears to differ significantly from 1to1, while differences between other strategies are less pronounced or uncertain. This may imply that NtoN offers unique advantages compared to other approaches, though further investigation is needed to confirm its behavior across diverse scenarios. The presence of values near the significance threshold (e.g., 0.05–0.066) highlights the need for larger sample sizes or more sensitive analytical methods to clarify these borderline results.
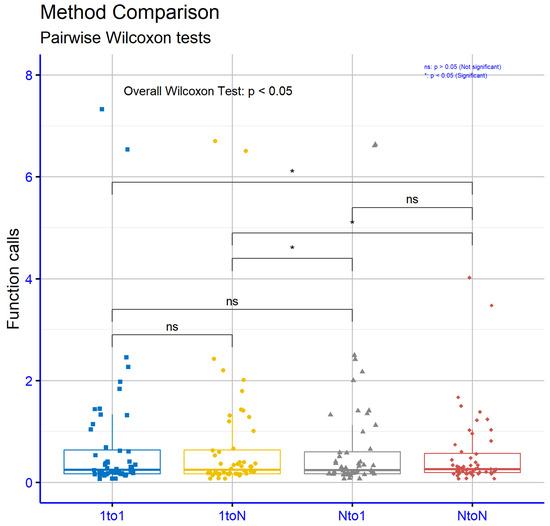
Figure 5.
Statistical comparison of times (seconds) with 10 subpopulations, using propagation every 4 iterations () and 5 agents propagated per event ().
Table 5 records the best functional values achieved for each subpopulation across different propagation strategies, 1to1, 1toN, Nto1, and NtoN, with propagation occurring at every iteration of the algorithm . Also, Table 6 presents average number of function calls with 10 subpopulations, using propagation every iterations () and 5 agents propagated per event (). The analysis begins with the 1to1 strategy, where the total values amount to 383838 with a success rate of 95.7%. In many functions, this strategy exhibits strong performance, such as in the ACKLEY function, where the value of 8667 is accompanied by high stability, and in the GRIEWANK10 function with a value of 12,224, indicating the reliability of this strategy for more complex functions. However, for higher-dimensional functions like POTENTIAL10 and ROSENBROCK16, the values of 15,959 and 15,679, respectively, while acceptable, fall short compared to other strategies. The 1toN strategy shows a slightly lower total sum compared to 1to1, with a value of 366,274 and a success rate of 95%. In functions such as GKLS350, this strategy excels, achieving a value of 2623 and a success rate of 87%. However, in more demanding functions like DIFFPOWER10, the 1toN strategy records high values (35,729), indicating that its effectiveness diminishes in more complex environments. The Nto1 strategy demonstrates similar overall performance to 1toN, with a total sum of 366,348 and a success rate of 95.4%. This strategy shows remarkable results in certain functions, such as TEST2N5, where the value of 4764 is accompanied by a high success rate of 97%. Meanwhile, in the HARTMAN3 function, the strategy achieves a lower value (3430), highlighting its adaptability to various search landscapes. The NtoN strategy shows the best overall performance, with a total sum of 259,119 and a success rate of 86.5%. Despite the slightly lower success rate, this strategy stands out for its significantly reduced values in many functions. For instance, in the DIFFPOWER10 function, the NtoN strategy achieves a value of 9662, which is notably lower than the other strategies. Similarly, in the POTENTIAL5 function, the value of 2795 is particularly noteworthy. Similar trends are observed in the SINUSOIDAL16 function, where NtoN records a value of 3365 and a success rate of 90%, which is remarkable relative to the lowest value achieved. The statistical overview of the overall results indicates that the NtoN strategy is the most effective in reducing functional values, particularly in complex or high-dimensional functions. The 1to1, 1toN, and Nto1 strategies exhibit slightly higher success rates but incur higher overall costs due to elevated values in most functions. The NtoN strategy proves ideal for scenarios where speed and optimization are critical, while maintaining competitive accuracy in finding the global minimum.

Table 6.
Comparison of function calls with 10 subpopulations, using propagation every iterations () and 5 agents propagated per event ().
In Figure 6, the statistical results from the comparison of subpopulation propagation strategies, based on the p-parameter, reveal significant differences. The NtoN (all-to-all) strategy stands out as the most effective, with extremely low p-values in all comparisons (e.g., 5 against 1toN), suggesting statistical superiority. The 1to1 strategy differs significantly from Nto1 (p = 7.6 ) and NtoN (p = 5.2 ), while 1toN and Nto1 show no significant difference between them (p = 0.75). The NtoN strategy also outperforms Nto1 (p = 4.1 ).
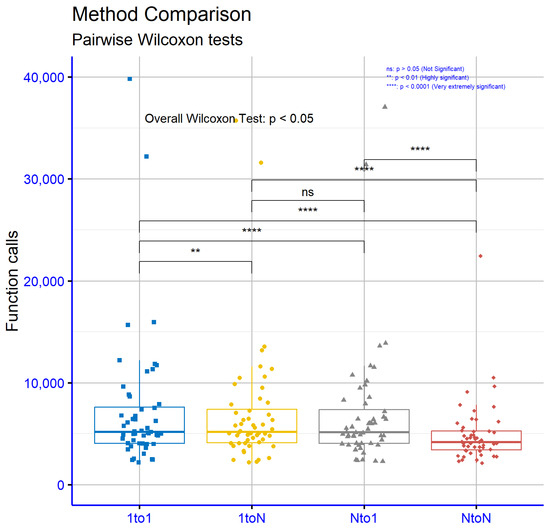
Figure 6.
Statistical comparison of function calls with 10 subpopulations, using propagation every iterations () and 5 agents propagated per event ().
Table 7 presents execution times (in seconds) required for achieving convergence under various propagation strategies between subpopulations: 1to1, 1toN, Nto1, and NtoN. Propagation occurs during each iteration () of the optimization algorithm. The 1to1 strategy exhibits a total runtime of 39.61 s, the highest among the evaluated strategies. Despite its slower performance, it maintains consistency across most functions. For example, the ACKLEY function has a runtime of 0.21 s, demonstrating efficiency in relatively simple landscapes. Similarly, in the GRIEWANK10 function, the runtime is 1.00 s, highlighting the strategy’s ability to manage complexity. However, for more demanding functions such as DIFFPOWER10 and POTENTIAL10, the strategy records significant runtimes of 6.85 and 6.56 s, respectively, indicating a higher computational cost for high-dimensional problems. The 1toN strategy achieves a total runtime of 36.70 s, which is slightly lower than that of the 1to1 strategy. This improvement is particularly evident in high-dimensional functions such as DIFFPOWER10, where the runtime decreases to 6.15 s, and POTENTIAL10, with a runtime of 5.67 s. However, in simpler functions like ELP10 and ELP20, the runtimes of 0.54 and 1.22 s, respectively, suggest only marginal gains. The 1toN strategy also exhibits strong performance in certain moderate-dimensional problems, such as ROSENBROCK16, where the runtime of 1.22 s reflects its efficiency. The Nto1 strategy records a total runtime of 37.63 s, falling between the 1to1 and 1toN strategies. Its runtime distribution is consistent across various functions, with notable improvements in specific cases. For instance, in the SINUSOIDAL16 function, the runtime decreases to 1.94 s compared to 2.21 s for 1to1. Similarly, for the HARTMAN3 function, a runtime of 0.23 s highlights the strategy’s adaptability. However, in more computationally intensive functions such as DIFFPOWER10 and POTENTIAL10, the runtimes remain relatively high at 6.37 and 5.81 s, respectively, indicating room for optimization. The NtoN strategy stands out as the most time-efficient, with a total runtime of 23.75 s, significantly lower than all other strategies. This advantage is evident across nearly all functions, particularly in high-dimensional and complex scenarios. For example, in the DIFFPOWER10 function, the runtime is reduced to 1.76 s, representing a substantial improvement. Similarly, in the POTENTIAL10 function, the runtime of 2.28 s underscores the strategy’s superiority. The NtoN strategy also performs well in simpler cases, such as the ROSENBROCK8 function, where the runtime of 0.42 s demonstrates its ability to handle diverse landscapes effectively. In summary, the NtoN strategy emerges as the most efficient in terms of runtime, especially for high-dimensional or computationally intensive problems. While the 1to1, 1toN, and Nto1 strategies offer competitive runtimes for simpler functions, their overall performance lags behind the NtoN approach. The significant reduction in runtime achieved by the NtoN strategy highlights its suitability for scenarios requiring rapid convergence and effective optimization across diverse problem landscapes.

Table 7.
Comparison of times (seconds) with 10 subpopulations and propagation, using propagation every 1 iterations () and 5 agents propagated per event ().
In Figure 7, the statistical results indicate only one statistically significant difference: the 1to1 vs. NtoN comparison (p = 0.00041). All other comparisons (1to1 vs. 1toN p = 0.12, 1to1 vs. Nto1 p = 0.98, 1toN vs. Nto1 p = 0.45, 1toN vs. NtoN p = 0.34, Nto1 vs. NtoN p = 0.43) show p-values above 0.05, indicating no statistically significant differences between these strategies.
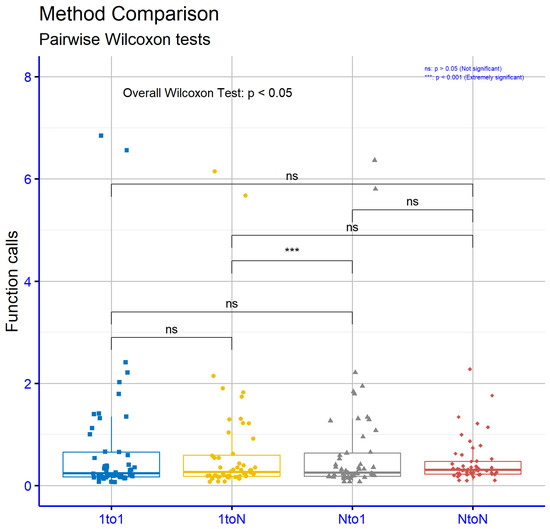
Figure 7.
Statistical comparison of times (seconds) with 10 subpopulations, using propagation every iteration () and 5 agents propagated per event ().
In Figure 8 and Figure 9, the optimization results using the parallel SAO method for three test functions ELP100 (dimension 100), ROSENBROCK100 (dimension 100), and DIFFPOWER30 (dimension 30) are presented. Figure 8 shows the number of function calls, while Figure 9 includes the corresponding execution times in seconds. For all functions, a significant reduction in both function calls and execution times is observed as the number of clusters increases. For example, for ELP100 with 1Cluster, 33,375 calls and 43.165 s are required, whereas with 20Cluster, the calls drop to 7537 and the time to 5.502 s. A similar trend is observed for the other functions: ROSENBROCK100 reduces calls from 49,697 (1Cluster) to 9841 (20Cluster) and time from 50.845 to 8.298 seconds, while DIFFPOWER30 decreases from 42,614 calls and 40.602 seconds to 8,351 calls and 6.873 s, respectively. The improvement is more pronounced when transitioning from fewer clusters (e.g., 1 to 5), with reductions slowing at higher cluster counts (e.g., 10 to 20). This suggests that parallel processing via the SAO method offers significant performance advantages, particularly in computationally complex scenarios. However, the variation in time differences between functions (e.g., ROSENBROCK100 vs. DIFFPOWER30) highlights the impact of problem nature and dimensionality on overall performance.
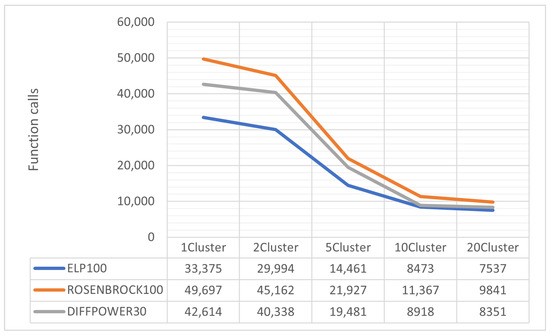
Figure 8.
Comparison of function calls of ELP, ROSENBROCK and DIFFPOWER with different numbers of clusters.
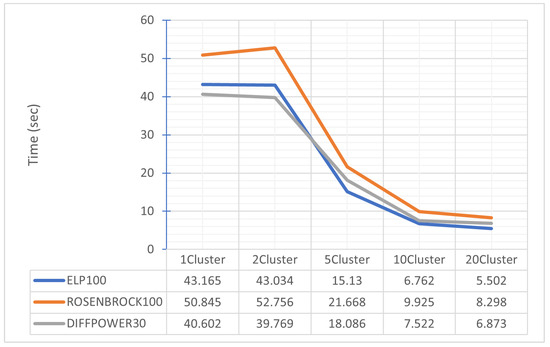
Figure 9.
Comparison of times of ELP, ROSENBROCK, and DIFFPOWER with different numbers of clusters.
Figure 10 presents the results of the parallel SAO method for the same functions with varying values of the parameter (number of agents). For all functions, a general decrease in function calls is observed as increases, though the improvement is nonlinear. For instance, in ELP100, calls drop from 14,925 ( = 1) to 7803 ( = 10), with the sharpest decline occurring between = 1 and = 5 (14,925 to 8473). Similarly, ROSENBROCK100 reduces calls from 22,030 ( = 1) to 10,473 ( = 10), albeit with fluctuations (e.g., an increase to 11,000 for = 8). DIFFPOWER30 shows the greatest relative improvement, with calls decreasing from 21,323 ( = 1) to 7746 ( = 10), particularly sharply between = 1 and = 7. The differences in behavior across functions suggest that optimization efficiency depends on the problem’s inherent characteristics. ELP100 benefits more significantly from increasing agents, while ROSENBROCK100 exhibits greater instability, likely due to its higher complexity. Additionally, for > 5, reductions in calls are slow, possibly indicating limits in parallel processing efficiency or increased computational coordination costs among agents.
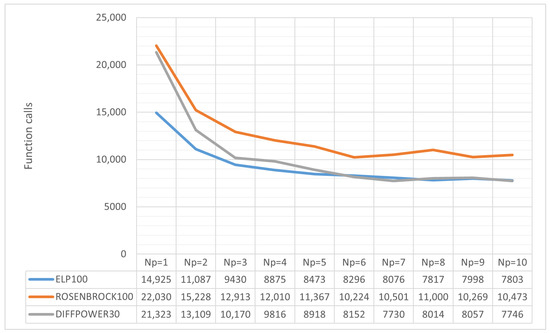
Figure 10.
Comparison of function calls with different values of (agents for propagation).
The results from the comparison Table 8 between the pSAOP (parallel SAO with propagation) method and the parallel algorithms pSAO (parallel SAO without propagation), pAOA, pAQUILA, and pDE reveal significant performance differences. Overall, the pSAOP method demonstrates the best total performance with a TOTAL value of 259.119, which is substantially lower than the values of the other methods (AQUILA: 554.293, AOA: 515.111, DE: 778.440, SAO: 387.927). This difference highlights the overall superiority of the pSAOP method over existing approaches, particularly in complex or high-dimensional functions. In specific functions, the pSAOP method shows remarkable improvements. For instance, in the DIFFPOWER10 function, the pSAOP method’s value (9.662) is up to six times lower than that of DE (60.024) and significantly better than the rest. A similar difference is observed in SCHWEFEL222, where the pSAOP method (4.062) dramatically outperforms DE (87.237). Furthermore, in functions like POTENTIAL5 (2.795) and POTENTIAL10 (4.899), the pSAOP method demonstrates notable performance advantages over all other algorithms. However, there are cases where other methods exhibit competitive performance. For example, in the ACKLEY function, SAO (8.307) performs slightly better than the pSAOP method (10.521). Similarly, in GRIEWANK2, SAO (6.736) appears to outperform the pSAOP method (9.109). These exceptions suggest that, while generally superior, the pSAOP method may not always be the optimal choice for certain types of problems. Additionally, the pSAOP method maintains consistent performance across a wide range of functions, as evidenced by its low values in SINUSOIDAL16 (3.365), TEST2N7 (3.707), and TEST30N4 (4.522), where it consistently outperforms the other algorithms. Its ability to minimize values across such diverse problems indicates flexibility and resilience. Overall, the findings support that the pSAOP method offers significant advantages, especially in complex and high-dimensional optimization problems. The improvements in specific functions, combined with its consistent performance, make it a favorable choice over existing methods. However, in some cases, combining it with other approaches may be required for optimal results.

Table 8.
Comparison of function calls of the proposed method with others.
The experiments shown in Table 8 and Figure 11 were performed according to the following parameterization:
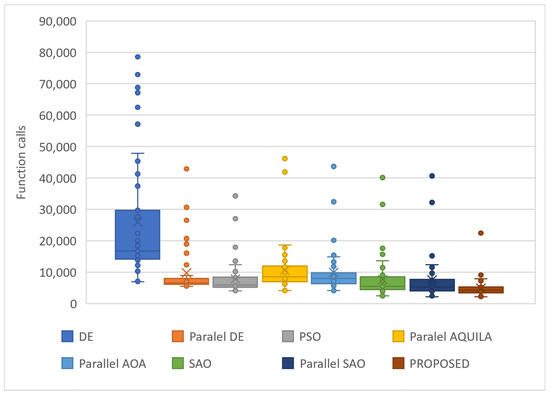
Figure 11.
Comparison of function calls of the proposed method with others.
- For PROPOSED (parallel SAO with propagation): = 1, = 5, = 1 and 10 subpopulations.
- For parallel SAO without propagation: 10 subpopulations.
- For parallel AOA (parallel Adaptive Optimization Algorithm): 10 subpopulations.
- For parallel AQUILA (parallel Aquila Optimizer): Coefficient = 0, Coefficient = 2 and 10 subpopulations.
- For parallel DE (Parallel Differential Evolution [66]): Crossover Probability = 09, Differential Weight = 0.8 and 10 subpopulations.
- For DE (Differential Evolution): Crossover Probability = 09 and Differential Weight = 0.8.
- For PSO (Particle Swarm Optimization):
- For all methods: m = 500, N = 10, = 200, Stopping Rule: = Similarity, = 8 and = 0.02 (2%).
The Table 8 presents the experimental results for a large number of benchmark functions, comparing the performance of various optimization algorithms. The analysis includes traditional algorithms such as DE and PSO, along with their parallel variants, like Parallel DE. It also includes newer metaheuristic algorithms such as AQUILA, AOA, and the proposed variant of Parallel SAO. The SAO algorithm is presented in both its sequential and parallel forms, and the set is completed with the proposed method, which integrates stochastic exploration, local exploitation, and cooperative information propagation strategies. It is observed that the proposed method consistently requires fewer objective function evaluations compared to the other algorithms across most benchmark functions. Notably, it demonstrates significant superiority on difficult and high-dimensional functions such as EXP16, EXP32, DIFFPOWER10, GRIEWANK10, ROSENBROCK16, and POTENTIAL10, where the reduction in required evaluations exceeds 50% compared to other methods. In most cases, the proposed method either outperforms or is highly competitive with the best alternatives, indicating its high effectiveness. Particular attention should be given to the last row of the table, which reports the total number of function evaluations across all benchmark problems. The proposed method achieves a total cost of 256,521, which is significantly lower than all other algorithms, including SAO (398,004), Parallel SAO (387,927), PSO (407,911), Parallel DE (507,525), and DE (1,347,623). The difference with the second-best algorithm (Parallel SAO) exceeds 130,000 evaluations, corresponding to a cost reduction of approximately 33%. This gap further supports the hypothesis that the combination of parallelization, improved propagation, and local exploitation proposed in this work contributes substantially to the efficiency of global optimization. Overall, the statistical results clearly demonstrate the superiority of the proposed method over the compared algorithms, confirming its effectiveness in solving both low- and high-complexity optimization problems.
Figure 11 expands on this analysis with box plots illustrating the statistical distribution of function calls. The pSAOP exhibits the most compact box plot, with a lower median and narrower range compared to the other methods. This indicates that pSAOP not only reduces the mean number of calls but also minimizes result variance, ensuring more predictable performance. Despite the presence of some outliers, the overall trend confirms that pSAOP is the most efficient choice for parallel optimization, especially in large-scale problems. The introduction of dynamic information exchange mechanisms between subpopulations (e.g., NtoN) appears to be the key factor driving this improvement, balancing exploration and exploitation within the search space.
4. Discussion
Collaboration is a fundamental factor contributing to the effectiveness of dissemination strategies in subpopulation-based approaches. Within the parallel implementation of the SAO method, the exchange of information among subpopulations extends beyond simple data sharing, focusing on enhancing collective dynamics. The adoption of dissemination strategies, such as the NtoN or Nto1 models, offers significant advantages. These strategies ensure the preservation of diversity in the search space, prevent premature convergence to local optima, and facilitate the faster discovery of optimal solutions. Specifically, subpopulations constantly collaborate by exchanging their best solutions, replacing less effective ones, and accelerating the overall convergence toward the global optimum. This collective approach strikes a balance between exploring new regions of the search space and exploiting the optimal solutions already identified. By employing mechanisms such as stochastic perturbations and targeted local searches, the dissemination of information acts as a catalyst for improving the algorithm’s performance. Although the results demonstrate a positive contribution of collaborative parallelism in terms of speed and accuracy, variations in performance are observed depending on the characteristics of each function. To understand these differences, a deeper analysis of the parameters that influence the algorithm’s behavior is essential. The first observation concerns the computational cost of evaluating the objective function. In problems with high computational load, the parallelization of SAO performs particularly well, as the speed-up achieved through workload distribution outweighs the synchronization time among agents. In contrast, in problems with lower computational demands, the benefit of parallelization decreases, since synchronization and communication among agents constitute a disproportionately large portion of the total execution time. This suggests that the parallel SAO is more efficient when applied to functions of higher complexity. Secondly, the topology of the search space significantly affects the behavior of the algorithm. Functions with strong multimodality, that is, multiple local optima, pose a challenge for SAO, as the likelihood of getting trapped in local optima increases. In such cases, parallelism can contribute positively only when it is accompanied by techniques that enhance search diversification. For example, the adoption of independent subpopulations with different initial positions and search strategies can strengthen exploration of the solution space and increase the probability of identifying the global optimum. Conversely, in functions that are smooth or possess a strong guiding gradient field, SAO tends to converge rapidly, and parallelization does not offer the same level of benefit. In these cases, static task distribution may lead to timing asymmetries due to thread lag, which delays the overall optimization process. It is therefore recommended to consider asynchronous parallelization schemes, where agents independently update the shared environment without requiring full synchronization at every iteration. Moreover, the internal dynamics of SAO, specifically its self-adaptive strategy, may behave differently depending on the function. The algorithm’s response to local fluctuations in the solution space depends on adaptation parameters, step-size ranges for agent movements, and the frequency of global updates. Parallelism can alter these dynamics by accelerating information propagation or enhancing diversity, provided it is appropriately leveraged. The optimization of these aspects could further improve the overall performance of the algorithm. In summary, the experimental results indicate that collaborative parallelization of SAO offers significant advantages, which, however, vary considerably depending on the nature of the problem. Evaluating the complexity, topology, and computational cost of the function in question is crucial in selecting an appropriate parallel strategy. Further exploration of alternative schemes such as asynchronous or multi-level parallel models constitutes a subject for future research and could lead to even more efficient implementations of SAO.
5. Conclusions
The findings of the present study highlight the capability of the parallel SAO to deliver significant improvements in both efficiency and accuracy of the optimization process, especially in cases involving high computational demand or complex search spaces. However, it is evident that the algorithm’s performance is not uniform across all types of functions, as it heavily depends on the characteristics of each particular case, such as the shape of the search landscape, the presence of local extrema, and the computational cost of each objective function evaluation. This observation underscores the need for a more targeted adaptation of the model to the specificities of each problem in order to maximize the benefits of parallelization. Beyond the academic evaluation of the parallel SAO, its potential application in real-world problems presents particular interest, where conditions are typically more complex and less controlled. In such settings, additional challenges arise that are not always apparent in synthetic or theoretical experiments. One of the major difficulties involves the uncertainty and instability of input data. In real applications, cost functions are often noisy or defined through temporary, empirical approximations, which may hinder the algorithm’s ability to converge to stable solutions. To address this challenge, smoothing techniques such as iterative estimation using moving averages or Kalman filters can be incorporated to mitigate the impact of noise during the search process. Another significant challenge relates to resource management and the implementation of parallelism in heterogeneous environments, such as computing networks or distributed systems with variable load. In these scenarios, the traditional assumption of uniform computing units does not hold, which may compromise the performance of the parallel algorithm due to temporal asymmetries or overload on specific nodes. A potential solution involves the use of adaptive scheduling and workload distribution strategies, aiming to dynamically balance the load and maximize resource utilization, even in environments with non-stationary conditions. Furthermore, in large-scale applications requiring multi-objective optimization or constraint handling, extending SAO to support multi-criteria optimization becomes a critical step. The parallel version of the algorithm can provide substantial advantages in this context, provided it is designed in a way that facilitates the exploration of alternative solutions along the Pareto front without compromising computational efficiency. Therefore, future research may focus on developing multi-objective extensions of the parallel SAO, incorporating techniques such as statistical weight distribution or progressive goal balancing. Finally, from a strategic perspective, the exploration of hybrid approaches is of particular interest, where the parallel SAO is integrated with other methods, such as local search techniques or heuristics based on domain knowledge. Such synergies can lead to more flexible and powerful solutions, especially in problems that simultaneously require high accuracy and speed.
Author Contributions
Conceptualization, V.C. and G.K.; methodology, I.G.T.; software, G.K.; validation, V.C., A.M.G. and I.G.T.; formal analysis, V.C.; investigation, I.G.T.; resources, I.G.T.; data curation, G.K.; writing—original draft preparation, V.C.; writing—review and editing, I.G.T.; visualization, V.C.; supervision, I.G.T.; project administration, I.G.T.; funding acquisition, I.G.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded by the European Union: Next Generation EU through the Program Greece 2.0 National Recovery and Resilience Plan, under the call RESEARCH–CREATE–INNOVATE, project name “iCREW: Intelligent small craft simulator for advanced crew training using Virtual Reality techniques” (project code: TAEDK-06195).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Carrizosa, E.; Molero-Río, C.; Romero Morales, D. Mathematical optimization in classification and regression trees. Top 2021, 29, 5–33. [Google Scholar] [CrossRef] [PubMed]
- Legat, B.; Dowson, O.; Garcia, J.D.; Lubin, M. MathOptInterface: A data structure for mathematical optimization problems. INFORMS J. Comput. 2022, 34, 672–689. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Stilck França, D.; Garcia-Patron, R. Limitations of optimization algorithms on noisy quantum devices. Nat. Phys. 2021, 17, 1221–1227. [Google Scholar] [CrossRef]
- Zhang, J.; Glezakou, V.A. Global optimization of chemical cluster structures: Methods, applications, and challenges. Int. J. Quantum Chem. 2021, 121, e26553. [Google Scholar] [CrossRef]
- Hu, Y.; Zang, Z.; Chen, D.; Ma, X.; Liang, Y.; You, W.; Zhang, Z. Optimization and evaluation of SO2 emissions based on WRF-Chem and 3DVAR data assimilation. Remote Sens. 2022, 14, 220. [Google Scholar] [CrossRef]
- Kaur, P.; Singh, R.K. A review on optimization techniques for medical image analysis. Concurr. Comput. Pract. Exp. 2023, 35, e7443. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hosney, M.E.; Mohamed, W.M.; Ali, A.A.; Younis, E.M. Fuzzy-based hunger games search algorithm for global optimization and feature selection using medical data. Neural Comput. Appl. 2023, 35, 5251–5275. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Hesami, M.; Jones, A.M.P. Application of artificial intelligence models and optimization algorithms in plant cell and tissue culture. Appl. Microbiol. Biotechnol. 2020, 104, 9449–9485. [Google Scholar] [CrossRef]
- Filip, M.; Zoubek, T.; Bumbalek, R.; Cerny, P.; Batista, C.E.; Olsan, P.; Bartos, P.; Kriz, P.; Xiao, M.; Dolan, A.; et al. Advanced computational methods for agriculture machinery movement optimization with applications in sugarcane production. Agriculture 2020, 10, 434. [Google Scholar] [CrossRef]
- Akintuyi, O.B. Adaptive AI in precision agriculture: A review: Investigating the use of self-learning algorithms in optimizing farm operations based on real-time data. Res. J. Multidiscip. Stud. 2024, 7, 16–30. [Google Scholar]
- Wang, Y.; Ma, Y.; Song, F.; Ma, Y.; Qi, C.; Huang, F.; Xing, J.; Zhang, F. Economic and efficient multi-objective operation optimization of integrated energy system considering electro-thermal demand response. Energy 2020, 205, 118022. [Google Scholar] [CrossRef]
- Alirahmi, S.M.; Mousavi, S.B.; Razmi, A.R.; Ahmadi, P. A comprehensive techno-economic analysis and multi-criteria optimization of a compressed air energy storage (CAES) hybridized with solar and desalination units. Energy Convers. Manag. 2021, 236, 114053. [Google Scholar] [CrossRef]
- Wolfe, M.A. Interval methods for global optimization. Appl. Math. Comput. 1996, 75, 179–206. [Google Scholar]
- Csendes, T.; Ratz, D. Subdivision direction selection in interval methods for global optimization. SIAM J. Numer. Anal. 1997, 34, 922–938. [Google Scholar] [CrossRef]
- Shezan, S.A.; Ishraque, M.F.; Shafiullah, G.M.; Kamwa, I.; Paul, L.C.; Muyeen, S.M.; NSS, R.; Saleheen, M.Z.; Kumar, P.P. Optimization and control of solar-wind islanded hybrid microgrid by using heuristic and deterministic optimization algorithms and fuzzy logic controller. Energy Rep. 2023, 10, 3272–3288. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, Z.; Liu, J. Deterministic Multi-Objective Optimization of Analog Circuits. Electronics 2024, 13, 2510. [Google Scholar] [CrossRef]
- Hsieh, Y.P.; Karimi Jaghargh, M.R.; Krause, A.; Mertikopoulos, P. Riemannian stochastic optimization methods avoid strict saddle points. Adv. Neural Inf. Process. Syst. 2024, 36, 29580–29601. [Google Scholar]
- Tyurin, A.; Richtárik, P. Optimal time complexities of parallel stochastic optimization methods under a fixed computation model. Adv. Neural Inf. Process. 2024, 36, 16515–16577. [Google Scholar]
- Sohail, A. Genetic Algorithms in the fields of artificial intelligence and data sciences. Ann. Data Sci. 2023, 10, 1007–1018. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.G.; Stavrou, V.N. An Intelligent Technique for Initial Distribution of Genetic Algorithms. Axioms 2023, 12, 980. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An improved Differential Evolution algorithm and its application in optimization problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar]
- Price, W. Global optimization by controlled random search. J. Optim. Theory Appl. 1983, 40, 333–348. [Google Scholar] [CrossRef]
- Křivý, I.; Tvrdik, J. The controlled random search algorithm in optimizing regression models. Comput. Stat. Data Anal. 1995, 20, 229–234. [Google Scholar] [CrossRef]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
- Eglese, R.W. Simulated Annealing: A tool for operational research. Eur. J. Oper. Res. 1990, 46, 271–281. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Lagaris, I.E. MinFinder: Locating all the local minima of a function. Comput. Phys. Commun. 2006, 174, 166–179. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, P. A multi-start central force optimization for global optimization. Appl. Soft Comput. 2015, 27, 92–98. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Pourpanah, F.; Wang, R.; Lim, C.P.; Wang, X.Z.; Yazdani, D. A review of artificial fish swarm algorithms: Recent advances and applications. Artif. Intell. Rev. 2023, 56, 1867–1903. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, F.M.; Li, F.; Wu, H.S. Improved artificial fish swarm algorithm. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 748–753. [Google Scholar]
- Kareem, S.W.; Mohammed, A.S.; Khoshabaa, F.S. Novel nature-inspired meta-heuristic optimization algorithm based on hybrid dolphin and sparrow optimization. Int. J. Nonlinear Anal. Appl. 2023, 14, 355–373. [Google Scholar]
- Wu, T.Q.; Yao, M.; Yang, J.H. Dolphin swarm algorithm. Front. Inf. Technol. Electron. 2016, 17, 717–729. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Asghari Varzaneh, Z.; Mirjalili, S. A systematic review of the whale optimization algorithm: Theoretical foundation, improvements, and hybridizations. Arch. Comput. Methods Eng. 2023, 30, 4113–4159. [Google Scholar] [CrossRef]
- Brodzicki, A.; Piekarski, M.; Jaworek-Korjakowska, J. The whale optimization algorithm approach for deep neural networks. Sensors 2021, 21, 8003. [Google Scholar] [CrossRef]
- Rokbani, N.; Kumar, R.; Abraham, A.; Alimi, A.M.; Long, H.V.; Priyadarshini, I.; Son, L.H. Bi-heuristic ant colony optimization-based approaches for traveling salesman problem. Soft Comput. 2021, 25, 3775–3794. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Z.M.; Chen, H.F. The simplified aquila optimization algorithm. IEEE Access 2022, 10, 22487–22515. [Google Scholar] [CrossRef]
- Abualigah, L.; Sbenaty, B.; Ikotun, A.M.; Zitar, R.A.; Alsoud, A.R.; Khodadadi, N.; Ezugwu, A.E.; Hanandeh, E.S.; Jia, H. Aquila optimizer: Review, results and applications. In Metaheuristic Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2024; pp. 89–103. [Google Scholar]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B. Improved arithmetic optimization algorithm and its application to discrete structural optimization. Structures 2022, 35, 748–764. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, G.; Huang, Y.; Kong, M. A novel enhanced arithmetic optimization algorithm for global optimization. IEEE Access 2022, 10, 75040–75062. [Google Scholar] [CrossRef]
- Salawudeen, A.T.; Mu’azu, M.B.; Yusuf, A.; Adedokun, A.E. A Novel Smell Agent Optimization (SAO): An extensive CEC study and engineering application. Knowl.-Based Syst. 2021, 232, 107486. [Google Scholar] [CrossRef]
- Salawudeen, A.T.; Mu’azu, M.B.; Sha’aban, Y.A.; Adedokun, E.A. On the development of a novel Smell Agent Optimization (SAO) for optimization problems. In Proceedings of the 2nd International Conference on Information and Communication Technology and Its Applications (ICTA 2018), Minna, Nigeria, 5–6 September 2018. [Google Scholar]
- Salawudeen, A.T.; Mu’azu, M.B.; Yusuf, A.; Adedokun, E.A. From smell phenomenon to Smell Agent Optimization (SAO): A feasibility study. In Proceedings of the International Conference on Global & Emerging Trends (ICGET), Abuja, Nigeria, 2–4 May 2018. [Google Scholar]
- Chakraborty, A.; Kar, A.K. Swarm intelligence: A review of algorithms. In Nature-Inspired Computing and Optimization: Theory and Applications; Springer: Cham, Switzerland, 2017; pp. 475–494. [Google Scholar]
- Brezočnik, L.; Fister, I., Jr.; Podgorelec, V. Swarm intelligence algorithms for feature selection: A review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef]
- Mohammed, S.; Sha’aban, Y.A.; Umoh, I.J.; Salawudeen, A.T.; Ibn Shamsah, S.M. A hybrid smell agent symbiosis organism search algorithm for optimal control of microgrid operations. PLoS ONE 2023, 18, e0286695. [Google Scholar] [CrossRef] [PubMed]
- Meadows, O.A.; Mu’Azu, M.B.; Salawudeen, A.T. A Smell Agent Optimization approach to capacitated vehicle routing problem for solid waste collection. In Proceedings of the 2022 IEEE Nigeria 4th International Conference on Disruptive Technologies for Sustainable Development (NIGERCON), Abuja, Nigeria, 5–7 April 2022; pp. 1–5. [Google Scholar]
- Kotte, S.; Injeti, S.K.; Thunuguntla, V.K.; Kumar, P.P.; Nuvvula, R.S.; Dhanamjayulu, C.; Rahaman, M.; Khan, B. Energy curve based enhanced smell agent optimizer for optimal multilevel threshold selection of thermographic breast image segmentation. Sci. Rep. 2024, 14, 21833. [Google Scholar] [CrossRef]
- Arumugam, M.; Thiyagarajan, A.; Adhi, L.; Alagar, S. Crossover smell agent optimized multilayer perceptron for precise brain tumor classification on MRI images. Expert Syst. Appl. 2024, 238, 121453. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.G. Toward an ideal particle swarm optimizer for multidimensional functions. Information 2022, 13, 217. [Google Scholar] [CrossRef]
- Powell, M.J.D. A tolerant algorithm for linearly constrained optimization calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Rabie, A.H. A Novel Musical Chairs Optimization Algorithm. Arab. J. Sci. Eng. 2023, 48, 10371–10403. [Google Scholar] [CrossRef]
- Geetha, S.; Poonthalir, G.; Vanathi, P.T. Nested particle swarm optimisation for multi-depot vehicle routing problem. Int. J. Oper. Res. 2013, 16, 329–348. [Google Scholar] [CrossRef]
- Koyuncu, H.; Ceylan, R. A PSO based approach: Scout particle swarm algorithm for continuous global optimization problems. J. Comput. Des. Eng. 2019, 6, 129–142. [Google Scholar] [CrossRef]
- Siarry, P.; Berthiau, G.; Durdin, F.; Haussy, J. Enhanced Simulated Annealing for globally minimizing functions of many-continuous variables. ACM Trans. Math. Softw. (TOMS) 1997, 23, 209–228. [Google Scholar] [CrossRef]
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Del Ser, J.; Herrera, F. A prescription of methodological guidelines for comparing bio-inspired optimization algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Gaviano, M.; Ksasov, D.E.; Lera, D.; Sergeyev, Y.D. Software for generation of classes of test functions with known local and global minima for global optimization. ACM Trans. Math. Softw. 2003, 29, 469–480. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the Determination of Molecular Fields. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar]
- Zabinsky, Z.B.; Graesser, D.L.; Tuttle, M.E.; Kim, G.I. Global optimization of composite laminates using improving hit and run. In Recent Advances in Global Optimization; De Gruyter Brill: Berlin, Germany, 1992; pp. 343–368. [Google Scholar]
- Charilogis, V.; Tsoulos, I.G. A Parallel Implementation of the Differential Evolution Method. Analytics 2023, 2, 17–30. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).