Numerical Solution for Fuzzy Fractional Differential Equations by Fuzzy Multi-Step Methods

Abstract

To solve fractional differential equations, they are typically converted into their corresponding crisp problems through a process known as the embedding method. This paper introduces a novel direct approach to solving fuzzy differential equations using fuzzy calculations, bypassing the need for this transformation. In this study, we develop the fuzzy Adams–Bashforth (A-B) method and the fuzzy Adams–Moulton (A-M) method to find numerical solutions for fuzzy fractional differential equations (FFDEs) with fuzzy initial values. To demonstrate the accuracy and efficiency of the proposed methods, we determine both the local truncation error and the global truncation error. Additionally, we establish the convergence and stability of these methods in detail. Finally, numerical examples are provided to illustrate the flexibility and effectiveness of the proposed methods.

1. Introduction

Fuzzy set theory is a robust tool for modeling uncertain problems, making it widely applicable to various natural phenomena. Specifically, fuzzy fractional differential equations (FFDEs) are commonly used in fields such as population modeling, weapon-system evaluation, civil engineering, and electro-hydraulics. The concept of fractional derivatives is crucial in fuzzy calculus, drawing significant attention from mathematicians and engineers.

The work on FFDEs was conducted by Agarwal et al. [1], who defined the Riemann-Liouville differentiability concept under Hukuhara differentiability to solve these equations. Recently, fractional calculus has proven effective in addressing complex mathematical and engineering problems, including aerodynamics, control systems, signal processing, and biomathematics.

Numerous authors have studied FFDEs, employing various methods to solve them. For instance, Hoa explored FFDEs using Caputo gH-differentiability, while Agarwal et al. [2] surveyed the topic to highlight its relevance to optimal control problems. Long et al. [3] demonstrated the solvability of FFDEs, and Salahshour et al. [4] applied fuzzy Laplace transforms to solve these equations.

The well-known theory of fuzzy sets is a very strong tool in mathematics, utilized for modeling problems involving uncertainty. It has been effectively applied to a widespread range of natural phenomena, which have been adoptly reformulated in fuzzy language. The well-known fuzzy fractional differential equation (FFDE), in particular, plays a pivotal role across various scientific disciplines, including but not limited to population models [5], evaluation of the systems of weapon [6], civil engineering [7], and electro-hydraulic systems modeling [8].

Fractional derivatives hold a significant place in fuzzy calculus, leading to the heightened interest in FFDEs among both mathematicians and engineers. In the early 1970s, Chang and Zadeh [9] introduced a very interesting notion of derivatives using fuzzy set theory, which paved the way for extensive subsequent researches. The first formal study in FFDEs, however, was conducted in 2010 by Agarwal et al. [2]. Indeed, they defined the differentiability of Riemann-Liouville in the context of the differentiability of Hukuhara and applied this novel approach to solve FFDEs. Since then, numerous researchers have delved into fractional calculus. This fascinating area of study has shown great applicability in solving complex problems in different fields such as biomathematics, aerodynamics, signal processing, and control systems (see, e.g., [2,10,11,12,13]).

In fuzzy mathematics, fractional differential equations (FDEs) have been extensively explored, with significant contributions from many authors, including the second author of this paper (see, e.g., [14,15,16,17,18,19]). Notable works include Salahshour, Allahviranloo, and Abbasbandy’s utilization of the fuzzy Laplace transform for solving FFDEs in 2012 [4], Hoa’s study of FFDEs through Caputo gH-differentiability in 2015 [20], and Long, Son and Tam’s demonstration of the solvability of FFDEs in 2017 [3]. More recently, in 2018, Agarwal et al. [1] conducted a survey on FFDEs, revealing their connection to a unique type of optimal control problems, specifically nonlocal evolution optimal control equations.

There are various numerical methods for reformulating the FFDEs into crisp problems to solve them (see, e.g., [21,22]). A fuzzy method based on the generalized fuzzy Taylor expansion, introduced in [16], is a one-step method. However, in the present paper, a novel multi-step fuzzy method is developed to find a numerical solution to the FFDEs directly in the fuzzy form without converting them to a crisp form. The Taylor series expansion and the Taylor-collocation method are two well-known, strong, and useful tools for solving both linear and nonlinear problems (see, e.g., [16,19,23,24,25]).

In the present work, first, the generalized fuzzy Taylor expansion using the notion of Caputo’s fractional differentiability is extended. Second, the Adams methods are applied to solve the FFDEs. Additionally, the local truncation error, consistency, convergence, and stability of these methods are demonstrated. Finally, several examples with switching points are provided and solved using these methods. The numerical simulations and results reported here show that the generalized fuzzy Adams methods have high accuracy and can be effectively applied to solve the FFDEs.

2. Basic Preliminaries

Here, some elementary notions and theorems that are needed in the paper are recalled. For a widespread discussion, the interested reader may see [16,26,27,28].

Definition 1 

([16]). Suppose that $n\in \mathbb{N}$ and ${\mathbb{R}}_{\mathcal{F}}$ denotes the family of all functions $t:{\mathbb{R}}^n\to [0,1]$, which satisfy the following statements:

1. 

t is normal in the sense that $t\left(x_0\right)=1$ for some $x_0\in {\mathbb{R}}^n$;

2. 

t is fuzzy convex, i.e.,

$$t\left(\eta x_1+(1-\eta )x_2\right)\ge min\left\{t\left(x_1\right),t\left(x_2\right)\right\}$$

for all $\eta \in [0,1]$ and all $x_1,x_2\in {\mathbb{R}}^n$;

3. 

t is upper semi-continuous at a point $x_0\in {\mathbb{R}}^n$, i.e.,

$$t\left(x_0\right)\ge \underset{x\to x_0^{\pm }}{lim}t\left(x\right);$$

4. 

The set

$${\left[t\right]}_0=\overline{supp\left(t\right)}=cl\left\{x\in {\mathbb{R}}^n:t\left(x\right)>0\right\}$$

is compact in ${\mathbb{R}}^n$ with the Euclidean metric.

The family ${\mathbb{R}}_{\mathcal{F}}$ introduced above is the space consisting of fuzzy numbers, and each $t\in {\mathbb{R}}_{\mathcal{F}}$ is a fuzzy number. Also, for all $\beta \in [0,1]$ and all $t\in {\mathbb{R}}_{\mathcal{F}}$, the β-level set ${\left[t\right]}_{\beta }$ of t is

$${\left[t\right]}_{\beta }=\left\{x\in {\mathbb{R}}^n:t\left(x\right)\ge \beta \right\}.$$

Remark 1 

([16]). It follows from Statements 1–4 in Definition 1 that the β-level sets ${\left[t\right]}_{\beta }$ of a fuzzy number $t\in {\mathbb{R}}_{\mathcal{F}}$ are all nonempty, bounded and closed (thus, compact) intervals.

Definition 2 

([16]). Every fuzzy set in ${\mathbb{R}}_{\mathcal{F}}$ defines a triangular fuzzy number t characterized by $t=(a,b,c)\in {\mathbb{R}}^3$, where $a\le b\le c$ as well as the lower bound $t^{-}\left(\beta \right)=a+(b-a)\beta$ and the upper bound $t^{+}\left(\beta \right)=c-(c-b)\beta$ of t are the endpoints of the β-level sets ${\left[t\right]}_{\beta }$ for all $\beta \in [0,1]$.

Remark 2 

([16]). A crisp number k is also called singleton. For simplicity, the singleton k is represented by

$$t^{-}\left(\beta \right)=t^{+}\left(\beta \right)=k\left(\beta \in [0,1]\right).$$

Two well-known operations, namely the addition ⊕ and the scalar multiplication ⊙ in ${\mathbb{R}}_{\mathcal{F}}$, can also be introduced and formulated naturally. In fact, if $t,s\in {\mathbb{R}}_{\mathcal{F}}$, then the addition of t and s is

$${[t\oplus s]}_{\beta }=\left[t^{-}\left(\beta \right)+s^{-}\left(\beta \right),t^{+}\left(\beta \right)+s^{+}\left(\beta \right)\right]\left(\beta \in [0,1]\right).$$

Moreover, if μ is a scalar, then the scalar multiplication of μ in t is

$${[\mu \odot t]}_{\beta }=\left\{\begin{array}{cc}\left[\mu t^{-}\left(\beta \right),t^{+}\left(\beta \right)\right],\hfill & \mu \ge 0,\hfill \\ \left[\mu t^{+}\left(\beta \right),t^{-}\left(\beta \right)\right],\hfill & \mu <0,\hfill \end{array}\right.\left(\beta \in [0,1]\right).$$

The Hausdorff distance of two fuzzy numbers is given by the function $\mathcal{H}:{\mathbb{R}}_{\mathcal{F}}\times {\mathbb{R}}_{\mathcal{F}}\to [0,+\infty )$ defined by the rule

$$\mathcal{H}(t,s)=\underset{0\le \beta \le 1}{sup}max\left\{|t^{-}\left(\beta \right)-s^{-}\left(\beta \right)|,|t^{+}\left(\beta \right)-s^{+}\left(\beta \right)|\right\}(t,s\in {\mathbb{R}}_{\mathcal{F}}),$$

where ${\left[t\right]}_{\beta }=\left[t^{-}\left(\beta \right),t^{+}\left(\beta \right)\right]$. Note that the function $\mathcal{H}$ satisfies the following statements:

1. 

For all $t,s,r\in {\mathbb{R}}_{\mathcal{F}}$ we have

$$\mathcal{H}(t\oplus s,s\oplus r)=\mathcal{H}(t,s);$$

2. 

For all $\mu \in \mathbb{R}$ and all $t,s\in {\mathbb{R}}_{\mathcal{F}}$ we have

$$\mathcal{H}(\mu t,\mu s)=\left|\mu \right|\mathcal{H}(t,s);$$

3. 

For all $t,s,r,u\in {\mathbb{R}}_{\mathcal{F}}$ we have

$$\mathcal{H}(t\oplus s,r\oplus u)\le \mathcal{H}(t,r)+\mathcal{H}(s,u).$$

Also, $\mathcal{H}$ defines a metric on ${\mathbb{R}}_{\mathcal{F}}$. It can be verified that $({\mathbb{R}}_{\mathcal{F}},\mathcal{H})$ is a complete, separable, and locally compact metric space.

Definition 3 

([16]). Suppose that $t,s\in {\mathbb{R}}_{\mathcal{F}}$.

1. 

If $t=s\oplus r$ for some $r\in {\mathbb{R}}_{\mathcal{F}}$, then r is called the Hukuhara difference (shortly, H-difference) of t and s. The H-difference of t and s is denoted by $t\ominus s$. In other words,

$$t\ominus s=r\iff t=s\oplus r.$$

2. 

If $t=s\oplus r$ or $s=t\oplus (-1)r$ for some $r\in {\mathbb{R}}_{\mathcal{F}}$, then r is called the generalized Hukuhara difference (shortly, gH-difference) of t and s. The gH-difference of t and s is simply denoted by $t{\ominus }_{\mathit{gH}}s$. In other words,

$$t{\ominus }_{\mathit{gH}}s=r\iff \left\{\begin{array}{c}\left(i\right)t=s\oplus r,\hfill \\ \left(\mathit{ii}\right)s=t\oplus (-1)r.\hfill \end{array}\right.$$

Remark 3 

([16]).

1. 

It can be easily verified that Statements (i) and (ii) in the definition of gH-difference are valid if r is crisp and vice versa.

2. 

The interested reader can see some other conditions that imply the existence of the gH-difference in [26]. However, for simplicity, we assume here that every two fuzzy numbers have a gH-difference.

Before going on the notion of continuity in the space of fuzzy numbers, notice that by a fuzzy-valued function, assume a function $f:A\subseteq \mathbb{R}\to {\mathbb{R}}_{\mathcal{F}}$ such that

$${\left[f\left(x\right)\right]}_{\beta }=\left[f^{-}(x;\beta ),f^{+}(x;\beta )\right]$$

is the $\beta$-level set or the parametric shape of f for all $\beta \in [0,1]$.

Definition 4 

([16]). A fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ is called continuous (regarding the Hausdorff metric $\mathcal{H}$) at a point $x_0\in [a,b]$ if for any arbitrary $\epsilon >0$, there is a $\delta >0$ such that $|x-x_0|<\delta$ implies $\mathcal{H}(f\left(x\right),f\left(x_0\right))<\epsilon$ for all $x\in [a,b]$. If f is continuous at each point $x_0\in [a,b]$, then f is called continuous on the whole interval $[a,b]$. The family of all continuous fuzzy-valued functions f, whose domain is the interval $[a,b]$, may be denoted by ${\mathcal{C}}_f([a,b],{\mathbb{R}}_{\mathcal{F}})$.

Remark 4 

([16]). A continuous function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ (regarding the Hausdorff metric $\mathcal{H}$) is also integrable on the interval $[a,b]$. Moreover, the function

$$x\mapsto {\int }_a^{x}f\left(\xi \right)d\xi \left(x\in [a,b]\right)$$

is continuous on $[a,b]$. Moreover,

$${\left[{\int }_a^{x}f\left(\xi \right)d\xi \right]}_{\beta }=\left[{\int }_a^x{f}^{-}(\xi ;\beta )d\xi ,{\int }_a^x{f}^{+}(\xi ;\beta )d\xi \right]$$

for all $\beta \in [0,1]$.

Definition 5 

([16]). Suppose for a fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ that both $f^{-}(x;\beta )$ and $f^{+}(x;\beta )$ are differentiable at a point $x_0\in (a,b)$ for all $\beta \in [0,1]$ and $D{f}_{\mathit{gH}}$ (i.e., the gH-derivative of f) exists.

1. 

f is called FD1-gH-differentiable at $x_0$ whenever

$${\left[D{f}_{1.\mathit{gH}}\left(x_0\right)\right]}_{\beta }=\left[D{f}^{-}(x_0;\beta ),D{f}^{+}(x_0;\beta )\right].$$

2. 

f is called FD2-gH-differentiable at $x_0$ whenever

$${\left[D{f}_{2.\mathit{gH}}\left(x_0\right)\right]}_{\beta }=\left[D{f}^{+}(x_0;\beta ),D{f}^{-}(x_0;\beta )\right].$$

Now are ready to go on fuzzy fractional generalized Hukuhara derivative.

Definition 6 

([16], see also [29]). Suppose that $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ is a fuzzy Lebesgue integrable fuzzy-valued function and $\alpha >0$. The α-th order fuzzy Reimann-Liouville fractional (shortly, FRLF) integral of f is

$${}^{\mathit{FRLF}}I_{[a,x]}^{\alpha }f\left(x\right)={\displaystyle \frac{1}{\mathit{\Gamma }\left(\alpha \right)}}{\int }_a^x{(x-\xi )}^{\alpha -1}f\left(\xi \right)d\xi \left(x\in (a,b]\right).$$

Definition 7 

([16], see also [29]). Suppose for a fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ that $D^m{f}_{\mathit{gH}}$ (i.e., the m-th gH-derivative of f) is integrable on $[a,b]$ for all $m\in \mathbb{N}$. The fuzzy fractional Caputo derivative (shortly, FFCD) of f is

$${}^{\mathit{FC}}D_{*}^{\alpha }f\left(x\right)={}^{\mathit{FRLF}}I_{[a,x]}^{m-\alpha }\left(D^m{f}_{\mathit{gH}}\right)\left(x\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(m-\alpha )}}{\int }_a^{\xi }{(x-\xi )}^{m-\alpha -1}{D}^m{f}_{\mathit{gH}}\left(\xi \right)d\xi$$

for all $m\in \mathbb{N}$, all $\alpha \in (m-1,m]$ and all $x\in (a,b]$.

Remark 5 

([16]). Suppose for a fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ that $D{f}_{\mathit{gH}}$ (i.e., the gH-derivative of f) is integrable on $[a,b]$. Consider the α-th order fuzzy Caputo generalized Hukuhara derivative (shortly, FC-gH-derivative) of f for some $\alpha \in (0,1]$. The FC-gH-derivative can be formulated by

$${}^{\mathit{FC}}D_{*}^{\alpha }f\left(x\right)={}^{\mathit{FRLF}}I_{[a,x]}^{m-\alpha }\left(D{f}_{\mathit{gH}}\right)\left(x\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\int }_a^x{(x-\xi )}^{-\alpha }D{f}_{\mathit{gH}}\left(\xi \right)d\xi \left(x\in (a,b]\right).$$

In this paper, authors are interested in working on the $\alpha$-th order FC-gH-derivatives of fuzzy-valued functions.

Lemma 1 

([16]). For a continuous fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$, the function ${}^{\mathit{FRLF}}I_{[a,·]}^{\alpha }f(·)$ is also continuous on the interval $[a,b]$ for all $\alpha \in (0,1]$.

Definition 8 

([16], see also [29]). Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ be a fuzzy-valued function and $x_0\in [a,b]$. The point $x_0$ is called a switching point for the FC-gH-derivative of f if, for every neighborhood V of $x_0$, there are $x_1,x_2\in V$ with $x_1<x_0<x_2$ such that

(I) 

f is FC1-gH-differentiable at $x_1$ but it is not FC2-gH-differentiable at $x_1$, and

f is FC2-gH-differentiable at $x_2$ but it is not FC1-gH-differentiable at $x_2$;

or

(II) 

f is FC2-gH-differentiable at $x_1$ but it is not FC1-gH-differentiable at $x_1$, and

f is FC1-gH-differentiable at $x_2$ but it is not FC2-gH-differentiable at $x_2$.

Theorem 1 

([16], fuzzy generalized Taylor). Suppose that $\alpha \in (0,1]$ and $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ is a fuzzy-valued function with ${}^{\mathit{FC}}D_{*}^{j\alpha }f\in {\mathcal{C}}_f([a,b],{\mathbb{R}}_{\mathcal{F}})$ for $j=1,\dots ,n$.

1. 

If ${}^{\mathit{FC}}D_{*}^{j\alpha }f$ is FC1-gH-differentiable for $j=0,\dots ,n-1$ and the type of the fuzzy Caputo differentiability remains unchanged on the interval $[a,b]$, then

$$\begin{array}{cc}\hfill f\left(x\right)& =f\left(a\right)\oplus {}^{\mathit{FC}}D_{*}^{\alpha }{f}_{1.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\oplus {}^{\mathit{FC}}D_{*}^{2\alpha }{f}_{1.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}\hfill \\ \hfill & \phantom{=}\oplus \cdots \oplus {}^{\mathit{FC}}D_{*}^{(n-1)\alpha }{f}_{1.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{(n-1)\alpha }}{\mathrm{\Gamma }\left(\right(n-1)\alpha +1)}}\oplus R_n(a,x)\left(x\in [a,b]\right),\hfill \end{array}$$

where

$$R_n(a,x):={}^{\mathit{FRLF}}I_{[a,x]}^{\alpha }\left({}^{\mathit{FRLF}}I_{[a,x]}^{\alpha }\cdots \left({}^{\mathit{FRLF}}I_{[a,x_{n-1}]}^{\alpha }\left({}^{\mathit{FC}}D_{*}^{n\alpha }{f}_{1.\mathit{gH}}\right)\left(x_n\right)\right)\cdots \right)\left(x\in [a,b]\right).$$

2. 

If ${}^{\mathit{FC}}D_{*}^{j\alpha }f$ is FC2-gH-differentiable for $j=0,\dots ,n-1$ and the type of the fuzzy Caputo differentiability remains unchanged on the interval $[a,b]$, then

$$\begin{array}{cc}\hfill f\left(x\right)& =f\left(a\right)\ominus (-1){}^{\mathit{FC}}D_{*}^{\alpha }{f}_{2.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\ominus (-1){}^{\mathit{FC}}D_{*}^{2\alpha }{f}_{2.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}\hfill \\ \hfill & \phantom{=}\ominus (-1)\cdots \ominus (-1){}^{\mathit{FC}}D_{*}^{(n-1)\alpha }{f}_{2.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{(n-1)\alpha }}{\mathrm{\Gamma }\left(\right(n-1)\alpha +1)}}\ominus (-1)R_n(a,x)\left(x\in [a,b]\right),\hfill \end{array}$$

where

$$R_n(a,x):={}^{\mathit{FRLF}}I_{[a,x]}^{\alpha }\left({}^{\mathit{FRLF}}I_{[a,x_1}^{\alpha }\cdots \left({}^{\mathit{FRLF}}I_{[a,x_{n-1}]}^{\alpha }\left({}^{\mathit{FC}}D_{*}^{n\alpha }{f}_{2.\mathit{gH}}\right)\left(x_n\right)\right)\cdots \right)\left(x\in [a,b]\right).$$

3. 

If ${}^{\mathit{FC}}D_{*}^{j\alpha }f$ exists for $j=1,\dots ,n$ and the type of the fuzzy Caputo generalized Hukuhara differentiability changes on the interval $[a,b]$, then

$$\begin{array}{cc}\hfill f\left(x\right)& =f\left(a\right)\ominus (-1){}^{\mathit{FC}}D_{*}^{\alpha }{f}_{2.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\oplus {}^{\mathit{FC}}D_{*}^{2\alpha }{f}_{i.gH}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}\hfill \\ \hfill & \phantom{=}\ominus (-1)\cdots \ominus (-1){}^{\mathit{FC}}D_{*}^{({\displaystyle \frac{j}{2}}-1)\alpha }{f}_{2.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{(\frac{j}{2}-1)\alpha }}{\mathrm{\Gamma }\left(\frac{j}{2}\alpha \right)}}\hfill \\ \hfill & \phantom{=}\oplus {}^{\mathit{FC}}D_{*}^{{\displaystyle \frac{j}{2}}\alpha }{f}_{1.\mathit{gH}}\left(a\right)\odot {\displaystyle \frac{{(x-a)}^{\frac{j}{2}\alpha }}{\mathrm{\Gamma }(\frac{j}{2}\alpha +1)}}\ominus (-1)\cdots \ominus (-1)R_n(a,x)\left(x\in [a,b]\right),\hfill \end{array}$$

where

$$R_n(a,x):={}^{\mathit{FRLF}}I_{[a,x]}^{\alpha }\left({}^{\mathit{FRLF}}I_{[a,x_1]}^{\alpha }\cdots \left({}^{\mathit{FRLF}}I_{[a,x_{n-1}]}^{\alpha }\left({}^{\mathit{FC}}D_{*}^{n\alpha }{f}_{1.\mathit{gH}}\right)\left(x_n\right)\right)\cdots \right)\left(x\in [a,b]\right).$$

4. 

Suppose that ${}^{\mathit{FC}}D_{*}^{k\alpha }f\in {\mathcal{C}}_f([a,b],{\mathbb{R}}_{\mathcal{F}})$ for all $k\ge 3$, and f is FC2-gH-differentiable on the subinterval $[a,c]$ and is FC1-gH-differentiable on the subinterval $[c,b]$, i.e., c is a Type (II) switching point for the α-th order derivative of f. Suppose further that there is a $x_0\in [a,c]$ such that the derivative of f of order $2\alpha$ at a point $c_1\in [x_0,c]$ has a Type (I) switching point. If the type of the fuzzy Caputo differentiability remains unchanged on the interval $[c,b]$, then

$$\begin{array}{cc}\hfill f\left(x\right)& =f\left(x_0\right)\ominus (-1){}^{\mathit{FC}}D_{*}^{\alpha }{f}_{2.\mathit{gH}}\left(x_0\right)\odot {\displaystyle \frac{{(c-x_0)}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\oplus (-1){}^{\mathit{FC}}D_{*}^{2\alpha }{f}_{1.\mathit{gH}}\left(x_0\right)\odot {\displaystyle \frac{{(x_0-c_1)}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\odot {\displaystyle \frac{{(c-x_0)}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\hfill \\ \hfill & \phantom{=}\ominus (-1){}^{\mathit{FC}}D_{*}^{2\alpha }{f}_{2.\mathit{gH}}\left(c_1\right)\odot \left[{\displaystyle \frac{{(c-c_1)}^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{{(x_0-c_1)}^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}\right]\hfill \\ \hfill & \phantom{=}\oplus {}^{\mathit{FC}}D_{*}^{\alpha }{f}_{1.\mathit{gH}}\left(c\right)\odot {\displaystyle \frac{{(x-c)}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\oplus {}^{\mathit{FC}}D_{*}^{2\alpha }{f}_{1.\mathit{gH}}\left(c\right)\odot {\displaystyle \frac{{(x-c)}^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}\hfill \\ \hfill & \phantom{=}\oplus {}^{\mathit{FRLF}}I_{[x_0,c]}^{\alpha }·{}^{\mathit{FRLF}}I_{[x_0,c_1]}^{\alpha }·{}^{\mathit{FRLF}}I_{[x_0,x_2]}^{\alpha }\left({}^{\mathit{FC}}D_{*}^{3\alpha }{f}_{1.\mathit{gH}}\right)\left(x_4\right)\hfill \\ \hfill & \phantom{=}\ominus (-1){}^{\mathit{FRLF}}I_{[x_0,c]}^{\alpha }·{}^{\mathit{FRLF}}I_{[c_1,x_1]}^{\alpha }·{}^{\mathit{FRLF}}I_{[c_1,x_3]}^{\alpha }\left({}^{\mathit{FC}}D_{*}^{3\alpha }{f}_{2.\mathit{gH}}\right)\left(x_5\right)\hfill \\ \hfill & \phantom{=}\oplus {}^{\mathit{FRLF}}I_{[c,x]}^{\alpha }·{}^{\mathit{FRLF}}I_{[c,y_1]}^{\alpha }·{}^{\mathit{FRLF}}I_{[a,y_2]}^{\alpha }\left({}^{\mathit{FC}}D_{*}^{3\alpha }{f}_{1.\mathit{gH}}\right)\left(y_3\right)\left(x\in [a,b]\right).\hfill \end{array}$$

3. Fuzzy Generalized Adams Methods

In this section, are delved into some intriguing aspects of the fuzzy generalized Taylor theorem (Theorem 1), with a specific focus on the fuzzy generalized Adams methods. Our approach begins with establishing the fuzzy generalized Adams–Bashforth (shortly, A-B) method and the fuzzy generalized Adams–Moulton (shortly, A-M) method, which is grounded in the concept of fuzzy fractional gH-differentiability.

To lay the groundwork for these methods, first are introduced the concepts of forward finite differences and backward finite differences using gH-differences. Following this, are formulated Newton’s forward interpolation polynomial and backward interpolation polynomial. Utilizing these foundations, we derived the fuzzy generalized A-B method and the fuzzy generalized A-M method.

Prior to embarking on our main discussion, are presented a concise overview of the formulation of linear multi-step methods. This introduction is aimed at providing a fundamental understanding necessary for grasping the subsequent advanced concepts. In the general case, a linear multi-step method for a continuous fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ is formulated by

$$\sum _{k=0}^n{a}_k{y}_{m+k}=h\sum _{k=0}^n{b}_k{f}_{m+k},$$

where $n\in \mathbb{N}\cup \left\{0\right\}$ is an integer, $h={\displaystyle \frac{b-a}{n}}$ and $a_k$’s and $b_k$’s are real constants such that $a_n\ne 0$ and $a_0^2+b_0^2>0$. It is noted that the family of Adams methods is a subfamily of the family of linear multi-step methods with

$$a_n=1,a_{n-1}=-1,a_k=0k=0,1,\dots ,n-2.$$

3.1. Forward Finite Differences, Backward Finite Differences and Newton’s Interpolation Polynomials

Definition 9 

([19]). A fuzzy interpolation polynomial of some data is a fuzzy-valued function $p:\mathbb{R}\to {\mathbb{R}}_{\mathcal{F}}$ satisfying the following statements:

1. 

$p\left(x_k\right)=f_k$ for $k=1,2,\dots ,n$;

2. 

p is continuous on the whole set $\mathbb{R}$;

3. 

The interpolation polynomial p is also crisp whenever the data are crisp.

To construct a fuzzy interpolation polynomial, i.e., a fuzzy-valued function p satisfying Conditions 1–3 in Definition 9, it is necessary to introduce forward finite differences and backward finite differences using the gH-differences between $f_k$ and $f_{k+1}$. Next do this in two separated subsections and then construct Newton’s fuzzy forward and backward interpolation polynomials that are used frequently in our methods. Newton’s fuzzy interpolation polynomials are two well-known examples of fuzzy interpolation polynomials.

3.1.1. Newton’s Fuzzy Forward Interpolation Polynomial

Consider a continuous fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ such that the values of f at

$$x_k=a+khk=0,1,\dots ,n$$

are known, where $h={\displaystyle \frac{b-a}{n}}$. For a fixed integer $k=0,1,\dots ,n-1$ and any $\beta \in [0,1]$, put

$${\mathrm{\Delta }}_{\mathrm{gH}}{f}_k\left(\beta \right)=f_{k+1}\left(\beta \right){\ominus }_{\mathrm{gH}}{f}_k\left(\beta \right)=\left\{\begin{array}{c}\left(\mathrm{i}\right)f_{k+1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_k\left(\beta \right),\hfill \\ \left(\mathrm{ii}\right)(-1)\odot \left(f_k\left(\beta \right){\ominus }_{\mathrm{H}}{f}_{k+1}\left(\beta \right)\right).\hfill \end{array}\right.$$

Also, the $\beta$-level sets of ${\mathrm{\Delta }}_{\mathrm{gH}}{f}_i$ are defined by

$$\begin{array}{cc}\hfill {\left[{\mathrm{\Delta }}_{\mathrm{gH}}{f}_k\left(\beta \right)\right]}_{\beta }& ={\left[f_{k+1}\left(\beta \right){\ominus }_{\mathrm{gH}}{f}_k\left(\beta \right)\right]}_r\hfill \\ \hfill & ={\left[min\left\{f_{k+1}^{-}\left(\beta \right)-f_k^{-}\left(\beta \right),f_{k+1}^{+}\left(\beta \right)-f_k^{+}\left(\beta \right)\right\},max\left\{f_{k+1}^{-}\left(\beta \right)-f_k^{-}\left(\beta \right),f_{k+1}^{+}\left(\beta \right)-f_k^{+}\left(\beta \right)\right\}\right]}_{\beta }\hfill \end{array}$$

Similarly, for $k=0,1,\dots ,n-2$ we have

$$\begin{array}{cc}\hfill {\mathrm{\Delta }}_{\mathrm{gH}}^2{f}_k\left(\beta \right)& ={\mathrm{\Delta }}_{\mathrm{gH}}\left({\mathrm{\Delta }}_{\mathrm{gH}}{f}_k\left(\beta \right)\right)={\mathrm{\Delta }}_{\mathrm{gH}}\left(f_{k+1}\left(\beta \right){\ominus }_{\mathrm{gH}}{f}_k\left(\beta \right)\right)\hfill \\ \hfill & =\left(f_{k+2}\left(\beta \right){\ominus }_{\mathrm{gH}}{f}_{k+1}\left(\beta \right)\right){\ominus }_{\mathrm{gH}}\left(f_{k+1}\left(\beta \right){\ominus }_{\mathrm{gH}}{f}_k\left(\beta \right)\right)\hfill \\ \hfill & =\left\{\begin{array}{c}\left(\mathrm{i}\right)f_{k+2}\left(\beta \right){\ominus }_{\mathrm{gH}}2\odot f_{k+1}\left(\beta \right)\oplus f_k\left(\beta \right),\hfill \\ \left(\mathrm{ii}\right)(-1)\odot \left(f_{k+1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_{k+2}\left(\beta \right)\right){\ominus }_{\mathrm{gH}}{f}_{k+1}\left(\beta \right)\oplus f_k\left(\beta \right)\hfill \end{array}\right.\hfill \\ \hfill & =\left\{\begin{array}{c}\left(\mathrm{i}\right)f_{k+2}\left(\beta \right){\ominus }_{\mathrm{H}}2\odot f_{k+1}\left(\beta \right)\oplus f_k\left(\beta \right),\hfill \\ \left(\mathrm{ii}\right)(-1)\odot \left(2\odot f_{k+1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_{k+2}\left(\beta \right)\right)\oplus f_k\left(\beta \right),\hfill \\ \left(\mathrm{iii}\right)(-1)\odot \left(f_{k+1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_{k+2}\left(\beta \right)\right){\ominus }_{\mathrm{gH}}{f}_{k+1}\left(\beta \right)\oplus f_k\left(\beta \right),\hfill \\ \left(\mathrm{iv}\right)(-1)\odot \left(f_{k+1}\left(\beta \right){\ominus }_{\mathrm{H}}(-1)\odot \left(f_{k+1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_{k+2}\left(\beta \right)\right)\right)\oplus f_k\left(\beta \right).\hfill \end{array}\right.\hfill \end{array}$$

(1)

Continuing this argument yields

$${\mathrm{\Delta }}_{\mathit{gH}}^3{f}_k\left(\beta \right)={\mathrm{\Delta }}_{\mathrm{gH}}\left({\mathrm{\Delta }}_{\mathrm{gH}}^2{f}_k\left(\beta \right)\right)k=0,1,\dots ,n-3$$

and so on. The fuzzy values ${\mathrm{\Delta }}_{\mathrm{gH}}^m{f}_k$, where $m\in \mathbb{N}$, are called the forward finite differences based on the generalized Hukuhara differences (shortly, forward finite gH-differences) of f.

Using these notations, Newton’s fuzzy forward interpolation polynomial may be defined as follows:

Definition 10 

([19]). For any $\beta \in [0,1]$, Newton’s fuzzy forward interpolation polynomial $p\left(x\right)$ at the point $(x_0,f_0)$ is

$$p\left(x\right)=f_0\left(\beta \right)\oplus \theta \odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_0\left(\beta \right)\oplus {\displaystyle \frac{\theta (\theta -1)}{2}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_0\left(\beta \right)\oplus \cdots \oplus {\displaystyle \frac{\theta (\theta -1)\cdots (\theta -n+1)}{n!}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^n{f}_0\left(\beta \right).$$

(2)

Remark 6 

([19]). The variable θ in Equation (2) is crisp since $\theta ={\displaystyle \frac{x-x_0}{h}}$ and x, $x_k$’s and h are all crisp variables.

3.1.2. Newton’s Fuzzy Backward Interpolation Polynomial

Similar to Newton’s fuzzy forward interpolation polynomial, one may formulate Newton’s fuzzy backward interpolation polynomial. To this end, consider again a continuous fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ such that the values of f at

$$x_k=a+khk=0,1,\dots ,n$$

are known, where $h={\displaystyle \frac{b-a}{n}}$. For a fixed integer $k=0,1,\dots ,n-1$ and any $\beta \in [0,1]$, put

$${\nabla }_{\mathit{gH}}{f}_k\left(\beta \right)=f_k\left(\beta \right){\ominus }_{\mathit{gH}}{f}_{k-1}\left(\beta \right)=\left\{\begin{array}{c}\left(\mathrm{i}\right)f_k\left(\beta \right){\ominus }_{\mathrm{H}}{f}_{k-1}\left(\beta \right),\hfill \\ \left(\mathrm{ii}\right)(-1)\odot \left(f_{k-1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_k\left(\beta \right)\right).\hfill \end{array}\right.$$

Also, the $\beta$-level sets of ${\nabla }_{\mathit{gH}}{f}_k$ are defined by

$$\begin{array}{cc}\hfill {\left[{\nabla }_{\mathit{gH}}{f}_k\left(\beta \right)\right]}_{\beta }& ={\left[f_k\left(\beta \right){\ominus }_{\mathit{gH}}{f}_{k-1}\left(\beta \right)\right]}_{\beta }\hfill \\ \hfill & ={\left[min\left\{f_k^{-}\left(\beta \right)-f_{k-1}^{-}\left(\beta \right),f_k^{+}\left(\beta \right)-f_{k-1}^{+}\left(\beta \right)\right\},max\left\{f_k^{-}\left(\beta \right)-f_{k-1}^{-}\left(\beta \right),f_i^{+}\left(\beta \right)-f_{k-1}^{+}\left(\beta \right)\right\}\right]}_{\beta }\hfill \end{array}$$

Similarly, for $k=2,3,\dots ,n$ we obtain

$$\begin{array}{cc}\hfill {\nabla }_{gH}^2{f}_k\left(\beta \right)& ={\nabla }_{\mathit{gH}}\left({\nabla }_{\mathit{gH}}{f}_k\left(\beta \right)\right)={\nabla }_{\mathit{gH}}\left(f_k\left(\beta \right){\ominus }_{\mathit{gH}}{f}_{k-1}\left(\beta \right)\right)\hfill \\ \hfill & =\left(f_k\left(\beta \right){\ominus }_{\mathit{gH}}{f}_{k-1}\left(\beta \right)\right){\ominus }_{\mathit{gH}}\left(f_{k-1}\left(\beta \right){\ominus }_{\mathit{gH}}{f}_{k-2}\left(\beta \right)\right)\hfill \\ \hfill & =\left\{\begin{array}{c}\left(\mathrm{i}\right)f_k\left(\beta \right){\ominus }_{\mathit{gH}}2\odot f_{k-1}\left(\beta \right)\oplus f_{k-2}\left(\beta \right),\hfill \\ \left(\mathrm{ii}\right)(-1)\odot \left(f_{k-1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_k\left(\beta \right)\right){\ominus }_{\mathit{gH}}{f}_{k-1}\left(\beta \right)\oplus f_{k-2}\left(\beta \right)\hfill \end{array}\right.\hfill \\ \hfill & =\left\{\begin{array}{c}\left(\mathrm{i}\right)f_k\left(\beta \right){\ominus }_{\mathrm{H}}2\odot f_{k-1}\left(\beta \right)\oplus f_{k-2}\left(\beta \right),\hfill \\ \left(\mathrm{ii}\right)(-1)\odot \left(2\odot f_{k-1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_k\left(\beta \right)\right)\oplus f_{k-2}\left(\beta \right),\hfill \\ \left(\mathrm{iii}\right)(-1)\odot \left(f_{k-1}\left(\beta \right){\ominus }_H{f}_k\left(\beta \right)\right){\ominus }_{\mathrm{H}}{f}_{k-1}\left(\beta \right)\oplus f_{k-2}\left(\beta \right),\hfill \\ \left(\mathrm{iv}\right)(-1)\odot \left(f_{k-1}\left(\beta \right){\ominus }_H(-1)\odot \left(f_{k-1}\left(\beta \right){\ominus }_{\mathrm{H}}{f}_k\left(\beta \right)\right)\right)\oplus f_{k-2}\left(\beta \right).\hfill \end{array}\right.\hfill \end{array}$$

(3)

Continuing this arguments yields

$${\nabla }_{\mathit{gH}}^3{f}_k\left(\beta \right)={\nabla }_{\mathit{gH}}\left({\nabla }_{\mathit{gH}}^2{f}_k\left(\beta \right)\right)k=3,4,\dots ,n$$

and so on. The fuzzy values ${\nabla }_{\mathit{gH}}^m{f}_k$, where $m\in \mathbb{N}$, are called the backward finite differences based on the generalized Hukuhara differences (shortly, backward finite gH-differences) of f.

Using these notations, Newton’s fuzzy backward interpolation polynomial may be defined as follows:

Definition 11 

([19]). For any $\beta \in [0,1]$, Newton’s fuzzy backward interpolation polynomial $p\left(x\right)$ at the point $(x_n,f_n)$ is

$$p\left(x\right)=f_n\left(\beta \right)\oplus \theta \odot {\nabla }_{\mathit{gH}}{f}_n\left(\beta \right)\oplus {\displaystyle \frac{\theta (\theta +1)}{2}}\odot {\nabla }_{\mathit{gH}}^2{f}_n\left(\beta \right)\oplus \cdots \oplus {\displaystyle \frac{\theta (\theta +1)\cdots (\theta +n-1)}{n!}}\odot {\nabla }_{\mathit{gH}}^n{f}_n\left(\beta \right).$$

(4)

Remark 7 

([19]). Similar to Equation (2), the variable θ in Equation (4) is crisp since $\theta ={\displaystyle \frac{x-x_0}{h}}$ and x, $x_i$’s and h are all crisp variables.

3.2. Fuzzy Generalized A-B Method and Fuzzy Generalized A-M Method

Consider the FFIVP

$$\left\{\begin{array}{cc}{}^{\mathit{FC}}D_{*}^{\alpha }{y}_{\mathrm{gH}}\left(x\right)=f\left(x,y\left(x\right)\right),\hfill & x\in [0,T],\hfill \\ y\left(0\right)=y_0\in {\mathbb{R}}_{\mathcal{F}},\hfill \end{array}\right.$$

(5)

where y is the unknown fuzzy-valued function of a crisp variable x, $f:[0,T]\times {\mathbb{R}}_{\mathcal{F}}\to {\mathbb{R}}_{\mathcal{F}}$ is a continuous fuzzy-valued function, $\alpha \in (0,1]$ and ${}^{\mathit{FC}}D_{*}^{\alpha }{y}_{\mathrm{gH}}$ is the $\alpha$-th order fuzzy fractional Caputo derivative of y with a finitely many switching points in $[0,T]$. By separating the closed interval $[0,T]$ into N subintervals with the same step length $h={\displaystyle \frac{T}{N}}$, obtain a partition $\mathcal{P}=\{x_0,x_1,\dots ,x_N\}$ of this interval, where

$$x_0=0,x_N=T,x_k=khk=0,1,\dots ,N.$$

Please note that $x_0<x_1<\cdots <x_N$. Further is assumed that the FFIVP (5) has a unique solution, and the authors wish to solve it using three fuzzy generalized Adams methods, namely:

• fuzzy generalized A-B two-step method with backward finite gH-differences,
• fuzzy generalized A-M two-step method with forward finite gH-differences, and
• fuzzy generalized A-M three-step method with forward finite gH-differences.

3.2.1. Fuzzy Generalized A-B Two-Step Method with Backward Finite gH-Differences

To solve the FFIVP (5) using the fuzzy generalized A-B two-step method with backward finite gH-differences, suppose that $k=1,2,\dots ,N-1$ is a fixed integer, $y\left(x_{k-1}\right)$ and $y\left(x_k\right)$ are fuzzy initial values, i.e., $f(x_{k-1},y\left(x_{k-1}\right))$ and $f(x_k,y\left(x_k\right))$ are known fuzzy numbers and also,

$${\nabla }_{\mathit{gH}}{f}_k=f_k{\ominus }_{\mathit{gH}}{f}_{k-1},\theta ={\displaystyle \frac{x-x_k}{h}}.$$

In particular, $x=x_k+\theta h$ and we obtain

$$x_{k+1}-x=x_{k+1}-x_k-\theta h=h-\theta h=(1-\theta )h.$$

Then the Newton’s fuzzy backward interpolation polynomial at $(x_k,f_k)$ and $(x_{k-1},f_{k-1})$ is

$$p\left(x,y\left(x\right)\right)=f_k\oplus \theta \odot {\nabla }_{\mathit{gH}}{f}_k.$$

Now, assume that Equation (3)(i) holds. Taking integral over the closed interval $[x_k,x_{k+1}]$ from the first equality in the FFIVP (5) leads us to

$${\int }_{x_k}^{x_{k+1}}{D}^{\alpha }{y}_{\mathit{gH}}\left(x\right)dx=I_{[x_k,x_{k+1}]}^{\alpha }f\left(x,y\left(x\right)\right),$$

and so

$$y_{k+1}{\ominus }_{\mathit{gH}}{y}_k={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{x_k}^{x_{k+1}}{(x_{k+1}-x)}^{\alpha -1}\odot f\left(x,y\left(x\right)\right)dx.$$

(6)

Thus, by substituting the fuzzy-valued function f with Newton’s fuzzy backward interpolation polynomial $p(x,y(x\left)\right)$ at the points $(x_k,f_k)$ and $(x_{k-1},f_{k-1})$ in Equation (6) as well as using the definition of backward finite gH-differences obtain

$$\begin{array}{cc}\hfill y_{k+1}{\ominus }_{\mathit{gH}}{y}_k& ={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}\odot {\int }_{x_k}^{x_{k+1}}{(x_{k+1}-x)}^{\alpha -1}\odot (f_k\oplus \theta \odot {\nabla }_{\mathit{gH}}{f}_k)dt\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot {\int }_0^1{(1-\theta )}^{\alpha -1}\odot (f_k\oplus \theta \odot {\nabla }_{\mathit{gH}}{f}_k)d\theta \hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot \left[\left({\int }_0^1{(1-\theta )}^{\alpha -1}d\theta \right)\odot f_k\oplus \left({\int }_0^1\theta {(1-\theta )}^{\alpha -1}d\theta \right)\odot {\nabla }_{\mathit{gH}}{f}_k\right]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot \left[\left(-{\displaystyle \frac{{(1-\theta )}^{\alpha }}{\alpha }}\right){|}_0^1\odot f_k\oplus \left(-{\displaystyle \frac{\theta }{\alpha }}{(1-\theta )}^{\alpha }-{\displaystyle \frac{{(1-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}\right){|}_0^1\odot {\nabla }_{\mathit{gH}}{f}_k\right]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot \left[{\displaystyle \frac{1}{\alpha }}\odot f_k\oplus {\displaystyle \frac{1}{\alpha (\alpha +1)}}\odot {\nabla }_{\mathit{gH}}{f}_k\right]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\alpha (\alpha +1)\mathrm{\Gamma }\left(\alpha \right)}}\odot \left[(\alpha +1)\odot f_k\oplus {\nabla }_{\mathit{gH}}{f}_k\right]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{(\alpha +1)\mathrm{\Gamma }(\alpha +1)}}\odot \left[(\alpha +1)\odot f_k\oplus \left(f_k{\ominus }_{\mathit{gH}}{f}_{k-1}\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{(\alpha +1)!}}\odot \left[(\alpha +2)\odot f_k{\ominus }_{\mathit{gH}}{f}_{k-1}\right].\hfill \end{array}$$

(7)

3.2.2. Fuzzy Generalized A-M Two-Step Method with Forward Finite gH-Differences

To solve the FFIVP (5) using the fuzzy generalized A-M two-step method with forward finite gH-differences, suppose again that $k=1,2,\dots ,N-1$ is a fixed integer, $y\left(x_k\right)$, $y\left(x_{k+1}\right)$ and $y\left(x_{k+2}\right)$ are fuzzy initial values, i.e., $(x_k,f_k)$, $(x_{k+1},f_{k+1})$ and $(x_{k+2},f_{k+2})$ are known fuzzy numbers and also,

$${\mathrm{\Delta }}_{\mathit{gH}}{f}_k=f_{k+1}{\ominus }_{\mathit{gH}}{f}_k,\theta ={\displaystyle \frac{x-x_k}{h}}.$$

In particular, $x=x_k+\theta h$ and we obtain

$$x_{k+2}-x=x_{k+2}-x_k-\theta h=(x_{k+2}-x_{k+1})+(x_{k+1}-x_k)-\theta h=h+h-\theta h=(2-\theta )h.$$

Then the Newton’s fuzzy forward interpolation polynomial at $(x_k,f_k)$, $(x_{k+1},f_{k+1})$ and $(x_{k+2},f_{k+2})$ is

$$p\left(x,y\left(x\right)\right)=f_k\oplus \theta \odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\oplus {\displaystyle \frac{\theta (\theta -1)}{2}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k.$$

Now, assume that Equation (1)(i) holds. Taking integral over the closed interval $[x_{k+1},x_{k+2}]$ from the first equality in the FFIVP (5) leads us to

$${\int }_{x_{k+1}}^{x_{k+2}}{D}^{\alpha }{y}_{\mathit{gH}}\left(x\right)dx=I_{[x_{k+1},x_{k+2}]}^{\alpha }f\left(x,y\left(x\right)\right),$$

and so

$$y_{k+2}{\ominus }_{\mathit{gH}}{y}_{k+1}={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{x_{k+1}}^{x_{k+2}}{(x_{k+2}-x)}^{\alpha -1}f\left(x,y\left(x\right)\right)dx.$$

(8)

Thus, by substituting the fuzzy-valued function f with the Newton’s fuzzy forward interpolation polynomial $p(x,y(x\left)\right)$ at the points $(x_k,f_k)$, $(x_{k+1},f_{k+1})$ and $(x_{k+2},f_{k+2})$ in Equation (8) as well as using the definition of forward finite gH-differences we obtain

$$\begin{array}{cc}\hfill y_{k+2}{\ominus }_{\mathit{gH}}{y}_{k+1}& ={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}\odot {\int }_{x_{k+1}}^{x_{k+2}}{(x_{k+2}-x)}^{\alpha -1}\odot (f_k\oplus \theta \odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\oplus {\displaystyle \frac{\theta (\theta -1)}{2}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k)dx\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot {\int }_1^2{(2-\theta )}^{\alpha -1}\odot (f_k\oplus \theta \odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\oplus {\displaystyle \frac{{\theta }^2-\theta }{2}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k)d\theta \hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\left({\int }_1^2{(2-\theta )}^{\alpha -1}d\theta \right)\odot f_k\oplus \left({\int }_1^2\theta {(2-\theta )}^{\alpha -1}d\theta \right)\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}\oplus {\displaystyle \frac{1}{2}}\left({\int }_1^2({\theta }^2-\theta ){(2-\theta )}^{\alpha -1}d\theta \right)\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\left(-{\displaystyle \frac{{(2-\theta )}^{\alpha }}{\alpha }}\right){|}_1^2\odot f_k\oplus \left(-{\displaystyle \frac{\theta {(2-\theta )}^{\alpha }}{\alpha }}-{\displaystyle \frac{{(2-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}\right){|}_1^2\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}\oplus [(\theta -1)\left(-{\displaystyle \frac{\theta {(2-\theta )}^{\alpha }}{\alpha }}-{\displaystyle \frac{{(2-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}\right)\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot \left[\right(\oplus [}+{\displaystyle \frac{\theta {(2-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}+{\displaystyle \frac{{(2-\theta )}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{{(2-\theta )}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}}]{|}_1^2\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [{\displaystyle \frac{1}{\alpha }}\odot f_k\oplus \left({\displaystyle \frac{1}{\alpha }}+{\displaystyle \frac{1}{\alpha (\alpha +1)}}\right)\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}{\ominus }_{\mathrm{H}}{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{\alpha (\alpha +1)}}+{\displaystyle \frac{2}{\alpha (\alpha +1)(\alpha +2)}}\right)\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot \left[{\displaystyle \frac{1}{\alpha }}\odot f_k\oplus {\displaystyle \frac{\alpha +2}{\alpha (\alpha +1)}}\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k{\ominus }_{\mathrm{H}}{\displaystyle \frac{\alpha +4}{2\alpha (\alpha +1)(\alpha +2)}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k\right]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\alpha (\alpha +1)(\alpha +2)\mathrm{\Gamma }\left(\alpha \right)}}\odot [(\alpha +1)(\alpha +2)\odot f_k\oplus {(\alpha +2)}^2\odot \left(f_{k+1}{\ominus }_{\mathit{gH}}{f}_k\right)\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\alpha (\alpha +1)(\alpha +2)\mathrm{\Gamma }\left(\alpha \right)}}\odot [}{\ominus }_{\mathrm{H}}{\displaystyle \frac{\alpha +4}{2}}\odot (f_{k+2}{\ominus }_{\mathit{gH}}2\odot f_{k+1}\odot f_k\left)\right].\hfill \end{array}$$

(9)

3.2.3. Fuzzy Generalized A-M Three-Step Method with Forward Finite gH-Differences

To solve the FFIVP (5) using the fuzzy generalized A-M three-step method with forward finite gH-differences, suppose one more time that $k=1,2,\dots ,N-1$ is a fixed integer, $y\left(x_k\right)$, $y\left(x_{k+1}\right)$, $y\left(x_{k+2}\right)$ and $y\left(x_{k+3}\right)$ are fuzzy initial values, i.e., $(x_k,f_k)$, $(x_{k+1},f_{k+1})$, $(x_{k+2},f_{k+2})$ and $(x_{k+3},f_{k+3})$ are known fuzzy numbers and also,

$${\mathrm{\Delta }}_{\mathit{gH}}{f}_k=f_{k+1}{\ominus }_{\mathit{gH}}{f}_k,\theta ={\displaystyle \frac{x-x_k}{h}}.$$

In particular, $x=x_k+\theta h$ and we obtain

$$\begin{array}{cc}\hfill x_{k+3}-x& =x_{k+3}-x_k-\theta h=(x_{k+3}-x_{k+2})+(x_{k+2}-x_{k+1})+(x_{k+1}-x_k)-\theta h\hfill \\ \hfill & =h+h+h-\theta h=(3-\theta )h.\hfill \end{array}$$

Then the Newton’s fuzzy forward interpolation polynomial at $(x_k,f_k)$, $(x_{k+1},f_{k+1})$, $(x_{k+2},f_{k+2})$ and $(x_{k+3},f_{k+3})$ is

$$p\left(x,y\left(x\right)\right)=f_k\oplus \theta \odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\oplus {\displaystyle \frac{\theta (\theta -1)}{2}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k\oplus {\displaystyle \frac{\theta (\theta -1)(\theta -2)}{6}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^3{f}_k.$$

Now, assume that Equation (1)(i) holds. Taking integral over the closed interval $[x_{k+2},x_{k+3}]$ from the first equality in the FFIVP (5) leads us to

$${\int }_{x_{k+2}}^{x_{k+3}}{D}^{\alpha }{y}_{\mathit{gH}}\left(x\right)dx=I_{[x_{k+2},x_{k+3}]}^{\alpha }f\left(x,y\left(x\right)\right),$$

and so

$$y_{k+3}{\ominus }_{\mathit{gH}}{y}_{k+2}={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{x_{k+2}}^{x_{k+3}}{(x_{k+3}-x)}^{\alpha -1}f\left(x,y\left(x\right)\right)dx.$$

(10)

Thus, by substituting the fuzzy-valued function f with Newton’s fuzzy forward interpolation polynomial $p(x,y(x\left)\right)$ at the points $(x_k,f_k)$, $(x_{k+1},f_{k+1})$, $(x_{k+2},f_{k+2})$ and $(x_{k+3},f_{k+3})$ in Equation (10) as well as using the definition of forward finite gH-differences obtain

$$\begin{array}{cc}\hfill y_{k+3}{\ominus }_{\mathit{gH}}{y}_{k+2}& ={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}\odot {\int }_{x_{k+2}}^{x_{k+3}}{(x_{k+3}-x)}^{\alpha -1}(f_k\oplus \theta \odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\oplus {\displaystyle \frac{\theta (\theta -1)}{2}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}\odot {\int }_{x_{k+2}}^{x_{k+3}}{(x_{k+3}-x)}^{\alpha -1}(}\oplus {\displaystyle \frac{\theta (\theta -1)(\theta -2)}{6}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^3{f}_k)dx\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot {\int }_2^3{(3-\theta )}^{\alpha -1}(f_k\oplus \theta \odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\oplus {\displaystyle \frac{\theta (\theta -1)}{2}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot {\int }_2^3{(3-\theta )}^{\alpha -1}(}\oplus {\displaystyle \frac{\theta (\theta -1)(\theta -2)}{6}}\odot {\mathrm{\Delta }}_{\mathit{gH}}^3{f}_k)d\theta \hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\left({\int }_2^3{(3-\theta )}^{\alpha -1}d\theta \right)\odot f_k\oplus \left({\int }_2^3{(3-\theta )}^{\alpha -1}\theta d\theta \right)\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}\oplus {\displaystyle \frac{1}{2}}\left({\int }_2^3\theta (\theta -1){(3-\theta )}^{\alpha -1}d\theta \right)\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}\oplus {\displaystyle \frac{1}{6}}\left({\int }_2^3\theta (\theta -1)(\theta -2){(3-\theta )}^{\alpha -1}d\theta \right)\odot {\mathrm{\Delta }}_{\mathit{gH}}^3]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\left(-{\displaystyle \frac{{(3-\theta )}^{\alpha }}{\alpha }}\right){|}_2^3\odot f_k\oplus \left(-{\displaystyle \frac{\theta {(3-\theta )}^{\alpha }}{\alpha }}-{\displaystyle \frac{{(3-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}\right){|}_2^3\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}\oplus {\displaystyle \frac{1}{2}}[(\theta -1)\left(-{\displaystyle \frac{\theta {(3-\theta )}^{\alpha }}{\alpha }}-{\displaystyle \frac{{(3-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}\right)\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\oplus {\displaystyle \frac{1}{2}}[}-{\displaystyle \frac{\theta {(3-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}-{\displaystyle \frac{2{(3-\theta )}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}}]{|}_2^3\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}\oplus {\displaystyle \frac{1}{6}}[(\theta -2)(\theta -1)\left(-{\displaystyle \frac{\theta {(3-\theta )}^{\alpha }}{\alpha }}-{\displaystyle \frac{{(3-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}\right)\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\oplus {\displaystyle \frac{1}{6}}[}-(\theta -2)\left({\displaystyle \frac{\theta {(3-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}+{\displaystyle \frac{2{(3-\theta )}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}}\right)\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\oplus {\displaystyle \frac{1}{6}}[}-(\theta -1)\left({\displaystyle \frac{\theta {(3-\theta )}^{\alpha +1}}{\alpha (\alpha +1)}}+{\displaystyle \frac{{(3-\theta )}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}}\right)\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\oplus {\displaystyle \frac{1}{6}}[}+{\displaystyle \frac{\theta {(3-\theta )}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{2{(3-\theta )}^{\alpha +3}}{\alpha (\alpha +1)(\alpha +2)(\alpha +3)}}\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\oplus {\displaystyle \frac{1}{6}}[}+{\displaystyle \frac{(\theta -1){(3-\theta )}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{2{(3-\theta )}^{\alpha +3}}{\alpha (\alpha +1)(\alpha +2)(\alpha +3)}}\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\oplus {\displaystyle \frac{1}{6}}[}+{\displaystyle \frac{\theta {(3-\theta )}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{2{(3-\theta )}^{\alpha +3}}{\alpha (\alpha +1)(\alpha +2)(\alpha +3)}}]{|}_2^3\odot {\mathrm{\Delta }}_{\mathit{gH}}^3{f}_k]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [{\displaystyle \frac{1}{\alpha }}\odot f_k{\ominus }_{\mathrm{H}}\left(-{\displaystyle \frac{2}{\alpha }}-{\displaystyle \frac{1}{\alpha (\alpha +1)}}\right)\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}{\ominus }_{\mathrm{H}}{\displaystyle \frac{1}{2}}\left(-{\displaystyle \frac{2}{\alpha }}-{\displaystyle \frac{1}{\alpha (\alpha +1)}}-{\displaystyle \frac{2}{\alpha (\alpha +1)}}-{\displaystyle \frac{1}{\alpha (\alpha +1)(\alpha +2)}}\right)\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}\oplus {\displaystyle \frac{1}{6}}({\displaystyle \frac{2}{\alpha (\alpha +1)}}+{\displaystyle \frac{1}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{2}{\alpha (\alpha +1)(\alpha +2)}}\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\oplus {\displaystyle \frac{1}{6}}(}+{\displaystyle \frac{2}{\alpha (\alpha +1)(\alpha +2)(\alpha +3)}}+{\displaystyle \frac{1}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{2}{\alpha (\alpha +1)(\alpha +2)(\alpha +3)}}\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [\oplus {\displaystyle \frac{1}{6}}(}+{\displaystyle \frac{2}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{2}{\alpha (\alpha +1)(\alpha +2)(\alpha +3)}}\left)\right]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [{\displaystyle \frac{1}{\alpha }}\odot f_k\oplus {\displaystyle \frac{2\alpha +3}{\alpha (\alpha +1)}}\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\oplus {\displaystyle \frac{1}{2}}\left({\displaystyle \frac{2(\alpha +1)(\alpha +2)+3(\alpha +2)+2}{\alpha (\alpha +1)(\alpha +2)}}\right)\odot {\mathrm{\Delta }}_{\mathit{gH}}^2{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}}\odot [}\oplus {\displaystyle \frac{1}{6}}\left({\displaystyle \frac{2(\alpha +2)(\alpha +3)+6(\alpha +3)+6}{\alpha (\alpha +1)(\alpha +2)(\alpha +3)}}\right)\odot {\mathrm{\Delta }}_{\mathit{gH}}^3]\hfill \\ \hfill & ={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +4)}}\odot [(\alpha +1)(\alpha +2)(\alpha +3)\odot f_k\oplus (2\alpha +3)(\alpha +2)(\alpha +3)\odot {\mathrm{\Delta }}_{\mathit{gH}}{f}_k\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +4)}}\odot [}\oplus {\displaystyle \frac{1}{2}}\left(2(\alpha +1)(\alpha +2)(\alpha +3)+3(\alpha +2)(\alpha +3)+2(\alpha +3)\right)\odot {\mathrm{\Delta }}_{\mathit{gH}}^2\hfill \\ \hfill & \phantom{={\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +4)}}\odot [}\oplus {\displaystyle \frac{1}{6}}\left(2(\alpha +2)(\alpha +3)+6(\alpha +3)+6\right)\odot {\mathrm{\Delta }}_{\mathit{gH}}^3].\hfill \end{array}$$

(11)

4. Analysis of the Fuzzy Generalized Adams Methods

Now, are explored the local truncation error (LTE) and the global truncation error (GTE) associated with the fuzzy generalized Adams methods. Our aim is to establish the consistency, the convergence as well as the stability of the developed methods. It is important to note that our investigation here is limited to the fuzzy generalized A-B two-step method. Here is focused on this method because the proofs for other methods in this category are quite similar and would follow analogous lines of reasoning.

4.1. Local Truncation Error (LTE)—Consistency

Let the FFIVP (5) have a unique solution y. First, define the residual of y. Therefore, consider the two types of differentiability of y separately.

Definition 12. 

Let y be the unique solution of the FFIVP (5). Define the residual ${\mathcal{R}}_k$ under two different cases:

1. 

In the case that y is FC1-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, have

$${\mathcal{R}}_k=y\left(x_{k+1}\right){\ominus }_{\mathit{gH}}\left(y\left(x_k\right)\oplus {\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\odot \left((\alpha +2)f\left(x_k,y\left(x_k\right)\right){\ominus }_{\mathit{gH}}f\left(x_{k-1},y\left(x_{k-1}\right)\right)\right)\right).$$

2. 

In the case that y is FC2-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, have

$${\mathcal{R}}_k=y\left(x_{k+1}\right){\ominus }_{\mathit{gH}}\left(y\left(x_k\right)\ominus (-1){\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\odot \left((\alpha +2)f\left(x_k,y\left(x_k\right)\right){\ominus }_{\mathit{gH}}f\left(x_{k-1},y\left(x_{k-1}\right)\right)\right)\right).$$

Now go on the local truncation error (LTE) as well as the consistency of y.

Definition 13. 

Let y be the unique solution of the FFIVP (5) and ${\mathcal{R}}_k$ is its residual.

1. 

The local truncation error (LTE) is denoted by ${\tau }_k$ and is defined as

$${\tau }_k={\displaystyle \frac{1}{h^{\alpha }}}{\mathcal{R}}_k.$$

2. 

The fuzzy generalized Adams methods are consistent if

$$\underset{h\to 0}{lim}\underset{t_k\le T}{max}\mathcal{H}({\tau }_k,0)=0.$$

Remark 8. 

Let y be the unique solution of the FFIVP (5). For ${\eta }_k\in [x_k,x_{k+1}]$, depending upon the type of the differentiability of y, the LTE ${\tau }_k$ and the residual ${\mathcal{R}}_k$ are formulated as follows:

1. 

In the case that y is FC1-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, have

$$\begin{array}{cc}\hfill & {\tau }_k=h^{\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)\odot {}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{1.\mathit{gH}}\left({\eta }_k\right),\hfill \\ \hfill & {\mathcal{R}}_k=h^{2\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)\odot {}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{1.\mathit{gH}}\left({\eta }_k\right).\hfill \end{array}$$

2. 

In the case that y is FC2-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, have

$$\begin{array}{cc}\hfill & {\tau }_k=\ominus (-1)h^{\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)\odot {}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{2.\mathit{gH}}\left({\eta }_k\right),\hfill \\ \hfill & {\mathcal{R}}_k=\ominus (-1)h^{2\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)\odot {}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{2.\mathit{gH}}\left({\eta }_k\right).\hfill \end{array}$$

Now, it is ready to prove the consistency of the fuzzy generalized Adams methods. To this end, let

$$\mathcal{H}\left({}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{1.\mathit{gH}}\left({\eta }_k\right),0\right)\le M,$$

where $M>0$. There are two cases:

Case One. If y is FC1-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, then

$$\begin{array}{cc}\hfill \underset{h\to 0}{lim}\underset{t_k\le T}{max}\mathcal{H}({\tau }_k,0)& =\underset{h\to 0}{lim}\underset{t_k\le T}{max}\mathcal{H}\left(h^{\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)\odot {}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{1.\mathit{gH}}\left({\eta }_k\right),0\right)\hfill \\ \hfill & =\underset{h\to 0}{lim}\left|h^{\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)\right|\underset{t_k\le T}{max}\mathcal{H}\left({}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{1.\mathit{gH}}\left({\eta }_k\right),0\right)\hfill \\ \hfill & =\underset{h\to 0}{lim}{h}^{\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)·\mathcal{H}\left({}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{1.\mathit{gH}}\left({\eta }_k\right),0\right)\hfill \\ \hfill & \le \underset{h\to 0}{lim}{h}^{\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)·M=0.\hfill \end{array}$$

Case Two. If y is FC2-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, then a similar argument proves the consistency of the methods.

It should be noted that the fuzzy generalized Adams methods are consistent until the solution y lies in ${\mathcal{C}}_f([0,T],{\mathbb{R}}_{\mathcal{F}})$.

4.2. Global Truncation Error (GTE)—Convergence

Lemma 2 

([30]). For every $z\in \mathbb{R}$, we have $1+z\le e^z$.

Definition 14. 

Let y be the unique solution of the FFIVP (5) and ${\mathcal{R}}_k$ is its residual.

1. 

The global truncation error (GTE) is denoted by $e_k$ and is defined as the accumulation of the LTE on all iterations, considering good information of y at the initial time step.

2. 

The fuzzy generalized Adams methods are convergent if the GTE tends to 0 whenever the step size approaches 0, i.e.,

$$\underset{h\to 0}{lim}\underset{k}{max}\mathcal{H}\left(y(x_{k+1},y_{k+1})\right)=0$$

whenever

$$\underset{h\to 0}{lim}\underset{k}{max}\mathcal{H}(e_{k+1},0)=0.$$

Remark 9. 

Let y be the unique solution of the FFIVP (5). Independent from the type of differentiability of y, the GTE $e_{k+1}$ can be written by $e_{k+1}=y\left(x_{k+1}\right){\ominus }_{\mathit{gH}}{y}_{k+1}$.

Now, start the proof of the convergence of our developed fuzzy methods. To this end, let ${}^{\mathrm{FC}}D_{*}^{2\alpha }y\left(t\right)$ exist and f satisfies the Lipschitz condition on the region

$$\left\{(x,y)|x\in [0,p],y\in \overline{B}(y_0,q),p,q>0\right\}.$$

We have two cases:

Case One. If y is FC1-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, then

$$y\left(x_{k+1}\right)=y\left(x_k\right)\oplus {\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\left[(\alpha +2)f\left(x_k,y\left(x_k\right)\right){\ominus }_{\mathit{gH}}f\left(x_{k-1},y\left(x_{k-1}\right)\right)\right]+r_k.$$

So have

$$\begin{array}{cc}\hfill \mathcal{H}\left(y\left(x_{k+1}\right),y_{k+1}\right)& =\mathcal{H}\left(y\left(x_k\right),y_k\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\left[\mathcal{H}\right((\alpha +2)f\left(x_k,y\left(x_k\right)\right){\ominus }_{\mathit{gH}}f\left(x_{k-1},y\left(x_{k-1}\right)\right),\hfill \\ \hfill & \phantom{=\mathcal{H}\left(y\left(x_k\right),y_k\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}[}f(x_k,y_k){\ominus }_{\mathit{gH}}f(x_{k-1},y_{k-1})\left)\right]+\mathcal{H}(r_k,0)\hfill \\ \hfill & \le \mathcal{H}\left(y\left(x_k\right),y_k\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}[(\alpha +2)\mathcal{H}\left(f\left(x_k,y\left(x_k\right)\right),f(x_k,y_k)\right)\hfill \\ \hfill & \phantom{\le \mathcal{H}\left(y\left(x_k\right),y_k\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}[}+\mathcal{H}\left(f\left(x_{k-1},y\left(x_{k-1}\right)\right),f(x_{k-1},y_{k-1})\right)]+\mathcal{H}(r_k,0).\hfill \end{array}$$

On the other hand,

$$\mathcal{H}\left(f\left(x_k,y\left(x_k\right)\right),f(x_k,y_k)\right)\le {\ell }_k\mathcal{H}\left(y\left(x_k\right),y_k\right)$$

and

$$\mathcal{H}\left(f\left(x_{k-1},y\left(x_{k-1}\right)\right),f(x_{k-1},y_{k-1})\right)\le {\ell }_{k-1}\mathcal{H}\left(y\left(x_{k-1}\right),y_{k-1}\right)\le {\ell }_{k-1}\mathcal{H}\left(y\left(x_k\right),y_k\right),$$

where ${\ell }_k$ is the Lipschitz constant of f. Therefore, putting

$$\ell =\underset{0\le k\le N-1}{max}{\ell }_k\mathrm{and}r=\underset{0\le k\le N-1}{max}\mathcal{H}(r_k,0)$$

gets

$$\begin{array}{cc}\hfill \mathcal{H}\left(y(x_{k+1}),y_{k+1}\right)& \le \mathcal{H}\left(y(x_k),y_k\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\left[(\alpha +2)\ell +\ell \right]\mathcal{H}\left(y(x_k),y_k\right)+r\hfill \\ \hfill & =\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)\mathcal{H}\left(y(x_k),y_k\right)+r.\hfill \end{array}$$

Because the last inequality is true for every positive integer k, hence

$$\begin{array}{cc}\hfill \mathcal{H}\left(y(x_{k+1}),y_{k+1}\right)& \le \left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)\left(\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)\mathcal{H}\left(y(x_{k-1}),y_{k-1}\right)+r\right)+r\hfill \\ \hfill & ={\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)}^2\mathcal{H}\left(y(x_{k-1}),y_{k-1}\right)+r\left[1+\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)\right].\hfill \end{array}$$

Repeating this argument yields

$$\mathcal{H}\left(y(x_{k+1}),y_{k+1}\right)\le {\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)}^{k+1}\mathcal{H}\left(y(x_0),y_0\right)+r\left[1+\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)+\cdots +\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)\right]$$

and from the summation formula

$$\sum _{i=0}^k{\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)}^i={\displaystyle \frac{1-{(1+\frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)})}^{k+1}}{-\frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}}$$

of geometric sequences obtain

$$\mathcal{H}\left(y(x_{k+1}),y_{k+1}\right)\le (1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\mathcal{H}\left(y(x_0),y_0\right)+{\displaystyle \frac{r\mathrm{\Gamma }(\alpha +2)}{h^{\alpha }\ell (\alpha +3)}}\left[1-{\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)}^{k+1}\right].$$

(12)

Now, set $z={\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}$ in Lemma 2. Then

$${\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)}^{k+1}\le e^{{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}·(k+1)}\le e^{{\displaystyle \frac{\ell T}{\mathrm{\Gamma }(\alpha +2)}}}$$

where $0\le (k+1)h^{\alpha }(\alpha +3)\le T$ for $k+1\le N-1$. Thus, in (12) find

$$\mathcal{H}\left(y(x_{k+1}),y_{k+1}\right)\le e^{{\displaystyle \frac{\ell T}{\mathrm{\Gamma }(\alpha +2)}}}\mathcal{H}\left(y(t_0),y_0\right)+{\displaystyle \frac{r\mathrm{\Gamma }(\alpha +2)}{h^{\alpha }\ell (\alpha +3)}}\left[1-e^{{\displaystyle \frac{\ell T}{\mathrm{\Gamma }(\alpha +2)}}}\right].$$

Moreover,

$$r=\underset{0\le k\le N-1}{max}\mathcal{H}(r_k,0)=h^{2\alpha }\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)\underset{0\le t\le T}{max}\mathcal{H}\left({}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{1.\mathit{gH}}(x),0\right).$$

If the initial value is chosen accurately enough, then we obtain $\mathcal{H}(y(x_0),y_0)=0$. Hence

$$\mathcal{H}\left(y(x_{k+1}),y_{k+1}\right)\le {\displaystyle \frac{r{h}^{\alpha }\mathrm{\Gamma }(\alpha +2)}{\ell (\alpha +3)}}\left({\displaystyle \frac{1}{\mathrm{\Gamma }(2\alpha +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha +2)\mathrm{\Gamma }(\alpha +1)}}\right)\underset{0\le t\le T}{max}\mathcal{H}\left({}^{\mathit{FC}}D_{*}^{2\alpha }{y}_{1.\mathit{gH}}(x),0\right).$$

Finally, letting $h\to 0$, find $\mathcal{H}(y(x_{k+1}),y_{k+1})\to 0$.

Case Two. If y is FC2-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, then a similar argument proves the convergence of the methods.

5. Stability

Now, is investigated the stability of our developed fuzzy methods. First, have a definition.

Definition 15. 

Let $y_0\in {\mathbb{R}}_{\mathcal{F}}$, $y_{k+1}$ for $k+1\ge 0$ be the solution obtained from the fuzzy generalized Adams methods and $z_{k+1}$ be the solution obtained from that method where $z_0=y_0\oplus {\delta }_0\in {\mathbb{R}}_{\mathcal{F}}$ determines the perturbed fuzzy initial condition. The fuzzy generalized Adams methods are stable whenever there are positive constants $\widehat{h}$ and $\mathcal{K}$ such that for all $k\in \mathbb{N}$ with $(k+1)h^{\alpha }(\alpha +3)\le T$ and $k+1<N-1$ and all $h\in (0,\widehat{h})$, $\mathcal{H}({\delta }_0,0)\le \delta$ implies $\mathcal{H}(z_{k+1},y_{k+1})\le \mathcal{K}\delta$.

Now, prove the stability of our developed fuzzy methods. There are two cases:

Case One. If y is FC2-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, then the perturbed problem can be formulated as

$$z_{k+1}=z_k\ominus (-1){\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\odot \left((\alpha +2)f(x_k,z_k){\ominus }_{\mathit{gH}}f(x_{k-1},z_{k-1})\right),z_0=y_0\oplus {\delta }_0.$$

Thus,

$$\mathcal{H}(z_{k+1},y_{k+1})\le \mathcal{H}(z_k,y_k)-{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\mathcal{H}\left((\alpha +2)f(x_k,z_k).(\alpha +2)f(x_k,y_z)\right)+\mathcal{H}\left(f(x_{k-1},z_{k-1}),f(x_{k-1},y_{k-1})\right),$$

Here, assume that the Hausdorff metric specifications hold. Therefore, applying the Lipschitz condition obtain

$$\mathcal{H}(z_{k+1},y_{k+1})\le \left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)\mathcal{H}(z_k,y_k).$$

Redoing this argument and using Lemma 2 yield

$$\begin{array}{cc}\hfill \mathcal{H}(z_{k+1},y_{k+1})& \le {\left(1+{\displaystyle \frac{h^{\alpha }\ell (\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}\right)}^{k+1}\mathcal{H}(z_0,y_0)\hfill \\ \hfill & \le e^{{\displaystyle \frac{h^{\alpha }(\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}}·\ell (k+1)}\mathcal{H}(z_0{\ominus }_{\mathit{gH}}{y}_0,0)\hfill \\ \hfill & \le e^{{\displaystyle \frac{\ell T}{\mathrm{\Gamma }(\alpha +2)}}}\mathcal{H}({\delta }_0,0)\le \mathcal{K}\delta \hfill \end{array}$$

for all $k\in \mathbb{N}$ with $(k+1)h^{\alpha }(\alpha +3)\le T$ and $k+1<N-1$ and all $h\in (0,\widehat{h})$, where $\mathcal{K}=e^{{\displaystyle \frac{\ell T}{\mathrm{\Gamma }(\alpha +2)}}}$.

Case Two. If y is FC1-gH-differentiable on the interval $[0,T]$ and the type of the differentiability remains unchanged, then a similar argument proves the stability of the methods.

Theorem 2. 

Let $y\left(t\right)$ be a solution to the fuzzy fractional differential equation (FFDE)

$$D^{\alpha }y\left(t\right)=f(t,y\left(t\right)),0<\alpha \le 1,$$

with the initial condition $y\left(0\right)=y_0$. If $f(t,y)$ is invariant under the transformation $t\to -t$ and $y\to -y$, then the solution $y\left(t\right)$ exhibits symmetry about the origin, i.e., $y(-t)=-y\left(t\right)$.

Proof. 

Consider the fuzzy fractional differential equation

$$D^{\alpha }y\left(t\right)=f(t,y\left(t\right)),$$

with the initial condition $y\left(0\right)=y_0$.

Apply the transformation $t\to -t$ and $y\to -y$. Let $v\left(t\right)=-y(-t)$. Then,

$$D^{\alpha }v\left(t\right)=D^{\alpha }(-y(-t)).$$

Using the property of the fractional derivative, we have

$$D^{\alpha }(-y(-t))=-D^{\alpha }\left(y(-t)\right).$$

Substitute $t\to -t$ in the original equation:

$$D^{\alpha }\left(y(-t)\right)=f(-t,y(-t)).$$

Given that $f(t,y)$ is invariant under the transformation $t\to -t$ and $y\to -y$, we have

$$f(-t,y(-t\left)\right)=-f(t,-y(t\left)\right).$$

Therefore,

$$-D^{\alpha }\left(y(-t)\right)=-f(t,-y\left(t\right)).$$

Simplifying, we obtain

$$D^{\alpha }v\left(t\right)=f(t,v\left(t\right)).$$

Since $v\left(t\right)=-y(-t)$ satisfies the same differential equation as $y\left(t\right)$, and given the initial condition $v\left(0\right)=-y\left(0\right)=-y_0$, it follows that $v\left(t\right)=y\left(t\right)$. Hence,

$$y(-t)=-y\left(t\right).$$

Thus, the solution $y\left(t\right)$ exhibits symmetry about the origin. □

6. Some Numerical Simulations

In the last section of the present paper, three examples of the FFDEs using present fuzzy generalized Adams methods are solved. Beside each example, the numerical results obtained by MATLAB R2023a are demonstrated in some tables and figures.

Example 1. 

Consider the initial value problem (IVP)

$$\left\{\begin{array}{c}{}^{\mathit{FC}}D_{*}^{\alpha }y\left(x\right)=(0,1,1.5)\odot \mathrm{\Gamma }(\alpha +1)(0<x\le 1),\hfill \\ y\left(0\right)=0.\hfill \end{array}\right.$$

(13)

The exact FC1-gH-differentiable solution to the IVP (13) is $y\left(x\right)=(0,1,1.5)\odot x^{\alpha }$. This problem has been solved using suggested methods. To this end, first construct the iteration

$$y_{k+1}=y_k\oplus {\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\odot \left[(\alpha +2)f_k{\ominus }_{\mathit{gH}}{f}_{k-1}\right]k=0,1,\dots ,N-1.$$

Table 1 demonstrates the numerical results based on our methods for different values of h and $\alpha$.

Table 1. Numerical results of the IVP (13) using our methods for different values of h and $\alpha$.

h	$\mathit{\alpha }=0.1$	$\mathit{\alpha }=0.3$	$\mathit{\alpha }=0.5$	$\mathit{\alpha }=0.9$
$0.1$	$(0.7943,11.52)$	$(1.504,6.766)$	$(1.581,3.953)$	$(1.133,1.322)$
$0.02$	$(3.381,49.03)$	$(4.639,20.87)$	$(3.536,8.839)$	$(1.331,1.553)$
$0.01$	$(6.31,91.49)$	$(7.536,33.91)$	$(5.0,12.5)$	$(1.426,1.664)$
$0.005$	$(11.77,170.7)$	$(12.24,55.09)$	$(7.071,17.68)$	$(1.529,1.784)$

Figure 1 shows the exact solution as well as the Caputo gH-derivative of the solution plots for $\alpha =0.6$.

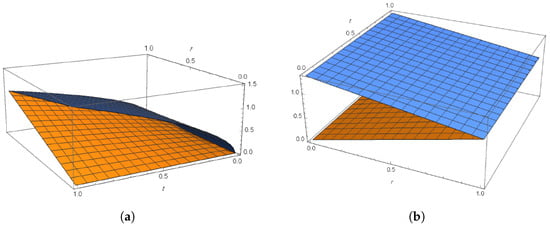
Figure 1. Plots of the exact solution as well as the Caputo gH-derivative of the solution of the IVP (13) for $\alpha =0.6$. (a) The exact solution. (b) The Caputo gH-derivative of the solution.

Example 2. 

Consider the IVP

$$\left\{\begin{array}{c}{}^{\mathit{FC}}D_{*}^{\alpha }y\left(x\right)=(-1)\odot y\left(x\right)(0\le x\le 1),\hfill \\ y\left(0\right)=(0,1,2).\hfill \end{array}\right.$$

(14)

The exact FC2-gH-differentiable solution to the IVP (14) is $y\left(x\right)=(0,1,2)\odot E_{\alpha }(-x^{\alpha })$. This IVP has been solved using the suggested methods. To this end, first construct the iteration

$$y_0=(0,1,2),y_{k+1}=y_k{\ominus }_{\mathit{gH}}{\displaystyle \frac{(-1)h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\odot \left[(\alpha +2)f_k{\ominus }_{\mathit{gH}}{f}_{k-1}\right]k=0,1,\dots ,N-1.$$

Table 2 demonstrates the numerical results based on methods for different values of h and $\alpha$.

Table 2. Numerical results of the IVP (14) using methods for different values of h and $\alpha$.

h	$\mathit{\alpha }=0.1$	$\mathit{\alpha }=0.3$	$\mathit{\alpha }=0.5$	$\mathit{\alpha }=0.9$
$0.1$	$(-0.1244,1.571)$	$(-0.005697,-1.606)$	$(0.0003713,1.606)$	$(0.03217,0.1281)$
$0.02$	$(-2.836\times {10}^{-5},0.7497)$	$(-2.501\times {10}^{-15},1.069)$	$(1.289\times {10}^{-14},-1.553)$	$(0.0335,-1.234)$
$0.01$	$(1.538\times {10}^{-11},2.831)$	$(3.151\times {10}^{-34},1.116)$	$(3.176\times {10}^{-16},-0.1067)$	$(0.02834,0.4973)$
$0.005$	$(1.224\times {10}^{-25},0.1847)$	$(6.112\times {10}^{-77},0.1062)$	$(2.266\times {10}^{-20},-1.101)$	$(0.02296,-1.268)$

Figure 2 shows the exact solution as well as the Caputo gH-derivative of the solution plots for $\alpha =0.3$.

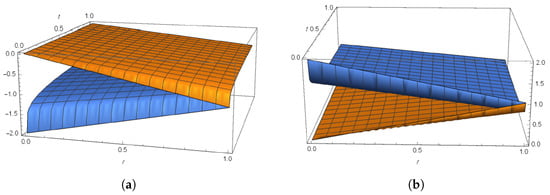
Figure 2. Plots of the exact solution as well as the Caputo gH-derivative of the solution of the IVP (14) for $\alpha =0.3$. (a) The exact solution. (b) The Caputo gH-derivative of the solution.

Example 3. 

Consider the nonlinear FDE under uncertainty

$$\left\{\begin{array}{c}{}^{\mathit{FC}}D_{*}^{\alpha }y\left(x\right)=g\left(x\right){\ominus }_{\mathit{gH}}{y}^2\left(x\right)\left(\alpha \in (0,1),x\in (0,1)\right),\hfill \\ y\left(0\right)=0.\hfill \end{array}\right.$$

(15)

where

$$g\left(x\right)=\left[{\displaystyle \frac{\mathrm{\Gamma }\left(6\right)}{\mathrm{\Gamma }(6-\alpha )}}{x}^{5-\alpha }-{\displaystyle \frac{\mathrm{\Gamma }\left(5\right)}{\mathrm{\Gamma }(5-\alpha )}}{x}^{4-\alpha }+{\displaystyle \frac{\mathrm{\Gamma }\left(4\right)}{\mathrm{\Gamma }(4-\alpha )}}{x}^{3-\alpha }+{(x^5-3x^4+2x^3)}^2\right]\odot \tilde{\eta },$$

and $\tilde{\eta }=(1,2,3)$ and $y\ne 0$. This problem has been solved using suggested methods. To find the FC1-gH-differentiable solution, first construct the iteration

$$y_{k+1}=y_k\oplus {\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\odot \left[(\alpha +2)f_k{\ominus }_{\mathit{gH}}{f}_{k-1}\right]k=0,1,\dots ,N-1.$$

Table 3 demonstrates the numerical results based on methods with different orders of differentiability and for different values of h and $\alpha$ at $x=1$.

Table 3. Numerical results of the nonlinear fractional differential Equation (15) using methods with different orders of differentiability and for different values of h and $\alpha$ at $x=1$.

h	$\mathit{\alpha }=0.5$	$\mathit{\alpha }=0.9$
$0.1$	$(3.8390,4.5277)$	$(2.3978,2.6392)$
$0.05$	$(4.18681,5.602055)$	$(2.77227,3.022708)$
$0.02$	$(4.339278,5.67121)$	$(2.98069,3.23426)$
$0.01$	$(4.4081617,5.738529)$	$(3.112012575,3.3697222)$

7. Conclusions

FDEs are one of the most interesting topics of fuzzy arithmetic. They have various applications in different branches, such as engineering and basic sciences. Therefore, developing numerical methods as well as analytical methods to solve the FDEs has a very high level of importance. In this work, the fuzzy generalized A-B method and the fuzzy generalized A-M method, which can be considered to be applications of the generalized Taylor expansion and applied for solving the FFDEs were introduced. Next, the LTE and the GTE, the convergence, the consistency, and the stability of the proposed methods were investigated, and finally, some examples were solved using the proposed methods. The numerical simulations done and the numerical results reported here showed that by reducing the step size, the convergence is established. The authors also hope to use these developed methods for solving impulsive fuzzy fractional differential equations (IFFDEs) in the next research.