Soliton Molecules, Multi-Lumps and Hybrid Solutions in Generalized (2 + 1)-Dimensional Date–Jimbo–Kashiwara–Miwa Equation in Fluid Mechanics
Abstract
:1. Introduction
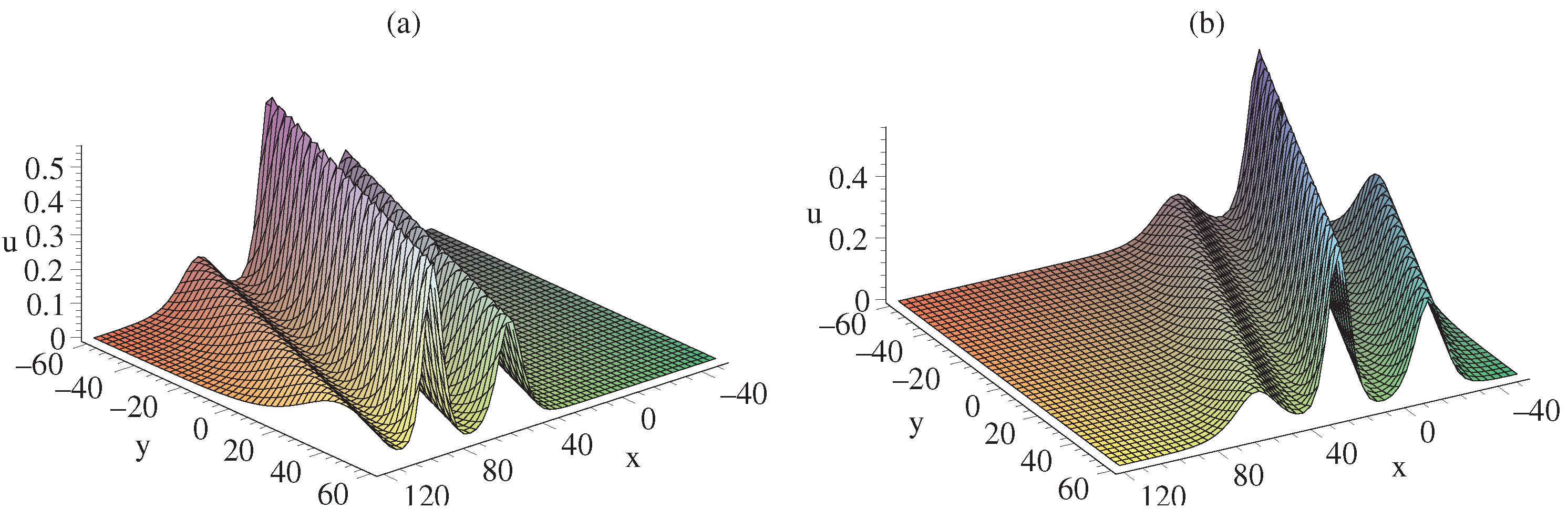
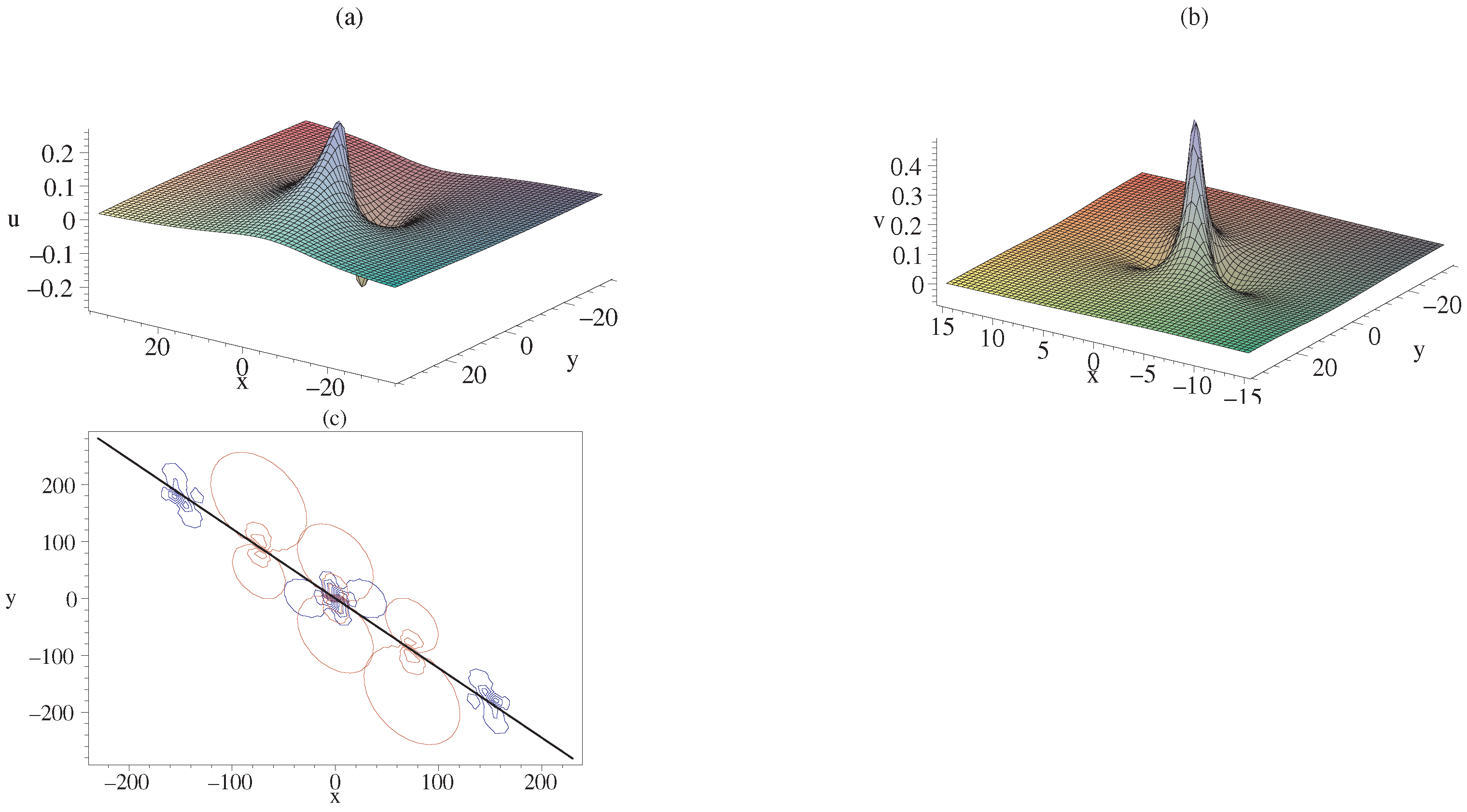
2. Soliton Molecules of gDJKM Equation
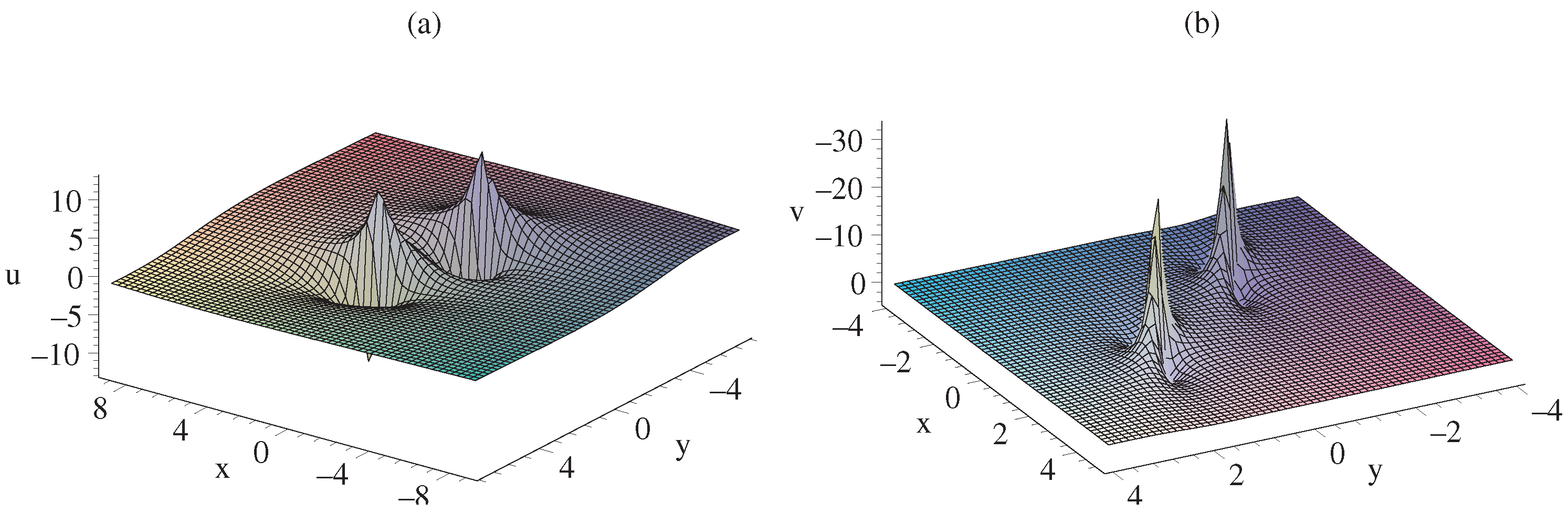
3. Multi-Order Lumps of gDJKM Equation
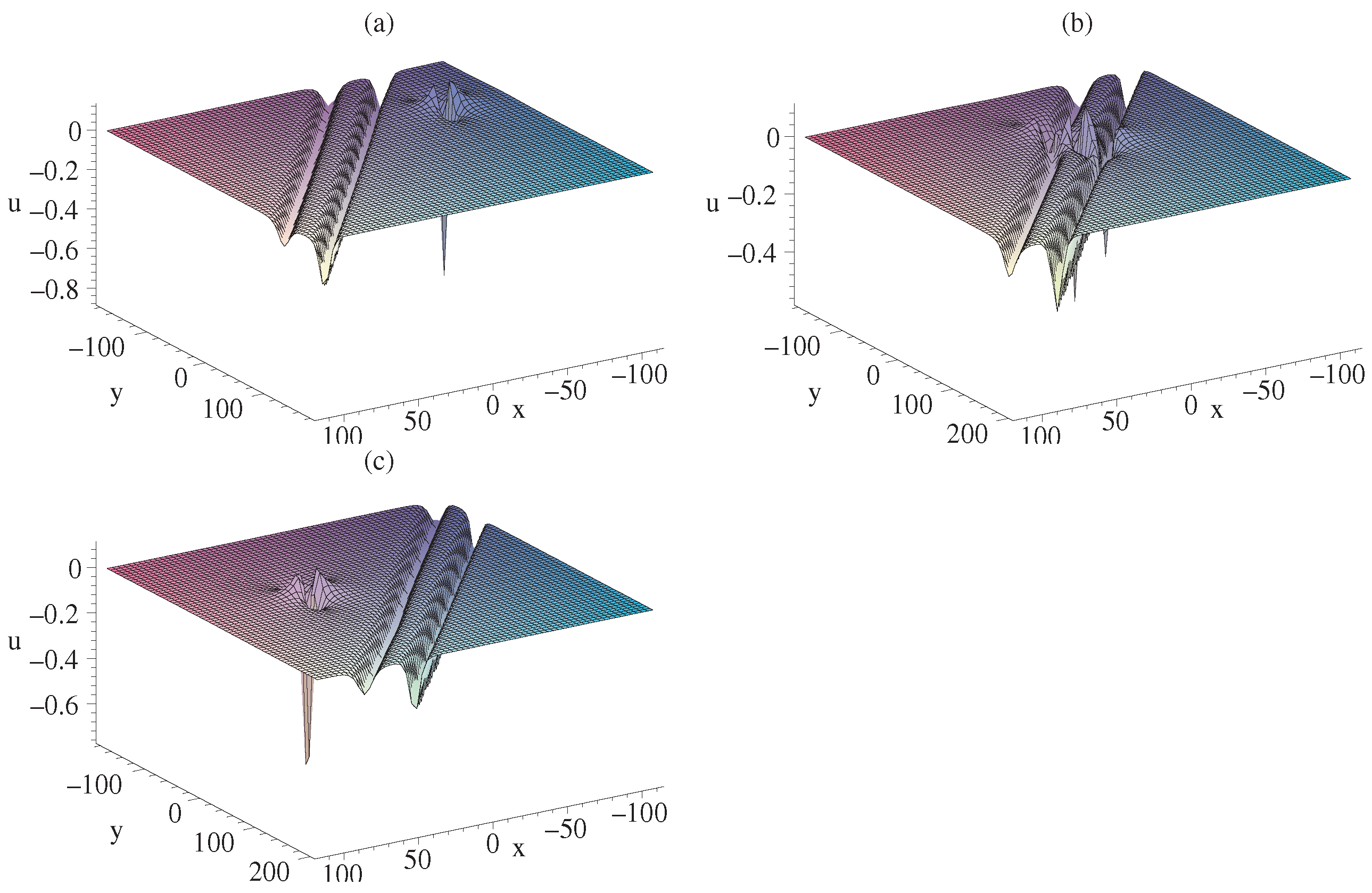
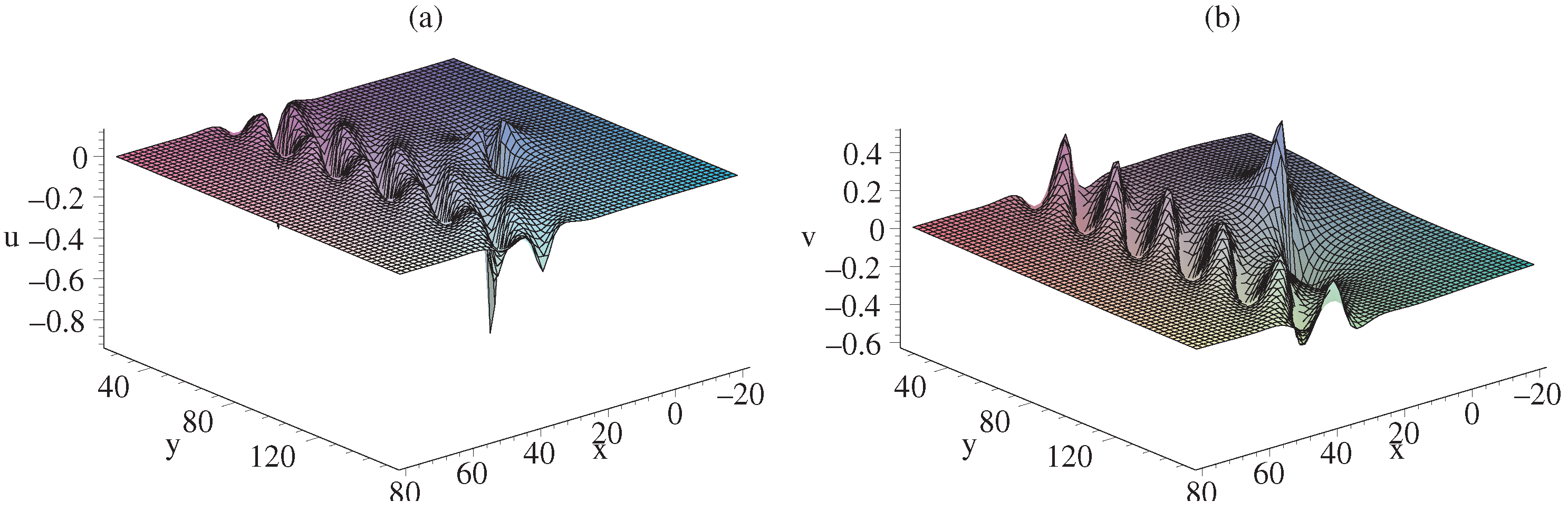
4. Interaction Among Lumps, Breathers and Soliton Molecules of gDJKM Equation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kadomtsev, B.B.; Petviashvili, V.I. On the stability of solitary waves in weakly dispersing media. Sov. Phys. Dokl. 1970, 15, 539. [Google Scholar]
- Lou, S.Y. Symmetries of the Kadomtsev-Petviashvili equation. J. Phys. A Math. Gen. 1993, 26, 4387. [Google Scholar]
- Lou, S.Y. A novel (2 + 1)-dimensional integrable KdV equation with peculiar solutions structures. Chin. Phys. B 2020, 29, 080502. [Google Scholar] [CrossRef]
- Wang, X.B.; Jia, M.; Lou, S.Y. Painlevé property, local and nonlocal symmetries, and symmetry reductions for a (2 + 1)-dimensional integrable KdV equation. Chin. Phys. B 2021, 30, 010501. [Google Scholar]
- Hietarinta, J. A search for bilinear equations passing Hirota’s three-soliton condition. I. KdV-type bilinear equations. J. Math. Phys. 1987, 28, 1732–1742. [Google Scholar] [CrossRef]
- Hietarinta, J. A search for bilinear equations passing Hirota’s three-soliton condition. II. mKdV-type bilinear equations. J. Math. Phys. 1987, 28, 2094–2101. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, Y.; Ma, W.X.; Hu, Y.W. Wronskian rational solutions to the generalized (2 + 1)-dimensional Date-Jimbo-Kashiwara-Miwa equation in fluid dynamics. Phys. Fluids 2024, 36, 017116. [Google Scholar]
- Guo, F.; Lin, J. Interaction solutions between lump and stripe soliton to the (2 + 1)-dimensional Date-Jimbo-Kashiwara-Miwa equation. Nonlinear Dyn. 2019, 96, 1233–1241. [Google Scholar] [CrossRef]
- Chauhan, A.; Sharma, K.; Arora, R. Lie symmetry analysis, optimal system, and generalized group invariant solutions of the (2 + 1)-dimensional Date-Jimbo-Kashiwara-Miwa equation. Math. Meth. Appl. Sci. 2020, 43, 8823–8840. [Google Scholar]
- Ozdemir, N.; Secer, A.; Ozisik, M.; Bayram, M. Soliton and other solutions of the (2 + 1)-dimensional Date-Jimbo-Kashiwara-Miwa equation with conformable derivative. Phys. Scr. 2023, 98, 015023. [Google Scholar]
- Malomed, B.A. Bound solitons in the nonlinear Schrödinger-Ginzburg-Landau equation. Phys. Rev. A 1991, 44, 6954. [Google Scholar] [PubMed]
- Wu, X.Q.; Peng, J.S.; Boscolo, S.; Finot, C.; Zeng, H.P. Synchronization, desynchronization, and intermediate regime of breathing solitons and soliton molecules in a laser cavity. Phys. Rev. Lett. 2023, 131, 263802. [Google Scholar] [PubMed]
- Wang, B.H.; Han, H.B.; Yu, L.J.; Wang, Y.Y.; Dai, C.Q. Generation and dynamics of soliton and soliton molecules from a VSe2/GO-based fiber laser. Nanophotonics 2022, 11, 129–137. [Google Scholar]
- Weng, W.L.; Bouchand, R.; Lucas, E.; Obrzud, E.; Herr, T.; Kippenberg, T.J. Heteronuclear soliton molecules in optical microresonators. Nat. Commun. 2020, 11, 2402. [Google Scholar] [PubMed]
- Lou, S.Y. Soliton molecules and asymmetric solitons in three fifth order systems via velocity resonance. J. Phys. Commun. 2020, 4, 041002. [Google Scholar]
- Li, Y.; Yao, R.X.; Xia, Y.R.; Lou, S.Y. Plenty of novel interaction structures of soliton molecules and asymmetric solitons to (2 + 1)-dimensional Sawada-Kotera equation. Commun. Nonlinear Sci. Numer. Simulat. 2021, 100, 105843. [Google Scholar]
- Xiong, Z.X.; Ren, B. Soliton molecules, breather molecules and stability analysis of the three-coupled nonlinear Schrödinger equation. Phys. Scr. 2024, 99, 055248. [Google Scholar]
- Ma, Y.L.; Wazwaz, A.M.; Li, B.Q. Soliton resonances, soliton molecules, soliton oscillations and heterotypic solitons for the nonlinear Maccari system. Nonlinear Dyn. 2023, 111, 18331–18344. [Google Scholar]
- Zhang, X.Q.; Ren, B. Resonance solitons, soliton molecules and hybrid solutions for a (2 + 1)-dimensional nonlinear wave equation arising in the shallow water wave. Nonlinear Dyn. 2024, 112, 4793–4802. [Google Scholar]
- Cheng, L.; Ma, W.X.; Zhang, Y.; Ge, J.Y. Integrability and lump solutions to an extended (2 + 1)-dimensional KdV equation. Eur. Phys. J. Plus 2022, 137, 902. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Chen, J.C.; Yang, B.; Feng, B.F. Rogue waves in the massive Thirring model. Stud. Appl. Math. 2023, 151, 1020–1052. [Google Scholar] [CrossRef]
- Chen, J.C.; Yan, Q.X. Bright soliton solutions to a nonlocal nonlinear Schrödinger equation of reverse-time type. Nonlinear Dyn. 2020, 100, 2807–2816. [Google Scholar] [CrossRef]
- Chen, J.C.; Feng, B.F.; Chen, Y.; Ma, Z.Y. General bright-dark soliton solution to (2 + 1)-dimensional multi-component long-wave-short-wave resonance interaction system. Nonlinear Dyn. 2017, 88, 1273–1288. [Google Scholar] [CrossRef]
- Ren, B.; Lin, J.; Liu, P. Soliton molecules and the CRE method in the extended mKdV equation. Commun. Theor. Phys. 2020, 72, 055005. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Satsuma, J. Solitons and rational solutions of nonlinear evolution equations. J. Math. Phys. 1978, 19, 2180–2186. [Google Scholar] [CrossRef]
- Satsuma, J.; Ablowitz, M.J. Two-dimensional lumpsin nonlinear dispersive systems. J. Math. Phys. 1979, 20, 1496–1503. [Google Scholar] [CrossRef]
- Zhao, Z.L.; He, L.C. Nonlinear superposition between lump waves and other waves of the (2 + 1)-dimensional asymmetrical Nizhnik-Novikov-Veselov equation. Nonlinear Dyn. 2022, 108, 555–568. [Google Scholar] [CrossRef]
- Wei, P.F.; Long, C.X.; Zhu, C.; Zhou, Y.T.; Yu, H.Z.; Ren, B. Soliton molecules, multi-breathers and hybrid solutions in (2 + 1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation. Chaos Solitons Fractals 2022, 158, 112062. [Google Scholar] [CrossRef]
- He, X.J.; Lü, X. M-lump solution, soliton solution and rational solution to a (3 + 1)-dimensional nonlinear model. Math. Comput. Simulat. 2022, 197, 327–340. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.Y.; Li, B.; Wazwaz, A.M.; Guo, Q. Generation mechanism of high-order rogue waves via the improved long-wave limit method: NLS case. Phys. Lett. A 2022, 450, 128395. [Google Scholar] [CrossRef]
- Baronio, F.; Wabnitz, S.; Kodama, Y. Optical Kerr spatiotemporal dark-lump dynamics of hydrodynamic origin. Phys. Rev. Lett. 2016, 116, 173901. [Google Scholar] [PubMed]
- Wei, P.F.; Zhao, Z.; Ling, S.Y.; Gui, R.; Chen, Y.; Wang, W.; Ren, B. Multi-soliton, breather, lump and their interactions of the (2 + 1)-dimensional generalized potential Kadomtsev-Petviashvili equation. J. Nonlinear Math. Phys. 2024, 31, 82. [Google Scholar]
- Wang, Q.; Mihalache, D.; Belić, M.R.; Lin, J. Mode conversion of various solitons in parabolic and cross-phase potential wells. Opt. Lett. 2024, 49, 1607–1610. [Google Scholar]
- Wang, Q.; Mihalache, D.; Belić, M.R.; Zeng, L.W.; Lin, J. Spiraling Laguerre Gaussian solitons and arrays in parabolic potential wells. Opt. Lett. 2023, 48, 4233–4236. [Google Scholar]
- Zhang, Z.; Yang, X.Y.; Li, B. Soliton molecules and novel smooth positons for the complex modified KdV equation. Appl. Math. Lett. 2020, 103, 106168. [Google Scholar]
- Xu, T.Z.; Liu, J.H.; Wang, Y.Y.; Dai, C.Q. Vector multipole solitons of fractional-order coupled saturable nonlinear Schrödinger equation. Chaos Solitons Fractals 2024, 186, 115230. [Google Scholar]
- Yin, Z.Y.; Tian, S.F. Nonlinear wave transitions and their mechanisms of (2 + 1)-dimensional Sawada-Kotera equation. Physica D 2021, 427, 133002. [Google Scholar] [CrossRef]
- Lü, X.; Zhang, L.L.; Ma, W.X. Oceanic shallow-water description with (2 + 1)-dimensional generalized variable-coefficient Hirota-Satsuma-Ito equation: Painlevé analysis, soliton solutions, and lump solutions. Phys. Fluids 2024, 36, 064110. [Google Scholar]
- Ren, B.; Lin, J. The integrability of a (2 + 1)-dimensional nonlinear wave equation: Painlev¨¦ property, multi-order breathers, multi-order lumps and hybrid solutions. Wave Motion 2023, 117, 103110. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Z.Y.; Zhao, L.C.; Yang, W.L. State transition induced by higher-order effects and backgroundfrequency. Phys. Rev. E 2015, 91, 022904. [Google Scholar]
- Zhang, X.Q.; Ren, B. Conversion mechanisms and transformed waves for the (3 + 1)-dimensional nonlinear equation. Phys. Fluids 2024, 36, 102129. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Song, H.-F.; Wang, W.-L.; Ren, B. Soliton Molecules, Multi-Lumps and Hybrid Solutions in Generalized (2 + 1)-Dimensional Date–Jimbo–Kashiwara–Miwa Equation in Fluid Mechanics. Symmetry 2025, 17, 538. https://doi.org/10.3390/sym17040538
Zhu W, Song H-F, Wang W-L, Ren B. Soliton Molecules, Multi-Lumps and Hybrid Solutions in Generalized (2 + 1)-Dimensional Date–Jimbo–Kashiwara–Miwa Equation in Fluid Mechanics. Symmetry. 2025; 17(4):538. https://doi.org/10.3390/sym17040538
Chicago/Turabian StyleZhu, Wei, Hai-Fang Song, Wan-Li Wang, and Bo Ren. 2025. "Soliton Molecules, Multi-Lumps and Hybrid Solutions in Generalized (2 + 1)-Dimensional Date–Jimbo–Kashiwara–Miwa Equation in Fluid Mechanics" Symmetry 17, no. 4: 538. https://doi.org/10.3390/sym17040538
APA StyleZhu, W., Song, H.-F., Wang, W.-L., & Ren, B. (2025). Soliton Molecules, Multi-Lumps and Hybrid Solutions in Generalized (2 + 1)-Dimensional Date–Jimbo–Kashiwara–Miwa Equation in Fluid Mechanics. Symmetry, 17(4), 538. https://doi.org/10.3390/sym17040538





