Hybrid Optimization of Phase Masks: Integrating Non-Iterative Methods with Simulated Annealing and Validation via Tomographic Measurements
Abstract
1. Introduction
2. Theory
2.1. LG Modes and HG Modes in Optical System
2.2. SA Algorithm
2.2.1. Initial Temperature
2.2.2. Decay of the Control Parameter
2.2.3. Cost Function
2.2.4. Metropolis Principle
2.3. Analytical Optimization Approaches for Hologram Generation
2.4. Tomographic Measurement
3. Experiment and Result
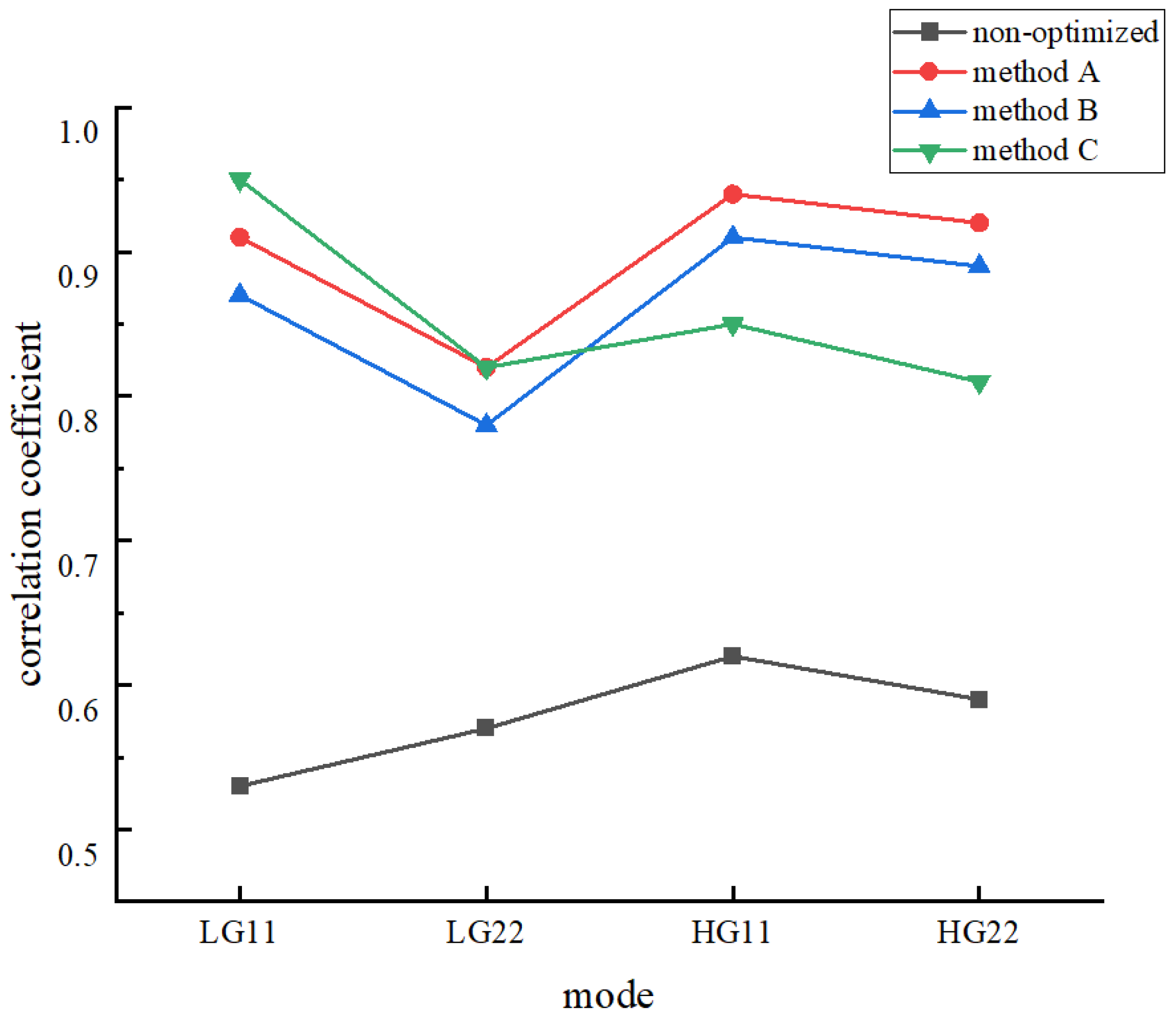
3.1. NI Algorithms for Hologram Generation
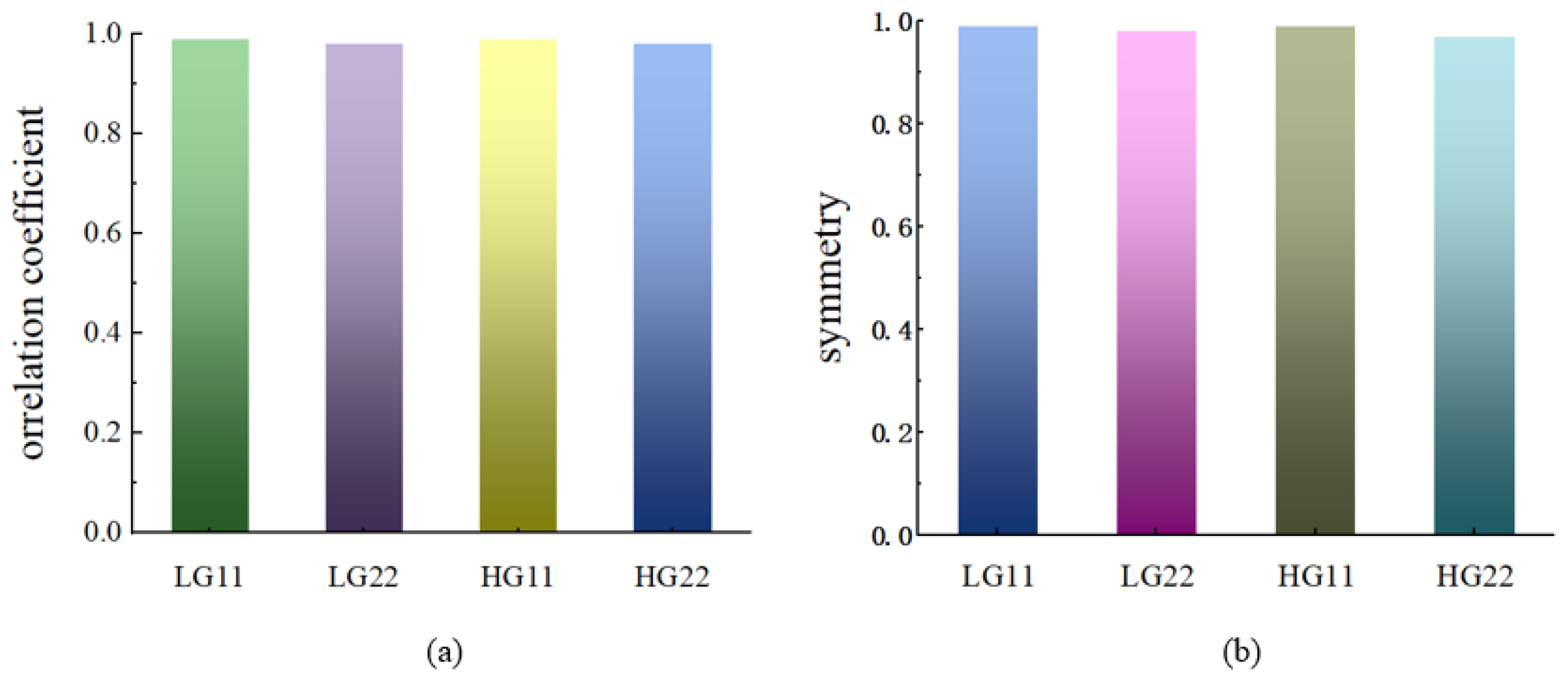
3.2. Combination of NI Algorithms and SA Algorithm for Hologram Generation
3.3. Experiment of Tomographic Measurement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SA | Simulated Annealing |
| SLM | Spatial Light Modulators |
| NI | Non-Iterative |
| MUB | Mutually Unbiased Bases |
| CGH | Computer-Generated Holography |
| POH | Phase-Only Holograms |
| AOH | Amplitude-Only Holograms |
| GS | Gerchberg-Saxton |
| OAM | Orbital Angular Momentum |
| HG | Hermite–Gaussian |
| LG | Laguerre–Gaussian |
| NOSAA | Numerical Optimization Strategy Based on Simulated Annealing Algorithm |
| OESAA | Optical Experiments Using the Simulated Annealing Algorithm |
References
- Schröter, J. Technologies beyond the Still and the Moving Image: The Case of the Multiplex Hologram. Hist. Photogr. 2011, 35, 23–32. [Google Scholar]
- Gentet, P.; Joung, J.; Gentet, Y.; Lee, S.H. A Zerotrope™ with an ultra-realistic full-color digital hologram. In Proceedings of the Digital Holography and Three-Dimensional Imaging 2019, Bordeaux, France, 19–23 May 2019; p. M3A.7. [Google Scholar]
- Yoneda, N.; Saita, Y.; Nomura, T. Computer-generated-hologram-based holographic data storage using common-path off-axis digital holography. Opt. Lett. 2020, 45, 2796–2799. [Google Scholar] [PubMed]
- Zeng, T.; Zhu, Y.; Lam, E.Y. Deep learning for digital holography: A review. Opt. Express 2021, 29, 40572–40593. [Google Scholar] [PubMed]
- Sahin, E.; Stoykova, E.; Mäkinen, J.; Gotchev, A. Computer-generated holograms for 3D imaging: A survey. ACM Comput. Surv. (CSUR) 2020, 53, 1–35. [Google Scholar]
- Shi, L.; Li, B.; Kim, C.; Kellnhofer, P.; Matusik, W. Towards real-time photorealistic 3D holography with deep neural networks. Nature 2021, 591, 234–239. [Google Scholar] [CrossRef]
- Shoydin, S.A.; Pazoev, A.L. Transmission of 3D holographic information via conventional communication channels and the possibility of multiplexing in the implementation of 3D hyperspectral images. Photonics 2021, 8, 448. [Google Scholar] [CrossRef]
- Kim, M.K. Principles and techniques of digital holographic microscopy. SPIE Rev. 2010, 1, 018005. [Google Scholar]
- Blinder, D.; Birnbaum, T.; Ito, T.; Shimobaba, T. The state-of-the-art in computer generated holography for 3D display. Light Adv. Manuf. 2022, 3, 572–600. [Google Scholar]
- Qin, H.; Han, C.; Shi, X.; Gu, T.; Sun, K. Complex-valued generative adversarial network for real-time and high-quality computer-generated holography. Opt. Express 2024, 32, 44437–44451. [Google Scholar] [CrossRef]
- Kara, K.; Lloret, J.; Romero, O.; Sendra, S. Performance Test of Holographic Video Communication System. In Proceedings of the 2024 International Conference on Multimedia Computing, Networking and Applications (MCNA), Valencia, Spain, 17–20 September 2024; pp. 15–20. [Google Scholar]
- Nazir, A.; Hussain, A.; Singh, M.; Assad, A. A novel approach in cancer diagnosis: Integrating holography microscopic medical imaging and deep learning techniques—Challenges and future trends. Biomed. Phys. Eng. Express 2025, 11, 022002. [Google Scholar]
- Ni, Y.; Feng, J.; Liu, J.; Yu, H.; Wei, H.; Du, Y.; Liu, L.; Sun, L.; Zhou, J.; Xu, W. An artificial nerve capable of UV-perception, NIR–vis switchable plasticity modulation, and motion state monitoring. Adv. Sci. 2022, 9, 2102036. [Google Scholar]
- Wang, J.Z.; Zhao, S.; Wu, C.; Adams, R.B.; Newman, M.G.; Shafir, T.; Tsachor, R. Unlocking the emotional world of visual media: An overview of the science, research, and impact of understanding emotion. Proc. IEEE 2023, 111, 1236–1286. [Google Scholar]
- Lee, C.; Song, G.; Kim, H.; Ye, J.C.; Jang, M. Deep learning based on parameterized physical forward model for adaptive holographic imaging with unpaired data. Nat. Mach. Intell. 2023, 5, 35–45. [Google Scholar]
- Lee, S.; Nam, S.W.; Lee, J.; Jeong, Y.; Lee, B. HoloSR: Deep learning-based super-resolution for real-time high-resolution computer-generated holograms. Opt. Express 2024, 32, 11107–11122. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, R.F. The Heterogeneous Network Community Detection Model Based on Self-Attention. Symmetry 2025, 17, 432. [Google Scholar] [CrossRef]
- Park, J.; Kang, H. Holo-VQVAE: VQ-VAE for phase-only holograms. arXiv 2024, arXiv:2404.01330. [Google Scholar]
- Fan, M.; Wang, J.; Du, C.; Yang, J.; Wang, H.; Xu, X. Generation of Non-Iterative POHs based on Optimized Hybrid Phase for Fresnel Lensless Holographic Projection. Teh. Vjesn. 2024, 31, 262–271. [Google Scholar]
- Liu, Q.; Chen, J.; Qiu, B.; Wang, Y.; Liu, J. DCPNet: A dual-channel parallel deep neural network for high quality computer-generated holography. Opt. Express 2023, 31, 35908–35921. [Google Scholar]
- Zhang, C.; Han, P.; Shi, J.; Zhou, H.; Zhang, Q.; Cheng, H.; Shen, C.; Zhang, F.; Han, C.; Wei, S. Non-Iterative 3D Computer-Generated Hologram Based on Single Full-Support Optimized Random Phase and Phase Compensation. New J. Phys. 2024, 26, 063032. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, F.; Zhou, J.; Wei, S. Non-iterative phase hologram generation for color holographic display. Opt. Express 2021, 30, 195–209. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Xu, B.; Chen, J. Optical image encryption and authentication using phase-only computer-generated hologram. Opt. Lasers Eng. 2021, 146, 106722. [Google Scholar]
- Tsang, P.; Chow, Y.T.; Poon, T.C. Generation of patterned-phase-only holograms (PPOHs). Opt. Express 2017, 25, 9088–9093. [Google Scholar] [CrossRef] [PubMed]
- Kishk, S.; Javidi, B. Information hiding technique with double phase encoding. Appl. Opt. 2002, 41, 5462–5470. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, H.; He, Z.; Wang, X.; Cao, L.; Jin, G. Weighted constraint iterative algorithm for phase hologram generation. Appl. Sci. 2020, 10, 3652. [Google Scholar] [CrossRef]
- Yang, G.Z.; Dong, B.Z.; Gu, B.Y.; Zhuang, J.Y.; Ersoy, O.K. Gerchberg–Saxton and Yang–Gu algorithms for phase retrieval in a nonunitary transform system: A comparison. Appl. Opt. 1994, 33, 209–218. [Google Scholar] [CrossRef]
- Guo, C.; Liu, S.; Sheridan, J.T. Iterative phase retrieval algorithms. I: Optimization. Appl. Opt. 2015, 54, 4698–4708. [Google Scholar] [CrossRef]
- Gaunt, A.; Hadzibabic, Z. Robust Digital Holography For Ultracold Atom Trapping. Sci. Rep. 2012, 2, 721. [Google Scholar]
- Zhao, T.; Chi, Y. Modified Gerchberg–Saxton (G-S) Algorithm and Its Application. Entropy 2020, 22, 1354. [Google Scholar] [CrossRef]
- Reddy, A.N.K.; Dev, V.; Pal, V.; Ganeev, R.A. The Effect of a Parabolic Apodizer on Improving the Imaging of Optical Systems with Coma and Astigmatism Aberrations. Photonics 2023, 11, 14. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Liu, L.; Zhao, M.; Mei, S. Coupling technology of OpenSURF and Shannon-Cosine wavelet interpolation for locust slice images inpainting. Comput. Electron. Agric. 2022, 198, 107110. [Google Scholar]
- Kelley, E.F. Calibration Requirements for Demanding Measurement Challenges. Inf. Disp. 2018, 34, 28–54. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J. Simulated annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Junior, H.A.; Ingber, L.; Petraglia, A.; Petraglia, M.R.; Machado, M.A.S. Stochastic Global Optimization and Its Applications with Fuzzy Adaptive Simulated Annealing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 35. [Google Scholar]
- Osaba, E.; Villar-Rodriguez, E.; Del Ser, J.; Nebro, A.J.; Molina, D.; LaTorre, A.; Suganthan, P.N.; Coello, C.A.C.; Herrera, F. A tutorial on the design, experimentation and application of metaheuristic algorithms to real-world optimization problems. Swarm Evol. Comput. 2021, 64, 100888. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Wang, M. Connectivity and matching preclusion for leaf-sort graphs. J. Interconnect. Netw. 2019, 19, 1940007. [Google Scholar] [CrossRef]
- Zhao, C.T.; Wang, R.F.; Tu, Y.H.; Pang, X.X.; Su, W.H. Automatic Lettuce Weed Detection and Classification Based on Optimized Convolutional Neural Networks for Robotic Weed Control. Agronomy 2024, 14, 2838. [Google Scholar] [CrossRef]
- Dong, H.; Dong, Z. Surrogate-assisted grey wolf optimization for high-dimensional, computationally expensive black-box problems. Swarm Evol. Comput. 2020, 57, 100713. [Google Scholar] [CrossRef]
- Lavin, A.; Krakauer, D.; Zenil, H.; Gottschlich, J.; Mattson, T.; Brehmer, J.; Anandkumar, A.; Choudry, S.; Rocki, K.; Baydin, A.G.; et al. Simulation intelligence: Towards a new generation of scientific methods. arXiv 2021, arXiv:2112.03235. [Google Scholar]
- Abdulazeez, D.H.; Askar, S.K. Offloading mechanisms based on reinforcement learning and deep learning algorithms in the fog computing environment. IEEE Access 2023, 11, 12555–12586. [Google Scholar] [CrossRef]
- Tu, Y.H.; Wang, R.F.; Su, W.H. Active Disturbance Rejection Control—New Trends in Agricultural Cybernetics in the Future: A Comprehensive Review. Machines 2025, 13, 111. [Google Scholar] [CrossRef]
- Yarmohamadi, H.; Mirhosseini, S. A new dynamic simulated annealing algorithm for global optimization. J. Math. Comput. Sci 2015, 14, 16–23. [Google Scholar] [CrossRef]
- Wang, S.; Wang, M. The strong connectivity of bubble-sort star graphs. Comput. J. 2019, 62, 715–729. [Google Scholar]
- Lalaoui, M.; El Afia, A.; Chiheb, R. A self-tuned simulated annealing algorithm using hidden markov model. Int. J. Electr. Comput. Eng. 2018, 8, 291–298. [Google Scholar] [CrossRef]
- Lalaoui, M.; El Afia, A.; Chiheb, R. Simulated Annealing with Adaptive Neighborhood using Fuzzy Logic Controller. In Proceedings of the International Conference on Learning and Optimization Algorithms: Theory and Applications, New York, NY, USA, 2–5 May 2018. LOPAL ’18. [Google Scholar]
- Weng, Y.; Pan, Z. Orbital angular momentum based sensing and their applications: A review. J. Light. Technol. 2022, 41, 2007–2016. [Google Scholar]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Mei, S.L. Shannon wavelet precision integration method for pathologic onion image segmentation based on homotopy perturbation technology. Math. Probl. Eng. 2014, 2014, 601841. [Google Scholar]
- Forbes, A.; Dudley, A.; McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photonics 2016, 8, 200–227. [Google Scholar]
- Ndagano, B.; Perez-Garcia, B.; Roux, F.S.; McLaren, M.; Rosales-Guzman, C.; Zhang, Y.; Mouane, O.; Hernandez-Aranda, R.I.; Konrad, T.; Forbes, A. Characterizing quantum channels with non-separable states of classical light. Nat. Phys. 2017, 13, 397–402. [Google Scholar]
- Mafu, M.; Dudley, A.; Goyal, S.; Giovannini, D.; McLaren, M.; Padgett, M.J.; Konrad, T.; Petruccione, F.; Lütkenhaus, N.; Forbes, A. Higher-dimensional orbital-angular-momentum-based quantum key distribution with mutually unbiased bases. Phys. Rev. A 2013, 88, 032305. [Google Scholar]
- Krenn, M.; Huber, M.; Fickler, R.; Lapkiewicz, R.; Ramelow, S.; Zeilinger, A. Generation and confirmation of a (100× 100)-dimensional entangled quantum system. Proc. Natl. Acad. Sci. USA 2014, 111, 6243–6247. [Google Scholar]
- Sit, A.; Bouchard, F.; Fickler, R.; Gagnon-Bischoff, J.; Larocque, H.; Heshami, K.; Elser, D.; Peuntinger, C.; Günthner, K.; Heim, B.; et al. High-dimensional intracity quantum cryptography with structured photons. Optica 2017, 4, 1006–1010. [Google Scholar]
- Fano, U. Description of States in Quantum Mechanics by Density Matrix and Operator Techniques. Rev. Mod. Phys. 1957, 29, 74–93. [Google Scholar]
- James, D.F.V.; Kwiat, P.G.; Munro, W.J.; White, A.G. Measurement of qubits. Phys. Rev. A 2001, 64, 052312. [Google Scholar]
- de Burgh, M.D.; Langford, N.K.; Doherty, A.C.; Gilchrist, A. Choice of measurement sets in qubit tomography. Phys. Rev. A 2008, 78, 052122. [Google Scholar]
- Jack, B.; Leach, J.; Ritsch, H.; Barnett, S.M.; Padgett, M.J.; Franke-Arnold, S. Precise quantum tomography of photon pairs with entangled orbital angular momentum. New J. Phys. 2009, 11, 103024. [Google Scholar]
- Spengler, C.; Huber, M.; Brierley, S.; Adaktylos, T.; Hiesmayr, B.C. Entanglement detection via mutually unbiased bases. Phys. Rev. A 2012, 86, 022311. [Google Scholar]
- Zhou, Y. Optical Communication with Structured Photons Propagating Through Dynamic, Aberrating Media; University of Rochester: Rochester, NY, USA, 2021. [Google Scholar]
- Bastiaans, M.J. Applications of the Wigner distribution to partially coherent light beams. Adv. Inf. Opt. Photonics 2008, 6, 27. [Google Scholar]
- Kovsh, D.I. Laser Beam Propagation Through Bulk Nonlinear Media: Numerical Simulation and Experiment; University of Central Florida: Orlando, FL, USA, 1999. [Google Scholar]
- Wang, M.; Lin, Y.; Wang, S. The nature diagnosability of bubble-sort star graphs under the PMC model and MM model. Int. J. Eng. Appl. Sci. 2017, 4, 2394–3661. [Google Scholar]
- Wang, M.; Ren, Y.; Lin, Y.; Wang, S. The tightly super 3-extra connectivity and diagnosability of locally twisted cubes. Am. J. Comput. Math. 2017, 7, 127–144. [Google Scholar]
- Sun, S.; Liu, J.; Sun, S. Hyperspectral subpixel target detection based on interaction subspace model. Pattern Recognit. 2023, 139, 109464. [Google Scholar]
- Wang, R.F.; Su, W.H. The application of deep learning in the whole potato production Chain: A Comprehensive review. Agriculture 2024, 14, 1225. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R.; Wang, M.; Lai, T.; Zhang, M. Self-supervised transformer-based pre-training method with General Plant Infection dataset. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Urumqi, China, 18–20 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 189–202. [Google Scholar]
- Ni, Y.; Wang, Y.; Xu, W. Recent process of flexible transistor-structured memory. Small 2021, 17, 1905332. [Google Scholar]
- Chen, J.; Wan, C.; Zhan, Q. Engineering photonic angular momentum with structured light: A review. Adv. Photonics 2021, 3, 064001. [Google Scholar]
- Noor, S.K.; Yasin, M.N.M.; Ismail, A.M.; Osman, M.N.; Soh, P.J.; Ramli, N.; Rambe, A.H. A review of orbital angular momentum vortex waves for the next generation wireless communications. IEEE Access 2022, 10, 89465–89484. [Google Scholar]
- Khare, K.; Lochab, P.; Senthilkumaran, P. Orbital Angular Momentum States of Light: Propagation Through Atmospheric Turbulence; IOP Publishing: Bristol, UK, 2024. [Google Scholar]
- Padgett, M.; Arlt, J.; Simpson, N.; Allen, L. An experiment to observe the intensity and phase structure of Laguerre-Gaussian laser modes. Am. J. Phys. 1996, 64, 77–81. [Google Scholar]
- Mardan Dezfouli, A. Generation and Detection of Optical Vortex Beam. Ph.D. Thesis, Department of Physics, Faculty of Science, University of Zagreb, Zagreb, Croatia, 2024. [Google Scholar]
- Bae, J.Y.; Jeon, C.; Pae, K.H.; Kim, C.M.; Kim, H.S.; Han, I.; Yeo, W.J.; Jeong, B.; Jeon, M.; Lee, D.H.; et al. Generation of low-order Laguerre-Gaussian beams using hybrid-machined reflective spiral phase plates for intense laser-plasma interactions. Results Phys. 2020, 19, 103499. [Google Scholar]
- Kovalev, A.; Kotlyar, V.; Porfirev, A. Asymmetric laguerre-gaussian beams. Phys. Rev. A 2016, 93, 063858. [Google Scholar]
- Ghaderi Goran Abad, M.; Mahmoudi, M. Laguerre-Gaussian modes generated vector beam via nonlinear magneto-optical rotation. Sci. Rep. 2021, 11, 5972. [Google Scholar]
- Longman, A.; Fedosejevs, R. Mode conversion efficiency to Laguerre-Gaussian OAM modes using spiral phase optics. Opt. Express 2017, 25, 17382–17392. [Google Scholar]
- Pampaloni, F.; Enderlein, J. Gaussian, hermite-gaussian, and laguerre-gaussian beams: A primer. arXiv 2004, arXiv:physics/0410021. [Google Scholar]
- Kim, H.C.; Lee, Y.H. Hermite–Gaussian and Laguerre–Gaussian beams beyond the paraxial approximation. Opt. Commun. 1999, 169, 9–16. [Google Scholar]
- Saghafi, S.; Sheppard, C.; Piper, J. Characterising elegant and standard Hermite–Gaussian beam modes. Opt. Commun. 2001, 191, 173–179. [Google Scholar] [CrossRef]
- Casperson, L.W.; Tovar, A.A. Hermite–sinusoidal-Gaussian beams in complex optical systems. J. Opt. Soc. Am. A 1998, 15, 954–961. [Google Scholar] [CrossRef]
- Laabs, H. Propagation of Hermite-Gaussian-beams beyond the paraxial approximation. Opt. Commun. 1998, 147, 1–4. [Google Scholar] [CrossRef]
- Hofer, L.; Jones, L.; Goedert, J.; Dragone, R. Hermite–Gaussian mode detection via convolution neural networks. J. Opt. Soc. Am. A 2019, 36, 936–943. [Google Scholar] [CrossRef]
- Luo, Y.Z.; Tang, G.J.; Zhou, L.N. Simulated annealing for solving near-optimal low-thrust orbit transfer. Eng. Optim. 2005, 37, 201–216. [Google Scholar] [CrossRef]
- Delahaye, D.; Chaimatanan, S.; Mongeau, M. Simulated annealing: From basics to applications. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2019; pp. 1–35. [Google Scholar]
- Burke, E.K.; Burke, E.K.; Kendall, G.; Kendall, G. Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Shakouri G., H.; Shojaee, K.; T. Behnam, M. Investigation on the choice of the initial temperature in the simulated annealing: A mushy state SA for TSP. In Proceedings of the 2009 17th Mediterranean Conference on Control and Automation, Thessaloniki, Greece, 24–26 June 2009; pp. 1050–1055. [Google Scholar]
- Glover, F.W.; Kochenberger, G.A. Handbook of metaheuristics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; Volume 57. [Google Scholar]
- Wang, H.; Zhang, X.; Mei, S. Shannon-Cosine Wavelet Precise Integration Method for Locust Slice Image Mixed Denoising. Math. Probl. Eng. 2020, 2020, 4989735. [Google Scholar] [CrossRef]
- Carpenter, J.; Wilkinson, T.D. Graphics processing unit–accelerated holography by simulated annealing. Opt. Eng. 2010, 49, 095801. [Google Scholar] [CrossRef]
- Gallego-Ruiz, R.; Álvarez-Castaño, M.; Herrera-Ramírez, J.; Correa, N. Optimization of phase masks using simulated annealing algorithm for mode conversion. J. Phys. Conf. Ser. 2020, 1547, 012007. [Google Scholar] [CrossRef]
- Berdagué, S.; Facq, P. Mode division multiplexing in optical fibers. Appl. Opt. 1982, 21, 1950–1955. [Google Scholar] [CrossRef]
- Fang, L.; Zuo, H.; Pang, L.; Yang, Z.; Zhang, X.; Zhu, J. Image reconstruction through thin scattering media by simulated annealing algorithm. Opt. Lasers Eng. 2018, 106, 105–110. [Google Scholar] [CrossRef]
- Davis, J.A.; Cottrell, D.M.; Campos, J.; Yzuel, M.J.; Moreno, I. Encoding amplitude information onto phase-only filters. Appl. Opt. 1999, 38, 5004–5013. [Google Scholar] [PubMed]
- Bolduc, E.; Bent, N.; Santamato, E.; Karimi, E.; Boyd, R.W. Exact solution to simultaneous intensity and phase encryption with a single phase-only hologram. Opt. Lett. 2013, 38, 3546–3549. [Google Scholar]
- Arrizón, V.; Ruiz, U.; Carrada, R.; González, L.A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. J. Opt. Soc. Am. A 2007, 24, 3500–3507. [Google Scholar]
- Lima, G.; Neves, L.; Guzmán, R.; Gómez, E.S.; Nogueira, W.; Delgado, A.; Vargas, A.; Saavedra, C. Experimental quantum tomography of photonic qudits via mutually unbiased basis. Opt. Express 2011, 19, 3542–3552. [Google Scholar] [PubMed]
- Adamson, R.; Steinberg, A.M. Improving quantum state estimation with mutually unbiased bases. Phys. Rev. Lett. 2010, 105, 030406. [Google Scholar] [CrossRef]
- Fernández-Pérez, A.; Klimov, A.; Saavedra, C. Quantum process reconstruction based on mutually unbiased basis. Phys. Rev. A 2011, 83, 052332. [Google Scholar]
- Giovannini, D.; Romero, J.; Leach, J.; Dudley, A.; Forbes, A.; Padgett, M.J. Characterization of high-dimensional entangled systems via mutually unbiased measurements. Phys. Rev. Lett. 2013, 110, 143601. [Google Scholar]
- Coles, P.J.; Berta, M.; Tomamichel, M.; Wehner, S. Entropic uncertainty relations and their applications. Rev. Mod. Phys. 2017, 89, 015002. [Google Scholar]
- Padgett, M.J.; Courtial, J. Poincaré-sphere equivalent for light beams containing orbital angular momentum. Opt. Lett. 1999, 24, 430–432. [Google Scholar] [CrossRef]
- Toninelli, E.; Ndagano, B.; Vallés, A.; Sephton, B.; Nape, I.; Ambrosio, A.; Capasso, F.; Padgett, M.J.; Forbes, A. Concepts in quantum state tomography and classical implementation with intense light: A tutorial. Adv. Opt. Photonics 2019, 11, 67–134. [Google Scholar] [CrossRef]
- Wu, K.D.; Streltsov, A.; Regula, B.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Experimental progress on quantum coherence: Detection, quantification, and manipulation. Adv. Quantum Technol. 2021, 4, 2100040. [Google Scholar]
- Krenn, M.; Malik, M.; Erhard, M.; Zeilinger, A. Orbital angular momentum of photons and the entanglement of Laguerre–Gaussian modes. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20150442. [Google Scholar]
- Jullien, T.; Roulleau, P.; Roche, B.; Cavanna, A.; Jin, Y.; Glattli, D. Quantum tomography of an electron. Nature 2014, 514, 603–607. [Google Scholar] [PubMed]
- Maire, E.; Withers, P.J. Quantitative X-ray tomography. Int. Mater. Rev. 2014, 59, 1–43. [Google Scholar]
- Kokail, C.; van Bijnen, R.; Elben, A.; Vermersch, B.; Zoller, P. Entanglement Hamiltonian tomography in quantum simulation. Nat. Phys. 2021, 17, 936–942. [Google Scholar]
- Cozzolino, D.; Da Lio, B.; Bacco, D.; Oxenløwe, L.K. High-dimensional quantum communication: Benefits, progress, and future challenges. Adv. Quantum Technol. 2019, 2, 1900038. [Google Scholar]
- Thekkadath, G.; England, D.; Bouchard, F.; Zhang, Y.; Kim, M.; Sussman, B. Intensity interferometry for holography with quantum and classical light. Sci. Adv. 2023, 9, eadh1439. [Google Scholar]
- Pachava, S.; Dharmavarapu, R.; Vijayakumar, A.; Jayakumar, S.; Manthalkar, A.; Dixit, A.; Viswanathan, N.K.; Srinivasan, B.; Bhattacharya, S. Generation and decomposition of scalar and vector modes carrying orbital angular momentum: A review. Opt. Eng. 2020, 59, 041205. [Google Scholar]
- Angelsky, O.; Bekshaev, A.Y.; Vasnetsov, M.; Zenkova, C.Y.; Maksimyak, P.; Zheng, J. Optical phase singularities: Physical nature, manifestations and applications. Front. Phys. 2022, 10, 1060787. [Google Scholar]
- Defienne, H.; Ndagano, B.; Lyons, A.; Faccio, D. Polarization entanglement-enabled quantum holography. Nat. Phys. 2021, 17, 591–597. [Google Scholar]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light Sci. Appl. 2018, 7, 17146. [Google Scholar]
- Ni, Y.; Yang, L.; Feng, J.; Liu, J.; Sun, L.; Xu, W. Flexible optoelectronic neural transistors with broadband spectrum sensing and instant electrical processing for multimodal neuromorphic computing. SmartMat 2023, 4, e1154. [Google Scholar]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Sun, C.; Wang, H.; Wang, R.-F. Hybrid Optimization of Phase Masks: Integrating Non-Iterative Methods with Simulated Annealing and Validation via Tomographic Measurements. Symmetry 2025, 17, 530. https://doi.org/10.3390/sym17040530
Li Z, Sun C, Wang H, Wang R-F. Hybrid Optimization of Phase Masks: Integrating Non-Iterative Methods with Simulated Annealing and Validation via Tomographic Measurements. Symmetry. 2025; 17(4):530. https://doi.org/10.3390/sym17040530
Chicago/Turabian StyleLi, Zhiwen, Chao Sun, Haihua Wang, and Rui-Feng Wang. 2025. "Hybrid Optimization of Phase Masks: Integrating Non-Iterative Methods with Simulated Annealing and Validation via Tomographic Measurements" Symmetry 17, no. 4: 530. https://doi.org/10.3390/sym17040530
APA StyleLi, Z., Sun, C., Wang, H., & Wang, R.-F. (2025). Hybrid Optimization of Phase Masks: Integrating Non-Iterative Methods with Simulated Annealing and Validation via Tomographic Measurements. Symmetry, 17(4), 530. https://doi.org/10.3390/sym17040530






