Spectrum-Constrained and Skip-Enhanced Graph Fraud Detection: Addressing Heterophily in Fraud Detection with Spectral and Spatial Modeling

Abstract

Fraud detection in large-scale graphs presents significant challenges, especially in heterophilic graphs where linked nodes often belong to dissimilar classes or exhibit contrasting attributes. These asymmetric interactions, combined with class imbalance and limited labeled data, make it difficult to fully leverage node labels in semi-supervised learning frameworks. This study aims to address these challenges by proposing a novel framework, Spectrum-Constrained and Skip-Enhanced Graph Fraud Detection (SCSE-GFD), designed specifically for fraud detection in heterophilic graphs. The primary objective is to enhance fraud detection performance while maintaining computational efficiency. SCSE-GFD integrates several key components to improve performance. It employs adaptive polynomial convolution to capture multi-frequency signals and utilizes relation-specific spectral filtering to accommodate both homophilic and heterophilic structures. Additionally, a relation-aware mechanism is incorporated to differentiate between edge types, which enhances feature propagation across diverse graph connections. To address the issue of over-smoothing, skip connections are used to preserve both low- and high-level node representations. Furthermore, supervised edge classification is used to improve the structural understanding of the graph. Extensive experiments on real-world datasets, including Amazon and YelpChi, demonstrate SCSE-GFD’s effectiveness. The framework achieved state-of-the-art AUC scores of 96.21% on Amazon and 90.58% on YelpChi, significantly outperforming existing models. These results validate SCSE-GFD’s ability to improve fraud detection accuracy while maintaining efficiency.

1. Introduction

The quick development of digital platforms has led to the emergence of many fraudulent activities, thereby posing significant risks to individuals, businesses, and global economies. Fraudulent activities, including online payment scams and misleading reviews, result in significant financial and reputational damage, drawing increased attention from industry stakeholders, academic researchers, and regulatory authorities [1,2,3,4]. Fraudulent online transactions exploit system weaknesses, resulting in significant financial losses, while malicious reviews damage merchants’ credibility and deceive consumers. To detect spam reviews effectively, rule-based learning methods [5] and statistical machine learning techniques have been commonly used in the past. However, these approaches often miss the relationships and connections between reviews, which can limit their ability to accurately identify fraudulent activity. A popular approach in fraud detection now involves using multi-relation graphs, which capture different types of connections between entities, like users, reviews, and the products they have reviewed. These graphs are then used to build supervised classifiers that extract features based on the graph’s structure [6,7]. However, these methods often require deep domain expertise to create meaningful features, which can make the process slow and resource heavy. Additionally, manually crafted features may fail to recognise the more complex, high-level relationships between entities that could improve fraud detection.

Graph-based methodologies have emerged as a fundamental aspect in the investigation of fraud detection [8,9,10]. These methods utilize graph architectures by representing entities as nodes and communications as edges to identify fraudulent behaviors. Graph Neural Networks (GNNs), recognized for their performance in graph representation learning [11,12,13], enable the aggregation of neighboring information to learn expressive node embeddings. Recent progress in GNNs applied to multi-relation graphs has led to the creation of more advanced frameworks for fraud detection. These frameworks capitalize on GNNs’ capacity to automatically learn rich representations, moving beyond the need for manually crafted features. Consequently, many new approaches have been proposed that leverage GNNs for detecting fraud, particularly by focusing on novel aggregation techniques. Some methods extract correlation features from local neighbors using convolutional layers [14,15,16]. Others take a hierarchical approach, first aggregating information from a node’s local neighborhood and then combining data from different views [17,18,19]. A shared characteristic of these methods is their focus on identifying clustering behaviors typical of fraudsters by aggregating neighborhood data. However, a significant drawback of this aggregation technique is its vulnerability to fraudsters who disguise their activities. These methods can be easily deceived when fraudsters hide their behaviors through feature manipulation or by altering relationships. When legitimate reviews are used in the aggregation process, the fraudulent behavior may be masked, making it harder to identify fraud accurately. Nonetheless, fraud detection graphs provide distinct challenges that constrain the effectiveness of conventional GNNs.

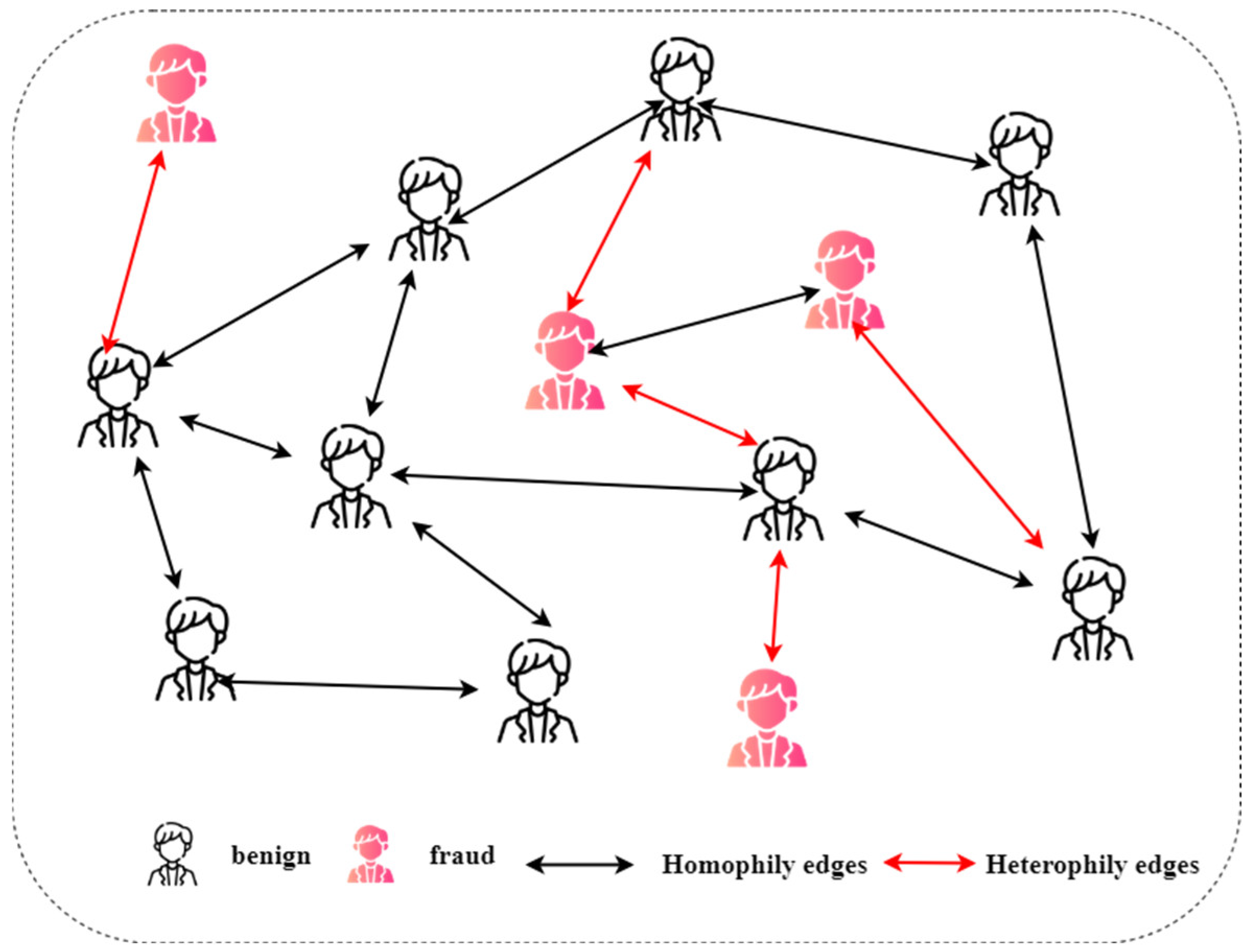
Fraud graphs frequently exhibit heterophily, characterized by connected nodes possessing dissimilar labels or attributes [20] as shown in Figure 1. This opposes the homophily assumption foundational to numerous GNNs, which states that connected nodes share similar properties. In fraudulent situations, malicious actors often engage with benign entities to conceal their actions or disseminate fraudulent behavior across multiple hops. This interaction between homophilic (symmetric) and heterophilic (asymmetric) connections introduces structural symmetry and asymmetry within the graph, which must be carefully analyzed. By understanding and leveraging these symmetric and asymmetric relationships, effective fraud detection frameworks can better capture the subtle patterns of malicious behavior and robustly distinguish fraudulent nodes from benign ones. For example, in e-commerce platforms like Amazon or Yelp, fraudsters often leverage legitimate accounts to post fake reviews or ratings, creating deceptive patterns that mask fraudulent activity. These fraudulent entities interact with benign users to amplify their influence, leading to intricate heterophilic relationships where fraudulent and legitimate accounts are connected. Conventional GNNs function as low-pass filters, smoothing node representations among neighbors and thereby reducing the discriminating attributes required to identify fraudulent entities. In addition, fraud detection datasets sometimes exhibit class imbalance, with fraudulent instances being substantially outnumbered by benign ones. This disparity intensifies the difficulty, as anomalous nodes are frequently overshadowed by prevailing normal nodes. This phenomenon, termed the common camouflage problem [21], is characterized by elevated homophily among normal nodes and strong heterophily among anomalous nodes, complicating the effective identification of fraudulent entities. Furthermore, existing semi-supervised fraud detection methodologies frequently neglect to properly leverage label information, disregarding the complex relationships between node labels, features, and their contextual environments.

Recent improvements in GNNs have been focused on addressing the unique challenges posed by heterophilic graphs, especially in the context of fraud detection. Spatial GNNs such as GraphConsis [22] and CARE-GNN [23] have tried to tackle heterophily by selecting similar neighbors for aggregation. These methods assume that fraudsters often share some traits with legitimate nodes, so focusing on similar neighbors seems like a good strategy. While this can work to some extent, it falls short because fraudsters typically display behaviors that are quite different from legitimate users. This means that when only local neighbors are considered, important fraud signals can be overlooked. To overcome this, H2-FDetector [24] takes a more refined approach by recognizing heterophilic edges and learning from the contrasting representations of nodes connected through these edges. It makes a clear distinction between homophilic and heterophilic connections, using labeled nodes to guide how features are aggregated. While H2-FDetector improves how heterophilic relationships are handled, it still does not fully take advantage of the graph’s spectral properties, which are essential for capturing the complexity of fraud patterns. Spectral-domain methodologies, such as AMNet [25] and BWGNN [26], have made progress in capturing both low- and high-frequency signals to enhance graph representations. These methods use spectral filtering to address heterophily by analyzing graph signals across various frequency bands. However, their primary focus has been on anomaly detection, which is different from fraud detection in this context because anomaly detection does not account for the structural and contextual complexities unique to fraud graphs, such as imbalances in labeled data or the ability of fraudsters to hide their actions through feature manipulation. These challenges highlight the need for more advanced strategies to improve fraud detection in graph-based systems. Despite significant progress in GNN-based fraud detection, existing methods still face key limitations. Heterophily handling remains a challenge, as models like GraphConsis and CARE-GNN assume that connected nodes share similar properties, which weakens their performance in heterophilic fraud networks. Computational efficiency is another concern, with reinforcement-learning-based models like CARE-GNN requiring substantial resources, making them impractical for large-scale fraud graphs. Additionally, loss of structural information affects models like PC-GNN, where adaptive sampling improves class imbalance but disrupts global graph patterns, reducing their overall effectiveness. Lastly, limited label utilization is a persistent issue in semi-supervised fraud detection, where available label information is often underutilized, leading to suboptimal predictions.

To address these gaps, this study presents a Spectrum-Constrained and Skip-Enhanced Graph Fraud Detector (SCSE-GFD), an innovative framework developed to overcome the limitations of current GNNs in fraud detection. SCSE-GFD is designed to address heterophily and class imbalance through an adaptive polynomial convolution module, relation-aware mechanisms, and skip connections for label utilization. The adaptive polynomial convolution module analyzes graph signals in the spectral domain, extracting information from various frequency bands. By dynamically modeling relationships across heterophilic and homophilic edges, it effectively accommodates the heterophilic characteristics of fraud graphs. Meanwhile, the relation-aware mechanism differentiates edge types and employs an edge classification task to improve structural understanding. This dual methodology improves the model’s capacity to recognize complex connections in the graph. Lastly, to mitigate the label utilization issue, skip connections are integrated, allowing both original node attributes and high-level representations to influence the final prediction. The main contribution is as follows.

This study proposes SCSE-GFD, a scalable framework for fraud detection, addressing heterophily and class imbalance through multi-frequency spectral filtering.

• ❖ A relation-aware mechanism and edge classification improve structural understanding and node classification.
• ❖ Skip connections enhance label utilization by preserving both low- and high-level node features.
• ❖ Experiments on real-world datasets validate SCSE-GFD’s effectiveness, outperforming state-of-the-art methods in accuracy and robustness.

The remainder of this manuscript is structured as follows: Section 2 provides a summary of related work. Section 3 presents a detailed explanation of the proposed SCSE-GFD framework, and the experimental setup. Section 4 discusses the results, analyzes key findings, and highlights limitations along with recommendations for future improvements. Finally, Section 5 concludes the study.

2. Related Work

2.1. Semi-Supervised Node Classification

Semi-supervised node classification has become a crucial task in graph learning, where the goal is to classify nodes using both labeled and unlabeled data. This task is essential in various real-world applications, such as social network analysis, recommender systems, and fraud detection. Recently, GNNs have gained prominence in addressing semi-supervised node classification tasks. Their ability to effectively model graph structures has enabled them to surpass traditional graph embedding methods in scalability and predictive accuracy. Classical models like GCN [27], GraphSAGE [28], GAT [29], and GIN [30] have shown impressive success in learning node representations by integrating both node features and graph structure into the learning process. These models surpass older approaches like DeepWalk [31] and Node2vec [32], which primarily focus on graph structure and rely on random walks to generate embeddings. The downside of these methods is that they often fail to capture the rich attribute information of nodes. What makes GNNs stand out is their ability to incorporate both node features and graph structure simultaneously. This dual consideration is especially valuable in semi-supervised settings, where labeled data are scarce, and the model must effectively use the unlabeled data to make accurate predictions. GNNs use a message-passing mechanism, where each layer combines information from neighboring nodes, allowing the model to iteratively improve node representations. By doing so, these representations are enhanced not only by the graph’s structure but also by the semantic features of neighboring nodes, making GNNs particularly effective in situations where both the graph structure and feature relationships are critical for accurate classification. The growing success of GNNs in semi-supervised node classification has sparked increasing interest in their applications, including fraud detection, recommendation systems, and social network analysis, where understanding the connections between entities is key. Additionally, by considering the entire graph during training, GNNs are able to generalize more effectively to previously unseen nodes, making them well-suited for large-scale and complex graph datasets.

2.2. GNN-Based Fraud Detection

Graph-based fraud detection has gained significant attention due to the ability of GNNs to model complex relationships between entities. However, fraud detection remains a challenging task due to issues such as fraudster camouflage, class imbalance, and the need for model interpretability. Several approaches have been developed to address these limitations, each with varying levels of effectiveness. GraphConsis [22] integrates contextual embeddings with node properties and employs node-specific relationship attention to capture the intricate dependencies between nodes. CARE-GNN [23] tackles fraudster camouflage by introducing a reinforcement-learning-based neighbor selection mechanism, which prioritizes trustworthy neighbors while filtering out misleading connections. This approach improves fraud detection accuracy but comes at a high computational cost, making it less scalable for large datasets. PC-GNN [4] focuses on handling class imbalance by using adaptive subgraph and neighbor sampling to ensure sufficient representation of minority-class (fraudulent) nodes. However, this technique sacrifices global graph structure in favor of localized sampling, which can lead to incomplete feature learning. GAGA [33] attempts to mitigate these limitations by introducing group aggregation and label-enhanced encoding, which improve fraud detection in low-homophily graphs where fraudsters do not share characteristics with their neighbors. While effective in some cases, this method requires extensive hyperparameter tuning, reducing its adaptability across diverse datasets. On the other hand, SEFraud [34] addresses the need for model interpretability by applying a self-explainable graph learning framework, which provides insights into why certain nodes are classified as fraudulent. However, this approach demands significant computational resources, making it less practical for real-time fraud detection.

Despite these advancements, a unified solution that effectively balances computational efficiency, class imbalance handling, and fraud camouflage resistance. SCSE-GFD addresses these gaps by integrating spectral and spatial modeling with a relation-aware mechanism, ensuring robust fraud detection across various graph structures while maintaining computational efficiency. By leveraging adaptive polynomial convolutions and skip connections, SCSE-GFD preserves both local and global structural information, effectively mitigating the limitations faced by previous models.

2.3. Graph Heterophily Learning

Heterophily in graphs presents a major challenge for traditional GNN-based fraud detection, as most models assume that connected nodes share similar properties (homophily). In fraud detection, however, fraudulent nodes often connect to legitimate ones, creating heterophilic structures that standard GNNs struggle to process effectively. Several methods have attempted to address this issue, each with varying levels of success. H2-FDetector [24] proposes a supervised edge-aware aggregation strategy that differentiates between homophilic and heterophilic connections. While this approach improves feature propagation by treating edge types differently, it heavily relies on labeled data, limiting its scalability in real-world fraud detection where labels are often scarce. SplitGNN [35] addresses heterophily by partitioning the graph into homophilic and heterophilic subgraphs and applying spectral band-pass filtering. This approach enhances fraud detection in heterophilic settings but introduces additional complexity due to the need for an edge classifier to separate subgraphs. BWGNN [26] takes a different approach by leveraging wavelet-based spectral filtering to capture both low- and high-frequency signals, making it better suited for anomaly detection rather than fraud classification. SEC-GFD [36] introduces spectral-based frequency partitioning to refine label utilization and feature extraction in multi-relational graphs, but its hybrid spectral modeling results in high computational costs. ACM attempts to refine node aggregation strategies by applying a homophily index, dynamically adjusting learning strategies based on the degree of node similarity [37]. However, its reliance on dataset-specific homophily indices limits its generalizability across different types of fraud graphs.

While these approaches provide valuable insights into handling heterophily, they often suffer from limited scalability, increased computational overhead, or reliance on extensive labeled data. SCSE-GFD addresses these challenges by dynamically learning edge importance without requiring prior homophily assumptions. By integrating adaptive polynomial convolutions and a relation-aware mechanism, it ensures that both homophilic and heterophilic structures are effectively captured, improving fraud detection in multi-relational graphs while maintaining computational efficiency.

Table 1. Comparison of existing graph-based fraud detection models.

Model	Method	Limitations
GraphConsis	Uses contextual embeddings to detect fraud patterns	Struggles with extreme heterophily, where node labels vary significantly
CARE-GNN	Reinforcement learning for fraud detection	High computational cost due to reinforcement learning
PC-GNN	Adaptive neighbor sampling for class imbalance	Loses global graph information
GAGA	Group aggregation and label-enhanced encoding	Requires extensive fine-tuning
H2-FDetector	Edge-aware aggregation	Requires labeled data
BWGNN	Beta wavelet-based spectral filtering	Focused on anomaly detection
SplitGNN	Graph partitioning with spectral filtering	Requires additional edge classification
SEC-GFD	Spectral-based frequency partitioning and local environmental constraints	Computationally expensive
SEFraud	Uses self-explainable graph learning with interpretative mask learning	Requires extensive model training to achieve accurate explainability

provides a comparative analysis of existing fraud detection models, highlighting their methodologies and limitations. Unlike previous methods, SCSE-GFD effectively addresses heterophily by integrating spectral and spatial modeling, ensuring robust fraud detection in multi-relational graphs.

3. Materials and Methodology

3.1. Problem Definition

A multi-relation graph $G=\left(V,X,{\left\{E_r\right\}}_{r=1}^R,Y\right)$ consists of sets of nodes $V$ where each node is associated with a d-dimensional feature vector $x\in X,$ and a set of edges $E_r$ for each relation $r\in \{1,\dots ,R\}$. The edge set $E_r$ can be further divided into $E_r^{+}$ and $E_r^{-},$ representing homophilic and heterophilic edges, respectively. Homophilic edges $E_r^{+}$ connect nodes that share a similar label, while heterophilic edges $E_r^{-}$ link nodes with different labels. Here, $R$ is the total count of relations, and $Y$ denotes the set of labeled nodes.

GFD is typically framed as semi-supervised, involving node-level binary classification. In this context, anomalies are often assigned a positive label (1), while normal nodes are given a negative label (0) [38]. The nodes in a fraud graph are categorized into labeled and unlabeled sets: the labeled nodes have their labels denoted as $Y_{train}$, while the labels of the unlabeled nodes, $Y_{test},$ remain hidden during training. The objective of GFD is to learn a labeling function for the unlabeled nodes using all available information, such that $Y_{test}=f(X,A,Y_{train})$.

Given the adjacency matrix $A$ of a graph $G,$ the graph Laplacian $L$ can be defined as either $L=D-A$ or $L=I-D^{-1/2}A{D}^{-1/2}$ [27], where $D$ is the degree matrix and $I$ is the identity matrix. The Laplacian matrix $L$ is positive semidefinite and can be decomposed as $L=U\Lambda U^T$, where $\Lambda$ is a diagonal matrix holding the eigenvalues ${\lambda }_1\le {\lambda }_2\le \dots \le {\lambda }_N,$ and $U=(u_1,u_2,\dots ,u_N)$ consists of the corresponding $N$ eigenvectors [39]. By defining an arbitrary threshold ${\lambda }_k$, the eigenvalues of the graph Laplacian can be grouped in two categories: low-frequency eigenvalues $\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k\}$ and high-frequency eigenvalues $\left\{{\lambda }_{k+1},{\lambda }_{k+2},\dots ,{\lambda }_N\right\}.$ This separation allows for the analysis of distinct spectral components within the graph. Based on the principles of graph signal analysis, the standardized Laplacian matrix’s eigenvectors, $U$, can be interpreted as the basis functions for the Graph Fourier Transform. These eigenvectors enable the decomposition of graph signals into different frequency components for analysis. Let $X=[x_1,x_2,\dots ,x_N]$ represent the graph signals. In the operation $U^{T}X$, $U,$ the eigenvectors of the normalized Laplacian matrix, is treated as the Graph Fourier Transform of the signal $X$ [40]. This transformation projects the graph signals onto the spectral domain. The energy distribution within the spectrum at ${\lambda }_k$ is defined in Equation (1) as

$$E\left({\lambda }_k\right)=\sum _{i=1}^k{\parallel U_i^{T}X\parallel }^2$$

(1)

The spectral energy proportion at ${\mathsf{\lambda }}_{\mathrm{k}}$ is defined as the total spectral energy allocation contributed by the initial k eigenvalues. It can be expressed in Equation (2) as follows:

$$R\left({\lambda }_k\right)={\displaystyle \frac{\sum _{i=1}^k{\parallel U_i^{T}X\parallel }^2}{\sum _{i=1}^N{\parallel U_i^{T}X\parallel }^2}}$$

(2)

In graph-based fraud detection, heterophily denotes the occurrence of an edge connecting nodes with dissimilar labels, shown by a fraudulent node linked to a benign node. This contrasts with homophily, in which connected nodes possess identical labels. Heterophily is popular in fraud detection, as fraudsters often disguise themselves by associating with benign users, making it a crucial element in the development of successful detection tools. For a specific node v, the heterophily degree measures the ratio of its neighbors having a different label. Likewise, the heterophily of the whole graph measures the ratio of heterophilic edges to the overall number of edges. These metrics can be defined in Equation (3) as follows:

$$\begin{gathered} \mathrm{h}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{o}\left(\mathrm{v}\right)={\displaystyle \frac{1}{\left|N\left(v\right)\right|}}\left|\left\{u:u\in N\left(v\right),y_u\ne y_v\right\}\right|, \\ \mathrm{h}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{o}\left(\mathrm{G}\right)={\displaystyle \frac{1}{\left|E\right|}}\left|\left\{ϵ:y_{\mathrm{s}\mathrm{r}\mathrm{c}}\ne y_{\mathrm{d}\mathrm{s}\mathrm{t}}\right\}\right| \end{gathered}$$

(3)

3.2. Proposed Framework

This study proposes the Spectrum-Constrained and Skip-Enhanced Graph Fraud Detector (SCSE-GFD), a novel framework designed to address heterophily and class imbalance in fraud detection. Figure 2 illustrates the SCSE-GFD architecture, which consists of four key components: adaptive polynomial convolution, relation-aware mechanism, skip connections, and edge classification. Each module plays a distinct role in enhancing fraud detection in graph-based settings. The adaptive polynomial convolution module enables multi-frequency spectral filtering to capture both low- and high-frequency signals. The relation-aware mechanism ensures effective feature propagation by dynamically weighting homophilic and heterophilic edges. Skip connections mitigate over-smoothing by preserving both low- and high-level node features. Finally, the edge classification task enhances the model’s structural understanding by predicting edge types. The following subsections provide a detailed explanation of each component.

3.2.1. Adaptive Polynomial Convolution

This study extends polynomial spectral filtering to enhance node feature propagation in multi-relational fraud graphs. Instead of directly applying graph convolution, SCSE-GFD approximates it using a polynomial function of the graph Laplacian. For a given node $v$, let $h_v^{(l-1)}$ be its feature at layer $l-1$. The feature update follows Equation (4):

$${\mathrm{h}}_v^{\left(l\right)}=\sum _{k=0}^K{\theta }_k{\mathrm{L}}^k{\mathrm{h}}_v^{(l-1)}$$

(4)

where $h_v^{\left(l\right)}$ is the updated node representation, ${\theta }_k$ are learnable coefficients for the polynomial filter, $L=D^{\frac{-1}{2}}{AD}^{\frac{-1}{2}}$ is the normalized Laplacian, and $K$ is the polynomial degree. To address heterophily and account for multi-relational graphs, the convolution is extended to include relation-specific Laplacians as shown in Equation (5):

$${\mathrm{h}}_v^{\left(l\right)}=\sum _{k=0}^K{\theta }_k\sum _{t\in T}{L}_t^k{\mathrm{h}}_v^{(l-1)}$$

(5)

where ${\mathit{L}}_t$ is the Laplacian matrix specific to edge type $t$. This enables the model to learn distinct feature representations for different types of relationships in the graph.

3.2.2. Relation-Aware Mechanism

The relation-aware mechanism is crucial for handling the heterophilic nature of fraud graphs. It distinguishes between different edge types, such as homophilic (symmetric) and heterophilic (asymmetric) edges to ensure that the features propagated across the graph are tailored to the relationships present. This mechanism leverages the concept of symmetry by treating homophilic edges as symmetric connections, where nodes share similar attributes, and heterophilic edges as asymmetric interactions, where connected nodes exhibit contrasting properties. By dynamically assigning weights to these edges, the relation-aware mechanism ensures that the structural balance between symmetric and asymmetric relationships is preserved.

For an edge $\left(u,v\right),$ let $h_u$ and $h_v$ represent the node embeddings of nodes $u$ and $v,$ respectively. The relation-aware score for the edge is computed as shown in Equation (6):

$$r\left(u,v\right)=\mathrm{tahn}\left(w_r^{⊺}\left[{\mathrm{h}}_u;{\mathrm{h}}_v;\left|{\mathrm{h}}_u-{\mathrm{h}}_v\right|\right]\right)$$

(6)

where ${\mathit{w}}_r$ are learnable weights for the relation-aware module and $\left[h_u;h_v;\left|h_u-h_v\right|\right]$ is the concatenation of the source, destination, and absolute difference of their features. This mechanism enables the model to adaptively weigh the significance of edges according to their types, enabling enhanced feature propagation across homophilic and heterophilic connections.

3.2.3. Skip Connections

The skip connections module resolves the label use issue sometimes faced in fraud detection. This component ensures that both low-level features and high-level features influence the final prediction. Without skip connections, deep GNN models suffer from over-smoothing, where nodes become indistinguishable due to excessive feature mixing. To prevent this, SCSE-GFD integrates skip connections across all layers, ensuring that meaningful information is preserved throughout the network. Let ${\mathrm{h}}_v^{\left(l\right)}$ represent the high-level feature at layer $l$ and ${\mathrm{x}}_v$ represent the initial (low-level) feature of node v, as shown in Equation (7). The final representation is computed as shown in Equation (8).

$${\mathrm{h}}_v^{\left(l\right)}={\mathrm{h}}_v^{\left(l\right)}+X_v$$

(7)

$${\mathrm{h}}_v^{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}={\mathrm{h}}_v^{\left(l\right)}+{\mathrm{x}}_v$$

(8)

3.2.4. Edge Classification

The edge classification task is introduced to improve the structural understanding of the graph. By learning to classify edge types, the model becomes more effective at handling heterophily. This classification helps reweight edge importance dynamically, improving the model’s ability to propagate features across meaningful connections. For an edge $\left(u,v\right),$ the model predicts the edge type ${\widehat{\mathit{y}}}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}$ using the concatenated features of the two nodes, as shown in Equation (9):

$${\widehat{y}}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathrm{W}}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}\right[{\mathrm{h}}_u;{\mathrm{h}}_v\left]\right)$$

(9)

where ${\mathrm{W}}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}$ is a learnable weight matrix and $\left[{\mathrm{h}}_u;{\mathrm{h}}_v\right]$ represents the concatenated node embeddings. The edge classification loss is calculated as shown in Equation (10).

$${\mathcal{L}}_{edge}=-\sum _{(u,v)\in E}\sum _{t\in T}{y}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}^{\left(t\right)}\log ({\widehat{y}}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}^{\left(t\right)})$$

(10)

This mechanism reinforces meaningful connections in the graph, improving node classification by leveraging relational structures. The predicted edge types are further used to reweight adjacency matrices during feature propagation, allowing SCSE-GFD to refine its learning process dynamically.

3.2.5. Training

SCSE-GFD optimizes both node classification and edge classification in a joint learning framework as shown in Algorithm 1. The loss function is defined in Equation (11) as follows:

$$\mathcal{L}={\mathcal{L}}_{node}+{\mathsf{\gamma }\mathcal{L}}_{edge}$$

(11)

where ${\mathcal{L}}_{node}$ represents cross-entropy loss for node classification and ${\mathcal{L}}_{edge}$ accounts for edge classification. The balancing parameter $\mathsf{\gamma }$ ensures that both tasks contribute effectively to learning without overshadowing each other. To determine an optimal $\mathsf{\gamma }$ value, we performed hyperparameter tuning across a range of values (0.1 to 1.0). Empirical results indicate that setting $\mathsf{\gamma }=0.5$ provides the best balance, preventing over-reliance on edge classification while still improving fraud detection performance.

Algorithm 1: The training process of SCSE-GFD

Input: fraud graph $\mathcal{G}=\left(\mathcal{V},\mathcal{E},\mathcal{X}\right)$ degree of polynomial $K$, frequency filters $\theta$

Output: logits $Z\in {\mathbb{R}}^{\left|V\right|\times C}$

Preprocessing: precompute relation-specific Laplacians $L_t$ for all edge types $t$

Initialize model parameters: polynomial filter coefficients $\left\{{\theta }_k\right\}$, relation-aware weights, and skip connection layers.

Training Loop For each epoch           for each batch B $\subset G:$

Extract node features $X_v$ Initialize node embeddings:${\mathrm{h}}_v^{\left(0\right)}⟵X_v$ for $v\in B$ Layer-wise feature propagation: For each layer $l=1toL$ Compute high-level features using adaptive polynomial convolution:${\mathrm{h}}_v^{\left(l\right)}=\sum _{k=0}^K{\theta }_k\sum _{t\in T}{L}_t^k{\mathrm{h}}_v^{(l-1)}$ Apply skip connection: ${\mathrm{h}}_v^{\left(l\right)}⟵{\mathrm{h}}_v^{\left(l\right)}+X_v$

4. Final node embedding after L-layers:${\mathrm{h}}_v^{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}={\mathrm{h}}_v^{\left(L\right)}$

5. Edge prediction: for each edge $\left(u,v\right)\in E$ Compute edge-type logits: ${\widehat{y}}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathrm{W}}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}\left[{\mathrm{h}}_u;{\mathrm{h}}_v\right]\right)$

6. Loss computation: Node classification loss: ${\mathcal{L}}_{node}=-\sum _{v\in V_{train}}{y}_v\log \left({\widehat{y}}_v\right)$        Edge classification loss:      ${\mathcal{L}}_{edge}=-\sum _{(u,v)\in E}\sum _{t\in T}{y}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}^{\left(t\right)}\log ({\widehat{y}}_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}^{\left(t\right)})$         Total loss: $\mathcal{L}={\mathcal{L}}_{node}+{\mathsf{\gamma }\mathcal{L}}_{edge}$

3.3. Datasets

To evaluate SCSE-GFD’s performance in fraud detection on graph-based data, we selected two widely used datasets: Amazon [41] and YelpChi [42], which focus on identifying fraudulent activity in reviews. Fraud detection in this context involves identifying deceptive or misleading reviews on products featured on e-commerce platforms. The key statistics of the datasets are summarized in

Table 2. Summary of dataset statistics.

Dataset	Nodes	Fraud (%)	Edges	Relations	Features
YelpChi	45,954	14.53%	R-U-R R-T-R R-S-R Homo	98,630 1,147,232 6,805,486 7,693,958	32
Amazon	11,944	6.87%	U-P-U U-S-U U-V-U Homo	351,216 7,132,958 2,073,474 8,796,784	24

.

The YelpChi dataset consists of hotel and restaurant reviews collected from Yelp.com, categorized into filtered (spam) and recommended (genuine) reviews. Each review is represented as a 32-dimensional feature vector, and the dataset captures multiple types of relationships that help in fraud detection. Specifically, YelpChi defines the following:

• ❖ R-U-R (Review-User-Review): This relationship connects two reviews posted by the same user. It helps identify users who generate multiple reviews, potentially revealing spam behavior.
• ❖ R-T-R (Review-Time-Review): this links reviews of similar products submitted within a short timeframe, useful for detecting coordinated review spam campaigns.
• ❖ R-S-R (Review-Score-Review): this associates reviews that share identical ratings for a specific product, helping to identify fraudulent patterns in rating manipulation.

The Amazon dataset contains reviews provided by clients for various products. They are categorized as normal if they have received over 80% helpful votes, while those with less than 20% helpful votes are marked as fraud [23]. To eliminate potential label leakage from the feature “minimum number of unhelpful votes” [23,24], this attribute is excluded, and the remaining features are used to construct 24-dimensional node representations. The dataset comprises three categories of relationships:

• ❖ U-P-U (User-Product-User): this relationship connects users who reviewed at least one common product, capturing potential coordinated manipulation.
• ❖ U-S-V (User-Score-Value): this links users who assigned identical star ratings within a one-week period, helping to detect groups that systematically inflate or deflate ratings.
• ❖ U-V-U (User-Vector-User): this represents user pairs with the top 5% similarity in their review texts, revealing users who may be working together to generate fraudulent content.

Once the datasets are collected and preprocessed, we proceed to define the evaluation metrics used to assess SCSE-GFD’s performance. These metrics provide a standardized way to compare SCSE-GFD against existing models, ensuring a rigorous evaluation of its effectiveness in fraud detection.

3.4. Evaluation Metrics

Given that GFD is inherently a class-imbalanced classification task, this study employs two commonly used evaluation metrics: F1-macro and AUC (area under the ROC curve).

F1-macro calculates the weighted mean of F1 scores across all classes as shown in Equation (12). It is frequently used to assess how the classification models perform, mainly in situations where the classes are imbalanced.

$$F1-\mathrm{m}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{F1}_i$$

(12)

where N is the total count of classes and ${F1}_i$ is the F1 score for class i. The F1 score for each class i is calculated as the harmonic mean of precision and recall, as shown in Equation (13).

$${F1}_i=2\times {\displaystyle \frac{{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}_{\mathrm{i}}\times {\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}_{\mathrm{i}}}{{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}_{\mathrm{i}}+{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}_{\mathrm{i}}}}$$

(13)

where precision for class i is ${\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{T}\mathrm{P}}_{\mathrm{i}}}{{\mathrm{T}\mathrm{P}}_{\mathrm{i}}+{\mathrm{F}\mathrm{P}}_{\mathrm{i}}}}$ (True Positives/(True Positives + False Positives) and recall for class i is ${\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{T}\mathrm{P}}_{\mathrm{i}}}{{\mathrm{T}\mathrm{P}}_{\mathrm{i}}+{\mathrm{F}\mathrm{N}}_{\mathrm{i}}}}$ (True Positives/(True Positives + False Negatives). Since fraud detection prioritizes correctly identifying fraudulent instances, F1-macro helps measure the model’s ability to reduce false negatives while maintaining precision, ensuring reliable classification despite class imbalance. AUC is a comprehensive evaluation of a model’s performance across all possible classification thresholds. This makes the AUC particularly robust when dealing with imbalanced datasets. AUC is detailed in Equation (14).

$$\mathrm{A}\mathrm{U}\mathrm{C}={\displaystyle \frac{1}{2}}\sum _{\mathrm{i}=1}^{\mathrm{m}-1}{(\mathrm{T}\mathrm{P}\mathrm{R}}_{\mathrm{i}+1}+{(\mathrm{T}\mathrm{P}\mathrm{R}}_{\mathrm{i}}\left)\right({\mathrm{F}\mathrm{P}\mathrm{R}}_{\mathrm{i}+1}-{(\mathrm{F}\mathrm{P}\mathrm{R}}_{\mathrm{i}})$$

(14)

where TPR is True Positive Rate and FPR is False Positive Rate. Higher values, along with F1-macro and AUC, indicate better overall performance of the evaluated methods.

3.5. Experimental Settings

We conducted all experiments using the Adam optimizer, running them on Python 3.7.12 within PyCharm on a system running Windows 10 Pro with an NVIDIA RTX 3070 GPU (8 GB VRAM) (NVIDIA Corporate, Santa Clara, CA, USA), an Intel Core i7-10750H CPU (Intel Corporation, Santa Clara, CA, USA), and 32 GB of RAM. The model was developed using PyTorch 2.1.0, DGL 1.1.2 + cu118, ensuring efficient execution of graph-based computations. For SCSE-GFD, we set the learning rate to 0.01 for YelpChi and 0.1 for Amazon, as these values provided the best balance between convergence speed and stability during training. A lower learning rate resulted in slower convergence, while a higher value led to instability. The model employed a weight decay of 0.00005 to prevent overfitting without excessively restricting model learning. A dropout rate of 0.1 was selected to maintain regularization while preserving sufficient information in the graph structure. The node embedding dimension was set to 16, ensuring efficient representation learning without excessive computational cost. Increasing this dimension did not yield significant performance improvements, while reducing it led to underfitting. Additionally, the high-frequency signal neighbor order (C) was set to 1, allowing the model to effectively capture high-frequency signals crucial for fraud detection in heterophilic graphs. Higher values of C resulted in increased noise propagation, reducing model performance. For fairness in experiments, we divided the datasets into training, validation, and test sets in a 40%/20%/40% ratio, ensuring a well-balanced evaluation. SCSE-GFD was implemented using the DGL library in PyTorch, while baseline methods were evaluated using publicly available implementations. To ensure convergence and comparability across models, all methods were trained for 1000 epochs, which was determined empirically as the point where performance stabilizes.

4. Results and Discussion

4.1. Baselines

We performed comparative experiments between SCSE-GFD and several advanced baseline models, categorized into three groups. The first includes homophily-based GNN models, such as GCN [27], GraphSAGE [28], GAT [29], and GIN [30]. The second focuses on state-of-the-art methods specifically developed for GFD, including GraphConsis [22], CARE-GNN [23], PC-GNN [4], GAGA [33], and SEfraud [34]. The third consists of GNN-based models tailored for heterophilic graphs, such as ACM [37], H2-FDetector [24], BWGNN [26], SplitGNN [35], and SEC-GFD [36].

4.2. Performance Comparison

This study presents a comprehensive comparison of SCSE-GFD against three groups of baseline models: (1) homophily-based GNNs, (2) graph-based fraud detection algorithms, and (3) heterophily-specific GNNs. The results, summarized in

Table 3. Performance comparison of SCSE-GFD and baseline models.

Methods		Datasets
		YelpChi		Amazon
		AUC	F1-Macro	AUC	F1-Macro
Homophily GNN	GCN	59.83	56.20	83.69	64.86
	GraphSAGE	89.38	75.46	93.16	88.26
	GAT	57.15	48.79	81.02	64.64
	GIN	75.28	63.42	81.38	71.14
GFD Algorithm	GraphConsis	69.55	57.91	87.27	78.46
	CARE-GNN	76.19	63.32	90.67	86.39
	PC-GNN	79.87	63.00	95.86	89.56
	GAGA	89.77	76.71	95.61	90.31
	SEFraud	86.77	73.01	93.23	89.50
Heterophily GNN	ACM	88.28	69.72	93.69	81.83
	H2-FDetector	89.48	74.38	96.03	86.91
	BWGNN	89.79	73.65	92.31	71.63
	SplitGNN	89.53	73.16	92.45	72.40
	SEC-GFD	90.13	75.98	94.32	90.24
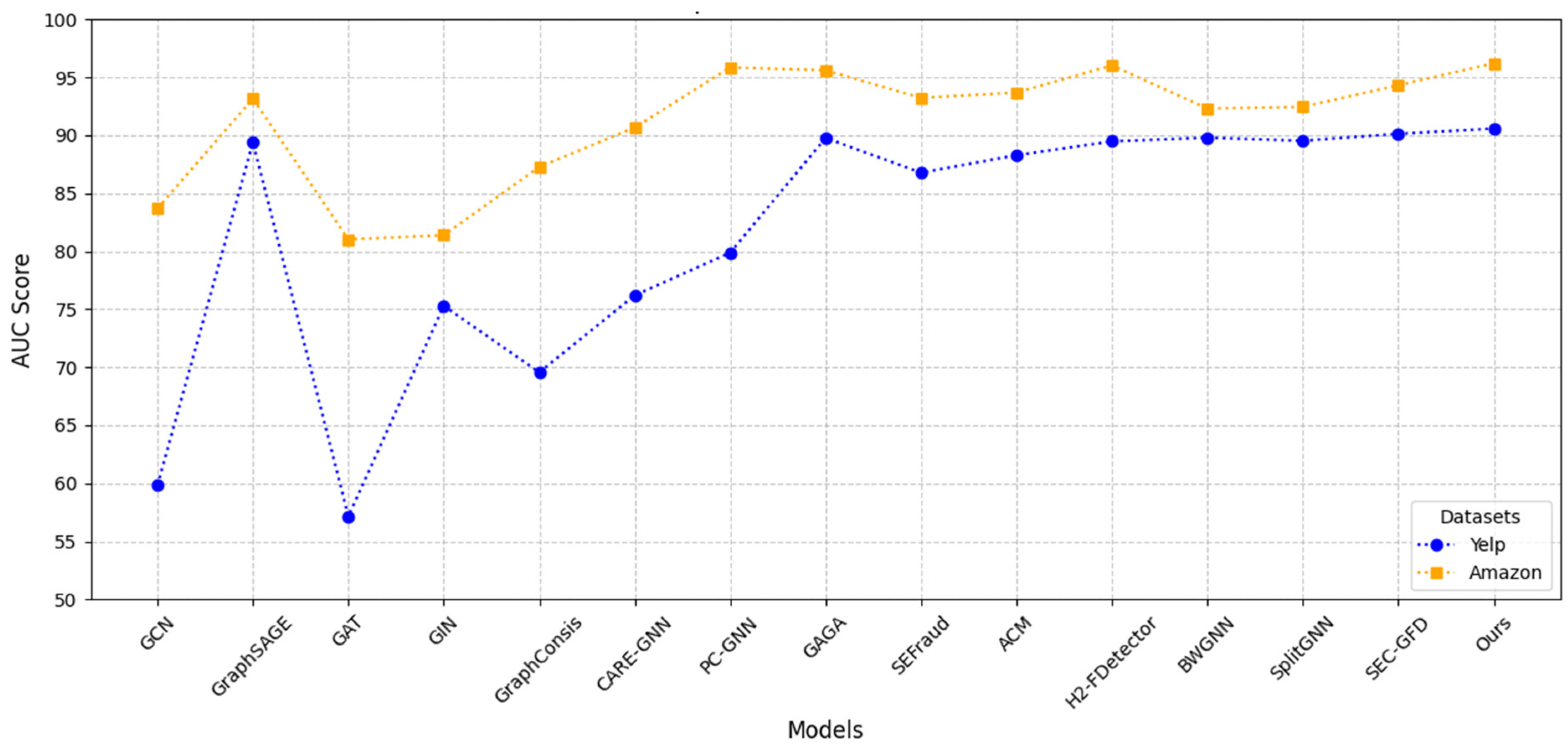
Ours	SCSE-GFD	90.58	76.12	96.21	92.28

, confirm the performance of SCSE-GFD across multiple datasets and evaluation metrics.

The first group of baselines consists of homophily-based GNNs, including GCN, GraphSAGE, GAT, and GIN. These models primarily function as low-pass filters, capturing only low-frequency graph signals. As a result, they fail to effectively utilize the high-frequency components that are critical for fraud detection in heterophilic graphs. On the YelpChi dataset, SCSE-GFD achieves an F1-macro score of 76.12, outperforming all homophily-based models. Compared to GIN, SCSE-GFD improves F1-macro by 12.70%, demonstrating its ability to retain discriminatory node features. Similarly, on the Amazon dataset, SCSE-GFD achieves an AUC of 96.21, surpassing GraphSAGE, the strongest homophily-based baseline, by 3.05%.

The second group consists of fraud-specific algorithms, including GraphConsis, CARE-GNN, PC-GNN, GAGA, and SEFraud. These models incorporate techniques to handle heterophily and fraud camouflage but rely on predefined neighbor selection or group aggregation, limiting their ability to capture complex high-frequency interactions. On YelpChi, SCSE-GFD achieves an AUC of 90.58, surpassing GAGA, the best-performing fraud detection baseline, by 0.81% in terms of the AUC. However, GAGA slightly outperforms SCSE-GFD in terms of F1-macro on YelpChi by 0.41%, which can be attributed to its label-enhanced encoding mechanism. Since YelpChi exhibits lower homophily, GAGA benefits from explicit label information when learning node representations, improving classification performance for minority-class nodes. Nevertheless, GAGA’s reliance on extensive hyperparameter tuning limits its adaptability across different datasets. In contrast, SCSE-GFD maintains robust performance across multiple datasets by leveraging spectral filtering and relation-aware modeling, ensuring consistent results without excessive fine-tuning. While GAGA excels in settings with low homophily and strong label dependencies, SCSE-GFD offers better adaptability, making it a more practical choice for large-scale fraud detection applications. Similarly, on Amazon, SCSE-GFD achieves an F1-macro of 92.28, outperforming PC-GNN and SEFraud, further showcasing its strength in fraud classification. The third group, shown in Table 3, includes heterophily-specific GNNs, such as ACM, H2-FDetector, BWGNN, and SplitGNN. While these models incorporate mechanisms to handle heterophily, they lack the flexibility to capture diverse spectral information across multiple frequency bands. On the Amazon dataset, SCSE-GFD achieves an F1-macro of 92.28, outperforming H2-FDetector by 5.37% and BWGNN by 20.65%. Many of these models focus on aggregation strategies and band-pass filtering but struggle with adaptability. SCSE-GFD overcomes this limitation through its adaptive polynomial convolutions, which dynamically adjust spectral learning based on the graph structure. On YelpChi, SCSE-GFD achieves an AUC of 90.58, slightly higher than both H2-FDetector and BWGNN, demonstrating its consistent performance across multiple heterophilic datasets. Figure 3 provides a visual summary of the AUC performance across all datasets, further confirming the advantages of SCSE-GFD over existing models.

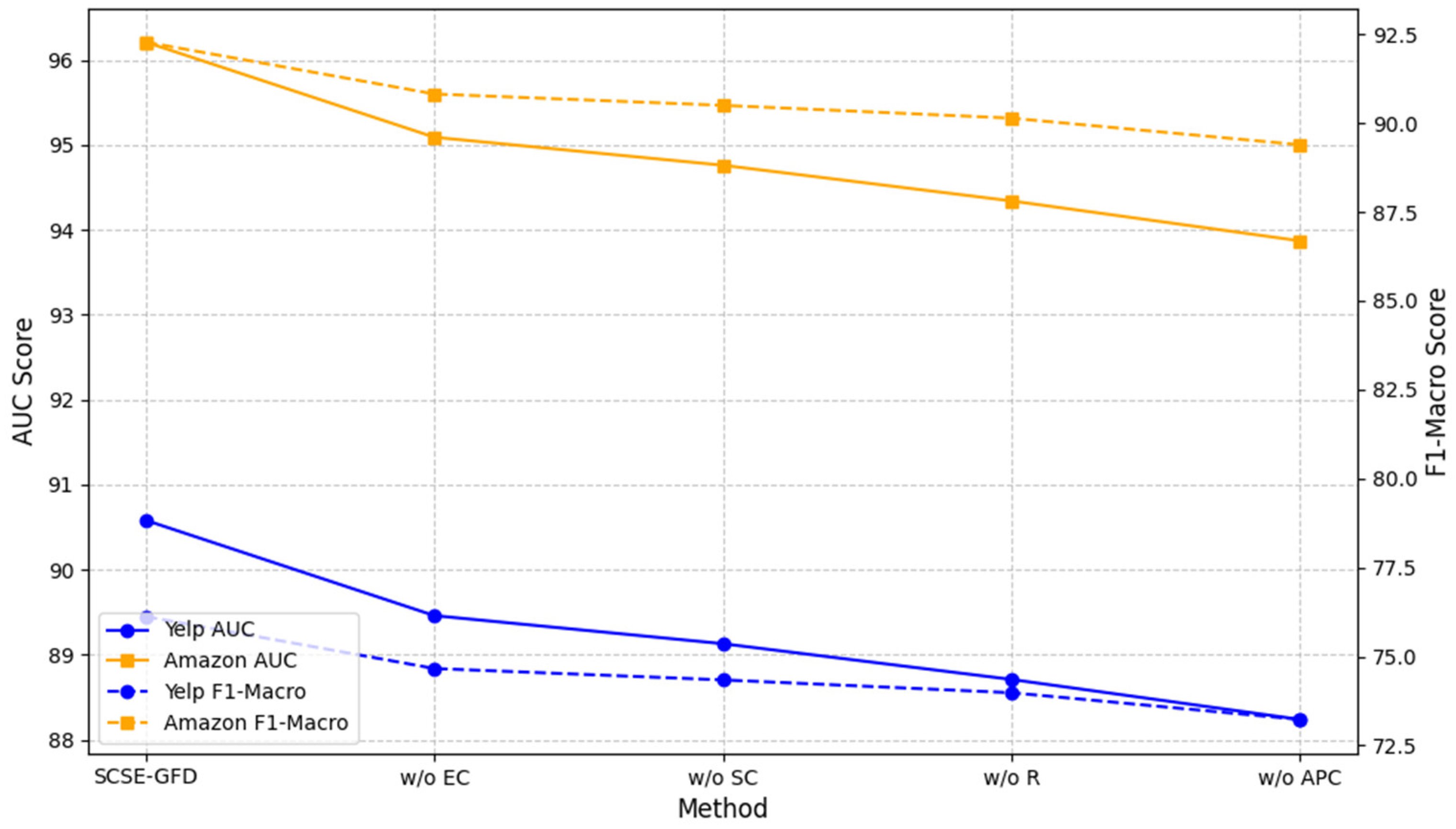
4.3. Ablation Study

To evaluate the contributions of different components within the SCSE-GFD framework, we conducted an ablation study by systematically removing or modifying specific modules. The results, presented in

Table 4. Performance of SCSE-GFD under different ablation settings; w/o (without) indicates that a specific module has been removed to evaluate its impact on model performance.

Method	Yelp		Amazon
	AUC	F1-Macro	AUC	F1-Macro
SCSE-GFD	90.58	76.12	96.21	92.28
w/o EC	89.46	74.66	95.09	90.82
w/o SC	89.13	74.34	94.76	90.50
w/o R	88.71	73.98	94.34	90.14
w/o APC	88.24	73.23	93.87	89.39

and Figure 4, highlight the critical role of each component in enhancing fraud detection performance.

When adaptive polynomial convolution (APC) is replaced with a standard graph convolution, a significant drop in performance is observed, with reductions of 2.34% and 2.89% in the AUC and F1-macro on the Yelp dataset. This indicates the importance of this module in capturing spectral signals and addressing heterophily through relation-specific Laplacians. Removing the relation-aware mechanism (R) results in further performance declines, particularly on the Amazon dataset, with reductions of 1.87% and 2.14% in the AUC and F1-macro. This underscores the value of distinguishing homophilic and heterophilic edges to propagate meaningful features effectively. The omission of skip connections (SC) also leads to a decline in performance, with the AUC and F1-macro dropping by 1.45% and 1.78% on Yelp. This highlights the importance of conserving both low- and high-level node features to combat over-smoothing and improve label utilization. Finally, excluding the edge classification (EC) task reduces the AUC and F1-macro by 1.12% and 1.46% on Amazon. While all components play a role in improving the model’s robustness, the adaptive polynomial convolution and relation-aware mechanism are particularly critical for addressing the challenges posed by heterophilic graphs.

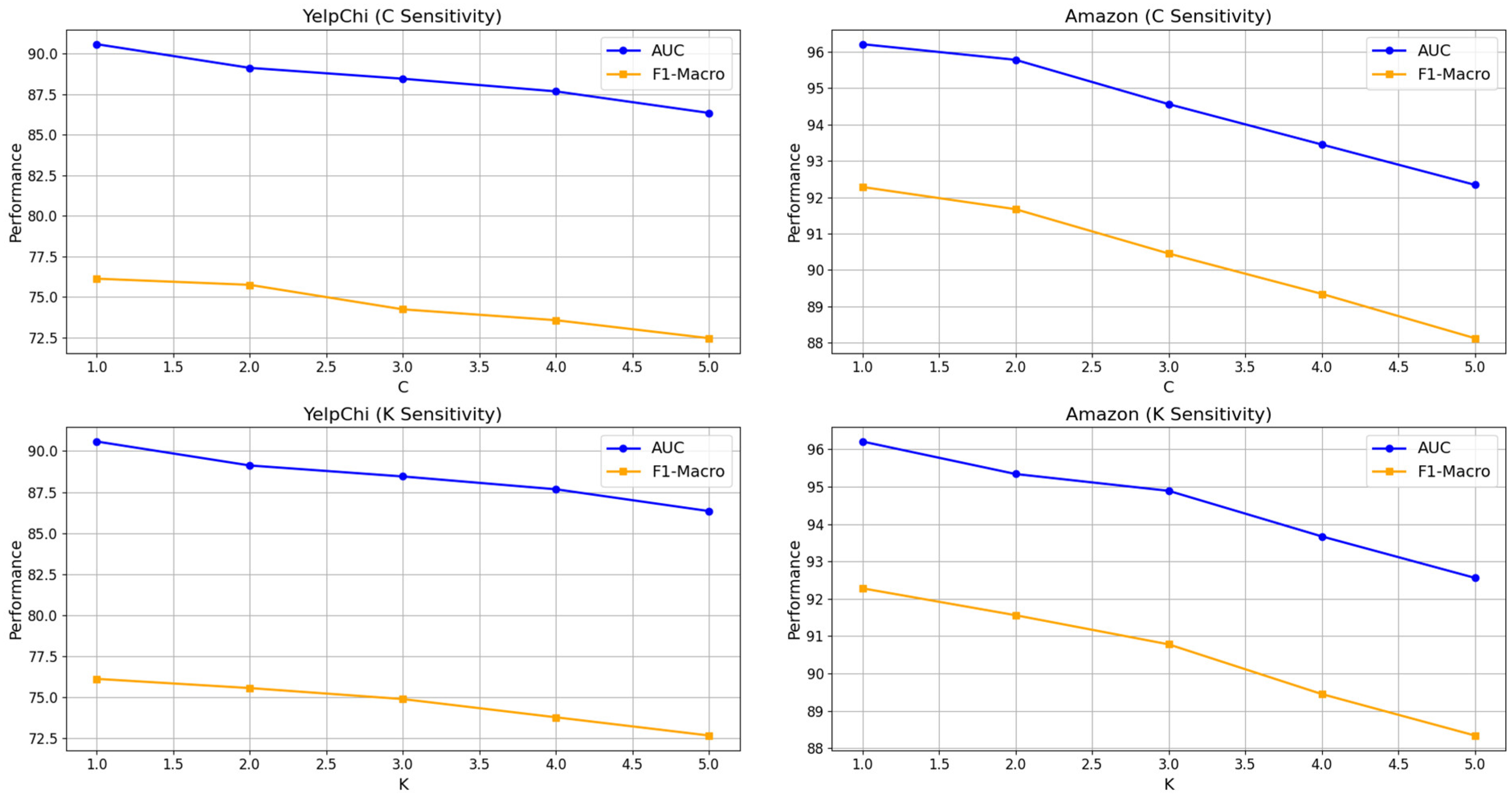
4.4. Parameter Study

The sensitivity analysis reveals that SCSE-GFD’s performance is highly influenced by C (neighbor order) and K (polynomial degree), as they determine how information is aggregated and filtered within the graph. The neighbor order C controls the number of hops considered during feature aggregation. In heterophilic graphs, where distant nodes often belong to different classes, higher values of C introduce noise rather than useful information. Our experiments indicate that SCSE-GFD performs optimally at lower values (C = 1 or 2) as seen in Figure 5. On YelpChi, increasing C from 1 to 5 results in a 4.5% drop in the AUC, demonstrating that aggregating information from distant, dissimilar nodes weakens fraud detection performance. Traditional GNNs designed for homophilic graphs benefit from information exchange across multiple hops, but in fraud detection, fraudulent nodes often interact with benign users deceptively, making distant neighbors less informative. Therefore, limiting aggregation to closer neighbors helps preserve relevant fraud-related patterns.

Similarly, the polynomial degree K, which controls the complexity of spectral filtering, plays a crucial role in SCSE-GFD’s effectiveness. Lower values of K (1 or 2) enable the model to focus on local structural differences, which are crucial for identifying fraudulent behavior. Increasing K from 1 to 5 on Amazon results in a 6% decline in the F1-macro, confirming that excessive spectral complexity leads to overfitting, where the model captures irrelevant noise instead of meaningful fraud patterns. Higher values of K tend to make the model more sensitive to small variations in node attributes, which may not be beneficial in fraud detection, where relationships are often heterogeneous. By keeping K low, SCSE-GFD effectively extracts high-frequency fraud indicators without amplifying irrelevant patterns, ensuring stable performance across different datasets.

Our findings emphasize the importance of carefully tuning C and K to maintain SCSE-GFD’s effectiveness. A larger C increases the risk of feature dilution, as distant nodes in heterophilic graphs are often weakly related. Similarly, a higher K amplifies unnecessary noise, reducing generalization. By balancing these values at C = 1 or 2 and K = 1 or 2, SCSE-GFD achieves superior fraud detection by capturing localized fraud patterns while avoiding feature corruption. These insights validate SCSE-GFD’s design and suggest that heterophilic fraud detection models should prioritize local interactions and controlled spectral filtering to avoid performance degradation. Future work could explore adaptive strategies where C and K are dynamically tuned based on the graph’s homophily–heterophily characteristics, further enhancing the model’s flexibility and performance.

4.5. Testing Time (Computational Complexity)

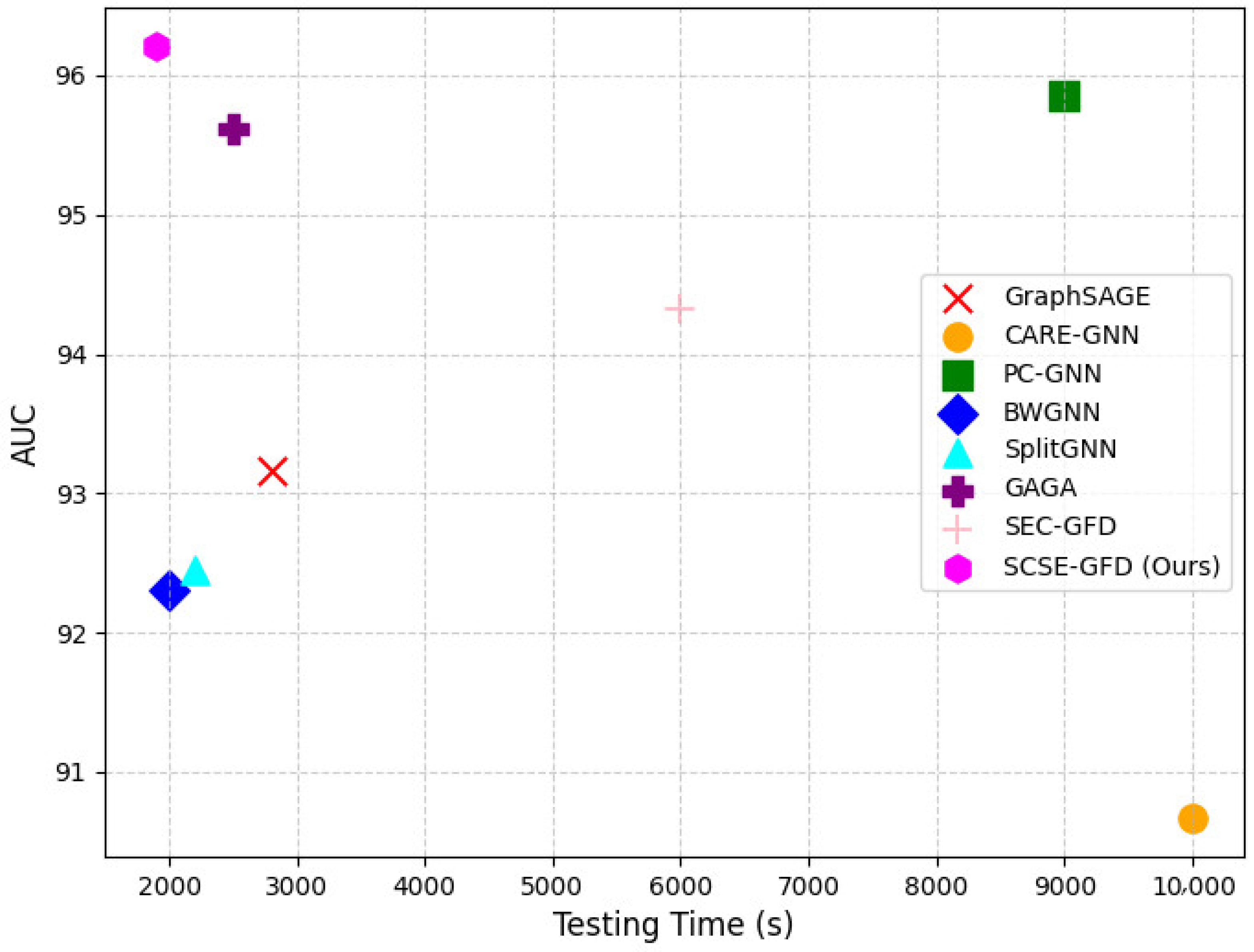
To evaluate the real-time efficiency of the proposed SCSE-GFD model, we conducted an inference speed comparison against several state-of-the-art models on the Amazon dataset. Large-scale fraud detection systems require both a high accuracy and computational efficiency, so it is essential to ensure that improvements in predictive performance do not come at the cost of increased inference time. Figure 6 shows that SCSE-GFD not only achieves the highest predictive accuracy but also maintains the lowest testing time, making it an effective approach for large-scale graph-based fraud detection. This efficiency is attributed to its spectral filtering and relation-aware mechanisms, which capture both low- and high-frequency signals without introducing excessive computational overhead. Some models, such as GraphSAGE and BWGNN, exhibit slightly lower inference times but fail to match SCSE-GFD in accuracy. GraphSAGE primarily relies on local neighborhood aggregation, limiting its ability to model complex fraud patterns in heterophilic graphs. BWGNN incorporates wavelet-based spectral filtering, which enhances efficiency but lacks the adaptive learning mechanisms of SCSE-GFD, leading to reduced predictive power. On the other hand, models like CARE-GNN and PC-GNN show significantly higher computational costs. CARE-GNN’s reinforcement-learning-based neighbor selection process increases its test time, making it less practical for real-time applications. PC-GNN, though effective at addressing class imbalance, suffers from slower inference due to its iterative neighbor sampling approach. Similarly, while GAGA and SEC-GFD achieve strong predictive performance, their longer test times suggest additional computational complexity from group aggregation and spectral partitioning techniques. Overall, SCSE-GFD demonstrates an optimal balance between accuracy and efficiency, making it highly suitable for real-time fraud detection in large-scale, dynamic environments like e-commerce platforms.

4.6. Limitations and Future Works

SCSE-GFD introduces a novel framework for fraud detection in heterophilic graphs by leveraging adaptive polynomial convolutions, relation-aware mechanisms, and skip connections. However, like any model, it has certain limitations that present opportunities for further improvement. One challenge is the dependence on edge classification to differentiate between homophilic and heterophilic edges. This makes the model sensitive to noisy or incomplete edge information, which could reduce its effectiveness in real-world scenarios where relationships between entities are unclear. To address this, future work will explore self-supervised learning techniques to enhance robustness against missing or inaccurate edge data, ensuring more reliable fraud detection in dynamic environments.

Another limitation is computational efficiency when applied to large-scale graphs, particularly due to spectral filtering. While SCSE-GFD optimizes efficiency through adaptive polynomial convolutions, further improvements can be made by integrating graph pruning techniques or model distillation to reduce computational overhead without sacrificing performance. Additionally, SCSE-GFD has been designed and evaluated specifically for fraud detection datasets. Its generalizability to other graph-based tasks, such as recommendation systems or social network analysis, remains unexplored. Future research will investigate domain adaptation strategies, such as transfer learning, to extend the model’s applicability beyond fraud detection.

Despite these challenges, SCSE-GFD represents a significant advancement in fraud detection by effectively modeling heterophilic structures, improving label utilization, and maintaining computational efficiency. Future enhancements will focus on self-supervised learning, scalability, and broader applications to further strengthen its effectiveness in complex graph-based tasks.

5. Conclusions

In this study, we introduced SCSE-GFD (Spectrum-Constrained and Skip-Enhanced Graph Fraud Detection), a novel framework aimed at addressing the challenges of fraud detection in heterophilic graphs. Fraud detection in multi-relational graphs is particularly difficult due to the complex interaction between homophilic and heterophilic edges, class imbalance, and the scarcity of labeled data. SCSE-GFD tackles these challenges through the use of adaptive polynomial convolutions, a relation-aware mechanism, and skip connections. These features allow the framework to capture intricate relationships and spectral properties, improving its ability to distinguish between homophilic and heterophilic connections.

Extensive experiments on several real-world datasets demonstrate that SCSE-GFD outperforms current state-of-the-art methods, achieving better results in terms of AUC and overall robustness. However, on the YelpChi dataset, GAGA achieves a slightly higher F1-macro score, which can be attributed to its label-enhanced encoding mechanism. This provides additional supervision in low-homophily settings, benefiting classification performance for minority-class nodes. While SCSE-GFD maintains a more adaptable and computationally efficient approach by integrating spectral filtering and relation-aware mechanisms, future work could explore hybrid approaches incorporating label-enhanced learning to further improve performance in highly heterophilic datasets.

These findings confirm SCSE-GFD’s effectiveness at improving fraud detection in heterogeneous graphs. Moreover, an ablation study highlights the importance of each component, adaptive polynomial convolution, the relation-aware mechanism, and skip connections, in enhancing the model’s robustness and accuracy. These results underscore SCSE-GFD’s potential as a powerful tool for fraud detection, leveraging both graph spectral features and structural relationships, and representing a significant advancement in the field.