Abstract
Robustness in networks plays a vital role in mitigating the effects of failures caused by nodes or links, which can disrupt essential services. Among the various vulnerability parameters in graph theory, such as connectivity and integrity, their applications to fuzzy graphs remain underexplored, despite fuzzy graphs being a powerful tool for modeling uncertainty. In this paper, we introduce the parameter ’fuzzy node integrity’, which considers both the number of disrupted elements and the strength of residual connections. We derive general formulas for different types of symmetric and asymmetric fuzzy graph structures, including cycle graphs, wheel graphs, and star graphs, to systematically demonstrate the utility of this parameter. The proposed parameter is then applied to a military logistics problem to gain insights into the identification of critical nodes and route optimization under uncertainty. This study bridges an important gap in fuzzy graph theory by redefining node integrity through the inclusion of connection strength, offering a promising tool for assessing network vulnerability. These findings lay the foundation not only for theoretical research but also for practical improvements in transportation, disaster management, and communication networks.
1. Introduction
Most modern systems consist of networks, including communication networks, transportation systems, and infrastructures for water distribution. In each of these, a failure in either a node or a link can have serious repercussions on their functions, underlining the importance of parameters related to their vulnerability in studies. Connectivity, integrity, tenacity, toughness, and rupture degree are some of the metrics for network vulnerability that are indispensable for understanding the resilience of a network to disruption and for developing effective measures to strengthen its resistance [1,2,3,4,5].
1.1. Literature Review
Fuzzy graphs were first proposed by Rosenfeld [6] and Yeh and Bang [7], based on the fuzzy sets and fuzzy relations introduced by Zadeh [8]. Thus, graph theory has been systematically extended to account for uncertainties in real-world systems. By allowing the relationships between nodes to be expressed as a degree of membership from 0 to 1, the representation using fuzzy graphs becomes seamless in modeling network dynamics. This flexibility makes fuzzy graphs even more useful for modeling systems where information is uncertain, imprecise, or incomplete.
Fuzzy graphs have applications in various fields, including research on directed networks, rough fuzzy digraphs, and toll road networks [9,10,11], as well as indices such as the Hyper–Wiener index and Zagreb indices, with applications in areas like the stock market, chemistry, and crime analysis [12,13,14,15,16]. Despite some advancements in fuzzy graph research, studies on its vulnerability parameters remain scarce compared to classical graph theory. Recent works investigated numerous methods for evaluating network vulnerabilities in the context of uncertainty, such as optimization-based methods [17]. Nevertheless, fuzzy graph-based methods remain critical in order to represent the gradual decline in network resilience. A few pioneering works have introduced new vulnerability concepts in fuzzy graphs, such as those by [18,19,20,21], which explore resilience against different types of structural attacks. Other advanced studies have examined various aspects of fuzzy connectivity, including generalized cycle connectivity [20], edge connectivity measures [21,22], and strong domination integrity [23]. Although these studies have significantly contributed to understanding fuzzy graph vulnerability, they fail to adequately capture the role of connection strength in maintaining network resilience.
1.2. Problem Statement
Network vulnerability has long been studied in classical graph theory, with integrity being one of the primary parameters used to measure network robustness. Integrity is typically defined as the sum of the number of disconnected components and the size of the largest remaining connected subgraph after disruption [2]. In fuzzy graphs, node failure does not necessarily lead to disconnection but rather to a reduction in the strength of connectedness between nodes. Existing definitions, such as those proposed by Saravanan et al. [24,25], fail to account for this and consider only the disconnection of graphs. Moreover, existing studies on fuzzy graph vulnerability do not explicitly address the role of network topology and redundancy in connectivity in resisting network failures.
1.3. Research Gap
Although integrity metrics have been extensively investigated in classical graphs, their extension to fuzzy graphs remains in its early stages. A fundamental gap exists in formulating a vulnerability index that captures the strength of connectedness between nodes rather than merely their disconnection. While some studies have explored connectivity measures in fuzzy graphs [26,27], they fail to account for the dynamic process of node failures and their impact on the residual network structure. Recent research on fuzzy graph-based vulnerability analysis [22,28] has proposed alternative approaches; however, these still lack an integrated framework that coherently incorporates both uncertainty and robustness.
1.4. Main Contributions
This study introduces a novel approach to measuring vulnerability, termed fuzzy node integrity. This method utilizes the strength of connectedness to assess network robustness under uncertainty. The key contributions of this study are as follows:
- Redefining the integrity parameter of fuzzy graphs to incorporate the strength of connectedness, providing a more comprehensive measure of network vulnerability and extending earlier works [23,29].
- Establishing general formulae for the fuzzy node integrity of various graph structures, including cycle graphs, wheel graphs, and star graphs, which exhibit different degrees of structural symmetry.
- Demonstrating the utility of the proposed measure through its application to a real-world military logistics problem, where fuzzy node integrity is used for critical node detection and route optimization under uncertainty, building upon previous works [10,15].
- Enhancing existing measures by introducing a parameter that balances both local and global structural resilience, capturing more subtle changes in network robustness than classical integrity measures. Unlike traditional integrity and connectivity metrics, the proposed measure accounts for gradual degradations in network strength rather than treating failures as binary disconnections.
- Providing a general and flexible framework that can be applied to a wide range of real-world problems, including transportation systems, communication networks, and cybersecurity, where network stability is influenced by uncertainty.
By addressing these limitations, this study contributes to the theoretical advancement of fuzzy graph vulnerability metrics and their application to real-world network systems. Future research will explore extensions of fuzzy node integrity to dynamic and time-evolving networks.
This research contributes both theoretically and practically by deriving general formulae for specific fuzzy graph structures and presenting an application to a military logistics case study, demonstrating its potential utility. Although this study highlights possible applications in fields such as disaster management and infrastructure planning, it serves as an initial step toward broader implementation. The role of symmetry in network failure scenarios can be further explored in future studies to refine these metrics. Future research should focus on further improving this metric, developing computationally efficient algorithms for large-scale networks, and exploring its applications in dynamic and evolving systems.
2. Preliminaries
Some fundamental definitions are provided in this section. Those not included here can be found in [26,30,31].
Definition 1
([32]). A fuzzy graph, referred to as an f-graph, is a structure , where V is the set of nodes, σ is a fuzzy subset of V, and μ is a fuzzy relation on σ, such that
Definition 2
([33]). An arc with the least membership value is called the weakest arc. Let and is called the depth of μ and is called the height of μ.
Definition 3
([32]). A fuzzy cycle is referred to as a multimin cycle if it has more than one weakest arc. It is called a locamin cycle if every node is incident with a weakest arc.
Definition 4
([34]). The strength of connectedness between two nodes, u and v, which is the maximum of the strengths of all paths between them, is represented by . A fuzzy graph is connected if, for every in
We accept that G is connected throughout this paper.
Definition 5
([30]). Let be an arc of G. It is called α-strong, if ; if , then it is β-strong, and if , then it is called a δ-arc.
Definition 6
([32]). If is a strong arc, then u and v are strong neighbors, and an path P is called a strong path if all the arcs in P are strong.
Definition 7
([30]). If the removal of an arc reduces the strength of connectedness between any pair of nodes, then that arc is called a fuzzy bridge. Accordingly, if the removal of a node results in a reduction in the strength of connectedness between any pair of nodes, then it is referred to as a fuzzy cut node. A connected fuzzy graph is a block if G has no fuzzy cut nodes. If a node has at most one strong arc incident with it, it is called a fuzzy end node of G.
Definition 8
([35]). Let be a fuzzy graph where Then, is called the arc-strength sequence of G with where is the strength of arc i for . Specifically, is the depth of μ and is the height of
Definition 9
([26]). Let be a connected fuzzy graph. Fuzzy node cut (FNC) is defined as a collection of nodes , for each pair of nodes and for , if either or is trivial.
If there are m nodes in then S is called an Obviously, a is a singleton set , where u is a fuzzy cut node.
Definition 10
([26]). Let S be a fuzzy node cut in G. The strong weight of S, denoted by , is defined as where is the minimum of the weights of strong arc incident on u.
Definition 11
([26]). The least strongest weight of fuzzy node cuts of a connected fuzzy graph G is called the fuzzy node connectivity of G. It is denoted by
3. Fuzzy Node Integrity
The concept of integrity for fuzzy graphs, as initially defined by Saravanan et al. [24], is
where denotes the sum of membership values of nodes in S, and is the total membership value of the largest connected component in . However, this definition does not take into consideration the strength of connectedness, which is an indispensable characteristic for network vulnerability modeling under uncertainty.
To handle this limitation, we have introduced a new parameter, fuzzy node integrity, which includes the strength of connectedness and thereby provides a more refined degree of network robustness under uncertain conditions.
Definition 12.
where . If is trivial, then .
The fuzzy node integrity of a connected fuzzy graph G is
where
- : The strong weight of the fuzzy node cut S, defined in [26], is calculated as the sum of membership values:where is the minimum of the membership values of strong arcs incident on u.
- : The strength of connectedness between nodes u and v in the residual graph .
- : The residual strength of connectedness is the maximum of the strengths of all paths among the nodes with diminishing strength of connectedness in the residual graph, defined in [35] as
Any set S of nodes that realizes the integrity value is called an -set.
The fuzzy node integrity parameter extends traditional metrics by incorporating the strength of connectedness into vulnerability analysis. It provides a systematic approach for evaluating network robustness in uncertain environments and lays the groundwork for further theoretical and practical developments.
In practical applications, membership values express the notion of reliability or strength of nodes and edges represented by and , respectively. These values will be determined based on real factors, such as terrain conditions, node reliability, traffic flow capacities, etc. In real-world applications, membership values may be estimated by expert judgment, data analysis, or simulations of one form or another, depending upon the system being modeled.
The newly defined parameter fuzzy node integrity value for a simple graph given in Figure 1 is evaluated in detail in the following example.
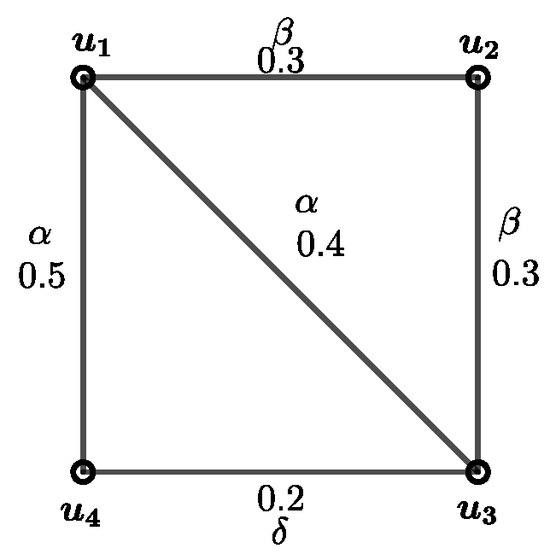
Figure 1.
A fuzzy graph with fuzzy node integrity value .
Example 1.

To compute the fuzzy node integrity of the fuzzy graph G shown in Figure 1, we will analyze all possible node cuts S. The membership values and the types of arcs, α-strong, β-strong or δ-arc, are given in the figure. The strong weight of each node is obtained as follows:
, , , .
The calculations are summarized in Table 1, which displays key values such as the strong weight , the strength of connectedness , the residual strength of connectedness , and the resulting fuzzy node integrity .

Table 1.
Summary of calculations for fuzzy node integrity of the graph in Figure 1.
From Table 1, we observe the following:
- Node Cut : The residual strength of connectedness is, and the strong weight of the node cut is . Combining these values, the fuzzy node integrity is
- Node Cut : Removing and , the residual strength of connectedness is , and the strong weight of this cut is . Thus,
- Node Cut : Removing , , and , only remains, leaving no connections in the residual graph. The strong weight is , and . Therefore,
By analyzing all possible cuts, the minimum fuzzy node integrity value of the fuzzy graph given in Figure 1 is
The fuzzy node integrity value for a fuzzy wheel graph given in Figure 2 is evaluated in the following example.
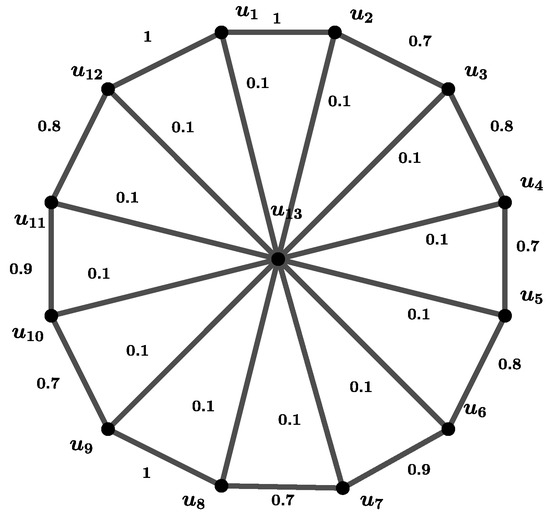
Figure 2.
A fuzzy wheel graph G.
Example 2.
According to Figure 2, let us consider the possible fuzzy node cuts.
For , and
,
and for , and
.
Also, are the only 1-FNC of G. We obtain for 1-FNC of G by definition. So,
For , , and . Hence, .
For , and . Thus, and
For , and . Then, . So, .
Among the fuzzy node cuts of G, and are sets of G. By taking the minimum, we obtain , according to the definition of fuzzy node integrity.
To determine the fuzzy node connectivity of the fuzzy graph in Figure 2, the fuzzy node cut of G with the minimum strong weight is , where and . Thus, . In addition, each of the nodes in provides the fuzzy node connectivity value since all the 1-FNC sets have the same strong weight value.
This example shows that the fuzzy node cuts may not be the same, which gives the fuzzy node connectivity and the fuzzy node integrity values for a fuzzy graph.
The general formulas for the fuzzy node integrity values of different types of fuzzy graphs are obtained and given below.
Theorem 1.
Let us consider the fuzzy wheel graph , where node is a fuzzy hub and the remaining nodes are located on the fuzzy cycle . Moreover, assume that the membership values of the arcs between nodes and are no greater than that of the weakest arc on the cycle, for , where all of the membership values of the arcs on the cycle are distinct. Consequently, the fuzzy node integrity value is
Proof.
All the paths on the fuzzy wheel graph are strong paths. Since a strong path contains only -strong or -strong arcs, the weakest arcs of are -strong and the rest of the arcs are -strong. Apart from , the membership values of the arcs and weakest arcs on the fuzzy cycle are equal; thus, Moreover, all the nodes for are adjacent to the fuzzy hub . By the definition of the fuzzy wheel graph, we obtain Thus, there are two cases according to the existence of a fuzzy cut node of since for
Case i. Let fuzzy wheel graph contain a fuzzy cut node, e.g., x, and let S be a fuzzy node cut such that Fuzzy hub is not a fuzzy cut node since all the arcs are arcs. Therefore, the fuzzy cut node x should lie on the fuzzy cycle A node on a fuzzy cycle is a fuzzy cut node if and only if the node is a common node of two fuzzy bridges. An arc of a fuzzy cycle is a fuzzy bridge if and only if the arc is [30].
In this case, the arcs and which are incident to the node x on fuzzy cycle are arcs. If the x node is removed from the graph, then
Since and the fuzzy node integrity is
Case ii. Let fuzzy wheel graph not contain a fuzzy cut node. For any arc of the wheel that is not strong, each path between these nodes u and v is a strong path since every path has the same strength between u and v. Therefore, the number of internally disjoint strongest paths between u and v is at most three. Hence, the cardinality of the minimal strength reducing set is at most three according to Menger’s theorem [36]. Thus, Since for all we obtain In this case, since is disconnected after removing three nodes. Thus, and the fuzzy node integrity is
The proof is completed by (11) and (12). □
Theorem 2.
Let be a fuzzy wheel graph where the node is a fuzzy hub and the nodes are on the fuzzy cycle Assume that , where all values, the membership values of the arcs lying on the cycle, are not equal for . Moreover, for , all are constant. Then, the fuzzy node integrity is
Proof.
Case i. Let for and , and let be constant. The nodes for lying on the cycle are incident to at most one of the strongest arcs on the fuzzy wheel graph Thus, each node is a fuzzy end node. Since a node should be incident to at least two strong arcs to be a fuzzy cut node, the nodes are not fuzzy cut nodes [34]. However, the node is a cut node since is adjacent to all the nodes and Hence, for Let S be a fuzzy cut set of If then where For Hence,
Therefore, and
If then and . Thus,
Via (15) and (16), the fuzzy node integrity is
Case ii. Let be constant for and for , where at least one of the arcs on the fuzzy cycle has the same membership value with All paths of length two where is the fuzzy hub and are the strongest paths. Thus, all arcs are strong for The e arcs on the cycle for are strong if ; otherwise, they would be -arcs. In this case, the node is the only fuzzy cut node of since is different for each by the assumption and for since is adjacent to all Let S be a fuzzy cut set of If then where for . Thus,
Therefore, and
The proof is completed by Case i and Case ii. □
Theorem 3.
Let be a fuzzy wheel graph where is a fuzzy hub and the nodes are on the fuzzy cycle If values are constant for and for then the fuzzy node integrity is
Proof.
Let be a fuzzy wheel graph and let values be constant for and for all , . In this case, all the paths on the wheel are strong paths. Since a strong path only contains or arcs, does not contain any arc. Since is adjacent to all the nodes and for and all the arcs are arcs and Therefore, fuzzy hub is not a fuzzy cut node. Thus, for and , where S is a fuzzy node cut of
There are two cases according to the existence of a fuzzy cut node of
Case i. Let have a fuzzy cut node, e.g., x. Thus, x is a fuzzy cut node if and only if x is a common vertex of two fuzzy bridges. Moreover, an arc is a fuzzy bridge if and only if the arc is For this reason, x is incident to the arcs and , where
If where then Hence,
for and Thus, the fuzzy node integrity is
If then Let where for Then,
for . Hence, and the fuzzy node integrity is
If then In this case, and the fuzzy node integrity is
By (22), (24) and (25),
Case ii. Let not contain a fuzzy cut node. Therefore, Let where and Thus, and By definition,
If then and Hence,
Via (27) and (28), we obtain
Thus, via (26) and (29), we obtain the result. □
Lemma 1.
Let be a fuzzy cycle graph without a fuzzy cut node. Then,
Proof.
Let S be a fuzzy node cut of a fuzzy cycle G. Since there is no fuzzy cut node,
Case i. If the remaining graph contains only one component, then S should contain nodes to be a fuzzy node cut. Thus, there is only one remaining node and
Case ii. If the remaining graph has two or more components, then since or for all Therefore,
The proof is completed via Case i and Case ii. □
Theorem 4.
Let be a locamin fuzzy cycle. Then, the fuzzy node integrity is
Proof.
Let S be a fuzzy cut set. since G has no fuzzy cut node. Therefore, where for . Moreover, via Lemma 1, Hence, the value of the of fuzzy node integrity is
□
Theorem 5.
Let be a fuzzy cycle graph with only one arc. Then, the fuzzy node integrity is
Proof.
If G has only one arc, then G is a locamin cycle. Thus, via Theorem 4, the following result is obtained:
□
Theorem 6.
Let be a self-centered fuzzy cycle graph with n nodes, and let the arcs be represented by for and If
Case i. if one of the following holds;
(1) for ;
(2) and for even integer n and ;
(3) and for where and .
Case ii. If and for where and then
Proof.
Case i. If G is a self-centered fuzzy cycle graph satisfying one of the conditions G is a multimin cycle since it has more than one weak arc [34]. G is also a locamin cycle since every node is incident to a weak arc. A multimin cycle is a locamin cycle if and only if it has no fuzzy cut nodes [34]. Thus, G does not have a fuzzy cut node. Then, by Lemma 1, Since G is a locamin fuzzy cycle, we obtain the following via Theorem 4:
Case ii. Let G be a self-centered fuzzy cycle with and where and Then, G is a multimin cycle since it has more than one weak arc. The node is the only cut node because it is incident to two arcs where Thus, and for Let S be a fuzzy cut set of G. If then where Therefore,
and Thus, by definition,
If then Because , we obtain or for Hence,
The equality holds for Thus,
For Hence,
By the definition of fuzzy node integrity, the minimum value is satisfied when Therefore,
By (38),(40) and (42), we obtain
□
Theorem 7.
Let be a regular fuzzy cycle graph. Then, the fuzzy node integrity value
Proof.
If G is a regular fuzzy cycle, then either the membership values of the arcs are equal or the membership values of the alternate arcs are equal [37]. Thus, there are two cases for the proof.
Case i. If the membership values of all arcs are equal, then all the arcs are weakest arcs. For this reason, all nodes are central nodes. Thus, G is a self-centered fuzzy cycle [38]. By Theorem 6, we obtain
Case ii. If the membership values of the alternate arcs are equal, then G has an even number of nodes [37]. Thus, G is a self-centered fuzzy cycle, and by Theorem 6
□
Theorem 8.
Consider a fuzzy graph with a single weakest arc and a cycle graph . Then, the fuzzy node integrity value is
Proof.
Let be the weakest arc of the cycle. It can thus be concluded that the nodes and are fuzzy end nodes, while the nodes labeled for are fuzzy cut nodes [33]. Hence, is -arc and . The other arcs are -strong. Hence, for , Assume that S is a fuzzy cut set and that there are two cases according to the cardinality of S.
Case i. Let Then, where and For any
for Hence, and
Case ii. Let Then, and Thus,
Therefore, by taking the minimum of Equations (49) and (50), we obtain the following result:
□
Theorem 9.
Let be a fuzzy star graph. Then, the fuzzy node integrity value is
Proof.
Let be the nodes of a fuzzy star, where is connected to all other nodes. Then, all arcs are arcs. For , the node is a fuzzy cut node. Assume that S is a fuzzy cut set of G.
Case i. If then and Hence,
and Thus, by the definition
Case ii. If then for Therefore,
Since contains only the node
Thus,
If then and since for any
Hence, by definition,
Via (53), (54) and (56), we obtain the following result:
□
4. Real-World Case Study: Military Logistics
In military logistics, identifying critical nodes and optimizing routes are crucial for ensuring the smooth movement of supplies and troops, even under uncertain conditions. This section utilizes the aforementioned fuzzy node integrity parameter to enhance network resilience and strategic movement planning.
4.1. Problem Definition
Military logistics is not solely concerned with finding the shortest or fastest route but rather with identifying the most suitable route between predefined nodes in a battle environment. This involves determining the optimal path based on factors beyond distance and duration, such as slope gradients, route traversability, water barriers, and vegetative obstacles.
Lytvynenko and Lytvynenko addressed the problem of determining the most comfortable routes for military unit movements between two points using fuzzy graph models in [39]. In their study, they utilized data on slope steepness, water and vegetative barriers, and other terrain features obtained through GIS analysis to define membership values for routes [39]. The fuzzy graph they obtained is illustrated in Figure 3 [39]. In this graph, as the membership values of the arcs decrease, the difficulty of crossing the roads increases.
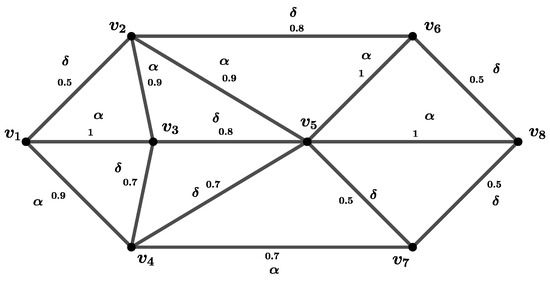
Figure 3.
The fuzzy graph G obtained in [39].
One such scenario analyzed in this study involves identifying the most comfortable route between nodes and for troop movement, as shown in Figure 3. Lytvynenko and Lytvynenko determined the most comfortable route as in [39]. However, their proposed solution does not fully consider network resilience against node failures. This study further extends their work by incorporating fuzzy node integrity, which not only verifies the feasibility of existing routes but also assesses network resilience against node failures.
4.2. Application of Fuzzy Node Integrity to Military Logistics
The logistics network is modeled as a fuzzy graph G, given in Figure 3, where nodes represent key military locations, edges represent roads between locations, and membership values indicate road suitability.
The objective of this analysis is to evaluate network susceptibility and identify the critical nodes and roads in the event of disruptions. The proposed strategy consists of the following steps:
- Finding the adjacency matrix of the fuzzy graph G, which is given in Figure 3.
- Finding the matrix including strength of connectedness for all possible node pairs.
- Determining the strong arcs.
- Finding the strongest weights of all nodes.
- Determining fuzzy cut nodes.
- Computing fuzzy node connectivity to identify the network’s weakest nodes and fuzzy node integrity to estimate the impact of node failures.
- Step 1: The adjacency matrix represents the membership values of the arcs between the nodes and given in Table 2.
 Table 2. Adjacency matrix A and strength of connectedness matrix C.
Table 2. Adjacency matrix A and strength of connectedness matrix C. - Step 2: The strength of the connectedness matrix represents the strength of connectedness between the nodes and , denoted by , which is the maximum of the strengths of all paths between these nodes given in Table 2.
- Step 3: If , then the arc between the nodes and is called a strong arc; otherwise, it is a -arc. If the off-diagonal entries of the strength of the connectedness matrix are equal to the non-zero off-diagonal entries of the adjacency matrix, then the corresponding arcs are called strong arcs. Checking these matrices gives the set of strong arcs for the fuzzy graph G. To decide if the arcs are -strong or -strong, we made a table to check if either for -strong or for -strong.According to Table 3, all the arcs in this graph are either -strong arcs or -arcs, as shown in Figure 3.
 Table 3. Strong arcs of the fuzzy graph G.
Table 3. Strong arcs of the fuzzy graph G. - Step 4: The strong weight of a node v is the minimum of the weights of strong arcs incident on v. The strongest weight of each node of G is given in Table 4.
 Table 4. The strongest weight of each node of G.
Table 4. The strongest weight of each node of G. - Step 5: The nodes are fuzzy cut nodes since each one is a common node of at least two -strong arcs [30].
- Step 6: The calculations are summarized in Table 5, which displays key values, such as fuzzy cut nodes; corresponding strong weights; the strength of connectedness and , where the values decrease for those nodes after removing S; the residual strength of connectedness ; and fuzzy node integrity values corresponding to the fuzzy cut nodes.
 Table 5. Summary of calculations for fuzzy node connectivity and fuzzy node integrity of the fuzzy graph G in Figure 3.
Table 5. Summary of calculations for fuzzy node connectivity and fuzzy node integrity of the fuzzy graph G in Figure 3.
Other fuzzy node cuts having two or more nodes were not considered since fuzzy node connectivity and fuzzy node integrity are equal to the minimum values.
Fuzzy node connectivity of this graph is and fuzzy node integrity is .
The strength of connectedness between and is equal to , and the strongest path with the strength of connectedness value 0.9 is , which is the same route as Lytvynenko and Lytvynenko found in their study [39].
In the event of any disruptions in the transport hubs during the transportation of vehicles and ammunition through routes, there may be a requirement to change the route or secure the concerned roads. Critical node identification is extremely necessary in order to counter the expected problem. Vulnerability parameters can be applied in the critical node identification. Applying the fuzzy node connectivity parameter to the graph yields , which aids in effectively identifying a different route. Specifically, is the cluster element that provides this value. This suggests that is a crucial node, and any malfunction in this node causes trouble when an army is transitioning from one point to another.
If a failure at node does occur, it is critical for alternative pathways to be identified. Therefore, when choosing a route, either this node should be excluded in the route or some necessary precautions should be assessed. The fuzzy node integrity parameter proposed in this paper provides a valuable tool for analyzing these issues. In that situation, graph analysis will give , meaning that a failure at node will equate to a diversion in the route with passability being lowered to 0.5. Since this measure is influenced by the arc between nodes and , a revalidation of road conditions is necessary. The combination of the two criteria indicates that the alternative route should try to avoid the node. If this is not feasible, either the road between the and nodes should be improved or the shipment should be modified to fit the requirements of the route.
If another fuzzy cut node would be chosen to be checked as a critical point, fuzzy node connectivity could not be utilized since four of the fuzzy cut nodes have the same strong weight. However, if fuzzy node integrity is used by performing a check, the minimum values of integrity state that the second critical node is and that it has a corresponding integrity value of . A failure at node will cause the route to be rerouted, with passability being reduced to . As this measure is influenced by the arc between nodes and , a revalidation of road conditions is necessary. During the transport of vehicles and military equipment along routes, it may be necessary to change the route or secure specific roads in the case of disruptions at transfer centers.
4.3. Comparative Analysis
In order to better validate the performance of the introduced fuzzy node integrity, we are comparing it with existing network vulnerability parameters. The key performance distinctions in fuzzy node integrity in relation to fuzzy node connectivity [26] and integrity for fuzzy graphs [24] are discussed in this section.
The comparative analysis is based upon the following aspects:
- Failure Impact: The measure in which a method incorporates node failures and how they impact network connectivity.
- Adaptability to Uncertainty: Whether or not the measure uses fuzzy or probabilistic aspects to deal with uncertainty.
- Resilience Estimation: The ability of the method to quantify remaining connectivity following disturbances.
- Alternative Path Planning: If the method provides alternative route suggestions in cases of failures.
Table 6 summarizes how different methods compare based on these criteria.

Table 6.
Comparative analysis of network vulnerability parameters.
This comparison highlights that fuzzy node integrity provides a more adaptive and realistic vulnerability measure than integrity and fuzzy node connectivity methods by incorporating partial degradation and a residual network strength assessment.
The fuzzy node connectivity parameter provides information about which node is critical, while the fuzzy node integrity parameter provides information not only about the critical node but also about which arcs need to be strengthened.
The concept of integrity for fuzzy graphs defined by Saravanan et al. in [24] only depends on the disconnection and the membership values of nodes. Therefore, this parameter cannot be evaluated for this type of fuzzy graph, which is given in Figure 3. It is not possible to accurately study the fuzziness of the situation as their definition relies on the disconnection. Consequently, their research motivated us to redefine the integrity parameter for fuzzy graphs.
5. Results and Discussion
The concept of ‘fuzzy node integrity’ was applied in a military logistics case study to measure its real-world efficacy. The implications and findings of this case study are presented in this section.
5.1. Key Insights from the Case Study
- Identification of Critical Nodes: The strategy was able to determine nodes whose removal would result in a substantial loss in the resilience of the network. This was especially true when taking into account the network’s nodes of passage, which are the nodes with the least strong weight but the highest difficulty.
- Scenario-based Analysis: The following two main failure scenarios were analyzed:
- –
- Targeted Node Failures: The removal of nodes with least strong weight affected the strength of connectedness by reducing the overall efficiency of the logistics network. The outcome showed a drop in network connectivity when critical nodes were targeted.
- –
- Random Node Failures: The network could tolerate some node failures with the backup routes still being effective. The capability of the system to reroute logistics was still maintained with node failures.
- Quantitative Performance Comparison:
- –
- Integrity for fuzzy graph is useless for this problem. It cannot be evaluated in these kinds of graphs since the definition depends only on the disconnection and the membership values of nodes.
- –
- Fuzzy node connectivity shows enhanced flexibility compared to traditional approaches while still being short of full resilience.
- –
- Fuzzy node integrity proves its high resilience estimation performance by providing information not only about the critical node but also about which arcs need to be strengthened.
- Real-Time Flexibility: The study showed how, by recalculating fuzzy node integrity in real time, logistical operations can be reallocated dynamically to optimize routes in line with fluctuating conditions, such as unexpected disruptions or road obstructions.
5.2. Practical Implications
The findings of this study have practical implications for real-world applications, such as the following:
- Transport Networks: Enhancing the resilience of road and rail networks against disruptions.
- Cybersecurity: Applying fuzzy node integrity to assess network vulnerability in critical communication infrastructures.
- Disaster Management: Planning for emergency responses in dynamic environments.
- Supply Chain Optimization: Identifying vulnerabilities in supply chains to ensure efficient distribution of products.
5.3. Limitations and Future Work
Even though the proposed method is a notable improvement in network vulnerability estimation, certain limitations exist, such as the following:
- Static Network Assumption: We have assumed a static network in this model, but real-world military logistics networks are highly dynamic in nature. Future research studies should incorporate real-time adaptability in line with time-dependent fuzzy graphs.
- Computational Complexity: The calculation for fuzzy node integrity is becoming complex as network sizes expand. Future studies should concentrate on creating efficient techniques for dealing with real-time large-scale networks.
- Limited Real-World Evaluation: The method is established in a theoretical case study but is in need of empirical testing in real logistics networks in order to validate its effectiveness.
- Interdependency Considerations: Interdependent networks are normally engaged in logistics in armed conflicts, such as supply networks and communications networks. The application may be extended to cover multi-layer fuzzy networks.
Future research can be directed towards merging machine learning mechanisms for adapting path selection in real-time conditions in fuzzy networks. Predictive modeling based on past network outages can be utilized for network vulnerability estimation improvement. A computational structure for efficient solutions for large-scale problems and applications in multiple-layered fuzzy networks will continue to have increased real-world applications in dynamic networks.
One promising direction for further research is the extension of the fuzzy node integrity framework to neutrosophic graphs, which would contribute to even more effective vehicles for quantifying network susceptibility by incorporating a more complete representation of indeterminacy and uncertainty in complex networks.
6. Conclusions
This paper addresses an important challenge in network vulnerability studies and introduces the fuzzy node integrity parameter, a metric specifically devised for fuzzy graphs. Contrary to other integrity metrics, this parameter considers the strength of connectedness; hence, it offers a subtler and more realistic appraisal of the robustness of a network in uncertain environments. Therefore, with this contribution, new definitions were openly extended, and an important gap in the fuzzy graph theory was covered by an integrated framework covering both theoretical improvements and practical applications.
The theoretical contributions of this work are related to the derivation of general formulas for fuzzy graph structures, such as cycle graphs, wheel graphs, and star graphs, which can serve as basic tools for future research studies in the stated field. The applicability of the proposed parameter is assured by its practical relevance in a case study related to military logistics, to which it was applied with a view to finding out the most critical nodes and route optimization in uncertain conditions. This example illustrates the potential of the parameter for modeling real-world problems such as disrupted supply chains and vulnerabilities in infrastructures.
Despite these contributions, there are still some limitations, and there are avenues for future research. One limitation is the stationarity assumed in current modeling when real logistics networks are highly dynamic in nature. Real-time adaptive, time-varying fuzzy graph-based algorithms must be incorporated in future research to better capture this dynamism. Also, as the network size is increased, computational complexity in fuzzy node integrity calculations is increased as well, and efficient algorithms for larger networks must be derived. A second major area is empirical validation; although we carried out a test on a hypothetical case study in this paper, real-world validation is needed for measuring practical performance in different application domains. Also, in typical military logistics, there are multiple-layer networks like supply chains, transportation networks, and communications networks. The model could be extended to account for interdependencies across them, and this could greatly enhance its applicability and resilience.
Fuzzy node integrity methodology, as a network vulnerability testing tool, can be extended to incorporate advanced path optimization techniques and predictive analyses for predicting network vulnerabilities in complex networks. The method can be applied for enhancing network resilience in unpredictable and dynamic environments.
Author Contributions
Conceptualization, G.B.-T.; formal analysis, F.N.M. and G.B.-T.; methodology, F.N.M. and G.B.-T.; resources, F.N.M.; software, F.N.M.; supervision, G.B.-T.; validation, F.N.M. and G.B.-T.; writing—original draft preparation, F.N.M.; writing—review and editing, G.B.-T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
This study was part of F.N. Murater’s Ph.D. thesis, which was approved at Manisa Celal Bayar University, Turkey, in 2021.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Harary, F. Graph Theory; Addison-Wesley Publishing Company Inc.: Reading, MA, USA, 1969. [Google Scholar]
- Barefoot, C.A.; Entringer, H.R.; Swart, H. Vulnerability in graphs—a comparative survey. J. Comb. Math. Comb. Comput. 1987, 1, 13–22. [Google Scholar]
- Cozzens, M.B.; Moazzami, D.; Stueckle, S. The tenacity of a graph. In Graph Theory, Combinatorics, and Algorithms; Alavi, Y., Allen, S., Eds.; Wiley: New York, NY, USA, 1995; pp. 1111–1112. [Google Scholar]
- Chvátal, V. Tough graphs and Hamiltonian circuits. Discret. Math. 1973, 5, 215–228. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Li, X. Rupture degree of a graph. Int. J. Comput. Math. 2005, 82, 793–803. [Google Scholar] [CrossRef]
- Rosenfeld, A. Fuzzy graphs. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Academic Press: Washington, DC, USA, 1975; pp. 77–95. [Google Scholar]
- Yeh, R.T.; Bang, S.Y. Fuzzy relations, fuzzy graphs and their applications to clustering analysis. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Academic Press: Washington, DC, USA, 1975; pp. 25–149. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Al-Shamiri, M.M.A.; Ahmad, U.; Maryam, A.; Akram, M. Cubic directed graphs with application. J. Appl. Math. Comput. 2024, 70, 2169–2196. [Google Scholar] [CrossRef]
- Ahmad, U.; Batool, T. Domination in rough fuzzy digraphs with application. Soft Comput. 2023, 27, 2425–2442. [Google Scholar] [CrossRef]
- Muhammad, A.; Shareef, A.; Al-Kenani, A.N. Pythagorean fuzzy incidence graphs with application in one-way toll road network. Granul. Comput. 2024, 9, 39. [Google Scholar]
- Islam, S.R.; Pal, M. Hyper-Wiener index for fuzzy graph and its application in share market. J. Intell. Fuzzy Syst. 2021, 41, 2073–2083. [Google Scholar] [CrossRef]
- Islam, S.R.; Pal, M. Second Zagreb index for fuzzy graphs and its application in mathematical chemistry. Iran. J. Fuzzy Syst. 2023, 20, 119–136. [Google Scholar]
- Islam, S.R.; Pal, M. Hyper-connectivity index for fuzzy graph with application. Twms J. Appl. Eng. Math. 2023, 13, 920–936. [Google Scholar]
- Islam, S.R.; Pal, M. Multiplicative version of first Zagreb index in fuzzy graph and its application in crime analysis. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2024, 94, 127–141. [Google Scholar]
- Islam, S.R.; Pal, M. An investigation of edge F-index on fuzzy graphs and application in molecular chemistry. Complex Intell. Syst. 2023, 9, 2043–2063. [Google Scholar]
- Wang, H.; Yu, X.; Lu, Y. A reinforcement learning-based ranking teaching-learning-based optimization algorithm for parameters estimation of photovoltaic models. Swarm Evol. Comput. 2025, 93, 101844. [Google Scholar]
- Sujithra, P.; Mathew, S.; Mordeson, J.N. Advanced fuzzy connectivity metrics for enhancing security in dynamic network environments. Inf. Sci. 2025, 700, 121857. [Google Scholar]
- Dhanya, C.M.; Mathew, S.; Mordeson, J.N. Connectivity in Cartesian products of fuzzy graphs: Application to decision making. J. Appl. Math. Comput. 2025. [Google Scholar] [CrossRef]
- Prabhath, A.; Mathew, S.; Mordeson, J.N. Generalized cycle connectivity in fuzzy graphs. Fuzzy Sets Syst. 2024, 482, 108909. [Google Scholar]
- Ma, J.; Li, Q.; Zhou, X. Fuzzy edge connectivity and fuzzy local edge connectivity with applications to communication networks. Fuzzy Sets Syst. 2021, 410, 109–125. [Google Scholar]
- Ma, J.; Li, L.; Li, J. Fuzzy average edge connectivity with its application to communication networks. Soft Comput. 2023, 27, 1367–1378. [Google Scholar]
- Ganesan, B.; Raman, S.; Pal, M. Strong domination integrity in graphs and fuzzy graphs. J. Intell. Fuzzy Syst. 2022, 43, 2619–2632. [Google Scholar]
- Saravanan, M.; Sujatha, R.; Sundareswaran, R. A study on regular fuzzy graphs and integrity of fuzzy graphs. Int. J. Appl. Eng. Res. 2015, 10, 160–164. [Google Scholar]
- Saravanan, M.; Sujatha, R.; Sundareswaran, R. Integrity of fuzzy graphs. Bull. Int. Math. Virtual Inst. 2016, 6, 89–96. [Google Scholar]
- Mathew, S.; Sunitha, M.S. Node connectivity and arc connectivity in fuzzy graphs. Inf. Sci. 2010, 180, 519–531. [Google Scholar]
- Binu, M.; Mathew, S.; Mordeson, J.N. Connectivity index of a fuzzy graph and its application to human trafficking. Fuzzy Sets Syst. 2019, 360, 117–136. [Google Scholar]
- Murater, F.N.; Bacak Turan, G.; Aslan, E. Bulanık çizgelerde zedelenebilirlik parametreleri: Bulanık tepe kararlılık değeri. J. Inst. Sci. Technol. 2025, 15, 316–329. [Google Scholar]
- Murater, F.N.; Bacak-Turan, G. Fuzzy node connectivity of some classes of graphs. J. Mod. Technol. Eng. 2024, 9, 2. [Google Scholar]
- Mathew, S.; Sunitha, M.S. Types of arcs in a fuzzy graph. Inf. Sci. 2009, 179, 1760–1768. [Google Scholar]
- Mordeson, J.N.; Nair, P.S. Fuzzy Graphs and Fuzzy Hypergraphs; Physica-Verlag: Heidelberg, Germany, 2000. [Google Scholar]
- Bhutani, K.R.; Rosenfeld, A. Strong arcs in fuzzy graphs. Inf. Sci. 2003, 152, 319–323. [Google Scholar]
- Bhutani, K.R.; Mordeson, J.N.; Rosenfeld, A. On degrees of end nodes and cut nodes in fuzzy graphs. Iran. J. Fuzzy Syst. 2004, 1, 57–64. [Google Scholar]
- Bhutani, K.R.; Rosenfeld, A. Fuzzy end nodes in fuzzy graphs. Inf. Sci. 2003, 152, 323–326. [Google Scholar]
- Altundag, F.N. Vulnerability Parameters of Fuzzy Graphs. PhD Thesis, Manisa Celal Bayar University, Manisa, Turkey, 2021. [Google Scholar]
- Mathew, S.; Sunitha, M.S. Menger’s theorem for fuzzy graphs. Inf. Sci. 2013, 222, 717–726. [Google Scholar]
- Gani, A.N.; Radha, K. On regular fuzzy graphs. J. Phys. Sci. 2008, 12, 33–40. [Google Scholar]
- Tom, M.; Sunitha, M.S. Strong sum distance in fuzzy graphs. SpringerPlus 2015, 4, 214. [Google Scholar] [PubMed]
- Lytvynenko, V.; Lytvynenko, O. Application of fuzzy graph models for finding rational routes. Adv. Mil. Technol. 2016, 10, 21–29. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).