An Unconditionally Stable Numerical Scheme for 3D Coupled Burgers’ Equations
Abstract
1. Introduction
2. Materials and Methods
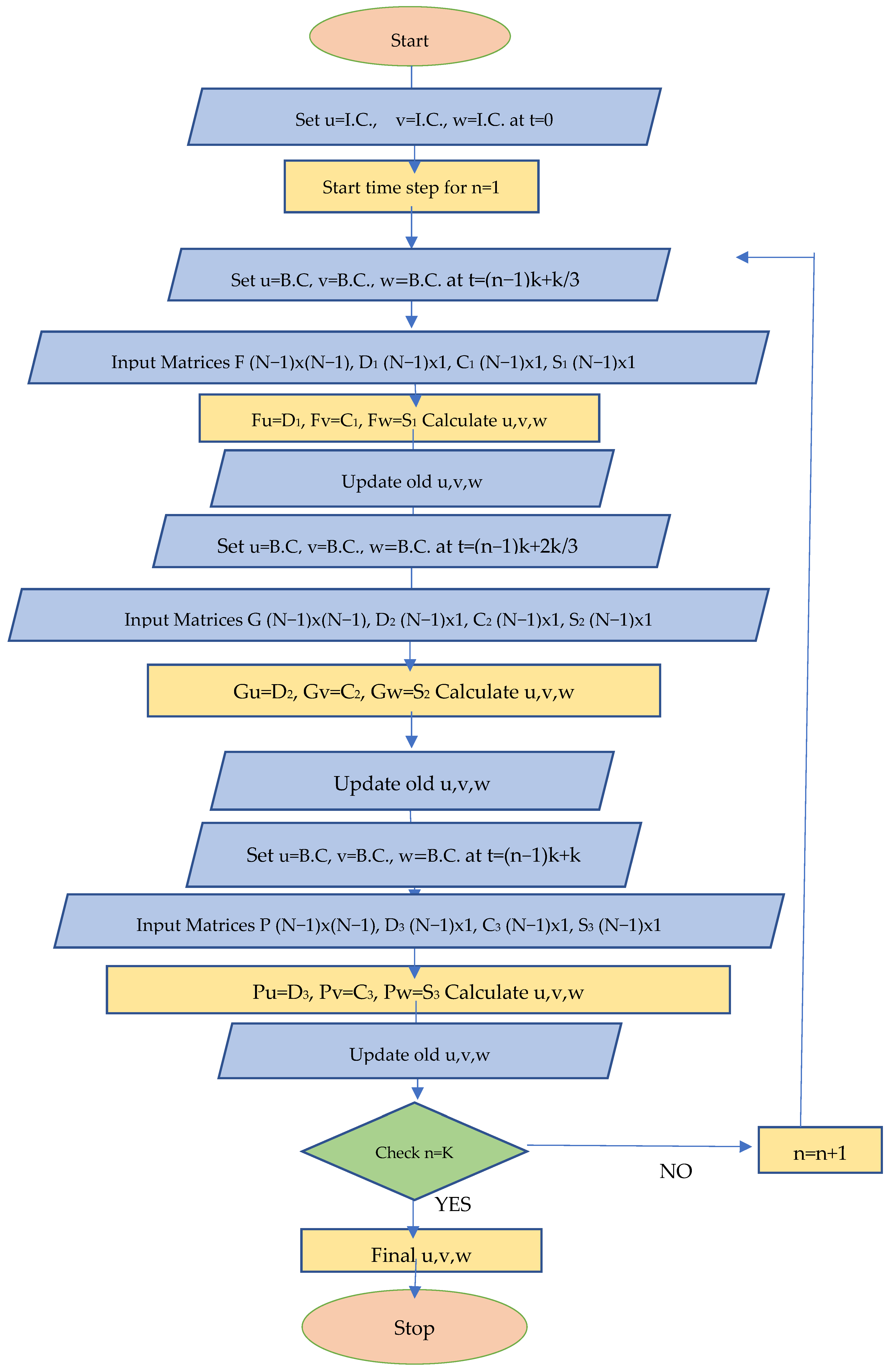
2.1. Fractional Step Method
- Fractional step decomposition—The three-dimensional coupled Burgers’ equations are efficiently transformed into simpler one-dimensional forms, reducing computational effort;
- Implicit finite difference scheme—Unlike explicit methods, the implicit approach enhances numerical stability and accuracy;
- Unconditional stability—A rigorous von Neumann stability analysis proves that the method is unconditionally stable, ensuring reliable numerical solutions;
- Benchmark validation—The method is tested on standard benchmark problems, demonstrating superior accuracy and robustness compared to existing techniques;
- Computational efficiency—The decomposition strategy reduces computational costs while maintaining high accuracy, making the approach suitable for large-scale simulations in fluid dynamics and related fields.
2.2. Local Truncation Error (LTE) and Consistency
2.3. Stability Analysis
2.4. Convergence
3. Results
4. Conclusions
5. Note
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abu Arqub, O. Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 828–856. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A Theoretical Basis for the Application of Fractional Calculus to Viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Uchaikin, V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Yousif, M.A.; Agarwal, R.P.; Mohammed, P.O.; Lupas, A.A.; Jan, R.; Chorfi, N. Advanced Methods for Conformable Time-Fractional Differential Equations: Logarithmic Non-Polynomial Splines. Axioms 2024, 13, 551. [Google Scholar] [CrossRef]
- Yousif, M.A.; Hamasalh, F.K. A Hybrid Non-Polynomial Spline Method and Conformable Fractional Continuity Equation. Mathematics 2023, 11, 3799. [Google Scholar] [CrossRef]
- Khalil, M.I.; Hashim, I.; Rasheed, M.A.; Ismail, E.S. Numerical finite difference approximations of a coupled parabolic system with blow-up. J. Math. Comput. Sci. 2023, 32, 387–407. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Tenreiro Machado, J.A. Numerical treatment of microscale heat transfer processes arising in thin films of metals. Int. Commun. Heat Mass Transf. 2022, 132, 105892. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, Y.; Luo, Z.; Liu, J. A spatial sixth-order numerical scheme for solving fractional partial differential equation. Appl. Math. Lett. 2025, 159, 109265. [Google Scholar] [CrossRef]
- Wei, L.; Yang, Y. Optimal order finite difference/local discontinuous Galerkin method for variable-order time-fractional diffusion equation. J. Comput. Appl. Math. 2021, 383, 113129. [Google Scholar] [CrossRef]
- Shukla, H.S.; Tamsir, M.; Srivastava, V.K.; Rashidi, M.M. Modified cubic B-spline differential quadrature method for numerical solution of three-dimensional coupled viscous Burger equation. Mod. Phys. Lett. B 2016, 30, 11. [Google Scholar] [CrossRef]
- Jain, P.C.; Holla, D.N. Numerical solution of coupled Burgers equations. Int. J. Numer. Methods Eng. 1978, 12, 213–222. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. A comparison of finite element and finite difference of the one- and two-dimensional Burgers’ equations. J. Comput. Phys. 1983, 51, 159–188. [Google Scholar] [CrossRef]
- Wubs, F.W.; de Goede, E.D. An explicit–implicit method for a class of time-dependent partial differential equations. Appl. Numer. Math. 1992, 9, 157–181. [Google Scholar] [CrossRef]
- Goyon, O. Multilevel schemes for solving unsteady equations. Int. J. Numer. Methods Fluids 1996, 22, 937–959. [Google Scholar] [CrossRef]
- Bahadir, A.R. A fully implicit finite-difference scheme for two dimensional Burgers’ equation. Appl. Math. Comput. 2003, 137, 131–137. [Google Scholar] [CrossRef]
- El Sayed, S.M.; Kaya, D. On the numerical solution of the system of two-dimensional Burgers’ equations by the decomposition method. Appl. Math. Comput. 2004, 158, 101–109. [Google Scholar] [CrossRef]
- Abdou, M.A.; Soliman, A.A. Variational iteration method for solving Burgers’ and coupled Burgers’ equations. J. Comput. Appl. Math. 2005, 181, 245–251. [Google Scholar] [CrossRef]
- Celikten, G.; Aksan, E.N. Alternating Direction Implicit (ADI) Method for Numerical Solutions of 2-D Burgers Equations. Therm. Sci. 2019, 23, 243–252. [Google Scholar] [CrossRef]
- Li, M.; Nikan, O.; Qiu, W.; Xu, D. An efficient localized meshless collocation method for the two-dimensional Burgers-type equation arising in fluid turbulent flows. Eng. Anal. Bound. Elem. 2022, 144, 44–54. [Google Scholar] [CrossRef]
- Yousif, M.A.; Hamasalh, F.K. Conformable non-polynomial spline method: A robust and accurate numerical technique. Ain Shams Eng. J. 2024, 15, 102415. [Google Scholar] [CrossRef]
- Yousif, M.A.; Hamasalh, F.K. Novel simulation of the time fractional Burgers–Fisher equations using a non-polynomial spline fractional continuity method. AIP Adv. 2022, 12, 115018. [Google Scholar] [CrossRef]
- Çelikten, G.; Cankurt, A. A Numerical Solution of the Generalized Burgers-Huxley Equation. Afyon Kocatepe Univ. J. Sci. Eng. 2022, 22, 75–84. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Ashutosh, M.T.; Tamsir, M. Generating Exact Solution of Three Dimensional Coupled Unsteady Nonlinear Generalized Viscous Burgers’ Equations. Int. J. Mod. Math. Sci. 2013, 5, 1. [Google Scholar]
- Rezaei, I.; Vaghefi, M. Numerical solution of the three-dimensional Burger’s equation by using the DQ-FD combined method in the determination of the 3D velocity of the flow. Appl. Water Sci. 2023, 13, 5. [Google Scholar] [CrossRef]
- Alhendi, F.A.; Alderremy, A.A. Numerical Solutions of Three-Dimensional Coupled Burgers’ Equations by Using Some Numerical Methods. J. Appl. Math. Phys. 2016, 4, 2011–2030. [Google Scholar] [CrossRef]
- Singh, G.; Singh, I. Semi-analytical solutions of three-dimensional (3D) coupled Burgers’ equations by new Laplace variational iteration method. Partial Differ. Equ. Appl. Math. 2022, 6, 100438. [Google Scholar] [CrossRef]
- Chung, T.J. Computational Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Duffy, D.J. Finite Difference Methods. In Financial Engineering a Partial Differential Equation Approach; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]


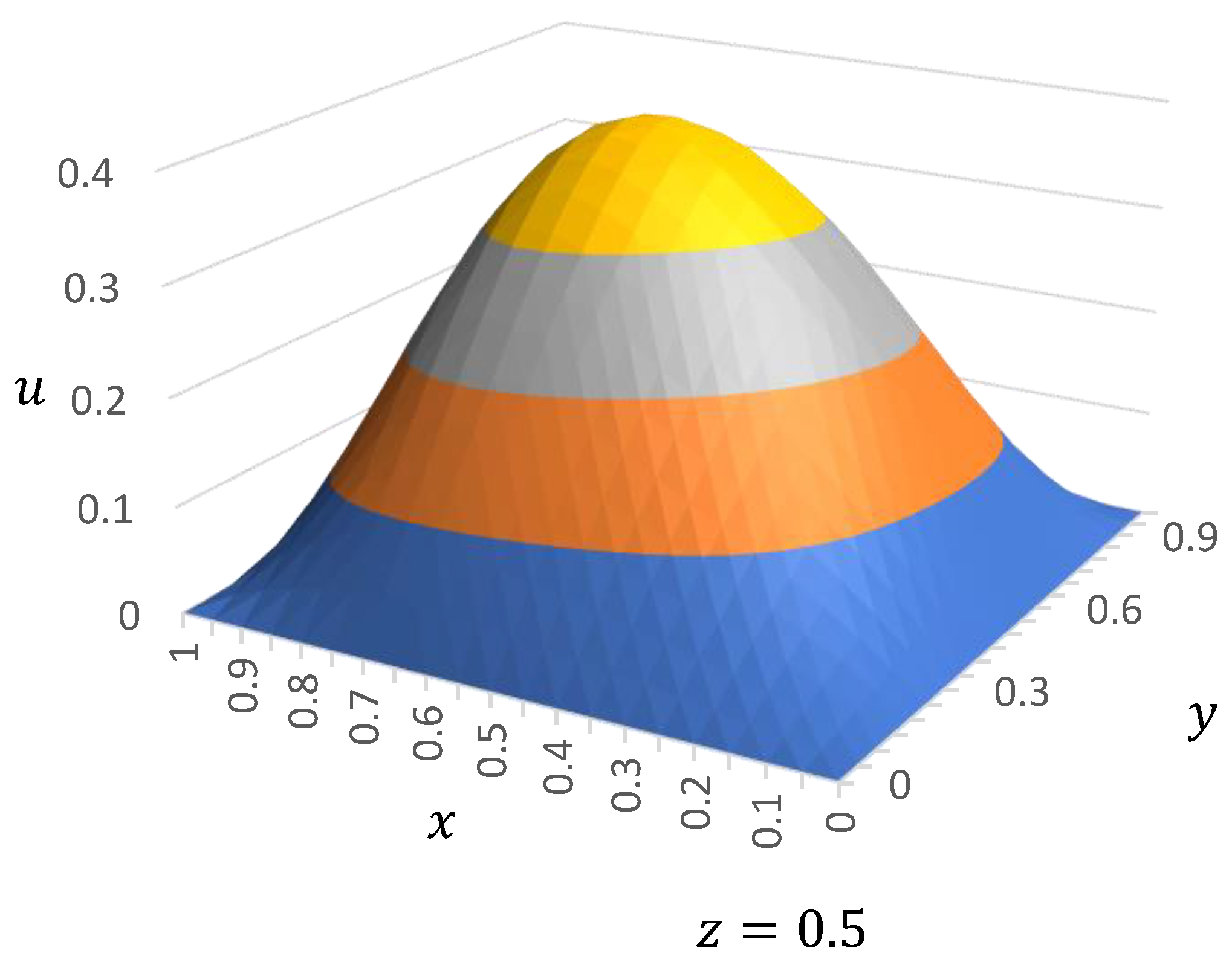
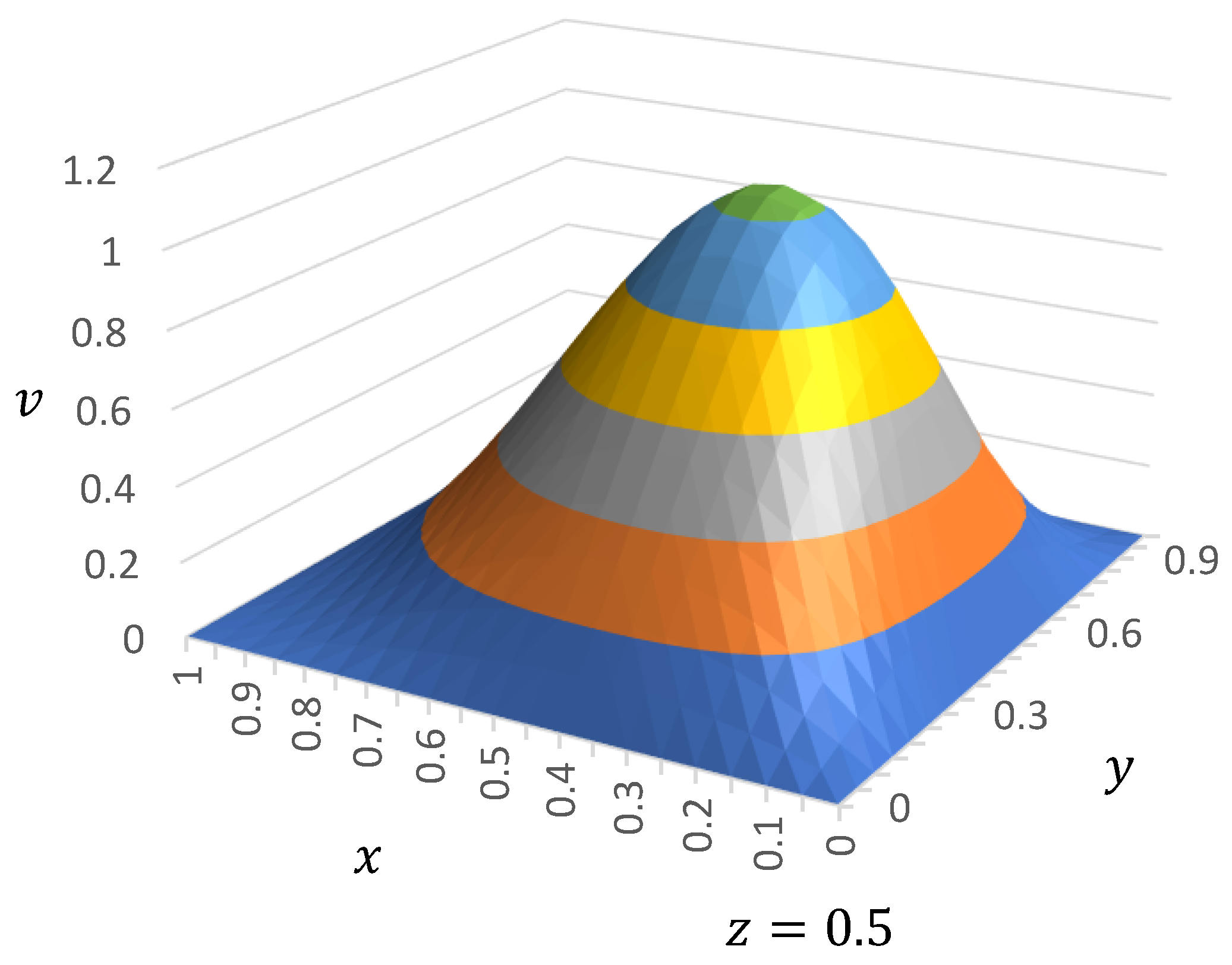
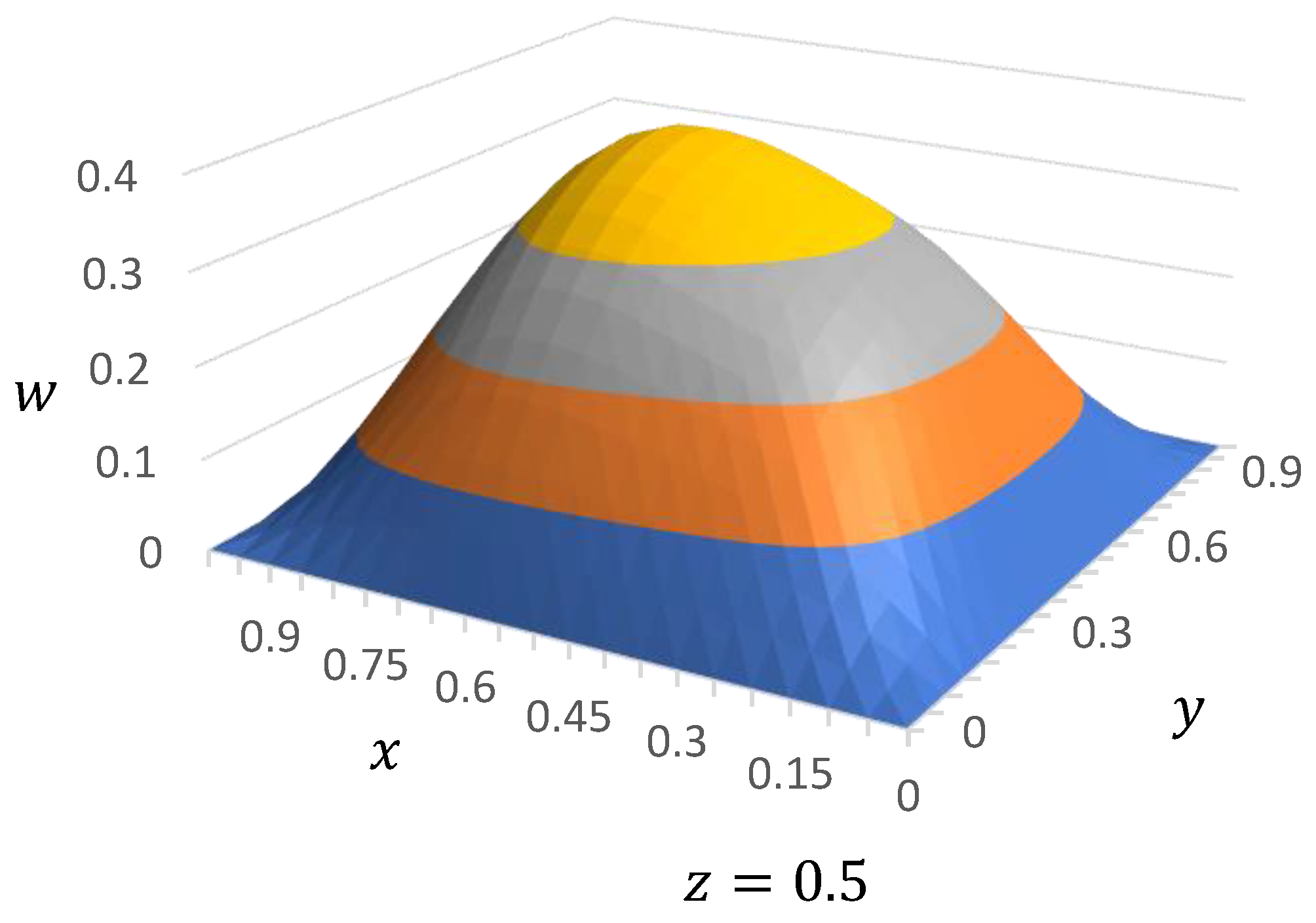



| Exact | Present | Absolute Error | ||
|---|---|---|---|---|
| 0.002 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.01834520 −0.01896376 −0.01945593 −0.01340710 −0.01368335 −0.01389983 −0.01492331 −0.01582336 −0.01054814 −0.01062954 −0.01098810 −0.01124165 −0.01160368 | −0.01834552 −0.01896527 −0.01945839 −0.01340724 −0.01368402 −0.01390090 −0.01492619 −0.01582768 −0.01054819 −0.01062973 −0.01098892 −0.01124285 −0.01160535 | |
| 0.006 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.01834455 −0.01896065 −0.01945088 −0.01340680 −0.01368198 −0.01389762 −0.01491740 −0.01581448 −0.01054806 −0.01062913 −0.01098642 −0.01123917 −0.01160025 | −0.01834550 −0.01896518 −0.01945824 −0.01340723 −0.01368398 −0.01390084 −0.01492601 −0.01582741 −0.01054818 −0.01062972 −0.01098887 −0.01124278 −0.01160525 | |
| 0.010 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.01834390 −0.01895756 −0.01944585 −0.01340651 −0.01368061 −0.01389542 −0.01491150 −0.01580563 −0.01054797 −0.01062873 −0.01098474 −0.01123671 −0.01159682 | −0.01834548 −0.01896508 −0.01945809 −0.01340722 −0.01368394 −0.01390077 −0.01492583 −0.01582715 −0.01054818 −0.01062971 −0.01098882 −0.01124270 −0.01160515 |
| Exact | Present | Absolute Error | ||
|---|---|---|---|---|
| 0.002 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.00017979 −0.00086042 −0.00140200 −0.00063170 −0.00299749 −0.00485131 −0.00250076 −0.00391638 −0.00081409 −0.00384970 −0.00316312 −0.00212417 −0.00319923 | −0.00018013 −0.00086209 −0.00140470 −0.00063293 −0.00300322 −0.00486050 −0.00250529 −0.00392317 −0.00081567 −0.00385704 −0.00316873 −0.00212774 −0.00320419 | |
| 0.006 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.00017907 −0.00085700 −0.00139644 −0.00062919 −0.00298570 −0.00483241 −0.00249146 −0.00390242 −0.00081086 −0.00383463 −0.00315158 −0.00211682 −0.00318902 | −0.00018011 −0.00086198 −0.00140453 −0.00063285 −0.00300286 −0.00485993 −0.00250501 −0.00392275 −0.00081557 −0.00385658 −0.00316838 −0.00212752 −0.00320388 | |
| 0.010 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.00017835 −0.00085360 −0.00139090 −0.00062669 −0.00297396 −0.00481359 −0.00248219 −0.00388849 −0.00080763 −0.00381962 −0.00314008 −0.00210949 −0.00317884 | −0.00018009 −0.00086188 −0.00140437 −0.00063278 −0.00300251 −0.00485936 −0.00250473 −0.00392233 −0.00081547 −0.00385613 −0.00316804 −0.00212730 −0.00320357 |
| Exact | Present | Absolute Error | ||
|---|---|---|---|---|
| 0.002 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.00017979 −0.00015803 −0.00011163 −0.00063170 −0.00055052 −0.00038626 −0.00250076 −0.00169783 −0.00081409 −0.00070704 −0.00316312 −0.00489982 −0.00319923 | −0.00018013 −0.00015833 −0.00011184 −0.00063293 −0.00055158 −0.00038700 −0.00250529 −0.00170077 −0.00081567 −0.00070839 −0.00316873 −0.00490806 −0.00320419 | |
| 0.006 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.00017907 −0.00015740 −0.00011119 −0.00062919 −0.00054836 −0.00038476 −0.00249146 −0.00169177 −0.00081086 −0.00070427 −0.00315158 −0.00488287 −0.00318902 | −0.00018011 −0.00015831 −0.00011183 −0.00063285 −0.00055151 −0.00038695 −0.00250501 −0.00170059 −0.00081557 −0.00070831 −0.00316838 −0.00490755 −0.00320388 | |
| 0.010 | (0.1, 0.1, 0.1) (0.1, 0.1, 0.5) (0.1, 0.1, 0.9) (0.5, 0.1, 0.1) (0.5, 0.1, 0.5) (0.5, 0.1, 0.9) (0.5, 0.5, 0.5) (0.5, 0.5, 0.9) (0.9, 0.1, 0.1) (0.9, 0.1, 0.5) (0.9, 0.5, 0.5) (0.9, 0.9, 0.5) (0.9, 0.9, 0.9) | −0.00017835 −0.00015677 −0.00011074 −0.00062669 −0.00054620 −0.00038326 −0.00248219 −0.00168574 −0.00080763 −0.00070152 −0.00314008 −0.00486597 −0.00317884 | −0.00018009 −0.00015829 −0.00011182 −0.00063278 −0.00055144 −0.00038691 −0.00250473 −0.00170041 −0.00081547 −0.00070822 −0.00316804 −0.00490704 −0.00320357 |
| Present | LT-ADM [25] | LT-HPM [25] | VIM [25] | VIDM [25] | VIHPM [25] | CPU | |
|---|---|---|---|---|---|---|---|
| 0.002 | 47 | ||||||
| 0.004 | 78 | ||||||
| 0.006 | 105 | ||||||
| 0.008 | 156 | ||||||
| 0.010 | 165 |
| Present | LT-ADM [25] | LT-HPM [25] | VIM [25] | VIDM [25] | VIHPM [25] | |
|---|---|---|---|---|---|---|
| 0.002 | ||||||
| 0.004 | ||||||
| 0.006 | ||||||
| 0.008 | ||||||
| 0.010 |
| Present | LT-ADM [25] | LT-HPM [25] | VIM [25] | VIDM [25] | VIHPM [25] | |
|---|---|---|---|---|---|---|
| 0.002 | ||||||
| 0.004 | ||||||
| 0.006 | ||||||
| 0.008 | ||||||
| 0.010 |
| CPU | |||||||
|---|---|---|---|---|---|---|---|
| 0.1 | 0.01607602 | 0.01701311 | 0.01701314 | 0.00078824 | 0.00052727 | 0.00052727 | 18 |
| 0.2 | 0.02885929 | 0.03118231 | 0.03118236 | 0.00136220 | 0.00094535 | 0.00094535 | 36 |
| 0.3 | 0.03925681 | 0.04314278 | 0.04314281 | 0.00180512 | 0.00129970 | 0.00129970 | 54 |
| 0.4 | 0.04777030 | 0.05327088 | 0.05327092 | 0.00211052 | 0.00158540 | 0.00158540 | 72 |
| 0.5 | 0.05473662 | 0.06183566 | 0.06183568 | 0.00234148 | 0.00182888 | 0.00182888 | 89 |
| 0.6 | 0.06040639 | 0.06904788 | 0.06904791 | 0.00256857 | 0.00203571 | 0.00203571 | 107 |
| 0.7 | 0.06497688 | 0.07508099 | 0.07508107 | 0.00273030 | 0.00220845 | 0.00220846 | 125 |
| 0.8 | 0.06860875 | 0.08008187 | 0.08008195 | 0.00283681 | 0.00234598 | 0.00234599 | 143 |
| 0.9 | 0.07144140 | 0.08418134 | 0.08418139 | 0.00289775 | 0.00245845 | 0.00245846 | 161 |
| 1.0 | 0.07357237 | 0.08747612 | 0.08747618 | 0.00292069 | 0.00254495 | 0.00254495 | 178 |
| CPU | |||||||
|---|---|---|---|---|---|---|---|
| 10 | 0.12595460 | 0.17624530 | 0.17628540 | 0.00398876 | 0.00496712 | 0.00496995 | |
| 20 | 0.14303290 | 0.19327000 | 0.19330240 | 0.00473712 | 0.00550840 | 0.00551130 | |
| 30 | 0.13336220 | 0.17461560 | 0.17464180 | 0.00461626 | 0.00496580 | 0.00496805 | |
| 40 | 0.12094910 | 0.15458880 | 0.15460980 | 0.00431160 | 0.00443582 | 0.00443767 | |
| 50 | 0.10965810 | 0.13755450 | 0.13757130 | 0.00401893 | 0.00393986 | 0.00394031 | 2 |
| 60 | 0.09998650 | 0.12355520 | 0.12356920 | 0.00377040 | 0.00356142 | 0.00356287 | |
| 70 | 0.09178136 | 0.11202780 | 0.11203940 | 0.00352644 | 0.00324337 | 0.00324450 | |
| 80 | 0.08479263 | 0.10243280 | 0.10244300 | 0.00329654 | 0.00296713 | 0.00296735 | |
| 90 | 0.07879200 | 0.09434658 | 0.09435534 | 0.00308419 | 0.00273646 | 0.00273663 | |
| 100 | 0.07359336 | 0.08744954 | 0.08745717 | 0.00291878 | 0.00254064 | 0.00254077 | |
| 1000 | 0.01124273 | 0.01200673 | 0.01200697 | 0.00054696 | 0.00036272 | 0.00036273 | |
| 10000 | 0.00122298 | 0.00127331 | 0.00127331 | 0.00006759 | 0.00003947 | 0.00003947 | 3 |
| Grid Point | ||||||
|---|---|---|---|---|---|---|
| (0.1, 0.1, 0.9) | 0.0239584 −0.1433502 −0.3098060 | 0.0251936 −0.0942885 −0.0444397 | 0.0198349 −0.0019673 0.0571594 | 0.0087784 0.0161314 0.0209709 | 0.0025408 0.0079498 0.0053030 | |
| (0.1, 0.1, 0.1) | 0.0130397 0.2961703 0.5933083 | 0.0086755 0.1819000 0.2619675 | 0.0042517 0.0713250 0.0521275 | 0.0021648 0.0258374 0.0125001 | 0.0010801 0.0071994 0.0034688 | |
| (0.9, 0.1, 0.1) | 0.0373669 −0.2133582 −0.3512228 | 0.0350676 −0.1539166 −0.0849666 | 0.0219688 −0.0399523 0.0298473 | 0.0091082 0.0024782 0.0171387 | 0.0024632 0.0052484 0.0049001 | |
| (0.9, 0.1, 0.9) | 0.0287756 0.0465253 0.1132805 | 0.0261095 0.0281507 0.0222440 | 0.0290998 0.0072191 0.0443088 | 0.0224096 0.0118066 0.0329812 | 0.0056462 0.0084688 0.0085465 | |
| (0.5, 0.5, 0.5) | 0.8804632 1.7752066 0.2335210 | 0.6788833 2.0130337 0.1981508 | 0.3317227 1.3315012 0.3736063 | 0.1704326 0.6964189 0.3278693 | 0.0806389 0.2940547 0.1650422 | |
| (0.1, 0.9, 0.9) | 0.0293427 0.0473384 0.1131651 | 0.0258647 0.0287051 0.0199498 | 0.0209887 0.0078080 0.0268328 | 0.0157792 0.0255877 0.0232304 | 0.0063097 0.0232738 0.0108606 | |
| (0.1, 0.9, 0.1) | 0.0285317 −0.1743388 −0.3571369 | 0.0222670 −0.1143676 −0.1186861 | 0.0122100 −0.0169228 0.0035327 | 0.0080087 0.0576209 0.0156805 | 0.0027520 0.0189870 0.0066534 | |
| (0.9, 0.9, 0.1) | 0.0274635 0.0434720 0.1061607 | 0.0280131 0.0281587 0.0114414 | 0.0204932 0.0042559 0.0088801 | 0.0117795 0.0117706 0.0139944 | 0.0049298 0.0145751 0.0080140 | |
| (0.9, 0.9, 0.9) | 0.0271956 −0.0122070 −0.0415867 | 0.0264742 −0.0067082 −0.0019528 | 0.0306129 0.0000573 0.0280496 | 0.0370216 0.0201885 0.0365225 | 0.0153747 0.0316911 0.0195732 | |
| CPU | 4 | 8 | 19 | 38 | 75 |
| Grid Point | Method | |||||
|---|---|---|---|---|---|---|
| (0.1, 0.1, 0.9) | Present DQ-FDM [24] FDM [24] | 0.0254111 0.02364 0.025403 | 0.0115768 0.01076 0.011756 | 0.0041839 0.00391 0.004266 | 0.0009462 0.00090 0.000983 | |
| Present DQ-FDM [24] FDM [24] | −0.1071553 −0.10201 −0.108493 | 0.0109503 0.00971 0.010697 | 0.0093759 0.00872 0.009521 | 0.0024052 0.00227 0.002498 | ||
| Present DQ-FDM [24] FDM [24] | −0.0680342 −0.07772 −0.089963 | 0.0185890 0.01747 0.020117 | 0.0058328 0.00545 0.005872 | 0.0012179 0.00115 0.001228 | ||
| (0.1, 0.1, 0.1) | Present DQ-FDM [24] FDM [24] | 0.0135700 0.01291 0.013941 | 0.0043702 0.00413 0.004521 | 0.0022730 0.00214 0.002331 | 0.0007671 0.00073 0.000798 | |
| Present DQ-FDM [24] FDM [24] | 0.2722870 0.26139 0.284202 | 0.0456060 0.04368 0.048848 | 0.0124520 0.01180 0.013223 | 0.0023299 0.00221 0.002449 | ||
| Present DQ-FDM [24] FDM [24] | 0.3243355 0.32746 0.379733 | 0.0148860 0.01391 0.016177 | 0.0042409 0.00391 0.004263 | 0.0010379 0.00097 0.001045 | ||
| (0.5, 0.5, 0.5) | Present DQ-FDM [24] FDM [24] | 0.8221614 0.82203 0.826809 | 0.3196220 0.32429 0.328282 | 0.1489025 0.15109 0.152905 | 0.0361105 0.03715 0.037998 | |
| Present DQ-FDM [24] FDM [24] | 1.5623827 1.57094 1.540632 | 0.9474787 0.94780 0.971748 | 0.4004099 0.40393 0.409879 | 0.0912639 0.09344 0.094790 | ||
| Present DQ-FDM [24] FDM [24] | 0.3610981 0.37251 0.401473 | 0.3579388 0.35500 0.340496 | 0.1880154 0.18819 0.185145 | 0.0451686 0.04595 0.045831 | ||
| (0.9, 0.9, 0.1) | Present DQ-FDM [24] FDM [24] | 0.0266505 0.02445 0.026479 | 0.0129122 0.01202 0.013229 | 0.0063366 0.00592 0.006476 | 0.0012449 0.00118 0.001334 | |
| Present DQ-FDM [24] FDM [24] | 0.0279643 0.02662 0.029084 | 0.0038226 0.00378 0.003146 | 0.0113319 0.01041 0.010327 | 0.0030525 0.00288 0.003158 | ||
| Present DQ-FDM [24] FDM [24] | 0.0139741 0.02232 0.032489 | 0.0133409 0.01219 0.012178 | 0.0068297 0.00626 0.006790 | 0.0015038 0.00141 0.001544 | ||
| (0.9, 0.9, 0.9) | Present DQ-FDM [24] FDM [24] | 0.0259294 0.02393 0.025940 | 0.0206922 0.01909 0.020358 | 0.0103278 0.00958 0.010436 | 0.0015613 0.00149 0.001669 | |
| Present DQ-FDM [24] FDM [24] | −0.0067402 −0.00660 −0.007179 | 0.0023861 0.00250 0.002243 | 0.0104624 0.00969 0.009546 | 0.0032999 0.00311 0.003387 | ||
| Present DQ-FDM [24] FDM [24] | −0.0027490 −0.00627 −0.006416 | 0.0218266 0.02055 0.020134 | 0.0103696 0.00968 0.010395 | 0.0018227 0.00172 0.001875 | ||
| CPU | 3 | 19 | 38 | 75 |
| Grid Point | Method | |||||
|---|---|---|---|---|---|---|
| (0.1, 0.1, 0.9) | Present DQ-FDM [24] FDM [24] | 0.0207517 0.01919 0.020817 | 0.0038962 0.00370 0.004033 | 0.0006396 0.00062 0.000682 | 0.0000164 0.00002 0.000019 | |
| Present DQ-FDM [24] FDM [24] | −0.0310491 −0.03350 −0.035715 | 0.0066557 0.00622 0.006890 | 0.0010418 0.00100 0.001105 | 0.0000260 0.00003 0.000030 | ||
| Present DQ-FDM [24] FDM [24] | 0.0279222 0.02000 0.026177 | 0.0042174 0.00401 0.004361 | 0.0006661 0.00064 0.000706 | 0.0000170 0.00002 0.000020 | ||
| (0.1, 0.1, 0.1) | Present DQ-FDM [24] FDM [24] | 0.0131351 0.01247 0.013573 | 0.0031357 0.00297 0.003242 | 0.0006058 0.00058 0.000645 | 0.0000164 0.00002 0.000019 | |
| Present DQ-FDM [24] FDM [24] | 0.1831330 0.17987 0.197984 | 0.0099416 0.00978 0.010907 | 0.0010810 0.00105 0.001159 | 0.0000260 0.00003 0.000030 | ||
| Present DQ-FDM [24] FDM [24] | 0.0690051 0.07888 0.095820 | 0.0035683 0.00339 0.003684 | 0.0006332 0.00061 0.000746 | 0.0000169 0.00002 0.000020 | ||
| (0.5, 0.5, 0.5) | Present DQ-FDM [24] FDM [24] | 0.6654563 0.66955 0.672757 | 0.1411316 0.14484 0.146526 | 0.0223667 0.02345 0.023959 | 0.0005572 0.00063 0.000654 | |
| Present DQ-FDM [24] FDM [24] | 1.0757338 1.06574 1.055410 | 0.2289045 0.23342 0.233923 | 0.0354140 0.03684 0.037139 | 0.0008814 0.00098 0.001013 | ||
| Present DQ-FDM [24] FDM [24] | 0.5259060 0.53003 0.531746 | 0.1456256 0.14901 0.149800 | 0.0231289 0.02420 0.024597 | 0.0005761 0.00065 0.000672 | ||
| (0.9, 0.9, 0.1) | Present DQ-FDM [24] FDM [24] | 0.0205042 0.01899 0.020760 | 0.0045598 0.00431 0.004726 | 0.0006817 0.00066 0.000733 | 0.0000165 0.00002 0.000019 | |
| Present DQ-FDM [24] FDM [24] | 0.0047205 0.00592 0.006935 | 0.0051581 0.00468 0.004731 | 0.0010428 0.00100 0.001076 | 0.0000260 0.00003 0.000030 | ||
| Present DQ-FDM [24] FDM [24] | 0.0080648 0.00749 0.0053180 | 0.0045400 0.00428 0.004689 | 0.0006999 0.00068 0.000747 | 0.0000170 0.00002 0.000020 | ||
| (0.9, 0.9, 0.9) | Present DQ-FDM [24] FDM [24] | 0.0212308 0.01971 0.021345 | 0.0053239 0.00502 0.005498 | 0.0007187 0.00070 0.000775 | 0.0000165 0.00002 0.000019 | |
| Present DQ-FDM [24] FDM [24] | −0.0006289 −0.00100 −0.001143 | 0.0035969 0.00323 0.003274 | 0.0010081 0.00096 0.001032 | 0.0000260 0.00003 0.000030 | ||
| Present DQ-FDM [24] FDM [24] | 0.0051624 0.00529 0.004513 | 0.0053273 0.00503 0.005506 | 0.0007364 0.00071 0.000788 | 0.0000171 0.00002 0.000020 | ||
| CPU | 4 | 19 | 37 | 75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çelikten, G. An Unconditionally Stable Numerical Scheme for 3D Coupled Burgers’ Equations. Symmetry 2025, 17, 452. https://doi.org/10.3390/sym17030452
Çelikten G. An Unconditionally Stable Numerical Scheme for 3D Coupled Burgers’ Equations. Symmetry. 2025; 17(3):452. https://doi.org/10.3390/sym17030452
Chicago/Turabian StyleÇelikten, Gonca. 2025. "An Unconditionally Stable Numerical Scheme for 3D Coupled Burgers’ Equations" Symmetry 17, no. 3: 452. https://doi.org/10.3390/sym17030452
APA StyleÇelikten, G. (2025). An Unconditionally Stable Numerical Scheme for 3D Coupled Burgers’ Equations. Symmetry, 17(3), 452. https://doi.org/10.3390/sym17030452








