Abstract
Since the 1960s, theorists have claimed that the electroweak force, which unifies parity-conserving electromagnetic and parity-violating weak nuclear forces, induces tiny parity-violating energy differences (10−10–10−21 eV) between mirror-image molecules. This study reports the dual mirror-symmetry-breaking and second-order phase transition characteristics of mirror-symmetric 73-helical poly(di-n-butylsilane) in n-alkanes under static (non-stirring) conditions. In particular, n-dodecane-h26 significantly enhances the circular dichroism (CD) and circularly polarized luminescence (CPL) spectra. A new (−)-CD band emerges at 299 nm below TC1 ~ 105 °C, with a helix–helix transition at TC2 ~ 28 °C, and exhibits gabs = +1.3 × 10−2 at −10 °C. Synchronously, the CPL band at 340 nm exhibiting glum = −0.7 × 10−2 at 60 °C inverts to glum = +2.0 × 10−2 at 0 °C. Interestingly, clockwise and counterclockwise stirring of the mixture induced non-mirror-image CD spectra. n-Dodecane-d26 weakens the gabs values by an order of magnitude, and oppositely signed CD and a lower TC1 of ~45 °C are observed. The notable H/D isotope effect suggests that the CH3 termini of the polysilane and n-dodecane-h26, which comprise a three identical nuclear spin-1/2 system in a triple-well potential, effectively work as unidirectional hindered rotors due to the handedness of nuclear-spin-dependent parity-violating universal forces. This is supported by the (−)-sign vibrational CD bands in the symmetric and asymmetric bending modes of the CH3 group in n-dodecane-h26.
1. Introduction
1.1. Hierarchy in Broken Symmetries
All hierarchical structures of nature are governed by four fundamental physical forces: the infinite range gravitational force (GF), the infinite range electromagnetic force (EMF), the ultrashort range (~10−9 nm) weak nuclear force (WF), and the ultrashort range (~10−6 nm) strong nuclear force (SF) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. Relative to the SF, the magnitudes of the GF, EMF, and WF are 10−43, 10−2, and 10−6, respectively [9,31]. The four forces are mediated by force-carrying vectoral bosons with integer spins: GF: the hypothetical massless graviton G (spin-2); WF: the massive charged W± (spin-1, 80.4 GeV) and neutral Z0 bosons (spin-1, 91.2 GeV); EMF: the massless photon γ (spin-1); and SF: the massless eight gluons (spin-1) [31,32,33]. Aiming at a deeper understanding of hierarchical structures, it has been theoretically and experimentally investigated whether the seven symmetries—parity (P), charge conjugation (C), time reversal (T), and their combinations, CP, PT, CT, and CPT—are rigorously conserved in the four forces [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,31,32,33]. P- and CP-symmetry breaking has been investigated in particle (neutrinos) and subatomic (K- and B-mesons) physics. P-symmetry breaking has been established in nuclear and atomic physics but not in chemistry, bioscience, or materials science.
Recently, P-symmetry breaking became a hot topic in cosmology [24,25,26,27,28,29,30]. In 2020, astrophysicists reported hidden handedness imprinted in the cosmic microwave background (CMB) at 2.73 K. The sign and magnitude of the birefringent rotation from an observer were evaluated to be βCMB = +0.35 ± 0.14° [28,29], corresponding to a Kuhn dissymmetry ratio, gem of +2.0 (±0.8) × 10−3. Our life, biomolecules, biopolymers, and chemical reactions may thus experience a cosmological dextrorotatory force ranging from 0.3 to 630 GHz (0.01–21 cm−1) with a peak of 160 GHz (5.35 cm−1). The W± bosons carry the handedness of the weak charged current (WCC) and permit exchange between quarks (fermions with spin-1/2), i.e., left-hand (LH) up quark (u, 2.2 MeV, charge +2/3) and LH down quark (d, 4.7 MeV, charge −1/3). However, interaction with right-hand (RH) u and RH d is not permitted [9,31,32,33]. Likewise, W+ and W−, respectively, transform between leptons (spin-1/2) from LH electron (e−, 0.51 MeV, charge −1) to LH electron-neutrino (νe < 2.2 × 10−6 MeV, charge 0) and from LH νe to LH e− [9,31,32]. The W−-WCC in 60Co → 60Ni and W+-WCC in 58Co → 58Fe nuclear fissions [4,5,33], as well as other β∓ decays of radiomarkers, i.e., 11C, 13N, 15O, 18F, 32P, are detectable as the opposite handedness of e− and its anti-matter positron, e+ [33,34].
1.2. Atomic Parity Violation—Theories and Experiments
Inspired by parity-violation (PV) in the β∓-decays [33], Weinberg, Glashow, and Salam in the 1960s proposed electroweak force (EWF) theory involving the Z0 boson to unify PV-WF and P-symmetry conserving (PC)-EMF. The EWF theory makes all of Z0, W±, and γ possible in a massless family above ~102 GeV (~1015 K) [31,32]. In 1973, the detection of weak neutral current (WNC) and WCC by an elastic νe–anti-νe scattering using a liquid bubble chamber detector (called Gargamelle) filled with CF3Br (possibly, C19F379/81Br) at Conseil Européen pour la Recherche Nucléaire (CERN) was reported, followed by, in 1983, the detection of the Z0 as a production of an e−e+ pair using the proton (p)-anti-p collider (Super Proton Synchrotron, SPS) at CERN [35,36,37,38,39]. By combining the SF theory and the Higgs scalar boson (spin-0, 125.1 GeV), the EWF theory became the standard model of particle physics [31,32]. Also, around that time, theorists further hypothesized atomic parity violation (APV) and molecular parity violation (MPV) induced by the handedness of the WNC mediated by the Z0-boson. Probing the APV hypothesis of stable atoms met difficulties due to the absence of chemical chirality [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. Although the APV of 1H was computationally visualized as a handed spiral torus of e− trajectory around p by admixing P-even 2s and P-odd 2p1/2 states, its APV magnitude was far from a detectable level [50]. Theoretical predictions to amplify APV ∝ Z3 (Z: atomic number) for non-relativistic atoms and APV ∝ Z5 for relativistic atoms [46,47,48,49] led to the successful detection of weak APV effects on the order of g ~ 10−7 at forbidden electronic transitions for several high-Z atoms, including 133Cs, 209Bi, 208Pb, 205Tl, and 174Yb, in a collision-free gas state using high-resolution optical rotatory dispersion spectroscopy (ORD), fluorescence-detective circular dichroism spectroscopy, and dc-Stark interferometer [9,49,51,52,53,54,55].
In 1964 Michel [43], followed by Stodolsky in 1974 and 1982 [44,45], predicted the use of neutron optical activity to detect APV effects. Actually, in recent years, spin-polarized neutron resonance scattering (SPNRS) has been used experimentally and detected clear APV effects. Almost a dozen half-integer nuclear spin (HINS) high-Z isotopes (spin number, I) as solids, i.e., 81Br (I = 3/2), 93Nb (I = 9/2), 103Rh (I = 7/2), 105Pd (I = 5/2), 107Ag (I = 1/2), 111Cd (I = 1/2), 115In (I = 9/2), 117Sn (I = 1/2), 127I (I = 5/2), 139La (I = 7/2), and integer nuclear spin (INS) radioisotope, 238U (I = 0), revealed huge APV effects on the order of g ~ 10–3–10–2 at resonance transitions by SPNRS experiments in the energy range of 0.5 to 1100 eV [56,57,58,59,60,61]. Among these HINS isotopes, 139La shows a particularly large g value of ~ 2 × 10–1 at 0.734 eV [58]. On the other hand, the INS isotopes, i.e., 82Br (I = 5), 112Cd (I = 0), 118Sn (I = 0), 140La (I = 3), showed greatly reduced APV effects even by the SPNRS [56,57]. These experiments strongly indicate the importance of HINS isotopes at the resonant transitions, enabling great amplification of APV effects, which is presumably also applicable to the nuclear-spin-dependent and/or the nuclear-spin-induced MPV effects.
1.3. Molecular Parity Violation—Theories and Experiments
In the 1960s and 1970s, MPV theorists estimated the order of magnitude of the parity-violating energy difference (PVED) between mirror-image molecules due to handed electron–nuclei interactions by admixing Z0-WNC to PC-EMF [62,63,64,65,66,67,68]. Comprehensive reviews covering those experiments, including the self-disproportionation of enantiomers (known as SDE), were published [69]. From the 1980s onward [4,5,6,7,8,10,16,17,18,19,20,68,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90], sophisticated theories of electroweak quantum chemistry facilitated the rigorous prediction of the sign and magnitude of PVED for mirror-image molecules in mostly double-well potential (DWP) with rotational and/or inversion barriers (EB). Because of the P-odd characteristics in the DWP, the potential energy for one mirror-image molecule is raised by EPV; conversely, the other is pushed down by EPV, similar to a seesaw. Therefore, the PVED is equal to 2EPV = +EPV − (−EPV). The magnitude of PVED for isolated molecules, however, is too small to detect, being on the order of 10−10–10−21 eV (cf. 0.026 eV at 300 K), corresponding to 10−6–10−17 cm−1 and 104–10−7 Hz [18,19,84,85,86,87,88].
The MPV hypothesis is in sharp contrast to the accepted concepts of enantiomerism, diastereomerism, and racemism in modern stereochemistry based on PC-EMF theory [91,92,93,94]. Conventional stereochemical theory is predicated upon the rigorous preservation of energetic equality between mirror-image molecules, supramolecules, macromolecules, micelles, colloids, aggregates, gels, liquid crystals, and crystals. Chiroptical spectroscopic techniques [91,92,93,94], including electronic circular dichroism (CD), vibrational circular dichroism (VCD), Raman optical activity (ROA), and ORD, which detect the ground state chirality, and circularly polarized luminescence (CPL) to measure photoexcited chirality should therefore afford absolutely ideal mirror-image chiroptical spectra between the mirror-image substances, exhibiting identical magnitudes with opposite chiroptical signs at the same wavelengths and wavenumbers to at least three significant figures. A few researchers appear to be aware that the experimental results do not rigorously obey conventional stereochemical theory, as evidenced by differences in the chiroptical spectra, physicochemical properties, chemical reactions, and other aspects between supposed mirror-image molecules, oligomers, polymers, colloids, and crystals, as discussed in Section 3.9 [12,21,22,23,24,66,69,78,89,90,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115].
Detecting MPV effects is therefore important in elucidating the missing link between the handedness of matter at all hierarchical levels of the matter world and the anti-matter world, ranging from LH-νe, LH-quarks, APV, L-amino acids and proteins, D-ribose and DNA/RNA, artificial molecules, and macromolecules; the homochiral living world, including helical bacteria, plants, and seashells; and the cosmological dextrorotatory rotation [1,3,8,12,13,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,49,55,60,62,70,71,72,74,82,86,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115]. Aiming at amplifying the tiny PVED to detectable levels, six theoretical scenarios have so far been proposed, as described below.
- Scenario A. An accumulation model, often called a linear amplification model, was proposed in 1966 by Yamagata [62]. The overall PVED is proportional to repeat unit number (N), yielding N × EPV in the systems. The idea is applicable to N-mer systems, i.e., macromolecules, supramolecules, micelles, colloids, micelles, colloids, aggregates, molecular liquids, liquid crystals, and crystals [12,66,71,78,95,96,97,98,99,100,101,102,103,104,105,106].
- Scenario B. EPV ∝ Z5 is possible for high-Z atoms, while Z2 and Z3, respectively, arise from spin-orbit-coupling (SOC, ξ) of constituents and the PV-WNC [5,6,67,70,73,75], which is similar to the Z3- and Z5-dependence of APV [42,46,47,48,49]. The idea is applicable to experiments using molecules involving high-Z atoms such as I, W, Re, Pb, Ir, Ru, and Os in periods 5 and 6 [17,18,69,73,75,76,77,78,79,95].
- Scenario C. In the early 1990s, a nonlinearly amplified MPV theory in a condensed phase was hypothesized by Salam based on Cooper e−(↑)-e−(↓) pairs (I = 0) in the Bardeen–Cooper–Schrieffer (BCS) theory of superconductivity and the 3He(↑)-3He(↑) pair (I = 1) and Bose–Einstein condensate (BEC) theory of superfluidity [107,108]. The hypothesis predicts that an L–D mixture of amino acids transforms into a single enantiomer at a critical temperature (Tc) by cooperative e−–n interactions. This cooperativity results in an entropy-driven, second-order phase transition detectable by emerging chiroptical signals and a jump of specific heat capacity [107,110,111,112]. Although Tc ~ 2.7 K was numerically obtained, a higher Tc ~ 250 K is optimistically conceivable [107]. However, because the rigid configuration of D-α-amino acids is unable to invert to L-configurations [96,97], non-rigid molecular rotamers in the absence of point chirality are suitable to validate the MPV hypothesis [18,19,67,109,110,111,112,113,114,115]. Similar phase transition models including mirror symmetric and dissymmetric bifurcations were proposed by Goldanskii et al. [2,3]. The selection between LH and RH at the bifurcation point is hypersensitive to external and internal fluctuations relative to the advantageous factors (rate constants in asymmetric chemical reactions) of chemical and physical chirality.
- Scenario D. The interplay between a smaller quantum tunneling splitting with an opposite parity, ΔE±, in a DWP with a larger EB and tiny P-odd EPV leads to the resonant amplification of the MPV effect when satisfying ΔE± ~ EPV. In the cases where EPV ≪ ΔE± or EPV ≫ ΔE±, there is no detectable amplification [16,17,18,19,67,80,81,84,85,86,87,88]. Modulating the EB vs. ΔE±, kT, and EPV causes a significant transition from coherence (oscillation) to decoherence (non-oscillation) due to environmental effects, leading to detectable MPV effects using steady-state and time-resolved chiroptical spectroscopy in a condensed phase [21,22,23,24,67,80,81,84,85,86,87,88,106,113,114,115].
- Scenario E. EPV ∝ (E0 − ET)−1 = ΔEST, where E0 and ET are the ground singlet (S0) and photoexcited triplet (T1) states [5,6], respectively, as confirmed by the direct S0 → T1 and T1 → S0 transition [116,117]. ΔEST is the difference in energy between the first excited (S1) and T1 states. Although the 1H atom has the weakest ξ of 0.45 cm−1 (5.5 × 10−5 eV, 1.3 × 10−3 kcal mol−1), several light- and medium-Z number atoms have significant ξ in cm−1: e.g., C (29), N (42), O (57), F (75), Si (211), P (247), S (288), Ge (1450), and Sn (4090) [118]. Molecules and polymers containing larger ξ atoms were found suitable for testing the MPV hypothesis. In particular, chain-like polysilanes consisting of Si–Si main chains with organic pendant side chains are one of the best candidates because summing up the SOCs amplifies the ξ of Si (211 cm−1) × N-mer (Scenario A). This ξ can be further enhanced by HINS 29Si (I = 1/2, natural abundance 4.7%, negative value of nuclear magnetic moment, μN = −0.55) [119]. For comparison, 13C (I = 1/2, natural abundance 1.1%, μN = +0.70), 1H (I = 1/2, natural abundance 99.99%, μN = +2.79), and 2H (I = 1, μN = +0.86), respectively, have positive values of μN. The sign and magnitude of μN and I should contribute differently to the observable MPV effects.
- Scenario F. Most APV and MPV theories neglect the contribution of the nuclear spins, although advanced APV and MPV theories involving the nuclear spin effect have also been proposed. The anapole moment (AM) of the HINS 1H atom was hypothesized in the late 1950s by Zel’dovich to account for PV β±-decays [40,41,42]. The first PV molecular anapole moment (MAM) of diatomic molecules was theoretically discussed in the 1980s by Flambaun and Khriplovich, who suggested that the PV-MAM may be detectable by optical activity [120,121,122,123,124]. In 1997, the first PV atomic anapole moment (AAM) of 133Cs vapor was detected using the dc-Stark technique [125,126]. So far, several hypothetical and realistic molecules and nanostructures [120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146], e.g., organometallic molecules involving 195Pt and 207Pb, [127] M19F (M = 203/205Tl, 38Ba, 223Ra) [121,122,123,128,129,130], 9Be(NC)2 and 25Mg(NC)2 [131], H2X2 (X = 17O, 33S, 77Se, 125Te, 209Po) [132,133,134], chiral fluorooxirane and CHFClBr [135,136,137], and others [89,90,138,139,140,141,142,143,144,145,146] have been theoretically and experimentally investigated. The simplest experiment to validate nuclear-spin-dependent MPV and MAM is to compare HINS and INS isotopomers, that is, ordinary organic substances and their fully or partly deuterated analogs.
For almost 130 years, starting with Kipping and Pope in 1897 and 1898 [147,148], the chiroptical and physicochemical properties and solid-state structures of LH and RH molecules in crystals, biological oligomers, micelles, aggregates, synthetic polymers, and systems have been investigated and statistical analyses carried out [21,22,23,24,69,78,95,96,97,98,99,100,101,102,103,104,105,106,109,110,111,112,113,114,115,148]. However, most of these experimental results, including our previous polysilanes bearing (S)- and (R)-3,7-dimethyloctyl pendants with 96% ee [21,22,23,24] and (S)- and (R)-2-methylbutyl pendants with 99% ee (Scenarios A, B, C, and E) [24,106], remain a matter of debate because of non-100% ee sources, unresolved impurities and chiral dust, differences in the crystal sizes and molecular weights of polymers, the action of directionally opposite Coriolis forces in the northern and southern hemispheres, and non-natural materials.
Recently, the present authors reported clear MPV-related (−)-sign CPL spectra (glum ~ –2 × 10−3) at 25 °C from nearly 70 kinds of mirror-symmetric π-conjugated molecular rotamers without point chirality in achiral solvents under static conditions (Scenarios A, C, and D) [113,114,115]. The rotamers possess small hindered barriers of EB ~ 1 kcal mol−1 along the C–C, C–N, C–O, and C–S single bonds (for example, refs. [113,114,115] Aiming at approaching the condition ΔE± ~ EPV, it was effectively possible to increase EB [113] by increasing the viscosity of the solvents (an environmental effect). The (−)-sign CPL spectra result from the S1-state of metastable chiral rotamers with handedness. Among these rotamers, two pyrromethenes, 546 and 597, carrying multiple methyl groups as hindered rotors (Chart S1, Supplementary Materials (SM)), coumarin 6, coumarin 545, and rhodamine B revealed clear (−)-CD spectra (gabs ~ −10−5) [114]. Additionally, Fujiki, Imai, and coworkers reported that a HINS molecular system, 151/153Eu(β-diketonate)3, involving six C19F3 groups coordinated with 31P-containing enantiomeric ligands, reveals P-odd (−)-sign CPL spectra at 5D0 → 4FJ (J = 3 at 650 nm and J = 4 at 700 nm) transitions [149]. This suggests nuclear-spin-induced MPV and/or PV-MAM effects (Scenario F) [150,151].
1.4. Our Experimental Approaches Toward Validation of Molecular Parity Violation Hypothesis
With the above six MPV scenarios in mind, our findings stimulated us to experimentally investigate the variable temperature (VT) CD and CPL spectral characteristics of rigid rod-like poly(di-n-butylsilane) (PDBS, Chart S1, Supplementary Materials) having a large characteristic ratio, C∞ = 42.3, in n-hexane (Θ solvent) at 19.1 °C, to validate the MPV hypothesis [152,153]. PDBS is well-known to adopt mirror-symmetric 73-helices with λmax = 319 nm in n-hexane and at λmax 313–320 nm in the solid state, although it possesses no chiral centers [152,153,154,155,156]. The family of poly(dialkylsilane)s including PDBS are acknowledged to be excellent examples of helical polymers because they exhibit narrow phonon-side-band-free absorption and photoluminescence (PL) in the near-UV region and show quasi-one-dimensional Wannier-like exciton behavior, characteristic of a Si quantum wire [157,158,159,160,161,162,163]. The nature of the exciton is extremely sensitive to the helicity of the wire [152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168].
The present study focuses on PDBS in medium-length n-alkane solvents using VT CD/UV and CPL/PL spectroscopy, ranging from −10 °C to 110 °C. Herein, we report the dual mirror-symmetry breaking second-order phase transitions (chiroptical generation and chiroptical inversion) of PDBS in a range of longer chain solvents: n-C11H24, n-C12H26, n-C13H28, n-C14H30, and n-C16H34 under static conditions. Similar, though less obvious, effects were found in shorter chain solvents: n-C8H18, n-C10H22, and isooctane. In particular, very large amplitude effects in the CD and CPL spectra of PDBS were induced in n-C12H26. A new (−)-sign CD band emerges at λmax 300 nm below TC1 ~ 105 °C, followed by a switch from (−)- to (+)-sign CD bands due to a helix–helix transition at TC2 ~ 28 °C, reaching gabs = +1.3 × 10−2 at −10 °C. Synchronously, the (−)-sign CPL band at 60 °C exhibited glum = –0.7 × 10−2 at λem 340 nm and inverted to (+)-sign CPL with glum = +2.0 × 10−2 at 0 °C. The signs and magnitudes of glum at TC2 show a large fluctuation between +2.0 × 10−2 and −1.0 × 10−2. Notably, in n-C12D26, these gabs values were an order of magnitude weaker, with opposite CD signs and a lower TC1 of ~45 °C. Unexpectedly, clockwise (CW) and counterclockwise (CCW) stirring of PDBS in n-alkanes at 0, 20, and 40 °C did not result in mirror-image CD spectra. The notable H/D isotope effect allows us to propose that the three-fold symmetric CH3 group, which is representative of three identical HINS systems (I = 3/2 (A) and 1/2 (Ea and Eb)) in a triple-well potential (TWP), works as a unidirectional hindered rotor, supporting several (−)-sign vibrational CD bands: symmetric bending (umbrella) at 1382 cm−1, asymmetric bending at 1455 cm−1, and other vibrational modes.
2. Results
2.1. Protocols for Reproducible Chiroptical Measurements of MPV Effects
To arrive at several protocols for testing for MPV effects, PDBS-H and PDBS-L were examined as homogeneous solutions in several n-alkanes and isooctane. The synthesis and characterization of PDBS–H and –L were reported in Section S2 and Figures S1 and S2 in the Supplementary Materials. PDBS-H has a higher number-average molecular weight (Mn) and weight-average molecular weight (Mw), and PDBS-L has lower Mn and Mw, while both have a similar polydispersity index (PDI): PDBS-H; Mn = 6.15 × 104, Mw = 11.6 × 104, PDI = 1.89 and PDBS-L; Mn = 4.55 × 104, Mw = 8.28 × 104, PDI = 1.82.
Furthermore, to validate a generality of MPV effects, poly{bis-(p-t-butylphenyl)silane), poly(n-hexyl-2-ethylbutylsilane), poly(methyl-n-propylsilane), poly(n-pentyl-n-propylsilane), poly(di-n-pentylsilane), poly(di-n-hexylsilane), and permethyldecasilane were examined (Chart S1, Supplementary Materials). The synthesis and characterization of the oligo- and polysilanes were mentioned in Section S2.4 and Figures S3 and S4 (Supplementary Materials). The MPV testing results are discussed in Section 3.8.
A prolonged search was carried out for a suitable system providing reproducible chiroptical measurements, the details of which are described in the experimental Section S2.2 in the Supplementary Materials. The protocol is briefly described below.
To exclude undesirable chiroptical effects induced by hydrodynamic lamellar/vortex/turbulent flow [169,170,171,172,173,174,175], the authors verified whether CW/CCW stirring, which mimics the P-symmetric Coriolis force in the northern and southern hemispheres resulting from the GF, and for comparison, static conditions, affects the resulting CD and UV spectra at 0, 20, and 40 °C. Although stirring direction-dependent CD spectra were obtained, it is still not yet clear why CW and CCW motions at the same stirring speeds did not induce mirror-symmetric CD spectra of PDBS-L and PDBS-H in n-C12H26, n-C13H28, n-C14H28, and n-C16H34. However, no obvious CD spectra of PDBS-L and PDBS-H in isooctane, n-C6H14, n-C8H18, and n-C10H22 under static and CW and CCW stirring conditions were induced. These unexpected results led to our adoption of static conditions to measure all the CD/UV spectra of the sample solutions and solvents at given temperatures. The anomaly in the effects of hydrodynamic flow on the CD spectral shapes and their chiroptical signs are described and discussed in Section 2.7 and Section 3.10 in the main text and Sections S3.7 and S3.8 in the Supplementary Materials.
More importantly, prior to the heating and cooling runs of the chiroptical experiments at a given temperature under static conditions, preliminary annealing at 60 °C for at least 15 min under static conditions was carried out to reorganize the n-butyl side chains and Si–Si main chains from their disordered conformations. The details are described in Section S3.1 of the Supplementary Materials.
2.2. Effects of n-Alkane Chain Length and Temperature on CD-UV Characteristics of PDBS-L
To clarify the carbon number dependence of the n-alkanes, the VT-CD/UV spectra of PDBS-L in isotropic dilute solutions of n-C8H18, n-C10H22, n-C12H26, n-C13H28, n-C14H30, n-C16H34, and isooctane were measured under static conditions at 40, 20, and 0 °C for both heating and cooling runs, starting from 60 °C.
The CD and UV spectra of PDBS-L in isooctane and n-C8H18, n-C10H22, n-C12H26, and n-C13H28 at 0, 20, and 40 °C are shown in Figure S5a–c (Supplementary Materials). Cotton CD spectra emerging at ~300 nm in n-C12H26 and n-C13H28 were generated at 0, 20, and 40 °C, and n-C16H34 at 20 °C and 40 °C: (+)-sign at 0 °C, but (−)-sign at 20 °C and 40 °C. Less obvious CD spectra were recorded for the lower viscosity solvents isooctane, n-C8H18, and n-C10H22 at these temperatures.
When solutions of PDBS-L in n-C12H26, n-C13H28, n-C14H30, and n-C16H34 were cooled from 40 °C to 0 °C, the broader UV band at approximately 315 nm abruptly blueshifted to a narrower UV band at 299–302 nm. Such a blueshift has not yet been reported for this polymer. According to previous studies upon cooling of PDBS in n-hexane [152,153,154,155,156], the UV band around λmax 320 nm at 22 °C undergoes an abrupt redshift around −35 °C, revealing a UV band at 355–360 nm at temperatures below −40 °C due to a change in conformation from the 73-helix of the Si main chain (dihedral angle (DH) ~ 150°) to other helices, e.g., 157-helix (~165°) and transoid 94-helix (~170°) [152,153,154,155,156,157,158,159,160].
The gabs values of the bands around 300 nm at 0, 20, and 40 °C as a function of the n-alkane carbon number are plotted in Figure S5d (Supplementary Materials): gabs = +6 × 10−4 in n-C12H26 at 0 °C was rather weak but fully recognizable. Importantly, the CD band at 299–302 nm emerges only when the corresponding UV band at 299–302 nm is the shorter tail of the 315 nm UV band, largely depending on the carbon number of n-alkanes and temperature. The sign of the CD band inverted between 0 °C and 20/40 °C, indicating the occurrence of a helix–helix transition. From the potential energy surfaces (PESs) of di-n-butyl 14-mer [152], diethyl-silane 4-mer [166], and diethylsilane 13-mer (discussed in Section 3.1), the 300 nm UV/CD band presumably derives from the DH 140–145° (and 220–225°) of the Si main chain as one of the local minima. These preliminary results encouraged a detailed investigation of the MPV effects of PDBS-H.
2.3. n-Alkane Carbon Number Dependence of CD-UV Characteristics of PDBS-H
The CD and UV spectra of PDBS-H in n-C12H26 and n-C13H28 over several temperatures are shown in Figure 1. For clarity, the corresponding raw CD and UV spectra of n-C12H26 are shown in Figure S6a–d, Supplementary Materials. The representative weaker CD and UV spectra of n-C11H24 and n-C14H30 are shown in Figure S7 (Supplementary Materials).
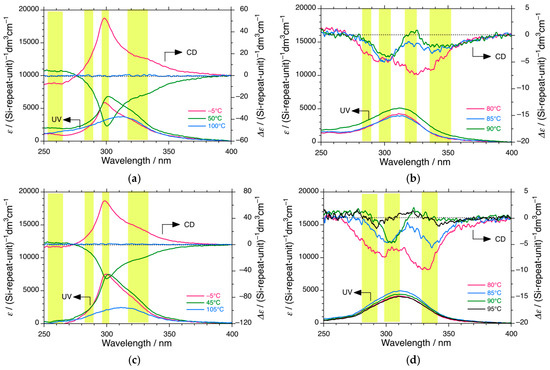
Figure 1.
Changes in the CD and UV spectra of PDBS-H in (a) n-C12H26 at −5 °C (red), 50 °C (green), and 100 °C (blue), (b) n-C12H26 at 80 °C (red), 85 °C (blue), and 90 °C (green), (c) n-C13H26 at −5 °C (red), 45 °C (green), and 105 °C (blue), and (d) n-C13H26 at 80 °C (red), 85 °C (blue), 90 °C (green), and 95 °C (black). Conditions: [Conc]0 = 1.0 × 10−5 M per Si-repeating unit, corresponding to [Polymer]0 = 5.2 × 10−8 M as the polymer chain. The path length is 1.0 cm under static conditions. The dashed lines in (a–d) indicate baselines of CD spectra at the right side of the ordinate. The yellow areas in (a–d) suggest chiroptical generation, inversion, and disappearance of the handed helices at ~260 nm, ~285 nm, ~300 nm, ~325 nm, ~335, and ~345 nm.
Clearly, PDBS-H in n-C12H26 reveals a (+)-sign 300 nm CD spectrum at the corresponding 300 nm UV band at −5 °C, and conversely, a (−)-sign 300 nm CD spectrum at the corresponding 300 nm UV band at 50 °C. The (+)/(−) 300 nm CD effects completely disappeared at 105 °C, coincident with a marked broadening of the UV band and bathochromic shift to 315 nm. Similarly, PDBS-H in n-C13H28 shows a (+)-300 nm CD band with coincident 300 nm UV absorption at −5 °C but a (−)-300 nm CD band and 300 nm UV absorption at 45 °C (Figure 1a,c).
The gabs value of PDBS-H reaches +1.3 × 10−2 in n-C12H26 at 0 °C and +0.9 × 10−2 in n-C13H28 at −5 °C but inverts to −0.8 × 10−2 in n-C12H26 at 50 °C and –0.7 × 10−2 in n-C13H28 at 45 °C. The 300 nm CD band with (+) and (−)-signs disappeared at 105 °C, coincident with a marked broadening of the UV band and bathochromic shift to 315 nm. PDBS adopts equal fractions of RH and LH 73-helices at 105 °C, resulting in a CD-silent racemic mixture of helices. PDBS-H in n-C12H26 and n-C13H28 at −5 °C additionally has three broad CD bands: (+)-CD at ~325 nm, (−)-CD at ~260 nm, and less obvious (+)-CD in the tail of the 300 nm CD at ~285 nm. However, the CD signals of the three additional bands were inverted at 50 °C.
When PDBS-H is in n-C12H26 and n-C13H28 at elevated temperatures in the range of 80–95 °C, three or four additional (−)-CD bands at ~285, ~305, ~320, and ~335 nm are commonly observed (Figure 1b,d), indicating the generation of three or four intermediate helices in hot solutions. The magnitudes of the 300 nm CD spectra in n-C11H24 and n-C14H30 were much weaker (Figure S7, Supplementary Materials). The 300 nm CD signals in n-C11H24 emerge below 40 °C as a shoulder of the broader main UV band at 315 nm due to the 73-helix.
The gabs values at the 300 nm CD bands of PDBS-H in n-C11H24, n-C12H26, n-C13H28, and n-C14H30 as a function of temperature are plotted in Figure 2. The temperature dependence of the gabs curves reveals marked cooperativity which does not obey the Arrhenius law of thermal activation. As shown in Figure 2a,b, the (−)-CD 300 nm-CD bands in n-C12H26 and n-C13H28 were evident below 100–105 °C, diminished at ~28 °C, and inverted to (+)-sign gabs below ~28 °C. The first critical temperature, TC1 (100–105 °C), relates to the second-order phase transition from mirror-symmetric 73-helices to the 300 nm CD helix with handedness. The second critical temperature, TC2 (~28 °C) relates to the second-order helix–helix transition of the 300 nm CD helix. From the temperature-independent gabs values between −10 °C and TC2 and between TC2 and ~50 °C, the transition characteristics result from quantum tunneling between the RH and LH helices responsible for the 300 nm CD/UV band. The 300 nm CD/UV band at TC2 indicates a superposition of the RH/LH helices with 50/50 populations. Similar quantum tunneling helix–helix transitions were reported for rigid rodlike polysilanes bearing (S)-3-methylpentyl and (R)-3,7-dimethyl-octyl co-pendants [21,22,23,24,167,168].
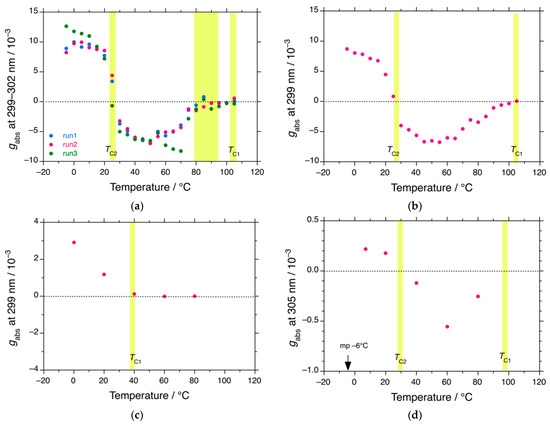
Figure 2.
Changes in the gabs values at 299–305 nm of PDBS-H in (a) n-C12H26 (runs 1,2, and 3), (b) n-C13H28, (c) n-C11H24, and (d) n-C14H30 as a function of temperature. Conditions: [Conc]0 = 1.0 × 10−5 M per Si-repeating unit. The path length is 1.0 cm under static conditions. The yellow areas in (a–d) indicate the second-order helix-helix transitions at TC1 and TC2. The dashed lines in (a–d) are a baseline of gabs at the left side of the ordinate.
As shown in Figure 2c, the TC1 value of PDBS-H in n-C11H24 decreased to 40 °C, and the TC2 value could not be observed. As shown in Figure 2d, although the TC1 and TC2 values in n-C14H30 are nearly identical to those in n-C12H26 and n-C13H28, the absolute magnitude of gabs over the entire temperature range is weaker by an order of magnitude. Thus, for PDBS-H, the values of gabs, TC1, and TC2, associated with the emergence and disappearance of the 300 nm CD and UV bands, are very susceptible to the temperature and carbon number of the n-alkane solvent.
Interestingly, less obvious alterations in the physicochemical properties of n-C12H26 are evident as a jump in specific volume (cm3·g−1, inverse of density) around 25 °C from an expected straight line of specific volume–temperature relationship (Figure S8 in Supplementary Materials) [176] and as a step-like increase in polarizability (dipole moment) of the CH3 group at 1 THz (33 cm−1, 4 × 10−3 eV) above 30 °C by VT-terahertz (THz) spectroscopy [177]. The occurrence of phase transitions due to change in the free-volume of n-C12H26 is weakly seen at ~30 °C, ~35 °C, and above 60 °C by the VT ortho-positronium (o-Ps) experiment [178]. These subtle transitions are reflected in TC2 (24–30 °C) of PDBS-H in n-C12H26, n-C13H28, n-C14H30, and n-C12D26, as discussed in Section 2.5.
2.4. Noticeable H/D Isotope Effects in n-Dodecane
The MPV theory (Scenario C) relies on the BCS theory of superconductivity. To solve such fundamental problems, it is important to test the substances in condensed phases rather than just as isolated collision-free species, as Philip Anderson discussed in a 1972 essay titled “More is different: Broken symmetry and the nature of the hierarchical structure of science” [179].
According to the BCS theory, a Cooper pair (a singlet boson, ↑↓) is formed by an attractive force between two repulsive fermions, e−(↑) and e−(↓), by indirect interactions between electrons and phonons (lattice vibrations) [180,181]. In an analogy of why a hydrogen molecule is spontaneously produced by two hydrogen atoms, roughly speaking, the Cooper pair constitutes a very weak chemical bond to bind two unpaired e−(↑) and e−(↓), due to the Pauli exclusion principle, and dissociates at Tc. The Debye frequency (θD) connecting θD ∝ Tc is chosen from the highest frequency of the phonon vibrations. Historically, from clear experimental evidence, the product m1/2·Tc is a constant for isotope effects of 198Hg and 202Hg and other metals (e.g., Sn, Pb, and Tl). θD is proportional to m−1/2, while m is the mass of metal isotopes [182,183,184]. In chemistry, θD is chosen from the reduced mass (μm) between 12C, 1H, and 2H, in the general form μm = (m1·m2)/(m1 + m2). In the present study, the highest θD values were obtained from the specific optically active vibrations of liquid n-C12H26 and n-C12D26, which involve stretching (symmetric and asymmetric), scissoring and rocking, wagging, twisting, and torsion modes of the methyl and methylene groups. In particular, chiral asymmetric stretching, rocking, and twisting phonons of n-alkanes are crucial for inducing handed helicity in PDBS. It is thus anticipated that the smaller θD values of n-C12D26 make TC1 and TC2 significantly lower than those in n-C12H26.
The CD and UV spectra of PDBS-H in n-C12D26 were measured as a function of temperature. Representative CD and UV spectra are shown in Figure 3a, although UV signals shorter than 280 nm were not clearly subtracted. A (−)-CD band emerged at −5 °C, whereas a (+)-CD band emerged at 40 °C; these CD bands completely disappeared at 55 °C. The gabs value of the 300 nm CD band in n-C12D26 as a function of temperature is plotted in Figure 3b. The absolute gabs values of PDBS-H in n-C12D26 were clearly an order of magnitude weaker compared with those in n-C12H26. TC1 decreased to ~42 °C, whereas TC2 at ~25 °C remained nearly unchanged. Interestingly, the signs of the CD signals in n-C12D26 below TC1 and TC2 are opposite to those in n-C12H26. This notable H/D isotope effect of n-dodecane suggests that the helix–helix transition characteristics at TC2 originate from PDBS-H itself since the difference in PES between n-C12H26 and n-C12D26 is almost negligible due to the bond length of C–D being only ~0.005 Å shorter than that of C–H [185].
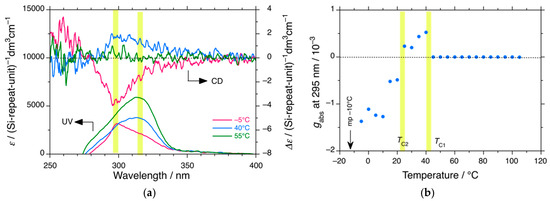
Figure 3.
(a) Changes in the CD and UV spectra of PDBS-H in n-C12D26 at −5 °C (red), 40 °C (blue), and 55 °C (green) and (b) the gabs values at 295 nm of the 300 nm CD band as a function of temperature. Conditions: [Conc]0 = 2.0 × 10−4 M−1 per Si-repeating unit. Path length is 0.2 cm under static conditions. The dashed lines in (a) and (b) are baselines of CD spectra at the right side of the ordinate and gabs at the left side of the ordinate, respectively. The yellow areas in (a) indicate chiroptical generation of the handed helices at ~295 nm and at ~315 nm. The yellow areas in (b) indicate two types of second-order helix-helix transitions at TC1 and TC2.
2.5. Effects of Carbon Number and H/D Isotopes in n-Alkanes
To summarize the VT-CD/UV spectral characteristics described above, the gabs values at the 300 nm CD band of PDBS-H at 0 and 20 °C as a function of the carbon number in n-alkanes are plotted in Figure 4a. The values of TC1 and TC2 as functions of the carbon number in n-alkanes are plotted in Figure 4b. A small difference in Mn and Mw between PDBS-H and PDBS-L resulted in a large difference in the MPV effects (Figure 4a and Figure S5, Supplementary Materials). According to Scenario A, there exist certain thresholds in DPn and DPw to cooperatively and nonlinearly elucidate the hidden MPV effects: PDBS-H (DPn = 194, DPw = 367) and PDBS-L (DPn = 143, DPw = 260).
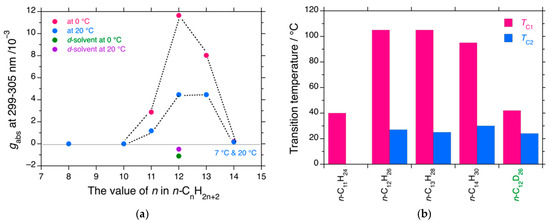
Figure 4.
(a) Changes in the gabs values at 299–305 nm at 0 °C and 20 °C as a function of chain length of n-alkanes, while for n-C14H30, gabs are taken at 7 °C and 20 °C. (b) Changes in TC1 and TC2 vs. chain length of n-alkanes. The thin solid line in (a) is a baseline of gabs at the left side of the ordinate.
Among the five medium-length n-alkane solvents, n-C12H26 exhibited the greatest MPV effects, accompanied by dual second-order phase transitions at TC1 and TC2 (Figure 4a). Similarly, n-C13H28 exhibited greater MPV effects, but the absolute gabs values were somewhat weaker than those of n-C12H26. However, no odd–even effect of the carbon number in n-alkanes is observed. The absolute gabs value of n-C12D26 was an order of magnitude lower than those of n-C12H26 and n-C13H28. As summarized in Figure 4b, n-C12H26, n-C13H28, and n-C14H28 had nearly identical TC1 values of 100–105 °C, whereas n-C11H24 had a markedly lower TC1 of 40 °C. All four of n-C12H26, n-C13H28, n-C14H28, and n-C12D26 showed nearly identical TC2 values of 25–28 °C, although TC2 in the shorter n-C11H24 should be observed below −10 °C.
2.6. Temperature Dependent CPL and CD Characteristics of PDBS-H in n-C12H26
The normalized CPL/PL and CD/UV spectra of PDBS-H in n-C12H26 at −5, 25, and 60 °C are compared in Figure 5a–d. For clarity, the normalized CD/UV and CPL/PL spectra at −5 °C as functions of photon energy (in eV) and wavenumbers (in cm−1) are shown in Figure 5e,f.
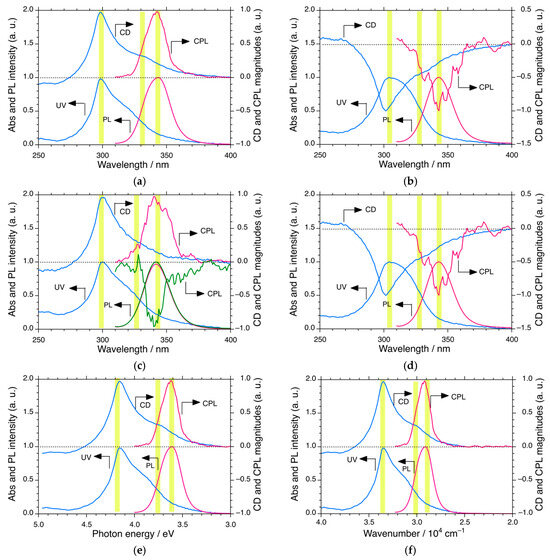
Figure 5.
Normalized CD/UV (blue lines) and CPL/PL (red lines and red/green lines) spectra excited at 290 nm of PDBS-H in n-C12H26 as a function of wavelength at (a) −5 °C, (b) 60 °C, and (c) 25 °C. (d) CPL/PL spectra excited at 290 nm as a function of the wavelength (nm) at 25 °C. Normalized CD/UV (blue lines) and CPL/PL (red lines) spectra of PDBS-H in n-C12H26 at −5 °C as functions of (e) photon energy in eV and (f) wavenumbers in cm−1. Data are taken from (a). The dashed lines in (a–f) are baselines of normalized CD and CPL magnitudes at the right side of the ordinate. The yellow areas in (a–d) suggest chiroptical generation and inversion of the handed helices at ~298 nm and ~328 nm in the ground state and the handed helix at ~ 340 nm in the photoexcited state.
At −5 °C below TC2, the (+)-sign CPL spectrum affords glum (= ΔI/I) = +1.9 × 10−2 at ~340 nm, while the corresponding CD spectrum shows gabs = +1.3 × 10−2 at 300 nm with an apparent Stokes’ shift of 4033 cm−1 (0.50 eV). Similarly, at 60 °C, between TC2 and TC1, the (−)-sign CPL spectrum affords glum = −0.7 × 10−2 at ~340 nm, whereas the corresponding CD spectrum has gabs = –0.5 × 10−2 at 300 nm with a similar Stokes shift at −5 °C. Interestingly, the CPL spectra at 25 °C near TC2 greatly fluctuate between glum = +2.0 × 10−2 and −1.0 × 10−2, as shown in Figure 5c,d.
The gabs values as a function of temperature and the glum value at the three temperatures are plotted in Figure 6. The spectra of PDBS at TC2 show no bands due to the superposition of LH and RH helicities. The histograms of eight and four independent CPL measurements at 25 and 60 °C, respectively, are shown in Figure S9 (Supplementary Materials). The eight glum values at 25 °C are likely to obey a stochastic resonance rather than a sinusoidal function with time, implying that CPL in the S1 state is hypersensitive to selection between RH and LH helicity due to the PVED-driven force to overcome fluctuations at 25 °C, whereas the four glum values at 60 °C are insensitive to fluctuations over time. In contrast, the results for the temperature region 25 °C ~ TC2 are indicative of bifurcation for selection between the LH and RH helicities in the S1 state of PDBS. The LH- or RH-helicity in the S1 state was not determined prior to the CPL measurement because of quantum entanglement between the LH- and RH-helicities.
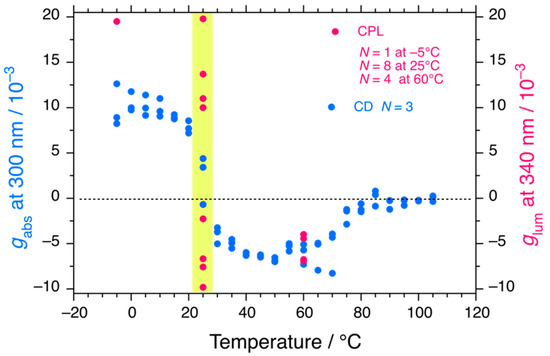
Figure 6.
Changes in the gabs values at the 300 nm CD/UV bands of PDBS-H in n-C12H26 (blue circles, N = 3 (runs 1, 2, and 3), data taken from Figure 2a) as a function of temperature and the corresponding glum values at 340 nm (red circles) at −5 °C, 25 °C, and 60 °C upon excitation at 290 nm. The yellow area indicates the second-order helix-helix transition at TC2 in the ground state of PDBS-H.
2.7. Non-Mirror-Symmetric CD Spectra of PDBS Under CW and CCW Stirring Directions
CD/UV spectra were recorded at 0 °C, 20 °C, and 40 °C for PDBS-L in n-C12H26, n-C13H28, n-C14H30, and n-C16H34 under static conditions and CW and CCW stirring at 100, 400, 600, and 800 rpm using a PTFE-coated cylindrical magnetic stir bar (2 mm in diameter × 7 mm in length) in a rectangular cuvette (10 mm path length and 35 mm in height) and the changes and differences are shown in Figure 7a–c and Figure S10a–h, Supplementary Materials, respectively. The changes in the CD/UV spectra of PDBS-H in n-C12H26 at 0 °C, 20 °C, and 40 °C under static and CW and CCW conditions at 1200 rpm are displayed in Figure S11 (Supplementary Materials).
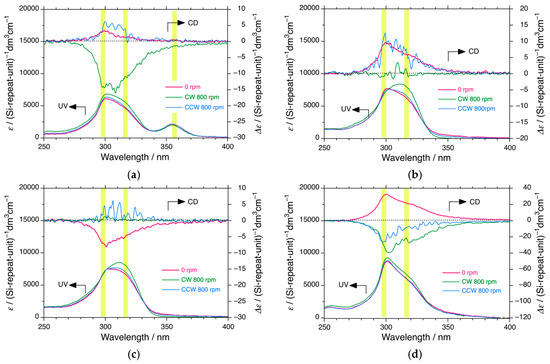
Figure 7.
Changes in CD/UV spectra of PDBS-L in n-C12H26 at (a) 0 °C, (b) 20 °C, and (c) 40 °C and (d) PDBS-H in n-C12H26 at 0 °C under static (red), CW (green), and CCW (blue) stirring at 800 rpm. In this experiment, a PTFE-coated cylindrical magnetic stir bar (2 mm diameter × 7 mm length) was placed in a rectangular cuvette (10 mm path length and 35 mm height). The dashed lines in (a–d) are baselines of CD spectra at the right side of the ordinate. The yellow areas (a–d) suggest chiroptical generation, inversion, and disappearance of the handed helices at ~ 295 nm and ~ 318 nm.
Hydrodynamic flow in CW and CCW directions is recognized to induce mirror-image CD and CPL spectra from achiral chromophores/luminophores during aggregation by the removal of solvent and by gelation upon cooling achiral chromophores [169,170,171,172,173,174,175]. The chiroptical signs and product chirality are determined by the CW and CCW directions. Actually, in 1989, Goldanskii et al. pointed out that rotational hydrodynamic flow causes local P-symmetry breaking as a PC-EMF event [3].
Evidently, the non-mirror-image CD spectra under the CW and CCW flows of PDBS-L and PDBS-H in n-C12H26, n-C13H28, n-C14H30, and n-C16H34 below and above TC2 and at ~TC2 indicate the occurrence of a mechanism other than local P-symmetry breaking. Under gentle stirring at 100, 400, and 600 rpm at 20 °C, PDBS-L in n-alkanes experienced an un-identified PV-related force (Figure S10a,b, Supplementary Materials). The hydrodynamic CW and CCW flow under the GF is no longer the local P-symmetry breaking force and becomes a global PV force, as discussed in Section 3.9 and Section 3.10.
3. Discussion
3.1. Potential Energy Surfaces at the Ground and Photoexcited States of PDBS
A primary question is the helical structure of PDBS in n-alkane solvents. The new helix responsible for the 300 nm CD and UV bands in a family of poly(di-n-alkylsilane)s and other poly(diorganosilane)s is yet not reported experimentally or theoretically [152,153,154,155,156,157,158,159,160,161,162,163]. Potential energy surfaces (PESs) at the ground and photoexcited states of Et-(Et2Si)13-Et (DES13) as a model of PDBS (Chart S2, Supplementary Materials) were calculated by semi-empirical PM3MM, DFT (B3LYP/6-31Gd), and TD-DFT, including three singlet and three triplet states (B3LYP/6-31Gd) using Gaussian 09 [186]. It is noted that the di-n-butylsilane 13-mer and its shorter 6-mer did not converge to optimized structures at the PM3MM level. The two PESs (PM3MM and DFT) normalized by 10 DH (dihedral angle) sets of the Si main chain as a function of DH are shown in Figure 8a,b. The photoexcitation energy (in nm) and oscillator strength (f) at the S1 state as a function of DH are shown in Figure 8c and Figure 8d, respectively. The magnitudes of UV (ε) and CD (Δε) obtained with a full-width-at-half-maximum (fwhm) of 0.333 eV, and their gabs values as a function of DH are depicted in Figure 8e and Figure 8f, respectively.
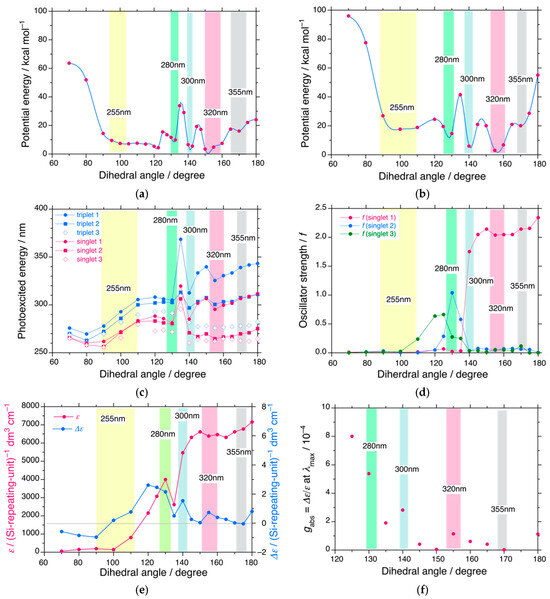
Figure 8.
(a) Potential energy (red spline curve) of Et-(Et2Si)13-Et vs. the dihedral angle (DH) of Si main chain obtained with PM3MM. (b) Potential energy (red circles with spline blue curve) of Et-(Et2Si)13-Et vs. the Si dihedral angle obtained using DFT (B3LYP with 6-31Gd basis set) based on the optimized models by PM3MM. (c) Photoexcitation energies (nm) of three triplets, T1 (blue circles), T2 (blue squares), T3 (blue cross), and three singlets, S1 (red circles), S2 (red squares), S3 (red crosses) vs. the Si dihedral angle obtained with TD-DFT (B3LYP with 6-31Gd basis set). (d) Oscillator strengths, f, at S1 (red), S2 (blue), and S3 (green) states vs. Si dihedral angle. (e) Magnitudes in UV, ε (red filled circles) and CD, Δε (blue filled circles) at λmax of Et-(Et2Si)13-Et obtained with fwhm 0.333 eV vs. Si dihedral angle. (f) gabs value at λmax vs. Si dihedral angle, with data taken from Figure 8e. The energies in (a) and (b) are normalized by 10 Si dihedral sets, whereas, in (e), the ε and Δε values are normalized by 13 Si repeating units. The thin solid line in (e) is a baseline of CD magnitude at the right side of the ordinate. The yellow, green, blue, red, and gray areas in (a–f), respectively, indicate the helices that afford the corresponding UV–CD spectra at 255 nm, 280 nm, 300 nm, 320 nm, and 355 nm.
As shown in Figure 8a,b, DES13 possesses five minima at 170° (gray), 155° (red), 140° (blue), 130° (green), and 100° (yellow) in the Si main chain. The helix at 155° is the global minimum. The first metastable helix at 140° was connected to the deviant (D±) helix of Et-(Et2Si)4-Et [166]. The 140°-helix is ascribed to the 300 nm CD/UV bands discussed in this work, presumably the 83-helix, while other local minima at 130° are likely to be 114-helices with λmax 280 nm. The 170°- and 155°-helices correspond to the 157-helix (λmax 355 nm) and 73-helix λmax 315–320 nm), respectively [152,153,154,155,156]. The CD/UV bands due to the 130°-helix can be weakly observed as the tail of the 300 nm CD/UV bands (Figure 1). The 100°-helix is experimentally observable as weak (−)-CD and broad UV bands around λmax 255–265 nm compared to the 300 nm (+)-CD band (Figure 1) because the chiroptical signs in the CD bands between 70° < DH < 100° and 100° < DH < 170° are theoretically opposite (Figure 8e).
The helix–helix transition capability between the four steep wells at ±140° and ±155°, associated with larger EB values, plays a key role in observable MPV effects. The EB between 140° and 150° was ~20 kcal mol−1 by PM3MM and ~25 kcal mol−1 by DFT. Similarly, the EB between 150° and 210° was ~25 kcal mol−1 by PM3MM and ~55 kcal mol−1 by DFT. Chiroptical generation and inversion between RH and LH helices from the most stable +155° helix to the other +140°, −140°, and −155° helices are unlikely to occur easily because of the large EB values.
The photoexcited energies (expressed in nm) at the S1, S2, and S3 states (marked in red) and T1, T2, and T3 states (marked in blue) significantly change as a function of DH due to the decrease in σ-conjugation of the Si wire (Figure 8c). The photoexcited energies at S1, S2, and S3 tended to progressively blueshift when the DH changed from 180° to 80°, except for 145–150° and 135° located at barriers between 140° and 155° and between 130° and 140°. The UV/CD bands in the S2 and S3 states can be observed experimentally at wavelengths shorter than 280 nm and partly overlap with the UV/CD bands of the 100°-helix, whereas the UV/CD bands in the S1 state appeared at wavelengths longer than 280 nm. The DH dependence of the photoexcited energies in the T1, T2, and T3 states was nearly identical to those in the S1, S2, and S3 states (Figure 8c). Their UV absorptions were experimentally less obvious because their f values (oscillator strengths) were theoretically zero.
It is noteworthy that when DH changes from 180° to 155°, the transition energy curve at the S1 state approaches the curve at the T2 state, and the curve at 140° is close to that of the T3 state (Figure 8c). These situations led to mixing between the S1, T2, and T3 states, resulting in a marked decrease in the e value, accompanied by an increase in De at 140°. Additionally, from EPV ∝ ΔEST (Scenario E), a smaller S0–T1 transition energy at three energy minima, 130°, 140°, and 155°, in the range of 3.81 eV (325 nm) and 4.13 eV (300 nm) effectively contributes to amplify EPV in the S0 state because the T1 is partly mixed with the S1 and T2 states.
The f values in the S1, S2, and S3 states were altered by the DH (Figure 8d). When the DH decreases from 170° to 70°, f in the S1 state progressively decreases from ~2.2 at 170° to ~0.0 at 130°. Conversely, f in the S2 state increases from ~0.1 at 170° to 0.7–1.0 at 130–135°. Likewise, f in the S3 state increases from ~0.1 at 170° to 0.7 at 120–125°. Consequently, when the DH changed from 180° to 125°, Δε increased; conversely, ε decreased (Figure 8e), leading to an increase in gabs (= Δε/ε) (Figure 8e,f). Focusing on the three helices with DHs of 155°, 140°, and 130°, the UV/CD bands at 280 nm and 320 nm mainly arose from the S1 state, while the UV/CD bands at 300 nm were mainly from the S2 state (Figure 8d). The gabs at 300 nm were approximately three times larger than those at 320 nm. This idea partly accounts for the reason why |gabs| at 300 nm reaches ~10−2 compared to |gabs| at 320 nm of ~10−4 [22,23,159,160].
A considerably large EB ranging from 15 to 50 kcal mol−1 is crucial to largely suppress ΔE± in multiple-well systems [113,187,188,189], leading to the emergence of observable MPV effects. These EB values are intermediate in racemization processes between temperature-independent quantum tunneling and classical temperature-dependent Arrhenius law mechanisms [189]. From ΔE± = 1/(2√π)·(hν·EB)1/2·exp(–EB/hν), where h is the Planck constant, and ν is the frequency of vibration in a single well, tunnel-driven dynamic racemization is expressed as Trac = h/ΔE± [10,113,187,189]. For comparison, in the case of the quantum tunneling inversion of ammonia in a DWP, H3N: ⇄ :NH3, an EB of 5 kcal mol−1 at ν = 950 cm−1 leads to a very fast Trac ~ 10−11 s, while the tunneling inversion of phosphine in a DWP, H3P: ⇄ :PH3, an EB of 37 kcal mol−1 at ν = 991 cm−1 results in a very slow Trac ~ 107 s [10,113,189]. By placing two adjustable parameters in the above ΔE± and Trac equations, the Trac values (in sec) as a function of EB (kcal mol−1) in the three cases of tunneling, Arrhenius law mechanisms, and their intermediate, are illustrated in Figure S12 (Supplementary Materials) [113,189]. The estimated EB (PM3MM) of DES13 with two EB ranges of ~20 kcal mol−1 and ~25 kcal mol−1 indicate an intermediate region, except for ~55 kcal mol−1 (DFT) around DH 180° (Figure 8b) [189].
Qualitatively, a larger EB in a DWP makes ΔE± exponentially smaller, thereby satisfying the ΔE± ~ EPV condition, whereas a tiny EPV is nearly unchanged around 10−10 eV. Experimentally, by increasing EB, it is, in principle, possible to achieve ΔE± ~ 10−10 eV by (i) increasing the viscosity of the solvents, (ii) increasing the steric hindrance between the side chains of chromophores, and (iii) cooling to a lower temperature. The cooperativity in the second-order phase transition originates from a continuous decrease from disordered to ordered states at low temperatures, i.e., superconductivity and BEC of HINS isotopes such as 87Rb, 23Na, 7Li, and 1H [190].
3.2. Potential Energy Surfaces of H-(H2Si)13-H, Me-(Me2Si)13-Me, and Et-(Et2Ge)13-Et
The other PESs of H-(SiH2)13-H, Me-(SiMe2)13-Me, and Et-(GeEt2)13-Et (Chart S2 (Supplementary Materials)) obtained using PM3MM and DFT (B3LYP-631Gd) are compared in Figure S13 (Supplementary Materials). The global and local minima of H-(SiH2)13-H exist at 180° (trans-planar (TP)) and 60–70° (gauche helical (GH)), respectively, and the EB values between TP and GH are as small as 0.6 kcal mol−1 (PM3MM) and 0.8 kcal mol−1 (DFT), respectively (Figure S13a,b, Supplementary Materials). However, the PES of Me-(SiMe2)13-Me suggests that the global and local minima are located at 180° (TP) and 90° (ortho helical (OH)), while the EB values between the TP and OH conformers are 12 kcal mol−1 (PM3MM) and 25 kcal mol−1 (DFT), respectively (Figure S13c,d, Supplementary Materials). Similarly, the shallow energy levels at the two minima with lower EB (indicated by yellow and gray) suggest a high susceptibility to fluctuations.
Similarly, the PES in hypothetical Et-(GeEt2)13-Et has two minima at ~155° and ~90°. Because of the similar shallow energy levels, the preference in the LH and RH helicity is rapidly lost owing to thermal fluctuations, as indicated by the blue, pink, and gray bars (Figure S13e,f, Supplementary Materials). Significant differences in local and global minima and their EB values between Et-(SiEt2)13-Et and Et-(GeEt2)13-Et are largely ascribed to a subtle difference in bond lengths between Si–Si (2.10 Å) and Ge–Ge (2.22 Å) [185]: a shorter bond length results in a stronger steric repulsive force (Pauli exclusion principle) between bulkier pendant groups.
3.3. Potential Energy Surface with PVED of n-Alkanes
In principle, GH in n-alkanes can result in a metastable rotamer. Kikuchi et al. calculated the EPV in a series of hypothetical GH n-alkanes [191,192]. The RH-GH of n-C11H24 is more stable by −5 × 10−18 kcal mol−1. The EPV of RH-GH linearly increases in proportion to the carbon number of n-alkanes (Scenario A) [191,192]. From studies of Raman, FT-IR, and theoretical simulations, the difference in energy between trans (t)- and gauche (g)-bonds per C–C bond, ΔEtg, is 0.65–0.90 kcal mol−1 in a series of n-alkanes from n-C4H10 to n-C16H34 [193,194,195,196,197,198]. DFT (B3LYP/6-311g**) calculations indicated that the EB from t- to g-bonds is commonly ~3 kcal mol−1 in a series of n-C4H10 to n-C10H22 [199,200]. In a series of carbon numbers from n-C5H12 to n-C14H30, liquid n-alkanes contain in total 34–41% as polar g-bonds, including one g-, two g-, and three g-sets, resulting in a weak dipole moment of 0.09 Debye [177,199,200,201,202,203,204,205,206,207,208,209]. Although n-C4H10 adopts ~16% g-bond, n-C5H12 and n-C11H24 contain ~25% g-bonds, and n-C16H34 is ~35% g-bonds [195,201,202,203,204,205,206]. According to a recent MM3 calculation of n-C12H26, the most dominant TP-conformer among the possible 7838 conformers is only ~15%, while five non-TP conformers, including one and two g-bonds, are ~15%, and other non-TP conformers are 70% [198]. On the other hand, Monte Carlo simulation indicates that TP-conformer content ranges from ~75% to ~85% for carbon numbers 6 to 12 in n-alkanes [197].
To confirm these results, we calculated two PESs of n-C12H26 as a function of DH 40–180° obtained using PM3MM and DFT (B3LYP/6-31Gd) (Figure S13g,h, Supplementary Materials). In both calculations, the PESs suggested a global minimum at 180° (TP) and a local minimum at 80° (OH), with an EB of ~5 kcal mol−1. The UV/CD spectra (fwhm 0.20 eV, TD-DFT) for several rotamers of n-C12H26 are summarized in Figure S14 (Supplementary Materials). Comparisons of the relative energy, dipole moments (μ, in Debye), and CD sign at λext for 10 rotamers, including g+ ~ 60–80° (9 DH sets of C–C bonds), are listed in Table S1, Supplementary Materials. These data were sorted by the relative energy against TP [(t)9], as shown in Figure S14 (Supplementary Materials).
The first metastable rotamer is the g+ rotamer [(g+)1-(t)8], which is unstable by 3.24 kcal mol−1 relative to [(t)9]. The value semi-quantitatively agrees well with the previous calculations [193,194,195,196,197,198,199,200]. The second metastable rotamers are a two g+ rotamer, [(g+)2-(t)7], and a one g+ rotamer, [(t)1-(g+)-(t)7], which are unstable by 4.23–4.45 kcal mol−1. The third metastable rotamer is a one g+ rotamer, [(t)2-(g+)-(t)6], which is unstable by 5.74 kcal mol−1. Interestingly, [(g+)-(t)9] showed (+)-sign CD; conversely, [(g+)2-(t)7] and [(t)-(g+)-(t)7] showed (−)-sign CD. Although the μ-value of TP is nearly zero, the other five rotamers, [(g+)9], [(g+)1-(t)8], [(g+)2-(t)7], [(t)2-(g+)-(t)6], and [(t)4-(g+)-(t)4], show fairly large μ values ranging from 0.049 to 0.087 Debye. The other four g+-containing rotamers, [(t)1-(g+)-(t)7], [(g+)3-(t)6], [(g+)4-(t)5 ], and [(t)3-(g+)-(t)5], had smaller μ values (0.015 and 0.029 Debye). Liquid n-C12H26 and other n-alkanes are thus likely to contain a considerable amount of polar one- and two-g+ and/or g− bonds and kinks (g+-t-g− and g−-(t)n-g+) [201,202,203,204,205,206,207,208,209]. The [(g+)1-(t)8], well-known as end-g+, is easily formed compared to interior g+-bonds, such as [(t)1-(g+)-(t)7], [(t)2-(g+)-(t)6], and [(t)4-(g+)-(t)4]. The fractions of the g-bonds increase as the temperature increases [201,202,203,204,205,206].
3.4. Electroweak Charges at Isotopes of PDBS and n-Alkanes
The electroweak charge, QW, is an important parameter in the Z0-force origin MPV theories [5,6,18,19,70,73,74,75,76,77,83]. QW is regarded as a naturally occurring additional charge on each spherical atom to afford the north and south poles induced by the handed WNC.
HPV = − Γ/2 ∑ ∑ QW{pi·σi, Δ3(ri − ra)}+,
Γ = GF/(2√2·me·c) = 5.731 × 10−17 a.u. equivalent to 1.559 × 10−15 eV.
QW = Na − (1 − 4·sin2θw)·Za
Herein, the HPV (PV-potential) is reduced by adding HPV(e−-e−), HPV(e−-p), and HPV(e−-n) terms when e−–e−, e−–p, and e−–n interactions between e−, n, and p are considered. Additionally, { }+ denotes an anticommutator. Γ combines the Fermi weak coupling constant GF with the electron mass me and speed of light c. Each electron i has a charge density at each atomic nucleus, which is represented by a three-dimensional Dirac delta function, Δ3(ri − ra). In addition, pi and σi are the electron momentum and Pauli spin-matrix operators, respectively. Na and Za (=Z, mentioned above), respectively, are numbers of n and p of each atomic nucleus a in a molecule, and θw is the Weinberg mixing angle between W and Z0 bosons.
Using the recent value of sin2θw = 0.223 [210], it can be shown that for 1H, QW = −0.108; for 2H (D), QW = +0.892; for 13C (NA 1.1%), +6.352; for 12C (NA 98.9%), +5.352; for 29Si (NA 4.7%), +13.488; for 28Si (NA 92.2%), +12.488; and for 30Si (NA 3.1%), +15.849, where NA is the natural abundance of stable isotopes. Only the 1H atom has a small (−)-sign QW. In contrast, 2H and other HINS and INS isotopes have a large (+)-QW. A large quantity of solvent organic molecules with multiple (−)-QW 1H atoms surround the PDBS. The opposite sign in the QW between 1H and 2H is related to the opposite CD sign characteristics between n-C12H26 and n-C12D26 and PDBS below TC1 and TC2 (Figure 2a and Figure 3b). In addition, (+)-QW HINS 29Si can contribute to an MPV-causing “sergeant” to cooperatively align in a handed helical geometry of 28Si and 30Si as “soldiers” in the Si main chain, leading to the weaker MPV effect of PDBS observed in n-C12D26 [107].
3.5. CH3 Hindered Rotor—Three Identical Nuclear Spin-1/2 System in a Triple-Well Potential
3.5.1. Ortho- and Para-Water to Account for the MPV-Experiment of L- and D-Oligopeptides
In 2006, Shinitzky et al. investigated the first-order α-helix-coil transition characteristics of an enantiomeric pair of L- and D-glutamic acid 24-mers [100]. They noticed subtle differences in the CD spectra between their random coils in H2O at pH 10.5; however, no such difference was observed in the D2O: H2O (4:1) cosolvent. Isothermal titration calorimetry detected subtle differences in ΔH ~ −0.14 kcal per residue between the L- and D-oligopeptides in H2O but did not show such ΔH in the D2O: H2O 4:1 mix. Based on the fact that H2O consists of two nuclear spin isomers, para (↑↓, I = 0) and ortho (↑↑, I = 1) in 1:3 ratio, ortho-H2O is assumed to solvate the L-oligopeptides preferentially over the D-oligopeptides [100]. The ortho- and para-spins in CH2 moieties are applicable to n-alkanes and the n-butyl pendants of PDBS, although their total I values are perpetually 0 and 1, respectively.
3.5.2. Bi-Directional CH3 Rotor by Tunneling and Non-Arrhenius Law Hopping
Based on the ortho-para spin states of H2O, the nuclear spin states of CH3 termini in n-alkanes and n-butyl pendants were first considered. A naive question is how three identical HINS atomic systems conserve P-symmetry, because even-number nuclear spin states (I = 0,1,2) are impossible. When considering a plausible explanation for the mechanism(s) of the observed MPV effects, the authors were aware of the uniqueness of the CH3 group. Historically, in 1940, Koehler and Dennison were the first to argue theoretically regarding hindered and free rotations of the OH group in methanol using the energy potential V = 1/2·H·(1 − cos3θ) and energy splitting [211]. In the 1960s, Hilt and Hubbard [212] and, independently, Runnels [213] theoretically treated how a three identical nuclear spin-1/2 system relaxes along the three-fold hindered rotation axis. These old questions can nowadays be reduced to a geometrical frustration, i.e., spin frustration and degeneracy of HINS in odd-number rings including triangular lattices in condensed matter physics and topological material science [214,215,216,217,218,219].
From the notable HINS isotope effects to the APV and PV-MAM hypotheses (Scenario F), the present study highlights three-fold symmetric CH3 and CD3 groups as a fundamental issue in soft condensed matter. Thus far, it has been more-or-less established over the last four decades that CH3 and CD3 groups act as hindered rotors in a TWP owing to temperature-dependent quantum tunneling and non-Arrhenius law hopping mechanisms in the framework of PC-EMF [220,221,222,223,224,225,226,227,228,229,230,231,232,233,234,235,236,237,238,239,240,241,242,243,244]. Rotating the symmetry-top CH4, NH4+, and CH3-group in a broad range of molecular crystals [220,221,222,223,224,225,226,227,228,229,230,231,232,233,234,235,236,237,238,239] and non-crystalline polymers [240,241,242,243,244] between 1 K and 390 K are elucidated by many theories and various measurements; i.e., inelastic neutron scattering (IENS), quasielastic neutron scattering (QENS), several 1H-NMR techniques (i.e., spin lattice relaxation (T1), low-magnetic-field, high-field to zero-field cycling, level crossing), 2H-NMR, electron nuclear double resonance (ENDOR), IR and Raman, microwave, viscoelastic relaxation, and photochemical hole burning [220]. The CH3 group possesses a perpetual I = 3/2 (↑↑↑, ↓↓↓, A-state) and I = 1/2 (↑↓↑ and ↑↓↓, E-state). Contrarily, the CD3 group of three identical 2H isotopes generates I = 0,1,3 (A-state) and I = 1,2 (E-state) [235,236,237,238,239]. However, theoretical and experimental investigations involving the nuclear spin-dependent MPV hypothesis have not yet been reported.
In 1991, Clough pointed out that the origins of CH3 and CD3 rotating motions in a TWP remain unanswered questions regarding the four symmetry breakings: geometrical, T-reversal, rotational, and permutational symmetries [227]. These issues can be reduced to the superposition of three identical 1/2-nuclear spin states among three indistinguishable 1H atoms that split into four A-sublevels and two sets of Ea-/Eb-sublevels under a non-zero external magnetic field in NMR. The A- and E-states contradict the Pauli exclusion principle. Zero-field NMR spectroscopy and sophisticated chiroptical spectroscopy can be used to answer these questions [90]. In addition, the CH3 rotating trajectory can be regarded as a set of helices in which the rotation is linked with environmental forces because the rotor acts as a clock and pendulum in the curvature of the space-time world [227]. However, no study has experimentally validated the four-symmetry breakings of CH3 and CD3 rotors.
The CH3 and CD3 hindered rotors can generate several g-bonds in liquid n-alkanes and n-butyl pendants due to the similar EB values in non-deuterated and deuterated polymers [240,241,242,243,244]. Their quantum tunneling and non-Arrhenius law hopping characteristics are significantly different due to the inherent moment of inertia (Irot) and rotational constant (B), B = ℏ2/(2IR) when considered as rigid rotors: for CH3, B = 0.655 meV (Irot = 0.535 × 10−46 kg m−2) and for CD3, B = 0.328 meV (Irot = 1.069 × 10−46 kg m−2) [220,222,238]. In fact, the differences in the B and IR of CD3 result in the marked suppression of tunneling splitting (EA–E) and tunneling frequency by one or two orders of magnitude [220,222,238]. The reduced tunneling frequency of the CD3 rotor causes inefficient intra- and intermolecular chirality transfers.
By considering several graphical explanations for the permutational quantum tunneling of the CH3 rotor in TWP [220,221,222,223,224,225,226,227,240,241,242,243,244], Figure 9a reproduces the hypothetical potential energy E(θ) as a function of CH3 rotation angle (θ); E(θ) = V3/2·{1 − cos(3θ)}, V3 ≃ EB = 25.2 meV (1.1 kcal mol−1) while the V3 is taken from CH3NO2 [221,224,225]. E(θ) exhibited three global minima at θ = ±120° and 0°. The E(θ) at each well (1, 2, 3) splits into A- and Ea-/Eb-states owing to quantum tunneling, whereas Ea and Eb have equal energies owing to degeneracy. The relative stability between A- and Ea/Eb-states alternatively changes with ν = 0, 1, 2 [222]. Representative IENS spectra at cryogenic temperatures revealed two well-resolved A → Ea/Eb and Ea → Eb/Eb → Ea transitions at zero frequency [221,227]. With an increase of temperature, tunneling splitting energy, EA–E (in eV, cm−1, Hz), exponentially decreases, approaching the zero-frequency. When Ea = Eb, a pair of CW and CCW rotations between three potential wells—well 1, well 2, and well 3—occurs equally, leading to a random hopping of bi-directional rotations resulting in the lack of macroscopic level optical activity.
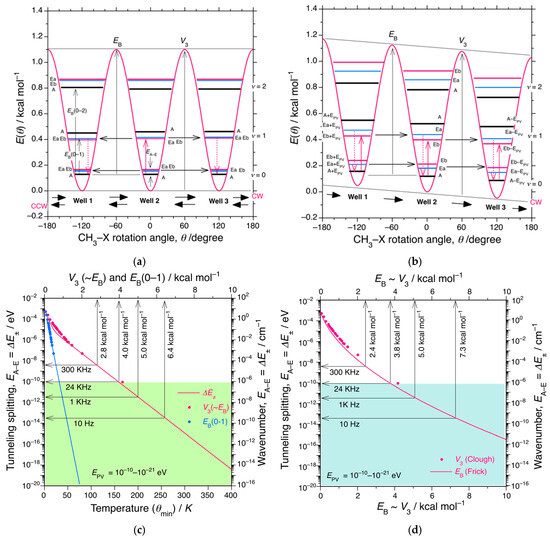
Figure 9.
(a) Symmetrical potential energy curves as functions of CH3 rotor angle (θ). E(θ) = V3/2·{1 − cos(3θ)}, V3 ≃ EB = 25.2 meV (1.1 kcal mol−1). V3 data were obtained from nitromethane (CH3NO2) [221]. (b) Asymmetrical potential energy curve as a function of θ by adding ±EPV to the A, Ea, and Eb levels. When the EPV term is added and subtracted from the Ea and Eb levels, Ea ≠ Eb, resulting in several VCD modes of n-alkanes. (c) A universal correlation curve for CH3 rotation in coherent tunneling, EA–E (= ΔE±) (in eV), and thermally activated incoherent non-Arrhenius hopping mechanisms as functions of θmin (in K) and V3 ≃ EB (in kcal mol−1). Here, EB (red circles) is the rotational barrier height of CH3 in the ground state (v = 0) and V3 (blue circles) is the rotational barrier height from the bottom of the wells. θmin was obtained at a reorientation rate of 2 × 108 s−1. An empirical equation, EA–E (in μeV) = 30·exp(−0.08·θmin) + 103·exp(−0.28·θmin), was obtained from the analysis of the crystalline molecular solids [221,222,223,224,225,226,227]. For readability, V3 ~ EB in X2-axis is added. A similar correlation between EA–E as a function of EB (in kJ mol−1) has been reported [222,228]. (d) Another universal correlation curve of EA–E (= ΔE±) as a function of EB (kcal mol−1) by analyzing INS spectroscopy in non-crystalline polymers: EA–E (in μeV) = a·(EB/b)0.75·exp[−(EB/b)0.5], a = 1.23 meV, b = 4.30 K [242]. For clarity, red circles are identical to those in (c). The green and blue areas in (c) and (d) suggest the CH3 rotations due to non-Arrhenius law hopping mechanism, respectively.
3.5.3. Unidirectional CH3 Rotor Induced by EPV
To address the four symmetry questions raised by Clough [227], the authors would like to mention a toy model of unidirectional CW (or CCW) rotation at a macroscopic level as a low-entropy state. The Ea–Eb degeneracy is “lifted” by an external magnetic field (Zeeman effect), an external electric field (Stark effect), a built-in internal electric field (dipole moment), and possibly Z0-WNC. When the EA–E ~ EPV condition is satisfied (Scenario D), a handed CH3 rotating action becomes possible. First, A, Ea, and Eb at well 2, biased by −EPV, were postulated. At well 3, A*(3) = A − EPV, Ea*(3) = Ea − EPV, and Eb*(3) = Eb − EPV; conversely, at well 1 biased by +EPV, A*(1) = A + EPV, Ea*(1)= Ea + EPV, and Eb*(1) = Eb + EPV.
Figure 9b illustrates the modified potential energy E(θ) biased by ±EPV as a function of θ. Because A(2) ≠ A*(1) ≠ A*(3), Ea(2) ≠ Ea*(1) ≠ Ea*(3), and Eb(2) ≠ Eb*(1) ≠ Eb*(3) at ν = 0,1,2.., there is unequal permutational tunneling between three potential wells—well 1, well 2, and well 3—with CW rotation, [well(2) → well (3) → well(1) → ]n, leading to handed CH3 rotation at low temperatures. When Ea in well 2 (ν = 0) is coincident with Eb + EPV in well 3 (ν = 0), resonant tunneling endowed with several chiral phonon modes occurs at ν = 0. Similarly, Eb in well 2 (ν = 1) is coincident with Ea + EPV in well 3 (ν = 1), and resonant tunneling with the help of several chiral phonons (from ν = 0 to ν = 1) is possible. Even if non-Arrhenius law hopping is dominant at higher temperatures, handed permutational rotation is likely to occur with a small probability because of the high cooperativity in the condensed phase to minimize the entropy at the macroscopic level. This assumption can be confirmed by the emergence of several (−)-sign vibrational circular dichroism (VCD) signals at the corresponding IR bands, characteristic of CH3 rotors and CH2 skeletal g-bonds in several liquid n-alkanes, as discussed in Section 3.6.
To determine the relationship between the EB dependence of the tunneling splitting/frequency (EA–E) with a small EPV, two universal correlation curves of EA–E in CH3 rotation at vibrational quantum number ν = 0 as functions of barrier heights, V3 ≃ EB (in kcal·mol−1), EB (from ν = 0 to ν = 1), and re-orientational temperature, θmin (in K) are compared [222,224,225,226,227,228]. Here, θmin determined by the T1 measurement of 1H-NMR is a crossover temperature between temperature-dependent quantum tunneling and non-Arrhenius law hopping processes, although the transition appears to be continuous.
Figure 9c shows the EA–E in molecular crystals as functions of θmin, V3 ≃ EB (red circles and red line), and EB(0–1) (blue circles and blue line) [222,224,225,226,227], while Figure 9d plots the EA–E obtained in non-crystalline polymers as a function of EB (red line) [240,241,242,243,244], with red circles taken from Figure 9c [224,225,226]. The two EA–E vs. EB correlation curves are very similar, regardless of whether considering crystalline molecular or non-crystalline polymer solids. When the EB of the CH3 rotor, EB(CH3), varies slightly from 2 to 7 kcal mol−1, the EA–E decreases exponentially from 10−7 to 10−14 eV, corresponding to 10−3 to 10−10 cm−1 (3 × 107 to 3 × 101 Hz). Consequently, EA–E becomes comparable to the theoretical EPV, and as a result, the EA–E (= ΔE±) ~ EPV condition (Scenario D) is experimentally feasible.
The EB(CH3) in the crystals ranges from 0.1 to 5 kcal mol−1 (50–2500 K, 0.004–0.21 eV, 35–1750 cm−1) [220]. At 4.2 K, the tunneling frequency of CH3 rotors is ~ 300 KHz for even-carbon number n-alkanes including n-C12H26, and 340 KHz for odd-carbon number n-alkanes, including n-C13H28 [220,232,233,234]. The two frequencies correspond to EA–E ~ (1.3–1.4) × 10−9 eV with EB(CH3) ~ 2.8 kcal mol−1. On the other hand, the rotational frequency of EB(CH3) directly attached to the main chain of PMMA, which is known as γ–relaxation, is only ~1 KHz (4 × 10−12 eV) below 120 K. The corresponding EB(CH3) values in isotactic- and syndiotactic-PMMA are evaluated to be 3.3 kcal mol−1 and 6.7 kcal mol−1, respectively [220,240,242].
The liquid n-alkanes containing PDBS in the range of −10 °C and 110 °C are likely to obey the EA–E–EB correlation curves in Figure 9c,d. When EB(CH3) ≳ 3.8 kcal mol−1, the EA–E approaches the predicted EPV value of 10−10 eV, and when EB(CH3) ≳ 6.4–7.3 kcal mol−1, the EA–E approaches the EPV value of 10−13 eV, as shown by the blue zone in Figure 9d and the green zone in Figure 9c. The rotational frequency of CH3 rotors in n-butyl pendants becomes very small and EB(CH3) is likely to be ≳ 6 kcal mol−1, which is considerably higher than EB(CH3) ~ 2.8 kcal mol−1 of n-alkanes. Even with a higher EB(CH3), the CH3 rotors of n-alkanes and n-butyl groups might feel the handed EPV force embedded in the non-Arrhenius law hopping process.
3.6. Are n-Alkanes Optically Active? VCD and IR Spectra of n-C12H26, n-C12D26, and Other n-Alkanes
3.6.1. Detecting the Gauche Bonds in n-Alkanes
The quantum tunneling of CH3 hinders the rotor in TP n-alkanes in the solid state, which is a dominant process at cryogenic temperatures. The CH3 rotation in odd-number carbon n-alkanes (carbon number from 9 to 29) results in non-TP conformers involving one and multiple g+ and g− bonds above their melting points and liquid states [220,232,233,234]. As discussed in Section 3.3, our calculated EB values from t- to one/two g-bonds of n-C12H26 are on the order of 3.24 to 5.74 kcal mol−1 (Table S1, Supplementary Materials). The production of single, double, and kink g+ and/or g−-bonds are experimentally detectable by IR and Raman spectroscopy [178,193,194,195,196,197,198,200,201,202,203,204,205,206,207,208,209]. For example, using IR spectroscopy, several characteristic bands, i.e., 873/975/1078/1164/1341 cm−1 for end-g bonds, 1353 cm−1 for gg-bonds, and 1306/1366 cm−1 for g-t-g* (kinks), respectively, can be recognized when compared to 1378 cm−1 for the CH3 group [178,201,202,203,204,205,206,207,208,209].
3.6.2. CD/UV Background Spectra of Liquid n-C12H26
In recent years, Ozaki et al. investigated the electronic transition states of n-C5H10 to n-C14H30 using attenuated total reflection far-ultraviolet (ATR-FUV) spectroscopy and TD-DFT/SAC-CI calculations [245,246,247]. They assigned several fundamental FUV bands of TP n-alkanes: the strongest FUV band around 145 nm was a mixture of HOMO → Rydberg 3p and HOMO-1 → Rydberg 3s transitions, and the weak shoulder FUV band around 165 nm was assigned to HOMO → Rydberg 3s. The major 145 nm and shoulder 165 nm bands should tail to the near-UV region in the range of 250–400 nm, which is seen as a structureless background (Figure S6a, Supplementary Materials). When n-alkanes are involved in a non-mirror-symmetric g+ or g− geometry, the 165 nm band tails more strongly in the CD/UV region. In fact, n-C12H26 showed weak temperature-dependent CD and UV spectra even after subtracting the instrumental background at −5 °C, 50 °C, and 100 °C (Figure S6b, Supplementary Materials).
3.6.3. VCD/IR Spectra of n-Alkanes
Assuming g+ > g− due to the EPV of RH-GH in n-C11H24 [191,192], the CH3 rotor then has a unique handedness, which is responsible for the transfer of solvent chirality to n-butyl pendants and hence the Si main chain. When n-C12H26 is between −10 °C and TC2, the [(g+)-(t)9] conformer showing (+)-sign CD as the dominant species strongly induces 300 nm RH-helicity and (+)-sign CD in PDBS. Conversely, when n-C12H26 is between TC2 and TC1, [(g+)2-(t)7] and [(g+)-(t)9] as the dominant species induce (−)-sign CD helicity. When n-C12H26 is above TC1, mutual cancellation between the (+)-and (−)-sign CD in g+-rotamers results in a lack of any induced MPV effects.
Inspired by the symmetry breakings proposed by Clough [227], if n-alkanes without point chirality adopt chiral conformers, VCD and ROA spectroscopy should detect several optically active vibration bands characteristic of the handedness of stretching, bending, rocking, and torsion modes of the CH3 group, and stretching, bending, and twisting modes for CH2. The VCD and IR spectra datasets of liquid n-C12H26 and n-C12D26 at 10 °C (below TC2), 25 °C (~TC2), and 40 °C (above TC2) are shown in Figure 10a–d and Figures S15 and S16, Supplementary Materials.
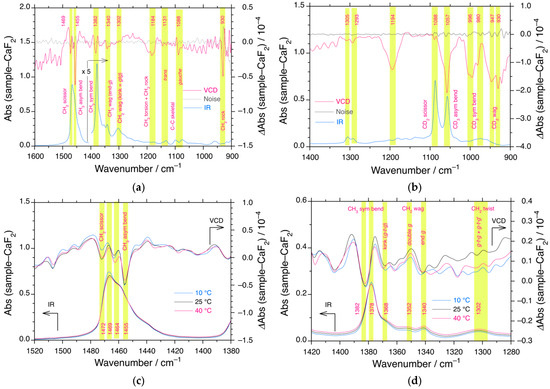
Figure 10.
VCD (red) and IR (blue) spectra and VCD background noise (black) (CaF2 windows) of (a) n-C12H26 at 25 °C in the range of 900 cm−1 and 1600 cm−1 and (b) n-C12D26 at 25 °C in the range of 900 cm−1 and 1400 cm−1. The zoomed-in VCD (red) and IR (blue) spectra of n-C12H26 at 10 °C (blue), 25 °C (black), and 40 °C (red) (c) in the range of 1380 cm−1 and 1520 cm−1, and (d) 1280 cm−1 and 1420 cm−1. The VCD and IR spectra were subtracted from the corresponding raw VCD and IR spectra of the CaF2 substrate, respectively. For n-C12H26, the VCD/IR bands at 1469 cm−1, 1455 cm−1, and 1382/1378 cm−1 were assigned to CH2 (scissoring), CH3 (asym, bending), and CH3 (sym, bending, “umbrella”) modes, respectively. The VCD/IR bands at 1368 cm−1, 1352 cm−1, 1341 cm−1, and 1302 cm−1 were assigned to CH2 wagging (g-t-g, double g, end g) and CH2 twisting (g-t-g + g-t-g′), respectively. For n-C12D26, the VCD/IR bands at 1088 cm−1, 1057 cm−1, 996/980, and 947/930 cm−1, respectively, are assignable to CD2 (scissoring), CD3 (asym, bending), CD3 (sym, bending), and CD2 (twisting) modes. The yellow areas in (a–d) indicate the detectable VCD signals relating to the corresponding IR bands, that are the region of interest discussed in the main text.
Several (−)-sign VCD signals of n-C12H26 and n-C12D26 are observed. The VCD spectral profiles are independent of temperature, as shown in Figures S15 and S16 (Supplementary Materials). In line with the handbooks of IR/Raman spectroscopies [248,249], a previous IR study of liquid and solid n-C12H26 [178,201,250] assigned three major characteristic IR bands at 1466 cm−1, 1456 cm−1, and 1382 cm−1, respectively, to CH2 (scissoring), CH3 (asym, bending), and CH3 (sym, bending or “umbrella”). The t- and g-bonds in the C–C skeletal IR bands are observed at 1133 cm−1 and 1076 cm−1, respectively (Figure 10a). The (−)-sign VCD band at 1088 cm−1 (a handed g-bond) is rather weak, and the VCD band of the t-bond is even less obvious. Although a sharper (−)-sign VCD band characteristic of CH3 (rocking) is observed at 930 cm−1, the corresponding IR bands around 929 cm−1 are very weak. The combination band of CH3 torsion and CH2 rocking modes at 1184 cm−1 is weak, and the corresponding IR bands are also not obvious.
The (−)-sign VCD band of n-C12H26 at 1456 cm−1, which is coincident with the 1456-cm−1 CH2 bending IR band, is observed as a shoulder of the 1466-cm−1 CH2 scissoring IR band (Figure 10c). The dissymmetry ratio of the vibration at 1456 cm−1, g = ΔAbs/Abs = −1.6 × 10−4, could be evidence of the unidirectional CH3 rotation in n-C12H26, for example, from the A*-state at ν = 0 to the Eb* (or Ea*)-state at ν = 1. The multiple (−)-sign VCD bands around 1470 cm−1 at the 1456-cm−1 CH2 scissoring IR band and the (−)-sign VCD and IR bands of the g-bond at 1088-cm−1 are related to the preference of g+ over g− bonds.
The VCD and IR spectra of liquid n-C12D26 can be observed more clearly, as shown in Figure 10b and Figure S16 (Supplementary Materials). Three major IR bands of n-C12D26 at 1088 cm−1, 1057 cm−1, and 975 cm−1 were assigned to the CD2 (scissoring), CD3 (asym, bending), and CD3 (sym, bending, ‘umbrella’) modes. Notably, the clear (−)-sign VCD band at 1057 cm−1 is coincident with the 1057-cm−1 CD3 IR band. The value of g = –4.0 × 10−4 at 1057 cm−1 is ~ two times larger than the corresponding 1456-cm−1 VCD/IR bands of CH3 in n-C12H26. This is evidence of the handed CD3 rotor in n-C12D26 being in the same direction as the CH3 rotor. At the shoulders of several broad IR bands centered at 980 cm−1, three (−)-sign VCD bands centered at 996 cm−1 accompanied by several (−)-sign VCD bands centered at 930 cm−1 are observed, suggesting the inequality of the CD3 bending modes. However, the VCD band at the CD2 (scissoring) IR band at 1088 cm−1 is less obvious, indicating no preference between g+ and g− bonds.
Similarly, the other five liquids, n-C8H18, n-C10H22, n-C13H28, n-C14H30, and n-C16H34, at 25 °C revealed several (−)-sign VCD bands in the range 900–1600 cm−1, as shown in Figure S17a–e (Supplementary Materials). Several characteristic VCD/IR bands of CH2 at 1464–1472 cm−1 (scissoring), CH3 at 1455–1466 cm−1 (asym, bending), CH3 1377–1380 cm−1 and 1360–1361 cm−1 (sym, bending), and the handed g-bonds at 1086–1088 cm−1, respectively, can be seen. The VCD bands due to CH2 around 1300 cm−1 (twisting) and the t-bonds in the C–C skeletal IR bands at 1131–1135 cm−1 were less obvious. Likewise, the combination band of CH3 torsion and CH2 rocking modes at 1172–1184 cm−1 was weak, and the corresponding IR bands were less obvious.
3.6.4. VCD, ROA, and Near-IR CD Spectroscopy
The detection of several VCD/ROA bands and high-resolution IENS signals as torsional modes (from ν = 0 to ν = 1) in Figure 9b in the range of 1–350 cm−1 might constitute direct evidence of MPV. The asymmetric (~2960 cm−1) and symmetric (~2870 cm−1) stretching modes of the CH3 group and the asymmetric (~2960 cm−1) and symmetric (~2850 cm−1) modes of the CH2 group provide additional evidence. Further, several overtones and combination bands, such as the first overtone CH3 (torsion) at ~620 cm−1, CH3 (torsion) + CH3 (asym, bending) at ~1800 cm−1, and CH3 (torsion) + CH2/CH3 (stretching) at ~3300 cm−1, are useful [244].
A near-IR CD spectropolarimeter with an InGaAs detector covering ~1600 nm (~1.29 eV, ~6250 cm−1) allowed the detection of optical activity in the second, third, and fourth overtones of C–H stretching, bending, and their combination bands as liquids as a function of temperature by choosing several path lengths in the range of 10–200 mm and subtracting the background spectra of the cuvette and window glass. The near-IR CD spectra of the CD3 and CD2 groups can be compared to those of the third and fourth overtone frequencies, which are reduced by ~1/√2.
3.7. Possible Scenarios for the MPV Effects of PDBS with n-Alkanes
Based on the above results and discussion, a possible scenario for the dual mirror-symmetry breaking of PDBS in n-dodecane is proposed. As mentioned in the Introduction, pyrromethenes 597 and 546, carrying three CH3 groups (Chart S1, Supplementary Materials), showed clear (−)-CD spectra in solution at 25 °C [114]. From the temperature-independent (−)-sign VCD spectra of liquid n-alkanes, the CH3 rotor consisting of three 1H atoms (QW = –0.108 × 3 = –0.324) is likely to function as a unidirectional hindered rotor mediated by EPV. The rotor characteristics obey the non-Arrhenius law of hopping at higher temperatures and quantum tunneling at lower temperatures, although there is no critical border and the transition between the two mechanisms is continuous as the temperature changes (Figure 9c,d, and Figure S12, Supplementary Materials). Similarly, the CD3 rotor consisting of three 2H atoms prefers CW rotation because of the same (−)-sign VCD bands and a similar magnitude of g ~ −10−4 for the symmetric bending modes of CH3 at 1456 cm−1 and CD3 at 1057 cm−1.
According to the MPV theory for GH n-alkanes, the RH helix consisting of all-g+ bonds is more stable than the LH helix with all-g− bonds, suggesting that the CH3 rotor prefers CW rotation. The enantiomeric pairs between the g+ and g− bonds and between the g+g+ and g−g− bonds are energetically unequal. The g+ and g+g+ bonds are in excess of the corresponding g− and g−g bonds. The CW-CH3 rotor generates end-g+, other g+, and g+g+ bonds in TP n-alkanes and TP n-butyl pendants. Non-TP n-alkanes involving one and multiple g+ bonds and g+g+ bonds thus become optically active chiral solvents, enabling the induction of handed helicity in mirror-symmetrical 73-helical PDBS via intermolecular chirality transfer interactions.
To explain the notable H/D isotope effect of TC1 evident in the gabs–T curves in Figure 2a and Figure 3b, the relative ratio of θD and θDrel between n-C12D26 and n-C12H26 was obtained from the asymmetric bending modes of CD3 (1057 cm−1) and CH3 (1456 cm−1), yielding θDrel = 0.726. θDrel predicted a TC1 of 274 K (1 °C) for n-C12D26 when a TC1 of 378 K for n-C12H26 was chosen. Similarly, the ratios of the highest asymmetric/symmetric stretching frequencies between CD3 (2216/2073 cm−1) and CH3 (2959/2875 cm−1) [251,252] led to θDrel = 0.748/0.721, corresponding to TC1 of 282 K (9 °C) and 273 K (0 °C), respectively. The fundamental vibrational modes of these solvent molecules account for TC1 as an observable MPV effect. These simple evaluations agree with Tc ∝ θD predicted by Salam’s theory. In contrast, the (−)-sign Qw of 1H and (+)-sign Qw of 2H as solvent molecules induced opposite helicity in PDBS below TC1 and TC2. The difference in |gabs| is ascribed to the inherent difference in Irot and B between CH3 and CD3 rotors, as indicated by the marked reductions in EA–E by two to three orders of magnitude [220,222,235,236,237,238,239].
From Table S1, Supplementary Materials, it is interesting to note that the end g+ bond, (g+)1-(t)8, and middle g+ bond, (t)2-(g+)1-(t)6, show (+)-sign CD spectra at λext of n-C12H26, whereas the g+g+ bond, (g+)2-(t)7, and other g+ bonds, like (t)1-(g+)1-(t)7, show (−)-sign CD effects.
First, intramolecular chirality transfer was considered. (a) When T < TC2, the 29Si-driven torque overcomes the CH3 torque, leading to a (+)-CD Si–Si bond helix in the presence of n-C12D26; conversely, when TC2 < T < TC1, the CH3-rotor driven torque overcomes that of 29Si, leading to a (−)-CD Si–Si bond helix (Figure 11a). On the other hand, below TC2, the CW-CH3 hindered rotor generates the (g+)1-(t)8 bond in n-C12H26 with (−)-sign CD (Figure 11b). When TC2 < T < TC1, the CW-CH3 hindered rotor induced (t)1-(g+)1-(t)7 and (g+)2-(t)7 rotamers with (−)-sign CD (Figure 11b). Next, intermolecular chirality transfer between n-C12H26 and PDBS was considered. When T < TC2, the (g+)1-(t)8 rotamer induces a (−)-CD Si–Si helix. In contrast, when TC2 < T < TC1, the (t)1-(g+)1-(t)7 and (g+)2-(t)7 rotamers induced the formation of a (+)-CD Si–Si helix. Another explanation for the observed optical activity of PDBS in n-C12H26 and n-C12D26 arises from the opposite Qw values between the three 1H isotopes in the CH3 rotor (Qw = −0.108 × 3 = −0.324) and the three 2H isotopes in the CD3 rotor (Qw = +0.892 × 3 = +2.772).
Figure 11.
A proposed rationale for nuclear-spin dependent intra- and inter-molecular chirality transfer between two types of CH3 rotors at the n-C12H26 and n-butyl pendants of PDBS and 29Si isotope of PDBS. The CD3 rotor in n-C12D26 diminishes the ability of the hindered rotor relative to that of CH3 as a result of the heavier isotopes of the three ENSs. First, with respect to intramolecular chirality transfer, (a) in the presence of n-C12D26, when T < TC2, the 29Si-driven torque overcomes the CH3 torque, leading to a (+)-CD Si–Si bond helix; conversely, when TC2 < T < TC1, the CH3-rotor driven torque overcomes the 29Si torque, leading to a (−)-CD Si–Si bond helix (a). On the other hand, in liquid n-C12H26, below TC2, the CW-CH3 hindered rotor generates a (g+)1-(t)8 bond in n-C12H26 with (−)-sign CD (b). When TC2 < T < TC1, the CW-CH3 hindered rotor induces (t)1-(g+)1-(t)7 and (g+)2-(t)7 rotamers with (−)-sign CD n-C12H26 (b). Next, intermolecular chirality transfer between n-C12H26 and PDBS was considered. When T < TC2, the (g+)1-(t)8 rotamer induces a (−)-CD Si–Si helix. In contrast, when TC2 < T < TC1, the (t)1-(g+)1-(t)7 and (g+)2-(t)7 rotamers induced formation of a (+)-CD Si–Si helix.
Two different CH3 rotors (I = 3/2, μN = +2.79 × 3 = +8.37) of n-C12H26 and n-butyl of PDBS are schematically illustrated in Figure 11. Because the tunneling frequency and splitting of the CD3 rotor markedly diminish relative to those of the CH3 rotor [220,222,235,236,237,238,239], the helix preference of the PDBS in n-C12D26 is dominantly determined by the relative magnitude and direction of the rotational torques between the two CH3 rotors and the 4.7% 29Si (I = 1/2, μN = –0.55). From NMR experiments, it is known that 1H and 13C isotopes prefer α-spin (↑), and conversely, 29Si prefers β-spin (↓) by Zeeman splitting under an external magnetic field (H0). It is possible that 1H and 29Si induce opposite rotational torque in the absence of H0.
3.8. Added in Proof—Other Oligo- and Polysilanes for the MPV Validation
To validate the calculated results of the PESs (Figure 8 and Figure S13c–f, Supplementary Materials) experimentally, the CD/UV spectra of permethyldecasilane (PMDS) and poly(diethylsilane) (PDES) (Chart S1, Supplementary Materials) were measured under static conditions. PMDS in n-propanol did not exhibit CD effects because of the lower EB in the tetra-wells (Figure S18a, Supplementary Materials). In contrast, PDES in n-propanol, n-butanol, and n-hexanol showed weak (+)-sign CD effects at longer λext values relative to the corresponding UV spectra at shorter λmax values (Figure S18b–d, Supplementary Materials); it is evident that the CD spectral profiles did not match the corresponding UV profiles. The (+)-sign gabs of PDES in n-propanol as a function of temperature indicated TC1 ~ 30 °C (Figure S18e, Supplementary Materials).
Prior to the VT-CD/UV spectral measurements of PDBS, PDES, and PMDS in n-alkanes, M.F. and J.R.K. at NTT Basic Research Labs in the 1980s and the 1990s were aware of the (−)-sign CD spectra of poly{bis-(p-t-butylphenyl)silane) (PBtBPS) (Chart S1, Supplementary Materials) in tetrahydrofuran (THF) at −10 °C, 25 °C, and 50 °C (Figure S19a, Supplementary Materials), in addition to the weak (−)-sign CD effects of poly(n-hexyl-2-methylpropylsilane) (PH2MPS) (Chart S1, Supplementary Materials) in isooctane at 0 °C (Figure S19b, Supplementary Materials). Importantly, the CD spectral profiles at shorter λext values do not match the corresponding UV spectra.
In 2018, T.M., M.F., and Dr. Ayako Nakao working at NAIST recognized that PDBS-H in a mixture of n-C12H26 98.3%/THF 1.7% (v/v) under static conditions reveals opposite signed temperature dependent CD spectra in n-C12H26 at 0 °C, 20 °C, and 45 °C when a small amount (50 μL) of 10−3 M THF solution of PDBS-H was added to 2.95 mL of n-C12H26 (Figure S19c, Supplementary Materials). However, the PDBS-H in pure THF did not exhibit any detectable CD effects at −10 °C. The oxygen atoms of a trace amount of THF coordinate to the Si 3d or Si σ* orbitals, resulting in intermolecular C–H/O interactions with the n-butyl pendants.
Interestingly, poly(n-hexyl-2-ethylbutylsilane) (PH2EBS) (Chart S1, Supplementary Materials) exhibited noticeable solvent and temperature dependence of the CD/UV spectra. The CD spectra of PH2EBS in n-C12H26 under static conditions are completely opposite to those in n-octanol at the three temperatures (Figure S19d,e, Supplementary Materials). The gabs values at 310 nm as a function of temperature are shown in Figure S19f, Supplementary Materials. Clearly, PH2EBS undergoes a second-order helix–helix transition at TC2 ~ 30 °C, which is associated with the oppositely signed CD signals in n-C12H26 and n-octanol. The CD spectrum of PH2EBS in n-octanol almost disappears at TC1 ~ 110 °C and recovers mirror-symmetric 73-helices absorbing at 320 nm. The oxygen atom of n-octanol coordinates to the 3d orbital or Si σ* of the Si atom and/or stimulates the intermolecular C–H/O interactions with alkyl pendants.
Five other poly(dialkylsilane)s, including poly(methyl-n-propylsilane), poly(n-pentyl-n-propylsilane), poly(di-n-pentylsilane), and poly(di-n-hexylsilane) (Chart S1, Supplementary Materials), did not induce clear CD spectra in n-alkanes, n-alkanols, THF, and CHCl3 at 0 °C. However, the authors found very clear CD and CPL spectra for several new polysilanes carrying designed achiral pendants in homogeneous solutions of n-alkanols, n-alkanes, and p-dioxane under static conditions. These results will be submitted elsewhere.
3.9. Other MPV-Related Experimental Studies
Most MPV scientists have sought possible answers to the issue of the origin of homochirality on Earth for the past 150 years: why and how have D-sugars and L-amino acids become the building blocks of our lives? And which deterministic or by-chance mechanism is the origin [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]? From the viewpoint of P-symmetry violation and CP-symmetry invariance in physics, true antipodes of D-sugars and L-amino acids are (L-sugars)* and (D-amino acids)* made up of anti-atoms [11,13,21,22,23,24]. The anti-atoms are comprised of anti-p, anti-n, and e+, whereas anti-p and anti-n, respectively, are made of anti-u and anti-d quarks [11,13,24]. Only e+ are manifested daily in regulated laboratories and hospitals utilizing short-half-life radioisotopes.
In recent years, synthetic biology, in designing mirror-image enzymes and pharmaceutics by producing non-natural DNA/RNA made up of L-sugars and non-natural proteins building-up D-amino acids, has received considerable attention in biotechnology and life science [253,254,255,256,257,258]. However, it remains unclear whether natural D- and non-natural L-sugars and natural L- and non-natural D-amino acids and their corresponding oligomers and macromolecules rigorously preserve mirror-image relationships in their structures and functionalities.
A few structural biologists are aware of noticeable differences between non-natural L- and natural D-RNA oligomers [259,260,261,262]. Single-strand RNA is classified as a floppy macromolecular rotamer with rotational and flip-flop freedom along C–C/C–O/C–N single bonds. When it produces a double-strand, there is a concomitant loss of freedom. In 2004, Betzel et al. reported clear dissimilarity between L- and D-RNA duplexes by crystallographic analysis: L-RNA adopts two types of helical duplexes with head-to-tail packing; conversely, D-RNA adopts a Watson–Crick type with an end-to-end duplex with a wobble-like pair. The discrepancy is ascribed to inherent differences in nature between D-ribose and L-ribose based on MPV calculations of D-ribose [259,260,261,262]. Subsequently, they reported other evidence, namely the different intensities of two Raman bands, at 1000 cm−1 and 1700 cm−1, between D- and L-RNA. The differences in intensity are ascribed to differences in the electronic levels between the D- and L-RNAs. Rypniewski et al. and Bolik et al. stated that the notable dissimilarity between D- and L-RNA crystals originates from the PVED-WNC of DL-ribose [259,260,261,262]. As an alternative explanation, phosphate O=PO3− with one HINS 31P atom (natural abundance: 100%) has a very large ξ = 475 cm−1 [= P (247 cm−1) + 4 × O (57 cm−1)] and works as a unidirectional rotor along P–O–C bonds, leading to dissimilarity between the D-/L-RNA.
Compared to D-/L-RNA, the MPV effect of L-/D-amino acids has a long history. In 1973, Garay et al. were the first to report the differences in positronium (Ps) annihilation characteristics between five kinds of L- and D-amino acids using e+ as a probe [263]. Note that Ps generates two e+-e− species of singlet (I = 0, para-Ps) with a shorter half-life (τs ~ 2·10−10 s) and triplet (I = 1, ortho-Ps) with a longer half-life (τt ~ (5–40)·10−9 s) in a 1-to-3 statistical ratio. The population of ortho-Ps relative to para-Ps is directly related to the annihilation intensity of ortho-Ps. Among the five DL pairs of amino acids, the annihilation intensity of ortho-Ps in L-amino acids was 6–33% weaker than that of the corresponding D-amino acids. D-Amino acids have greater free volumes and lower specific densities than L-amino acids. Although further clarification is needed, this astonishing result implies violations of CP- and P-symmetries between natural L- and non-natural D-α-amino acids. This means a violation of T-symmetry invariance between L- and D-α-amino acids.
Inspired by Salam’s hypothesis [107,108], in the early 2000s, Wang et al. reported differences between D-L-α-alanine crystals using VT solid-state 13C-/1H-NMR, Raman spectroscopy, magnetic susceptibility, and DSC from room temperature to cryogenic temperatures [96,97]. An independent research team, however, did not observe such significant differences and ascribed the differences to unresolved impurities imbedded in non-natural D-alanine [264]. If Wang’s results are correct, IENS tunneling spectroscopy will detect differences in the CH3 rotor between D- and L-α-alanine crystals at 4 K because the D-L chirality is unchanged. Recently, Bordallo et al. reported dissimilarity between crystalline L- and D-α-alanine by VT-polarized Raman spectroscopy and neutron diffraction [265] but had many debates regarding their results [266,267].
In 2021, Koralewski et al. reported that H2O commonly shows (+)-sign-specific Verde constants at 546.1 nm in magneto-optical rotatory dispersion (MORD) spectroscopy at 291 K [268]. However, they ascribed the unexpected results to metal ion contamination, although L-α-threonine (CH3) and L-α-leucine (isobutyl) had particularly large (−)-sign specific Verde constants. The anomaly can be connected to the handed CH3 rotor action, although the handedness will depend on the solution temperature, pH, ortho-/para-H2O ratio, and H2O/D2O ratio.
In 2006 and 2013, Romalis et al. reported nuclear-spin-induced optical rotation (NSOR) with (+)-sign rotation of 1–13 μrad·cm−1·M−1 (0.06–0.7 mdeg·cm−1·M−1) at 405 nm under B0 = 5 G of achiral molecular liquids carrying CH3 and C19F3 rotors, i.e., methanol, ethanol, n-propanol, isopropanol, n-hexane, n-hexene, and perfluoro-n-hexane when the liquids were placed in a 0.85 T permanent magnet based on the early work with 129Xe [144,145]. Interestingly, even H2O exhibits a weak NSOR. The results suggest a nuclear-spin-dependent PV-MAM phenomenon because the organic molecules adopt chiral and/or helical geometries owing to the rotors. An enantiomeric pair of liquid molecules carrying CH3 and C19F3 revealed clear differences in absolute magnitude with the same or opposite signs of NSOR signals.
In 2015, Pandey et al. reported non-mirror-symmetric Cu2+ metal organic framework (MOF) crystals coordinated to D- and L-leucine derivatives [269]. The D- and L-homochiral Cu2+-MOFs revealed structurally distinct crystal packing, leading to notable difference in proton conductivity: the L-MOF showed significantly higher conductivity than the D-MOF. The D- and L-leucine residues induce mirror-symmetry-breaking MOFs differently, presumably leading to observable MPV functionality. The handedness of multiple CH3 rotors due to the isopropyl groups of the D-L-leucine residues is responsible for the non-mirror MOF crystals.
Recently, to validate Salam’s hypothesis [107,108], Kozlova et al. designed a new MOF crystal incorporating diamagnetic Zn2+, diazabizyclooctane (DABCO), and terephthalate. DABCO, a two-fold symmetric hindered rotor, can exist as a mixture of LH and RH geometries [109,110,111,112]. The DABCO-Zn2+ MOF revealed three second-order phase transitions at 130 K (terephthalate), 60 K (DABCO), and 14 K (DABCO) from specific heats using adiabatic calorimetry and the solid-state 1H-NMR T1 value. The two transitions at 60 K and 14 K are ascribed to the structural transition of DABCO due to the dynamic Jahn–Teller effect of DABCO, whereas the transition at 130 K arises from the structural transition of BDC2−. A LH–RH preference at 60 K and 14 K of the MOF is not characterized because neither the calorimeter nor 1H-NMR are chiroptical approaches [109,110,111,112]. It is interesting to note that the existence of two transitions of the MOF is very similar to that of TC1 and TC2 of PDBS in n-alkanes.
3.10. Perspectives
3.10.1. Is Parity Conserved Under the Gravitational Force?
From the non-mirror CD spectra of PDBS in n-alkanes in the CW and CCW flow, it is unclear whether the P-symmetry of GF is rigorously preserved. In materials science, CW and CCW flow under the GF has recently been recognized as a local PC-EMF event enforced by mirror-symmetrical hydrodynamics [3,169,170,171,172,173,174,175]. The hypersensitive hydrodynamic force under the GF is likely to break P-symmetry in response to a tiny local PV advantage factor and nuclear spin frustration beyond the P-symmetric Coriolis force [3,169,170,171,172,173,174,175]. To account for the non-mirror characteristics of the CW and CCW flow experiments, the authors came across a research community of PV-GF.
The general relativity theory of GF formulated by Albert Einstein in the early 20th century relies on a uniformly accelerated reference frame that conserves P-symmetry [270,271,272,273,274,275,276,277,278,279,280,281,282,283,284,285,286,287,288,289,290,291]. Since 1964, many researchers have theoretically discussed PV-GF: do LH- and RH-chiral objects placed in curved spacetime follow equally geodesic trajectories [274,275,276]? The possibility of theoretical and experimental breakthroughs in gravitational wave theory owing to differences between LH and RH polarization modes has prompted several experiments to validate the PV-GF hypothesis.
For PV-GF testing, researchers often use the Eötvös ratio, η = 2·(aA − aB)/(aA + aB) ≃ (mg/mi)A − (mg/mi)B = Δ(A, B), which is similar to Kuhn’s dissymmetry ratios, gabs and glum, where aA and aB are the accelerations of two free-falling bodies A and B, and mg and mi are their gravitational and inertial masses, respectively [272]. Similar to the subtle EPV of MPV theories, a tiny Eötvös ratio, η, in the PV-GF is estimated to be η = 10−15–10−21 eV and the spin-gravity coupling constant is |Asg| = 10−18–10−22 eV [272]. To validate the PV-GF hypothesis on Earth, a precision rotational torsion pendulum under magnetic shielding at cryogenic temperature has been designed [270,271,272,273]. Carefully designed experiments to search for PV-GF have been proposed utilizing spin-particles, such as polarized e− [277,278,279], a pair of HINS isotopes and a pair of HINS-INS isotopes (i.e., 85Rb-87Rb, 39K-87Rb, 87Sr-88Sr, 129X-131Xe) [280,281,282,283,284], different masses and densities in Ti-Pt alloys [285,286], l- and d-quartz [287], nuclear-spin-induced chiral molecules [88,288,289], and nuclear-spin-independent chiral CHBrClF and helical H2X2 (X = O, S, Se, Te, Po) [290,291]. From his essay, it seems that Shinitzky might have been aware that subtle but detectable differences in density (specific gravity) and optical rotation between L- and D-molecular liquids and between L- and D-NaClO3 crystals, stem from the handedness of the spatiotemporal galaxy and universe [103].
In 2008, 2015, and 2024, Bargueño et al. discussed the importance of nuclear spin dependence when enantiomers experienced PV-GF [88,288,289]. Molecules possessing CH3 rotors are candidates to investigate the magnitude of the PV-GF on Earth. The role of the CH3 rotor in the CW and CCW flow of n-alkanes on a macroscopic scale is to dynamically drive the CH3 rotor and generate g+ > g− (or g+ < g−) bonds by chirally sheared intra- and intermolecular interactions between n-alkane molecules. PDBS is a chiroptical probe that responds to the dynamic behavior of n-alkanes. The external hydrodynamic CW and CCW flow at 400–800 rpm (7–15 Hz) results in non-mirror-image CD spectra of PDBS in n-alkanes. Organic solvents with CH3 rotors are likely to feel sensitively the coupling between the EMF and GF. Enantiomeric pairs of terpenes with multiple CH3 rotors, such as limonene, pinene, carvone, and camphor, are thus candidates as rotating torsional pendulum chemical probes. Actually, noticeable non-mirror-image CD spectra under CW and CCW stirring were found when two optically active aggregates of π-conjugated polymers were stirred in the presence of (S)- and (R)-limonene carrying two CH3 rotors [292,293].
3.10.2. Olfactory Receptors Discriminate Between CH3 and CD3 Groups of Molecules
One might be aware of the fact that the CH3 group is ubiquitous in homochiral biomolecules such as lipids, L-amino acids (alanine, threonine, cysteine, valine, leucine, isoleucine, methionine), and thymine. In contrast, no CD3-containing natural compounds have been detected. Actually, it was demonstrated that olfactory receptor proteins (ORPs) of fruit flies (Drosophila melanogaster) at 25 °C and honeybees (Apis mellifera) favor acetophenone-h8 and n-octanol-h17 but disfavor acetophenone-d3 (Me), -d5 (Ph), -d8 (Me and Ph), and n-octanol-d18 [294,295]. Interestingly, the fruit flies could not discriminate between benzaldehyde-h8 and -d8, presumably because of the lack of a CH3 group. These odorants might therefore exist as racemic mixtures of rotamers due to the lack of rigid chirality.
To explain the discrimination capability of H-D isotopomers, a molecular vibration theory of olfaction has been proposed in addition to the traditional molecular shape theory of fitting odorant molecules in pocket-shaped ORPs, which belongs to classical biology [296]. However, the vibration theory neglects the CH3 rotor dynamics of achiral odorants. Recently, quantum smell theories for ORPs have been proposed in quantum biology in terms of the asymmetric DWP and MPV of enantiomeric odorants [297,298]. Sensing odorant chirality is influenced by quantum tunneling between enantiomers in double-well potential. This theory led to the conjecture that the handed CH3 rotor dynamics of odorants are crucial to ORPs. The hidden handedness of the CH3 and CD3 rotors and the handed intermolecular chirality transfer affect the discrimination capability of ORPs. The MPV hypothesis thus shines a light on a new horizon in quantum biology [299].
3.10.3. Candidates of the Handed Rotors
Non-radioactive non-rare molecules containing HINS isotopes, e.g., 1H (I = 1/2), 11B (I = 3/2), 13C (I = 1/2), 15N (I = 1/2), 17O (I = 5/2), 19F (I = 1/2), 31P (I = 1/2), 29Si (I = 1/2), 33S (I = 3/2), 35/37Cl (I = 3/2), 79/81Br (I = 3/2) and 127I (I = 5/2), can be utilized to investigate nuclear-spin-dependent MPV and PV-GF hypotheses in odd-number wells. Several three-fold rotors, that is, CH3, CF3, NH3+, and SO3− as pendants and BF4−, NH4+, and O=PO33− as counter ions, can be introduced into various chromophores/luminophores and solvents. VCD/IR [300], ROA/Raman [300], THz (microwave) CD [301,302,303], and cavity-ring-down ORD/CD spectroscopy [304,305] allows the characterization of the simplest molecules with C3v symmetry, i.e., CH3X (X = CN, NC, 2H, 19F, 35/37Cl, 79/81Br, 127I) and CHX3 (X = 19F, 35/37Cl, 79/81Br, 127I), by probing the C–H stretching and bending bands in CHX3 and the asymmetric and symmetric bending bands of CH3 in CH3X [306,307,308,309,310,311,312,313,314]. When the NH3+ group in zwitterionic species of L-amino acids acts as a handed rotor in ortho- and/or para-H2O, L- and D-amino acids are no longer enantiomeric, which could provide a possible answer to biomolecular handedness on Earth. To our knowledge, time-dependent MPV theories that treat HINS isotopomers in odd-number wells, including three-, five-, seven-, and nine-wells, are rare or have not yet been reported because most MPV theories deal with even-number wells, typically DWP, in the ground state.
Simpler small molecules containing three-fold symmetric rotors in the absence of rigid chemical chirality, that is, methanol, ethanol, n-propanol, isopropanol, di-n-propyl ether, n-butane (a minimal g-bond), methylcyclohexane, zwitterions (glycine, β-alanine, and choline), acetaldehyde, acetone, diacetyl, t-butyl methyl ether, acetic acid, toluene, p-cymene, o-/m-/p-xylenes, several terpenes (i.e., geraniol, nerol, α-terpinene, γ-terpinene), and, for comparison, their 2H, 13C, and 15N isotopomers are commercially available candidates.
Particularly, it is vital to validate the generality of whether other three-fold symmetric rotors, such as C19F3 in n-C4F10, n-C6F14, n-C8F18, 2,3,3,3-tetrafluoropropene, and fluorinated myristic acid generate non-mirror molecules and vibrational spectra [315,316,317,318,319,320]. The VCD/IR spectra of n-C6F14 and n-C8F18, which are molecular models of 136- and 157-helical poly(tetrafluoroethylene) [321,322,323], are shown in Figure S20a,b (Supplementary Materials), respectively. Hence, (−)-sign VCD signals due to the CF3 symmetric stretching modes at 1335 cm−1 (n-C6F14) and 1347 cm−1 (n-C8F18) can be observed. Additionally, several (−)-sign VCD signals due to the CF2 asymmetric and symmetric stretching modes are observed in the range of 1265–1150 cm−1.
The nuclear-spin-dependent VCD/IR spectra of the methyl groups in C3v symmetric CH3CN and CD3CN are compared in Figure S20c,d (Supplementary Materials), respectively. The VCD/IR spectra of CH3CN clearly show several broader VCD bands due to the CH3 group around ~1400 cm−1 including sharper asymmetric bending (ν6) at 1442 cm−1 and symmetric bending (ν3) at 1378 cm−1 [307,324]. The broad VCD/IR bands are ascribed to anti-parallel dimers, tetramers, hexamers, and octamers [307,324]. However, CD3CN showed less obvious VCD signals in the CD3 group. Further, the VCD/IR spectra of monomeric CH3CN/CD3CN species in the gas phase and/or in a dilute solution in C35/37Cl4 will provide direct evidence of intermolecular hindered rotation transfer with handedness.
Another example is the comparison between toluene-h8 and toluene-d8, which are the simplest methyl-substituted aromatics. The nuclear-spin-dependent VCD/IR spectra are shown in Figure S20e,f (Supplementary Materials), respectively. Previously, polycrystalline samples of partially and fully deuterated toluene (C6D5CH3 and C6D5CD3) at cryogenic temperatures clearly showed INS spectra and well-resolved Raman scattering (<140 cm−1) due to the hindered rotation of methyl groups in the TWP [220,325,326]. The (−)-sign VCD band of the C=C stretching mode at 1494 cm−1 of toluene-h8 is obvious, although the VCD bands of CH3 bending modes (1456 and 1378 cm−1) are weak, as is evident in Figure S20e (Supplementary Materials). Two intense (−)-sign VCD signals (1941 and 1858 cm−1) at four weaker IR bands (1941, 1858, 1800, and 1731 cm−1), which are unique overtone characteristics of monosubstituted benzene derivatives, are clearly observed [249,325,326]. However, the corresponding VCD signals of toluene-d8 in the range of 1300–1400 cm−1 range are very weak (Figure S20f, Supplementary Materials). The VCD-active IR modes are likely to be enhanced as overtones due to effective coupling of the two fundamental vibrational modes of toluene-h8 [326].
Notably, p-cymene (4-isopropyltoluene), which is an aromatic monoterpene, exhibited clear VCD signals in the corresponding IR spectra (Figure S20g–i, Supplementary Materials). The two intense (−)-sign VCD signals (1941 and 1800 cm−1) at two weaker IR bands (1941 and 1800 cm−1), are overtones characteristic of 1,4-substituted benzene derivatives [249]. Conversely, a number of intense (+)-sign VCD signals at the corresponding IR bands in the range of 1000–1550 cm−1 are clearly detected, i.e., C–H(CH3) wagging mode at 1514 cm−1, isopropyl symmetric and asymmetric bending modes (1382 and 1363 cm−1) and p-substituted skeletal mode (1057 cm−1) [327]. Because p-cymene is often used as a ligand in various ruthenium complexes, its optically active vibrational modes may be crucial for catalytic activity.
The calculated results can be readily validated using commercial and homemade VCD, ROA, and near-IR CD spectrometers. A theoretical and experimental understanding of the generality of the handedness of perpetual molecular rotors will allow the synthesis of both RH- and LH-chiral molecules and/or helical polymers without chiral catalysts with minimal energy, time, and cost in the near future.
4. Conclusions
Since the 1960s, many theorists have argued that the electroweak force (EWF) induces a parity-violating energy difference (EPV) on the order of 10−10–10−21 eV between mirror-image molecules induced by the handedness of the weak neutral electron current (WNC). The six major theoretical scenarios are as follows: (i) linear amplification model (EPV ∝ N), (ii) EPV ∝ Z5 (Z: atomic number), (iii) nonlinear amplification model, (iv) tuning ΔE± to adjust EPV, (v) EPV ∝ ΔEST, and (vi) nuclear-spin-induced anapole moment. In 1991/1992, Salam predicted that non-natural D-amino acids should undergo an EWF-origin P-symmetry violating second-order phase transition at 250 K (–23 °C) but that natural L-amino acids would not.
Inspired by Salam’s hypothesis and other theoretical MPV approaches, the present work investigates the detailed CD and CPL spectroscopic characteristics of rod-like poly(di-n-butylsilane) (PDBS) in homogeneous solutions of n-alkanes and isooctane ranging from −10 °C to 110 °C under static conditions, and, for comparison, under clockwise (CW) and counterclockwise (CCW) stirring conditions. PDBS adopts mirror-symmetric 73-helices in n-hexane and in the solid state.
This paper reports the serendipitous finding of dual mirror-symmetry breaking in PDBS: second-order phase transitions as a result of chiroptical generation at TC1 ~ 105 °C, and chiroptical inversion due to a helix–helix transition at TC2 ~ 28 °C. In particular, the solvent n-dodecane-h26 induced a gigantic enhancement in the CD and CPL spectra of PDBS. A (−)-sign CD band newly emerged at a shorter λmax (300 nm) below TC1, followed by a helix–helix transition at TC2, and eventually exhibited gabs = +1.3 × 10−2 at −10 °C. In a similar manner, (−)-sign CPL at 60 °C exhibited glum = –0.7 × 10−2 at λem 340 nm but was inverted to (+)-CPL with glum = +2.0 × 10−2 at 0 °C. Notably, in n-dodecane-d26, these gabs values are weaker by an order of magnitude at the lower TC1 and associated with opposite CD signs.
The notable H/D effects between n-dodecane-h26 and -d26 led to the proposal that the three-fold symmetrical CH3 groups of n-dodecane and the n-butyl pendants of PDBS work cooperatively as a unidirectional perpetual hindered rotor with handedness owing to three non-vanishing nuclear spin-1/2 systems in a triple-well potential. The CD3 group is an inefficient hindered rotor compared to the CH3 group because of the inherent difference in the moments of inertia and rotational constants between the CD3 and CH3 rotors. Several (−)-sign VCD signals characteristic of the asymmetric and symmetric bending modes of CH3/CD3, scissoring and twisting modes of CH2/CD2, and gauche-bonds of n-dodecane-h26 were detected.
More interestingly, CW and CCW stirring in several n-alkanes at 0–40 °C induced completely non-mirror-image CD spectra of PDBS, which is consistent with the coupling of EWF with gravitational force, and which causes apparent P-symmetry breaking on Earth. The handedness of the CH3 rotor may provide a possible answer to the issue of the missing link of handedness at all hierarchical levels, ranging from LH–νe, LH quarks, optically active atoms, biological proteins, DNA/RNA, homochiral living biospheres, and cosmological dextrorotatory rotation. Several handed molecular rotors of three identical nuclear spin-1/2 atoms in a triple-well potential could allow the future synthesis of RH- and LH-chiral molecules and/or helical polymers by optimizing achiral solvents at specific temperatures in the absence of conventional chemical chirality.
Several experimental studies that may provide evidence for the MPV hypothesis have been introduced and briefly discussed. A dozen of the simplest molecules carrying handed rotors without point chirality were proposed to verify the MPV hypothesis.
The term “chirogenesis” in the title was coined by Victor Borovkov and Yoshihisa Inoue in supramolecular chemistry and materials chemistry, based on the nuclear-spin-independent PC-EMF [328,329,330,331]. Nuclear-spin-dependent chirogenesis may be widely applicable to PV-EWF in general chemistry, a range of spectroscopy, molecular dynamics and molecular mechanics, materials science, quantum dynamics and quantum mechanics, particle physics, atomic physics, molecular physics, biology, astronomy, gravity theory, and cosmology.
5. Experimental Section
The synthesis and characterization of the monomers and polymers are summarized in the Supplementary Materials. All solvents were used as received. Instrumentation and analysis of NMR (1H, 13C, 29Si), VT-CD/UV, VT-CPL/PL, VT-VCD/IR spectroscopic data, and Gaussian 09 calculations obtained with PM3MM, DFT (B3LYP with 6-31G(d) basis set), and TD-DFT(B3LYP with 6-31G(d) basis set) are described in the Supplementary Materials. PBtBPS was synthesized by Wurtz-coupling of the corresponding diaryldichlorosilane [332]. PH2MPS and PH2EBS were synthesized by Wurtz-coupling of n-hexyl-2-methylpropyldichlorosilane and n-hexyl-2-ethylbutyldichlorosilane, respectively [106,333].
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/sym17030433/s1, Chart S1: The chemical structures of nine polysilanes, one oligosilane, and pyrromethenes 546 and 597; Chart S2: Three tridecasilane derivatives, tridecagermane derivative, and n-dodecane were studied theoretically using Gaussian 09; Figure S1: 1H-, 13C-, and 29Si-NMR spectra of PDBS-H in CDCl3; Figure S2: 1H-, 13C-, and 29Si-NMR spectra of PDBS-L in CDCl3; Figure S3: 1H-NMR spectrum of PMDS and PDES in CDCl3; Figure S4: GPC chart of PH2EBS, 13C-NMR spectrum of n-hexyl-2-ethybutyldichlorosilane in CDCl3, 29Si-NMR spectrum of n-hexyl-2-ethybutyldichlorosilane in CDCl3, 13C-NMR spectrum of PH2EBS in CDCl3, and 29Si-NMR spectrum of PH2EBS in CDCl3; Figure S5: CD and UV spectra of PDBS-L in isooctane, n-C8H18, n-C10H22, n-C12H26, n-C14H30, and n-C16H34 at 0 °C, 20 °C, and 40 °C, and the gabs value at 300 nm as a function of the carbon number of n-alkanes at 0 °C, 20 °C, and 40 °C; Figure S6: Raw CD and UV spectra of PDBS-H in n-C12H26 at three temperatures under static condition, including sample solution with a quartz cuvette subtracted from J-820 instrumental background, neat solvent with quartz cuvette subtracted from J-820 instrumental background, subtracted spectra, and a CD baseline of zero at 400 nm; Figure S7: CD and UV spectra of PDBS-H in n-C11H24 at 0 °C, 20 °C, and 40 °C and n-C14H30 at 7 °C, 40 °C, and 60 °C under static conditions; Figure S8: Specific volumes (cm3·g−1) of n-C11H24 and n-C12H26 as a function of temperature; Figure S9: Histograms of eight and three independent CPL measurements of PDBS-H excited at 300 nm in n-C12H26 at 25 °C (~TC2) and 60 °C (>TC2), respectively; Figure S10: CD/UV spectra of PDBS-L under static and CW, and CCW stirring conditions in n-C12H26 at 20 °C, n-C13H28 at 20 °C, n-C13H28 at 40 °C, n-C14H30 at 20 °C, n-C14H30 at 40 °C, n-C16H34 at 20 °C, and n-C16H34 at 40 °C; Figure S11: CD/UV spectra of PDBS-L in n-C12H26 at 0 °C (<TC2), 20 °C (~TC2), and 40 °C (>TC2) under static, CW, and CCW stirring at 1200 rpm; Figure S12: Schematic diagrams of racemization time in Trac as a function of EB; Figure S13: Potential energy surfaces as a function of the main chain dihedral angle obtained using PM3MM and DFT (B3LYP with 631Gd basis set, including H-(SiH2)13-H, Me-(SiMe2)13-Me, Et-(GeEt2)13-Et, and n-C12H26; Figure S14: Simulated CD and UV spectra including three singlet and three triplet states, dipole moments, and graphical geometries of ten conformations of n-C12H26; Figure S15: VCD and IR spectra of n-C12H26 at 10 °C, 25 °C, and 40 °C; Figure S16: VCD and IR spectra of n-C12D26 at 10 °C, 25 °C, and 40 °C; Figure S17: VCD and IR spectra at 25 °C of n-C8H18, n-C10H22, n-C13H28, n-C14H30, and n-C16H34; Figure S18: CD and UV spectra of PMDS in n-propanol at –10 °C, PDES in n-propanol at −10 °C, 10 °C, and 30 °C, PDES in n-butanol at 0 °C and 20 °C, PDES in n-hexanol at –10°C and 0°C, gabs at 315–319 nm of PDES in n-propanol as a function of temperature; Figure S19: CD and UV spectra of PBtBPS in THF at −10 °C, 25 °C, and 50 °C, PH2MPS in isooctane at 0 °C, PDBS-H in a mixture of n-C12H26 2.95 mL and THF 0.05 mL at 0 °C, 20 °C, and 45 °C, PH2EBS in n-dodecane at 20 °C, 30 °C, and 105 °C, PH2EBS in n-octanol at 0 °C, 20 °C, and 45 °C, gabs at 310 nm of PH2EBS in n-C12H26 and n-octanol as a function of temperature; Figure S20: VCD and IR spectra at 25 °C of n-C6F13, n-C8F17, CH3CN, CD3CN, toluene-h8, toluene-d8, and p-cymene (4-isopropyltoluene); Table S1: Comparisons of relative energy, dipole moment, and CD sign at λext of ten rotamers in n-C12H26.
Author Contributions
Conceptualization, M.F.; methodology, M.F.; validation, M.F., T.M., and M.M.A.; formal analysis, M.F., T.M., and M.M.A.; investigation, T.M., M.F., J.R.K., and M.M.A.; resources, M.F., J.R.K., and T.M.; data curation, M.F. and T.M.; writing—original draft preparation, M.F.; writing—review and editing, J.R.K., M.F., and M.M.A.; visualization, T.M. and M.F.; supervision, M.F.; project administration, M.F.; funding acquisition, M.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Japan Society for the Promotion of Science (JSPS)–KAKENHI Grants-in-Aid for Scientific Research [16655046 (FY2003–2005) and 22350052 (FY2010–2013)], the Sekisui Integrated Research Co. (SRI) (non-traditional design of helical polymers learning from the origin of homochirality, FY2009), the NAIST Foundation (FY2009), Japan Science and Technology Agency (JST): CREST program (design of hyperhelical polymers and understanding of structure-property-functionality relationship, FY1998–2003), and an in-house proposal at NTT Basic Research Laboratory (FY1994–1998).
Data Availability Statement
The data presented in this study are available on reasonable request from the corresponding author.
Acknowledgments
The authors are grateful to the respected scholars, researchers, and students listed in the acknowledgements of refs. [113,114], particularly Masaaki Ishikawa, Anubhav Saxena, Yoshihiro Kimura, Fumiko Ichiyanagi, Yasuko Nakamura, Yoko Nakano, Makoto Taguchi, Ayako Nakao, Nozomu Suzuki, Puhup Puneet, Nanami Ogata, and Seiko Amazumi in their days as students and researchers (FY 2002–2019) when they joined the MPV validation projects at NAIST. M.M.A. and M.F. thank Kotohiro Nomura (Tokyo Metropolitan University) for fruitful discussion and valuable comments. M.F. is thankful to Takashi Takakuwa, Yoshirou Kondo, Koushi Nagamori, and Nobuyuki Sakayanagi at JASCO for technical advice over three decades. Special thanks are given to Yasuo Nakanishi and Yoshio Morikage at JASCO Engineering Service (Osaka, Japan), who maintained the chiroptical spectrometers for many years. M.F. and J.R.K. express their gratitude to the late Hideki Sakurai (1931–2024, Tohoku University) and the late Robert West (1928–2022, University of Wisconsin–Madison) for stimulating comments and discussion around the helical polysilane projects over many years. M.F. is grateful to the late Meir Shinitzky (1939–2015, Weizmann Institute of Science) for sharing the MPV hypothesis.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hegstrom, R.A.; Kondepudi, D.K. The handedness of the universe. Sci. Am. 1990, 262, 108–115. [Google Scholar] [CrossRef]
- Morozov, L.L.; Kuz’min, V.V.; Goldanskii, V.I. Comparative analysis of the role of statistical fluctuations and factor of advantage (parity nonconservation) in the origins of optical activity. Orig. Life 1983, 13, 119–138. [Google Scholar] [CrossRef]
- Avetisov, V.A.; Goldanskii, V.I.; Kuz’min, V.V. Handedness, Origin of life and evolution. Phys. Today 1991, 44, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Mason, S.F. Chapter 11: Chiral energy discrimination. In Molecular Optical Activity and the Chiral Discriminations; Cambridge University Press: Cambridge, UK, 1982; ISBN 978-0521105637. [Google Scholar]
- Mason, S.F.; Tranter, G.E. The parity-violating energy difference between enantiomeric molecules. Mol. Phys. 1984, 53, 1091–1111. [Google Scholar] [CrossRef]
- Mason, S.F.; Tranter, G.E. The electroweak origin of biomolecular handedness. Proc. R. Soc. A Math. Phys. Sci. 1985, 397, 45–65. [Google Scholar] [CrossRef]
- Mason, S.F. Biomolecular homochirality. Chem. Soc. Rev. 1988, 17, 347–359. [Google Scholar] [CrossRef]
- Mason, S.F. Chemical Evolution: Origin of the Elements, Molecules, and Living Systems; Clarendon: Oxford, UK, 1991; ISBN 978-0198552727. [Google Scholar]
- Latal, H. Chapter 1: Parity violation in atomic physics. In Chirality: From Weak Bosons to the α–Helix; Janoschek, R., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 1–17. ISBN 978-3642765711. [Google Scholar] [CrossRef]
- Janoschek, R. Chapter 2: Theories on the origin of biomolecular homochirality. In Chirality: From Weak Bosons to the α–Helix; Janoschek, R., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 18–33. ISBN 978-3642765711. [Google Scholar] [CrossRef]
- Gardner, M. The New Ambidextrous Universe: Symmetry and Asymmetry from Mirror Reflections to Superstrings, 3rd ed.; Dover: Mineola, NY, USA, 1995; ISBN 978-0716720935. [Google Scholar]
- Compton, R.N.; Pagni, R.M. The chirality of biomolecules. Adv. Atom. Mol. Opt. Phys. 2002, 48, 219–261. [Google Scholar] [CrossRef]
- Barron, L. Molecular Light Scattering and Optical Activity, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; ISBN 978-0521121378. [Google Scholar]
- Wagnière, G.H. On Chirality and the Universal Asymmetry: Reflections on Image and Mirror Image; Wiley-VCH: Weinheim, GE, USA, 2007; ISBN 978-3906390383. [Google Scholar]
- Guijarro, A.; Yus, M. The Origin of Chirality in the Molecules of Life: A Revision from Awareness to the Current Theories and Perspectives of this Unsolved Problem; RSC: Cambridge, UK, 2008; ISBN 978-0854041565. [Google Scholar]
- Quack, M. On the measurement of the parity violating energy difference between enantiomers. Chem. Phys. Lett. 1986, 132, 147–153. [Google Scholar] [CrossRef]
- Quack, M. How important is parity violation for molecular and biomolecular chirality? Angew. Chem. Int. Ed. 2002, 41, 4618–4630. [Google Scholar] [CrossRef]
- Quack, M.; Stohner, J.; Willeke, M. High-resolution spectroscopic studies and theory of parity violation in chiral molecules. Annu. Rev. Phys. Chem. 2008, 59, 741–769. [Google Scholar] [CrossRef]
- Quack, M.; Seyfang, M.G.; Wichmann, G. Perspectives on parity violation in chiral molecules: Theory, spectroscopic experiment and biomolecular homochirality. Chem. Sci. 2022, 13, 10598–10643. [Google Scholar] [CrossRef] [PubMed]
- Sallembien, Q.; Bouteiller, L.; Crassous, J.; Raynal, M. Possible chemical and physical scenarios towards biological homochirality. Chem. Soc. Rev. 2022, 51, 3436–3476. [Google Scholar] [CrossRef]
- Fujiki, M. Experimental tests of parity violation at helical polysilylene level. Macromol. Rapid Commun. 2001, 22, 669–674. [Google Scholar] [CrossRef]
- Fujiki, M. Mirror symmetry breaking of silicon polymers—From weak bosons to artificial helix. Chem. Rec. 2009, 9, 271–298. [Google Scholar] [CrossRef]
- Fujiki, M. Mirror symmetry breaking in helical polysilanes: Preference between left and right of chemical and physical origin. Symmetry 2010, 2, 1625–1652. [Google Scholar] [CrossRef]
- Fujiki, M. Chapter 1: Chirogenesis in parity violation and weak forces. In Chirogenesis in Chemical Science; Borovkov, V., Aav, R., Eds.; World Scientific: Singapore, 2023; pp. 1–68. ISBN 978-9811259210. [Google Scholar] [CrossRef]
- Seljuk, U. Measuring polarization in the cosmic microwave background. Atrophys. J. 1997, 482, 6–16. [Google Scholar] [CrossRef]
- Kovac, J.M.; Leitch, E.M.; Pryke, C.; Carlstrom, J.E.; Halverson, N.W.; Holzapfel, W.L. Detection of polarization in the cosmic microwave background using DASI. Nature 2002, 420, 772–787. [Google Scholar] [CrossRef] [PubMed]
- National Research Council; Division on Engineering, Physical Sciences; Board on Physics; Committee on the Physics of the Universe. Connecting Quarks with the Cosmos: Eleven Science Questions for the New Century; National Academic Press: Washington, DC, USA, 2003; ISBN 978-0309074063. [Google Scholar]
- Minami, Y.; Komatsu, E. New extraction of the cosmic birefringence from the Planck 2018 polarization Data. Phys. Rev. Lett. 2020, 125, 221301. [Google Scholar] [CrossRef]
- Komatsu, E. New physics from the polarised light of the cosmic microwave background. Nat. Rev. Phys. 2022, 4, 452–469. [Google Scholar] [CrossRef]
- Hou, J.; Slepian, Z.; Cahn, R.N. Measurement of parity-odd modes in the large-scale 4-point correlation function of Sloan digital survey baryon oscillation spectroscopic survey twelfth data release CMASS and LOWZ galaxies. Mon. Not. R. Astron. Soc. 2023, 522, 5701–5739. [Google Scholar] [CrossRef]
- Standard Model. Available online: https://en.wikipedia.org/wiki/Standard_Model (accessed on 20 January 2025).
- Particle Physics. Available online: https://en.wikipedia.org/wiki/Particle_physics (accessed on 8 January 2025).
- Beta Decay. Available online: https://en.wikipedia.org/wiki/Beta_decay (accessed on 19 January 2025).
- Sgouros, G.; Bodei, L.; McDevitt, M.R.; Nedrow, J.R. Radiopharmaceutical therapy in cancer: Clinical advances and challenges. Nat. Rev. Drug Discov. 2020, 19, 589–608. [Google Scholar] [CrossRef]
- Hasert, F.J.; Kabe, S.; Krenz, W.; Von Krogh, J.; Lanske, D.; Morfin, J.; Schultze, K.; Weerts, H.; Bertrand-Coremans, G.; Sacton, J.; et al. Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment. Nucl. Phys. B 1974, 73, 1–22. [Google Scholar] [CrossRef]
- Haidt, D. Chapter 7: The discovery of weak neutral currents. In 60 Years of CERN Experiments and Discovery; Schopper, H., Di Lella, L., Eds.; World Scientific: Singapore, 2015; pp. 165–183. ISBN 978-9814644143. [Google Scholar] [CrossRef]
- Bagnaia, P.; Banner, M.; Battiston, R.; Bloch, P.; Bonaudi, F.; Borer, K.; Borghini, M.; Chollet, J.-C.; Clark, A.G.; Conta, C.; et al. (The UA2 Collaboration). Evidence for Z0→e+e− at the CERN pp collider. Phys. Lett. B 1983, 129, 130–140. [Google Scholar] [CrossRef]
- Arnison, G.T.; Astbury, A.; Aubert, B.; Bacci, C.; Bauer, G.; Bezaguet, A.; Böck, R.; Bowcock, T.J.V.; Calvetti, M.; Catz, P.; et al. (The UA2 Collaboration). Experimental observation of lepton pairs of invariant mass around 95 GeV/c2 at the CERN SPS collider. Phys. Lett. B 1983, 126, 398–410. [Google Scholar] [CrossRef]
- Di Lella, L.; Rubbia, C. Chapter 6: The discovery of the W and Z particles. In 60 Years of CERN Experiments and Discovery; Schopper, H., Di Lella, L., Eds.; World Scientific: Singapore, 2015; pp. 137–163. ISBN 978-9814644143. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. Electromagnetic interaction with parity violation. Sov. Phys. JETP 1958, 6, 1184–1186. Available online: http://www.jetp.ras.ru/cgi-bin/dn/e_006_06_1184.pdf (accessed on 7 March 2025).
- Zel’dovich, Y.B. Parity nonconservation in the first order in the weak-interaction constant in electron scattering and other effects. Sov. Phys. JETP Lett. 1959, 9, 682–683. Available online: www.jetp.ras.ru/cgi-bin/dn/e_009_03_0682.pdf (accessed on 7 March 2025).
- Zel’dovich, Y.B.; Perelomov, A.M. The effect of weak interaction on the electromagnetic properties of particles. Sov. Phys. JETP 1961, 12, 777–784. Available online: https://www.osti.gov/biblio/4097351 (accessed on 7 March 2025).
- Michel, F.C. Parity nonconservation in nuclei. Phys. Rev. 1964, 133, B329–B349. [Google Scholar] [CrossRef]
- Stodolsky, L. Neutron optics and weak currents. Phys. Lett. B 1974, 50, 352–356. [Google Scholar] [CrossRef]
- Stodolsky, L. Parity violation in threshold neutron scattering. Nucl. Phys. B 1982, 197, 213–227. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Bouchiat, C. Weak neutral currents in atomic physics. Phys. Lett. B 1974, 48, 111–114. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Bouchiat, C.I. Parity violation induced by weak neutral currents in atomic physics. J. Phys. 1974, 35, 899–927. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Bouchiat, C. Parity violation induced by weak neutral currents in atomic physics. Part II. J. Phys. 1975, 36, 493–509. [Google Scholar] [CrossRef]
- Bouchiat, M.-A.; Bouchiat, C. Parity Violation in Atoms and Polarized Electron Scattering; Atomic parity violation: An overview; Frois, B., Bouchiat, M.-A., Eds.; World Scientific: Singapore, 1999; pp. 191–243. ISBN 978-9810237318. [Google Scholar]
- Hegstrom, R.A.; Chamberlain, J.P.; Seto, K.; Watson, R.G. Mapping the weak chirality of atoms. Am. J. Phys. 1988, 56, 1086–1091. [Google Scholar] [CrossRef]
- Baird, P.E.G.; Brimicombe, M.W.S.M.; Roberts, G.J.; Sandars, P.G.H.; Soreide, D.C.; Fortson, E.N.; Lewis, L.L.; Lindahl, E.G.; Soreide, D.C. Search for parity non-conserving optical rotation in atomic bismuth. Nature 1976, 264, 528–529. [Google Scholar] [CrossRef]
- Fortson, E.N.; Wilets, L. Parity nonconservation in atoms: Status of theory and experiment. Adv. Atom. Mol. Phys. 1980, 16, 319–373. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Guena, J.; Hunter, L.; Pottier, L. Observation of a parity violation in cesium. Phys. Lett. B 1982, 117, 358–364. [Google Scholar] [CrossRef]
- Fortson, E.N.; Lewis, L.L. Atomic parity nonconservation experiments. Phys. Rep. 1984, 113, 289–344. [Google Scholar] [CrossRef]
- Bouchiat, M.-A.; Bouchiat, C. Parity violation in atoms. Rep. Prog. Phys. 1997, 60, 1351–1396. [Google Scholar] [CrossRef]
- Forte, M.; Heckle, B.R.; Ramsey, N.F.; Green, K.; Ramsey, G.L.; Byrne, J.; Pendlebury, J.M. First measurement of parity-nonconserving neutron-spin rotation: The tin isotopes. Phys. Rev. Lett. 1980, 45, 2088–2091. [Google Scholar] [CrossRef]
- Alfimenkov, V.P.; Borzakov, S.B.; Van Thuan, V.; Mareev, Y.D.; Pikelner, L.B.; Khrykin, A.S.; Sharapov, E.I. Parity nonconservation in neutron resonances. Nucl. Phys. A 1983, 398, 93–106. [Google Scholar] [CrossRef]
- Yuan, V.W.; Bowman, C.D.; Bowman, J.D.; Bush, J.E.; Delheij, P.P.J.; Frankle, C.M.; Gould, C.R.; Haase, D.G.; Knundson, J.N.; Mitchell, G.E.; et al. Parity nonconservation in polarized-neutron transmission through 139La. Phys. Rev. C 1991, 44, 2187–2194. [Google Scholar] [CrossRef] [PubMed]
- Crawford, B.E.; Bowman, J.D.; Bowman, C.D.; Bush, J.E.; Delheij, P.P.J.; Frankle, C.M.; Gould, C.R.; Haase, D.G.; Knudson, J.; Mitchell, G.E.; et al. Parity nonconservation for neutron resonances in 238U. Phys. Rev. Lett. 1990, 65, 1192–1195. [Google Scholar] [CrossRef]
- Mitchell, G.E.; Bowman, J.D.; Weidenmüller, H.A. Parity violation in the compound nucleus. Rev. Mod. Phys. 1999, 71, 445–457. [Google Scholar] [CrossRef]
- Smith, D.A.; Bowman, D.; Crawford, B.E.; Grossmann, C.A.; Haseyama, T.; Johnson, M.B.; Masaike, A.; Matsuda, Y.; Mitchell, G.E.; Nazarenko, V.A.; et al. Parity violation in neutron resonances of 117Sn. Phys. Rev. C 2001, 64, 015502. [Google Scholar] [CrossRef]
- Yamagata, Y. A hypothesis for the asymmetric appearance of biomolecules on Earth. J. Theor. Biol. 1966, 11, 495–498. [Google Scholar] [CrossRef]
- Rein, D.W. Some remarks on parity violating effects of intramolecular interactions. J. Mol. Evol. 1974, 4, 15–22. [Google Scholar] [CrossRef]
- Letokhov, V.S. On difference of energy levels of left and right molecules due to weak interactions. Phys. Lett. A 1975, 53, 275–276. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Saakyan, D.B.; Sobel’Man, I.I. Energy difference between right–hand and left-hand molecules, due to parity nonconservation in weak interactions of electrons with nuclei. Sov. Phys. JETP Lett. 1977, 25, 94–97. Available online: http://jetpletters.ru/ps/1388/article_21066.pdf (accessed on 7 March 2025).
- Keszthelyi, L. Origin of the asymmetry of biomolecules and weak interaction. Orig. Life 1977, 8, 299–340. [Google Scholar] [CrossRef]
- Harris, R.A.; Stodolsky, L. Quantum beats in optical activity and weak interactions. Phys. Lett. B 1978, 78, 313–317. [Google Scholar] [CrossRef]
- Rein, D.W.; Hegstrom, R.A.; Sandars, P.G.H. Parity non-conserving energy difference between mirror image molecules. Phys. Lett. A 1979, 71, 499–502. [Google Scholar] [CrossRef]
- Thiemann, W.; Darge, W. Experimental attempts for the study of the origin of optical activity on earth. Orig. Life 1974, 5, 263–283. [Google Scholar] [CrossRef] [PubMed]
- Hegstrom, R.A.; Rein, D.W.; Sandars, P.G.H. Calculation of the parity nonconverging energy difference between mirror-image molecules. J. Chem. Phys. 1980, 73, 2329–2341. [Google Scholar] [CrossRef]
- Mason, S.F.; Tranter, G.E. Energy inequivalence of peptide enantiomers from parity non-conservation. J. Chem. Soc. Chem. Commun. 1983, 117–119. [Google Scholar] [CrossRef]
- Tranter, G.E. Preferential stabilization of the D-sugar series by the parity-violating weak interactions. J. Chem. Soc. Chem. Commun. 1986, 60–61. [Google Scholar] [CrossRef]
- Wiesenfeld, L. Effect of atomic number on parity-violating energy differences between enantiomers. Mol. Phys. 1988, 64, 739–745. [Google Scholar] [CrossRef]
- Laerdahl, J.K.; Wesendrup, R.; Schwerdtfeger, P. D- or L-alanine: That is the question. ChemPhysChem 2000, 60–62. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Gierlich, J.; Bollwein, T. Large parity-violation effects in heavy-metal-containing chiral compounds. Angew. Chem. Int. Ed. 2003, 42, 1293–1296. [Google Scholar] [CrossRef]
- Crassous, J.; Chardonnet, C.; Saue, T.; Schwerdtfeger, P. Recent experimental and theoretical developments towards the observation of parity violation (PV) effects in molecules by spectroscopy. Org. Biomol. Chem. 2005, 3, 2218–2224. [Google Scholar] [CrossRef]
- Fiechter, M.R.; Haase, P.A.B.; Saleh, N.; Soulard, P.; Tremblay, B.; Havenith, R.W.A.; Timmermans, R.G.E.; Schwerdtfeger, P.; Crassous, J.; Darquié, B.; et al. Toward detection of the molecular parity violation in chiral Ru(acac)3 and Os(acac)3. J. Phys. Chem. Lett. 2022, 13, 10011–10017. [Google Scholar] [CrossRef]
- Pagni, R.M.; Compton, R.N. Asymmetric synthesis of optically active sodium chlorate and bromate crystals. Cryst. Grow. Des. 2002, 2, 249–253. [Google Scholar] [CrossRef]
- Macdermott, A.J.; Tranter, G.E. The search for large parity-violating energy differences between enantiomers. Chem. Phys. Lett. 1989, 163, 1–4. [Google Scholar] [CrossRef]
- MacDermott, A.J.; Hegstrom, R.A. A proposed experiment to measure the parity-violating energy difference between enantiomers from the optical rotation of chiral ammonia-like “cat” molecules. Chem. Phys. 2004, 305, 55–68. [Google Scholar] [CrossRef]
- Macdermott, A.J. Chiroptical signatures of life and fundamental physics. Chirality 2012, 24, 764–769. [Google Scholar] [CrossRef]
- Zanasi, R.; Lazzeretti, P. On the stabilization of natural L-enantiomers of α-amino acids via parity-violating effects. Chem. Phys. Lett. 1998, 286, 240–242. [Google Scholar] [CrossRef]
- Zanasi, R.; Lazzeretti, P.; Ligabue, A.; Soncini, A. Theoretical results which strengthen the hypothesis of electroweak bioenantioselection. Phys. Rev. E 1999, 59, 3382–3385. [Google Scholar] [CrossRef]
- Bargueño, P.; Gonzalo, I.; de Tudela, R.P. Detection of parity violation in chiral molecules by external tuning of electroweak optical activity. Phys. Rev. A 2009, 80, 012110. [Google Scholar] [CrossRef]
- Gonzalo, I.; Bargueño, P.; de Tudela, R.P.; Miret-Artés, S. Towards the detection of parity symmetry breaking in chiral molecules. Chem. Phys. Lett. 2010, 489, 127–129. [Google Scholar] [CrossRef]
- Bargueño, P.; de Tudela, R.P.; Miret-Artés, S.; Gonzalo, I. An alternative route to detect parity violating energy differences through Bose–Einstein condensation of chiral molecules. Phys. Chem. Chem. Phys. 2011, 13, 806–810. [Google Scholar] [CrossRef]
- Dorta-Urra, A.; Peñate-Rodríguez, H.C.; Bargueño, P.; Rojas-Lorenzo, G.; Miret-Artés, S. Dissipative geometric phase and decoherence in parity-violating chiral molecules. J. Chem. Phys. 2012, 136, 174505. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Gil, D.; Bargueño, P.; Miret-Artés, S. The interplay between tunneling and parity violation in chiral molecules. Entropy 2024, 26, 456. [Google Scholar] [CrossRef] [PubMed]
- Eills, J.; Blanchard, J.W.; Bougas, L.; Kozlov, M.G.; Pines, A.; Budker, D. Measuring molecular parity nonconservation using nuclear-magnetic-resonance spectroscopy. Phys. Rev. A 2017, 96, 042119. [Google Scholar] [CrossRef]
- Blanchard, J.W.; King, J.P.; Sjolander, T.F.; Kozlov, M.G.; Budker, D. Molecular parity nonconservation in nuclear spin couplings. Phys. Rev. Res. 2020, 2, 023258. [Google Scholar] [CrossRef]
- Wilen, S.H.; Eliel, E.L.; Mander, L.N. Stereochemistry of Organic Compounds; Wiley-Interscience: New York, NY, USA, 1994; ISBN 978-0471016700. [Google Scholar]
- Mislow, K. Introduction to Stereochemistry; Dover: Mineola, NY, USA, 2003; ISBN 978-0486425306. [Google Scholar]
- Berova, N.; Polavarapu, P.; Nakanishi, K.; Woody, R.W. Comprehensive Chiroptical Spectroscopy, Volume 1: Instrumentation, Methodologies, and Theoretical Simulations; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-1118012932. [Google Scholar]
- Berova, N.; Polavarapu, P.; Nakanishi, K.; Woody, R.W. Comprehensive Chiroptical Spectroscopy, Volume 2: Applications in Stereochemical Analysis of Synthetic Compounds, Natural Products, and Biomolecules; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-1118012925. [Google Scholar]
- Szabó-Nagy, A.; Keszthelyi, L. Demonstration of the parity-violating energy difference between enantiomers. Proc. Natl. Acad. Sci. USA 1999, 96, 4252–4255. [Google Scholar] [CrossRef]
- Wang, W.; Yi, F.; Ni, Y.; Zhao, Z.; Jin, X.; Tang, Y. Parity violation of electroweak force in phase transitions of single crystals of D-and L-alanine and valine. J. Biol. Phys. 2000, 26, 51–65. [Google Scholar] [CrossRef]
- Wang, W.-Q.; Min, W.; Liang, Z.; Wang, L.-Y.; Chen, L.; Deng, F. NMR and parity violation: Low-temperature dependence in 1H CRAMPS and 13C CP/MAS ssNMR spectra of alanine enantiomer. Biophys. Chem. 2003, 103, 289–298. [Google Scholar] [CrossRef]
- Shinitzky, M.; Haimovitz, R. Chiral surfaces in micelles of enantiomeric N-palmitoyl- and N-stearoylserine. J. Am. Chem. Soc. 1993, 115, 12545–12549. [Google Scholar] [CrossRef]
- Shinitzky, M.; Nudelman, F.; Barda, Y.; Haimovitz, R.; Chen, E.; Deamer, D.W. Unexpected differences between D-and L-tyrosine lead to chiral enhancement in racemic mixtures. Orig. Life Evol. Biosph. 2002, 32, 285–297. [Google Scholar] [CrossRef]
- Scolnik, Y.; Portnaya, I.; Cogan, U.; Tal, S.; Haimovitz, R.; Fridkin, M.; Elitzur, A.C.; Deamer, D.W.; Shinitzky, M. Subtle differences in structural transitions between poly-L- and poly-D-amino acids of equal length in water. Phys. Chem. Chem. Phys. 2006, 8, 333–339. [Google Scholar] [CrossRef]
- Shinitzky, M.; Elitzure, A.C. Ortho–para spin isomers of the protons in the methylene group—Possible implications for protein structure. Chirality 2006, 18, 754–756. [Google Scholar] [CrossRef] [PubMed]
- Deamer, D.W.; Dick, R.; Thiemann, W.; Shinitzky, M. Intrinsic asymmetries of amino acid enantiomers and their peptides: A possible role in the origin of biochirality. Chirality 2007, 19, 751–763. [Google Scholar] [CrossRef] [PubMed]
- Shinitzky, M. Space asymmetry as a possible global feature. Chirality 2013, 25, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Shinitzky, M. Information storage in liquids with ordered molecular assemblies. Entropy 2011, 13, 1–10. [Google Scholar] [CrossRef]
- Kodona, E.K.; Alexopoulos, C.; Panou-Pomonis, E.; Pomonis, P.J. Chirality and helix stability of polyglutamic acid enantiomers. J. Colloid Interface. Sci. 2008, 319, 72–80. [Google Scholar] [CrossRef]
- Fujiki, M.; Okazaki, S.; Rahim, N.A.A.; Yamada, T.; Nomura, K. Synchronization in non-mirror-symmetrical chirogenesis: Non-helical π–conjugated polymers with helical polysilane copolymers in co-colloids. Symmetry 2021, 13, 594. [Google Scholar] [CrossRef]
- Salam, A. The role of chirality in the origin of life. J. Mol. Evol. 1991, 33, 105–113. [Google Scholar] [CrossRef]
- Salam, A. Chirality, phase transitions and their induction in amino acids. Phys. Lett. B 1992, 288, 153–160. [Google Scholar] [CrossRef]
- Gabuda, S.P.; Kozlova, S.G. Abnormal difference between the mobilities of left- and right-twisted conformations of C6H12N2 roto-symmetrical molecules at very low temperatures. J. Chem. Phys. 2015, 142, 234302. [Google Scholar] [CrossRef]
- Kozlova, S.G.; Mirzaeva, I.V.; Ryzhikov, M.R. DABCO molecule in the M2(C8H4O4)2·C6H12N2 (M = Co, Ni, Cu, Zn) metal-organic frameworks. Coord. Chem. Rev. 2018, 376, 62–74. [Google Scholar] [CrossRef]
- Kozlova, S.G.; Gabuda, S.P. Thermal properties of Zn2(C8H4O4)2·C6H12N2 metalorganic framework compound and mirror symmetry violation of dabco molecules. Sci. Rep. 2017, 7, 11505. [Google Scholar] [CrossRef] [PubMed]
- Kozlova, S.; Ryzhikov, M.; Pishchur, D.; Mirzaeva, I. Overview of low-temperature heat capacity data for Zn2(C8H4O4)2·C6H12N2 and the Salam hypothesis. Symmetry 2019, 11, 657. [Google Scholar] [CrossRef]
- Fujiki, M.; Koe, J.R.; Mori, T.; Kimura, Y. Questions of mirror symmetry at the photoexcited and ground states of non-rigid luminophores raised by circularly polarized luminescence and circular dichroism spectroscopy: Part 1. Oligofluorenes, oligophenylenes, binaphthyls and fused aromatics. Molecules 2018, 23, 2606. [Google Scholar] [CrossRef]
- Fujiki, M.; Koe, J.R.; Amazumi, S. Questions of mirror symmetry at the photoexcited and ground states of non-rigid luminophores raised by circularly polarized luminescence and circular dichroism spectroscopy. Part 2: Perylenes, BODIPYs, molecular scintillators, coumarins, rhodamine B, and DCM. Symmetry 2019, 11, 363. [Google Scholar] [CrossRef]
- Puneet, P.; Singh, S.; Fujiki, M.; Nandan, B. Handed mirror symmetry breaking at the photo-excited state of π-conjugated rotamers in solutions. Symmetry 2021, 13, 272. [Google Scholar] [CrossRef]
- McGlynn, S.P.; Azumi, T.; Kinoshita, M. Molecular Spectroscopy of The Triplet State; Prentice-Hall: Englewood Coffs, NJ, USA, 1969; ISBN 978-0135996621. [Google Scholar]
- Turro, N.J. Modern Molecular Photochemistry; University Science Books: Sausalito, CA, USA, 1991; ISBN 978-0935702712. [Google Scholar]
- Matin, W.C. Table of spin-orbit energies for p-electrons in neutral atomic (core) np configurations. J. Res. Natl. Bur. Stand. A Phys. Chem. 1971, 75, 109–111. [Google Scholar] [CrossRef]
- Stone, N.J. Table of nuclear magnetic dipole and electric quadruple moments. At. Data Nucl. Data Tables 2014, 90, 75–176. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Khriplovich, I.B. P-odd nuclear force—A source of parity violation in atoms. Sov. Phys. JETP 1980, 52, 835–839. Available online: http://jetp.ras.ru/cgi-bin/dn/e_052_05_0835.pdf (accessed on 7 March 2025).
- Sushkov, O.P.; Flambaum, V.V.; Khriplovich, I.B. Possibility of investigating P- and T-odd nuclear forces in atomic and molecular experiments. Sov. Phys. JETP 1984, 60, 873–883. Available online: http://www.jetp.ras.ru/cgi-bin/dn/e_060_05_0873.pdf (accessed on 7 March 2025).
- Khriplovich, I.B. P-odd difference of hyperfine structure constants in optical isomers. Z. Phys. A 1985, 322, 507–509. [Google Scholar] [CrossRef]
- Khriplovich, I.B.; Pospelov, M.E. Anapole moment of a chiral molecule. Z. Phys. 1990, 47, 81–84. [Google Scholar] [CrossRef]
- Roberts, B.M.; Dzuba, V.A.; Flambaum, V.V. Parity and time-reversal violation in atomic systems. Annu. Rev. Nucl. Part. Sci. 2015, 65, 63–86. [Google Scholar] [CrossRef]
- Wood, C.S.; Bennett, S.C.; Cho, D.; Masterson, B.P.; Roberts, J.L.; Tanner, C.E.; Wieman, C.E. Measurement of parity nonconservation and an anapole moment in cesium. Science 1997, 275, 1759–1763. [Google Scholar] [CrossRef]
- Haxton, W.C.; Wieman, C.E. Atomic parity violation and nuclear anapole moments. Annu. Rev. Nucl. Part. Sci. 2001, 51, 261–293. [Google Scholar] [CrossRef]
- Barra, A.L.; Robert, J.B.; Wiesenfeld, L. Possible observation of parity nonconservation by high-resolution NMR. Europhys. Lett. 1988, 5, 217–222. [Google Scholar] [CrossRef]
- Kozlov, M.G.; Labzowsky, L.N. Parity Violation effects in diatomics. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 1933–1961. [Google Scholar] [CrossRef]
- DeMille, D.; Cahn, S.B.; Murphree, D.; Rahmlow, D.A.; Kozlov, M.G. Using molecules to measure nuclear spin-dependent parity violation. Phys. Rev. Lett. 2008, 100, 023003. [Google Scholar] [CrossRef]
- Altuntaş, E.; Ammon, J.; Cahn, S.B.; DeMille, D. Demonstration of a sensitive method to measure nuclear-spin-dependent parity violation. Phys. Rev. A 2018, 120, 142501. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Navrátil, P.; Norrgard, E.B.; Iliaš, M.; Eliav, E.; Timmermans, R.G.E.; Flambaum, V.V.; Borschevsky, A. Nuclear spin-dependent parity-violating effects in light polyatomic molecules. Phys. Rev. A 2020, 102, 052828. [Google Scholar] [CrossRef]
- Laerdahl, J.K.; Schwerdtfeger, P. Fully relativistic ab initio calculations of the energies of chiral molecules including parity-violating weak interactions. Phys. Rev. A 1999, 60, 4439–4453. [Google Scholar] [CrossRef]
- Aucar, I.A.; Borschevsky, A. Relativistic study of parity-violating nuclear spin-rotation tensors. J. Chem. Phys. 2021, 155, 134307. [Google Scholar] [CrossRef] [PubMed]
- Aucar, A.; Jofré, M.T.C.; Aucar, G.A. Relativistic relationship between nuclear-spin-dependent parity-violating NMR shielding and nuclear spin-rotation tensors. J. Chem. Phys. 2023, 152, 094306. [Google Scholar] [CrossRef] [PubMed]
- Fabian, H.; Berger, R.; Stohner, J. Investigation of parity violation in nuclear spin-rotation interaction of fluorooxirane. Mol. Phys. 2013, 111, 2345–2362. [Google Scholar] [CrossRef]
- Rauhut, G.; Schwerdtfeger, P. Parity-violation effects in the vibrational spectra of CHFClBr and CDFClBr. Phys. Rev. A 2021, 103, 042819. [Google Scholar] [CrossRef]
- Aucar, I.A.; Chamorro, Y.; Borschevsky, A. Parity-violating contributions to nuclear spin-rotation interactions and to NMR shielding constants in tetrahedral molecules. Phys. Rev. A 2022, 106, 062802. [Google Scholar] [CrossRef]
- Fukuyama, T.; Momose, T.; Nomura, D. Anapole moment of a chiral molecule revisited. Eur. Phys. J. D 2015, 69, 264. [Google Scholar] [CrossRef]
- Zarycz, N.; Provasi, P.F.; Pagola, G.I.; Ferraro, M.B.; Pelloni, S.; Lazzeretti, P. Computational study of basis set and electron correlation effects on anapole magnetizabilities of chiral molecules. J. Comput. Chem. 2016, 37, 1552–1558. [Google Scholar] [CrossRef]
- Norrgard, E.B.; Barker, D.S.; Eckel, S.; Fedchak, J.A.; Klimov, N.N.; Scherschligt, J. Nuclear-spin dependent parity violation in optically trapped polyatomic molecules. Commun. Phys. 2019, 2, 77. [Google Scholar] [CrossRef]
- Kaelberer, T.; Fedotov, V.A.; Papasimakis, N.; Tsai, D.P.; Zheludev, N.I. Toroidal dipolar response in a metamaterial. Science 2010, 330, 1510–1512. [Google Scholar] [CrossRef]
- Ungur, L.; Lin, S.-Y.; Tang, J.; Chibotaru, L.F. Single-molecule toroics in Ising-type lanthanide molecular clusters. Chem. Soc. Rev. 2014, 43, 6894–6905. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Evlyukhin, A.B.; Yu, Y.F.; Bakker, R.M.; Chipouline, A.; Kuznetsov, A.I.; Luk’yanchuk, B.; Chichkov, B.N.; Kivshar, Y.S. Nonradiating anapole modes in dielectric nanoparticles. Nat. Commun. 2015, 6, 8069. [Google Scholar] [CrossRef] [PubMed]
- Savukov, I.M.; Lee, S.-K.; Romalis, M.V. Optical detection of liquid-state NMR. Nature 2006, 442, 1021–1024. [Google Scholar] [CrossRef]
- Shi, J.; Ikäläinen, S.; Vaara, J.; Romalis, M.V. Observation of optical chemical shift by precision nuclear spin optical rotation measurements and calculations. J. Phys. Chem. Lett. 2013, 4, 437–441. [Google Scholar] [CrossRef][Green Version]
- Vaara, J.; Rizzo, A.; Kauczor, J.; Norman, P.; Coriani, S. Nuclear spin circular dichroism. J. Chem. Phys. 2014, 140, 134103. [Google Scholar] [CrossRef] [PubMed]
- Kipping, F.S.; Pope, W.J. LXXXVIIL—Racemism and pseudoracemism. J. Chem. Soc. Trans. 1897, 71, 989–1001. [Google Scholar] [CrossRef]
- Kipping, F.S.; Pope, W.J. LXIIL—Enantiomorphism. J. Chem. Soc. Trans. 1898, 73, 606–617. [Google Scholar] [CrossRef]
- Mishima, K.; Kaji, D.; Fujiki, M.; Imai, Y. Remarkable effects of external magnetic field on circularly polarized luminescence of EuIII(hfa)3 with phosphine chirality. ChemPhysChem 2021, 22, 1728–1737. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V.; Khriplovich, I.B. Enhancement of P- and T-nonconserving effects in rare-earth atoms. Z. Phys. D 1986, 1, 243–245. [Google Scholar] [CrossRef]
- Labzowsky, L.N.; Nefiodov, A.V.; Plunien, G.; Soff, G.; Marrus, R.; Liesen, D. Parity-violation effect in heliumlike gadolinium and europium. Phys. Rev. A 2001, 63, 054105. [Google Scholar] [CrossRef]
- Sasanuma, Y.; Kato, H.; Kaito, A. Conformational analysis of poly(di-n-butylsilane), poly(di-n-hexylsilane), and poly(methyl-n-propylsilane) by a rotational isomeric state scheme with molecular dynamics simulations. J. Phys. Chem. B 2003, 107, 11852–11860. [Google Scholar] [CrossRef]
- Kato, H.; Sasanuma, Y.; Kaito, A.; Tanigaki, N.; Tanabe, Y.; Kinugasa, S. Unperturbed chain dimensions of poly(di-n-hexylsilane), poly(methyl-n-propylsilane), and poly(di-n-butylsilane). Macromolecules 2001, 34, 262–268. [Google Scholar] [CrossRef]
- Schilling, F.C.; Lovinger, A.J.; Zeigler, J.M.; Davis, D.D.; Bovey, F.A. Solid-state structures and thermochromism of poly(di-n-butylsilylene) and poly(di-n-pentylsilylene). Macromolecules 1989, 22, 3055–3063. [Google Scholar] [CrossRef]
- Schweizer, K.S.; Harrah, L.A.; Zeigler, J.M. Chapter 22: Order-disorder transitions and thermochromism of polysilylenes in solution. In Silicon-Based Polymer Science: A Comprehensive Resource; Zeigler, J.M., Fearon, F.G., Eds.; ACS: Washington, DC, USA, 1989; pp. 379–395. ISBN 978-0841215467. [Google Scholar]
- Miller, R.D.; Michl, J. Polysilane high polymers. Chem. Rev. 1989, 89, 1359–1410. [Google Scholar] [CrossRef]
- Teramae, H.; Takeda, K. Ab initio studies on silicon compounds. 2. On the gauche structure of the parent polysilane. J. Am. Chem. Soc. 1989, 111, 1281–1285. [Google Scholar] [CrossRef]
- Tachibana, H.; Matsumoto, M.; Tokura, Y.; Moritomo, Y.; Yamaguchi, A.; Koshihara, S.; Miller, R.D.; Abe, S. Spectra of one-dimensional excitons in polysilanes with various backbone conformations. Phys. Rev. B 1993, 47, 4363–4371. [Google Scholar] [CrossRef]
- Fujiki, M. Effect of main chain length in the exciton spectra of helical-rod polysilanes as a model of a 5 Å wide quantum wire. Appl. Phys. Lett. 1994, 65, 3251–3253. [Google Scholar] [CrossRef]
- Fujiki, M. Optically active polysilylenes: State-of-the-art chiroptical polymers. Macromol. Rapid Commun. 2001, 22, 539–563. [Google Scholar] [CrossRef]
- Seki, S.; Terashima, Y.; Kunimi, Y.; Kawamori, T.; Tashiro, M.; Honda, Y.; Tagawa, S. The effects of free volumes on charge carrier transport in polysilanes probed by positron annihilation. Rad. Phys. Chem. 2003, 68, 501–505. [Google Scholar] [CrossRef]
- Seki, S.; Koizumi, Y.; Kawaguchi, T.; Habara, H.; Tagawa, S. Dynamics of positive charge carriers on Si chains of polysilanes. J. Am. Chem. Soc. 2004, 126, 3521–3528. [Google Scholar] [CrossRef]
- Kitao, T.; Bracco, S.; Comotti, A.; Sozzani, P.; Naito, M.; Seki, S.; Uemura, T.; Kitagawa, S. Confinement of single polysilane chains in coordination nanospaces. J. Am. Chem. Soc. 2015, 137, 5231–5238. [Google Scholar] [CrossRef]
- Neumann, F.; Teramae, H.; Downing, J.W.; Michl, J. Gauche, ortho, and anti conformations of saturated A4X10 chains: When will all six conformers exist? J. Am. Chem. Soc. 1998, 120, 573–582. [Google Scholar] [CrossRef]
- Michl, J.; West, R. Conformations of linear chains. Systematics and suggestions for nomenclature. Acc. Chem. Res. 2000, 33, 821–823. [Google Scholar] [CrossRef] [PubMed]
- Fogarty, H.A.; Ottosson, C.-H.; Michl, J. The five favored backbone conformations of n-Si4Et10: Cisoid, gauche, ortho, deviant, and transoid. J. Mol. Struct. Theochem. 2000, 506, 243–255. [Google Scholar] [CrossRef]
- Fujiki, M. Helix magic. Thermo-driven chiroptical switching and screw-sense inversion of flexible rod helical polysilylenes. J. Am. Chem. Soc. 2000, 122, 3336–3343. [Google Scholar] [CrossRef]
- Fujiki, M.; Koe, J.R.; Motonaga, M.; Nakashima, H.; Terao, K.; Teramoto, A. Computing handedness: Quantized and superposed switch and dynamic memory of helical polysilylene. J. Am. Chem. Soc. 2001, 123, 6253–6261. [Google Scholar] [CrossRef] [PubMed]
- Ohno, O.; Kaizu, Y.; Kobayashi, H. J-aggregate formation of a water-soluble porphyrin in acidic aqueous media. J. Chem. Phys. 1993, 99, 4128–4139. [Google Scholar] [CrossRef]
- Ribó, J.M.; Crusats, J.; Sagués, F.; Claret, J.; Rubires, R. Chiral sign induction by vortices during the formation of mesophases in stirred solutions. Science 2001, 292, 2063–2066. [Google Scholar] [CrossRef]
- Crusats, J.; El-Hachemi, E.; Ribó, J.M. Hydrodynamic effects on chiral induction. Chem. Soc. Rev. 2010, 39, 569–577. [Google Scholar] [CrossRef]
- Okano, K.; Taguchi, M.; Fujiki, M.; Yamashita, T. Circularly polarized luminescence of rhodamine B in a supramolecular chiral medium formed by a vortex flow. Angew. Chem. Int. Ed. 2011, 50, 12474–12477. [Google Scholar] [CrossRef]
- Tang, X.; Ji, X.; Li, Y.; Li, B.; Yang, Y. Achiral polydialkylsilane aggregates that record stirring direction. Chem. Asian J. 2016, 11, 852–857. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y.; Yan, F.; Liu, C.; Sang, Y.; Tian, F.; Feng, Q.; Duan, P.; Zhang, L.; Shi, X.; et al. Control over the emerging chirality in supramolecular gels and solutions by chiral microvortices in milliseconds. Nat. Commun. 2018, 9, 2599. [Google Scholar] [CrossRef] [PubMed]
- Kuroha, M.; Nambu, S.; Hattori, S.; Kitagawa, Y.; Niimura, K.; Mizuno, Y.; Hamba, F.; Ishii, K. Chiral Supramolecular nanoarchitectures from macroscopic mechanical rotations: Effects on enantioselective aggregation behavior of phthalocyanines. Angew. Chem. Int. Ed. 2019, 58, 18454–18459. [Google Scholar] [CrossRef] [PubMed]
- Landau, R.; Würflinger, A. PVT-daten von acetonitril, undecan und dodecan bis 3 kbar und –50 °C. druckabhangigkeit der umwandlungsvolumina, -enthalpien und -entropien. Ber. Bunsenges. Phys. Chem. 1980, 84, 895–902. [Google Scholar] [CrossRef]
- Laib, P.; Mittleman, D.M. Temperature-dependent terahertz spectroscopy of liquid n-alkanes. J. Infrared Millim. Terahertz Waves 2010, 31, 1015–1021. [Google Scholar] [CrossRef]
- Naidu, S.V.; Smith, F.A. Defects in the rotator and liquid phases of n-alkanes: A study using FTIR and positron annihilation. J. Phys. Cond. Matter 1994, 6, 3865–3878. [Google Scholar] [CrossRef]
- Anderson, P.W. More is different—Broken symmetry and the nature of the hierarchical structure of science. Science 1972, 177, 393. [Google Scholar] [CrossRef] [PubMed]
- Cooper, L.N. Bound electron pairs in a degenerate fermi gas. Phys. Rev. 1956, 104, 1189–1190. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Maxwell, E. Isotope effect in the superconductivity of mercury. Phys. Rev. 1950, 78, 477. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Serin, B.; Wright, W.H.; Nesbitt, L.B. Superconductivity of isotopes of mercury. Phys. Rev. 1950, 78, 487. [Google Scholar] [CrossRef]
- Garland, J.W., Jr. Isotope effect in superconductivity. Phys. Rev. Lett. 1963, 11, 114–119. [Google Scholar] [CrossRef]
- Power, P.P. Silicon, germanium, tin and lead analogues of acetylenes. Chem. Commun. 2003, 2091–2101. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09 (Rev.D.01); Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Narayanamurtic, V.; Pohl, R.O. Tunneling states of defects in solids. Rev. Mod. Phys. 1970, 42, 201–236. [Google Scholar] [CrossRef]
- Merzbacher, E. The early history of quantum tunneling. Phys. Today 2002, 55, 44–49. [Google Scholar] [CrossRef]
- Fujiki, M.; Jalilah, A.J.; Koe, J.R.; Nomura, K.; Suzuki, N.; Rahim, N.A.A.; Zhang, W. Chapter 17: Ultraweak intermolecular interactions in chirogenesis from noncharged CPL-/CD-silent molecules, oligomers, and polymers endowed with noncharged chiral terpenes, mono-/polysaccharides, and helical polysilanes. In Chiral Luminescence: From Molecules to Materials and Devices; Akagi, K., Ed.; Wiley-VCH: Weinheim, Germany, 2024; pp. 381–415. ISBN 978-3527351800. [Google Scholar] [CrossRef]
- Leggett, A.J. Bose-Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307–356. [Google Scholar] [CrossRef]
- Kikuchi, O.; Kiyonaga, H. Parity-violating energy shift of helical n-alkanes. J. Mol. Struct. Theochem. 1994, 312, 271–274. [Google Scholar] [CrossRef]
- Kiyonaga, H.; Morihashi, K.; Kikuchi, O. Calculation of contributions of one- and two-electron spin-orbit coupling terms to the parity-violating energy shifts for amino acids and helical alkanes. J. Chem. Phys. 1998, 108, 2041–2043. [Google Scholar] [CrossRef]
- Scherer, J.R.; Snyder, R.G. Raman spectra of liquid n-alkanes. II. Longitudinal acoustic modes and the gauche-trans energy difference. J. Chem. Phys. 1980, 72, 5798–5808. [Google Scholar] [CrossRef]
- Snyder, R.G. The structure of chain molecules in the liquid state: Low frequency Raman spectra of n-alkanes and perfluoro-n-alkanes. J. Chem. Phys. 1982, 76, 3921–3927. [Google Scholar] [CrossRef]
- Snyder, R.G.; Kim, Y. Conformation and low-frequency isotropic Raman spectra of the liquid n-alkanes C4–C9. J. Phys. Chem. 1991, 95, 602–610. [Google Scholar] [CrossRef]
- Snyder, R.G. Chain conformation from the direct calculation of the Raman spectra of the liquid n-alkanes C12–C20. J. Chem. Soc. Faraday Trans. 1992, 88, 1823–1833. [Google Scholar] [CrossRef]
- Thomas, L.L.; Christakis, T.J.; Jorgensen, W.L. Conformation of alkanes in the gas phase and pure liquids. J. Phys. Chem. B 2006, 110, 21198–21204. [Google Scholar] [CrossRef] [PubMed]
- Sěbek, J.; Pele, L.; Potma, E.O.; Gerber, R.B. Raman spectra of long chain hydrocarbons: Anharmonic calculations, experiment and implications for imaging of biomembranes. Phys. Chem. Chem. Phys. 2011, 13, 12724–12733. [Google Scholar] [CrossRef] [PubMed]
- Vansteenkiste, P.; van Speybroeck, V.; Marin, G.B.; Waroquier, M. Ab initio calculation of entropy and heat capacity of gas-phase n-alkanes using internal rotations. J. Phys. Chem. A 2003, 107, 3139–3145. [Google Scholar] [CrossRef]
- Smith, G.D.; Jaffe, R.L. Quantum chemistry study of conformational energies and rotational energy barriers in n-alkanes. J. Phys. Chem. 1996, 100, 18718–18724. [Google Scholar] [CrossRef]
- Snyder, R.G. Vibrational study of the chain conformation of the liquid n-paraffins and molten polyethylene. J. Chem. Phys. 1967, 47, 1316–1360. [Google Scholar] [CrossRef]
- Maroncelli, M.; Strauss, H.L.; Snyder, R.G. The distribution of conformational disorder in the high-temperature phases of the crystalline n-alkanes. J. Chem. Phys. 1980, 82, 2811–2827. [Google Scholar] [CrossRef]
- Maroncelli, M.; Qi, S.P.; Strauss, H.L.; Snyder, R.G. Nonplanar conformers and the phase behavior of solid n-alkanes. J. Am. Chem. Soc. 1982, 104, 6237–6247. [Google Scholar] [CrossRef]
- Brown, K.G.; Bicknell-Brown, E.; Ladjadj, M. Raman-active bands sensitive to motion and conformation at the chain termini and backbones of alkanes and lipids. J. Phys. Chem. 1987, 91, 3436–3442. [Google Scholar] [CrossRef]
- Menger, F.M.; D’Angelo, L.L. Does the conformation of hydrocarbon chains depend on solvation? J. Am. Chem. Soc. 1988, 110, 8241–8242. [Google Scholar] [CrossRef]
- Lüttschwager, N.O.B.; Suhm, M.A. Stretching and folding of 2-nanometer hydrocarbon rods. Soft Matter 2014, 10, 4885–4901. [Google Scholar] [CrossRef] [PubMed]
- Stumper, U. Dielectric absorption of liquid normal alkanes in the microwave and far infrared regions. Adv. Mol. Relax. Proc. 1975, 7, 189–208. [Google Scholar] [CrossRef]
- Hermiz, N.A.; Hasted, J.B.; Rosenberg, C. Microwave dielectric losses of n-alkanes. J. Chem. Soc. Faraday Trans. 1982, 78, 147–161. [Google Scholar] [CrossRef]
- Vij, J.K. Microwave and far-infra-red dielectric absorption in n-alkanes. II Nuovo Cimento D 1983, 2, 751–762. [Google Scholar] [CrossRef]
- Weinberg angle. Available online: https://en.wikipedia.org/wiki/Weinberg_angle (accessed on 9 March 2025).
- Koehler, J.S.; Dennison, D.M. Hindered rotation in methyl alcohol. Phys. Rev. 1940, 57, 1006–1021. [Google Scholar] [CrossRef]
- Hilt, R.; Hubbard, P.S. Nuclear magnetic relaxation of three spin systems undergoing hindered rotations. Phys. Rev. 1964, 134, A392–A398. [Google Scholar] [CrossRef]
- Runnels, L.K. Nuclear spin-lattice relaxation in three-spin molecules. Phys. Rev. 1964, 134, A28–A36. [Google Scholar] [CrossRef]
- Gabay, M.; Toulouse, G. Coexistence of spin-glass and ferromagnetic orderings. Phys. Rev. Lett. 1981, 47, 201–203. [Google Scholar] [CrossRef]
- Khan, O. Competing spin interactions and degenerate frustration for discrete molecular species. Chem. Phys. Lett. 1997, 265, 109–114. [Google Scholar] [CrossRef]
- Schnack, J. Effects of frustration on magnetic molecules: A survey from Olivier Kahn till today. Dalton Trans. 2010, 39, 4677–4686. [Google Scholar] [CrossRef]
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Krzyaniak, M.D.; Stoddart, J.F.; Wasielewski, M.R. Spin frustration in the triradical trianion of a naphthalenediimide, molecular triangle. J. Am. Chem. Soc. 2017, 139, 2948–2951. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Wang, X. Spin frustration in organic radicals. Angew. Chem. Int. Ed. 2024, 63, e202310147. [Google Scholar] [CrossRef]
- Prager, M.A. Heidemann. Rotational tunneling and neutron spectroscopy: A compilation. Chem. Rev. 1997, 97, 2933–2966. [Google Scholar] [CrossRef]
- Horsewill, A.J. Rotational tunneling in organic molecules. Spectrochim. Acta A 1992, 48, 379–403. [Google Scholar] [CrossRef]
- Horsewill, A.J. Quantum tunnelling aspects of methyl group rotation studied by NMR. Prog. Nucl. Magn. Res. Spectrosc. 1999, 35, 359–389. [Google Scholar] [CrossRef]
- Zachariou, A.; Hawkins, A.P.; Collier, P.; Howe, R.F.; Lennon, D.; Parker, S.F. The methyl torsion in unsaturated compounds. ACS Omega 2020, 5, 2755–2765. [Google Scholar] [CrossRef]
- Clough, S.; Heidemann, A.; Horsewill, A.J.; Lewis, J.D.; Paley, M.N.J. The correlation of methyl tunnelling and thermally activated reorientation. J. Phys. C 1981, 14, L525–L529. [Google Scholar] [CrossRef]
- Clough, S.; McDonald, P.J. The correlation of methyl tunnelling and thermally activated reorientation: II. J. Phys. C 1982, 15, L1039–L1042. [Google Scholar] [CrossRef]
- Clough, S.; Heidemann, A.; Horsewill, A.J.; Lewis, J.D.; Paley, M.N.J. The rate of thermally activated methyl group rotation in solids. J. Phys. C 1982, 15, 2495–2508. [Google Scholar] [CrossRef]
- Clough, S. The tunnelling methyl group: A probe of the quantum classical transition. Sci. Progr. Oxford 1991, 75, 121–139. Available online: https://www.jstor.org/stable/43421264 (accessed on 7 March 2025).
- Montjoie, A.-S.; Müller-Warmuth, W. CH3 rotational tunnelling in alkali acetates and correlation between NMR spin-lattice relaxation and neutron scattering Data. Z. Naturforsch. A 1985, 40, 596–601. [Google Scholar] [CrossRef]
- Plazanet, M.; Neumann, M.A.; Trommsdorff, H.P. Methyl group rotational tunneling in vibrational spectra of crystals at low temperatures. Chem. Phys. Lett. 2000, 320, 651–657. [Google Scholar] [CrossRef]
- Perras, F.A.; Matsuki, Y.; Southern, S.A.; Dubroca, T.; Flesariu, D.F.; Van Tol, J.; Constantinides, C.P.; Koutentis, P.A. Mechanistic origins of methyl-driven Overhauser DNP. J. Chem. Phys. 2023, 158, 154201. [Google Scholar] [CrossRef]
- Jescheke, G. Rotational coupling in methyl-tunneling electron spin echo envelope modulation. Appl. Magn. Reson. 2022, 53, 635–651. [Google Scholar] [CrossRef] [PubMed]
- Abed, K.J.; Clough, S. Methyl tunneling rotation in the n-alkanes. Chem. Phys. Lett. 1987, 142, 209–212. [Google Scholar] [CrossRef]
- Tomkinson, J.; Parker, S.F.; Bradeny, D.A.; Hudson, B.S. Inelastic neutron scattering spectra of the transverse acoustic modes of the normal alkanes. Phys. Chem. Chem. Phys. 2002, 4, 716–772. [Google Scholar] [CrossRef]
- Neumann, M.A.; Johnson, M.R.; Radaelli, P.G. The low temperature phase transition in octane and its possible generalization to other n-alkanes. Chem. Phys. 2011, 266, 53–68. [Google Scholar] [CrossRef]
- Soulard, L.; Fillaux, F.; Braathen, G.; Le Calve, N.; Pasquier, B. Rotational dynamics of the methyl group in the 4-methyl pyridine crystal. Chem. Phys. Lett. 1986, 125, 41–46. [Google Scholar] [CrossRef]
- Diezemann, G.; Häusler, W. Symmetry-species conversion in CD3 systems. J. Phys. Cond. Matter 1993, 5, 6121–6138. [Google Scholar] [CrossRef][Green Version]
- Orth, K.; Rohlfing, F.; Friedrich, J. Rotational tunneling dynamics of methyl groups in n-alkane host lattices: An optical investigation and external isotope effect. Z. Phys. B 1994, 95, 493–501. [Google Scholar] [CrossRef]
- Takeda, S.; Kataoka, H.; Ikeda, S.; Yamaguchi, K. Rotational tunneling of methyl groups of Sc(CH3COO)3 and Sc(CD3COO)3. Phys. B 1996, 226, 174–177. [Google Scholar] [CrossRef]
- Somoza, M.M.; Friedrich, J. The physics of rotational tunneling: Hole-burning spectroscopy of methyl groups. Low Temp. Phys. 2006, 32, 1020–1027. [Google Scholar] [CrossRef]
- Williams, J.; Eisenberg, A. Methyl group tunneling and viscoelastic relaxation in poly(methyl methacrylate). Macromolecules 1978, 11, 700–707. [Google Scholar] [CrossRef]
- Gabryi, B.; Higgins, J.S.; Ma, K.T.; Roots, J.E. Rotational motion of the ester methyl group in stereoregular poly(methyl methacrylate): A neutron scattering study. Macromolecules 1984, 17, 560–566. [Google Scholar] [CrossRef]
- Colmenero, J.; Mukhopadhyay, R.; Alegría, A.; Frick, B. Quantum rotational tunneling of methyl groups in polymers. Phys. Rev. Lett. 1998, 80, 2350–2353. [Google Scholar] [CrossRef]
- Colmenero, J.; Moreno, A.J.; Alegría, A. Neutron scattering investigations on methyl group dynamics in polymers. Prog. Polym. Sci. 2005, 30, 1147–1184. [Google Scholar] [CrossRef]
- Adams, M.A.; Gabrys, B.J.; Zajac, W.M.; Peiffer, D.G. High-resolution incoherent inelastic neutron scattering spectra of polyisobutylene and polyisoprene. Macromolecules 2005, 38, 160–166. [Google Scholar] [CrossRef]
- Tachibana, S.; Morisawa, Y.; Ikehata, A.; Sato, H.; Higashi, N.; Ozaki, Y. Far-Ultraviolet spectra of n-alkanes and branched alkanes in the liquid phase observed using an attenuated total reflection-far ultraviolet (ATR-FUV) spectrometer. Appl. Spectrosc. 2011, 65, 221–226. [Google Scholar] [CrossRef]
- Morisawa, Y.; Tachibana, S.; Ehara, M.; Ozaki, Y. Elucidating electronic transitions from σ orbitals of liquid n- and branched alkanes by far-ultraviolet spectroscopy and quantum chemical calculations. J. Phys. Chem. A 2012, 116, 11957–11964. [Google Scholar] [CrossRef]
- Ozaki, Y.; Morisawa, Y.; Tanabe, I.; Beć, K. ATR-far-ultraviolet spectroscopy in the condensed phase—The present status and future perspectives. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 253, 119549. [Google Scholar] [CrossRef] [PubMed]
- Lin-Vien, D.; Colthup, N.B.; Fateley, W.G.; Grasselli, J.G. Chapter 2: Alkanes. In The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules; Elsevier: Amsterdam, The Netherlands, 1991; ISBN 978-0124511606. [Google Scholar]
- Socrates, G. Chapter 2: Alkane Group Residue: C–H Group. In Infrared and Raman Characteristic Group Frequencies: Tables and Charts, 3rd ed.; Wiley: Chichester, UK, 2001; ISBN 978-0470093078. [Google Scholar]
- Gorai, K.K.; Shastri, A.; Singh, P.J.; Jha, S.N. Experimental and theoretical studies on the absorption spectra of n-dodecane in the IR and VUV regions. J. Quant. Spectrosc. Radiat. Transf. 2019, 236, 106582. [Google Scholar] [CrossRef]
- Knapp, D.; Brunschwig, B.S.; Lewis, N.S. Transmission infrared spectra of CH3, CD3, and C10H21-Ge(111) surfaces. J. Phys. Chem. C 2011, 115, 16389–163970. [Google Scholar] [CrossRef]
- Tyrode, E.; Hedberg, J. A comparative study of the CD and CH stretching spectral regions of typical surfactants systems using VSFS: Orientation analysis of the terminal CH3 and CD3 groups. J. Phys. Chem. C 2012, 116, 1080–1091. [Google Scholar] [CrossRef]
- Urata, H.; Shinohara, K.; Ogura, E.; Ueda, Y.; Akagi, M. Mirror-image DNA. J. Am. Chem. Soc. 1993, 113, 8174–8175. [Google Scholar] [CrossRef]
- Milton, R.C.D.L.; Miton, S.C.F.; Kent, S.B.H. Total chemical synthesis of a D-enzyme: The Enantiomers of HIV-1 protease show demonstration of reciprocal chiral substrate specificity. Science 1992, 256, 1445–1448. [Google Scholar] [CrossRef]
- Zawadzke, L.E.; Berg, J.M. A racemic protein. J. Am. Chem. Soc. 1992, 114, 4002–4003. [Google Scholar] [CrossRef]
- Weinstock, M.T.; Jacobsen, M.T.; Kay, M.S. Synthesis and folding of a mirror-image enzyme reveals ambidextrous chaperone activity. Proc. Natl. Acad. Sci. USA 2014, 111, 11679–11684. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, W.; Liu, L.; Zhu, T.F. A synthetic molecular system capable of mirror-image genetic replication and transcription. Nat. Chem. 2016, 8, 698–704. [Google Scholar] [CrossRef]
- Fan, C.; Deng, Q.; Zhu, T.F. Bioorthogonal information storage in L-DNA with a high-fidelity mirror-image Pfu DNA polymerase. Nat. Biotechnol. 2021, 39, 1548–1555. [Google Scholar] [CrossRef]
- Vallazza, M.; Perbandt, M.; Klussmann, S.; Rypniewski, W.; Einspahr, H.M.; Erdmann, V.A.; Betzel, C. First look at RNA in L-configuration. Acta Cryst. D 2004, 60, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Bolik, S.; Rübhausen, M.; Binder, S.; Schulz, B.; Perbandt, M.; Genov, N.; Erdmann, V.; Klussmann, S.; Betzel, C. First experimental evidence for the preferential stabilization of the natural D- over the nonnatural L-configuration in nucleic acids. RNA 2007, 13, 1877–1880. [Google Scholar] [CrossRef] [PubMed]
- Kiliszek, A.; Błaszczyk, L.; Bejger, M.; Rypniewski, W. Broken symmetry between RNA enantiomers in a crystal lattice. Nucleic Acids Res. 2021, 49, 12535–12539. [Google Scholar] [CrossRef] [PubMed]
- Kiliszek, A.; Rypniewski, W. The emergence of biological homochirality. Acta Biochim. Pol. 2023, 70, 481–485. [Google Scholar] [CrossRef]
- Garay, A.S.; Keszthelyi, L.; Demeter, I.; Hraskó, P. Differences in the annihilation of positrons in optical isomers. Chem. Phys. Lett. 1973, 23, 549–552. [Google Scholar] [CrossRef]
- Sullivan, R.; Pyda, M.; Pak, J.; Wunderlich, B.; Thompson, J.R.; Pagni, R.; Barnes, C.; Schwerdtfeger, P.; Compton, R. Search for electroweak interactions in amino acid crystals. II. The Salam hypothesis. J. Phys. Chem. A 2003, 107, 6674–6680. [Google Scholar] [CrossRef]
- Belo, E.A.; Pereira, J.E.; Freire, P.T.; Argyriou, D.N.; Eckert, J.; Bordallo, H.N. Hydrogen bonds in crystalline D-alanine: Diffraction and spectroscopic evidence for differences between enantiomers. IUCrJ 2018, 5, 6–12. [Google Scholar] [CrossRef]
- Bürgia, H.-B.; Macchi, P. Comments on ‘Hydrogen bonds in crystalline D-alanine: Diffraction and spectroscopic evidence for differences between enantiomers’. IUCrJ 2018, 5, 654–657. [Google Scholar] [CrossRef]
- Belo, E.A.; Pereira, J.E.; Freire, P.T.; Argyriou, D.N.; Eckert, J.; Bordallo, H.N. Response to comment on ‘Hydrogen bonds in crystalline D-alanine: Diffraction and spectroscopic evidence for differences between enantiomers’. IUCrJ 2018, 5, 658–659. [Google Scholar] [CrossRef]
- Koralewski, M.; Baranowski, M.; Ryzner, A. Probing physical invariance between enantiomers: The magnetooptical and refractive properties of the simplest chiral amino acid—Alanine. J. Mol. Liq. 2021, 339, 117279. [Google Scholar] [CrossRef]
- Dubey, M.; Kumar, A.; Dhavale, V.M.; Kurungot, S.; Pandey, D.S. Can enantiomer ligands produce structurally distinct homochiral MOFs? CrystEngComm 2015, 17, 8202–8206. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoedl, S.; Schlamminger, S. Torsion balance experiments: A low-energy frontier of particle physics. Prog. Part. Nucl. Phys. 2009, 62, 102–134. [Google Scholar] [CrossRef]
- Ni, W.-T. Searches for the role of spin and polarization in gravity: A five-year update. Int. J. Mod. Phys. Conf. Ser. 2016, 40, 1660010. [Google Scholar] [CrossRef]
- Safronova, M.S.; Budker, D.; DeMille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Qiao, J.; Li, Z.; Zhu, T.; Ji, R.; Li, G.; Zhao, W. Testing parity symmetry of gravity with gravitational waves. Front. Astron. Space Sci. 2023, 9, 1109086. [Google Scholar] [CrossRef]
- Leitner, J.; Okubo, S. Parity, charge conjugation, and time reversal in the gravitational interaction. Phys. Rev. 1964, 136, B1542–B1546. [Google Scholar] [CrossRef]
- Dass, N.D.H. Test for C, P, and T nonconservation in gravitation. Phys. Rev. Lett. 1976, 36, 393–395. [Google Scholar] [CrossRef]
- Anandan, J. Tests of parity and time-reversal noninvariance using neutron Interference. Phys. Rev. Lett. 1982, 48, 1660–1663. [Google Scholar] [CrossRef]
- Hou, L.-S.; Ni, W.-T.; Li, Y.-C.M. Test of cosmic spatial isotropy for polarized electrons using a rotatable torsion balance. Phys. Rev. Lett. 2003, 90, 201101. [Google Scholar] [CrossRef]
- Heckel, B.R.; Cramer, C.E.; Cook, T.S.; Adelberger, E.G.; Schlamminger, S.; Schmidt, U. New CP-violation and preferred-frame tests with polarized electrons. Phys. Rev. Lett. 2006, 97, 021603. [Google Scholar] [CrossRef]
- Terrano, W.A.; Adelberger, E.G.; Lee, J.G.; Heckel, B.R. Short-range, spin-dependent interactions of electrons: A probe for exotic pseudo-Goldstone bosons. Phys. Rev. Lett. 2015, 115, 201801. [Google Scholar] [CrossRef]
- Fray, S.; Diez, C.A.; Hänsch, T.W.; Weitz, M. Atomic interferometer with amplitude gratings of light and its applications to atom based tests of the equivalence principle. Phys. Rev. Lett. 2004, 93, 240404. [Google Scholar] [CrossRef]
- Tarallo, M.G.; Mazzoni, T.; Poli, N.; Sutyrin, D.V.; Zhang, X.; Tino, G.M. Test of Einstein equivalence principle for 0-Spin and half-integer-spin atoms: Search for spin-gravity coupling effects. Phys. Rev. Lett. 2014, 113, 023005. [Google Scholar] [CrossRef] [PubMed]
- Rosi, G.; D’Amico, G.; Cacciapuoti, L.; Sorrentino, F.; Prevedelli, M.; Zych, M.; Brukner, Č.; Tino, G.M. Quantum test of the equivalence principle for atoms in coherent superposition of internal energy states. Nat. Commun. 2016, 8, 15529. [Google Scholar] [CrossRef]
- Duan, X.-C.; Deng, X.-B.; Zhou, M.-K.; Zhang, K.; Xu, W.-J.; Xiong, F.; Xu, Y.-Y.; Shao, C.-G.; Luo, J.; Hu, Z.-K. Test of the universality of free fall with atoms in different spin orientations. Phys. Rev. Lett. 2016, 117, 023001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.-B.; Ba, Z.-L.; Ning, D.-H.; Zhai, N.-F.; Lu, Z.-T.; Sheng, D. Search for spin-dependent gravitational interactions at earth range. Phys. Rev. Lett. 2023, 130, 201401. [Google Scholar] [CrossRef] [PubMed]
- Touboul, P.; Métris, G.; Rodrigues, M.; André, Y.; Baghi, Q.; Bergé, J.; Boulanger, D.; Bremer, S.; Carle, P.; Chhun, R.; et al. MICROSCOPE mission: First results of a space test of the equivalence principle. Phys. Rev. Lett. 2017, 119, 231101. [Google Scholar] [CrossRef]
- Touboul, P.; Métris, G.; Rodrigues, M.; Bergé, J.; Robert, A.; Baghi, Q.; André, Y.; Bedouet, J.; Boulanger, D.; Bremer, S.; et al. MICROSCOPE mission: Final results of the test of the equivalence principle. Phys. Rev. Lett. 2022, 129, 121102. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, Q.; Zhao, H.-H.; Gong, Q.-L.; Yang, S.-Q.; Luo, P.; Shao, C.-G.; Wang, Q.-L.; Tu, L.-C.; Luo, J. Test of the equivalence principle with chiral masses using a rotating torsion pendulum. Phys. Rev. Lett. 2018, 121, 261101. [Google Scholar] [CrossRef]
- Bargueño, P.; de Tudela, R.P. Constraining long-range parity violation in gravitation using high resolution spectroscopy of chiral molecules. Phys. Rev. D 2008, 78, 102004. [Google Scholar] [CrossRef]
- Bargueño, P. Chirality and gravitational parity violation. Chirality 2015, 27, 375–381. [Google Scholar] [CrossRef] [PubMed]
- Gaul, K.; Kozlov, M.G.; Isaev, T.A.; Berger, R. Chiral molecules as sensitive probes for direct detection of P-odd cosmic fields. Phys. Rev. Lett. 2020, 125, 123004. [Google Scholar] [CrossRef]
- Gaul, K.; Kozlov, M.G.; Isaev, T.A.; Berger, R. Parity-nonconserving interactions of electrons in chiral molecules with cosmic fields. Phys. Rev. A 2020, 102, 032816. [Google Scholar] [CrossRef]
- Kawagoe, Y.; Fujiki, M.; Nakano, Y. Limonene magic: Noncovalent molecular chirality transfer leading to ambidextrous circularly polarised luminescent p-conjugated polymers. New J. Chem. 2010, 34, 637–647. [Google Scholar] [CrossRef]
- Fujiki, M.; Kawagoe, Y.; Nakano, Y.; Nakao, A. Mirror-symmetry-breaking in poly[(9,9-di-n-octylfluorenyl-2,7-diyl)-alt-biphenyl] (PF8P2) is susceptible to terpene chirality, achiral solvents, and mechanical stirring. Molecules 2013, 18, 7035–7057. [Google Scholar] [CrossRef] [PubMed]
- Franco, M.I.; Turin, L.; Mershin, A.; Skoulakis, E.M.C. Molecular vibration-sensing component in Drosophila melanogaster olfaction. Proc. Natl. Acad. Sci. USA 2011, 108, 3797–3802. [Google Scholar] [CrossRef]
- Gronenberg, W.; Raikhelkar, A.; Abshire, E.; Stevens, J.; Epstein, E.; Loyola, K.; Rauscher, M.; Buchmann, S. Honeybees (Apis mellifera) learn to discriminate the smell of organic compounds from their respective deuterated isotopomers. Proc. Roy. Soc. B 2014, 281, 20133089. [Google Scholar] [CrossRef]
- Turin, L. A Spectroscopic mechanism for primary olfactory reception. Chem. Sens. 1996, 21, 773–791. [Google Scholar] [CrossRef] [PubMed]
- Tirandaz, A.; Ghahramani, F.T.; Shafiee, A. Dissipative vibrational model for chiral recognition in olfaction. Phys. Rev. E 2015, 92, 032724. [Google Scholar] [CrossRef]
- Asogwa, C. Quantum biology: Can we explain olfaction using quantum phenomenon? arXiv 2019, arXiv:1911.02529. [Google Scholar] [CrossRef]
- Mokhtari, M.; Khoshbakht, S.; Ziyaei, K.; Akbari, M.E.; Moravveji, S.S. New classifications for quantum bioinformatics: Q-bioinformatics, QCt-bioinformatics, QCg-bioinformatics, and QCr-bioinformatics. Brief. Bioinform. 2024, 25, bbae074. [Google Scholar] [CrossRef]
- Nafie, L.A. Vibrational Optical Activity—Principles and Applications; Wiley: Chichester, UK, 2011; ISBN 978-0470032480. [Google Scholar]
- Xu, J.; Ramian, G.J.; Galan, J.F.; Savvidis, P.G.; Scopatz, A.M.; Birge, R.R.; Allen, S.J.; Plaxco, K.W. Terahertz circular dichroism spectroscopy: A potential approach to the in situ detection of life’s metabolic and genetic machinery. Astrobiology 2003, 3, 489–504. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.J.; Lee, S.H.; Park, B.C.; Kotov, N.A. Terahertz circular dichroism spectroscopy of molecular assemblies, and nanostructures. J. Am. Chem. Soc. 2022, 144, 22789–22804. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Liu, J.; Shi, W.; Fan, F.; Chang, S. Enhancing terahertz circular dichroism spectrum of amino acid chiral enantiomers by all-dielectric metasurface. Sens. Actuat. A 2022, 348, 114001. [Google Scholar] [CrossRef]
- Müller, T.; Wiberg, K.B.; Vaccaro, P.H. Cavity ring-down polarimetry (CRDP): A new scheme for probing circular birefringence and circular dichroism in the gas phase. J. Phys. Chem. A 2000, 104, 5959–5968. [Google Scholar] [CrossRef]
- Bougas, L.; Katsoprinakis, G.E.; von Klitzing, W.; Rakitzis, T.P. Fundamentals of cavity-enhanced polarimetry for parity-nonconserving optical rotation measurements: Application to Xe, Hg, and I. Phys. Rev. A 2014, 89, 052127. [Google Scholar] [CrossRef]
- Prager, M.; Stanislawski, J.; Häusler, W. Inelastic incoherent neutron scattering study of the methyl rotation in various methyl halides. J. Chem. Phys. 1987, 86, 2563–2575. [Google Scholar] [CrossRef]
- Kosower, E.M.; Markovich, G.; Borz, G. Thin-film infrared spectroscopy of acetonitrile. ChemPhysChem 2007, 8, 2513–2519. [Google Scholar] [CrossRef] [PubMed]
- Wong, J.S.; Green, W.H., Jr.; Cheng, C.-k.; Moore, C.B. Coupling of CH stretching and bending vibration of trihalomethanes. J. Chem. Phys. 1987, 86, 5994–5999. [Google Scholar] [CrossRef]
- Nishida, J.; Shigeto, S.; Yabumoto, S.; Hamaguchi, H. Anharmonic coupling of the CH-stretch and CH-bend vibrations of chloroform as studied by near-infrared electroabsorption spectroscopy. J. Chem. Phys. 2012, 137, 234501. [Google Scholar] [CrossRef]
- Nolasco, M.M.; Coimbra, M.M.; Parker, S.F.; Vaz, P.D.; Ribeiro-Claro, P.J. Structural dynamics of chloromethanes through computational spectroscopy: Combining INS and DFT. Molecules 2022, 27, 7661. [Google Scholar] [CrossRef] [PubMed]
- Ratcliffe, C.I.; Waddington, T.C. Internal torsional modes in methyl halogenocarbons studied by inelastic neutron scattering. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1976, 72, 1821–1839. [Google Scholar] [CrossRef]
- Macleod, N.A.; Lawley, K.P.; Donovan, R.J. Internal rotation of the CF3 group in the (trifluoromethyl)anilines: A zero-kinetic-energy pulsed-field-ionization study. J. Phys. Chem. A 2001, 105, 5646–5654. [Google Scholar] [CrossRef]
- Beckmann, P.A.; Rosenberg, J.; Nordstrom, K.; Mallory, C.W.; Mallory, F.B. CF3 rotation in 3-(trifluoromethyl)phenanthrene: Solid state 19F and 1H NMR relaxation and Bloch-Wangsness-Redfield theory. J. Phys. Chem. A 2006, 110, 3947–3953. [Google Scholar] [CrossRef]
- Beckmann, P.A.; Rheingold, A.L. 1H and 19F spin-lattice relaxation and CH3 or CF3 reorientation in molecular solids containing both H and F atoms. J. Chem. Phys. 2016, 144, 154308. [Google Scholar] [CrossRef]
- Charmet, A.P.; Bizzocchi, L.; Giuliano, B.M.; Caselli, P.; Craig, N.C.; Krasnoshchekov, S. Disentangling the IR spectra of 2,3,3,3-tetrafluoropropene using an ab initio description of vibrational polyads by means of canonical van Vleck perturbation theory. J. Quant. Spectrosc. Radia. Transfer. 2019, 239, 106656. [Google Scholar] [CrossRef]
- Campos-Vallette, M.; Rey-Lafon, M. Molecular structure of the rotational isomers in short chain n-perfluoroalkanes. J. Mol. Struct. 1984, 118, 245–255. [Google Scholar] [CrossRef]
- Kim, C.S.; Mowrey, C.; Butler, J.E.; Russell, J.N., Jr. Photochemical attachment of fluorobutyl moieties on a diamond (110)-oriented surface: A multiple internal reflection infrared spectroscopic (MIRIRS) investigation. J. Phys. Chem. B 1998, 102, 9290–9296. [Google Scholar] [CrossRef]
- Jang, S.S.; Blanco, M.; Goddard, W.A., III; Caldwell, G.; Ross, R.B. The source of helicity in perfluorinated N-alkanes. Macromolecules 2003, 36, 5331–5341. [Google Scholar] [CrossRef]
- Hasegawa, T.; Shimoaka, T.; Tanaka, Y.; Shioya, N.; Morita, K.; Sonoyama, M.; Amii, H.; Takagi, T.; Kanamori, T. An origin of complicated infrared spectra of perfluoroalkyl compounds involving a normal alkyl group. Chem. Lett. 2015, 44, 834–836. [Google Scholar] [CrossRef]
- Shimoaka, T.; Sonoyama, M.; Amii, H.; Takagi, T.; Kanamori, T.; Hasegawa, T. Raman optical activity on a solid sample: Identification of atropisomers of perfluoroalkyl chains having a helical conformation and no chiral center. J. Phys. Chem. A 2019, 123, 3985–3991. [Google Scholar] [CrossRef] [PubMed]
- Zerbi, G.; Sacchi, M. Dynamics of polymers as structurally disordered systems. Vibrational spectrum and structure of poly(tetrafluoroethylene). Macromolecules 1973, 6, 692–698. [Google Scholar] [CrossRef]
- Starkweather, H.W., Jr.; Ferguson, R.C.; Chase, D.B.; Minor, J.M. Infrared spectra of amorphous and crystalline poly(tetrafluoro-ethylene). Macromolecules 1985, 18, 1684–1686. [Google Scholar] [CrossRef]
- Dixon, D.A.; Van-Cadedge, F.A. A molecular model for the helicity of polytetrafluoroethylene (Tefloin®). Int. J. Supercomput. Appl. 1988, 2, 62–81. [Google Scholar]
- Mathieu, D.; Defranceschi, M.; Delhalle, J. Ab initio study of the influence of aggregation on the infrared spectrum of acetonitrile. Int. J. Quantum Chem. 1993, 45, 735–746. [Google Scholar] [CrossRef]
- Cavagnat, D.; Lascombe, J.; Lassegues, J.C.; Horsewill, A.J.; Heidemann, A.; Suck, J.B. Neutron and Raman scattering studies of the methyl dynamics in solid toluene and nitromethane. J. Phys. 1984, 45, 97–105. [Google Scholar] [CrossRef]
- Wilmshurst, J.K.; Bernstein, H.J. The infrared and Raman spectra of toluene, toluene-α-d3, m-xylene, and m-xylene-αα’-d6. Can. J. Chem. 1957, 35, 911–925. [Google Scholar] [CrossRef]
- Valderrama, A.C.S.; De, G.C.R. Traceability of active compounds of essential oils in antimicrobial food packaging using a chemometric method by ATR-FTIR. Am. J. Anal. Chem. 2017, 8, 726–741. [Google Scholar] [CrossRef]
- Borovkov, V.V.; Hembury, G.A.; Inoue, Y. The origin of solvent-controlled supramolecular chirality switching in a bis(zinc porphyrin) system. Angew. Chem. Int. Ed. 2003, 42, 5310–5314. [Google Scholar] [CrossRef]
- Borovkov, V.V.; Hembury, G.A.; Inoue, Y. Origin, control, and application of supramolecular chirogenesis in bisporphyrin-based systems. Acc. Chem. Res. 2004, 37, 449–459. [Google Scholar] [CrossRef]
- Hembury, G.A.; Borovkov, V.V.; Inoue, Y. Chirality-sensing supramolecular systems. Chem. Rev. 2008, 108, 1–73. [Google Scholar] [CrossRef] [PubMed]
- Borovkov, V.V. Effective supramolecular chirogenesis in ethane-bridged bis-porphyrinoids. Symmetry 2010, 2, 184–200. [Google Scholar] [CrossRef]
- Fujiki, M.; Yoshida, K.; Suzuki, N.; Rahim, N.A.A.; Jalil, J.A. Tempo-spatial chirogenesis. Limonene-induced mirror symmetry breaking of Si–Si bond polymers during aggregation in chiral fluidic media. J. Photochem. Photobiol. A Chem. 2016, 331, 120–129. [Google Scholar] [CrossRef]
- Nakano, Y.; Ichiyanagi, F.; Naito, M.; Yang, Y.; Fujiki, M. Chiroptical generation and inversion during the mirror-symmetry-breaking aggregation of dialkylpolysilanes due to limonene chirality. Chem. Commun. 2012, 48, 6636–6638. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).