Abstract
In the field of manufacturing, complex products with a tree structure often naturally exhibit asymmetric characteristics due to the uniqueness of their constituent elements and hierarchical relationships. In the production scheduling of such small-batch and multi-variety products, due to the influence of process constraints, many pieces of equipment will be idle for a long time in the production process. This increases the makespan of production and reduces the utilization rate of the equipment. Aiming at improving this situation, a resource cooperative scheduling algorithm is proposed to dynamically adjust the idle time of equipment: the integrated scheduling algorithm with dynamic adjustment of machine idle time based on an improved semi-numerical algorithm (ISA_DA). This algorithm adopts the critical path chain and the optimal scheduling strategy. On this basis, an adjustment strategy based on the semi-numerical algorithm considering the backward movement of the process is proposed, which improves the strength of the close connection of the process and the strength of parallel processing. Experimental results show that the effect of the proposed algorithm is better than the comparison algorithms: the hierarchical scheduling order algorithm and the process tree cyclic decomposition algorithm. It can increase the equipment utilization rate by 10% and 11.5%, respectively, and reduce the makespan by 28.6%. These experimental results strongly prove that the proposed algorithm can effectively reduce the total processing time and improve the production efficiency, whether it is for complex products with a symmetric structure or asymmetric structure.
1. Introduction
Integrated scheduling is applied to the production of treelike structured products with process constraints, and it deals with both the stages of the processing and the assembly. In addition, it involves the activity of allocating limited equipment, personnel and other resources to obtain the best time efficiency and equipment utilization rate, which meets the requirements of the state to vigorously develop process technology to adapt to intelligent manufacturing. Therefore, as a direct influence on the production efficiency and social benefits of enterprises, the scheduling problem has always been a hot issue studied by experts and scholars.
With the rapid development of AI, IoT and other information technologies, the scheduling mode of various products has also undergone great changes [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. For example, reference [1] proposed integrating Internet of Things technology and applying 5G technology to build a power wireless private network to solve the problem that the optimal scheduling design of an intelligent distribution network and its key technologies needs to be deeply analyzed and explored. Reference [2] constructed a regional integrated energy system based on an improved particle swarm optimization algorithm to solve the problem of excessive scheduling energy consumption and load in the current regional integrated energy optimization scheduling method. Reference [3] proposed a hybrid scheduling algorithm based on parallel team scheduling, worker ability and transportation time. Reference [4] proposed a polar fox optimization algorithm (PFA) based on the group life and hunting behavior of Arctic foxes, which solved the optimization problems in nonlinear optimization and engineering applications. However, the customization and diversification of product process requirements make the problem of product scheduling, which is small-scale but complicated in process, increasingly prominent. Therefore, as the third type of product manufacturing scheduling mode with complex constrained processes, integrated scheduling came into being, which can be summarized as follows:
- When depicting the complex process of the product, a tree structure is adopted, which can clearly and intuitively present the hierarchical relationship and internal logic between the processes in a symmetrical or asymmetrical form.
- The product quantity is single or small-batch.
- The processing and assembly of the product are coordinated [18].
In recent years, in the research of complex product integrated scheduling, researchers have carried out in-depth exploration on symmetric and asymmetric product structures [19,20,21,22,23,24,25,26,27,28,29,30,31], and achieved a series of valuable results, which has effectively promoted the development of this field. For example, reference [23] proposes a strategy of combining the genetic algorithm and improved whale algorithm and introducing a fitness function, which solves the problems of slow scheduling speed and uneven energy distribution in traditional energy scheduling systems. However, it only focuses on the processing time of the process and ignores the overall utilization of the equipment, resulting in a large number of idle time periods for the equipment. In reference [26], the sub-tree decomposition strategy and the adjustment strategy based on priority and constraint relationship are proposed. The manufacturing efficiency of complex products is improved by using the idle time of equipment. In reference [27], based on the hierarchical characteristics of the tree structure, a three-level scheduling strategy of ‘priority + leaf node + short time’ is designed. The scheduling simulation is carried out by using the production process model based on a Petri net. The algorithm designed and implemented effectively reduces the product scheduling time and improves the overall utilization rate of the equipment. In reference [28], a Q-learning-based Cangying optimizer (QL-AO) strategy is proposed. Combined with the initialization method based on the NEH heuristic and five local search strategies, the integrated optimization problem of blocking flow shop scheduling and preventive maintenance is solved to balance the production completion time and total maintenance cost.
In the above results, from the research perspective of vertical optimization, for example, the algorithm in reference [26] simply takes a long path as the main line of research, there will be delayed scheduling of leaf node processes on short paths on the device, and unusable idle time will be generated in the scheduling process. Therefore, vertical scheduling optimization can be further improved. In the results, from the research perspective of horizontal optimization, for example, the algorithm in reference [27] gives priority to the hierarchical structure of the process tree, the short-time strategy will fail when the path length of the subsequent processes with tight constraints is the same. It results in idle equipment corresponding to subsequent processes. Therefore, the horizontal scheduling effect can be further optimized.
At present, in the field of integrated scheduling of complex products, both products with a symmetrical structure and asymmetric products with significant structural differences are generally faced with the problem of unreasonable process scheduling. This problem results in a large amount of idle time being wasted, which greatly prolongs the total processing time of product scheduling. In summary, in order to effectively solve this problem, the integrated scheduling algorithm with dynamic adjustment of machine idle time based on a symmetry-improved semi-numerical algorithm (ISA_DA) is proposed. The algorithm uses key links to improve the tightness of process processing, improves the semi-numerical algorithm according to the symmetry principle to determine whether the process moves backward and uses the process backward strategy to dynamically adjust the order of process processing on a device, thereby reducing the idle time or excessive load of the device and improving production efficiency.
2. Related Concepts and Definitions
Whether it is a product with a symmetrical structure or an asymmetric structure, there are usually the following requirements when conducting integrated scheduling:
- (1)
- The processing and the assembly are collaborative processes, and collectively referred to as ‘processing’;
- (2)
- The process has three basic characteristics: (unique) identification serial number, matching equipment serial number, and fixed processing time;
- (3)
- At a certain scheduling time, the process and the equipment have a unique correspondence;
- (4)
- No identical equipment exists;
- (5)
- The constraint process of the product is represented by a treelike structure;
- (6)
- The arrow points to indicate the precedence constraint between the processes; that is, the arrow points to the process with high priority, and the processing can only begin after its immediate predecessor process is completed.
Accordingly, the mathematical model is established as follows:
Assuming n is the number of processes and m is the number of pieces of equipment, different products can start processing at different times and there is a constraint relationship between the processes. is the set of all processes; is the set of all equipment; TPij is the processing time of the ith process on the jth machine; TEij is the processing end time of the ith process on the jth machine; STij is the best scheduling time of the ith process on the jth machine; EPj is the idle time of the jth machine; SPij is the ith process being processed on the jth machine; EDj is the completion time on the jth machine; and SPTi is the processing time of the ith process. Then, there are the following:
Objective function:
subject to
Formula (1) represents the optimization objective of this paper: minimizing the completion time of the complex product. Formula (2) represents the process constraint relationship, that is, regardless of the ith process, the (i − 1)th process has a precedence constraint relationship with it. The start time of the former must not be less than the end time of the latter; Formula (3) represents the processing conditions of the equipment; that is, on the same equipment, Mj, the optimal scheduling time of the uth process cannot affect the vth process being processed.
Definition 1.
Process path value. The sum of the processing time of each process in the product process tree is defined as the path values between adjacent constrained processes, and the path values of the predecessor and successor are superimposed according to the shortest path principle.
Definition 2.
Tightly concatenated sub-string. A string of processes with a unique immediate predecessor and a unique immediate successor.
Definition 3.
Critical path chain. The tightly concatenated sub-string with the largest path value in the product process tree.
Definition 4.
Optimal scheduling time. The time when the process can start being processed earliest on the corresponding equipment under the premise of satisfying the constraint relationship.
3. Algorithm Design and Analysis
3.1. Symmetry Principle Improves Semi-Numerical Algorithm
The semi-numerical algorithm is a global optimization method for solving optimization problems with nonlinear constraints, and the optimal solution is found through an iterative process. Aiming at the problem of the excessive idle time of equipment in process machining, the algorithm proposed in this paper improves the semi-numerical algorithm by using the symmetry principle, so that it can find the global optimal solution in each iteration. For the general real number distribution probability problem, it can be represented by the distribution function f(x). When f(x) traverses all the probability values between 0 and 1, the probability k shows the symmetry property of being divided equally in the local non-random judgment, that is, k is the average and the value is 1/2. By using this symmetry principle, it lays a foundation for the next step to judge whether the processing procedure is moved backward.
3.2. Backward Movement Strategy
The half value of the idle time, EPj, on the corresponding equipment and the processing time, TPij, of the corresponding process are taken as the judgment basis. SPTw denotes the processing time of the wth process that needs to be inserted in the backward movement strategy. According to the improved semi-numerical algorithm, for the common real number distribution probability problem, in the local non-random judgment, the probability k is usually divided into a half. Based on this, when the idle time of a device is longer than half of the time required for the corresponding processing procedure, it shows that the device has sufficient idle time to accommodate the processing time that needs to be inserted into the process. At this time, you can consider moving the process on the device backwards; that is, the condition of is satisfied at this time. In addition, the delay time must meet the following requirements:
Formula (4) indicates that on the equipment, Mj, the interval between the start time of the backward (i + 1)th process and the end time of the processed ith process must satisfy at least the processing time of the inserted wth process. Formula (5) indicates that on the corresponding equipment, Mj, the wth process to be scheduled seamlessly connects to the completed ith process.
3.3. Algorithm Description
Step 1: Calculate the path value of each process, and establish the critical path chain of the complex product based on the path value.
Step 2: Take each node in the critical path chain as the vertex, and establish the tightly concatenate sub-strings.
Step 3: Calculate the path value of each sub-string, and establish a descending sequence of the path value set of all the sub-strings.
Step 4: Arrange sub-strings in descending order according to the path value of each sub-string.
Step 5: Schedule each node in the critical path chain.
Step 6: Schedule each tightly concatenate sub-string according to the descending order of the path values. If there are sub-strings with the same path value, prioritize the sub-string with a larger number of nodes.
Step 7: If there is an optimal scheduling time on the corresponding device for the process to be scheduled in the sub-string, then go to Step 8. Otherwise, go to Step 9.
Step 8: Determine whether this process can be fully scheduled from the optimal scheduling time of the process to be scheduled. If it can be scheduled, then schedule the process. Otherwise, go to Step 9.
Step 9: If the post-operation strategy is satisfied, then the scheduled processes on the corresponding device are about to move to the optimal scheduling time of the process to be scheduled. Otherwise, according to the precedence constraint relationship between the processes, schedule them in turn.
Step 10: If all the sub-strings are scheduled, then go to Step 11 and end the procedure. Otherwise, go to Step 7.
Step 11: According to the precedence constraint relationship between the processes, adjust the starting times of the subsequent processes affected by the movement backward of the process to the optimal scheduling time in turn.
The algorithm flow chart is shown in Figure 1.
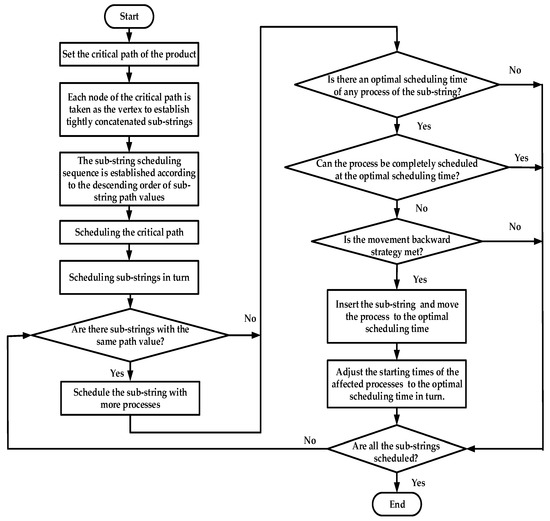
Figure 1.
Flowchart of the proposed algorithm.
3.4. Algorithm Code
The pseudo-code of the proposed algorithm is shown in Algorithm 1.
| Algorithm 1 Consider the step-back algorithm |
|
3.5. Algorithm Complexity
Assuming that the number of processing operations and the amount of processing equipment of complex products are known, which are set to n and m, respectively, the complexity of the algorithm is analyzed as follows:
- (1)
- In the complex product process tree, the parts of the symmetrical structure are consistent in space, shape and process. Each part of the asymmetric structure is significantly different, which is caused by personalized design or production constraints. But no matter what kind of structure there is, each node corresponds to the product processing process, forming a complete processing flow. According to the tight constraint relationship between the procedures, when determining the key link of the process tree, it is necessary to calculate the process link value for n procedures, and a total of n operations are required. Therefore, the time complexity of calculating the process link value and establishing the key link operation is O(n).
- (2)
- After the establishment of the key link is completed, according to which each node is a vertex, it needs n times to traverse and establish the closely connected process sub-string, and the time complexity of the algorithm is also O(n).
- (3)
- When searching for the best scheduling time, we need to perform an operation on each process a total of n times; the time complexity is O(n). Then, according to the optimal scheduling time, the half value of the processing time of the process and the length of the idle time of the equipment are judged. In the worst case, n processes need to be judged in turn, so the time complexity is O(n).
In summary, after fully considering the characteristics of the symmetric structure, as well as the irregularity and diversity of the asymmetric structure, it is concluded that the time complexity of the algorithm in this paper is the maximum value of the above operation time complexity, that is, O(n), and it is simple and easy to implement.
4. Scheduling Examples
Assume that the complex product P with a tight-front tight-back constraint process is a randomly generated asymmetric structure, as shown in Figure 2; the scheduling process will be described in combination with the algorithm in this paper. However, it should be noted that symmetry is actually a special case of asymmetry. Although this paper takes the product P with an asymmetric structure as an example for analysis, in fact, the algorithm in this paper can show good scheduling results for examples with tree process constraints, whether they are complex products with an asymmetric structure or symmetric structure.
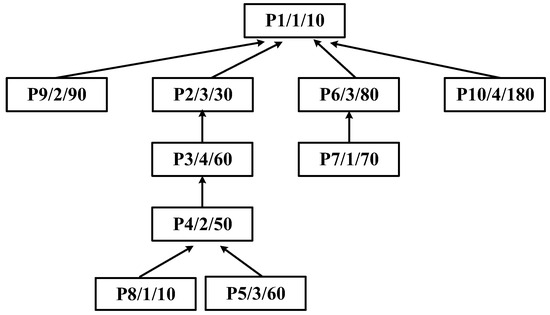
Figure 2.
Process tree of complex product P.
The specific scheduling procedure is as follows:
Step 1: Identify the critical path chain {P5, P4, P3, P2, P1}.
Step 2: As shown in Figure 3, take the process nodes P5, P4, P3, P2 and P1 in the critical path chain as vertices. These processes are marked in red in Figure 3 to establish tightly concatenated sub-strings {P8}, {P9}, {P7, P6}, {P10}, and marked in blue in Figure 3.
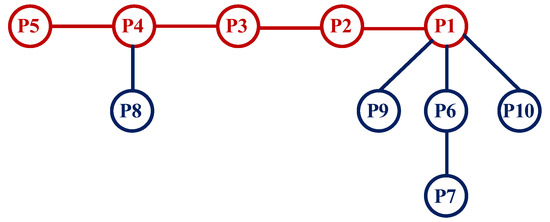
Figure 3.
Sub-string diagram of tightly concatenated sub-strings.
Step 3: Calculate the path values of the sub-strings {P8}, {P9}, {P7, P6}, {P10}, respectively, which are =1, =9, =18 and =15. Build the process set in descending order of path values: {{P10}, {P7, P6}, {P9}, {P8}}.
Step 4: Schedule each node in the critical path chain, as shown in Figure 4.
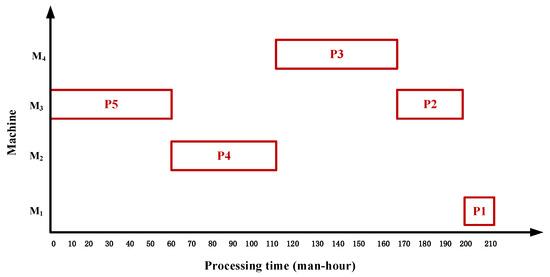
Figure 4.
Gantt chart of critical path chain for scheduling.
Step5: Schedule the process set according to the sub-string path values: {{P10}, {P7, P6}, {P9}, {P8}}.
Firstly, {P10} is scheduled: (1) Process P10 is a leaf node process, and there is no tight pre-process constraint. (2) The optimal scheduling time on M4 is t = 0. (3) The processing time of P10 on equipment M4 is , the idle time of M4 from t = 0 is 110 working hours, greater than , so the process, P3, on M4 is moved to t = 180, that is, the optimal scheduling time of P3. (4) Schedule process P10 at t = 0, as shown in Figure 5. Among them, red is used to represent the process on the critical path, blue is used to represent the closely connected sub-string process P10 to be inserted, and green is used to represent the process position after the process is moved backward according to the backward movement strategy.
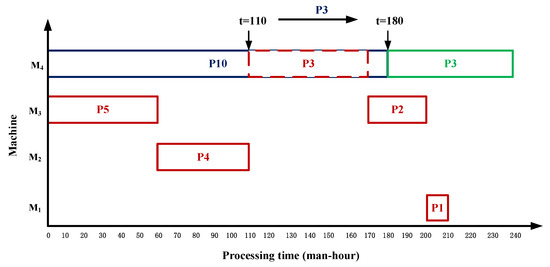
Figure 5.
Gantt diagram of scheduling sub-string {P10} and moving P3 backward.
Secondly, scheduling {P7, P6}: (1) Process P7 is a leaf node process without tight pre-process constraints. (2) The best scheduling time on device is t = 0 time. (3) The processing time of P7 on device is , and the idle time of device from t = 0 time is 210 man-hours, which is greater than (1/2). (4) The scheduling process P7 starts at t = 0 time on device . (5) The best scheduling time of process P6 on device is t = 70 time. (6) The processing time of P6 on device is t = 80, and the idle time of device from t = 60 is 170 man-hours, which is greater than (1/2). (7) Schedule operation P6 at time t = 70 on device .
Then, scheduling {P9}: (1) Process P9 is a leaf node process, without tight pre-process constraints. (2) The best scheduling time on the device is t = 0. (3) The processing time of P9 on the device is . The idle time of the device from t = 0 is 60 man-hours, which is greater than (1/2), so P4 on the device is moved back to t = 90, that is, the best scheduling time of P4. (4) Start scheduling process P9 at t = 0 on the device , as shown in Figure 6. Among them, red is used to represent the process on the critical path, blue is used to represent the inserted closely connected substring process, and green is used to represent the process position after the process is moved backward according to the process backward strategy.
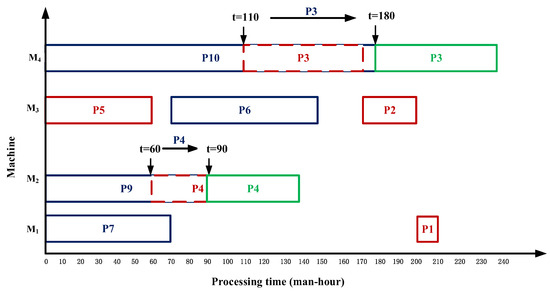
Figure 6.
Gantt diagram of scheduling sub-strings {P7, P6} and{P9} and moving P4 backward.
Finally, scheduling {P8}: (1) Process P8 is a leaf node process without tight pre-process constraints. (2) The best scheduling time on the equipment is t = 70. (3) The processing time of P8 on the equipment is . The idle time of the equipment from t = 0 is 140 man-hours, which is greater than (1/2). (4) The scheduling process P8 starts at t = 70 on the equipment .
Step 6: According to the constraint relationship between the tight front and tight back of the process, the process P2 needs to be processed after the completion of the tight-front process P3 before starting processing, and the process P1 needs to be processed after the completion of the tight-front processes P9, P2, P6 and P10 before starting processing. Therefore, adjust the starting times of process P8 on equipment M3 and process P1 on equipment M1 to t = 240 and t = 270, respectively. Then, the final scheme by the proposed algorithm is {P5, P4, P3, P2, P1, P7, P6, P10, P9, P8}. The makespan of the product is 280 working hours, as shown in Figure 7.
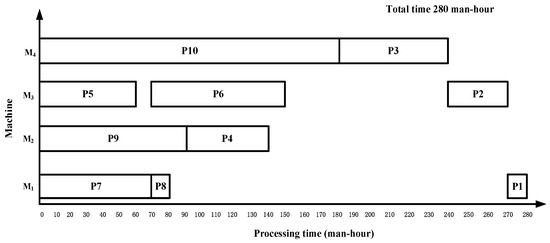
Figure 7.
Gantt chart of product P by the proposed algorithm with 280 working hours.
5. Comparative Analysis of Asymmetric Algorithms
5.1. Scheduling Results of Three Asymmetric Complex Products
In order to show the outstanding advantages of the algorithm in this paper more intuitively, the asymmetric complex product P presented in Figure 2 is selected as a case. The product has high requirements for production scheduling algorithms due to its irregular structure and complex processes. The algorithm in this paper is compared with the latest research results in the same research field. The experimental results show that the proposed algorithm achieves a better effect of general integrated scheduling.
Comparison Algorithm CHSO: The algorithm that considers a hierarchical scheduling order (CHSO)
CHSO is adopted, with the scheduling strategies layer priority, leaf node priority and short-time priority applied in turn. The scheme of complex product P by CHSO is {P7, P8, P5, P4, P3, P9, P10, P2, P6, P1}, and the makespan is 360 working hours., as shown in Figure 8.
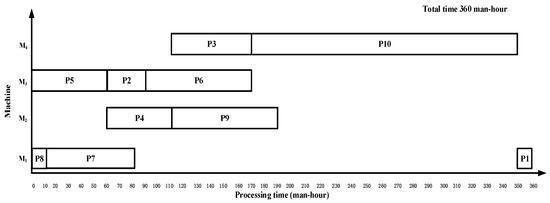
Figure 8.
Gantt chart of complex product P by CHSO algorithm with 360 working hours.
Comparison Algorithm BSCDPT: Process tree loop decomposition (BSCDPT) algorithm
The algorithm, BSCDPT, first takes the sub-tree as the unit to cycle decompose the process tree until the sub-tree is a leaf node or a serial sub-tree with constraint degree 1. And then the strategy is adjusted according to the audit strategy and a tight constraint relation is ensured between processes. The scheme of product P by BSCDPT is {P5, P8, P4, P7, P3, P10, P9, P6, P2, P1}, and the makespan is 360 working hours, as shown in Figure 9.
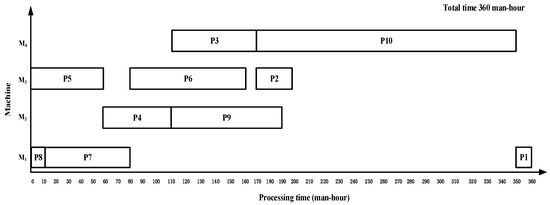
Figure 9.
Gantt chart of complex product P by algorithm BSCDPT with 360 working hours.
For complex product P with an asymmetric structure with an irregular layout and complex process, the maximum completion time of the ISA_DA algorithm proposed in this paper is 280 working hours, which is less than the other two algorithms. The comparison and analysis of the scheduling results of these three algorithms are shown in Table 1; the relative reduction ratio of total time is the ratio of the relative reduction in total time of the two comparison algorithms to the total time of the algorithm in this paper. The equipment utilization rate is shown in Table 2, and the calculation method of the equipment utilization rate is based on the scheduling result Gantt chart. Specifically, it is necessary to calculate the time when each device is in the processing state, accumulate it, and then divide it by the total length of the processing duration of each device. Taking the algorithm in this paper as an example, the processing time of the equipment M1, M2, M3 and M4 is 240 h, 170 h, 140 h and 90 h, respectively, and the processing time of the four pieces of equipment is 240 h, 270 h, 140 h and 280 h, respectively. The total time of the processing state is divided by the total time of the processing, that is, 640 ÷ 930 × 100% ≈ 68.8%, and the equipment utilization rate of the algorithm in this paper is 68.8%. The equipment utilization rate of the other two comparison algorithms is also calculated according to this method. Compared with the other two algorithms, the equipment utilization rate of the proposed algorithm is increased by 10% and 11.5%, respectively. The equipment utilization rate of the proposed algorithm is also higher.

Table 1.
Comparative analysis of scheduling results of three algorithms.

Table 2.
Equipment utilization of three algorithms.
5.2. Comparative Analysis of Three Asymmetric Complex Products
In order to verify the effectiveness of the proposed algorithm, its wide universality and its adaptability to complex products with a symmetric or asymmetric structure, it should have a better scheduling effect than any other algorithm for symmetric or asymmetric complex products with a tree structure. Therefore, the process tree used in the comparative analysis of the algorithm is randomly generated by the computer. In order to verify the optimization of the scheduling effect of the proposed algorithm in this paper, 100 complex product process trees of [20, 40, 80, 100] four kinds of data are randomly selected on four devices in the same computer Matlab R2021b experimental environment; that is, each process tree contains 20, 40, 80 and 100 processes. On average, 25 process trees are selected for each group of data for experiments, and the processing end time of each group of data is compared. Since the number of devices is four, the average number of processing processes per device in the four sets of data are [5, 10, 20, 25] in an ascending order. The scheduling effects of the CHSO algorithm, BSCDPT algorithm and ISA_DA algorithm are shown in Figure 10. In Figure 10, the four subgraphs of a, b, c and d, respectively, show the processing completion time (unit: working hours) of the ISA-DA, CHSO and BSCDPT algorithms when the process tree contains 20, 40, 80 and 100 processing procedures. In order to facilitate the summary, the three algorithms are represented by orange, green and purple in the four subgraphs. As the number of processing operations in the process tree increases, the processing completion time of the algorithm generally shows an increasing trend. In order to more clearly and accurately present the total processing time of each algorithm under different process number conditions, the y-axis of each subgraph is scaled in 500 units.
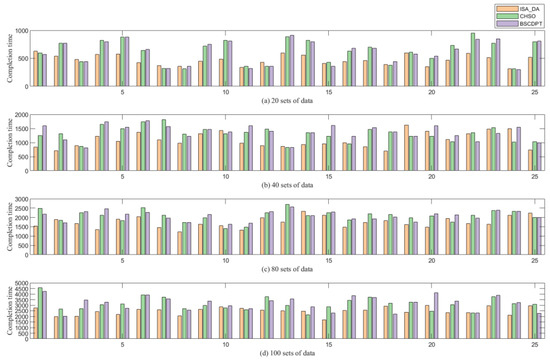
Figure 10.
Comparative analysis diagram of scheduling 100 random instances by three algorithms.
The experimental data are derived from four sets of data of different sizes, and each set of data is processed on 25 complex product process trees. These process trees cover both symmetric and asymmetric structures. Among them, the layout and characteristics of each part of the symmetrical structure of the process tree are similar; however, the process tree layout of asymmetric structure has no rules to follow, and the process execution sequence and resource allocation are more complex, which requires higher flexibility and adaptability of the scheduling algorithm, and in most cases, the completion time of this algorithm is earlier than the other two algorithms. Therefore, compared with the other two algorithms, the ISA_DA algorithm has a better scheduling effect in each process scale.
In order to verify the adaptability and superiority of algorithm ISA_DA to different symmetric and asymmetric treelike process complex products, 40 product process trees with different scales and process constraint structures were randomly generated under the same computer Matlab R2021 b experimental environment. The 40 product process trees were divided into four groups; on average, each group contained 10 different process tree instances. The number of processes in these four sets was [20, 40, 80, 100], that is, 10 process trees with 20 processes, 10 process trees with 40 processes, 10 process trees with 80 processes and 10 process trees with 100 processes. The ISA_DA algorithm is compared with the optimal solution ratio of each set of data of the other two groups of the CHSO algorithm and BSCDPT algorithm. This ratio is used to measure the performance of the algorithm. The closer the optimal solution ratio is to 100%, the closer the solution obtained by the algorithm is to the optimal solution, and the better the performance of the algorithm. The experimental results are shown in Figure 11.
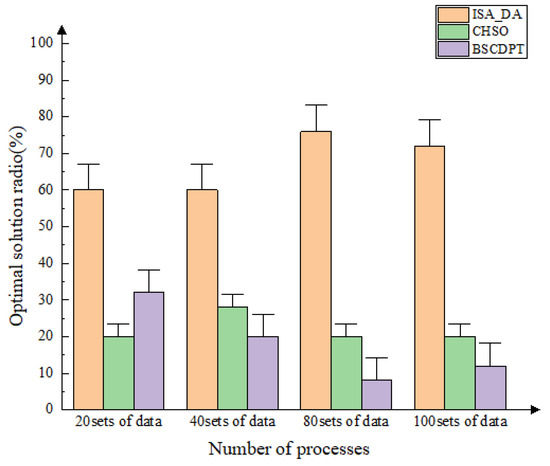
Figure 11.
Ratio of optimal solutions of three algorithms corresponding to process trees of 40 products.
The experimental results show that in the tree complex products, the symmetrical structure with uniform distribution and rules and the asymmetric structure with an irregular layout, complex process sequence and flexible resource allocation need to be adjusted, and the ISA_DA algorithm in this paper has a higher proportion of optimal solutions than the other two algorithms, and maintains a high ratio, and the stability is also the best; that is, the solution obtained by algorithm ISA_DA is closer to the optimal solution.
In summary, compared with the latest research results on the CHSO and BSCDPT algorithms in the field of integrated scheduling research, these two algorithms cannot accurately capture the key links when they are actually applied to process scheduling, which makes the process connection not close enough. The total processing time is long, and the equipment utilization rate cannot be effectively improved. From the perspective of specific performance indicators, under the same test conditions, for the complex product scheduling problem studied in this paper, these two comparison algorithms are not as good as the algorithm in this paper in terms of the rationality of the process scheduling sequence, the control of total time and the improvement of equipment utilization. With an accurate grasp of the key links and scientific process adjustment basis, the algorithm in this paper shows higher practicability and superiority in practical application, and can better meet the needs of complex product production scheduling.
5.3. Advantage Analysis of the Algorithm
The algorithm in this paper has achieved better results in the same field. It not only meets the scheduling requirements of asymmetric structure products, but also plays an equally good role in the scheduling of symmetric structure products. The main reasons are as follows:
- (1)
- In the aspect of vertical optimization, the critical path chain is first scheduled in this paper, which improves the intensity of the tightly concatenated sub-strings; in the aspect of horizontal optimization, this paper adopts the strategy of descending scheduling for the tightly concatenated sub-strings and optimal scheduling time, which improves the intensity of high-density processing.
- (2)
- In order to make full use of the idle resources of the equipment, this paper adopts the movement backward strategy, which not only improves the utilization rate of the equipment, but also effectively shortens the makespan of complex products. For example, the equipment utilization rate of M4 by the proposed algorithm is 100%, and the seamless scheduling of P3 and P10 is realized. Compared with the hierarchical scheduling order algorithm and the process tree loop decomposition algorithm, the equipment utilization rate of M4 is increased by 31.4%.
5.4. Applicability Analysis of the Algorithm
In this paper, the key link and the best scheduling strategy are comprehensively used, and based on an improved semi-numerical algorithm, an adjustment strategy considering the backward movement of the process is proposed to dynamically adjust the idle time of the equipment. Whether it is a symmetrical complex tree product with a uniform distribution of each part, or an asymmetric complex tree product with significant differences in each part and a complex process sequence, this strategy can exert excellent performance and effectively improve production efficiency. In the case of the increasing demand for multi-variety and small-batch complex products in the market, the algorithm in this paper can flexibly deal with complex constraints and dynamic conditions, dynamically adjust the process processing sequence according to the actual situation, avoid idle time or the excessive load of equipment, improve production efficiency and realize the efficient utilization of resources and the equalization of production.
In addition, regarding the potential limitations of this paper, for symmetric or asymmetric complex products, the use of semi-numerical algorithms may require a long calculation time, and in large-scale production systems, this may become a problem that affects the timeliness of production decisions. In this regard, intelligent optimization algorithms can be introduced, such as genetic algorithms, simulated annealing algorithms, etc., combined with semi-numerical algorithms to reduce computational complexity and improve solution speed under the premise of ensuring production efficiency.
In short, the algorithm in this paper has high applicability in actual production, whether it is tree complex products with a highly symmetrical layout or asymmetric treelike complex products with an irregular structure, which can effectively improve production efficiency and reduce costs. However, its applicability and effectiveness may vary according to different industries and production scales. Therefore, this algorithm can be customized according to its own actual situation when it is used to ensure that the algorithm can maximize its effectiveness.
6. Summary and Outlook
In the near future, China will vigorously promote the digital transformation of complex products and promote the digitalization and intellectualization of processes. In this paper, aiming at the production scheduling problem of complex tree products with precedence constraints between processes, a semi-numerical algorithm improved from the principle of symmetry and the movement backward strategy is proposed from the perspective of optimizing the idle time of the equipment, which shortens the total scheduling time of symmetric and asymmetric complex products and increases the innovation of process technology. The experimental results show that the algorithm has achieved better scheduling results in the field of general integrated scheduling of complex products. In the future, more actual production constraints can be considered on the basis of the algorithm in this paper, such as the actual production constraints under different characteristics such as symmetrical structure product layout rules and process stability, as well as the actual production constraints under different characteristics such as asymmetric product structure complexity and process variability, such as equipment maintenance plan, energy consumption, order change, etc., so that the algorithm can better adapt to different production environments. It provides a new research idea for the subsequent research of integrated scheduling considering complex multi-products, flexible integrated scheduling, distributed integrated scheduling, and other related fields. It also expands the research ideas for carrying out research of ‘intelligent + process’ and accelerating the process of intelligent manufacturing.
Author Contributions
Conceptualization, X.D. and W.Z.; methodology, Z.X.; software, X.D. and W.C.; data curation, Z.T. and M.S.; writing—original draft preparation, X.D.; writing—review and editing, W.Z. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Natural Science Foundation of China (61772160, Funder: Z.X.); National Social Science Foundation of China (20BZS058, Funder: M.S.); Natural Science Foundation Project of Heilongjiang Province (LH2024F045, Funder: W.C.); Key Projects of Education Department of Jilin Province (JJKH20250946KJ, Funder: W.Z.); and Jilin Normal University Doctoral Program (2022014, Funder: W.Z.).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pei, C.W. Research on intelligent optimal dispatching of distribution networks based on artificial intelligence. Electr. Eng. 2023, S1, 36–38. [Google Scholar] [CrossRef]
- Wang, Y.R.; Zhao, X.L.; Yu, Z. Regional integrated energy optimal scheduling method based on improved particle swarm optimization algorithm. Control Instrum. Chem. Ind. 2024, 51, 693–698. [Google Scholar]
- Li, H.T.; Liu, J.H.; Wang, Y.; Zhuang, C.B. A multi-objective complex product assembly scheduling problem considering transport time and worker competencies. Adv. Eng. Inform. 2023, 58, 102233. [Google Scholar] [CrossRef]
- Ghiaskar, A.; Amiri, A.; Mirjalili, S. Polar fox optimization algorithm: A novel meta-heuristic algorithm. Neural Comput. Appl. 2024, 36, 20983–21022. [Google Scholar] [CrossRef]
- Wang, P.; Lu, Y.; Wang, S.; Yao, W.D. A Reservation and Reuse Combined Q-learning Semi Persistent Scheduling for C-V2X Communication. J. Electron. Inf. Technol. 2022, 44, 2785–2791. [Google Scholar] [CrossRef]
- Wen, H.B. On the Innovative Practice of Intelligent Manufacturing Technology in Precision Mold Design and Manufacture. In Proceedings of the 8th International Conference on Machinery, Mechanics, Materials, and Computer Engineering, Huhhot, China, 28–30 June 2021; Available online: https://webofproceedings.org/proceedings_series/article/artId/19837.html (accessed on 13 February 2025).
- Deng, S.; Zhao, S.; Zhao, X. The Design of Mufti-task Management System Based on Mufti-core Parallel Real-time Simulation Platform. In Proceedings of the 21 National Conference on Simulation Technology, Hangzhou, China, 2–4 April 2021; pp. 48–52. [Google Scholar]
- Shi, H.Y.; Jing, D.X. Research on the Construction and Key Technologies of Cloud Manufacturing Platform for Intelligent Manufacturing. In Proceedings of the International Conference on Applied Science, Engineering and Technology (ICASET 2021), Qingdao, China, 25–26 July 2021; p. 204. [Google Scholar] [CrossRef]
- Su, M.F.; Wang, G.J.; Li, R.F. Resource Diployment with Prediction and Task Scheduling Optimization in Edge Cloud Collaborative Computing. J. Comput. Res. Dev. 2021, 58, 2558–2570. [Google Scholar] [CrossRef]
- Tang, L.; Wei, Y.N.; Tan, Q.; Tang, R.; Chen, Q.B. Joint Congestion Control and Resource Allocation Dynamic Scheduling Strategy for Network Slices in Heterogeneous Cloud Raido Access Network. J. Electron. Inf. Technol. 2020, 42, 1244–1252. [Google Scholar] [CrossRef]
- Zhao, C.Z.; Zhang, Y.H.; Li, M.; Ye, X.Y.; Sun, E.C. Computing Resource Optimization and Allocation for Internet of Thing Systems Assisted by Unmanned Aerial Vehicle. In Proceedings of the 14th National Conference on Signal and Intelligent Information Processing and Applications, Beijing, China, 25–27 June 2021; Volume 7, pp. 184–190. [Google Scholar]
- Khorsand, R.; Ramezanpour, M. An energy-efficient task-scheduling algorithm based on a multi-criteria decision-making method in cloud computing. Int. J. Commun. Syst. 2020, 33, 4379–4386. [Google Scholar] [CrossRef]
- Tang, H.L.; Wu, B.L.; Hu, W.; Kang, C.X. Earthquake Emergency Resource Multiobjective Schedule Algorithm Based on Particle Swarm Optimization. J. Electron. Inf. Technol. 2020, 42, 737–745. [Google Scholar] [CrossRef]
- Dong, H. Research on the Transformation and Upgrading Path of Traditional Industries Based on Intelligent Manufacturing. In Proceedings of the 8th International Education, Economics, Social Science, Arts, Sports and Management Engineering Conference, Chengdu, China, 30–31 October 2020; p. 64. [Google Scholar]
- Zhao, B.F.; Zhao, Q.Q.; Zhao, J.; Xu, Z.H.; Shao, Z.J. Event-driven Monthly Scheduling System for Multiple Air Separation Units. In Proceedings of the Conference on China Automation Conference (CAC2020), Shanghai, China, 6–8 November 2020; pp. 290–295. [Google Scholar] [CrossRef]
- Chong, C.; Ki, M.; Ting, N.; Yuen, N. Prediction of Production Performance in Smart Manufacturing Using Multivariate Adaptive Regression Spline. In Proceedings of the ASME 2021 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, Online, 17–19 August 2021; p. 41. [Google Scholar] [CrossRef]
- Li, X.L.; Si, J.J.; Yin, C.C.; Li, Y.P. Single-machine scheduling problem considering jobs’release times and flexible maintenances. Comput. Integr. Manuf. Syst. 2023, 29, 581–592. [Google Scholar] [CrossRef]
- Xie, Z.Q. Study on Operation Scheduling of Complex Product with Constraint among Jobs. Ph.D. Thesis, Harbin University of Science and Technology, Harbin, China, January 2009. [Google Scholar]
- Wang, L.; Li, B.; Zhao, X. Multi-objective predictive maintenance scheduling models integrating remaining useful life prediction and maintenance decisions. Comput. Ind. Eng. 2024, 197, 110581. [Google Scholar] [CrossRef]
- Gui, Z.Y.; Zhang, Z.; Wang, Q.; Jiang, L.L. Reversed flexible integrated scheduling algorithm based on device driving and essential path. Mod. Inf. Technol. 2024, 8, 152–156. [Google Scholar]
- Sugianto, C.W.; Kim, S.B. Iterated variable neighborhood search for integrated scheduling of additive manufacturing and multi-trip vehicle routing problem. Comput. Oper. Res. 2024, 167, 106659. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, P.W.; Zheng, Y.; Xie, Z.Q. A Heuristic Integrated Scheduling Algorithm via Processing Characteristics of Various Machines. Symmetry 2022, 14, 2150–2170. [Google Scholar] [CrossRef]
- Wei, L.; An, G. Optimization of building integrated energy scheduling using an improved genetic whale algorithm. Sci. Rep. 2024, 14, 2386. [Google Scholar] [CrossRef]
- Ece, Y.; Erhan, S.K. Integrated production scheduling and vehicle routing problem with energy efficient strategies: Mathematical formulation and metaheuristic algorithms. Expert Syst. Appl. 2024, 237, 121586. [Google Scholar] [CrossRef]
- Zhang, B.N.; Tu, X.; Fu, W.L.; Gao, Y.H. Fully distributed dispatch algorithm for integrated energy system based on state decomposition. Power Syst. Technol. 2024, 48, 4928–4937. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Zhou, W.; Yang, J. Resource Cooperative Integrated Scheduling Algorithm Based on Sub-tree Cycle Decomposition of Process Tree. J. Mech. Eng. 2022, 58, 228–239. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Zhou, W.; Yang, J. Resource cooperative integrated scheduling algorithm considering hierarchical scheduling order. Comput. Integr. Manuf. Syst. 2022, 28, 3391–3402. [Google Scholar] [CrossRef]
- Ge, Z.P.; Wang, H.F. Integrated optimization of blocking flowshop scheduling and preventive maintenance using a Q-Learning-Based aquila optimizer. Symmetry 2023, 15, 1600. [Google Scholar] [CrossRef]
- Ding, X.Y.; Xie, Z.Q.; Zhou, W.; Tan, Z.J.; Sun, M. Flexible Integrated Scheduling Considering Periodic Maintenance. Electronics 2024, 13, 3730. [Google Scholar] [CrossRef]
- Yang, D.; Xie, Z.Q.; Zhang, C.T. Multi-flexible integrated scheduling algorithm for multi-flexible integrated scheduling problem with setup times. Math. Biosci. Eng. 2023, 20, 9781–9817. [Google Scholar] [CrossRef]
- Yang, D.; Xie, Z.Q.; Liu, Q.; Yu, X. A signal-driven based flexible integrated scheduling algorithm with bidirectional coordination mechanism. Multimed. Tools Appl. 2023, 82, 34029–34051. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).