The Heterogeneous Network Community Detection Model Based on Self-Attention
Abstract
1. Introduction
2. BP-GCN Model
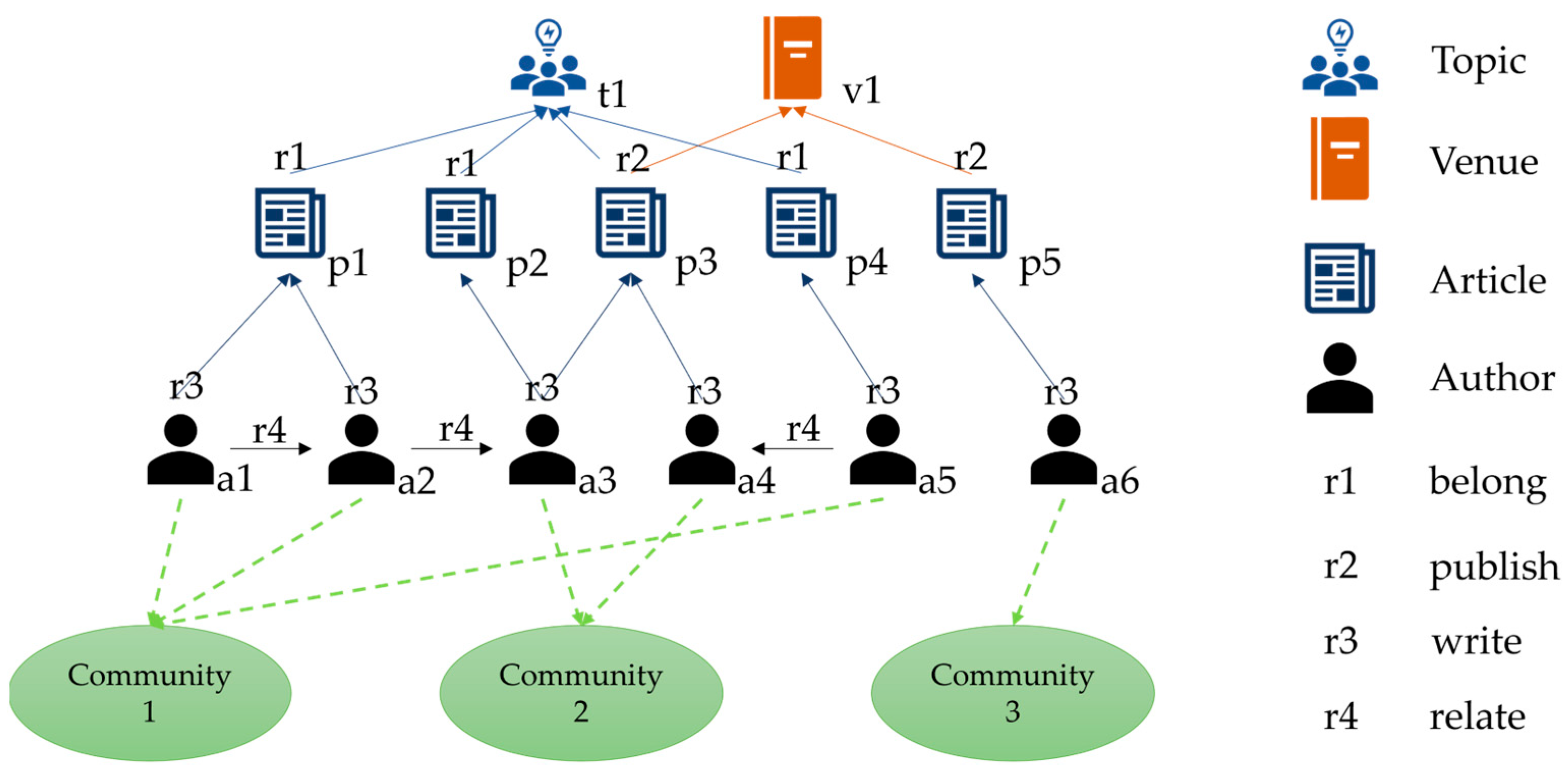
2.1. Concept Definition
2.2. Loss Function
2.3. BP-GCN Model Architecture
3. Experiments
3.1. Dataset
3.2. Benchmark Methods
3.3. Comparative Experiments
3.4. Parameter Sensitivity Analysis
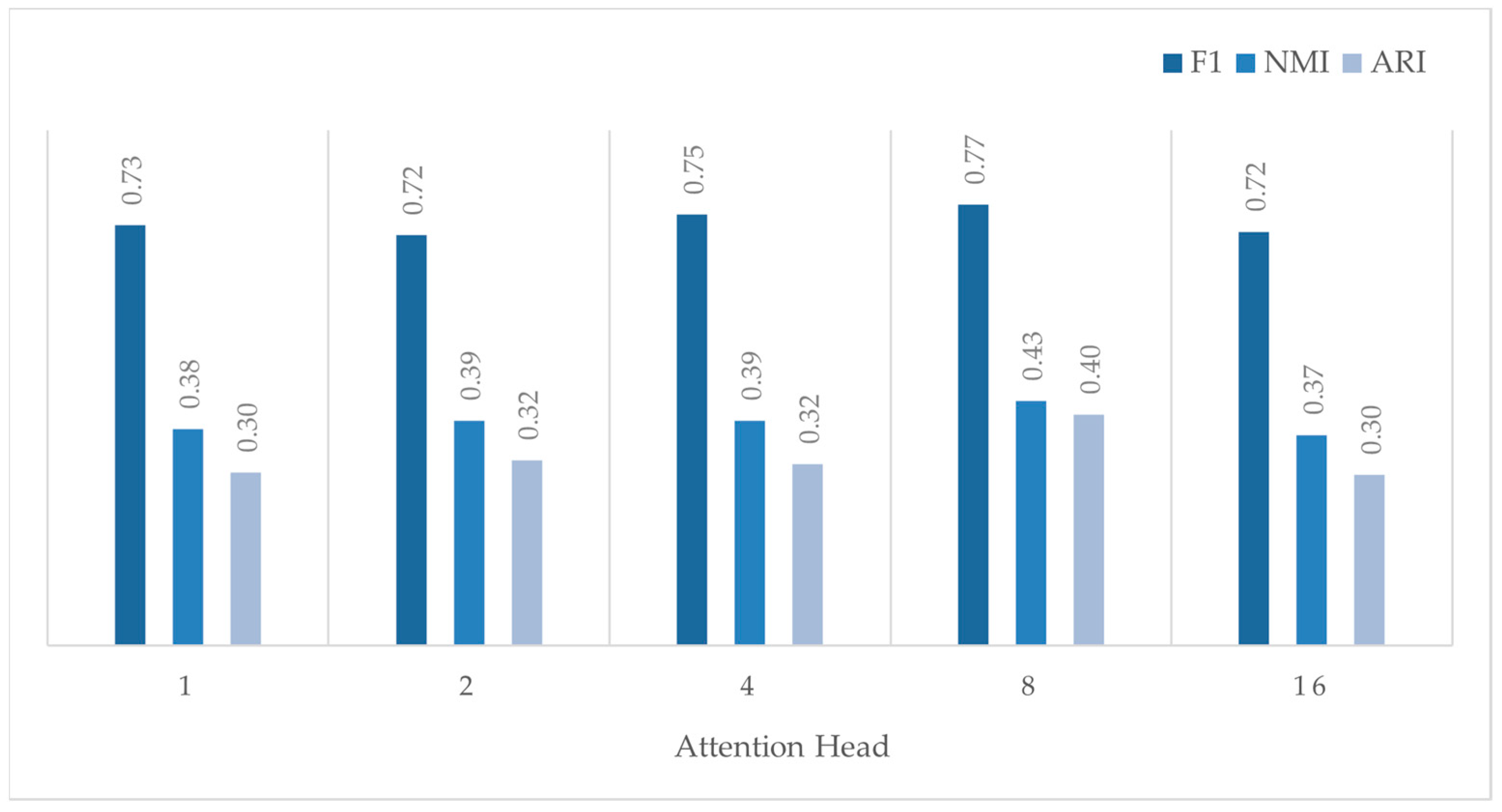
3.4.1. Number of Attention Heads
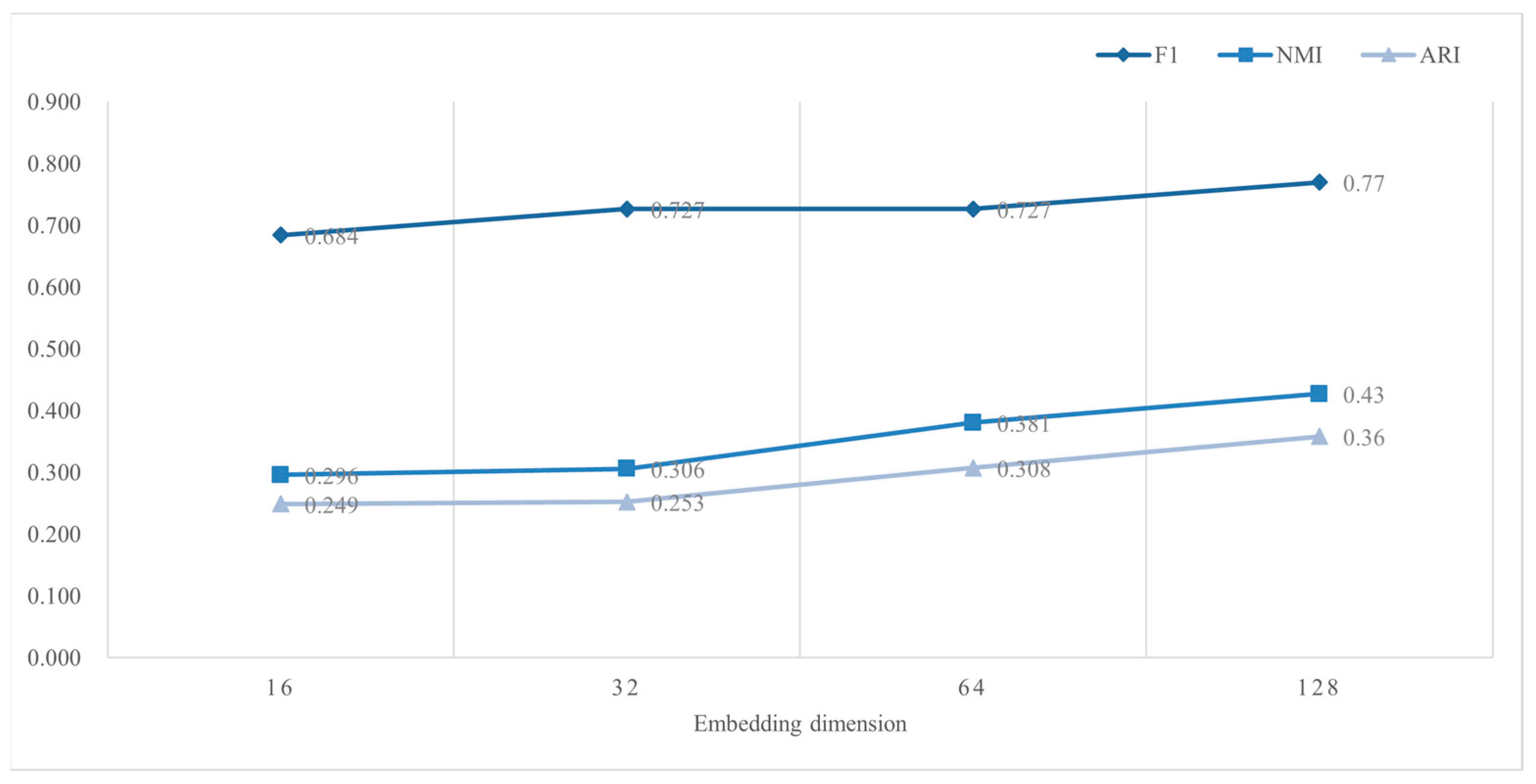
3.4.2. Embedding Dimensions
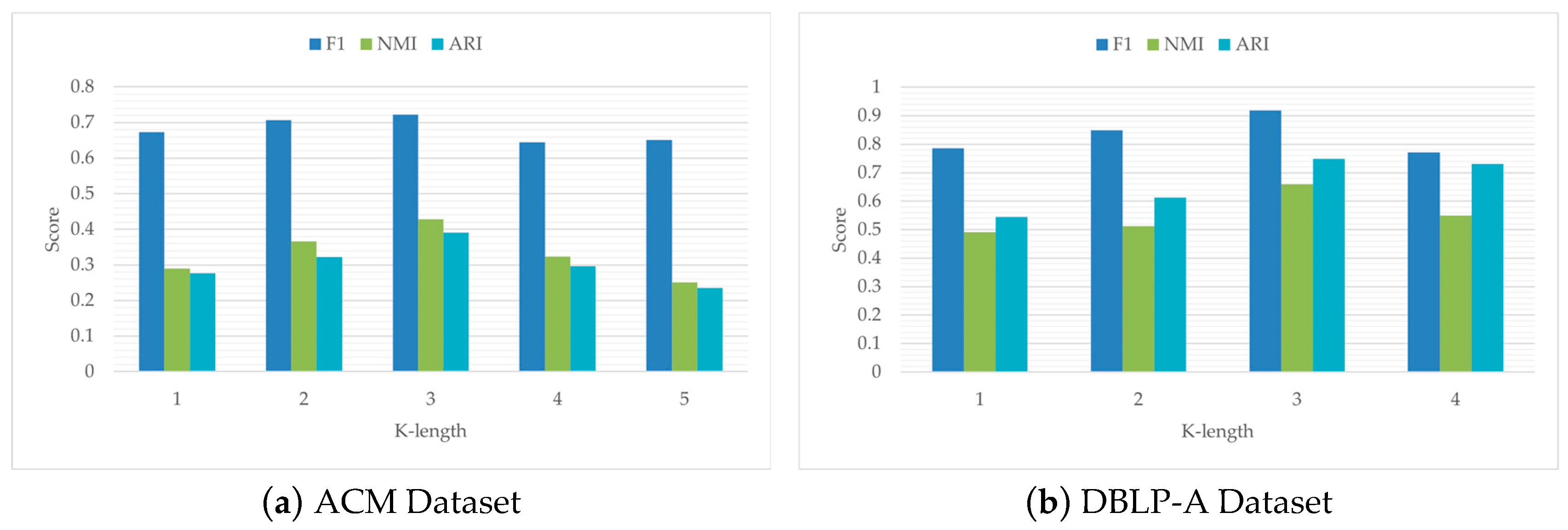
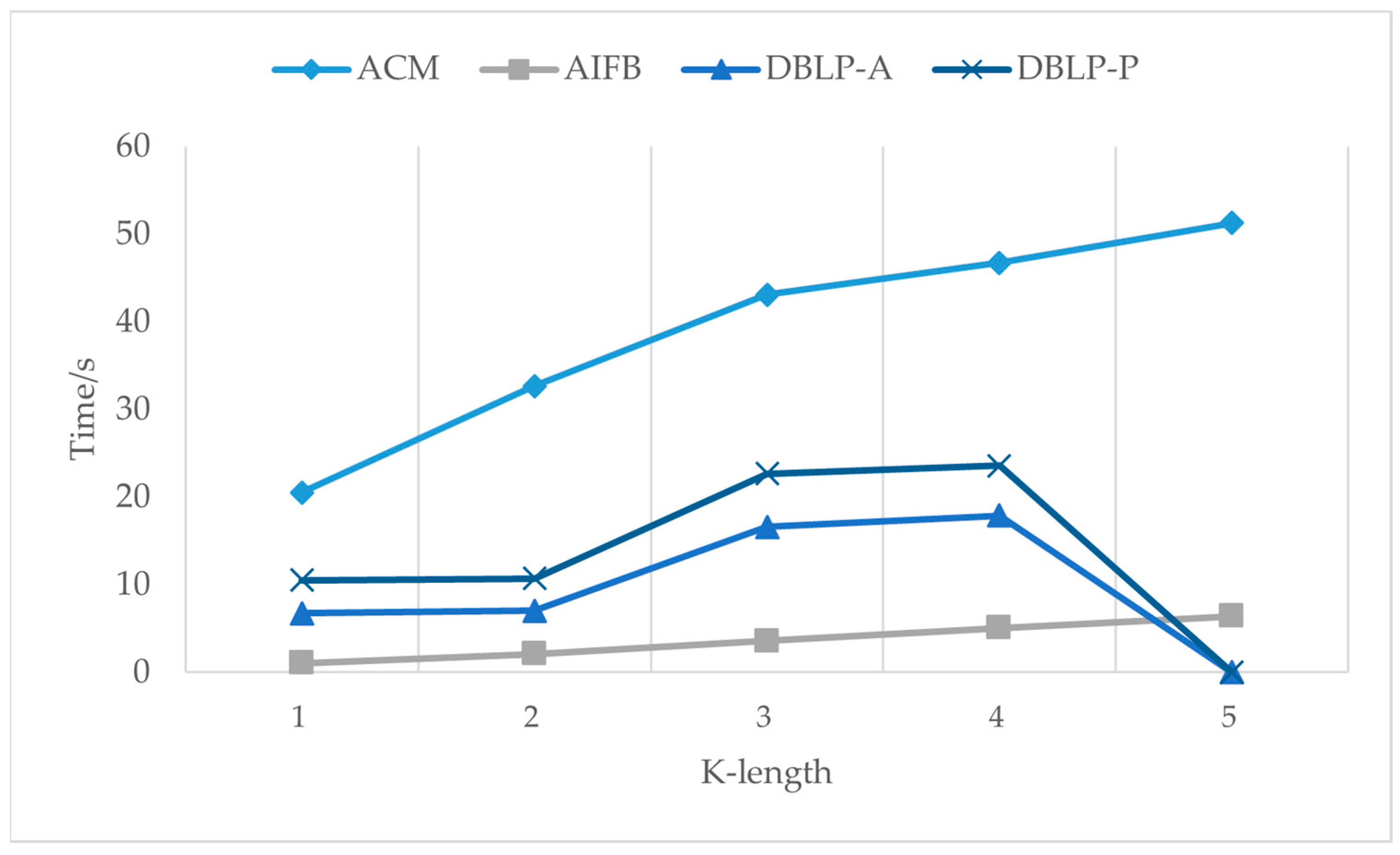
3.4.3. Context Path Length
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Explanation | Relation |
|---|---|---|
| HG | Heterogeneous graph | |
| HGP | Primary graph of the heterogeneous graph | |
| HGA’ | Auxiliary graph of the heterogeneous graph | |
| A | Node set of the heterogeneous graph | |
| P | Primary node type | |
| A’ | Auxiliary node type | |
| Edge set of the heterogeneous graph | ||
| Context path of length k | ||
| F | Community membership matrix |
References
- Wang, M.; Xiang, D.; Qu, Y.; Li, G. The diagnosability of interconnection networks. Discret. Appl. Math. 2024, 357, 413–428. [Google Scholar] [CrossRef]
- Wang, X.; Ji, H.; Shi, C.; Wang, B.; Ye, Y.; Cui, P.; Yu, P.S. Heterogeneous graph attention network. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 2022–2032. [Google Scholar]
- Wu, C.-Y.; Beutel, A.; Ahmed, A.; Smola, A.J. Explaining reviews and ratings with paco: Poisson additive co-clustering. In Proceedings of the 25th International Conference Companion on World Wide Web, Montréal, QC, Canada, 11–15 April 2016; pp. 127–128. [Google Scholar]
- Cai, D.; Shao, Z.; He, X.; Yan, X.; Han, J. Mining hidden community in heterogeneous social networks. In Proceedings of the 3rd International Workshop on Link Discovery, Chicago, IL, USA, 21–25 August 2005; pp. 58–65. [Google Scholar]
- Qi, G.-J.; Aggarwal, C.C.; Huang, T.S. On clustering heterogeneous social media objects with outlier links. In Proceedings of the Fifth ACM International Conference on Web Search and Data Mining, Seattle, WA, USA, 8–12 February 2012; pp. 553–562. [Google Scholar]
- Shi, C.; Wang, R.; Li, Y.; Yu, P.S.; Wu, B. Ranking-based clustering on general heterogeneous information networks by network projection. In Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014; pp. 699–708. [Google Scholar]
- Fan, S.; Zhu, J.; Han, X.; Shi, C.; Hu, L.; Ma, B.; Li, Y. Metapath-guided heterogeneous graph neural network for intent recommendation. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2478–2486. [Google Scholar]
- Pan, C.-H.; Qu, Y.; Yao, Y.; Wang, M.-J.-S. HybridGNN: A Self-Supervised Graph Neural Network for Efficient Maximum Matching in Bipartite Graphs. Symmetry 2024, 16, 1631. [Google Scholar] [CrossRef]
- Wang, R.-F.; Su, W.-H. The application of deep learning in the whole potato production Chain: A Comprehensive review. Agriculture 2024, 14, 1225. [Google Scholar] [CrossRef]
- Cui, K.; Tang, W.; Zhu, R.; Wang, M.; Larsen, G.D.; Pauca, V.P.; Alqahtani, S.; Yang, F.; Segurado, D.; Fine, P.; et al. Real-time localization and bimodal point pattern analysis of palms using uav imagery. arXiv 2024, arXiv:2410.11124. [Google Scholar]
- Wang, M.; Lin, Y.; Wang, S. The nature diagnosability of bubble-sort star graphs under the PMC model and MM∗ model. Int. J. Eng. Appl. Sci. 2017, 4, 2394–3661. [Google Scholar]
- Cui, K.; Li, R.; Polk, S.L.; Murphy, J.M.; Plemmons, R.J.; Chan, R.H. Unsupervised spatial-spectral hyperspectral image reconstruction and clustering with diffusion geometry. In Proceedings of the 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Rome, Italy, 13–16 September 2022; pp. 1–5. [Google Scholar]
- Tu, Y.-H.; Wang, R.-F.; Su, W.-H. Active Disturbance Rejection Control—New Trends in Agricultural Cybernetics in the Future: A Comprehensive Review. Machines 2025, 13, 111. [Google Scholar] [CrossRef]
- Xiang, D.; Hsieh, S.-Y. G-good-neighbor diagnosability under the modified comparison model for multiprocessor systems. Theor. Comput. Sci. 2025, 1028, 115027. [Google Scholar]
- Cui, K.; Li, R.; Polk, S.L.; Lin, Y.; Zhang, H.; Murphy, J.M.; Plemmons, R.J.; Chan, R.H. Superpixel-based and Spatially-regularized Diffusion Learning for Unsupervised Hyperspectral Image Clustering. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 1–18. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z.; Wang, Z.; Li, P. CDBMA: Community Detection in Heterogeneous Networks Based on Multi-attention Mechanism. In Proceedings of the Chinese National Conference on Social Media Processing, Hefei, China, 23–26 November 2023; pp. 174–187. [Google Scholar]
- Fu, T.-Y.; Lee, W.-C.; Lei, Z. Hin2vec: Explore meta-paths in heterogeneous information networks for representation learning. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 1797–1806. [Google Scholar]
- Dong, Y.; Chawla, N.V.; Swami, A. metapath2vec: Scalable representation learning for heterogeneous networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 135–144. [Google Scholar]
- Hu, Z.; Dong, Y.; Wang, K.; Sun, Y. Heterogeneous graph transformer. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 2704–2710. [Google Scholar]
- Yang, J.; Leskovec, J. Community-affiliation graph model for overlapping network community detection. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 1170–1175. [Google Scholar]
- Shchur, O.; Günnemann, S. Overlapping community detection with graph neural networks. arXiv 2019, arXiv:1909.12201. [Google Scholar]
- Luo, L.; Fang, Y.; Cao, X.; Zhang, X.; Zhang, W. Detecting communities from heterogeneous graphs: A context path-based graph neural network model. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Queensland, Australia, 1–5 November 2021; pp. 1170–1180. [Google Scholar]
- Barman, D.; Bhattacharya, S.; Sarkar, R.; Chowdhury, N. k-Context Technique: A Method for Identifying Dense Subgraphs in a Heterogeneous Information Network. IEEE Trans. Comput. Soc. Syst. 2019, 6, 1190–1205. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Li, S.; Yue, Z.; Yang, X. Research on Community Structure of Small-World Networks and Scale-Free Networks. Chin. Phys. Soc. 2007, 56, 6886–6893. [Google Scholar]
- Guare, J. Six degrees of separation. In The Contemporary Monologue: Men; Routledge: London, UK, 2016; pp. 89–93. [Google Scholar]
- Zhang, L.; Tu, W. Six Degrees of Separation in Online Society. 2009. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=1febc4cc5199d36e50ec7d3533a8ac8a32889d7c (accessed on 10 March 2025).
- Zhao, C.-T.; Wang, R.-F.; Tu, Y.-H.; Pang, X.-X.; Su, W.-H. Automatic Lettuce Weed Detection and Classification Based on Optimized Convolutional Neural Networks for Robotic Weed Control. Agronomy 2024, 14, 2838. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R.; Wang, M.; Lai, T.; Zhang, M. Self-supervised transformer-based pre-training method with General Plant Infection dataset. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Urumqi, China, 18–20 October 2024; pp. 189–202. [Google Scholar]
- Tinto, V. Dropout from higher education: A theoretical synthesis of recent research. Rev. Educ. Res. 1975, 45, 89–125. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Li, L.; Wang, H.; Wu, Y.; Chen, S.; Wang, H.; Sigrimis, N.A. Investigation of Strawberry Irrigation Strategy Based on K-Means Clustering Algorithm. Trans. Chin. Soc. Agric. Mach. 2020, 51, 295–302. [Google Scholar]
- Voita, E.; Talbot, D.; Moiseev, F.; Sennrich, R.; Titov, I. Analyzing multi-head self-attention: Specialized heads do the heavy lifting, the rest can be pruned. arXiv 2019, arXiv:1905.09418. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Sun, S.; Liu, J.; Sun, S. Hyperspectral subpixel target detection based on interaction subspace model. Pattern Recognit. 2023, 139, 109464. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Mei, S. Shannon-Cosine Wavelet Precise Integration Method for Locust Slice Image Mixed Denoising. Math. Probl. Eng. 2020, 2020, 4989735. [Google Scholar] [CrossRef]
- Gao, J.; Liang, F.; Fan, W.; Sun, Y.; Han, J. Graph-based consensus maximization among multiple supervised and unsupervised models. In Proceedings of the 23rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; Volume 22. [Google Scholar]
- Ristoski, P.; De Vries, G.K.D.; Paulheim, H. A collection of benchmark datasets for systematic evaluations of machine learning on the semantic web. In Proceedings of the Semantic Web–ISWC 2016: 15th International Semantic Web Conference, Kobe, Japan, 17–21 October 2016; Proceedings, Part II 15. pp. 186–194. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. stat 2017, 1050, 4. [Google Scholar]
- Chen, Z.; Li, X.; Bruna, J. Supervised community detection with line graph neural networks. arXiv 2017, arXiv:1705.08415. [Google Scholar]
- Danon, L.; Diaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005, 2005, P09008. [Google Scholar] [CrossRef]




| Dataset | Node Type | Nodes | Edge Type | Edges | Meta-Path |
|---|---|---|---|---|---|
| ACM | * Paper (P) | 12,499 | Paper–Paper | 30,789 | PAP |
| Author (A) | 17,431 | Paper–Author | 37,055 | ||
| Subject (S) | 73 | Paper–Subject | 12,499 | PSP | |
| Facility (F) | 1804 | Author–Facility | 30,424 | ||
| DBLP | * Paper (P) | 14,475 | Paper–Conference Author–Paper Paper–Term | 14,736 41,794 114,624 | APCPA APA APTPA |
| * Author (A) | 14,736 | ||||
| Conference (C) | 20 | ||||
| Term (T) | 8920 | ||||
| IMDB | * Movie | 4275 | Movie–Actor Movie–Director Movie–Keyword | 12,831 4181 20,428 | MAM MDM MKM |
| Actor | 5432 | ||||
| Director | 2083 | ||||
| Keyword | 7313 | ||||
| AIFB | A total of 7 types of nodes | 7262 | A total of 104 types of edges | 48,810 | - |
| Dataset | Metric | Node2vec | Metapath2vec | GCN | GAT | LGNN | HAN | HGT | BP-GCN |
|---|---|---|---|---|---|---|---|---|---|
| ACM | F1 | 0.6954 | 0.7142 | 0.5366 | 0.6876 | 0.6987 | 0.7922 | 0.7599 | 0.7496 |
| NMI | 0.2666 | 0.3596 | 0.0966 | 0.2577 | 0.2746 | 0.394 | 0.4509 | 0.4231 | |
| ARI | 0.2469 | 0.2956 | 0.1022 | 0.1422 | 0.2368 | 0.319 | 0.3813 | 0.4039 | |
| DBLP-A | F1 | 0.7572 | 0.7144 | 0.32 | 0.9023 | 0.321 | 0.9023 | 0.9386 | 0.9261 |
| NMI | 0.0638 | 0.2554 | 0.0186 | 0.618 | 0.0069 | 0.624 | 0.7032 | 0.6934 | |
| ARI | 0.0409 | 0.2722 | 0.0166 | 0.5264 | −0.0012 | 0.665 | 0.7322 | 0.7626 | |
| DBLP-P | F1 | 0.3 | 0.3125 | 0.31 | 0.3 | 0.225 | 0.3375 | 0.4 | 0.4875 |
| NMI | 0.0655 | 0.0034 | 0.0171 | 0.0495 | 0.0431 | 0.0732 | 0.1086 | 0.4392 | |
| ARI | −0.0016 | 0.0013 | −0.0048 | −0.0029 | 0.0016 | −0.0103 | 0.0724 | 0.0564 | |
| IMDB | F1 | 0.5494 | 0.488 | 0.3628 | 0.3587 | 0.3646 | 0.4888 | 0.3634 | 0.546 |
| NMI | 0.0745 | 0.027 | 0.0018 | 0.0012 | 0.0158 | 0.1172 | 0.0101 | 0.2298 | |
| ARI | 0.0471 | 0.0146 | 0.0013 | −0.0009 | −0.0079 | 0.131 | 0.0083 | 0.1135 | |
| AIFB | F1 | 0.7517 | - | 0.6524 | 0.7375 | 0.6809 | - | 0.7163 | 0.7659 |
| NMI | 0.2401 | - | 0.1567 | 0.2117 | 0.2435 | - | 0.3812 | 0.3854 | |
| ARI | 0.1518 | - | 0.1248 | 0.1142 | 0.079 | - | 0.3011 | 0.2836 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Wang, R.-F. The Heterogeneous Network Community Detection Model Based on Self-Attention. Symmetry 2025, 17, 432. https://doi.org/10.3390/sym17030432
Zhou G, Wang R-F. The Heterogeneous Network Community Detection Model Based on Self-Attention. Symmetry. 2025; 17(3):432. https://doi.org/10.3390/sym17030432
Chicago/Turabian StyleZhou, Gaofeng, and Rui-Feng Wang. 2025. "The Heterogeneous Network Community Detection Model Based on Self-Attention" Symmetry 17, no. 3: 432. https://doi.org/10.3390/sym17030432
APA StyleZhou, G., & Wang, R.-F. (2025). The Heterogeneous Network Community Detection Model Based on Self-Attention. Symmetry, 17(3), 432. https://doi.org/10.3390/sym17030432







