Sharp Bounds of Hermitian Toeplitz Determinants for Bounded Turning Functions

Abstract

Hermitian Toeplitz determinants are used in multiple disciplines, including functional analysis, applied mathematics, physics, and engineering sciences. We calculate the sharp upper and lower bounds on the fourth-order Hermitian Toeplitz determinant for the subclass of bounded turning functions associated with the nephroid function represented by $R_n$. A nephroid function is associated with the geometric shape of a nephroid (a kidney-shaped curve) and refers to a specific type of epicycloid with two cusps. In geometric function theory, a bounded turning function is an analytic function whose derivative has a positive real part, ensuring that its tangent vector does not turn too sharply at any point.

1. Introduction and Definitions

Following the Bieberbach conjecture in 1916, there was a notable rise in the exploration of sharp bounds for the coefficient functionals of normalized analytic functions defined on the unit disk. The investigation of the bounds for the coefficients of various classes of analytic functions continued even after L. de Branges [1] presented the historical proof of the Bieberbach conjecture in 1984 since the bounds on coefficients also revealed other geometric characteristics of analytic functions. For example, the growth and distortion of an analytic function can be calculated using the bound on the second coefficient of an analytic univalent function [2]. Cantor [3] presented rationality criteria for analytic functions using the Hankel determinant of their coefficients. The estimated coefficient functionals become much more remarkable with results of this kind. Let A represent the set of functions that are analytic within the unit disk $\psi :=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$ and of the specified form

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{b}_n{z}^n,z\in \psi .$$

(1)

Let S consist of those functions from A which are univalent in $\psi$. When an open unit disk is inverted for a certain point, it reveals a characteristic called "inversion symmetry". The open unit disk reveals an inversion symmetry to the origin since any complex number z in the disk is inverted, for it shows the complex number $-z$, whose inversion is also in symmetry with respect to its center, the origin. In general, the open unit disk contains an array of symmetries useful in many mathematical and geometric situations. We aimed to explore additional geometric properties within this symmetrical region. Assume that f and g are two analytic functions in $\psi$. Then, we say that the function f is subordinate to the function g, written symbolically as

$$f\left(z\right)\prec g\left(z\right),\left(z\in \psi \right),$$

if there exists a Schwarz function $w\left(z\right)$ that meets the following conditions:

$$w\left(0\right)=0\mathrm{and}\left|w\left(z\right)\right|<1,\left(z\in \psi ,\right)$$

(2)

such that

$$f\left(z\right)=g\left(w\left(z\right)\right),\left(z\in \psi \right).$$

Hermitian Toeplitz matrices are important in functional analysis within applied mathematics, physics, and technical sciences. The Hermitian Toeplitz matrix $T_{q,n}\left(f\right)$ of a function $f\in A$, as defined by Equation (1), is obtained by selecting q,$n\in N$.

$$T_{q,n}\left(f\right)=\left(\begin{array}{ccc}{b}_n& b_{n+1}& \cdots b_{n+q-1}\\ {\overline{b}}_{n+1}& b_n& \cdots b_{n+q-2}\\ \begin{array}{c}⋮\\ {\overline{b}}_{n+q-1}\end{array}& \begin{array}{c}⋮\\ {\overline{b}}_{n+q-2}\end{array}& \begin{array}{c}⋮\\ \cdots \end{array}\begin{array}{c}⋮\\ b_n\end{array}\end{array}\right).$$

(3)

In recent years, many studies have focused on determining bounds for determinants, where elements are coefficients of functions of class A or its subclasses. The generalized Zalcman functional $j_{m,n}\left(f\right)$:$=b_{m+n-1-}{b}_m{b}_n,$$m,n$,$\in \mathbb{N}$, and Hankel matrices, or square matrices with constant entries along the reverse diagonal, are of particular significance. Many papers and related works have discussed the bounds for the generalized Zalcman functional, specifically $j_{2,3}\left(f\right)$ by Equation (3) for certain values q of n we obtain the “following”.

$$det\left(T_{2,1}\right)=\left|\begin{array}{cc}{b}_1& b_2\\ {\overline{b}}_2& b_1\end{array}\right|,det\left(T_{3,1}\right)=\left|\begin{array}{ccc}{b}_1& b_2& b_3\\ {\overline{b}}_2& b_1& b_2\\ {\overline{b}}_3& {\overline{b}}_2& b_1\end{array}\right|,$$

and

$$det\left(T_{4,1}\right)=\left|\begin{array}{cccc}{b}_1& b_2& b_3& b_4\\ {\overline{b}}_2& b_1& b_2& b_3\\ {\overline{b}}_3& {\overline{b}}_2& b_1& b_2\\ {\overline{b}}_4& {\overline{b}}_3& {\overline{b}}_2& b_1\end{array}\right|,$$

respectively. Note that for $f\in A$, $b_1=1,det\left(T_{2,1}\right)\left(f\right)$, $det\left(T_{3,1}\right)\left(f\right)$ and $det\left(T_{4,1}\right)\left(f\right)$ reduce to

$$det\left(T_{2,1}\right)\left(f\right)=1-{\left|b_2\right|}^2,$$

(4)

$$det\left(T_{3,1}\right)\left(f\right)=1-2{\left|b_2\right|}^2-{\left|b_3\right|}^2+2\Re \left(b_2^2{\overline{b}}_3\right),$$

(5)

and

$$\begin{array}{cc}\hfill det\left(T_{4,1}\right)\left(f\right)& =1-3{\left|b_2\right|}^2+{\left|b_2\right|}^4-2{\left|b_2\right|}^2{\left|b_3\right|}^2-2{\left|b_3\right|}^2+{\left|b_3\right|}^4\hfill \\ \hfill & +{\left|b_2\right|}^2{\left|b_4\right|}^2-{\left|b_4\right|}^2+4\Re \left(b_2^2{\overline{b}}_3\right)+4\Re \left(b_2{b}_3{\overline{b}}_4\right)\hfill \\ \hfill & -2\Re \left(b_2^3{\overline{b}}_4\right)-2\Re \left(b_2{\overline{b}}_3^2{b}_4\right).\hfill \end{array}$$

(6)

The focus of many articles in recent years has been to determine the bounds of determinants, the elements of which are coefficients of functions in A or its subclasses. Determinants are crucial in Geometric Function Theory (GFT), especially in conformal mappings, complex analysis, and transformations. Various real-world applications highlight their importance. For a 2D area or a 3D volume, the local scaling factor is given by the absolute value of the Jacobian determinant. It is utilized for image processing, computer graphics, and cartography transformations. Möbius transformations, used in control theory and signal processing, classify many transformations based on their determinants. When identifying if a transformation is rotation, dilation, or inversion, determinant conditions are useful. Symmetric Toeplitz determinants and Hankel matrices, square matrices with constant values along the anti-diagonal, are commonly encountered [2].

Hermitian Toeplitz’s determinants about normalized analytic functions are a fascinating study area. Hermitian Toeplitz determinants for specific classes of normalized analytic functions have been a topic of study since the findings presented in [4]. The sharp bounds of Hermitian Toeplitz determinants for various classes of univalent functions are explored in references [4,5,6,7,8,9,10,11,12]. Jastrzebski et al. [7] examined the precise upper and lower bounds of the second- and third-order Hermitian Toeplitz determinants for particular subclasses of close-to-star functions. In 2021, Kumar [8] established accurate upper and lower bounds for second- and third-order Hermitian–Toeplitz matrices within several subclasses of close-to-convex functions. For the classes of extremely starlike functions, lemniscate starlike functions, and lune starlike functions, Kumar et al. [13] determined the sharp upper and lower bounds for the Hermitian–Toeplitz determinant of the third order $det\left(T_{4,1}\left(f\right)\right)$ in 2021. Lecko et al. [14] calculated that $0\le det\left(T_{4,1}\left(f\right)\right)\le 1$ by analyzing the sharp upper and lower bounds for the Hermitian Toeplitz determinant of the fourth order for the class of convex functions in 2020.

Let P represent the class of Carathéodory functions p that is normalized by

$$p\left(z\right)=1+\sum _{n=1}^{\infty }{c}_n{z}^{n}z\in \psi ,$$

(7)

and satisfy the condition $\Re \left(p\left(z\right)\right)>0.$

We now consider the following class.

$$R_n=\left\{f\in \mathcal{S}:f\prime \left(z\right)\prec \Phi \left(z\right)\right\},$$

where

$$\Phi \left(z\right)=1+z-{\displaystyle \frac{z^3}{3}},$$

which maps the domain E into the nephroid-shaped region, as shown in Figure 1.

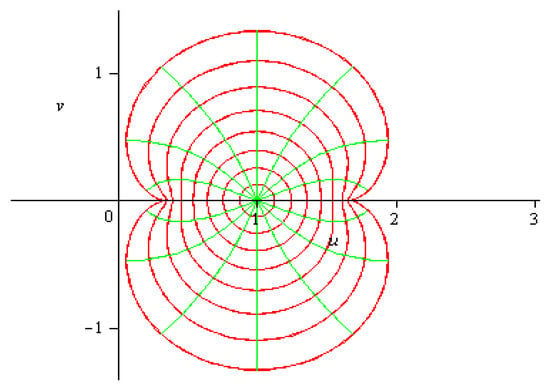
Figure 1. The image domain of the Nephroid function $\Phi \left(z\right)$.

We intend to find the sharpness of the first, second, third, and fourth orders for this defined class $R_n$. To proceed further, we need the following lemma.

Lemma 1

([15,16]). If $p\in P$, then

$$2c_2=c_1^2+\left(4-c_1^2\right)\xi ,$$

(8)

and

$$4c_3=c_1^3+\left(4-c_1^2\right)c_1\xi \left(2-\xi \right)+2\left(4-c_1^2\right)\left(1-{\left|\xi \right|}^2\right)\eta$$

(9)

for some $\xi ,\eta \in \overline{\psi }:=\left\{z\in \mathbb{C}:\left|z\right|\le 1\right\}.$

Theorem 2. 

Let $f\in R_n$, then

$${\displaystyle \frac{3}{4}}\le det\left(T_{2,1}\right)\left(f\right)\le 1.$$

The bounds are sharp.

Proof. 

For the function $f\in R_n$ as defined by Equation (1), it is understood that there is an analytic function $p\in P$ inside the unit disk $\psi$ with $p\left(0\right)=1$ and $\Re \left(p\left(z\right)\right)>0$ in (2).

$$f\prime \left(z\right)=1+w\left(z\right)-{\displaystyle \frac{w{\left(z\right)}^3}{3}}.$$

(10)

If $p\in P$, then

$$p\left(z\right)={\displaystyle \frac{1+w\left(z\right)}{1-w\left(z\right)}}=1+c_{1}z+c_2{z}^2+c_3{z}^3+\cdots .$$

By using, (10), we obtain

$$\begin{array}{ccc}\hfill 1+w\left(z\right)-{\displaystyle \frac{w{\left(z\right)}^3}{3}}& =& 1+{\displaystyle \frac{1}{2}}{c}_{1}z+({\displaystyle \frac{1}{2}}{c}_2-{\displaystyle \frac{1}{4}}{c}_1^2)z^2+({\displaystyle \frac{1}{2}}{c}_3-{\displaystyle \frac{1}{2}}{c}_{1}c+{\displaystyle \frac{1}{12}}{c}_1^3)z^3\hfill \\ & & +\left({\displaystyle \frac{1}{2}}{c}_1{c}_3+{\displaystyle \frac{1}{4}}{c}_1^2{c}_2+{\displaystyle \frac{1}{2}}{c}_4-{\displaystyle \frac{1}{4}}{c}_2^2\right)z^4+\cdots .\hfill \end{array}$$

(11)

Considering that the series is defined in (1), it implies that

$$f\prime \left(z\right)=1+2b_{2}z+3b_3{z}^2+4b_4{z}^3+\cdots .$$

(12)

Comparing (11) and (12), we obtain

$$b_2={\displaystyle \frac{1}{4}}c,b_3={\displaystyle \frac{1}{6}}{c}_2-{\displaystyle \frac{1}{12}}{c}^2.$$

(13)

Since the classes $f\in R_n$ and $det\left(T_{2,1}\right)\left(f\right)$ are rotationally invariant, we can say that $c:=c_1\in \left[0,2\right]$. Using (4) and $|c_1|\le 2$, we see that

$$det\left(T_{2,1}\right)\left(f\right)=1-{\displaystyle \frac{1}{16}}{\left|c_1\right|}^2\in \left[{\displaystyle \frac{3}{4}},1\right].$$

The function reaches the lower bound precisely.

$$f_0={\int }_0^z\left(1+\left(t-{\displaystyle \frac{t^3}{3}}\right)\right)dt=z+{\displaystyle \frac{1}{2}}{z}^2-{\displaystyle \frac{1}{12}}{z}^4+\cdots .$$

and the upper bound on $det\left(T_{2,1}\right)$ is exact of this function

$$f_1={\int }_0^z\left(1+{\left(t-{\displaystyle \frac{t^3}{3}}\right)}^2\right)dt=z+{\displaystyle \frac{1}{3}}{z}^3-{\displaystyle \frac{2}{15}}{z}^5+{\displaystyle \frac{1}{63}}{z}^7+\cdots .$$

□

Theorem 3.

 If $f\in R_n$, then

$${\displaystyle \frac{1}{2}}\le det\left(T_{3,1}\right)\left(f\right)\le 1.$$

(14)

The bounds are sharp.

Proof. 

For the function $f\in R_n$ as defined in Equation (1), it is understood that there exists an analytic function $p\in P$ within the unit disk $\psi$, such that $p\left(0\right)=1$ and $\Re \left(p\left(z\right)\right)>0$ in (2).

$$f\prime \left(z\right)=1+w\left(z\right)-{\displaystyle \frac{w{\left(z\right)}^3}{3}}.$$

(15)

If $p\in P$, then

$$p\left(z\right)={\displaystyle \frac{1+w\left(z\right)}{1-w\left(z\right)}}=1+c_{1}z+c_2{z}^2+c_3{z}^3+\cdots .$$

Using (15), we obtain

$$\begin{array}{ccc}\hfill 1+w\left(z\right)-{\displaystyle \frac{w{\left(z\right)}^3}{3}}& =& 1+{\displaystyle \frac{1}{2}}{c}_{1}z+({\displaystyle \frac{1}{2}}{c}_2-{\displaystyle \frac{1}{4}}{c}_1^2)z^2+({\displaystyle \frac{1}{2}}{c}_3-{\displaystyle \frac{1}{2}}{c}_{1}c+{\displaystyle \frac{1}{12}}{c}_1^3)z^3\hfill \\ & & +\left({\displaystyle \frac{1}{2}}{c}_1{c}_3+{\displaystyle \frac{1}{4}}{c}_1^2{c}_2+{\displaystyle \frac{1}{2}}{c}_4-{\displaystyle \frac{1}{4}}{c}_2^2\right)z^4+\cdots .\hfill \end{array}$$

(16)

Considering that the series is defined in (1), it implies that

$$f\prime \left(z\right)=1+2b_{2}z+3b_3{z}^2+4b_4{z}^3+\cdots .$$

(17)

Comparing (16) and (17), we obtain

$$b_2={\displaystyle \frac{1}{4}}c,b_3={\displaystyle \frac{1}{6}}{c}_2-{\displaystyle \frac{1}{12}}{c}^2.$$

(18)

By using (4) and (18), we have

$$det\left(T_{3,1}\right)\left(f\right)=1-{\displaystyle \frac{1}{8}}{c}^2-{\displaystyle \frac{1}{36}}{c}_2^2+{\displaystyle \frac{1}{36}}{c}_2{c}^2-{\displaystyle \frac{1}{144}}{c}^4+{\displaystyle \frac{1}{8}}\Re \left(c^2({\displaystyle \frac{1}{6}}{c}_2-{\displaystyle \frac{1}{12}}{c}^2)\right).$$

By (8), we have

$$det\left(T_{3,1}\right)\left(f\right)=1-{\displaystyle \frac{1}{8}}{c}^2+{\displaystyle \frac{1}{96}}{c}^2\left(4-c^2\right)\Re \left(\xi \right)-{\displaystyle \frac{1}{144}}{\left(4-c^2\right)}^2{\left|\xi \right|}^2=:\psi \left(c,\left|\xi \right|,\Re \left(\xi \right)\right)$$

(19)

for some $c\in \left[0,2\right]$ and $\xi \in \overline{\psi .}$

$\mathbf{A}$. First, we show that (14) has a right-side inequality.

By mean (19), we obtain

$$det\left(T_{3,1}\right)\left(f\right)=\psi \left(c,\left|\xi \right|,\Re \left|\xi \right|\right)\le \psi \left(c,\left|\xi \right|,-\left|\xi \right|\right)$$

$$=:G\left(c^2,\left|\xi \right|\right)\left(\left(c,\left|\xi \right|\right)\in \left[0,2\right]\times \left[0,1\right]\right).$$

(20)

Let $G:$ $\left[0,4\right]\times \left[0,1\right]\to R$ be defined by

$$G\left(\alpha ,\beta \right)=1-{\displaystyle \frac{1}{8}}\alpha -{\displaystyle \frac{1}{96}}\left(4-\alpha \right)\alpha \beta -{\displaystyle \frac{1}{144}}{\left(4-\alpha \right)}^2{\beta }^2.$$

${\mathbf{A}}_1$. Put $\alpha =0$, then we have

$$G\left(0,\beta \right)=1-{\displaystyle \frac{1}{9}}{\beta }^2\le 1\left(\beta \in \left[0,1\right]\right).$$

${\mathbf{A}}_2$. Put $\alpha =4$, we have

$$G\left(4,\beta \right)={\displaystyle \frac{1}{2}}\left(\beta \in \left[0,1\right]\right).$$

${\mathbf{A}}_3$. Put $\beta =0$, we obtain

$$G\left(\alpha ,0\right)=1-{\displaystyle \frac{1}{8}}\alpha \left(\alpha \in \left[0,4\right]\right).$$

${\mathbf{A}}_4$. Put $\beta =1,$ we observe that

$$G\left(\alpha ,1\right)=1-{\displaystyle \frac{1}{8}}\alpha -{\displaystyle \frac{1}{96}}\left(4-\alpha \right)\alpha -{\displaystyle \frac{1}{144}}{\left(4-\alpha \right)}^2\le G\left(0,1\right)={\displaystyle \frac{8}{9}}\left(\alpha \in \left[0,4\right]\right).$$

${\mathbf{A}}_5$. Let $\left(\alpha ,\beta \right)$ be an element of the interval $\left(0,4\right)\times \left(0,1\right).$

$${\displaystyle \frac{\partial G}{\partial \beta }}=-{\displaystyle \frac{1}{96}}(4-\alpha )-{\displaystyle \frac{1}{72}}{(4-\alpha )}^2\beta =0$$

If and only if

$${\beta }_0={\displaystyle \frac{3\alpha }{4(\alpha -4)}}.$$

Therefore we see that

$${\displaystyle \frac{\partial G}{\partial \alpha }}\left(\alpha ,{\beta }_0\right)=0$$

If and only if

$$-{\displaystyle \frac{1}{8}}+{\displaystyle \frac{{\alpha }^2}{32(4\alpha -16)}}-{\displaystyle \frac{\left(4-\alpha \right)\alpha }{32\left(4\alpha -16\right)}}+{\displaystyle \frac{\left(4-\alpha \right){\alpha }^2}{8{\left(4\alpha -16\right)}^2}}=0.$$

(21)

Equation (21) has the following solution:

$${\alpha }_1=16,{\alpha }_2=4.$$

Hence, $G(\alpha ,\beta )$ does not have a critical point within the interval $\left(0,4\right)\times \left(0,1\right).$

Form ${\mathbf{A}}_1$ to ${\mathbf{A}}_5$ it is obviously

$$det\left(T_{3,1}\right)\left(f\right)\le max\left\{1,{\displaystyle \frac{1}{2}}\right\}=1.$$

Now, with $\left(\alpha ,\beta \right)\in \left[0,4\right]\times \left[0,1\right]$, we can infer from (20), that the upper bound given in (14) is valid.

$\mathbf{B}$. The inequality on the left side of the Equation (14) has been defined.

$$det\left(T_{3,1}\right)\left(f\right)=\psi \left(c,\left|\xi \right|\right)\ge \psi \left(c,\left|\xi \right|,-\left|\xi \right|\right)$$

$$=:Q\left(c^2,\left|\xi \right|\right)\left(\left(c,\left|\xi \right|\right)\in \left[0,2\right]\times \left[0,1\right]\right).$$

(22)

Let $Q:$$\left[0,4\right]\times \left[0,1\right]\to R$ be defined by

$$Q\left(\alpha ,\beta \right)=1-{\displaystyle \frac{1}{8}}+{\displaystyle \frac{1}{96}}\left(4-\alpha \right)\alpha \beta -{\displaystyle \frac{1}{144}}{\left(4-\alpha \right)}^2{\beta }^2.$$

${\mathbf{B}}_1$. Put $\alpha =0$, we obtain

$$Q\left(0,\beta \right)=1-{\displaystyle \frac{1}{9}}{\beta }^2\ge {\displaystyle \frac{8}{9}}\left(\beta \in \left[0,1\right]\right).$$

${\mathbf{B}}_2$. Put $\alpha =4$, we have

$$Q\left(4,\beta \right)={\displaystyle \frac{1}{2}}\left(\beta \in \left[0,1\right]\right).$$

${\mathbf{B}}_3$. Put $\beta =0,$ then we have

$$Q\left(\alpha ,0\right)=1-{\displaystyle \frac{1}{8}}\alpha \left(\alpha \in \left[0,4\right]\right).$$

${\mathbf{B}}_4$. Put $\beta =1,$ we obtain

$$Q\left(\alpha ,1\right)=1-{\displaystyle \frac{1}{8}}\alpha +{\displaystyle \frac{1}{96}}\left(4-\alpha \right)\alpha -{\displaystyle \frac{1}{144}}{\left(4-\alpha \right)}^2={\displaystyle \frac{1}{2}}\left(\alpha \in \left[0,4\right]\right).$$

${\mathbf{B}}_5$. Let $\left(\alpha ,\beta \right)\in \left(0,4\right)\times \left(0,1\right).$ Then

$${\displaystyle \frac{\partial Q}{\partial \beta }}={\displaystyle \frac{1}{96}}(4-\alpha )-{\displaystyle \frac{1}{72}}{(4-\alpha )}^2\beta =0$$

If and only if

$$\beta ={\beta }_0=-{\displaystyle \frac{3\alpha }{4(\alpha -4)}}.$$

Therefore, $Q\left(\alpha ,\beta \right)$ has no critical points within the region $(0,4)\times (0,1$).

From section ${\mathbf{B}}_{\mathbf{1}}$ to ${\mathbf{B}}_{\mathbf{5}}$, it shows that

$$Q\left(\alpha ,\beta \right)\ge min\left\{{\displaystyle \frac{8}{9}},{\displaystyle \frac{1}{2}}\right\}$$

$$={\displaystyle \frac{1}{2}}.$$

If we consider parts $\mathbf{A}$ and $\mathbf{B}$, the right side inequality in (14) is true.

The following function gives the lower bound.

$$f_0={\int }_0^z\left(1+\left(t-{\displaystyle \frac{t^3}{3}}\right)\right)dt=z+{\displaystyle \frac{1}{2}}{z}^2-{\displaystyle \frac{1}{12}}{z}^4+\cdots ,$$

and the upper bound of $det\left(T_{3,1}\right)$ is given by the following function;

$$f_1={\int }_0^z\left(1+{\left(t-{\displaystyle \frac{t^3}{3}}\right)}^3\right)dt=z+{\displaystyle \frac{1}{4}}{z}^4-{\displaystyle \frac{1}{6}}{z}^6+{\displaystyle \frac{1}{24}}{z}^8-{\displaystyle \frac{1}{270}}{z}^{10}+\cdots .$$

□

Theorem 4.

 If $f\in R_n$, then

$${\displaystyle \frac{64}{81}}\le det\left(T_{4,1}\right)\left(f\right)\le 1.$$

(23)

The bounds are sharp.

Proof. 

For the function $f\in R_n$ as defined in Equation (1), it is understood that there exists an analytic function $p\in P$ within the unit disk $\psi$, such that $p\left(0\right)=1$ and $\Re \left(p\left(z\right)\right)>0$ in (2).

$$f\prime \left(z\right)=1+w\left(z\right)-{\displaystyle \frac{w{\left(z\right)}^3}{3}}.$$

(24)

If $p\in P$, then

$$p\left(z\right)={\displaystyle \frac{1+w\left(z\right)}{1-w\left(z\right)}}=1+c_{1}z+c_2{z}^2+c_3{z}^3+\cdots .$$

Using (24), we obtain

$$\begin{array}{ccc}\hfill 1+w\left(z\right)-{\displaystyle \frac{w{\left(z\right)}^3}{3}}& =& 1+{\displaystyle \frac{1}{2}}{c}_{1}z+({\displaystyle \frac{1}{2}}{c}_2-{\displaystyle \frac{1}{4}}{c}_1^2)z^2+({\displaystyle \frac{1}{2}}{c}_3-{\displaystyle \frac{1}{2}}{c}_{1}c+{\displaystyle \frac{1}{12}}{c}_1^3)z^3\hfill \\ & & +\left({\displaystyle \frac{1}{2}}{c}_1{c}_3+{\displaystyle \frac{1}{4}}{c}_1^2{c}_2+{\displaystyle \frac{1}{2}}{c}_4-{\displaystyle \frac{1}{4}}{c}_2^2\right)z^4+\cdots .\hfill \end{array}$$

(25)

Considering that the series is defined in (1), it implies that

$$f\prime \left(z\right)=1+2b_{2}z+3b_3{z}^2+4b_4{z}^3+\cdots .$$

(26)

Comparing (25) and (26), we obtain

$$b_2={\displaystyle \frac{1}{4}}c,b_3={\displaystyle \frac{1}{6}}{c}_2-{\displaystyle \frac{1}{12}}{c}^2,b_4={\displaystyle \frac{1}{8}}{c}_3-{\displaystyle \frac{1}{8}}c{c}_2+{\displaystyle \frac{1}{48}}{c}^3.$$

(27)

By using (27) in equation (6), we get

$$\begin{array}{ccc}\hfill det\left(T_{4,1}\right)\left(f\right)& =& 1-{\displaystyle \frac{3}{16}}{c}^2-{\displaystyle \frac{23}{2304}}{c}^4+{\displaystyle \frac{1}{48}}\Re c{c}_2{c}_3-{\displaystyle \frac{1}{576}}\Re c_2^2{c}_3+{\displaystyle \frac{1}{576}}\Re c^3{c}_2{c}_3\hfill \\ & & +{\displaystyle \frac{1}{1296}}{c}_2^4-{\displaystyle \frac{1}{2304}}\Re c^5{c}_3+{\displaystyle \frac{1}{24}}\Re c^2{c}_2+{\displaystyle \frac{5}{6912}}\Re c^6{c}_2+{\displaystyle \frac{41}{2304}}\Re c^4{c}_2\hfill \\ & & +{\displaystyle \frac{1}{576}}\Re c^2{c}_2^3+{\displaystyle \frac{1}{32}}{c}_{3}c{c}_2-{\displaystyle \frac{11}{768}}\Re c^3{c}_3-{\displaystyle \frac{1}{512}}{c}^3{c}_3{c}_2-{\displaystyle \frac{7}{3456}}\Re c^4{c}_2^2\hfill \\ & & -{\displaystyle \frac{1}{48}}\Re c^2{c}_2^2-{\displaystyle \frac{1}{18}}{c}_2^2+{\displaystyle \frac{1}{18}}{c}_2{c}^2-{\displaystyle \frac{11}{576}}{c}^2{c}_2^2+{\displaystyle \frac{5}{576}}{c}^4{c}_2-{\displaystyle \frac{1}{648}}{c}^2{c}_2^3\hfill \\ & & +{\displaystyle \frac{59}{27,648}}{c}^4{c}_2^2-{\displaystyle \frac{59}{82,944}}{c}^6{c}_2-{\displaystyle \frac{1}{192}}{c}_3{c}^3+{\displaystyle \frac{1}{1024}}{c}^2{c}_3^2+{\displaystyle \frac{1}{3072}}{c}^5{c}_3\hfill \\ & & -{\displaystyle \frac{1}{48}}\Re c^4-{\displaystyle \frac{11}{4608}}\Re c^6-{\displaystyle \frac{1}{13,824}}\Re c^8-{\displaystyle \frac{1}{768}}{c}^6+{\displaystyle \frac{25}{331,776}}{c}^8-{\displaystyle \frac{1}{64}}{c}_3^2.\hfill \end{array}$$

Thus, by using (8) and (9), we obtain

$$\begin{array}{ccc}\hfill det\left(T_{4,1}\right)\left(f\right)& =& 1-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{48}}\Re c^2(4-c^2)\zeta -{\displaystyle \frac{1}{768}}(4-c^2)c^3\eta {\left|\zeta \right|}^2+{\displaystyle \frac{1}{256}}c{(4-c^2)}^2\eta {\zeta }^2\hfill \\ & & +{\displaystyle \frac{1}{12,288}}{c}^5(4-c^2)\eta {\left|\zeta \right|}^2-{\displaystyle \frac{1}{4096}}{c}^3{(4-c^2)}^2\eta {\zeta }^2-{\displaystyle \frac{1}{2048}}{c}^2{(4-c^2)}^2{\eta }^2{\zeta }^2\hfill \\ & & +{\displaystyle \frac{1}{4096}}{c}^2{(4-c^2)}^2{\eta }^2{\zeta }^4-{\displaystyle \frac{1}{1152}}\Re c^4(4-c^2)\zeta -{\displaystyle \frac{1}{384}}\Re c^2{(4-c^2)}^2{\zeta }^3\hfill \\ & & +{\displaystyle \frac{1}{1024}}\Re c^4(4-c^2){\zeta }^2-{\displaystyle \frac{1}{512}}\Re c^3(4-c^2)\eta +{\displaystyle \frac{1}{27,648}}\Re c^4{(4-c^2)}^2{\zeta }^2\hfill \\ & & +{\displaystyle \frac{1}{9216}}\Re c^2{(4-c^2)}^3{\zeta }^4-{\displaystyle \frac{1}{192}}\Re c{(4-c^2)}^2\zeta \eta {\left|\zeta \right|}^2+{\displaystyle \frac{1}{4608}}\Re c{(4-c^2)}^3{\zeta }^2\eta {\left|\zeta \right|}^2\hfill \\ & & +{\displaystyle \frac{1}{16,384}}{c}^4{(4-c^2)}^2{\zeta }^4+{\displaystyle \frac{1}{768}}{c}^3(4-c^2)\eta -{\displaystyle \frac{1}{12,288}}{c}^5(4-c^2)\eta \hfill \\ & & -{\displaystyle \frac{1}{1536}}{c}^4(4-c^2){\zeta }^2+{\displaystyle \frac{1}{128}}{(4-c^2)}^2{\eta }^2{\left|\zeta \right|}^2-{\displaystyle \frac{1}{1152}}{c}^2{(4-c^2)}^2{\zeta }^2\hfill \\ & & -{\displaystyle \frac{1}{1024}}{c}^2{(4-c^2)}^2{\zeta }^4-{\displaystyle \frac{1}{256}}{(4-c^2)}^2{\eta }^2{\left|\zeta \right|}^4+{\displaystyle \frac{1}{4096}}{c}^2{(4-c^2)}^2{\eta }^2\hfill \\ & & +{\displaystyle \frac{1}{24,576}}{c}^6(4-c^2){\zeta }^2-{\displaystyle \frac{1}{256}}c{(4-c^2)}^2{\zeta }^4\eta +{\displaystyle \frac{1}{192}}\Re c{(4-c^2)}^2\zeta \eta \hfill \\ & & +{\displaystyle \frac{1}{512}}\Re c^3(4-c^2)\eta {\left|\zeta \right|}^2-{\displaystyle \frac{1}{4608}}\Re c{(4-c^2)}^3{\zeta }^2\eta +{\displaystyle \frac{1}{4096}}{c}^3{(4-c^2)}^2{\eta }^2{\zeta }^4\hfill \\ & & +{\displaystyle \frac{1}{3072}}\Re c^6-{\displaystyle \frac{1}{72}}{(4-c^2)}^2{\zeta }^2+{\displaystyle \frac{1}{20,736}}{(4-c^2)}^4{\zeta }^4-{\displaystyle \frac{1}{256}}{(4-c^2)}^2{\eta }^2\hfill \\ & & +{\displaystyle \frac{1}{256}}{c}^4-{\displaystyle \frac{1}{9216}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8,\hfill \end{array}$$

(28)

for some $c\in \left[0,2\right]$ and $\zeta ,\eta \in \overline{\psi }$.

The next step is to study the lower and upper bounds of the class $R_n$ under various conditions. A. Let $\zeta =0.$ Then

$$\begin{array}{cc}\hfill 0& \le det\left(T_{4,1}\right)\left(f\right)=1+{\displaystyle \frac{1}{4096}}{c}^2{(4-c^2)}^2{\eta }^2+{\displaystyle \frac{1}{768}}{c}^3(4-c^2)\eta \hfill \\ \hfill & -{\displaystyle \frac{1}{12,288}}{c}^5(4-c^2)\eta -{\displaystyle \frac{1}{256}}{(4-c^2)}^2{\eta }^2-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{256}}{c}^4\hfill \\ \hfill & +{\displaystyle \frac{1}{4608}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8:=T_0(c,\eta )\hfill \end{array}$$

(29)

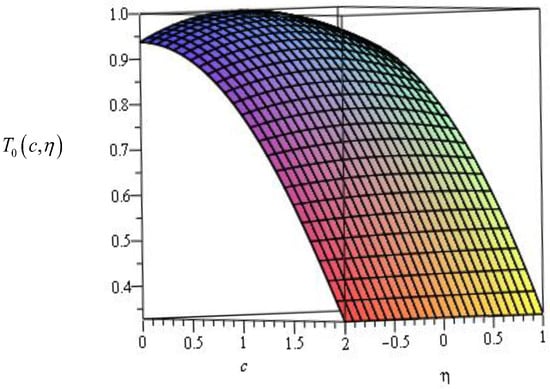
The right hand side of (29) gives the bound of 1 over the intervals $c\in \left[0,2\right]$ and $\eta \in [-1,1]$. This fact can also be seen from Figure 2.

Figure 2. The graph of $T_0(c,\eta )$.

Let $\eta =0.$ Then

$$\begin{array}{cc}\hfill det\left(T_{4,1}\right)\left(f\right)& =1-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{256}}{c}^4-{\displaystyle \frac{2}{9}}{\zeta }^2+{\displaystyle \frac{1}{81}}{\zeta }^4+{\displaystyle \frac{1}{147,456}}{c}^8-{\displaystyle \frac{1}{9216}}{c}^6\hfill \\ \hfill & +{\displaystyle \frac{1}{3072}}\Re c^6+{\displaystyle \frac{1}{12}}\Re c^2\zeta -{\displaystyle \frac{1}{24}}\Re c^2{\zeta }^3+{\displaystyle \frac{31}{6912}}\Re c^4{\zeta }^2+{\displaystyle \frac{1}{144}}\Re c^2{\zeta }^4\hfill \\ \hfill & +{\displaystyle \frac{1}{48}}\Re c^4{\zeta }^3+{\displaystyle \frac{1}{1152}}\Re c^6\zeta -{\displaystyle \frac{1}{384}}\Re c^6{\zeta }^3-{\displaystyle \frac{7}{288}}\Re c^4\zeta +{\displaystyle \frac{371}{27,648}}{c}^4{\zeta }^4\hfill \\ \hfill & -{\displaystyle \frac{11}{1152}}{c}^4{\zeta }^2-{\displaystyle \frac{145}{5184}}{c}^2{\zeta }^4+{\displaystyle \frac{7}{72}}{c}^2{\zeta }^2+{\displaystyle \frac{1}{27,648}}\Re c^8{\zeta }^2+{\displaystyle \frac{1}{768}}\Re c^6{\zeta }^4\hfill \\ \hfill & -{\displaystyle \frac{1}{192}}\Re c^4{\zeta }^4-{\displaystyle \frac{1}{9216}}\Re c^8{\zeta }^4-{\displaystyle \frac{35}{27,648}}\Re c^6{\zeta }^2-{\displaystyle \frac{371}{165,888}}{c}^6{\zeta }^4\hfill \\ \hfill & +{\displaystyle \frac{145}{1,327,104}}{c}^8{\zeta }^4-{\displaystyle \frac{1}{18,432}}{c}^6{\zeta }^2-{\displaystyle \frac{1}{24,576}}{c}^8{\zeta }^2.\hfill \end{array}$$

(30)

It follows that

$$\begin{array}{cc}\hfill det\left(T_{4,1}\right)\left(f\right)& \ge 1-{\displaystyle \frac{1}{12}}{c}^2\zeta +{\displaystyle \frac{7}{288}}{c}^4\zeta +{\displaystyle \frac{7}{72}}{c}^2{\zeta }^2+{\displaystyle \frac{31}{6912}}{c}^4{\zeta }^2-{\displaystyle \frac{11}{1152}}{c}^4{\zeta }^2\hfill \\ \hfill & -{\displaystyle \frac{1}{1152}}{c}^6\zeta -{\displaystyle \frac{35}{27,648}}{c}^6{\zeta }^2-{\displaystyle \frac{1}{18,432}}{c}^6{\zeta }^2-{\displaystyle \frac{1}{24}}{c}^2{\zeta }^3+{\displaystyle \frac{1}{48}}{c}^4{\zeta }^3\hfill \\ \hfill & -{\displaystyle \frac{1}{384}}{c}^6{\zeta }^3+{\displaystyle \frac{1}{27,648}}{c}^8{\zeta }^2-{\displaystyle \frac{1}{24,576}}{c}^8{\zeta }^2-{\displaystyle \frac{145}{5184}}{c}^2{\zeta }^4+{\displaystyle \frac{1}{144}}{c}^2{\zeta }^4\hfill \\ \hfill & +{\displaystyle \frac{371}{27,648}}{c}^4{\zeta }^4-{\displaystyle \frac{1}{192}}{c}^4{\zeta }^4-{\displaystyle \frac{371}{165,888}}{c}^6{\zeta }^4+{\displaystyle \frac{1}{768}}{c}^6{\zeta }^4-{\displaystyle \frac{1}{9216}}{c}^8{\zeta }^4\hfill \\ \hfill & +{\displaystyle \frac{145}{1,327,104}}{c}^8{\zeta }^4-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{256}}{c}^4-{\displaystyle \frac{1}{9216}}{c}^6+{\displaystyle \frac{1}{3072}}{c}^6\hfill \\ \hfill & +{\displaystyle \frac{1}{147,456}}{c}^8-{\displaystyle \frac{2}{9}}{\zeta }^2+{\displaystyle \frac{1}{81}}{\zeta }^4\hfill \\ \hfill & =:P(c^2,\zeta ),\hfill \end{array}$$

(31)

and

$$\begin{array}{cc}\hfill det\left(T_{4,1}\right)\left(f\right)& \le 1+{\displaystyle \frac{1}{12}}{c}^2\zeta -{\displaystyle \frac{7}{288}}{c}^4\zeta +{\displaystyle \frac{7}{72}}{c}^2{\zeta }^2+{\displaystyle \frac{31}{6912}}{c}^4{\zeta }^2-{\displaystyle \frac{11}{1152}}{c}^4{\zeta }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{1152}}{c}^6\zeta -{\displaystyle \frac{35}{27,648}}{c}^6{\zeta }^2-{\displaystyle \frac{1}{18,432}}{c}^6{\zeta }^2-{\displaystyle \frac{1}{24}}{c}^2{\zeta }^3+{\displaystyle \frac{1}{48}}{c}^4{\zeta }^3\hfill \\ \hfill & -{\displaystyle \frac{1}{384}}{c}^6{\zeta }^3+{\displaystyle \frac{1}{27,648}}{c}^8{\zeta }^2-{\displaystyle \frac{1}{24,576}}{c}^8{\zeta }^2-{\displaystyle \frac{145}{5184}}{c}^2{\zeta }^4+{\displaystyle \frac{1}{144}}{c}^2{\zeta }^4\hfill \\ \hfill & +{\displaystyle \frac{371}{27,648}}{c}^4{\zeta }^4-{\displaystyle \frac{1}{192}}{c}^4{\zeta }^4-{\displaystyle \frac{371}{165,888}}{c}^6{\zeta }^4+{\displaystyle \frac{1}{768}}{c}^6{\zeta }^4-{\displaystyle \frac{1}{9216}}{c}^8{\zeta }^4\hfill \\ \hfill & +{\displaystyle \frac{145}{1,327,104}}{c}^8{\zeta }^4-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{256}}{c}^4-{\displaystyle \frac{1}{9216}}{c}^6+{\displaystyle \frac{1}{3072}}\Re c^6\hfill \\ \hfill & +{\displaystyle \frac{1}{147,456}}{c}^8-{\displaystyle \frac{2}{9}}{\zeta }^2+{\displaystyle \frac{1}{81}}{\zeta }^4\hfill \\ \hfill & =:Q(c^2,\zeta ),\hfill \end{array}$$

(32)

let P, Q: $\left[0,4\right]\times \left[0,1\right]\to R$ be defined by

$$\begin{array}{cc}\hfill P(u,\alpha )& =1+{\displaystyle \frac{7}{72}}u{\alpha }^2-{\displaystyle \frac{35}{6912}}{u}^2{\alpha }^2-{\displaystyle \frac{73}{55,296}}{u}^3{\alpha }^2-{\displaystyle \frac{1}{24}}u{\alpha }^3\hfill \\ \hfill & +{\displaystyle \frac{1}{48}}{u}^2{\alpha }^3-{\displaystyle \frac{1}{384}}{u}^3{\alpha }^3-{\displaystyle \frac{1}{221,184}}{u}^4{\alpha }^2-{\displaystyle \frac{109}{5184}}u{\alpha }^4-{\displaystyle \frac{13}{48}}u\hfill \\ \hfill & +{\displaystyle \frac{227}{27,648}}{u}^2{\alpha }^4-{\displaystyle \frac{155}{165,888}}{u}^3{\alpha }^4+{\displaystyle \frac{1}{1,327,104}}{u}^4{\alpha }^4+{\displaystyle \frac{65}{2304}}{u}^2\hfill \\ \hfill & +{\displaystyle \frac{1}{1536}}{u}^3+{\displaystyle \frac{1}{147,456}}{u}^4-{\displaystyle \frac{2}{9}}{\alpha }^2+{\displaystyle \frac{1}{81}}{\alpha }^4,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill Q(u,\alpha )& =& 1+{\displaystyle \frac{1}{12}}u\alpha -{\displaystyle \frac{7}{288}}{u}^2\alpha +{\displaystyle \frac{7}{72}}u{\alpha }^2-{\displaystyle \frac{35}{6912}}{u}^2{\alpha }^2+{\displaystyle \frac{1}{1152}}{u}^3\alpha \hfill \\ & & -{\displaystyle \frac{73}{55,296}}{u}^3{\alpha }^2-{\displaystyle \frac{1}{24}}u{\alpha }^3+{\displaystyle \frac{1}{48}}{u}^2{\alpha }^3-{\displaystyle \frac{1}{384}}{u}^3{\alpha }^3-{\displaystyle \frac{1}{221,184}}{u}^4{\alpha }^2\hfill \\ & & -{\displaystyle \frac{109}{5184}}u{\alpha }^4+{\displaystyle \frac{227}{27,648}}{u}^2{\alpha }^4-{\displaystyle \frac{155}{165,888}}{u}^3{\alpha }^4+{\displaystyle \frac{1}{1,327,104}}{u}^4{\alpha }^4\hfill \\ & & -{\displaystyle \frac{3}{16}}u+{\displaystyle \frac{1}{256}}{u}^2+{\displaystyle \frac{1}{4608}}{u}^3+{\displaystyle \frac{1}{147,456}}{u}^4-{\displaystyle \frac{2}{9}}{\alpha }^2+{\displaystyle \frac{1}{81}}{\alpha }^4,\hfill \end{array}$$

respectively.

$\mathbf{B}\mathbf{1}$. The lower bound of $P(u,\alpha )$ is examined.

$\left(i\right)$ We have $\left[0,4\right]\times \left[0,1\right]$ on its vertices.

$$P(0,0)\ne P(0,1)\ne P(4,0)\ne P(4,1).$$

$\left(ii\right)$ Put $u=0$, we obtain

$$P(0,\alpha )={\left(1-{\displaystyle \frac{1}{9}}{\alpha }^2\right)}^2\ge 0,\left(\alpha \in \left[0,1\right]\right).$$

$\left(iii\right)$ Put $u=4$, we obtain

$$P(4,\alpha )={\displaystyle \frac{21}{64}},\left(\alpha \in \left[0,1\right]\right).$$

$\left(iv\right)$ Put $\alpha =0$, we have

$$P(u,0)=1-{\displaystyle \frac{13}{48}}u+{\displaystyle \frac{65}{2304}}{u}^2-{\displaystyle \frac{1}{1536}}{u}^3+{\displaystyle \frac{1}{147,456}}{u}^4\ge 0.$$

$\left(v\right)$ Putt $\alpha =1$, we obtain

$$P(u,1)={\displaystyle \frac{64}{81}}-{\displaystyle \frac{1225}{5184}}u+{\displaystyle \frac{481}{9216}}{u}^2-{\displaystyle \frac{457}{82,944}}{u}^3+{\displaystyle \frac{1}{331,776}}{u}^4=:\Phi \left(u\right)\left(u\in \left[0,4\right]\right).$$

Note that

$$\Phi \prime \left(u\right)=-{\displaystyle \frac{1225}{5184}}+{\displaystyle \frac{481}{1536}}u-{\displaystyle \frac{457}{27,648}}{u}^2+{\displaystyle \frac{1}{82,944}}{u}^3,\left(u\in \left[0,4\right]\right),$$

for $0\le u\le 4$, we observed that $\Phi \prime \left(u\right)\le 0$, which mean that

$$\Phi \left(u\right)\ge \Phi \left(0\right)={\displaystyle \frac{64}{81}},$$

Therefore, we conclude that

$$P(u,1)=\Phi \left(u\right)\ge {\displaystyle \frac{64}{81}}\left(u\in \left[0,4\right]\right).$$

$\left(vi\right)$ It is evident that P does not have critical points within the interior $\left(0,4\right)\times \left(0,1\right)$. Consider the system of equations

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial p}{\partial \alpha }}& =-{\displaystyle \frac{1}{12}}u+{\displaystyle \frac{7}{288}}{u}^2+{\displaystyle \frac{7}{36}}\alpha u-{\displaystyle \frac{35}{3456}}{u}^2\alpha -{\displaystyle \frac{1}{1152}}{u}^3-{\displaystyle \frac{73}{27,648}}{u}^3\alpha \hfill \\ \hfill & -{\displaystyle \frac{1}{8}}u{\alpha }^2+{\displaystyle \frac{1}{16}}{u}^2{\alpha }^2-{\displaystyle \frac{1}{128}}{u}^3{\alpha }^2-{\displaystyle \frac{1}{110,592}}{u}^4\alpha -{\displaystyle \frac{109}{1296}}u{\alpha }^3\hfill \\ \hfill & +{\displaystyle \frac{227}{6912}}{u}^2{\alpha }^3-{\displaystyle \frac{155}{41,472}}{u}^3{\alpha }^3+{\displaystyle \frac{1}{331,776}}{u}^4{\alpha }^3-{\displaystyle \frac{4}{9}}\alpha +{\displaystyle \frac{4}{81}}{\alpha }^3\hfill \\ \hfill & =0.\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial p}{\partial u}}& ={\displaystyle \frac{7}{72}}{\alpha }^2-{\displaystyle \frac{70}{6912}}u{\alpha }^2-{\displaystyle \frac{219}{55,296}}{\alpha }^2{u}^2-{\displaystyle \frac{1}{24}}{\alpha }^3+{\displaystyle \frac{1}{24}}u{\alpha }^3-{\displaystyle \frac{1}{128}}{u}^2{\alpha }^3\hfill \\ \hfill & -{\displaystyle \frac{4}{221,184}}{u}^3{\alpha }^2-{\displaystyle \frac{109}{5184}}{\alpha }^4-{\displaystyle \frac{13}{48}}+{\displaystyle \frac{454}{27,648}}u{\alpha }^4-{\displaystyle \frac{465}{165,888}}{u}^2{\alpha }^4\hfill \\ \hfill & +{\displaystyle \frac{4}{1,327,104}}{u}^3{\alpha }^4+{\displaystyle \frac{130}{2304}}u+{\displaystyle \frac{3}{1536}}{u}^2+{\displaystyle \frac{4}{147,456}}{u}^3\hfill \\ \hfill & =0.\hfill \end{array}$$

(33)

For ${\displaystyle \frac{\partial p}{\partial \alpha }}=0$ and ${\displaystyle \frac{\partial p}{\partial u}}=0$, we have solved these equations by using the Newton Raphson method and we obtain $\alpha =-3.25\times {10}^{-21}$ and $c=4.164834762$. We see that $u\notin (0,4), c\notin (0,1)$. We observed that there is no critical point within the interior $(0,4)\times (0,1)$. So it has no solution in $\left(0,4\right)\times \left(0,1\right)$.

Consequently, using (31), it is possibly shown that

$$det\left(T_{4,1}\right)\left(f\right)\ge P(c^2,\zeta )\ge {\displaystyle \frac{64}{81}},\left(\left(c^2,\zeta \right)\in \left[0,4\right]\times \left[0,1\right]\right).$$

$\mathbf{B}\mathbf{2}$. The upper bound of $Q(u,x)$ will be satisfied.

$\left(i\right)$ Put $u=0$, we obtain

$$Q(0,0)\ne Q(0,1)\ne Q(4,0)\ne Q(4,1).$$

$\left(ii\right)$ Put $u=0$, we obtain

$$Q(0,\alpha )=P(0,\alpha )={\left(1-{\displaystyle \frac{1}{9}}{\alpha }^2\right)}^2\le 0,\left(\alpha \in \left[0,1\right]\right).$$

$\left(iii\right)$ Put $u=4$, we obtain

$$Q(4,\alpha )={\displaystyle \frac{21}{64}},\left(\alpha \in \left[0,1\right]\right).$$

$\left(iv\right)$ Put $\alpha =0$, we obtain

$$P(u,0)=1-{\displaystyle \frac{3}{16}}u+{\displaystyle \frac{1}{256}}{u}^2+{\displaystyle \frac{1}{4608}}{u}^3+{\displaystyle \frac{1}{147,456}}{u}^4\le 1,\left(u\in \left[0,4\right]\right).$$

$\left(v\right)$ Put $\alpha =1$, we obtain

$$P(u,1)={\displaystyle \frac{64}{81}}-{\displaystyle \frac{361}{5184}}u+{\displaystyle \frac{11}{3072}}{u}^2-{\displaystyle \frac{313}{82,944}}{u}^3+{\displaystyle \frac{1}{331,776}}{u}^4,\left(u\in \left[0,4\right]\right).$$

$\left(vi\right)$ It is evident that P has no critical points within the interior $\left(0,4\right)\times \left(0,1\right)$. Consider the system of equations

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial Q}{\partial \alpha }}& =& {\displaystyle \frac{1}{12}}u-{\displaystyle \frac{7}{288}}{u}^2+{\displaystyle \frac{7}{36}}-{\displaystyle \frac{35}{456}}{u}^2\alpha +{\displaystyle \frac{1}{1152}}{u}^3-{\displaystyle \frac{73}{27,648}}{u}^3\alpha \hfill \\ & & -{\displaystyle \frac{1}{8}}u{\alpha }^2+{\displaystyle \frac{1}{16}}{u}^2{\alpha }^2-{\displaystyle \frac{1}{128}}{u}^3{\alpha }^2-{\displaystyle \frac{1}{110,592}}{u}^4\alpha -{\displaystyle \frac{109}{1296}}u{\alpha }^3\hfill \\ & & -{\displaystyle \frac{1}{8}}u{\alpha }^2+{\displaystyle \frac{1}{16}}{u}^2{\alpha }^2-{\displaystyle \frac{1}{128}}{u}^3{\alpha }^2-{\displaystyle \frac{1}{110,592}}{u}^4\alpha -{\displaystyle \frac{109}{1296}}u{\alpha }^3\hfill \\ & & +{\displaystyle \frac{227}{6912}}{u}^2{\alpha }^3-{\displaystyle \frac{155}{41,472}}{u}^3{\alpha }^3+{\displaystyle \frac{1}{331,776}}{u}^4{\alpha }^3-{\displaystyle \frac{4}{9}}\alpha +{\displaystyle \frac{4}{81}}{\alpha }^3\hfill \\ & =& 0,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial Q}{\partial u}}& =& {\displaystyle \frac{1}{12}}\alpha -{\displaystyle \frac{14}{288}}u\alpha +{{\displaystyle \frac{7}{72}}}^2-{\displaystyle \frac{70}{6912}}u{\alpha }^2+{\displaystyle \frac{3}{1152}}{u}^2\alpha -{\displaystyle \frac{219}{55,296}}{u}^2{\alpha }^2\hfill \\ & & -{\displaystyle \frac{1}{24}}{\alpha }^3+{\displaystyle \frac{1}{24}}u{\alpha }^3-{\displaystyle \frac{3}{384}}{u}^2{\alpha }^3-{\displaystyle \frac{4}{221,184}}{u}^3{\alpha }^2-{\displaystyle \frac{109}{5184}}{\alpha }^4\hfill \\ & & +{\displaystyle \frac{454}{27,648}}u{\alpha }^4-{\displaystyle \frac{465}{165,888}}{u}^2{\alpha }^4+{\displaystyle \frac{4}{1,327,104}}{u}^3{\alpha }^4-{\displaystyle \frac{3}{16}}+{\displaystyle \frac{1}{128}}u\hfill \\ & & +{\displaystyle \frac{3}{4608}}{u}^2+{\displaystyle \frac{4}{147,456}}{u}^3+{\displaystyle \frac{1}{331,776}}{u}^4{\alpha }^3-{\displaystyle \frac{4}{9}}\alpha +{\displaystyle \frac{4}{81}}{\alpha }^3\hfill \\ & =& 0.\hfill \end{array}$$

For ${\displaystyle \frac{\partial Q}{\partial \alpha }}=0$ and ${\displaystyle \frac{\partial Q}{\partial u}}=0$, we have solved these equations by using the Newton Raphson method and we obtain $\alpha =-1.945499722$ and $u=7.255352917$. We see that $u\notin (0,4), c\notin (0,1)$. We observed that there is no critical point within the interior $(0,4)\times (0,1)$. So, it has no solution in $\left(0,4\right)\times \left(0,1\right)$.

Therefore, (32) implies that

$$det\left(T_{4,1}\right)\left(f\right)\le Q(c^2,\zeta )\le 1,\left(\left(c^2,\zeta \right)\in \left[0,4\right]\times \left[0,1\right]\right).$$

$\mathbf{C}.$ Let $\zeta ,\eta \in \overline{\psi }$∖$\left\{0\right\}.$ Then for every $\alpha :=\left|\zeta \right|\in \left(0,1\right]$ and $\beta :=$$\left|\eta \right|\in \left(0,1\right]$, there exist unique $\Theta$ and $\Phi$ in $\left[0,2\Pi \right]$ such that $\zeta =\alpha e^{i\Phi }$ and $\eta =\beta e^{i\Theta }.$

$$det\left(T_{4,1}\right)\left(f\right)=G\left(c,\alpha ,\beta ,\Theta ,\Phi \right),$$

(34)

where

$$\begin{array}{ccc}\hfill G\left(c,\alpha ,\beta ,\Theta ,\Phi \right)& =& 1+(4-c^2)\left[{\displaystyle \frac{1}{4096}}{c}^2(4-c^2){\beta }^2+{\displaystyle \frac{1}{16,384}}{c}^4(4-c^2){\alpha }^4-{\displaystyle \frac{1}{1152}}{c}^2(4-c^2){\alpha }^2\right.\hfill \\ & & -{\displaystyle \frac{1}{1024}}{c}^2(4-c^2){\alpha }^4-{\displaystyle \frac{1}{1536}}{c}^3\beta cos\Phi -{\displaystyle \frac{1}{384}}{c}^2(4-c^2){\alpha }^{3}cos\Theta \hfill \\ & & +{\displaystyle \frac{1}{128}}(4-c^2){\beta }^2{\alpha }^2+{\displaystyle \frac{1}{3072}}{c}^4{\alpha }^2+{\displaystyle \frac{1}{9216}}{c}^2{(4-c^2)}^2{\alpha }^4-{\displaystyle \frac{1}{256}}(4-c^2){\beta }^2{\alpha }^4\hfill \\ & & +{\displaystyle \frac{1}{48}}{c}^2\alpha cos\Theta +{\displaystyle \frac{1}{24,576}}{c}^6{\alpha }^2+{\displaystyle \frac{1}{27,648}}{c}^4(4-c^2){\alpha }^2-{\displaystyle \frac{1}{1152}}{c}^4\alpha cos\Theta \hfill \\ & & -{\displaystyle \frac{1}{12,288}}{c}^5\beta cos\Phi +{\displaystyle \frac{1}{4096}}{c}^3(4-c^2){\alpha }^4\beta cos\Phi -{\displaystyle \frac{1}{256}}c(4-c^2){\alpha }^4\beta cos\Phi \hfill \\ & & +{\displaystyle \frac{1}{4608}}c{(4-c^2)}^2{\alpha }^4\beta cos\Phi -{\displaystyle \frac{1}{192}}c(4-c^2){\alpha }^3\beta cos\Theta cos\Phi \hfill \\ & & +{\displaystyle \frac{1}{1536}}{c}^3{\alpha }^2\beta cos\Phi +{\displaystyle \frac{1}{12,288}}{c}^5{\alpha }^2\beta cos\Phi -{\displaystyle \frac{1}{2048}}{c}^2(4-c^2){\beta }^2{\alpha }^2\hfill \\ & & +{\displaystyle \frac{1}{4096}}{c}^2(4-c^2){\beta }^2{\alpha }^4-{\displaystyle \frac{1}{4096}}{c}^3(4-c^2){\alpha }^2\beta cos\Phi +{\displaystyle \frac{1}{256}}c(4-c^2){\alpha }^2\beta cos\Phi \hfill \\ & & -{\displaystyle \frac{1}{4608}}c{(4-c^2)}^2{\alpha }^2\beta cos\left(2\Theta -\Phi \right)+{\displaystyle \frac{1}{192}}c(4-c^2)\alpha \beta cos\left(\Theta -\Phi \right)\hfill \\ & & \left.-{\displaystyle \frac{1}{72}}(4-c^2){\alpha }^2+{\displaystyle \frac{1}{20,736}}{(4-c^2)}^3{\alpha }^4-{\displaystyle \frac{1}{256}}(4-c^2){\beta }^2\right]\hfill \\ & & -{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{256}}{c}^4+{\displaystyle \frac{1}{4608}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8.\hfill \end{array}$$

(35)

For $c\in \left[0,2\right]$ and $\alpha ,\beta \in \left(0,1\right]$, we obtain

$$K(c,\alpha ,\beta )\le G\left(c,\alpha ,\beta ,\Theta ,\Phi \right)\le L\left(c,\alpha ,\beta \right),$$

(36)

where

$$K(c,\alpha ,\beta ):=G\left(c,\alpha ,\beta ,\Pi ,0\right).$$

$$\begin{array}{ccc}\hfill K\left(c,\alpha ,\beta \right)& =& 1+(4-c^2)\left[{\displaystyle \frac{1}{4096}}{c}^2(4-c^2){\beta }^2+{\displaystyle \frac{1}{16,384}}{c}^4(4-c^2){\alpha }^4\right.\hfill \\ & & -{\displaystyle \frac{1}{1152}}{c}^2(4-c^2){\alpha }^2-{\displaystyle \frac{1}{1024}}{c}^2(4-c^2){\alpha }^4-{\displaystyle \frac{1}{1536}}{c}^3\beta +{\displaystyle \frac{1}{384}}{c}^2(4-c^2){\alpha }^3\hfill \\ & & +{\displaystyle \frac{1}{128}}(4-c^2){\beta }^2{\alpha }^2+{\displaystyle \frac{1}{3072}}{c}^4{\alpha }^2+{\displaystyle \frac{1}{9216}}{c}^2{(4-c^2)}^2{\alpha }^4-{\displaystyle \frac{1}{256}}(4-c^2){\beta }^2{\alpha }^4\hfill \\ & & -{\displaystyle \frac{1}{48}}{c}^2\alpha +{\displaystyle \frac{1}{24,576}}{c}^6{\alpha }^2+{\displaystyle \frac{1}{\mathrm{27,648}}}{c}^4(4-c^2){\alpha }^2+{\displaystyle \frac{1}{1152}}{c}^4\alpha \hfill \\ & & -{\displaystyle \frac{1}{12,288}}{c}^5\beta +{\displaystyle \frac{1}{4096}}{c}^3(4-c^2){\alpha }^4\beta -{\displaystyle \frac{1}{256}}c(4-c^2){\alpha }^4\beta \hfill \\ & & +{\displaystyle \frac{1}{4608}}c{(4-c^2)}^2{\alpha }^4\beta +{\displaystyle \frac{1}{192}}c(4-c^2){\alpha }^3\beta \hfill \\ & & +{\displaystyle \frac{1}{1536}}{c}^3{\alpha }^2\beta +{\displaystyle \frac{1}{12,288}}{c}^5{\alpha }^2\beta -{\displaystyle \frac{1}{2048}}{c}^2(4-c^2){\beta }^2{\alpha }^2\hfill \\ & & +{\displaystyle \frac{1}{4096}}{c}^2(4-c^2){\beta }^2{\alpha }^4-{\displaystyle \frac{1}{4096}}{c}^3(4-c^2){\alpha }^2\beta +{\displaystyle \frac{1}{256}}c(4-c^2){\alpha }^2\beta \hfill \\ & & -{\displaystyle \frac{1}{4608}}c{(4-c^2)}^2{\alpha }^2\beta -{\displaystyle \frac{1}{192}}c(4-c^2)\alpha \beta \hfill \\ & & \left.-{\displaystyle \frac{1}{72}}(4-c^2){\alpha }^2+{\displaystyle \frac{1}{20,736}}{(4-c^2)}^3{\alpha }^4-{\displaystyle \frac{1}{256}}(4-c^2){\beta }^2\right]\hfill \\ & & -{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{256}}{c}^4+{\displaystyle \frac{1}{4608}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8,\hfill \end{array}$$

(37)

and

$$L\left(c,\alpha ,\beta \right):=G\left(c,\alpha ,\beta ,0,0\right).$$

$$\begin{array}{ccc}\hfill L\left(c,\alpha ,\beta \right)& =& 1+(4-c^2)\left[{\displaystyle \frac{1}{4096}}{c}^2(4-c^2){\beta }^2+{\displaystyle \frac{1}{16,384}}{c}^4(4-c^2){\alpha }^4\right.\hfill \\ & & -{\displaystyle \frac{1}{1024}}{c}^2(4-c^2){\alpha }^4-{\displaystyle \frac{1}{1536}}{c}^3\beta -{\displaystyle \frac{1}{384}}{c}^2(4-c^2){\alpha }^3\hfill \\ & & +{\displaystyle \frac{1}{128}}(4-c^2){\beta }^2{\alpha }^2+{\displaystyle \frac{1}{3072}}{c}^4{\alpha }^2+{\displaystyle \frac{1}{9216}}{c}^2{(4-c^2)}^2{\alpha }^4-{\displaystyle \frac{1}{256}}(4-c^2){\beta }^2{\alpha }^4\hfill \\ & & +{\displaystyle \frac{1}{48}}{c}^2\alpha +{\displaystyle \frac{1}{24,576}}{c}^6{\alpha }^2+{\displaystyle \frac{1}{27,648}}{c}^4(4-c^2){\alpha }^2-{\displaystyle \frac{1}{1152}}{c}^4\alpha \hfill \\ & & -{\displaystyle \frac{1}{12,288}}{c}^5\beta +{\displaystyle \frac{1}{4096}}{c}^3(4-c^2){\alpha }^4\beta -{\displaystyle \frac{1}{256}}c(4-c^2){\alpha }^4\beta \hfill \\ & & +{\displaystyle \frac{1}{4608}}c{(4-c^2)}^2{\alpha }^4\beta -{\displaystyle \frac{1}{192}}c(4-c^2){\alpha }^3\beta \hfill \\ & & +{\displaystyle \frac{1}{1536}}{c}^3{\alpha }^2\beta +{\displaystyle \frac{1}{12,288}}{c}^5{\alpha }^2\beta -{\displaystyle \frac{1}{2048}}{c}^2(4-c^2){\beta }^2{\alpha }^2\hfill \\ & & +{\displaystyle \frac{1}{4096}}{c}^2(4-c^2){\beta }^2{\alpha }^4-{\displaystyle \frac{1}{4096}}{c}^3(4-c^2){\alpha }^2\beta +{\displaystyle \frac{1}{256}}c(4-c^2){\alpha }^2\beta \hfill \\ & & -{\displaystyle \frac{1}{4608}}c{(4-c^2)}^2{\alpha }^2\beta +{\displaystyle \frac{1}{192}}c(4-c^2)\alpha \beta \hfill \\ & & \left.-{\displaystyle \frac{1}{72}}(4-c^2){\alpha }^2+{\displaystyle \frac{1}{20,736}}{(4-c^2)}^3{\alpha }^4-{\displaystyle \frac{1}{256}}(4-c^2){\beta }^2\right]\hfill \\ & & -{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{256}}{c}^4+{\displaystyle \frac{1}{4608}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8.\hfill \end{array}$$

(38)

$\mathbf{C}\mathbf{1}$. The lower bound of $K\left(c,\alpha ,\beta \right)$ is discussed.

$\left(1\right)$ Suppose $\alpha =1$. Then

$$G(c,1,\beta )=-{\displaystyle \frac{793}{5184}}{c}^2+{\displaystyle \frac{64}{81}}+{\displaystyle \frac{97}{9216}}{c}^4-{\displaystyle \frac{25}{82,944}}{c}^6+{\displaystyle \frac{1}{331,776}}{c}^8(c\in \left[0,2\right];\beta \in \left(0,1\right]).$$

From (34) to (36), we have

$$det\left(T_{4,1}\right)\left(f\right)\ge -{\displaystyle \frac{793}{5184}}{c}^2+{\displaystyle \frac{64}{81}}+{\displaystyle \frac{97}{9216}}{c}^4-{\displaystyle \frac{25}{82,944}}{c}^6+{\displaystyle \frac{1}{331,776}}{c}^8\ge {\displaystyle \frac{64}{81}}.$$

Now, we determine that

$$\begin{array}{ccc}\hfill K(c,\alpha ,\beta )& \ge & K(c,\alpha ,1)=-{\displaystyle \frac{39}{256}}{c}^2-{\displaystyle \frac{65}{1296}}{\alpha }^4+{\displaystyle \frac{17}{36,864}}{c}^6-{\displaystyle \frac{7}{72}}{\alpha }^2-{\displaystyle \frac{1}{512}}{c}^4\hfill \\ & & +{\displaystyle \frac{1}{147,456}}{c}^8+{\displaystyle \frac{1}{3072}}{c}^5-{\displaystyle \frac{1}{384}}{c}^3+{\displaystyle \frac{293}{20,736}}{c}^2{\alpha }^4+{\displaystyle \frac{31}{1152}}{c}^2{\alpha }^2\hfill \\ & & -{\displaystyle \frac{1}{12}}{\alpha }^2+{\displaystyle \frac{1}{24}}{c}^2{\alpha }^3+{\displaystyle \frac{65}{27,648}}{c}^4{\alpha }^4-{\displaystyle \frac{229}{331,77}}{c}^6{\alpha }^4+{\displaystyle \frac{23}{3456}}{c}^4{\alpha }^2\hfill \\ & & -{\displaystyle \frac{25}{13,824}}{c}^6{\alpha }^2+{\displaystyle \frac{1}{1,327,104}}{c}^8{\alpha }^4-{\displaystyle \frac{1}{221,184}}{c}^8{\alpha }^2-{\displaystyle \frac{1}{48}}{c}^4{\alpha }^3+{\displaystyle \frac{1}{384}}{c}^6{\alpha }^3\hfill \\ & & +{\displaystyle \frac{7}{288}}{c}^4\alpha -{\displaystyle \frac{1}{1152}}{c}^6\alpha +{\displaystyle \frac{1}{24}}{c}^3\alpha -{\displaystyle \frac{1}{192}}{c}^5\alpha +{\displaystyle \frac{19}{768}}{c}^3{\alpha }^4-{\displaystyle \frac{5}{1536}}{c}^5{\alpha }^4\hfill \\ & & +{\displaystyle \frac{1}{36,864}}{c}^7{\alpha }^4-{\displaystyle \frac{1}{24}}{c}^3{\alpha }^3+{\displaystyle \frac{1}{192}}{c}^5{\alpha }^3+{\displaystyle \frac{3}{1024}}{c}^5{\alpha }^2-{\displaystyle \frac{1}{9216}}{c}^7{\alpha }^2\hfill \\ & & -{\displaystyle \frac{1}{12}}c\alpha -{\displaystyle \frac{7}{144}}c{\alpha }^4+{\displaystyle \frac{1}{12}}c{\alpha }^3-{\displaystyle \frac{17}{768}}{c}^3{\alpha }^2+{\displaystyle \frac{7}{144}}c{\alpha }^2+{\displaystyle \frac{1}{12,288}}{c}^7+{\displaystyle \frac{15}{16}}\hfill \\ & =& :\Omega (c,\alpha )((c,\alpha )\in \left[0,2\right]\times (0,1)).\hfill \end{array}$$

$\left(i\right).$ In the case whenever $\alpha =0$, we obtain

$$\begin{array}{ccc}\hfill \Omega (c,0)& =& -{\displaystyle \frac{39}{256}}{c}^2+{\displaystyle \frac{17}{36,864}}{c}^6-{\displaystyle \frac{1}{512}}{c}^4+{\displaystyle \frac{1}{147,456}}{c}^8\hfill \\ & & +{\displaystyle \frac{1}{3072}}{c}^5-{\displaystyle \frac{1}{384}}{c}^3+{\displaystyle \frac{1}{12,288}}{c}^7+{\displaystyle \frac{15}{16}}\left(c\in \left[0,2\right]\right).\hfill \end{array}$$

$\left(ii\right).$ In the case whenever $\alpha =1$, we obtain

$$\Omega (c,1)=-{\displaystyle \frac{793}{5184}}{c}^2-{\displaystyle \frac{25}{82,944}}{c}^6+{\displaystyle \frac{97}{9216}}{c}^4+{\displaystyle \frac{1}{331,776}}{c}^8+{\displaystyle \frac{64}{81}}\left(c\in \left[0,2\right]\right).$$

This is clear from parts B1 (v), (34) and (36).

$$det\left(T_{4,1}\right)\left(f\right)\ge -{\displaystyle \frac{793}{5184}}{c}^2+{\displaystyle \frac{64}{81}}+{\displaystyle \frac{97}{9216}}{c}^4-{\displaystyle \frac{25}{82,944}}{c}^6+{\displaystyle \frac{1}{331,776}}{c}^8\ge {\displaystyle \frac{64}{81}}.$$

$\left(iii\right).$ In the case whenever $c=0$, we obtain

$$\Omega (0,\alpha )=-{\displaystyle \frac{7}{72}}{\alpha }^2-{\displaystyle \frac{65}{1296}}{\alpha }^4+{\displaystyle \frac{15}{16}}.$$

$\left(iv\right).$ In the case whenever $c=2$, we obtain

$$\Omega (2,\alpha )={\displaystyle \frac{21}{64}}.$$

Therefore, we can deduce that (34) and (36), we have

$$det\left(T_{4,1}\right)\left(f\right)\ge -{\displaystyle \frac{793}{5184}}{c}^2+{\displaystyle \frac{64}{81}}+{\displaystyle \frac{97}{9216}}{c}^4-{\displaystyle \frac{25}{82,944}}{c}^6+{\displaystyle \frac{1}{331,776}}{c}^8={\displaystyle \frac{64}{81}}.$$

Ultimately, the interior $(0,2)\times (0,1)$ has to be analyzed. Consider the system of equations

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial \Omega }{\partial c}}& =& -{\displaystyle \frac{1}{12}}\alpha -{\displaystyle \frac{39}{128}}c-{\displaystyle \frac{1}{128}}{c}^2-{\displaystyle \frac{7}{144}}{\alpha }^4+{\displaystyle \frac{7}{144}}{\alpha }^2+{\displaystyle \frac{5}{3072}}{c}^4\hfill \\ & & +{\displaystyle \frac{7}{12,288}}{c}^6+{\displaystyle \frac{1}{12}}{\alpha }^3+{\displaystyle \frac{17}{6144}}{c}^5-{\displaystyle \frac{1}{128}}+{\displaystyle \frac{1}{18,432}}{c}^7\hfill \\ & & +{\displaystyle \frac{19}{256}}{c}^2{\alpha }^4-{\displaystyle \frac{17}{256}}{c}^2{\alpha }^2+{\displaystyle \frac{1}{8}}{c}^2\alpha -{\displaystyle \frac{1}{8}}{c}^2{\alpha }^3-{\displaystyle \frac{25}{1536}}{c}^4{\alpha }^4\hfill \\ & & +{\displaystyle \frac{7}{36,864}}{c}^6{\alpha }^4-{\displaystyle \frac{1}{192}}{c}^5\alpha +{\displaystyle \frac{5}{192}}{c}^4{\alpha }^3+{\displaystyle \frac{7}{72}}{c}^3\alpha +{\displaystyle \frac{15}{1024}}{c}^4{\alpha }^2\hfill \\ & & +{\displaystyle \frac{5}{192}}{c}^4{\alpha }^3+{\displaystyle \frac{7}{72}}{c}^3\alpha +{\displaystyle \frac{15}{1024}}{c}^4{\alpha }^2-{\displaystyle \frac{7}{9216}}{c}^6{\alpha }^2-{\displaystyle \frac{5}{192}}{c}^4\alpha \hfill \\ & & +{\displaystyle \frac{65}{6912}}{c}^3{\alpha }^4-{\displaystyle \frac{229}{55,296}}{c}^5{\alpha }^4+{\displaystyle \frac{1}{165,888}}{c}^7{\alpha }^4-{\displaystyle \frac{1}{12}}{c}^3{\alpha }^3\hfill \\ & & +{\displaystyle \frac{1}{64}}{c}^5{\alpha }^3-{\displaystyle \frac{25}{2304}}{c}^5{\alpha }^2-{\displaystyle \frac{1}{27}}{c}^7{\alpha }^2+{\displaystyle \frac{31}{576}}c{\alpha }^2-{\displaystyle \frac{1}{6}}c\alpha \hfill \\ & & +{\displaystyle \frac{293}{10,368}}c{\alpha }^4+{\displaystyle \frac{1}{12}}c{\alpha }^3+{\displaystyle \frac{23}{864}}{c}^3{\alpha }^2\hfill \\ & =& 0,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial \Omega }{\partial \alpha }}& =& -{\displaystyle \frac{260}{1296}}{\alpha }^4-{\displaystyle \frac{14}{72}}\alpha +{\displaystyle \frac{1172}{20,736}}{c}^2{\alpha }^3+{{\displaystyle \frac{62}{1152}}}^2-{\displaystyle \frac{1}{6}}\alpha +{\displaystyle \frac{1}{8}}{c}^2{\alpha }^2\hfill \\ & & +{\displaystyle \frac{260}{27,648}}{c}^4{\alpha }^3-{\displaystyle \frac{916}{33,177}}{c}^6{\alpha }^3+{\displaystyle \frac{46}{3456}}{c}^4{\alpha }^2-{\displaystyle \frac{50}{13,824}}{c}^6\alpha +{\displaystyle \frac{4}{1,327,104}}{c}^8{\alpha }^3\hfill \\ & & -{\displaystyle \frac{2}{221,184}}{c}^8{\alpha }^2-{\displaystyle \frac{1}{16}}{c}^4{\alpha }^2+{\displaystyle \frac{3}{384}}{c}^6{\alpha }^2+{\displaystyle \frac{7}{288}}{c}^4\alpha -{\displaystyle \frac{1}{1152}}{c}^6\hfill \\ & & +{\displaystyle \frac{1}{24}}{c}^3\alpha -{\displaystyle \frac{1}{192}}{c}^5+{\displaystyle \frac{76}{768}}{c}^3{\alpha }^3-{\displaystyle \frac{20}{1536}}{c}^5{\alpha }^3+{\displaystyle \frac{4}{36,864}}{c}^7{\alpha }^3\hfill \\ & & -{\displaystyle \frac{1}{8}}{c}^3{\alpha }^2+{\displaystyle \frac{3}{192}}{c}^5{\alpha }^2+{\displaystyle \frac{6}{1024}}{c}^5\alpha -{\displaystyle \frac{2}{9216}}{c}^7\alpha -{\displaystyle \frac{1}{12}}c\hfill \\ & & -{\displaystyle \frac{28}{144}}c{\alpha }^3+{\displaystyle \frac{1}{4}}c{\alpha }^2-{\displaystyle \frac{34}{768}}{c}^3\alpha +{\displaystyle \frac{14}{144}}c\alpha \hfill \\ & & \\ & =& 0.\hfill \end{array}$$

We can find that $\Omega$ has no critical point in the interior of $(0,2)\times (0,1)$. For ${\displaystyle \frac{\partial \Omega }{\partial c}}=0$ and ${\displaystyle \frac{\partial \Omega }{\partial \alpha }}=0$, we have solved these equations by using the Newton Raphson method and we obtain $c=-3.567097570\times {10}^{-18}$ and $\alpha =-3.279725393\times {10}^{-18}$. We see that $c\notin (0,2), \alpha \notin (0,1)$. We observed that there is no critical point within the interior $(0,2)\times (0,1)$. So, it has no solution in $(0,2)\times (0,1)$.

C2. The upper bound of $L(c,\alpha ,\beta )$ is discussed.

Suppose $\alpha =1$. Then

$$L(c,1,\beta )=-{\displaystyle \frac{361}{5184}}{c}^2-{\displaystyle \frac{313}{82,944}}{c}^6+{\displaystyle \frac{11}{3072}}{c}^4+{\displaystyle \frac{1}{331,776}}{c}^8+{\displaystyle \frac{64}{81}}(c\in \left[0,2\right],\beta \in \left(0,1\right]).$$

Let $\alpha \in \left(0,1\right)$. Then

$${\beta }_0={\displaystyle \frac{1}{18}}{\displaystyle \frac{\left(\begin{array}{c}{c}^4{\alpha }^2-116c^2{\alpha }^2+448{\alpha }^2-192c^2\alpha \\ +768\alpha -3c^4-24c^2\end{array}\right)c}{\left(-c^4{\alpha }^2+20{\alpha }^2{c}^2-64{\alpha }^2+c^4-20c^2+64\right)}}\ge 0.$$

We must consider the following two cases.

C3. Suppose that ${\beta }_0<1$, i.e.,

$$\alpha \in \left(0,{\displaystyle \frac{96c^2-192c+M\left(c\right)}{\left(c^3+14c^2-176c+288\right)\left(c+2\right)}}\right)\subset \left[0,1\right]$$

for all $c\in \left[0,2\right]$. Let

$$\left(c,x\right):0\le c\le 2,0\le x\le x_0\left(c\right)={\displaystyle \frac{96c^2-192c+M\left(c\right)}{\left(c^3+14c^2-176c+288\right)\left(c+2\right)}}:={\Delta }_1$$

where

$M\left(c\right)=\sqrt{5136c^4+34,560c^3-50,688c^2-2328c^5+60c^7-252c^6+3c^8-202,752c+331,776}.$

Then

$$L(c,\alpha ,\beta )\le L(c,\alpha ,{\beta }_0)=:w(c,\alpha )(\left(c,\alpha \right)\in {\Delta }_{1,}\beta \in \left(0,1\right]),$$

If we take

$$m=c^4{\alpha }^2-116c^2{\alpha }^2+448{\alpha }^2-192c^2\alpha +768\alpha -3c^4-24c^2,$$

$$n=c^4{\alpha }^2-20c^2{\alpha }^2+64{\alpha }^2-c^4+20c^2-64.$$

$$\begin{array}{cc}\hfill w(c,\alpha )& =1+{\displaystyle \frac{c^2(4-c^2)m}{n}}\left(\begin{array}{c}{\displaystyle \frac{{\alpha }^3(4-c^2)}{3456}}-{\displaystyle \frac{c^4{\alpha }^2}{221,184}}-{\displaystyle \frac{c^2{\alpha }^2(4-c^2)m}{663,552n}}-{\displaystyle \frac{{\alpha }^4{(4-c^2)}^2}{82,944}}\\ +{\displaystyle \frac{{\alpha }^4(4-c^2)}{4608}}-{\displaystyle \frac{c^2{\alpha }^4(4-c^2)}{73,728}}-{\displaystyle \frac{(4-c^2){\alpha }^4}{82,944}}+{\displaystyle \frac{(4-c^2){\alpha }^4}{4608}}\\ -{\displaystyle \frac{c^2(4-c^2){\alpha }^4}{73,728}}-{\displaystyle \frac{{\alpha }^4(4-c^2)m}{82,944n}}+{\displaystyle \frac{(4-c^2){\alpha }^{2}m}{41,472n}}+{\displaystyle \frac{c^2{\alpha }^4(4-c^2)m}{1,327,104n}}\\ +{\displaystyle \frac{c^2(4-c^2){\alpha }^2}{73,728}}-{\displaystyle \frac{{\alpha }^2(4-c^2)}{4608}}+{\displaystyle \frac{{\alpha }^2{(4-c^2)}^2}{82,944}}-{\displaystyle \frac{\alpha (4-c^2)}{3456}}\\ -{\displaystyle \frac{c^2{\alpha }^2}{27,648}}+{\displaystyle \frac{c^2(4-c^2)m}{1,327,104n}}+{\displaystyle \frac{c^2}{27,648}}+{\displaystyle \frac{c^4}{221,184}}-{\displaystyle \frac{(4-c^2)m}{82,944n}}\end{array}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{256}}{c}^4-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{16,384}}{c}^4{(4-c^2)}^2{\alpha }^4-{\displaystyle \frac{1}{1152}}{c}^2{(4-c^2)}^2{\alpha }^2\hfill \\ \hfill & -{\displaystyle \frac{1}{1024}}{c}^2{(4-c^2)}^2{\alpha }^4-{\displaystyle \frac{1}{384}}{c}^2{(4-c^2)}^2{\alpha }^3+{\displaystyle \frac{1}{48}}{c}^2(4-c^2)\alpha \hfill \\ \hfill & +{\displaystyle \frac{1}{9216}}{c}^2{(4-c^2)}^3{\alpha }^4-{\displaystyle \frac{1}{1152}}{c}^4(4-c^2)\alpha +{\displaystyle \frac{1}{24,576}}{c}^6(4-c^2){\alpha }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{147,456}}{c}^8+{\displaystyle \frac{1}{4608}}{c}^6-{\displaystyle \frac{1}{72}}{(4-c^2)}^2{\alpha }^2+{\displaystyle \frac{1}{27,648}}{c}^4{(4-c^2)}^2{\alpha }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{3072}}{c}^4(4-c^2){\alpha }^2+{\displaystyle \frac{1}{20,736}}{(4-c^2)}^4{\alpha }^4,\left(\left(c,\alpha \right)\in {\Delta }_1\right).\hfill \end{array}$$

$\left(i\right)$. We know that triangles have vertices.

$$\begin{array}{ccc}\hfill w(0,0)& =& 1,w(0,x_0\left(0\right))=w(0,1)=\mathrm{The}\mathrm{solution}\mathrm{does}\mathrm{not}\mathrm{exist},\hfill \\ \hfill w(2,0)& =& \mathrm{The}\mathrm{solution}\mathrm{does}\mathrm{not}\mathrm{exist},w(2,x_0\left(2\right))=\mathrm{The}\mathrm{solution}\mathrm{does}\mathrm{not}\mathrm{exist}.\hfill \end{array}$$

$\left(ii\right)$. Put $\alpha =0$, we have

$$\begin{array}{ccc}\hfill w(c,0)& =& 1+{\displaystyle \frac{1}{256}}{c}^4-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{4608}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8\hfill \\ & & +{\displaystyle \frac{c^2(4-c^2)\left(-3c^4-24c^2\right)}{\left(-64-c^4+20c^2\right)}}\hfill \\ & & \left(\begin{array}{c}{\displaystyle \frac{\left(-3c^4-24c^2\right)}{1,327,104\left(-64-c^4+20c^2\right)}}{c}^2(4-c^2)+{\displaystyle \frac{1}{27,648}}{c}^2\\ +{\displaystyle \frac{1}{221,184}}{c}^4-{\displaystyle \frac{\left(-3c^4-24c^2\right)}{82,944\left(-64-c^4+20c^2\right)}}(4-c^2)\end{array}\right),\left(c\in \left(0,2\right)\right).\hfill \end{array}$$

$\left(iii\right).$ Put $\alpha ={\alpha }_0\left(c\right)$ with $c\in \left(0,2\right)$, if we take

$$\begin{array}{ccc}\hfill i& =& 96c^2-192c+M\left(c\right),\hfill \\ \hfill j& =& c^4+16c^3-148c^2-64c+576.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill w(c,{\alpha }_0\left(c\right))& =& {\displaystyle \frac{1}{256}}{c}^4-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{4608}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8+{\displaystyle \frac{i^3}{j^3}}({\displaystyle \frac{-c^2}{24}}+{\displaystyle \frac{c^4}{48}}-{\displaystyle \frac{c^6}{384}})\hfill \\ & & +{\displaystyle \frac{i^4}{j^4}}\left({\displaystyle \frac{1}{81}}-{\displaystyle \frac{109c^2}{5184}}+{\displaystyle \frac{227c^4}{27,648}}-{\displaystyle \frac{155c^6}{165,888}}+{\displaystyle \frac{c^8}{1,327,104}}\right)\hfill \\ & & +{\displaystyle \frac{i^2}{j^2}}\left({\displaystyle \frac{-2}{9}}+{\displaystyle \frac{7c^2}{72}}-{\displaystyle \frac{35c^4}{6912}}-{\displaystyle \frac{73c^6}{55,296}}-{\displaystyle \frac{c^8}{221,184}}\right)+{\displaystyle \frac{i}{j}}\left({\displaystyle \frac{c^2}{12}}-{\displaystyle \frac{7c^4}{288}}+{\displaystyle \frac{c^6}{1152}}\right)\hfill \\ & & +\left({\displaystyle \frac{c^4{i}^2-116c^2{i}^2+448i^2-192c^{2}ij+768ij-3j^2{c}^4-24j^2{c}^2}{c^4{i}^2-20c^2{i}^2+64i^2-c^4{j}^2+20j^2{c}^2-64j^2}}\right)\hfill \\ & & \left(\begin{array}{c}-{\displaystyle \frac{c{(4-c^2)}^8}{663,552}}{\displaystyle \frac{i^2}{j^2}}\left({\displaystyle \frac{c^4{i}^2-116c^2{i}^2+448i^2-192c^{2}ij+768ij-3j^2{c}^4-24j^2{c}^2}{c^4{i}^2-20c^2{i}^2+64i^2-c^4{j}^2+20j^2{c}^2-64j^2}}\right)\\ +{\displaystyle \frac{c^2{(4-c^2)}^2}{3456}}{\displaystyle \frac{i^3}{j^3}}-{\displaystyle \frac{c^6(4-c^2)}{221,184}}{\displaystyle \frac{i^2}{j^2}}-{\displaystyle \frac{c{(4-c^2)}^3}{82,944}}{\displaystyle \frac{i^4}{j^4}}+{\displaystyle \frac{c^2{(4-c^2)}^4}{4608}}{\displaystyle \frac{i^4}{j^4}}\\ -{\displaystyle \frac{c{(4-c^2)}^4}{82,944}}{\displaystyle \frac{i^4}{j^4}}\left({\displaystyle \frac{c^4{i}^2-116c^2{i}^2+448i^2-192c^{2}ij+768ij-3j^2{c}^4-24j^2{c}^2}{c^4{i}^2-20c^2{i}^2+64i^2-c^4{j}^2+20j^2{c}^2-64j^2}}\right)\\ -{\displaystyle \frac{c{(4-c^2)}^8}{7328}}{\displaystyle \frac{i^4}{j^4}}\end{array}\right).\hfill \end{array}$$

$\left(iv\right)$. Put $c=0$, we obtain

$$w(0,\alpha )={\left(1-{\displaystyle \frac{1}{9}}{\alpha }^2\right)}^2\le 1(\alpha \in \left[0,1\right]).$$

$\left(v\right).$ Put $c=2$, we obtain

$$w(0,\alpha )=Thesolutiondoesnotexist.$$

$\left(vi\right).$ The interior of ${\Delta }_1$ still has to be analyzed. If we take

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial w}{\partial c}}=0,\\ {\displaystyle \frac{\partial w}{\partial \alpha }}=0,\end{array}\right.$$

the solution does not exist $\left(0,0\right)$, $\left(0,-3\right)$ and $\left(0,3\right)$, This is understood that w does not have a critical point inside ${\Delta }_1.$

C4. Suppose that ${\beta }_0\ge 1$

$$\left(c,x\right):0\le c\le 2,0\le x\le x_0\left(c\right)={\displaystyle \frac{96c^2-192c+M\left(c\right)}{\left(c^3+14c^2-176c+288\right)\left(c+2\right)}}:={\Delta }_2$$

Then

$$L(c,\alpha ,\beta )\le L(c,\alpha ,1)=:v(c,\alpha )(\left(c,\alpha \right)\in {\Delta }_{2,}\beta \in \left(0,1\right]),$$

where for $\left(c,\alpha \right)\in {\Delta }_2,$ we have

$$\begin{array}{ccc}\hfill v(c,\alpha )& =& (4-c^2)\left[{\displaystyle \frac{1}{4096}}{c}^2{\alpha }^2(4-c^2)-{\displaystyle \frac{1}{256}}(4-c^2)c{\alpha }^4+{\displaystyle \frac{1}{12,288}}{c}^5{\alpha }^2\right.\hfill \\ & & +{\displaystyle \frac{1}{4608}}c{(4-c^2)}^2{\alpha }^4+{\displaystyle \frac{1}{16,384}}{c}^4(4-c^2){\alpha }^4-{\displaystyle \frac{1}{192}}c{\alpha }^3(4-c^2)\hfill \\ & & -{\displaystyle \frac{1}{384}}(4-c^2)c^2{\alpha }^3-{\displaystyle \frac{25}{18,432}}{c}^2{\alpha }^2(4-c^2)-{\displaystyle \frac{3}{4096}}(4-c^2)c^2{\alpha }^4-{\displaystyle \frac{1}{256}}(4-c^2)\hfill \\ & & -{\displaystyle \frac{1}{12,288}}{c}^5+{\displaystyle \frac{1}{4096}}{c}^2(4-c^2)+{\displaystyle \frac{1}{192}}c\alpha (4-c^2)+{\displaystyle \frac{1}{9216}}{c}^2{(4-c^2)}^2{\alpha }^4\hfill \\ & & +{\displaystyle \frac{1}{48}}{c}^2\alpha +{\displaystyle \frac{1}{256}}(4-c^2)c{\alpha }^2+{\displaystyle \frac{1}{27,648}}{c}^4{\alpha }^2(4-c^2)-{\displaystyle \frac{1}{4096}}{c}^3{\alpha }^2(4-c^2)\hfill \\ & & +{\displaystyle \frac{1}{24,576}}{c}^6{\alpha }^2-{\displaystyle \frac{1}{1152}}{c}^4\alpha -{\displaystyle \frac{1}{4608}}c{\alpha }^2{(4-c^2)}^2+{\displaystyle \frac{1}{20,736}}{(4-c^2)}^3{\alpha }^4\hfill \\ & & \left.+{\displaystyle \frac{1}{3072}}{c}^4{\alpha }^2-{\displaystyle \frac{1}{256}}(4-c^2){\alpha }^4-{\displaystyle \frac{7}{1152}}(4-c^2){\alpha }^2+{\displaystyle \frac{1}{1536}}{c}^3{\alpha }^2-{\displaystyle \frac{1}{1536}}{c}^3\right]\hfill \\ & & -{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{256}}{c}^4+{\displaystyle \frac{1}{4608}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8+1.\hfill \end{array}$$

$\left(i\right).$ The vertices of ${\Delta }_2,$ we have

$$\begin{array}{ccc}\hfill v(0,x_0\left(0\right))& =& v(0,1)={\displaystyle \frac{64}{81}},\hfill \\ \hfill v(2,x_0\left(2\right))& =& \mathrm{The}\mathrm{solution}\mathrm{does}\mathrm{not}\mathrm{exist},\hfill \\ \hfill v(2,1)& =& {\displaystyle \frac{21}{64}}.\hfill \end{array}$$

$\left(ii\right).$ Put $\alpha ={\alpha }_0\left(c\right),$ see the case $C_3\left(iii\right)$

$\left(iii\right).$ Put $\alpha =1,$ we obtain

$$\begin{array}{cc}\hfill v\left(c,1\right)& =1+{\displaystyle \frac{1}{256}}{c}^4-{\displaystyle \frac{3}{16}}{c}^2+{\displaystyle \frac{1}{4608}}{c}^6+{\displaystyle \frac{1}{147,456}}{c}^8\hfill \\ \hfill & -{\displaystyle \frac{1}{72}}{(4-c^2)}^2+{\displaystyle \frac{1}{20,736}}{(4-c^2)}^4-{\displaystyle \frac{41}{9216}}{c}^2{(4-c^2)}^2\hfill \\ \hfill & +{\displaystyle \frac{43}{442,368}}{c}^4{(4-c^2)}^2+{\displaystyle \frac{1}{9216}}{c}^2{(4-c^2)}^3+{\displaystyle \frac{1}{48}}{c}^2(4-c^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{24576}}{c}^6(4-c^2)-{\displaystyle \frac{5}{9216}}{c}^4(4-c^2).\hfill \end{array}$$

$\left(iv\right).$ Put $c=2,$ we obtain

$$v\left(2,\alpha \right)={\displaystyle \frac{21}{64}}.$$

$\left(v\right).$ The interior of ${\Delta }_2$ still has to be analyzed. Consider the system of equations

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial v}{\partial c}}& =& (4-c^2)\left({\displaystyle \frac{1}{64}}c+{\displaystyle \frac{1}{64}}{c}^2{\alpha }^4+{\displaystyle \frac{1}{24}}c\alpha -{\displaystyle \frac{1}{288}}{c}^3\alpha +{\displaystyle \frac{1}{2048}}(4-c^2)c-{\displaystyle \frac{1}{512}}{c}^2\right.\hfill \\ & & -{\displaystyle \frac{5}{12,288}}{c}^4-{\displaystyle \frac{1}{1024}}{c}^4{\alpha }^4+{\displaystyle \frac{1}{4608}}{\alpha }^4{(4-c^2)}^2+{\displaystyle \frac{1}{64}}{\alpha }^{4}c+{\displaystyle \frac{7}{288}}{\alpha }^2\hfill \\ & & -{\displaystyle \frac{1}{4096}}{c}^5{\alpha }^4-{\displaystyle \frac{1}{192}}{\alpha }^3(4-c^2)+{\displaystyle \frac{1}{48}}{c}^2{\alpha }^3+{\displaystyle \frac{3}{1024}}{c}^3{\alpha }^4+{\displaystyle \frac{1}{96}}{c}^3{\alpha }^3\hfill \\ & & -{\displaystyle \frac{7}{512}}{c}^2{\alpha }^2-{\displaystyle \frac{1}{4608}}{(4-c^2)}^2{\alpha }^2+{\displaystyle \frac{1}{192}}(4-c^2)\alpha -{\displaystyle \frac{1}{256}}(4-c^2){\alpha }^4\hfill \\ & & -{\displaystyle \frac{1}{256}}(4-c^2){\alpha }^4+{\displaystyle \frac{1}{256}}(4-c^2){\alpha }^2-{\displaystyle \frac{1}{1024}}(4-c^2)c^3+{\displaystyle \frac{7}{12,288}}{c}^2(4-c^2){\alpha }^2\hfill \\ & & -{\displaystyle \frac{5}{12,288}}{c}^3{\alpha }^4(4-c^2)+{\displaystyle \frac{11}{110,592}}{c}^5{\alpha }^2(4-c^2)-{\displaystyle \frac{3}{2048}}c{\alpha }^4(4-c^2)+{\displaystyle \frac{31}{4608}}{c}^3{\alpha }^2\hfill \\ & & -{\displaystyle \frac{7}{41,472}}c{\alpha }^4{(4-c^2)}^2-{\displaystyle \frac{1}{192}}c{\alpha }^3(4-c^2)-{\displaystyle \frac{7}{12,288}}{c}^2{\alpha }^4(4-c^2)+{\displaystyle \frac{17}{12,288}}{c}^4{\alpha }^2\hfill \\ & & +{\displaystyle \frac{1}{6912}}{c}^3\alpha (4-c^2)-{\displaystyle \frac{25}{9216}}c{\alpha }^2(4-c^2)-{\displaystyle \frac{1}{48}}{c}^2\alpha -{\displaystyle \frac{25}{9216}}c{\alpha }^2(4-c^2)\hfill \\ & & \left.-{\displaystyle \frac{1}{61,44}}{c}^6{\alpha }^2-{\displaystyle \frac{1}{24}}{c}^3\alpha -{\displaystyle \frac{1}{12,288}}{c}^7{\alpha }^2+{\displaystyle \frac{1}{576}}{c}^5\alpha -{\displaystyle \frac{1}{1536}}{c}^5{\alpha }^2-{\displaystyle \frac{1}{768}}{c}^4{\alpha }^2\right)\hfill \\ & & +{\displaystyle \frac{1}{18,432}}{c}^7+{\displaystyle \frac{1}{768}}{c}^4+{\displaystyle \frac{1}{6144}}{c}^6+{\displaystyle \frac{1}{768}}{c}^5+{\displaystyle \frac{1}{64}}{c}^3-{\displaystyle \frac{3}{8}}c\hfill \\ & =& 0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial v}{\partial \alpha }}& =(4-c^2)\left({\displaystyle \frac{1}{13,824}}{c}^4\alpha (4-c^2)-{\displaystyle \frac{1}{128}}{c}^2{\alpha }^2(4-c^2)-{\displaystyle \frac{1}{1152}}{c}^4\right.\hfill \\ \hfill & +{\displaystyle \frac{1}{12,288}}{c}^6\alpha -{\displaystyle \frac{1}{2304}}c\alpha {(4-c^2)}^2-{\displaystyle \frac{25}{9216}}{c}^2\alpha (4-c^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{1024}}{c}^3{\alpha }^3(4-c^2)+{\displaystyle \frac{1}{6144}}{c}^5\alpha -{\displaystyle \frac{1}{64}}c{\alpha }^3(4-c^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{1152}}c{\alpha }^3{(4-c^2)}^2-{\displaystyle \frac{1}{64}}c{\alpha }^2(4-c^2)-{\displaystyle \frac{3}{1024}}{c}^2{\alpha }^3(4-c^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{48}}{c}^2-{\displaystyle \frac{1}{2048}}{c}^3\alpha (4-c^2)+{\displaystyle \frac{1}{128}}c\alpha (4-c^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{1536}}{c}^4\alpha +{\displaystyle \frac{1}{768}}{c}^3\alpha -{\displaystyle \frac{1}{64}}{\alpha }^3(4-c^2)-{\displaystyle \frac{7}{576}}\alpha (4-c^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{4096}}{c}^4{\alpha }^3(4-c^2)+{\displaystyle \frac{1}{2304}}{c}^2{\alpha }^3{(4-c^2)}^2\hfill \\ \hfill & \left.+{\displaystyle \frac{1}{192}}c(4-c^2)+{\displaystyle \frac{1}{5184}}{\alpha }^3{(4-c^2)}^3\right)\hfill \\ \hfill & =0,\hfill \end{array}$$

For ${\displaystyle \frac{\partial v}{\partial c}}=0$ and ${\displaystyle \frac{\partial v}{\partial \alpha }}=0$, we have solved these equations by using the Newton Raphson method and we obtain $c=-2\times {10}^{-90}$ and $\alpha =-1.040488710\times {10}^{-160}$. We see that $c\notin (0,2), \alpha \notin (0,1)$. We observed that there is no critical point within the interior $(0,2)\times (0,1)$. So $(-2\times {10}^{-90},-1.040488710\times {10}^{-160})\cong (0,0)\notin (0,2)\times (0,1)$. So, it has no solution in $(0,2)\times (0,1)$.

In part $\mathbf{C}4$ its implies that by using (35),

$$det\left(T_{4,1}\right)\left(f\right)=G\left(c,\alpha ,\beta ,\Theta ,\Phi \right)=1.$$

The upper bound on $det\left(T_{4,1}\right)$ is exact of this function;

$$f_0={\int }_0^z\left(1+{\left(t-{\displaystyle \frac{t^3}{3}}\right)}^5\right)dt=z+{\displaystyle \frac{1}{5}}{z}^5-{\displaystyle \frac{4}{21}}{z}^7+{\displaystyle \frac{2}{27}}{z}^9-{\displaystyle \frac{4}{296}}{z}^{11}+\cdots .$$

For the sharpness of the lower bound of (23), B1 (v) and C1 (ii), let

$$f_1={\int }_0^z\left(1+{\left(t-{\displaystyle \frac{t^3}{3}}\right)}^2\right)dt=z+{\displaystyle \frac{1}{3}}{z}^3-{\displaystyle \frac{2}{15}}{z}^5+\cdots .$$

Thus we find that

$$det\left(T_{4,1}\right)\left(f\right)={\displaystyle \frac{64}{81}}.$$

□

2. Conclusions

This paper has found the sharpness of the second, third, and fourth order Hermitian Toeplitz determinants for the defined class $R_n$. We determined the lower and upper bounds of second, third, and fourth order Hermitian–Toeplitz determinants for the subclass of bounded turning function is associated with the nephroid function through the subordination relation. These results may open new directions in the estimation of coefficient functionals.