Novel Fractional-Order Chaotic System Applied to Mobile Robot Path Planning and Chaotic Path Synchronization

Abstract

In this paper, a novel fractional-order chaotic system equipped with symmetric attractors was proposed for the full-coverage path-planning problem of mobile robots, especially in application scenarios where path privacy needs to be protected. By coupling this system with a kinematic model of a mobile robot, a novel path-planning algorithm was designed to realize encrypted full-coverage path planning. A predefined time-synchronization control strategy effectively resolved inconsistencies in the path caused by initial position, time delay, and uncertain disturbances. Numerical simulation results demonstrated that the proposed path-planning method, based on the novel chaotic system, significantly improved coverage and randomness, compared to existing studies. Moreover, it maintained accuracy and stability in path planning, even in the presence of time delays and uncertain disturbances.

1. Introduction

Complete coverage path-planning (CCPP) technology has seen increasing application in mobile robots [1,2,3,4], with extensive use in areas such as patrolling [5,6], security [7], household cleaning [8,9], and agricultural management [10]. The primary task of this technology is to design a path that ensures the robot can navigate the entire working area while avoiding existing obstacles [11]. However, in certain specialized scenarios, such as surveillance systems, military operations, or adversarial environments, path planning must not only achieve full area coverage but also incorporate a degree of path encryption to enhance unpredictability and ensure operational security [12].

In adversarial and high-security environments, traditional deterministic path-planning methods may expose vulnerabilities, making them susceptible to prediction and interception by adversaries. To address this challenge, Nakamura [13] first proposed the introduction of chaotic mapping as a path input in 2001. By leveraging the sensitivity and randomness of chaotic systems, this approach enabled the design of unpredictable movement trajectories, offering a novel perspective on enhancing the security of path planning. This breakthrough quickly garnered significant attention within the research community.

Subsequently, research on full-coverage path planning based on the chaos theory has gained momentum, leading to methods utilizing systems, such as the Lorenz [14], Chen [15], Lv [12], Arnold [16], and Chua [17,18]. Sridharan [19] optimized coverage schemes by partitioning regions to enhance efficiency. Sánchez-López [20] proposed an adaptive approach for scaled region coverage paths. Additionally, Moysis [21] introduced a chaotic path-planning method for drones using a modulus strategy with chaotic mapping. According to Nasr [22], by controlling chaotic systems to generate multi-scroll chaotic attractors, their application in chaotic path planning can significantly enhance coverage efficiency.

With the advancement of chaos theory, research on fractional-order chaotic systems has become increasingly sophisticated. Fractional-order systems display a wider range of characteristics than their integer-order counterparts, including increased complexity, greater sensitivity, and a stronger dependence on time [23,24]. Fractional-order systems inherently introduce memory and global characteristics, making them more dependent on past states [25]. This enables fractional-order systems to describe real-world physical systems, such as electrical circuits [26] and biological systems [27].

In recent years, there has been growing interest in the study of 4D chaotic systems. Xiaoyue Tang et al. [28] explored a 4D fractional-order chaotic system based on sinusoidal functions, revealing how fractional-order variations lead to complex bifurcations and coexisting symmetric attractors. Meng Jiao Wang et al. [29] proposed a novel system with hidden attractors, examining its dynamic behaviors through the nonlinear theory, simulations, and circuit implementations. Chengyi Zhou et al. [30] introduced a new system, investigating the coexistence of single-wing and double-wing attractors, as well as transitions from periodic to chaotic states. A variable fractional-order circuit was designed to experimentally validate these findings. In comparison, the system proposed in this study also incorporates fractional-order dynamics but distinguishes itself by its ability to model chaotic behaviors relevant to mobile robot path planning.

Specifically, in the chaotic path planning of mobile robots, the primary objective is to enhance the unpredictability of the generated paths. Fractional-order systems demonstrate superior performance, compared to integer-order chaotic systems, in achieving this goal, owing to their increased dynamical complexity and greater sensitivity to initial conditions. However, research on the application of fractional-order systems in chaotic path planning for mobile robots remains limited.

Current research on chaotic mobile robots primarily focuses on autonomous robots, which emphasize minimizing human intervention—a significant advantage over traditional mobile robots. This design integrates path-planning algorithms directly into the robot system, enabling fully autonomous mobility. However, in practical applications, ensuring that the robot autonomously follows a predefined trajectory relies on the coordination of various sensors to maintain consistency between the actual trajectory and the target trajectory. According to [31], chaotic mobile robots face numerous challenges in real-world applications. Since the path planner is based on chaotic systems, it is inevitably affected by time delays, uncertain disturbances, and hardware performance limitations during operation. These factors often result in significant deviations between the chaotic path and the expected outcome, leading to what is referred to as “chaotic degradation”. This phenomenon significantly weakens the system’s randomness, coverage, and stability. Therefore, current research should focus on minimizing the impact of internal system errors and employing effective control methods to eliminate trajectory inconsistencies caused by hardware limitations. These efforts aim to enhance the robustness of chaotic path planning, ensuring a reliable and stable performance in complex environments.

The primary objectives of this study are threefold:

• To develop a novel fractional-order chaotic system and thoroughly analyze its dynamic properties, including stability and bifurcation behavior.
• To apply this system in mobile robot path planning to enhance coverage and unpredictability.
• To address trajectory inconsistencies caused by system errors using a predefined time sliding mode control approach.

The paper is structured as follows: Section 2 develops and analyzes the novel fractional-order chaotic system, focusing on its dynamic properties. Section 3 applies this system to mobile robot path planning, with comprehensive coverage and entropy evaluations. Section 4 addresses control challenges through a predefined time sliding mode control scheme. Finally, Section 5 concludes the paper and outlines future research directions.

2. Novel Fractional-Order Chaotic System

Fractional-order systems, characterized by their higher dynamic complexity, have demonstrated significant advantages over traditional integer-order systems in the field of information encryption [32]. This section presents a fractional-order chaotic system tailored for mobile robot coverage path planning, with a comprehensive analysis focusing on its stability, dynamic characteristics, and complexity.

2.1. Novel Fractional-Order Chaotic System Model

Research on chaotic mobile robot path planning typically focuses on integer-order systems like the Lorenz [14], Lu [12], and Arnold systems [16] and the logistic map [33]. This paper builds on [34] by introducing new variables to develop a fractional-order hyperchaotic system, which increases path complexity and enhances navigation security.

In this paper, we used the Caputo fractional derivative of order $q$, which generalizes the classical derivative to non-integer orders. The Caputo fractional derivative is particularly advantageous in handling initial value problems. Unlike other fractional derivative definitions, the Caputo derivative includes only the initial values of the integer-order derivatives in its Laplace transform [28]. The Caputo fractional derivative of a function $f\left(t\right)$ of order $q$ is defined as:

$$D^{q}f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(n-q\right)}}{\int }_0^t{\left(t-\tau \right)}^{\left(n-q-1\right)}{f}^{\left(n\right)}\left(\tau \right)d\tau$$

(1)

where $n\in Z^{+}$ is the smallest integer greater than or equal to $q$, and $\Gamma \left(\cdot \right)$ is the gamma function.

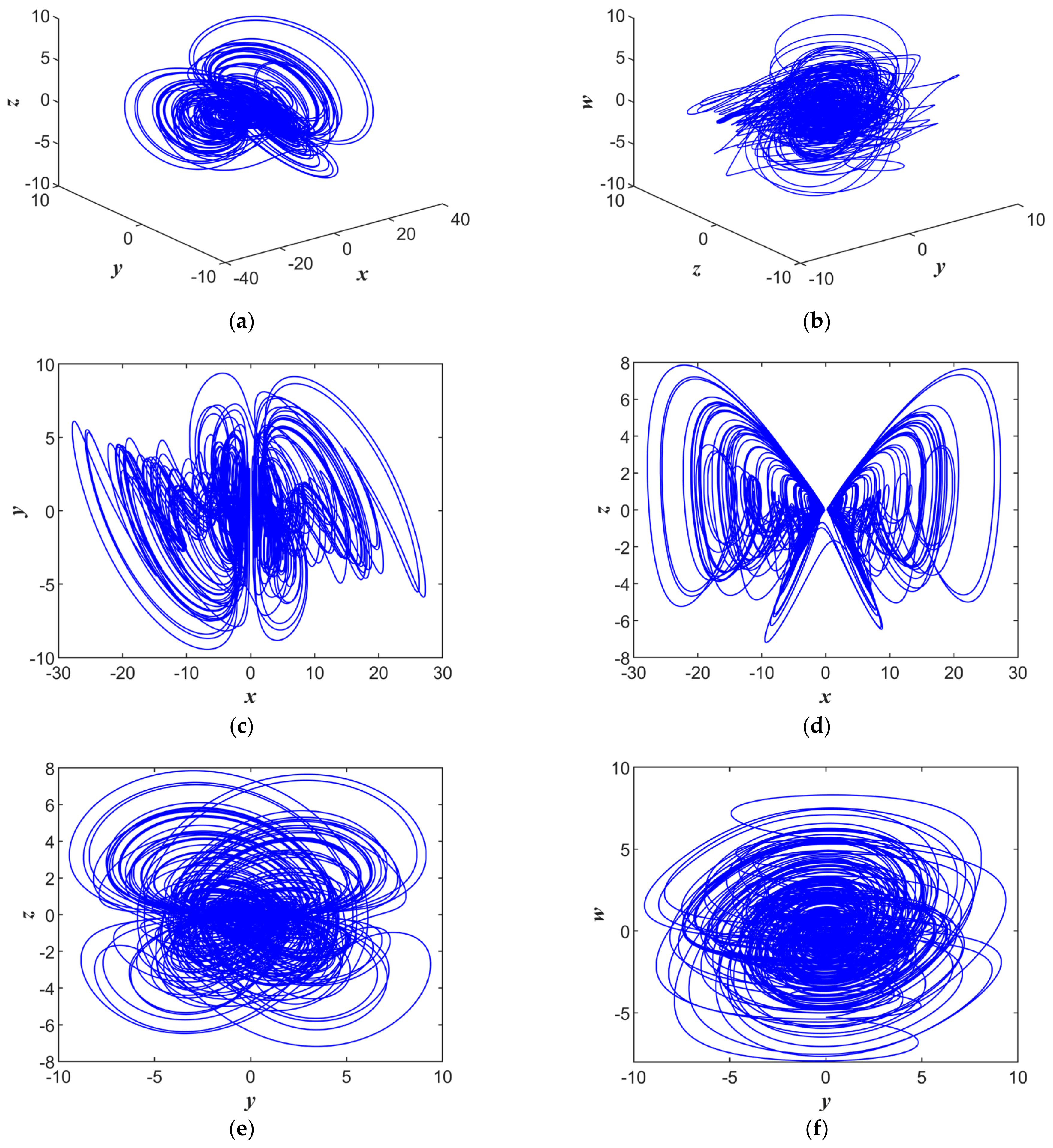
The proposed system is defined by:

$$\left\{\begin{array}{l}{D}^{q}x\left(t\right)=-x+xz+ayz\\ D^{q}y\left(t\right)=by-xz-3w\\ D^{q}z\left(t\right)=-cz+xy+d{z}^2\\ D^{q}w\left(t\right)=ey\end{array}\right.$$

(2)

where $x,y,z, \mathrm{and} w\in \mathrm{R}$ represent the system state variables, and $a=2.3, b=2, c=6, d=-0.25, \mathrm{and} e=3$ represent the system parameters. The system exhibited a symmetric attractor, and the attractor for the initial values [$1,0,0,1]$ and order $q=0.98$ is shown in Figure 1.

2.2. Stability Analysis

The equilibrium points of system 2 were determined by setting all derivatives equal to zero and solving the resulting algebraic equations for $x, y, z$, and $w$. The equilibrium state equations for system 2 are expressed as follows:

$$\left\{\begin{array}{l}0=-x+xz+ayz\\ 0=by-xz-3w\\ 0=-cz+xy+d{z}^2\\ 0=ey\end{array}\right.$$

(3)

The system equilibrium points are shown in

Table 1. Equilibrium points of system 2.

Equilibrium Point	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$
$E_1$	0	0	0	0
$E_2$	0	0	−24	0

.

By linearizing system 2, the Jacobian matrix is represented as Equation (3):

$$J=\left[\begin{array}{cccc}-1+z& az& x+ay& 0\\ -z& b& -x& -3\\ y& x& -c+2dz& 0\\ 0& e& 0& 0\end{array}\right]$$

(4)

The characteristic equation corresponding to the Jacobian matrix is given by Equation (4):

$$\left|\lambda E-J\right|=\left|\begin{array}{cccc}\lambda +1-z& -az& -x-ay& 0\\ z& \lambda -b& x& 3\\ -y& -x& \lambda +c-2dz& 0\\ 0& -e& 0& \lambda \end{array}\right|$$

(5)

When the equilibrium point is set to $E_1$ and the parameter’s values are $a=2.3, b=2, c=6, d=-0.25, \mathrm{and} e=3$, we can obtain:

$$\left|\lambda E-J\right|={\lambda }^4+5{\lambda }^3+{\lambda }^2+51\lambda +54=0$$

(6)

The characteristic roots of Equation (6) were ${\lambda }_1=-6, {\lambda }_2=-1,{ \lambda }_3=1-2\sqrt{2}i, {\mathrm{and} \lambda }_4=1+2\sqrt{2}i$. We can obtain $\left|\arg \left({\lambda }_1\right)\right|=\pi$, $\left|\arg \left({\lambda }_2\right)\right|=\pi$, $\left|\arg \left({\lambda }_3\right)\right|=1.231$, and $\left|\arg \left({\lambda }_4\right)\right|=1.231$. It can be deduced that system 2 exhibited asymptotic stability at equilibrium point $E_1$ when the order $q<{\displaystyle \frac{2\left|\arg \left({\lambda }_i\right)\right|}{\pi }}=0.78$.

Similarly, by analyzing the equilibrium point $E_2$, we obtained the characteristic roots ${\lambda }_1=6, {\lambda }_2=-11.412+31.927i, {\lambda }_3=-11.412-31.927i, \mathrm{and} {\lambda }_4=-0.176$, indicating that the system behaved as an unstable saddle point at this equilibrium.

2.3. Dynamics Analysis

Lyapunov exponents and bifurcation diagrams can effectively demonstrate whether a nonlinear system exhibits chaotic or periodic behavior [35].

Table 2. Maximum Lyapunov exponents for the various parameter values.

Order (q)	Parameter (b)	${\mathit{L}\mathit{E}}_1$	${\mathit{L}\mathit{E}}_2$	${\mathit{L}\mathit{E}}_3$	${\mathit{L}\mathit{E}}_4$
0.98	1.17	0.037	0.040	−0.117	−6.916
0.98	1.44	0.069	0.036	−0.188	−6.623
0.98	2	0.478	0.054	−0.366	−6.378
0.893	2	0.022	−0.151	−0.450	−10.788
0.934	2	0.193	−0.033	−0.625	−8.241

displays the maximum Lyapunov exponents for the four components of the fractional-order system as they varied with the order q and the parameter b.

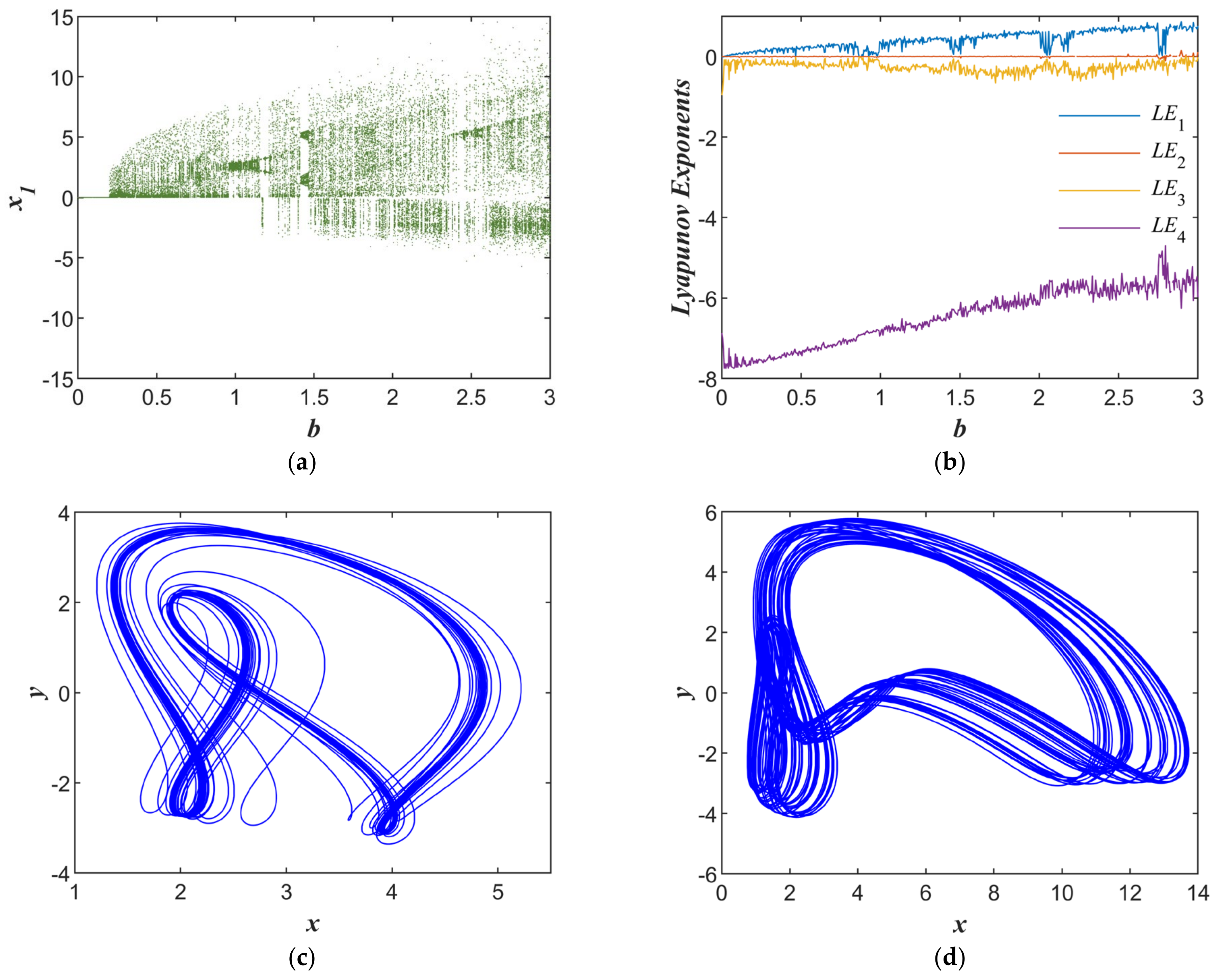
To provide a clearer illustration of the fractional-order system 2 state, with initial conditions [1, 0, 0, 1] and keeping the parameters $a, b, c, d, \mathrm{and} e$ constant, Figure 2a illustrates the system bifurcation as parameter b varied from 0 to 3. It was evident that the system demonstrated periodic, quasi-periodic, and chaotic behaviors. Figure 2c,d shows the phase trajectories in the x-y plane for $b=1.17$ and $b=1.44$, respectively. A comparison with the Lyapunov exponent graph revealed that the system underwent a brief period of quasi-periodic motion around $b=1$ and $b=1.5$. For $b>1.5$, the system exhibited a double-sided attractor, indicating that the chaotic behavior of the system became more complex and was more suitable for generating pseudorandom sequences.

The parameters and initial conditions constant were kept, and Figure 3a,b presents the bifurcation and Lyapunov exponent plots for system 2, with the fractional order q ranging from 0.8 to 1. The bifurcation diagram indicates that as q increased from 0.8 to 1, the system experienced periodic motion and quasi-periodic motion and ultimately transitioned into a chaotic state.

The Lyapunov exponent diagram verified this conclusion. Figure 3c,d displays the phase trajectories in the x-y plane for $q=0.893$ and $q=0.934$, respectively, illustrating the rich dynamical behavior of the system as the fractional order $q$ changed.

2.4. Complexity Analysis

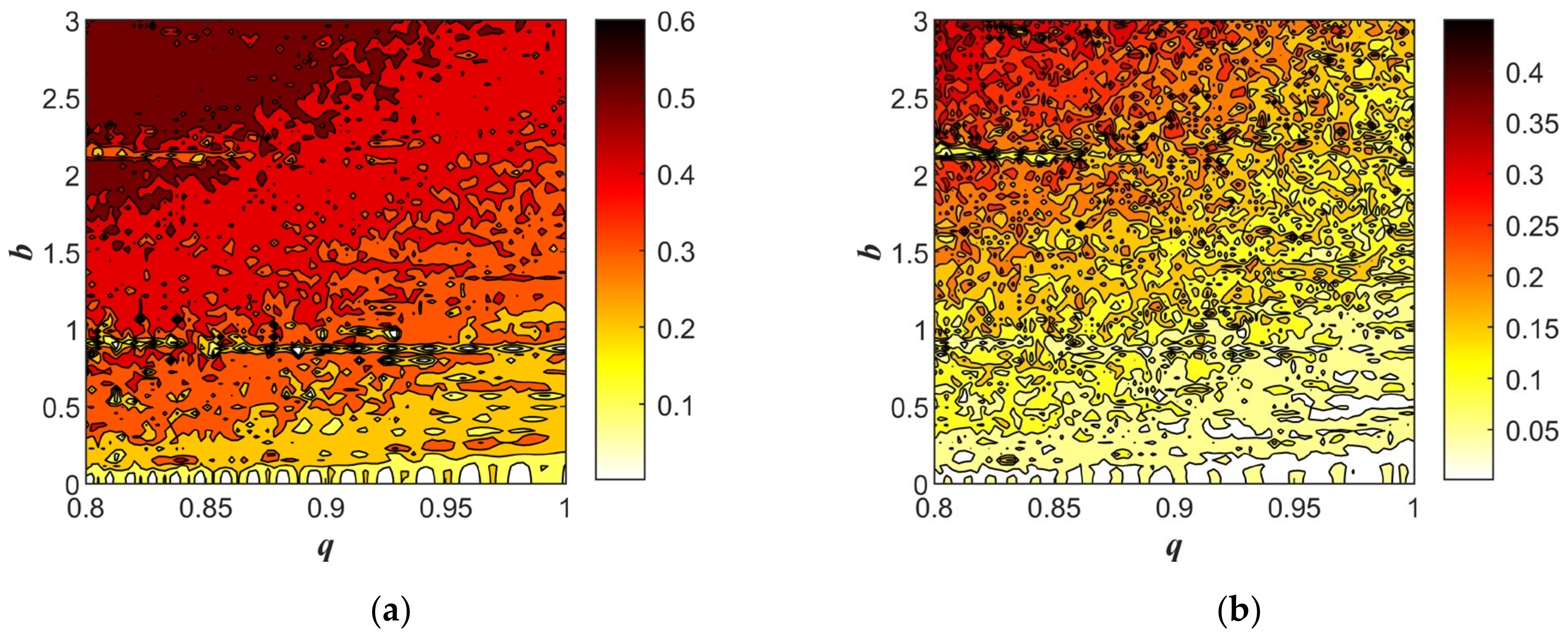
Fractional-order nonlinear systems exhibit higher unpredictability and complexity than integer-order systems [36]. To assess the complexity of the system, this work will perform a complexity analysis of the fractional-order system (1) from two perspectives: SE complexity and CO complexity. This approach provides valuable insights into parameter selection in the practical implementation of fractional-order systems.

The spectral entropy algorithm primarily leverages the energy distribution in the Fourier-transform domain, integrated with Shannon entropy, to derive the corresponding spectral entropy value. The CO complexity algorithm, based on FFT transformation, removes the regular components of a sequence while retaining irregular components. We considered the parameters $\left(a,c,d,e\right)=(2.3, 6,-0.25, 3)$ with parameters $b\in \left(0,3\right)$ and $q\in \left(0.8,1\right)$. Figure 4a shows the SE complexity, and Figure 4b shows the CO complexity. It was evident that as the order increased, the system complexity decreased progressively. However, when the parameter b was fixed, the increase in order had a smaller impact on the complexity. In contrast, when the order was held constant, variations in parameter b exerted a more pronounced influence on complexity.

3. Chaotic Mobile Robot Path Planning

The application of chaotic system signals in path planning for differential drive robots, such as those used in firefighting, inspection, and unknown environment exploration, leverages the sensitivity and unpredictability of chaotic systems. In this paper, we proposed a chaotic path-planning method based on a novel fractional-order chaotic system. Compared to traditional integer-order chaotic systems, the paths generated by this approach demonstrated significantly higher coverage and enhanced randomness. Drawing inspiration from chaos theory applications in image encryption, we introduced entropy as a metric to assess both the coverage and pseudo-randomness of the chaotic paths.

3.1. Chaotic Mobile Robot Model

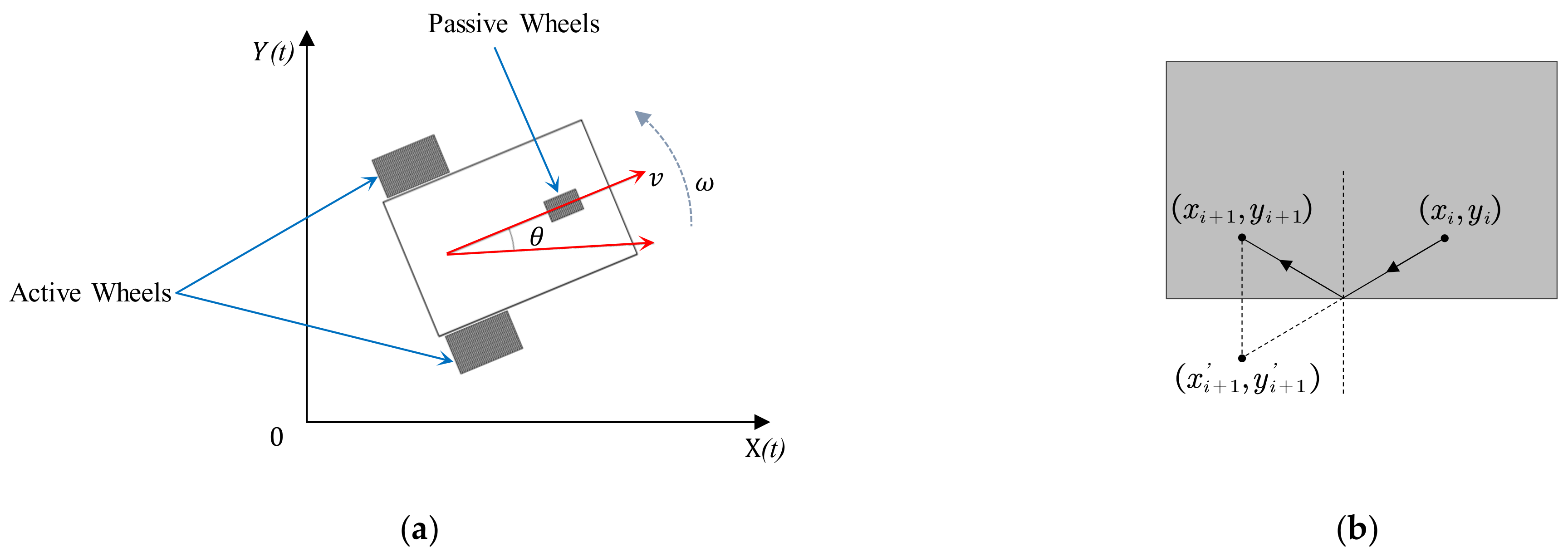
This paper employed a mathematical model to describe the dynamics of the wheeled mobile robot (WMR) with nonholonomic independent constraints. The motion diagram of the mobile robot is shown in Figure 5a, resembling the systems discussed in the works of Li, C [14] and Sridharan, K [19].

The model can be expressed in matrix form as:

$$\dot{P}=\left[\begin{array}{c}\dot{X}\\ \dot{Y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{c}\cos \theta \\ \sin \theta \\ 0\end{array}\begin{array}{c} 0\\ 0\\ 1\end{array}\right]\left[\begin{array}{c}{V}_x\\ V_y\\ w_z\end{array}\right]$$

(7)

Here, X and Y are the robot’s horizontal and vertical coordinates, $V_x$ and $V_y$ are the linear velocities, and $w_z$ is the angular velocity. By using the variables in system 2 as a mapping and coupling them with the kinematic equations of the mobile robot, the angular displacement in the kinematic equations was replaced to construct the chaotic robot path planner, as shown in Equation (8).

$$\left\{\begin{array}{l}{D}^q{x}_1\left(t\right)=-x_1\left(t\right)+x_1\left(t\right)x_3\left(t\right)+a{x}_2\left(t\right)x_3\left(t\right)\\ D^q{x}_2\left(t\right)=b{x}_2\left(t\right)-x_1\left(t\right)x_3\left(t\right)-3x_4\left(t\right)\\ D^q{x}_3\left(t\right)=-c{x}_3\left(t\right)+x_1\left(t\right)x_2\left(t\right)+d{x}_3{\left(t\right)}^2\\ D^q{x}_4\left(t\right)=e{x}_2\left(t\right)\\ D^q{X}_n\left(t\right)=vcos\left(x_i\left(t\right)\right)\\ D^q{Y}_n\left(t\right)=vsin\left(x_i\left(t\right)\right)\\ D^q\theta \left(t\right)=x_i\left(t\right)\end{array}\right.$$

(8)

Here, n represents the iteration count, and $X_n$ and $Y_n$ denote the horizontal and vertical coordinates at iteration n. By using the variable $x_i$ as a mapping, a path planner was constructed, resulting in highly randomized path points. Utilizing the fourth-order Runge–Kutta method to iterate Equation (8), given system parameters and initial values, enabled the determination of the position coordinates of the mobile robot at time t.

The schematic diagram of the mirror mapping method is shown in Figure 5b. References [12,14,18,19] all adopted the mirror mapping obstacle avoidance approach, which not only facilitates static obstacle avoidance but also improves operational efficiency. Assuming that the current coordinates of the mobile robot are $\left(x_0,y_0\right)$, and the next planned path point is $\left(x_0^{\prime },y_0^{\prime }\right)$, if $\left(x_0^{\prime },y_0^{\prime }\right)$ exceeds the boundaries of the working area, it can be mirrored with respect to the boundary of the working area or the obstacle boundary to obtain new coordinates $\left(x_1,y_1\right)$ within the working area. This method is equally applicable for static obstacle avoidance.

3.2. Performance Evaluation

To evaluate the effectiveness of the proposed strategy, coverage was used to define efficiency, representing the surface area covered by the robot during its operation [19]. Coverage can be expressed as:

$$C={\displaystyle \frac{1}{M}}\sum _{i=1}^M I\left(i\right), I\left(i\right)=\left\{\begin{array}{l}1,\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{i}\mathrm{f} \mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l} i \mathrm{i}\mathrm{s} \mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}\\ 0,\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\mathrm{i}\mathrm{f} \mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l} i \mathrm{i}\mathrm{s} \mathrm{u}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}.\end{array}\right.$$

(9)

where $C$ denotes the coverage rate, and $I\left(i\right)$ indicates whether each cell in the robot’s partitioned workspace is covered.

To assess the complexity of the chaotic path-planning method proposed in this paper, Shannon entropy was introduced for analyzing the path’s complexity. By calculating the entropy of the path, we can quantitatively evaluate its unpredictability. The calculation is defined as:

$$H=-\sum _{i=1}^N P_i\mathrm{l}\mathrm{o}\mathrm{g}\left(P_i\right)$$

(10)

where $P_i$ represents the probability of the path points falling within the $i$th grid cell, and $N$ is the total number of grid cells covered by the path. A higher entropy value indicates a more uniform distribution of path points, greater complexity, and an increased unpredictability of the path, making it suitable for applications that require a thorough exploration of the environment.

3.3. Numerical Simulation

Using system 1 as the framework for path planning, the chaotic variables $x_1$, $x_2$, $x_3$, and $x_4$ were individually mapped to the robot’s angular velocity ω. The workspace was defined as a 10 × 10 grid, with an iteration step size of $h=0.01$. The minimum statistical unit for coverage was set to 0.1. Figure 6 illustrates the path simulation results for four different mapping strategies ($x_1$, $x_2$, $x_3$, and $x_4$) at run times of 200 s, 500 s, and 800 s. It can be observed that when the iteration time reached 800 s, all mapping strategies produced paths with a high degree of unpredictability, and the coverage rate exceeded 90%. Among them, the $x_3$ mapping, shown in Figure 6g–i, achieved the best coverage performance, while the paths generated by $x_1$, shown in Figure 6a–c, and $x_4$, shown in Figure 6j–l, were smoother. The $x_2$ mapping, shown in Figure 6d–f, on the other hand, was particularly effective for prioritizing access to specific regions within the operational area. With the increase in run time, any of the mapping strategies can achieve full coverage of the operational area.

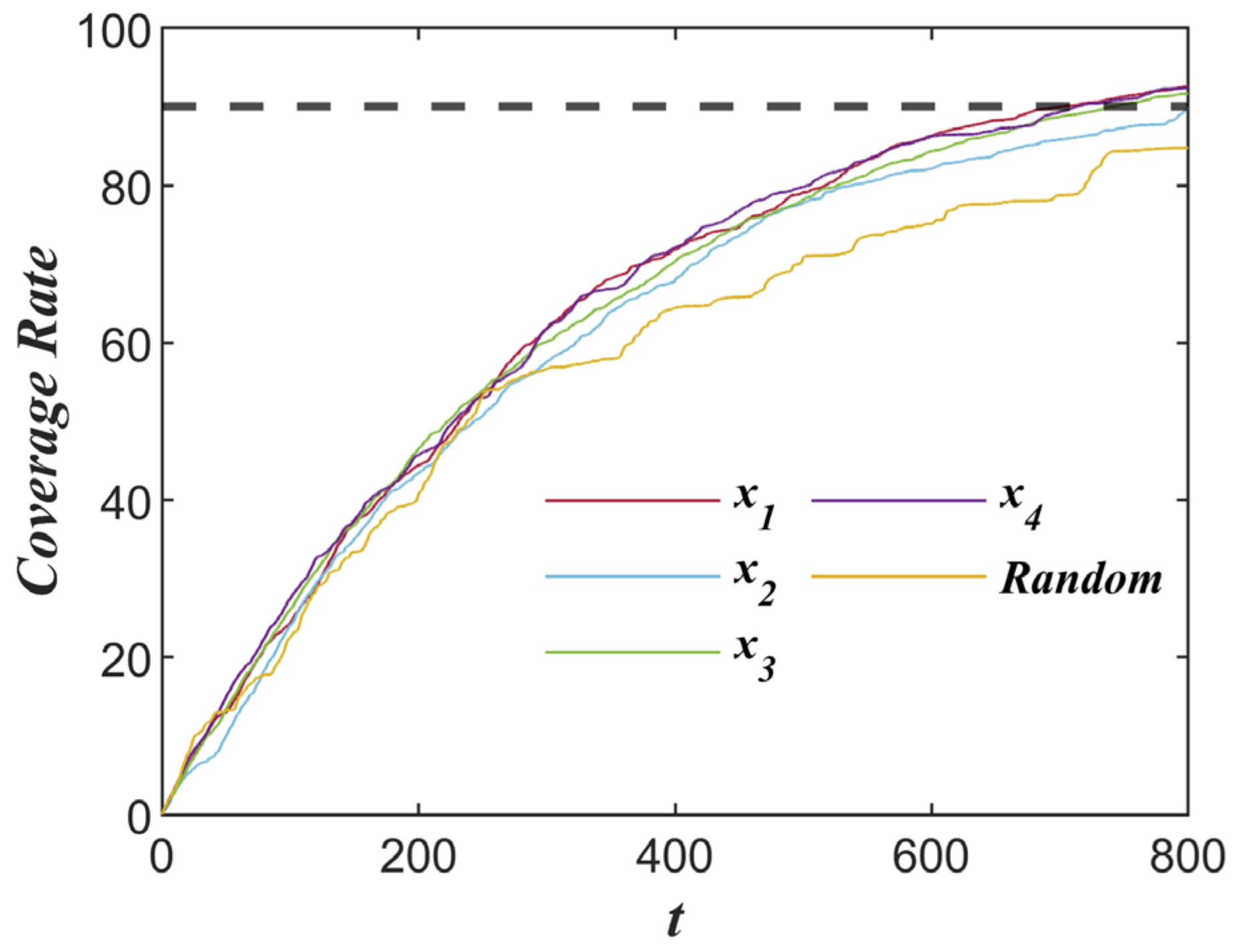
By observing Figure 7, it is evident that the coverage performance of the full-coverage path-planning strategy based on fractional-order chaotic systems was significantly higher than that of the random walk approach.

Additionally, by comparing its performance with existing research, the unique advantages of the fractional-order system in enhancing the pseudo-randomness and coverage efficiency of the path were demonstrated.

Table 3. Comparison of coverage rates in reported works.

Model	System	Coverage Rate	Path Entropy	Iteration Count
Classical Chaotic System	Lorenz	0.532	8.23	8 × 104
	Chen	0.431	7.98	8 × 104
Reference [38]	Logistic	0.799	NA	1 × 104
Reference [22]	Chua	0.898	NA	8 × 104
Reference [31]	Integer-order	0.82	NA	NA
This work	$x_1$	0.92	8.95	8 × 104
This work	$x_2$	0.896	8.85	8 × 104
This work	$x_3$	0.927	8.97	8 × 104
This work	$x_4$	0.917	8.94	8 × 104

presents the coverage rates of chaotic paths generated by different chaotic systems. Under the same number of iterations, compared to the classical chaotic systems, such as the Lorenz system and the Chen system, the fractional-order chaotic system proposed in this study achieved at least a 68.4% improvement in coverage rate and a 12.4% increase in path entropy. Furthermore, compared to the strategies employed in references [22,37], there was a significant improvement. The integer-order system 2 in reference [34] showed a 13.1% increase in coverage rate.

4. Synchronization Control Scheme for Chaotic Paths

As noted in [31], the chaotic path planning of mobile robots can experience chaotic degradation under real-world conditions, driven by the sensitivity of chaotic systems to unknown disturbances. This section examines uncontrollable chaos in planned paths caused by time delays and uncertainties when applying chaotic system-based planning. To address these challenges, we proposed a predefined sliding mode control strategy that effectively mitigates the impact of internal uncertainties, ensuring that the chaotic path remains consistent with the predefined trajectory, even in the presence of system imperfections. By employing this approach, we enhanced the robustness and reliability of chaotic path planning, maintaining consistency even when faced with real-world challenges, such as time delays and disturbances.

4.1. Synchronization Scheme

With chaotic path planner 8 as the main system, the secondary system can be configured as:

$$\left\{\begin{array}{l}{D}^q{y}_1\left(t\right)=-y_1\left(t\right)+y_1\left(t\right)y_3\left(t\right)+a{y}_2\left(t\right)y_3\left(t\right)+u_1\\ D^q{y}_2\left(t\right)=b{y}_2\left(t\right)-y_1\left(t\right)y_3\left(t\right)-3y_4\left(t\right)+u_2\\ D^q{y}_3\left(t\right)=-c{y}_3\left(t\right)+y_1\left(t\right)y_2\left(t\right)+d{y}_3{\left(t\right)}^2+u_3\\ D^q{y}_4\left(t\right)=e{y}_2\left(t\right)+u_4\\ D^q{X}_n\left(t\right)=vcos\left(y_i\left(t-\tau \right)\right)+d_{m1}+u_5\\ D^q{Y}_n\left(t\right)=vsin\left(y_i\left(t-\tau \right)\right)+d_{m2}+u_6\\ D^q\theta \left(t\right)=y_i(t-\tau )+d_{m3}+u_7\end{array}\right.$$

(11)

Here, $\tau >0$ represents the delay disturbance, and $d_m$ denotes an uncertain disturbance with a defined upper bound. When these disturbances interfered, the mobile robot’s path experienced chaotic degradation, deviating from the intended trajectory and resulting in a loss of path control.

The error system between Equations (8) and (11) can be expressed as:

$$e_i\left(t\right)=y_i\left(t\right)-x_i\left(t\right)$$

(12)

Then, the state equation of the error system is expressed as:

$$\left\{\begin{array}{l}{D}^q{e}_1\left(t\right)=-e_1\left(t\right)+y_1\left(t\right)y_3\left(t\right)+a{y}_2\left(t\right)y_3\left(t\right)-x_1\left(t\right)x_3\left(t\right)-a{x}_2\left(t\right)x_3\left(t\right)+u_1\\ D^q{e}_2\left(t\right)=b{e}_2\left(t\right)-3e_4\left(t\right)-y_1\left(t\right)y_3\left(t\right)+x_1\left(t\right)x_3\left(t\right)+u_2\\ D^q{e}_3\left(t\right)=-c{e}_3\left(t\right)+d\left(y_3{\left(t\right)}^2-x_3{\left(t\right)}^2\right)+y_1\left(t\right)y_2\left(t\right)-x_1\left(t\right)x_2\left(t\right)+u_3\\ D^q{e}_4\left(t\right)=e{e}_2\left(t\right)+u_4\\ D^q{e}_5\left(t\right)=vcos\left(y_i\left(t-\tau \right)\right)-vcos\left(x_i\left(t\right)\right)+d_{m1}+u_5\\ D^q{e}_6\left(t\right)=vsin\left(y_i\left(t-\tau \right)\right)-vsin\left(x_i\left(t\right)\right)+d_{m2}+u_6\\ D^q{e}_7\left(t\right)=e_i\left(t\right)+d_{m3}+u_7\end{array}\right.$$

(13)

Lemma 1

([38]). Let $T_c$ be a predefined time. If the function $D^{q}x\left(t\right)=\varphi \left(t,x\right)$ admits an unbounded Lyapunov function $V\left(x\right)$, it satisfies:

$$\dot{V}\le -{\displaystyle \frac{1}{T_c}}{\displaystyle \frac{2}{\alpha }}\left(2V+V^{1-{\displaystyle \frac{\alpha }{2}}}+V^{1+{\displaystyle \frac{\alpha }{2}}}\right)$$

(14)

Then, $D^{q}x\left(t\right)=\varphi \left(t,x\right)$is predefined-time stable. The stabilization time $T⩽T_c$, where $T_c$ is the predefined stabilization time, and the parameter $\alpha \in (0, 1)$.

Lemma 2

([39]). For any $x_i>0\left(i=1,2,3\dots n\right)$, it holds:

$${\left(\sum _{i=1}^n{x}_i\right)}^p⩽\sum _{i=1}^n{x_i}^p,n^{1-q}\left(\sum _{i=1}^n{x}_i\right)⩽\sum _{i=1}^n{x_i}^q⩽{\left(\sum _{i=1}^n{x}_i\right)}^q$$

(15)

where $0<p<1, 1⩽q<\infty$.

Assumption 1

([40]). We assumed that the time delay and uncertain disturbances in the system were bounded, satisfying $\left|{\tau }_m\right|<\left|{\Gamma }_m\right|,\left|d_m\right|<\left|D_m\right|$, where $\Gamma$ and $D_m$ are positive constants, and $\left|{\Gamma }_m\right|+\left|D_m\right|\le L$.

Using main system 8 as the predefined trajectory and secondary system 11 as the simulation trajectory, eliminating the chaotic degradation phenomenon in the trajectory can be transformed into ensuring that error system 13 converged to 0 or stabilized at 0.

4.2. Sliding Surface Design

Based on Lemma 1 and error system 13, the synchronization control sliding mode surface can be defined as:

$$s_i=D^{q-1}{e}_i+D^{q-2}(c_1{e}_i+c_{2}sign\left(e_i\right){\left|e_i\right|}^{1+{\displaystyle \frac{{\gamma }_1}{2}}}+c_{3}sign\left(e_i\right){\left|e_i\right|}^{1-{\displaystyle \frac{{\gamma }_1}{2}}}+c_{4}sign\left(e_i\right))$$

(16)

where $c_i(i=1,2 ,3,4)$ is the control input, with $c_1={\displaystyle \frac{4}{{\gamma }_1{T}_1}},c_2={\displaystyle \frac{2n^{\left(\frac{1-r_1}{2}\right)}}{{\gamma }_1{T}_1}},c_3={\displaystyle \frac{2}{{\gamma }_1{T}_1}},c_4>0, 0<{\gamma }_1<1$.

The Lyapunov function is chosen as:

$$V=\sum _{i=1}^N\left|e_i\right|$$

(17)

Differentiating Equation (17), we obtain:

$$\begin{array}{l}{\dot{V}}_1\left(e_i\right)={\displaystyle \sum _{i=1}^N}sign\left(e_i\right){\dot{e}}_i\\ \hspace{1em}\hspace{1em} ={\displaystyle \sum _{i=1}^N}sign\left(e_i\right)\left(D^{1-q}\left(D^q{e}_i\right)\right)\\ \hspace{1em}\hspace{1em} ⩽{\displaystyle \sum _{i=1}^N}\begin{array}{c}-c_1\left|e_i\right|-c_2{\left|e_i\right|}^{1+{\displaystyle \frac{{\gamma }_1}{2}}}-c_3{\left|e_i\right|}^{1-{\displaystyle \frac{{\gamma }_1}{2}}}-c_4\end{array}\\ \hspace{1em}\hspace{1em} ⩽-{\displaystyle \frac{2}{{\gamma }_1{T}_1}}\left(2V_1+V_1^{1+{\displaystyle \frac{{\gamma }_1}{2}}}+V_1^{1-{\displaystyle \frac{{\gamma }_1}{2}}}\right)\end{array}$$

(18)

where $T_1$ is the predefined stabilization time. Then the settling time can be expressed as:

$$\begin{array}{l}T\left(x_0\right)⩽\underset{V_0}{\overset{0}{\int }} -{\displaystyle \frac{{\gamma }_1{T}_{1}d{V}_1}{2\left(2V_1+{V_1}^{1+\frac{{\gamma }_1}{2}}+{V_1}^{1-\frac{{\gamma }_1}{2}}\right)}}={\displaystyle \frac{{\gamma }_1{T}_1}{2}}\underset{0}{\overset{V_0}{\int }} {\displaystyle \frac{d{V}_1}{2V_1+{V_1}^{1+\frac{{\gamma }_1}{2}}+{V_1}^{1-\frac{{\gamma }_1}{2}}}}\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{{\gamma }_1{T}_1}{2}}\underset{0}{\overset{V_0}{\int }} {\displaystyle \frac{d{V}_1}{{V_1}^{1-\frac{{\gamma }_1}{2}}{\left(V_1^{\frac{{\gamma }_1}{2}}+1\right)}^2}}={\displaystyle \frac{{\gamma }_1{T}_1}{2}}\underset{0}{\overset{V_0}{\int }} {\displaystyle \frac{d\left(V_1^{\frac{{\gamma }_1}{2}}\right)}{{\left(V_1^{\frac{{\gamma }_1}{2}}+1\right)}^2}}\\ \hspace{1em}\hspace{1em} =T_1\underset{0}{\overset{V_0}{\int }} {\displaystyle \frac{d\left(V_1^{\frac{{\gamma }_1}{2}}\right)}{\left(V_1^{{\gamma }_1}+1\right)}}=T_1\left(1-{\displaystyle \frac{1}{V_1^{\frac{{\gamma }_1}{2}}+1}}\right)⩽T_1\end{array}$$

(19)

From this, we can conclude that $T\left(x_0\right)⩽T_1$. According to Lemma 1, the error system $e_i$ can converge to 0 within the predefined time $T_1$.

4.3. Controller Design

The controller was devised to reach the sliding mode surface and accomplish synchronization within a specified time $T_p$. Thus, the controllers for system 8 and system 11 can be set as shown in Equation (20):

$$\begin{array}{c}{u}_i=e_i-D^{q-1}\left(c_1{e}_i+c_{2}sign\left(e_i\right){\left|e_i\right|}^{1+{\displaystyle \frac{{\gamma }_1}{2}}}+c_{3}sign\left(e_i\right){\left|e_i\right|}^{1-{\displaystyle \frac{{\gamma }_1}{2}}}+c_{4}sign\left(e_1\right)\right)\\ -\left(c_5\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(s_i\right){\left|s_i\right|}^{1+{\displaystyle \frac{{\gamma }_2}{2}}}+c_6\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(s_i\right){\left|s_i\right|}^{1-{\displaystyle \frac{{\gamma }_2}{2}}}+c_7\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(s_i\right)\right)-Lsign\left(s_i\right)\end{array}$$

(20)

where $c_i(i=5, 6, 7)$ is the control input, and $c_5={\displaystyle \frac{2n^{\left(\frac{1-r_1}{2}\right)}}{{\gamma }_2{T}_2}}, c_6={\displaystyle \frac{2}{{\gamma }_2{T}_2}},c_7>0, 0<{\gamma }_2<1$, $L>0$ represents the upper bound of the uncertain disturbance. This means that it is not necessary to know the specific nature of the disturbance, but the upper bound must be determined to achieve synchronization.

The Lyapunov function ${\dot{V}}_2$ for the sliding mode surface $s_i$ 16 is as follows:

$$\begin{array}{l}{\dot{V}}_2={\displaystyle \sum _{i=1}^N}sign\left(s_i\right){\dot{s}}_i\\ \hspace{1em}\hspace{1em} ⩽{\displaystyle \sum _{i=1}^N}\begin{array}{c}-c_5{\left|s_i\right|}^{1+{\displaystyle \frac{{\gamma }_2}{2}}}-c_6{\left|s_i\right|}^{1-{\displaystyle \frac{{\gamma }_2}{2}}}-c_7\end{array}\\ \hspace{1em}\hspace{1em} ⩽-{\displaystyle \frac{2}{{\gamma }_2{T}_2}}\left(2V_2+V_2^{1+{\displaystyle \frac{{\gamma }_2}{2}}}+V_2^{1-{\displaystyle \frac{{\gamma }_2}{2}}}\right)\end{array}$$

(21)

where $T_2$ is the predefined stabilization time. Then, the settling time can be expressed as:

$$\begin{array}{l}T\left(S_0\right)⩽\underset{V_0}{\overset{0}{\int }} -{\displaystyle \frac{{\gamma }_2{T}_{2}d{V}_2}{2\left(2V_2+{V_2}^{1+\frac{{\gamma }_2}{2}}+{V_2}^{1-\frac{{\gamma }_2}{2}}\right)}}={\displaystyle \frac{{\gamma }_2{T}_2}{2}}\underset{0}{\overset{V_0}{\int }} {\displaystyle \frac{d{V}_2}{2V_2+{V_2}^{1+\frac{{\gamma }_2}{2}}+{V_2}^{1-\frac{{\gamma }_2}{2}}}}\\ \hspace{1em}\hspace{1em} ={\displaystyle \frac{{\gamma }_2{T}_2}{2}}\underset{0}{\overset{V_0}{\int }} {\displaystyle \frac{d{V}_2}{{V_2}^{1-\frac{{\gamma }_2}{2}}{\left(V_2^{\frac{{\gamma }_2}{2}}+1\right)}^2}}={\displaystyle \frac{{\gamma }_2{T}_2}{2}}\underset{0}{\overset{V_0}{\int }} {\displaystyle \frac{d\left(V_2^{\frac{{\gamma }_2}{2}}\right)}{{\left(V_2^{\frac{{\gamma }_2}{2}}+1\right)}^2}}\\ \hspace{1em}\hspace{1em} =T_2\underset{0}{\overset{V_0}{\int }} {\displaystyle \frac{d\left(V_2^{\frac{{\gamma }_2}{2}}\right)}{\left(V_2^{{\gamma }_2}+1\right)}}=T_2\left(1-{\displaystyle \frac{1}{V_2^{\frac{{\gamma }_2}{2}}+1}}\right)⩽T_2\end{array}$$

(22)

Using Equations (19) and (22), it can be deduced that error system 13 and sliding mode surface 16 converged within the time intervals $T_1$ and $T_2$, respectively. The global predefined time $T_c=p_1{T}_1+p_2{T}_2$, where $p_1+p_2=1$.

4.4. Numerical Simulation

This section conducts simulations to evaluate the synchronization performance under varying initial conditions, different predefined synchronization times, and scenarios with and without disturbances. The parameters of controller 20 were configured as $r_1=r_2=0.5$ and $c_4$ = 2, and the time delay was set to $\tau =0.1$ s. Uncertain disturbances were simulated using Gaussian white noise with an amplitude of 2.5, and the disturbance upper bound was set to $L=6$.

The initial state of fractional-order chaotic system 8 was set to [1, 0, 0, 1], while the initial state of slave system 11 was configured as [3, 4, 4, 6]. The fractional order for both systems was set to q = 0.98. The mobile robot in the master system started from an initial position of [1, 1], with an orientation angle of $\theta =2$, while the slave system started from [1.5, 1.5], with an orientation angle of $\theta =1.5$. 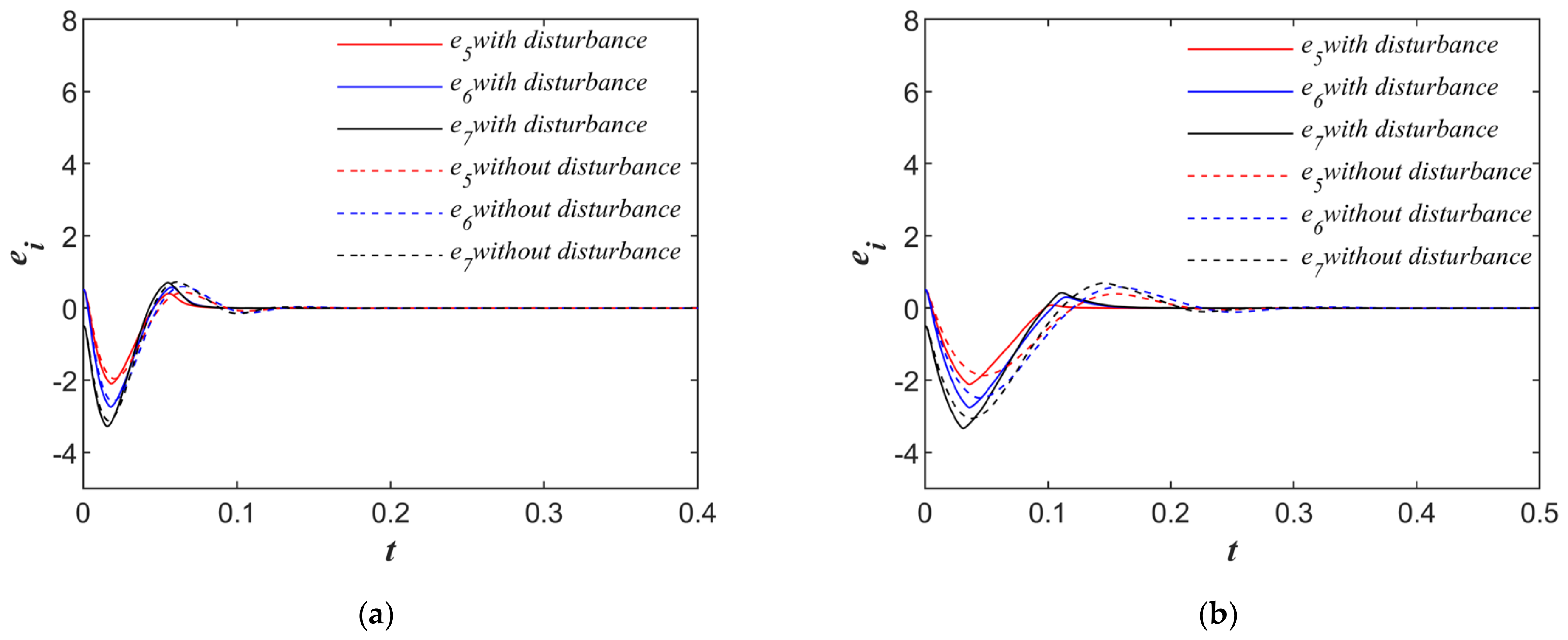Figure 8a presents the time-domain response of the error system under a control period of $T_c=0.2$ s. The solid line represents the synchronization performance under disturbances, whereas the dashed line corresponds to the scenario without disturbances. It can be observed that in the presence of disturbances, the robot’s pose stabilized at zero after 0.087 s, achieving synchronization between the master and slave systems. In the absence of disturbances, synchronization was achieved after 0.165 s. Figure 8b presents the results for $T_c=0.5$ s. Under disturbance conditions, the error system converged to zero after 0.17 s, whereas without disturbances, synchronization occurred at 0.347 s. These results indicate that the slave system consistently synchronized with the master system within the predefined time, regardless of disturbances. This validates that the proposed synchronization control strategy can achieve synchronization control within the preset time and exhibits excellent robustness.

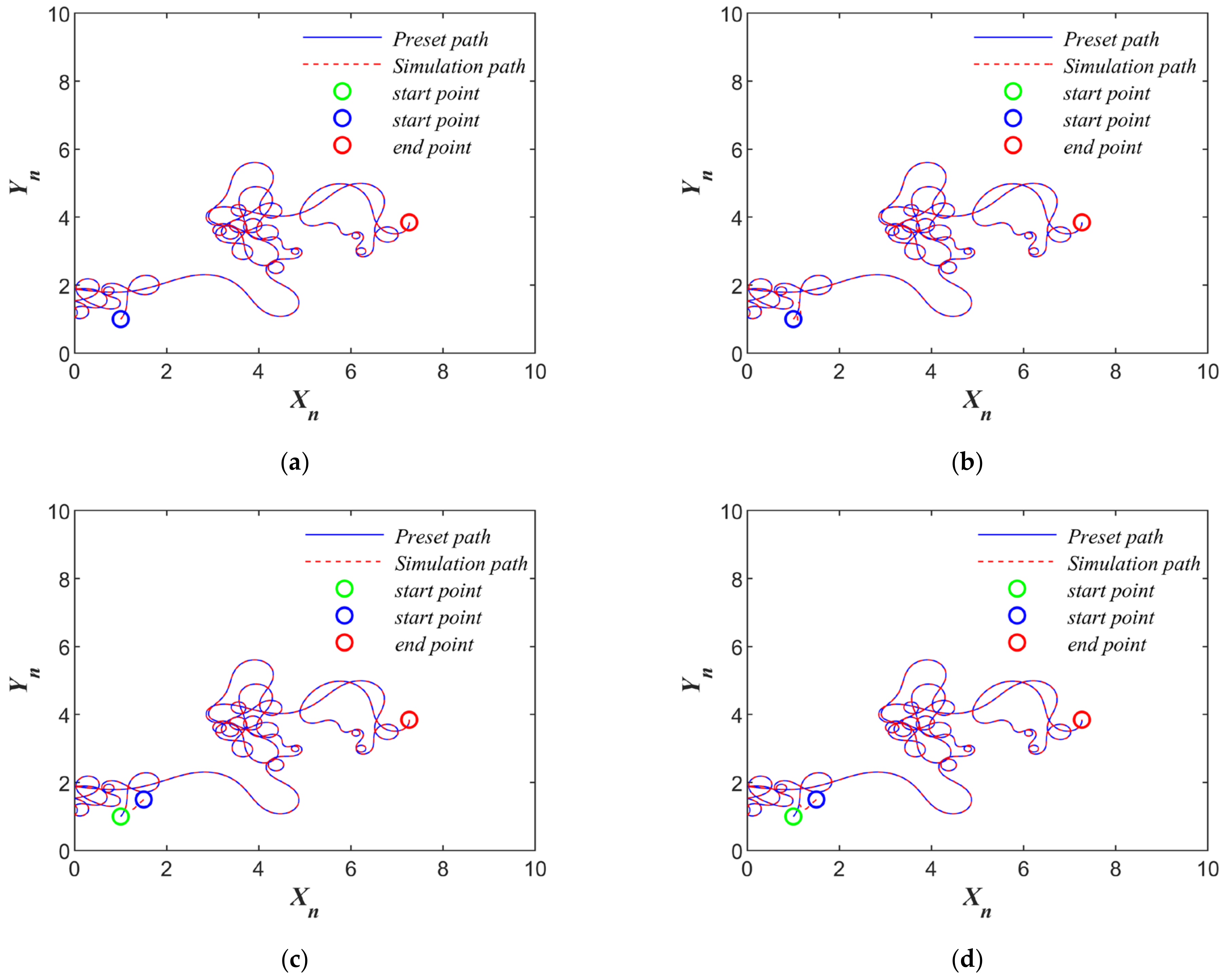
Figure 9 present the trajectory performance of the mobile robot with an initial position set to [1, 1] and a time delay of $\tau =0.1$ s and subjected to Gaussian white noise disturbances with an amplitude of 2.5. Under these conditions, the simulated trajectory (dashed line) significantly deviated from the desired trajectory (solid line), indicating that the robot’s path control was severely compromised under strong disturbance, leading to the loss of its intended operational functionality. By employing the proposed synchronization controller for trajectory regulation, Figure 10a,b demonstrates the trajectory synchronization results under the same initial position, with synchronization time periods of $T_{\mathrm{c}}=0.2 \mathrm{s}$ and $T_{\mathrm{c}}=0.5 \mathrm{s}$. The results indicate that the simulated trajectory can accurately follow the desired trajectory, despite the presence of disturbances. Figure 10c,d present the trajectory synchronization results when the initial position deviated from the desired path, with synchronization time periods of $T_{\mathrm{c}}=0.2 \mathrm{s}$ and $T_{\mathrm{c}}=0.5 \mathrm{s}$, further validating the effectiveness of the proposed controller. These simulation results demonstrated that the designed controller achieved the trajectory synchronization of chaotic mobile robots within the predefined time and exhibited excellent robustness.

5. Conclusions

In this paper, a novel fractional-order chaotic system with symmetric attractors was proposed and applied to a full-coverage mobile robot path-planning task. By analyzing the stability, maximum Lyapunov exponent, bifurcation map, and complexity of the system, the results showed that the system exhibited a variety of complex dynamic behaviors. By adjusting the system parameters, the flexibility and variability of the attractor can be realized, which enhances its adaptability in practical applications.

In terms of mobile robot path planning, the chaotic system-based path-planning method proposed in this paper showed unique advantages in maintaining path unpredictability in special scenarios. Compared with the existing integer-order chaotic systems, the proposed fractional-order system improved the path coverage by 13.1% and also showed significant advantages in the path entropy value. In addition, by introducing a predefined time sliding mode synchronization control strategy, this study successfully eliminated the deviation between the actual path and the preset path due to time lag, uncertainty perturbation, initial position deviation, and hardware accuracy error during the integration of the chaotic path planner into the mobile robot. Numerical simulation results showed that the proposed synchronization control strategy can ensure that the master–slave system completes the synchronization within the predefined time, and the synchronization effect remained stable, even in the presence of uncertain perturbations, which further verified the robustness of the proposed control strategy.

Although fractional-order chaotic systems still face challenges in practical engineering applications, future research can further explore more efficient control strategies, optimize the system parameters, and enhance the robustness and practicality of the system.