Abstract
Randomness plays a crucial role in numerous applications, with cryptography being one of the most significant areas where its importance is evident. A major challenge in cryptographic applications is designing a reliable key generator that meets stringent security requirements. Existing methods often suffer from predictability and fail to provide robust randomness, necessitating novel mathematical approaches. In this study, we propose an innovative mathematical framework that integrates quantum wave functions with chaotic systems to enhance the unpredictability and security of random number generation. The proposed approach leverages the inherent uncertainty of quantum mechanics and the dynamic behavior of chaos to generate statistically strong random sequences. The analysis results confirm that the proposed generator successfully passes all standard statistical randomness tests, demonstrating its effectiveness in cryptographic applications. Additionally, we present a practical implementation of the proposed method as an image encryption algorithm, showcasing its potential for real-world information security solutions. The findings suggest that this approach can contribute significantly to secure communication systems, financial transactions, and other domains requiring high-level cryptographic security.
1. Introduction
Electronic commerce, or e-commerce, has played a significant role in shaping our digital lives in recent years. E-commerce refers to the buying and selling of goods and services online, and it has become increasingly popular due to the convenience and efficiency it offers. There is a very strong link between e-commerce and cryptology science. This is because the main factor that triggered developments in both electronic commerce and cryptology science is trading habits. The determining factor in the exponential growth of electronic commerce volume on the internet is cryptographic algorithms, which are mathematically proven to be secure. The sense of trust that forms the infrastructure of this digital market that brings together buyers and sellers who are thousands of kilometers away from each other is provided by cryptology algorithms based on the beauties offered by mathematics [1]. The strong designs of both public-key encryption algorithms such as RSA and ECC and private-key encryption algorithms such as AES are some of the most widely accepted examples of these mathematically proven robust algorithms. Although algorithms such as RSA, ECC, and AES have different design principles, one of their common requirements is that they need strong key design (planning/scheduling) algorithms, which is a difficult task. This is because demonstrating that the randomness requirements required by cryptological applications are met is not an easy process [2,3]. These requirements can be grouped into two main categories: statistical randomness and unpredictability. In some sources, these requirements are collected in more detail under four main categories. The most widely accepted randomness requirements in the literature are listed in Table 1 [4,5].

Table 1.
Requirements for random numbers.
Depending on the security level required by different applications, which of the requirements listed in Table 1 should meet may vary. For example, in applications such as simulation, modeling, and games, it will be sufficient to meet the R1 requirement, while all requirements must be met to guarantee critical information security applications. However, while providing good statistical features, it is not easy to guarantee unpredictability at the same time. For example, while random number generators such as linear congruential generator (LCG) [6], the middle square method, and linear feedback shift register (LFSR) show good statistical properties [7], they facilitate the predictability of deterministic structures. Designs such as radioactive decay, noise in electrical circuits, and chaotic systems do not show good statistical properties, but their predictability is difficult. The main problem of researchers working on this subject is to be able to develop a design that can meet all requirements together [8].
Random numbers, which are one of the fields of mathematics, are numbers that are defined for a certain range, have an equal probability of occurrence, and have no relationship between them. Random numbers play a very important role in many different fields from games to cryptology, from statistics to simulations, and from computer programs to scientific studies. Especially in cryptology, random numbers are required in key generation. This is because the key generation is very important in terms of protecting information and preventing it from being interfered with by unwanted people. In today’s systems, keys emerge as digital numbers. The focus is on increasing the level of unpredictability to increase their security. Various physical processes or algorithms are used for this reason. Many random number generators (RNGs) have been developed to obtain random numbers. These random number generators are used to generate sequences of numbers that are difficult to predict. These are classified as pseudo-random number generators (PRNGs) and true random number generators (TRNGs) because of their way of generating numbers [9,10,11,12,13].
Recent advancements in random number generation, cryptographic security, and chaotic encryption methodologies have been extensively explored in the literature. Bikos et al. [14] provide an overview of RNGs, their principles, and their applications in cryptography, emphasizing the importance of true randomness for secure communications. Crocetti et al. [15] review methodologies and metrics for assessing RNG quality, while Zhao et al. [16] introduced a pseudorandom number generator integrating chaotic maps and quantum random walks. Fouzar et al. [17] explore secure video communication using a multi-equation, multi-key hybrid cryptographic system. Jiang et al. [18] discuss quantum obfuscation techniques applied to quantum power functions, highlighting its potential for secure computation. Ref. [19] presents a novel multi-channel image encryption algorithm using pixel reorganization and hyperchaotic maps, whereas Ref. [20] proposes an encryption approach using plane-level image filtering and discrete logarithmic transforms. Ref. [21] examines fractional-order 3D Lorenz chaotic systems and 2D discrete polynomial hyper-chaotic maps for multi-image encryption. Feng et al. [22] introduced a secure and efficient image transmission scheme leveraging two chaotic maps, while Feng et al. [23] developed a quadratic polynomial hyperchaotic map with a pixel fusion strategy for enhanced image encryption. Qian et al. [24] investigated a memristor-enhanced polynomial hyper-chaotic map for multi-channel image encryption. Lin et al. [25] analyzed diversified butterfly attractors in memristive Hopfield neural networks (HNNs) and their applications in IoMT privacy protection. Ref. [26] presents a grid multi-butterfly memristive neural network with three memristive systems, demonstrating its application in police IoT security. This structured overview provides a comprehensive summary of current research efforts in RNGs and cryptographic security.
Quantum random number generators have been added to this classification in recent years [27]. A new concept of a quantum random number generator related to the application of a quantum entanglement to produce several mutually coupled in a random manner bit strings is proposed [28]. A fast quantum random number generator based on a photonic integrated circuit directly embedded in an electronic platform is proposed [29]. A more efficient two-fold statistical approach is proposed to ensure the quantumness of optical sources with the desired confidence level [30].
This study aimed to design a robust random number generator algorithm that can be used to ensure the security of critical information. For this purpose, the advantages and disadvantages of the random number generators mentioned above were examined and the quantum wave function was used to solve several problems. Both the good statistical properties and the unpredictable nature of the random numbers produced by the proposed method stood out as the original aspect of the study. In this study, an architecture based on quantum wave equations was used to satisfy the unpredictability requirement. Since it is predicted that quantum wave equations will play a critical role in the encryption requirements that will change especially after the spread of quantum computers, such a design approach is thought to be useful both today and in the future. In addition to the unique properties of quantum wave equations, the use of chaos theory in parameter selection is another advantage of the proposed method. Both the success of the analysis results and the realization of a practical application as an image encryption algorithm are important indicators that the proposed method can be used effectively in many applications in the future.
The rest of the study is organized as follows: In Section 2, RNGs are briefly explained. In the Section 3, firstly, a short discussion about the importance of quantum wave equations in science and engineering studies is presented. Then, the relationship between unpredictable behavior and quantum wave equations is explained. Also, in the third chapter, a summary of the literature on random number generator designs based on quantum wave equations is presented, and the advantages and disadvantages of the proposed method can be evaluated more fairly. In the Section 4, the solution of the Schrödinger equation and how to obtain the values to be used in the generation of random numbers are explained in a stepwise manner. It is shown how to create an entropy source over a small numerical example. In Section 5, the details of the algorithm that converts the entropy source into random bit sequences are presented. In Section 6, analysis results on whether the generated numbers meet the randomness requirements are given. In Section 7, a practical application of random bit sequences generated by an image-encoding algorithm is shown. In Section 8, the study is summarized by discussing all the results obtained and possible future studies.
2. Random Number Generators
RNGs are quite vital in secure communication, because it is known that encryption made with keys obtained by generators, where sufficient randomness cannot be achieved, causes security vulnerabilities [2,3,4,5]. RNGs can be grouped as physical generators, generators based on software algorithms, generators based on probability distribution functions, and generators that generate random numbers with data produced by humans depending on the way the number is generated. However, in the programming field, randomness is not an easy task. Algorithms are highly deterministic structures, that is, they are reproducible processes that give the same results under the same initial conditions. Therefore, the question arises, can these pieces of code generate “random” numbers? Based on this question, they can be classified as pseudo-random number generators, real random number generators, and quantum random number generators.
The PRNGs are deterministic (mathematical or computable) number generators that generate random numbers according to a specific algorithm. Such generators need randomly chosen initial values. The most important advantages of PRNGs are that they are cheap and can be implemented simply and fast. However, the numbers produced by these generators are predictable when the initial value is determined or when the mathematical notations used in the system are not complex enough. The TRNGs are non-deterministic. The generated random numbers using real physical processes are more difficult to predict instead of algorithms. The most distinctive feature of random numbers obtained with such generators is that their randomness depends on the randomness of physical processes.
TRNGs have some disadvantages, such as that they are slow, costly, and hardware-dependent. The quantum random number generators (QRNGs) are generators that use many undetectable mechanisms of the quantum world, based on the Heisenberg uncertainty principle, and generate random numbers using the laws of quantum physics [31,32,33]. The random numbers obtained with such generators are derived from the random behavior of photons in certain situations. Since the QRNG can generate random numbers regardless of the processes used during number generation, they are the most suitable generators for cryptology applications. They have more advantages than other generators. However, since QRNGs cannot provide a sufficient level of randomness by themselves, randomness is strengthened by using classical physics [33,34,35]. Also, it creates a deficiency in terms of communication speed as cumbersome contrivances are used. However, detectors used during production are also very costly. Is it possible to eliminate such troubles? Is it possible to eliminate such problems? In our study, a hybrid random number generator is proposed as an alternative for QRNG applications using the quantum wave function in TRNGs.
3. Quantum Wave Function in Science and Engineering
In quantum mechanics, the states of physical systems are usually determined by a function of virtual value called the state function or wave function. The maximum information about the system and in particular the probability distributions related to the other observables of the system are encoded in these functions, which are interpreted as probability amplitudes [36]. The wave function provides all the information about a quantum system. Each particle is represented by a wave function. This wave function multiplied by itself gives the probability of the particle at a particular time and location. The wave function should have the following properties:
- Contains all measurable information about the particle.
- If there are particles, the probability should be 1. In other words, the probability of a certain particle to be found at a certain time is 1.
- The wave function and its derivative should be continuous to satisfy the conservation of particles and conservation of momentum, respectively.
- Provides three-dimensional probability distribution.
- Allows the calculation of the effective average value of a given variable.
- The wave function for a free particle is a sinus wave. This means that the position is completely uncertain.
- Their norms should be finite, i.e., they can be normed.
- They must be continuous, univalent, and not divergent.
As is known, the special part of quantum mechanics provides the properties of the behavior of a system rather than the future behaviors of a system. This is achieved by the wave function. The equation that shows the change of a wave function concerning space and time is the quantum wave equation known as the Schrödinger equation. This equation plays a role in conserving energy in Newton’s laws and classical mechanics and provides information about the future behavior of a dynamic system. It also predicts the probability of events analytically and precisely. The Schrödinger equation also estimates the distribution of the results. The evolution of probability amplitudes in space and time again is determined by the Schrödinger wave equation, which is a partial differential linear equation. The success of quantum mechanics is in the solutions of the Schrödinger equation that provide results that are fully compatible with many experimental facts that exist, especially in the microstructure of nature.
4. Schrödinger Equation-Based Entropy Source
The Schrödinger equation: It is a quadratic differential equation shown in Equation (1).
Equation (2) has two independent solutions, like . Based on these solutions, the general solution is a linear combination as follows:
A and B are determined by the boundary conditions (x) and Ψ′ (x). For these solutions to be considered physically reasonable, the functions Ψ (x) and Ψ′ (x) must be continuous. The Schrödinger equation has solutions in two separate cases: a free particle and a particle in a box.
- (I)
- Free Particle Condition:
Equation (3) turns into
Provided that it is
is found.
Where
If de Broglie wave formulas are used, the wave equation becomes whose solutions are
- (II)
- Particle Condition in a Box:
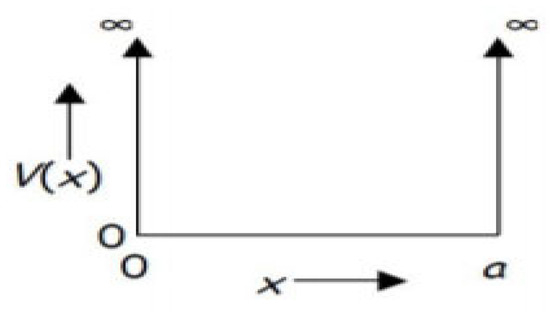
Figure 1.
The particle situation in a box.
There cannot be a particle with anywhere. In this case, .
The Schrödinger equation with the free particle for becomes
Using the definitions of and the solution , the result is obtained. However, this time there are boundary conditions.
Since it is known that k is continuous, is not continuous, and it takes values in the form of ; the solutions of the Schrödinger equation are as follows [34]:
Equation (5) is the solution obtained in both cases, provided that : time, : wave vector , : wavelength is rearranged as : position, and : frequency; a new quantum wave function is obtained as follows [37]:
Similarly, solutions to the Schrödinger equation with different methods are available in the literature [38,39,40,41].
5. Random Bit Generator Algorithm
This section provides a detailed explanation of the proposed algorithm, including its workflow, parameter selection process, and boundary conditions. The algorithm begins by generating an entropy source based on initial conditions and parameters set within a chaotic system. Random number generation is achieved by leveraging the uncertainty properties of quantum wave functions. The parameter selection process involves optimizing the initial values and equations of chaotic maps (e.g., logistic map, tent map) to ensure maximum randomness. Various chaotic systems were tested, and the combinations yielding the highest statistical randomness were identified. During this process, different parameter configurations were evaluated, and the most optimal set was selected based on predefined randomness metrics. Additionally, nonlinear transformations and differential equations were incorporated to enhance the stability of entropy sources. The boundary conditions of the algorithm were defined to maintain the continuity of the quantum wave function while analyzing the impact of varying initial conditions in chaotic maps on the system’s randomness level. The conducted analyses and tests demonstrate that the proposed method provides high statistical randomness and unpredictability. A detailed flowchart of the algorithm is presented in Figure 2. The architecture suggested in Figure 2 consists of three basic blocks. These blocks are the prime number parameter frequency calculator (PNPFC), chaotic selection for real and imaginary parts of the complex number, and the quantum wave function-based random number generator by using determined parameters. The blocks other than the dashed arrows represent the analysis stages of the statistical randomness processes, which is the basic condition that must be met for the generated random numbers.
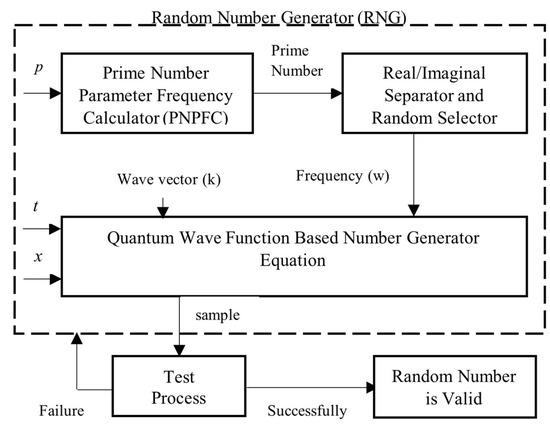
Figure 2.
Overview of the proposed random number generator.
A complex number value is calculated with the help of the PNPFC block. Details of the pseudocode regarding the chaotic selection principle of the real and imaginary parts of the complex number are given in Algorithm 1.
| Algorithm 1. Prime Number Parameter Frequency Calculator (PNPFC) |
| parameters: pList (Prime Number List) P ← pList loop n to range(P) ListFC[n] ← ((1-i√2)Pn-1-(i√2)Pn)/(Pn(-i√2)(1-i√2)(3-i√2)) endloop // ListFC contains complex number loop n to listFC xPrior ← RandomSelector[0,1] /* xPior is a decimal number xNext ← 4*xPrior*(1-xPrior) between 0 and 1 */ if xNext<0.5 ListPNPFC[n] ← ListFC[n].real else ListPNPFC[n] ← ListFC[n].imag xPrior ← xNext endloop return ListPNPFC |
The pseudo-codes for the bit values to be produced through the quantum wave equation by using the parameter values determined using the pseudo-codes given by Algorithm 1 are given in Algorithm 2.
| Algorithm 2. Random Number Generator (RNG) |
| parameters: ListPNPFC, t, x wList ← ListPNPFC maxhour ← 60 maxminute ← 60 loop t to maxhour loop w to wList loop x to maxminute lmd ← w k ← 2π/lmd frequency ← (1/√2(cos(wt - kx) + sin(wt - kx))).real frequencyBinaryList ← binary(frequency) endloop endloop endloop return frequencyBinaryList |
The pseudo-code given in Algorithm 2 produces bit values as output. These bit values are collected in an entropy pool. It is the case that 256-bit long values are taken from the entropy pool to generate random numbers with decimal values in a specific bit range. These values are passed through the SHA3 hash function to generate a new 256-bit value. In other words, there is no reduction in the bit output rate of the generator. When the values are obtained to reach the 1,000,000-length bitstream, whether they are statistically random or not is checked with the help of various hypothesis tests. The general view of this post-processing approach is given in Figure 3.
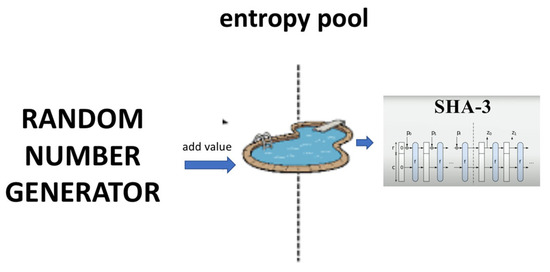
Figure 3.
Proposed post-processing approach.
6. Analysis Results
The science of cryptology is like a two-legged table. Since missing one of these legs, known as cryptography and cryptanalysis, will affect the security of the entire system, a newly proposed generator must be analyzed in detail to meet the randomness requirements. It has been previously stated that four requirements must be met in random number generators to be used for cryptographical purposes. The first of these requirements is the statistical randomness requirement. There are various tools for checking statistical randomness. One of the most widely accepted comprehensive test tools among these tools is the NIST test suite [42]. The NIST test package contains 15 different test tools. To perform these tests, 1,000,000 length bit strings are required. By using the proposed method detailed in Section 5, 1,000,000 bits were generated. NIST test results for this sample-generated bitstream are given in Table 2.

Table 2.
NIST randomness analysis results.
The NIST test suite contains hypothesis tests. It is observed in Table 4 of the NIST test suite [42] that all tests were successfully provided for all acceptable confidence values. These results indicate that statistically random numbers have a uniform distribution and that an attacker cannot make a better statistical inference than a blind guess. However, as stated in the first section, statistical randomness is only one of four requirements. It is not native alone. Therefore, it should be verified that the proposed generator has an unpredictable nature. In the study, unpredictable architecture is fed by two sources. These sources are chaotic systems and a quantum wave equation known as the Schrödinger equation. However, to further validate these results and address any concerns regarding potential weaknesses in the generator’s output, additional analyses were conducted. These analyses include multiple test iterations under different initial conditions. To confirm the stability of the generator, we repeated the NIST test suite under various conditions. These included different initial values and control parameters for the chaotic system, different sequence lengths (1,000,000 bits, 10,000,000 bits, and 100,000,000 bits), and different entropy extraction techniques. In all cases, the results remained consistent, indicating that the generator’s statistical properties do not degrade with changes in input parameters. This ensures that the system maintains its randomness and unpredictability across different scenarios.
The widespread use of chaos theory for the design of RNGs in the literature is a hot topic for researchers. Thus, for many years, what might be best practices for various chaotic systems have been extensively studied. In this study, by using the best chaos-based entropy sources previously published [43] in the literature, the negativities that can be experienced (such as avoiding the initial conditions that are negative for different chaotic systems and not providing statistical randomness) are prevented. The chaotic system based on the study was chosen as a discrete-time tent map [44]. A tent map discrete-time chaotic system was used to determine the parameters of the Schrödinger equation. If the random number generator is to be used as the secret parameter of the encryption system, its predictability will theoretically not be possible since it has a large key space. The width of the key space and its resistance to brute force attacks are analyzed in the next section. The other leg of the unpredictable structure of the proposed generator is provided by the unpredictable structure of the Schrödinger equation.
The two other requirements that random number generators need to meet, the unpredictability of the previous and next sub-sequences of random numbers, are related to the second requirement, although the use of cryptographic hash functions in the proposed architecture to guarantee these requirements cryptographically is important in terms of providing the provable security characteristics of the study is an advantage. The SHA3 algorithm, which is the hash function accepted as the latest standard, was used in the study. If a general evaluation is made, if the SHA3 algorithm is safe, the generator will not be predictable. To express it in a simpler and understandable language, the random number generator requirements and the cryptographical components used in the generator proposed to meet these requirements are given in Table 3.

Table 3.
Randomness analysis of the proposed generator.
The comparison presented in the Table 4 emphasizes the advantages and trade-offs of the proposed random number generator relative to chaotic and quantum-based approaches.

Table 4.
Randomness analysis of proposed generator.
One of the key strengths of the proposed method is its high unpredictability, achieved by integrating chaotic systems with quantum wave functions. This provides an advantage over traditional chaotic RNGs, which may exhibit structural weaknesses and patterns that can be exploited under certain conditions. Additionally, while QRNGs also offer high unpredictability, they often require post-processing to refine their entropy sources, making implementation more complex. The resistance to brute-force attacks is another critical factor where the proposed generator demonstrates superiority over chaotic RNGs. Due to its combination of chaos and quantum principles, the proposed method ensures a high entropy output, making it highly resistant to attacks. Although QRNGs also possess strong security properties, their reliance on quantum hardware poses implementation challenges. From a computational complexity standpoint, the proposed generator falls in the moderate to high range, as solving quantum wave equations requires additional processing power compared to standard chaotic maps. Chaotic RNGs generally have the lowest computational burden, making them suitable for real-time applications with limited resources. However, QRNGs remain the most complex, given the need for specialized quantum computations. Regarding hardware requirements, the proposed generator provides flexibility, as it can be implemented purely in software while benefiting from hardware acceleration for efficiency improvements. In contrast, chaotic RNGs are predominantly software-based and easy to implement, whereas QRNGs necessitate dedicated quantum hardware, making them less practical for widespread cryptographic applications at present. The randomness quality of the proposed generator is validated through extensive statistical testing, particularly with NIST SP 800-22 evaluations. This ensures that the generated sequences exhibit true randomness characteristics, a property that some chaotic RNGs struggle to achieve consistently. While QRNGs also generate high-quality randomness, their reliability is contingent on the integrity of their entropy sources. Implementation complexity is a notable consideration. The proposed generator, though more complex than chaotic RNGs, remains significantly more accessible than quantum-based methods, which require a deep understanding of quantum mechanics. Finally, in terms of potential applications, the proposed generator is well-suited for cryptographic key generation, secure communications, and high-security environments—areas where strong unpredictability and resistance to attacks are paramount. While chaotic RNGs are often used in simulation, gaming, and moderate-security applications, QRNGs find their niche in high-security cryptographic applications and emerging quantum computing environments. Overall, this evaluation highlights the balanced approach of the proposed generator, leveraging both chaotic and quantum properties to achieve a secure, efficient, and flexible solution for cryptographic random number generation.
7. A Practical Application: One-Time Key-Based Image Encryption Algorithm
Various image encryption algorithms have been proposed recently based on the strongest components of modern cryptology [45,46,47]. The basic principle in these image encryption algorithms is based on the principle of XOR processing of each pixel value (pixel values range from 0 to 255) and a key value of the image to be encrypted. Using the key generator algorithm proposed in this study, key values (random values ranging from 0 to 255) are generated as much as the number of pixels in the picture to be encrypted. A step-by-step detailed explanation of the proposed encryption algorithm is given below.
- The image is selected in M × N size. The M value denotes the number of rows, and the N value indicates the number of columns. The image contains T = M × N pixels. If the image is a color image, it contains T = 3 × M × N pixels.
- To solve the correlation problem specific to the images, the working logic is visualized in Figure 4 is applied, and the image has been transformed into a one-dimensional array in 1 × T size by using the zig-zag transformation approach suggested in Ref [2].
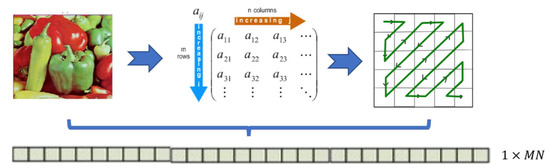 Figure 4. Proposed approach to solve the correlation problem.
Figure 4. Proposed approach to solve the correlation problem. - T random numbers are generated using the proposed random number generator. These random numbers are placed in an array of 1 × T size.
- A new mixed sequence is obtained by applying the XOR process to the cells of both sequences in the same position.
- The encryption process is completed by converting the 1 × T size array back to the M × N size image.
Various design guidelines have been published to evaluate the security level of an image encryption algorithm. An analysis scenario that is widely used among these design guides and evaluation criteria has been published [48,49,50,51]. This analysis scenario contains 12 different analysis stages. Each of these analysis stages and the processes to be provided with these stages in the proposed image encoding algorithm are given in Table 5 [52].

Table 5.
Cryptanalysis of the image encryption algorithm.
8. Conclusions and Discussion
In conclusion, our study demonstrates the potential of using quantum wave equations to develop a true random number generator and image encryption algorithm. By exploiting the unpredictable nature of quantum mechanics, we were able to create a highly secure encryption key that is resistant to attacks from cryptanalysis techniques. The successful analysis results of our generator and encryption algorithm indicate that they have important potential for practical applications in the future, especially in fields that require high-level security, such as finance, defense, and telecommunications. Furthermore, the development of this technology may pave the way for the creation of other secure cryptographic systems that can benefit from the power of quantum mechanics.
Despite the promising results, the proposed method has certain limitations that must be addressed in future research. One primary challenge is the computational complexity associated with solving quantum wave equations, which may impact real-time implementations in resource-constrained environments. Additionally, while the integration of chaotic systems with quantum mechanics enhances unpredictability, further investigations are needed to evaluate the stability of the generator under different operational conditions. Another limitation lies in hardware dependencies; although software implementations are feasible, optimizing the generator for hardware-based architectures remains an open research area. To address these limitations, several future research directions are proposed:
- Exploration of Alternative Chaotic Maps: Investigating different chaotic functions to optimize entropy extraction and improve the efficiency of randomness generation.
- Hybridizing Quantum Entropy Sources: Combining quantum randomness with additional entropy sources to further strengthen the statistical properties of the generator.
- Real-Time Hardware Implementations: Developing FPGA- and ASIC-based implementations to improve processing speed and optimize performance for cryptographic applications.
- Extended Security Evaluations: Conducting additional security tests beyond NIST, such as machine-learning-based randomness assessments, to ensure robustness against evolving attack strategies.
- Quantum-Resilient Cryptographic Applications: Exploring post-quantum cryptographic frameworks that integrate the proposed generator to ensure security against future quantum adversaries.
The unique aspects of the proposed image encryption algorithm and its advantages in cryptographic applications are listed below:
- The proposed random number generator algorithm successfully meets all the requirements for cryptographic applications.
- The proposed generator shows no weakness in terms of statistical randomness, and it has been shown that it can be used in various practical application areas such as simulation, modeling, and games.
- The unpredictable structure of the proposed generator based on both chaos theory and the Schrödinger equation has been shown to meet critical requirements in cryptographic applications, especially the secret key generator.
- Generator design performed specifically for the Schrödinger equation draws attention to the critical role that quantum wave equations will play in the future to address the cryptographic requirements that will change with the widespread use of quantum computers.
- The use of cryptographic components such as hash functions in the proposed generator mathematically proves that security concerns against attacks are addressed with a provable security model in future designs.
- The fast and high-bit output rate of the proposed generator is an important advantage over similar generators.
- It has been evaluated that the image encryption algorithm designed as a practical application example can successfully provide fast encryption performance and security analysis and can be used in successful designs in different applications in the future.
Author Contributions
Conceptualization, M.T.G. and F.Ö.; methodology, M.T.G.; software, Ö.K.; validation, M.T.G., Ö.K. and F.Ö.; formal analysis, F.Ö.; investigation, M.T.G.; resources, F.Ö.; data curation, F.Ö.; writing—original draft preparation, F.Ö.; writing—review and editing, M.T.G., Ö.K. and F.Ö.; visualization, Ö.K.; supervision, M.T.G., Ö.K. and F.Ö.; project administration, M.T.G.; funding acquisition, M.T.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by Institution of Firat University Scientific Research Projects (FUBAP) under project number TBMYO.24.04, with the APC funded by FUBAP.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors sincerely thank the editor(s) and the anonymous reviewers contributed positively to this paper’s academic development with their constructive and quick feedback. Muharrem Tuncay Gencoglu has been supported by TÜBİTAK (223N142-CHISTERA).
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
References
- Araki, S.; Wu, J.-H.; Yan, J.-J. A Novel Design of Random Number Generators Using Chaos-Based Extremum Coding. IEEE Access 2024, 12, 24039–24047. [Google Scholar] [CrossRef]
- Muhammad, A.S.; Özkaynak, F. SIEA: Secure Image Encryption Algorithm Based on Chaotic Systems Optimization Algorithms and PUFs. Symmetry 2021, 13, 824. [Google Scholar] [CrossRef]
- Schindler, W. Random Number Generators for Cryptographic Applications. In Cryptographic Engineering; Koç, Ç.K., Ed.; Springer: Berlin, Germany, 2009; pp. 1–25. [Google Scholar]
- Topaloğlu, F. Development of a New Hybrid Method for Multi-Criteria Decision Making (MCDM) Approach: A Case Study for Facility Location Selection. Oper. Res. 2024, 24, 60. [Google Scholar] [CrossRef]
- Yakut, S.; Tuncer, T.; Özer, A.B. A New Secure and Efficient Approach for TRNG and Its Post-Processing Algorithms. J. Circuits Syst. Comput. 2020, 29, 2050244. [Google Scholar] [CrossRef]
- Eröz, E.; Tanyıldızı, E.; Özkaynak, F. A New Method Based on Particle Swarm Optimization Algorithm to Improve Statistical Randomness Properties. In Proceedings of the 2023 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE), Dubai, United Arab Emirates, 9–10 March 2023; pp. 209–214. [Google Scholar] [CrossRef]
- Eröz, E.; Tanyıldızı, E.; Özkaynak, F. Determination of Suitable Configuration Parameters for Linear Feedback Shift Register Using Binary Bat Optimization Algorithm. In Proceedings of the IEEE EUROCON 2021—19th International Conference on Smart Technologies, Lviv, Ukraine, 6–8 July 2021; pp. 348–351. [Google Scholar] [CrossRef]
- Özkaynak, F. Cryptographically Secure Random Number Generator with Chaotic Additional Input. Nonlinear Dyn. 2014, 78, 2015–2020. [Google Scholar] [CrossRef]
- Paul, G.; Basak, B.; Das, S. Evaluating Quantumness, Efficiency and Cost of Quantum Random Number Generators via Photon Statistics. arXiv 2024, arXiv:2405.14085. [Google Scholar]
- Persohn, K.J.; Povinelli, R.J. Analyzing Logistic Map Pseudorandom Number Generators for Periodicity Induced by Finite Precision Floating-Point Representation. Chaos Solit. Fract. 2012, 45, 238–245. [Google Scholar] [CrossRef]
- Prajapati, R.B.; Panchal, S.D. Enhanced Approach to Generate One Time Password (OTP) Using Quantum True Random Number Generator (QTRNG). Int. J. Comput. Digit. Syst. 2024, 15, 279–292. [Google Scholar] [CrossRef]
- Garipcan, A.M.; Erdem, E. A TRNG Using Chaotic Entropy Pool as a Post-Processing Technique: Analysis, Design, and FPGA Implementation. Analog Integr. Circ. Sig. Process. 2020, 103, 391–410. [Google Scholar] [CrossRef]
- Garipcan, A.M.; Erdem, E. Implementation and Performance Analysis of True Random Number Generator on FPGA Environment by Using Non-Periodic Chaotic Signals Obtained from Chaotic Maps. Arab J. Sci. Eng. 2019, 44, 9427–9441. [Google Scholar] [CrossRef]
- Bikos, A.; Nastou, P.E.; Petroudis, G.; Stamatiou, Y.C. Random Number Generators: Principles and Applications. Cryptography 2023, 7, 54. [Google Scholar] [CrossRef]
- Crocetti, L.; Nannipieri, P.; Di Matteo, S.; Fanucci, L.; Saponara, S. Review of Methodologies and Metrics for Assessing the Quality of Random Number Generators. Electronics 2023, 12, 723. [Google Scholar] [CrossRef]
- Zhao, W.; Chang, Z.; Ma, C.; Shen, Z. A Pseudorandom Number Generator Based on the Chaotic Map and Quantum Random Walks. Entropy 2023, 25, 166. [Google Scholar] [CrossRef] [PubMed]
- Fouzar, Y.; Lakhssassi, A.; Mundugar, R. Secure Video Communication Using Multi-Equation Multi-Key Hybrid Cryptography. Future Internet 2023, 15, 387. [Google Scholar] [CrossRef]
- Jiang, Y.; Shang, T.; Tang, Y.; Liu, J. Quantum Obfuscation of Generalized Quantum Power Functions with Coefficient. Entropy 2023, 25, 1524. [Google Scholar] [CrossRef]
- Feng, W.; Yang, J.; Zhao, X.; Qin, Z.; Zhang, J.; Zhu, Z.; Wen, H.; Qian, K. A Novel Multi-Channel Image Encryption Algorithm Leveraging Pixel Reorganization and Hyperchaotic Maps. Mathematics 2024, 12, 3917. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, X.; Zhang, J.; Qin, Z.; Zhang, J.; He, Y. Image Encryption Algorithm Based on Plane-Level Image Filtering and Discrete Logarithmic Transform. Mathematics 2022, 10, 2751. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting Newly Designed Fractional-Order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map for High-Performance Multi-Image Encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Qin, Z. A Secure and Efficient Image Transmission Scheme Based on Two Chaotic Maps. Complexity 2021, 2021, 1898998. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Woźniak, M. Exploiting Robust Quadratic Polynomial Hyperchaotic Map and Pixel Fusion Strategy for Efficient Image Encryption. Expert Syst. Appl. 2023, 246, 123190. [Google Scholar] [CrossRef]
- Qian, K.; Xiao, Y.; Wei, Y.; Liu, D.; Wang, Q.; Feng, W. A Robust Memristor-Enhanced Polynomial Hyper-Chaotic Map and Its Multi-Channel Image Encryption Application. Micromachines 2023, 14, 2090. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Deng, X.; Yu, F.; Sun, Y. Grid Multi-Butterfly Memristive Neural Network with Three Memristive Systems: Modeling, Dynamic Analysis, and Application in Police IoT. IEEE Internet Things J. 2024, 99, 29878–29889. [Google Scholar] [CrossRef]
- Lin, H.; Deng, X.; Yu, F.; Sun, Y. Diversified Butterfly Attractors of Memristive HNN with Two Memristive Systems and Application in IoMT for Privacy Protection. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2024, 44, 304–316. [Google Scholar] [CrossRef]
- Jacak, J.E.; Jacak, W.A.; Donderowicz, W.A.; Jacak, L. Quantum Random Number Generators with Entanglement for Public Randomness Testing. Sci. Rep. 2020, 10, 164. [Google Scholar] [CrossRef]
- Jóźwiak, P.; Jacak, J.E.; Jacak, W.A. New Concepts and Construction of Quantum Random Number Generators. Quantum Inf. Process. 2024, 23, 132. [Google Scholar] [CrossRef]
- Marangon, D.G.; Smith, P.R.; Walk, N.; Paraïso, T.K.; Dynes, J.F.; Lovic, V.; Sanzaro, M.; Roger, T.; De Marco, I.; Lucamarini, M.; et al. A Fast and Robust Quantum Random Number Generator with a Self-Contained Integrated Photonic Randomness Core. Nat. Electron. 2024, 7, 396–404. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172. [Google Scholar] [CrossRef]
- Schmidt, H. Quantum-Mechanical Random-Number Generator. J. Appl. Phys. 1970, 41, 2. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Zurek, W.H. The Physical Content of Quantum Kinematics and Mechanics. In Quantum Theory of Measurement; Princeton University Press: Princeton, NJ, USA, 1927. [Google Scholar]
- Gabriel, C.; Wittmann, C.; Sych, D.; Dong, R.; Mauerer, W.; Andersen, U.L.; Marquardt, C.; Leuchs, G. A Generator for Unique Quantum Random Numbers Based on the Vacuum States. Nat. Photonics 2010, 4, 711–715. [Google Scholar] [CrossRef]
- Herrero-Collantes, M.; Garcia-Escartin, J.C. Quantum Random Number Generators. Rev. Mod. Phys. 2017, 89, 015004. [Google Scholar] [CrossRef]
- Wei, W.; Guo, H. Bias-Free True Random-Number Generator. Opt. Lett. 2009, 34, 1876–1878. [Google Scholar] [CrossRef]
- Dereli, T.; Verçin, A. Kuantum Mekaniği: Temel Kavramlar ve Uygulamaları. TÜBA Ders Kitapları: Ankara, Türkiye, 2014. [Google Scholar]
- Gençoğlu, M.T.; Agarwal, P. Use of Quantum Differential Equations in Sonic Processes. Appl. Math. Nonlinear Sci. 2021, 6, 21–28. [Google Scholar] [CrossRef]
- Gençoğlu, M.T. Complex solutions for Burgers-Like equation. Turk. J. Sci. Technol. 2013, 8, 121–123. [Google Scholar]
- Gümüş, H.; Yılmaz, H. Nonlineer Schrödinger Denkleminin Tam Çözümleri. Turk. J. Appl. Sci. Technol. 2019, 2, 11–19. [Google Scholar]
- Inç, M.; Aliyu, A.I.; Yusuf, A. Optical solitons to the nonlinear Shrödinger’s equation with Spatio-temporal dispersion using complex amplitude ansatz. J. Mod. Opt. 2017, 64, 2273–2280. [Google Scholar] [CrossRef]
- Jorgensen, L.; Cardozo, D.L.; Thibierge, E. Numerical Resolution of The Schrödinger Equation. Master’s Thesis, Normale Supérieure de Lyon, Lyon, France, 2011. [Google Scholar]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; US Department of Commerce, Technology Administration, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Muhammad, Z.M.Z.; Özkaynak, F. An Image Encryption Algorithm Based on Chaotic Selection of Robust Cryptographic Primitives. IEEE Access 2020, 8, 56581–56589. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Özkaynak, F. A New Chaotic S-Box Generation Method Using Parameter Optimization of One-Dimensional Chaotic Maps. IEEE Access 2019, 7, 117829–117838. [Google Scholar] [CrossRef]
- Al-Daraiseh, A.; Sanjalawe, Y.; Fraihat, S.; Al-E’mari, S. Novel, Fast, Strong, and Parallel: A Colored Image Cipher Based on SBTM CPRNG. Symmetry 2024, 16, 593. [Google Scholar] [CrossRef]
- Ge, B.; Ge, G.; Xia, C.; Duan, X. High-Capacity Reversible Data Hiding in Encrypted Images Based on 2D-HS Chaotic System and Full Bit-Plane Searching. Symmetry 2023, 15, 1423. [Google Scholar] [CrossRef]
- Alexan, W.; Chen, Y.-L.; Por, L.Y.; Gabr, M. Hyperchaotic Maps and the Single Neuron Model: A Novel Framework for Chaos-Based Image Encryption. Symmetry 2023, 15, 1081. [Google Scholar] [CrossRef]
- Rabie, O.; Ahmad, J.; Alghazzawi, D. Modified SHARK Cipher and Duffing Map-Based Cryptosystem. Mathematics 2022, 10, 2034. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, B.; Wu, Z. Research on Color Image Encryption Algorithm Based on Bit-Plane and Chen Chaotic System. Entropy 2022, 24, 186. [Google Scholar] [CrossRef] [PubMed]
- Lawnik, M.; Moysis, L.; Volos, C. Chaos-Based Cryptography: Text Encryption Using Image Algorithms. Electronics 2022, 11, 3156. [Google Scholar] [CrossRef]
- Huang, R.; Han, F.; Liao, X.; Wang, Z.; Dong, A. A Novel Intermittent Jumping Coupled Map Lattice Based on Multiple Chaotic Maps. Appl. Sci. 2021, 11, 3797. [Google Scholar] [CrossRef]
- Ozkaynak, F. Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dyn 2018, 92, 305–313. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).