Sensory or Intelligence Data Compression Can Drive the Yerkes–Dodson Effect

Abstract

New probability models of inherently embodied cognition derived from the asymptotic limit theorems of information and control theories show, where the Weber–Fechner, Stevens, Hick–Hyman, and Pieron’s psychophysics laws—and analogous processes of sensory data rate compression—operate, that sufficient arousal will engender the classic Yerkes–Dodson effect responses for ‘easy’ and ‘difficult’ challenges, depending on the level of ‘noise’ impeding the cognition rate. A ‘hallucination’ mode is found to arise at low arousal, and, in the face of sufficient noise, a ‘panic’ mode at high arousal. Systems that are ‘ductile’ in a formal sense, however, are not afflicted by such hallucination, although panic remains for difficult challenges. Similar dynamics that surround organized conflict on ‘Clausewitz landscapes’ of fog, friction, and deadly adversarial intent have long been studied. We find a central mechanism for cognitive failure under increasing stress across a very broad range of modalities to be enough—usually badly needed—compression of sensory/intelligence and internal information transmission rates. It seems possible, with some effort, to convert the probability models developed here into robust statistical tools for the study and limited control of critical real-time, real-world embodied cognitive phenomena associated with cellular, neural, individual, machine, and institutional systems and their many composites.

A wide consensus has emerged in recent years that successful policymaking and programming in conflict situations must start with an accurate understanding of local context, conflict actors, causes, and the dynamic relationships among them.

—Woocher [1].

...[A]ccurate and stable neural networks exist, however, modern algorithms do not compute them.

—Bastounis et al. [2].

1. Introduction

The Weber–Fechner law [3] that sensation perception is proportional to the logarithm of sensation energy has been found to approximately hold across a surprising range of modalities in human enterprise [4,5]:

• Weight perception.
• Sound intensity perception.
• Brightness perception.
• Numerical cognition.
• Dose–response chemoreception.
• Public finance in mature democracies.
• Emotional intensity.

The usual mathematical form of the Weber–Fechner (WF) law is that the strength of the perceived ‘sensation’ P varies as the ‘energy’ of the sensory impulse S according to

$$P\approx kln\left({\displaystyle \frac{S}{S_0}}\right)$$

(1)

where k is an appropriate constant and $S_0$ a characteristic minimum detection level.

The WF law is most often applied to ‘local’ psychophysics for which results can be found with only 50 percent accuracy. So-called ‘global’ psychophysical observations, to higher precision, are often subsumed under the Stevens law [6]:

$$P\approx k{I}^a$$

(2)

where I is an intensity measure and a an appropriate exponent. As Mackey [7] shows, however, the Stevens law can, in a sense, be derived from the WF law.

‘Sensory’ or ‘intelligence’ data compression are essential for cognitive systems that must act in real-world environments of fog, friction, and adversarial intent. Without some form of data-sorting, winnowing, or other form of compression, one is simply overwhelmed by unredacted sensation and left paralyzed. This is, indeed, a central purpose of misinformation in organized conflict.

From another perspective, the widely observed Hick–Hyman law [8] states that the response time $T_R$ of a cognitive agent to an incoming sensory or other data stream will be proportional to the Shannon uncertainty of that stream. That is, more complex information takes longer to process, in direct proportion to that complexity, as measured by the Shannon uncertainty expression:

$$T_R\propto -\sum _j{P}_{j}ln\left(P_j\right)$$

(3)

where $P_j$ are the (perceived) probabilities of the different possible options.

Likewise, Pieron’s law finds response time given as [5]

$$T_R\propto I^{-b}$$

(4)

where I is the intensity of the sensory signal and b a positive constant.

Reina et al. [5] characterize these matters as follows:

Psychophysics, introduced in the nineteenth century by Fechner, studies the relationship between stimulus intensity and its perception in the human brain. This relationship has been explained through a set of psychophysical laws that hold in a wide spectrum of sensory domains, such as sound loudness, musical pitch, image brightness, time duration, vibrotactile frequency, weight, and numerosity. More recently, numerous studies have shown that a wide range of organisms at various levels of complexity obey these laws. For instance, Weber’s law, which Fechner named after his mentor Weber, holds in humans as well as in other mammals, fish, birds, and insects. Surprisingly, also organisms without a brain can display such behaviour, for instance slime moulds and other unicellular organisms.

...[F]or the first time, we show that superorganismal behaviour, such as honeybee nest-site selection, may obey the same psychophysical laws displayed by humans in sensory discriminatory tasks.

Superorganismal cognitive behavior in organized conflict, however, has long been observed to obey something qualitatively similar to these psychophysics laws. Examples abound, e.g., during the Japanese attack on Pearl Harbor [9]:

On the morning of 7 December 1941, the SCR-270 radar at the Opana Radar Site on northern Oahu detected a large number of aircraft approaching from the north. This information was conveyed to Fort Shafter’s Intercept Center. The report was dismissed by Lieutenant Kermit Tyler who assumed that it was a scheduled flight of aircraft from the continental United States. The radar had in fact detected the first wave of Japanese Navy aircraft about to launch the attack on Pearl Harbor.

US radar subsequently—and accurately—traced Japanese aircraft in their post-attack return flights to their carriers.

Here, essential data—complex, and, at the time, highly novel, radar observations—were compressed to what in probability theory would be characterized as a set of measure zero. The result might well be described as a form of ‘hallucination’, the arbitrary assignment of meaning to some (or to the absence of) signal.

Half a year later, however, the US Navy’s institutional cognition had considerably progressed. Wirtz [10], in a prize-winning essay, writes

The story of how Naval intelligence paved the way for victory at Midway is embedded in the culture of the U.S. Navy, but the impact of this narrative extends far beyond the service. Today, scholars use the events leading up to Midway to define intelligence success—an example of a specific event prediction that was accurate, timely, and actionable, creating the basis for an effective counterambush of the Imperial Japanese Navy. Yet an important element of the Midway intelligence story has been overlooked over the years: Those who received intelligence estimates understood the analysis and warnings issued and acted effectively on them.

Wirtz [10] emphasizes, for this success, the tight bonding of the newly enhanced intelligence component, under Lieutenant Commander Edwin Layton, with the overall Pacific Command, under Admiral Chester W. Nimitz. This bonding represented, in a formal sense, an enhanced coupling channel capacity.

As Wirtz [10] put the matter, “...[O]nly nine days elapsed between Layton’s forecast of coming events and the detection of Japanese carriers northwest of Midway”.

This was barely sufficient time for Nimitz to assemble the needed countermeasures. The rest, as they say, is history.

In short, a sufficiently large channel capacity linking intelligence with command obviated both Pearl Harbor-style institutional hallucination and panic.

There is yet another longstanding ‘psychophysics’ context to such matters.

With regard to the dynamics of hallucination and panic in embodied cognitive agents, the Yerkes–Dodson effect—studied as early as 1905 [11,12,13]—states that, for a simple task, ‘performance’ varies as an S-shaped curve with increasing ‘arousal’, while for a difficult task, the pattern is an inverse-U (see Figure 1).

Here, we will show that it is possible to derive versions of Figure 1 from the Weber–Fechner, Stevens, Hick–Hyman, and Pieron laws (and analogous de facto sensory compression modes), using probability models based on the asymptotic limit theorems of information and control theories. These are interpreted through the lenses of first- and second-order models abducted from statistical physics and the Onsager approximation to nonequilibrium thermodynamics. While (at least to the author) surprisingly straightforward, this effort is not without subtlety.

With some further—and necessarily considerable—investment of resources, the probability models explored here can be developed into robust statistical tools for application to a broad spectrum of embodied cognitive phenomena at and across various scales and levels of organization. Such tools would be particularly useful in systems where it is necessary to condense incoming ‘sensory’ and/or ‘intelligence’ information in real time. Possible applications to embodied entities and processes range from the cellular through the neural, individual, machine, institutional, and their many possible composites.

As Wirtz [10] implies, those familiar with the planning or direction of organized conflict are sadly familiar with the general dynamics studied here.

We begin with some necessary methodological boilerplate.

2. Rate Distortion Control Theory

French et al. [14] modeled the Yerkes–Dodson effect using a neural network formalism, interpreting the underlying mechanism in terms of a necessary form of real-time data compression that eventually fails as task complexity increases. Data compression implies matters central to information theory, for which there is a formal context, i.e., the Rate Distortion Theorem [15].

Information theory has three classic asymptotic limit theorems [15,16]:

• The Shannon Coding Theorem. For a stationary transmission channel, a message recoded as ‘typical’ with respect to the probabilities of that channel can be transmitted without error at a rate C characteristic of the channel, i.e., its capacity. Vice versa, it is possible to argue for a tuning theorem variant in which a transmitting channel is tuned to be made typical with respect to the message being sent, so that, formally, the channel is ‘transmitted by the message’ at an appropriate dual-channel capacity.
• The Shannon–McMillan or Source Coding Theorem. Messages transmitted by an information source along a stationary channel can be divided into sets: a very small one congruent with a characteristic grammar and syntax, and a much larger one of vanishingly small probability not so congruent. For stationary (in time), ergodic sources, where long-time averages are cross-sectional averages, the splitting criterion dividing the two sets is given by the classic Shannon uncertainty. For nonergodic sources, which are likely to predominate in biological and ecological circumstances, matters require a ‘splitting criterion’ to be associated with each individual high-probability message [16].
• The Rate Distortion Theorem (RDT). This involves message transmission under conditions of noise for a given information channel. There will be, for that channel, assuming a particular scalar measure of average distortion, D, between what is sent and what is received, a minimum necessary channel capacity $R\left(D\right)$. The theorem asks what is the ‘best’ channel for transmission of a message with the least possible average distortion. $R\left(D\right)$ can be defined for nonergodic information sources via a limit argument based on the ergodic decomposition of a nonergodic source into a ‘sum’ of ergodic sources.

The RDT can be reconfigured in an inherently embodied control theory context, if we envision a system’s topological information from the DRT as ‘simply’ another form of noise, adding to the average distortion D (see Figure 2). The punctuation implied by the DRT [17] emerges from this model if there is a critical maximum average distortion that characterizes the system. Other systems may degrade more gracefully, or, as we show below, have even more complicated patterns of punctuation that, in effect, generalize the Data Rate Theorem.

We will expand perspectives on the dynamics of cognition/regulation dyads across rates of arousal, across the possibly manifold set of basic underlying probability distributions that characterize such dyads at different scales, levels of organization, and indeed, across various intrinsic patterns of arousal.

We again reiterate that inherent to Figure 2 is a fundamental ‘real-time’ embodiment directly instantiated by the Comparison and Control Channel feedback loop and the definition of the average distortion D.

3. Scalarizing Essential Resource Rates

The RDT holds that, under a given scalar measure of average distortion D between a sequence of signals that has been sent and the sequence that has actually been received in message transmission—measuring the difference between what was ordered and what was observed—there is a minimum necessary channel capacity $R\left(D\right)$ determined by the rate at which a set of essential resources, indexed by some scalar measure Z, can be provided to the system ‘sending the message’ in the presence of noise and an opposing rate of topological information characteristic of the inherent instability of the control system under study.

The Rate Distortion Function (RDF) $R\left(D\right)$ is necessarily convex in D, so that $d^{2}R/d{D}^2\ge 0$ [15]. For a nonergodic process in which the cross-sectional mean is not the same as the time-series mean, the RDF can still be defined as the average across the RDFs of the ergodic components of that process, and is thus convex in D.

The relations between the minimum necessary channel capacity $R\left(D\right)$ and the rates of any essential resources will usually be quite subtle.

A ‘simple’ scalar resource rate index—say Z—which we adopt as a first approximation, must be composed of a minimum of three interacting components:

• The rate at which subcomponents of the system of interest can communicate with each other, defined by a channel capacity $\mathcal{C}$.
• The rate at which ‘sensory’ information is available from the embedding environment, associated with a channel capacity $\mathcal{H}$.
• The rate $\mathcal{M}$ at which ‘metabolic’ or other free-energy ‘materiel’ resources can be provided to a subsystem of a full entity, organism, institution, machine, and so on.

These rates must be compounded into an appropriate scalar measure:

$$Z(\mathcal{C},\mathcal{H},\mathcal{M}).$$

Most simply, this might perhaps be taken as their product, the sum of their logs, or some other component.

Following [13], ‘Z’ will most likely be a 3 by 3 matrix, including necessary interaction crossterms. An n-dimensional matrix $\mathbf{Z}$ has n scalar invariants $r_i$ under appropriate transformations that are determined by the characteristic equation

$$\det [\mathbf{Z}-\gamma \mathbf{I}]=\sum _{i=1}^n{(-1)}^{i-1}{\gamma }^{i-1}{r}_i$$

(5)

$\mathbf{I}$ is the n-dimensional identity matrix, det is the determinant, and $\gamma$ is a real-valued parameter. $r_1$ is the matrix trace and $r_n$ the matrix determinant. Given these n scalar invariants, it will often be possible to construct $Z(r_1,0\dots ,r_n)$ as their scalar function, analogous to the principal component analysis of a correlation matrix.

Wallace [18] provides an example in which two such indices are minimally necessary, a matter requiring sophisticated Lie Group methods.

4. The Fundamental Model

Feynman [19] and Bennett [20] argue that information is a form of free energy, not an ‘entropy’, in spite of information theory’s Shannon uncertainty taking the same mathematical form as entropy for a simple—indeed, simplistic—ergodic system. Feynman [19] illustrates this equivalence using a simple ideal machine to convert information from a message into useful work.

We next apply something much like the standard formalism of statistical mechanics—given a proper definition of ‘temperature’—for a cognitive, as opposed to a ‘simply’ physical, system.

We consider the full ensemble of high-probability developmental trajectories available to the system, writing these as $Y_j,j=1,2,\dots$. Each trajectory is associated with a Rate Distortion Function-defined minimum-necessary-channel capacity $R_j$ for a particular maximum average scalar distortion $D_j$. Then, assuming some basic underlying probability model having the distribution $\rho (c,x)$, where c is a parameter set, we can define a pseudoprobability for a meaningful ‘message’ $Y_j$ sent into the system of Figure 2 as

$$dP={\displaystyle \frac{\rho (c,R/g(Z\left)\right)dR}{{\int }_0^{\infty }\rho (c,R/g\left(Z\right))dR}}={\displaystyle \frac{\rho (c,R_j/g\left(Z\right))dR}{g\left(Z\right)}}$$

(6)

since $\rho$ is a probability density that integrates to unit value.

Again, $Y_j$ is a particular trajectory, while the (possibly generalized) integral is over all possible ‘high probability’ paths available to the system.

We implicitly impose the Shannon–McMillan Source Coding Theorem so that the overall set of possible system trajectories can be divided in two distinct equivalence classes defining a ‘fundamental groupoid’ whose ‘symmetry-breaking’ imposes the essential two-fold structure. These are, first, a very large set of measure zero—vanishingly low probability—that is not consistent with the underlying grammar and syntax of some basic information source, and a much smaller consistent set [16].

Again, $R_j$ is the RDT channel capacity, keeping the average distortion less than a given limit $D_j$ for message $Y_j$. $g\left(Z\right)$ is a yet-to-be-determined temperature analog depending on the scalar resource rate Z. $\rho (c,x)$, for physical systems, is usually taken as the Boltzmann distribution: $\rho \left(x\right)=exp[-x]$. We suggest that, for cognitive phenomena—from the living and institutional to the machine and composite—it is necessary to move beyond analogs with physical system analogs. That is, it becomes necessary to explore the influence of a variety of different probability distributions, including those with ‘fat tails’ [21,22], on the dynamics of cognition/regulation stability.

The standard methodology from statistical physics [23] identifies the denominator of Equation (3) as a partition function. This allows for the definition of an iterated free-energy analog F as

$$\rho (c,F/g\left(Z\right))\equiv {\int }_0^{\infty }\rho (c,R/g\left(Z\right))dR=g\left(Z\right).$$

(7)

Once again, adapting a standard argument, now from chemical physics [24], we can define a cognition rate for the system as a reaction rate analog:

$$L\equiv {\displaystyle \frac{{\int }_{R_0}^{\infty }\rho (c,R/g\left(Z\right))dR}{{\int }_0^{\infty }\rho (c,R/g\left(Z\right))dR}}={\displaystyle \frac{1}{g\left(Z\right)}}{\int }_{R_0}^{\infty }\rho (c,R/g\left(Z\right))dR$$

(8)

where $R_0$ is the minimum channel capacity needed to keep the average distortion below a critical value $D_0$ for the full system of Figure 2.

The basic underlying probability model of Equation (6)—via Equation (8)—determines system dynamics, but not system structure, and cannot be associated with a particular underlying network form, although they are related [25,26]. More specifically, a set of distinctly different networks may all be mapped onto any single given dynamic behavior pattern; and, indeed, vice versa, the same static network may display a spectrum of behaviors [27]. We focus on dynamics rather than network topology.

Abducting a canonical first-order approximation from nonequilibrium thermodynamics [28], we can now define a ‘real’ entropy—as opposed to a ‘Shannon uncertainty’ that is basically Feynman’s [19] free energy—from the iterated free energy F by taking the standard Legendre Transform [23], so that

$$S\equiv -F+ZdF/dZ$$

(9)

The standard first-order Onsager approximation from nonequilibrium thermodynamics is then [28]

$$\partial Z/\partial t\approx dS/dZ=Zd{F}^2/d{Z}^2$$

(10)

where the scalar diffusion coefficient has been set equal to one.

For a second-order model,

$$\begin{array}{c}\hfill S_2=-F+ZdF/dZ+Z^2{d}^{2}F/d{Z}^2\\ \hfill \partial Z/\partial t=d{S}_2/dZ+Zd{S}_2^2/d{Z}^2=\\ \hfill 3Z{d}^{2}F/d{Z}^2+Z^2{d}^{3}F/d{Z}^3+\\ \hfill Z\left(3d^{2}F/d{Z}^2+5Z{d}^{3}F/d{Z}^3+Z^2{d}^{4}F/d{Z}^4\right)\end{array}$$

(11)

5. Two Probability Distributions

We consider rates of cognition for two different underlying probability models, according to their underlying ‘hazard rates’ $Q\left(x\right)$, defined as

$$Q\left(x\right)={\displaystyle \frac{\rho \left(x\right)}{1-{\int }_0^x\rho \left(u\right)du}}$$

(12)

We choose hazard rates $Q\left(x\right)=1,1/(1+x)$. The resulting integral equations lead to probability distributions $\rho \left(x\right)=exp[-x],1/{(1+x)}^2$. The first is simply the Boltzmann distribution and the second is ‘fat-tailed’, without finite mean or variance.

For the Boltzmann distribution, the ‘temperature’ and cognition rate relations from Equations (7) and (8) are

$$\begin{array}{c}\hfill g={\displaystyle \frac{-F}{W(n,-F)}}\\ \hfill L=exp[-R_0/g]\end{array}$$

(13)

where $W(n,x)$ is the Lambert W-function of order n that satisfies the relation

$$W(n,x)exp\left[W\right(n,x\left)\right]=x$$

It is real-valued only for $n=0,-1$ and $x>-exp[-1]$. This condition ensures the existence of Fisher zero phase transitions in the system [29,30,31].

For the $1/{(1+x)}^2$ distribution,

$$\begin{array}{c}\hfill g=-F+{\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sqrt{1-4F}}{2}}\\ \hfill L={\displaystyle \frac{g}{g+R_0}}\end{array}$$

(14)

Here, there is also a necessary condition for a real-valued temperature analog, leading again to the possibility of Fisher zero phase transition.

6. Weber–Fechner Implies Yerkes–Dodson

In addition to noise inherent to the RDT approach, suppose that there is a ‘noise’ representing the difficulty of the problem addressed, which is what Figure 1 identifies as ‘impairment of divided attention, working memory, decision-making and multitasking’. That ‘noise’ is incorporated via the second term in the stochastic differential equations

$$\begin{array}{c}\hfill d{Z}_t=(dS/dZ)dt+\sigma Z_{t}d{B}_t\\ \hfill d{Z}_t=\left(d{S}_2/dZ+Z{d}^2{S}_{2}d{Z}^2\right)dt+\sigma Z_{t}d{B}_t\end{array}$$

(15)

where $\sigma$ is the magnitude of the difficulty noise and $d{B}_t$ is ordinary Brownian noise.

We next replace the $(dZ/dt)dt$ terms with their full expressions in their respective free-energy constructs F, to first and second order.

It is here that the Weber–Fechner law forecloses possibilities. For Equation (1), we set $k=S_0=1,S=Z$ and assume that perception must be stabilized under the Ito Chain Rule [32,33]. That is, we require that $<dln\left(Z_t\right)>=0$ for both first- and second-order models.

Surprisingly, F, the first-, and $F_2$, the second-order expressions are ‘easily’ found to be

$$\begin{array}{c}\hfill F\left(Z\right)={\displaystyle \frac{1}{4}}{\sigma }^2{Z}^2+C_{1}Z+C_2\\ \hfill F_2=C_4+{\displaystyle \frac{1}{24}}{\sigma }^2{Z}^2+C_{1}Z+{\displaystyle \frac{C_3}{Z}}+C_{2}ln\left(Z\right)\end{array}$$

(16)

calculated, for example, using the elementary MAPLE computer algebra programs given by Cyganowski et al. [33] for the Ito Chain Rule of an SDE (see the mathematical appendix).

Both expressions have potentially dominant terms in ${\sigma }^2{Z}^2$ that ensure the punctuated emergence of imaginary-valued cognition rates via the algebraic forms of the temperature analogs $g\left(Z\right)$.

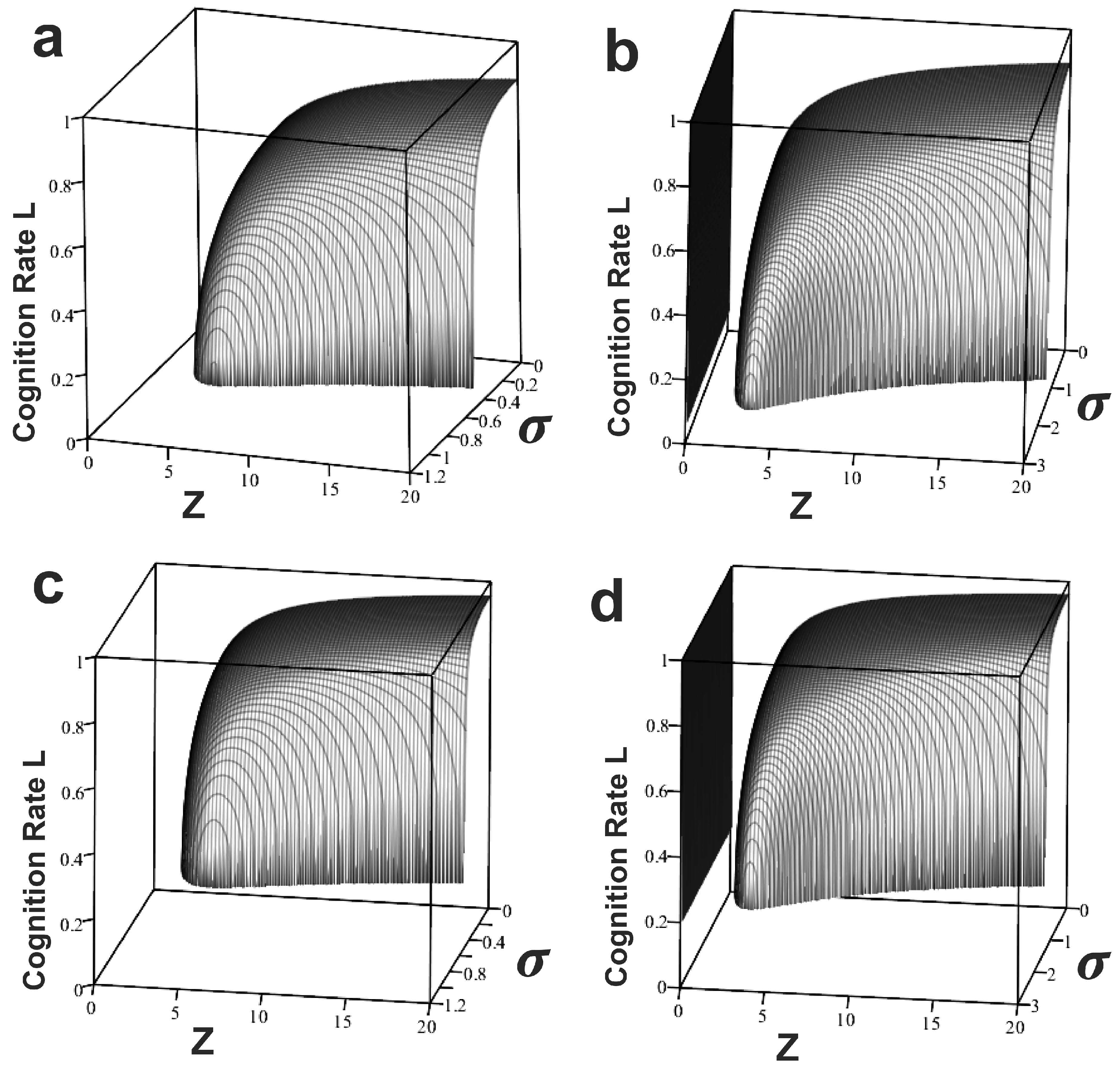
In what follows, for F, $C_1=-1,C_2=3$, and for $F_2$, $C_4=3,C_1=-1,C_2=C_3=1$. In the expressions for cognition rate L, we set $n=0,R_0=1$ and calculate cognition rates vs. $\{\sigma ,Z\}$ for both distributions and both orders of approximation. The results are shown in Figure 3. The top two are, respectively, from left to right, first and second order for the Boltzmann distribution. The bottom two, again left to right, first and second order, for the $1/{(1+x)}^2$ distribution.

Although there are detailed differences between orders and distribution form results—the Boltzmann with finite mean and variance, and the other fat-tailed and without—the general pattern is that increasing ‘noise’ $\sigma$ transforms the cognition rate from the simple task of Figure 1 into the inverse-U of the Yerkes–Dodson relation. Note that sufficient ‘noise’ $\sigma$ fully collapses all systems. A subsequent section explores this dynamic in deeper detail, focusing on the character of the assumed underlying probability distribution.

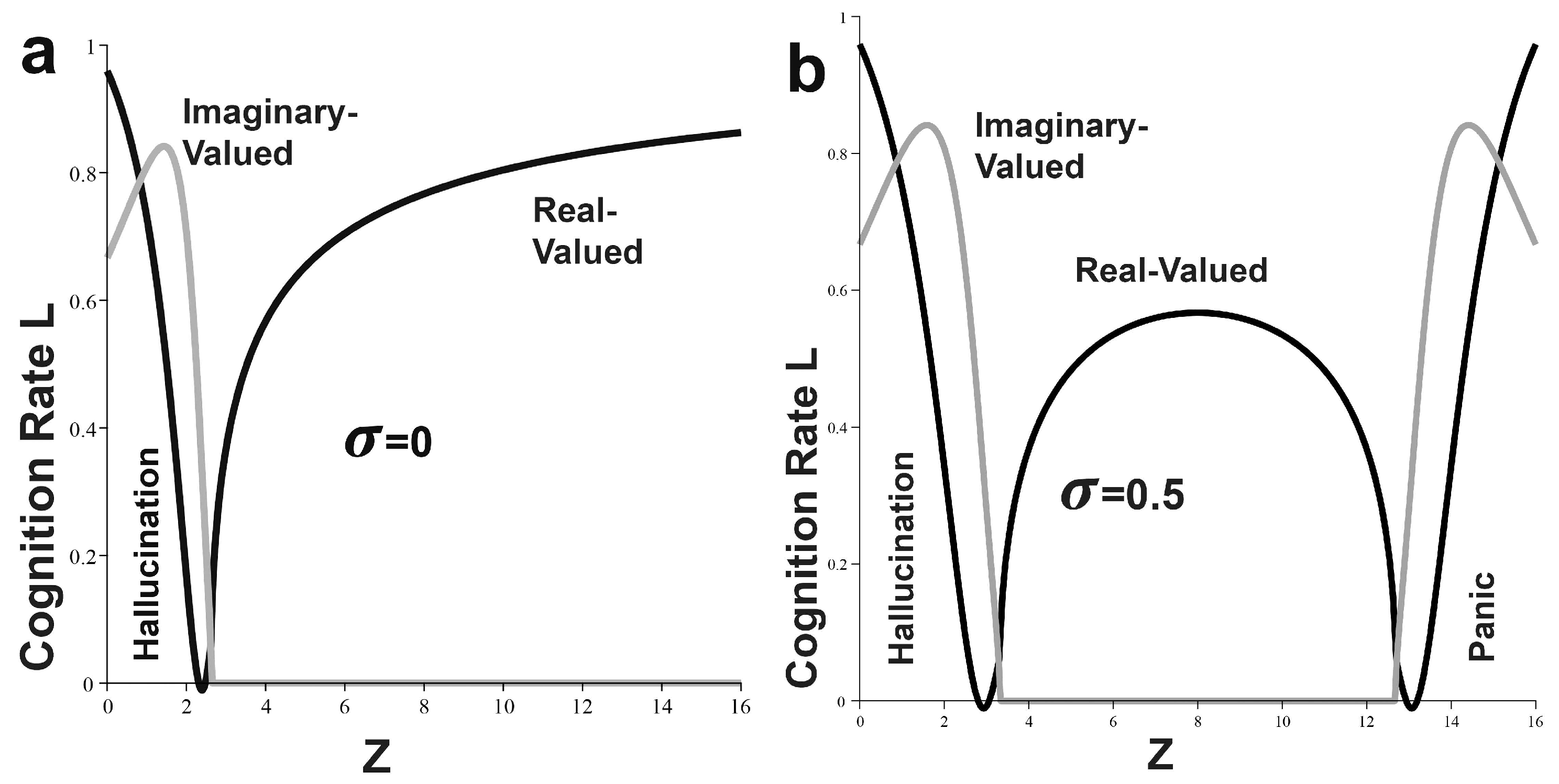
In more detail, Figure 4 takes two-dimensional cross-sections across Figure 3a, setting $\sigma =0,0.5$, letting Z vary as ‘arousal’, and dividing cognition rate into real- and imaginary-valued components. At low arousal, both systems suffer a nonzero imaginary-valued ‘hallucination’ mode. For $\sigma =0.5$, the intermediate zone, with a zero imaginary-valued component, follows the classic inverse-U of the Yerkes–Dodson effect, and imaginary-valued ‘panic’ emerges at high Z. The $\sigma =0$ system corresponds to the ‘easy’ problem of the Yerkes–Dodson.

7. Stevens Implies Yerkes–Dodson

If, instead of WF data compression according to $<dln\left(Z_t\right)>=0$, we impose a version of Stevens law compression [7,34,35] as $<d{Z}_t^{1/n}>=0,n>1$, then ‘elementary’ calculation based on the Ito Chain Rule finds

$$\begin{array}{c}\hfill F\left(Z\right)={\displaystyle \frac{\left({\sigma }^{2}n-{\sigma }^2\right)Z^2}{4n}}+C_{1}Z+C_2\\ \hfill F_2\left(Z\right)=-{\displaystyle \frac{C_1}{2Z}}-C_{2}ln\left(Z\right)+{\displaystyle \frac{Z^2{\sigma }^2}{24}}-{\displaystyle \frac{Z^2{\sigma }^2}{24n}}+C_{3}Z+C_4\end{array}$$

(17)

For large enough n, the results are similar to those following from Equation (16), producing, in Figure 5, for $n=3$, close analogs to Figure 3 and Figure 4, given appropriate boundary conditions. In particular, the condition for the term in Z is again taken as −1, and the constant boundary condition as 3, with the other two again set equal to one.

8. Hick–Hyman Implies Yerkes–Dodson

Recall that the Hick–Hyman law’s [8] assertion of an individual-level response time to a multimodal task challenge increases as the Shannon uncertainty across the modes of that challenge.

For what we perform here, defining $Z(\mathcal{C},\mathcal{H},\mathcal{M})$ in terms of appropriate information and ‘materiel’ streams, the rate of response will be determined as $\propto Z^{-1}$. In the formalism of this study, we must now examine the nonequilibrium steady-state condition $<d{Z}_t^{-1}>=0$, leading to

$$\begin{array}{c}\hfill F\left(Z\right)={\displaystyle \frac{1}{2}}{\sigma }^2{Z}^2+C_{1}Z+C_2\\ \hfill F_2\left(Z\right)={\displaystyle \frac{{\sigma }^2{Z}^2}{12}}-{\displaystyle \frac{C_1}{2Z}}-C_{2}ln\left(Z\right)+C_{3}Z+C_4\end{array}$$

(18)

These relations again produce analogs to Figure 3 and Figure 5 in first and second order across the Boltzmann and $1/{(1+x)}^2$ distributions.

9. Pieron Implies Yerkes–Dodson

The Pieron law [5] states that system response time will be proportional to the intensity I of the sensory input signal as $T_R\propto I^{-b},b>0$. Calculation finds, for first- and second-order Onsager approximations and letting $I=Z_t$, the following:

$$\begin{array}{c}\hfill F\left(Z\right)={\displaystyle \frac{{\sigma }^2\left(b+1\right)Z^2}{4}}+C_{1}Z+C_2\\ \hfill F_2\left(Z\right)=-{\displaystyle \frac{C_1}{2Z}}-C_{2}ln\left(Z\right)+{\displaystyle \frac{Z^2{\sigma }^{2}b}{24}}+{\displaystyle \frac{{\sigma }^2{Z}^2}{24}}+C_{3}Z+C_4\end{array}$$

(19)

Given the same boundary conditions as above, one again obtains, for Boltzmann and $1/{(1+x)}^2$ distributions, close analogs to Figure 3 and Figure 4.

10. Other Compression Schemes

Suppose that we are constructing a cognitive embodied machine, institution, or composite entity, and are able to choose a particular data compression scheme $V\left(Z\right)$ under some given environmental or other selection pressure, according to the first- and second-order ‘ordinary volatility’ schemes of Equation (15). Then, in the first and second orders, the Ito Chain Rule calculation gives

$$\begin{array}{c}\hfill F\left(Z\right)=\int \left(\int -{\displaystyle \frac{{\sigma }^{2}Z\left(\frac{d^2}{d{Z}^2}V\left(Z\right)\right)}{2\left(\frac{d}{dZ}V\left(Z\right)\right)}}dZ\right)dZ+C_{1}Z+C_2\\ \hfill F_2\left(Z\right)=\\ \hfill \int \left(\int {\displaystyle \frac{-\frac{\left(\int \frac{{\sigma }^2\left(\int \frac{Z^3\left(\frac{d^2}{d{Z}^2}V\left(Z\right)\right)}{\frac{d}{dZ}V\left(Z\right)}dZ\right)-2C_1}{Z^2}dZ\right)}{2}+C_2}{Z^2}}dZ\right)dZ+C_{3}Z+C_4\end{array}$$

(20)

For appropriate boundary conditions, in all cases, $\sigma =0$ collapses system dynamics to the ‘easy’ Y-D problem.

Details for $V\left(Z_t\right)=arctan\left(Z_t\right)$ are left as an exercise.

A mathematically sophisticated reader might derive general results across sufficiently draconian compression schemes using methods similar to those of Appleby et al. [36]. Indeed, Equations (16)–(20) can probably be used to bracket most reasonable approaches.

French et al. [14] were right: data compression provides a possible route to the Yerkes–Dodson effect.

11. The Ductile-Brittle Transition

Figure 3, Figure 4 and Figure 5, as constructed, display disconcerting patterns of instability at low and, under significant noise $\sigma$, at high levels of arousal Z. These patterns are, in a sense, ‘artifacts’ of the boundary conditions imposed in the definitions of the free-energy constructs F. Such ‘artifacts’ haunted materials science and engineering until the latter part of the 20th century when a broad range of substances, from glasses to ceramics and metals, were understood to undergo sharp temperature-dependent phase transitions from ductile to brittle under sudden stress.

Many readers will be familiar with the standard laboratory demonstration of freezing a normally ductile substance in liquid nitrogen, and then easily shattering it with a light blow. Cognitive systems subject to the Yerkes–Dodson effect, it seems, are likewise subject to kinds of brittleness that can, perhaps, be more formally characterized.

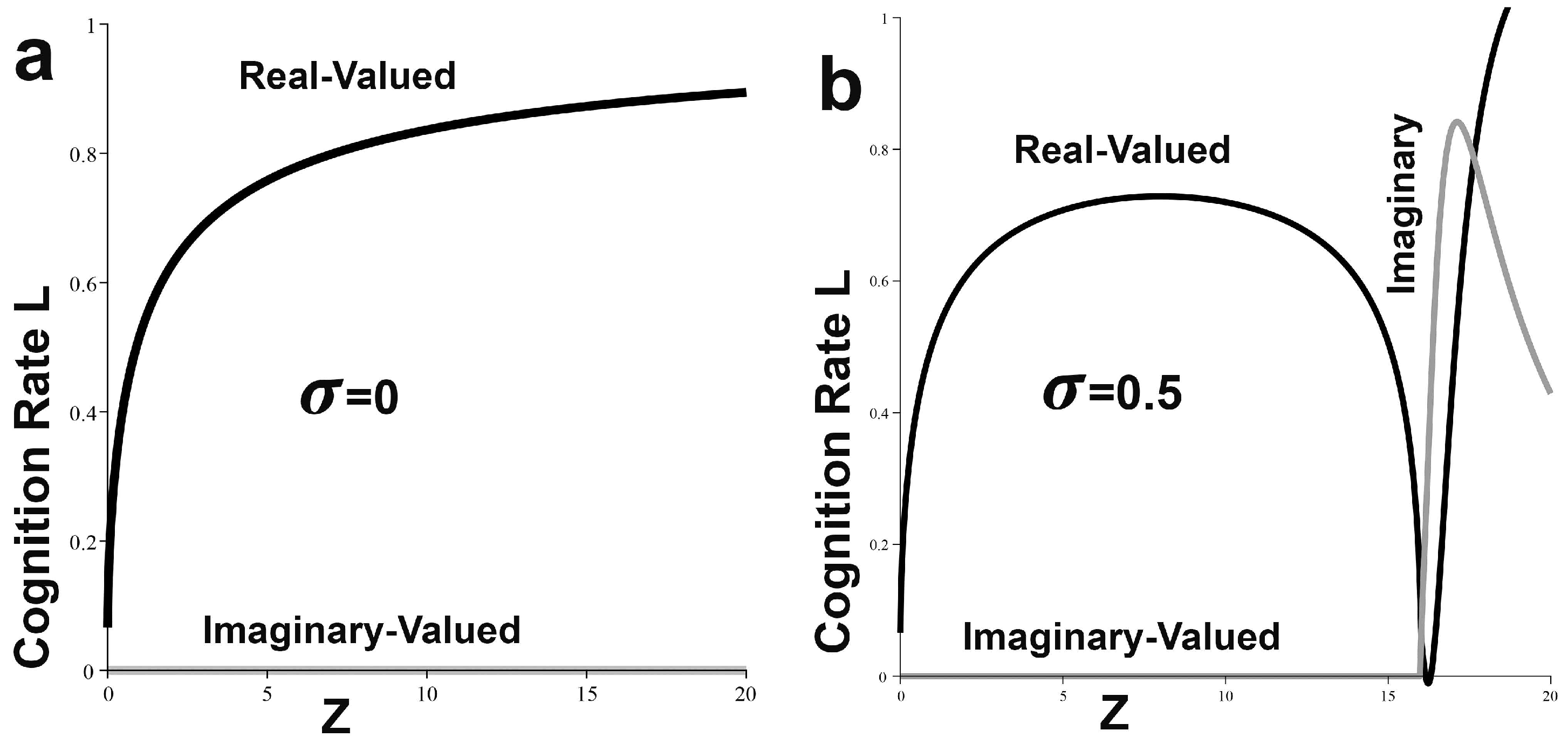
Recall the first expression of Equation (16) for F under the Weber–Fechner law, and Figure 4a,b, where $C_1=-1,C_2=3$ for $\sigma =0,0.5$, the ‘easy’ and ‘difficult’ modes of the Yerkes–Dodson effect. Figure 6 displays the analog to Figure 4, for which, again, $C_1=-1$, but now $C_2=exp[-1]$. Hallucination has disappeared.

Boundary conditions, it seems, together define another ‘temperature’, characterizing the onset of both ‘hallucination’ and ‘panic’ modes. Indeed, for Figure 4b, panic begins at $Z=12.678$, while in Figure 6b, in the absence of hallucination, panic onset is increased to $Z=16$.

The keys to the matter are found in Equation (16), expressing the form of F under the WF law, and the expressions for g and L in Equation (13) under the Boltzmann distribution. Both g and L depend on the Lambert W-function of orders 0 and $-1$. Recall that the natures of both g and L are determined by $W(0,-F)$, real-valued only for $-F>-exp[-1]$. Some elementary algebra, based on the first form of Equation (16), finds the Z-values determining the limits and onset of hallucination and panic given as

$$\begin{array}{c}\hfill Z_H=-{\displaystyle \frac{2\left(C_1+\sqrt{{\sigma }^2{\mathrm{e}}^{-1}-{\sigma }^2{C}_2+C_1^2}\right)}{{\sigma }^2}}\\ \hfill Z_P={\displaystyle \frac{-2C_1+2\sqrt{{\sigma }^2{\mathrm{e}}^{-1}-{\sigma }^2{C}_2+C_1^2}}{{\sigma }^2}}\end{array}$$

(21)

Further, solving the relation $Z_P-Z_H=0$ for ${\sigma }^2$ gives the maximum tolerable level of ‘noise’ as

$${\sigma }^2=-{\displaystyle \frac{C_1^2}{{\mathrm{e}}^{-1}-C_2}}$$

(22)

These relations can ‘easily’ be extended to various orders of F and to different underlying probability distributions, for example, the $1/{(1+x)}^2$ distribution leading to the expressions of Equation (14).

12. The Tyranny of Time

An extension of the formalism to a multiple-subsystem structure involves time as well as resource constraints. That is, not only are the individual components of the composite rate index Z constrained, but the time available for effective action is limited.

This can be addressed in first order as a classic Lagrangian optimization under environmental shadow price constraints abducted from economic theory [37,38]. Here, time and other resource limits are assumed to very strongly dominate system dynamics.

The aim is to maximize the total cognition rate across a full system of n subcomponents. Each has an associated cognition rate $L_j$ and is allotted resources at the rate $Z_j$ for time $T_j$.

A Lagrangian optimization can be conducted as

$$\begin{array}{c}\hfill \mathcal{L}\equiv \sum _i{L}_i+\lambda \left(Z-\sum _i{Z}_i\right)+\mu \left(T+\sum _i{T}_i\right)\\ \hfill \partial \mathcal{L}/\partial Z=\lambda ,\partial \mathcal{L}/\partial T=\mu \\ \hfill \partial L_i/\partial Z_i=\lambda ,\partial L_i/\partial T_i=\mu \end{array}$$

(23)

To reiterate, from economic theory, $\lambda$ and $\mu$ are shadow prices imposed by environmental externalities including fog, friction, and usually skilled adversarial intent.

After some heuristics,

$$\partial Z_i/\partial T_i={\displaystyle \frac{\mu }{\lambda }}\equiv \omega$$

(24)

Taking $g\left(Z_i\right)$ as the volatility function, the fundamental stochastic differential equation under draconian constraints of time and resource rates is

$$d{Z}_t^i=\omega dt+{\sigma }_i{g}_i\left(Z_t^i\right)d{B}_t$$

(25)

If the data compression function is $V\left(Z\right)=ln\left(Z\right),Z^{-1},Z^{1/n}$, and so on, then application of the Ito Chain Rule to determine the nonquilibrium steady-state condition $<dV\left(Z_t^i\right)>=0$ gives, by suppressing indices, the following:

$$\begin{array}{c}\hfill {\displaystyle \frac{2\omega }{{\sigma }^2}}=-{\displaystyle \frac{g{\left(Z\right)}^2\left(\frac{d^2}{d{Z}^2}V\left(Z\right)\right)}{\frac{d}{dZ}V\left(Z\right)}}\equiv Q\left(Z\right)\\ \hfill Z_i=Q_i^{-1}\left(2\omega /{\sigma }^2\right)\end{array}$$

(26)

Typically, $Q^{-1}\to 0$ as $\sigma$ increases or $\omega$ declines.

For the three forms of $V\left(Z\right)$, given just the above, under ordinary volatility, so that $g_i\left(Z_i\right)=Z_i$,

$$Z_i={\displaystyle \frac{2\omega }{{\sigma }^2}},{\displaystyle \frac{\omega }{{\sigma }^2}},{\displaystyle \frac{2\omega n}{{\sigma }^2(n-1)}}$$

(27)

Declining environmental shadow price ratio is thus synergistic with rising ‘noise’ to drive essential resource rates below critical values for important subcomponents across a variety of data compression schemes.

13. The Tyranny of Adaptation

Another necessary extension is, however, much less direct, even in first order.

Wirtz [10] presents the matter thusly:

Standard operating procedures that continue for years or even decades give opponents the time they need to devise innovative tactics, technologies, and stratagems that are hard to detect, analyze, and forecast. Small changes can delay opponents’ schemes, while larger changes can invalidate their plans altogether. Routine can be exploited. It is possible for planners and commanders to minimize the challenge facing intelligence by providing opponents with a new problem to plan against before they devise a way to solve the old one. And rest assured, they are working on finding ways to sidestep current force postures.

That is, while institutional cognition rates are most often perceived by combatatants/participants on tactical and operational levels and relatively short time frames, strategic enterprise takes place over Darwinian and Lamarckian evolutionary spatial, social, and time scales. Wallace ([39], Chs. 1 and 9) explores the dynamics of such an evolutionary process in terms of ‘punctuated equilibrium’ phase transitions analogous to the Fisher zero phase changes studied here. Extension and application of the cognitive dynamics models studied here to evolutionary time scales, however, remains to be conducted.

14. The Compression/Sensitivity Explosion

We have, thus far, explored systems for which the underlying fundamental distribution was characterized by either a fixed or declining hazard rate function—Equation (12)—under Weber–Fechner or Stevens data compression schemes, to first and second orders. It is conceivable, perhaps even to be expected, however, that some systems may need—or be driven—to increase the rate of signal detection with rising system burden, so that, from Equation (12), $Q\left(x\right)=x^m,m>0$. This diktat generates an extended version of the Rayleigh Distribution as

$$\begin{array}{c}\hfill \rho (m,x)=x^{m}exp[-{\displaystyle \frac{x^{m+1}}{m+1}}]\\ \hfill <x>={\left(1+m\right)}^{{\displaystyle \frac{1}{1+m}}}\Gamma \left({\displaystyle \frac{2+m}{1+m}}\right)\end{array}$$

(28)

Given a free-energy measure F, calculation finds the temperature analog and cognition rate as

$$\begin{array}{c}\hfill g\left(m,F\right)=-{\displaystyle \frac{F{\left(1+m\right)}^{-\frac{1}{1+m}}{\left(-\frac{1}{W\left(-\frac{F}{1+m}\right)}\right)}^{-\frac{m}{1+m}}}{W\left(-\frac{F}{1+m}\right)}}\\ \hfill L(m,g)={\mathrm{e}}^{-{\displaystyle \frac{g^{-1-m}}{1+m}}}\end{array}$$

(29)

where, again, W is the Lambert W-function and we have again set the ‘trigger level’ as $H_0=1$.

Recall, by contrast, the expressions for the Boltzmann distribution:

$$g=-F/W(-F),L=exp[-1/g].$$

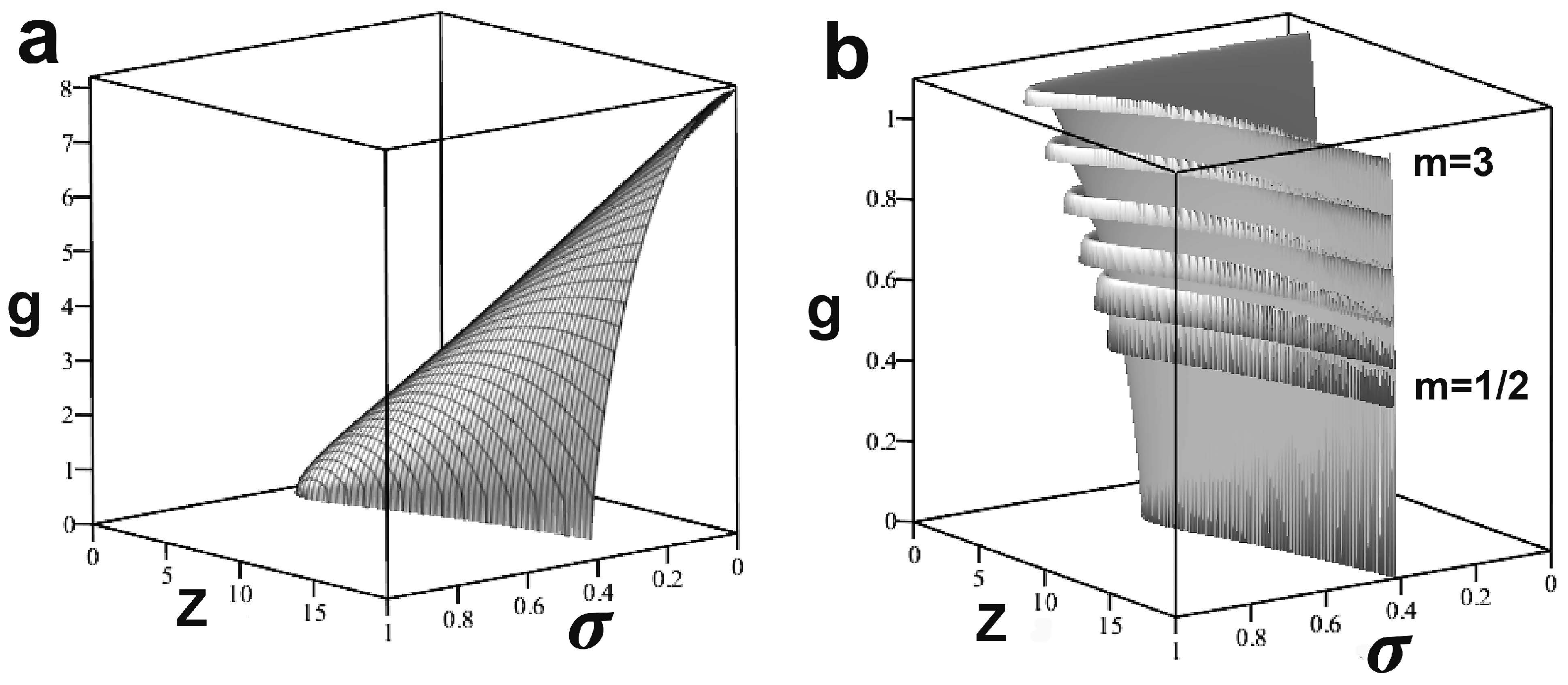
We define F by again imposing Weber–Fechner compression, i.e., stability as $<dln\left(x\right)>=0$, according the first-order relation of Equation (16). Figure 7a shows, for comparison, the Boltzmann distribution form of $g(\sigma ,Z)$, subsequently filtered through the relation $L=exp[-1/g]$ to produce the cognition rate model of Figure 3a. Figure 7b shows $g(m,\sigma ,Z)$ from Equation (29), taking $m=1/2\to 3$ by increments of $1/2$. These results are then fed through the second expression of Equation (29) to give highly complex and counterintuitive variants of Figure 3 and Figure 4 that are left as an exercise.

Requiring, or imposing, rising signal detection rates with increasing signal strength, under conditions of signal compression and ‘noise’, can produce incomprehensively complicated cognitive dynamics.

Somewhat heuristically, in signal detection systems, sensitivity is often represented by a threshold value chosen above the mean noise level. As sensitivity increases, the system becomes more responsive to smaller changes in signal strength. This can be visualized as lowering the threshold for detection, allowing weaker signals to be recognized. Combining increasing sensitivity with data compression schemes like the Weber–Fechner law creates a system that is highly responsive to small changes in input while also compressing the range of those inputs. This combination can lead to instabilities for several reasons:

• Amplification of Noise: As sensitivity increases, the system becomes more susceptible to detecting noise as signals, potentially leading to false positives.
• Compression of Dynamic Range: The Weber–Fechner law—like similar schemes—compresses the perceived intensity of stimuli, which can make it difficult for the system to distinguish between important signals and background noise at higher intensities.
• Feedback Loops: In complex systems with multiple interconnected modules, increased sensitivity can create feedback loops that amplify small fluctuations, potentially leading to system-wide instabilities that extend far beyond those illustrated in Figure 7.

15. Discussion

One art of science is the ability to infer the general from the particular. The probability models of inherently embodied cognitive systems studied here suggest that, in a surprisingly general manner, compression of sensory/intelligence and necessary internal data streams can drive some form of the Yerkes–Dodson effect’s contrast between ‘easy’ and ‘difficult’ tasks.

This occurs through such mechanisms as the increasing impairment of divided attention, limits on working memory, difficulties in decision-making, and the burdens of multitasking [11,12]. Further, the inverse-U patterns of difficult problems appear routinely bracketed by hallucination at low, and panic at high, arousal, depending critically on the interaction between ‘boundary conditions’ and the basic underlying probability distribution or distributions. A ‘ductile’, as opposed to a ‘brittle’ system, from these perspectives, emerges when boundary conditions have been adjusted to eliminate the hallucination mode. For noisy systems also burdened by the topological information stream of an embedding—and often adversarial—Clausewitzian ‘roadway’, however, panic remains a risk at sufficient arousal.

These general patterns were found across a variety of modeling modes, including different basic underlying probability distributions and two orders of approximation in an Onsager nonequilibrium approach.

Another important art of science, however, is recognizing the severe limitations of mathematical modeling in the study of complex real-world phenomena. As Pielou [40] argues in the context of theoretical ecology, the principal utility of mathematical models is speculation, the raising of questions to be answered by the analysis of observational and experimental data, the only sources of new knowledge.

This being said, similar arguments have often been made regarding the dynamics of organized conflict on Clausewitz landscapes of fog, friction, and deadly adversarial intent (e.g., Refs. [18,39,41,42] and the many classic and classical references therein). One underlying mechanism, then, seems related to sufficient—and usually badly needed—compression scaling of sensory/intelligence information data rates, enabling Maskirovka, spoofing, and related deceptions. Internal data streams are, likewise, often compressed, leading to the synergisms explored in Figure 3, Figure 4 and Figure 5, and suggesting the possibility of some mitigation in Figure 6 and Equations (21) and (22).

The Fisher zero phase transitions implied by Equations (13) and (14), and related distribution models, suggest, however, that inverse-U signal transduction and patterns of hallucination or panic will not be constrained to circumstances of data compression. We have explored only one tree in a very large forest.

In addition—and perhaps centrally—new probability models of poorly understood complex phenomena, if solidly based on appropriate asymptotic limit theorems, can serve as the foundation for building new and robust statistical tools useful in the analysis and modest control of those phenomena.

The development, testing, and validation of such statistical tools, however, is not a project for the timid.

16. Mathematical Appendix: Stochastic Differential Equations

We first recall Einstein’s 1905 [43] analysis of Brownian motion for a large number of particles N:

$$\begin{array}{c}\hfill \partial \rho (x,t)/\partial t=\mu {\partial }^2\rho (x,t)/\partial x^2\\ \hfill \rho (x,t)={\displaystyle \frac{N}{\sqrt{4\pi \mu t}}}exp[-{\displaystyle \frac{x^2}{4\mu t}}]\\ \hfill <x^2>\propto t\end{array}$$

(30)

where t is the time, x is a location variate, and $\mu$ is a ‘diffusion coefficient’.

The last relation represents the average value of x for a particle across the jittering system.

More generally, as a consequence of this insight, it is possible to write, for a Brownian ‘stochastic differential’ $d{B}_t$ that might be seen as perturbing some base function, the fundamental relation

$$<d{B}_t^2>=dt$$

(31)

and on this result hangs a considerable tale.

We follow something of Cyganowski et al. ([33], Section 8.4), who provide related programs in the computer algebra program MAPLE.

We are given a base ‘ordinary’ differential equation $dX/dt=f(t,X(t\left)\right)$ perturbed by a Brownian stochastic variate $d{B}_t$ that follows Equation (31). The ‘perturbed’ solution $X_t$ solves the stochastic differential equation (SDE)

$$d{X}_t=f(t,X_t)dt+g(t,X_t)d{B}_t$$

(32)

We are then given a function Y that depends on both t and $X_t$. Some calculation—based on Equation (31)—finds that $Y(t,X_t)$ solves the SDE

$$d{Y}_t=L^0{Y}_{t}dt+L^1{Y}_{t}d{B}_t$$

(33)

where $L^0$ and $L^1$ are the operators

$$\begin{array}{c}\hfill L^{0}Y=\partial Y/\partial t+f\partial Y/\partial x+{\displaystyle \frac{1}{2}}{g}^2\partial Y^2/\partial x^2\\ \hfill L^{1}Y=g\partial Y/\partial x\end{array}$$

(34)

This is the famous Ito Chain Rule.

To prove this, as Cyganowski et al. ([33], Section 8.4) show, one expands

$$\Delta Y_t=Y(t+\Delta t,X_t+\Delta X_t)-Y(t,X_t)$$

to second order, using $\Delta X_t=f\Delta t+g\Delta B_t+\dots$. Some tedious algebra produces a second-oder term in $B_t$

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}{g}^2{\partial }^{2}Y/\partial x^2{(\Delta B_t)}^2\to \\ \hfill {\displaystyle \frac{1}{2}}{g}^2{\partial }^{2}Y/\partial x^{2}dt\end{array}$$

(35)

by Equation (31) that is then brought into the ‘$dt$’ part of the expression. This is one source of the inherent strangeness of stochastic differential equations.

We are concerned with ‘nonequilibrium steady states’ averaged across the stochastic jitter and represented as

$$<d{Y}_t>=L^{0}Y=0$$

(36)

A simple MAPLE computer algebra program for the Ito Chain Rule is given in Cyganowski et al. ([33], p. 238), adapted here as

L0 := proc(X,a,b) local Lzero, U;

Lzero := diff(U(x,t),t)+a*diff(U(x,t),t,x)+

1/2 * b*b * diff(U(x,t), x, x);

eval(subs(U(x,t)=X,Lzero));

end:

where X is the expression of Y in Equation (31) in terms of x. a is $f(t,X_t)$ and b is $g(t,X_t)$ in Equation (31), likewise expressed in terms of the base-variable x.