Hybrid Nanofluid Flow and Heat Transfer in Inclined Porous Cylinders: A Coupled ANN and Numerical Investigation of MHD and Radiation Effects
Abstract
1. Introduction
2. Novelty
3. Research Gap
- Experimental validation and AI-based modeling of hybrid nanofluids, especially and systems, are still limited.
- Few studies integrate MHD, radiation, porous media, and activation energy effects within a single framework.
- The activation energy term has rarely been justified or applied to non-reactive fluids like kerosene.
- Existing AI approaches focus mainly on ANN models without benchmarking against other surrogates such as Gaussian Processes or Physics-Informed Neural Networks (PINNs).
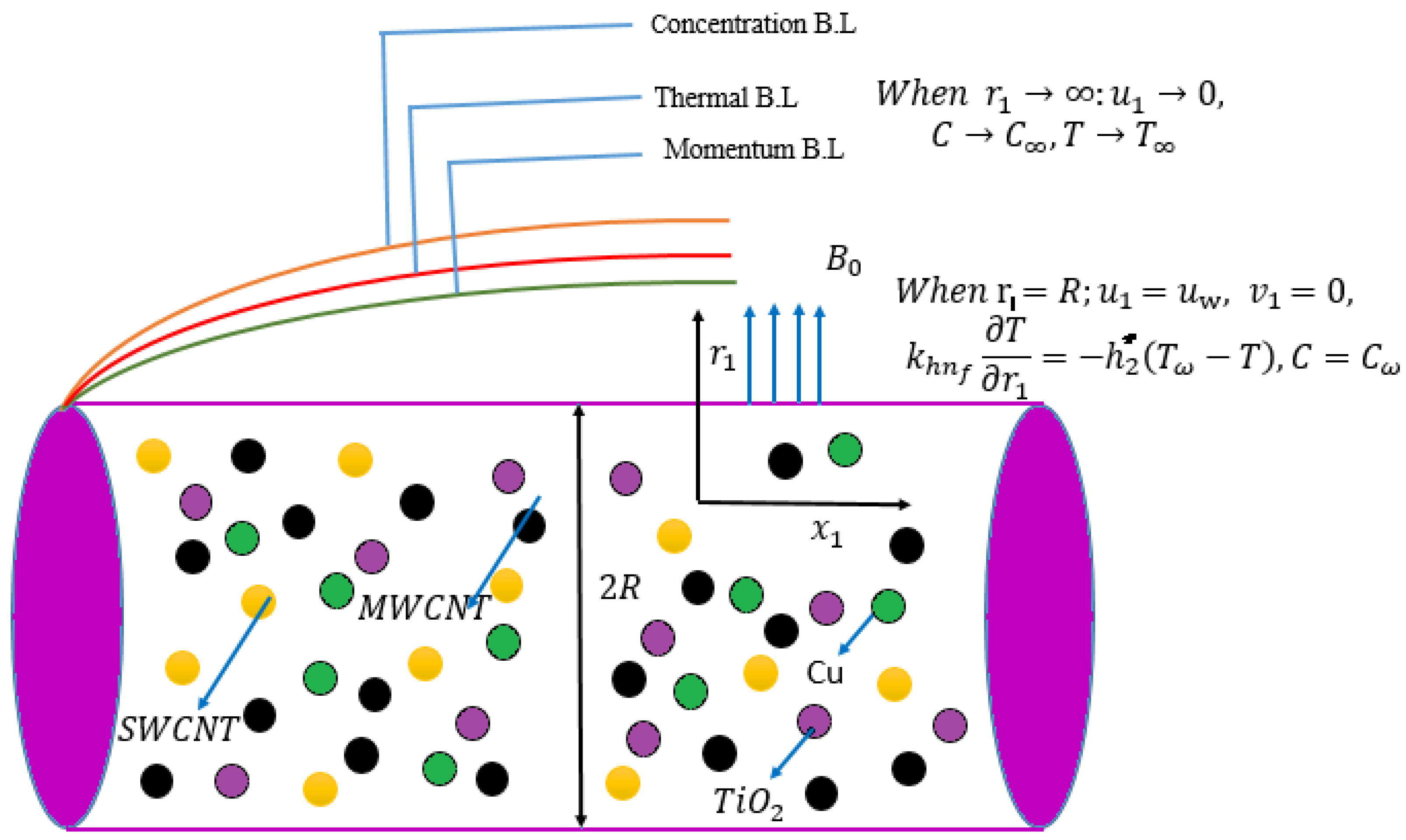
4. Mathematical Formulation
5. Physical Quantities
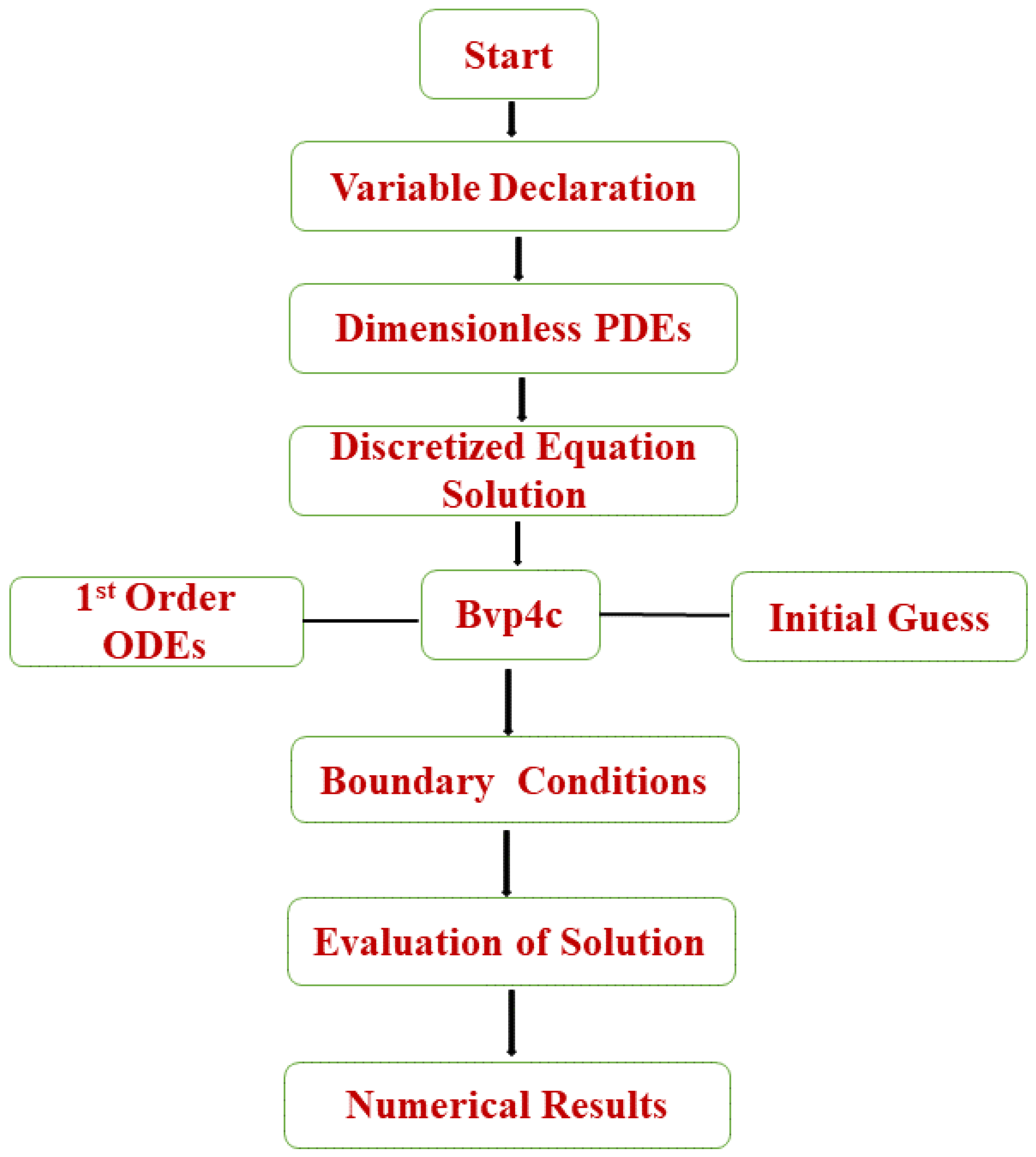
6. Numerical Solution
Dimensionless Parameters
7. Results and Discussion
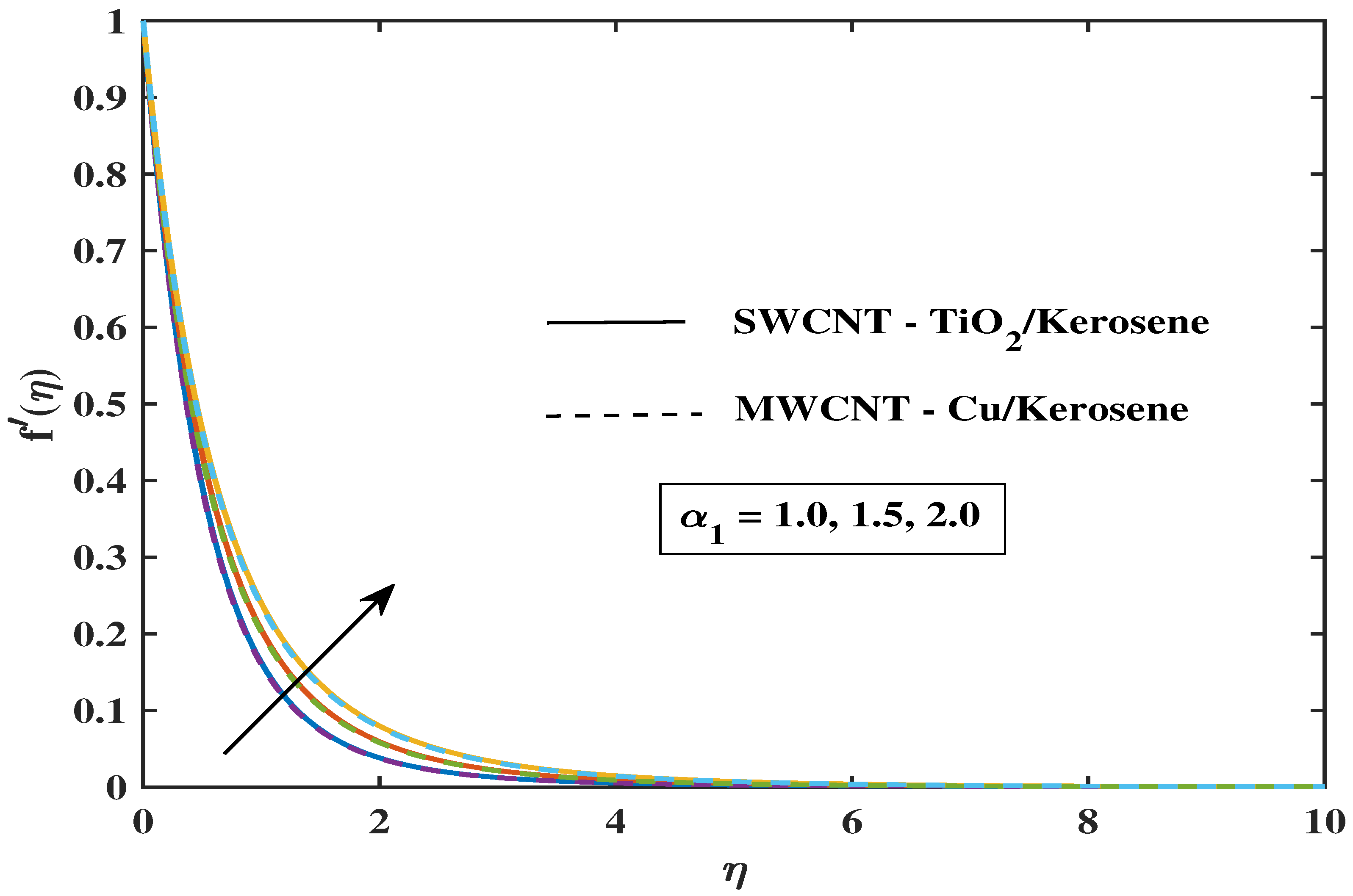
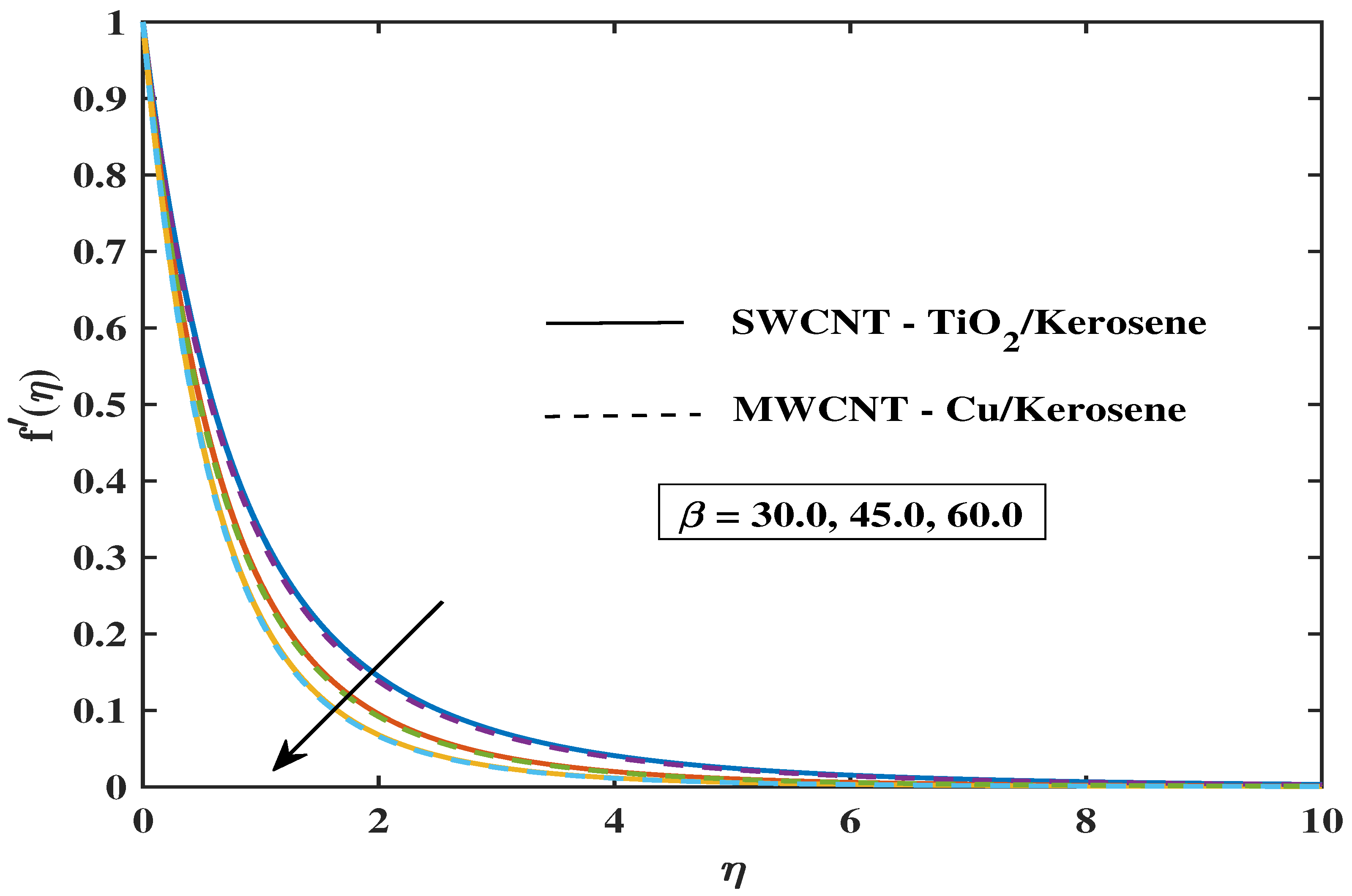
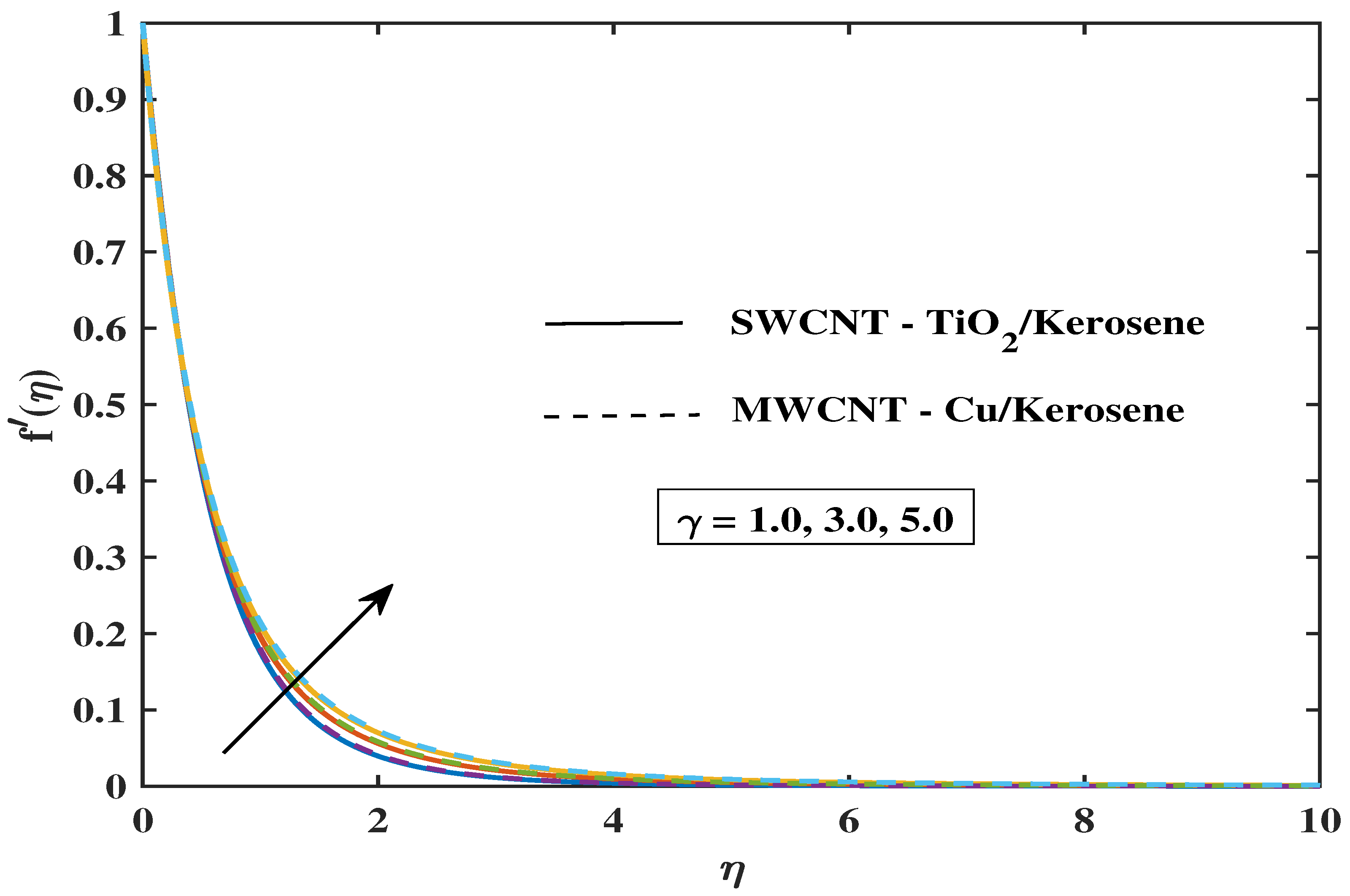
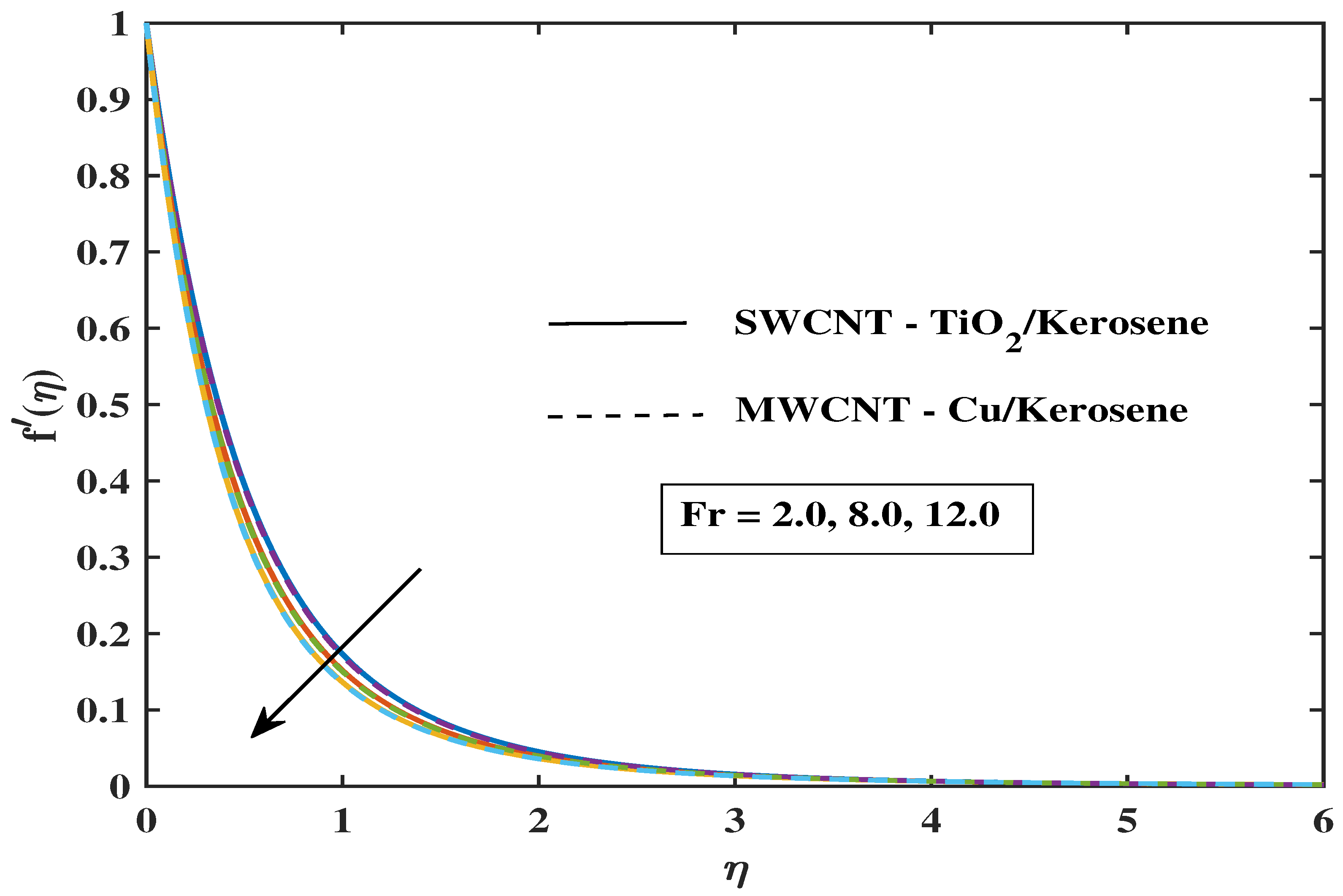
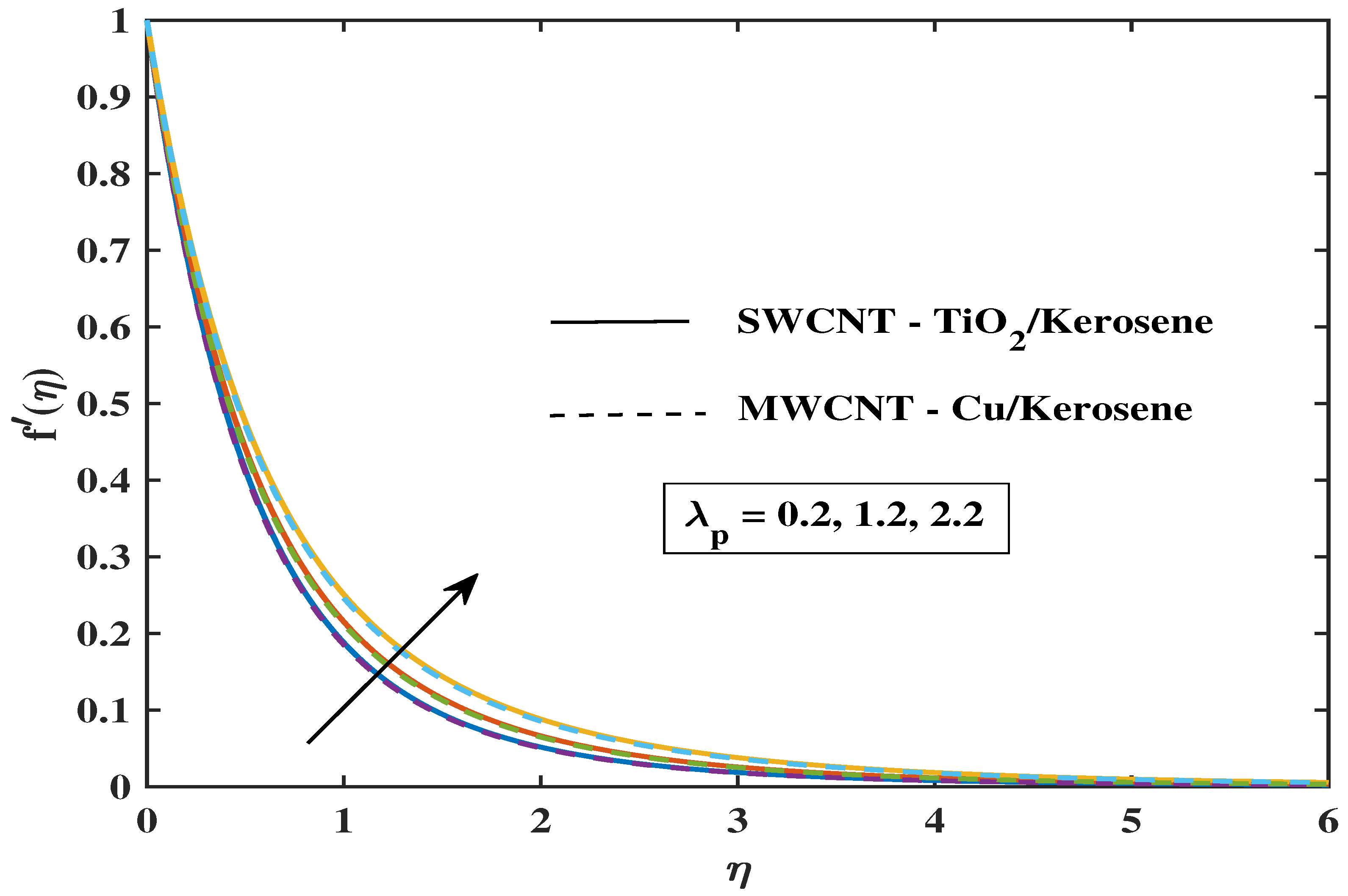
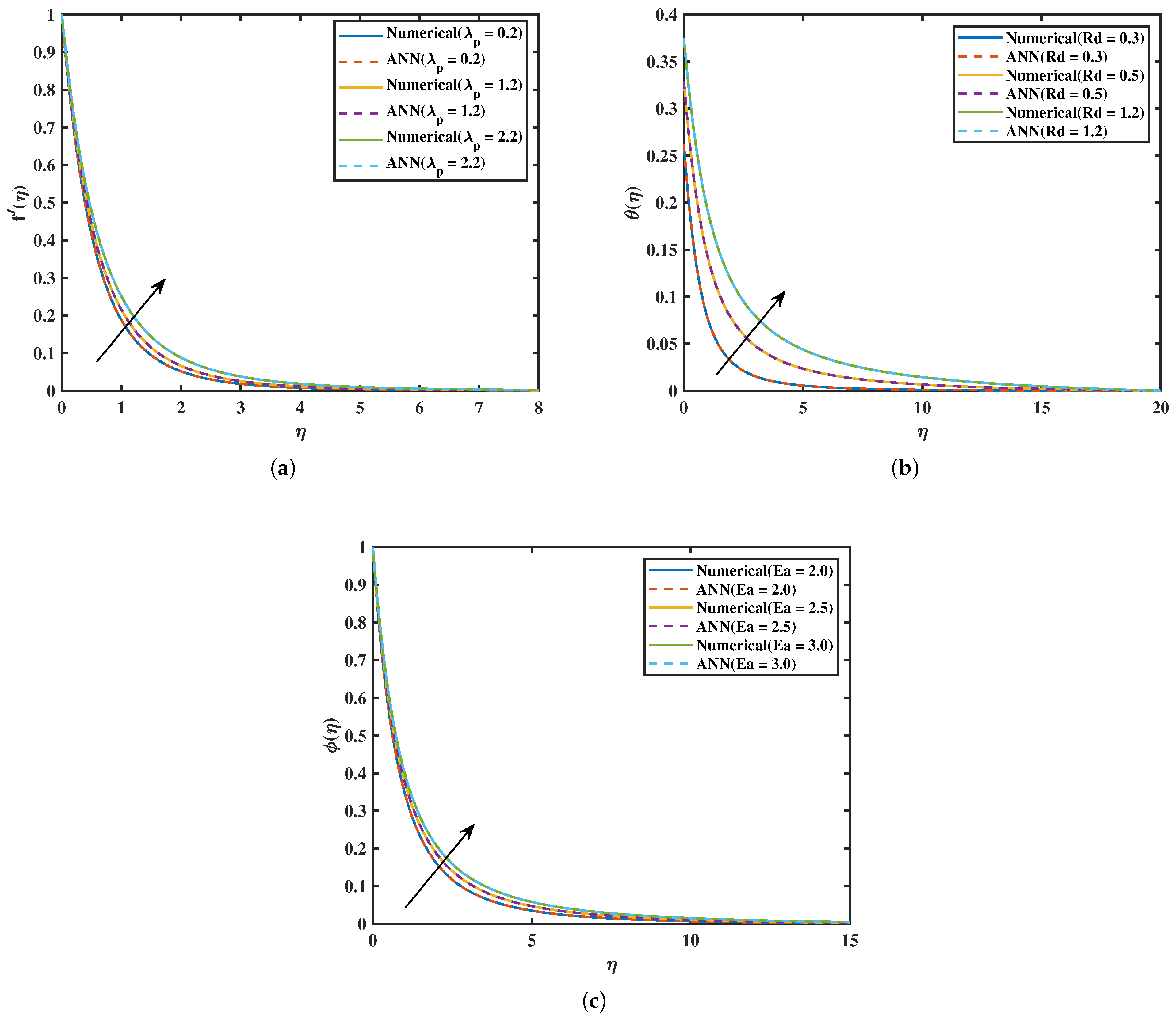
7.1. Velocity Profile
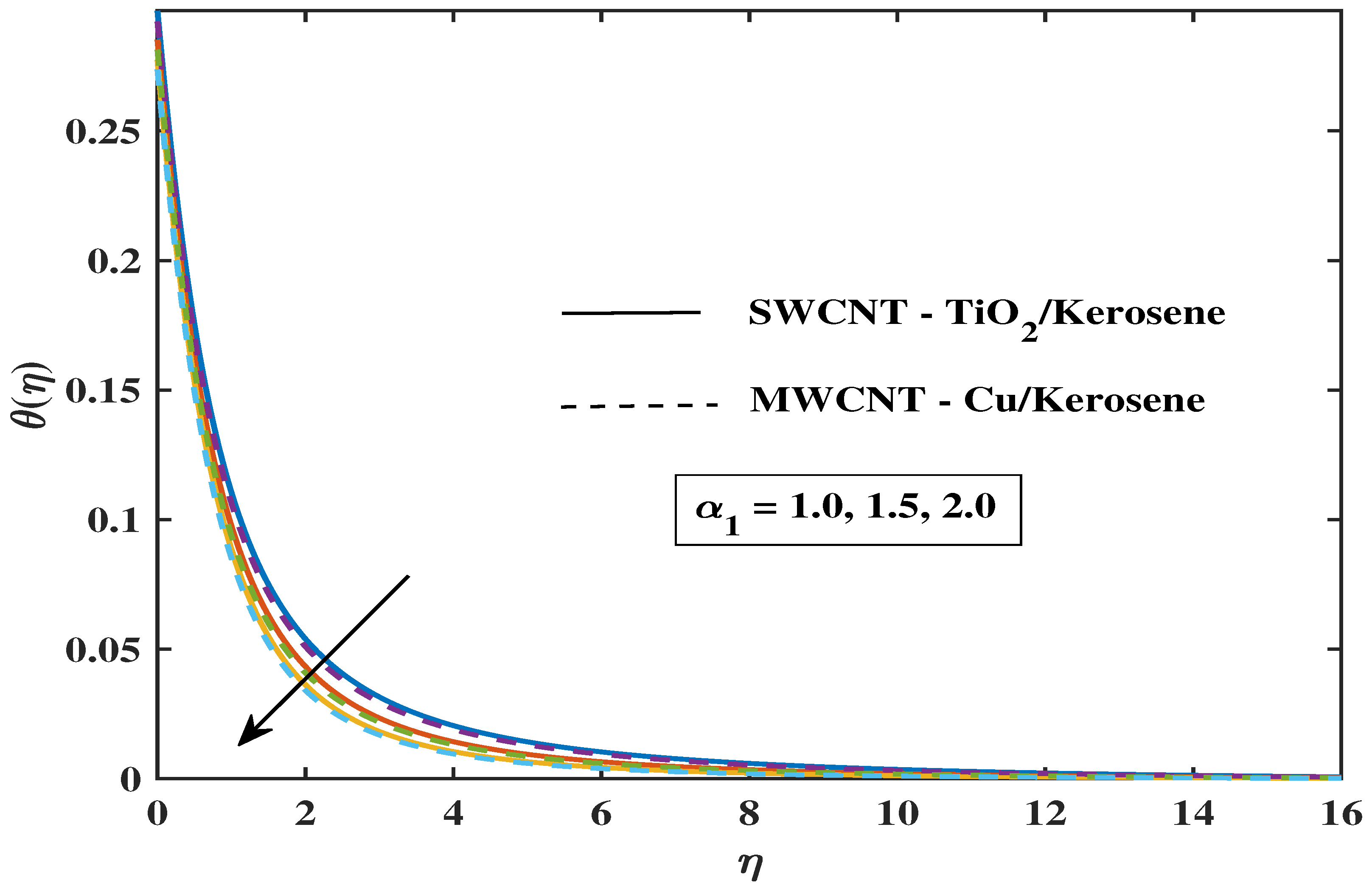
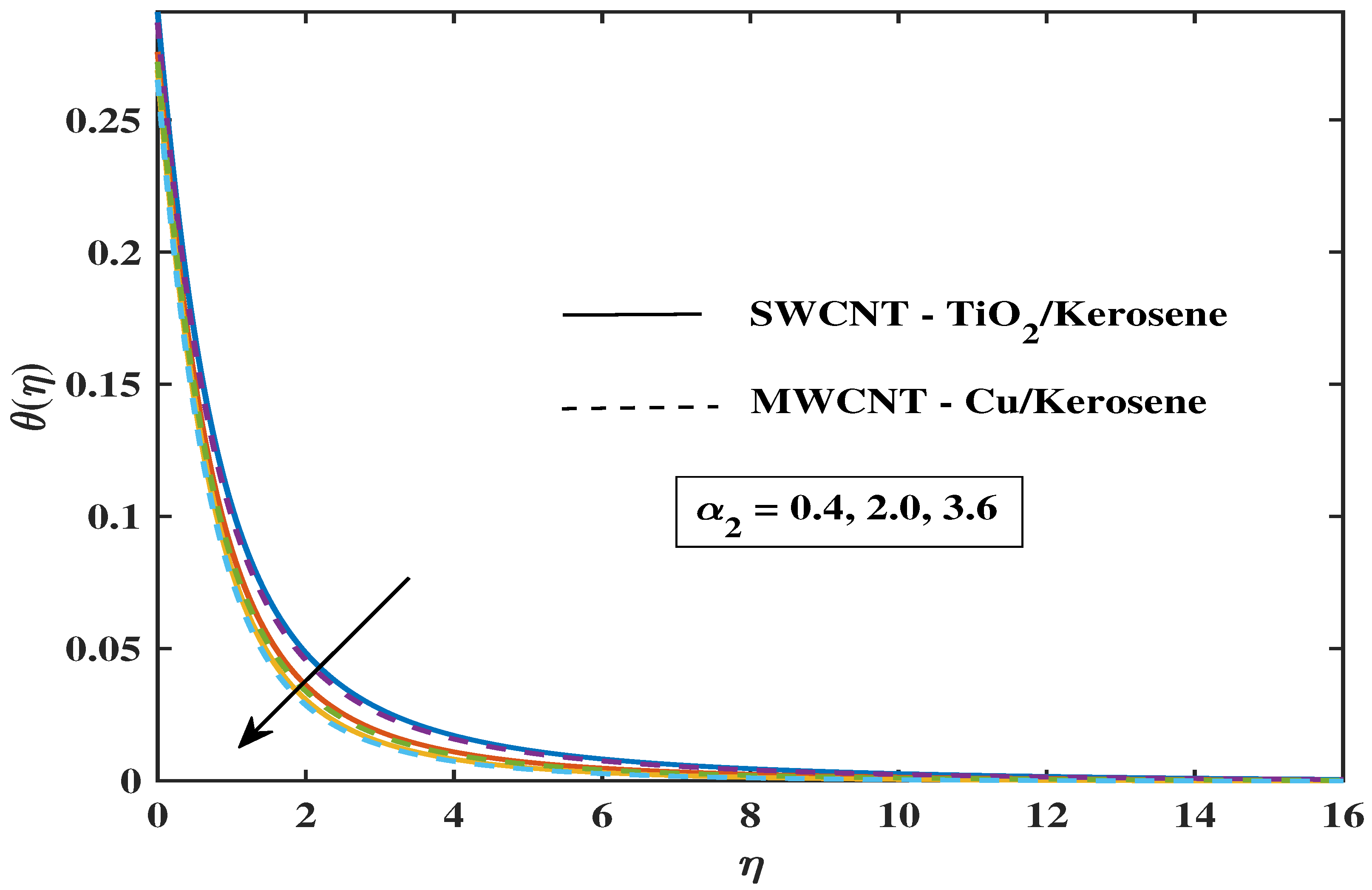
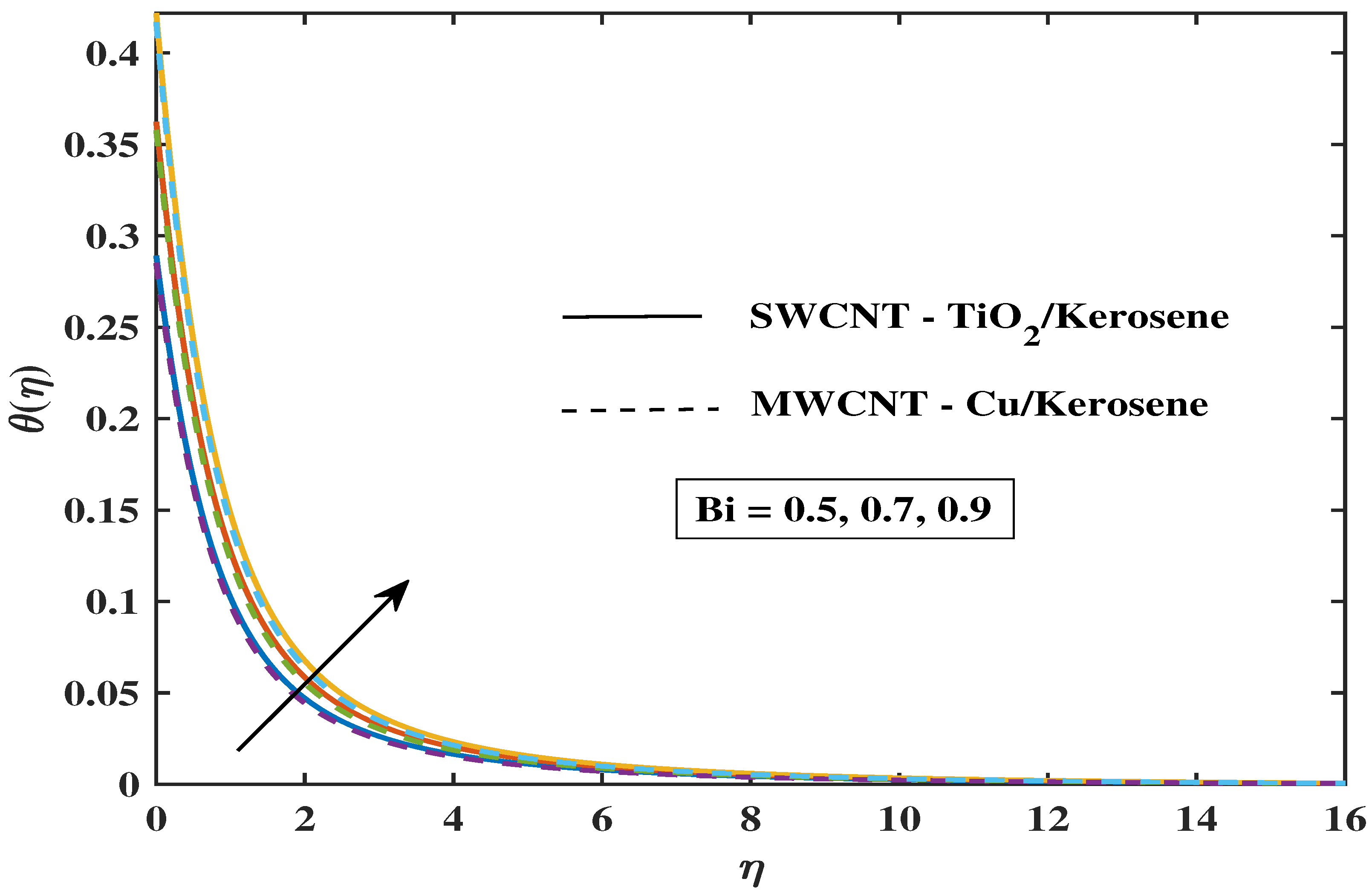
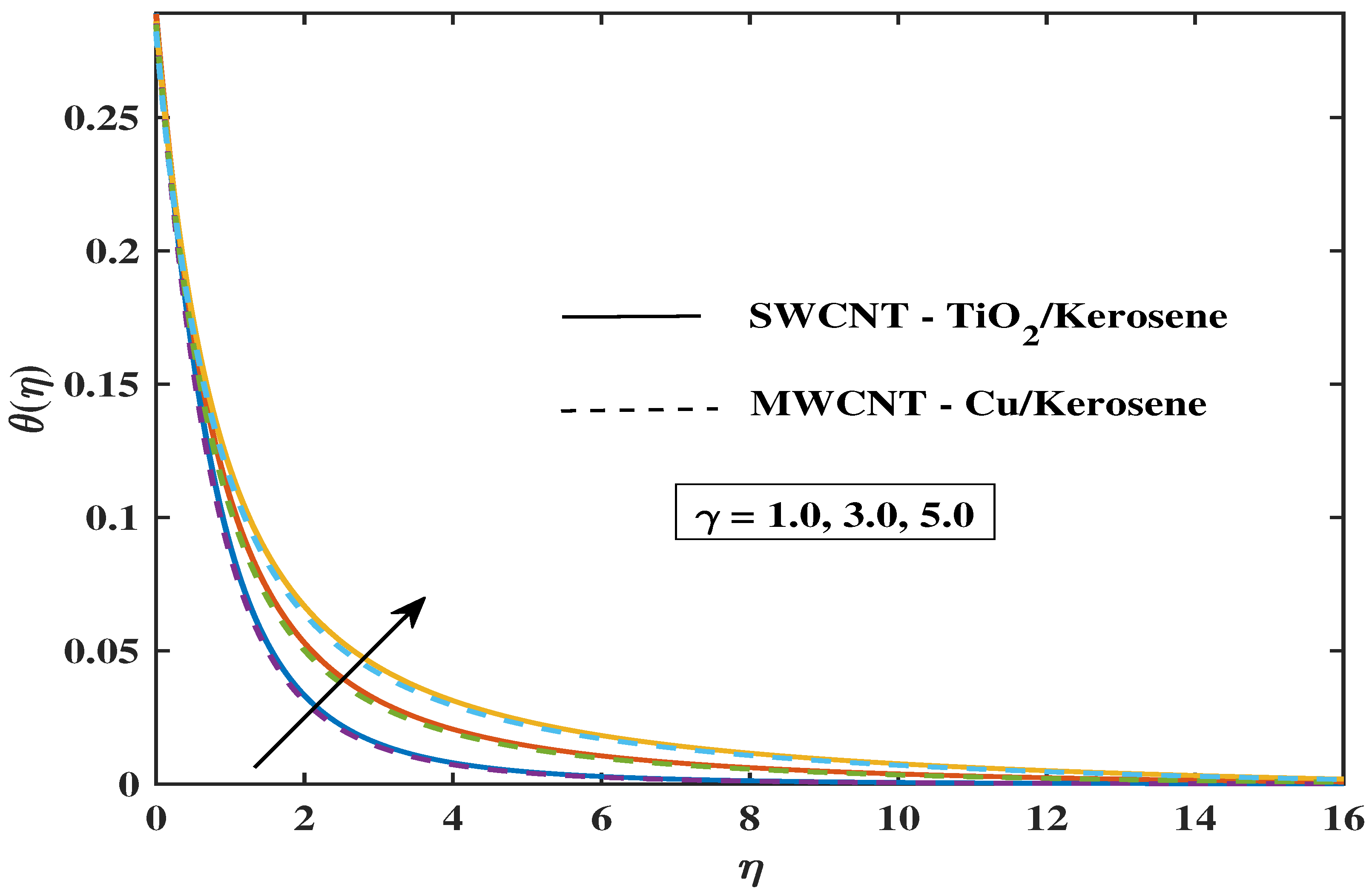
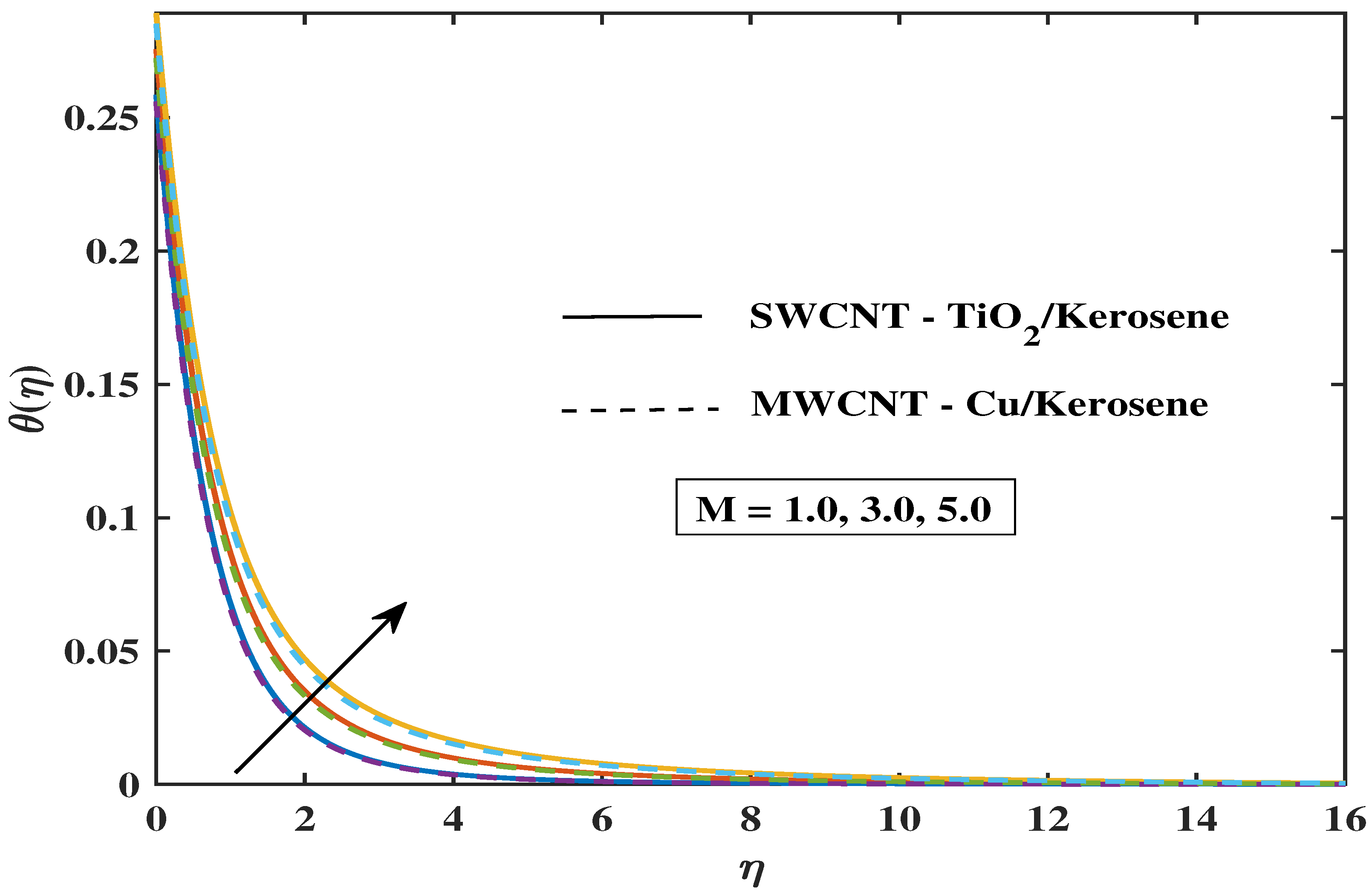
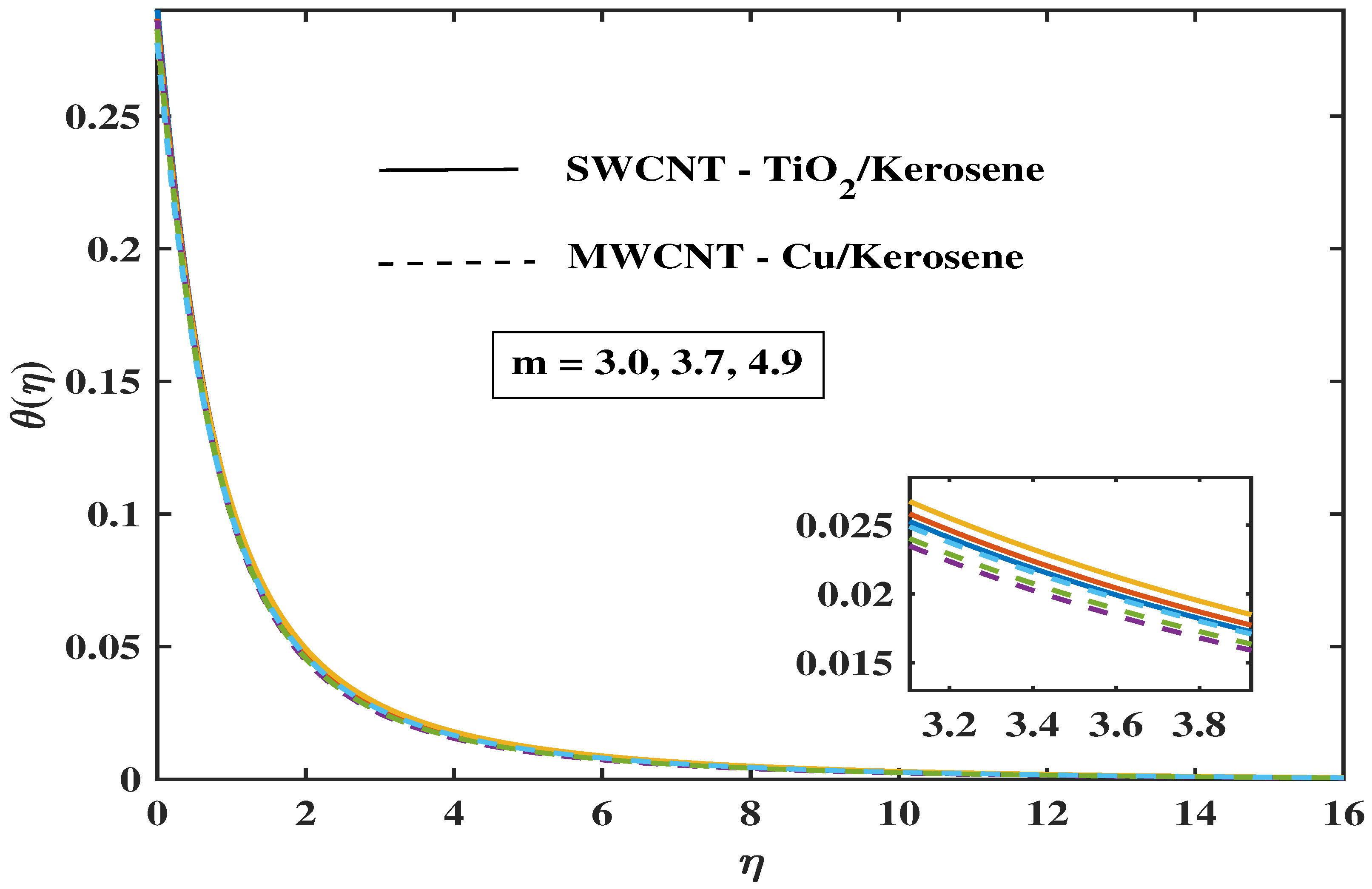
7.2. Temperature Profile
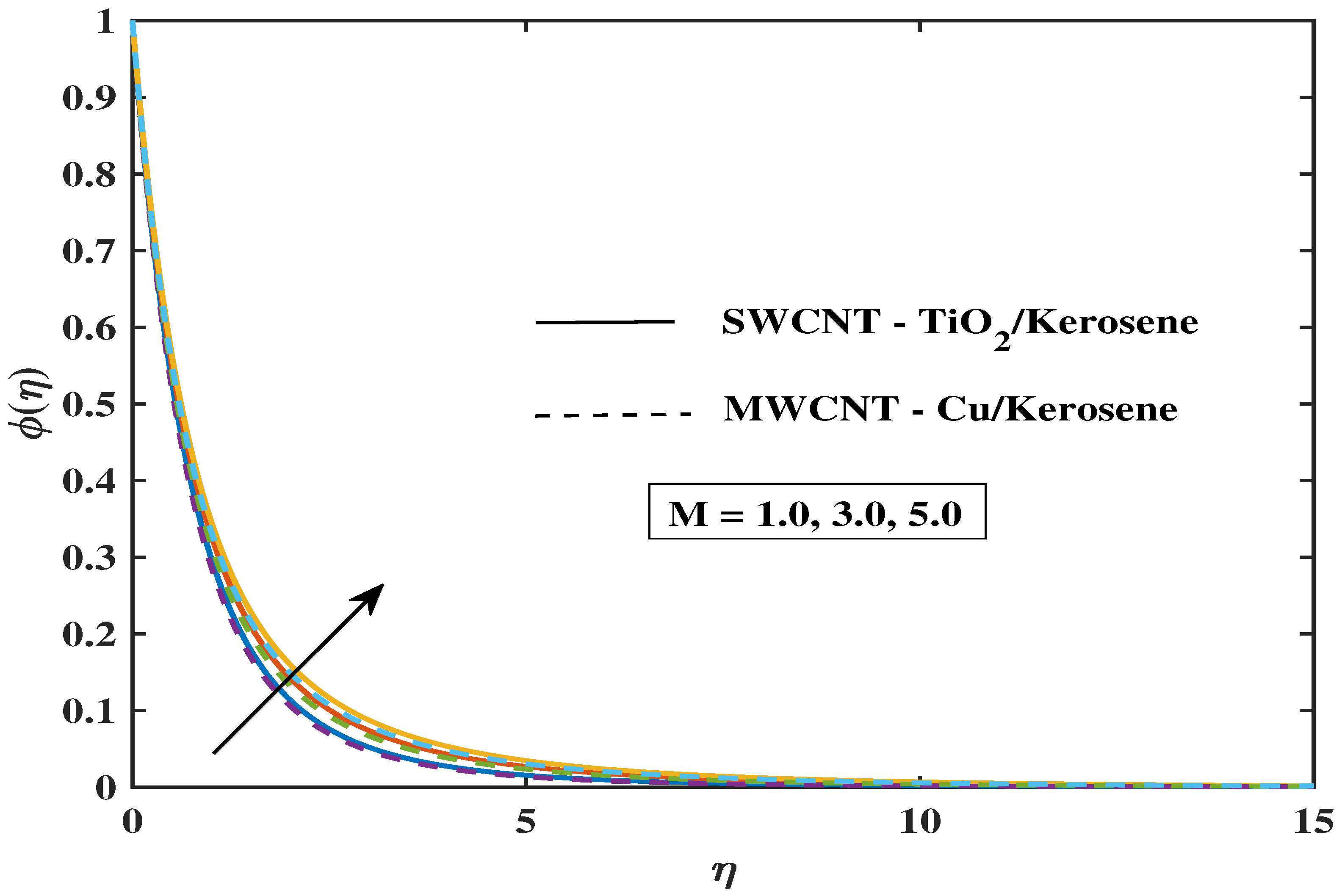
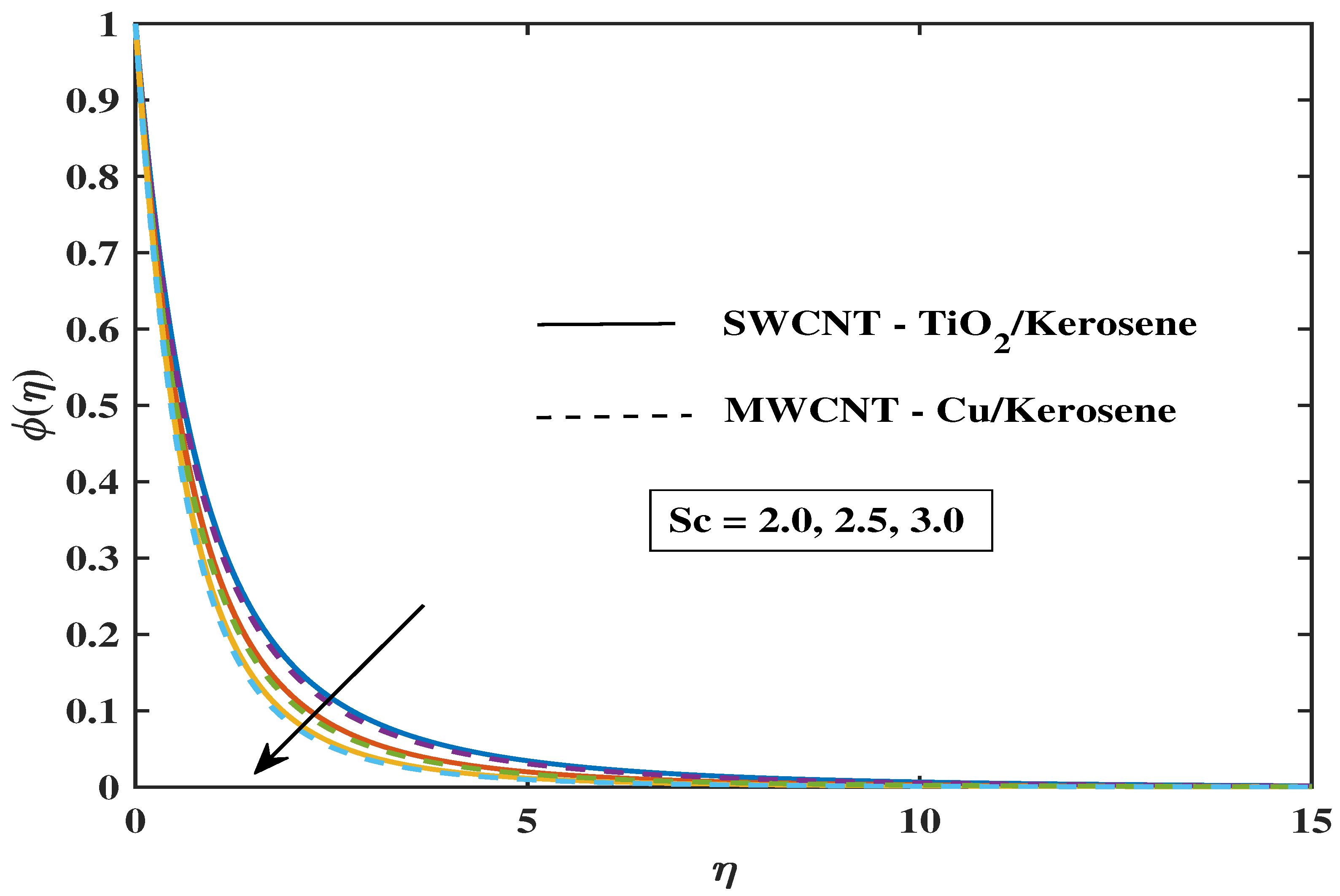
7.3. Concentration Profile
7.4. Model Validation
7.5. Applications and Relevance
- Magnetic field strength (M = 1–5) corresponds to fields of 0.1–0.5 T, typical of MHD cooling channels.
- Porosity values ( = 0.1–0.5) match metallic or ceramic porous inserts used in compact heat exchangers.
- Nanoparticle volume fractions () are within experimentally stable limits for and dispersions.
8. The Artificial Neural Network Modeling (ANN)
9. Concluding Remarks
- The fluid’s velocity drops as the values of magnetic parameter M, , and enhance, but it climbs when the values of , , , and improve.
- The hybrid exhibits superior heat transfer performance (higher Nusselt number) compared with the case across the considered parameter ranges.
- A modification in the angle of inclination, Biot number, curvature, magnetic parameter, and thermal radiation enhances the thermal profile.
- The temperature of both hybrid nanofluids decreases as the Prandtl fluid parameters increase.
- The shape factor strongly affects heat transfer: cylindrical nanoparticles (CNT-type) enhance thermal conductivity through elongated conduction paths, whereas brick-shaped particles yield weaker enhancement.
- Within the studied context, the created artificial neural network (ANN) model predicts outcomes with great efficiency and accuracy. Despite being tested using a brand-new hybrid nanofluid, it was able to accurately forecast heat transfer.
- The ANN surrogate (single hidden layer, 20 neurons, Levenberg–Marquardt training) reproduced the bvp4c results with <1.5% error and achieved a ≈93.8% reduction in computation time, enabling real-time prediction and design optimization.
- Sherwood numbers rise in tandem with the values of , , , and . On the other hand, it has a declining trend when M and increase.
- As , , , and grow, so does the number of skin friction. Conversely, when the porosity parameter increases, it decreases.
- Nusselet numbers rise with increasing values of , , , , and , but they decrease with increasing megnatic parameter M.
- Future research might focus on transient and three-dimensional expansions of the model, multi-objective optimization utilizing the trained ANN surrogate, and experimental measurements of hybrid nanofluid stability and heat transport in cylindrical geometries.
Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nanofluid density (kg·m−3) | Electrical conductivity (S·m−1) | ||
| f | Velocity Profile | Prandtl Number | |
| Dimensionless temperature | Cartesian coordinates (m) | ||
| Kinematic viscosity of nanofluid (m2s−1) | Curvature parameter | ||
| Temperature away from the surface (K) | Radiation parameter | ||
| T | Non-dimensional temperature (K) | Sherwood number | |
| Skin-friction factor | Temperature at surface (K) | ||
| Thermal conductivity (W.m−1·K−1) | Heat capacity (J·kg−1·K−1) | ||
| Darcy forchheimer coefficient | Activation energy (J·mol−1) | ||
| Dimentionless concentration | Inclination angle parameter | ||
| Reynolds number | Nusselt Number | ||
| Connective variable | Diffusion variable | ||
| Velocity components (m/s1) | Schmidt Number | ||
| Brownian Diffusion factor | Mean fluid temperature | ||
| porosity coefficient (s−1) | Stream function | ||
| Electrical conductivity | Specific heat (J·kg−1·K−1) | ||
| Temperature difference parameter | Biot number |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29); Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Toghraie, D.; Chaharsoghi, V.A.; Afrand, M. Measurement of thermal conductivity of ZnO-TiO2/EG hybrid nanofluid: Effects of temperature and nanoparticles concentration. J. Therm. Anal. Calorim. 2016, 125, 527–535. [Google Scholar] [CrossRef]
- Xian, H.W.; Sidik, N.A.C.; Aid, S.R.; Ken, T.L.; Asako, Y. Review on preparation techniques, properties and performance of hybrid nanofluid in recent engineering applications. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 45, 1–13. [Google Scholar]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Muneeshwaran, M.; Srinivasan, G.; Muthukumar, P.; Wang, C.C. Role of hybrid-nanofluid in heat transfer enhancement: A review. Int. Commun. Heat Mass Transf. 2021, 125, 105341. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical investigation of solar system equipped with innovative turbulator and hybrid nanofluid. Sol. Energy Mater. Sol. Cells 2022, 243, 111786. [Google Scholar] [CrossRef]
- Ai, C.; Liu, C.; Sun, P.; Liu, C. Na2CO3-SiO2-H2O nanofluid synergistically treats coal dust and hydrogen sulfide. J. Environ. Chem. Eng. 2025, 13, 119365. [Google Scholar] [CrossRef]
- Li, Y.; Xia, Y.; Deng, W.; Gao, X.; Li, H.; Gao, X. Nucleate boiling heat transfer and critical heat flux in controllable droplet trains cooling. Appl. Therm. Eng. 2025, 267, 125824. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Malik, M.Y. Inspection of hybrid based nanofluid flow over a curved surface. Comput. Methods Programs Biomed. 2020, 189, 105193. [Google Scholar] [CrossRef]
- Sudarmadji, S.; Bambang, I.; Susilo, S.H. The Effect of Hybrid Nanofluid CuO-TiO2 on Radiator Performance. East.-Eur. J. Enterp. Technol. 2022, 118, 21–29. [Google Scholar] [CrossRef]
- Rehman, K.U.; Fatima, N.; Shatanawi, W.; Kousar, N. Mathematical solutions for coupled nonlinear equations based on bioconvection in MHD Casson nanofluid flow. AIMS Math. 2025, 10, 598–633. [Google Scholar] [CrossRef]
- Wu, J.; Lin, J.; Yan, Y.; You, Z.; Su, Z.; Long, J. Grooved-porous composite wick structures for highly efficient capillary-fed boiling heat transfer. Appl. Therm. Eng. 2024, 256, 124029. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Naseem, R.; Hussain, S.; Alghamdi, M. Impact of MHD radiative flow of hybrid nanofluid over a rotating disk. Case Stud. Therm. Eng. 2021, 26, 101015. [Google Scholar] [CrossRef]
- Bi, Y.; Xia, G.; Wang, C.; Peng, M.; Xu, Y.; Wu, J. Design and transient analysis of a novel type passive residual heat removal system. Nucl. Eng. Des. 2025, 445, 114446. [Google Scholar] [CrossRef]
- Chabani, I.; Mebarek-Oudina, F.; Ismail, A.A.I. MHD flow of a hybrid nano-fluid in a triangular enclosure with zigzags and an elliptic obstacle. Micromachines 2022, 13, 224. [Google Scholar] [CrossRef]
- Tetik, T.; Armagan, M.; Demir, E.K.; Arbak, A.; Teksan, A.E.; Pusat, S.; Karagoz, Y. An experimental study on the heat transfer performance of a radiator using MWCNT-SiO2 hybrid nanofluid. Energy Sources Part A Recover. Util. Environ. Eff. 2023, 45, 12590–12603. [Google Scholar]
- Manimaran, M.; Norizan, M.N.; Kassim, M.H.M.; Adam, M.R.; Abdullah, N.; Norrrahim, M.N.F. Critical review on the stability and thermal conductivity of water-based hybrid nanofluids for heat transfer applications. RSC Adv. 2025, 15, 14088–14125. [Google Scholar] [CrossRef]
- Abdollahi, S.A.; Alizadeh, A.A.; Zarinfar, M.; Pasha, P. Investigating heat transfer and fluid flow betwixt parallel surfaces under the influence of hybrid nanofluid suction and injection with numerical analytical technique. Alex. Eng. J. 2023, 70, 423–439. [Google Scholar] [CrossRef]
- Choudhary, S.; Kumar Jarwal, V.; Choudhary, P.; Loganathan, K.; Pattanaik, B. Mass-Based Hybrid Nanofluid Model for Thermal Radiation Analysis of MHD Flow over a Wedge Embedded in Porous Medium. J. Eng. 2024, 2024, 9528362. [Google Scholar] [CrossRef]
- Shoaib, M.; Raja, M.A.Z.; Sabir, M.T.; Islam, S.; Shah, Z.; Kumam, P.; Alrabaiah, H. Numerical investigation for rotating flow of MHD hybrid nanofluid with thermal radiation over a stretching sheet. Sci. Rep. 2020, 10, 18533. [Google Scholar] [CrossRef]
- Huang, J.; Li, Y.; Zhou, Z.; Xiang, M. Study on the impact of the atomized water droplet size on the performance of magnesium-based water ramjet engine. Appl. Therm. Eng. 2025, 279, 127849. [Google Scholar] [CrossRef]
- Yaseen, M.; Kumar, M.; Rawat, S.K. Assisting and opposing flow of a MHD hybrid nanofluid flow past a permeable moving surface with heat source/sink and thermal radiation. Partial. Differ. Equ. Appl. Math. 2021, 4, 100168. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I.; Bachok, N.; Hafidzuddin, M.E.H. MHD mixed convection flow of a hybrid nanofluid past a permeable vertical flat plate with thermal radiation effect. Alex. Eng. J. 2022, 61, 3323–3333. [Google Scholar] [CrossRef]
- Mahesh, R.; Mahabaleshwar, U.S.; Kumar, P.V.; Öztop, H.F.; Abu-Hamdeh, N. Impact of radiation on the MHD couple stress hybrid nanofluid flow over a porous sheet with viscous dissipation. Results Eng. 2023, 17, 100905. [Google Scholar] [CrossRef]
- Raisee, M.; Vahedi, N.; Rostamzadeh, A. Prediction of gas flow through short and long 2-D micro and nano-channels using a generalized slip model. Int. Conf. Nanochannels Microchannels Minichannels 2008, 48345, 103–109. [Google Scholar]
- Shah, S.A.A.; Awan, A.U.; Ali, B.; Ragab, E.A. Dynamics of methanol conveying mono and hybrid nanoparticles to optimization of heat transfer across stretching cylinder. Numer. Heat Transf. A 2025, 86, 6462–6477. [Google Scholar] [CrossRef]
- Islam, S.; Khan, A.; Kumam, P.; Alrabaiah, H.; Shah, Z.; Khan, W.; Zubair, M.; Jawad, M. Radiative mixed convection flow of maxwell nanofluid over a stretching cylinder with joule heating and heat source/sink effects. Sci. Rep. 2020, 10, 17823. [Google Scholar] [CrossRef]
- Patil, P.M.; Kulkarni, M. Analysis of MHD mixed convection in a Ag-TiO2 hybrid nanofluid flow past a slender cylinder. Chin. J. Phys. 2021, 73, 406–419. [Google Scholar] [CrossRef]
- Ahmad, W.; Ur Rehman, M.I.; Hamid, A.; Hou, M. Numerical investigation of bioconvection flow of Sutterby nanofluid with Darcy—Forchheimer porous media past an inclined stretching cylinder. Eur. Phys. J. Plus 2024, 139, 842. [Google Scholar] [CrossRef]
- Jiang, X.; Hatami, M.; Abderrahmane, A.; Younis, O.; Makhdoum, B.M.; Guedri, K. Mixed convection heat transfer and entropy generation of MHD hybrid nanofluid in a cubic porous cavity with wavy wall and rotating cylinders. Appl. Therm. Eng. 2023, 226, 120302. [Google Scholar] [CrossRef]
- Tang, Y.; Wei, X.; Liu, Y. Hybrid RANS-LES simulation of rotor–stator interaction in a compressor stage using a grid-adaptive simulation method. J. Turbomach. 2025, 147, 071001. [Google Scholar] [CrossRef]
- Wang, X.; Hu, X.; Liu, Z.; Zhu, C.; Shen, R.; Quan, B.; Qu, J. Interpenetrating double-network ANF/MXene-K+ aerogels enable integrated electromagnetic interference shielding, infrared camouflage, and Joule Heating in adaptive multifunctional systems. Nano Res. 2025, 18, 94907702. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Ahammad, N.A.; Ali, B.; Guedri, K.; Awan, A.U.; Gamaoun, F.; Tag-ElDin, E.M. Significance of bio-convection, MHD, thermal radiation and activation energy across Prandtl nanofluid flow: A case of stretching cylinder. Int. Commun. Heat Mass Transf. 2022, 137, 106299. [Google Scholar] [CrossRef]
- Awan, A.U.; Shah, S.A.A.; Ali, B. Bio-convection effects on Williamson nanofluid flow with exponential heat source and motile microorganism over a stretching sheet. Chin. J. Phys. 2022, 77, 2795–2810. [Google Scholar] [CrossRef]
- Zafar, S.S.; Alfaleh, A.; Zaib, A.; Ali, F.; Faizan, M.; Abed, A.M.; Elattar, S.; Khan, M.I. Simulation of Prandtl nanofluid in the mixed convective flow of activation energy with gyrotactic microorganisms: Numerical outlook features of micro-machines. Micromachines 2023, 14, 559. [Google Scholar] [CrossRef]
- Ul-Haq, S.; Tanveer, A.; Ashraf, M.B.; Nawaz, R. Artificial neural network (ANN) analysis of non-similar solution of MHD nanofluid flow past a curved stretching surface. Numer. Heat Transf. Part A Appl. 2023, 86, 2399–2422. [Google Scholar] [CrossRef]
- Das, P.; Mamun, M.A.H. Predicting MHD mixed convection in a semicircular cavity with hybrid nanofluids using AI. Heliyon 2024, 10, e38303. [Google Scholar] [CrossRef]
- Abbas, Z.; Abdullah, A.R.; Malik, M.F.; Shah, S.A.A. Artificial Neural Network Modeling of Darcy–Forchheimer Nanofluid Flow over a Porous Riga Plate: Insights into Brownian Motion, Thermal Radiation, and Activation Energy Effects on Heat Transfer. Symmetry 2025, 17, 1582. [Google Scholar] [CrossRef]
- Ramasekhar, G.; Alkarni, S.; Shah, N.A. Machine learning approach of Casson hybrid nanofluid flow over a heated stretching surface. AIMS Math. 2024, 9, 18746–18762. [Google Scholar] [CrossRef]
- Reddy, S.R.R.; Jakeer, S.; Sathishkumar, V.E.; Basha, H.T.; Cho, J. Numerical study of TC4-NiCr/EG+ Water hybrid nanofluid over a porous cylinder with Thompson and Troian slip boundary condition: Artificial neural network model. Case Stud. Therm. Eng. 2024, 53, 103794. [Google Scholar] [CrossRef]
- Mehta, R.; Senthilvadivu, K. Artificial Neural Network Analysis on Heat and Mass Transfer in MHD Carreau Ternary Hybrid Nanofluid Flow across a Vertical Cylinder: A Numerical Computation. Int. J. Thermofluids 2025, 27, 101171. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Awan, A.U. Significance of magnetized Darcy-Forchheimer stratified rotating Williamson hybrid nanofluid flow: A case of 3D sheet. Int. Commun. Heat Mass Transf. 2022, 136, 106214. [Google Scholar] [CrossRef]
- Awan, A.U.; Qayyum, S.; Nadeem, S.; Ahammad, N.A.; Gepreel, K.A.; Alharthi, M.; Alosaimi, M. Analysis of chemical characteristics of engine-oil-based Prandtl hybrid nanofluid flow. Zamm-J. Appl. Math. Mech. Angew. Math. Mech. 2024, 104, e202400050. [Google Scholar] [CrossRef]
- Awan, A.U.; Ali, B.; Shah, S.A.A.; Oreijah, M.; Guedri, K.; Eldin, S.M. Numerical analysis of heat transfer in Ellis hybrid nanofluid flow subject to a stretching cylinder. Case Stud. Therm. Eng. 2023, 49, 103222. [Google Scholar] [CrossRef]
- Kumbhakar, B.; Nandi, S.; Chamkha, A.J. Unsteady hybrid nanofluid flow over a convectively heated cylinder with inclined magnetic field and viscous dissipation: A multiple regression analysis. Chin. J. Phys. 2022, 79, 38–56. [Google Scholar] [CrossRef]
- Malik, M.F.; Shah, S.A.A.; Bilal, M.; Hussien, M.; Mahmood, I.; Akgul, A.; Alshomrani, A.S.; Az-Zo’bi, E.A. New insights into the dynamics of heat and mass transfer in a hybrid (Ag-TiO2) nanofluid using Modified Buongiorno model: A case of a rotating disk. Results Phys. 2023, 53, 106906. [Google Scholar] [CrossRef]
- Farooq, U.; Liu, H.; Basem, A.; Fatima, N.; Alhushaybari, A.; Imran, M.; Ali, N.B.; Muhammad, T. Computational investigation of methanol-based hybrid nanofluid flow over a stretching cylinder with Cattaneo—Christov heat flux. J. Comput. Des. Eng. 2024, 11, 73–82. [Google Scholar] [CrossRef]
- Song, Y.Q.; Hamid, A.; Sun, T.C.; Khan, M.I.; Qayyum, S.; Kumar, R.N.; Prasannakumara, B.C.; Khan, S.U.K.; Chinram, R. Unsteady mixed convection flow of magneto-Williamson nanofluid due to stretched cylinder with significant non-uniform heat source/sink features. Alex. Eng. J. 2022, 61, 195–206. [Google Scholar] [CrossRef]







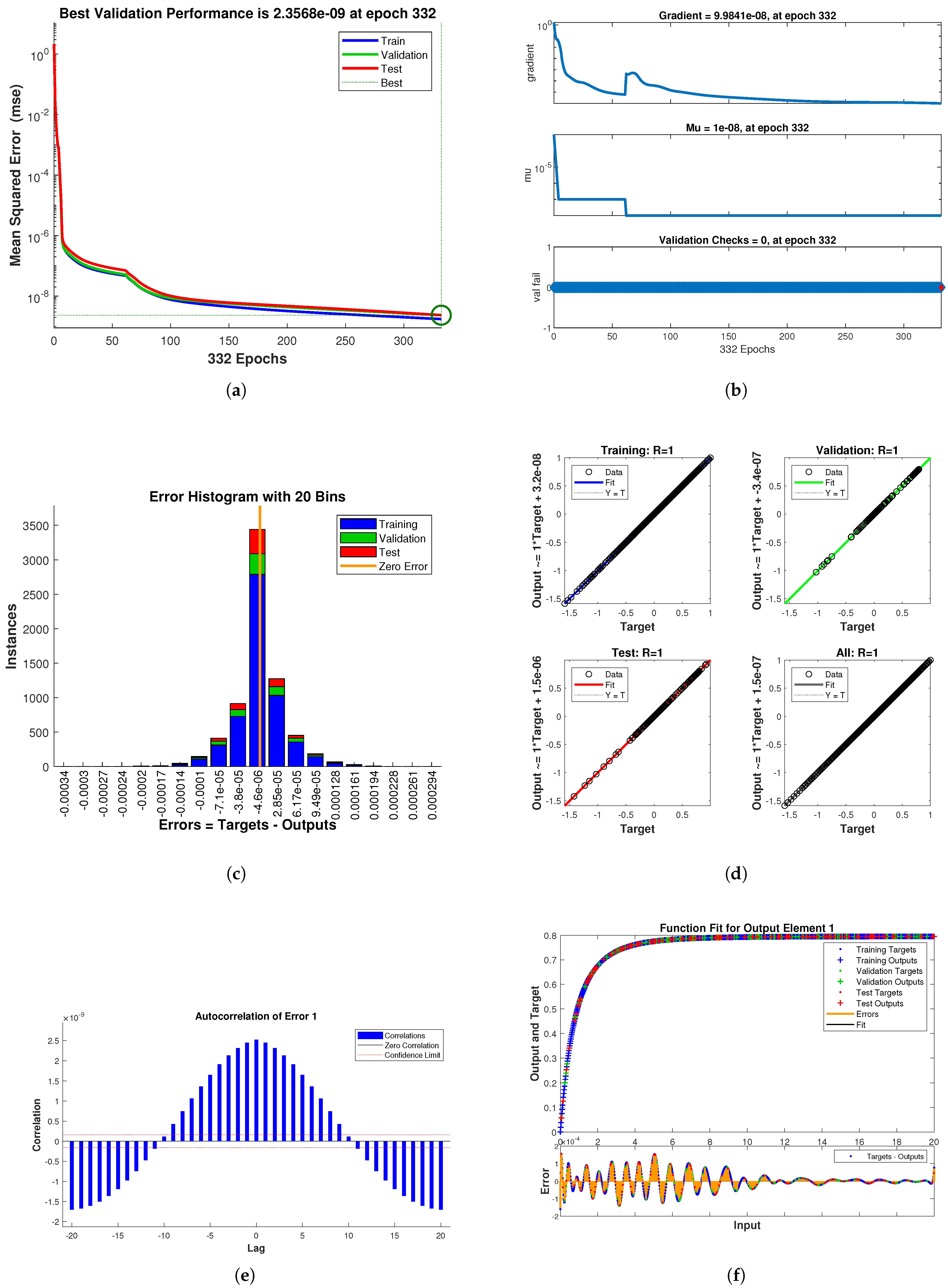
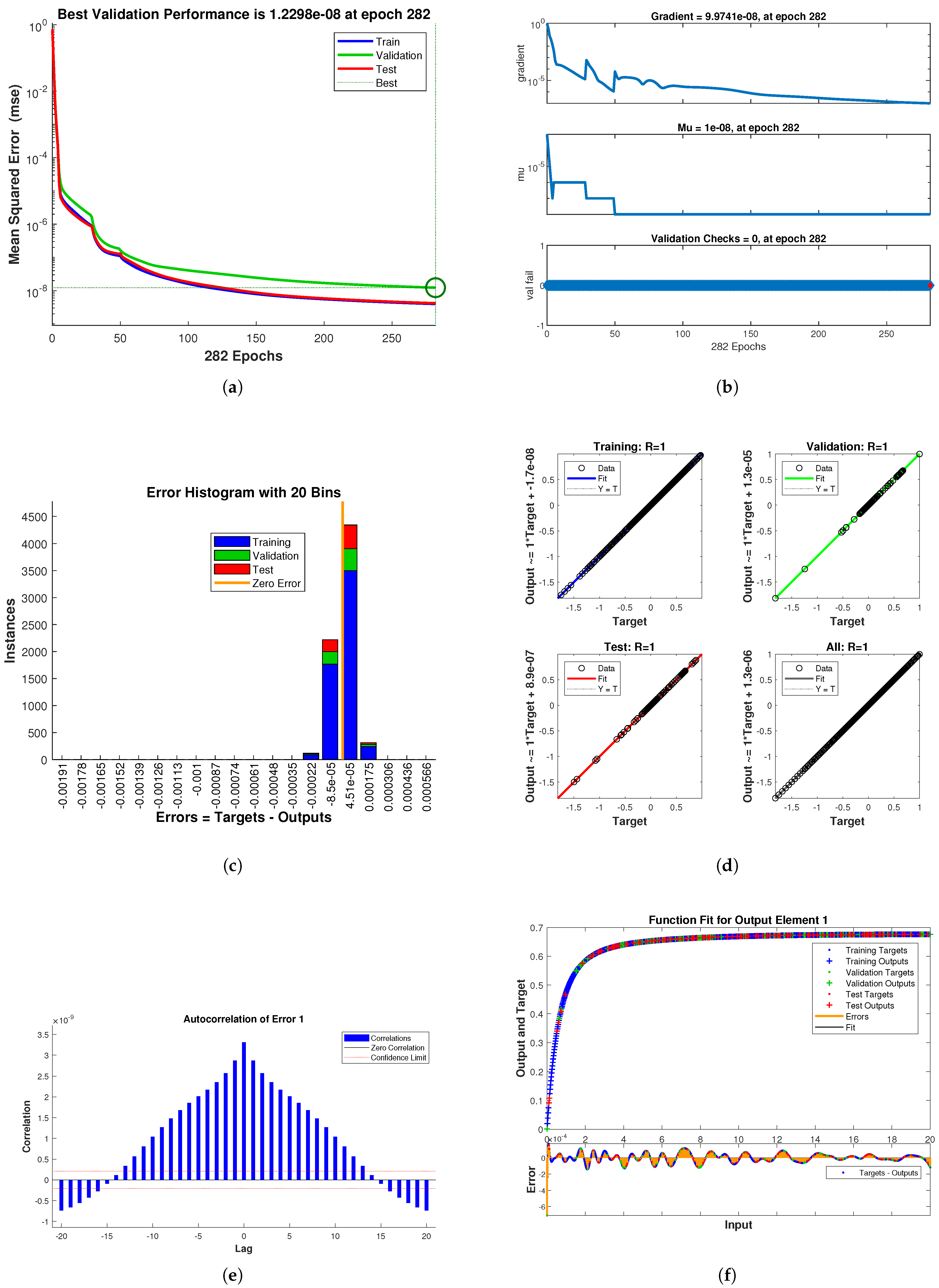
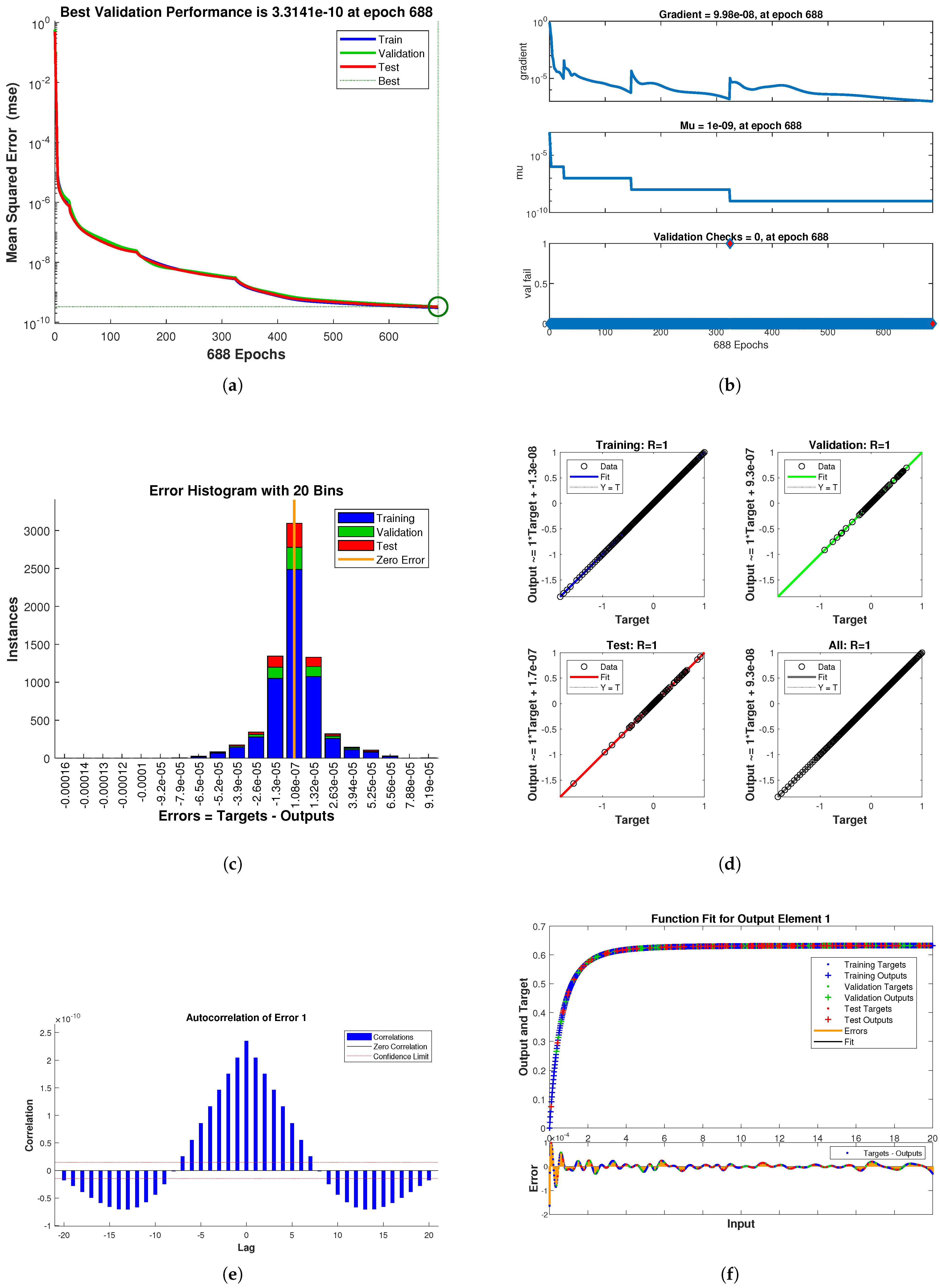
| Epoch | MSE | Gradient | mu | |
|---|---|---|---|---|
| 332 | 2.3568 | 9.9841 | 1 | |
| 282 | 1.2298 | 9.9741 | 1 | |
| 688 | 3.3141 | 9.98 | 1 |
| Properties | Hybrid Nanofluid |
|---|---|
| Viscosity | |
| Density | |
| Heat Capacity | |
| Thermal Conductivity | |
| Electrical Conductivity |
| Properties | Kerosene | ||||
|---|---|---|---|---|---|
| (kg/m3) | 783 | 2600 | 1600 | 4230 | 8933 |
| (J/kg1·K1) | 2090 | 425 | 796 | 692 | 385 |
| k (W/m1·K1) | 0.15 | 6600 | 3000 | 8.4 | 401 |
| Parameter | Present Study | Nadeem et al. [9] | Patil & Kulkarni. [28] | Deviation (%) |
|---|---|---|---|---|
| 0.5331 | 0.5425 | 0.5280 | <1.9 | |
| 3.4102 | 3.4628 | 3.3870 | <1.7 |
| Farooq et al. [47] | Song at al. [48] | This Study | CPU Time (s) | |
|---|---|---|---|---|
| 0.0 | −1.0000 | −1.0000 | −1.0000 | 2.760355 |
| 0.25 | −1.0943743 | −1.0943742 | −1.094377 | 2.746383 |
| 0.5 | −1.1887304 | −1.1887303 | −1.188727 | 3.298879 |
| 0.75 | −1.2818245 | −1.2818242 | −1.281833 | 2.205832 |
| 1.0 | −1.4593752 | −1.4593751 | −1.459372 | 2.797052 |
| M | |||||||
|---|---|---|---|---|---|---|---|
| Kerosene | Kerosene | ||||||
| 1.0 | 0.5 | 2.0 | 0.5 | 1.0 | 90.0 | 3.4059 | 3.4449 |
| 1.2 | 3.8797 | 3.9250 | |||||
| 1.4 | 4.3078 | 4.3588 | |||||
| 1.3 | 0.3 | 3.8710 | 3.9143 | ||||
| 0.6 | 4.1963 | 4.2466 | |||||
| 0.9 | 4.4463 | 4.5018 | |||||
| 0.5 | 1.5 | 2.6710 | 2.7355 | ||||
| 2.5 | 3.1231 | 3.1810 | |||||
| 3.5 | 3.5339 | 3.5871 | |||||
| 2.0 | 0.5 | 3.9782 | 4.0274 | ||||
| 1.0 | 3.7719 | 3.8228 | |||||
| 1.5 | 3.5583 | 3.6112 | |||||
| 0.2 | 2.5 | 4.4370 | 4.4828 | ||||
| 3.0 | 4.5467 | 4.5917 | |||||
| 3.5 | 4.6550 | 4.6993 | |||||
| 1.0 | 30.0 | 2.5487 | 2.6154 | ||||
| 45.0 | 3.1231 | 3.1810 | |||||
| 60.0 | 3.6319 | 3.6840 |
| M | |||||||
|---|---|---|---|---|---|---|---|
| Kerosene | Kerosene | ||||||
| 1.0 | 0.5 | 2.0 | 0.5 | 0.5 | 0.5 | 0.5600 | 0.5634 |
| 1.2 | 0.5640 | 0.5672 | |||||
| 1.4 | 0.5674 | 0.5705 | |||||
| 1.3 | 0.3 | 0.5629 | 0.5661 | ||||
| 0.6 | 0.5669 | 0.5701 | |||||
| 0.9 | 0.5698 | 0.5730 | |||||
| 0.5 | 1.5 | 0.5858 | 0.5880 | ||||
| 2.5 | 0.5792 | 0.5818 | |||||
| 3.5 | 0.5734 | 0.5763 | |||||
| 2.0 | 0.4 | 0.5339 | 0.5367 | ||||
| 0.7 | 0.6258 | 0.6297 | |||||
| 1.0 | 0.7077 | 0.7131 | |||||
| 0.5 | 0.4 | 0.4803 | 0.4826 | ||||
| 0.6 | 0.6419 | 0.6461 | |||||
| 0.8 | 0.7720 | 0.7780 | |||||
| 0.5 | 0.3 | 0.5657 | 0.5689 | ||||
| 0.6 | 0.5661 | 0.5693 | |||||
| 0.9 | 0.5683 | 0.5714 |
| M | |||||||
|---|---|---|---|---|---|---|---|
| Kerosene | Kerosene | ||||||
| 1.0 | 0.5 | 2.0 | 2.0 | 0.9 | 0.5 | 1.1996 | 1.1966 |
| 1.2 | 1.2090 | 1.2061 | |||||
| 1.4 | 1.2178 | 1.2148 | |||||
| 1.3 | 0.3 | 1.2057 | 1.2027 | ||||
| 0.6 | 1.2169 | 1.2139 | |||||
| 0.9 | 1.2255 | 1.2226 | |||||
| 0.5 | 1.5 | 1.2806 | 1.2759 | ||||
| 2.5 | 1.2550 | 1.2511 | |||||
| 3.5 | 1.2355 | 1.2322 | |||||
| 0.5 | 2.2 | 1.2761 | 1.2731 | ||||
| 2.4 | 1.3365 | 1.3333 | |||||
| 2.6 | 1.3947 | 1.3914 | |||||
| 2.0 | 2.1 | 1.1921 | 1.1891 | ||||
| 2.4 | 1.1353 | 1.1323 | |||||
| 2.7 | 1.0886 | 1.0856 | |||||
| 2.0 | 0.3 | 1.1410 | 1.1379 | ||||
| 0.6 | 1.2492 | 1.2463 | |||||
| 0.9 | 1.3541 | 1.3514 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, M.F.; Aljethi, R.A.; Shah, S.A.A.; Yasmeen, S. Hybrid Nanofluid Flow and Heat Transfer in Inclined Porous Cylinders: A Coupled ANN and Numerical Investigation of MHD and Radiation Effects. Symmetry 2025, 17, 1998. https://doi.org/10.3390/sym17111998
Malik MF, Aljethi RA, Shah SAA, Yasmeen S. Hybrid Nanofluid Flow and Heat Transfer in Inclined Porous Cylinders: A Coupled ANN and Numerical Investigation of MHD and Radiation Effects. Symmetry. 2025; 17(11):1998. https://doi.org/10.3390/sym17111998
Chicago/Turabian StyleMalik, Muhammad Fawad, Reem Abdullah Aljethi, Syed Asif Ali Shah, and Sidra Yasmeen. 2025. "Hybrid Nanofluid Flow and Heat Transfer in Inclined Porous Cylinders: A Coupled ANN and Numerical Investigation of MHD and Radiation Effects" Symmetry 17, no. 11: 1998. https://doi.org/10.3390/sym17111998
APA StyleMalik, M. F., Aljethi, R. A., Shah, S. A. A., & Yasmeen, S. (2025). Hybrid Nanofluid Flow and Heat Transfer in Inclined Porous Cylinders: A Coupled ANN and Numerical Investigation of MHD and Radiation Effects. Symmetry, 17(11), 1998. https://doi.org/10.3390/sym17111998






