High-Performance Sensorless Control of Induction Motors via ANFIS and NPC Inverter Topology
Abstract
1. Introduction
2. Induction Motor
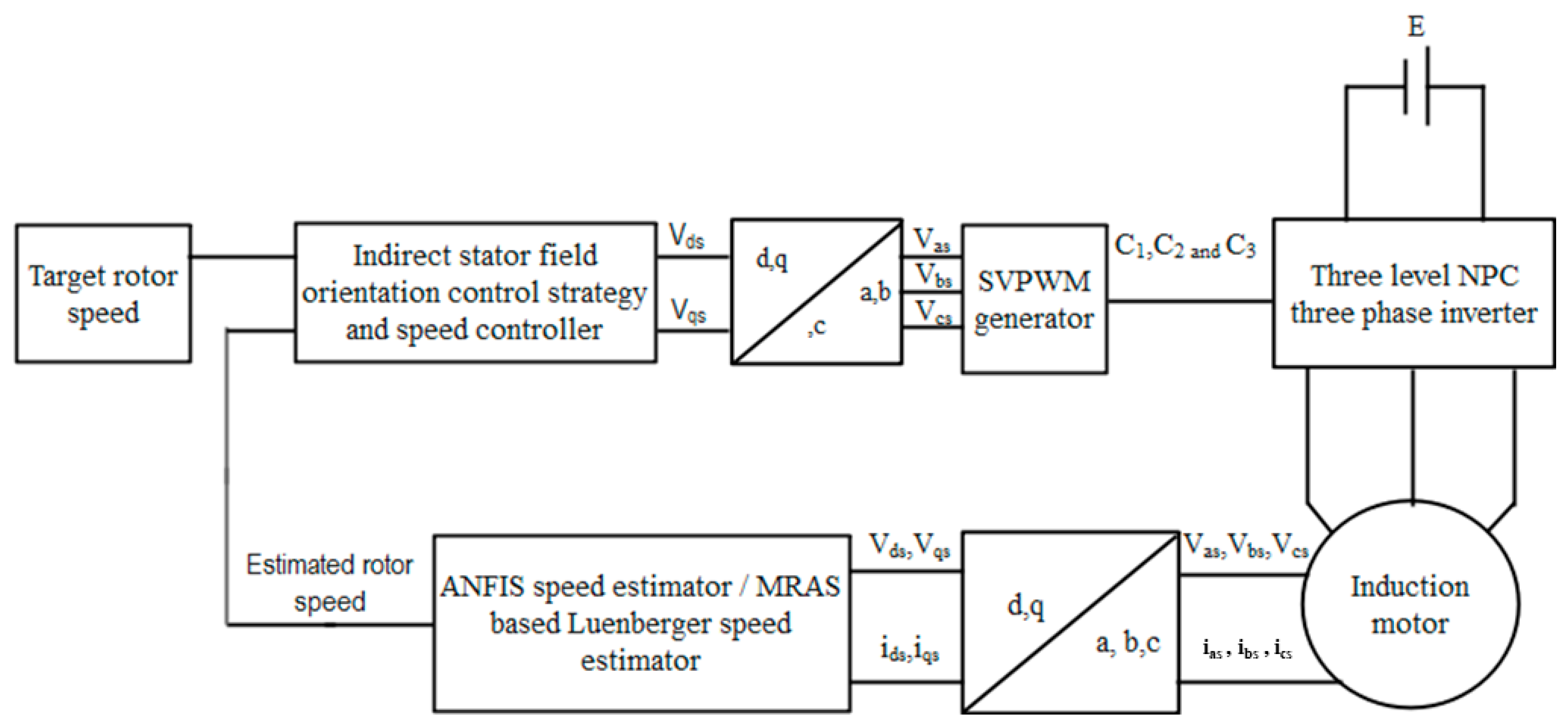
3. ISFOC Vector Control by Stator Flux Orientation
4. Speed Estimation
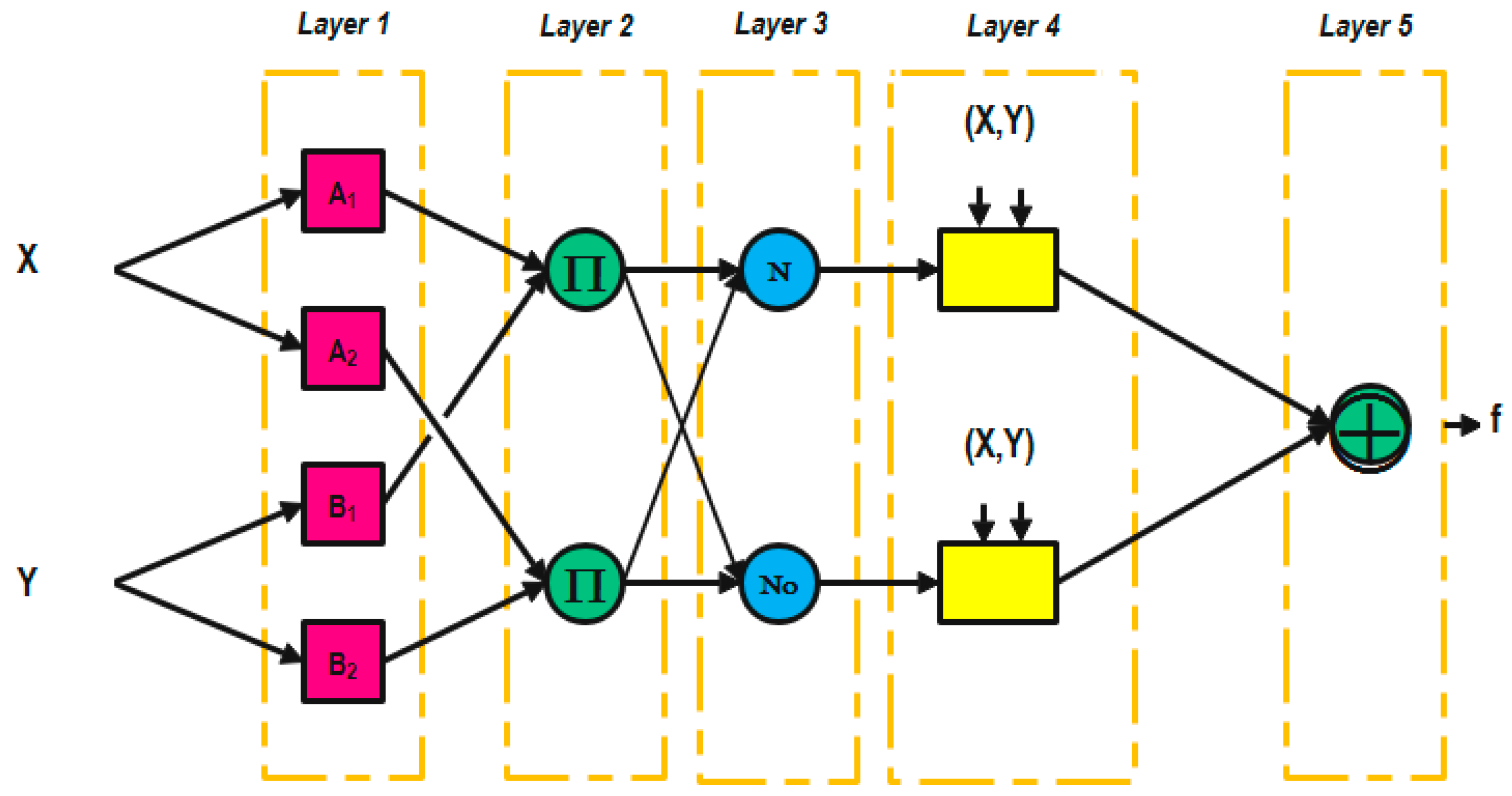
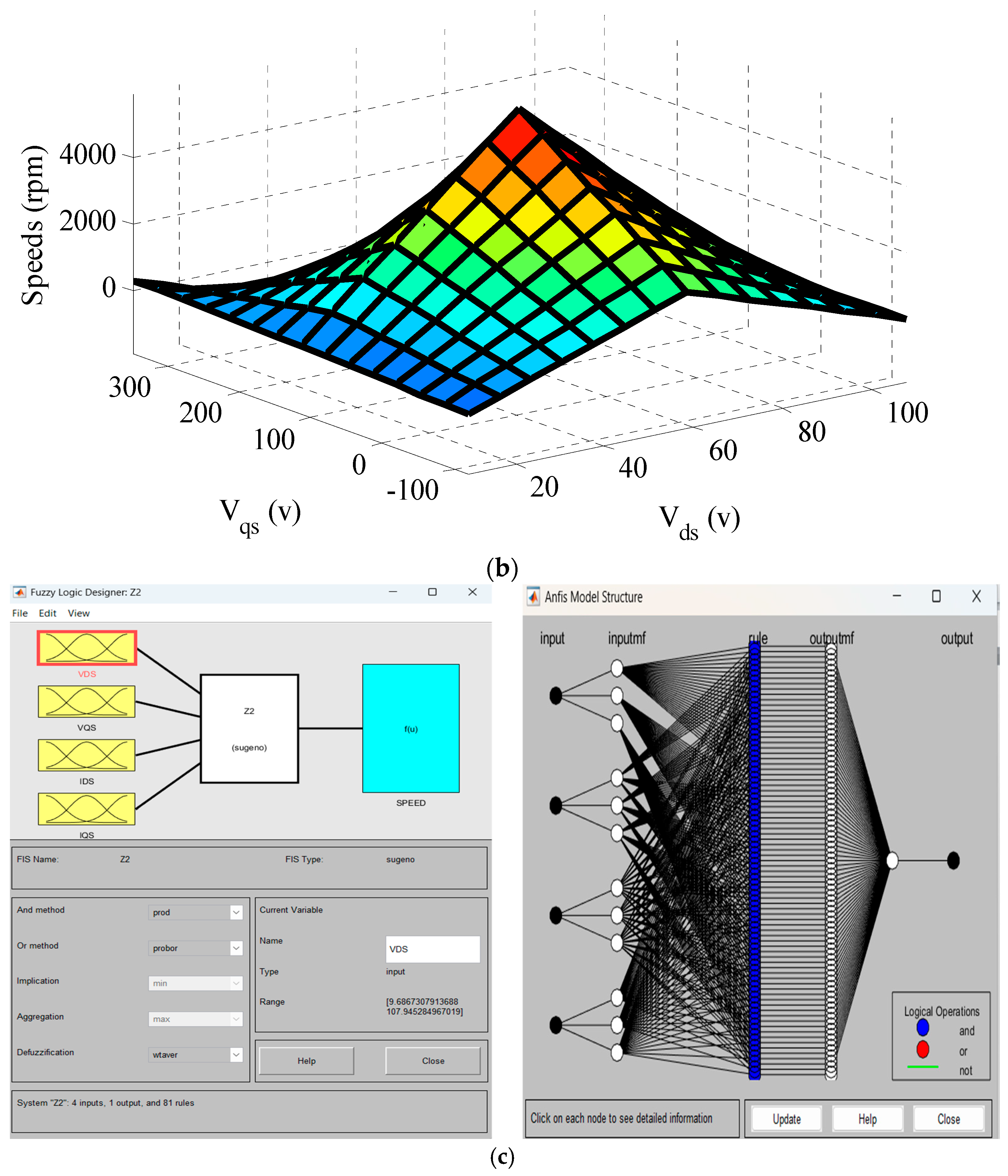
4.1. ANFIS Algorithm
- Layer 1: Generation of the membership degree:
- Layer 2: Rule i generation weight:
- Layer 3: Rule i normalization weight:
- Layer 4: Rules calculation output:
- Layer 5: ANFIS calculation by sum generation:
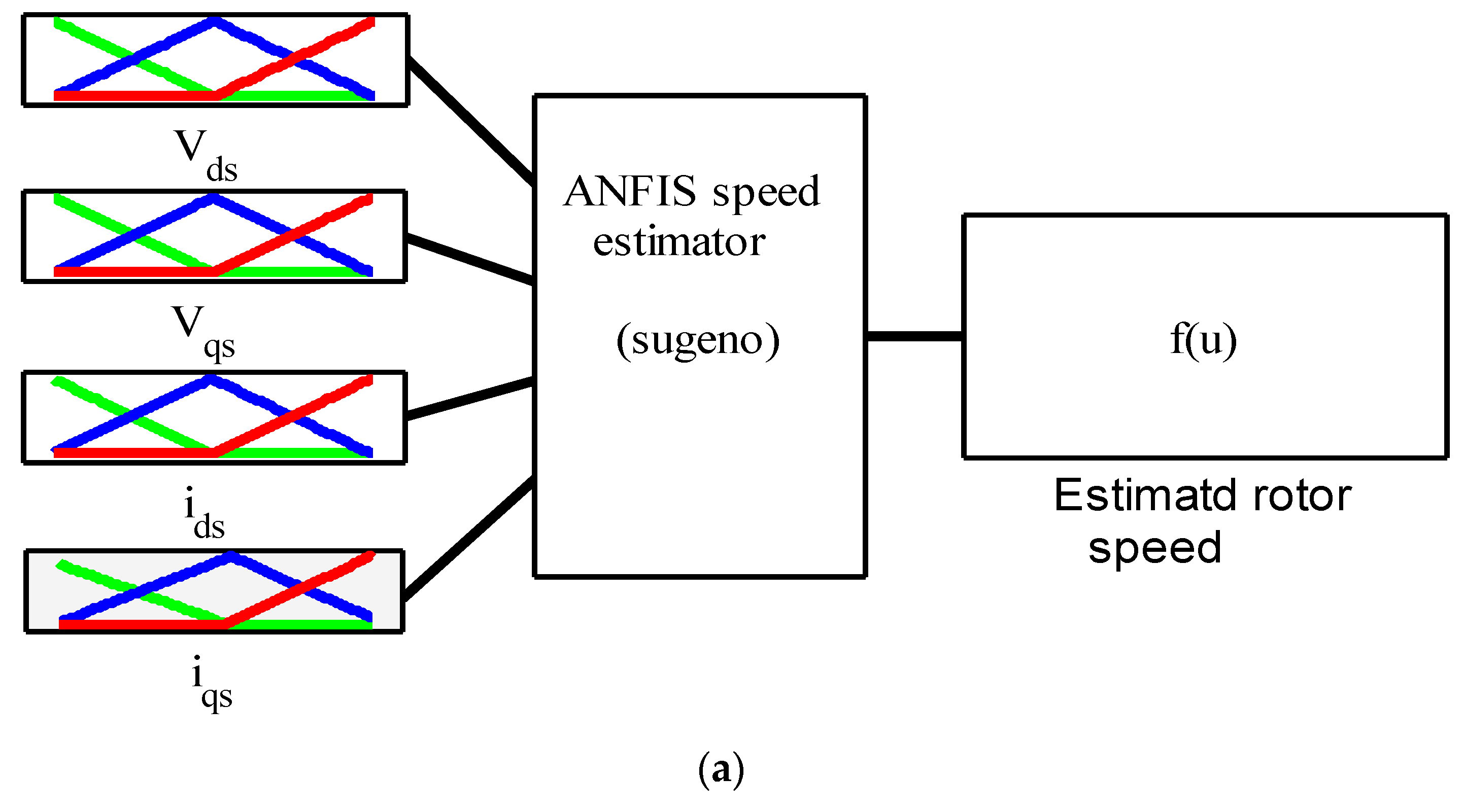
4.2. ANFIS Speed Estimator
- Select an appropriate set of membership functions.
- Provide the input–output data required for ANFIS training.
4.3. MRAS-Based Luenberger Speed Observer
4.4. Comparative Study of Performance of Speed Estimators
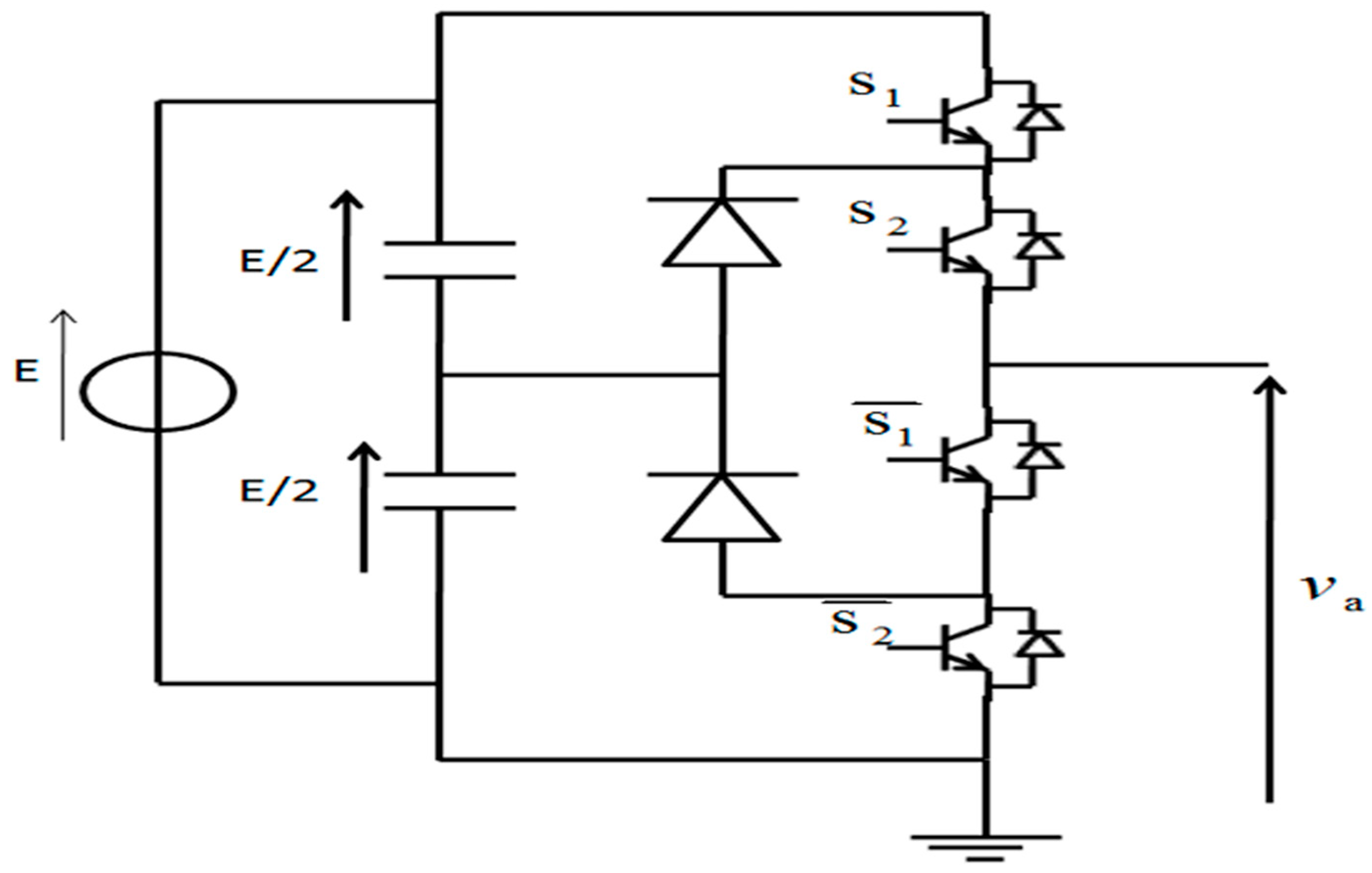
5. NPC Inverter
5.1. NPC Topology
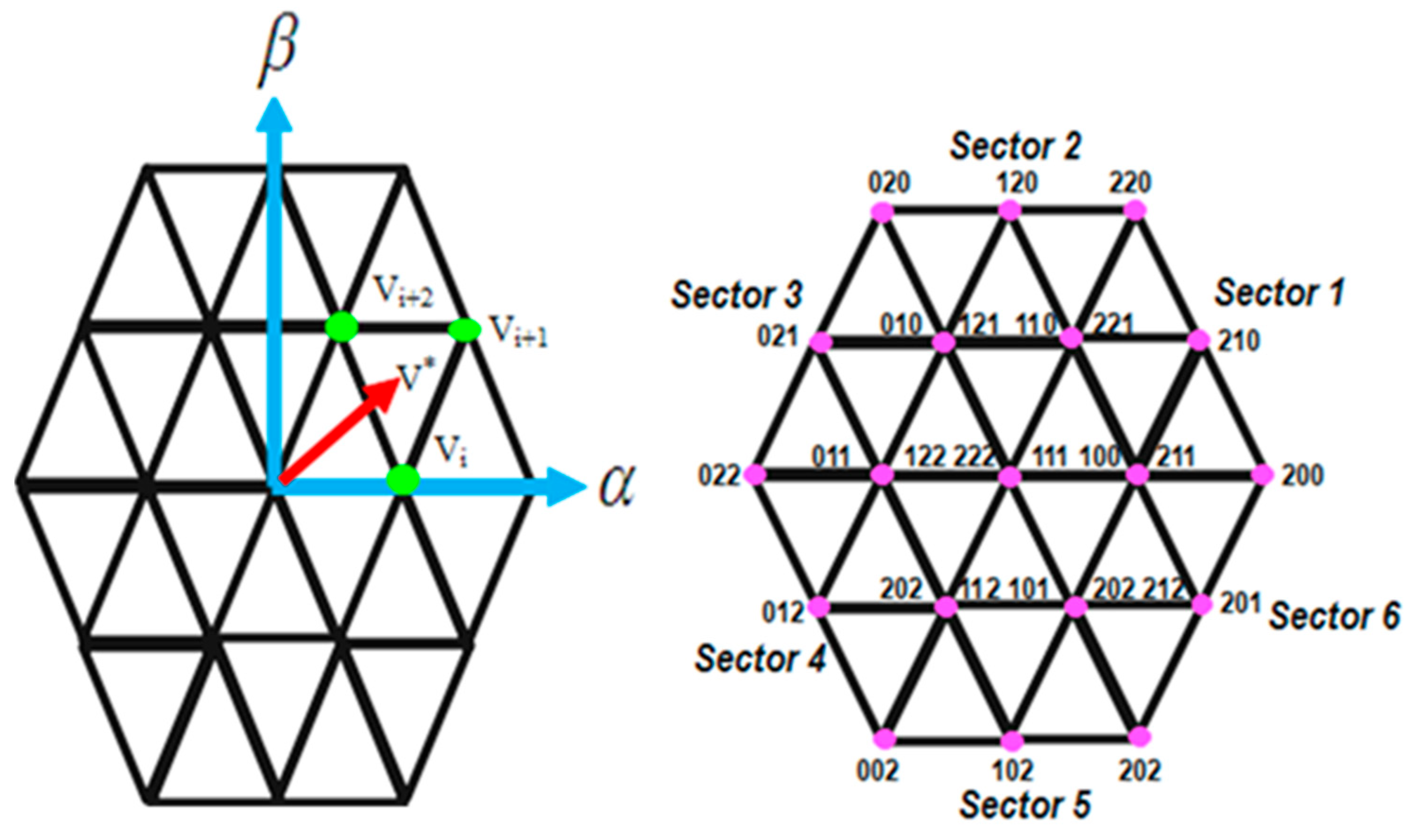
5.2. SVM Topology
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tounsi, M.M.; Allali, A.; Boulouiha, H.M.; Denaï, M. ANFIS control of a shunt active filter based with a five-level NPC inverter to improve power quality. Int. J. Electr. Comput. Eng. (IJECE) 2021, 11, 1886–1893. [Google Scholar] [CrossRef]
- Vargas, O.S.; Aldaco, S.E.D.L.; Alquicira, J.A.; Vela-Valdés, L.G.; Núñez, A.R.L. Adaptive network-based fuzzy inference system (ANFIS) applied to inverters: A survey. IEEE Trans. Power Electron. 2023, 39, 869–884. [Google Scholar] [CrossRef]
- Karaboga, D.; Kaya, E. Adaptive network based fuzzy inference system (ANFIS) training approaches: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2263–2293. [Google Scholar] [CrossRef]
- Anjan Kumar, S. A novel metaheuristic approach for simultaneous loss minimization and torque ripple reduction of DTC-IM driven EV. Green Energy Intell. Transp. 2025, 4, 1–10. [Google Scholar]
- Lin, S.; Jian, Z.; Kai, C.; Xuhui, W. A Static Current Error Elimination Algorithm for Predictive Current Control in PMSM for Electric Vehicles. Green Energy Intell. Transp. 2025, 100306. [Google Scholar] [CrossRef]
- Jenkal, H.; Bossoufi, B.; Boulezhar, A.; Lilane, A.; Hariss, S. Vector control of a Doubly Fed Induction Generator wind turbine. Mater. Today Proc. 2020, 30, 976–980. [Google Scholar] [CrossRef]
- Dyanamina, G.; Kakodia, S.K. Adaptive neuro fuzzy inference system based decoupled control for neutral point clamped multi-level inverter fed induction motor drive. Chin. J. Electr. Eng. 2021, 7, 70–82. [Google Scholar] [CrossRef]
- Boussada, Z.; Elbeji, O.; Benhamed, M. Different topologies and control techniques of multi-level inverter: A literature survey. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; IEEE: New York, NY, USA, 2017; pp. 1–5. [Google Scholar]
- Ramprasad, A.; Giribabu, D.; Kakodia, S.K.; Panda, A.K. Performance analysis of three-level NPC inverter Fed PMSM drives. In Proceedings of the 2022 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 19–20 February 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Baschera, N.E.L.; Di Benedetto, M.; Lidozzi, A.; Solero, L. FPGA Based Space Vector Modulation Strategy for the Three-Phase 7-Level Multiplexed Converter. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024; IEEE: New York, NY, USA, 2024; pp. 3405–3412. [Google Scholar]
- Younes, D.; El Mehdi, A.S.A.; Houcine, C.; Mouloud, D. Sensorless Torque Control of an Electric Vehicle Driven by an Open End Winding Induction Motor: An Experimental Study. In Proceedings of the 2023 Second International Conference on Energy Transition and Security (ICETS), Adrar, Algeria, 12–14 December 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Pabbewar, A.S.; Kowsalya, M. Three level neutral point clamped inverter using space vector modulation with proportional resonant controller. Energy Procedia 2016, 103, 286–291. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Durairaj, S.; Padmavathi, S. A performance improvement of the fuzzy controller-based multi-level inverter-fed three-phase induction motor with enhanced time and speed of response. J. Electr. Eng. Technol. 2021, 16, 1131–1141. [Google Scholar] [CrossRef]
- Homaeinezhad, M.; Beik, O. Development of a Generalized Multilevel SVM and Capacitor Voltage Balancing Strategy for Multiphase Three-Level NPC Converters. IEEE Open J. Power Electron. 2024, 5, 1059–1070. [Google Scholar] [CrossRef]
- Balal, A.; Dinkhah, S.; Shahabi, F.; Herrera, M.; Chuang, Y.L. A review on multilevel inverter topologies. Emerg. Sci. J. 2022, 6, 185–200. [Google Scholar] [CrossRef]
- Kanaujia, A.K.; Kumar, S. A Novel Multi-Level SVPWM Scheme for High Power Induction Motor Drive Applications. In Proceedings of the IEEE 1st International Conference on Smart and Sustainable Developments in Electrical Engineering (SSDEE), Dhanbad, India, 28 February–2 March 2025; pp. 1–7. [Google Scholar]
- Elbeji, O.; Boussada, Z.; Ben Hamed, M. Inverter control: Comparative study between SVM and PWM. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Benbouhenni, H.; Bizon, N. A new direct power control method of the DFIG-DRWT system using neural PI controllers and four-level neural modified SVM technique. J. Appl. Res. Technol. 2023, 21, 36–55. [Google Scholar] [CrossRef]
- Oukassi, A.; Elamri, O.; Boulghasoul, Z. ADRC and IFOC Control of a Sensorless Induction Motor Driven by a Multilevel Converter Using SVM Approach and PV Generators. Math. Probl. Eng. 2024, 2024, 6183332. [Google Scholar] [CrossRef]
- Beniak, R.; Górecki, K.; Rogowski, K. Real-Time Switching Number Reduction SVM for a Two-Phase Motor Powered by Three-Level NPC Inverter. Energies 2023, 16, 749. [Google Scholar] [CrossRef]
- Khamlich, S.; Khamlich, F.; Atouf, I.; Benrabh, M. Performance evaluation and implementations of MFCC, SVM and MLP algorithms in the FPGA board. Int. J. Electr. Comput. Eng. Syst. 2021, 12, 139–153. [Google Scholar] [CrossRef]
- Govindharaj, I.; Rampriya, R.; Balamurugan, S. Improving robustness and dynamic performance of sensorless vector-controlled IM drives with ANFIS-enhanced MRAS. Int. J. Electr. Electron. Res. 2024, 12, 975–980. [Google Scholar]
- Korzonek, M.; Orlowska-Kowalska, T. Discrete implementation of sensorless IM drive with MRAS-type speed estimator. In Proceedings of the 2019 International Conference on Electrical Drives & Power Electronics (EDPE), The High Tatras, Slovakia, 24–26 September 2019; pp. 242–247. [Google Scholar]
- Ammar, A.; Kheldoun, A.; Metidji, B.; Ameid, T.; Azzoug, Y. Feedback linearization based sensorless direct torque control using stator flux MRAS-sliding mode observer for induction motor drive. SA Trans. 2020, 98, 382–392. [Google Scholar] [CrossRef]
- Misra, P.; Kumar, B. Rotor resistance estimation for improved performance of MRAS-based sensorless speed estimation of induction motor drives. In Intelligent Algorithms for Analysis and Control of Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2021; pp. 177–187. [Google Scholar]
- Korzonek, M.; Tarchala, G.; Orlowska-Kowalska, T. A review on MRAS-type speed estimators for reliable and efficient induction motor drives. ISA Trans. 2019, 93, 1–13. [Google Scholar] [CrossRef]
- Karlovsky, P.; Lipcak, O.; Lettl, J. Estimation of stator voltage of inverter-supplied induction motor using Kalman Filter. In AETA 2019; Springer: Berlin/Heidelberg, Germany, 2021; pp. 64–73. [Google Scholar]
- Banu, S.; Johnson, T.; Moger, T. A comparative analysis of speed estimation techniques of induction motor drive using non-linear Kalman Filters. In Proceedings of the 2021 31st Australasian Universities Power Engineering Conference (AUPEC), Online, 26–30 September 2021; pp. 1–6. [Google Scholar]
- Quan, V.; Long, T. Sensorless sliding mode control method for a three-phase induction motor. Electr. Eng. 2022, 104, 3685–3695. [Google Scholar] [CrossRef]
- Ilten, E.; Demirtas, M. Fractional order super-twisting sliding mode observer for sensorless control of induction motor. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 878–892. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Javadi, M.S.; Heidari, R.; Catalão, J.P.S. Improved double-surface sliding mode observer for flux and speed estimation of induction motors. ET Electr. Power Appl. 2020, 14, 1002–1010. [Google Scholar] [CrossRef]
- El Daoudi, S.; Lazrak, L.; Lafkih, M.A. Sliding mode approach applied to sensorless direct torque control of cage asynchronous motor via multi-level inverter. Prot. Control Mod. Power Syst. 2020, 5, 13. [Google Scholar] [CrossRef]
- Feng, F.; Yang, J.; Hu, H.; Liang, J.; Yu, S. Speed-sensorless model predictive thrust control of linear induction motor based on improved extended Kalman filter observer. Trans. Inst. Meas. Control 2025, 10, 01423312241307713. [Google Scholar] [CrossRef]
- Caramori, G.; Oliani, I.; Lunardi, A.S.; Sguarezi Filho, A.J. Robust Predictive Current Control of IMs with MRAS-Based Parameter Estimation. IEEE Access 2025, 13, 90921–90931. [Google Scholar] [CrossRef]
- Sengamalai, U.; Anbazhagan, G.; Thentral, T.M.T.; Vishnuram, P.; Khurshaid, T.; Kamel, S. Three phase induction motor drive: A systematic review on dynamic modeling, parameter estimation, and control schemes. Energies 2022, 15, 8260. [Google Scholar] [CrossRef]
- Savarapu, S.; Qutubuddin, M.; Narri, Y. Modified brain emotional controller-based ripple minimization for SVM-DTC of sensorless induction motor drive. IEEE Access 2022, 10, 40872–40887. [Google Scholar] [CrossRef]
- Hasan, F. Vector Control of the Induction Motor Based on Whale Optimization Algorithm. Int. J. Electr. Comput. Eng. Syst. 2025, 16, 31–37. [Google Scholar] [CrossRef]
- Govindharaj, I.; Dinesh Kumar, K.; Balamurugan, S.; Yazhinian, S.; Anandh, R.; Rampriya, R.; Karthick, G.; Michael, G. Sensorless vector-controlled induction motor drives: Boosting performance with Adaptive Neuro-Fuzzy Inference System integrated augmented Model Reference Adaptive System. MethodsX 2024, 13, 102992. [Google Scholar]
- Abdullah, Q.; Farah, N.; Ahmed, M.S.; Shah, N.S.M.; Aydoğdu, Ö.; Talib, H.N.; Al-Moliki, Y.M.; Uğurenver, A.; Al-Mekhalfi, M.A.A.; Aihsan, M.Z.; et al. Sensorless Speed Control of Induction Motor Drives Using Reinforcement Learning and Self-Tuning Simplified Fuzzy Logic Controller. IEEE Access 2024, 12, 136485–136501. [Google Scholar] [CrossRef]
- Benayad, N.; Aouiche, A.; Djeddi, A. Fuzzy Logic Speed Controller for Dual Stator Induction Motor Based on Indirect Vector Control. IAM 2023, 3694, 126–135. [Google Scholar]
- Ben Regaya, C.; Farhani, F.; Hamdi, H.; Zaafouri, A.; Chaari, A. Robust ANFIS vector control of induction motor drive for high-performance speed control supplied by a photovoltaic generator. WSEAS Trans. Syst. Control. 2020, 15, 356–365. [Google Scholar] [CrossRef]
- Fahassa, C.; Akherraz, M.; Zahraoui, Y. ANFIS speed controller and intelligent dual observer based DTC of an induction motor. In Proceedings of the 2018 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Rabat-Kenitra, Morocco, 21–23 November 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Kamaleshwar, R.; Prahadeeshwaran, A.; Srivats Athindran, N. Sensorless sliding mode control SVPWM fed induction motor drive using DSS speed estimator. In Proceedings of the 2017 International Conference on Innovative Research in Electrical Sciences (IICIRES), Nagapattinam, India, 16–17 June 2017; pp. 1–6. [Google Scholar]
- Hasan, M.M. Artificial neural network based speed estimator for sensorless field oriented control of three phase induction motor. In Proceedings of the 3rd International Conference on Electrical, Computer & Telecommunication Engineering (ICECTE), Rajshahi, Bangladesh, 26–28 December 2019; pp. 57–60. [Google Scholar]
- Reddy, S.; Kumar, B.; Swaroop, D. Investigations on training algorithms for neural networks based flux estimator used in speed estimation of induction motor. In Proceedings of the 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; pp. 1090–1094. [Google Scholar]
- Omri, B. Software method versus hardware method to balance capacitors voltages for three level NPC converter. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; IEEE: New York, NY, USA, 2017; pp. 1–4. [Google Scholar]
- Purwanto, E.; Ferdiansyah, I.; Nugraha, S.D.; Qudsi, O.A. The effect of ANFIS controller on the performance of induction motor drives in low-speed operation based on IFOC. Int. J. Adv. Sci. Eng. Inf. Technol. 2021, 11, 440–450. [Google Scholar] [CrossRef]
- Soni, S.K.; Khemariya, M.; Singh, A. Sensorless speed control of induction machine with adaptive-neuro fuzzy technique integrated MRAS module. Int. J. Eng. Trends Technol. 2022, 70, 405–413. [Google Scholar] [CrossRef]
- Ramdani, D.R.; Windarko, N.A.; Purwanto, E. Sensorless speed estimation of induction motor using ANFIS. J. Inf. Syst. Eng. Manage. 2025, 10. [Google Scholar] [CrossRef]
- Miloud, I.; Cauet, S.; Etien, E.; Salameh, J.P.; Ungerer, A. Real-time speed estimation for an induction motor: An automated tuning of an extended Kalman filter using voltage–current sensors. Sensors 2024, 24, 1744. [Google Scholar] [CrossRef]
- Çavuş, B.; Aktaş, M. Sliding mode speed estimation of induction motor with MPC-based flux weakening control for electric vehicle. Afyon Kocatepe Univ. J. Sci. Eng. 2024, 24, 1403–1411. [Google Scholar] [CrossRef]
- Hamdi, W.; Hammoudi, M.Y.; Betka, A. Sensorless speed control of induction motor using Model Reference Adaptive System and deadbeat regulator. Eng. Proc. 2023, 56, 16. [Google Scholar]
- Zaky, M.S.; Metwaly, M.K. Sensitivity analysis of a stator current-based MRAS estimator for sensorless induction motor drives. Eng. Technol. Appl. Sci. Res. 2024, 14, 17584–17590. [Google Scholar] [CrossRef]



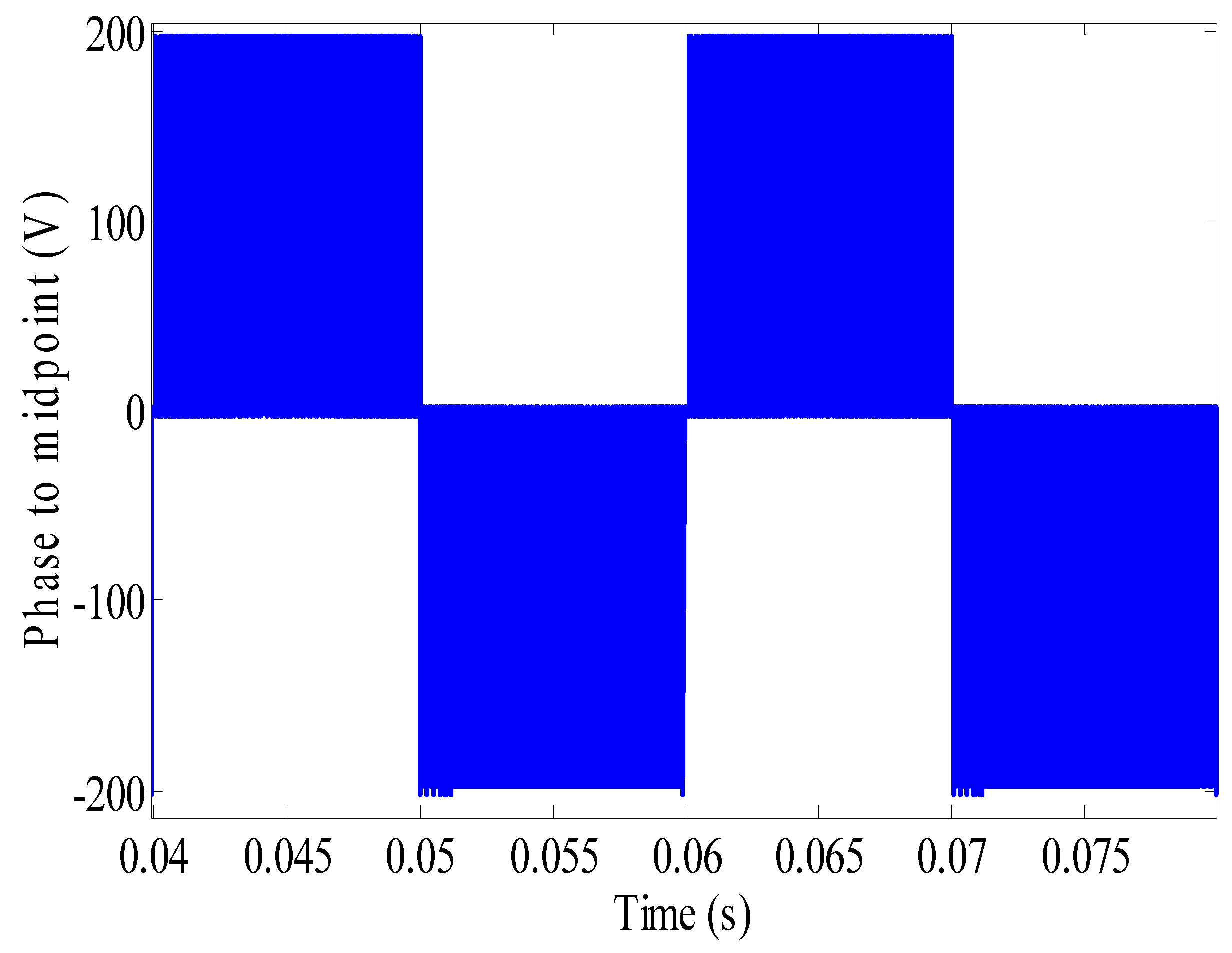
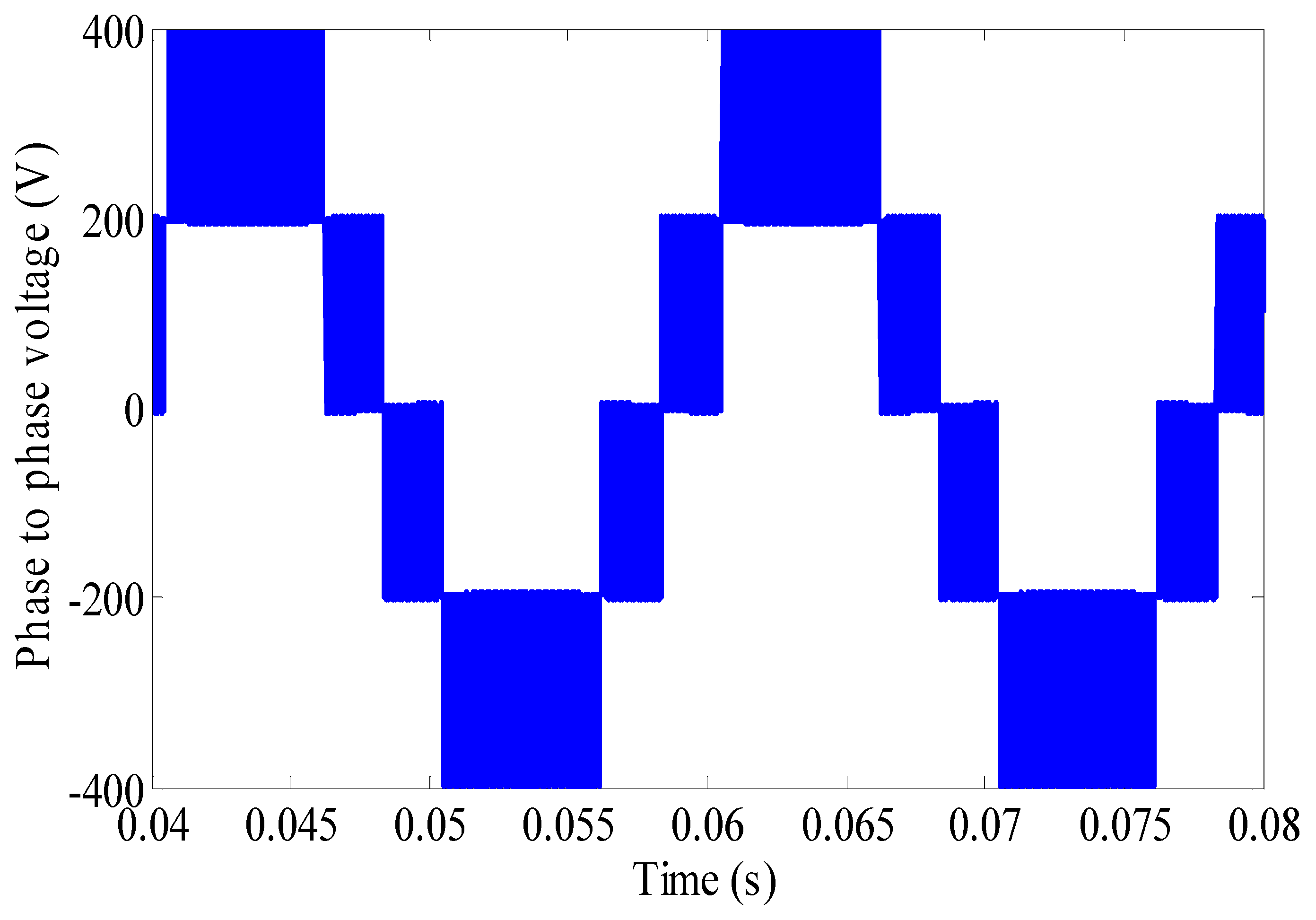
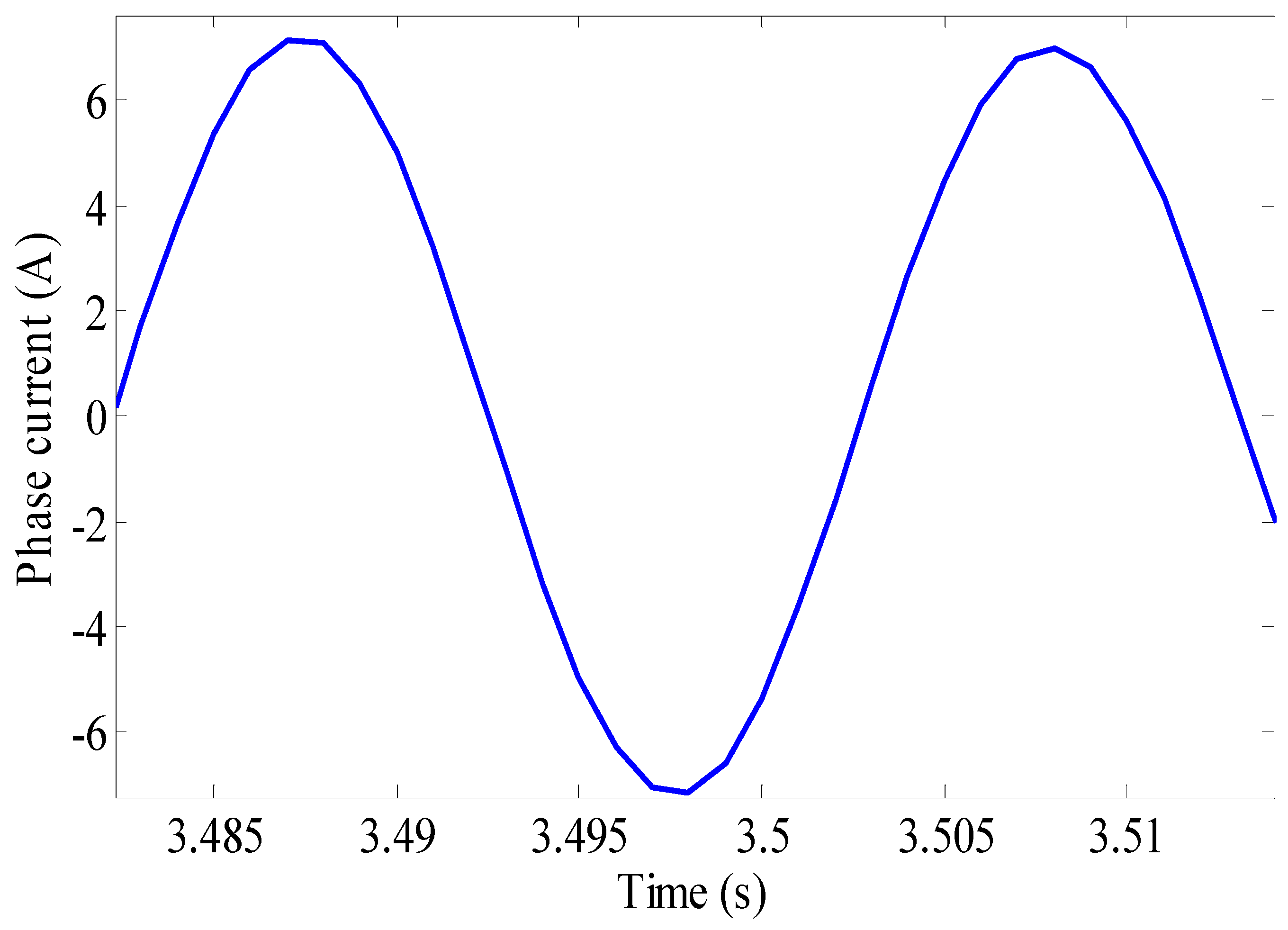
| Parameter | Design |
|---|---|
| Vds and Vqs | d-q axis stator voltages respectively |
| Ids, Iqs, Idr, and Iqr | d-q axis stator currents d-q axis rotor currents respectively |
| Rs, Rr | Stator and rotor resistance per phase respectively |
| p | Number of poles |
| ωs, ωr | Speed of the rotating magnetic field and the rotor speed respectively |
| Ce | Electromagnetic developed torque. |
| Ls, Lr, M | Self-inductances of the stator and rotor and the mutual inductance respectively |
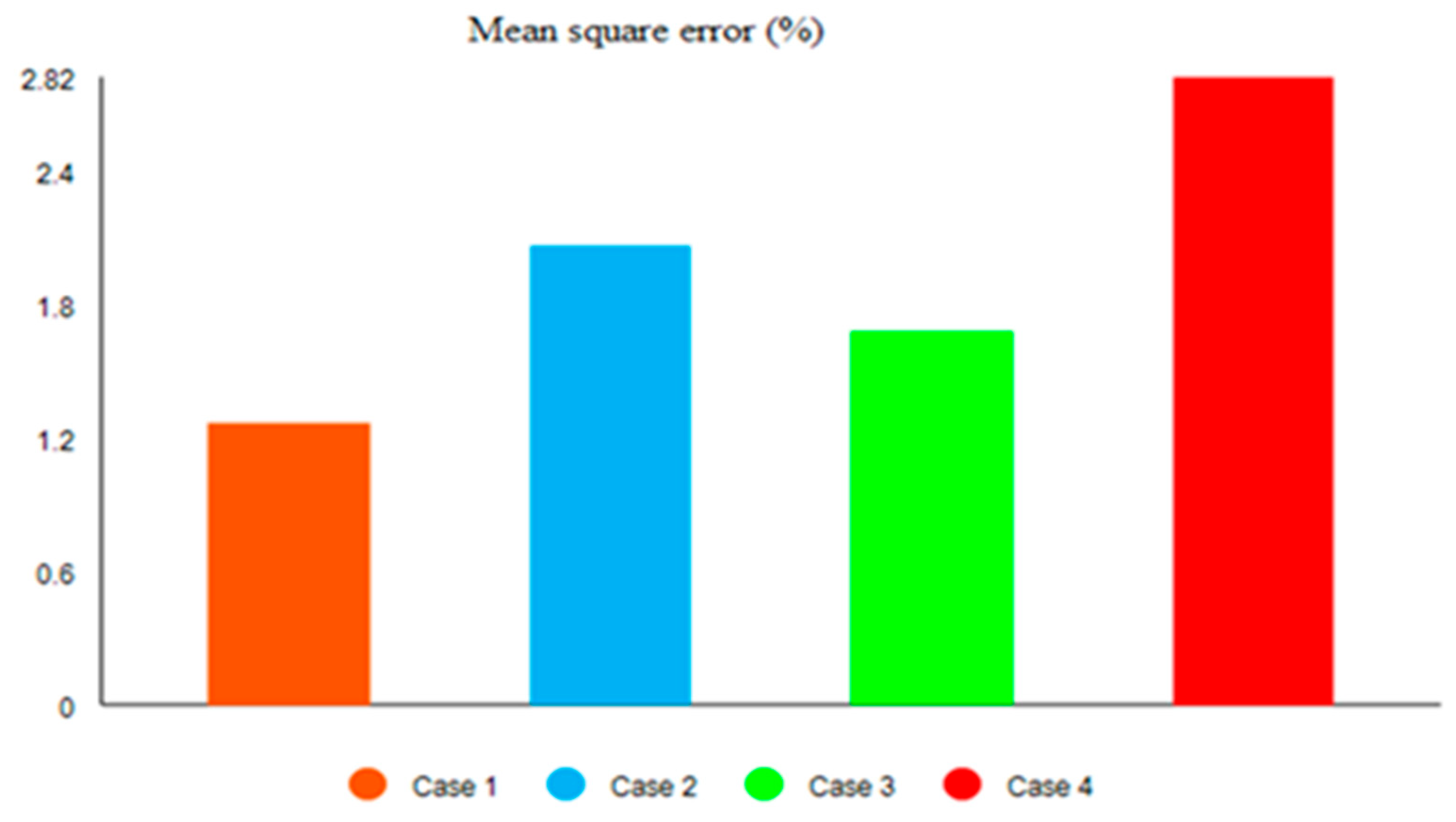
| No | Type of Membership Function | Root Mean Square Error (%) |
|---|---|---|
| 1 | Trimf | 1.27 |
| 2 | Trapmf | 2.06 |
| 3 | Gbellmf | 1.681 |
| 4 | Gaussmf | 2.82 |
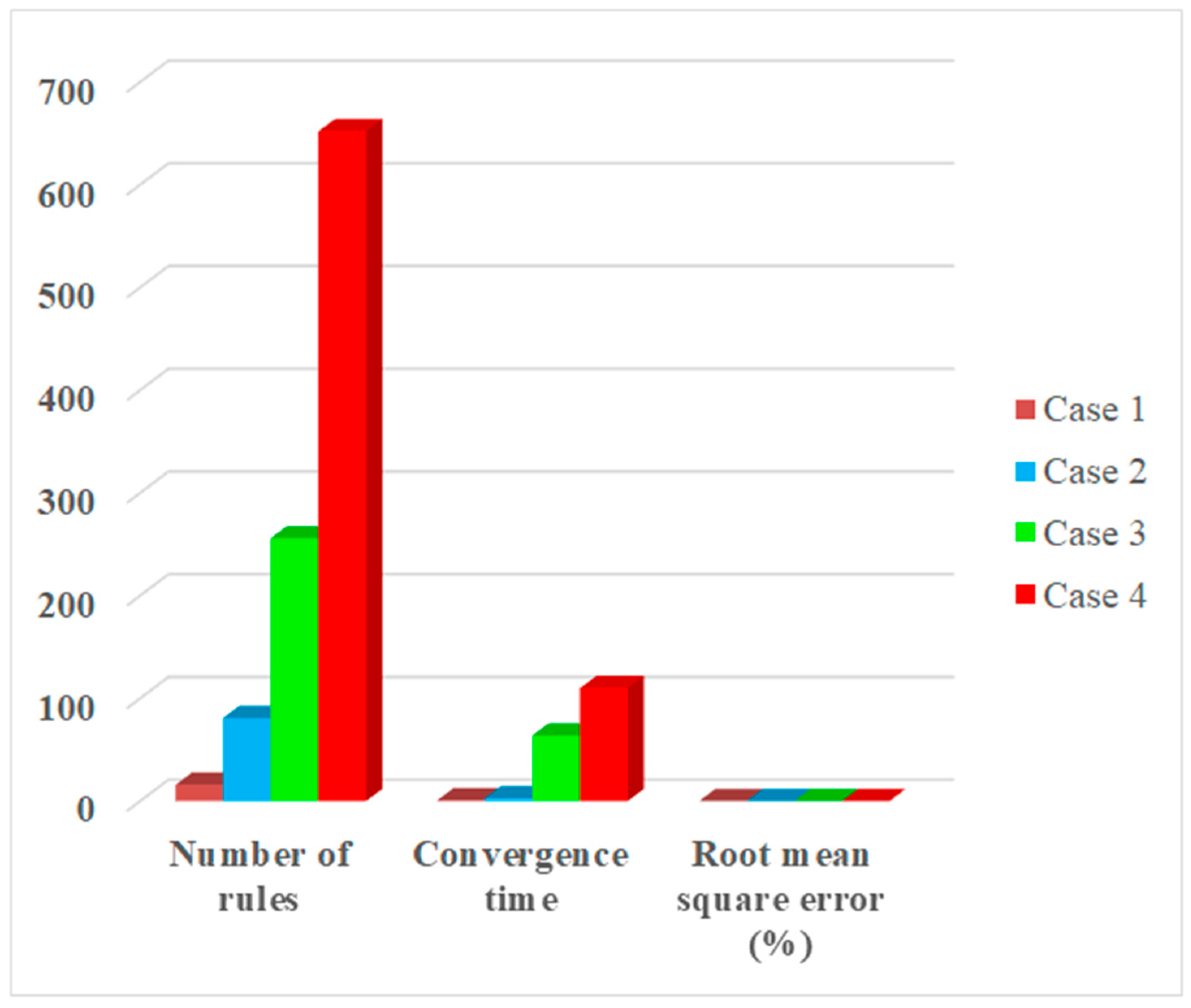
| No | Number of Membership Functions | Number of Rules | Convergence Time (s) | Root Mean Square Error at Training Phase (%) |
|---|---|---|---|---|
| 1 | 2 2 2 2 | 16 | 1 | 5.64 |
| 2 | 3 3 3 3 | 81 | 3 | 4.48 |
| 3 | 4 4 4 4 | 256 | 64 | 2.17 |
| 4 | 5 5 5 5 | 652 | 110 | 1.75 |
| Parameter | Design |
|---|---|
| Type | Sugeno |
| Inputs number | 4 |
| Number of membership functions for inputs | 3 |
| Membership function of input | type trimf |
| Number of outputs | 1 |
| Number of rules | 81 |
| Estimator | RMSE (rpm) | Convergence Time (s) | Rules/Complexity | Robustness to Load |
|---|---|---|---|---|
| ANFIS | 0.005 | 5 | 81 (3 MFs) | High |
| MRAS-Luenberger | 0.008 | 7 | Low (model-based) | Moderate |
| EKF | 0.01 | 8 | High (matrix ops) | High |
| SMO | 0.012 | 6 | Moderate | Moderate |
| C1 | C2 | C3 | Van | Vbn | Vcn | Vα | Vβ | Vab |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | |||||
| 0 | 0 | 2 | − | − | 0 | |||
| 0 | 1 | 0 | ||||||
| 0 | 1 | 1 | − | 0 | ||||
| 0 | 1 | 2 | 0 | |||||
| 0 | 2 | 0 | ||||||
| 0 | 2 | 1 | 0 | |||||
| 0 | 2 | 2 | 0 | |||||
| 1 | 0 | 0 | 0 | |||||
| 1 | 0 | 1 | ||||||
| 1 | 0 | 2 | 0 | 0 | ||||
| 1 | 1 | 0 | − | 0 | ||||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 2 | 0 | |||||
| 1 | 2 | 0 | 0 | 0 | ||||
| 1 | 2 | 1 | ||||||
| 1 | 2 | 2 | − | 0 | ||||
| 2 | 0 | 0 | − | − | 0 | |||
| 2 | 0 | 2 | ||||||
| 2 | 0 | 1 | 0 | |||||
| 2 | 1 | 1 | 0 | |||||
| 2 | 1 | 2 | ||||||
| 2 | 2 | 0 | 0 | |||||
| 2 | 2 | 1 | 0 | |||||
| 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boussada, Z.; Omri, B.; Hamed, M.B. High-Performance Sensorless Control of Induction Motors via ANFIS and NPC Inverter Topology. Symmetry 2025, 17, 1996. https://doi.org/10.3390/sym17111996
Boussada Z, Omri B, Hamed MB. High-Performance Sensorless Control of Induction Motors via ANFIS and NPC Inverter Topology. Symmetry. 2025; 17(11):1996. https://doi.org/10.3390/sym17111996
Chicago/Turabian StyleBoussada, Zina, Bassem Omri, and Mouna Ben Hamed. 2025. "High-Performance Sensorless Control of Induction Motors via ANFIS and NPC Inverter Topology" Symmetry 17, no. 11: 1996. https://doi.org/10.3390/sym17111996
APA StyleBoussada, Z., Omri, B., & Hamed, M. B. (2025). High-Performance Sensorless Control of Induction Motors via ANFIS and NPC Inverter Topology. Symmetry, 17(11), 1996. https://doi.org/10.3390/sym17111996





