Behavior-Based Optimization of Emergency Shelter Siting: A TPB–NSGA-III Approach Applied to Hangzhou
Abstract
1. Introduction
1.1. Conventional Approaches to Shelter Siting
1.2. Applying Heuristic Algorithms to Shelter Siting
1.3. Multi-Criteria Techniques for Shelter Siting
1.4. Application of TPB and NSGA-III in This Research
- RQ1: Can integrating TPB-based modeling into an NSGA-III siting optimizer significantly improve population coverage and travel time accessibility compared to the current situation?
- RQ2: Can integrating TPB-based behavioral modeling into the NSGA-III optimizer yield greater relative improvements in shelter accessibility and population coverage under the vulnerable scenario than in general or emergency scenarios?
2. Method
2.1. Technical Framework
- Data Foundation Construction: The entire area of Hangzhou is divided into 285,792 grids with a size of 50 m × 50 m each. Each grid cell contains three types of data, namely (1) the total population within the grid, (2) the coordinate values of the grid’s central point, and (3) a unique identifier for each grid, referred to as a population point. In addition, 3600 emergency shelters are randomly allocated based on population density, and each shelter is assigned a unique identifier.
- Calculations Based on the TPB: Using the TPB framework, two key metrics are calculated, namely (1) the total population served by each emergency shelter site for any given population point and (2) the time satisfaction of the population point in terms of reaching the emergency shelter site.
- NSGA-III Iterative Optimization Objectives: Based on the TPB-calculated results, two iterative optimization objectives are set for NSGA-III following the Pareto optimal concept, including (1) serving as many people as possible () and (2) minimizing the maximum satisfaction time (). The maximum time threshold for rapid access to emergency shelter sites is set at 5 or 15 min as a boundary condition.
- NSGA-III High-Dimensional Calculation Model: A high-dimensional NSGA-III model is established using the coordinate data of emergency shelter sites (j). Gene iteration calculations are performed based on objective .
- Point Optimization and Analysis: Based on the results from NSGA-III, optimization and analysis of the emergency shelter site locations are carried out.
2.2. Demand Simulation and Goal Setting Based on the Theory of Planned Behavior
2.3. Multi-Objective Optimization Based on NSGA-III
- Selecting one gene segment from each reference point.
- Adding these gene segments to the queue, with segments from reference points containing fewer gene segments ranked higher.
- If a reference point no longer contains any unselected gene segments, removing it from the process.
- Returning to step 1 and selecting the next round of gene segments until all segments are sorted.
3. Results
3.1. The Convergence Process of NSGA-III
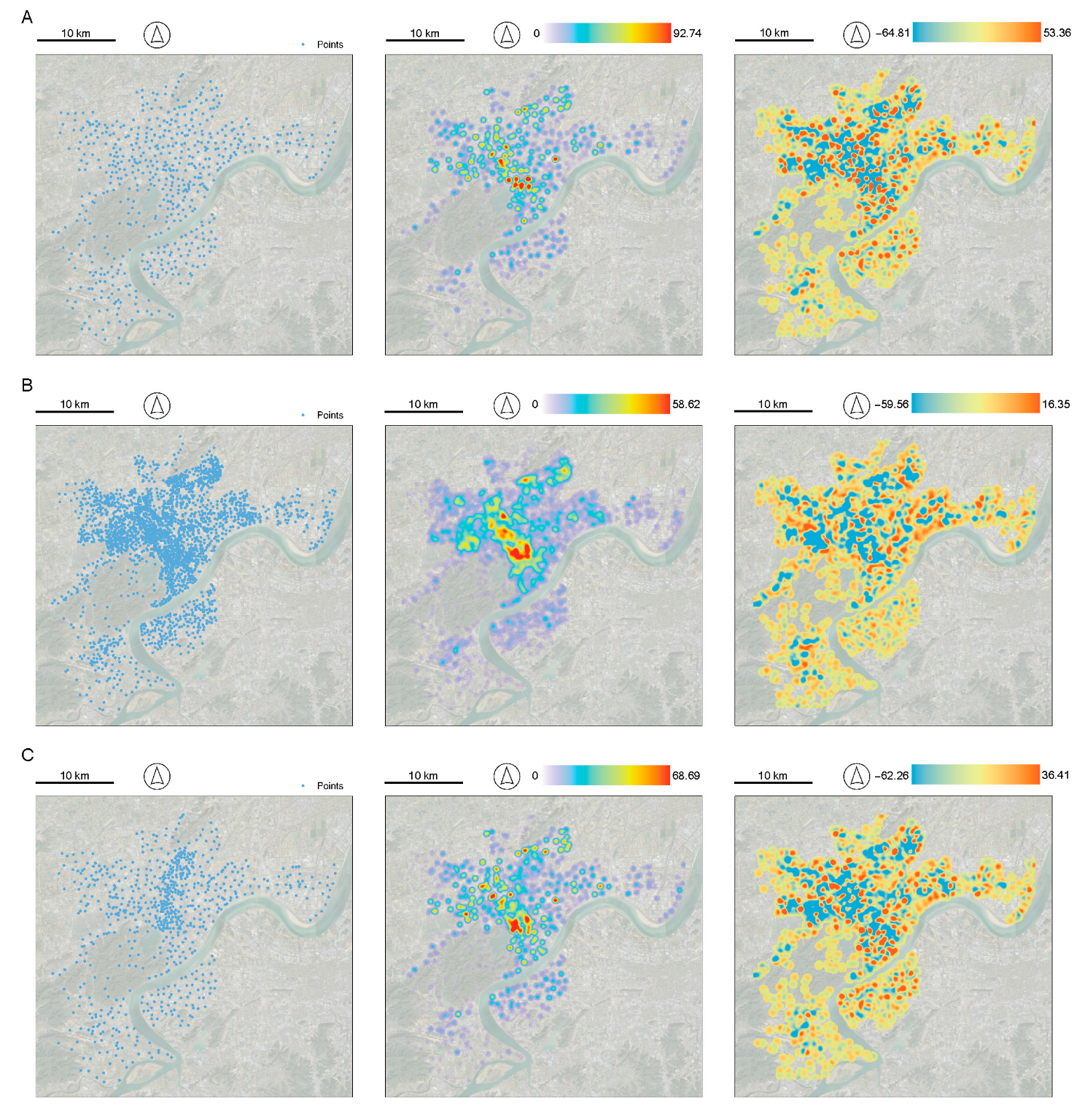
3.2. The Optimization Results of the General Situation Using the NSGA-III Method Based on the TPB
3.3. The Optimization Results for an Emergency Using the NSGA-III Method Based on the TPB
3.4. The Optimization Results of Focusing on Vulnerable Groups Using the NSGA-III Method Based on the TPB
3.5. The Comparison Between Three Optimization Results
3.6. Summary
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TPB | Theory of Planned Behavior |
| NSGA-III | Non-dominated Sorting Genetic Algorithm III |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| ACO | Ant Colony Optimization |
| PSO | Particle Swarm Optimization |
References
- Gai, C.; Weng, W.; Yuan, H. Review of Public Safety in Viewpoint of Complex Networks. AIP Conf. Proc. 2010, 1233, 801–805. [Google Scholar] [CrossRef]
- Huang, L.; Shi, P.; Zhu, H.; Chen, T. Early detection of emergency events from social media: A new text clustering approach. Nat. Hazards 2022, 111, 851–875. [Google Scholar] [CrossRef] [PubMed]
- Sajjad, M.; Chan, J.C.; Chopra, S.S. Rethinking disaster resilience in high-density cities: Towards an urban resilience knowledge system. Sustain. Cities Soc. 2021, 69, 102850. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Y.; Luo, A.; Xu, S.; Chen, J.; Liu, W. Site selection and prediction of urban emergency shelter based on VGAE-RF model. Sci. Rep. 2024, 14, 14368. [Google Scholar] [CrossRef]
- Park, H.S.; Kwon, S.A.; Azam, M. A study on GIS-based spatial analysis of emergency response for disaster management: Focusing on Seoul. Heliyon 2024, 10, e28669. [Google Scholar] [CrossRef]
- Sheu, J.-B. An emergency logistics distribution approach for quick response to urgent relief demand in disasters. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 687–709. [Google Scholar]
- Huang, K.; Rafiei, R. Equitable last mile distribution in emergency response. Comput. Ind. Eng. 2019, 127, 887–900. [Google Scholar] [CrossRef]
- Khayal, D.; Pradhananga, R.; Pokharel, S.; Mutlu, F. A model for planning locations of temporary distribution facilities for emergency response. Socio-Econ. Plan. Sci. 2015, 52, 22–30. [Google Scholar]
- Mete, H.O.; Zabinsky, Z.B. Stochastic optimization of medical supply location and distribution in disaster management. Int. J. Prod. Econ. 2010, 126, 76–84. [Google Scholar] [CrossRef]
- Rawls, C.G.; Turnquist, M.A. Pre-positioning of emergency supplies for disaster response. Transp. Res. Part B Methodol. 2010, 44, 521–534. [Google Scholar] [CrossRef]
- Rawls, C.G.; Turnquist, M.A. Pre-positioning planning for emergency response with service quality constraints. OR Spectr. 2011, 33, 481–498. [Google Scholar] [CrossRef]
- Sheu, J.-B.; Pan, C. A method for designing centralized emergency supply network to respond to large-scale natural disasters. Transp. Res. Part B Methodol. 2014, 67, 284–305. [Google Scholar]
- Huang, K.; Jiang, Y.; Yuan, Y.; Zhao, L. Modeling multiple humanitarian objectives in emergency response to large-scale disasters. Transp. Res. Part E Logist. Transp. Rev. 2015, 75, 1–17. [Google Scholar]
- Caunhye, A.M.; Zhang, Y.; Li, M.; Nie, X. A location-routing model for prepositioning and distributing emergency supplies. Transp. Res. Part E Logist. Transp. Rev. 2016, 90, 161–176. [Google Scholar] [CrossRef]
- Fu, L.; Sun, D.; Rilett, L.R. Heuristic shortest path algorithms for transportation applications: State of the art. Comput. Oper. Res. 2006, 33, 3324–3343. [Google Scholar] [CrossRef]
- Silver, E.A. An overview of heuristic solution methods. J. Oper. Res. Soc. 2004, 55, 936–956. [Google Scholar] [CrossRef]
- Wang, X.; Choi, T.-M.; Liu, H.; Yue, X. A novel hybrid ant colony optimization algorithm for emergency transportation problems during post-disaster scenarios. IEEE Trans. Syst. Man Cybern. Syst. 2016, 48, 545–556. [Google Scholar]
- Yi, W.; Kumar, A. Ant colony optimization for disaster relief operations. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 660–672. [Google Scholar] [CrossRef]
- Mohammadi, R.; Ghomi, S.F.; Jolai, F. Prepositioning emergency earthquake response supplies: A new multi-objective particle swarm optimization algorithm. Appl. Math. Model. 2016, 40, 5183–5199. [Google Scholar] [CrossRef]
- Mondal, T.; Boral, N.; Bhattacharya, I.; Das, J.; Pramanik, P. Distribution of deficient resources in disaster response situation using particle swarm optimization. Int. J. Disaster Risk Reduct. 2019, 41, 101308. [Google Scholar] [CrossRef]
- Wang, J.; Situ, C.; Yu, M. The post-disaster emergency planning problem with facility location and people/resource assignment. Kybernetes 2020, 49, 2385–2418. [Google Scholar] [CrossRef]
- Wang, B.C.; Qian, Q.Y.; Gao, J.J.; Tan, Z.Y.; Zhou, Y. The optimization of warehouse location and resources distribution for emergency rescue under uncertainty. Adv. Eng. Inform. 2021, 48, 101278. [Google Scholar] [CrossRef]
- Bo, Y.; Cheng, W.; Hua, H.; Lijun, L. A multi-agent and PSO based simulation for human behavior in emergency evacuation. In Proceedings of the 2007 International Conference on Computational Intelligence and Security (CIS 2007), Harbin, China, 15–19 December 2007; pp. 296–300. [Google Scholar]
- Nayeri, S.; Tavakkoli-Moghaddam, R.; Sazvar, Z.; Heydari, J. A heuristic-based simulated annealing algorithm for the scheduling of relief teams in natural disasters. Soft Comput. 2022, 26, 1825–1843. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Mason, S.J. A bi-objective optimisation of post-disaster relief distribution and short-term network restoration using hybrid NSGA-II algorithm. Int. J. Prod. Res. 2022, 60, 5769–5793. [Google Scholar] [CrossRef]
- Niu, X.; Tang, H.; Wu, L. Satellite scheduling of large areal tasks for rapid response to natural disaster using a multi-objective genetic algorithm. Int. J. Disaster Risk Reduct. 2018, 28, 813–825. [Google Scholar] [CrossRef]
- Yan, L.; Jinsong, B.; Xiaofeng, H.; Ye, J. A heuristic project scheduling approach for quick response to maritime disaster rescue. Int. J. Proj. Manag. 2009, 27, 620–628. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, W.; Qin, L.; Zhao, X. Site Selection Models in Natural Disaster Shelters: A Review. Sustainability 2019, 11, 399. [Google Scholar] [CrossRef]
- Shadkam, E.; Cheraghchi, M. Prioritization of earthquake relief using a hybrid two-phase approach. J. Appl. Res. Ind. Eng. 2022, 9, 493–506. [Google Scholar] [CrossRef]
- Najafi, M.; Ardalan, A.; Akbarisari, A.; Noorbala, A.A.; Elmi, H. The theory of planned behavior and disaster preparedness. PLoS Curr. 2017, 9. [Google Scholar]
- Kinateder, M.T.; Kuligowski, E.D.; Reneke, P.A.; Peacock, R.D. Risk perception in fire evacuation behavior revisited: Definitions, related concepts, and empirical evidence. Fire Sci. Rev. 2015, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Freiberger, E.; Sieber, C.C.; Kob, R. Mobility in older community-dwelling persons: A narrative review. Front. Physiol. 2020, 11, 881. [Google Scholar] [CrossRef]
- Department of Economic. World Population Prospects 2024: Summary of Results; Stylus Publishing, LLC: Sterling, VA, USA, 2024. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Ajzen, I. The theory of planned behavior. Organ. Behav. Hum. Decis. Process. 1991, 50, 179–211. [Google Scholar] [CrossRef]
- Train, K.E. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Snyder, L.V. Facility location under uncertainty: A review. IIE Trans. 2006, 38, 547–564. [Google Scholar] [CrossRef]
- Poikolainen, I.; Neri, F.; Caraffini, F. Cluster-based population initialization for differential evolution frameworks. Inf. Sci. 2015, 297, 216–235. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, W.; Ma, Y.; Hu, F. Scenario-based multi-objective optimum allocation model for earthquake emergency shelters using a modified particle swarm optimization algorithm: A case study in Chaoyang District, Beijing, China. PLoS ONE 2015, 10, e0144455. [Google Scholar] [CrossRef]
- Moreno, C.; Allam, Z.; Chabaud, D.; Gall, C.; Pratlong, F. Introducing the “15-Minute City”: Sustainability, Resilience and Place Identity in Future Post-Pandemic Cities. Smart Cities 2021, 4, 93–111. [Google Scholar] [CrossRef]
- Nazif, S.; Mohammadpour Khoie, M.M.; Eslamian, S. Urban disaster management and resilience. In Handbook of Disaster Risk Reduction for Resilience: New Frameworks for Building Resilience to Disasters; Springer: Cham, Switzerland, 2021; pp. 157–185. [Google Scholar]
- Etinay, N.; Egbu, C.; Murray, V. Building urban resilience for disaster risk management and disaster risk reduction. Procedia Eng. 2018, 212, 575–582. [Google Scholar] [CrossRef]
- Rana, I.A.; Asim, M.; Aslam, A.B.; Jamshed, A. Disaster management cycle and its application for flood risk reduction in urban areas of Pakistan. Urban Clim. 2021, 38, 100893. [Google Scholar] [CrossRef]
- Akgün, İ.; Gümüşbuğa, F.; Tansel, B. Risk based facility location by using fault tree analysis in disaster management. Omega 2015, 52, 168–179. [Google Scholar] [CrossRef]
- Park, K.; Oh, H.; Won, J.-h. Analysis of disaster resilience of urban planning facilities on urban flooding vulnerability. Environ. Eng. Res. 2021, 26, 190529. [Google Scholar] [CrossRef]






| Walking Time Threshold Range | General | Emergency | For Vulnerable | |
|---|---|---|---|---|
| F1 | Initial Value | 5,657,327 | 5,177,386 | 5,382,346 |
| Optimized Value | 5,668,054 | 5,569,283 | 5,608,284 | |
| Population Coverage Change | 10,727 | 391,897 | 225,938 | |
| Increased Coverage Rate | 99.93% | 98.19% | 98.87% | |
| Coverage Increase | 0.19% | 6.91% | 3.98% | |
| F2 | Initial Value | 0.552 | 0.424 | 0.552 |
| Optimized Value | 0.647 | 0.581 | 0.648 | |
| Original Required Time | 305.96 | 122.34 | 313.75 | |
| Optimized Time | 261.98 | 100.26 | 261.62 | |
| Optimization Ratio | 14.37% | 18.05% | 16.62% | |
| Converged Quantity | 561 | 2291 | 577 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, N.; Huang, S.; Wu, Y.; Liu, J.; Cheng, M. Behavior-Based Optimization of Emergency Shelter Siting: A TPB–NSGA-III Approach Applied to Hangzhou. Symmetry 2025, 17, 1964. https://doi.org/10.3390/sym17111964
Yu N, Huang S, Wu Y, Liu J, Cheng M. Behavior-Based Optimization of Emergency Shelter Siting: A TPB–NSGA-III Approach Applied to Hangzhou. Symmetry. 2025; 17(11):1964. https://doi.org/10.3390/sym17111964
Chicago/Turabian StyleYu, Ningzhe, Shan Huang, Yanxi Wu, Jiale Liu, and Mingjun Cheng. 2025. "Behavior-Based Optimization of Emergency Shelter Siting: A TPB–NSGA-III Approach Applied to Hangzhou" Symmetry 17, no. 11: 1964. https://doi.org/10.3390/sym17111964
APA StyleYu, N., Huang, S., Wu, Y., Liu, J., & Cheng, M. (2025). Behavior-Based Optimization of Emergency Shelter Siting: A TPB–NSGA-III Approach Applied to Hangzhou. Symmetry, 17(11), 1964. https://doi.org/10.3390/sym17111964







