A Chaos-Initiated and Adaptive Multi-Guide Control-Based Crayfish Optimization Algorithm for Image Analysis
Abstract
1. Introduction
- We present CMCOA, an improved optimization algorithm that integrates chaotic initialization and adaptive multi-guide control, showing consistent gains in exploration, convergence speed, and robustness on benchmarks and multispectral datasets.
- CMCOA combines logistic-map chaos with opposition-based learning to enhance initial diversity and accelerate early search, while an MIT-inspired adaptive mechanism adjusts parameters to maintain a balance between exploration and exploitation.
- A multi-guide stage-switching strategy enables flexible transitions across search phases, reducing leader bias and supporting more reliable solution quality.
- Applied to multispectral image clustering, CMCOA improves cluster balance and texture preservation, yielding meaningful segmentation with practical efficiency in high-dimensional tasks.
2. The Chaotic Initialization and Adaptive Multi-Guide Control-Based Crayfish Optimization Algorithm
2.1. Overview of the Original Crayfish Optimization Algorithm
2.1.1. Initialization
2.1.2. Temperature Schedule
2.1.3. Summer Resort Stage
2.1.4. Competition Stage
2.1.5. Foraging Stage
- Shredding (when ): If the food is large relative to the agent’s state, the crayfish first “shreds” it. The global best position is scaled to simulate processing:Then the crayfish advances toward the food with an alternating step:Here is the food intake proportion, determined by a Gaussian function of the temperature:Among them, µ refers to the temperature most suitable for crayfish, σ and are used to control the intake of crayfish at different temperatures, where and in the original COA formulation. The sine-cosine term is designed to emulate the alternating use of claws when manipulating larger food items, thereby enabling fine-grained local search behavior within the optimization process.
- Direct Feeding (when ): If the food is small enough, the crayfish moves directly toward it:This accelerates convergence by exploiting the gradient toward the best solution. These stages are repeated until the iteration limit T is reached. Throughout, the algorithm updates global and local bests. In summary, COA embeds exploration and exploitation within a unified framework.
2.2. Improved Strategy Framework of CMCOA
2.2.1. Chaotic Initialization Strategy
2.2.2. Adaptive Parameter Control Rule
2.2.3. Multi-Guide and Stage-Switching Update Mechanism
- Multi-guide update
- Stage-switching rule
2.3. Complexity Analysis
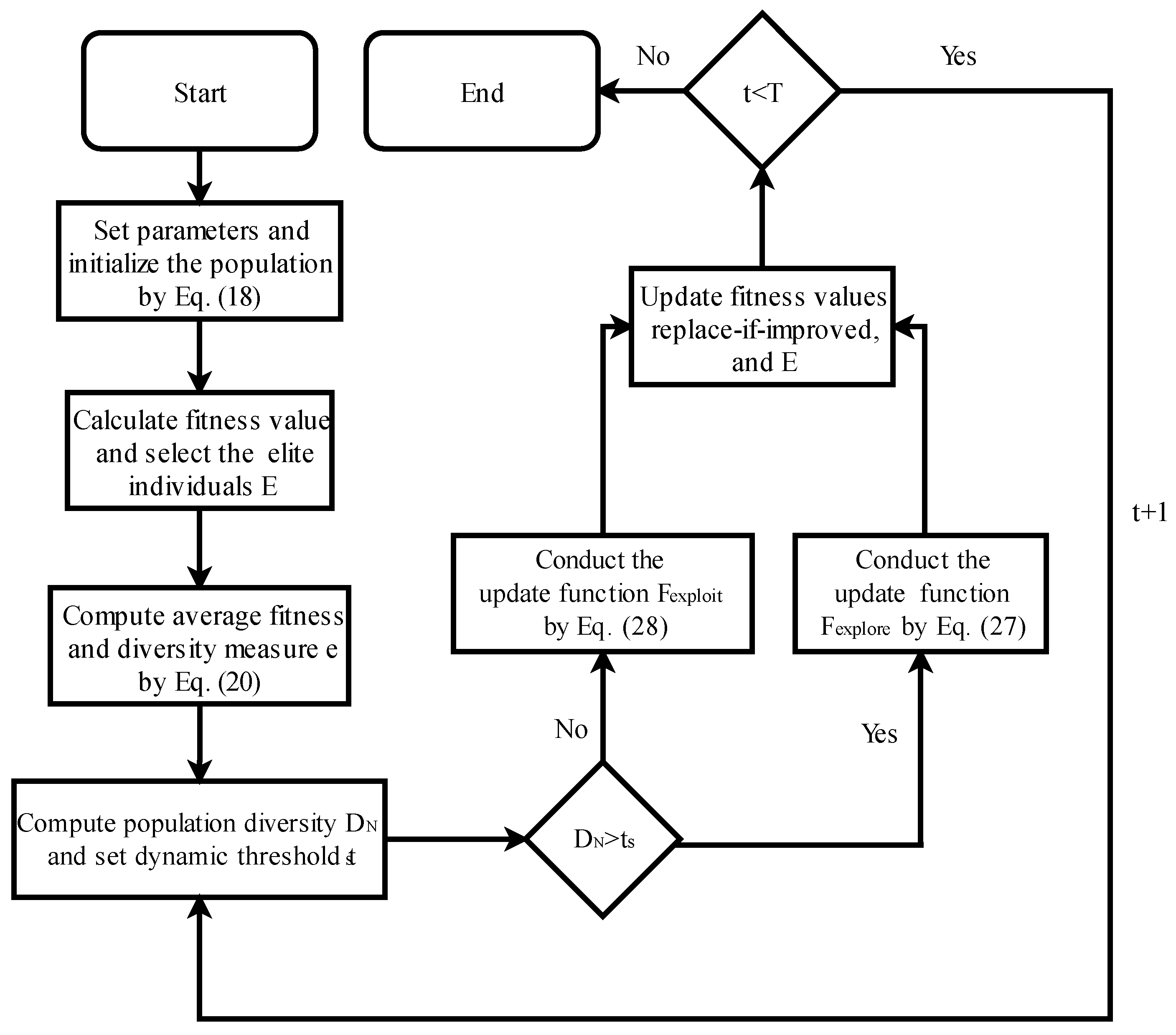
2.4. Pseudo Code and Flow Chart of CMCOA
| Algorithm 1: The CMCOA algorithm |
|
2.5. Numeric Experiments
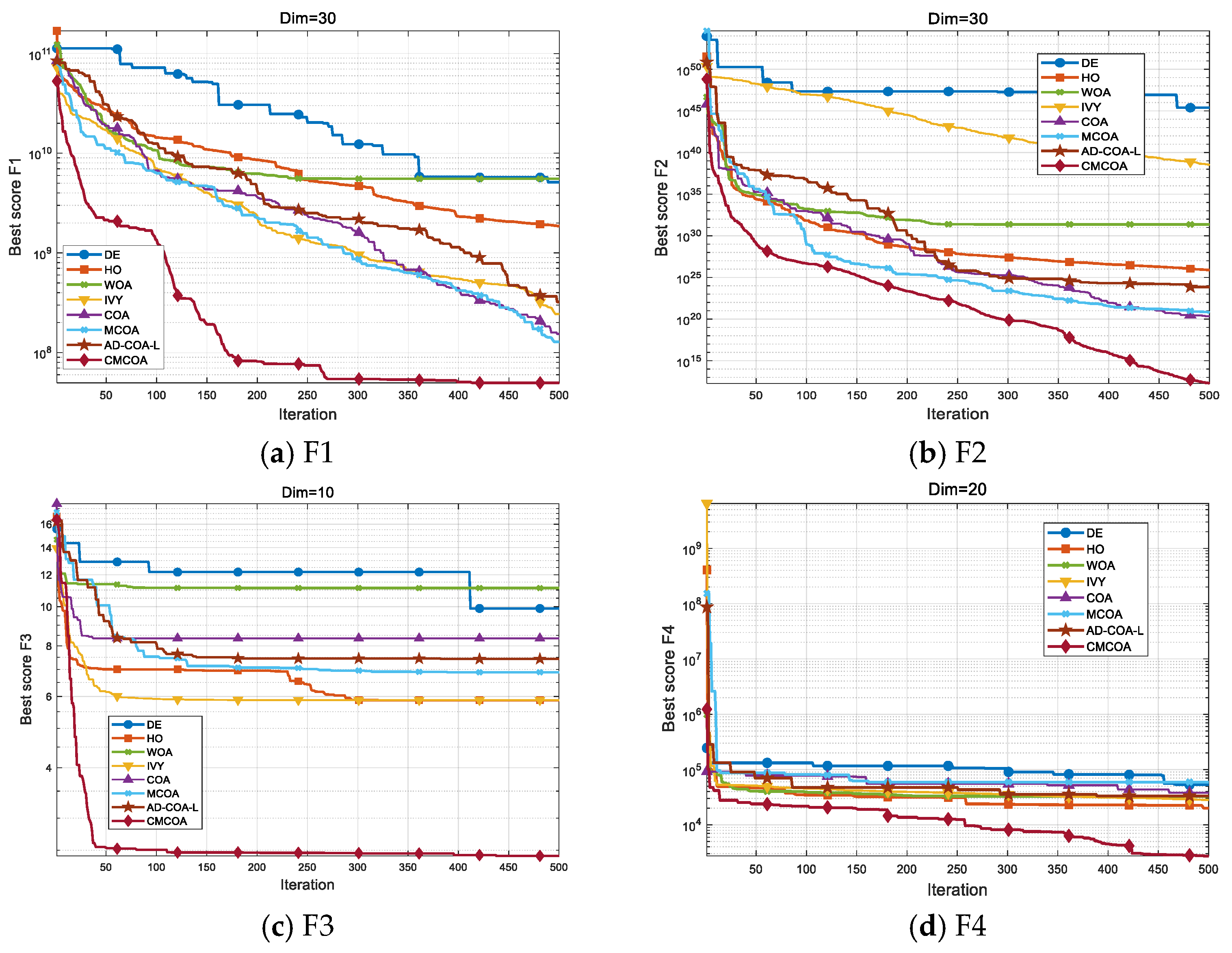
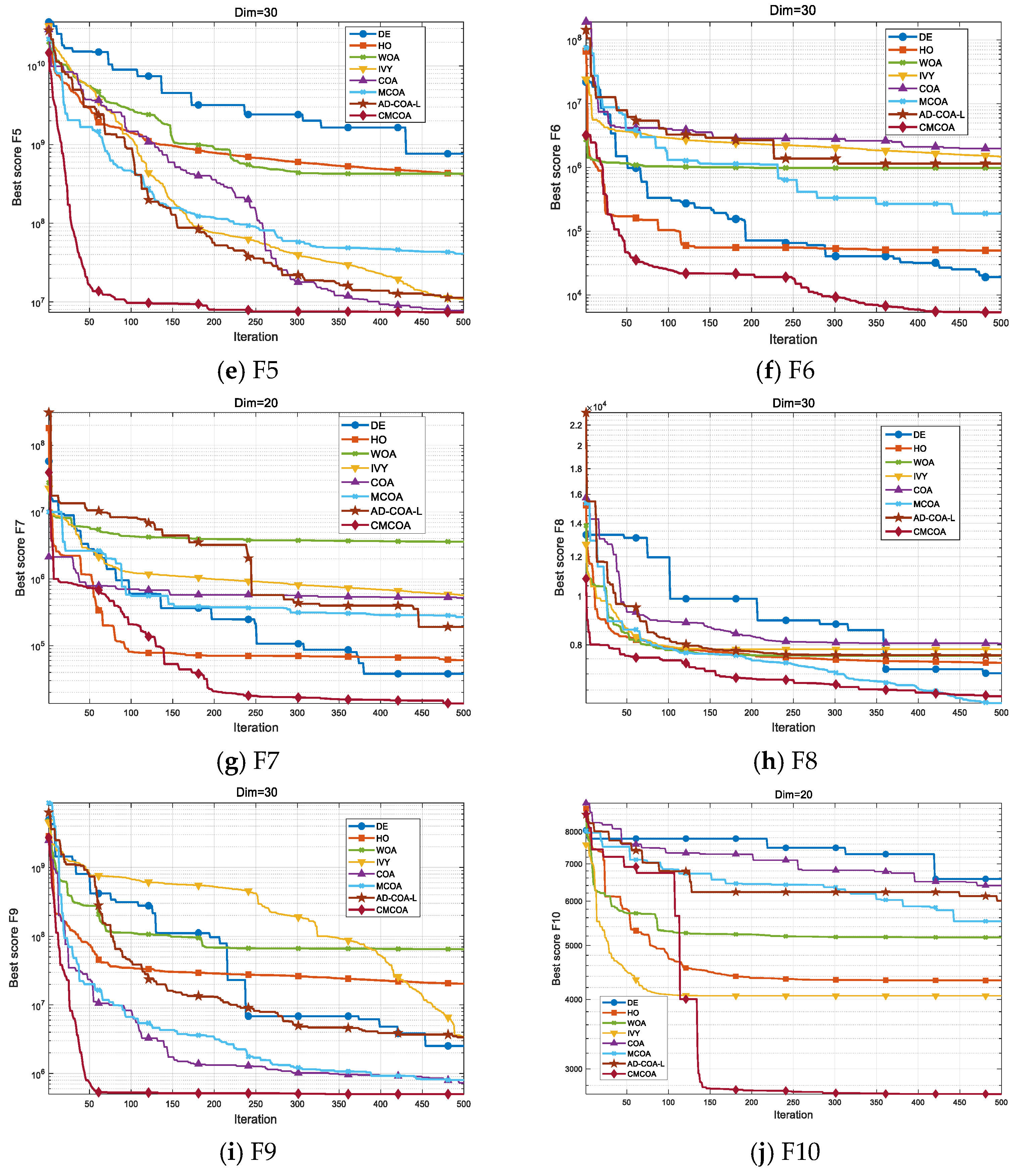
2.5.1. Algorithm Performance Analysis on Test Functions
2.5.2. Analysis of Non-Parametric Statistical Significance Test of CMCOA
2.5.3. Engineering Design Problems
- Gear Train Design Problem
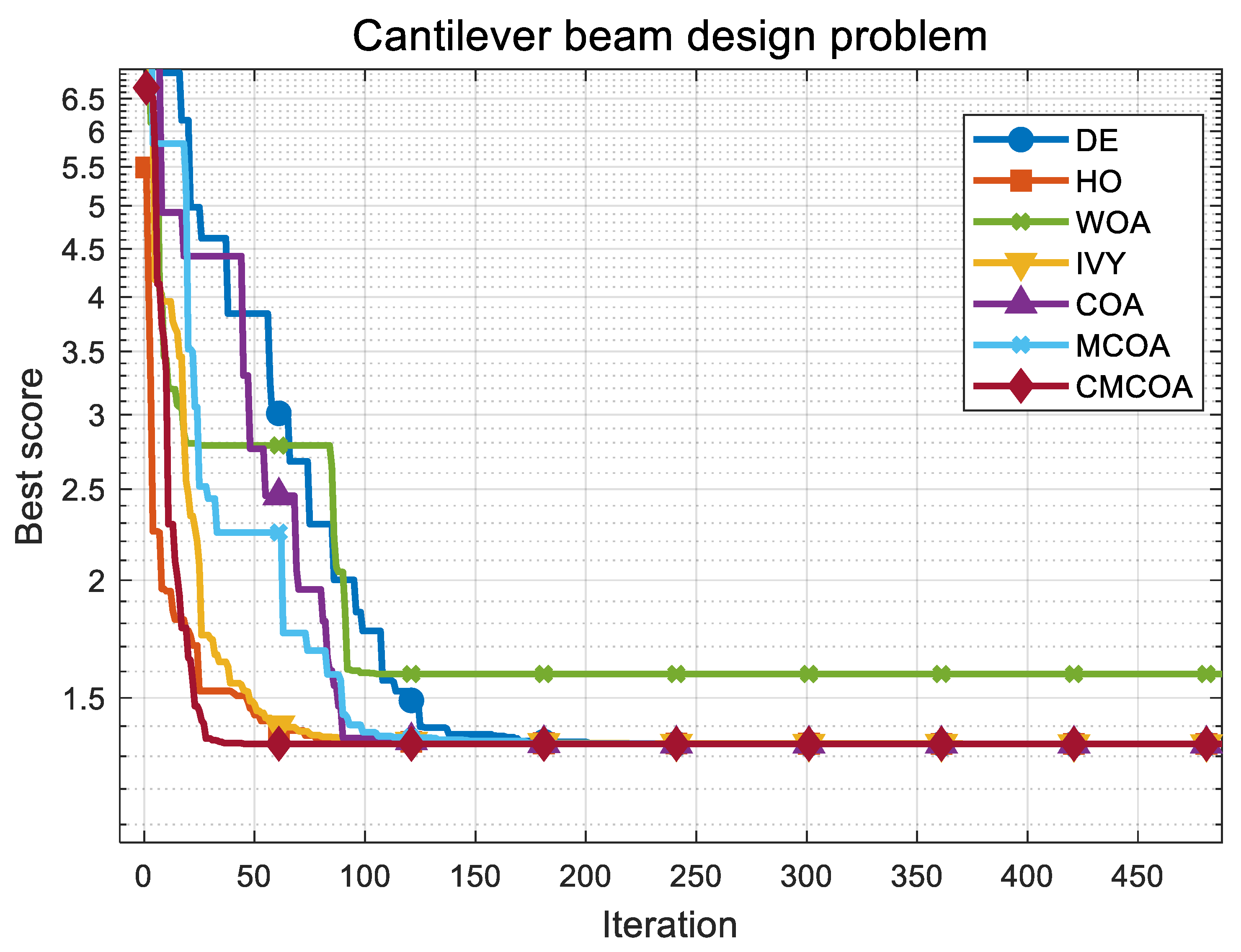
- Cantilever Beam Design Problem
- Experimental analysis
3. Application and Evaluation of CMCOA for Image Analysis
3.1. Experimental Setup
3.2. Analysis of Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMCOA | Chaos-initiated and Adaptive Multi-guide Control-based Crayfish Optimization Algorithm |
| COA | Crayfish Optimization Algorithm |
| MIT rule | Massachusetts Institute of Technology Rule from Model Reference Adaptive Control |
| BinCOA | Binary Crayfish Optimization Algorithm |
| MCOA | Modified Crayfish Optimization Algorithm |
| AD-COA-L | Adaptive Dynamic COA with a Locally enhanced escape operator |
| PSO | Particle Swarm Optimization |
| OBL | Opposition-Based Learning |
| Eq | Equation |
| rand | random number in the interval of [0, 1] |
| DE | Differential Evolution |
| HO | Hippopotamus Optimization |
| WOA | Whale Optimization Algorithm |
| IVY | Ivy Algorithm |
| CEC | IEEE Congress on Evolutionary Computation competition |
| Symbols | |
| dimension | |
| the problem dimension | |
| -dimensional vector which is generated uniformly at random from the interval [0, 1] | |
| dimension search space | |
| dimension search space | |
| a random value from the interval [0, 1] | |
| the global best solution | |
| the local best solution | |
| total iterations and current iteration | |
| the linearly decreasing coefficient | |
| N | the population size |
| round() | to round a decimal to the nearest integer |
| the food location | |
| a constant food factor which equals 3 and represents the largest food | |
| the food size | |
| the food intake proportion | |
| µ | for crayfish |
| factors to control the intake of crayfish at different temperatures, which are equal to 3 and 0.2, respectively | |
| the chaotic value | |
| the logistic-map parameter, which equals 4 | |
| the positive Lyapunov exponent | |
| the opposite solution of each candidate | |
| the control parameter in the adaptive parameter control rule | |
| generation population | |
| the relative deviation between the population average and the best solution | |
| the learning rate controlling the update speed set as 0.03 | |
| E | the top-performing solutions |
| the elite set of size | |
| the guiding position in the multi-guide strategy | |
| best solution | |
| the feasible domain of elite solutions | |
| the switching threshold | |
| generation population fitness standard deviation | |
| M | the number of basic functions |
| R | the desired target ratio |
| feature vector of the i-th pixel | |
| the k-th cluster center | |
| the total number of pixels and cluster centers, respectively |
References
- Peng, D.; Gui, Z.; Wu, H. Interpreting the Curse of Dimensionality from Distance Concentration and Manifold Effect. arXiv 2023, arXiv:2401.00422. [Google Scholar]
- Simpson, C.; Tabatsky, E.; Rahil, Z.; Eddins, D.J.; Tkachev, S.; Georgescauld, F.; Papalegis, D.; Culka, M.; Levy, T.; Gregoretti, I.; et al. Lifting the Curse from High-Dimensional Data: Automated Projection Pursuit Clustering for a Variety of Biological Data Modalities. GigaScience 2025, 14, giaf052. [Google Scholar] [CrossRef]
- Fakhouri, H.N.; Al-Shamayleh, A.S.; Ishtaiwi, A.; Makhadmeh, S.N.; Fakhouri, S.N.; Hamad, F. Hybrid Four Vector Intelligent Metaheuristic with Differential Evolution: Opportunities and Challenges for Structural Single-Objective Engineering Optimization. Algorithms 2024, 17, 417. [Google Scholar] [CrossRef]
- Wang, C.-H.; Hu, K.; Wu, X.; Ou, Y. Rethinking Metaheuristics: Unveiling the Myth of “Novelty” in Metaheuristic Algorithms. Mathematics 2025, 13, 2158. [Google Scholar] [CrossRef]
- Rajwar, K.; Deep, K.; Das, S. An Exhaustive Review of the Metaheuristic Algorithms for Search and Optimization: Taxonomy, Applications, and Open Challenges. Artif. Intell. Rev. 2023, 56, 13187–13257. [Google Scholar] [CrossRef]
- Tian, D.; Xu, Q.; Yao, X.; Zhang, G.; Li, Y.; Xu, C. Diversity-Guided Particle Swarm Optimization with Multi-Level Learning Strategy. Swarm Evol. Comput. 2024, 86, 101533. [Google Scholar] [CrossRef]
- Choi, K.P.; Lai, T.L.; Tong, X.T.; Tsang, K.W.; Wong, W.K.; Zhang, H. Adaptive Parameter Tuning of Evolutionary Computation Algorithms. Stat. Biosci. 2025, 13, 2158. [Google Scholar] [CrossRef]
- Prado-Rodríguez, R.; González, P.; Banga, J.R. A Parameter Control Strategy for Parallel Island-Based Metaheuristics. Expert Syst. 2025, 42, e70061. [Google Scholar] [CrossRef]
- Grewal, R.; Kasana, S.S.; Kasana, G. Hyperspectral Image Segmentation: A Comprehensive Survey. Multimed. Tools Appl. 2023, 82, 20819–20872. [Google Scholar] [CrossRef]
- Wang, N.; Cui, Z.; Lan, Y.; Zhang, C.; Xue, Y.; Su, Y.; Li, A. Large-Scale Hyperspectral Image-Projected Clustering via Doubly Stochastic Graph Learning. Remote Sens. 2025, 17, 1526. [Google Scholar] [CrossRef]
- Jia, H.; Rao, H.; Wen, C.; Mirjalili, S. Crayfish Optimization Algorithm. Artif. Intell. Rev. 2023, 56 (Suppl. S2), 1919–1979. [Google Scholar] [CrossRef]
- Shikoun, N.H.; Al-Eraqi, A.S.; Fathi, I.S. BinCOA: An Efficient Binary Crayfish Optimization Algorithm for Feature Selection. IEEE Access 2024, 12, 28621–28635. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, X.; Zhang, J.; Abualigah, L.; Yildiz, A.R.; Hussien, A.G. Modified crayfish optimization algorithm for solving multiple engineering application problems. Artif. Intell. Rev. 2024, 57, 127. [Google Scholar] [CrossRef]
- Elhosseny, M.; Abdel-Salam, M.; El-Hasnony, I.M. Adaptive dynamic crayfish algorithm with multi-enhanced strategy for global high-dimensional optimization and real-engineering problems. Sci. Rep. 2025, 15, 10656. [Google Scholar] [CrossRef]
- Jayakrishna, N.; Prasanth, N.N. Detection and mitigation of distributed denial of service attacks in vehicular ad hoc network using a spatiotemporal deep learning and reinforcement learning approach. Results Eng. 2025, 26, 104839. [Google Scholar] [CrossRef]
- Padmashree, A.; Sankar, P.; Alkhayyat, A.; Muniyand, E. A novel similarity navigated graph neural networks and crayfish optimization algorithm for accurate brain tumor detection. Res. Biomed. Eng. 2025, 41, 31. [Google Scholar]
- Dinh, P.H. MIF-BTF-MRN: Medical image fusion based on the bilateral texture filter and transfer learning with the ResNet-101 network. Biomed. Signal Process. Control 2025, 100, 106976. [Google Scholar] [CrossRef]
- Luo, T.; Xie, J.; Zhang, B.; Zhang, Y.; Li, C.; Zhou, J. An improved Lévy chaotic particle swarm optimization algorithm for energy-efficient cluster routing scheme in industrial wireless sensor networks. Expert Syst. Appl. 2024, 241, 122780. [Google Scholar] [CrossRef]
- Li, M.-W.; Xu, R.-Z.; Yang, Z.-Y.; Yeh, Y.-H.; Hong, W.-C. Optimizing berth–crane allocation considering tidal effects using chaotic quantum whale optimization algorithm. Appl. Soft Comput. 2024, 162, 111811. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, K.; Zhang, J.; Zhao, X.; Chen, Y.; Cai, B.; Zhu, Z.; Wen, H.; Ye, C. Integrating fractional-order Hopfield neural network with differentiated encryption: Achieving high-performance privacy protection for medical images. Fractal Fract. 2025, 9, 426. [Google Scholar] [CrossRef]
- Ye, C.; Tan, S.; Wang, J.; Shi, L.; Zuo, Q.; Feng, W. Social image security with encryption and watermarking in hybrid domains. Entropy 2025, 27, 276. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Woźniak, M. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Mahdavi, S.; Rahnamayan, S.; Deb, K. Opposition-based learning: A literature review. Swarm Evol. Comput. 2018, 39, 1–23. [Google Scholar] [CrossRef]
- Rothe, J.; Zhang, Y.; Schmidt, M.; Müller-Stoll, S. A modified Model Reference Adaptive Controller (M-MRAC): Comparison of MIT-rule and SPR-rule. Electronics 2020, 9, 1104. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Amiri, M.H.; Mehrabi Hashjin, N.; Montazeri, M.; Mirjalili, S.; Khodadadi, N. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep. 2024, 14, 5032. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zare, M.; Trojovský, P.; Rao, R.V.; Trojovská, E.; Kandasamy, V. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl.-Based Syst. 2024, 295, 111850. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; National University of Defense Technology: Changsha, China, 2017. [Google Scholar]
- Xue, B.; Zhang, M.; Browne, W.; Ma, H.; Mei, Y.; Song, A.; Andreae, P.; Chen, A.; Chen, Q.; Al-Sahaf, H.; et al. 2019 IEEE Congress on Evolutionary Computation (CEC 2019). In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019. [Google Scholar]
- Liang, J.J.; Qu, B.; Gong, D.; Yue, C. Problem Definitions and Evaluation Criteria for the CEC 2019 Special Session on Multimodal Multiobjective Optimization; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China, 2019. [Google Scholar]
- Kumar, A.; Price, K.V.; Mohamed, A.W.; Hadi, A.A.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the 2022 Special Session and Competition on Single Objective Bound Constrained Numerical Optimization; Nanyang Technological University: Singapore, 2021. [Google Scholar]
- Su, H.; Dong, Z.; Liu, Y.; Mu, Y.; Li, S.; Xia, L. Symmetric projection optimizer: Concise and efficient solving engineering problems using the fundamental wave of the Fourier series. Sci. Rep. 2024, 14, 6032. [Google Scholar] [CrossRef]
- Hu, G.; Guo, Y.; Wei, G.; Abualigah, L. Genghis Khan shark optimizer: A novel nature-inspired algorithm for engineering optimization. Adv. Eng. Inform. 2023, 58, 102210. [Google Scholar] [CrossRef]
- Zhong, R.; Yu, J.; Zhang, C.; Munetomo, M. Surrogate ensemble-assisted hyper-heuristic algorithm for expensive optimization problems. Int. J. Comput. Intell. Syst. 2023, 16, 169. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H. Surrogate-assisted hybrid evolutionary algorithm with local estimation of distribution for expensive mixed variable optimization problems. Appl. Soft Comput. 2023, 133, 109957. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-Visual-Words and Spatial Extensions for Land-Use Classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM SIGSPATIAL GIS 2010), San Jose, CA, USA, 2–5 November 2010; ACM: New York, NY, USA, 2010; pp. 270–279. [Google Scholar]
- Lloyd, S.P. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]





| Mechanism | CMCOA | AD-COA-L | BinCOA | MCOA |
|---|---|---|---|---|
| Initialization | Uses a chaotic system (Logistic Map). | Uses a Bernoulli map for initialization. | Uses refracted opposition-based learning to select a better starting point. | Standard random initialization. |
| Adaptation | Dynamically adjusts the key control parameter C based on the population’s fitness change, replacing . | Introduces a dynamic inertia weight to balance exploration and exploitation. | A special mechanism for binary problems, converting continuous values to binary. | Guides the algorithm to seek a better “environment” based on a fitness-related “water quality” factor. |
| Update Rule | Guides the search using the average position of the elites and switches between exploration and exploitation. | Encourages information sharing and helps escape local optima via random movement. | A crossover mechanism that averages two random individuals’ positions to increase diversity. | A strategy to escape local optima by generating and evaluating an “opposite” solution. |
| Algorithm | Parameter | Value |
|---|---|---|
| DE | F | 0.8 |
| CR | 0.9 | |
| HO | ϑ | 1.5 |
| WOA | a | Linear reduction 2 to 0 |
| r | [0, 1] | |
| l | [−1, 1] | |
| IVY | β | [1, 1.5] |
| COA | 0.2 | |
| 3 | ||
| µ | 25 | |
| σ | 3 | |
| CMCOA | 4 | |
| 0.03 |
| No. | Functions | Dimension | Search Range | Optimum | |
|---|---|---|---|---|---|
| Unimodal Functions | 1 | Shifted and Rotated Bent Cigar Function | 30 | [−100, 100] | 100 |
| 2 | Shifted and Rotated Sum of Different Power Functions | 30 | [−100, 100] | 200 | |
| 3 | Weierstrass Function | 10 | [−100, 100] | 1 | |
| 4 | Shifted and full Rotated Zakharov Function | 20 | [−100, 100] | 300 | |
| Hybrid Functions | 5 | Hybrid Function 1 (M = 3) | 30 | [−100, 100] | 1200 |
| 6 | Hybrid Function 2 (M = 4) | 30 | [−100, 100] | 1400 | |
| 7 | Hybrid Function 3 (M = 5) | 20 | [−100, 100] | 2100 | |
| Composition Functions | 8 | Composition Function 1 (M = 5) | 30 | [−100, 100] | 2600 |
| 9 | Composition Function 2 (M = 3) | 30 | [−100, 100] | 3000 | |
| 10 | Composition Function 3 (M = 4) | 20 | [−100, 100] | 2400 |
| Function | DE [25] | HO [26] | WOA [27] | IVY [28] | COA [11] | MCOA [13] | AD-COA-L [14] | CMCOA | |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.88 × 1010 | 2.72 × 108 | 2.32 × 109 | 6.3 × 107 | 1.09 × 108 | 9.56 × 107 | 1.70 × 108 | 1.30 × 108 | |
| 5.58 × 109 | 2.69 × 108 | 9.68 × 108 | 1.50 × 108 | 1.54 × 108 | 3.08 × 1016 | 1.10 × 1016 | 1.73 × 107 | ||
| TIME | 0.208 | 3.192 | 0.0913 | 0.589 | 0.123 | 0.120 | 0.187 | 0.0957 | |
| F2 | 2.33 × 1046 | 1.55 × 1031 | 4.33 × 1039 | 4.39 × 1039 | 5.56 × 1024 | 2.72 × 1022 | 9.22 × 1023 | 7.38 × 1013 | |
| 8.36 × 1046 | 6.35 × 1031 | 2.37 × 1040 | 2.20 × 1040 | 2.99 × 1025 | 9.79 × 1045 | 1.39 × 1049 | 3.13 × 1014 | ||
| TIME | 0.239 | 3.103 | 0.0972 | 0.525 | 0.136 | 0.140 | 0.215 | 0.108 | |
| F3 | 10.4946 | 6.264 | 8.7262 | 5.7342 | 9.9109 | 4.4447 | 5.3074 | 4.3841 | |
| 0.70196 | 1.3226 | 1.9108 | 2.0109 | 0.9925 | 1.9738 | 2.0936 | 1.536 | ||
| TIME | 1.639 | 4.681 | 0.779 | 1.223 | 1.292 | 1.308 | 2.077 | 1.236 | |
| F4 | 154,587.69 | 17,565.24 | 26,152.7 | 36,470.94 | 41,746.72 | 40,935.48 | 26,690.80 | 4910.69 | |
| 1364.85 | 5347.51 | 11,212.3 | 14,025.44 | 15,320.54 | 1.08 × 108 | 3.106 × 107 | 1923.38 | ||
| TIME | 0.184 | 2.502 | 0.0694 | 0.527 | 0.0952 | 0.095 | 0.150 | 0.0758 | |
| F5 | 2.59 × 109 | 1.09 × 108 | 2.01 × 108 | 3.23 × 106 | 8.08 × 106 | 9.24 × 106 | 8.36 × 106 | 1.7 × 106 | |
| 8.64 × 108 | 9.46 × 107 | 1.39 × 108 | 2.46 × 106 | 8.21 × 106 | 2.76 × 1013 | 1.28 × 1014 | 1.7 × 106 | ||
| TIME | 0.271 | 3.005 | 0.113 | 0.572 | 0.163 | 0.185 | 0.274 | 0.147 | |
| F6 | 1.02 × 105 | 3.33 × 105 | 2.95 × 106 | 1.37 × 106 | 3.73 × 105 | 2.61 × 105 | 4.19 × 105 | 47,615.86 | |
| 51,916.22 | 4.63 × 105 | 2.86 × 106 | 1.21 × 106 | 3.46 × 105 | 4.52 × 1010 | 1.81 × 1011 | 26,653.6 | ||
| TIME | 0.313 | 3.016 | 0.136 | 0.608 | 0.198 | 0.201 | 0.325 | 0.141 | |
| F7 | 2.24 × 105 | 51,662.08 | 1.22 × 106 | 7.99 × 105 | 2.19 × 105 | 2.21 × 105 | 5.11 × 105 | 1.08 × 105 | |
| 1.11 × 105 | 34,314.9 | 1.21 × 106 | 8.26 × 105 | 2.80 × 105 | 3.85 × 105 | 8.63 × 105 | 81,411.68 | ||
| TIME | 0.224 | 2.606 | 0.0902 | 0.541 | 0.122 | 0.135 | 0.206 | 0.0957 | |
| F8 | 7476.37 | 7192.30 | 8559.44 | 5756.80 | 5994.25 | 5561.52 | 5948.29 | 5719.08 | |
| 533.74 | 1361.35 | 675.96 | 1778.69 | 1348.80 | 1672.66 | 2732.49 | 182.09 | ||
| TIME | 0.675 | 3.731 | 0.327 | 0.772 | 0.488 | 0.500 | 0.807 | 0.317 | |
| F9 | 1.44 × 107 | 2.09 × 107 | 3.98 × 107 | 61,498.20 | 5.25 × 105 | 4.43 × 105 | 7.12 × 105 | 1.1 × 105 | |
| 8.07 × 106 | 2.21 × 107 | 2.68 × 107 | 41,016.21 | 6.54 × 105 | 2.44 × 105 | 2.85 × 105 | 1.5 × 105 | ||
| TIME | 1.242 | 4.521 | 0.611 | 1.095 | 1.007 | 1.046 | 1.635 | 0.715 | |
| F10 | 6688.12 | 4028.24 | 4829.55 | 3774.09 | 4300.92 | 3585.02 | 2862.07 | 3369.18 | |
| 1124.06 | 1088.57 | 1076.81 | 281,291.09 | 2258.22 | 1351.52 | 5908.71 | 945.03 | ||
| TIME | 0.334 | 2.761 | 0.138 | 0.606 | 0.211 | 0.214 | 0.330 | 0.202 |
| Function | CMCOA vs. DE | CMCOA vs. HO | CMCOA vs. WOA | CMCOA vs. IVY | CMCOA vs. COA | CMCOA vs. MCOA | CMCOA vs. AD-COA-L |
|---|---|---|---|---|---|---|---|
| F1 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 4.28 × 10−6 | 1.73 × 10−6 | 0.845 | 0.198 |
| F2 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 3.88 × 10−6 | 1.73 × 10−6 |
| F3 | 1.73 × 10−6 | 0.000174 | 2.12 × 10−6 | 0.503 | 0.0936 | 0.0185 | 2.16 × 10−5 |
| F4 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| F5 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 3.72 × 10−5 | 1.23 × 10−5 | 0.05709 | 0.00196 |
| F6 | 1.92 × 10−6 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.92 × 10−6 | 5.75 × 10−6 | 1.23 × 10−5 |
| F7 | 8.18 × 10−5 | 0.115 | 1.73 × 10−6 | 5.75 × 10−6 | 1.79 × 10−5 | 0.00773 | 3.88 × 10−6 |
| F8 | 1.73 × 10−6 | 0.00499 | 1.92 × 10−6 | 0.318 | 0.845 | 0.0147 | 0.2802 |
| F9 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 0.749 | 1.97 × 10−5 | 0.000331 | 0.00984 |
| F10 | 0.00927 | 0.00499 | 0.428 | 0.000528 | 0.00159 | 0.781 | 0.141 |
| Algorithm | Optimal Objective Value | Optimal Variables |
|---|---|---|
| DE | 2.3078 × 10−11 | [51, 30, 13, 53] |
| HO | 2.3576 × 10−9 | [39, 12, 15, 32] |
| WOA | 2.3078 × 10−11 | [53, 15, 26, 51] |
| IVY | 1.8274 × 10−8 | [37, 12, 12, 27] |
| COA | 2.3576 × 10−9 | [48, 12, 15, 26] |
| MCOA | 9.9399 × 10−11 | [49, 31, 13, 57] |
| AD-COA-L | 6.6021 × 10−10 | [56, 23, 13, 37] |
| CMCOA | 2.7009 × 10−12 | [49, 16, 19, 43] |
| SPO [33] | 2.7009 × 10−12 | [43, 16, 19, 49] |
| GKSO [34] | 2.7009 × 10−12 | [49, 19, 16, 43] |
| Algorithm | Optimal Objective Value | Optimal Variables |
|---|---|---|
| DE | 1.3400 | [6.0160, 5.3092, 4.4943, 3.5015, 2.1527] |
| HO | 1.3400 | [6.0288, 5.3229, 4.4922, 3.4981, 2.1322] |
| WOA | 1.4092 | [6.2557, 4.6792, 4.0823, 4.5797, 2.9872] |
| IVY | 1.3402 | [6.0974, 5.2295, 4.4873, 3.5063, 2.1578] |
| COA | 1.3400 | [5.9890, 5.3216, 4.4963, 3.5137, 2.1537] |
| MCOA | 1.3400 | [6.0098, 5.3300, 4.4990, 3.4804, 2.1551] |
| AD-COA-L | 1.3401 | [6.0183, 5.3328, 4.4474, 3.5215, 2.1555] |
| CMCOA | 1.3400 | [6.0329, 5.3202, 4.4808, 3.5072, 2.1332] |
| SEA-HHA [35] | 1.4037 | [5.3868, 5.4171, 5.1441, 3.3892, 3.1576] |
| SHEALED [36] | 1.3540 | [5.7524, 5.7174, 4.1701, 3.9365, 2.1216] |
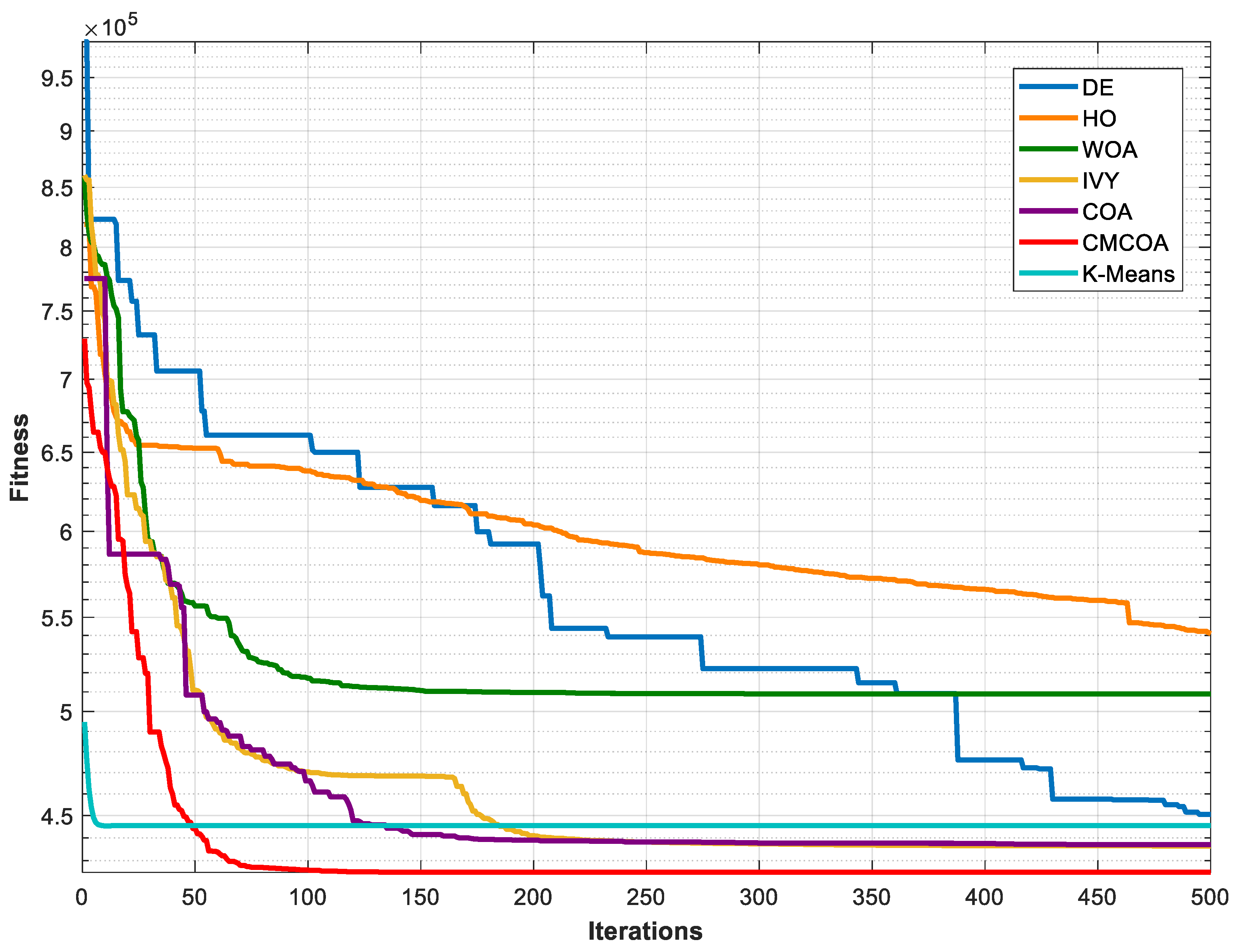
| Test Image 1 | DE [25] | HO [26] | WOA [27] | IVY [28] | COA [11] | K-Means [38] | CMCOA |
| Fit Silhouette | 458,837.75 | 541,011.41 | 508,927.69 | 438,185.77 | 437,017.73 | 445,498.86 | 424,886.16 |
| 0.6021 | 0.6101 | 0.4040 | 0.5910 | 0.5990 | 0.6128 | 0.6432 | |
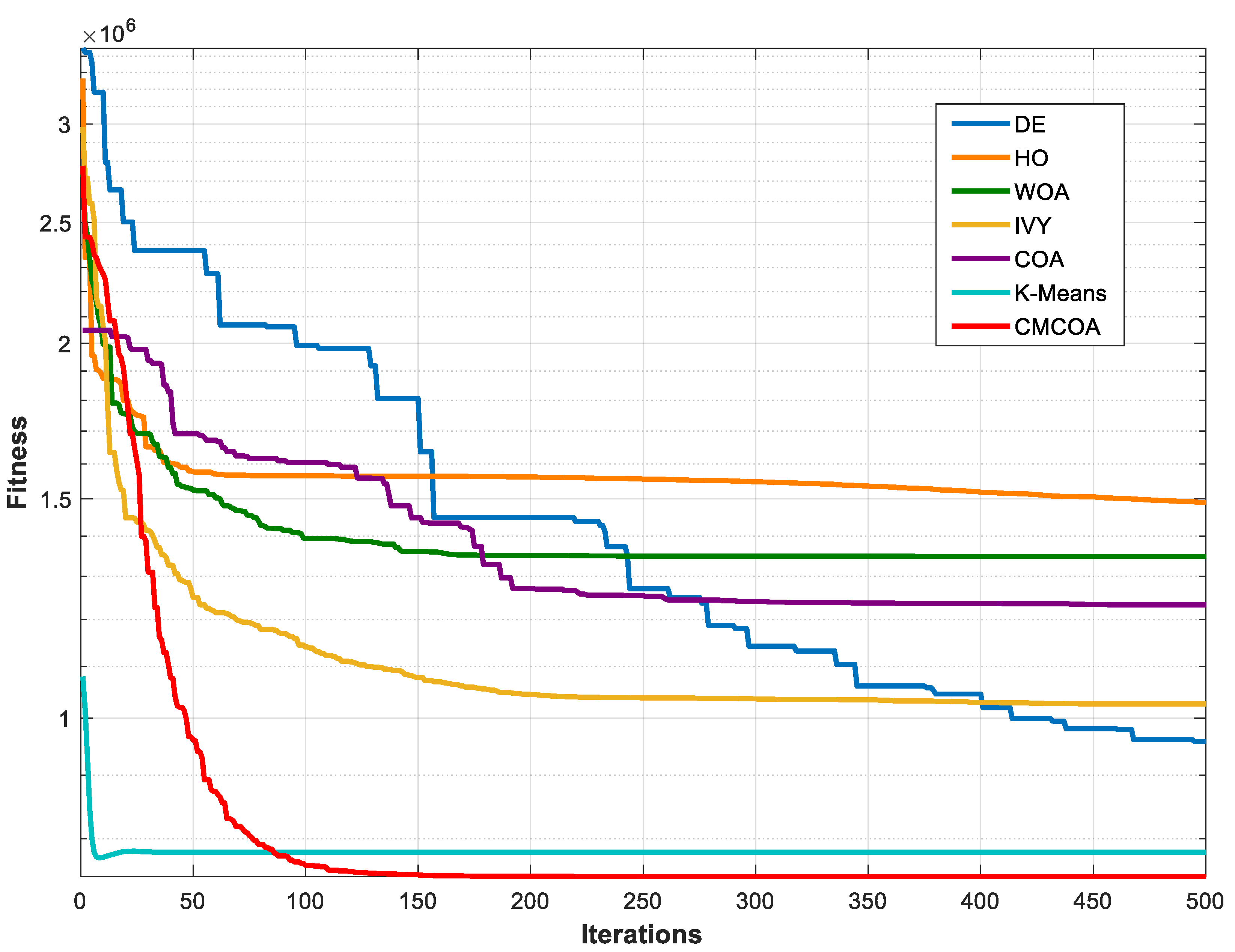
| Test Image 2 | DE [25] | HO [26] | WOA [27] | IVY [28] | COA [11] | K-Means [38] | CMCOA |
| Fit Silhouette | 958,164.06 | 1,490,353.64 | 1,349,062.02 | 1,026,513.97 | 1,232,848.03 | 780,546.27 | 746,342.75 |
| 0.6423 | 0.5719 | 0.6219 | 0.4575 | 0.6348 | 0.6722 | 0.6623 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Sun, Z.; Bi, Y.; Sun, Z. A Chaos-Initiated and Adaptive Multi-Guide Control-Based Crayfish Optimization Algorithm for Image Analysis. Symmetry 2025, 17, 1940. https://doi.org/10.3390/sym17111940
Shen Z, Sun Z, Bi Y, Sun Z. A Chaos-Initiated and Adaptive Multi-Guide Control-Based Crayfish Optimization Algorithm for Image Analysis. Symmetry. 2025; 17(11):1940. https://doi.org/10.3390/sym17111940
Chicago/Turabian StyleShen, Ziyang, Zhe Sun, Yunrui Bi, and Zhixin Sun. 2025. "A Chaos-Initiated and Adaptive Multi-Guide Control-Based Crayfish Optimization Algorithm for Image Analysis" Symmetry 17, no. 11: 1940. https://doi.org/10.3390/sym17111940
APA StyleShen, Z., Sun, Z., Bi, Y., & Sun, Z. (2025). A Chaos-Initiated and Adaptive Multi-Guide Control-Based Crayfish Optimization Algorithm for Image Analysis. Symmetry, 17(11), 1940. https://doi.org/10.3390/sym17111940






